Determination of Density and Surface Tension of CaO–Al2O3 Molten Slag Using Pendant Drop Method
Abstract
1. Introduction
2. Experimental
2.1. Slag Preparation
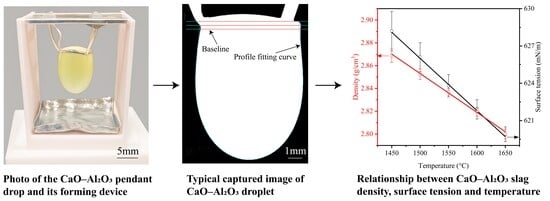
2.2. Experimental Equipment
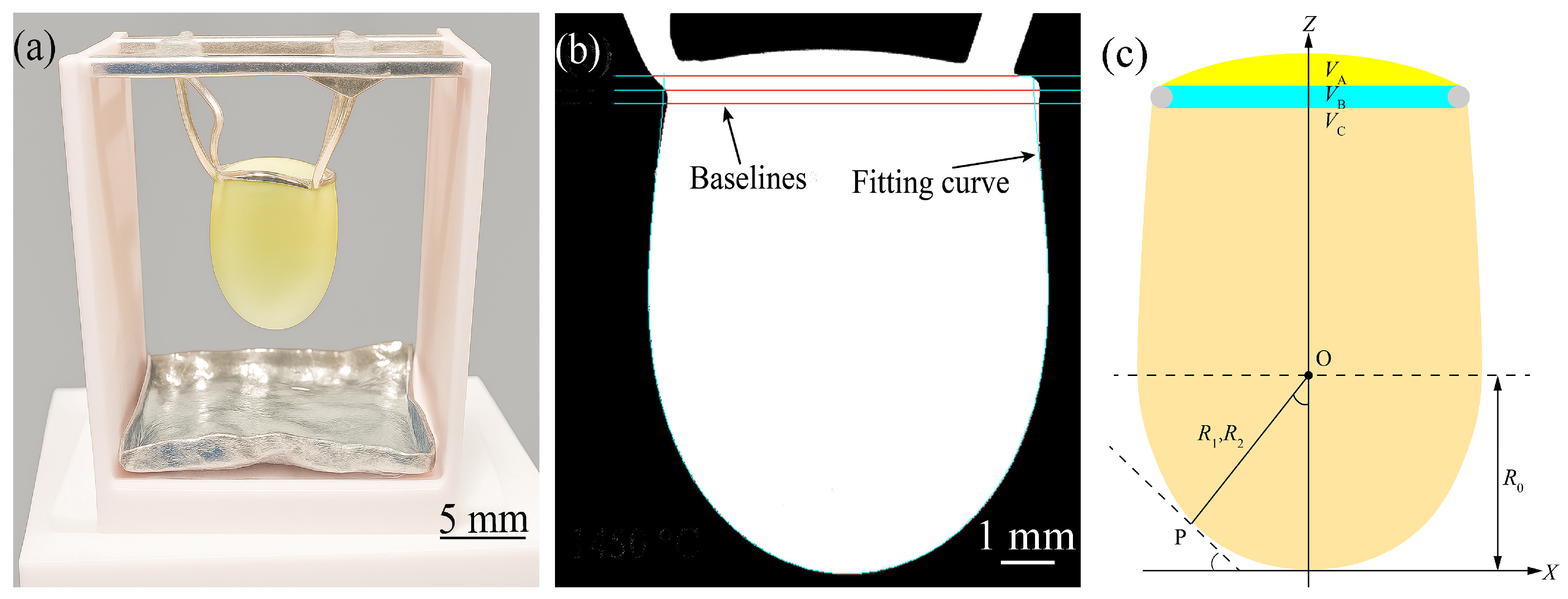
2.3. Experimental Method
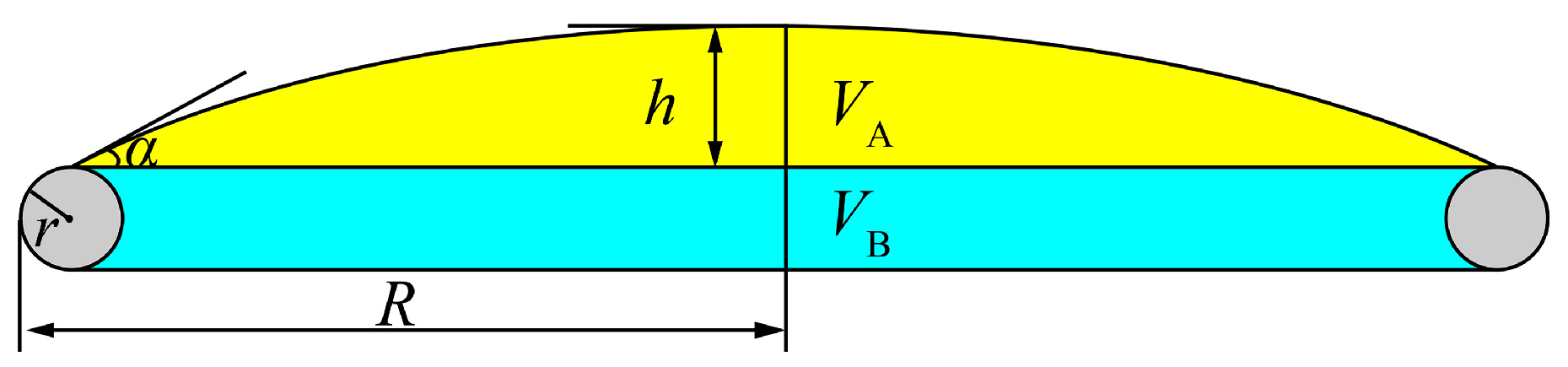
3. Theoretical Bases
4. Results and Discussion
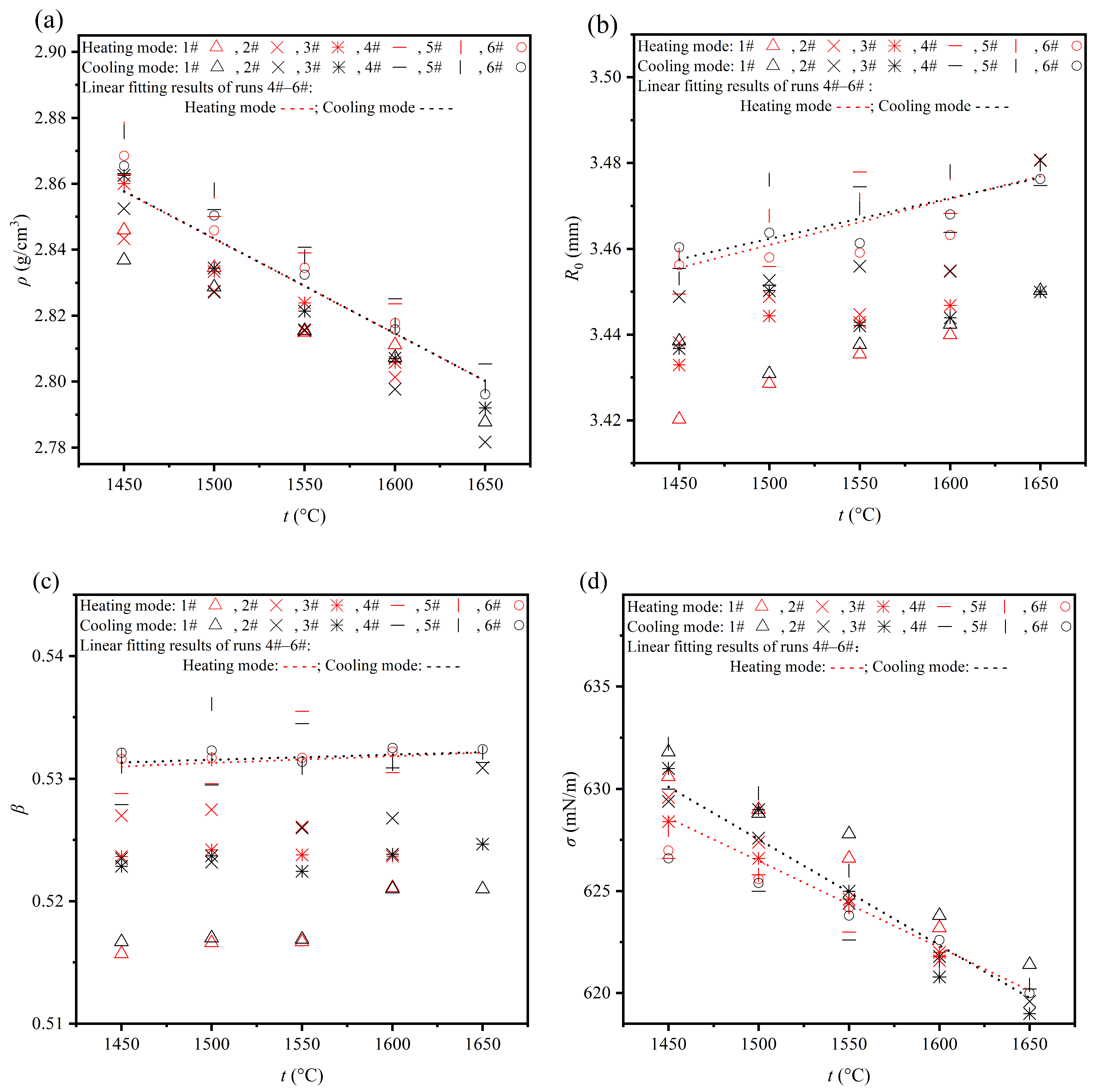
4.1. Effects of Measurement Mode and Droplet Mass
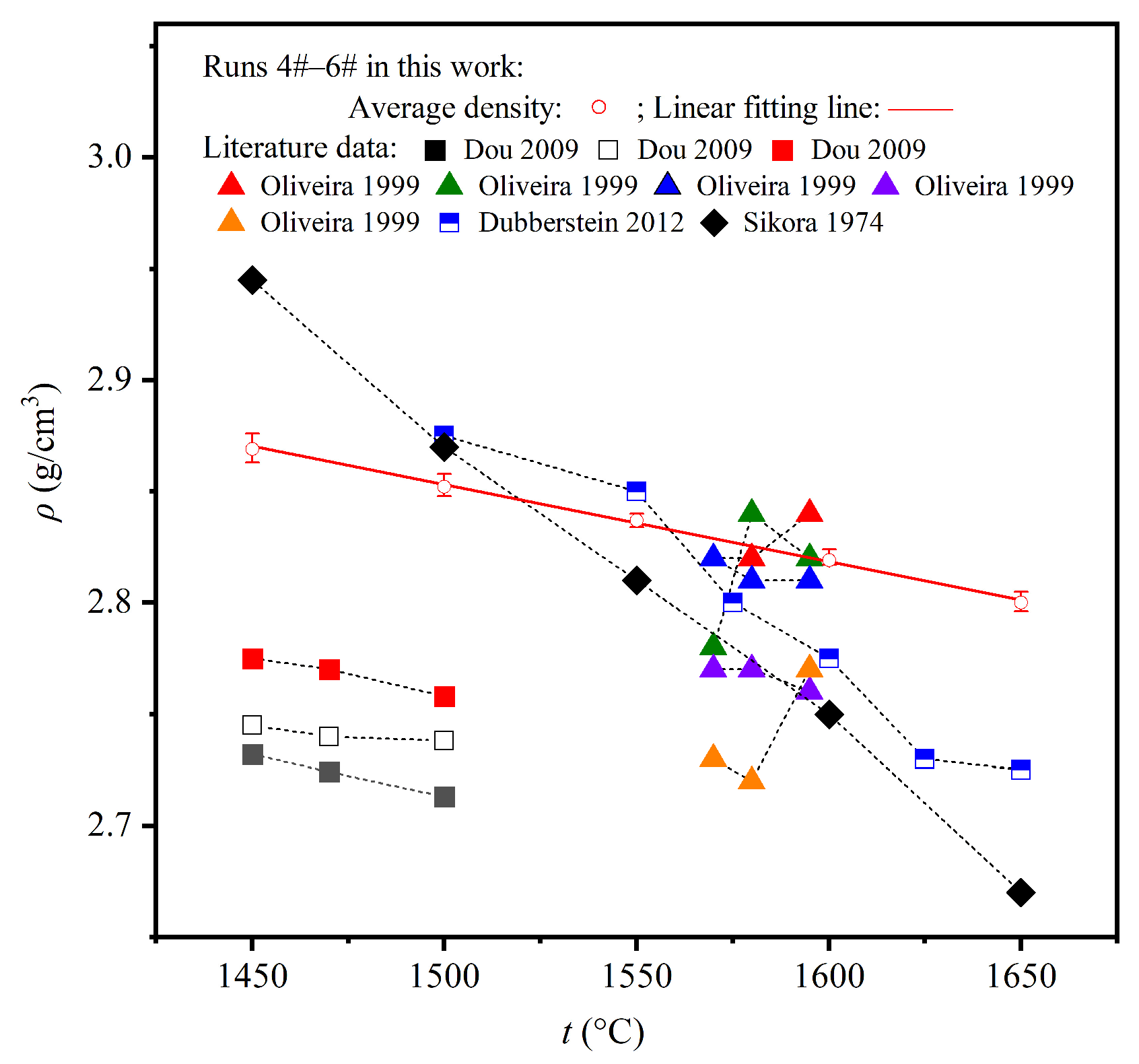
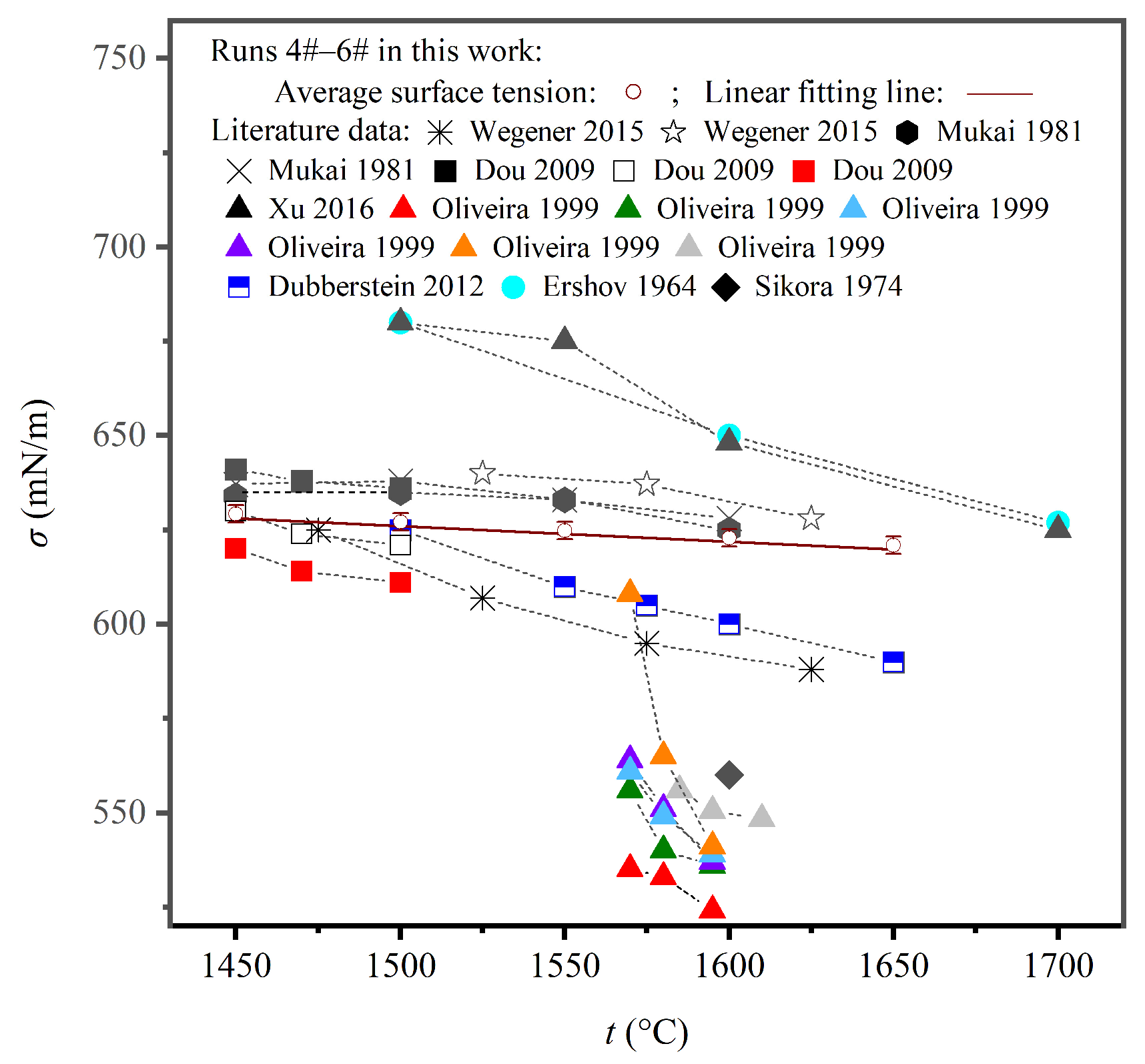
4.2. Comparison of the Measured Density and Surface Tension with the Literature Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Dn | Inner diameter of the alloy ring (mm) | t | Experimental temperature (°C) |
| g | Gravitational acceleration constant (g = 9.7933 m/s2) | VA, VB, and VC | Volumes of parts A, B, and C of the slag, respectively (mm3) |
| h | Height of crown-shaped slag on the upper horizontal plane of the alloy ring (mm) | Vm | Total volume of slag (mm3) |
| L20 °C and Lt | Maximum outer diameter of the alloy ring at room and experimental temperatures, respectively (mm), or scale length | Wo | Dimensionless number |
| Lpixel,20°C and Lpixel,t | Pixel length of the maximum outer diameter of the alloy ring at room and experimental temperatures, respectively (px) | z | Height difference between the vertex of the pendant drop and the measurement position (mm) |
| Mag | Magnification factor of image (px/mm) | α | Inclination angle (°) |
| m | Final pendant droplet mass (g) | β | Shape factor |
| m0 and m1 | Mass of the slag or pendant drop-forming device before and after the experiment (g) | φ | Diameter of cylindrical compact (mm) |
| m2 | Mass of adhered slag on the alloy bracket after experiment (g) | π | Constant (π = 3.1416) |
| r | Half of the diameter of the alloy ring wire (mm) | ρ | Density of droplet (g/cm3) |
| R | Half of the outer diameter of the alloy ring (mm) | ρAr | Density of argon gas (g/cm3) |
| R0 | Curvature radius of the pendant drop vertex (mm) | ∆ρ | Density difference between the pendant drop and the environment atmosphere (that is, Ar gas in this work) (g/cm3) |
| R1 and R2 | Main curvature radius on both sides of the pendant drop (mm) | σ | Surface tension of droplet (mN/m) |
| L | Scale length (mm) | Average surface tension of droplet (mN/m) | |
| u(B) | Uncertainty of physical quantity B | Average density of droplet (g/cm3) |
References
- Zhang, H.; Peng, Y.B.; Zhang, S.; Liu, C.S. Effects of refining slag on transformation and removal of inclusions in type 430 stainless steel. Metall. Mater. Trans. B 2022, 53, 702–715. [Google Scholar] [CrossRef]
- Liu, C.S.; Ran, X.G.; Zhang, H.; Li, J.; Wang, Y.; Lu, Y.Y.; Xiong, L.; Ni, H.W. Influence of refining slag on transformation and separation of nonmetallic inclusions in 316L stainless steel. Mater. Res. Technol. 2023, 26, 7199–7217. [Google Scholar] [CrossRef]
- Zheng, D.L.; Ma, G.J.; Zhang, X.; Liu, M.K.; Xu, J.F. Effect of CaO/Al2O3 on structure, viscosity, and surface tension of electroslag remelting-type CeO2-bearing slag. Iron Steel Res. Int. 2023, 30, 717–725. [Google Scholar] [CrossRef]
- Cheremisina, E.; Zhang, Z.; Bilbao, E.; Schenk, J. Density, viscosity and surface tension of high-silicate CaO–SiO2–Fe2O3 slags derived by aerodynamic levitation. The behavior of Fe3+ in high-silicate melts. Cream. Int. 2023, 49, 4460–4472. [Google Scholar] [CrossRef]
- Ju, J.T.; He, K.; Guo, W.K.; Zhou, Y. Effects of TiO2 and CaO/Al2O3 on melting characteristics, surface tension, and structure electroslag-remelting-type low-fluorine slag. Steel Res. Int. 2024, 95, 2400241. [Google Scholar] [CrossRef]
- Chang, Y.E.; Lin, C.M.; Shen, J.M.; Luo, S.F.; Yu, K.W.; Wu, W. The effect of the addition of alumina on the viscosity, surface tension, and foaming efficiency of 2.5(CaO/SiO2)–xAl2O3–yFeO–MgO melts. Ceram. Int. 2023, 49, 1994–2003. [Google Scholar] [CrossRef]
- Hoorfar, M.; Neumann, A.W. Recent progress in axisymmetric drop shape analysis (ADSA). Adv. Colloid Interface Sci. 2006, 121, 25–49. [Google Scholar] [CrossRef]
- Berry, J.D.; Neeson, M.J.; Dagastine, R.R.; Chan, D.Y.C.; Tabor, R.F. Measurement of surface and interfacial tension using pendant drop tensiometry. J. Colloid Interface Sci. 2015, 454, 226–237. [Google Scholar] [CrossRef]
- Saad, S.M.I.; Policova, Z.; Neumann, A.W. Design and accuracy of pendant drop methods for surface tension measurement. Colloids Surf. A 2011, 384, 442–452. [Google Scholar] [CrossRef]
- Sravya, S.; Thomas, W. Stability and critical volume of a suspended pendant drop in air via experiments and eigenvalue analysis. Colloids Surf. A 2023, 66, 131346. [Google Scholar] [CrossRef]
- Wegener, M.; Muhmood, L.; Sun, S.; Deev, A.V. Surface tension measurements of calcia-alumina slags: A comparison of dynamic methods. Metall. Mater. Trans. B 2015, 46, 316–327. [Google Scholar] [CrossRef]
- Chang, Y.Y.; Wu, M.Y.; Hung, Y.L.; Lin, S.Y. Accurate surface tension measurement of glass melts by the pendant drop method. Rev. Sci. Instrum. 2011, 82, 055107. [Google Scholar] [CrossRef] [PubMed]
- Kingery, W.D. Surface tension of some liquid oxides and their temperature coefficients. J. Am. Cream. Soc. 1959, 42, 6–10. [Google Scholar] [CrossRef]
- Mukai, K.; Ishikawa, T. Surface tension measurements on liquid slags in CaO–SiO2, CaO–Al2O3 and CaO–Al2O3–SiO2 systems by a pendant drop method. J. Jpn. Inst. Met. 1981, 45, 147–154. (In Japanese) [Google Scholar] [CrossRef]
- Lihrmann, J.M.; Haggerty, J.S. Surface tensions of alumina-containing liquids. American. J. Am. Ceram. Soc. 1985, 68, 81–85. [Google Scholar] [CrossRef]
- Lee, J.; Kiyose, A.; Nakatsuka, S.; Nakamoto, M.; Tanaka, T. Improvements in surface tension measurements of liquid metals having low capillary constants by the constrained drop method. ISIJ Int. 2004, 44, 1793–1799. [Google Scholar] [CrossRef]
- Duchesne, M.A.; Hughes, R.W. Slag density and surface tension measurements by the constrained sessile drop method. Fuel 2017, 188, 173–181. [Google Scholar] [CrossRef]
- Paras, J.; Takeda, O.; Wu, M.; Allanore, A. The surface tension and density of molten Sc2O3, La2O3, Y2O3, Al2O3, and MgO measured via a pendant droplet method. Metall. Mater. Trans. B 2022, 53, 2077–2087. [Google Scholar] [CrossRef]
- Stephan, H.W.; Wang, B.; Wang, T.; Stadler, F.J. Measurement principles for room temperature liquid and fusible metals’ surface tension. Surf. Interfaces 2023, 39, 102921. [Google Scholar] [CrossRef]
- Xin, J.J.; Wang, N.; Chen, M.; Gan, L. Surface tension calculation of molten slag in SiO2–Al2O3–CaO–MgO systems based on a statistical modelling Approach. ISIJ Int. 2019, 59, 759. [Google Scholar] [CrossRef]
- Shi, C.B.; Seo, M.D.; Cho, J.W.; Kim, S.H. Crystallization characteristics of CaO–Al2O3–based mold flux and their effects on in-mold performance during high-aluminum TRIP steels continuous casting. Metall. Mater. Trans. B 2014, 45, 1081–1090. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, L.S.; Wang, J.; Wang, H.C.; Dong, Y.C. Alumina extraction from high-alumina ladle furnace refining slag. Hydrometallurgy 2013, 140, 14–19. [Google Scholar] [CrossRef]
- Dou, Z.H.; Zhang, Y.A.; Yao, J.M.; Jang, X.L.; Niu, L.P.; He, J.C. Research on the character of CaO–Al2O3 slag. Chin. J. Process. Eng. 2009, 9, 4–8. [Google Scholar] [CrossRef]
- Xu, J.F.; Zhang, J.Y.; Chen, D.; Sheng, M.Q.; Weng, W.P. Effects of MgO content and CaO/Al2O3 ratio on surface tension of calcium aluminate refining slag. J. Cent. South Univ. 2016, 23, 3079–3084. [Google Scholar] [CrossRef]
- Oliveira, F.A.; Miller, A.; Madias, J. Surface tension, densities and viscosities of some CaO–Al2O3 slags. Rev. Metal. Madrid. 1999, 35, 91–99. [Google Scholar] [CrossRef][Green Version]
- Dubberstein, T.; Heller, H.P.; Scheller, P.R. Determination of Thermophysical Properties for Molten Slags by Maximum Bubble Pressure Method; Institute of Iron and Steel Technology IEST, Technical University Bergakademie Freiberg: Freiberg, Germany, 2012; Available online: https://api.semanticscholar.org/CorpusID:204920674 (accessed on 11 November 2025).[Green Version]
- Ershov, G.S.; Popova, E.A. Dissolution kinetics of silica in oxide melt. Russ. J. Inorg. Chem. 1964, 9, 654–659. [Google Scholar][Green Version]
- Sikora, B.; Zielinski, M. Density surface tension, viscosity, and electric conductivity of fused calcium oxide-alumina-calcium fluoride systems. Hutnik 1974, 41, 433–437. Available online: https://www.mendeley.com/catalogue/375c1e4e-ea67-3558-8dd2-70ae18b6931a/ (accessed on 11 November 2025).[Green Version]
- Gao, Y.; Zhang, H.; Wang, Q.; Li, G. Effect of applied voltage on wetting and corrosion of corundum refractory by CaO–SiO2–MgO molten slag. Ceram. Int. 2022, 48, 9753–9764. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Y.; Wang, Q.; Li, G. Determination of density and surface tension of CaO–SiO2–Al2O3 molten slag by pendant drop method. Metall. Mater. Trans. B 2023, 54, 1499–1510. [Google Scholar] [CrossRef]
- Saad, S.M.I.; Neumann, A.W. Axisymmetric drop shape analysis (ADSA): An outline. Adv. Colloid Interface Sci. 2016, 238, 62–87. [Google Scholar] [CrossRef]
- GB/T 4842-2017; Argon. Standardization Administration of China (SAC): Beijing, China. (In Chinese)
- Alcock, C.B.; Hooper, G.W. Thermodynamics of the gaseous oxides of the platinum-group metals. Phys. Math. Sci. 1960, 254, 551–561. Available online: http://www.jstor.org/stable/2413869 (accessed on 11 November 2025).
- Wimber, R.T.; Kraus, H.G. Oxidation of iridium. Metall. Mater. Trans. B 1974, 5, 1565–1571. [Google Scholar] [CrossRef]
- Wimber, R.T.; Hills, S.W.; Wahl, N.K.; Tempero, C.R. Kinetics of evaporation/oxidation of iridium. Metall. Mater. Trans. A 1977, 8, 193–199. [Google Scholar] [CrossRef]
- Cordfunke, E.H.P.; Meyer, G. The system iridium-oxygen I. Measurements on the volatile oxide of iridium. J. Chem. Soc. 1962, 81, 495–504. [Google Scholar] [CrossRef]
- Gesing, T.M.; Jeitschko, W. The crystal structure and chemical properties of U2Al3C4 and structure refinement of Al4C3. Z. Naturforsch. B 1995, 50, 196–200. [Google Scholar] [CrossRef]
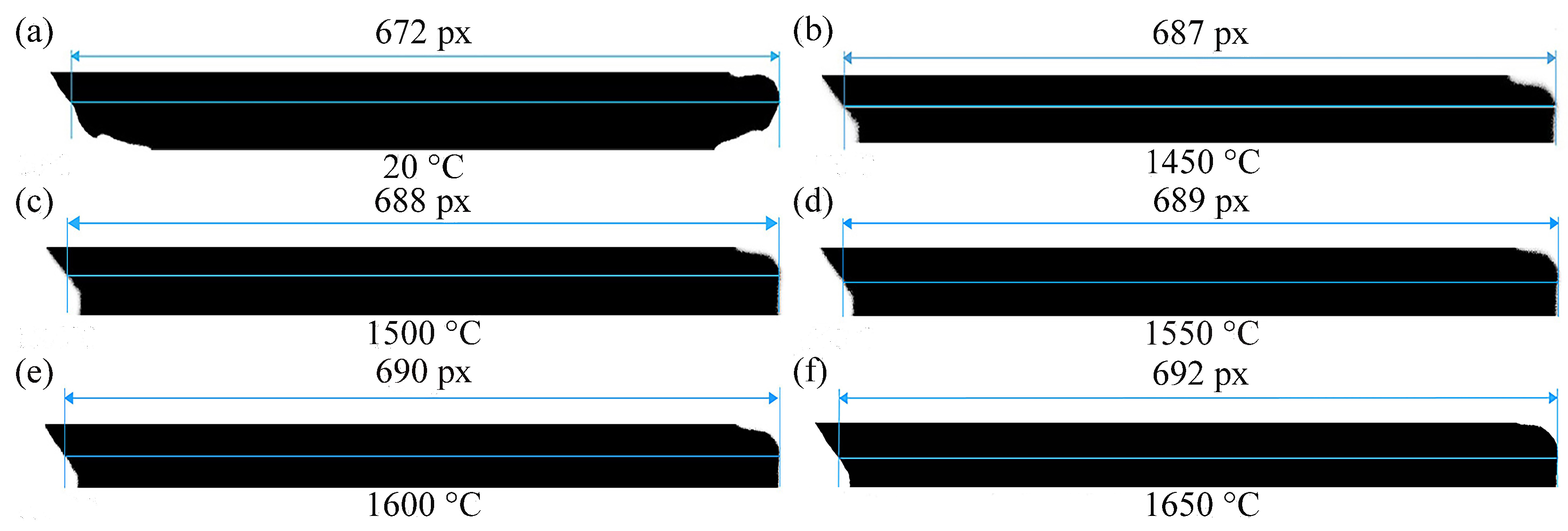

| t (°C) | Mag (px/mm) | Lpixel,t (px) | Pixel Length of 2r (px) | 2R (mm) | 2r (mm) |
|---|---|---|---|---|---|
| 20 | 94.285 | 672 | 43 | 7.1273 | 0.4598 |
| 1450 | 94.285 | 687 | 44 | 7.2864 | 0.4701 |
| 1500 | 94.285 | 688 | 44 | 7.2970 | 0.4707 |
| 1550 | 94.285 | 689 | 44 | 7.3076 | 0.4714 |
| 1600 | 94.285 | 690 | 45 | 7.3182 | 0.4721 |
| 1650 | 94.285 | 692 | 45 | 7.3394 | 0.4735 |
| Run No. | Category | m0 (g) | m1 (g) | ∆m (g) * | m2 (g) | m (g) ** |
|---|---|---|---|---|---|---|
| 1# | Slag | 0.8827 | 0.8664 | −0.0163 | - | 0.8664 |
| Pendant drop-forming device | 2.9332 | 2.9332 | 0 | - | - | |
| Total mass | 3.8159 | 3.7996 | −0.0163 | - | - | |
| 2# | Slag | 0.9640 | 0.9503 | −0.0137 | −0.0282 | 0.9221 |
| Pendant drop-forming device | 2.9324 | 2.9317 | −0.0007 | - | - | |
| Total mass | 3.8964 | 3.8820 | −0.0144 | - | - | |
| 3# | Slag | 0.9382 | 0.9286 | −0.0096 | - | 0.9286 |
| Pendant drop-forming device | 2.9332 | 2.9324 | −0.0008 | - | - | |
| Total mass | 3.8714 | 3.8610 | −0.0104 | - | - | |
| 4# | Slag | 0.9797 | 0.9609 | −0.0188 | −0.0167 | 0.9442 |
| Pendant drop-forming device | 2.9304 | 2.9300 | −0.0004 | - | - | |
| Total mass | 3.9101 | 3.8909 | −0.0192 | - | - | |
| 5# | Slag | 0.9989 | 0.9831 | −0.0158 | −0.0259 | 0.9572 |
| Pendant drop-forming device | 2.9313 | 2.9308 | −0.0005 | - | - | |
| Total mass | 3.9302 | 3.9139 | −0.0163 | - | - | |
| 6# | Slag | 1.0022 | 0.9898 | −0.0132 | −0.0153 | 0.9745 |
| Pendant drop-forming device | 2.9313 | 2.9310 | −0.0003 | - | - | |
| Total mass | 3.9335 | 3.9208 | −0.0127 | - | - |
| Measurement Mode | α (°) | VA (mm3) | VB (mm3) | VC (mm3) | Vm (mm3) | ρ (g/cm3) | R0 (mm) | β | σ (mN/m) |
|---|---|---|---|---|---|---|---|---|---|
| Heating | 16.8 | 9.249 | 15.350 | 305.127 | 329.726 | 2.864 | 3.4434 | 0.5272 | 627 |
| 305.221 | 329.819 | 2.863 | 3.4498 | 0.5277 | 627 | ||||
| 305.356 | 329.955 | 2.862 | 3.4514 | 0.5293 | 627 | ||||
| 305.132 | 329.731 | 2.864 | 3.4524 | 0.5297 | 626 | ||||
| 305.266 | 329.865 | 2.862 | 3.4502 | 0.5299 | 626 | ||||
| (Average) | 16.8 | 9.249 | 15.350 | 305.220 | 329.819 | 2.863 | 3.4494 | 0.5288 | 627 |
| Cooling | 16.8 | 9.249 | 15.350 | 305.245 | 329.884 | 2.863 | 3.4562 | 0.5285 | 630 |
| 305.075 | 329.674 | 2.864 | 3.4556 | 0.5278 | 630 | ||||
| 305.074 | 329.673 | 2.864 | 3.4555 | 0.5279 | 630 | ||||
| 305.319 | 329.918 | 2.862 | 3.4541 | 0.5274 | 630 | ||||
| 305.139 | 329.738 | 2.863 | 3.4557 | 0.5278 | 630 | ||||
| (Average) | 16.8 | 9.249 | 15.350 | 305.110 | 329.709 | 2.863 | 3.4554 | 0.5279 | 630 |
| Author | Symbol | Property * | Method ** | Atmosphere | Mass % | Ref. | |
|---|---|---|---|---|---|---|---|
| CaO | Al2O3 | ||||||
| Wegener |  | S | P | Ar | 49 | 51 | [11] |
 | D | 50 | 50 | ||||
| Mukai |  | S | P | Ar | 51 | 49 | [14] |
 | 48 | 52 | |||||
| Dou |  | D/S | Hammer/Slide | Ar | 52 | 48 | [23] |
 | 49 | 51 | |||||
 | 46 | 54 | |||||
| Xu |  | S | Slide | Ar | 50 | 50 | [24] |
| Oliveira |  | D/S | M | Ar | 55 | 45 | [25] |
 | 52 | 48 | |||||
 | 50 | 50 | |||||
 | 48 | 52 | |||||
 | 47 | 53 | |||||
| Dubberstein |  | D/S | M | Ar | 50 | 50 | [26] |
| Ershov |  | S | M | - | 50 | 50 | [27] |
| Sikora |  | D/S | M | - | 50 | 50 | [28] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Gao, Y. Determination of Density and Surface Tension of CaO–Al2O3 Molten Slag Using Pendant Drop Method. Metals 2025, 15, 1252. https://doi.org/10.3390/met15111252
Chen J, Gao Y. Determination of Density and Surface Tension of CaO–Al2O3 Molten Slag Using Pendant Drop Method. Metals. 2025; 15(11):1252. https://doi.org/10.3390/met15111252
Chicago/Turabian StyleChen, Jian, and Yunming Gao. 2025. "Determination of Density and Surface Tension of CaO–Al2O3 Molten Slag Using Pendant Drop Method" Metals 15, no. 11: 1252. https://doi.org/10.3390/met15111252
APA StyleChen, J., & Gao, Y. (2025). Determination of Density and Surface Tension of CaO–Al2O3 Molten Slag Using Pendant Drop Method. Metals, 15(11), 1252. https://doi.org/10.3390/met15111252