The Time–Frequency Analysis and Prediction of Mold Level Fluctuations in the Continuous Casting Process
Abstract
1. Introduction
- A novel time–frequency analysis and prediction framework is developed for mold level fluctuations in continuous casting, which can visualize and quantify dynamic correlations between fluctuation patterns and key process variables with improved interpretability.
- An integrated feature extraction strategy combining time–domain and frequency–domain analyses is utilized to identify the potential factors influencing mold level behavior and to reveal the coupling mechanisms between casting signals and liquid level responses.
- An Informer-based long-sequence prediction model is established to achieve accurate forecasting of mold level trends and to effectively suppress abnormal fluctuation events under multivariable casting conditions.
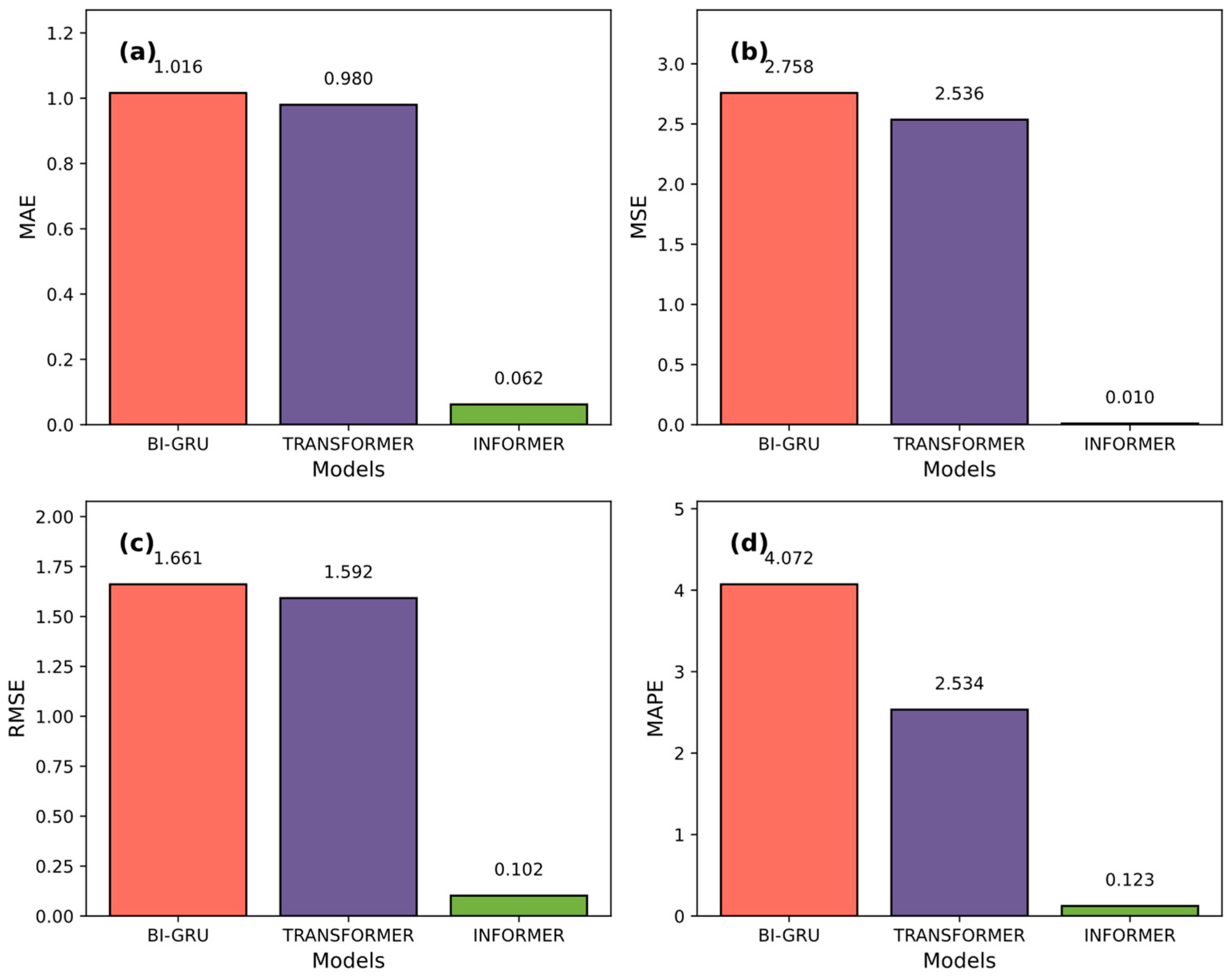
- Comprehensive validation using real industrial production data demonstrates that the proposed system achieves substantial improvement in prediction accuracy (over 90% reduction in MAE compared with baseline models) and provides a scalable solution for adaptive optimization of the continuous casting process.
2. Related Work
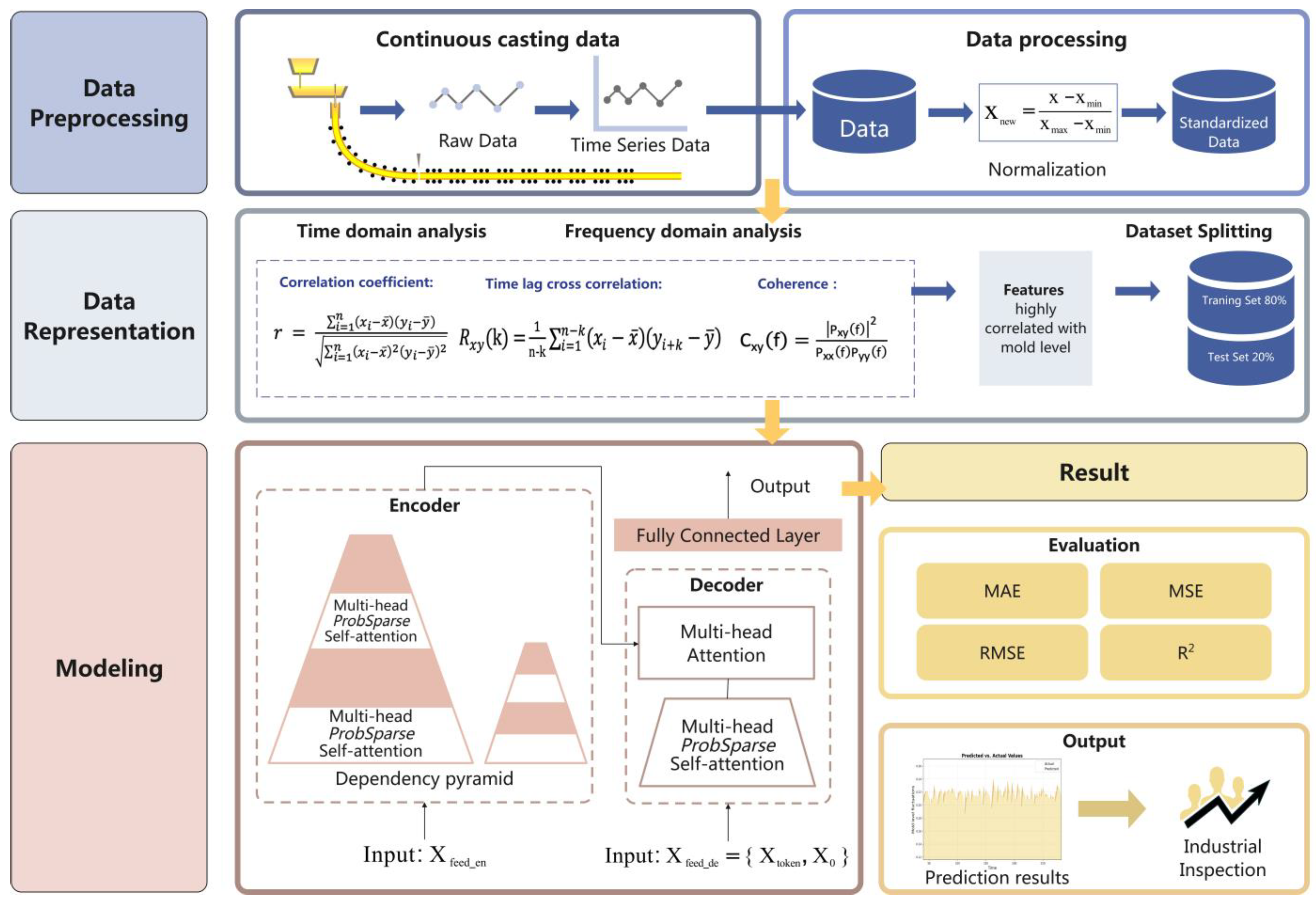
3. Proposed Framework
3.1. Data Preprocessing
3.2. Time Domain Analysis
3.3. Frequency Domain Analysis
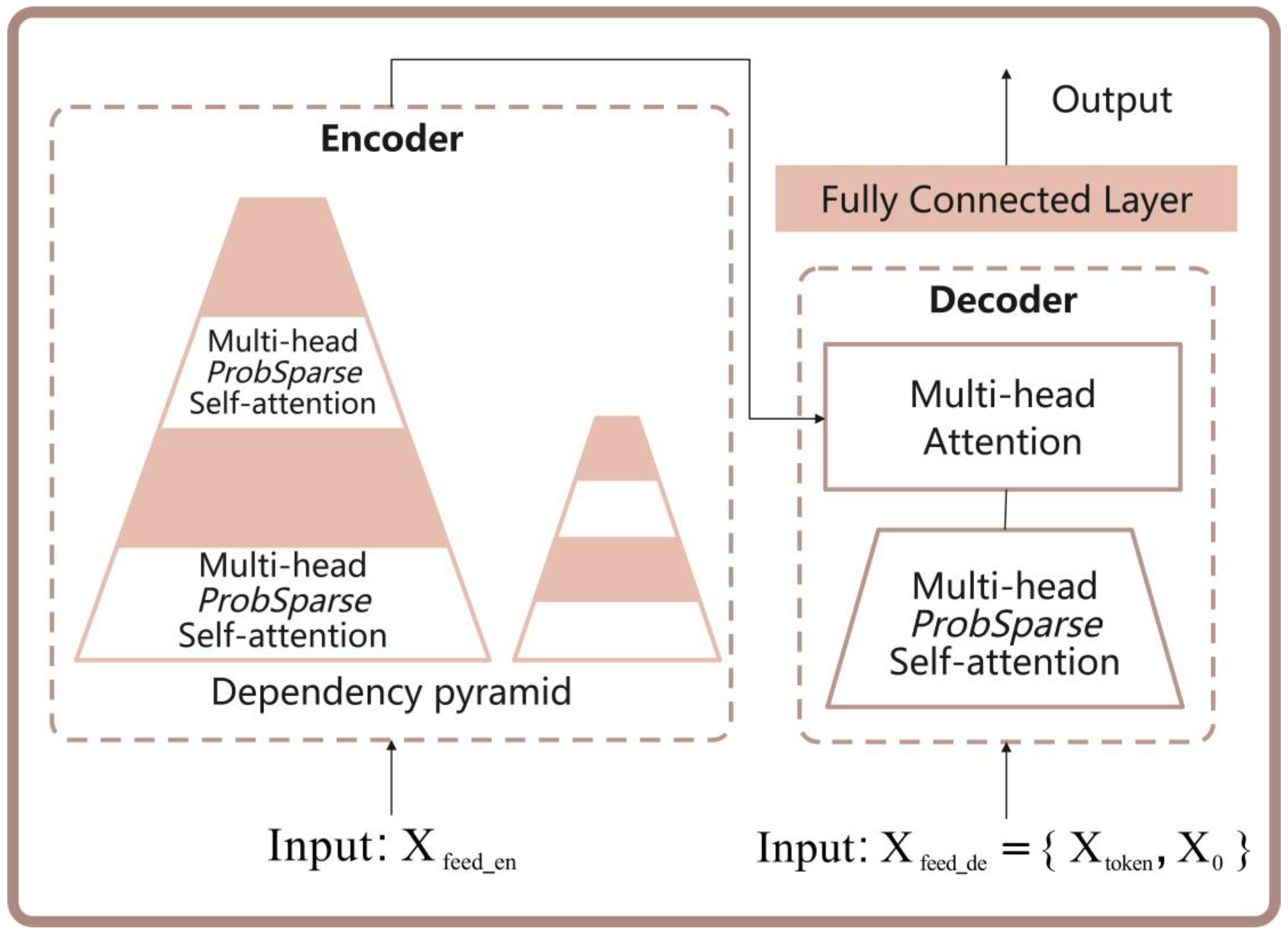
3.4. Informer
3.4.1. Probabilistic Sparse Self-Attention Mechanism
3.4.2. Self-Attention Distillation
3.4.3. Generative Decoder
3.5. Evaluation Methods
4. Experiments and Results
4.1. Experimental Platform
4.2. Results of Time Domain Analysis
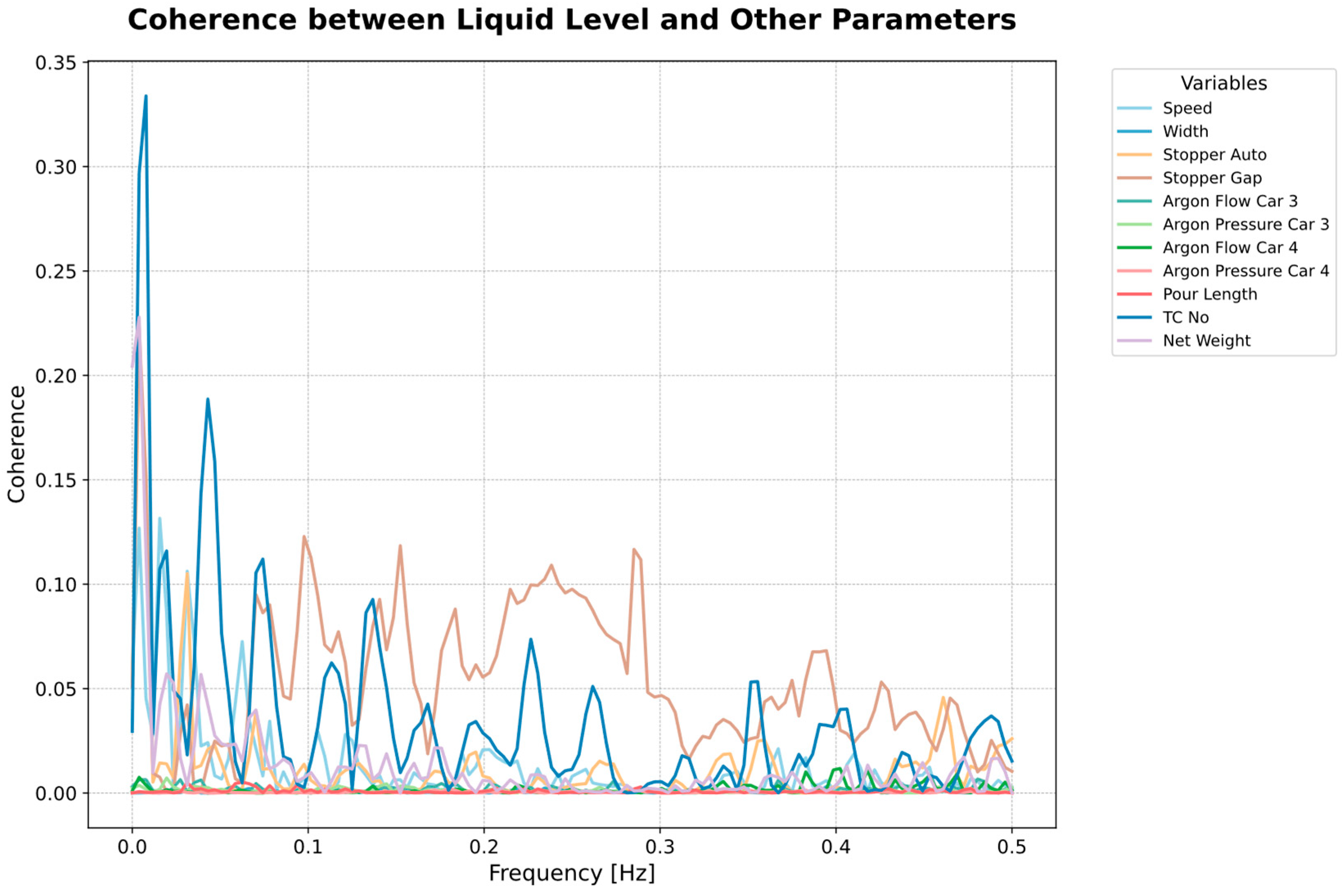
4.3. Results of Frequency Domain Analysis
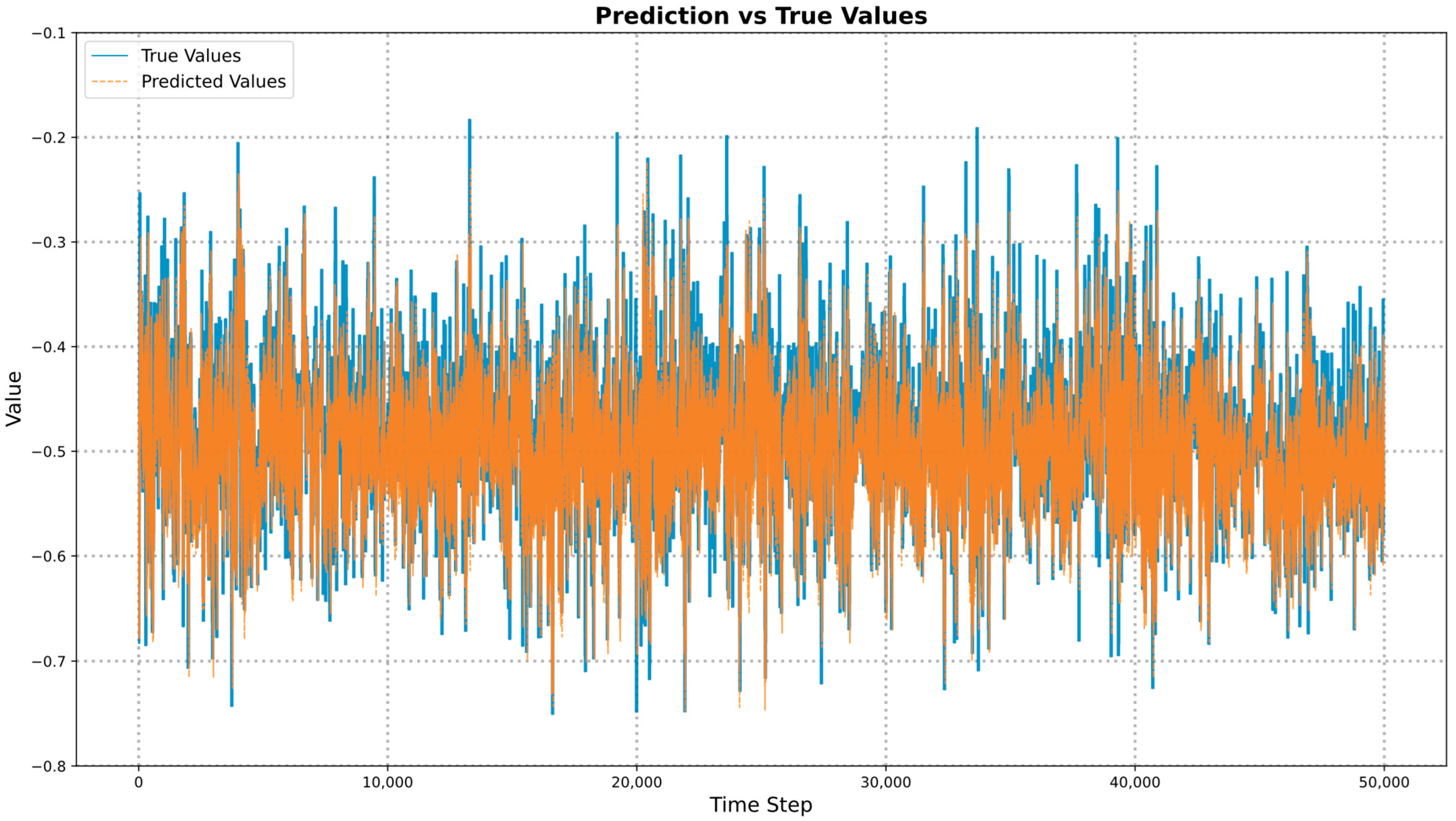
4.4. Results of Three Deep Learning Models
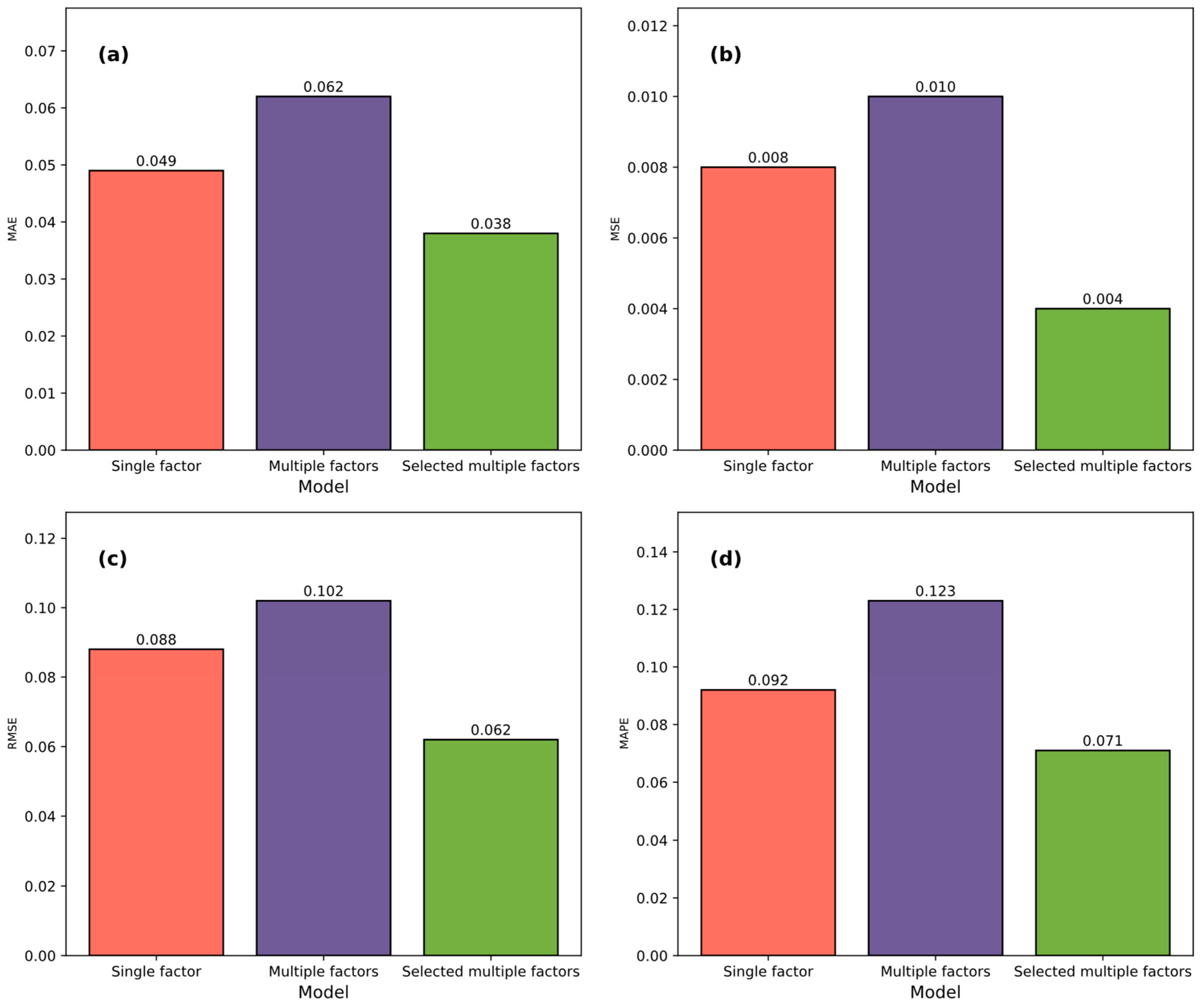
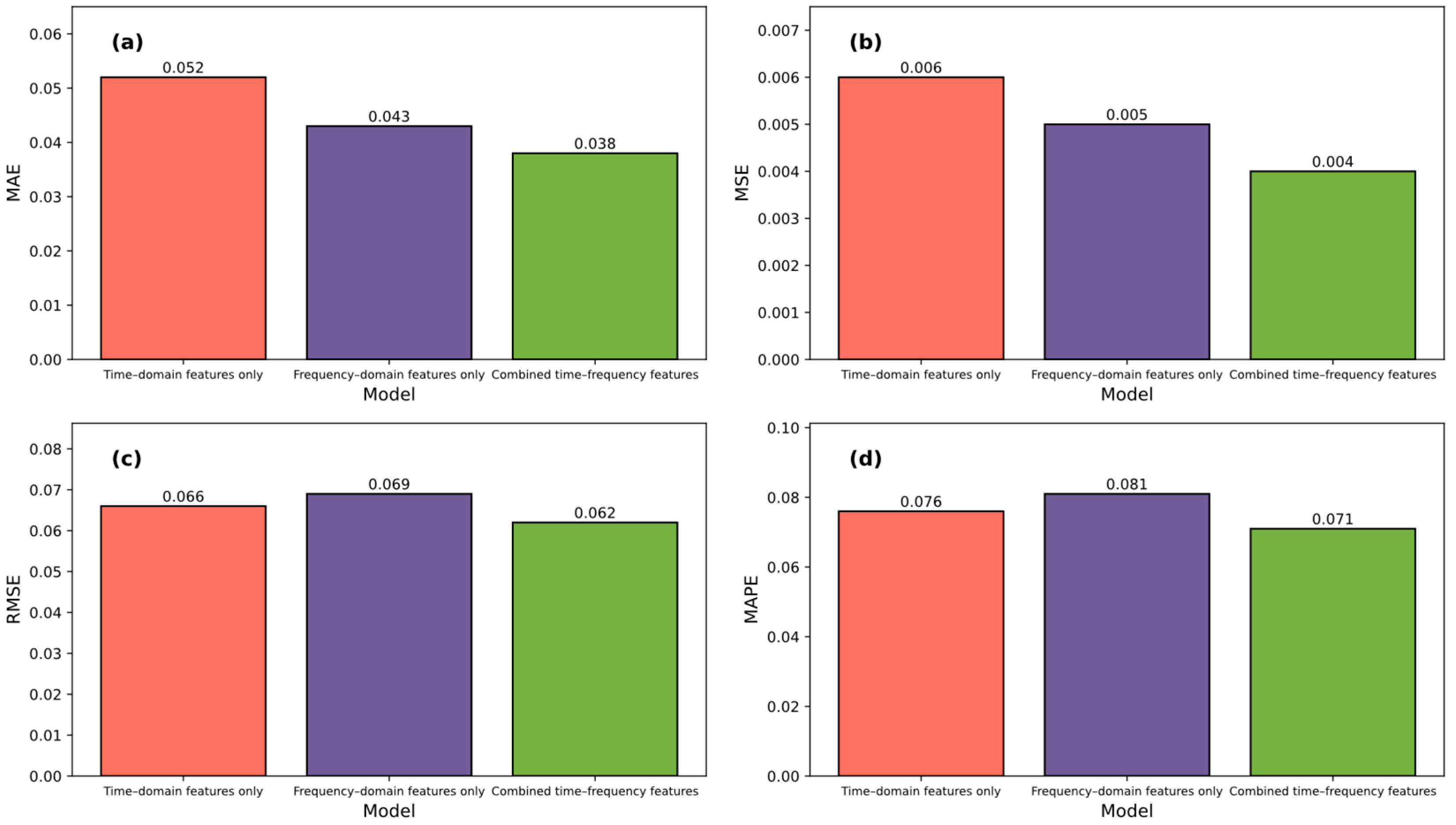
4.5. Results of Different Input Strategies Evaluated Using Multiple Metrics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saini, D.K.; Jha, P.K. Fabrication of aluminum metal matrix composite through continuous casting route: A review and future directions. J. Manuf. Process. 2023, 96, 138–160. [Google Scholar] [CrossRef]
- Li, C.; Zhang, T.; Liu, Y.; Liu, J. Effect of process parameters on surface quality and bonding quality of brass cladding copper stranded wire prepared by continuous pouring process for clad. J. Mater. Res. Technol. 2023, 26, 8025–8035. [Google Scholar] [CrossRef]
- Li, Q.; Wen, G.; Chen, F.; Tang, P.; Hou, Z.; Mo, X. Irregular initial solidification by mold thermal monitoring in the continuous casting of steels: A review. Int. J. Miner. Metall. Mater. 2024, 31, 1003–1015. [Google Scholar] [CrossRef]
- Zhao, P.; Li, Q.; Kuang, S.B.; Zou, Z. LBM-LES simulation of the transient asymmetric flow and free surface fluctuations under steady operating conditions of slab continuous casting process. Metall. Mater. Trans. B 2017, 48, 456–470. [Google Scholar] [CrossRef]
- Zhang, Q. Numerical simulation of influence of casting speed variation on surface fluctuation of molten steel in mold. J. Iron Steel Res. Int. 2010, 17, 15–19. [Google Scholar] [CrossRef]
- Lei, H.; Liu, J.; Tang, G.; Zhang, H.; Jiang, Z.; Lv, P. Deep insight into mold level fluctuation during casting different steel grades. JOM 2023, 75, 914–919. [Google Scholar] [CrossRef]
- Ma, Y.; Fang, B.; Ding, Q.; Wang, F. Analysis of mold friction in a continuous casting using wavelet transform. Metall. Mater. Trans. B 2018, 49, 558–568. [Google Scholar] [CrossRef]
- Yong, M.; Fangyin, W.; Cheng, P.; Wei, G.; Bohan, F. Analysis of Mold Friction in a Continuous Casting Using Wavelet Entropy. Metall. Mater. Trans. B 2016, 47, 1565–1572. [Google Scholar] [CrossRef]
- Wei, Z.J.; Wang, T.; Feng, C.; Li, X.-Y.; Liu, Y.; Wang, X.-D.; Yao, M. Modeling and Simulation of Multi-phase and Multi-physical Fields for Slab Continuous Casting Mold Under Ruler Electromagnetic Braking. Metall. Mater. Trans. B 2024, 55, 2194–2208. [Google Scholar] [CrossRef]
- Jin, Y.; Luo, S.; Meng, X.; Liu, Z.; Wang, C.; Wang, W.; Zhu, M. A Real-Time Prediction Method for Heat Flux in Continuous Casting Mold with Optical Fibers. Metall. Mater. Trans. B 2025, 56, 1865–1878. [Google Scholar] [CrossRef]
- Xie, Z.; Yu, D.; Zhan, C.; Zhao, Q.; Wang, J.; Liu, J.; Liu, J. Ball screw fault diagnosis based on continuous wavelet transform and two-dimensional convolution neural network. Meas. Control 2023, 56, 518–528. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, L.; Ren, Y.; Chen, W.; Liu, F. Formation and prevention of nozzle clogging during the continuous casting of steels: A review. ISIJ Int. 2024, 64, 1–20. [Google Scholar] [CrossRef]
- Dong, X.; Li, L.; Tang, Z.; Huang, L.; Liu, H.; Liao, D.; Yu, H. The Effect of Continuous Casting Cooling Process on the Surface Quality of Low-Nickel Austenitic Stainless Steel. Steel Res. Int. 2025, 2400957, 108–117. [Google Scholar] [CrossRef]
- Guo, D.; Zeng, Z.; Peng, Z.; Guo, K.; Hou, Z. Effect of Casting Speed on CET Position Fluctuation Along the Casting Direction in Continuous Casting Billets. Metall. Mater. Trans. B 2023, 54, 450–464. [Google Scholar] [CrossRef]
- Landauer, J.; Marko, L.; Kugi, A.; Steinboeck, A. Mathematical modeling and system analysis for preventing unsteady bulging in continuous slab casting machines. J. Process Control 2024, 139, 103232. [Google Scholar] [CrossRef]
- Han, K.; Xiao, A.; Wu, E.; Guo, J.; Xu, C.; Wang, Y. Transformer in transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 15908–15919. [Google Scholar]
- Deng, Z.; Zhang, Y.; Zhang, L.; Cong, J. A Transformer and Random Forest Hybrid Model for the Prediction of Non-metallic Inclusions in Continuous Casting Slabs. Integr. Mater. Manuf. Innov. 2023, 12, 466–480. [Google Scholar] [CrossRef]
- Fang, X.; Liu, C.; Yang, H.; Zheng, X.; Chen, X. Noise-Reduced Anomaly Attention Transformer for Intelligent Microscale Defects Detection in Metal Materials. IEEE Trans. Instrum. Meas. 2024, 73, 6505313. [Google Scholar] [CrossRef]
- Zhang, C. Application of neural network in steelmaking and continuous casting: A review. Ironmak. Steelmak. 2024, 03019233241301144. [Google Scholar] [CrossRef]
- Sun, F.; Jin, W. CAST: A convolutional attention spatiotemporal network for predictive learning. Appl. Intell. 2023, 53, 23553–23563. [Google Scholar] [CrossRef]
- Yang, R.; Cao, L.; Li, J.; Yang, J. Variational Hierarchical N-BEATS Model for Long-term Time-series Forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 19398–19410. [Google Scholar] [CrossRef]
- Van Belle, J.; Crevits, R.; Caljon, D.; Verbeke, W. Probabilistic forecasting with modified N-BEATS networks. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 18872–18885. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, K.; He, F.; Zhang, Z. Application of time series data anomaly detection based on deep learning in continuous casting process. ISIJ Int. 2022, 62, 689–698. [Google Scholar] [CrossRef]
- Yang, H.; Fang, Y.; Liu, L.; Ju, H.; Kang, K. Improved YOLOv5 based on feature fusion and attention mechanism and its application in continuous casting slab detection. IEEE Trans. Instrum. Meas. 2023, 72, 1–16. [Google Scholar] [CrossRef]
- Wang, T.; Li, K.; Li, S.; Wang, L.; Yang, J.; Feng, L. Asymmetric flow behavior of molten steel in thin slab continuous casting mold. Metall. Mater. Trans. B 2023, 54, 3542–3553. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Z.; Xiong, Y.; Yang, J.; Xu, G.; Li, B. A Novel Feedforward Neural Network Model for Predicting the Level Fluctuation in Continuous Casting Mold. Metall. Mater. Trans. B 2025, 56, 5009–5026. [Google Scholar] [CrossRef]
- Brezina, M.; Mauder, T.; Klimes, L.; Stetina, J. Comparison of Optimization-Regulation Algorithms for Secondary Cooling in Continuous Steel Casting. Metals 2021, 11, 237. [Google Scholar] [CrossRef]
- Brezocnik, M.; Župerl, U. Optimization of the Continuous Casting Process of Hypoeutectoid Steel Grades Using Multiple Linear Regression and Genetic Programming—An Industrial Study. Metals 2021, 11, 972. [Google Scholar] [CrossRef]
- Yang, J.; Ji, Z.; Liu, W.; Xie, Z. Digital-Twin-Based Coordinated Optimal Control for Steel Continuous Casting Process. Metals 2023, 13, 816. [Google Scholar] [CrossRef]
- Rao, R.V.; Davim, J.P. Optimization of Different Metal Casting Processes Using Three Simple and Efficient Advanced Algorithms. Metals 2025, 15, 1057. [Google Scholar] [CrossRef]
- Kovačič, M.; Zupanc, A.; Vertnik, R.; Župerl, U. Optimization of Billet Cooling after Continuous Casting Using Genetic Programming—Industrial Study. Metals 2024, 14, 819. [Google Scholar] [CrossRef]
- Wang, Z.; Shan, Q.; Gao, Y.; Pan, H.; Lu, B.; Wen, J.; Cui, H. Physical Simulation of Mold Level Fluctuation Characteristics. Metall. Mater. Trans. B 2023, 54, 2591–2604. [Google Scholar] [CrossRef]
- Meng, X.; Luo, S.; Zhou, Y.; Wang, W.; Zhu, M. Time–Frequency Characteristics and Predictions of Instantaneous Abnormal Level Fluctuation in Slab Continuous Casting Mold. Metall. Mater. Trans. B 2023, 54, 2426–2438. [Google Scholar] [CrossRef]
- Wang, Z.; Shan, Q.; Cui, H.; Pan, H.; Lu, B.; Shi, X.; Wen, J. Characteristic analysis of mold level fluctuation during continuous casting of Ti-bearing IF steel. J. Mater. Res. Technol. 2024, 31, 1367–1378. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, R.; Liu, J.; Yu, W.; Li, G.; Cui, H. Exploration of the causes of abnormal mold level fluctuation in thin slab continuous casting mold. J. Mater. Res. Technol. 2024, 33, 1460–1469. [Google Scholar] [CrossRef]
- Lu, M.; Xu, X. TRNN: An efficient time-series recurrent neural network for stock price prediction. Inf. Sci. 2024, 657, 119951. [Google Scholar] [CrossRef]
- Wang, Y.; Long, H.; Zheng, L.; Shang, J. Graphformer: Adaptive graph correlation transformer for multivariate long sequence time series forecasting. Knowl.-Based Syst. 2024, 285, 111321. [Google Scholar] [CrossRef]
- Das, A.; Kong, W.; Sen, R.; Zhou, Y. A decoder-only foundation model for time-series forecasting. In Proceedings of the Forty-first International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Yadav, H.; Thakkar, A. NOA-LSTM: An efficient LSTM cell architecture for time series forecasting. Expert Syst. Appl. 2024, 238, 122333. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Meng, X.; Luo, S.; Zhou, Y.; Wang, W.; Zhu, M. Control of Instantaneous Abnormal Mold Level Fluctuation in Slab Continuous Casting Mold Based on Bidirectional Long Short-Term Memory Model. Steel Res. Int. 2025, 96, 2400656. [Google Scholar] [CrossRef]
- He, Y.; Zhou, H.; Zhang, B.; Guo, H.; Li, B.; Zhang, T.; Yang, K.; Li, Y. Prediction model of liquid level fluctuation in continuous casting mold based on GA-CNN. Metall. Mater. Trans. B 2024, 55, 1414–1427. [Google Scholar] [CrossRef]
- He, Y.; Zhou, H.; Li, Y.; Zhang, T.; Li, B.; Ren, Z.; Zhu, Q. Multi-task learning model of continuous casting slab temperature based on DNNs and SHAP analysis. Metall. Mater. Trans. B 2024, 55, 5120–5132. [Google Scholar] [CrossRef]
- Diniz, A.P.M.; Ciarelli, P.M.; Salles, E.O.T.; Coco, K.F. Use of deep neural networks for clogging detection in the submerged entry nozzle of the continuous casting. Expert Syst. Appl. 2024, 238, 121963. [Google Scholar] [CrossRef]
- Xu, E.; Zou, F.; Shan, P. A multi-stage fault prediction method of continuous casting machine based on Weibull distribution and deep learning. Alex. Eng. J. 2023, 77, 165–175. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; AAAI Press: Washington, DC, USA, 2021; Volume 35, pp. 11106–11115. [Google Scholar]

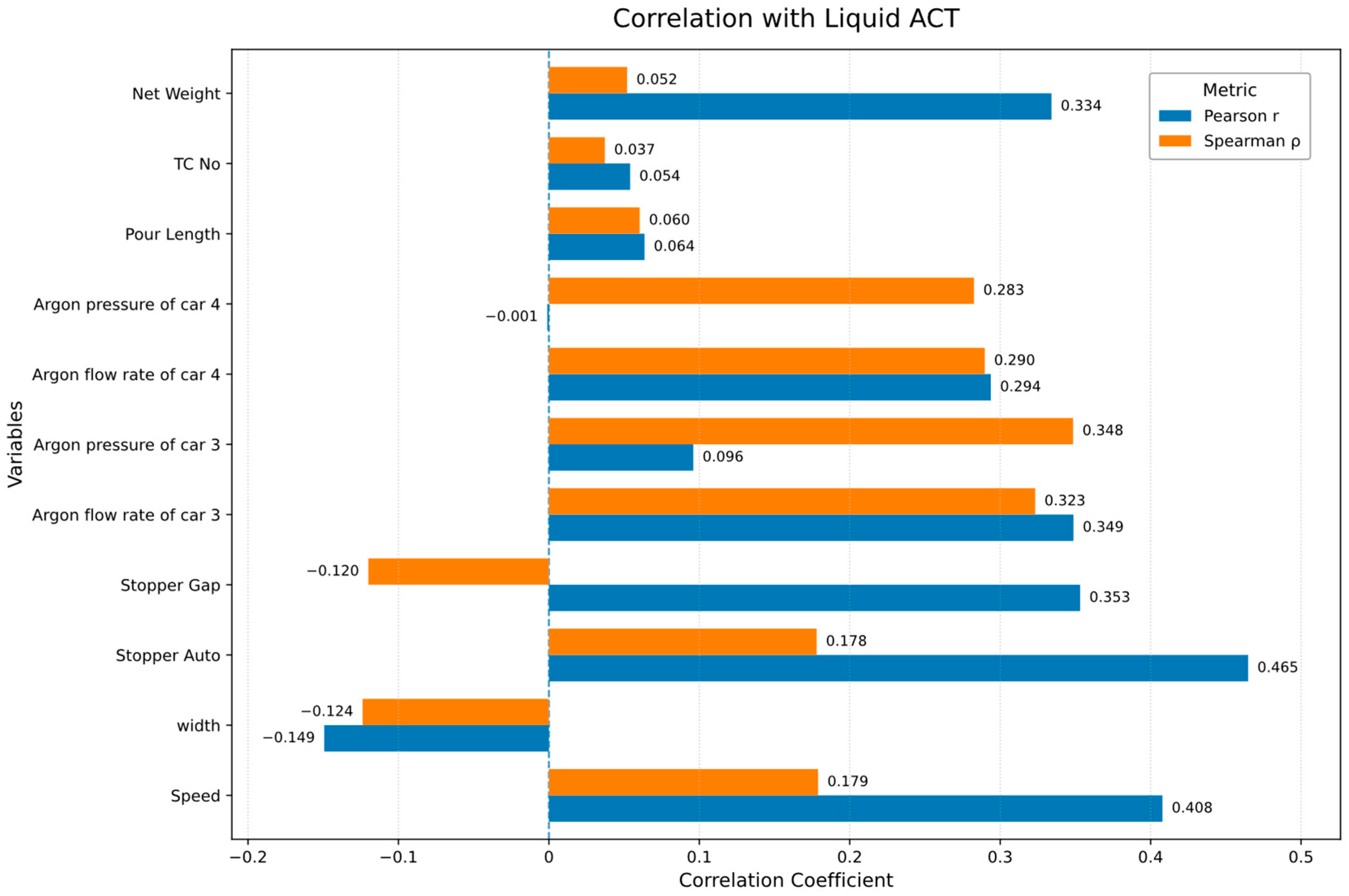
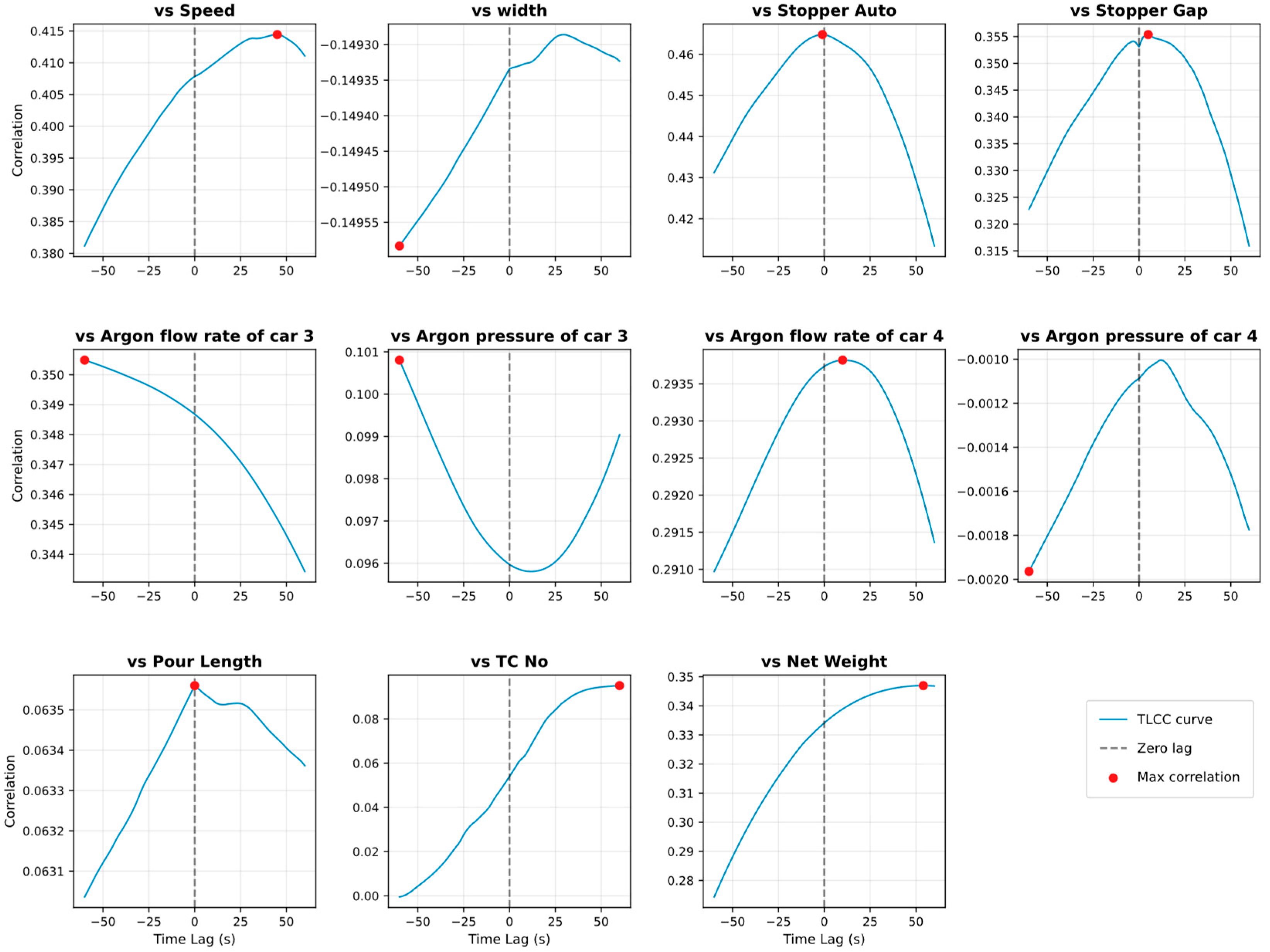
| Parameter | Definition |
|---|---|
| Net weight | The net weight of molten steel in the tundish that is fed into the mold during the casting process. It represents the amount of steel available for casting. The identification number of the tundish car, which transports the tundish (the vessel holding molten steel) to the caster for continuous casting. |
| TC No (Tundish Car Number) | |
| Pour length | The length of the casting, representing the portion of steel being continuously poured into the mold. It is critical for determining the quality of the steel slab or billet. |
| Argon pressure of Car 3 | The argon gas pressure applied to Tundish Car 3. Argon is used to reduce gas bubble formation and control molten steel flow for smooth casting. |
| Argon pressure of Car 4 | The argon gas pressure applied to Tundish Car 4, used similarly to regulate flow and prevent casting defects. |
| Argon flow rate of Car 3 | The flow rate of argon gas in Tundish Car 3, which plays a similar role in controlling steel flow. |
| Argon flow rate of Car 4 | The flow rate of argon gas in Tundish Car 4. Proper control of this flow rate helps stabilize the mold and improve casting uniformity. |
| Stopper gap | The opening of the stopper rod that controls molten steel flow from the tundish into the mold. This gap is critical for maintaining stable mold levels. |
| Width | The adjustable width of the cast product (slab or billet), influencing the overall geometry and surface quality. |
| Speed (Casting speed) | The linear withdrawal speed of the mold from the continuous casting machine, which directly affects solidification rate and product quality. |
| Mold level fluctuation | Mold level fluctuation refers to the time-varying oscillation of the molten steel surface height within the mold during the continuous casting process. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, M.; Fu, M.; Li, W.; Wang, Q.; Chen, N.; Ma, Z.; Sun, L.; Zhang, R.; Wang, H.; Wang, J. The Time–Frequency Analysis and Prediction of Mold Level Fluctuations in the Continuous Casting Process. Metals 2025, 15, 1253. https://doi.org/10.3390/met15111253
Cai M, Fu M, Li W, Wang Q, Chen N, Ma Z, Sun L, Zhang R, Wang H, Wang J. The Time–Frequency Analysis and Prediction of Mold Level Fluctuations in the Continuous Casting Process. Metals. 2025; 15(11):1253. https://doi.org/10.3390/met15111253
Chicago/Turabian StyleCai, Mohan, Meixia Fu, Wei Li, Qu Wang, Na Chen, Zhangchao Ma, Lei Sun, Ronghui Zhang, Hongbin Wang, and Jianquan Wang. 2025. "The Time–Frequency Analysis and Prediction of Mold Level Fluctuations in the Continuous Casting Process" Metals 15, no. 11: 1253. https://doi.org/10.3390/met15111253
APA StyleCai, M., Fu, M., Li, W., Wang, Q., Chen, N., Ma, Z., Sun, L., Zhang, R., Wang, H., & Wang, J. (2025). The Time–Frequency Analysis and Prediction of Mold Level Fluctuations in the Continuous Casting Process. Metals, 15(11), 1253. https://doi.org/10.3390/met15111253








