Abstract
This paper presents a physics-free Bayesian approach for the learning and inference of probabilistic stability charts in milling operations. The approach does not require any information from machine tool structural dynamics or cutting force coefficients, and the underlying learning algorithm can operate with limited training data. A Fully Bayesian Gaussian Process with distributions on its kernel hyperparameters is employed to enable information transfer between different machine and process configurations. The vision system further automates the detection of necessary dimensions from the tool–holder assembly in the machine’s tool magazine, further enhancing the applicability of the approach. Experiments demonstrated the effectiveness of this approach, offering great promise as an industry-friendly solution.
1. Introduction
Chatter has been the main factor limiting the productivity of milling operations for many years. The importance of chatter lies in the serious damages it can cause, threatening the lifespan of machines and tools, as well as degrading the surface quality. Consequently, the manufacturing industry has resorted to using highly conservative process parameters, resulting in reduced productivity and higher production costs.
Scholars have attempted to predict chatter-free process parameters using Stability Lobe Diagrams (SLDs), where the critical stable depth of a cut is plotted as a function of the spindle speed. The zero-order solution (ZOS) by Altintas and Budak [1] is a well-known method for generating such SLDs, requiring tooltip dynamics and cutting force coefficients. While the ZOS has gained popularity due to its computational efficiency, more sophisticated chatter prediction methods have been developed. For instance, the multi-frequency approach by Budak and Altintas [2] is particularly precise for situations involving interrupted cuts, such as those with low radial immersion. Additionally, the Nyquist criterion has been employed for milling stability analysis, as demonstrated in Eynian’s study on process stability with process damping [3]. Chatter analysis can also be conducted in the time domain using the Semi-Discretization Method (SDM) developed by Insperger and Stepan [4]. The required dynamics at the tooltip are typically obtained by coupling the Timoshenko beam model of the tool–holder assembly to the experimentally measured machine tool dynamics through receptance coupling [5,6]. However, the demand for modeling and measurement efforts limits the practicality of such physics-based approaches on the shop floor.
With the rise of machine learning, researchers have explored the effectiveness of these data-driven methods for predicting the chatter state of a process. Cherukuri et al. [7] trained a multi-layer neural network classifier on 600 training samples to predict chatter in turning operations, using the spindle speed and width of a cut as inputs, and the predicted stability state as the output. While neural networks are powerful tools for such classification tasks, their demand for extensive training datasets hinders their practicality for industrial applications. Addressing this, Postel et al. [8] used physics-based models to generate a supplementary training dataset of 1000–10,000 samples for pretraining Deep Neural Networks (DNNs) and an affordable set of 10–100 experimental samples for fine-tuning the DNNs, within a transfer learning concept.
In instances where data are limited, Bayesian learning enables effective learning by quantifying the probability of predictions and the underlying uncertainty, known as epistemic uncertainty. Ostad Ali Akbari et al. [9] proposed a physics-supported probabilistic artificial intelligence technique to refine stability predictions with a limited number of experimental training datasets, where uncertainties in the tool–holder assembly model [10] and cutting force coefficients are refined through Bayesian learning. Within a federated learning concept, they leveraged the physics-based models to enable knowledge transfer between various machines sharing similar components, leading to enhanced stability prediction even for unseen but comparable configurations. The remaining uncertainties in the model were further utilized for active data collection through active learning. While the resulting probabilistic SLDs were useful for informing machine operators about the reliability of predictions, this hybrid approach requires the establishment of a sufficiently comprehensive physics-based model and the measurement of machine tool dynamics through inverse receptance coupling [11] or indirect identification techniques [12].
This study followed a probabilistic perspective to propose an industrial-friendly solution by offering two main advantages: (i) eliminating the complexities and efforts associated with physics-driven models and (ii) reducing the need for extensive large training datasets associated with data-driven models. Section 2 presents the methodology of using Bayesian learning to learn probabilistic SLDs for given tool–holder combinations, and it employs a Fully Bayesian Gaussian Process (FBGP) to propagate knowledge with the degree of certainty to other tool–holder and process configurations. This approach does not require human effort and merely necessitates an ordinary camera installed inside the machine’s tool magazine and a microphone to detect chatter based on process noise. The effectiveness of the proposed approach was investigated through experimental studies, as presented in Section 3, and the paper is concluded in Section 4.
2. Methodology
This section presents the methodology and its background theory. For each machine and process configuration , specified by the tool stick-out length in pixels and tool–workpiece radial immersion (within the scope of this study), Bayesian learning is applied using importance sampling. This approach refines the prior distributions of the parametric SLD parameters, , to their posteriors based on their alignment with the training data through the likelihood function. These posteriors, along with those from other machine and process configurations, are fed into FBGPs with a hyperparameter vector . This process aims to estimate the corresponding parameters for a new machine and process configuration and predict the probabilistic stability diagram. This procedure is illustrated in Figure 1. Note that throughout this article, non-scalar variables are represented in bold.
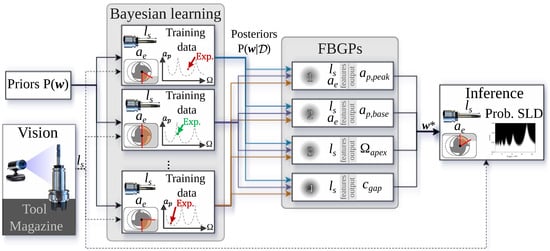
Figure 1.
Overview of the proposed learning framework. After the priors of the SLD parameters are refined according to the training data, they are fed into four independent FBGPs to estimate the SLD parameters for a new machine and process configuration.
2.1. Parametric SLD
As previously introduced, SLDs delineate the boundary of the critical depth of cut as a function of the spindle speed, exclusively for a given machine and process configuration . In this study, the characteristic shape of SLDs for a single-mode system was assumed to be generated through a second-order polynomial that is defined by four parameters: the unconditional depth of cut under which the process remains stable regardless of the spindle speed, the depth of the cut at the last peak for the maximum attainable cutting depth, the spindle speed at the last valley that adjusts the lobe placements depending on the most flexible vibration mode, and the pocket spacing scale that adjusts the frequency of the appearance of the lobes in the SLD based on the number of cutting teeth. Figure 2 presents an exemplary case where the parametric SLD is tuned to align with experimental cutting tests. The agreement between the two suggests the validity of using such a parametric SLD to represent actual stability boundaries. Nevertheless, in general, the lobes may not necessarily be symmetric, and such additional complexities can be considered by introducing extra parameters to the formulation of the parametric SLD.
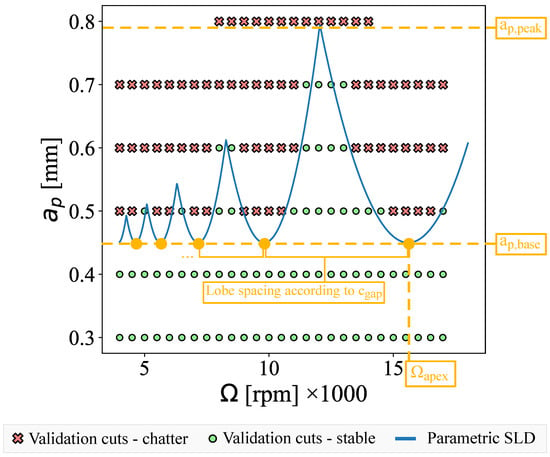
Figure 2.
Generating SLDs through the parametric model based on the four characterizing parameters, underlining its effectiveness in representing actual stability borders. In this particular example, the SLD parameters are tuned manually to fit the experimental chatter detection.
In this representation, a parametric SLD consists of multiple second-order polynomials, each representing a stability lobe defined as
for the lobe number . The complete parametric SLD contains multiples of these lobes, with the minimum depth of the cut being selected and scaled by additional linear terms to feature the desired unconditional and peak depths of the cut:
where is the depth of the cut at the intersection of lobes and . Therefore, the parametric SLD that is defined by for a given provides the value for at a requested . In the end, the parameter vector contains the normalized values of these four parameters, i.e., , to improve the efficiency of the learning algorithm, which is presented in the following sections.
2.2. Likelihood Function for Stability Refinement
The likelihood function assesses the probability of specific observations as training data given a particular sample of model parameter . The binary-valued represents the experimental stability state of the process, with 1 indicating instability and 0 indicating stability. In this binary classification of chatter stability states, the likelihood function is formulated using a logistic function [13]. This involves comparing the experimental depth of cut with the critical depth of the cut predicted by the parametric SLD . The likelihood for one unstable observation is defined as follows [9]:
with k adjusting the steepness of the state transition at the stability border. Since follows a Bernoulli distribution for the binary outcome of process stability state according to [9], the likelihood for one stable observation can be computed as
Assuming that the observations are independent, the total likelihood from all training data is computed as
2.3. Bayesian Learning through Importance Sampling
When dealing with problems involving uncertainty, the Bayesian approach offers powerful tools to account for and refine uncertainties [14]. Bayesian learning begins with a prior distribution of model parameter , which suggests a prior belief about possible values of model parameters. Upon acquiring training data , the prior distribution can be refined into an updated posterior distribution using the Bayes rule [15]:
where Z is meant to normalize the summation of probabilities and is defined as
Thus, the posterior distribution is derived based on the compatibility of the prior distribution with the training data, as quantified by the likelihood function in Section 2.2. Often, obtaining closed-form expressions for posterior distributions is intractable, especially in high-dimensional parameter spaces. Therefore, techniques such as variational inference [16] and Markov Chain Monte Carlo (MCMC) simulations [17] are employed to approximate the posterior distributions.
In small parameter spaces, such as for the parametric SLD where the parameter space of has four dimensions and the computation of likelihood is inexpensive, an approximation approach based on importance sampling [18] can be employed. In assuming that the posterior distribution of remains an independent multivariate normal distribution after learning is performed, the posterior mean and covariance matrix of are computed by
Also, for the inference and generation of the updated probabilistic SLD for a test case represented as , the following equation is used
In the above formulations, represents the expectation operation and needs to be computed with respect to the posterior distribution of , which is currently unavailable. The following provides an alternative direction based on importance sampling to approximate this expectation from existing prior distributions. Let this expectation for a generic function be defined as
which describes the expected value of when is drawn from the posterior distribution, . As the posterior distribution is not yet available, the integration can be written in the following form by substituting with Bayes rule:
The right-hand-side integration represents the expectation with respect to the prior distribution of ; therefore,
This expectation can be estimated through the following Monte Carlo approximation:
where is drawn from the prior distribution, . The normalizing factor is also approximated by
In summary, the expectation with respect to the posterior distribution can be estimated with samples drawn from the prior distribution using the following equation:
2.4. Fully Bayesian Gaussian Process (FBGP)
A standard Gaussian Process (GP) is a probabilistic model that defines a distribution over functions, serving as a versatile tool for capturing uncertainty in various scientific domains. This approach has gained popularity and interest over the last two decades [19,20,21]. Unlike conventional parametric models, GPs treat functions as random variables, providing a non-parametric framework for flexible function estimation. GPs find applications in regression tasks, Bayesian optimization, and other fields where the estimation of uncertainties is important. Their elegance lies in their capacity to model complex relationships and yield predictive distributions that account for the inherent uncertainty in scientific data analysis and decision-making processes. An FBGP refers to an approach that treats all model parameters, including the hyperparameters of the kernel, as probabilistic variables with associated probability distributions.
After the Bayesian learning for the machine and process configuration for which training data were available , a posterior distribution for SLD parameters for each is obtained as . The goals of using an FBGP are to establish a connection for a new machine and process configuration and provide an estimation for its corresponding SLD parameters leading to the generation of a corresponding probabilistic SLD. Since is a four-element vector, separate independent FBGPs are trained for each element in this vector; let each of these scalar variables be represented by w. The posterior mean and standard deviation of w for case m after Bayesian learning are indicated by and , respectively. The FBGP is based on the following joint Gaussian distribution [20]:
The prior mean of the FBGP, either or , is a vector with equal scalar values of . The covariance matrix considers a fixed Gaussian noise for the training data, i.e., with being the posterior standard deviation of . The mean values of the posterior SLD parameters are fed to the FBGP as the target values, i.e., . The covariance matrix is established based on a measure of similarity between the feature vectors of different cases using a kernel function in the following arrangement:
and analogously for , , and . The kernel in this study is a Radial Basis Function (RBF) [22], which is formulated as
with as the output scale and ℓ as the length scale. In the end, the mean and covariance matrix at the test points are calculated as follows:
Usually, in standard GPs, the hyperparameters are considered deterministic values and are adjusted to maximize the marginal likelihood of the data [20]. In FBGPs, the distributions of hyperparameters are tuned based on the Bayes rule through MCMC approximations. In this study, an FBGP was implemented using the GPyTorch library [23]. Uniform distributions were assigned as priors to the length scale and output scale, and their distributions were refined via Bayesian learning through MCMC approximations. Additionally, a normal distribution with a mean of 0.5 and a standard deviation of 0.2 was assigned to the FBGP mean, i.e., , to consider a feasible range between 0 and 1 for normalized SLD parameters.
2.5. Vision-Assisted Estimation of Tooling System Dimensions
In pursuit of advancing the full automation of stability prediction, a tool dimension recognition system was developed using image processing techniques. This system enables predictions with the aid of vision, eliminating the need to remove the tool from the milling machine for measurements, such as for determining the stick-out length. The entire process occurs rapidly and automatically within the unused space inside the CNC machine’s tool magazine.
The system configuration is detailed in Figure 3. A key requirement involves securing the camera onto a fixture. The camera must be accurately oriented perpendicular to the tool, ensuring a perpendicular side view rather than an elevated view.

Figure 3.
Vision system for automatically capturing tooling system dimensions, installed inside the machine’s tool magazine.
The image processing algorithm operates in three self-operating stages, eliminating the need for manual intervention. The algorithm takes a captured image as input and estimates the stick-out length of the tool as output. The algorithmic steps are illustrated in Figure 4. In the initial phase, the raw image is cropped and reoriented to select a pre-defined region of the image, and then it is converted into grayscale. Following this, a pixel brightness threshold is applied to the grayscale image to enhance contrast, resulting in a binary representation of the image. In the final stage, the algorithm analyzes the number of dark pixels per row from top to bottom and identifies the first significant increase in the number of dark pixels as the tooltip. The subsequent significant increase corresponds to the starting point of the holder, for which its distance to the tooltip is measured as the stick-out length in pixels. The average value of pixels per row in this region also serves as a representative of the tool diameter.
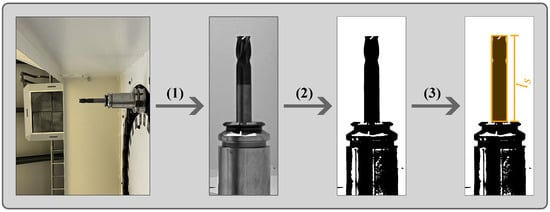
Figure 4.
Image processing steps for the estimation of tool stick-out length: (1) the raw image is cropped, rotated, and converted into grayscale; (2) the grayscale is converted into a binary image based on a brightness threshold; (3) the tool region is detected, and the stick-out length is estimated.
3. Experimental Validations
This section is devoted to the evaluation of the proposed method through experimental case studies. In these case studies, four different cases, varying in holder–tool clamping length and immersion conditions, are considered. Validation cuts were performed for each case on a GF Mikron HPM 800U (Biel/Bienne, Switzerland) five-axis milling machine and AL6082 workpiece material (HABA AG, Pfäffikon, Switzerland), where the actual stability states of the process for various combinations of spindle speeds and depths of cuts were recorded. Chatter detection during these cuts was conducted by recording process noise with a microphone and analyzing its frequency spectrum for detecting anomaly frequencies possibly originating from chatter. Chatter detection mechanisms have been reviewed in the literature [24,25,26], where the time-domain process noise signal is transferred to the frequency domain using a short-time Fourier transform (STFT). This method extracts the development of frequencies over time, revealing the presence of chatter frequencies that do not coincide with rotation frequency harmonics. The holder and tool used in these experiments are presented in Table 1.

Table 1.
The specific holder and milling tool employed in this study, which remained consistent across all cases.
In Table 2, the three cases of A, B, and C indicate the training cases, whereas the fourth case, labeled as D, was considered to validate the predictive capabilities of the proposed learning method.

Table 2.
Machine and process configurations in the experimental evaluations. represents feed per tooth.
In Table 3 the estimated stick-out lengths are compared to the actual stick-out lengths using a calibrated pixel-to-length ratio from the image processing setup. The percentage errors resulting from the comparisons underscore the stability and accuracy of the image processing procedure. The conversion of the estimated lengths from pixels to millimeters was performed solely to evaluate the precision of the vision system. For the FBGP, the pixel values are used directly.

Table 3.
Evaluating the precision of vision-based estimations compared to the actual values of the tool stick-out length.
The experimental chatter observations that are used for training are listed in Table 4. The training points are used for each case through Bayesian learning (in Section 2.3) to refine the distribution of SLD parameters from their prior to posterior distributions, as listed in Table 5. The prior distribution embraces a wide and general range of feasible parameter values based on the insights and understanding of the milling stability. As shown in Figure 5, Monte Carlo samples from prior distributions generate multiple parametric SLDs, which are overlaid to visually represent the variability in stability predictions. The broad range of possible SLDs and the lack of distinguishable stability pockets highlight the considerable uncertainty in the initial predictions and emphasizes the need for further learning and refinement. As an optional advantage, the selection of priors also allows the algorithm to benefit from the experience of machine operators that can guide and facilitate learning with a lower number of training data.

Table 4.
Experimental process monitoring data used for Bayesian learning per case.

Table 5.
Prior and posterior distributions of SLD parameters after Bayesian learning, characterized by a mean and a standard deviation (std).
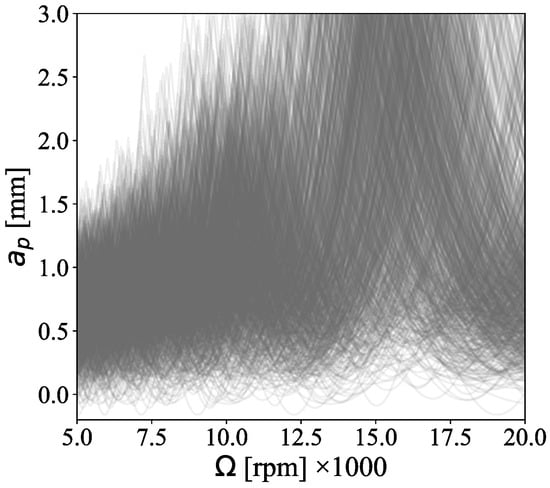
Figure 5.
Monte Carlo samples of SLD from the prior distribution serve to illustrate the inherent generality of the initial distribution, emphasizing the need for refinement.
This learning stage also allows for the inference of posterior probabilistic SLDs for each individual case, as shown in Figure 6. The complete sets of validation cutting tests are plotted over the probabilistic SLDs for validation purposes. As the agreement suggests, the learning was able to successfully refine the stability predictions for each individual case, despite providing only a limited number of training data.
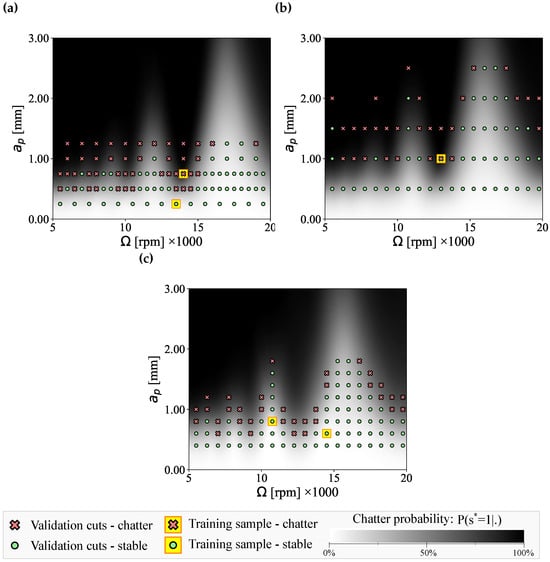
Figure 6.
The updated posterior probabilistic SLDs for each training case alongside the corresponding validation cuts. (a) represents case A, (b) represents case B, and (c) represents case C.
The primary goal was to apply the acquired knowledge through Bayesian learning to new machine and process configurations. The use of FBGPs can enable this connection by correlating values and uncertainties across different cases. To facilitate effective learning using the FBGPs, all input and target values were normalized to fall within the range of 0 to 1. Table 6 outlines the range within which each variable was normalized, denoted by for a given generic variable v:

Table 6.
The range of values assumed for normalization spanning the entire possible range of each parameter.
A total number of four FBGPs were used in this study:
- To predict the distribution of based on and .
- To predict the distribution of based on and .
- To predict the distribution of based on .
- To predict the distribution of based on .
This choice is grounded in the physical intuition that the tool stick-out length affects the natural frequency of the tooltip dynamics, thereby influencing the lobe locations determined by and . Additionally, the stick-out length influences the flexibility of the tooltip, which, together with the cutting load corresponding to , determines the vertical positioning of the lobes through and . Figure 7 illustrates the four FBGPs trained using the posterior distributions of the SLD parameters for cases A, B, and C, obtained from Bayesian learning and listed in Table 5. This figure showcases the impact of the training data across different combinations of machine and process configurations. As particularly evident in the one-dimensional FBGPs, having a distribution instead of a fixed value for the kernel’s hyperparameters allows for the inclusion of function samples with diverse characteristic shapes.
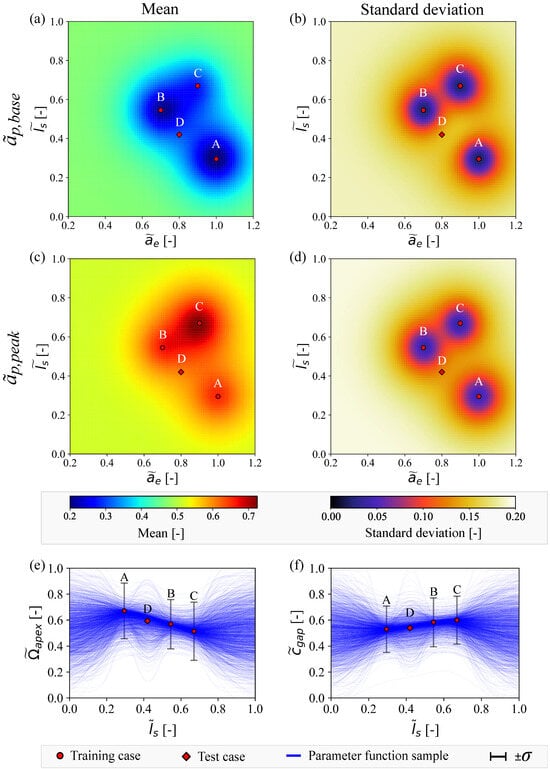
Figure 7.
Four independent FBGPs, each represents one of the four SLD parameters: prediction of FBGPs with a two-dimensional feature vector for in (a,b), and for in (c,d). Also, prediction of FBGPs with a one-dimensional feature vector for in (e), and for in (f).
To assess the validity of the FBGP predictions for the new machine and process configuration of case D, the predicted distributions of , , , and at case D are utilized to generate the corresponding probabilistic SLD, as depicted in Figure 8. The agreement with the experimentally collected validation points confirms the effectiveness of transferring the underlying knowledge for stability predictions through FBGPs to new machine and process configurations. In order to have a benchmark to evaluate the performance of the proposed physics-free learning approach based on FBGPs versus state-of-the-art methods, the prediction for case D reported in [9] is also provided in Figure 8 for comparison. As can be seen, the performance of the approach proposed in this paper is comparable to and even exceeds those of the state-of-the-art methods. It is worth noting that the approach presented in [9] requires a physics-driven model for modeling the tooling system dynamics and also requires the experimental measurement of the machine tool dynamics at the spindle flange using impact tests. In contrast, the physics-free approach in this study eliminates these complexities and offers a more attractive solution for industrial applications.
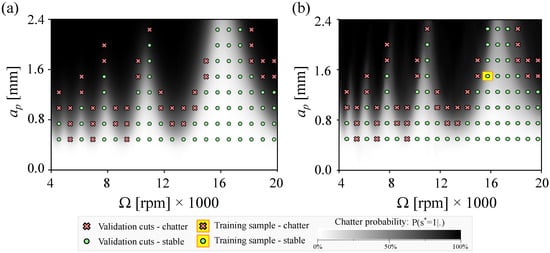
Figure 8.
Evaluating the effectiveness of the FBGPs for probabilistic SLD prediction for case D: (a) prediction from the proposed physics-free learning approach; (b) prediction from the physics-informed Bayesian machine learning reported in [9].
To illustrate chatter detection from process noise in practice, Figure 9 includes the spectrum analysis of process noise for case D at two cutting conditions: a stable process, where the dominant frequency in the sound spectrum coincides with the tooth-passing harmonics; and an unstable process, where an anomaly frequency appears in the sound spectrum.
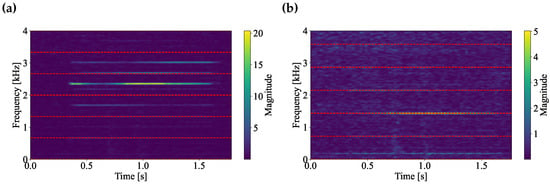
Figure 9.
Process noise spectrum analysis for chatter detection in case D: (a) unstable cut at = 10,000 rpm and mm; (b) stable cut at = 10,750 rpm and mm. The red dashed lines indicate the harmonics of the tooth-passing frequency.
4. Discussion and Conclusions
As chatter continues to be a costly problem that drastically limits productivity in the manufacturing industry, further developments toward the shop floor practicality of chatter suppression solutions holds utmost importance. Unlike existing physics-driven methods, the physics-free Bayesian approach presented in this paper requires no knowledge of machine tool dynamics or cutting force coefficients. Consequently, it eliminates the need for experimental impact testing on machine tools and/or theoretical modeling. Unlike methods based on deep neural networks, the proposed approach builds upon a limited observation of the experimental process state to identify stability regions and incorporates the remaining uncertainty due to this limited training data through probabilities. Considering probability distributions in the FBGPs’ hyperparameters allows for a rich comprehensive propagation of knowledge and uncertainty to other machine and process configurations. Moreover, the vision system effectively provides the often varying stick-out length as an automatic alternative to manual measurements using a caliper. Also, it is superior to the laser system for measuring the tool length installed on modern machine tools since it can provide comprehensive information about the holder–tool geometry, which is important for process stability prediction. As a future development of the algorithm, the following advancements may be considered: (i) expanding the FBGP inputs to include more features, such as the tool diameter or holder dimensions, which are obtainable from the vision system; and (ii) the current parametric SLD applied to a system with one mode involved in chatter, as overlaying multiple SLDs may handle systems with multiple modes involved in chatter. These advancements could prepare the algorithm to be installed on each machine tool, providing continuously improved stability predictions as more observations are collected during arbitrary cuts.
Author Contributions
V.O.A.A.: conceptualization, methodology, software, analysis, resources, final draft, and supervision; A.E.: methodology, software, validation, analysis, data curation, visualization, and writing original draft; K.W.: review of final draft and supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors would like to thank Michal Kuffa for his support in project management, including the allocation of financial resources.
Conflicts of Interest
Author Andrea Eichenberger was employed by the company Inspire AG. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DNN | Deep Neural Network; |
| FBGP | Fully Bayesian Gaussian Process; |
| GP | Gaussian Process; |
| MCMC | Markov Chain Monte Carlo; |
| RBF | Radial Basis Function; |
| SDM | Semi-Discretization Method; |
| STFT | Short-Time Fourier Transform; |
| SLD | Stability Lobe Diagram; |
| std | Standard Deviation; |
| ZOS | Zero-Order Solution. |
References
- Altintaş, Y.; Budak, E. Analytical prediction of stability lobes in milling. CIRP Ann. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Budak, E.; Altintas, Y. Analytical prediction of chatter stability in milling—Part I: General formulation. J. Dyn. Sys. Meas. Control 1998, 120, 22–30. [Google Scholar] [CrossRef]
- Eynian, M. Chatter Stability of Turning and Milling with Process Damping. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2010. [Google Scholar]
- Insperger, T.; Stépán, G. Semi-discretization method for delayed systems. Int. J. Numer. Methods Eng. 2002, 55, 503–518. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Donalson, R. Predicting high-speed machining dynamics by substructure analysis. CIRP Ann. 2000, 49, 303–308. [Google Scholar] [CrossRef]
- Ostad Ali Akbari, V.; Ahmadi, K. Substructure analysis of vibration-assisted drilling systems. Int. J. Adv. Manuf. Technol. 2021, 113, 2833–2848. [Google Scholar] [CrossRef]
- Cherukuri, H.; Perez-Bernabeu, E.; Selles, M.; Schmitz, T. Machining chatter prediction using a data learning model. J. Manuf. Mater. Process. 2019, 3, 45. [Google Scholar] [CrossRef]
- Postel, M.; Bugdayci, B.; Wegener, K. Ensemble transfer learning for refining stability predictions in milling using experimental stability states. Int. J. Adv. Manuf. Technol. 2020, 107, 4123–4139. [Google Scholar] [CrossRef]
- Akbari, V.O.A.; Kuffa, M.; Wegener, K. Physics-informed Bayesian machine learning for probabilistic inference and refinement of milling stability predictions. CIRP J. Manuf. Sci. Technol. 2023, 45, 225–239. [Google Scholar] [CrossRef]
- Akbari, V.O.A.; Postel, M.; Kuffa, M.; Wegener, K. Improving stability predictions in milling by incorporation of toolholder sound emissions. CIRP J. Manuf. Sci. Technol. 2022, 37, 359–369. [Google Scholar] [CrossRef]
- Namazi, M.; Altintas, Y.; Abe, T.; Rajapakse, N. Modeling and identification of tool holder–spindle interface dynamics. Int. J. Mach. Tools Manuf. 2007, 47, 1333–1341. [Google Scholar] [CrossRef]
- Akbari, V.O.A.; Mohammadi, Y.; Kuffa, M.; Wegener, K. Identification of in-process machine tool dynamics using forced vibrations in milling process. Int. J. Mech. Sci. 2023, 239, 107887. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Markov, S. Sigmoid Functions: Some Approximation and Modelling Aspects; AP LAMBERT Academic Publishing: Saarbrucken, Germany, 2015; Volume 4. [Google Scholar]
- Yuan, C.; Druzdzel, M.J. Importance sampling algorithms for Bayesian networks: Principles and performance. Math. Comput. Model. 2006, 43, 1189–1207. [Google Scholar] [CrossRef]
- Neal, R.M. Bayesian Learning for Neural Networks; Springer Science & Business Media: Berlin, Germany, 2012; Volume 118. [Google Scholar]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight uncertainty in neural network. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1613–1622. [Google Scholar]
- Brooks, S. Markov chain Monte Carlo method and its application. J. R. Stat. Soc. 1998, 47, 69–100. [Google Scholar] [CrossRef]
- Tokdar, S.T.; Kass, R.E. Importance sampling: A review. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 54–60. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Evaluation of Gaussian Processes and other Methods for Non-Linear Regression. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 1997. [Google Scholar]
- Seeger, M. Gaussian processes for machine learning. Int. J. Neural Syst. 2004, 14, 69–106. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.G.; Knowles, D.A.; Ghahramani, Z. Gaussian process regression networks. arXiv 2011, arXiv:1110.4411. [Google Scholar]
- Wilson, A.; Nickisch, H. Kernel interpolation for scalable structured Gaussian processes (KISS-GP). In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1775–1784. [Google Scholar]
- Gardner, J.; Pleiss, G.; Weinberger, K.Q.; Bindel, D.; Wilson, A.G. Gpytorch: Blackbox matrix-matrix gaussian process inference with gpu acceleration. Adv. Neural Inf. Process. Syst. 2018, 31, 7576–7586. [Google Scholar]
- Riviére, E.; Stalon, V.; Van den Abeele, O.; Filippi, E.; Dehombreux, P. Chatter detection techniques using microphone. In Proceedings of the Seventh National Congress on Theoretical and Applied Mechanics, Mons, Belgium, 30–31 May 2006; Volume 2006. [Google Scholar]
- Huda, F.; Darman, D.; Rusli, M. Chatter detection in turning process using sound signal and simple microphone. IOP Conf. Ser. Mater. Sci. Eng. 2020, 830, 042027. [Google Scholar] [CrossRef]
- Wang, W.K.; Wan, M.; Zhang, W.H.; Yang, Y. Chatter detection methods in the machining processes: A review. J. Manuf. Process. 2022, 77, 240–259. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

