Abstract
A population balance model (PBM) is used to describe flocculation of particle tailings in seawater at pH 8 for a range of mixing intensities. The size of the aggregates is represented by the mean chord length, determined by the focused beam reflectance measurement (FBRM) technique. The PBM follows the dynamics of aggregation and breakage processes underlying flocculation and provides a good approximation to the temporal evolution of aggregate size. The structure of the aggregates during flocculation is described by a constant or time-dependent fractal dimension. The results revealed that the compensations between the aggregation and breakage rates lead to a correct representation of the flocculation kinetics of the tailings of particles in seawater and, in addition, that the representation of the flocculation kinetics in optimal conditions is equally good with a constant or variable fractal dimension. The aggregation and breakage functions and their corresponding parameters are sensitive to the choice of the fractal dimension of the aggregates, whether constant or time dependent, however, under optimal conditions, a constant fractal dimension is sufficient. The model is robust and predictive with a few parameters and can be used to find the optimal flocculation conditions at different mixing intensities, and the optimal flocculation time can be used for a cost-effective evaluation of the quality of the flocculant used.
1. Introduction
The sustainability of the mining industry faces a challenging scenario for mineral processing, with low grade ore deposits, water scarcity and seawater as an alternative to freshwater. One of the operational priorities is to close the water cycle, a process that can be successful with proper management of the thickening stages. Generally, the concentration stages are carried out at alkaline pH, which means that both particles and flocculant molecules (such as hydrolyzed polyacrylamide) carry anionic charges. Although reagents may have a low affinity with the particles, it is sufficient to form porous aggregates with low density, which facilitate the transport of the thick pulp from the bottom of the thickener to the tailing dams. The fact that industrial water has some ionic charge can be beneficial. There is evidence in the literature that the presence of ions in the liquor is necessary for adequate flocculation, because ions allow the adsorption of polymeric molecules on the charged surfaces [1,2,3]. There is also evidence that flocculants may exhibit different behaviors when interacting in saline media. For example, studies have indicated that flocculated kaolinite shows decreasing sedimentation rates in environments with high salinity [4,5], while other studies show the opposite [6]. We recently demonstrated that the increase in salinity promotes the adsorption of polyelectrolytes on mineral surfaces but decreases the size of the polymer in solution, resulting in a competitive effect that can benefit or impair particle agglomeration. Thus, varied behaviors are expected [7,8].
There is great interest in studying flocculation from a microscopic level because the mechanisms involved during the aggregation of colloidal particles determine the efficiency of thickeners. Various particle characterization techniques are available, such as laser analysis, dynamic image analysis (DIA), and microscopy [9], however, the focused beam reflectance measurement (FBRM) has significant advantages for flocculation, since it can be used directly in feed slurries, allowing online monitoring of aggregate size without sampling and without dilution [10,11,12,13,14]. Through this technique, the effect of shear rate has been studied in several works [15,16,17,18]. In some cases, a maximum aggregate size is reached in a short time after the addition of the flocculant, but then fragmentation of the aggregates and polymer depletion occurs. Interestingly, the systems studied by He et al. [19] have shown that the maximum floc size is reached at low shear rate values and that any further increase in the intensity of the mixture leads to fragmentation.
Several researchers have described the kinetics of growth and fragmentation of aggregates using population balance models (PBM) [20,21,22] of a wide variety of systems, such as coagulation and flocculation [23], crystallization [24], reduction in mill size [25], and polymerization [26]. A century ago, Smoluchowski [27] was the first to formulate the PBM equations to describe the coalescence growth phenomena. Since then, this procedure has been the basis for describing new systems with mechanisms of aggregation of particles with increasingly richer physics, which has required modifications to the original equations.
Consideration of the fractal dimension as an indicator of the irregular structure of the aggregates has been key [20,28,29]. The fractal dimension has allowed describing the decrease in aggregate size over time due to restructuring mechanisms [30,31,32]. In all these cases, the fractal dimension increases while flocculation takes place. Recently, Jeldres et al. [33] showed that the fractal dimension of aggregates of flocculated mineral tailings in seawater decreases, while flocculation time and/or mixing intensity increase. These results are important because they define the mechanisms involved during the growth of aggregates, such as fragmentation, collision efficiency, permeability of structures [32,34] and flocculant depletion [21,35].
In this work, PBM is used to describe the flocculation kinetics of quartz-kaolinite tailing particles flocculated in seawater with a high-molecular-weight anionic polymer for a range of mixing intensities. The effect of the shear stress on the flocculation kinetics and on the aggregation and breakage rates of aggregates is analyzed. Optimum mixing conditions are determined to achieve the largest aggregate size. The structure of the aggregates during flocculation is described by a constant and time-dependent fractal dimension. Finally, an attempt is made to determine whether the representation of flocculation kinetics requires a constant average fractal dimension or a time-varying fractal dimension.
2. Model
The PBM equations used in this work were derived from from the work proposed by Spicer and Pratsinis [36] for particle grouping, which combines the discretization approach of Hounslow et al. [37] for aggregations and Kusters et al. [38] for breakage, in which the aggregate size distribution is discretized into a number of bins or channels according to a geometric progression of the volume distribution of the aggregates, that is, . The population balance equation is given by:
where is the number concentration of aggregates in bin . The first two term on the right-hand side of Equation (1) describe the formation of aggregates of size from smaller aggregates. The following two terms describe the loss of aggregates of size to greater aggregates. The fifth term on the right-hand side represents the loss of aggregates of size by fragmentation. The last term represents the gain of aggregates of size by fragmentation of larger aggregates. The superscript max1 and max2 stand for the maximum number of intervals used to represent the complete aggregate size spectrum by aggregation and fragmentation, respectively. Functions , and represent aggregation rate, fragmentation rate, and breakage distribution function of aggregates, respectively. All the functions in Equation (1) are empirical in origin and thus parameters involved need to be determined by solving Equation (1) against experimental data. The functions are described next.
2.1. Aggregation Kernel
The function is the aggregation kernel defined by the product between the collision frequency (β) and the capture efficiency (α):
Collision frequency
Fluid flow can penetrate and pass through particle aggregates [39], meaning that the genuine collision frequency is considerably lower than that predicted from rectilinear flow models. To incorporate permeability effects, we use a parameter called ‘fluid collection efficiency’ which is the ratio between flow passing through an aggregate and that approaching it (undisturbed). Veerapaeni and Wiesner [40] proposed the function in Equation (3) to account for the collision frequency which includes permeability and fractal dimension, as:
where and are the diameters of the aggregates of sizes and , respectively, is the mean value of shear rate, and is derived from the Brinkman extension to Darcy’s law in function of a dimensionless permeability , that is:
where is defined as and is the permeability, for which the expression from the Li and Logan [41] is used:
The porosity is related to fractal dimension () by the expression of Vainshtein et al. [42]:
where is a packing coefficient (generally assumed to be 0.65) and is the primary particle diameter; and are related by the expression by Mandelbrot [43]:
Collision efficiency
Several models allow estimating collision efficiency, depending on the type of aggregate and the additive used. In this work, the three-parameter expression of Vajihinejad and Soares [35] is used to capture the depletion of adsorbed high-molecular-weight polymer of the type used here and its rearrangement on the surface of the particles, that is:
where and are maximum and minimum collision efficiency, respectively, at steady state conditions and is a decay constant.
2.2. Breakage Kernel
The function in Equation (1) is the fragmentation rate and the function is the breakage distribution function; these two represent the breakage kernel. The term is difficult to predict since it has not been theorized; it is common to adjust it to size distribution data. For this work, a two-parameter power law function of the aggregate mass is used [44]:
where and are the fitted parameters.
For the breakage distribution function, a binary distribution without parameters is used:
2.3. Shear Rate
The shear rate required by the aggregation and breakage kernels is calculated from:
where is the average energy dissipation rate given by:
where is the impeller power number which for a plane disk with gentle agitation, as is our case, is 0.6 [45], is the rotation speed, and and are the diameter of the impeller and the working volume of the vessel, respectively. The density of the suspension is calculated from:
where is the mass solid fraction of the solution and and are the solid and water densities, respectively. Finally, the viscosity of the solution is measured.
2.4. PBM Solution
In this work, the PBM equation (Equation (1)) is used to describe the flocculation kinetics of synthetic copper tailings in seawater. A solver based on a numerical differentiation formula for stiff ODEs (ode23s) is used in MATLAB environment. The numerical solution requires parameters which are obtained by minimizing the objective function:
where is the experimental diameter of the aggregates and is the volume-weighted mean aggregate diameter from the model:
To solve Equation (14) the MATLAB function fminsearch is used; this function uses the Nelder–Mead direct search to find the minimum of an unconstrained multivariable function.
Two criteria validate the model fit and predictions, one is the coefficient of determination () that measures the closeness of the model values to the experimental values:
The other is the goodness of fit:
where std stands for the standard error calculated from:
where is the number of data values and is the number of parameters to be fitted. A of 90% or higher means that the proposed model is able to predict the flocculation kinetics [10]. Finally, conservation of the total volume of particles is verified after every integration to ensure that the simulations are maintaining the particle population.
3. Materials and Methods
3.1. Materials
Quartz particles with a density of 2.65 g/cm3 acquired from Donde Capo (Chilean Store, Santiago, Chile) were used, which were pulverised and screened with -#325 mesh. The SiO2 content, estimated by XRD analysis, was higher than 99 wt%. Kaolin particles were acquired from Ward’s Science (Rochester, NY 14586, Rochester, United States), and the XRD analysis indicated 84% kaolinite and 16% halloysite. Seawater from the coast of Antofagasta (Chile) was provided by the Department of Marine Resources from the University of Antofagasta and subsequently filtered by UV for the removal of microorganisms. The ionic composition was determined with varied chemical methods depending on the ion type. By atomic absorption spectrometry: Na+ 10.5 g/L, Mg2+ 1.42 g/L, Ca2+ 0.38 g/L, K+ 0.40 g/L. The composition of Cl− was determined by argentometric method and was 19.1 g/L. The concentration of HCO3− was determined by acid–base volumetry to be 0.17 mg/L. NaOH was used as a pH modifier; anionic SNF704 and high molecular weight were used as a flocculant.
3.2. Flocculation Kinetics
A suspension of 270 g was prepared, considering a total solids content of 8 wt%, corresponding to a mixture of 80 wt% quartz and 20 wt% kaolin. The slurry was vigorously mixed for 30 min using a 30 mm diameter turbine-type stirrer, placed in the axial position, in a 1 L capacity, 100 mm diameter vessel. The stirrer was placed 20 mm above the vessel bottom. Subsequently, the mixing rate was reduced to 250 rpm, and an established volume of a solution (seawater and polymer) was added, at a proportion fixed by the required polymer dosage. The size distribution was traced using the FBRM technique, which consists of a sensor that measures reflection pulses of a laser beam on suspended particles in the range of 0.25–1000 μm. The main advantage of this technique is that the data is collected in-situ and in real-time; therefore, it does not require sampling or isolation that could contribute to changes in the size and distribution of aggregates by the eventual breakage or agglomeration. The FBRM probe was submerged vertically in the reaction vessel, 10 mm over the stirrer and 20 mm off-axis. The measurement began by tracking the primary particles of the tailings, and after 1 min, the flocculant was added with subsequent growth and destruction of aggregates for 3 min. The flocculation assays where done at pH 8, under ambient temperature and different mixing intensities.
3.3. Viscosity
The calculation of the shear rate requires the viscosity of the slurry. For this, a flocculation process was carried out with the methodology defined in Section 3.2. Subsequently, an aliquot of 56 mL was taken for rheological analysis. An Anton Paar MCR 102 rheometer with the RheoCompass Software was operated in controlled-rate mode, and a sandblasted #CC39 with bob-in-cup geometry was used to reduce wall slip effects. The gap generated between both concentric cylinders was 1.5 mm. Each sample remained for 15 min, ensuring that the rheological properties were obtained in steady state. The range of shear rate was preset between 10–300 s−1.
3.4. Sedimentation
After a pre-set flocculation period (10–80 s), the pulp was gently poured into closed cylinders of 300 cm3 (35 mm internal diameter) and then slowly inverted twice by hand (the whole cylinder rotation process took 4 s). After 10 min of settling, the supernatant fluid was rescued and stirred to homogenize the suspended solids. Then, a 50 mL aliquot was used for turbidity measurements in a Hanna HI98713 turbidimeter, which performed ten readings in 20 s, delivering the average of the point readings.
3.5. Conditions
Table 1 summarizes parameters and conditions used in this study. With these conditions, shear rate was calculated for all the cases, using Equations (11)–(13).

Table 1.
Input parameters and conditions.
4. Results
4.1. Initial Particle Size
Solving the PBM equations requires an initial particle number concentration for each size class and per unit of volume of suspension (), for that, a number distribution from experimental volume distribution is obtained from:
where is the experimental volume fraction of particles with diameter , obtained from Equation (7), and is the volume of the primary particles following the geometric progression . Figure 1 shows the normalized volume for synthetic tailings in seawater at pH 8. is obtained by interpolating the data in Figure 1 at the required values of . The initial distribution is sensitive to the shear rate, where the tendency is for the particles to aggregate as the intensity of mixing increases. The initial primary particle size is set to 5 µm, which is the mean minimal size with non-zero value in the distribution.
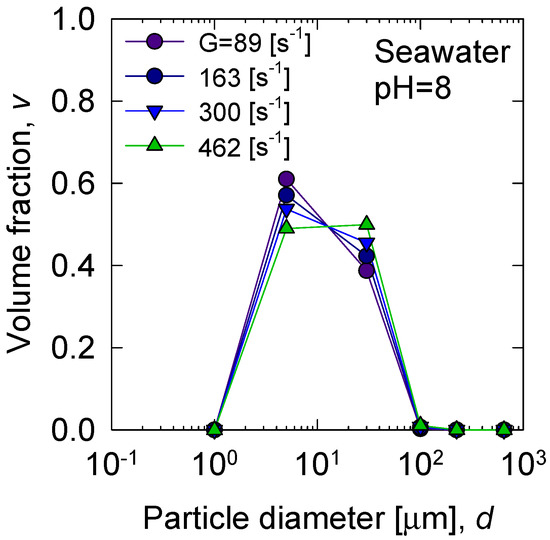
Figure 1.
Normalized initial volume distribution of particles of synthetic tailings in seawater at pH 8 for different mixing intensities (shear rate G).
4.2. Fractal Dimension
The fractal dimension defines the structure of the aggregates and appears in several equations describing particle agglomeration. In this study, the fractal dimension (Figure 2) is obtained from combined sedimentation tests with aggregate size measurements using the FBRM probe. The experimental data of hindered settling velocity, mean particle size, and mean aggregate size were used to extract the fractal dimension from the settling velocity model of Heath et al. [11]. In previous work, we found that the fractal dimension of particle tailing aggregates is very close to constant for low values of shear rate [46], in agreement with results from Heath et al. [15,21]. The results of Figure 2 confirm that, for low shear rate, the fractal dimension is a constant independent of flocculation time. However, when the shear rate values are high, the fractal dimension decreases monotonously over time, indicating that fragmentation of aggregates leads to lower-dimension Euclidean structures. In this work, the consequences of using constant fractal dimension in the determination of flocculation kinetics and aggregation and breakage functions for all flocculation conditions are analyzed. The results are compared with those obtained using fractal dimension as a function of time. Note that the constant fractal dimension is defined here as the average between the lowest and highest fractal dimensions for the same system and identical flocculation conditions.
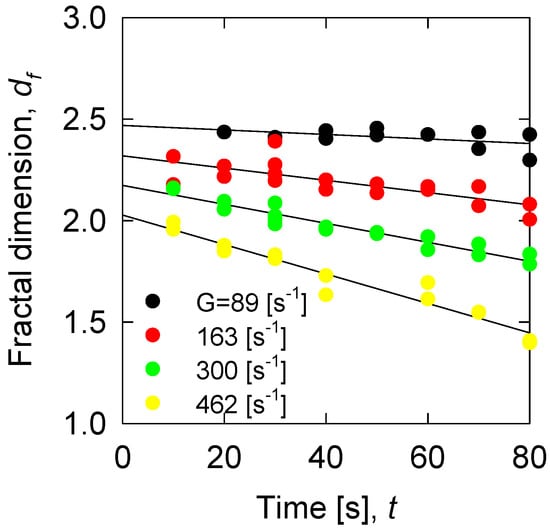
Figure 2.
Temporal evolution of the fractal dimension during flocculation of synthetic tailing particles in seawater at pH 8 as a function of shear stress (G).
4.3. Flocculation Kinetics Modelling
The flocculation kinetics of synthetic tailing particles in seawater are shown in Figure 3 as a function of shear stress. While the open circles correspond to experimental data, the solid lines correspond to the best fit with the PBM and the fractal dimension from Figure 2. Low shear requires a long time to give life to small aggregates, while high shear in a short time leads approximately to the same small aggregates; in the first case collisions and captures are unimportant, while in the second case the ruptures are important. There is clearly a mixing intensity that maximizes the size of the aggregates; however, the necessary flocculation time is critical because it defines the utility or lack of utility of the chosen flocculant. In the case of synthetic tailing particles in seawater with the flocculant chosen in this work, the optimum size of the aggregates is ca. 225 µm when the shear rate is 163 s−1. The PBM captures all the complex stages of particle flocculation, that is, initial growth of aggregates by particle bridging and subsequent size reduction as a result of fragmentation.
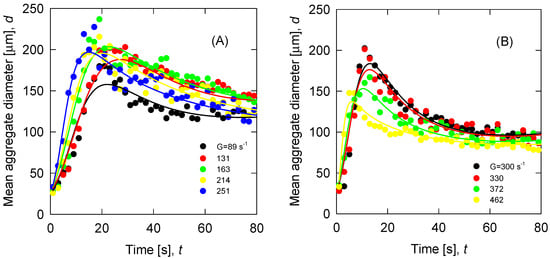
Figure 3.
Flocculation kinetics of synthetic tailing particles in seawater at pH 8 as a function of shear stress (G). Open circles correspond to experimental data and solid lines to the best fit with the population balance model (PBM). (A): Shear rate range from 89–251 s−1. (B): Shear rate range from 300–462 s−1.
Figure 3 shows qualitatively that the model correctly describes the experimental data for all mixing intensities. The quantitative results of GoF and R2 summarized in Table 2 show that the quality of the PBM is very good in all the cases analyzed and that the effect of representing the fractal dimension of the aggregates as a constant independent of the flocculation time is a correct decision, at least to represent the flocculation kinetics.

Table 2.
Quantitative results of GoF and R2 when the PBM is used with constant fractal dimension ( mean) or variable ( var) fractal dimension dependent on flocculation time.
4.4. Aggregation, Breakage, and Permeability Modelling
The aggregation, rupture, and permeability functions of particle aggregates are the building blocks to describe the flocculation kinetics, in the present case of synthetic tailing particles. Therefore, it is of great interest to evaluate the quality of the PBM representation of these functions when using the fractal dimension of the aggregates as a constant or variable dependent on the flocculation time. Figure 4 summarizes the four results.
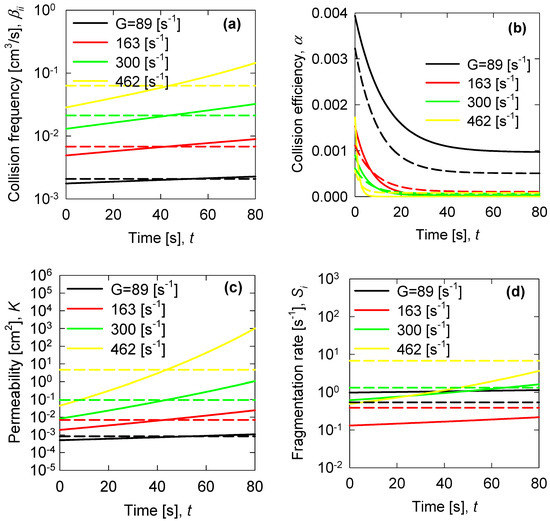
Figure 4.
PBM representation of collision frequency (a), collision efficiency (b), aggregate permeability (c) and fragmentation rate (d) for the largest aggregates considering constant fractal dimension of the aggregates (dashed lines) and time-dependent fractal dimension (solid lines) for different mixing intensities. Aggregate size range is 200–600 µm (bin i = 15).
As expected, the collision frequency increases and the collision efficiency decreases with mixing intensity (Figure 4a,b). The collision frequency remains constant when the fractal dimension is considered constant and grows over time when the fractal dimension is considered dependent on the flocculation time. The collision efficiency shows an exponential decay with flocculation time, at low shear rate the efficiency decreases rapidly when the fractal dimension is used as a function of time, and at high shear rate the collision efficiency is not so different if the fractal dimension is constant or variable. The results suggest that when aggregates are more porous and irregularly structured they are less likely to adhere once they collide.
The permeability of the aggregates increases with the intensity of the mixing and does so more strongly when the shear rate is very high. Permeability is constant when considering a constant fractal dimension and increases with flocculation time when considering a fractal dimension dependent on flocculation time. The product of the collision frequency and the collision efficiency is the aggregation rate; it is expected to be quite different when using constant or variable fractal dimension, however, to represent the optimal mixing (163 s−1) that leads to the larger aggregates (225 µm) the results of Figure 4a,b for collision frequency and collision efficiency, respectively, and the results of Figure 4c for aggregate permeability, suggest that there are no large differences if one or the other fractal dimension is used.
The fragmentation rate is not a monotonous function of the mixing intensity for both constant and variable fractal dimensions (Figure 4d). For low shear rate values, the rate decreases when the mixing intensity increases, and for high shear rate values, the rate increases with the mixing intensity. The fragmentation rate is constant when the constant fractal dimension is used and in general it is very different from the fragmentation rate obtained with a variable fractal dimension. Under optimal mixing conditions (163 s−1), the results of Figure 4c suggest that the fragmentation rate is better represented by the variable fractal dimension, the use of a constant fractal dimension can lead to significant deviations.
It is well known that compensations between aggregation and breakage rates lead to a very good representation of flocculation kinetics; the results in Figure 3 are a good demonstration. However, in addition, this study reveals that under optimal mixing conditions the representation of flocculation kinetics is equally good with a constant or variable fractal dimension.
4.5. Optimized Parameters
The optimization of the PBM model is performed against experimental flocculation data resulting in five parameters: the maximum and minimum collision efficiency (), the collision efficiency decay constant (), and two breakage rate kernel parameters ( and ). Of great interest is the effect of mixing intensity and the fractal dimension, constant or variable, on these parameters. The three parameters that describe the collision efficiency versus shear rate are presented in Figure 5, for the two conditions of fractal dimension. In general, and decrease with the shear rate, for the whole range of shear rate, except for at the lowest rate, and increases with the shear rate. The effect of the fractal dimension either constant or variable is small except at very high shear rate for and . is not affected by the choice of fractal dimension. For the optimal mixing conditions (163 s−1), the three parameters of the collision efficiency can be estimated considering a constant fractal dimension. Finally, the two parameters of the breakage rate (, ) change erratically with the shear rate but are not affected by the choice of the fractal dimension, whether constant or variable. For the optimal mixing conditions, the breakage rate parameters can be determined assuming a constant fractal dimension.
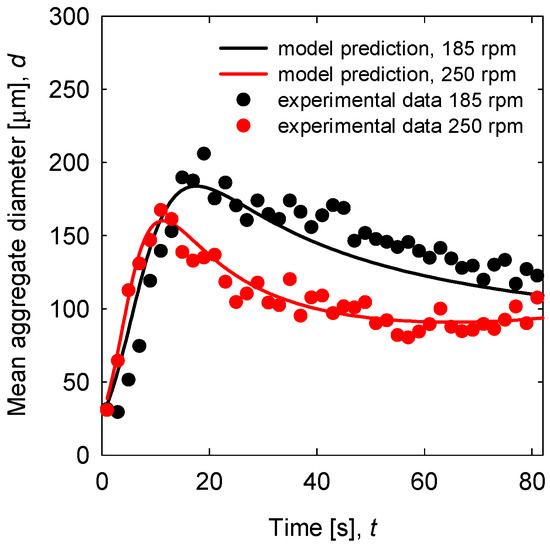
Figure 5.
Experimental (symbols) vs. calculated (continuous lines) time evolution of the mean diameter of aggregates of tailing particles as a function of pH in seawater. Constant pH condition at 8.
4.6. Prediction Capability
To test the predictive capacity of PBM with the parameters determined in the preceding sections, new experiments were carried out to determine the kinetics of flocculation of tailing particles in seawater at 185 and 250 rpm. Pulps with the same composition and percentage of solids were considered as in the trials in Section 4.3. The size of primary particles was again 5 µm. Also, the same flocculant and the same operating conditions were used, that is, temperature, flocculant dose, agitation time, and pH. Figure 5 shows the experimental and modeling results. The parameters for PBM were interpolated from Figure 2 for the fractal dimension, Figure 6 for the aggregation kernel and Figure 7 for the breakage rate for each pH. The adjustments are generally good, with GoF of 87.17 for 185 rpm and 92.02 for 250 rpm, which demonstrates the predictive capacity of PBM. Unlike what was found in our previous paper [46] where pH has little influence in kinetics, the shear rate has marked nonlinear dependence on the results of kinetics. Therefore, modeling was possible with good prediction for intervals of 30 s–1.
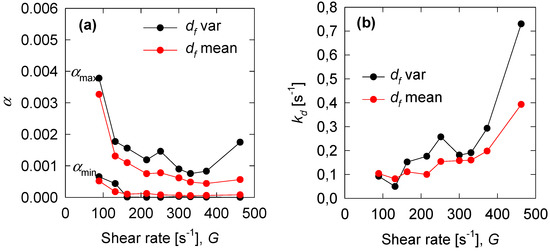
Figure 6.
Optimum aggregation parameters vs. shear rate for constant and variable fractal dimension, (a) maximum and minimum collision efficiencies and (b) collision efficiency decay constant .
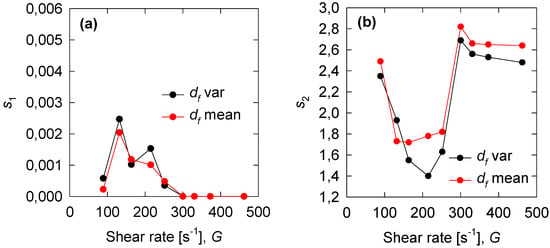
Figure 7.
Optimum breakage parameters vs. shear rate for constant and variable fractal dimension, (a) and (b) .
5. Conclusions
PBM equations were used to describe the aggregation kinetics of synthetic copper tailings in seawater with a high molecular weight polyacrylamide at pH 8 and a range of mixing intensities. It is common to consider that the fractal dimension of the aggregates is constant throughout the flocculation process, however in this work we found that when the mixing intensity is high, >100 s–1, the fractal dimension of the aggregates decreases monotonously over time, indicating that fragmentation of aggregates leads to lower-dimension Euclidean structures. This study revealed that compensations between aggregation and breakage rates lead to a very good representation of the flocculation kinetics of the particle tailings in seawater, and in addition, that the representation of flocculation kinetics under optimal conditions is equally good with a constant or variable fractal dimension. The mixing intensity of 163 s–1 was found to maximize the size of the tailing aggregates, that is, ca. 225 µm at ca. 20 s. The aggregation and breakage functions and corresponding parameters are sensitive to the choice of the fractal dimension of the aggregates, whether constant or time-dependent; however, under optimal conditions, a constant average of the fractal dimension is sufficient. The predictive capacity of the model can be used to find the optimal flocculation conditions based on a few experimental flocculation data at different mixing intensities, and the optimal flocculation time can be used to make decisions regarding the effectiveness of the flocculant used.
Author Contributions
G.R.Q. and W.H.L. contributed in research and wrote paper, N.T., P.R. and R.I.J. contributed in project administration, L.A. contributed resources and P.G.T. contributed in review and validation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Conicyt Fondecyt 11171036 and Centro CRHIAM Project ANID/FONDAP/15130015.
Acknowledgments
The authors thank Centro CRHIAM Project Conicyt/Fondap/15130015. RIJ thanks CONICYT Fondecyt 11171036. Pedro Robles thanks the Pontificia Universidad Católica de Valparaíso for the support provided.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Burlamacchi, L.; Ottaviani, M.F.; Ceresa, E.M.; Visca, M. Stability of colloidal TiO2 in the presence of polyelectrolytes and divalent metal ions. Colloids and Surfaces 1983, 7, 165–182. [Google Scholar] [CrossRef]
- Sommerauer, A.; Sussman, D.L.; Stumm, W. The role of complex formation in the flocculation of negatively charged sols with anionic polyelectrolytes. Kolloid-Zeitschrift Zeitschrift für Polym. 1968, 225, 147–154. [Google Scholar] [CrossRef]
- Nabzar, L.; Pefferkorn, E.; Varoqui, R. Polyacrylamide-sodium kaolinite interactions: Flocculation behavior of polymer clay suspensions. J. Colloid Interface Sci. 1984, 102, 380–388. [Google Scholar] [CrossRef]
- Peng, F.F.; Di, P. Effect of multivalent salts-calcium and aluminum on the flocculation of kaolin suspension with anionic polyacrylamide. J. Colloid Interface Sci. 1994, 164, 229–237. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, L.; Yan, B.; Xu, H.; Liu, Q.; Zeng, H. Molecular and surface interactions between polymer flocculant chitosan- g -polyacrylamide and kaolinite particles: Impact of salinity. J. Phys. Chem. C 2015, 119, 7327–7339. [Google Scholar] [CrossRef]
- Ji, Y.; Lu, Q.; Liu, Q.; Zeng, H. Effect of solution salinity on settling of mineral tailings by polymer flocculants. Colloids Surfaces A Physicochem. Eng. Asp. 2013, 430, 29–38. [Google Scholar] [CrossRef]
- Jeldres, R.I.; Piceros, E.C.; Leiva, W.H.; Toledo, P.G.; Herrera, N. Viscoelasticity and yielding properties of flocculated kaolinite sediments in saline water. Colloids Surfaces A Physicochem. Eng. Asp. 2017, 529, 1009–1015. [Google Scholar] [CrossRef]
- Quezada, G.R.; Jeldres, R.I.; Fawell, P.D.; Toledo, P.G. Use of molecular dynamics to study the conformation of an anionic polyelectrolyte in saline medium and its adsorption on a quartz surface. Miner. Eng. 2018, 129. [Google Scholar] [CrossRef]
- Liang, L.; Peng, Y.; Tan, J.; Xie, G. A review of the modern characterization techniques for flocs in mineral processing. Miner. Eng. 2015, 84, 130–144. [Google Scholar] [CrossRef]
- Biggs, C.A.; Lant, P.A. Activated sludge flocculation: On-line determination of floc size and the effect of shear. Water Res. 2000. [Google Scholar] [CrossRef]
- Heath, A.R.; Bahri, P.A.; Fawell, P.D.; Farrow, J.B. Polymer flocculation of calcite: Relating the aggregate size to the settling rate. AIChE J. 2006, 52, 1987–1994. [Google Scholar] [CrossRef]
- Gregory, J. Monitoring particle aggregation processes. Adv. Colloid Interface Sci. 2009, 147–148, 109–123. [Google Scholar] [CrossRef]
- Meng, Z.; Hashmi, S.M.; Elimelech, M. Aggregation rate and fractal dimension of fullerene nanoparticles via simultaneous multiangle static and dynamic light scattering measurement. J. Colloid Interface Sci. 2013, 392, 27–33. [Google Scholar] [CrossRef]
- Rong, H.; Gao, B.; Li, J.; Zhang, B.; Sun, S.; Wang, Y.; Yue, Q.; Li, Q. Floc characterization and membrane fouling of polyferric–polymer dual/composite coagulants in coagulation/ultrafiltration hybrid process. J. Colloid Interface Sci. 2013, 412, 39–45. [Google Scholar] [CrossRef]
- Heath, A.R.; Bahri, P.A.; Fawell, P.D.; Farrow, J.B. Polymer flocculation of calcite: Experimental results from turbulent pipe flow. AIChE J. 2006, 52, 1284–1293. [Google Scholar] [CrossRef]
- Owen, A.T.; Fawell, P.D.; Swift, J.D.; Labbett, D.M.; Benn, F.A.; Farrow, J.B. Using turbulent pipe flow to study the factors affecting polymer-bridging flocculation of mineral systems. Int. J. Miner. Process. 2008, 87, 90–99. [Google Scholar] [CrossRef]
- Bubakova, P.; Pivokonsky, M.; Filip, P. Effect of shear rate on aggregate size and structure in the process of aggregation and at steady state. Powder Technol. 2013, 235, 540–549. [Google Scholar] [CrossRef]
- Benn, F.A.; Fawell, P.D.; Halewood, J.; Austin, P.J.; Costine, A.D.; Jones, W.G.; Francis, N.S.; Druett, D.C.; Lester, D. Sedimentation and consolidation of different density aggregates formed by polymer-bridging flocculation. Chem. Eng. Sci. 2018, 184, 111–125. [Google Scholar] [CrossRef]
- He, W.; Nan, J.; Li, H.; Li, S. Characteristic analysis on temporal evolution of floc size and structure in low-shear flow. Water Res. 2012, 46, 509–520. [Google Scholar] [CrossRef]
- Thomas, D.N.; Judd, S.J.; Fawcett, N. Flocculation modelling: a review. Water Res. 1999, 33, 1579–1592. [Google Scholar] [CrossRef]
- Heath, A.R.; Bahri, P.A.; Fawell, P.D.; Farrow, J.B. Polymer flocculation of calcite: Population balance model. AIChE J. 2006, 52, 1641–1653. [Google Scholar] [CrossRef]
- Jeldres, R.I.; Fawell, P.D.; Florio, B.J. Population balance modelling to describe the particle aggregation process: A review. Powder Technol. 2018, 326, 190–207. [Google Scholar] [CrossRef]
- Runkana, V.; Somasundaran, P.; Kapur, P.C. A population balance model for flocculation of colloidal suspensions by polymer bridging. Chem. Eng. Sci. 2006, 61, 182–191. [Google Scholar] [CrossRef]
- Costa, C.B.B.; Maciel, M.R.W.; Filho, R.M. Considerations on the crystallization modeling: Population balance solution. Comput. Chem. Eng. 2007, 31, 206–218. [Google Scholar] [CrossRef]
- Datta, A.; Rajamani, R.K. A direct approach of modeling batch grinding in ball mills using population balance principles and impact energy distribution. Int. J. Miner. Process. 2002, 64, 181–200. [Google Scholar] [CrossRef]
- Kiparissides, C.; Alexopoulos, A.; Roussos, A.; Dompazis, G.; Kotoulas, C. Population balance modeling of particulate polymerization processes. Ind. Eng. Chem. Res. 2004, 43, 7290–7302. [Google Scholar] [CrossRef]
- Von Smoluchowski, M. Versuch einer mathematischen Theorie der Koagulations kinetik kolloider Lösungen. Zeitschrift fuer Phys. Chemie 1917, 129, 129–168. [Google Scholar]
- Flesch, J.C.; Spicer, P.T.; Pratsinis, S.E. Laminar and turbulent shear-induced flocculation of fractal aggregates. AIChE J. 1999, 45, 1114–1124. [Google Scholar] [CrossRef]
- Filippov, A.V.; Zurita, M.; Rosner, D.E. Fractal-like aggregates: Relation between morphology and physical properties. J. Colloid Interface Sci. 2000, 229, 261–273. [Google Scholar] [CrossRef]
- Selomulya, C.; Bushell, G.; Amal, R.; Waite, T.D. Understanding the role of restructuring in flocculation: The application of a population balance model. Chem. Eng. Sci. 2003, 58, 327–338. [Google Scholar] [CrossRef]
- Antunes, E.; Garcia, F.A.P.; Ferreira, P.; Blanco, A.; Negro, C.; Rasteiro, M.G. Modelling PCC flocculation by bridging mechanism using population balances: Effect of polymer characteristics on flocculation. Chem. Eng. Sci. 2010, 65, 3798–3807. [Google Scholar] [CrossRef]
- Jeldres, R.I.; Concha, F.; Toledo, P.G. Population balance modelling of particle flocculation with attention to aggregate restructuring and permeability. Adv. Colloid Interface Sci. 2015, 224, 62–71. [Google Scholar] [CrossRef] [PubMed]
- Jeldres, M.; Piceros, E.C.; Toro, N.; Torres, D.; Robles, P.; Leiva, W.H.; Jeldres, R.I. Copper tailing flocculation in seawater: Relating the yield stress with fractal aggregates at varied mixing conditions. Metals (Basel). 2019, 9, 1295. [Google Scholar] [CrossRef]
- Ahmad, A.L.; Chong, M.F.; Bhatia, S. Population Balance Model (PBM) for flocculation process: Simulation and experimental studies of palm oil mill effluent (POME) pretreatment. Chem. Eng. J. 2008, 140, 86–100. [Google Scholar] [CrossRef]
- Vajihinejad, V.; Soares, J.B.P. Monitoring polymer flocculation in oil sands tailings: A population balance model approach. Chem. Eng. J. 2018, 346, 447–457. [Google Scholar] [CrossRef]
- Spicer, P.T.; Pratsinis, S.E. Shear-induced flocculation: The evolution of floc structure and the shape of the size distribution at steady state. Water Res. 1996, 30, 1049–1056. [Google Scholar] [CrossRef]
- Hounslow, M.J.; Ryall, R.L.; Marshall, V.R. A discretized population balance for nucleation, growth, and aggregation. AIChE J. 1988, 34, 1821–1832. [Google Scholar] [CrossRef]
- Kusters, K.A.; Pratsinis, S.E.; Thoma, S.G.; Smith, D.M. Ultrasonic fragmentation of agglomerate powders. Chem. Eng. Sci. 1993, 48, 4119–4127. [Google Scholar] [CrossRef]
- Thill, A.; Moustier, S.; Aziz, J.; Wiesner, M.R.; Bottero, J.Y. Flocs restructuring during aggregation: Experimental evidence and numerical simulation. J. Colloid Interface Sci. 2001, 243, 171–182. [Google Scholar] [CrossRef]
- Veerapaneni, S.; Wiesner, M.R. Hydrodynamics of fractal aggregates with radially varying permeability. J. Colloid Interface Sci. 1996, 177, 45–57. [Google Scholar] [CrossRef]
- Li, X.Y.; Logan, B.E. Permeability of fractal aggregates. Water Res. 2001. [Google Scholar] [CrossRef]
- Vainshtein, P.; Shapiro, M.; Gutfinger, C. Mobility of permeable aggregates: effects of shape and porosity. J. Aerosol Sci. 2004, 35, 383–404. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Self-affine fractals and fractal dimension. Phys. Scr. 1985, 32, 257–260. [Google Scholar] [CrossRef]
- Pandya, J.D.; Spielman, L.A. Floc breakage in agitated suspensions: Effect of agitation rate. Chem. Eng. Sci. 1983, 38, 1983–1992. [Google Scholar] [CrossRef]
- Pretorius, C.; Wicklein, E.; Rauch-Williams, T.; Samstag, R.; Sigmon, C. How oversized mixers became an industry standard. Proc. Water Environ. Fed. 2015, 11, 4379–4411. [Google Scholar] [CrossRef]
- Quezada, G.R.; Ramos, J.; Jeldres, R.I.; Robles, P.; Toledo, P.G. Analysis of the flocculation process of fine tailings particles in saltwater through a population balance model. Sep. Purif. Technol. 2019, 116319. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).