Abstract
Increasing quality demands of combustion engines require, amongst others, improvements of the engine’s acoustics and all (sub)components mounted to the latter. A significant impact to the audible tonal noise spectrum results from the vibratory motions of fast-rotating turbocharger rotor systems in multiple hydrodynamic bearings such as floating bearing rings. Particularly, the study of self-excited non-linear vibrations of the rotor-bearing systems is crucial for the understanding, prevention or reduction of the noise and, consequently, for a sustainable engine acoustics development. This work presents an efficient modeling approach for the investigation, optimization, and design improvement of complex turbocharger rotors in hydrodynamic journal bearings, including floating bearing rings with circular and non-circular bearing geometries. The capability of tonal non-synchronous vibration prevention using non-circular bearing shapes is demonstrated with dynamic run-up simulations of the presented model. These findings and the performance of our model are compared and validated with results of a classical Laval/Jeffcott rotor-bearing model and a specific turbocharger model found in the literature. It is shown that the presented simulation method yields fast and accurate results and furthermore, that non-circular bearing shapes are an effective measure to reduce or even prevent self-excited tonal noise.
1. Introduction
The recent development of combustion engines shows not only a clear trend towards “downsizing”, i.e., the reduction of quantity and/or volumetric size of the cylinders but also an increased demand of higher specific power of such new engines together with lower carbon dioxide emissions. These requirements may only be achieved by using highly efficient turbocharger systems.
In addition, the representative customer of the premium segment vehicle demands significantly higher expectations regarding vibration and acoustic comfort. Engine noises have been continuously reduced, such that the noise emitted by turbocharging systems has become a focus of the engine sound design. A special case of disturbing turbocharger noises are tonal noises which result from imbalance-excited or self-excited resonances of the rotor-bearing system. In [1] it was demonstrated how the subjective perception of tonal turbocharger noises can be assessed objectively.
Turbochargers are usually supported by hydrodynamic floating bearing rings, a bearing concept consisting of a freely rotating journal bearing bushing with separate oil films between the bushing and both the shaft and the center housing. Depending on the size and the load of the application other bearing concepts exist using a non-rotating bearing ring. These structures allow very high rotational speeds, but come with the challenge of acoustically perceivable self-excited shaft vibrations. Literature often refers to these vibrations as “oil whirl”, “constant tone” or “subsynchronous whining” [2,3,4,5,6,7].
A good understanding of the cause and impact of self-excited vibratory motions in exhaust gas turbocharger systems is crucial to enhance the comfort of premium segment vehicles. To understand the dynamics of complex turbocharger rotors, one possible approach is the study of reduced models such as the Laval/Jeffcott rotor. In an earlier publication [7], the self-excited shaft whirls of customized Laval/Jeffcott rotor simulation models were identified and a sensitivity study of rotor dimensions, bearing geometry and tribological properties was performed. Furthermore, it was shown that based on the Laval/Jeffcott rotor model, a system optimization can be conducted regarding reductions of self-excited shaft motion durations as well as displacement amplitudes. In the literature measures of how to reduce displacement amplitudes of plain hydrodynamic bearing self-excited vibrations can be found, however, the complete removal of the addressed vibrations of single and multiple bearing assemblies, including their modeling, is rarely covered. The stabilizing effect of asymmetrical or even non-circular bearing shapes is known in the literature, e.g., lemon bore bearings or tilting pad bearings [8,9], however, extended research and especially a validated and efficient simulation method of non-circular hydrodynamic journal bearings is hardly reported to the best of the authors’ knowledge. Using a complete turbocharger model, the present work shows the possibility of completely preventing self-excited motions using non-circular bearing designs. For comparison and model validation, the non-circular shape was introduced into the abovementioned customized Laval rotor and into a turbocharger model from the literature, [10]. Analyzed orbits and spectrograms of these models show detailed insights about the sensitivities of onset rotational speeds, durations, and frequency characteristics of self-excited motions. As the outlook, a detailed comparison of simulation results and advanced measurements of a turbocharger during run-ups on a component hot gas test rig are subject of ongoing and future work.
2. Modeling Methods
2.1. Rotordynamic Model for Efficient Run-Up Simulations in HOTINT
In the present work we utilize the simulation tool HOTINT (High Order Time Integration, [11]) which provides a versatile framework for the efficient numerical modeling and simulation of general flexible multibody systems, and furthermore, includes functionality for simulator coupling, visualization, post-processing, and optimization (for further information, see, for instance, [12]). HOTINT is available online (www.hotint.org) both as maintained freeware release and open source version.
Used as simulation tool for a broad range of applications in mechanics and mechatronics, as well as coupled multi-physics problems, HOTINT features a modular structure which allows for an efficient implementation of extensions and additional functionality. In the context of the present work, the software was extended by hydrodynamic bearing elements based on analytical models (short and long bearing theory) and a numerical solution of the Reynolds equation.
The rotordynamic models used in the present work were defined in terms of the HOTINT script language which allows for a fully parametrized and generic model setup. Further details on the general structure of multibody simulation models in HOTINT, the employed model components, and the hydrodynamic bearing modeling are presented in the following sections.
2.2. Element and Model Description
A turbocharger rotor system consists of several rotating and non-rotating parts. For the simulation of the vibratory motion of the turbocharger, however, the rotating shaft with turbine and compressor wheel as well as the radial bearing elements (here, hydrodynamic bearings) are the most important components. Other elements such as the thrust bearing, spacer elements, or turbocharger housing, are not modeled in the present investigations or accounted for in a reduced way. For instance, the thrust bearing and spacer are represented by effective shaft stiffnesses, but not modeled as separate parts. Axial thrust is not considered in the model. Regarding the bearings, since we are primarily interested in the radial movement of the shafts and the bearing rings (in case of floating bearing rings), only the radial hydrodynamic forces are taken into account. The axial motion is not considered (to be exact, kinematically constrained) in the present investigations, since the axial hydrodynamic bearing forces are negligible compared to the radial forces and the coupling between axial and the radial motion is assumed to be small due to the small tilt angles of the shaft. Note that, furthermore, no tilting motion of the floating rings is taken into account.
Figure 1 shows a sketch of the basic object structure in HOTINT. In general, a model is composed of a set of rigid or flexible bodies which may be independent of each other or linked together by means of some kind of connectors (kinematic constraints, contact, etc.). The bodies may be subject to external loads, and furthermore, so-called IO elements (Input-Output elements) may be used to implement control or dynamically modify model parameters during a simulation. The run-up profile, for instance, is implemented by a set of IO elements which compute the angular frequency according to a specified mathematical expression in dependency of time and prescribe the result by modifying the offset of a kinematic velocity constraint with respect to the corresponding degree of freedom of a beam element node. Finally, sensors are used to measure physical quantities such as (generalized) displacements, velocities, and forces which in turn may be used either for post-processing purposes or as input for IO elements.

Figure 1.
HOTINT object library.
The rotordynamic model employed in the present work relies on rotor beam elements based on a linear beam formulation, including the Rayleigh model to represent material damping [13], which are used to discretize the turbocharger’s shaft along its rotor axis combined with rigid disk elements which correctly represent gyroscopic effects (e.g., of the turbine or compressor wheel). The hydrodynamic bearings are implemented as special constraints which act on the respective nodes of the rotor beam elements. Further details on the implemented bearing formulation are given in Section 2.4. Imbalances can be modeled either by point masses connected to a local position on beam or disk elements, or by centrifugal forces , where denotes the k-th imbalance mass, the respective radial distance, and the rotor’s angular frequency.
2.3. Equations of Motion and Time Integration
The equations of motion for the considered rotordynamic system within the framework of multibody system dynamics may be written as:
where is the vector of generalized coordinates, denotes the mass matrix, is a matrix which includes both damping as well as the gyroscopic terms, is the stiffness matrix, and is a vector of (generalized) external forces which may depend on the generalized coordinates and velocities. denotes a set of algebraic equations which represent kinematic constraints, and is the corresponding vector of Lagrange multipliers.
The global system of Equations (1) is assembled from element-wise contributions. Each body contributes a mass matrix, flexible bodies additionally contribute an element-wise stiffness matrix, and damping and gyroscopic terms are accounted for in . Connector elements can either be described by algebraic equations and associated Lagrange multipliers, or, in terms of a Penalty formulation, included in the force vector . The latter is the case for the employed hydrodynamic bearing elements.
The integration of the above governing equations with respect to time is performed numerically in HOTINT by means of stable implicit integrators based on Lobatto-IIIA or Radau-IIA formulas [12,14]. The algebraic equations are typically reduced to index two (velocity-level) to enhance stability. Note that the efficient discretization of the rotor by means of beam elements and a fast implementation of the bearing elements within the discussed multibody dynamics framework (cf. also the following section) allow for efficient dynamic analyses of the non-linear rotor-bearing system. A typical computational effort for the simulation of a rotor run-up within 10 s of physical time, including the numerical solution of the Reynolds Equation (3) for each bearing, amounts to a few hours CPU time, which is still sufficient to reasonably conduct parameter studies.
To perform eigenvalue analyses, all algebraic constraints are replaced by stiff penalty constraints, such that no algebraic equations remain, and the system is linearized about a configuration which may either be its initial state or the current solution resulting from a dynamic simulation. In any case, the generalized eigenvalue problem
is solved, where denotes the -th eigenvector corresponding to the complex eigenvalue . Here, the imaginary part represents the eigenmode’s angular frequency, whereas a negative real part corresponds to its damping.
2.4. Hydrodynamic Bearing Elements with Finite Length and Non-Circular Geometry
The starting point for the analysis and modeling of hydrodynamic bearings with circular geometry without a tilt between shaft and shell is the Reynold’s equation for the hydrodynamic pressure field ,
where and denote the cirumferential and axial coordinate of the oil film, the oil film thickness, and the inner and outer bearing radius (i.e., the radius of shaft and shell), and the respective angular velocities, and the dynamic viscosity of the lubricant [15]. Here, the local oil film thickness only depends on and the relative position of the centers of shaft and shell. For the most general case, i.e., non-circular bearing shapes including axial and radial grooves, as well as a tilt of the shaft, Equation (3) is extended,
Now, the oil film thickness is a function of both coordinates and , as well as of the relative position and orientation between shaft and shell. Note that and here are functions of as well as the respective angular positions of shaft and shell and represent any general non-circular bearing geometry. Whereas Equation (3) can be simplified for the limit cases of infinitely short and long bearings and solved analytically (based on the short and long bearing theory, cf. [15] or [16]), the solution of (3) for finite-length bearings and of the generalized form (4) can only be obtained numerically.
In the present work, a finite differences scheme is used to discretize the governing equations. Depending on the dominance of the convective parts of Equation (4), i.e., the terms proportional to and , the scheme is switched from second-order central differences to a first-order upwind scheme (forward or backward differences) to preserve stability. Figure 2 shows a sketch of the computational domain with the regular finite difference grid of the , with and the bearing length . As to the boundary conditions of the differential equation, first of all, the periodic boundary conditions require , and specifically, , for the pressure field. Furthermore, the inlet pressure needs to be specified at the bearing’s ends, i.e., and , respectively, and can be additionally set on an oil inlet zone (cf. the orange area in the sketch in Figure 2 as well as Figure 3 for illustration). The additional inlet area does not need to conform to the underlying finite difference grid and is accounted for in a consistent way by adapted finite difference formulas in adjacent grid cells. For illustration of this approach, the second-order difference formulas used to approximate first and second derivatives with respect to in a grid point adjacent to a cell partly lying inside the inlet area (cut cell) are given by
or
respectively. Here, denotes the regular (equidistant) resolution of the finite difference grid (i.e., the cell size), and is the fraction of a cut cell (in the direction of that lies outside the inlet area. Similar expressions can be derived for first-order forward or backward finite difference formulas for the upwinding scheme. Finally, since no cavitation model is used in the present investigations, the pressure is cut off at in order to prevent the unphysical occurrence of negative pressure values. The transition to the zero-pressure cut-off is made smooth, i.e., no discontinuity in the pressure field nor its gradient occurs, which is consistent with the so-called Reynolds boundary condition [15].
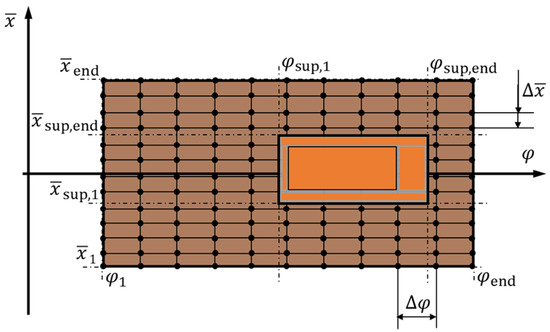
Figure 2.
Schematic of the computational domain of the pressure field . A rectangular zone for a pressure supply area is marked in orange.

Figure 3.
Computed pressure field of a generalized shaft model supported in hydrodynamic radial bearings including a pressure supply area. Screenshots at different instants of time during a run-up simulation.
The system of linear equations resulting from the finite difference discretization is finally solved by SOR (Successive Over Relaxation) Gauss-Seidel iterations for both a preconditioning phase as well as the actual solution phase [17], which yields the discrete pressure field at all points of the finite difference grid. See Figure 2 for the schematic of the computational domain and Figure 3 for the illustration of a computed pressure field with an oil inlet area.
Based on the pressure field , the velocity field , and subsequently, the hydrodynamic stress tensor
consisting of the pressure contribution and the viscous contribution can be computed (for further details on the relation between pressure and velocity field cf. again [15]).
Consequently, the bearing forces and moment about the rotor axis acting on the shaft and the corresponding counterforces and moments on the shell are given by integration over the bearing surface as
and
respectively, where denotes the surface normal, and the rotor axis is aligned with the x-direction of the coordinate system. The dominating contribution to the bearing force (8) originates from the pressure terms. Note that is always assumed as cylindrical bearing surface with a constant radius of and its axis aligned with the x-axis of the coordinate system. For circular geometries, is set to , in case of general bearing geometries, a reasonable value, e.g., the circumferential average of is chosen. The errors due to integration over that aligned cylindrical bearing surface instead of the actual surface, possibly with additional tilt between shaft and shell, are on the order , with the bearing clearance , and , and thus, usually negligible in agreement with the underlying assumptions for the Reynolds Equations (3) and (4). Only in the vicinity of grooves, the term may be large, which violates the above assumptions, yet introduces only local errors over a small range of .
The integrals (8) and (9) are finally evaluated numerically according to the discrete finite difference solution. The pressure contribution of the bearing force in (8), for instance, is approximated by
with and . The resulting forces and moments are applied to the corresponding bodies in the multibody system and accounted for in the non-linear force vector of the equation of motion (1). In case of full-floating bearing rings (without rotation constraints), where the floating ring is modeled as rigid body, the sum of the moments (9) from both the inner and outer oil film determines the ring speed about the rotor axis in the dynamic simulations.
2.5. Post Processing Methods
Post processing was done in Matlab 2015 [18]. For the computation of the spectrograms based on data of run-up simulations, a fast Fourier transform (FFT) time window with a length of was used, which was shifted from 0 to 10 s consecutively by a time span of . The FFT frequency resolution is determined by the FFT time window length as . The maximum analyzable frequency is given by the Nyquist criterion as the inverse of the time resolution (time step size) of the numerical solution data.
3. Results
This section shows results of simulated run-ups of three different rotor-bearing assembly models. Detailed descriptions of the model parameters are given in Appendix A.
3.1. Customized Laval/Jeffcott-Rotor in Plain Hydrodynamic Bearings
In [5], Schweizer presented a customized, extended version of the well-known Laval/Jeffcott-rotor [19], where the usually linear elastic and damped bearings were replaced by plain hydrodynamic bearings with circular geometry which introduce non-linear bearing forces. In this section such a rotor model is investigated using the simulation tool HOTINT [11]. In a first step, for model validation a comparison between the results of Schweizer and the HOTINT implementation is drawn for circular-shaped bearings. Then, the model is extended by non-circular journal bearings in order to study the potential of preventing self-excited vibrations. Figure 4 shows a sketch of the investigated rotor system.
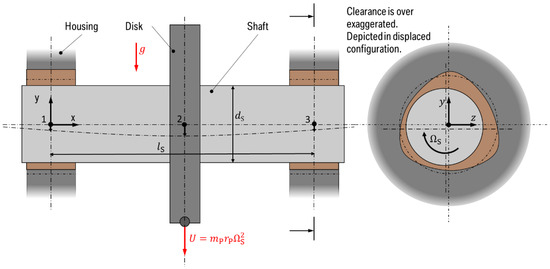
Figure 4.
Model of a customized Laval/Jeffcott rotor using single hydrodynamic bearings. The solid and dash-dotted contours in the cross-sectional view on the right hand side correspond to a non-circular and circular shaped bearing, respectively. Finite element nodes are numbered .
The simulated structure consists of an elastic Laval/Jeffcott rotor with a rigid disk mass centered on a massless shaft. Identical single hydrodynamic journal bearings on the left and right end support the assembly. A point mass is fixed to the disk at a given radial distance from the center of the shaft to account for the centrifugal imbalance force , where is the shaft’s rotational speed and is the time variable. To simulate a smooth run-up for and for is used.
Figure 5 shows a comparison of results for the Laval/Jeffcott rotor model using HOTINT and the solution presented by Schweizer [5]. The same parameter setup as in [5] was used, for details see the Appendix A. A spectrogram of the central node’s displacement (node 2), i.e., the disk displacement, is shown in Figure 5a. The abscissa corresponds to the vibration frequency, the ordinate depicts the time of the simulated run-up and the color displays the displacement value within one FFT-window. Clearly two kinds of displacements can be observed: () results from imbalance and () represents a self-excited, also called subsynchronous vibration, starting with , with an initial frequency of (). The frequency of this phenomenon varies only slightly during the run-up, which is why the acoustical effect of this motion is often called “constant tone” in technical literature [7,20,21,22,23,24,25,26,27,28]. However, the term might be misleading as the frequency is not exactly constant over time. Since the addressed vibration is a consequence of a resonant shaft displacement, in the present work we refer to it as shaft whirl instead. The onset of the self-excited motion occurs slightly earlier in the authors’ results than in the article by Schweizer. The difference can be accounted to of a cavitation model [29] in [5], which is not used in the HOTINT model. The difference in onset rotational speeds is also small.

Figure 5.
Comparison of results obtained with HOTINT and from [5]. (a) Displacement spectrogram of the central node in direction; (b) Vibration frequencies from the spectrograms in [5] (cf. again Figure 4 for node numbers). Vibrations () and () result from imbalance- and self-excitation, respectively.
Figure 6 shows results for shaft displacements at the central node (Figure 6a) and the bearing eccentricities (Figure 6b). Again, the agreement is satisfactory.
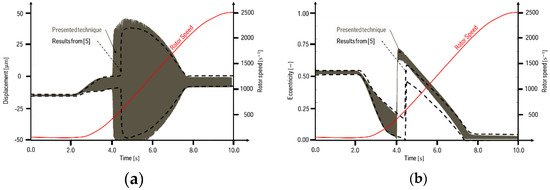
Figure 6.
Comparison of results obtained with HOTINT (brown) against reference data from [5] (black dashed lines show envelopes). (a) Displacements of the central shaft node in direction; (b) Bearing eccentricities in the nodes and (cf. again Figure 4 for node numbers).
The good agreement between the obtained results and the reference solution from literature with respect to frequency characteristics, displacement amplitudes, and bearing eccentricities confirms the validity of the implementation in HOTINT.
In view of practical applications, in some cases, self-excited motions of turbochargers can be audible and unwanted. Reduction methods mostly employ geometrical changes towards a certain asymmetry in the bearing design, which usually only results in a reduction of the amplitude or change of the onset speed of subsynchronous effects. In the following, we show that non-circular bearing shapes may allow a complete prevention of self-excited vibrations. To this end, a three-lobe sinusoidal clearance shape, as depicted in the cross-section in Figure 4, with a variation of 10% in the radial clearance with respect to the nominal clearance, , is used instead of the circular bearing geometry. This modification is sufficient to completely suppress the occurrence of self-excited motions as shown by the comparison of the results for circular vs. non-circular bearing geometries in Figure 7a,b. Further insights in the systems’ characteristics may be obtained by a linearized eigenvalue analysis. Figure 7c,d show the frequencies , of the lowest eigenmodes of a linearization of the system around a transient steady-state solution at a given constant rotational speed (see Equation (2)) for further details) after simulated time. Hence, we do not compute the linearization around a specifically chosen point. However, as can be seen in Figure 6 and Figure 8, before the onset of the self-excited vibration, the orbit radius is small, and beyond the onset, the orbits in the bearings are almost circular such that the self-excited forces dominate the dynamic behavior. Therefore, the exact choice of the point of linearization is not crucial. The corresponding modes are a shaft bending mode at an almost constant frequency of around , a cylindrical rigid-body whirl mode at half the current rotational frequency of the shaft (i.e., where the effective hydrodynamic velocity amounts to zero, cf., for instance, [5,15,16]), and two coupled modes. The lowest coupled mode, which starts at zero at a shaft frequency of and locks in the bending mode at higher shaft speeds, corresponds to the self-excited subsynchronous motion as shown in Figure 7a. In the linearized analysis, the other modes show stronger damping (negative real parts of the respective eigenvalues, cf. again Equation (2)) and thus are not excited during the dynamic run-up procedure. The lowest mode, in contrast, exhibits significantly smaller damping values and even instable behavior indicated by a positive real part of the complex eigenvalue in case of the circular bearing geometry, cf. Figure 7e. Note that the rotor speed at which this instability occurs at the first time corresponds well with the onset of the self-excited motion in the results of the run-up simulation in Figure 7a. From this perspective, the main effect of the non-circular bearing geometry can be described as a shift of the damping of the instable mode to the stable region, which is clearly visible in Figure 7e. The eigenfrequencies, in contrary, do not change significantly, cf. Figure 7c,d. Physically, the additional damping, and thus, increased stability of the bearings with non-circular geometry is related to an additional pressure build-up in the oil film. It should be noted that the linearized eigenvalue analysis may only give indications on the actual run-up dynamics, however, it does not fully resemble the non-linearity of the system. Particularly, it does not include information about the energy transfer to (or from) self-excited vibrations which are characterized by the interplay between the dissipation and excitation. Stable limit cycle oscillations are defined by the equilibrium between transferred and dissipated energy (see, e.g., [30]). Having a closer look at the comparison between Figure 7a,e again, as discussed above, the onset of the subsynchronous motion corresponds well with the point where the corresponding eigenmode of the linearized systems becomes unstable (i.e., exhibits a positive real part of the eigenvalue). With increasing rotor speed, the eigenmode becomes stable again (negative real parts of the eigenvalue), which corresponds to a stable limit cycle oscillation where the energy transfer to the mode is compensated by its damping. Starting with a rotor speed of around , however, the amplitude of the self-excited oscillation starts to decrease, despite a decrease, in some points even negative damping of the respective eigenmode. These results lead to the conclusion that, in that range of rotor speeds, the energy transfer to the self-excited vibration gradually vanishes.
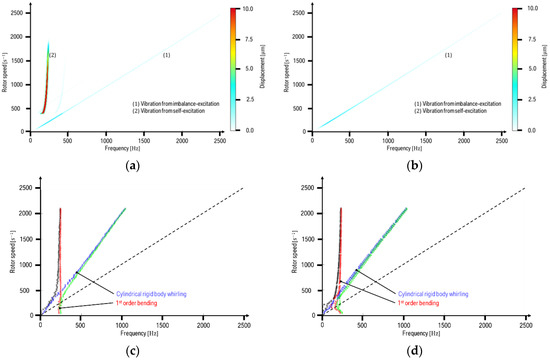

Figure 7.
Spectrograms of the bearing nodes’ (1 or 3 in Figure 4) -displacement of a run-up of a customized Laval/Jeffcott rotor in two identical single hydrodynamic bearings using (a) circular shaped and (b) non-circular shaped bearings; () and () indicate the imbalance-excited and the self-excited motions, respectively; (c,d) show the lowest four eigenfrequencies (first: black, second: blue, third: red, fourth: green) of the system linearized about a transient steady-state solution with a given constant rotational speed (see Equation (2)) for circular and non-circular bearing shapes; (e,f) show the damping parameter (again Equation (2)) of the first eigenmode (cf. black eigenfrequency in c,d)).
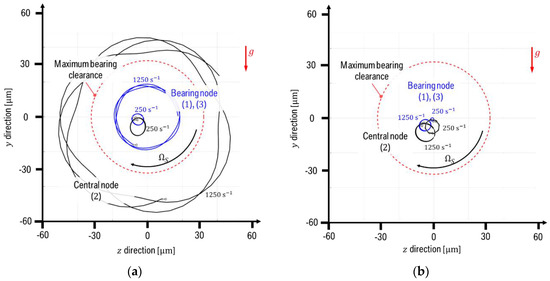
Figure 8.
Shaft motion at the central node (black, 2) and at the bearing nodes (blue, or ) during a run-up. The depicted orbits results from ten shaft revolutions at rotational speeds of and . (a) Circular bearing shape; (b) non-circular bearing shape.
In literature, the abrupt change of displacement or eccentricities at , c.f. Figure 6, is often described as a jump-like phenomenon of the shaft orbits to so-called limit cycles, see, e.g., [6,31,32,33]. Before the occurrence of the self-excited vibration, the shaft rotational axis performs small motions around a quasi-equilibrium state of the rotor at the particular rotational speed. At the disk and bearing node orbits jump to the their maximum displacements (limit cycle) as indicated in the spectrograms and move around the bearing with an orbital frequency of . The orbit sizes decrease for increasing shaft rotational speeds until the self-excited motion completely fades out. The shaft orbit within a circular-shaped bearing is depicted in Figure 8a demonstrating the sharp increase of the shaft displacements in the limit cycle beyond the onset speed. One orbit recirculation resulting from the self-excited vibration takes a time-period of and is modulated by the significantly smaller imbalance-excited motion with a period of .
Figure 8b shows the bearing node shaft orbits in the non-circular bearings described above for ten shaft revolutions at speeds of and in comparison with the maximum clearance in the bearings. The orbit size increases with rotational speed but is much smaller compared to a Laval/Jeffcott rotor with circular bearing shapes which illustrates the suppression of self-excited resonance phenomena.
To conclude, the validity of the employed simulation approach was shown by comparison with reference results from the literature. Furthermore, the potential of non-circularly shaped bearings for the prevention of self-excited shaft vibrations was investigated and demonstrated.
3.2. Reduced Turbocharger Model with Floating-Bearing Rings
This section shows results of numerical rotor run-ups of a reduced turbocharger model presented in [10]. There, simulated results for rotors with circular and lobe-shaped full-floating bearing rings are compared accordingly with experimental results from run-ups on a turbocharger balancing rig. Using the described validated simulation technique the reduced turbocharger model is reproduced and the results are compared with [10].
The reduced turbocharger model consists of two rigid disks representing the turbine and compressor wheel mounted to a rotating, elastic shaft modeled by twelve beam elements. Independently rotating floating rings support the structure at nodes and , see also the sketch of the cross-section in Figure 9. The floating ring’s inner and outer contours consist of six circumferentially in-phase sinusoidal lobes with an amplitude of 25% of the nominal radial clearance.
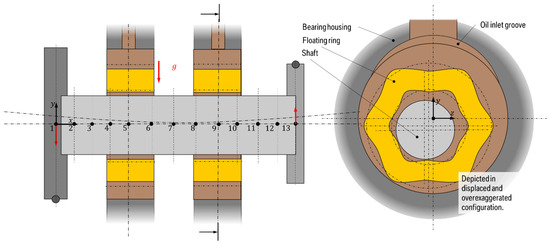
Figure 9.
Model of a reduced turbocharger model using floating bearing rings according to [10]. Finite element nodes are numbered - .
Imbalances with opposite orientation are added by mass points fixed to both disks. The oil inlets are represented as rectangular areas with constant oil pressure. For further details on the implementation and exact model data the reader is referred to Section 2 and Appendix A.
Unlike as in [10] the hydrodynamic pressure communication in the oil connecting channels of the floating rings is not considered in the HOTINT model. However, as it will be shown, the effects on the bearing ring speeds are small. In both studies some simplifications, such as neglected eddy flow within the oil connecting channels as well as the assumption of constant oil viscosities and bearing clearances during the run-up, are introduced.
Calculated displacements of the shaft in the turbine-sided bearing (node ) are depicted for the floating ring in Figure 10a and the relative displacement between shaft and ring in Figure 10b, respectively. Compared to the analysis of the shaft displacement only, which is commonly done in the literature, the investigation of the absolute difference between the -displacements of the floating ring and the shaft makes the difference between instabilities in the inner and outer oil film, here denoted as ring whirl and shaft whirl, more obvious. Shaft whirls can be observed in both spectrograms of and , whereas ring whirls only in the spectrogram. Note that in a spectrogram the ring whirl would be dominant, as discussed in the following. In general, corresponding displacements in Figure 10a,b indicate shaft whirls.
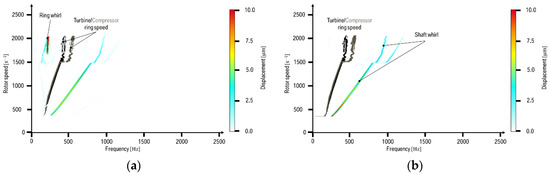
Figure 10.
Results from simulated run-ups using the reduced turbocharger model in full-floating bearing rings. (a) Spectrogram of the turbine side floating ring displacement in direction, ; (b) spectrogram of the shaft displacement in direction at the turbine side bearing node relative to the bearing ring displacement, ; The calculated turbine and compressor ring speeds are laid on top.
The shaft starts to perform a self-excited motion beneath the minimum rotor speed. After a bifurcation at a shaft rotational speed of an additional self-excited motion comes into play. The sharp increase of the compressor ring speed indicates that the bifurcation can be assigned to a shaft whirl at the compressor side. Conversely, a higher shaft eccentricity leads to an increased acceleration of the floating ring. At a shaft speed of the motion of the floating ring becomes resonant and a ring whirl occurs. Note that, since the floating rings carry the shaft, the ring whirl dominates the overall shaft motion (i.e., the displacement amplitudes).
The shaft whirl and the ring whirl become even more apparent in Figure 11 in the orbits of and of . From to (Figure 11a) both the bearing orbit and the relative shaft orbit are characterized by the shaft whirl. After the onset of the ring whirl the orbits are shaped by the resonant bearing displacements (Figure 11b). Both the bearing and the shaft displacements are now dominated by the ring whirl (blue solid line) such that the vector difference between the two is small (black solid line).
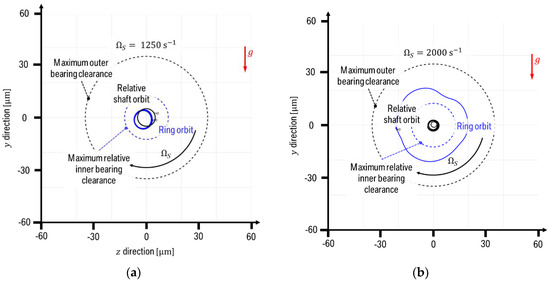
Figure 11.
Reduced turbocharger model with circular bearing shape. Maximum inner and outer clearance and turbine side bearing ring orbit and shaft orbits at the turbine bearing node at shaft rotational speeds of (a) ; (b) .
An introduction of a non-spherical bearing shape as depicted in the sketch of the cross-section of Figure 9 leads to a strikingly different characteristic of the shaft’s and bearing rings’ orbital motion. Figure 12 compares spectrograms of the vectorial sum of the bearing forces in the direction for the turbocharger model with circular vs. non-circular bearing shapes. Furthermore, a comparison with spectrograms of accelerations obtained from measurements of the real turbocharger mounted on a balancing machine [10] is given. However, since the transfer function between bearing forces and accelerations is unknown, only the frequencies and relative values of the traces have been extracted. Additionally, [10] neither gives details about the exact rotor or bearing geometry nor about the mounting on the balancing machine. The agreement between our simulation results and the measurement data can therefore be seen as satisfactory, particularly the bifurcation of the shaft whirl corresponds well. It should be noted that the comparison between the simulation results and the measurement data needs to be taken with care, since the model still contains simplifications (e.g., oil connecting channels in floating rings not modeled, constant temperature and viscosity assumed during run-up, housing and axial thrust not considered). Thus, the focus here is mainly on the correct representation of the qualitative dynamic behavior.
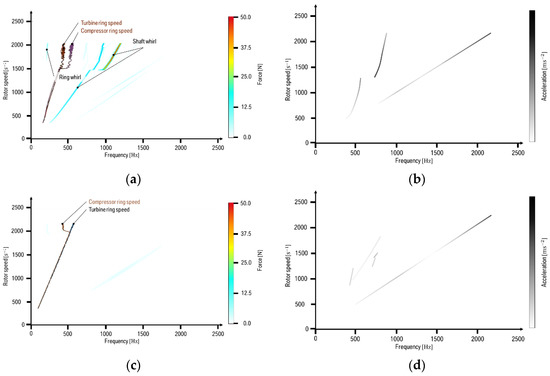
Figure 12.
Comparison of a reduced turbocharger model using floating bearing rings with (a) circular bearing shape from the present work; (b) circular bearing shape from data by Eling et al. [10]; (c) non-circular bearing shape from the present work; (d) non-circular bearing shape from data by Eling et al. [10].
The simulation of the turbocharger with non-circular bearings indicates that shaft whirls are no longer existent. The dominant ring whirl—with respect to the displacements—can be recognized by the deceleration of the turbine ring speed. It still occurs in case of non-circular bearings, however, the bifurcation and its onset shaft rotational speed is higher than in the turbocharger with circular shapes and its contribution to the bearing forces is small. A similar conclusion can be drawn from the experimental results of the balancing machine. Self-excited vibrations are still existent, but their acceleration amplitudes are minor and perhaps result from production imperfection.
Comparing the simulated displacement spectrograms, Figure 10a,b, with the acceleration spectrograms, Figure 12b,d, it should be noted that the highest displacement value, the ring whirl, is responsible for the large orbit motion, the largest force and acceleration amplitudes, however, are found in the shaft whirls. For this reason, the ring whirl is not visible in the measured sensor acceleration.
In conclusion, in the simulation models as well as in agreement with measurements, non-circular bearing shapes have again proven to be an effective measure to (fully) suppress self-excited vibrations.
4. Conclusions and Outlook
An earlier published efficient hydrodynamic and rotordynamic modeling technique was used for the investigation of self-excited vibratory shaft and bearing ring motions of Laval/Jeffcott and turbocharger rotors. A detailed study of academic and real rotordynamic structures, validated by comparison to results from literature, was performed with special focus on the impact of non-spherical bearing shapes onto the shaft motion and the resulting bearing forces during rotor run-ups. Non-spherical bearing shapes such as lobes around the bearing’s circumferential direction are shown to be promising as a means against self-excited shaft motions. In order to further qualify the simulation models as a tool for the early development stage of both Otto and Diesel combustion engines in parallel with their turbochargers, orbital measurements of shaft and bearing rings are important. A comparison of modeled and advanced measurement results is subject to future work—again with a focus on the effect and design of circular and non-circular bearing shapes (for a sketch see Figure 13, first simulation results are shown in Figure 14) with the perspective on the optimization of engine acoustics.
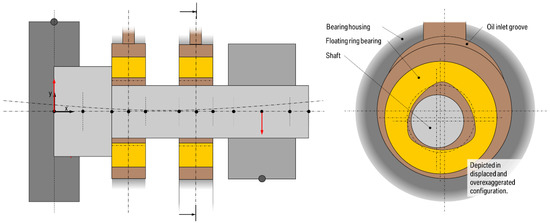
Figure 13.
Model of a turbocharger with floating-bearing rings. The sketch on the right-hand side shows a cross-section through a bearing which features an oil-inlet groove in the outer oil film and a non-circular geometry on the inside of the floating ring.
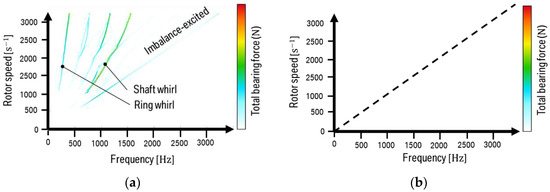
Figure 14.
Comparison of simulation results of a reduced turbocharger model using floating bearing rings with (a) circular inner bearing shape; (b) non-circular inner bearing shape.
Accelerations and kinematical data (e.g., floating ring motion and shaft orbits) will be obtained from experimental run-up studies with an advanced measurement setup on a turbocharger hot gas test rig. References [34,35] show that the influence of viscosity models can be large. In the future study, the effects of changing viscosity and clearance during the run-up will also be discussed.
The combination of validated simulation models and state-of-the-art measurement techniques will lead to detailed insights into the rotordynamic characteristics of the investigated turbocharger model specifically, and the effect of non-circular bearing designs in general. Moreover, well-known results from the literature, such as distinct mode shapes of ring and shaft whirl (often referred to as conical vs. cylindrical motions, see, e.g., [3,20,23,36,37,38,39]) will be studied based on measurement data.
Author Contributions
Markus Schörgenhumer and Lukas Bernhauser built-up the simulation models, conducted the simulations and wrote the paper; Martin Heinisch and Manfred Nader introduced useful information and discussions relevant for the article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Model Data of Customized Laval/Jeffcott-Rotor in Plain Hydrodynamic Bearings
The run-up simulation model in Section 3.1 consisted of a massless shaft with a shaft stiffness of (assuming steel as a material with a Young’s modulus of results in a rotor length of ) and an inner bearing radius of . The model does not take into account outer damping, . An imbalance of is attached to the central node between the bearings onto a stiff disk with . Also it has two bearings with a bearing length of , a relative bearing clearance of (absolute nominal clearance is ) and an oil viscosity of each.
Appendix A.2. Model Data of Turbocharger Model with Floating Bearing Rings
In accordance with [10], the reduced turbocharger model in HOTINT used for the studies in Section 3.2 is composed of the following components and parameters: The model consists of twelve linear beam elements representing the rotor and one rigid disk at the left and the right end of the structure in place of the turbine and the compressor wheel, respectively. The two times four beam elements between disk nodes and bearing nodes are equal in length, , as well as the four beam elements between the bearing nodes, . The shaft radius is common to all beam elements, , and the material is assumed as steel (Young’s modulus , Poisson ratio and density ).
The disk masses are and and their moments of inertia are set to and with respect to the rotation axis, and two orthogonal (radial) directions, respectively. Imbalance forces act onto the shaft using two mass points at each of the disk nodes showing in radial distance and in radial distance. As such, the imbalance vectors oppose each other.
The floating bearing rings are designed symmetrically such that the inner and outer bearing lengths are equal for compressor and turbine side, and . Radial clearances are and . The ring’s mass is and its moment of inertia, , is set to negligible values. The outer bearing diameter (bearing housing diameter) is .
For the consideration of a non-spherical bearing geometry, the inner ring radius follows .
The pressures at the axial boundaries of the hydrodynamic bearings is atmospheric pressure, .
The oil inlet is a rectangular domain on top of the outside hydrodynamic FDM grid with a constant (absolute) pressure, . It extends from to and from to (cf. again the sketch of the domains in Figure 4) symmetrically around the center of the outer bearings.
A small numerical damping of is added to both disks.
The run-up is done numerically using a penalty constraint for the shaft’s angular velocity with a stiffness of in order to prescribe the rotational speed between to according to the formula
The shaft’s and the ring’s axial motion is fixed at the first bearing node for numerical reasons. The tilting motion of the rings is also constrained.
Sensors measure the - and -displacement of the turbine node, the compressor node, the bearing nodes, and accordingly the displacements of both floating rings. For the floating rings an inner and an outer eccentricity is evaluated. The static and dynamic eccentricity gives rise to inner and outer bearing forces and inner and outer bearing torques, which are observed as well. The rotational speed is stored for the shaft and for each ring individually.
References
- Bernhauser, L.; Steinwender, L.; Irschik, H. Designing a Metric for the Customer Relevance of Synchronous Turbocharger Whistling in the Driver’ s Cabin. In Proceedings of the Inter-Noise 2016, Hamburg, Germany, 21–24 August 2016.
- Boyaci, A.; Lu, D.; Schweizer, B. Stability and bifurcation phenomena of Laval/Jeffcott rotors in semi-floating ring bearings. Nonlinear Dyn. 2015, 79, 1535–1561. [Google Scholar] [CrossRef]
- Nguyen-Schäfer, H. Rotordynamics of Automotive Turbochargers; Springer-Verlag: Berlin, Germany, 2012. [Google Scholar]
- Nguyen-Schäfer, H. Aero and Vibroacoustics of Automotive Turbochargers; Springer-Verlag: Berlin, Germany, 2013. [Google Scholar]
- Schweizer, B. Oil whirl, oil whip and whirl/whip synchronization occurring in rotor systems with full-floating ring bearings. Nonlinear Dyn. 2009, 57, 509–532. [Google Scholar] [CrossRef]
- Schweizer, B. Total instability of turbocharger rotors-Physical explanation of the dynamic failure of rotors with full-floating ring bearings. J. Sound Vib. 2009, 328, 156–190. [Google Scholar] [CrossRef]
- Bernhauser, L.; Steinwender, L.; Neumayer, R.; Schörgenhumer, M.; Nader, M. Efficient Transient Run-up Simulations for the Investigation of Acoustically Relevant Vibrations of Turbocharger Structures with Floating-Ring Bearings. In Proceedings of the DAGA 2016—Jahrestagung für Akustik, Aachen, Germany, 14–17 March 2016.
- Nishida, H.; Kamata, K.; Tomita, I.; Shiraishi, T.; Hayashi, N.; Ebisu, M.; Suzuki, H.; Ogita, H. Turbocharger and Method of Manufacturing Floating Bush. U.S. Patent 20140010647 A1, 9 January 2014. [Google Scholar]
- Aktiengesellschaft Kühnle, K. Lagerung eines Abgasturboladers. Patent DE3936069 A1, 2 May 1991. [Google Scholar]
- Eling, R.; van Ostayen, R.; Rixen, D. Multilobe Floating Ring Bearings for Automotive Turbochargers. In Proceedings of the 9th IFToMM International Conference on Rotor Dynamics, Mechanisms and Machine Science, Milan, Italy, 22–25 September 2014; Volume 21, pp. 1103–1113.
- Gerstmayr, J.; Al, E. HOTINT—A Script Language Based Framework for the Simulation of Multibody Dynamics Systems. In Proceedings of the ASME 2013 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference IDETC/CIE, Portland, OR, USA, 4–7 August 2013.
- Gerstmayr, J.; Stangl, M. High-Order Implicit Runge—Kutta Methods for Discontinuous Mechatronical Systems. In Proceedings of the 32nd Summer School APM, Saint Petersburg, Russia, 2004; pp. 1–13.
- Dresig, H.; Holzweißig, F. Maschinendynamik; Springer-Verlag: Berlin, Germany, 2016. [Google Scholar]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations I (II); Springer-Verlag: Berlin, Germany, 1991. [Google Scholar]
- Lang, R.; Steinhilper, W. Hydrodynamische Schmierung und hydrodynamische Lager. In Gleitlager. Berechnung und Konstruktion von Gleitlagern mit konstanter und Zeitlich Veränderlicher Belastung; Springer-Verlag: Berlin, Germany, 1978. [Google Scholar]
- Krämer, E. Dynamics of Rotors and Foundations; Springer-Verlag: Berlin, Germany, 1993. [Google Scholar]
- Meister, A. Numerik Linearer Gleichungssysteme; Vieweg + Teubner Verlag: Wiesbaden, Germany, 2008. [Google Scholar]
- The MathWorks Inc. MATLAB, version 8.6.0 (R2015b); The MathWorks Inc.: Natick, MA, USA, 2015. [Google Scholar]
- Jeffcott, H.H. The Lateral Vibration of Loaded Shafts in the Neighbourhood of a Whirling Speed—The Effect of Want of Balance. Philos. Mag. 1919, 37, 304–314. [Google Scholar] [CrossRef]
- Leonetti, M. Experimental investigation of operating parameters on constant-tone-noise of turbochargers. In Proceedings of the Internationales Stuttgarter Symposium 2016, Wiesbaden, Germany, 2016; pp. 687–705.
- Nguyen-Schäfer, H. Nonlinear Rotordynamic Computations of Automotive Turbochargers Using Rotating Floating Ring Bearings at High Rotor Speeds. In Proceedings of SIRM 2013—10th International Conference on Vibrations in Rotating Machines, Berlin, Germany, 25–27 February 2013.
- Koutsovasilis, P. Mode shape degeneration in linear rotor dynamics for turbocharger systems. Arch. Appl. Mech. 2017, 87, 575–592. [Google Scholar] [CrossRef]
- Koutsovasilis, P.; Driot, N. Turbocharger rotors with oil-film bearings: Sensitivity and optimization analysis in virtual prototyping. In Proceedings of the 11th International Conference on Vibrations in Rotating Machines, Wiesbaden, Germany, 23–25 Februray 2015.
- Deng, D.; Shi, F.; Begin, L.; Du, I. The Effect of Oil Debris in Turbocharger Journal Bearings on Subsynchronous NVH. SAE Tech. Pap. 2015. [Google Scholar] [CrossRef]
- Nowald, G.; Boyaci, A.; Schmoll, R.; Koutsovasilis, P.; Driot, N.; Schweizer, B. Influence of Circumferential Grooves on the Non-Linear Oscillations of Turbocharger Rotors in Floating Ring Bearings. In Proceedings of the 14th IFToMM World Congress, Taipei, Taiwan, 25–30 October 2015; pp. 1–8.
- Koutsovasilis, P.; Driot, N.; Lu, D.; Schweizer, B. Quantification of sub-synchronous vibrations for turbocharger rotors with full-floating ring bearings. Arch. Appl. Mech. 2015, 85, 481–502. [Google Scholar] [CrossRef]
- Leonetti, M.; Bargende, M.; Kreschel, M.; Meier, C.; Schulze, H. An Investigation of Sub-Synchronous Oscillations in Exhaust Gas Turbochargers. SAE Tech. Pap. 2015. [Google Scholar] [CrossRef]
- Nguyen-Schäfer, T.-H. Exhaust Gas Turbocharger with Plain Bearing for Reducing Fluid Turbulence. Patent EP 2576996 B1, 15 July 2015. [Google Scholar]
- Goenka, P.K. Dynamically Loaded Journal Bearings: Finite Element Method Analysis. J. Tribol. 1984, 106, 429. [Google Scholar] [CrossRef]
- Magnus, K.; Popp, K.; Walter, S. Schwingungen—Eine Einführung in die Physikalischen Grundlagen und die Theoretische Behandlung von Schwingungsproblemen; Vieweg + Teubner Verlag: Wiesbaden, Germany, 2008; Volume 8. [Google Scholar]
- Amamou, A.; Chouchane, M. Nonlinear stability analysis of long hydrodynamic journal bearings using numerical continuation. Mech. Mach. Theory 2014, 72, 17–24. [Google Scholar] [CrossRef]
- Boyaci, A.; Hetzler, H.; Seemann, W.; Proppe, C.; Wauer, J. Analytical bifurcation analysis of a rotor supported by floating ring bearings. Nonlinear Dyn. 2009, 57, 497–507. [Google Scholar] [CrossRef]
- Chouchane, M.; Amamou, A. Bifurcation of limit cycles in fluid film bearings. Int. J. Non Linear Mech. 2011, 46, 1258–1264. [Google Scholar] [CrossRef]
- Allmaiera, H.; Priestnera, C.; Reicha, F.M.; Priebscha, H.H.; Forstnerb, C.; Novotny-Farkasc, F. Predicting friction reliably and accurately in journal bearings—The importance of extensive oil-models. Tribol. Int. 2012, 48, 93–101. [Google Scholar] [CrossRef]
- Sander, D.E.; Allmaier, H.; Priebsch, H.H.; Reich, F.M.; Witt, M.; Füllenbach, T.; Skiadas, A.; Brouwer, L.; Schwarze, H. Impact of high pressure and shear thinning on journal bearing friction. Tribol. Int. 2015, 81, 29–37. [Google Scholar] [CrossRef]
- Fryščok, T.; Zatko, M. Subsynchronous frequency of a turbocharger rotor. J. Middle Eur. Constr. Des. Cars 2013, 11, 1–4. [Google Scholar] [CrossRef]
- Schweizer, B.; Sievert, M. Nonlinear oscillations of automotive turbocharger turbines. J. Sound Vib. 2009, 321, 955–975. [Google Scholar] [CrossRef]
- Alsaeed, A.A. A Study of Methods for Improving the Dynamic Stability of High-Speed Turbochargers. Ph.D. Thesis, Virginia Polytechnic and State University, Blacksburg, VA, USA, 2010. [Google Scholar]
- Boyaci, A.; Schweizer, B. Nonlinear oscillations of high-speed rotor systems in semi-floating ring bearings. In Proceedings of the 9th IFToMM International Conference on Rotor Dynamics, Milan, Italy, 22–25 September 2014; Volume 21, pp. 845–854.
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).