Abstract
This study presents multi-band photometric observations and detailed period analysis of a totally eclipsing binary system exhibiting low photometric amplitude. The system exhibits characteristic W Ursae Majoris (EW)-type light curves with complete eclipses. In our light curve modeling, we tested two setups: one excluding third light and the other including it as a free parameter (accounting for a potential tertiary component). Photometric analysis reveals that ASASSN-V J171815.10+450432.9 (hereafter J171815) represents a marginal contact binary system with an extreme mass ratio (the more massive component is designated as the primary star), approaching the theoretical lower limit for stable contact configurations. Furthermore, our investigation of orbital period variations uncovers a long-term period increase at a rate of , which is likely attributable to ongoing mass transfer between components. This interpretation aligns with the system’s geometric configuration and observed light curve asymmetries. The unique characteristics presented by this binary system serve as a rare opportunity for in-depth research on the mass ratio theory, and also provide an important opportunity for testing the Thermal Relaxation Oscillation (TRO) theory.
1. Introduction
Near-contact binaries (NCBs), defined by Shaw [1] as close binaries where at least one component approaches but does not fully fill its Roche lobe, exhibit diverse morphological states including marginal contact, semi-detached, and near-detached configurations [2], serving as critical transitional objects bridging detached and fully contact binaries. According to TRO theory [3,4], NCBs undergo cyclic oscillations between shallow contact (where stars have just begun sharing a common envelope) and semi-detached states, making them ideal for testing evolutionary mechanisms of over-contact binaries; however, their short evolutionary timescales [5,6] result in relative rarity, necessitating more observational data to constrain their physical properties. While TRO remains a fundamental framework, alternative mechanisms are increasingly recognized, including Angular Momentum Loss (AML) driving contact [7], mass ratio oscillations around critical values [8,9], and hierarchical fragmentation/magnetic braking in triple systems [10], with the near-contact stage interpreted differently across models (as a precursor to stable contact in AML scenarios, a transient phase in TRO cycles, or a post-contact configuration). Recent studies [11] further indicate that modern contact binaries likely originate from multiple evolutionary channels.
Prior theoretical investigations (e.g., [12,13]) established that tidal instability arises in close binaries when the system’s orbital angular momentum falls below three times the rotational angular momentum of the primary component (). Beyond this threshold, the breakdown of synchronized rotation initiates rapid orbital inspiral, ultimately leading to coalescence into a single object. This instability criterion for contact binaries aligns with the theoretically predicted minimum mass ratio , below which systems are predicted to undergo catastrophic orbital decay. However, because different studies employ different research methods, the proposed values for are different. For instance, Yang and Qian [14] statistically deduced that could be as low as 0.044. In contrast, Pešta and Pejcha [15] demonstrated that the value of is contingent upon the type of contact binary. Specifically, for late-type systems with orbital periods exceeding 0.3 days, is approximately 0.087; systems with shorter periods, conversely, exhibit a higher of around 0.246. Early - type contact binaries, on the other hand, display a lower , approximately 0.030. Recent comprehensive reviews by Arbutina and Wadhwa [16] and Wadhwa et al. [17] have thoroughly examined the critical mass ratio and orbital stability of low-q contact binaries. Detection of contact binary systems with observed q values below theoretical predictions poses a significant challenge to existing astrophysical models. Until now, only a few systems with have been identified, including TIC 55007847 (, Cheng et al. [18]), TYC 4002-2628-1 (, Guo et al. [19]), TYC 3801-1529-1 (, Li et al. [20]) and ASASSN-V J175200.35+361805.2 (, Guo et al. [21]). These ultra-low-q systems provide a unique perspective for observing stellar merger processes. To further expand the sample of such low-mass-ratio systems and deepen related studies, we have conducted a dedicated research program targeting the search for ultra-low mass ratio contact binaries [19,20,21,22,23]. Candidate systems from this program were selected from archival photometric data of large-scale sky surveys, such as Wide Angle Search for Planets (SuperWASP; Butters et al. [24]), Catalina Sky Survey (CSS; Drake et al. [25]), All-Sky Automated Survey for SuperNovae (ASAS-SN; Shappee et al. [26], Jayasinghe et al. [27]). In the selection process, we focused specifically on eclipsing binaries and applied two key criteria: complete eclipses (which allow for reliable determination of stellar parameters—such as the mass ratio—under the assumption of negligible third-light contamination) and light curve amplitudes < 0.3 mag (a well-recognized signature of low mass ratios). This targeted selection strategy is designed to efficiently identify potential low-mass ratio systems.
Based on the International Variable Star Index1, CSS-J171815.1+450432 (other names: ASASSN-V J171815.10+450432.9) was a newly discovered contact binary with a low amplitude (0.24 CV band) and a short period (0.317907d) by Drake et al. [25]. In this paper, photometric observations and their corresponding photometric solutions for the totally eclipsing binary J171815 are presented. Meanwhile, orbital period variations are also investigated, revealing a continuous period increase.
2. Observations and Data Reduction
2.1. Ground-Based Observation
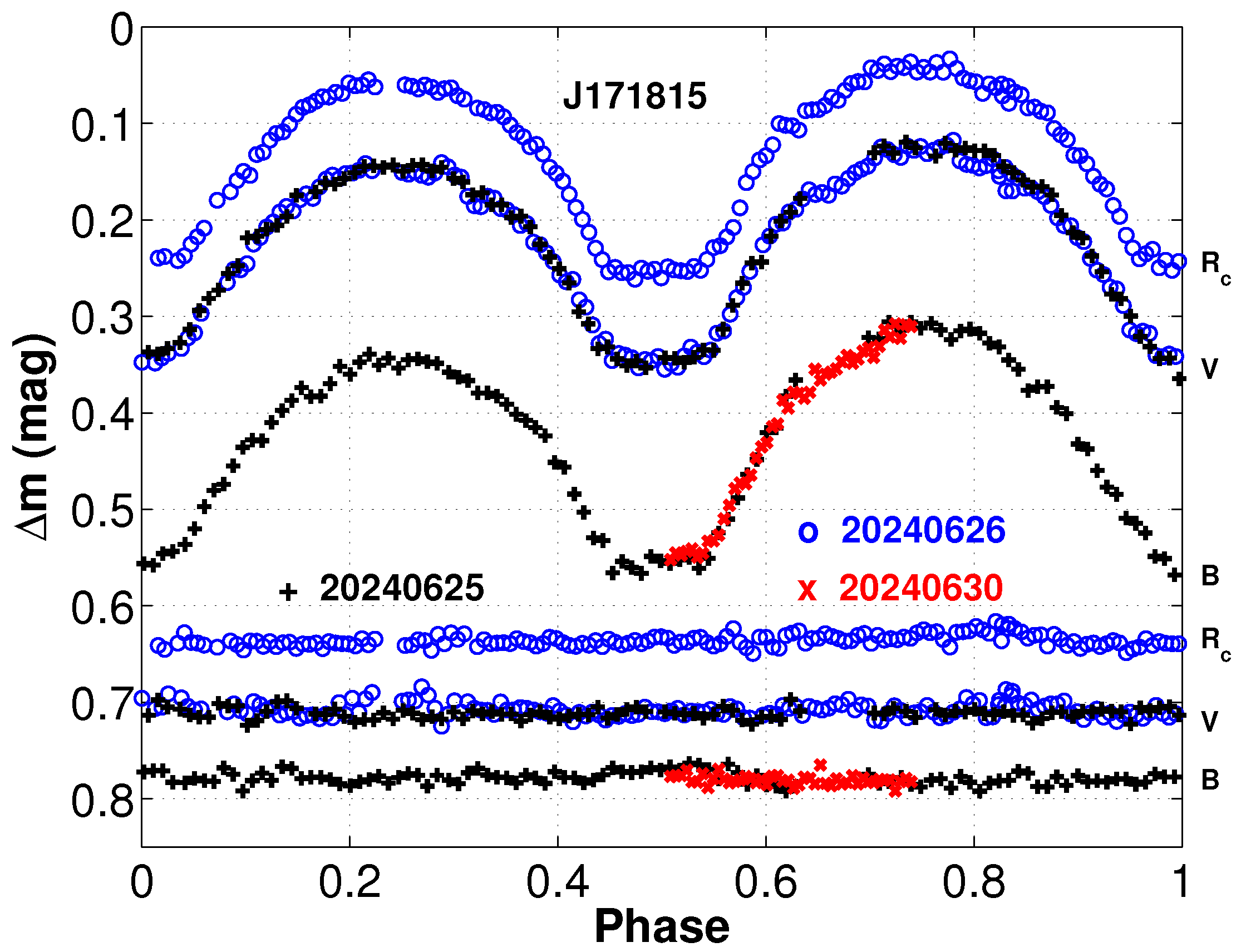
Multi-band photometric observations for the totally eclipsing binary J171815 were conducted using the newly installed 50 cm telescope located at Wendeng Biblical Mountain in Weihai (WH50, N, E). The observational system consists of a PlaneWave CDK20 telescope (f/6.8) coupled with a Dhyana 4040BSI sCMOS detector featuring square pixels. With an image scale of ∼ , the system provides a × field of view. Image acquisition was done with MaxIm DL. During the photometric observation, the standard Cousins filters () were employed. Bias, dark, and flat frames were obtained and used to calibrate the target images, with all data reduction carried out using the Image Reduction and Analysis Facility (IRAF) software package2. A completed band light curves () were obtained on 25, 26 and 30 June 2024. The typical exposure times for B, V and bands are 140 s, 90 s and 60 s, respectively. Differential photometry was performed using aperture techniques with carefully selected reference stars: the comparison star (; ) and check star (; ). The phase-folded light curves (Figure 1) were computed using the ephemeris: .
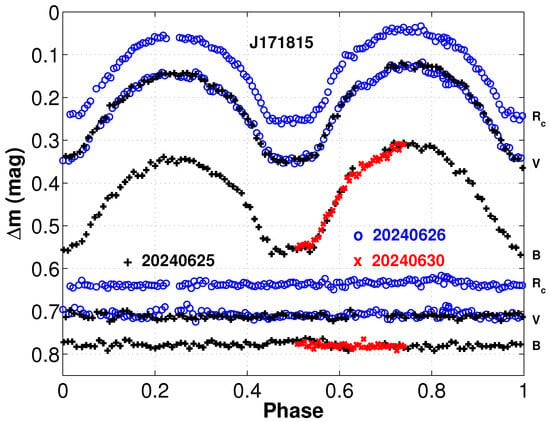
Figure 1.
BVRc light curves of J171815 observed by 50 cm telescope at Wendeng station of Weihai observatory.
2.2. TESS Observation
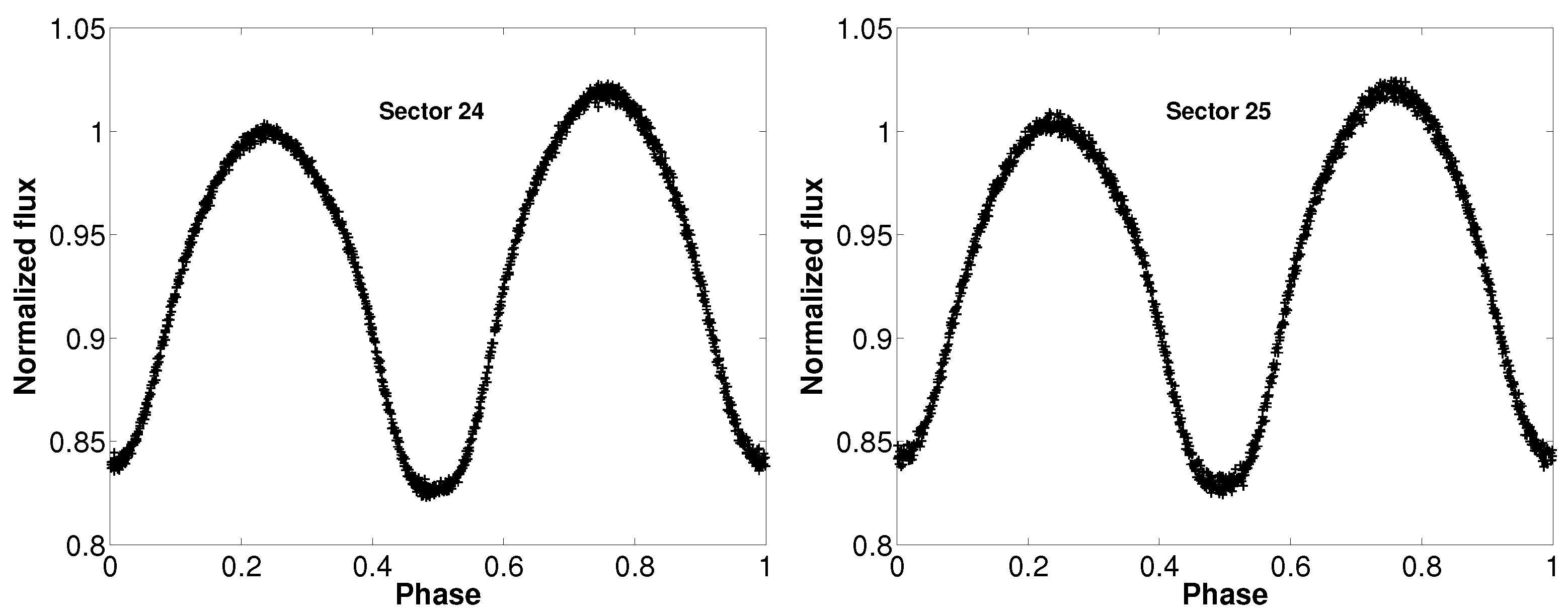
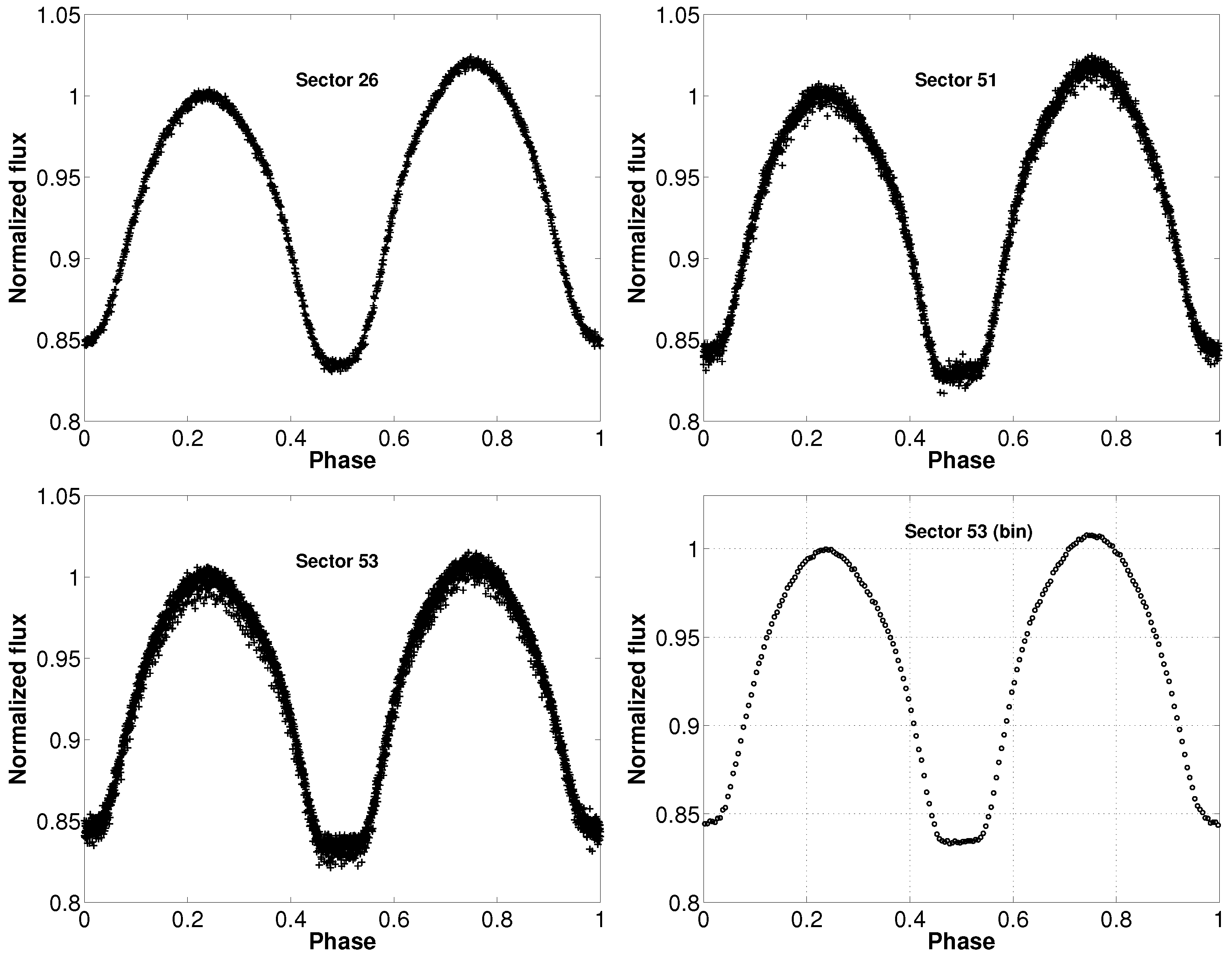
NASA’s Transiting Exoplanet Survey Satellite (TESS; [28]) provides continuous photometric observations, making it possible to conduct a detailed analysis of the light curve shapes of eclipsing binary systems. We found that J171815 was observed by TESS in Sectors 24, 25, 26 at 30-min cadence, while in sectors 51 and 53 at 10-min cadence. Then, we downloaded the relevant data from the Mikulski Archive for Space Telescopes (MAST)3. After acquiring the local minimum times and applying them to phase the light curves, we excluded data points with evident discrepancies in our analysis. Then, we normalized the light curves according to the values at phase 0.25. All phased light curves from TESS are illustrated in Figure 2. To better reveal the subtle features of the light curves, we selected Sector 53 (the highest-quality dataset among all sectors) and binned its observational data by phase, with the results presented in the last panel of the figure. As illustrated, the secondary minimum exhibits a distinct flat-bottom characteristic.
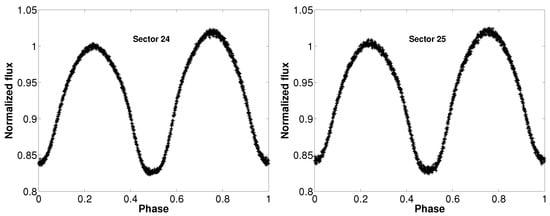
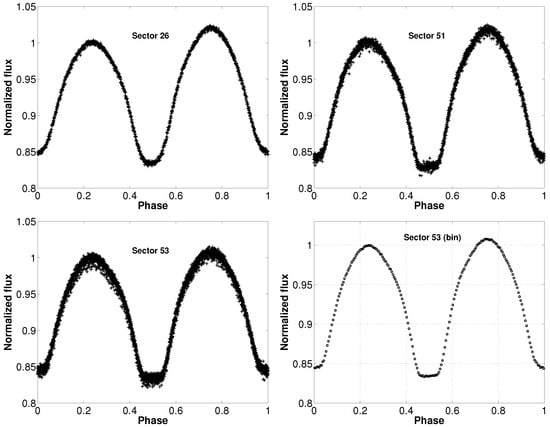
Figure 2.
The normalized TESS light curves observed of J171815 at different sectors.
3. Orbital Period Investigation
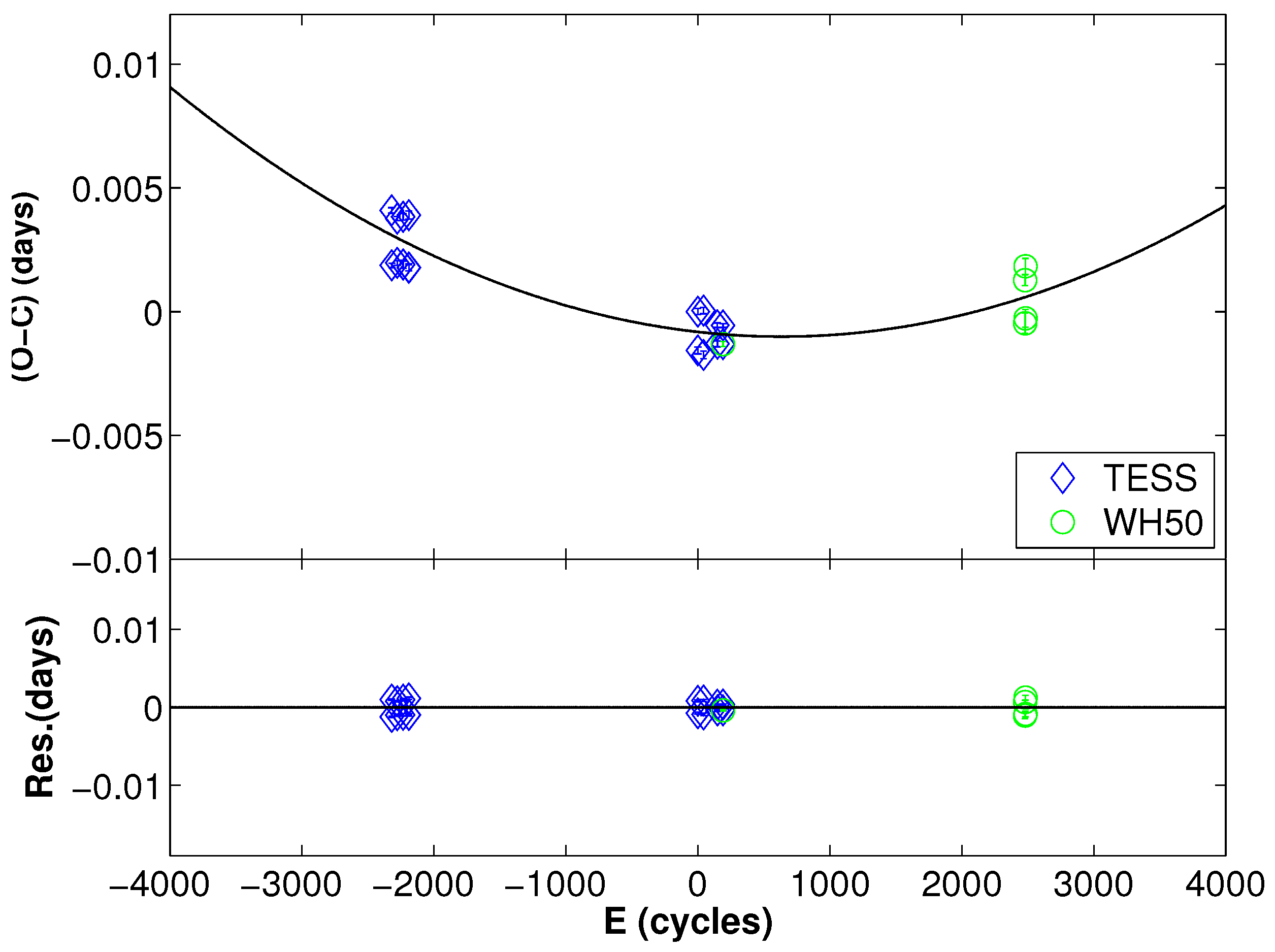
For the purpose of examining the orbital period’s variation, we adhered to the procedures described in [29,30,31] to calculate the minimum times of TESS data. As a result, 20 minimum times were obtained. Since the TESS data use the Barycentric Julian Date (BJD), we transformed the minimum times determined by our observations to BJD using online tools4 [32]. Through these efforts, we identified 24 eclipsing minima, which are listed in Table 1. Using the following equation:
the diagrams of are obtained and displayed in Figure 3. The diagram of illustrates an upward parabolic change. By using the least square method to fit the curve, we derived the following ephemeris formula:

Table 1.
CCD times of light minimum for J171815.
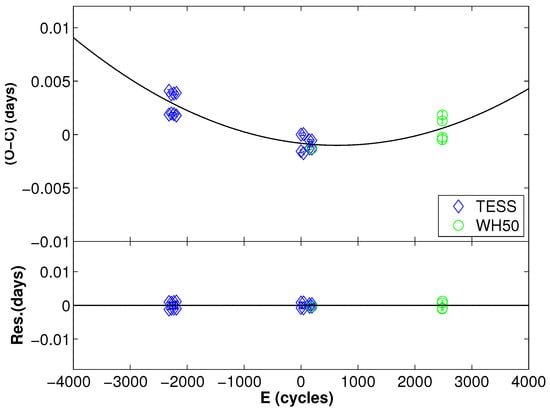
Figure 3.
O-C diagram of J171815. Different symbols refer to different observations.
According to Equation (2), the residuals are calculated and displayed at the bottom of Figure 3. The increase in the secular period of Equation (2) is calculated to be . Considering the short timescale and the limited observational data available for J171815, the observed long-term orbital trend may represent only a portion of the actual orbital period variation. Therefore, additional observations are required to confirm and further understand these findings.
4. Photometric Solutions
We employed the Wilson-Devinney (W-D) code [33,34,35,36,37,38] to obtain photometric solutions for the binary system. A pivotal step in deriving the photometric parameters of the binary system was determining the effective temperatures, as accurate temperature values are essential for reliable modeling. Using data from the Gaia mission [39,40], we calculated the effective temperature to be 5495 K. As reported by Andrae et al. [41], Gaia-derived effective temperatures within the 3000–10,000 K range are typically associated with uncertainties of approximately 324 K.
Notably, the light curves of J171815 display extremely low amplitudes, suggesting that the primary component predominantly contributes to the system’s overall luminosity. Consequently, we adopted the effective temperatures obtained from the Gaia mission as the effective temperature for the primary component. In accordance with the guidelines proposed by Lucy [42] and Ruciński [43], we set the bolometric albedo coefficients and gravity darkening coefficients for both components. The bolometric albedo coefficients were assigned as , while the gravity darkening coefficients were set to .
The light curves of the target exhibit small amplitudes, suggesting an extremely low mass ratio. This presents a considerable challenge in directly measuring the mass ratio from radial velocity (RV) observations. However, the presence of total eclipses in the system supports the reliability of the photometric solution obtained with the W–D code under the assumption of negligible third light, as corroborated by earlier studies [44,45]. Given that the target displays typical EW-type light curves, we initially adopted mode 3 for the photometric analysis, which is suitable for overcontact binary systems. To estimate the initial mass ratio, we applied the q-search method, beginning with a sequence of trial mass ratios starting at 0.06. For each tested mass ratio, parameters including the surface potential (Ω), orbital inclination (i), secondary component temperature (), and the luminosity of the primary component () were allowed to vary. Light curve models were generated for each q and compared to the observed data. The optimal model, selected by minimizing a statistical indicator such as the chi-squared () value, yielded an estimate for the initial mass ratio.
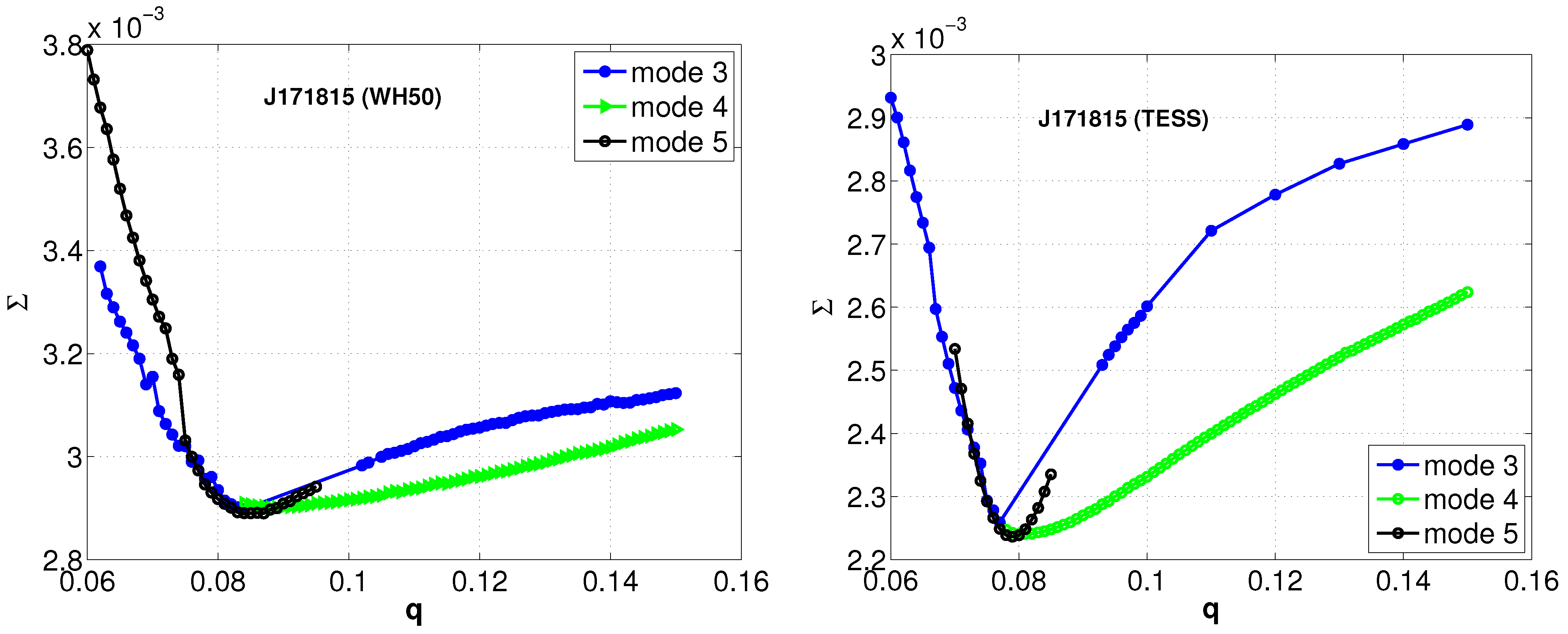
During the q-search process, we observed that certain trial mass ratios did not converge even after 200 iterations for the target J171815. To address this, we expanded the q-search approach to incorporate modes 4 and 5. Mode 4 is intended for semi-detached binary systems in which the primary star fills its critical Roche lobe, whereas mode 5 applies to semi-detached systems where the less massive component reaches its Roche lobe. Eventually, convergent solutions for J171815 were obtained under modes 3, 4, and 5. The plots illustrating the correlation between the tested mass ratios q and the sums of weighted squared deviations are displayed in the left panel of Figure 4.
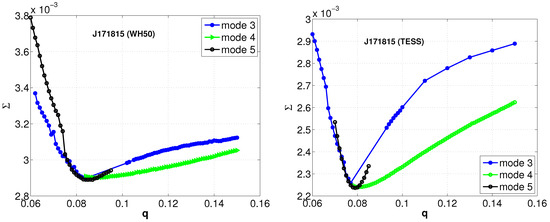
Figure 4.
The left panel displays the q-search results derived from data obtained using the WH50 telescope, while the right panel presents the q-search results utilizing data from TESS.
As previously stated, the TESS mission observed the binary system. It monitored sectors 24, 25, and 26 at a 30-min sampling rate, while sectors 51 and 53 were observed at a more frequent 10-min cadence, as depicted in Figure 2. The figure clearly reveals that the 30 min cadence data suffered substantially from phase-smearing effects. These effects can distort the true shape of the light curve and lead to inaccuracies in the photometric analysis. Furthermore, the light curves obtained from different sectors exhibit remarkable similarity in their profiles. This similarity strongly suggests that there were no significant intrinsic changes in the system’s brightness during the observation period. Given these factors, the phase-binned light curves from sector 53 were selected for deriving the photometric solutions. Sector 53’s data stood out because of its higher data density and lower scatter. For comparison, the q-search method was applied to the TESS data set. The plots in the right panels of Figure 4 illustrate the relationships between the tested mass ratios q and Σ.
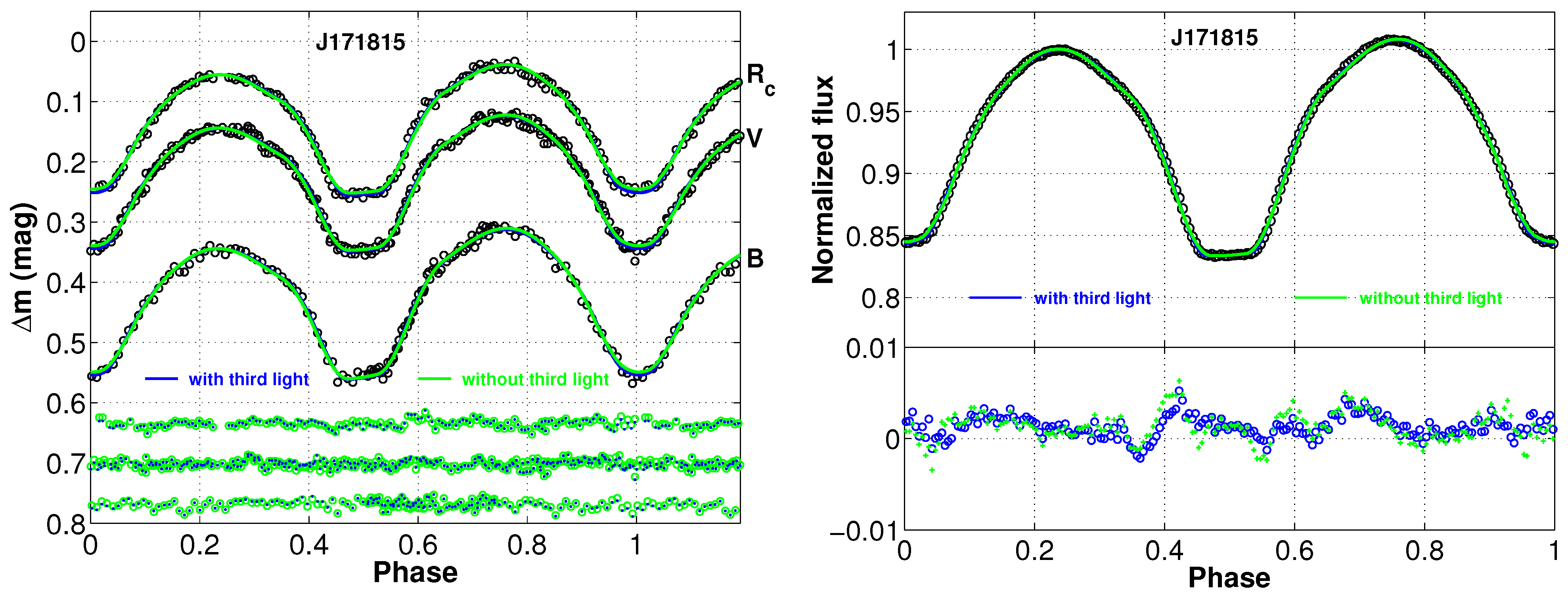
Based on the left panel of Figure 4, the minimum values of derived from modes 3, 4, and 5 are 0.084, 0.088, and 0.087, respectively. They are quite similar to the results derived from TESS, which yielded a minimum value of at , , and for modes 3, 4, and 5, respectively. Given the long-term increasing trend in the orbital period, which indicates mass transfer from the less massive component to the more massive one, modes 3 and 5 are considered more plausible than mode 4. Given that the phase-binned light curves of TESS displays typical EW-type light curves and shows no abrupt slope variations near orbital phases 0.36 and 0.64—where such features would be indicative of a semi-detached configuration—we adopted a contact binary model for the analysis. The corresponding mass ratios from our data and TESS data were used as initial mass ratios. These values were then treated as adjustable parameters in the following analysis, together with other key parameters such as the luminosity of the primary (), phase shift, secondary temperature (), potential (), and inclination (i). From Figure 1 and Figure 2, we can see that all the light curves show asymmetry with brightness enhancement at the secondary light maximum. Just as the asymmetry in some NCBs [46,47,48] has been explained by a hot spot on the binaries, we added a hot spot to the primary component. The final photometric solutions from the data and the TESS data are summarized in Table 2, labeled and , respectively. The theoretical light curves are shown in Figure 5 with green solid lines.

Table 2.
Photometric solutions for J171815 derived from the observations and TESS data.
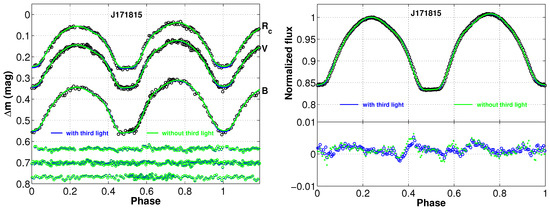
Figure 5.
In the (left) panel, the fitted light curves for the bands are shown, whereas in the (right) panel, those for TESS are provided. The green solid line represents the theoretical fit without third light, while the blue solid line represents the theoretical fit with third light.
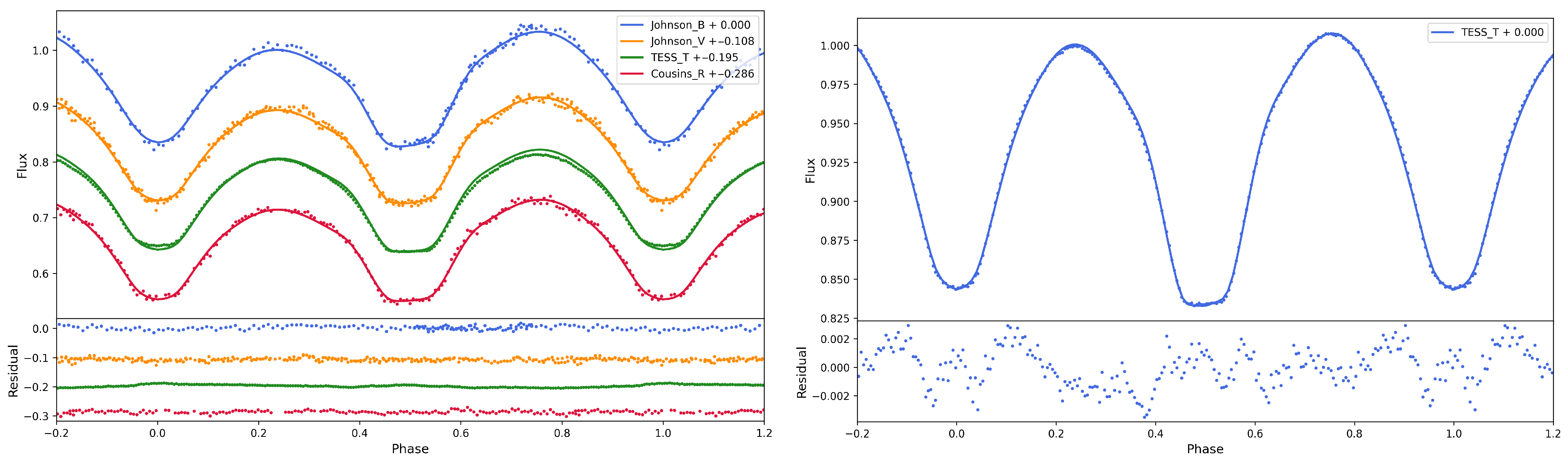
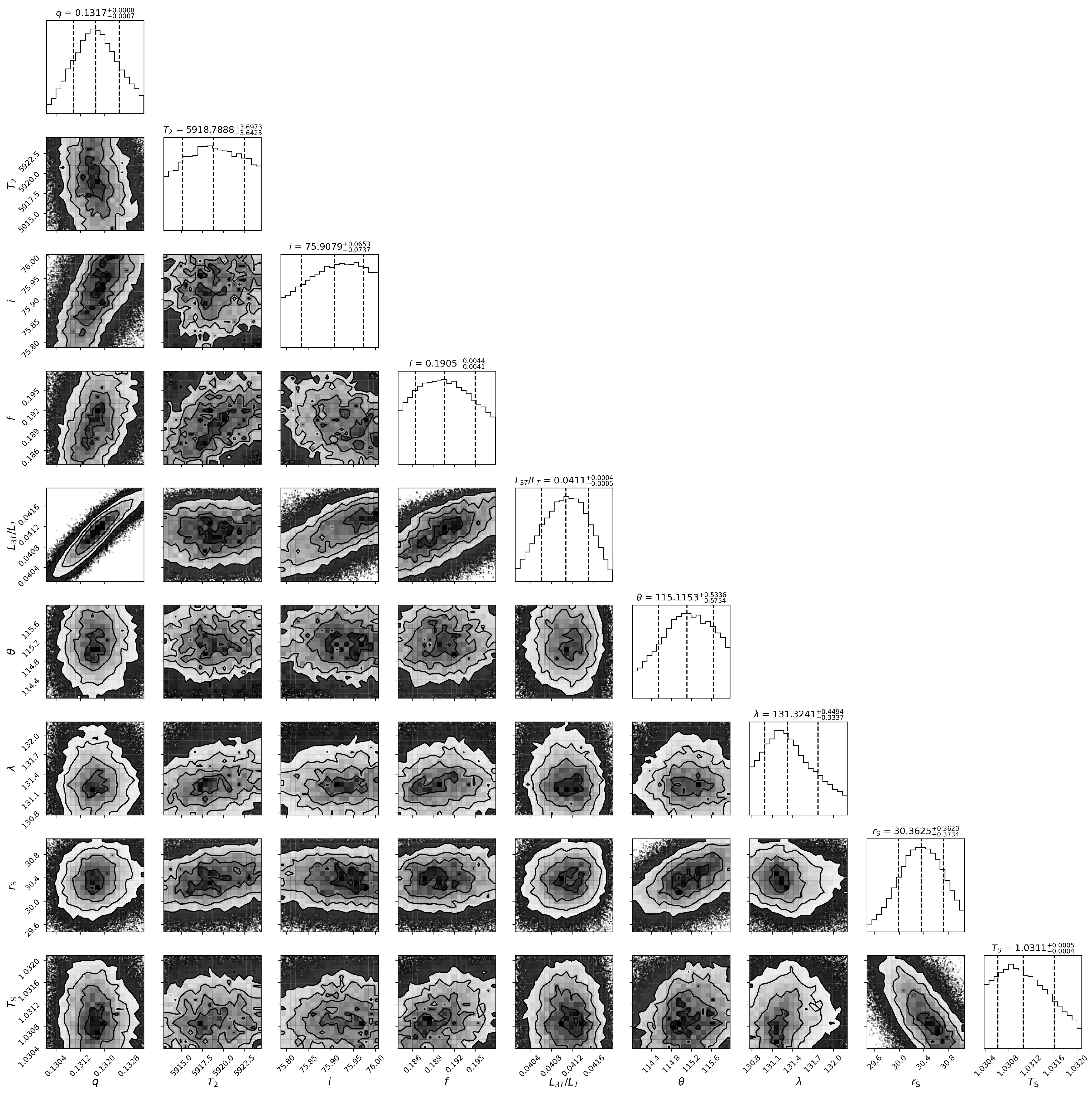
Given that third components are prevalent in most W UMa-type contact binary systems, we explicitly treated the third-light component (l3) as a free parameter in the photometric modeling using the W–D code. The corresponding fitting results have been supplemented in Table 2, labeled as “ (with third light)” and “TESS (with third light)”, respectively. These results demonstrate that even when the third-light parameter is freely optimized, the system retains its extreme low-mass-ratio nature (). To obtain more precise results, we employed the Contact Binary Light-curve Analyzer (CBLA; Li et al. [49]), a software package based on PHOEBE [50,51,52,53] that utilizes a neural-network model for rapid multi-band light-curve analysis of contact binaries. Figure 6 displays the corner plots derived from CBLA, while the left panel of Figure 7 presents the corresponding light-curve fits. We found that simultaneous fitting of all four bands yielded suboptimal results, potentially due to magnetic activity effects, as the observations were not obtained simultaneously. Given the high precision of TESS data, we separately processed the TESS observations using CBLA. The resulting corner plots and fitted light curves are shown in Figure 8 and the right panel of Figure 7, respectively. The derived physical parameters, presented in Table 3, are similar with those obtained from the W–D analysis. It is important to note that since the actual contribution fraction of third light cannot be uniquely determined from the available photometric data, there is an inherent degeneracy between third light and other parameters such as mass ratio and luminosity ratio. This phenomenon is a common challenge in multi-parameter photometric modeling, especially for systems with low-amplitude light curves, where the dilution effect of third light and the luminosity contribution of the secondary component are difficult to fully disentangle.

Figure 6.
Posterior probability distributions of key parameters obtained from the simultaneous analysis of and TESS light curves using CBLA.
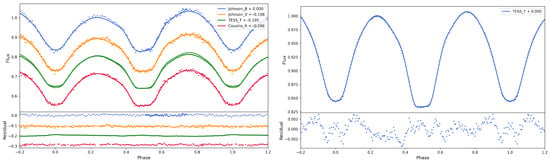
Figure 7.
Modeled light curves from CBLA are presented. The solid lines represent the best-fit models based on MCMC parameter estimation, with residuals shown in the bottom panels. The (left) panel displays the simultaneous fitting of four-band light curves, while the (right) panel shows the results for TESS data alone.
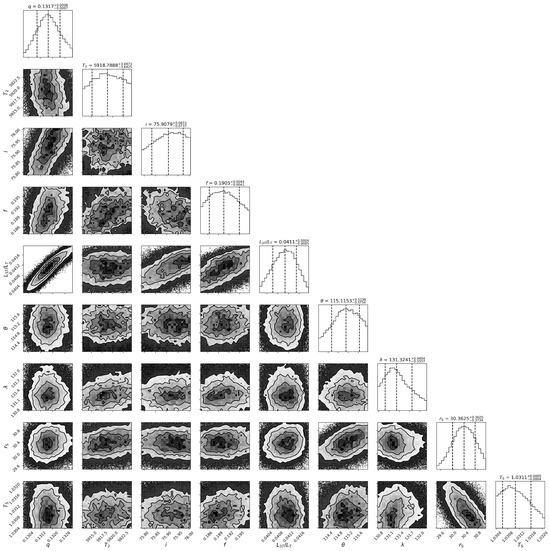
Figure 8.
Posterior probability distributions of key parameters obtained from the analysis of TESS light curves using CBLA.

Table 3.
Physical parameters obtained by CBLA.
5. Discussions and Conclusions
The photometric solutions and detailed orbital period analysis for J171815 are carried out for the first time. Table 2 and Table 3 presents the photometric solutions obtained from multi-band ground-based observations and TESS data, including models both with and without a third-light component. Photometric solutions suggest that J171815 is a W-type contact binary system, where the more massive star is cooler than the less massive one. The system has an ultra low mass ratio and a shallow contact degree, where f is defined as , with being the Roche lobe potential at the Lagrangian point, the potential at the Lagrangian point and the actual potential of the star.
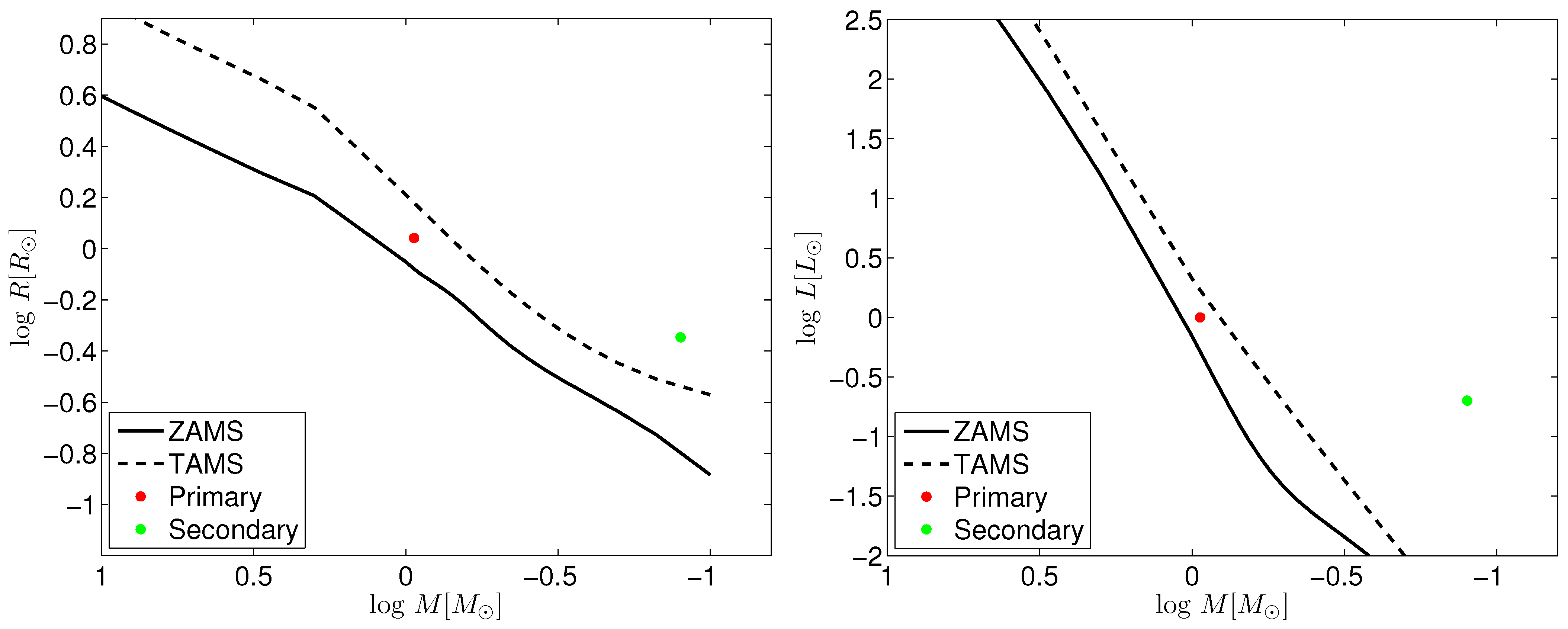
To constrain the global parameters of J171815, we selected the light-curve solution with third light (mode 3 from the TESS analysis) as the final result. This decision is justified by two key considerations: first, a large number of W UMa-type binaries are known to belong to triple or higher-multiplicity systems, which makes the inclusion of third light physically reasonable; second, compared to the solution without third light, the one incorporating third light yields smaller residuals (), signifying a more accurate fit to the observed data. Assuming that the more massive primary star in the system is on the main sequence, we estimated its mass using data from an online table [54]. This led to a mass estimate of . Applying Kepler’s third law (), we calculated the semi-major axes (the separations between the components) to be approximately . Based on the photometric solutions provided in Table 2, the radii of the primary and secondary components were calculated. These values are (primary) and (secondary). The luminosities of the binaries were then computed based on the Stefan - Boltzmann law (), which resulted in and . To gain more insights into how the two components of this system have evolved, we present the mass-radius and mass-luminosity diagrams in Figure 9. Both the ZAMS (Zero-Age Main Sequence) and TAMS (Terminal-Age Main Sequence) lines in the figures are derived from the binary evolution code by [55]. Notably, the primary star’s location between the ZAMS and TAMS lines demonstrates it is still in the main sequence stage, whereas the secondary star’s position above the TAMS line indicates it has evolved beyond the main sequence.
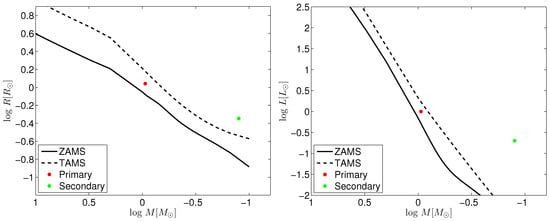
Figure 9.
The (left) panel shows the mass-radius diagram, while the (right) panel presents the mass-luminosity diagram. Solid lines correspond to ZAMS, and dashed lines to TAMS.
For the first time, we analyzed the minimum times calculated for constructing and plotting the diagrams for J171815, which are shown in Figure 3, which reveal an upward parabolic trend. The quadratic term in the orbital period ephemeris (Equation (2)) reveals a secular increase in the orbital period at a rate of (), which indicates mass transfer from the less massive primary component to the more massive secondary star. Then, using Equation (3),
we calculate the mass accretion rate of the primary component as .
As TRO theory predicts, contact binaries must undergo oscillations around the state of marginal contact, with each oscillation cycle consisting of a shallow contact phase followed by a semi-detached phase, and during the shallow contact phase, orbital periods should increase due to conservative mass transfer from the less massive component to the more massive one [3,4]—and our observational data for the target system is consistent with these predictions: our photometric analyses confirm the system is currently in the shallow contact phase, and our measurement of the orbital period derivative yields a positive value, directly indicating the orbital period is increasing, which matches TRO’s expectation for the shallow contact phase driven by conservative mass transfer from the less massive secondary to the more massive primary [56,57]. Since the observed long-term orbital trend may represent only a segment of a more complex, possibly cyclic orbital variation, additional observations are required to confirm and further elaborate on these findings.
In summary, our analysis based on photometric solutions and orbital period studies indicates that J171815 has an ultra-low mass ratio. The observed positive () supports this scenario, suggesting mass transfer from the less massive star to the more massive one through Roche lobe overflow, which may cause brightness enhancement around the secondary light maximum [46,48]. Given its very small mass ratios and marginal critical states, J171815 is an important candidate for continuous monitoring. Such observations are crucial for testing theories of binary mergers and thermal relaxation oscillations, providing valuable insights into the evolution of these systems.
Author Contributions
Conceptualization, F.L. and D.G.; methodology, F.L. and K.L.; software, X.C.; validation, D.G. and K.L.; formal analysis, F.L.; investigation, X.C.; resources, D.G.; data curation, F.L. and J.A.; writing—original draft preparation, F.L.; writing—review and editing, D.G.; visualization, F.L. and C.Z.; supervision, D.G.; project administration, D.G.; funding acquisition, D.G. and K.L. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge supports Shandong Provincial Natural Science Foundation (Project No.: ZR2025MS90), and by the instrument Enducation Funds of Shandong University (yr20240103), and by the Qilu Young Researcher Project of Shandong University.
Data Availability Statement
The -band photometric data utilized in this study are available from the corresponding author upon reasonable request. Those interested are invited to contact Dr. Guo at difu@sdu.edu.cn. All other data used in this research are publicly accessible.
Acknowledgments
We sincerely appreciate the meticulous reviews and valuable suggestions from all referees. These comments have not only helped us correct the expressive inconsistencies in the study but also significantly enhanced the scientific rigor, precision, and completeness of the manuscript. This work makes use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia, accessed on 3 April 2025), processed by the Gaia Data Processing and Analysis Consortium (https://www.cosmos.esa.int/web/gaia/dpac/consortium, accessed on 3 April 2025). This work makes use of data collected by the TESS mission which are funded by NASA Science Mission directorate. We acknowledge the TESS team for its support of this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Notes
| 1 | https://www.aavso.org/vsx/index.php, accessed on 3 March 2025 |
| 2 | https://iraf.readthedocs.io/en/latest/, accessed on 3 March 2025 |
| 3 | https://archive.stsci.edu/, accessed on 3 April 2025 |
| 4 | https://astroutils.astronomy.osu.edu/time/hjd2bjd.html, accessed on 3 April 2025 |
References
- Shaw, J.S. Near-Contact Binary Stars. In Proceedings of the Active Close Binaries Proceedings, NATO Advanced Study Institute, Kusadasi, Turkey, 11–22 September 1989; NATO Advanced Study Institute (ASI) Series C; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990; Volume 319, p. 241. [Google Scholar]
- Zhu, L.; Qian, S.; Liu, L.; Liao, W.P.; He, J.J.; Li, L.J.; Zhao, E.G.; Dai, Z.B.; Zhang, J.; Li, K. A Preliminary Photometric Study of the HW Vir-like Binary NSVS14256825. In Proceedings of the 9th Pacific Rim Conference on Stellar Astrophysics, Lijiang, China, 14–20 April 2011; Astronomical Society of the Pacific Conference Series. Qain, S., Leung, K., Zhu, L., Kwok, S., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2011; Volume 451, p. 155. [Google Scholar]
- Lucy, L.B. W Ursae Majoris systems with marginal contact. Astrophys. J. 1976, 205, 208–216. [Google Scholar] [CrossRef]
- Flannery, B.P. A Cyclic Thermal Instability in Contact Binary Stars. Astrophys. J. 1976, 205, 217–225. [Google Scholar] [CrossRef]
- Zhu, L.; Qian, S. BL Andromedae and GW Tauri: Close binary stars in a key evolutionary stage. Mon. Not. R. Astron. Soc. 2006, 367, 423–432. [Google Scholar] [CrossRef]
- Meng, Z.B.; Wang, H.W.; Yu, Y.X.; Hu, K.; Xiang, F.Y. HT Lyn and IR Lyn: Two Semi-detached-type Near-contact Binaries with Stable Orbital Period. Res. Astron. Astrophys. 2022, 22, 115015. [Google Scholar] [CrossRef]
- Rucinski, S.M. Contact Binaries. In Instrumentation and Research Programmes for Small Telescopesm, Proceedings of the 118th Symposium of the International Astronomical Union Christchurch (IAU Symposium), New Zealand, 2–6 December 1985; Hearnshaw, J.B., Cottrell, P.L., Eds.; Springer: Berlin/Heidelberg, Germany, 1986; Volume 118, p. 159. [Google Scholar]
- Qian, S. A possible relation between the period change and the mass ratio for W-type contact binaries. Mon. Not. R. Astron. Soc. 2001, 328, 635–644. [Google Scholar] [CrossRef]
- Qian, S. Orbital period changes of contact binary systems: Direct evidence for thermal relaxation oscillation theory. Mon. Not. R. Astron. Soc. 2001, 328, 914–924. [Google Scholar] [CrossRef]
- Eggleton, P.P. Formation and Evolution of Contact Binaries. J. Astron. Space Sci. 2012, 29, 145–149. [Google Scholar] [CrossRef]
- Qian, S.B.; Zhang, J.; He, J.J.; Zhu, L.Y.; Zhao, E.G.; Shi, X.D.; Zhou, X.; Han, Z.T. Physical Properties and Evolutionary States of EA-type Eclipsing Binaries Observed by LAMOST. Astrophys. J. Suppl. Ser. 2018, 235, 5. [Google Scholar] [CrossRef]
- Darwin, G.H. The Determination of the Secular Effects of Tidal Friction by a Graphical Method. Proc. R. Soc. Lond. Ser. I 1879, 29, 168–181. [Google Scholar]
- Hut, P. Stability of tidal equilibrium. Astron. Astrophys. 1980, 92, 167–170. [Google Scholar]
- Yang, Y.G.; Qian, S.B. Deep, Low Mass Ratio Overcontact Binary Systems. XIV. A Statistical Analysis of 46 Sample Binaries. Astron. J. 2015, 150, 69. [Google Scholar] [CrossRef]
- Pešta, M.; Pejcha, O. Mass-ratio distribution of contact binary stars. Astron. Astrophys. 2023, 672, A176. [Google Scholar] [CrossRef]
- Arbutina, B.; Wadhwa, S. The Critical Mass Ratio for W-UMa-Type Contact Binary Sytems. Serbian Astron. J. 2024, 208, 1–15. [Google Scholar] [CrossRef]
- Wadhwa, S.S.; Landin, N.R.; Arbutina, B.; Tothill, N.F.H.; De Horta, A.Y.; Filipović, M.D.; Petrović, J.; Djurašević, G. Low-mass contact binaries: Orbital stability at extreme low mass ratios. Mon. Not. R. Astron. Soc. 2024, 535, 2494–2502. [Google Scholar] [CrossRef]
- Cheng, Q.; Xiong, J.; Ding, X.; Ji, K.; Li, J.; Liu, C.; Li, J.; Luo, J.; Lyu, X.; Han, Z.; et al. The First Photometric Analysis of Two Low-mass-ratio Contact Binary Systems in TESS Survey. Astron. J. 2024, 167, 148. [Google Scholar] [CrossRef]
- Guo, D.F.; Li, K.; Liu, F.; Li, H.Z.; Xia, Q.Q.; Gao, X.; Gao, X.; Chen, X.; Gao, D.Y.; Sun, G.Y. The first photometric and orbital period investigation of an extremely low mass ratio contact binary with a sudden period change TYC 4002-2628-1. Mon. Not. R. Astron. Soc. 2022, 517, 1928–1936. [Google Scholar] [CrossRef]
- Li, K.; Gao, X.; Guo, D.F.; Gao, D.Y.; Chen, X.; Wang, L.H.; Xin, Y.X.; Han, Y.X.; Kim, C.H.; Jeong, M.J. Detection of the lowest mass ratio contact binary in the universe: TYC 3801-1529-1. Astron. Astrophys. 2024, 692, L4. [Google Scholar] [CrossRef]
- Guo, D.F.; Li, K.; Liu, F.; Wang, L.h.; Li, H.Z.; Chen, X.; Gao, X. Two Ultralow-mass-ratio Binary Systems at Critical Evolutionary Stages. Astron. J. 2025, 170, 101. [Google Scholar] [CrossRef]
- Guo, D.F.; Li, K.; Liu, F.; Li, H.Z.; Liu, X.Y. WISE J185503.7+592234: A particularly low mass ratio contact binary approaching merger. Mon. Not. R. Astron. Soc. 2023, 521, 51–59. [Google Scholar] [CrossRef]
- Guo, D.; Li, K.; Liu, F.; Li, H.; Liu, X.; Chen, X. WISE J141530.7+592234: A Very Low Mass Ratio Contact Binary with Significant Light Curve Variations. Publ. Astron. Soc. Pac. 2023, 135, 044201. [Google Scholar] [CrossRef]
- Butters, O.W.; West, R.G.; Anderson, D.R.; Collier Cameron, A.; Clarkson, W.I.; Enoch, B.; Haswell, C.A.; Hellier, C.; Horne, K.; Joshi, Y.; et al. The first WASP public data release. Astron. Astrophys. 2010, 520, L10. [Google Scholar] [CrossRef]
- Drake, A.J.; Graham, M.J.; Djorgovski, S.G.; Catelan, M.; Mahabal, A.A.; Torrealba, G.; García-Álvarez, D.; Donalek, C.; Prieto, J.L.; Williams, R.; et al. The Catalina Surveys Periodic Variable Star Catalog. Astrophys. J. Suppl. Ser. 2014, 213, 9. [Google Scholar] [CrossRef]
- Shappee, B.J.; Prieto, J.L.; Grupe, D.; Kochanek, C.S.; Stanek, K.Z.; De Rosa, G.; Mathur, S.; Zu, Y.; Peterson, B.M.; Pogge, R.W.; et al. The Man behind the Curtain: X-Rays Drive the UV through NIR Variability in the 2013 Active Galactic Nucleus Outburst in NGC 2617. Astrophys. J. 2014, 788, 48. [Google Scholar] [CrossRef]
- Jayasinghe, T.; Kochanek, C.S.; Stanek, K.Z.; Shappee, B.J.; Holoien, T.W.S.; Thompson, T.A.; Prieto, J.L.; Dong, S.; Pawlak, M.; Shields, J.V.; et al. The ASAS-SN catalogue of variable stars I: The Serendipitous Survey. Mon. Not. R. Astron. Soc. 2018, 477, 3145–3163. [Google Scholar] [CrossRef]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS). J. Astron. Telesc. Instrum. Syst. 2015, 1, 014003. [Google Scholar] [CrossRef]
- Li, K.; Kim, C.H.; Xia, Q.Q.; Michel, R.; Hu, S.M.; Gao, X.; Guo, D.F.; Chen, X. The First Light Curve Modeling and Orbital Period Change Investigation of Nine Contact Binaries around the Short-period Cutoff. Astron. J. 2020, 159, 189. [Google Scholar] [CrossRef]
- Li, K.; Xia, Q.Q.; Kim, C.H.; Gao, X.; Hu, S.M.; Guo, D.F.; Gao, D.Y.; Chen, X.; Guo, Y.N. Photometric Study and Absolute Parameter Estimation of Six Totally Eclipsing Contact Binaries. Astron. J. 2021, 162, 13. [Google Scholar] [CrossRef]
- Li, K.; Gao, X.; Liu, X.Y.; Gao, X.; Li, L.Z.; Chen, X.; Sun, G.Y. Extremely Low Mass Ratio Contact Binaries. I. The First Photometric and Spectroscopic Investigations of Ten Systems. Astron. J. 2022, 164, 202. [Google Scholar] [CrossRef]
- Eastman, J.; Siverd, R.; Gaudi, B.S. Achieving Better Than 1 Minute Accuracy in the Heliocentric and Barycentric Julian Dates. Publ. Astron. Soc. Pac. 2010, 122, 935. [Google Scholar] [CrossRef]
- Wilson, R.E.; Devinney, E.J. Realization of Accurate Close-Binary Light Curves: Application to MR Cygni. Astrophys. J. 1971, 166, 605. [Google Scholar] [CrossRef]
- Wilson, R.E.; Van Hamme, W.; Terrell, D. Flux Calibrations from Nearby Eclipsing Binaries and Single Stars. Astrophys. J. 2010, 723, 1469–1492. [Google Scholar] [CrossRef]
- Wilson, R.E. Accuracy and Efficiency in the Binary Star Reflection Effect. Astrophys. J. 1990, 356, 613. [Google Scholar] [CrossRef]
- Wilson, R.E. Spotted Star Light Curves with Enhanced Precision. Astron. J. 2012, 144, 73. [Google Scholar] [CrossRef]
- Wilson, R.E. Eclipsing Binary Solutions in Physical Units and Direct Distance Estimation. Astrophys. J. 2008, 672, 575–589. [Google Scholar] [CrossRef]
- Van Hamme, W.; Wilson, R.E. Third-Body Parameters from Whole Light and Velocity Curves. Astrophys. J. 2007, 661, 1129–1151. [Google Scholar] [CrossRef]
- Prusti, T.; de Bruijne, J.H.J.; Brown, A.G.A.; Vallenari, A.; Babusiaux, C.; Bailer-Jones, C.A.L.; Bastian, U.; Biermann, M.; Evans, D.W.; Gaia Collaboration; et al. The Gaia mission. Astron. Astrophys. 2016, 595, A1. [Google Scholar] [CrossRef]
- Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Babusiaux, C.; Bailer-Jones, C.A.L.; Biermann, M.; Evans, D.W.; Eyer, L.; Gaia Collaboration; et al. Gaia Data Release 2. Summary of the contents and survey properties. Astron. Astrophys. 2018, 616, A1. [Google Scholar] [CrossRef]
- Andrae, R.; Fouesneau, M.; Creevey, O.; Ordenovic, C.; Mary, N.; Burlacu, A.; Chaoul, L.; Jean-Antoine-Piccolo, A.; Kordopatis, G.; Korn, A.; et al. Gaia Data Release 2. First stellar parameters from Apsis. Astron. Astrophys. 2018, 616, A8. [Google Scholar] [CrossRef]
- Lucy, L.B. Gravity-Darkening for Stars with Convective Envelopes. Z. FüR Astrophys. 1967, 65, 89. [Google Scholar]
- Ruciński, S.M. The Proximity Effects in Close Binary Systems. II. The Bolometric Reflection Effect for Stars with Deep Convective Envelopes. Acta Astron. 1969, 19, 245. [Google Scholar]
- Terrell, D.; Wilson, R.E. Photometric Mass Ratios of Eclipsing Binary Stars. Astrophys. Space Sci. 2005, 296, 221–230. [Google Scholar] [CrossRef]
- Li, K.; Xia, Q.Q.; Kim, C.H.; Hu, S.M.; Guo, D.F.; Jeong, M.J.; Chen, X.; Gao, D.Y. Two Contact Binaries with Mass Ratios Close to the Minimum Mass Ratio. Astrophys. J. 2021, 922, 122. [Google Scholar] [CrossRef]
- Zhu, L.Y.; Qian, S.B.; Zola, S.; Kreiner, J.M. Near-Contact Binaries with Mass Transfer: V473 Cassiopeiae and II Persei. Astron. J. 2009, 137, 3574–3580. [Google Scholar] [CrossRef]
- Tian, X.M.; Chang, L.F. Investigation on the mass transferring near-contact binary TT Cet. Publ. Astron. Soc. Aust. 2020, 37, e031. [Google Scholar] [CrossRef]
- Chang, L.F.; Zhu, L.Y. V505 Cyg: A Mass-transferring Marginal Contact Binary. Publ. Astron. Soc. Pac. 2022, 134, 054202. [Google Scholar] [CrossRef]
- Li, K.; Wang, L.H.; Gao, X. A Neural-network Model for Quickly Solving Multiple-band Light Curves of Contact Binaries. Astrophys. J. Suppl. Ser. 2025, 281, 1. [Google Scholar] [CrossRef]
- Prša, A.; Zwitter, T. A Computational Guide to Physics of Eclipsing Binaries. I. Demonstrations and Perspectives. Astrophys. J. 2005, 628, 426–438. [Google Scholar] [CrossRef]
- Prša, A.; Conroy, K.E.; Horvat, M.; Pablo, H.; Kochoska, A.; Bloemen, S.; Giammarco, J.; Hambleton, K.M.; Degroote, P. Physics Of Eclipsing Binaries. II. Toward the Increased Model Fidelity. Astrophys. J. Suppl. Ser. 2016, 227, 29. [Google Scholar] [CrossRef]
- Conroy, K.E.; Kochoska, A.; Hey, D.; Pablo, H.; Hambleton, K.M.; Jones, D.; Giammarco, J.; Abdul-Masih, M.; Prša, A. Physics of Eclipsing Binaries. V. General Framework for Solving the Inverse Problem. Astrophys. J. Suppl. Ser. 2020, 250, 34. [Google Scholar] [CrossRef]
- Kobulnicky, H.A.; Molnar, L.A.; Cook, E.M.; Henderson, L.E. A Bayesian Analysis of Physical Parameters for 783 Kepler Close Binaries: Extreme-mass-ratio Systems and a New Mass Ratio versus Period Lower Limit. Astrophys. J. Suppl. Ser. 2022, 262, 12. [Google Scholar] [CrossRef]
- Pecaut, M.J.; Mamajek, E.E. Intrinsic Colors, Temperatures, and Bolometric Corrections of Pre-main-sequence Stars. Astrophys. J. Suppl. Ser. 2013, 208, 9. [Google Scholar] [CrossRef]
- Hurley, J.R.; Tout, C.A.; Pols, O.R. Evolution of binary stars and the effect of tides on binary populations. Mon. Not. R. Astron. Soc. 2002, 329, 897–928. [Google Scholar] [CrossRef]
- Yakut, K.; Eggleton, P.P. Evolution of Close Binary Systems. Astrophys. J. 2005, 629, 1055–1074. [Google Scholar] [CrossRef]
- Zhu, L.; Qian, S.B.; Mikulášek, Z.; Zejda, M.; Zvěřina, P.; Diethelm, R. Photometric Study of the Very Short Period Shallow Contact Binary DD Comae Berenices. Astron. J. 2010, 140, 215–223. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).