An Accuracy Design Method for a Linear Feed System of Machine Tools Considering the Geometric Error Shape of the Guideway
Abstract
1. Introduction
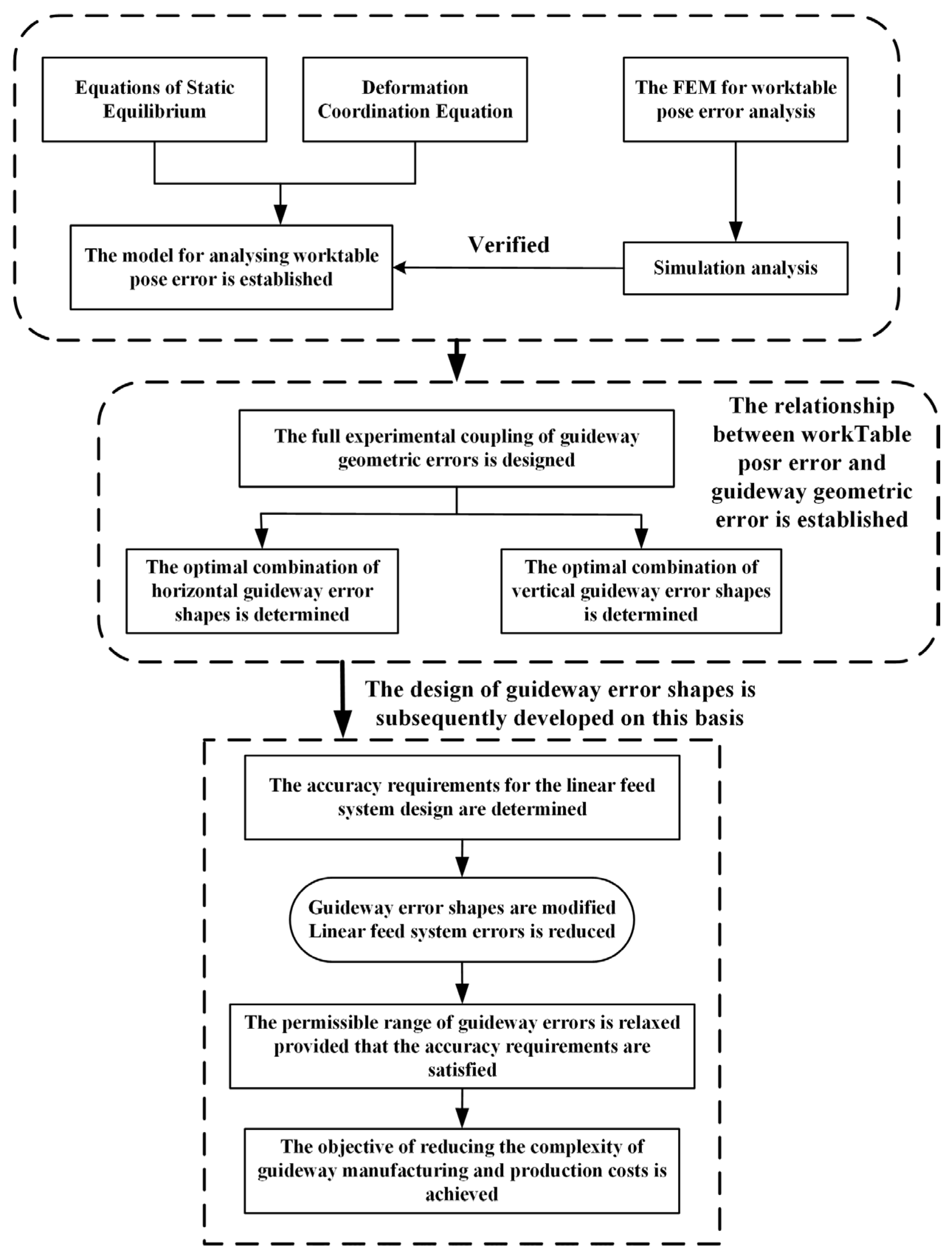
2. Theoretical Analysis
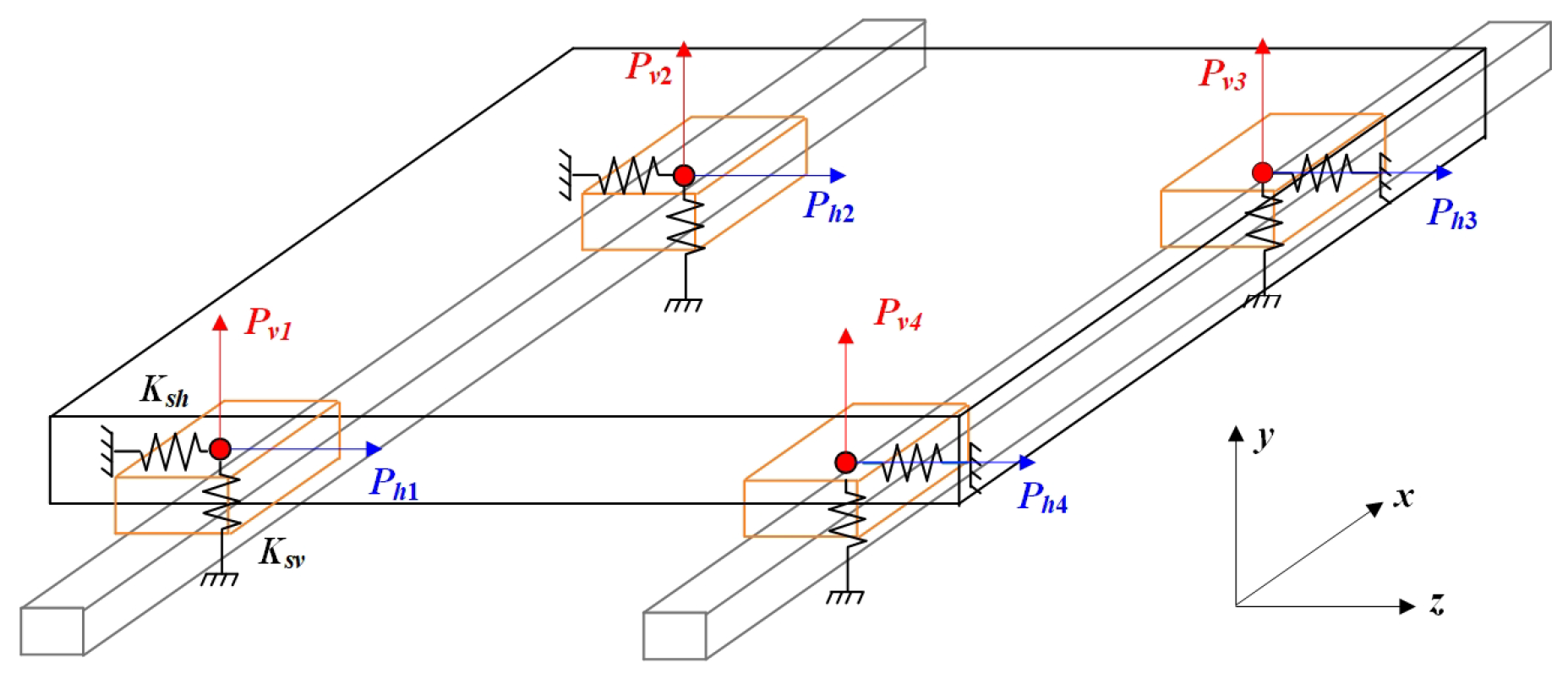
2.1. Theoretical Model
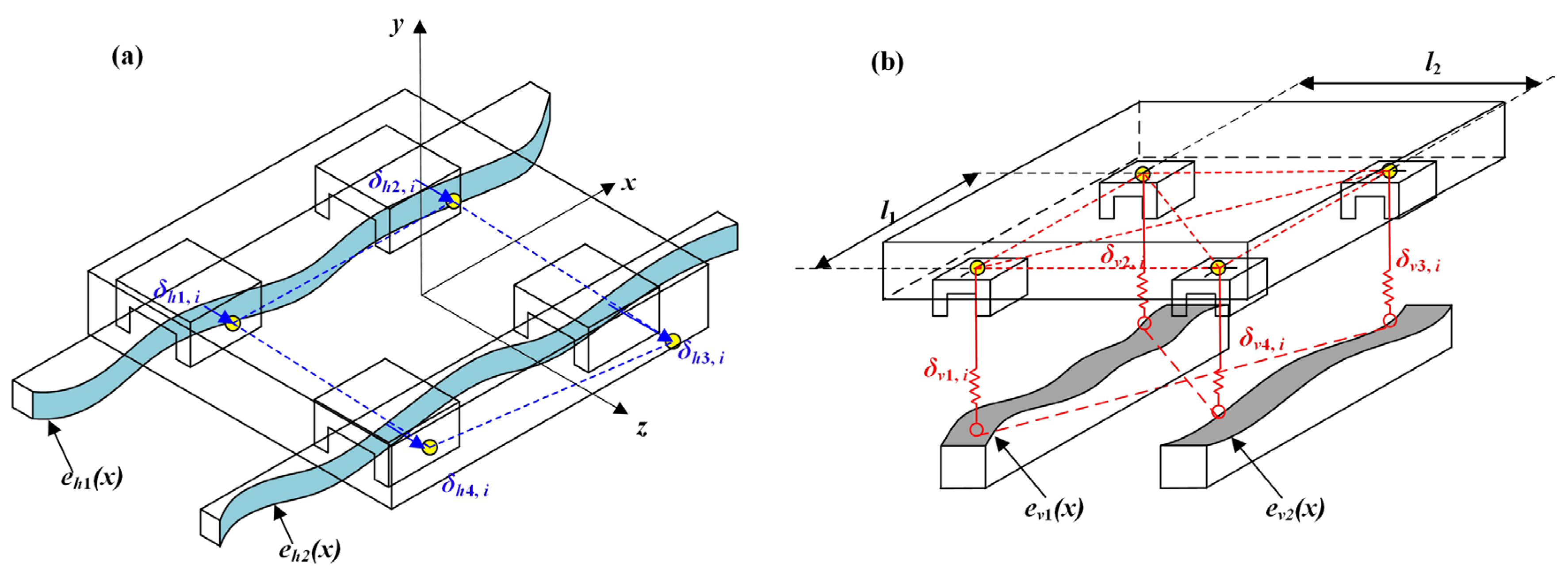
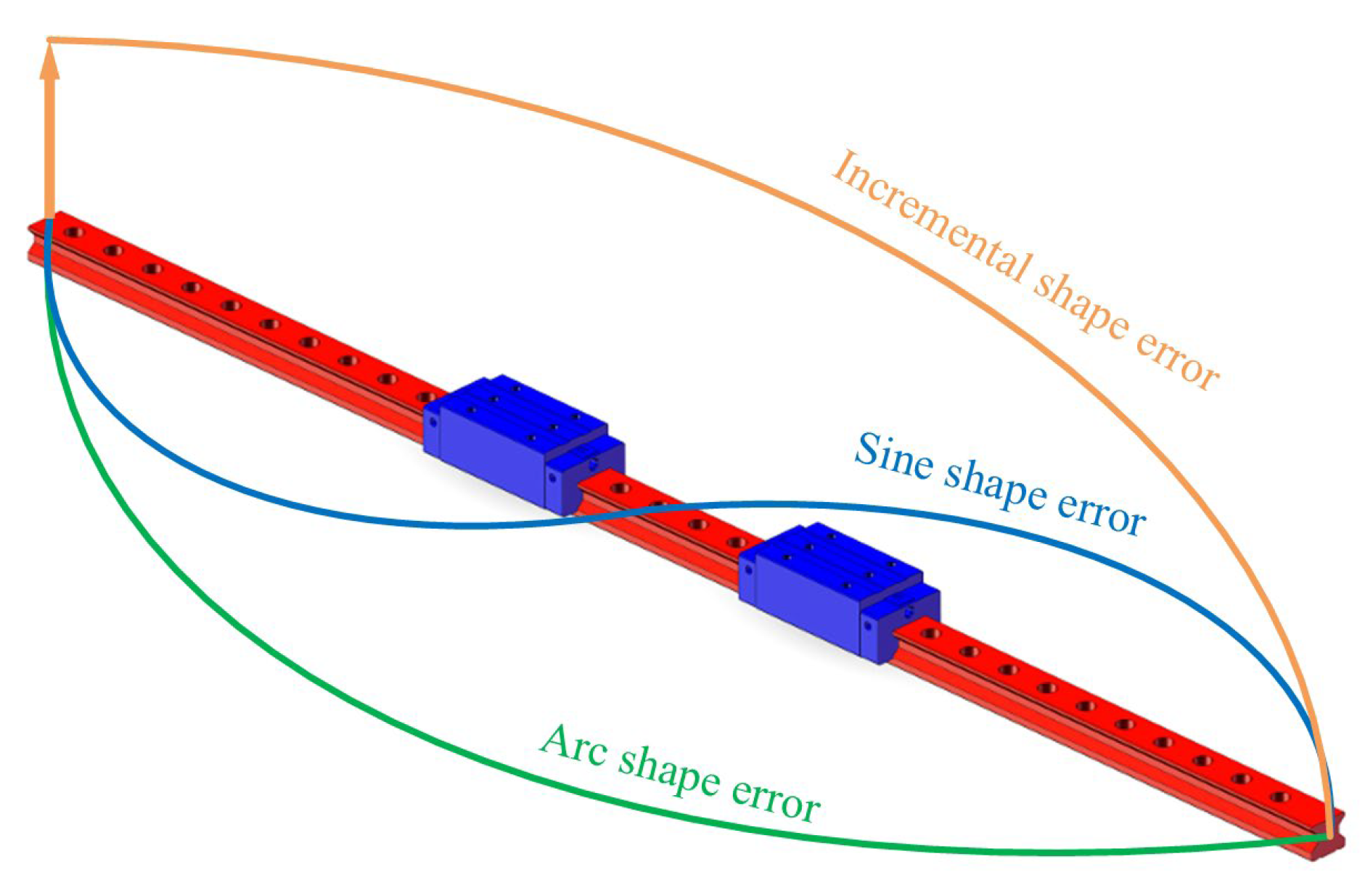
2.2. Analysis of the Geometric Error Shape of Guideways
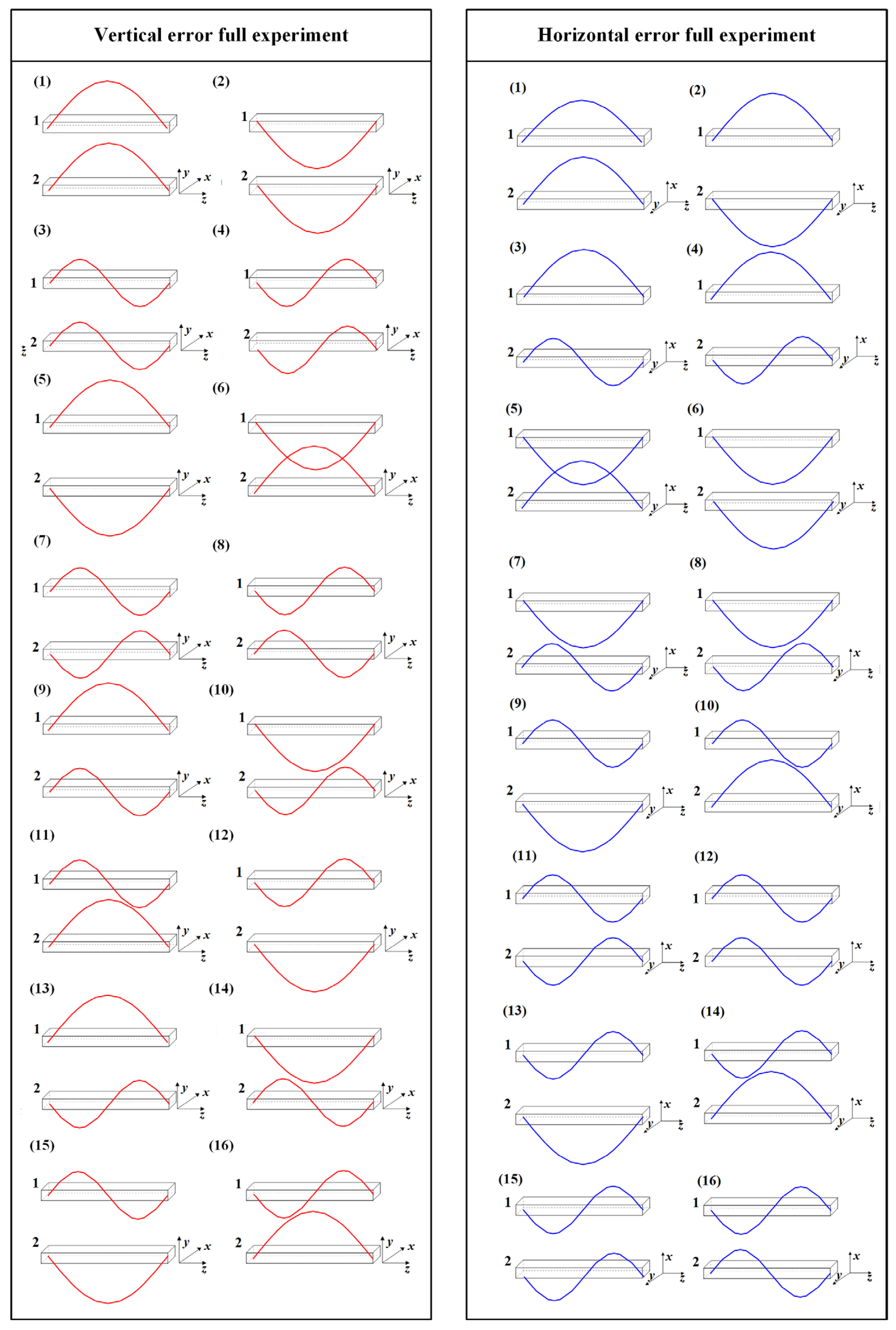
2.3. Full Experimental Design of Guideway Error Shapes
2.4. Analysis of Theoretical Results
3. Finite Element Analysis
3.1. Single-Slider Modeling
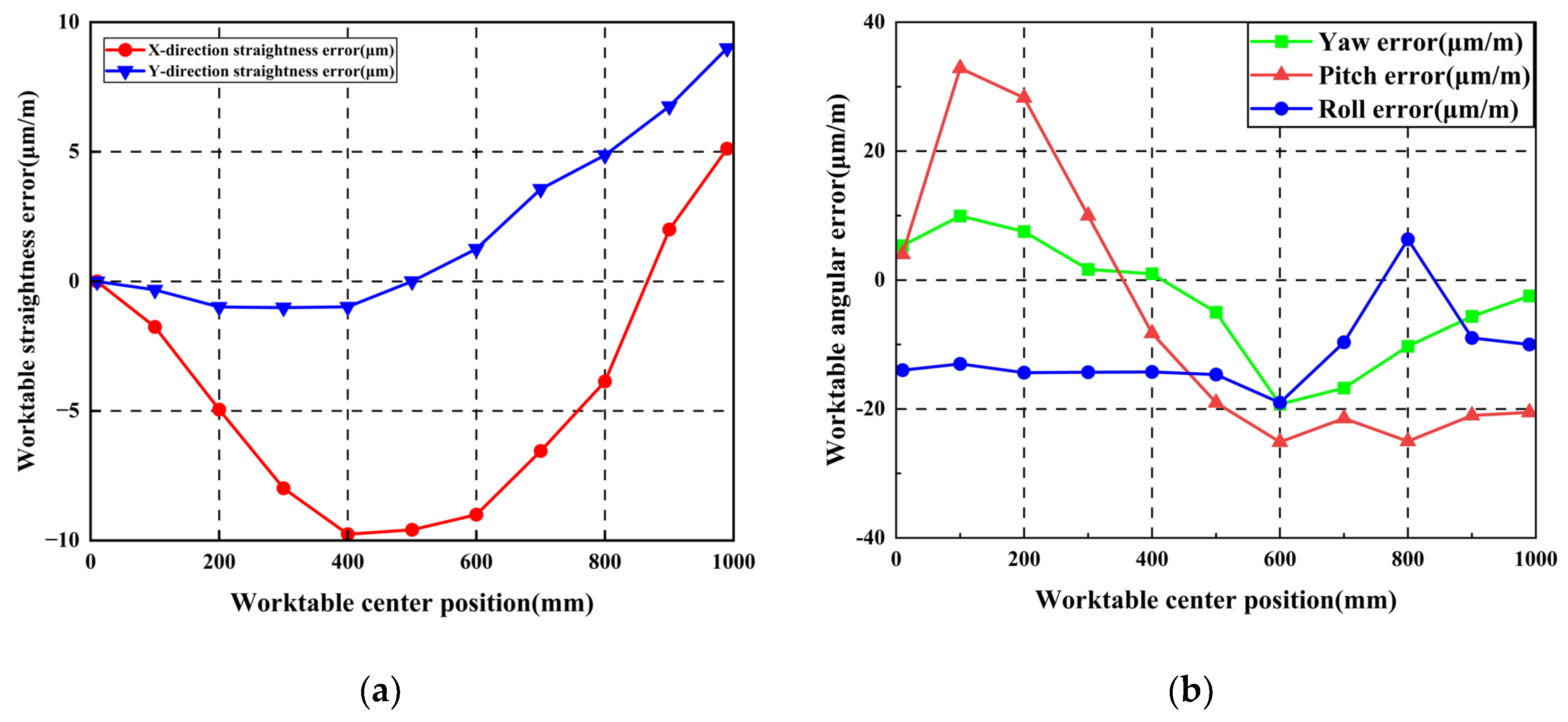
3.2. Analysis of Finite Element Simulation Result
3.3. Error-Averaging Coefficient Analysis
3.4. Design of Guideway Error Shapes
4. Experiment Verification
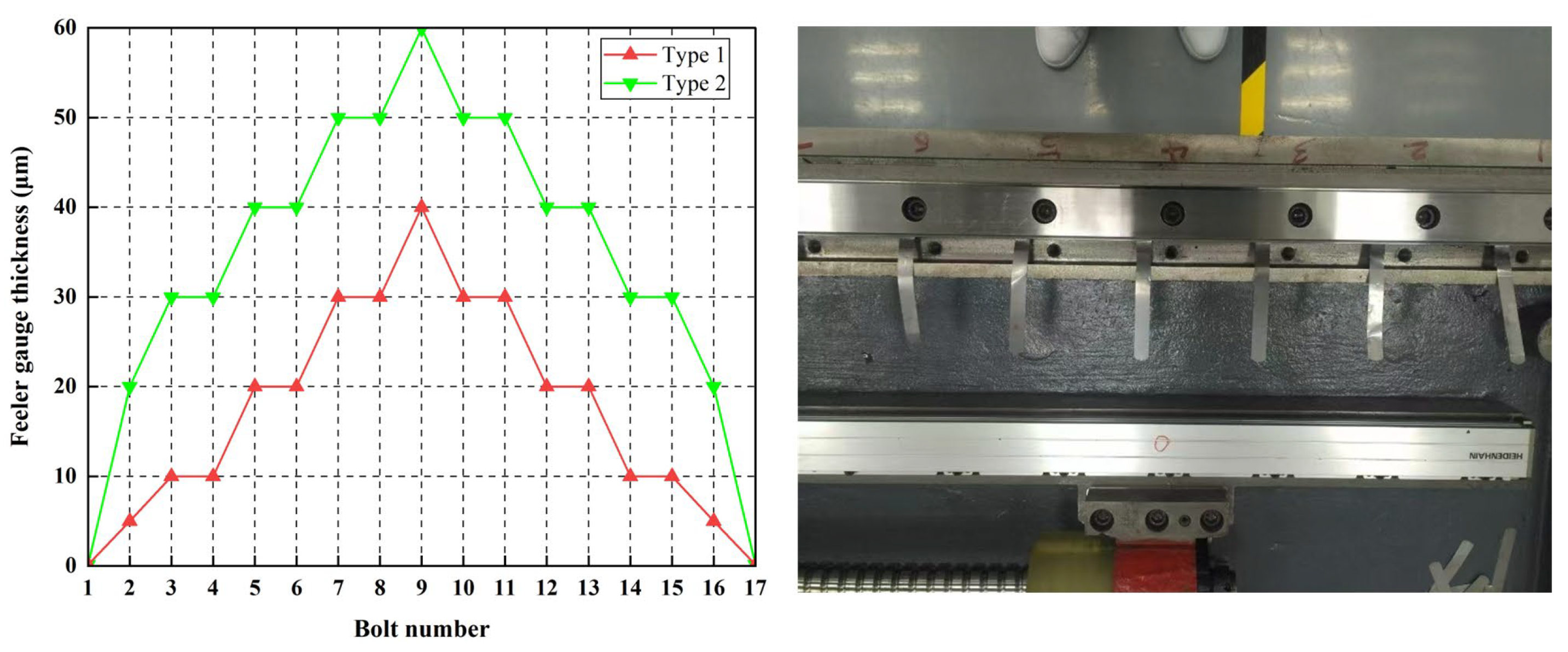
4.1. Experimental Setup
4.2. Experimental Results
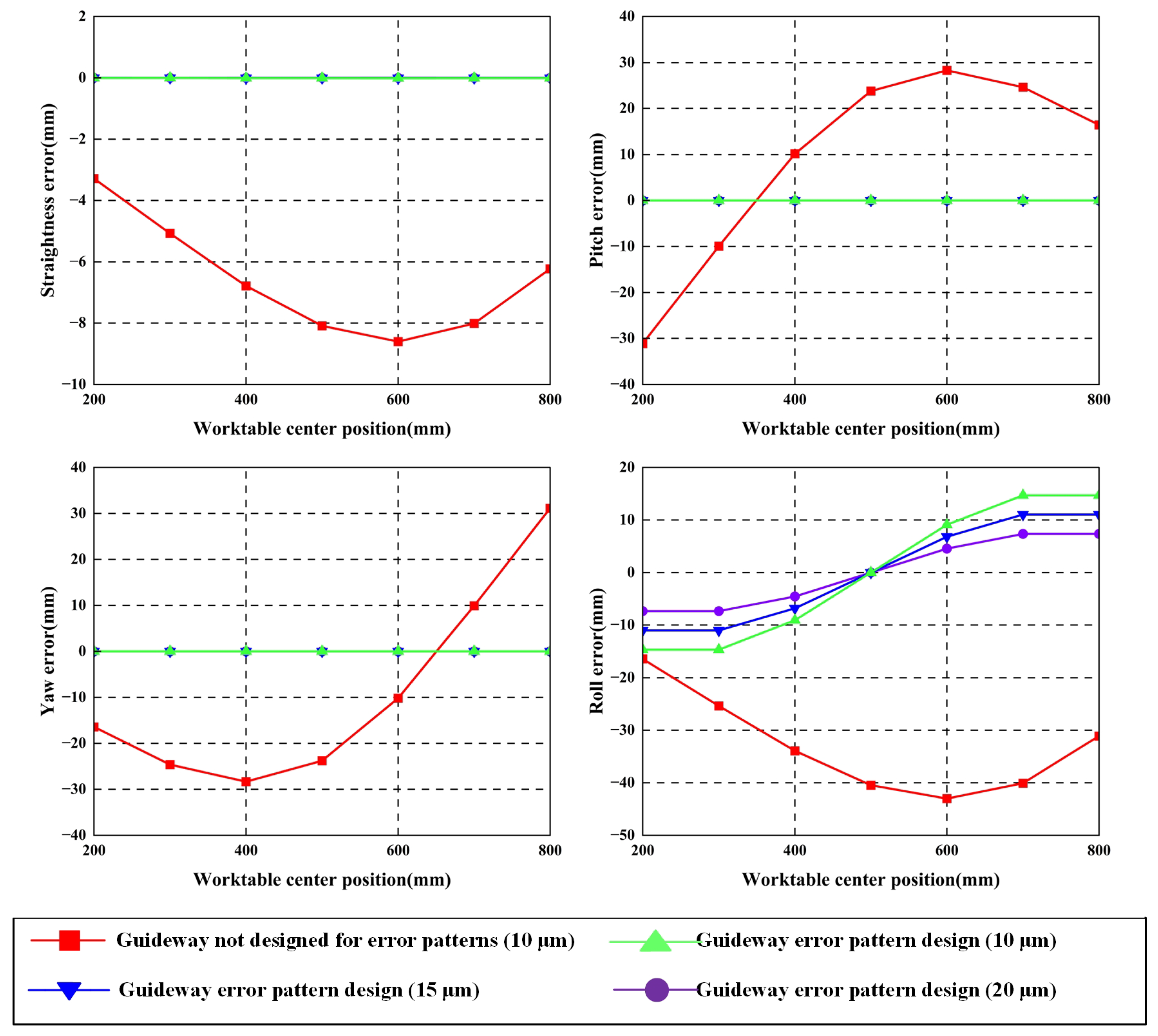
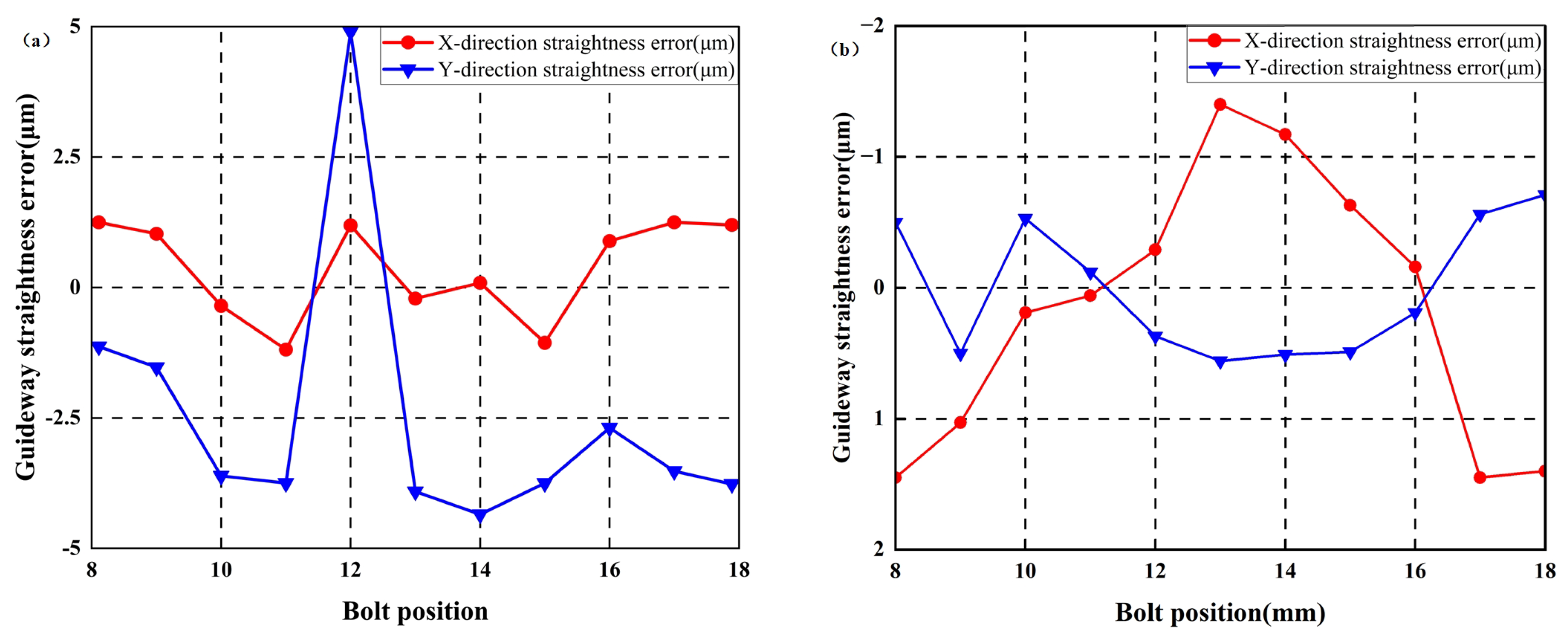
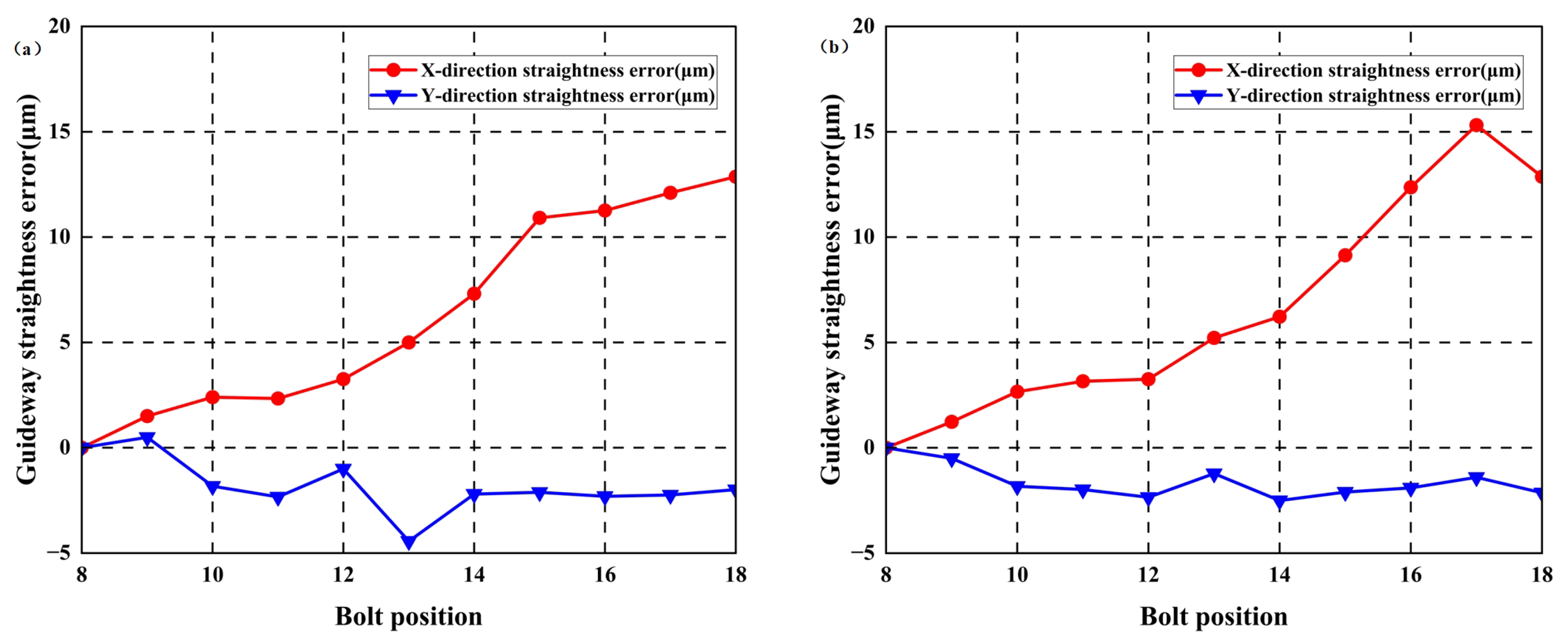
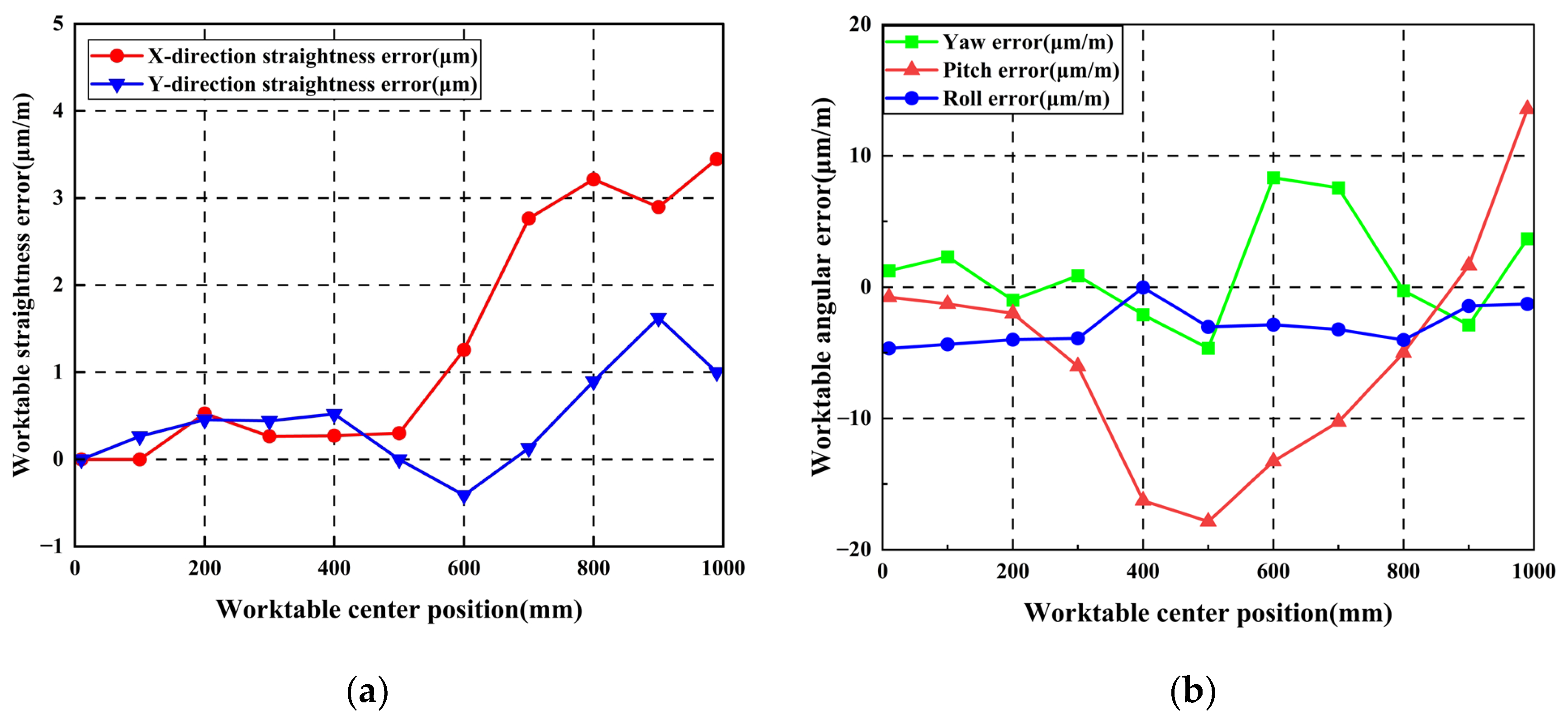
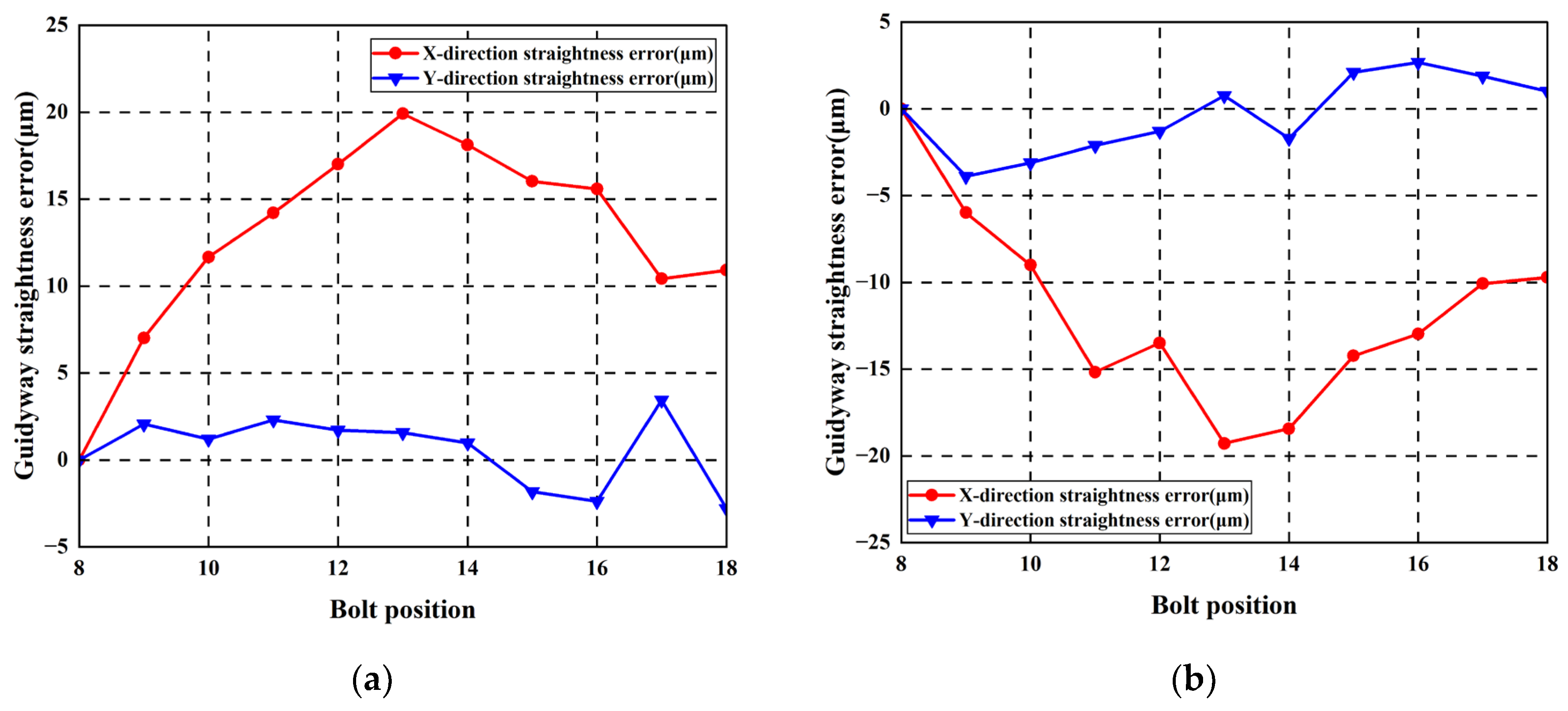
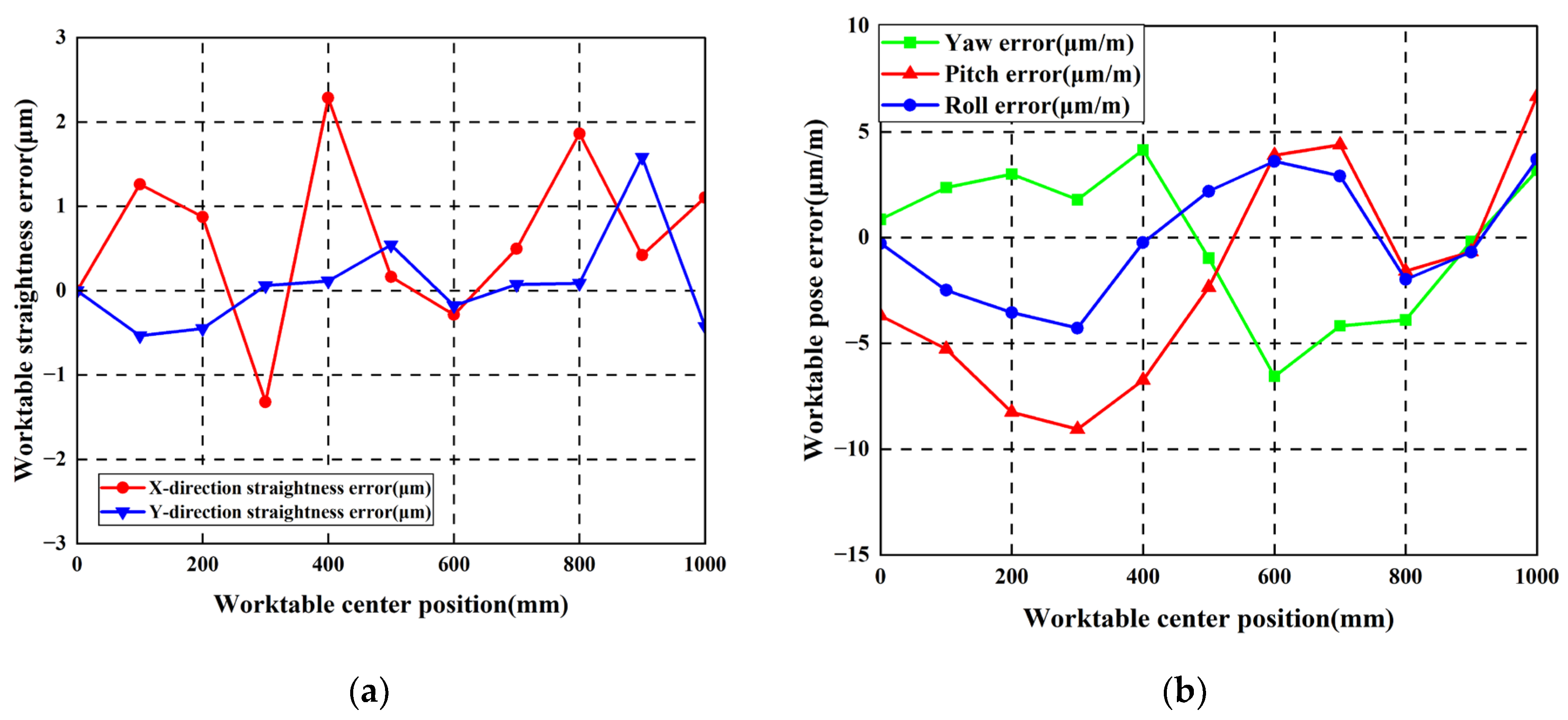
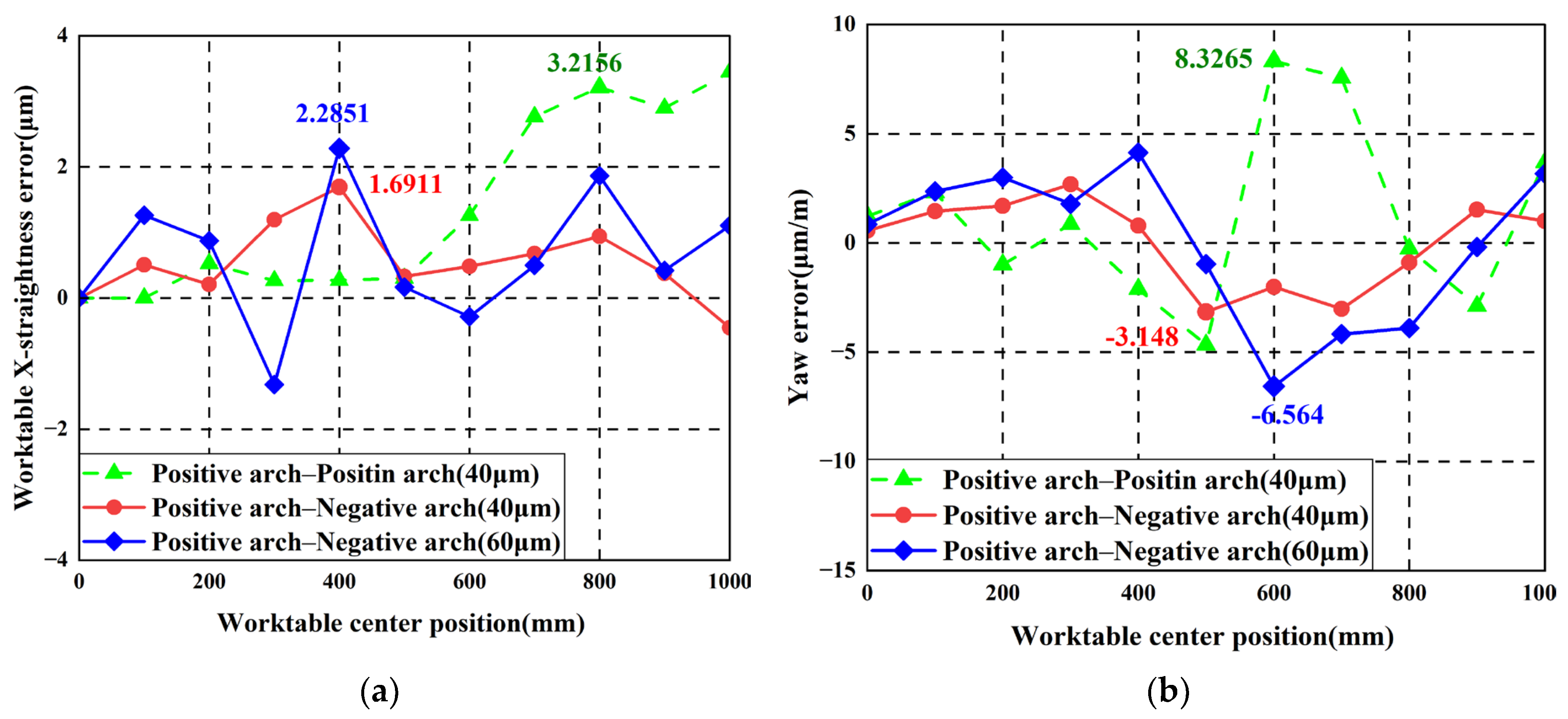
4.2.1. Analyzing Guideways Without Additive Geometric Errors
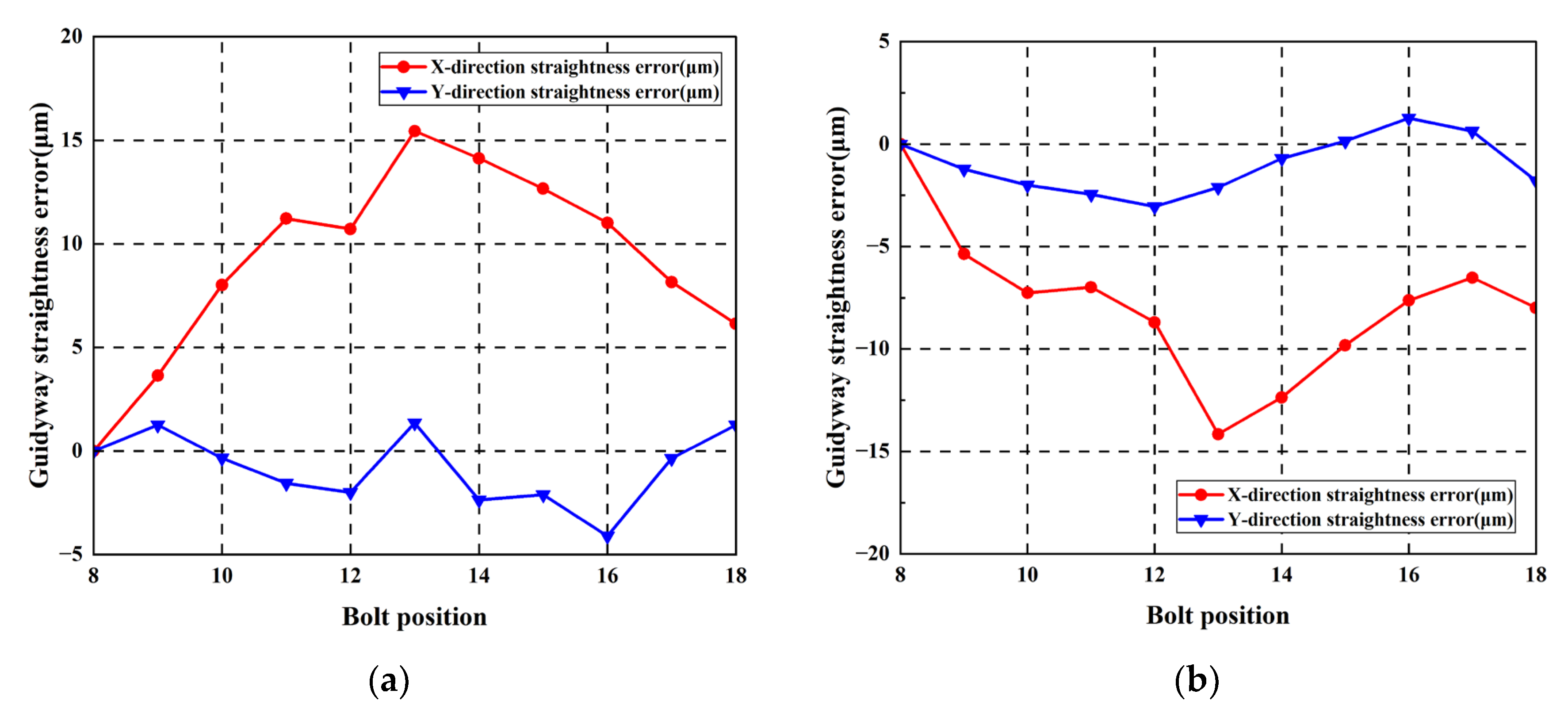
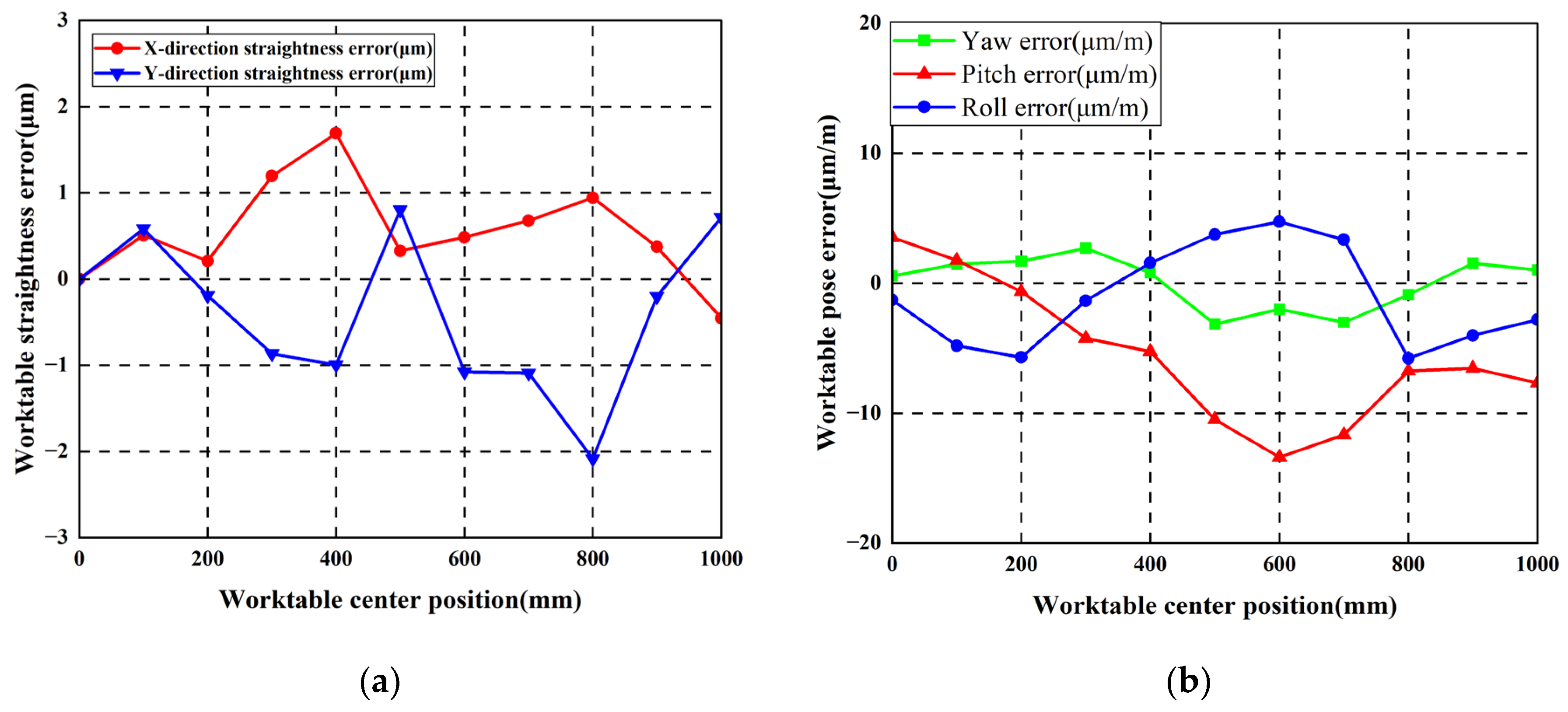
4.2.2. Identical Horizontally Arched Geometrishijiaxiangtongc Error of Guideway Is Applied
4.2.3. Reverse Horizontally Arched Geometric Error of Guideway Is Applied
4.2.4. Analysis of Experimental Results
5. Conclusions
- (1)
- The research results indicate that the pose error of the worktable is influenced by the amplitude and shape of the guideway geometric errors in the linear feed system. Consequently, conducting guideway shape design is meaningful.
- (2)
- The highest accuracy for the linear feed system is achieved under the guideway condition of sine–negative sine or positive arch–negative arch error shapes in the horizontal direction, and under the condition of sine–negative sine error shapes in the vertical direction.
- (3)
- Implementing accuracy design based on the optimal guideway shape combination significantly relaxes the geometric tolerance requirements for guideways, thereby reducing manufacturing difficulty and production costs.
- (4)
- The proposed accuracy design method provides a valuable reference for the development and manufacturing of other precision equipment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, C.; Zheng, P.; Xu, X. Digitalisation and servitisation of machine tools in the era of Industry 40: A review. Int. J. Prod. Res. 2023, 61, 4069–4101. [Google Scholar] [CrossRef]
- Ilangkumaran, M.; Sasikumar, R.; Sakthivel, G. Parametric optimization for the production of nanostructure in high carbon steel chips via machining. Ain Shams Eng. J. 2015, 6, 957–965. [Google Scholar] [CrossRef]
- Yang, K.Z.; Pramanik, A.; Basak, A.; Dong, Y.; Prakash, C.; Shankar, S.; Dixit, S.; Kumar, K.; Vatin, N.I. Application of coolants during tool-based machining—A review. Ain Shams Eng. J. 2023, 14, 101830. [Google Scholar] [CrossRef]
- Fan, K.C.; Chen, H.M.; Kuo, T.H. Prediction of machining accuracy degradation of machine tools. Precis. Eng. 2012, 36, 288–298. [Google Scholar] [CrossRef]
- Khim, G.; Park, C.H.; Shamoto, E.; Kim, S.W. Prediction and compensation of motion accuracy in a linear motion bearing table. Precis. Eng. 2011, 35, 393–399. [Google Scholar] [CrossRef]
- Shamoto, E.; Park, C.H.; Moriwaki, T. Analysis and improvement of motion accuracy of hydrostatic feed table. CIRP Ann. 2001, 50, 285–290. [Google Scholar] [CrossRef]
- Ma, J.; Lu, D.; Zhao, W. Assembly errors analysis of linear axis of CNC machine tool considering component deformation. Int. J. Adv. Manuf. Technol. 2016, 86, 281–289. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; Wang, L.; Li, T.; You, Z. Research on the stiffness of a 5-DOF hybrid machine tool with actuation redundancy. Mech. Mach. Theory 2009, 44, 289–305. [Google Scholar] [CrossRef]
- Zha, J.; Xue, F.; Chen, Y.L. Straightness error modeling and compensation for gantry type open hydrostatic guideways in grinding machine. Int. J. Mach. Tools Manuf. 2017, 112, 1–6. [Google Scholar] [CrossRef]
- Guo, S.; Mei, X.; Jiang, G. Geometric accuracy enhancement of five-axis machine tool based on error analysis. Int. J. Adv. Manuf. Technol. 2019, 105, 137–153. [Google Scholar] [CrossRef]
- Wu, H.; Li, X.; Sun, F.; Zheng, H.; Zhao, Y. Optimization design method of machine tool static geometric accuracy using tolerance modeling. Int. J. Adv. Manuf. Technol. 2022, 118, 1793–1809. [Google Scholar] [CrossRef]
- Wu, H.; Zheng, H.; Li, X.; Wang, W.; Xiang, X.; Meng, X. A geometric accuracy analysis and tolerance robust design approach for a vertical machining center based on the reliability theory. Measurement 2020, 161, 107809. [Google Scholar] [CrossRef]
- Wang, S.; He, G.; Zhang, D.; Yang, Y.; Yan, Y.; Song, Y. B-Spline Curve-Based Machine Tool Guideways Geometric Accuracy Design. Int. J. Mech. Sci. 2025, 301, 110550. [Google Scholar] [CrossRef]
- Park, C.H.; Jeong, J.H.; Lee, H.S.; Kim, S.T. Finite Element Analysis on the Motion Accuracy of Hydrostatic Table (1st Analysis and Experimental Verification on Single-side Table). J. Korean Soc. Precis. Eng. 2000, 17, 137–144. [Google Scholar]
- Park, C.H.; Lee, H.S.; Kim, T.H.; Kim, M.G. Finite Element Analysis on the Motion Accuracy of Hydrostatic Table (2nd Analysis and Experimental Verification on Double Sides Table). J. Korean Soc. Precis. Eng. 2002, 19, 65–70. [Google Scholar]
- Wang, S.; He, G.; Zhang, D.; Chen, F.; Yao, C.; Yan, Y. Innovative design methods for the geometric accuracy of machine tool guideway oriented to spatial accuracy. J. Manuf. Process. 2024, 119, 483–498. [Google Scholar] [CrossRef]
- Ni, Y.; Zhou, H.; Shao, C.; Li, J. Research on the error averaging effect in a rolling guide pair. Chin. J. Mech. Eng. 2019, 32, 72. [Google Scholar] [CrossRef]
- Sun, G.; Chen, S.; Sun, M.; Gao, R.; Zhang, D.; Guo, X.; Zhao, J. Research on the error averaging effect of linear feed systems for precision machine tools. Ain Shams Eng. J. 2024, 15, 103101. [Google Scholar] [CrossRef]
- Song, L.; Zhang, Q.; Xu, L.; Zhao, X.; Sun, T. Investigation of the error averaging effect on design and assembly of external slider closed hydrostatic guideways. Tribol. Int. 2024, 199, 110036. [Google Scholar] [CrossRef]
- Lin, Z.; Tian, W.; Zheng, Y.; Xu, Y.; Shi, K.; Chen, J.; Zhang, D.; Gao, W. Analysis of the Finite Element Simulation of the Linear Rolling Guide Pair Error Averaging Effect. In Artificial Intelligence Technologies and Applications; IOS Press: Amsterdam, The Netherlands, 2024; pp. 200–206. [Google Scholar]
- Hu, P.H.; Yu, C.W.; Fan, K.C.; Dang, X.M.; Li, R.J. Error averaging effect in parallel mechanism coordinate measuring machine. Appl. Sci. 2016, 6, 383. [Google Scholar] [CrossRef]
- Sun, G.; Wang, Y.; Wang, W.; Liu, J.; Yu, M.; Zhao, J. Stiffness effects on repeatability of positioning of linear axes. J. Mech. Sci. Technol. 2022, 36, 4659–4669. [Google Scholar] [CrossRef]
- Wu, H.; Zheng, H.; Wang, W.; Xiang, X. A method for tracing key geometric errors of vertical machining center based on global sensitivity analysis. Int. J. Adv. Manuf. Technol. 2020, 106, 3943–3956. [Google Scholar] [CrossRef]
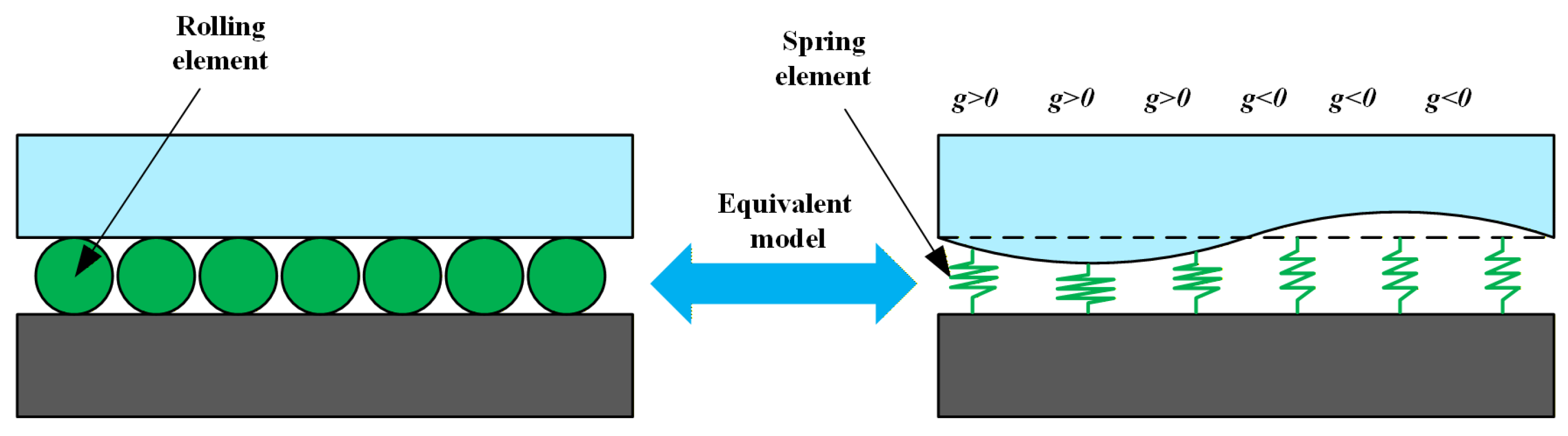
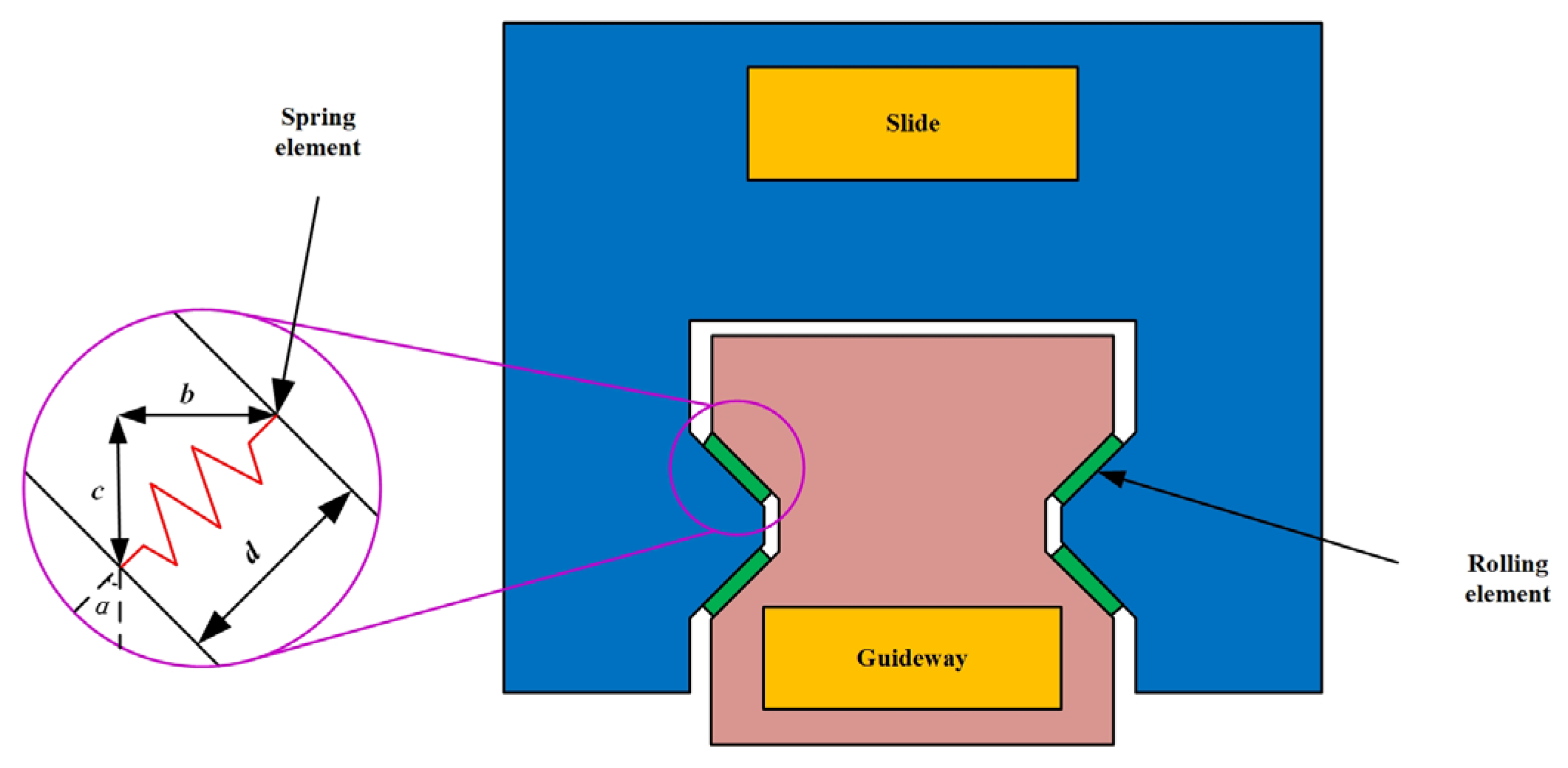
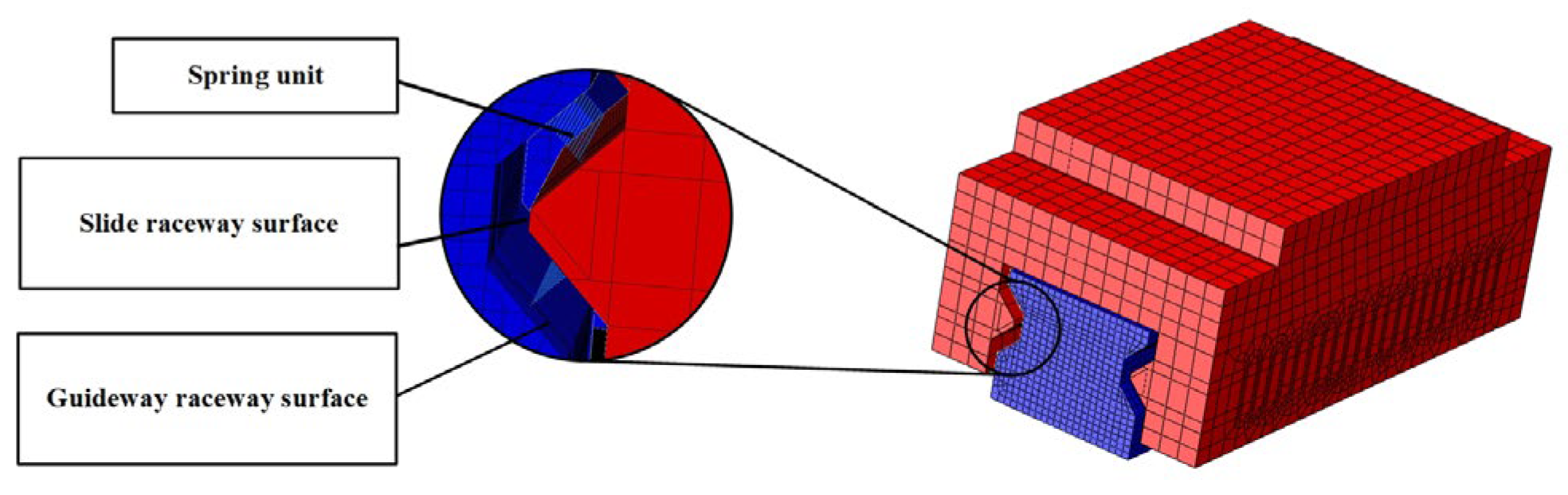
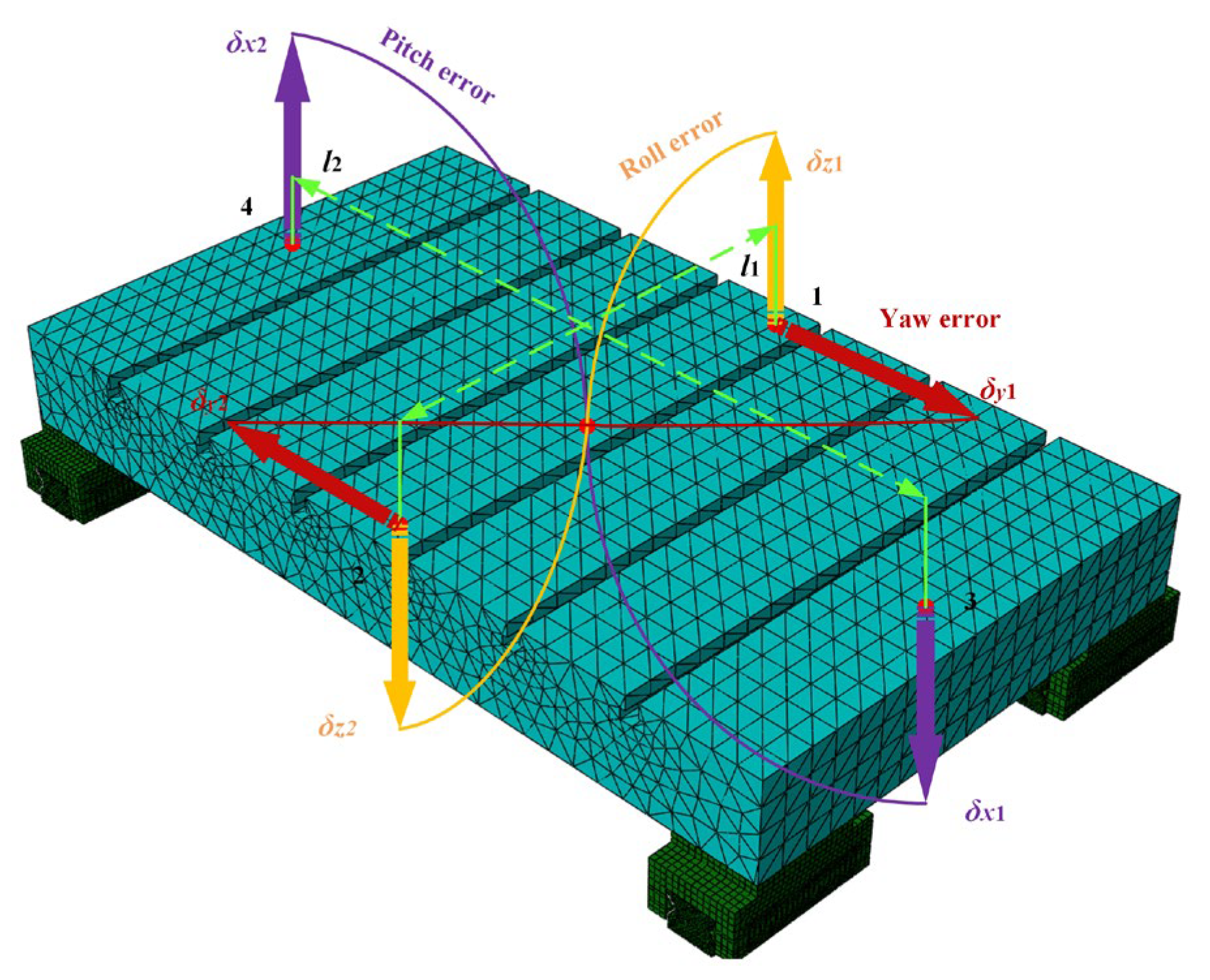
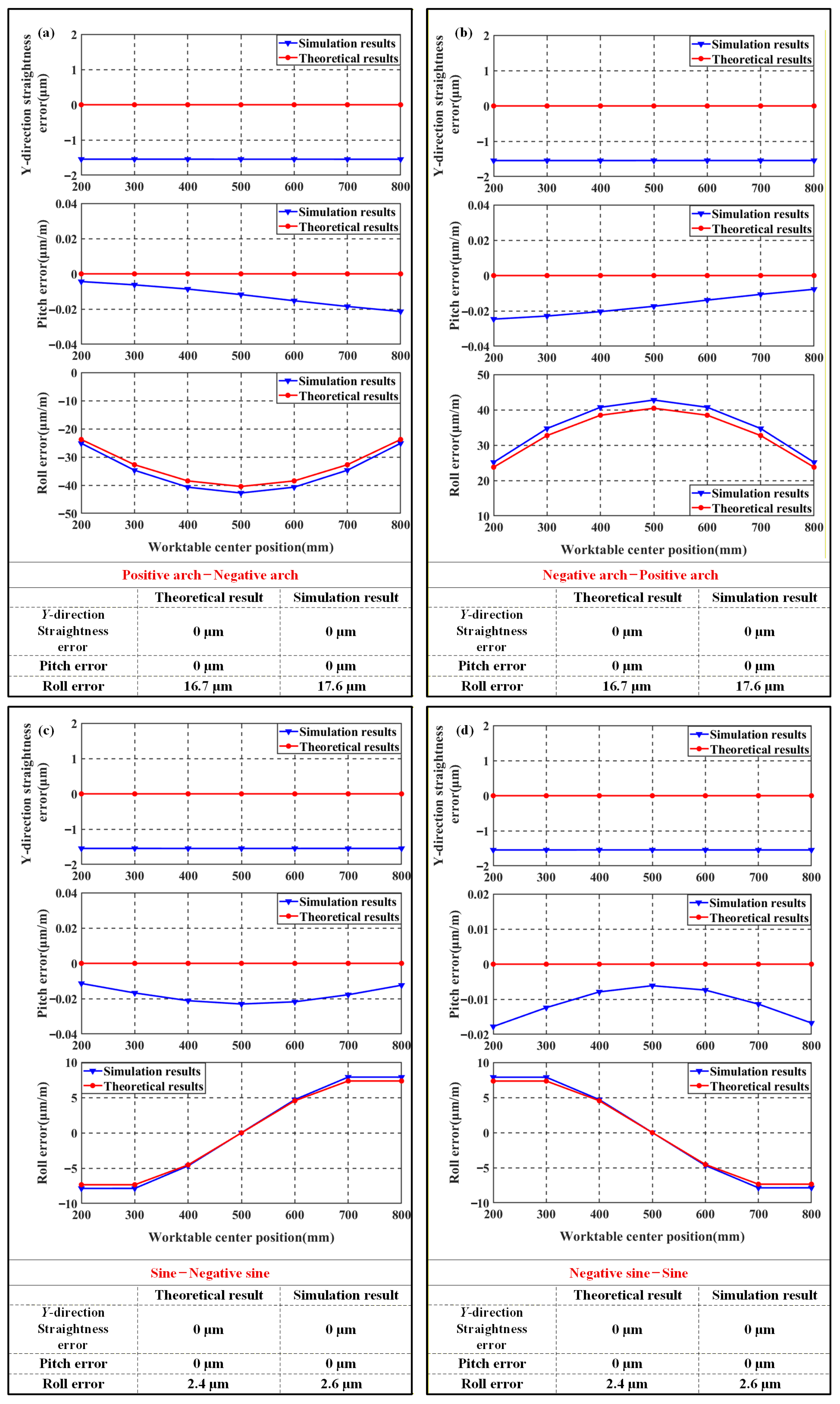
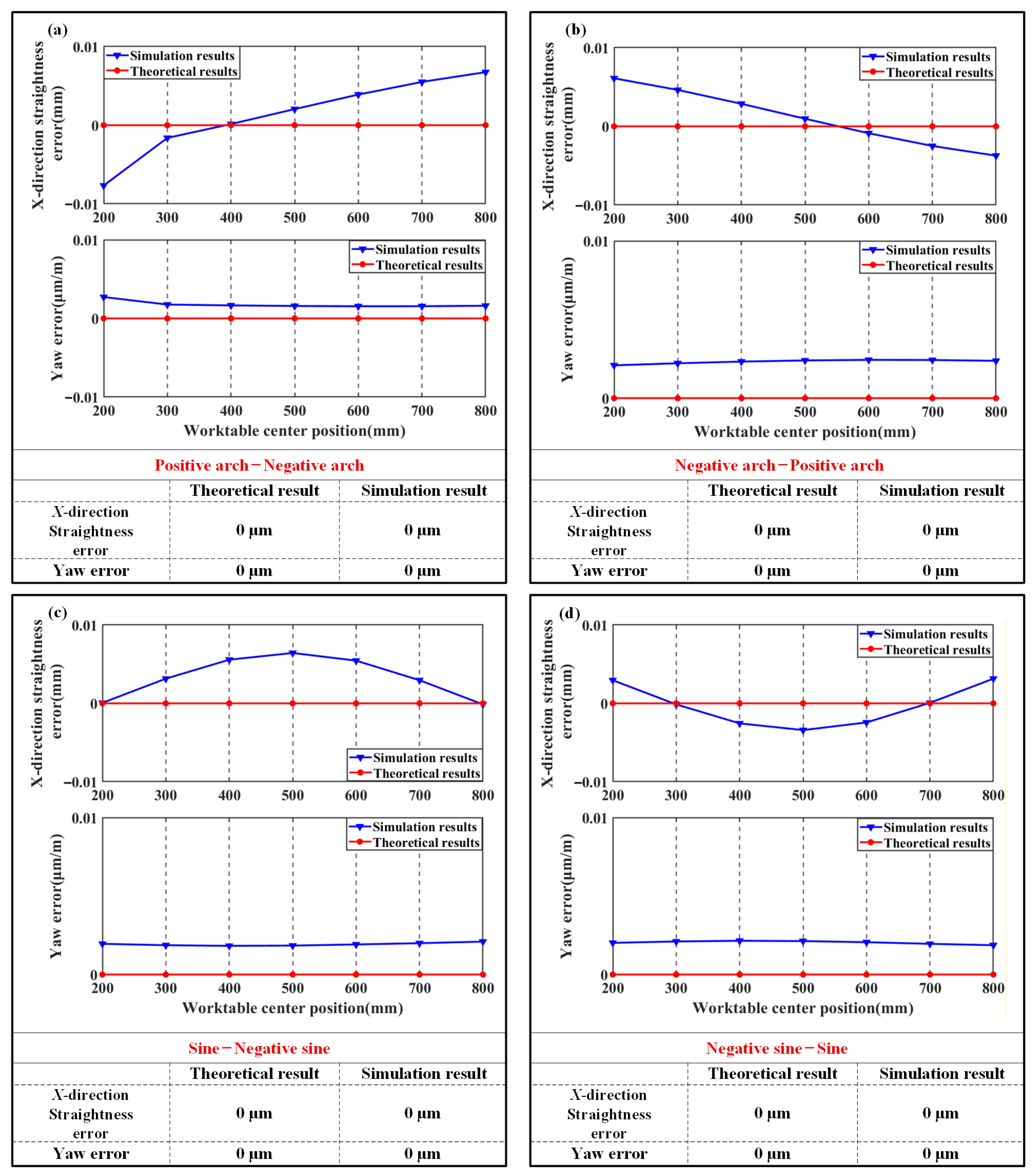
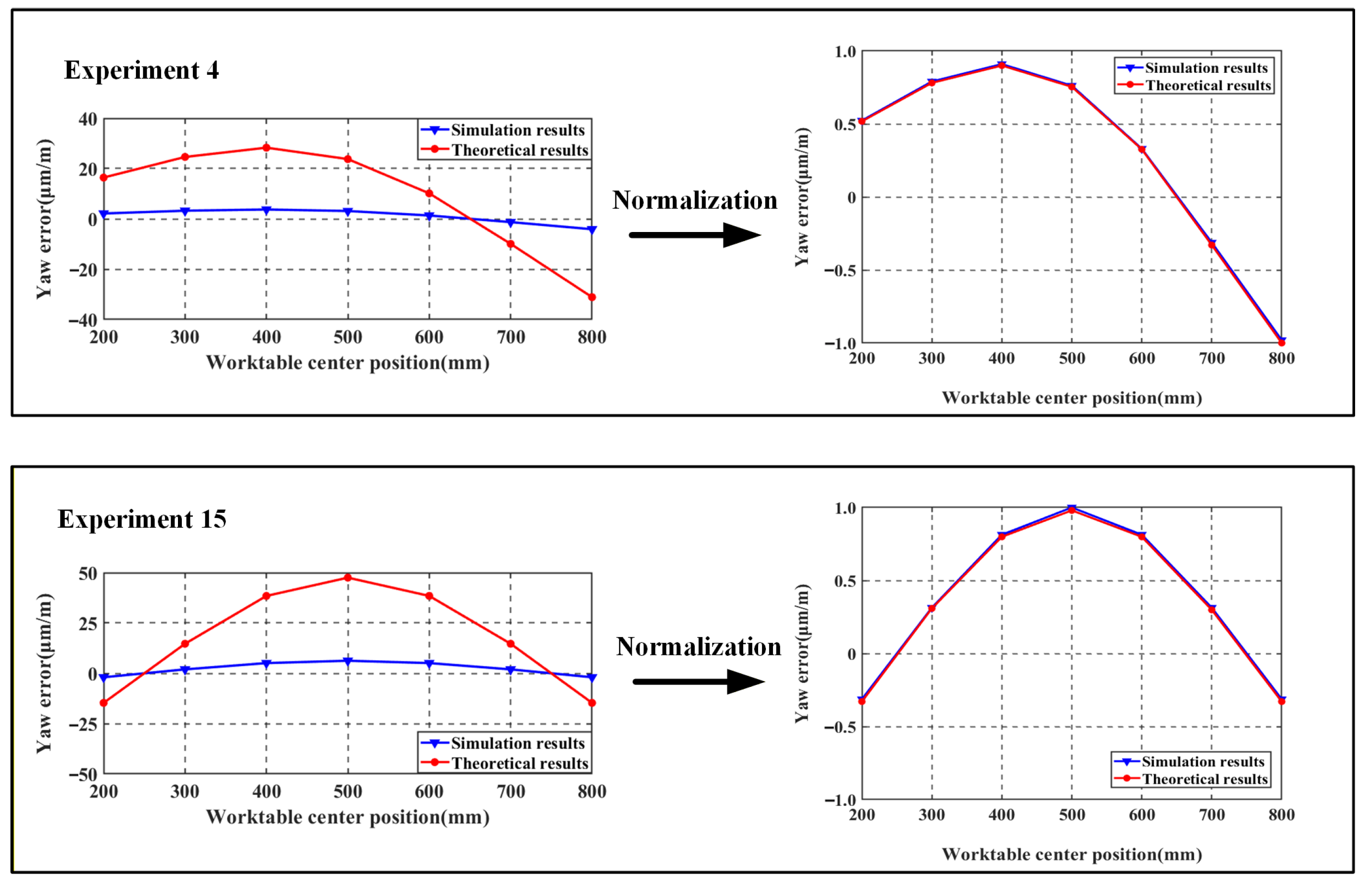


| Parameters | Guideway | Slider | Worktable |
|---|---|---|---|
| Materials | Martensitic stainless steel | Martensitic stainless steel | QT500 |
| Density (g/cm3) | 7.75 | 7.75 | 7.0 |
| Modulus of elasticity (MPa) | 206,000 | 206,000 | 162,000 |
| Poisson’s ratio | 0.3 | 0.3 | 0.293 |
| Experimental Number | Vertical Experimental Design | |
|---|---|---|
| Guideway 1 Error (ev1) | Guideway 2 Error (ev2) | |
| 1 | positive arch | positive arch |
| 2 | negative arch | negative arch |
| 3 | sine | sine |
| 4 | negative sine | negative sine |
| 5 | positive arch | negative arch |
| 6 | negative arch | positive arch |
| 7 | sine | negative sine |
| 8 | negative sine | sine |
| 9 | positive arch | sine |
| 10 | negative arch | negative sine |
| 11 | sine | positive arch |
| 12 | negative sine | negative arch |
| 13 | positive arch | negative sine |
| 14 | negative arch | sine |
| 15 | sine | negative arch |
| 16 | negative sine | positive arch |
| Experimental Number | Horizontal Experimental Design | |
|---|---|---|
| Guideway 1 Error (eh1) | Guideway 2 Error (eh1) | |
| 1 | positive arch | positive arch |
| 2 | positive arch | positive arch |
| 3 | positive arch | positive arch |
| 4 | positive arch | positive arch |
| 5 | negative arch | negative arch |
| 6 | negative arch | negative arch |
| 7 | negative arch | negative arch |
| 8 | negative arch | negative arch |
| 9 | sine | sine |
| 10 | sine | sine |
| 11 | sine | sine |
| 12 | sine | sine |
| 13 | negative sine | negative sine |
| 14 | negative sine | negative sine |
| 15 | negative sine | negative sine |
| 16 | negative sine | negative sine |
| Error Type | X-Direction Straightness Error (μm) | Y-Direction Straightness Error (μm) | Yaw Error (μm/m) | Pitch Error (μm/m) | Roll Error (μm/m) |
|---|---|---|---|---|---|
| 1 | 3.3 | 3.3 | 2.8 | 2.8 | 0 |
| 2 | 0 | 3.3 | 0 | 2.8 | 0 |
| 3 | 1.7 | 0.5 | 31.1 | 62.2 | 0 |
| 4 | 1.7 | 0.5 | 31.1 | 62.2 | 0 |
| 5 | 0 | 0 | 0 | 0 | 16.7 |
| 6 | 3.3 | 0 | 2.8 | 0 | 16.7 |
| 7 | 1.7 | 0 | 31.1 | 0 | 2.4 |
| 8 | 1.7 | 0 | 31.1 | 0 | 2.4 |
| 9 | 1.7 | 1.7 | 31.1 | 31.1 | 8.4 |
| 10 | 1.7 | 1.7 | 31.1 | 31.1 | 8.4 |
| 11 | 0 | 1.7 | 0 | 31.1 | 8.4 |
| 12 | 0.5 | 1.7 | 62.2 | 31.1 | 8.4 |
| 13 | 1.7 | 1.7 | 31.1 | 31.1 | 8.4 |
| 14 | 1.7 | 1.7 | 31.1 | 31.1 | 8.4 |
| 15 | 0.5 | 1.7 | 62.2 | 31.1 | 8.4 |
| 16 | 0 | 1.7 | 0 | 31.1 | 8.4 |
| Error Combination Type | X-Direction Straightness Error (μm) | Y-Direction Straightness Error (μm) | Yaw Error (μm/m) | Pitch Error (μm/m) | Roll Error (μm/m) |
|---|---|---|---|---|---|
| 1 | 6.6 | 6.7 | 0.6 | 2.6 | 0 |
| 2 | 0 | 6.6 | 0 | 2.7 | 0 |
| 3 | 3.3 | 1.0 | 4.1 | 60.0 | 0 |
| 4 | 3.3 | 1.0 | 4.1 | 60.0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 17.6 |
| 6 | 6.6 | 0 | 0.4 | 0 | 17.6 |
| 7 | 3.3 | 0 | 4.1 | 0 | 2.6 |
| 8 | 3.3 | 0 | 4.1 | 0 | 2.6 |
| 9 | 3.3 | 3.3 | 4.1 | 30.0 | 8.8 |
| 10 | 3.3 | 3.3 | 4.1 | 30.0 | 8.8 |
| 11 | 0 | 3.3 | 0 | 30.0 | 8.8 |
| 12 | 1.0 | 3.3 | 8.2 | 30.0 | 8.8 |
| 13 | 3.3 | 3.3 | 4.1 | 30.0 | 8.8 |
| 14 | 3.3 | 3.3 | 4.1 | 30.0 | 8.8 |
| 15 | 1.0 | 3.3 | 8.2 | 30.0 | 8.8 |
| 16 | 0 | 3.3 | 0 | 30.0 | 8.8 |
| Left-Guideway Error Shape | Right-Guideway Error Shape | X-Direction Error- Averaging Coefficient | Y-Direction Error- Averaging Coefficient |
|---|---|---|---|
| positive arch | positive arch | 0.66405 | 0.66505 |
| positive arch | negative arch | 0.00036 | 0.000029 |
| positive arch | sine | 0.33143 | 0.33225 |
| positive arch | negative sine | 0.33345 | 0.33238 |
| negative arch | positive arch | 0.000043 | 0.000029 |
| negative arch | negative arch | 0.6646 | 0.664 |
| negative arch | sine | 0.33345 | 0.3324 |
| negative arch | negative sine | 0.33143 | 0.3323 |
| sine | negative arch | 0.33285 | 0.33255 |
| sine | positive arch | 0.33203 | 0.33215 |
| sine | negative sine | 0.00065 | 0.000104 |
| sine | sine | 0.0997 | 0.099 |
| negative sine | negative arch | 0.33203 | 0.3322 |
| negative sine | positive arch | 0.33285 | 0.3332 |
| negative sine | negative sine | 0.0997 | 0.099 |
| negative sine | sine | 0.00065 | 0.000103 |
| Name | Application | Note |
|---|---|---|
| Micrometer | Measurement | Resolution: 1 μm |
| Optical collimator | Slider displacement deviation measurement | Accuracy: 0.1”, Resolution: 0.01” |
| Laser interferometer | Measurement of worktable pose error | Renishaw XM60 |
| Spirit level | Measurement accuracy | 00-Level |
| Feeler gauges | Adjustment error shape | Specifications: 5–60 μm |
| Torque wrench | Bolt tightening | Torque range: 28–210 N·m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Guo, X.; Wang, H.; Sun, G.; Zhang, D.; Su, Z.; Hu, G. An Accuracy Design Method for a Linear Feed System of Machine Tools Considering the Geometric Error Shape of the Guideway. Machines 2026, 14, 82. https://doi.org/10.3390/machines14010082
Guo X, Wang H, Sun G, Zhang D, Su Z, Hu G. An Accuracy Design Method for a Linear Feed System of Machine Tools Considering the Geometric Error Shape of the Guideway. Machines. 2026; 14(1):82. https://doi.org/10.3390/machines14010082
Chicago/Turabian StyleGuo, Xin, Hongxu Wang, Guangming Sun, Dawei Zhang, Zhe Su, and Gaofeng Hu. 2026. "An Accuracy Design Method for a Linear Feed System of Machine Tools Considering the Geometric Error Shape of the Guideway" Machines 14, no. 1: 82. https://doi.org/10.3390/machines14010082
APA StyleGuo, X., Wang, H., Sun, G., Zhang, D., Su, Z., & Hu, G. (2026). An Accuracy Design Method for a Linear Feed System of Machine Tools Considering the Geometric Error Shape of the Guideway. Machines, 14(1), 82. https://doi.org/10.3390/machines14010082




