Trajectory Tracking Control for Wheeled Mobile Robots with Unknown Slip Rates Based on Improved Rapid Variable Exponential Reaching Law and Sliding Mode Observer
Abstract
1. Introduction
- (1)
- Innovative Control Architecture: Unlike the independent design methods of sliding mode observer and approaching law in existing research, the sliding mode state observer and the improved rapid exponential convergence law are integrated into the same control framework in this paper. The observer is used to estimate unmeasurable slip ratios (, ) in real time, and the observation results are directly embedded into the control law. The parameters of the improved rapid exponential convergence law are adjusted in real time according to the motion situation. This deep coupling not only achieves adaptive parameter adjustment and disturbance compensation but also maintains high-precision trajectory tracking performance under unknown sideslip conditions.
- (2)
- Algorithmic Advancements: Proposes a dual-phase adaptive convergence mechanism that simultaneously accelerates convergence speed and effectively suppresses chattering. Designs a novel sliding surface whose structural parameters can be tuned to regulate the convergence rate of pose errors, guaranteeing finite-time convergence.
- (3)
- Performance Breakthroughs: Both simulations and experimental results validate the proposed method’s rapid convergence characteristics and strong robustness in unknown slip scenarios.
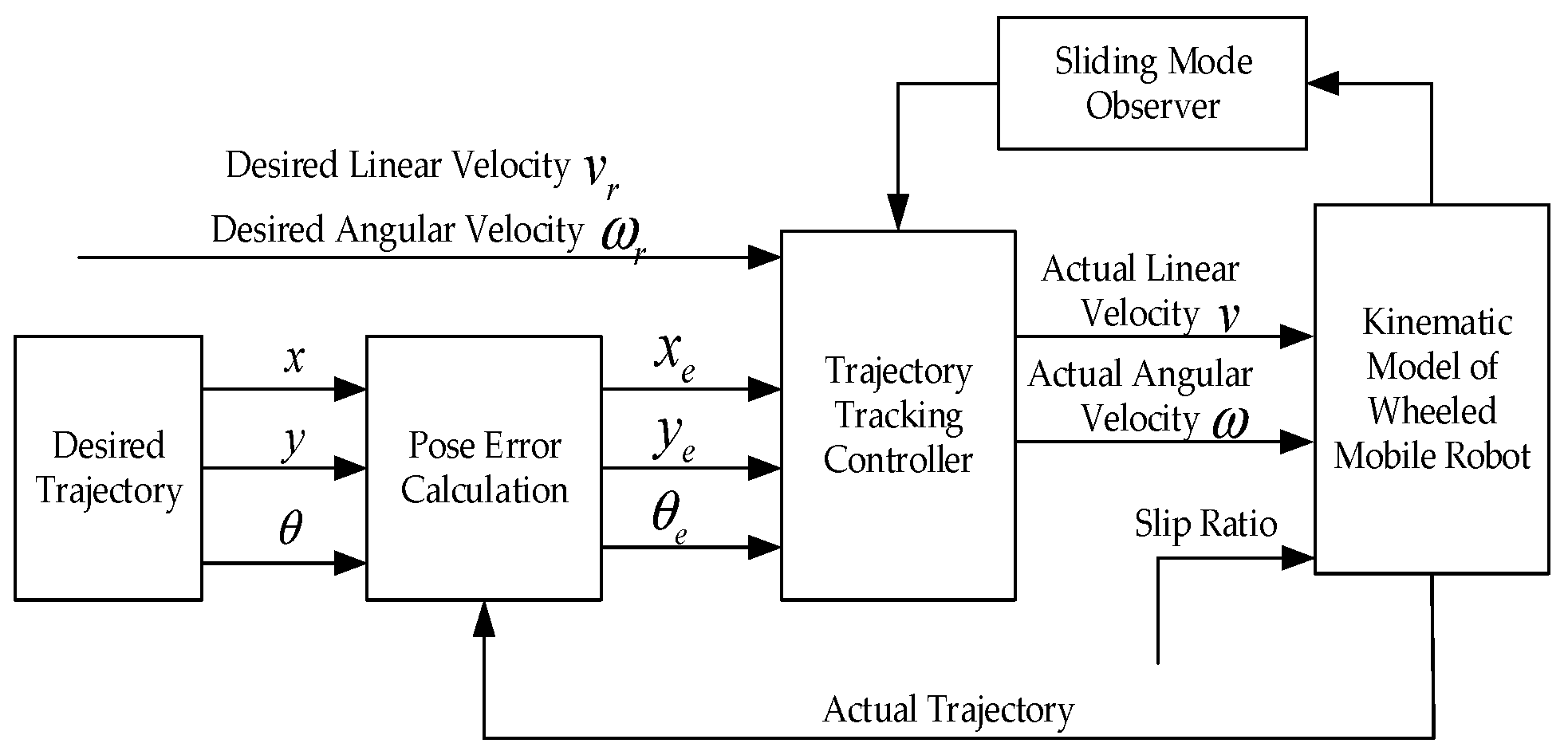
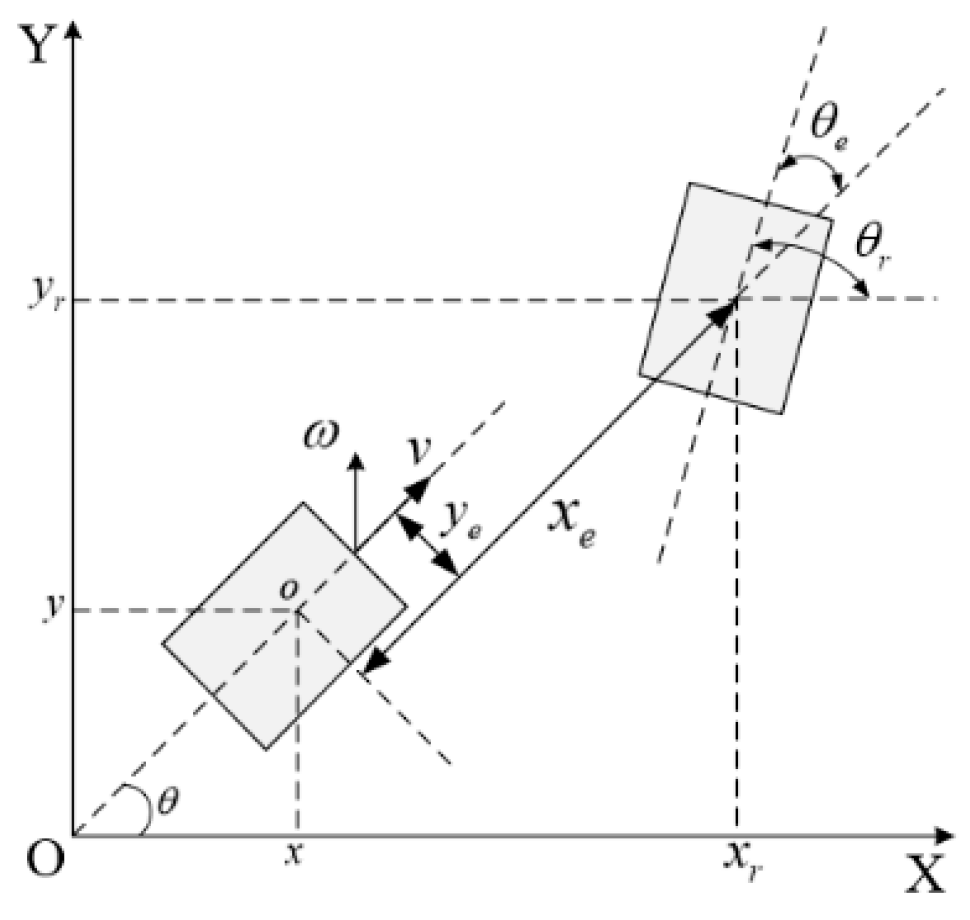
2. Establishment of Kinematic Model of Wheeled Mobile Robot in Slipping State
3. Estimation of Slippage Parameters
3.1. Design of Sliding Mode Observer
3.2. Stability Analysis of Sliding Mode Observer
4. Design of Trajectory Tracking Controller
4.1. Establishment of Trajectory Tracking Error Model in Slip State
4.2. Design of Trajectory Tracking Controller Improved Rapid Variable Exponential Reaching Law and Its Performance Analysis Under Different Parameters
4.2.1. Improved Rapid Variable Exponential Reaching Law
4.2.2. Analysis of the Influence of Reaching Law Parameters on Performance
- (1)
- and exponent a: Govern the convergence speed in the large-error phase (). Increasing accelerates initial convergence, while ensures high-power terms () dominate far from the sliding surface, significantly improving initial convergence speed. Excessively large or a may exacerbate chattering.
- (2)
- and exponent b: Regulate dynamics near the sliding surface (). Increasing shortens convergence time for small errors but may intensify chattering. Setting enables fractional-power terms () near the sliding surface, smoothing transitions and suppressing chattering.
- (3)
- : Ensures linear convergence and steady-state robustness against disturbances. Increasing accelerates overall convergence but may cause oscillations if oversized.
4.3. Design and Stability Analysis of Sliding Mode Trajectory Tracking Controller with Parameter Influence on Control Performance
4.3.1. Design of Trajectory Tracking Controller
4.3.2. Stability Analysis
4.3.3. Analysis of the Influence of Sliding Mode Trajectory Tracking Controller Parameters on Control Performance
- (1)
- (Linear term coefficients): Directly determine the exponential convergence rate of errors. Increasing them accelerates linear error convergence but may induce overshoot and oscillations.
- (2)
- (High-power term coefficients): Dominate rapid convergence in the large-error phase ().
- (3)
- (Fractional-power terms): Optimize smoothness in the small-error phase (), avoiding steady-state chattering.
- (4)
- ratio: Determines the convergence speed of position error via Equation (58). Increasing the ratio accelerates convergence but may cause oscillations (e.g., oversized or undersized in simulations). The optimal ratio balances speed and smoothness. Simulations use = 16.4, = 17.8 (ratio ≈ 0.92) to ensure convergence while suppressing oscillations.
5. Simulation and Experiment
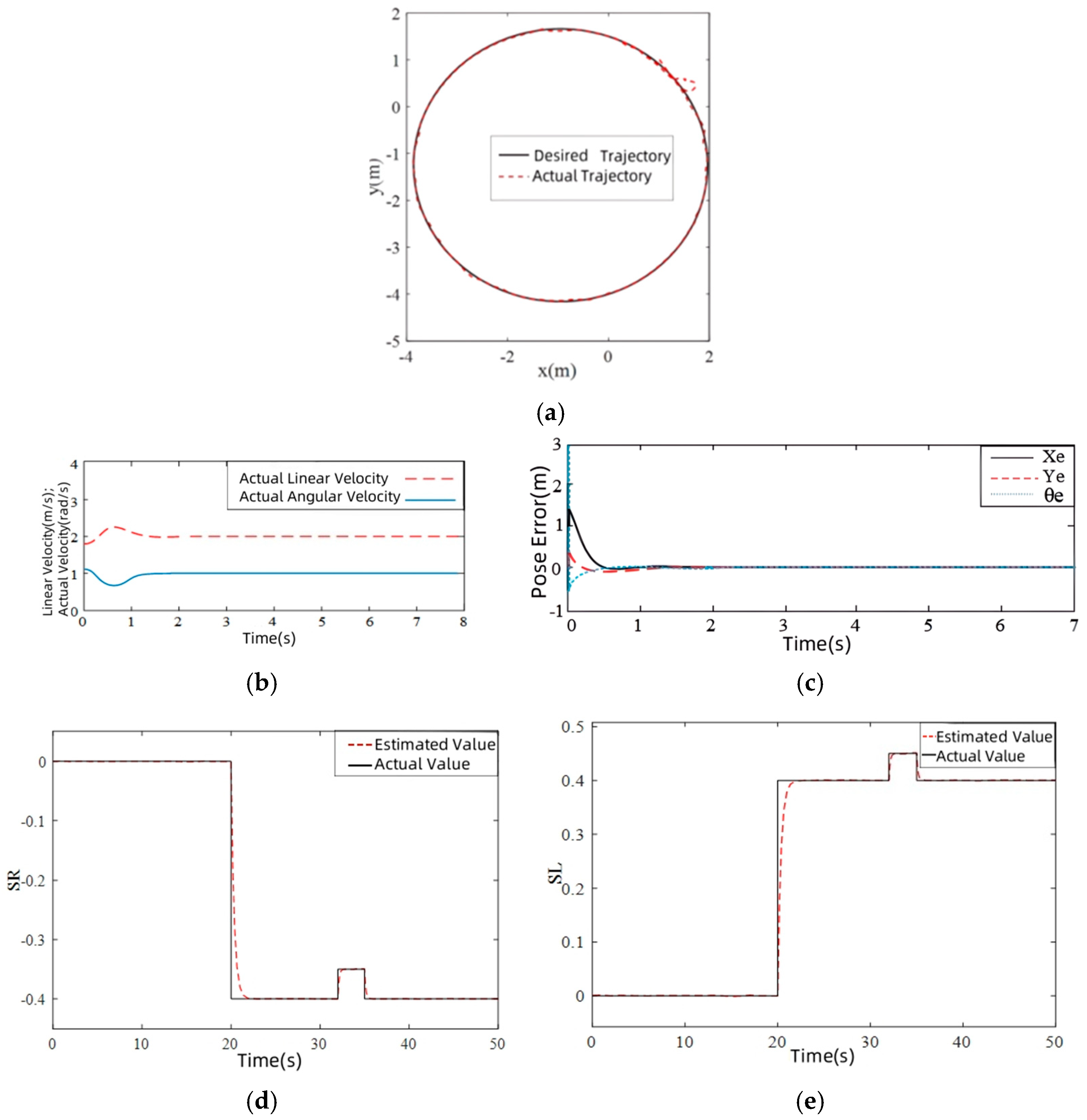
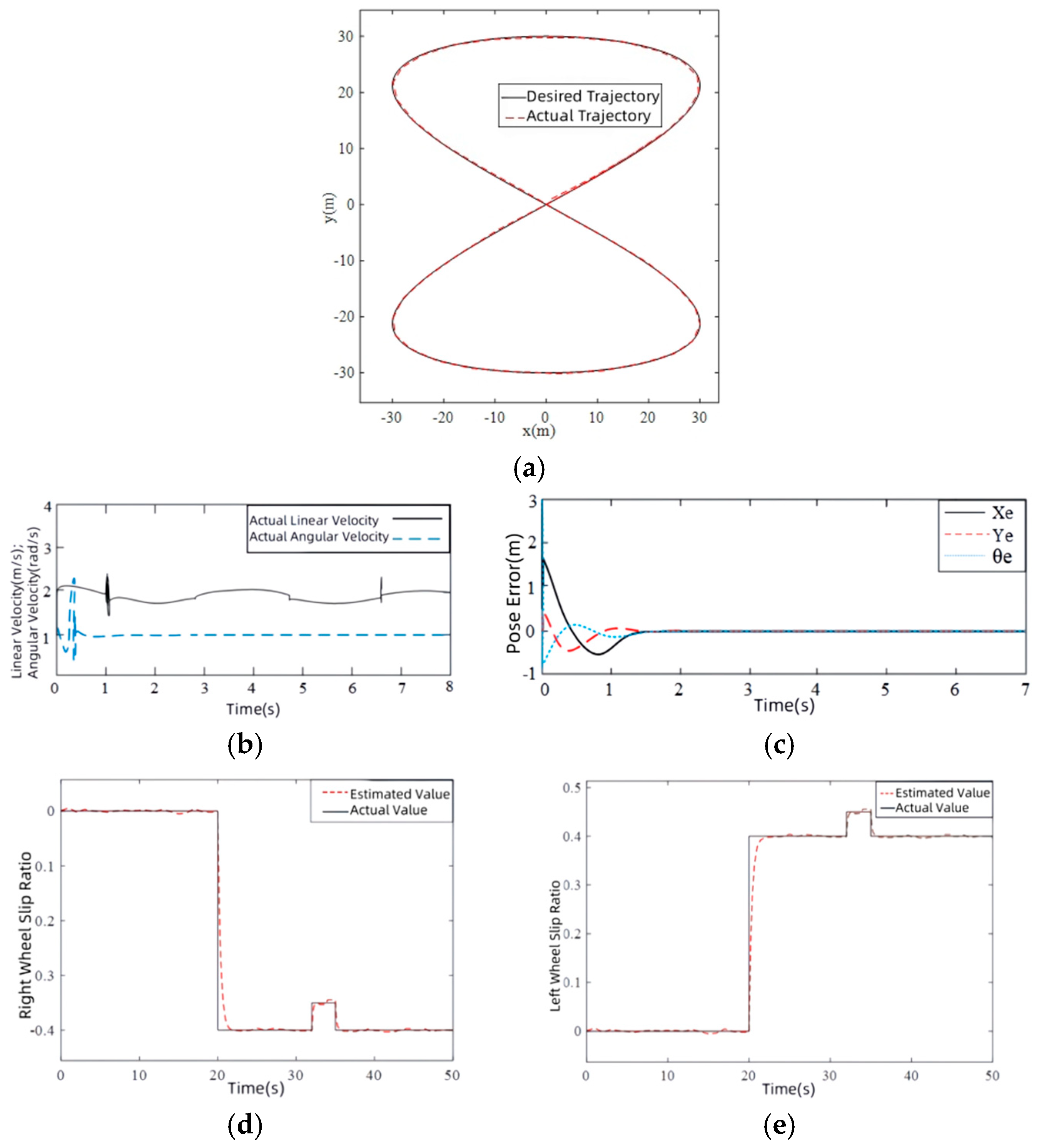
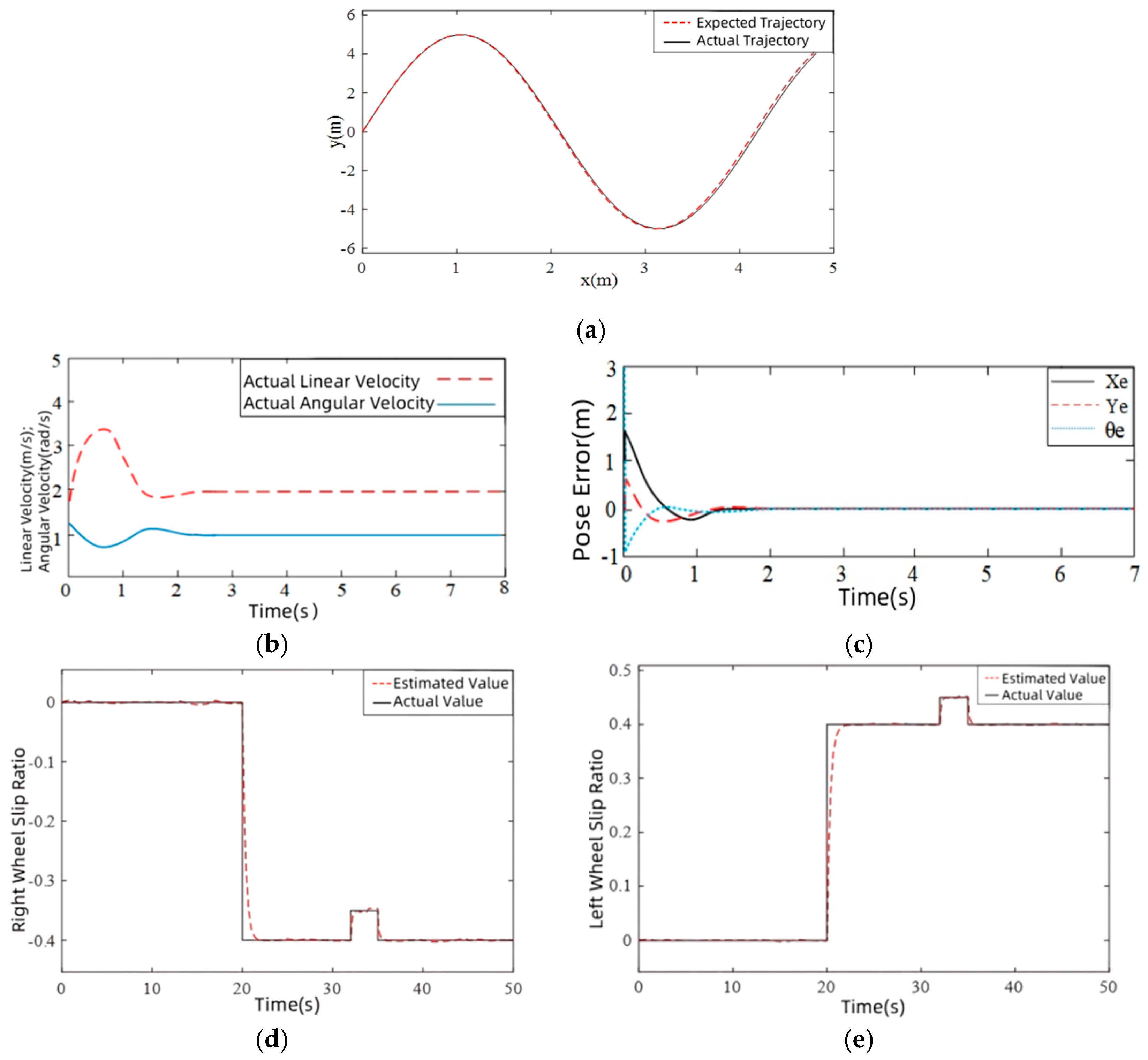
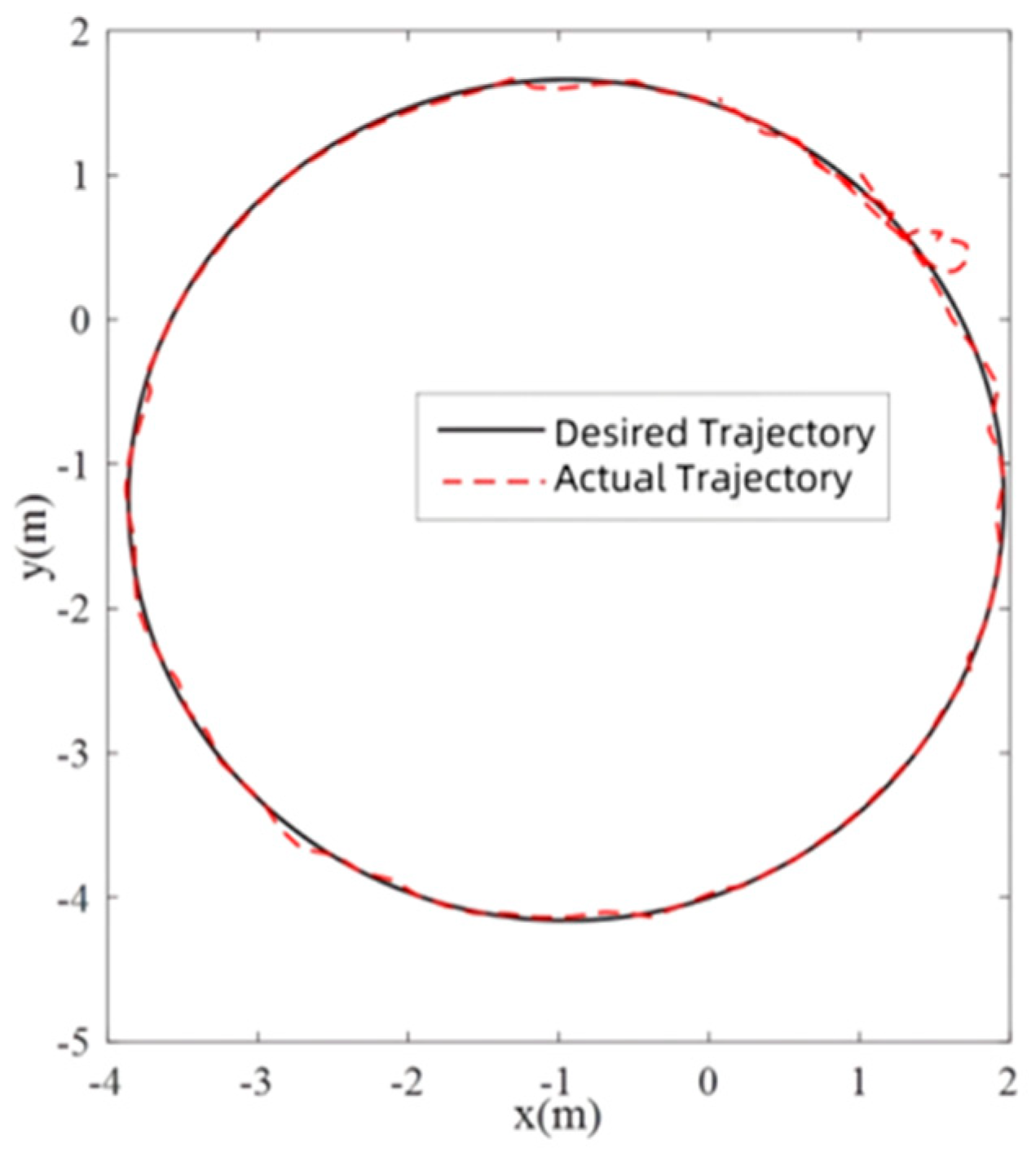
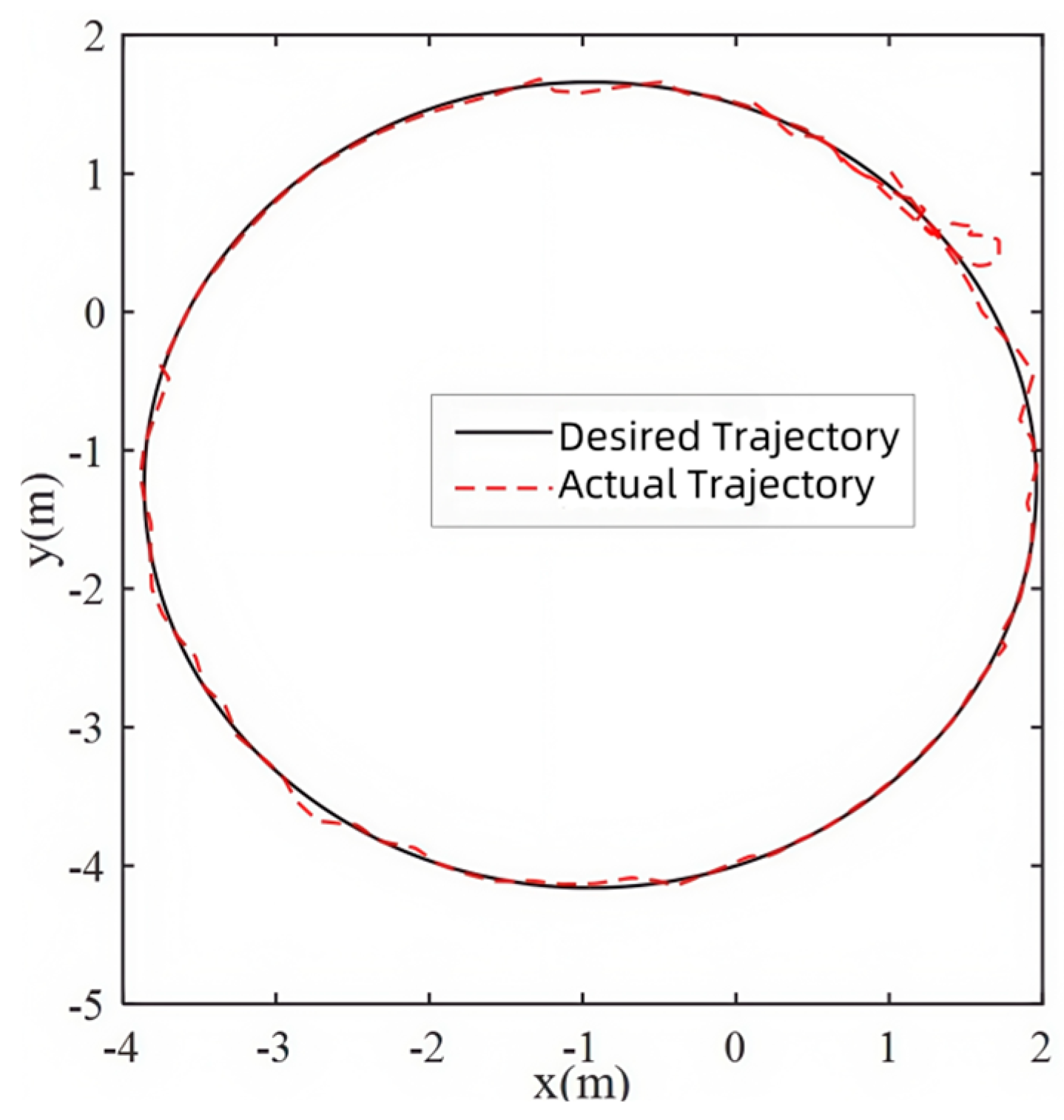
5.1. Simulation Verification
- (1)
- The tracking path of the robot is selected as a circular shape, and its reference trajectory is as follows:
- (2)
- The tracking path of the robot is selected as “8” shape, and its reference trajectory is as follows:
- (3)
- The tracking path of the robot is selected as a sinusoidal shape, with its reference trajectory being the following:
5.2. Simulation Comparison Verification
- (1)
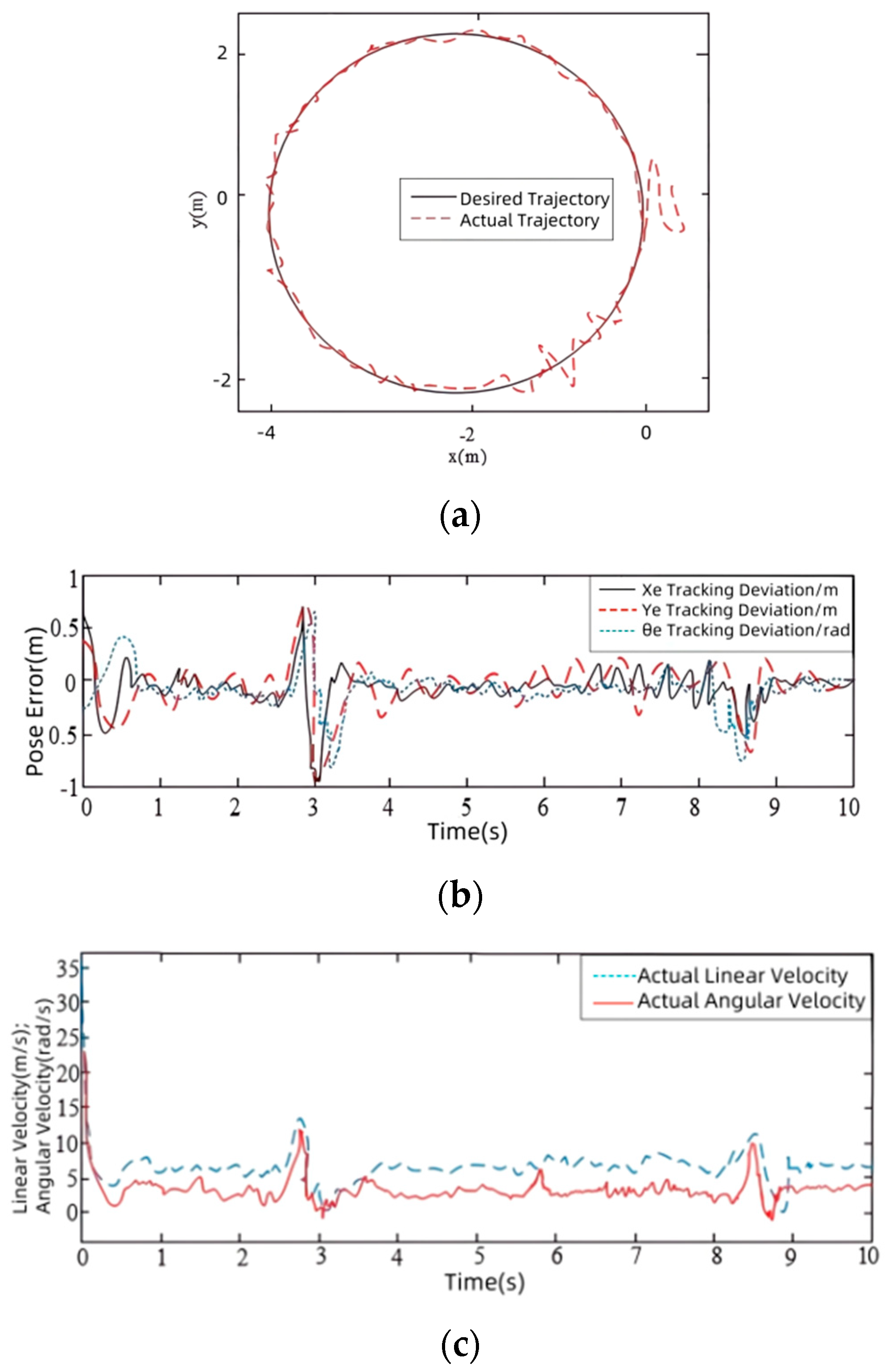
- Replace the convergence law of the sliding mode trajectory tracking controller designed in Section 3.2 with a rapid double exponential reaching law, keeping other aspects unchanged. The result of tracking the circular trajectory is shown in Figure 7.
- (2)
- Let the slip rate parameters and in Equation (35) be 0; the sliding mode observer is not used to estimate the slip rate, nor is the influence of the slip rate considered in the control; the others remain unchanged. The result of tracking the circular trajectory is shown in Figure 8.
- (3)
- Due to the ability of fuzzy PID controller to adjust PID parameters in real time according to environmental changes, it has strong environmental adaptability and robustness. Therefore, in this section, the fuzzy PID control algorithm was used to design a trajectory tracking controller. Other experimental conditions remain unchanged; the result of tracking the circular trajectory is shown in Figure 9.
5.3. Experimental Verification
6. Limitations and Future Work
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Li, B.; Wang, C.H.; Ma, L.; Zhang, H.C. Fixed-time trajectory tracking control for a wheel mobile robot. Control Decis. 2024, 39, 845–852. [Google Scholar]
- Xu, S.; Ou, Y.S.; Wang, Z.Y.; Li, H. Learning-based kinematic control using position and velocity errors for robot trajectory tracking. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1100–1110. [Google Scholar] [CrossRef]
- Kim, Y.; Singh, T. Energy-time optimal trajectory tracking control of wheeled mobile robots. IEEE/ASME Trans. Mechatron. 2024, 29, 1283–1294. [Google Scholar] [CrossRef]
- Liu, X.; Wang, W.; Li, X.; Liu, F.; He, Z.; Yao, Y.; Ruan, H.; Zhang, T. MPC-based high-speed trajectory tracking for 4WIS robot. ISA Trans. 2022, 123, 413–424. [Google Scholar] [CrossRef]
- Wang, S.; Li, G.; Song, J.; Liu, B. Research on an intelligent vehicle trajectory tracking method based on optimal control theory. World Electr. Veh. J. 2024, 15, 160. [Google Scholar] [CrossRef]
- Wu, H.; Wang, S.; Xie, Y.; Li, H.; Zheng, S.; Jiang, L. Adaptive abrupt disturbance rejection tracking control for wheeled mobile robots. IEEE Robot. Autom. Lett. 2024, 9, 7787–7794. [Google Scholar] [CrossRef]
- Li, H.; Bi, L.Z.; Yi, J. Sliding-mode nonlinear predictive control of brain-controlled mobile robots. IEEE Trans. Cybern. 2022, 52, 5419–5431. [Google Scholar] [CrossRef] [PubMed]
- Ryoo, Y.J. Trajectory-tracking control of a transport robot for smart logistics using the fuzzy controller. Int. J. Fuzzy Log. Intell. Syst. 2022, 22, 69–77. [Google Scholar] [CrossRef]
- Dong, C.; Yu, Z.; Chen, X.; Huang, Y.; Huang, Q. Adaptability control towards complex ground based on fuzzy logic for humanoid robots. IEEE Trans. Fuzzy Syst. 2022, 30, 1574–1584. [Google Scholar] [CrossRef]
- Falsafi, M.H.; Alipour, K.; Tarvirdizadeh, B. Tracking-error fuzzy-based control for nonholonomic wheeled robots. Arab. J. Sci. Eng. 2019, 44, 881–892. [Google Scholar] [CrossRef]
- Tan, W.; Wang, M.; Ma, K. Research on intelligent vehicle trajectory tracking control based on improved adaptive MPC. Sensors 2024, 24, 2316. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.J.; Zhao, F.H.; Lou, Y.J. Interactive model predictive control for robot navigation in dense crowds. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 2289–2301. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, X.; Huang, J.; Yuan, L. Adaptive model predictive control for intelligent vehicle trajectory tracking considering road curvature. Int. J. Automot. Technol. 2024, 25, 1051–1064. [Google Scholar] [CrossRef]
- Yang, H.; Wang, J.; Li, S.; Chen, W. Trajectory tracking for wheeled mobile robots via model predictive control with softening constraints. IET Control Theory Appl. 2018, 12, 206–214. [Google Scholar] [CrossRef]
- Silaa, M.Y.; Bencherif, A.; Barambones, O. Indirect adaptive control using neural network and discrete extended Kalman filter for wheeled mobile robot. Actuators 2024, 13, 51. [Google Scholar] [CrossRef]
- Lu, X.; Fei, J. Velocity tracking control of wheeled mobile robots by iterative learning control. Int. J. Adv. Robot. Syst. 2016, 13, 103. [Google Scholar] [CrossRef]
- Hassan, N.; Saleem, A. Neural network-based adaptive controller for trajectory tracking of wheeled mobile robots. IEEE Access 2022, 10, 13582–13597. [Google Scholar] [CrossRef]
- Wu, X.; Li, X.; Zhang, D.; Wang, Y.; Zhang, Q. A control strategy for point stabilization and trajectory tracking of wheeled mobile robots. Robot. Auton. Syst. 2025, 173, 105040. [Google Scholar] [CrossRef]
- Kang, Z.; Zhang, H.; Huang, K.; Zhao, H.; Zhang, Y. Adaptive trajectory tracking of wheeled mobile robots based on a fish-eye camera. Int. J. Control Autom. Syst. 2019, 17, 2297–2309. [Google Scholar] [CrossRef]
- Zhang, K.; Chai, B.; Tan, M. Optimal enhanced backstep method for trajectory tracking control of the wheeled mobile robot. Optim. Control Appl. Methods 2024, 45, 2762–2790. [Google Scholar] [CrossRef]
- Binh, N.T.; Tung, N.A.; Nam, D.P.; Quang, N.H. An adaptive backstep trajectory tracking control of a tractor trailer wheeled mobile robot. Int. J. Control Autom. Syst. 2019, 17, 465–473. [Google Scholar] [CrossRef]
- Villalobos-Aranda, C.; Pliego-Jiménez, J.; Montañez-Molina, C.; Arellano-Delgado, A. An almost global trajectory tracking controller for differential-drive wheeled mobile robots. Int. J. Control Autom. Syst. 2024, 22, 3684–3693. [Google Scholar] [CrossRef]
- Petrov, P.; Kralov, I. Exponential trajectory tracking control of nonholonomic wheeled mobile robots. Mathematics 2024, 13, 1. [Google Scholar] [CrossRef]
- Yuan, L.; Li, J.N. Consensus of discrete-time nonlinear multiagent systems using sliding mode control based on optimal control. IEEE Access 2022, 10, 47275–47283. [Google Scholar] [CrossRef]
- Sharma, A.K.; Bhushan, B. Comparison of various fuzzy sliding mode based controller on single link inverted pendulum. J. Intell. Fuzzy Syst. 2022, 42, 679–688. [Google Scholar] [CrossRef]
- Lin, H.Z.; Li, Y.M.; Yuan, Z.H.; Wu, T.; Liu, C.L. Sliding mode anti-interference path tracking method for autonomous operation of paddy field plant protection machine. Trans. Chin. Soc. Agric. Mach. 2021, 52, 383–388. [Google Scholar]
- Wang, Z.; Pang, A.M.; Ma, S.B. Novel sliding mode control of mobile robot based on differential evolution algorithm. Modul. Mach. Tool Autom. Manuf. Tech. 2022, 9, 72–75+79. [Google Scholar]
- Geng, Z.W.; Wang, S.; Yang, S.Y. Tracking control of wheeled mobile robot based on backstepping and hierarchical sliding mode control. Manuf. Autom. 2022, 44, 109–112. [Google Scholar]
- Wang, L.L.; Dong, L.Y.; Ma, D.; Liu, X.L.; Wang, H.R. Active disturbance rejection tracking control of wheeled mobile robots under sliding and slipping conditions. Control Theory Appl. 2020, 37, 431–438. [Google Scholar]
- Li, Z.Y.; Dong, F.M.; Dian, S.Y.; Zhao, T. Anti-windup fuzzy super-twisting sliding mode control of WMRs with skidding and slipping. Comput. Simul. 2022, 39, 387–393+398. [Google Scholar]
- Jia, S.M.; Lu, X.Y.; Zhang, X.Y.; Zhang, G.L. Trajectory tracking control for omnidirectional mobile robot in presence of wheel slipping. Control Decis. 2020, 35, 833–842. [Google Scholar]
- Han, X.; Ge, M.; Cui, J.; Wang, H.; Zhuang, W. Motion modeling of a non-holonomic wheeled mobile robot based on trajectory tracking control. Trans. Can. Soc. Mech. Eng. 2020, 44, 228–233. [Google Scholar] [CrossRef]
- Yang, X. Research on Key Technology of Multi-Mode Motion Control for Reconfigurable Mobile Robot. Ph.D. Thesis, Chongqing University, Chongqing, China, 2023. [Google Scholar]
- Bai, H.; Song, X.G.; Ding, L.; Xia, K.R.; Li, N.; Deng, Z.Q. Adaptive motion control of wheeled mobile robot with unknown slippage. Int. J. Control 2014, 87, 1513–1522. [Google Scholar]
- Sergiyenko, O.; Tyrsa, V.; Zhirabok, A.; Zuev, A. Sensor fault identification in linear and nonlinear dynamic systems via sliding mode observers. IEEE Sens. J. 2022, 22, 10173–10182. [Google Scholar] [CrossRef]
- Li, Y.; Sun, R.; Xia, Y.; Gu, C. A sliding mode control method with improved rapid power approximation law. J. Xi’an Jiaotong Univ. 2022, 56, 118–126. [Google Scholar]




| Performance Indicators | |||||
|---|---|---|---|---|---|
| Adjust time/s | 0.66 | 0.51 | 0.76 | 1.37 | 1.24 |
| Number of oscillations | 1 | 0 | 0 | 1 | 1 |
| Overshoot | 0.06 | 0 | 0 | 0.17 | 0.5 |
| Performance Indicators | |||||
|---|---|---|---|---|---|
| Adjust time/s | 1.48 | 1.47 | 1.45 | 1.53 | 0.44 |
| Number of oscillations | 1 | 1 | 1 | 2 | 2 |
| overshoot | 0.67 | 0.53 | 0.14 | 0.33 | 1.17 |
| Performance Indicators | |||||
|---|---|---|---|---|---|
| Adjust time/s | 1.37 | 1.56 | 1.45 | 2.12 | 2.04 |
| Number of oscillations | 1 | 1 | 1 | 1 | 1 |
| overshoot | 0.16 | 0.09 | 0.18 | 0.78 | 0.25 |
| Adjustment Time/s | |||||
|---|---|---|---|---|---|
| Improved Rapid Variable Exponential Reaching Law + Observe | 0.66 | 0.51 | 0.76 | 1.37 | 1.24 |
| Rapid Double Exponential Reaching Law + Observe | 1.01 | 0.79 | 0.94 | 2.23 | 2.01 |
| Improved Rapid Power Approximation Law | 1.38 | 1.16 | 1.67 | 2.43 | 2.26 |
| Fuzzy PID Trajectory Tracking Controller | 2.62 | 2.48 | 3.05 | 3.98 | 3.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Guo, J.; Wang, T.; Xiong, X.; Feng, Y.; Li, X. Trajectory Tracking Control for Wheeled Mobile Robots with Unknown Slip Rates Based on Improved Rapid Variable Exponential Reaching Law and Sliding Mode Observer. Machines 2025, 13, 765. https://doi.org/10.3390/machines13090765
Li Z, Guo J, Wang T, Xiong X, Feng Y, Li X. Trajectory Tracking Control for Wheeled Mobile Robots with Unknown Slip Rates Based on Improved Rapid Variable Exponential Reaching Law and Sliding Mode Observer. Machines. 2025; 13(9):765. https://doi.org/10.3390/machines13090765
Chicago/Turabian StyleLi, Zexu, Jun Guo, Taiyuan Wang, Xiufang Xiong, Yong Feng, and Xingshu Li. 2025. "Trajectory Tracking Control for Wheeled Mobile Robots with Unknown Slip Rates Based on Improved Rapid Variable Exponential Reaching Law and Sliding Mode Observer" Machines 13, no. 9: 765. https://doi.org/10.3390/machines13090765
APA StyleLi, Z., Guo, J., Wang, T., Xiong, X., Feng, Y., & Li, X. (2025). Trajectory Tracking Control for Wheeled Mobile Robots with Unknown Slip Rates Based on Improved Rapid Variable Exponential Reaching Law and Sliding Mode Observer. Machines, 13(9), 765. https://doi.org/10.3390/machines13090765





