MHSAEO Index for Fault Diagnosis of Rolling Bearings in Electric Hoists
Abstract
1. Introduction
2. Theoretical Foundation of the MHSAEO
3. Property Analysis of the MHSAEO
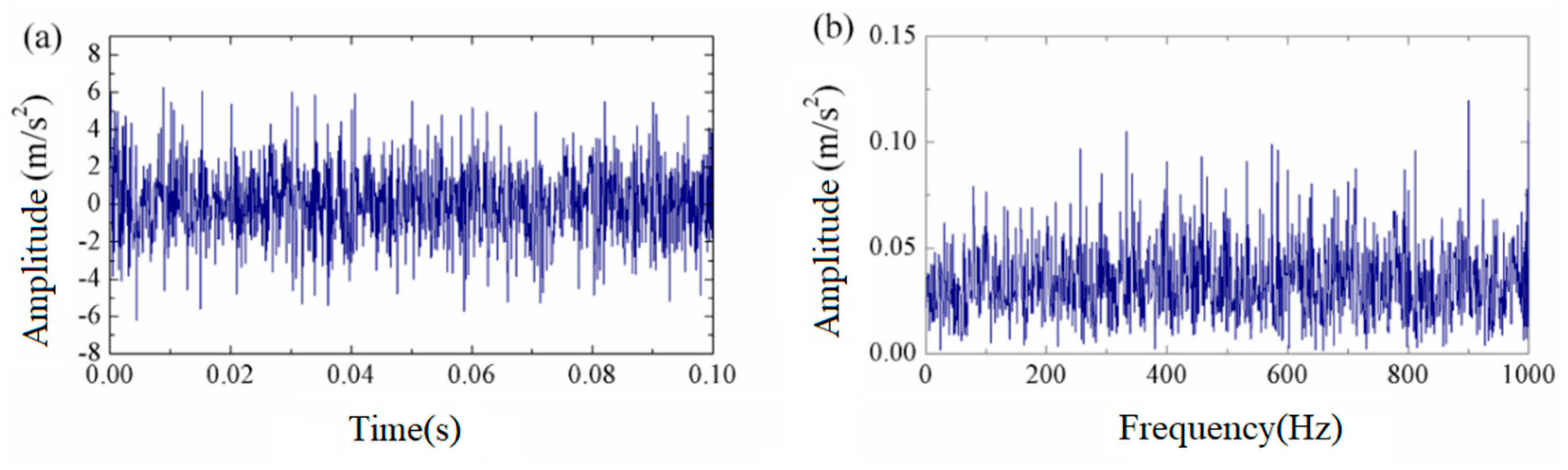
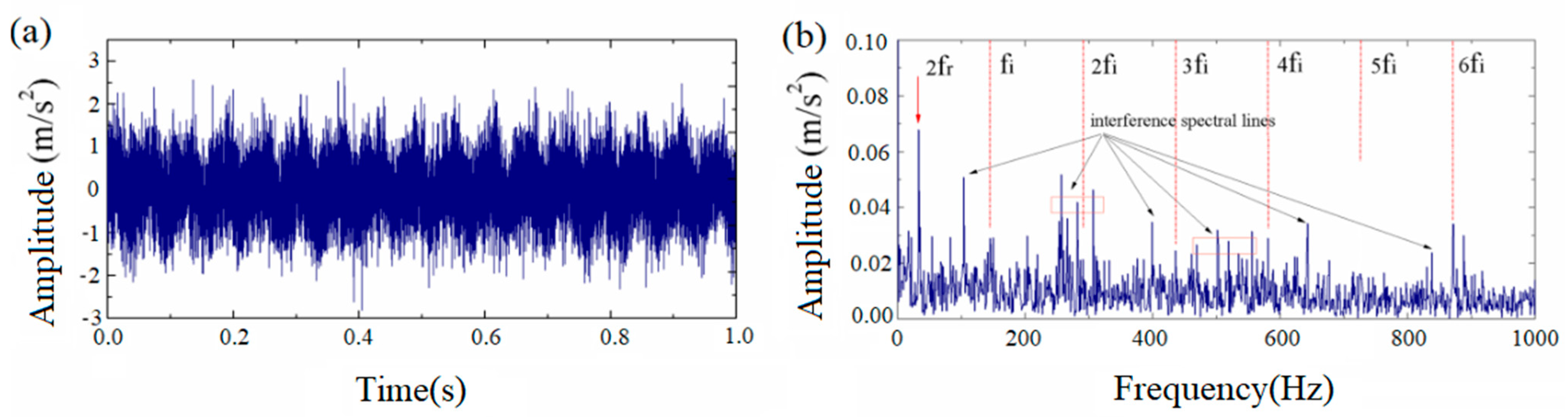
3.1. Anti-Interference Characteristic Analysis
3.2. Signal-to-Noise Ratio Enhancement
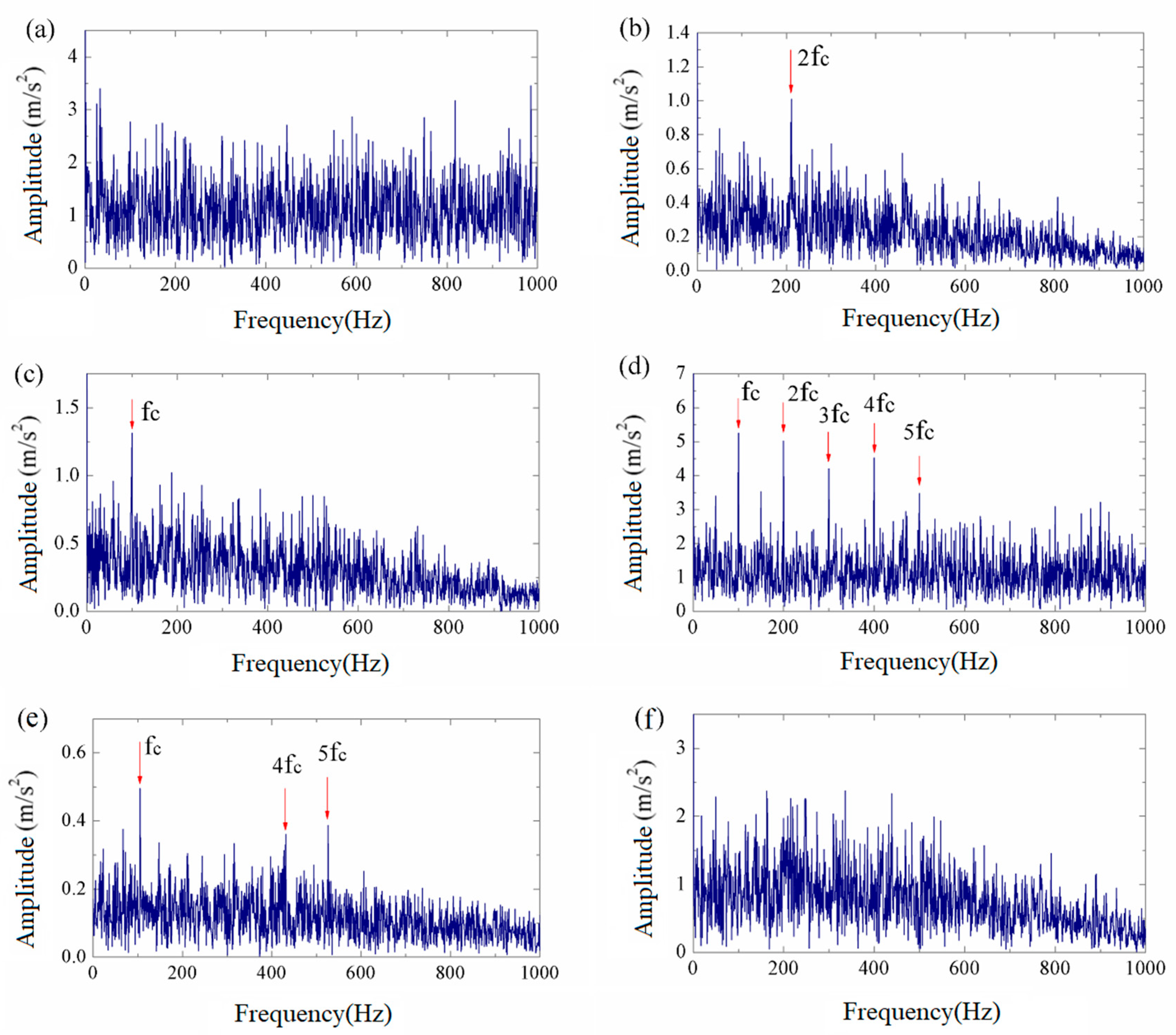
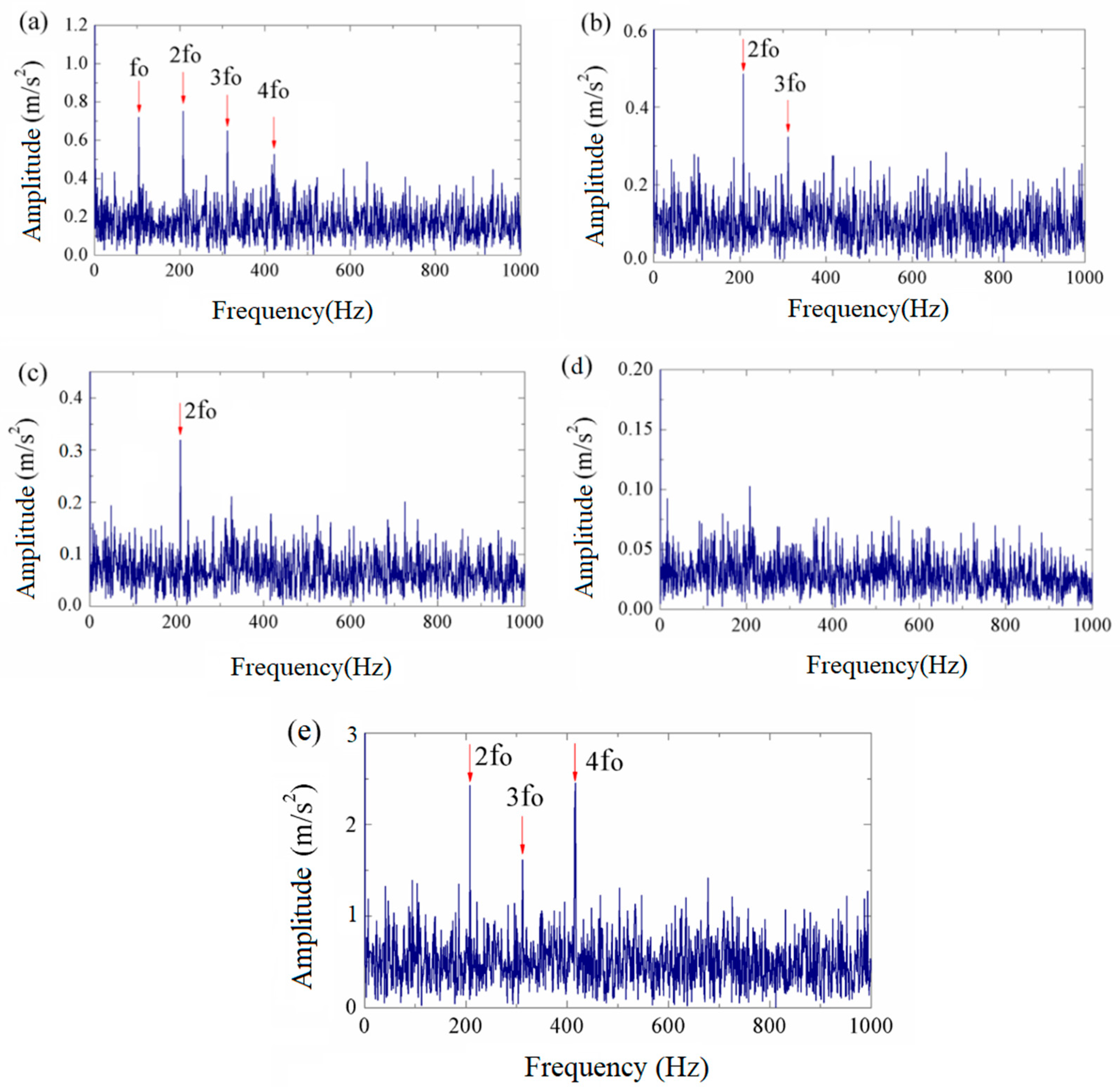
4. Bearing Fault Diagnosis Experiment for Electric Hoist
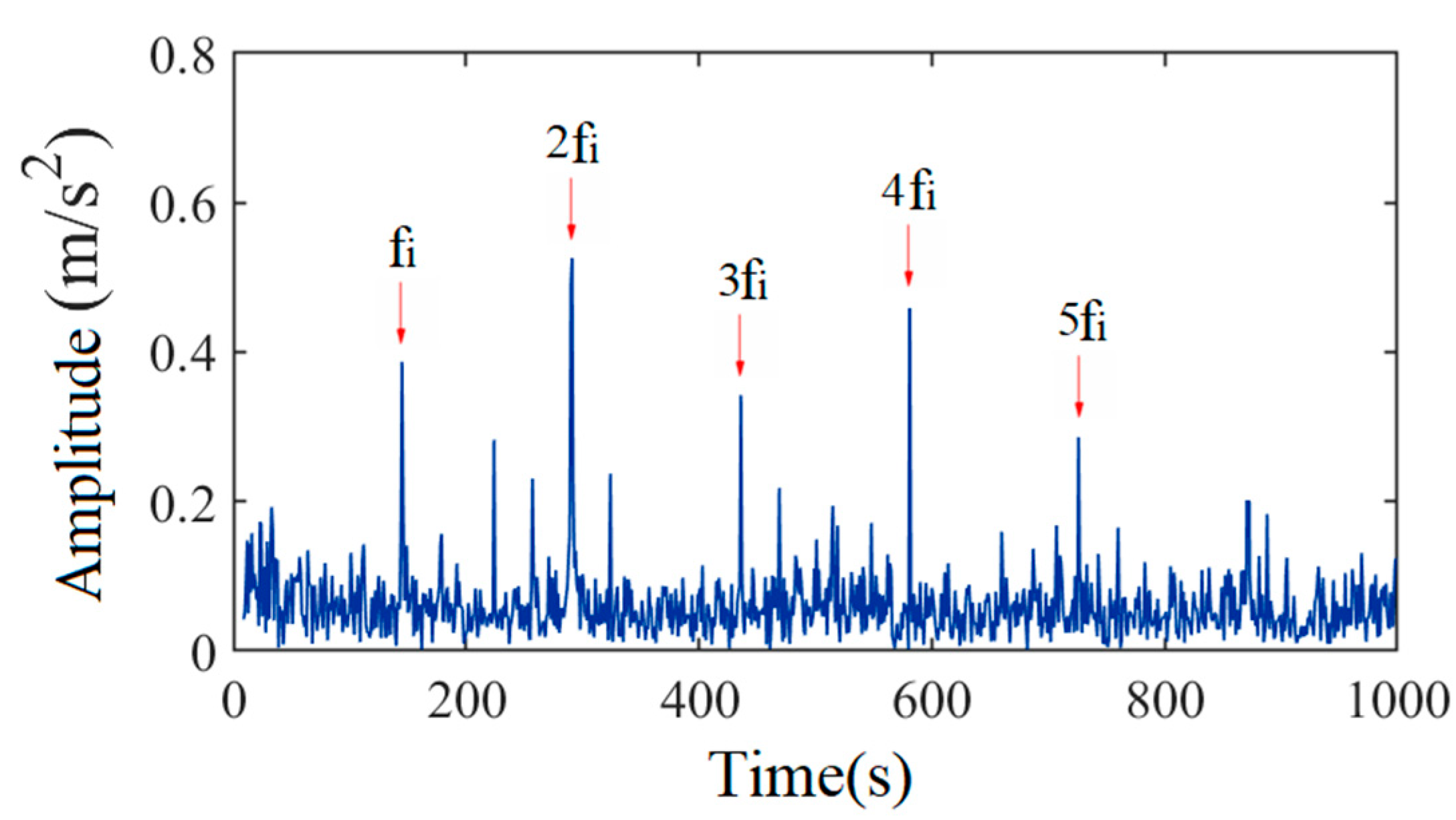
4.1. Outer Race Fault Diagnosis
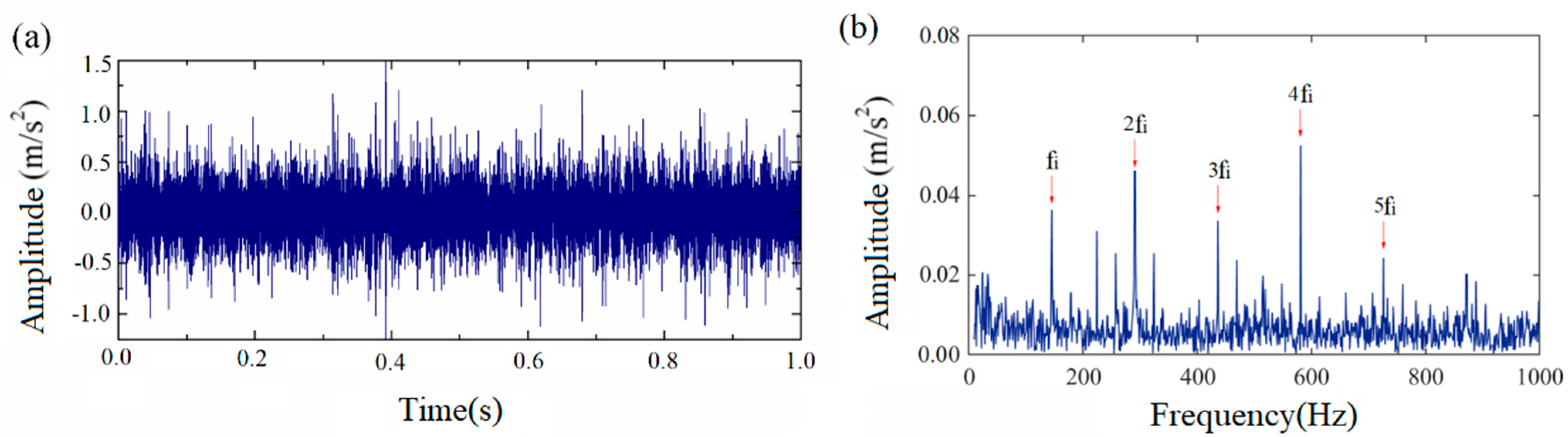
4.2. Inner Race Fault Diagnosis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mikić, D.; Desnica, E.; Kiss, I.; Mikić, V. Reliability analysis of rolling ball bearings considering the bearing radial clearance and operating temperature. Adv. Eng. Lett 2022, 1, 16–22. [Google Scholar] [CrossRef]
- Desnica, E.; Ašonja, A.; Radovanović, L.; Palinkaš, I.; Kiss, I. Selection, dimensioning and maintenance of roller bearings. In Proceedings of the International Conference on Organization and Technology of Maintenance, Austin, TX, USA, 13–16 October 2022; pp. 133–142. [Google Scholar]
- Feng, C.; Zhang, D.; Chen, K.; Wang, D.; Li, X.; Cao, Y. Effect of Dynamic Load on Adhesive Friction at the Interface Between Friction Lining and Wire Rope of Hoist. J. Tribol. 2022, 144, 091704. [Google Scholar] [CrossRef]
- Wu, K.; Xiang, D.; Cai, D.; Feng, Y.; Xu, Y.; Jiang, Z. Extraction of incipient fault features of rolling bearings based on CWSSMD and 1.5 D-EDEO demodulation. Meas. Sci. Technol. 2023, 34, 045011. [Google Scholar] [CrossRef]
- Li, C.G.; Qi, Q.S.; Dong, Q.; Yu, Y.N.; Fan, Y. Research on fatigue remaining life of structures for a dynamic lifting process of a bridge crane. J. Mech. Sci. Technol. 2023, 37, 1789–1801. [Google Scholar] [CrossRef]
- Liu, T.; Li, X.; Lyu, M.; Yan, S. A bearing fault extraction method combining time–frequency mode decomposition based on local maxima with amplitude z-scores. Adv. Eng. Inform. 2025, 64, 103002. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, Y.; Zhang, L.; Ma, C.; Xu, Y. Frequency slice graph spectrum model and its application in bearing fault feature extraction. Mech. Syst. Signal Process. 2025, 226, 112383. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, K.; Sheng, Z.; Zhang, X.; Xu, Y. The amplitude modulation bispectrum: A weak modulation features extracting method for bearing fault diagnosis. Reliab. Eng. Syst. Saf. 2024, 250, 110241. [Google Scholar] [CrossRef]
- Xu, Y.; Fan, F.; Jiang, X. A fast iterative filtering decomposition and symmetric difference analytic energy operator for bearing fault extraction. ISA Trans. 2021, 108, 317–332. [Google Scholar] [CrossRef]
- Lv, J.; Yu, J. Average combination difference morphological filters for fault feature extraction of bearing. Mech. Syst. Signal Process. 2018, 100, 827–845. [Google Scholar] [CrossRef]
- Liao, J.-X.; He, C.; Li, J.; Sun, J.; Zhang, S.; Zhang, X. Classifier-guided neural blind deconvolution: A physics-informed denoising module for bearing fault diagnosis under noisy conditions. Mech. Syst. Signal Process. 2025, 222, 111750. [Google Scholar] [CrossRef]
- Liu, T.; Li, L.; Noman, K.; Li, Y. Local maximum instantaneous extraction transform based on extended autocorrelation function for bearing fault diagnosis. Adv. Eng. Inform. 2024, 61, 102487. [Google Scholar] [CrossRef]
- Li, B.; Li, C.; Liu, J. Incipient detection of bearing fault using impulse feature enhanced weighted sparse representation. Tribol. Int. 2023, 184, 108467. [Google Scholar] [CrossRef]
- Zhu, D.; Chen, J.; Yin, B. Fault feature extraction of rolling element bearing based on TPE-EVMD. Measurement 2021, 183, 109880. [Google Scholar] [CrossRef]
- Li, X.; Ma, J.; Wang, X.; Wu, J.; Li, Z. An improved local mean decomposition method based on improved composite interpolation envelope and its application in bearing fault feature extraction. ISA Trans. 2020, 97, 365–383. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Y.; Jiang, L.; Zhou, L. Fault feature extraction for rolling bearings based on parameter-adaptive variational mode decomposition and multi-point optimal minimum entropy deconvolution. Measurement 2021, 173, 108469. [Google Scholar] [CrossRef]
- Chen, W.; Li, J.; Wang, Q.; Han, K. Fault feature extraction and diagnosis of rolling bearings based on wavelet thresholding denoising with CEEMDAN energy entropy and PSO-LSSVM. Measurement 2021, 172, 108901. [Google Scholar] [CrossRef]
- Zheng, K.; Yao, D.; Shi, Y.; Wei, B.; Yang, D.; Zhang, B. An adaptive group sparse feature decomposition method in frequency domain for rolling bearing fault diagnosis. ISA Trans. 2023, 138, 562–581. [Google Scholar] [CrossRef]
- Yan, H.; Zhou, H.; Wang, Y.; Wu, N.; Zhou, W.; Zhou, J. Combining the synchrosqueezing generalized S-transform of variational mode decomposition with the Teager–Kaiser energy operator to calculate the attenuation gradient for identifying oil and gas reservoirs. Acta Geophys. 2023, 71, 795–812. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, J.; Li, H.; Zhen, D.; Gu, F.; Ball, A. Improved cyclostationary analysis method based on TKEO and its application on the faults diagnosis of induction motors. ISA Trans. 2022, 128, 513–530. [Google Scholar] [CrossRef]
- Agah, G.R.; Rahideh, A.; Khodadadzadeh, H.; Khoshnazar, S.M.; Hedayatikia, S. Broken rotor bar and rotor eccentricity fault detection in induction motors using a combination of discrete wavelet transform and Teager–Kaiser energy operator. IEEE Trans. Energy Convers. 2022, 37, 2199–2206. [Google Scholar]
- Song, X.; Huang, Z.; Liang, G.; Niu, J.; Jia, B.; Liao, Z. Rotating Machinery Structural Faults Feature Enhancement and Diagnosis Base on Low-pass Teager Energy Operator Intrinsic Time-scale Decomposition. Meas. Sci. Technol. 2025, 36, 036113. [Google Scholar] [CrossRef]
- Krishnendu, K.; Pradhan, P.M. Diagnosis of Bearing Faults using Optimal Teager-Kaiser Energy Concentrated Time-Frequency Transforms. IEEE Trans. Instrum. Meas. 2025, 74, 3516311. [Google Scholar] [CrossRef]
- Yang, N.; Liu, Y.; Wei, Y.; Feng, K. Iterative Laplace of Gaussian filter and improved Teager energy operator for bearing fault detection in gearboxes. Meas. Sci. Technol. 2024, 35, 096135. [Google Scholar] [CrossRef]
- Bendjama, H. Bearing fault diagnosis based on optimal Morlet wavelet filter and Teager-Kaiser energy operator. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 392. [Google Scholar] [CrossRef]
- Gu, R.; Chen, J.; Hong, R.; Wang, H.; Wu, W. Incipient fault diagnosis of rolling bearings based on adaptive variational mode decomposition and Teager energy operator. Measurement 2020, 149, 106941. [Google Scholar] [CrossRef]
- Bendjama, H. Feature extraction based on vibration signal decomposition for fault diagnosis of rolling bearings. Int. J. Adv. Manuf. Technol. 2024, 130, 821–836. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, L.; Xu, Y. Enhancement of bearing fault detection using an alternative analytic energy operator and sparse Bayesian step-filtering. J. Mech. Sci. Technol. 2021, 35, 905–920. [Google Scholar] [CrossRef]
- Wu, K.; Xu, Y.; Yang, N.; Zhao, L. A multiresolution higher-order symmetric envelope-derivative operator and its application to bearing fault detection. J. Mech. Sci. Technol. 2023, 37, 1165–1175. [Google Scholar] [CrossRef]
- Feldman, M. Hilbert transform in vibration analysis. Mech. Syst. Signal Process. 2011, 25, 735–802. [Google Scholar] [CrossRef]
- Han, T.; Ding, L.; Qi, D.; Li, C.; Fu, Z.; Chen, W. Compound faults diagnosis method for wind turbine mainshaft bearing with Teager and second-order stochastic resonance. Measurement 2022, 202, 111931. [Google Scholar] [CrossRef]
- Liao, Z.; Song, X.; Jia, B.; Chen, P. Bearing fault feature enhancement and diagnosis based on statistical filtering and 1.5-dimensional symmetric difference analytic energy spectrum. IEEE Sens. J. 2021, 21, 9959–9968. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Bu, P.; Ye, M. Incipient fault feature extraction of rolling element bearings based on SOSO boosting technique and improved energy operator. Meas. Sci. Technol. 2023, 35, 025012. [Google Scholar] [CrossRef]
- Fu, Q.; Wang, H.; Zhang, H. Fault diagnosis of rolling bearing based on wavelet threshold denoising and energy operator. J. Beijing Inf. Sci. Technol. Univ. 2017, 32, 40–43. [Google Scholar]



| k | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| SNRI (dB) | −1.27 | −1.29 | −0.35 | −0.81 | −3.18 |
| Inner Diameter (mm) | Outer Diameter (mm) | Roller Diameter (d/mm) | Pitch Diameter (D/mm) | Ball Complement Z | Contact Angle (θ/°) | Rotational Frequency (fr/Hz) |
|---|---|---|---|---|---|---|
| 40 | 80 | 12.5 | 65 | 14 | 30 | 16.7 |
| k | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| SNRI (dB) | −5.03 | −3.83 | −5.35 | −4.84 | −4.45 |
| k | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| SNRI (dB) | −4.21 | −2.12 | −3.25 | −5.53 | −6.78 |
| Algorithm | MHSAEO | Wavelet Threshold Denoising + TEO |
|---|---|---|
| Time(s) | 0.0328 | 0.9872 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wang, Y.; He, Y. MHSAEO Index for Fault Diagnosis of Rolling Bearings in Electric Hoists. Machines 2025, 13, 508. https://doi.org/10.3390/machines13060508
Wang X, Wang Y, He Y. MHSAEO Index for Fault Diagnosis of Rolling Bearings in Electric Hoists. Machines. 2025; 13(6):508. https://doi.org/10.3390/machines13060508
Chicago/Turabian StyleWang, Xinhui, Yan Wang, and Yutian He. 2025. "MHSAEO Index for Fault Diagnosis of Rolling Bearings in Electric Hoists" Machines 13, no. 6: 508. https://doi.org/10.3390/machines13060508
APA StyleWang, X., Wang, Y., & He, Y. (2025). MHSAEO Index for Fault Diagnosis of Rolling Bearings in Electric Hoists. Machines, 13(6), 508. https://doi.org/10.3390/machines13060508






