Abstract
In recent years, due to the growing imbalance between energy consumption and available resources, as well as strict CO2 emission regulations, turbochargers have become increasingly important in applications such as automobiles, ships, and aerospace. Turbochargers can effectively increase the intake volume of engine cylinders, improving fuel combustion efficiency and engine power. In order to meet the growing demand for more energy-efficient, lower-carbon-emission systems, it is necessary to design more compact, efficient, durable, and affordable supercharging systems. Compared with traditional floating ring bearings, rolling bearing turbochargers have become a greater focus of research due to their excellent transient performance, low friction loss, and strong load-bearing capacity. Due to the large number of components, complex structure, lightweight high-load rotor, complicated operating conditions, and unclear nonlinear vibration mechanism of rolling bearing turbochargers, it is necessary to establish a refined model to clarify how factors such as bearing and squeeze film damper parameters and rotor operating parameters affect the system response. Therefore, this study reviews relevant research in this field from the perspectives of modeling and system characteristics and points out directions for future research.
1. Introduction
Since the advent of the Industrial Revolution in the 18th century, humanity’s consumption of Earth’s resources and the resultant pollution have accelerated dramatically, with automobile exhaust being a major source of the latter [1]. Europe has proposed that CO2 emissions be reduced by nearly one-third by 2030 compared to 2019 levels. To achieve emission and fuel consumption reductions, it is necessary to simultaneously improve the thermodynamic efficiency of internal combustion engines and the electrification of powertrains. The use of turbocharging technology is an effective method for achieving this goal. Compared to naturally aspirated superchargers, turbochargers have a higher performance range and require lower fuel consumption due to their high compression ratios, Miller cycles, and cooled external exhaust gas recirculation [2]. Traditional turbochargers typically use two radial bearings and one double-direction thrust bearing to support the rotor. Due to their low cost and simple structure, they have been developed and applied for a long period. However, they also have inherent drawbacks: high bearing friction resistance, a significant “lag effect” at low speeds and during gear changes, complex oil circuits and high lubricant requirements, oil film instability (particularly severe overall instability), large radial clearance, low dynamic control accuracy of the rotor, and susceptibility to thrust bearing failure [3,4,5,6,7]. Although these issues can be improved through the use of various technologies, such as twin turbines, sequential turbines, variable nozzles, and electric assistance, these technologies themselves have varying degrees of drawbacks: large size, complex structure, and difficulty in control; these drawbacks have prevented them from being widely adopted [8,9]. In recent years, rolling bearing turbochargers have attracted increasing attention due to their advantages, such as eliminating the need for separate thrust bearings, significantly reducing friction resistance, minimizing the rotor’s lateral vibration displacement, reducing the sealing clearance between the compressor wheel and turbine, improving aerodynamic efficiency, and enhancing vehicle handling while effectively reducing emissions, making them particularly suitable for special vehicles (such as military vehicles) operating in variable conditions and providing supplementary power in high-altitude and low-temperature environments [8,10,11]. The earliest literature investigated in this study can be traced back to 1984. The most recent literature was released in 2025. The literature from the past 10 years accounts for 60% of the body of research, and studies from the past 3 years account for 30%.
1.1. The Development and Application of Turbocharging Technology
Turbochargers utilize the exhaust gas emitted by an engine to drive the turbine, which in turn drives the compressor to increase the intake volume of the engine cylinder, thereby increasing the oxygen content and combustion pressure in the cylinder, improving fuel combustion efficiency, and purifying the exhaust gas. In 1905, Swiss scientist Dr. Buechi first proposed the idea of exhaust gas turbocharging and obtained patents in the United States and Germany simultaneously. From 1909 to 1912, Buechi designed the world’s first exhaust-driven axial flow turbocharger and completed bench testing on a single-cylinder engine. In the industry, turbocharging technology was first successfully applied in aircraft engines. In 1925, ABB of Switzerland successfully applied its turbochargers to marine diesel engines. Since then, turbocharging technology has been widely promoted and applied to large marine and land-based engines. The production of automotive turbochargers began in the late 1940s, with slow initial development. It was not until the 1960s that they began to be widely promoted [12]. Turbocharging technology has been continuously improved over 120 years of development. Its types are classified into axial flow and radial flow based on the movement of fluids. Multi-stage axial flow is suitable for high-flow equipment, while radial flow is suitable for low-flow equipment. The support structure includes floating bearings, semi-floating bearings, rolling bearings, foil bearings, etc. The current support structure mostly uses a double internal support system. Boost systems are generally divided into two types: constant-pressure boost and pulse boost. In addition, to improve performance, technologies such as composite supercharging, multi-stage supercharging, electric assistance, exhaust bypass valves, and variable geometry turbocharger (VGT) have been developed. To date, turbochargers are used in large diesel engines in developed countries and regions such as Europe, the United States, and Japan. Even in medium and small diesel engines, the installation rate of turbochargers can reach 80%. Figure 1 shows that there is still significant room for improvement in the adoption rate of turbochargers. Driven by the trends toward smaller passenger vehicles, stricter emissions standards, and strong market demand, the development of turbochargers remains a key focus for the future.
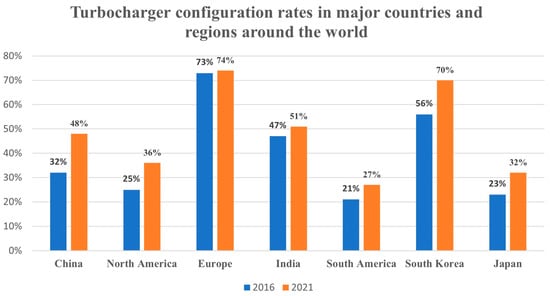
Figure 1.
Turbocharger configuration rates in major countries and regions around the world.
1.2. The Development and Application of Rolling Bearing Turbochargers
In 1993, rolling bearing turbochargers manufactured by Honeywell in the United States were tested in Nissan vehicles. In 1994, Swiss company ABB began using rolling bearings in its VTR-4 series of turbochargers. In the same year, Garrett Corporation in the United States began researching rolling bearing turbochargers and applying them to its own products [13]. Japan’s IHI Corporation uses rolling bearings in its RHB5 and other models of superchargers, achieving mechanical efficiencies of over 95% [14]. Previously, rolling bearing turbochargers were not widely used due to cost constraints. In recent years, driven by mandatory emission reduction treaties in Europe, North America, Japan, and other regions, major automobile, engine, and bearing manufacturers have increased their development of rolling bearing turbochargers. IHI Corporation has developed rolling bearing turbochargers suitable for use in passenger cars, buses, and trucks [15]. NSK has developed high-performance cassette rolling bearings suitable for use in automotive turbochargers. This bearing has the following three features: (I) It uses friction analysis technology to ensure low wear, long life, low vibration, low noise, and high stability; (II) heat-resistant steel is used to improve durability; (III) a heat-resistant resin cage is included to improve transient response [16]. Companies such as SKF [17,18] and Schaeffler [19] have also successfully developed rolling bearing turbochargers and begun mass production, while companies such as Honeywell [20], Garrett [21], and BorgWarner [2] already have mature rolling bearing turbocharger products. In 2023, Ningbo Weifu Tianli Supercharging Technology Co., Ltd., successfully developed a self-lubricating rolling bearing rotor system for drone piston engine superchargers, and this system was used in the final design of drones [22]. It is evident that rolling bearing turbochargers have a wide range of applications, are developing rapidly, and have ample market prospects.
1.3. Features, Research Challenges, and Focal Topics of Rolling Bearing Turbochargers
1.3.1. Features of Rolling Bearing Turbochargers
First, rolling bearing turbochargers have the following characteristics: light loads, high speeds (up to 250,000 rpm), compact size, high flexibility, variable operating conditions (spanning first- and second-order critical speeds, with automotive turbochargers frequently accelerating and decelerating, causing load fluctuations), strong nonlinearity (nonlinear oil film forces), high temperatures (turbocharger inlet temperatures reaching 800–1000 °C), multiple components, and high precision. Their structure consists of a turbine, a compressor wheel, a rotor shaft, and rolling bearings, as shown in Figure 2. The core component is a double-row angular-contact ball bearing, which typically consists of two inner rings arranged back-to-back and a common outer ring. When considering axial forces, axial preload must be added to create negative clearance between the balls and raceways.
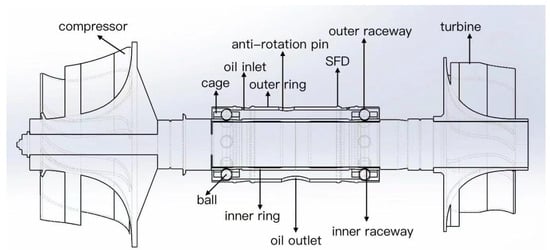
Figure 2.
Rolling bearing turbocharger structure.
Secondly, compared with floating ring bearings, the friction mechanism experiences fundamental changes. Under high shear conditions, multiple rolling elements replace the oil film, significantly reducing system friction. This significantly improves system friction at operating temperatures (typically up to 50%) and even more so during the first minute of cold engine start-up, as shown in Figure 3. This is because, under cold start conditions, the engine’s oil is very viscous, and the viscous resistance of the floating ring bearings hinders the effective rotation of the shaft, preventing it from providing torque in a timely manner. In contrast, rolling bearings can still rotate the shaft at low speeds in cold conditions. This not only alleviates turbo lag but also improves the original emission quality due to improved fresh air supply. Through experimental comparative analyses of ball bearings versus sliding bearings at different rotational speeds, Jebur and Soud [23] demonstrated that bearing selection must be based on operational characteristics—such as speed range and primary load direction—to enhance system stability and mitigate vibration-related issues.
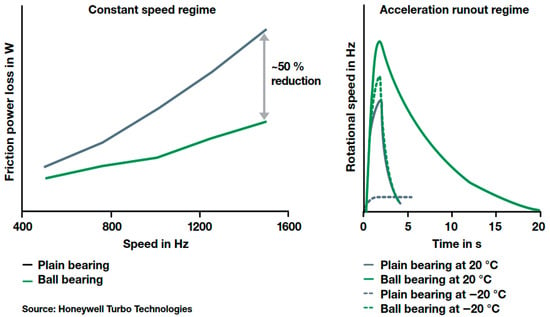
Figure 3.
Friction loss benefits of ball bearing turbochargers [19].
Furthermore, compared with floating ring bearings, lubricating oil in rolling bearings mainly serves to provide lubrication, cooling, and damping functions. These bearings also require less oil, have a lower risk of oil leakage from the shaft seal, and exhibit longer failure durations when the oil supply is interrupted, thereby enhancing the robustness of the system. These bearings’ characteristics include the following: ① Lubricity: Considering the high Diameter × Nominal (DN) value and common characteristic speed value of bearings, the operating speed of turbocharger bearings is six times faster than any other bearings in vehicles. Due to this high-speed operating condition, oil quantity control is extremely important. On the one hand, excessive oil volumes can result in agitation losses. On the other hand, insufficient oil volumes can result in inadequate lubrication. Lubrication is typically achieved through oil spray lubrication, where the oil jet must penetrate the air turbulence surrounding each bearing row to lubricate the contact areas between the rolling elements and the cage. Therefore, the internal surfaces of the cage and the geometric shapes of the components should be considered during the design process. ② Cooling Properties: Due to the high-temperature, high-pressure exhaust gas impact on the turbine side, the high temperature is ultimately transferred through the multi-body system to the ball bearings via heat conduction during normal operations, and heat is transferred by the oil flow at the oil outlet. However, focus should also be centered on the possibility of lubrication interruption and thermal shutdown conditions. Under such conditions, the bearing’s temperature will increase by about 100 °C, seriously affecting system operations. In addition, there are significant temperature differences between various components of the bearing. Therefore, heat-resistant materials are generally selected in the construction of these bearings. According to the authors of [24], for example, nickel–iron alloys are used for turbines, and aluminum is used for compressors. Steel is generally used for rotor shafts and inner and outer rings. The authors of [25] indicate that ceramic ball materials have the following characteristics: such as low density, heat resistance, high hardness, corrosion resistance, and wear resistance. Therefore, silicon nitride is generally used as the ball material in rolling bearings and turbochargers. The advantages of silicon nitride are as follows: (1) Lower density reduces the weight of the bearing, thereby reducing the centrifugal force of the ball at high speeds; (2) the presence of covalent bonds reduces bearing failure caused by reduced oil volumes under high-speed operating conditions; (3) silicon nitride can be used under high-temperature conditions; (4) the fatigue life is more than twice that of bearing steel; (5) less friction loss occurs. Cages are generally used to evenly space rolling elements. In this structure, they are affected by high temperatures; thus, materials that are high in strength, light in weight, and exhibit high temperature resistance are generally selected [26]. Using polyetheretherketone (PEEK), the authors of [25] show that the friction loss of hybrid ceramic ball bearings with polyimide resin cages is more than 15% lower than that of bearings with high-pressure brass cages. ③ Damping: The squeeze film damper acts in a fluid dynamic manner, i.e., it establishes a pressure field based on the speed of the bearing outer ring relative to the bearing’s housing, providing the necessary damping for the dynamic stability of the rotor.
Finally, compared with floating ring bearings, rolling bearings are more durable and have more complex dynamics. During supercharger operation, contaminants in the engine oil include engine wear, combustion by-products, and foreign substances introduced during engine maintenance or repair. These contaminants often reduce the life of the bearing system, and the authors of [27] show that the life of rolling bearings contaminated by lubricating oil is seven times that of floating ring bearings under the same conditions. However, due to the large number of components in double-row angular-contact ball bearings, when they are coupled with the rotor during high-speed operations, the components interact with each other, resulting in more complex dynamics.
1.3.2. Research Challenges of Rolling Bearing Turbochargers
The analysis of this complex system involves multiple fundamental scientific theories, including elasticity mechanics, fluid mechanics, rotor dynamics, tribology, and thermodynamics. The outer ring of the rolling bearing turbocharger is supported by a squeeze film damper (SFD), and oil film lubrication is also present inside the bearing. Therefore, challenges in this system comprise a fluid–structure interaction problem, requiring the coupling and simultaneous solution of the pressure–viscosity equation, Reynolds equation, and elastic deformation equation for fluid lubrication. Currently, these are generally solved by carrying out simplification under certain assumptions and then using numerical iteration methods to solve nonlinear equations.
There is relatively little research on rolling bearing turbochargers. The related research is mainly concentrated among the three major turbocharger manufacturers (Honeywell, Garrett, and BorgWarner in the United States) and some well-known engine manufacturers (such as Cummins and Caterpillar in the United States). Due to confidentiality reasons, there is very little publicly available information. To date, there is no publicly available comprehensive theory or methodology for analyzing the characteristics of rolling bearing turbocharger systems.
1.3.3. Focal Topics of Rolling Bearing Turbochargers
Research on high-speed rolling bearing turbochargers is currently focused on studying their system characteristics, including dynamics, mechanical efficiency, and thermal effects. Dynamics also include rotor dynamics and bearing dynamics, entailing the analysis of the effects of various parameters to optimize designs.
2. Modeling Study of Rolling Bearing Turbochargers
Figure 4 shows the number of published papers in the field of rolling bearing turbochargers over the past 40 years. It can be observed that there was a wave of growth around 2015, mainly due to the fact that its mechanical efficiency was significantly improved compared to sliding bearings at that time. However, its popularity gradually declined later due to reasons such as bearing lifespan and price. In recent years, due to the development of computers and artificial intelligence, the research on their mechanisms and structural optimization design have become more convenient, and thus their popularity is still gradually increasing.
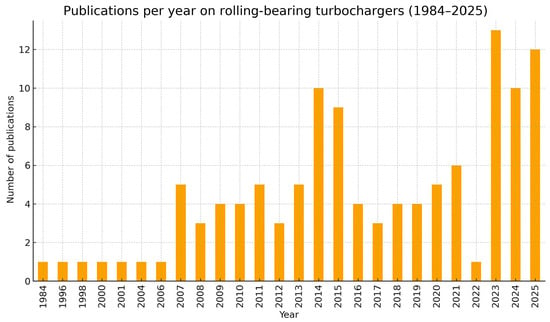
Figure 4.
The number of published papers in the field of rolling bearing turbochargers over the past 40 years.
For modeling rolling bearing turbochargers, detailed models mostly integrate the modeling of rotors, bearings, and squeeze film dampers. The rotors are modeled using finite element discrete grids for flexibility, while the bearings are mostly modeled using the discrete element method. Squeeze film dampers are modeled using different approximate theories or simplified models depending on the oil film’s length-to-diameter ratio. Huang et al. [28,29,30,31,32] used the Riccati transfer matrix method and the DyRoBeS finite element method to calculate the natural characteristics of the rotor, simplifying the bearing force to equivalent stiffness. Based on their experimental work in 2011 [33], Ashtekar A et al. [11] conducted a modeling analysis of a turbocharger with angular-contact ceramic ball bearings. The bearings were modeled using the discrete element method. The normal force between the balls and raceways was modeled using the Hertz contact force model, and tangential force was modeled using a dry friction model. Friction forces in the short axis direction were neglected, and friction forces were integrated along the long axis. The squeeze oil film force was modeled using the short bearing theory assumption, and the rotor was modeled using finite element modeling. Brouwer and Sadeghi [24] used a modeling method similar to that by the authors of [11], but they applied a linearization method to the contact force, which affected the accuracy of the contact force to a certain extent. Conley B and Sadeghi F [34] built upon their 2019 experimental work [35] to model a turbocharger using the discrete element method, equating it to a deep groove ball bearing. The rotating shaft, compressor wheel, and turbine were treated as a single rigid body, with the unbalanced mass acting on the inner ring. The SFD was simplified to a bilinear spring and damper, with the low-stiffness segment corresponding to the equivalent linear stiffness of the oil film and the high-stiffness segment corresponding to the contact stiffness with the intermediate housing. This simplification clearly cannot accurately describe the oil film’s force. Conley B and Sadeghi F [36,37] built upon the work of the authors of [34] in 2020, artificially adding two cross-stiffness terms to the bilinear model, and the steady-state axial load on the outer ring was simulated using spring dampers. Although this represented an improvement over previous work, the two cross-stiffness terms could not be effectively determined, and the rotor shaft was considered flexible and modeled using commercial software. With the development of technologies such as finite element analysis and multibody dynamics, establishing detailed virtual prototype models through software comprises the future research trend. Shan [7] and Wan [38] used ADAMS software combined with FORTRAN language to write a program for internal forces in angular-contact ball bearings and established a multibody dynamics model for rolling bearings. Lu [39] used collaborative simulation technology to establish a relatively accurate rolling bearing turbocharger model. Majer, M. et al. [40] outlined the advantages and disadvantages of dry gas seals and contact seals, considering four factors: ball bearings, SFD, gas seals, and impeller aerodynamics. He analyzed the impact of the cross-coupled stiffness between the impeller and gas seal on the stiffness of rolling bearings and the instability forces. The dynamics of rolling bearing elements (REBs) is modeled through linearized coefficients using classical stiffness and damping matrices. The values of direct stiffness were obtained by averaging the stiffness estimated using Hertz contact theory as a function of the radial and axial loads on the bearings, which changed with the rotational speed. The effect of the squeeze film damper is considered by introducing a stiffness and damping matrix with non-null direct terms and null cross-coupled terms. The results indicate that the bending modes of the shaft are significantly influenced by the dynamic response of the SFD as rotational speed varies, while the stiffness of the rolling elements has a relatively minor effect on the shaft’s bending modes. Bala Murugan, S. et al. [41] established a rocket turbocharger model incorporating rolling bearings, Muszynska-relation sealing forces, gyroscopic effects, and imbalance factors based on Hamilton’s principle. Using Houbolt’s implicit time-integration scheme to solve rotor dynamics equations, he observed the sub-synchronous motion of the rotor. Most major bearing manufacturers have their own specialized software for designing rolling bearings for turbochargers—such as CABA 3D, developed by Schaeffler, and BFree, developed by SKF [11,17,19]—but there is very little publicly available information.
Figure 5 shows some general methods, design ideas and research directions in this field. It enables readers to quickly understand the current research status and future development in the field of rolling bearing turbochargers. The train of thought is similar to the structure of this article.
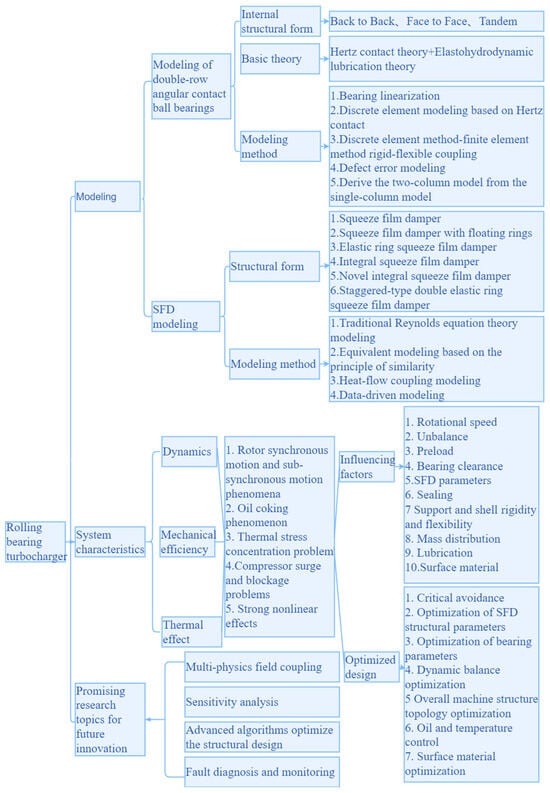
Figure 5.
Research architecture of rolling bearing turbochargers.
2.1. Rolling Bearing Modeling
Turbocharger rolling bearings are double-row angular-contact ball bearings. There are a few published studies on their modeling, and the models considered are relatively simple. Therefore, this study reviews the relevant literature on the dynamics of single-row and double-row angular-contact ball bearings as a theoretical supplement to their modeling design. When designing double-row angular-contact ball bearings, it is important to maximize the rated dynamic load capacity while ensuring minimal axial play. Such bearings can withstand overturning moments, offer high rotational accuracy, high limiting speed ratios, and strong stability, and they significantly outperform single-row ball bearings in terms of stiffness. In the context of load analysis, the two bearings are very similar, with the core of their modeling being the contact forces between their internal components. Compared to single-row angular-contact ball bearings, double-row bearings share a common outer ring, and the centrifugal force of the balls has a significant impact on internal bearing forces. This impact is even more important in bearings with large contact angles. Since the axial component of centrifugal forces increases with the contact angle and acts in the same direction, the two bearings in a paired angular-contact ball bearing arrangement will therefore load each other. After the double row is subjected to combined radial and axial loads, the two rows of rolling elements are loaded unevenly. Double-row angular-contact ball bearings with different internal configurations are shown in Figure 6.
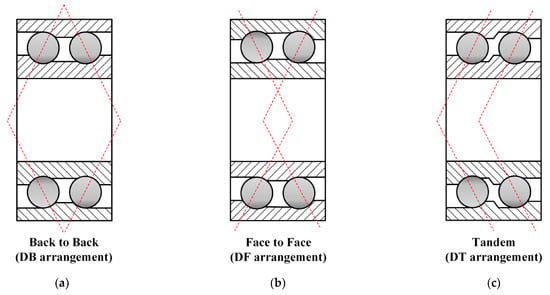
Figure 6.
Three configurations of double-row angular-contact ball bearings: (a) DB arrangement; (b) DF arrangement; (c) DT arrangement [42].
Desai [43] established a flexible shaft and bearing system in the ADAMS software. Wensing [44] used a finite element method based on component modal synthesis to model the shaft, bearing housing, and outer ring. Yao [45,46] used the C-B modal synthesis method to analyze the dynamics of rigid-flexible coupling. The normal contact force of angular-contact ball bearings was calculated using the Hertz contact model, taking into account contact deformation caused by centrifugal force, friction force, and gyroscopic torque. The calculation of contact stiffness was mainly related to the principal curvature of the ball and the inner and outer rings. Subsequently, the authors of [47,48], based on the assumption of an infinite elastic half-space and Boussinesq theory, considered an elastic non-coordinated contact surface model for the inner and outer rings and balls, formed tetrahedral load elements in the contact zone, and used the Newton–Raphson time integration method to iteratively calculate the dynamic average stiffness coefficient of angular-contact ball bearings with variable contact angles using time sub-steps. Moreover, the Timoshenko beam element was used to discretize the flexible outer ring. The authors of [49] divided the contact area between the ball and the raceway into three parts, and equivalent contact stiffness and damping were established. Zhu et al. [50] analyzed the load relationship between the two rows of rolling elements in double-row angular-contact ball bearings, using Hertz contact theory to combine numerical calculations and ANSYS for load distribution and contact stress analysis. Li et al. [51] established a five-degree-of-freedom double-row angular-contact ball bearing quasi-static numerical analysis model based on nonlinear elastic Hertz contact theory and elastic fluid dynamic lubrication theory. This model comprehensively considers the effects of centrifugal force, friction force, gyroscopic torque, bearing clearance, oil film thickness, and bearings. Deng et al. [52,53] considered the contact force and friction force between the ball, inner and outer rings, cage, and guide ring under elastic flow lubrication. In order to deal with the tilting of the cage, the slice method was used to obtain segmented circular slices for the solution. The authors of [54] considered both rolling friction and sliding friction when establishing the fluid dynamic friction force between the ball and the cage [55]. Their model is very similar to the rolling bearings in a turbocharger. By calculating the Hertzian contact and oil film stiffnesses, the stiffness of the balls and inner and outer rings is connected in series and parallel to obtain the overall dynamic stiffness of the bearing. Gunduz et al. [56] established a stiffness matrix for a 5-degree-of-freedom shaft system to calculate the equivalent bearing force, ignoring factors such as the ball’s centrifugal force and gyroscopic torque. Yu and Zhang [57] did not consider the influence of torque and calculated the axial force based on deformation coordination conditions. Zhuo et al. [58] established a numerical analysis model for a three-degree-of-freedom double-row self-aligning ball bearing based on classical Hertz contact theory and deformation coordination theory. Cheng and Wang [59] established an elastic contact model for double-row angular-contact ball bearings based on Hertz’s elastic contact theory and analyzed the contact load distribution characteristics under combined loads. Liu et al. [60] established a set of differential equations for the dynamics of double-row bearings. Saheta, V [61] described the contact rules between spherical pocket retainers and cylindrical pocket retainers. Cylindrical pockets do not radially constrain the retainer; thus, the retainer must be guided by the outer ring. Cao [62] used the discrete element method to establish ball bearings and finite elements to establish flexible shells and rotors, and a robust detection algorithm was designed for rigid–flexible coupling contact. Ashtekar A [63,64] designed a new method for modeling bearing surface defects, considering surface indentations, protrusions, debris, and other defects to modify the Hertz contact model. Moreover, the simulation results with and without defects were compared, focusing on the effects of dent size, inner ring speed, dent location, dent clusters on the inner ring, cage movement, and contact force. Doro, A. M. K. [65] reported that damping in rolling bearings within turbochargers comprises four components: damping of the elasto-hydrodynamic (EHD) lubrication film within the Hertzian contact zone between the rolling elements and raceways; bearing interface damping between the bearing rings and housings or shaft; damping due to squeezing lubricants within the so-called entry region where oil is entrained into the Hertzian zone; material damping due to Hertzian deformation of the rolling elements and raceways. Luo Zhong et al. [66] systematically introduced five modeling methods for combined support rotor systems and their corresponding dynamic solution approaches. Sawalem and Aburwais [67] employed SolidWorks and finite element analysis to model and simulate a double-row angular-contact ball bearing after verifying mesh convergence, demonstrating that the bearing’s failure was more likely attributable to lubrication and asymmetric loading. Zhang, H. et al. [68] examined the internal structure of bearings and demonstrated that double-row angular-contact ball bearings in a back-to-back configuration exhibit superior dynamic performance. Wen, B. et al. [69] established a quasi-dynamic model for double-row angular-contact ball bearings by considering inner ring axial clearance. The oil film thickness was calculated using the elasto-hydrodynamic lubrication (EHL) formula, while ball-and-raceway friction was modeled using a classical friction model, neglecting variations in the sliding friction coefficient. Fang, B. et al. [42] derived the load–displacement relationship between double-row and single-row bearings through vector transformations across multiple coordinate systems based on an improved quasi-static model for single-row angular-contact ball bearings. He analytically derived the stiffness matrices for double-row bearings with different internal structures and implemented model solutions using a double-layer nested iterative algorithm based on the Newton–Raphson method.
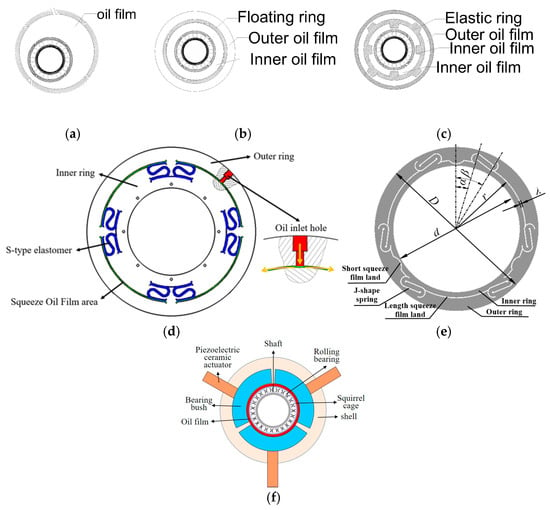
2.2. Modeling of a Squeeze Film Damper
Due to the high rigidity and low damping of rolling bearings, significant displacement may occur during high-speed operations. The synchronous excitation generated by the imbalance has a significant impact on the vibration of the rotor. Therefore, it is necessary to install a squeeze oil film damper on the outer ring to provide support and reduce contact with the housing. Kim and Ryu [70] demonstrated that the meticulous design of dampening components can enhance vibration isolation and system stability. There are many types of SFD structures, mainly including traditional SFD, SFD with floating rings (FSFD), and elastic ring squeeze film damper (ERSFD). Recently, new types of extrusion oil film dampers, such as integral squeeze film damper (ISFD), novel integral squeeze film damper (NISFD), and piezoelectric-driven split SFD, have emerged, as shown in Figure 7. Gunter, E. J. [71] indicated that rolling bearings themselves do not exhibit instability issues compared to floating ring bearings. However, due to the presence of Alford cross-coupling forces in compressors and turbines, damping is required to control the resulting instability. Traditional non-centered extruded oil film dampers experience a rapid increase in radial stiffness when eccentricity exceeds 0.5, rendering stiffness-damping optimization difficult and introducing lockup issues. Their study demonstrates that closed-end air squeeze film dampers maintain linear stiffness within an eccentricity of 0.8 without locking. The specific nonlinear oil film force is generally approximated using the Reynolds equation based on the circular precession assumption. According to the oil film’s length-to-width ratio, it is divided into short bearing, wide bearing, and finite-width bearing models, while according to the presence or absence of cavities, it is divided into 2Π theory and Π theory. Zhou et al. [72] established a rolling bearing–rotor coupling system dynamic model based on the short bearing assumption and Reynolds boundary conditions. The authors of [73] investigated the differences between FSFD and SFD. Compared with SFD, FSFD can suppress bistable responses and has better damping effects with smaller displacement amplitudes, effectively preventing sub-synchronous and non-synchronous operation and having a larger periodic operating range. Matthew Brouwer [74] used a cylindrical coordinate system to derive and calculate the radial and tangential forces of the oil film based on the short bearing theory. Since the radial clearance of the oil film is very small, the fluid inertia effect was ignored. Garrett Corporation [75] used short bearings and Π theory to calculate oil film stiffness and damping on high-speed balancing machines for rolling bearings. Heidari and Ashkooh [76] analyzed the stability and bifurcation of a rigid rotor with a compression membrane damper and a concentrated spring, focusing on the effects of asymmetric concentrated spring stiffness in the x and y directions. The results show that increasing the spring stiffness in the y-direction has no effect on the nature of the system response and bifurcation, but increasing the stiffness in the x-direction causes the response system to become unstable, resulting in a period-doubling bifurcation phenomenon. Wang et al. [77] used the Reynolds equation and neural network models to numerically predict the oil film stiffness and damping of SFD, providing a new approach to calculating nonlinear oil film forces. Due to the high computational cost of numerical solutions to the Reynolds equations, Groves and Bonello [78] used Chebyshev polynomial fitting to identify finite difference (FD) solutions to the incompressible Reynolds equations. Liu [79] derived oil film forces by considering the differential equations of oil film pressure distributions without inertia—using time inertia terms and full inertia terms—and then calculated the oil film’s force using the finite difference method. Ding et al. [80], based on the Reynolds equation considering fluid inertia, used the finite difference method to calculate the internal and external oil film distribution pressure and the resultant oil film force of the elastic ring squeeze film damper, and they analyzed the dynamics of the ERSFD-rotor system. Wang et al. [81] also calculated the inner and outer oil film stiffness and damping of ERSFD using the difference method and applied it to rolling bearing turbochargers. Nerg, J. et al. [82] employed the singular value decomposition (SVD) method to simulate worst-case unbalanced responses and thereby back-calculated the optimal stiffness and damping for SFD. Fan and Behdinan [83] introduced Prandtl’s mixed length within the short-bearing theoretical framework to derive the effective flow viscosity, thereby calculating the SFD damping coefficient for high-speed SFDs with large clearances where turbulent effects are present. He, F. et al. [84] derived dynamic similarity relations for rotor systems with squeeze film dampers based on the Buckingham π theorem and similarity theory, establishing a distortion model based on the scaling ratio. Luo, Z. et al. [85] coupled the energy equation with the Reynolds equation and the viscosity–temperature equation to establish an ERSFD model incorporating oil film temperature, investigating the distribution of oil film forces and temperature. Li, Y. et al. [86] developed a mathematical model for a rigid–elastic–oil-coupled elastic ring support squeeze film dampers, considering elastic ring deformations and unbalanced forces. The results indicate that the flexibility coefficient has the greatest influence on the dynamic characteristic coefficients of ERSFD, followed by the oil film’s radius clearance. The effects of journal eccentricity and damper hole diameter are the smallest. Sun, K. et al. [87] established a mathematical model for ERSFD under different sealing conditions (no end-face seal, full end-face seal, piston ring seal, and O-ring seal) by modifying the initial boundary equations of the ERSFD flow field. Yan, W. et al. [88] established separate solid and fluid models of the ISFD and obtained numerical analytical values for the ISFD’s damping and stiffness coefficients. Lu, Q. et al. [89] designed a novel piezoelectric-driven split SFD structure capable of rapidly adjusting the oil film gap online to control rotor system vibrations. Dong, H. et al. [90] designed a NISFD incorporating three pairs of elastomer characteristics, ensuring uniform distributions of stiffness and damping while featuring a simpler structure and easier manufacturing process. Zhang, Y. et al. [91] constructed a finite element model of the staggered-type double elastic ring squeeze film damper (SDERSFD) and developed an innovative interleaved bidirectional pressure transmission iterative calculation method. A nonlinear rotor SDERSFD dynamic model considering impact and maneuvering excitations is established utilizing the finite element method (FEM) to investigate the SDERSFD’s damping characteristics under complex operating conditions.
3. Research on the Characteristics of Rolling Bearing Turbocharger Systems
3.1. Dynamics Research
For ball bearing rotors, critical instability occurs at critical speeds. Avoiding the operation of ball bearing rotors at critical speeds can effectively prevent large vibrations. For bearings, coupled changes in contact angle and contact force during high-speed operation can cause damage to bearing components and even failure, rendering the entire system inoperable. Huang et al. [31] studied the effect of acceleration on the dynamic characteristics of the ball bearing rotor system of a turbocharger by considering the sealing fluid and airflow excitation forces at the blade tip gap. They concluded the following: (i) The first-order critical speed of ball bearing turbochargers decreases as acceleration increases, while the second-order critical speed increases as acceleration increases. (ii) Under acceleration (deceleration) conditions, the amplitude of the ball bearing turbocharger rotor increases with increasing acceleration (deceleration) near the critical speed, but it does not change significantly in the non-critical speed range. (iii) The maximum amplitude near the critical speed of the ball bearing turbocharger in the acceleration (deceleration) state is much smaller than the maximum amplitude of the steady-state response. Huang et al. analyzed the relationship between stiffness and rotor transient response [32], indicating that changes in bearing load only cause minor changes in the amplitude of the turbocharger’s transient response, which can generally be ignored. The authors of [28,92] analyzed the effects of axial load, bearing stiffness, span, and material properties on critical speed. Huang et al. [29,30] showed that sealed fluid excitation forces increase system damping, reduce the amplitude of the ball bearing turbocharger rotor system, and improve system stability; airflow excitation forces increase the system’s cross-stiffness and reduce the amplitude of the system’s steady-state response. Ashtekar A analyzed the effects of imbalance and preload [11,33,93], showing that imbalance forces increase the amplitude of the rotor—resulting in greater contact forces between the balls and inner ring, in addition to greater impact forces between the balls and the cage. These factors all affect bearing life. Without preload, fluctuations in the contact force between the balls and inner ring increase, with ball angular velocity fluctuations being 200% higher than in preloaded conditions. Additionally, the inner ring’s motion trajectory becomes larger, and the cage’s motion trajectory becomes less stable. However, excessive preload can result in premature bearing fatigue failure; thus, preload must be set appropriately. Brouwer MD et al. compared the rotor response and bearing wear of floating ring bearing turbocharger (FRBT) and ball bearing turbocharger (BBT) [10] through experiments, showing that the average vibration amplitude of BBT was reduced by 47%, and the average deceleration time was extended by 14%. FRBT rotors primarily exhibit sub-synchronous vibration, while BBT rotors primarily exhibit synchronous vibration. The authors of [24] investigated the effects of four types of ball materials on rotor vibration amplitude, ball–outer ring contact force, and ball–inner/outer ring contact angle. Conley B et al. [34,35,36] first conducted experimental tests on bearing axial forces and friction forces, and they observed that the rotor response exhibited half-frequency vortex motion and bifurcation. They investigated the effects of half-frequency vortex motion, rotor axial movement, bearing clearance, and preload on bearing wear; the influence of preload on rotor half-frequency vortex motion, ball rotational angular velocity, and ball–inner/outer ring contact angle; and the impact of bearing clearance and oil film gap on ball–inner ring contact force. Shan [7] used ADAMS software to analyze the effects of preload and inner and outer ring groove curvature on bearing raceway contact stress, life, and power loss. He et al. [81] applied ERSFD to rolling bearing turbochargers. Their study showed that compared with traditional SFD, the nonlinearity of ERSFD stiffness damping was significantly suppressed, resulting in better vibration suppression. The stiffness of the elastic ring was significantly lower than that of ball bearings, and connecting them in series reduced the stiffness of the system. The number of bosses had a significant impact on the stiffness of the elastic ring. Zhen [94] used static analysis to examine the effect of bearing stiffness caused by changes in the contact angle due to bearing loads, and dynamic analysis was carried out to examine the nonlinear changes in bearing stiffness caused by centrifugal forces and gyroscopic torque. Shafiee, A. et al. [95] developed a flexible rotor–rigid bearing–flexible bearing housing model using ABAQUS and ADAMS, revealing the significant impact of rotor and bearing housing flexibility on the system, including the generation of overturning moments and ovality. Li, T. et al. [96] investigated the nonlinear behavior of a turbocharger rotor system with coupled rolling bearings using an improved incremental harmonic balancing method incorporating arc length extension. Their study reveals a bistable phenomenon at the resonance peak of the bending mode. The cone mode exhibits high sensitivity to variations in bearing clearance and bearing spacing, with the amplitude within the nonlinear resonance speed range positively correlated with the cone mode resonance peak. Simultaneously, the frequency and amplitude of the bending mode are sensitive to changes in bearing spacing. Increasing the number of balls, enhancing Hertzian contact stiffness, and reducing bearing clearance can improve the system’s high-speed impact resistance. While meeting other parameter requirements, bearing clearance should be minimized as much as possible. Compared to the Runge–Kutta (R-K) solution method, this approach offers higher computational efficiency and yields a complete solution for the system. Li, Y. et al. [97] established a rotor–ERSFD–ball bearing structural dynamic model to simulate and analyze the dynamic response of the ball bearing’s outer ring under sudden imbalances. Their study examined the effects of speed ratio, damping ratio, and mass ratio on the transient response time to a steady state, the bearing’s vibration suppression performance, and the sensitivity of relevant parameters to oil film force. Wen, B. et al. [69] investigated the effects of single and overall overturning moments on the load capacity and service life of double-row angular-contact ball bearings. The study revealed that when subjected to an overall overturning moment, the equivalent dynamic load on the outer raceway exceeds that on the inner raceway. In practical applications, distributing the overturning moment uniformly across all bearing directions can prevent concentrated bending moments, thereby extending bearing service life. Fang, B. et al. [42] demonstrated that the back-to-back double-row angular-contact ball bearing structure exhibits a nonlinear spring characteristic, with stiffness that first softens and then stiffens as external force increases.
3.2. Mechanical Efficiency Research
Huang et al. [98] proposed a new acceleration performance parameter A in response to the phenomenon of “turbo lag” during acceleration. They analyzed the factors affecting A, which mainly included turbine flow, engine exhaust temperature, and supercharger efficiency, and they conducted a weight analysis using the analytic hierarchy process to determine the advantages and disadvantages of different turbochargers. Tian et al. [99] indicated that the overall efficiency and maximum speed of hybrid ceramic ball bearing turbochargers were significantly improved compared with sliding bearings. Zhang et al. [100] showed that, compared with journal bearings, ball bearings in turbochargers produce greater transient torque during cold starts, enabling faster acceleration to improve mechanical efficiency, and this method can reduce engine back pressure during steady-state operations, thereby reducing engine fuel consumption. SKF [18] confirmed that the efficiency of the Carnot cycle can be increased to 49% when using a turbine system with a damper and ball bearings. Huang et al. [101] proposed a method combining theoretical calculations and experiments to obtain the mechanical loss power of a turbocharger and designed an experimental measurement device. RC Griffith et al. [27] developed a test rig by removing the compressor side blades and used the basic power balance equation for turbochargers, to precisely measure the power consumption of the bearing and shaft seal systems. They analyzed the relationship between bearing power loss and rotational speed and compared the turbine efficiency under different pressure ratio conditions. Simultaneously, improvements in mechanical efficiency also reduce fuel consumption. Ozaki, M. et al. [102] indicates that turbochargers still hold development potential in hybrid vehicles. By optimizing the compressor inlet, volute passages, and bearings, mechanical efficiency can be significantly enhanced. Faraj and Hadi [103] compared the stress, strain, and total deformation of turbine blades under high-speed impact loads across three blade configurations and four different materials. The findings demonstrate that selecting appropriate materials and blade counts can significantly enhance the performance, durability, efficiency, and lifespan of turbocharger blades. An, Y. et al. [104] conducted a detailed study of ball bearings as a single variable affecting engine combustion, emissions, and performance. The research indicates that ball bearings significantly enhance turbine-side efficiency within the low-expansion-ratio range, markedly improve brake specific fuel consumption (BSFC) at low speeds, and exert minimal impact on combustion and particulate emissions. Conley [37] measured the axial load primarily concentrated on the compressor side by constructing an experimental test rig. By comparing the effects of bearing internal geometry, SFD clearance, and SFD width on bearing wear, he determined the optimal parameter design under wear conditions. Fasolia, V. et al. [105] reviewed methods for enhancing the wear resistance of turbocharger components to improve system reliability and efficiency. These include bearing cooling using compressed air, plasma spraying technology, chemical vapor deposition (CVD) repair and strengthening techniques for components and electrical discharge machining (EDM) technology. Riera, P. et al. [106] established a method for calculating bearing life under rolling element wear, analyzing the effects of radial load, eccentric load angle, bearing clearance, and preload clearance on bearing life. The study revealed that contact load and radial load, in addition to contact stress and eccentric load angle, all exhibit a positive correlation. Conversely, bearing life shows a negative correlation with radial force and eccentric load angle while maintaining a positive correlation with bearing clearance.
3.3. Thermal Effect Research
When a turbocharger is in operation, high-temperature exhaust gases transfer a large amount of heat to the turbine wheel, while the compressor wheel remains in a normal temperature environment. The turbocharger, which is heated by high temperatures, generates significant temperature gradients in both the radial and axial directions, resulting in severe thermal–mechanical stresses. Additionally, temperature changes can alter material properties such as the elastic modulus, Poisson’s ratio, and damping, which in turn affect the system’s characteristics. Ensuring optimal lubrication quality is critical for the stable operation, bearing temperature, and service life of turbochargers. Serrano, J. R. et al. [107] investigated changes in turbocharger temperature and efficiency under transient and steady-state conditions to determine the impact of degraded oil on turbocharging systems. High temperatures cause the formation of high concentrations of carbon deposits inside the turbocharger, resulting in greater performance loss. Hu and Lin [108] established a two-phase flow model for double-row ball bearings based on computational fluid dynamics (CFD) methods and conducted an optimization analysis of the bearing lubrication system. The study revealed that the oil supply rate is the key parameter determining the total oil delivery volume, while the inner ring rotational speed can indirectly regulate the oil flow’s direction. Increased oil viscosity suppresses oil dispersion. The oil volume fraction on the raceway’s surface exhibits a negative correlation with inner ring rotational speed and a positive correlation with oil supply rates. Ball spin significantly influences the oil volume fraction distribution within the bearing cavity under low-speed conditions but becomes negligible at high speeds. Zhou, H. et al. [109] employed a hybrid multiphase flow model and the Zwart–Gerber–Belamri (Z–G–B) cavitation model to solve the three-dimensional Navier–Stokes equations, obtaining the pressure field within the SFD fluid domain. Using ANSYS, he first investigated the SFD temperature–viscosity relationship and subsequently studied the thermal effects on steam cavitation and air ingestion. An SFD thermo-fluid dynamics model was established to analyze the path by which extrusion heating affects oil film viscosity, thereby influencing steam cavitation and air ingestion. Tian et al. [99,110] derived heat generation formulas for high-speed hybrid ceramic ball bearings and sliding bearings, compared the heat generation of the two, and analyzed the effects of rotational speed, bearing load, initial contact angle, and lubricant viscosity on heat generation. The results show the following: (A) The friction heat generated by mixed ceramic ball bearings is the combined result of friction losses and rolling resistance caused by contact between the rolling elements and raceways, in addition to the friction heat generated by the rotation of the rolling elements. (B) Under the same rotational speed and load conditions, the friction heat generated by mixed ceramic ball bearings is significantly lower than that of sliding bearings. (C) Bearing friction heat increases with an increase in speeds and loads. Methods to reduce bearing friction heat include reducing the diameter of the rolling elements, reducing the contact angle, reducing the preload, and lowering the viscosity of the lubricating oil. Shan [7] analyzed the effects of temperature on the stress and deformation of the outer ring, balls, and inner ring separately; then, they analyzed the overall deformation after coupling the three components. They determined the assembly clearance and the axial stiffness of the bearing under optimal parameters. Brouwer and Sadeghi [24] studied the effect of temperature on ball–outer ring pressure. In another study [26], they applied ball bearing cage radio frequency (RF) sensors to superchargers and analyzed the main causes of temperature changes at different supercharger positions and at different speeds.
4. Conclusions
This review summarizes the development of rolling bearing turbochargers over the past four decades and outlines updates on new research in this field within the last three years. It aims to give readers a concise understanding of the topic from multiple perspectives, including history, structure, modeling, and system characteristics. The following are the important conclusions of this review.
For an accurate analysis of the complex rolling bearing structure, establishing an accurate model requires the consideration of not only multiple degrees of freedom but also the contact forces between components. Currently, for ball bearings and inner and outer rings, the normal force of the cage is generally calculated using Hertzian contact theory to determine contact stiffness. Additionally, the oil film force within the contact area can be introduced to calculate the equivalent contact stiffness. The internal friction force of the bearing is typically calculated using a dry friction model. When the cage is guided by the outer ring, the contact force between the outer ring and the cage is calculated using a fluid dynamic pressure lubrication model. SFD generally selects different approximate models based on the aspect ratio to calculate nonlinear oil film forces. New methods, such as neural networks, can also be used to predict oil film stiffness and damping. Currently, there are studies using ERSFD to support the outer ring, which has better results than traditional SFD.
The establishment and analysis of the vast majority of models are determined by several considerations. The calculation of basic contact stiffness, damping, and oil film force is as described in the previous paragraph. If lubrication and thermal effects are taken into account, most faults are corrected on the basis of the basic model. This study compares various modeling methods and theories of double-row angular-contact ball bearings and SFD from the perspectives of applicability, advantages, and limitations, as shown in Table 1, Table 2 and Table 3, aiming to guide their modeling design.

Table 1.
Comparison of the modeling methods in numerical analysis of double-row angular-contact ball bearings.

Table 2.
Comparison of the modeling methods in theoretical analysis of double-row angular-contact ball bearings.

Table 3.
Comparison of modeling methods for squeeze film dampers.
For dynamic studies, the main factors currently being researched that affect rotor dynamics and bearing dynamics include rotor acceleration, seal fluid excitation force, blade tip clearance airflow excitation force, axial load, bearing stiffness, bearing span, material properties, imbalance, preload, and inner and outer groove curvature.
In terms of mechanical efficiency research, rolling bearing turbochargers and systems have significantly higher mechanical efficiency than traditional journal bearings, and the reduction in friction loss also greatly alleviates the turbo lag effect.
Research on thermal effects indicates that the friction heat generated by mixed ceramic ball bearings is the result of the combined effects of friction losses and rolling resistance caused by the contact between rolling elements and the raceway, in addition to the friction heat generated by the rotation of rolling elements. To reduce the friction heat generated by the bearings, methods such as reducing the diameter of the rolling elements, reducing the contact angle, reducing the preload, and lowering the viscosity of the lubricating oil can be employed. Additionally, simulation calculations can be used to assess the impact of temperature on the deformation of bearing components, enabling the design of appropriate assembly clearances.
5. Promising Research Topics for Future Innovation
Turbochargers operate in a unique environment and are exposed to high-temperature exhaust gases. Currently, no research has been conducted on refined models of the coupling between temperature and fluid fields and rolling bearing turbochargers. In the future, multi-physical field coupling research should be prioritized wherever possible.
Research on dynamics has not yet determined the extent to which design parameters and their mutual coupling affect dynamics. Sensitivity analysis and other methods should be used to determine the most important design parameters in order to provide a basis for design optimization.
Cheng, C. et al. [111,112] established a mathematical model for the structural optimization of double-row angular-contact ball bearings with rated dynamic and static loads as the objective functions, and they optimized the design of the bearings with a genetic and immune algorithm, respectively, which greatly improved the rated dynamic and static loads of the bearings. Hu, Q. G. et al. [113] established a multi-objective optimization model for the structure of a double-row angular-contact ball bearing, with the maximum rated dynamic load and rated static load of the double-row angular-contact ball bearing as the optimization objective, and they used a penalty function particle swarm algorithm to optimize the design of the bearing. Consequently, he rated dynamic and static loads of the bearing were greatly increased. Xu, Y. [114] introduced the predatory optimization HPO algorithm to optimize key parameters of the SFD with an overall vibration reduction in the rotor system as the optimization objective. This indicates that the use of advanced algorithms for the optimized design of rolling bearing turbocharger components is also a topic worthy of study.
Sharko, O. [115] analyzed the structural vibration spectrum of marine turbocharger rolling bearings using principal component analysis and proposed a novel point defect vibration diagnostic parameter for bearing fault detection. Nnaji, O. E. [116] performed Weibull reliability assessments and failure predictions for supercharger ball bearings based on ship data. Chen, Y. [117] employed a genetic algorithm based on the MATLAB platform to determine the optimal structural parameters of bearings. Using service life as the objective function and the inner and outer ring curvature radius coefficients, ball diameter, and number of balls as design variables, the approach achieved rapid convergence and high precision and eliminated cumbersome programming tasks. This indicates that the fault diagnosis and monitoring, as well as the life and reliability analysis of rolling bearing turbocharger components, are also worthy research topics.
Author Contributions
Z.Y.: Conceptualization, data curation, investigation, methodology, validation, visualization, writing—original draft, and writing—review and editing. Z.Z.: Supervision, project administration, funding acquisition, and writing—review and editing. J.P.: Data curation, investigation, validation, and writing—review and editing. Q.X.: Validation, project administration, and writing—review and editing. Y.L.: Project administration, funding acquisition, and writing—review and editing. T.W.: Project administration, funding acquisition, and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Open Subject of State Key Laboratory of Engines of Tianjin University (Grant Number: K2023-09).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this manuscript.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| VGT | variable geometry turbocharger; | NISFD | novel integral squeeze film damper; |
| DN | Diameter × Nominal; | FD | finite difference; |
| PEEK | polyetheretherketone; | SVD | singular value decomposition; |
| SFD | squeeze film damper; | SDERSFD | staggered-type double elastic ring squeeze film damper; |
| REBs | rolling bearing elements; | FEM | finite element method; |
| EHD | damping of the elasto-hydrodynamic; | FRBT | floating ring bearing turbocharger; |
| EHL | elasto-hydrodynamic lubrication; | BBT | ball bearing turbocharger; |
| FSFD | SFD with floating rings; | R-K | Runge–Kutta; |
| ERSFD | elastic ring squeeze film damper; | BSFC | brake specific fuel consumption; |
| ISFD | integral squeeze film damper; | CVD | chemical vapor deposition; |
| EDM | electrical discharge machining; | CFD | computational fluid dynamics; |
| Z–G–B | Zwart–Gerber–Belamri; | RF | radio frequency; |
| DEM | Discrete Element Method; | NVH | Noise, Vibration, Harshness; |
| MBD | Multibody Dynamics; | HPO | Hunter-Prey Optimization; |
| PSO | Particle Swarm Optimization |
References
- Jin, X.; Liu, H. The impact of vehicle exhaust emissions on the environment and their control. Resour. Econom. Environ. Prot. 2015, 33, 80. [Google Scholar] [CrossRef]
- Christmann, R.; Rohi, A.; Weiske, S.; Gugau, M. VTG Turbochargers with Ball Bearings for Gasoline Engines. MTZ Worldw. 2019, 80, 18–25. [Google Scholar] [CrossRef]
- Schweizer, B. Total instability of turbocharger rotors—Physical explanation of the dynamic failure of rotors with full-floating ring bearings. J. Sound Vib. 2009, 328, 156–190. [Google Scholar]
- Schweizer, B.; Sievert, M. Nonlinear oscillations of automotive turbocharger turbines. J. Sound Vib. 2009, 321, 955–975. [Google Scholar] [CrossRef]
- Keller, R.; Scharrer, J.; Pelletti, J. Alternative Performance Turbocharger Bearing Design; No. 962500; SAE International: Warrendale, PA, USA, 1996. [Google Scholar]
- Koutsovasilis, P. Automotive turbocharger rotordynamics: Interaction of thrust and radial bearings in shaft motion simulation. J. Sound Vib. 2019, 455, 413–429. [Google Scholar] [CrossRef]
- Shan, R. Design and Performance Analysis of Rolling Bearing for Vehicle Turbocharger. Master’s Thesis, Henan University of Science and Technology, Luoyang, China, 2017. [Google Scholar]
- Nguyen-Schäfer, H. Rotordynamics of Automotive Turbochargers; Springer International Publishing: Cham, Switzerland, 2015; Volume 17. [Google Scholar]
- Peng, F. Turbocharging technology has great potential, and BorgWarner is accelerating its expansion into China’s electric drive market. Automob. Parts 2018, 2, 54–55. [Google Scholar] [CrossRef]
- Brouwer, M.D.; Sadeghi, F.; Lancaster, C.; Archer, J.; Donaldson, J. Whirl and friction characteristics of high speed floating ring and ball bearing turbochargers. J. Tribol. 2013, 135, 041102. [Google Scholar] [CrossRef]
- Ashtekar, A.; Tian, L.; Lancaster, C. An analytical investigation of turbocharger rotor-bearing dynamics with rolling element bearings and squeeze film dampers. In Proceedings of the 11th International Conference on Turbochargers and Turbocharging, London, UK, 13–14 May 2014; Woodhead Publishing: Oxford, UK, 2014; pp. 361–373. [Google Scholar]
- Wang, Y.; Huang, Y. Vehicle Engine Exhaust Turbocharger; National Defense Industry Press: Beijing, China, 1984. [Google Scholar]
- Wan, H.; Zhang, Z.; Fan, Y. Design of tester for rolling bearing used in automotive turbocharger. Bearing 2015, 4, 47–49+54. [Google Scholar] [CrossRef]
- Zhou, G.; Hao, S.; Zhou, P.; Ren, X.; Shang, Y.; Wang, Q. Measures on improving low-speed torque performance of turbocharged I.C. engine. Intern. Combust. Engine Powerpl. 2010, 27, 7–11. [Google Scholar]
- Onitsuka, K.; Peng, H. The potential of turbochargers to improve vehicle environmental performance. Foreign Intern. Combust. Engine 2015, 47, 57–59. [Google Scholar]
- NSK Develop New Bearing Products. Automob. Parts 2013, 8, 29. Available online: https://d.wanfangdata.com.cn/periodical/CiFQZXJpb2RpY2FsQ0hJU29scjlTMjAyNTEwMjEwOTUwNDYSDnFjbGJqMjAxMzEyMDE4GghoYjl2NGtkMQ%3D%3D (accessed on 4 November 2025).
- Schweitzer, F.; Adleff, K. Rolling bearings in turbocharger applications. MTZ Worldw. 2006, 67, 16–19. [Google Scholar] [CrossRef]
- Bearing innovation technology of SKF used for complex turbo changer. Automob. Parts 2008, 28, 44–46. Available online: https://d.wanfangdata.com.cn/periodical/CiFQZXJpb2RpY2FsQ0hJU29scjlTMjAyNTEwMjEwOTUwNDYSDnFjeXBqMjAwODAxMDE0GghqZjk3bnp6bg%3D%3D (accessed on 4 November 2025).
- Schaeffler Technologies GmbH. Rolling Bearings in Turbochargers. In Solving the Powertrain Puzzle: 10th Schaeffler Symposium April 3/4, 2014; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2014; pp. 202–210. [Google Scholar]
- Bauer, K.H.; Balis, C.; Paja, D.; Davies, P.; Marsal, D. High volume series production of ball bearing turbochargers. MTZ Worldw. Emagazine 2011, 72, 48–51. [Google Scholar] [CrossRef]
- Garrett Motion. Basic Understanding the Parts of the Turbocharger; Garrett Motion Inc.: Rolle, Switzerland, 2023. [Google Scholar]
- Yang, Y. Innovation and R&D lead the way, adapting to trends to secure the future—Ningbo Weifu Tianli Turbocharging Technology Co., Ltd. deeply rooted in the turbocharger industry. Sci. Technol. Ind. China 2023, 37, 32–33. Available online: https://d.wanfangdata.com.cn/periodical/zgkjcy202307016 (accessed on 4 November 2025).
- Jebur, N.A.; Soud, W.A. A Comparative Analysis of the Performance of Ball Bearings and Journal Bearings Under Varying Rotational Speeds. J. Fail. Anal. Prev. 2025, 25, 1528–1538. [Google Scholar] [CrossRef]
- Brouwer, M.D.; Sadeghi, F. Investigation of turbocharger dynamics using a combined explicit finite and discrete element method rotor–cartridge model. J. Tribol. 2017, 139, 012201. [Google Scholar] [CrossRef]
- Tanimoto, K.; Kajihara, K.; Yanai, K. Hybrid Ceramic Ball Bearings for Turbochargers; SAE Transactions: Warrendale, PA, USA, 2000; pp. 763–775. [Google Scholar]
- Brouwer, M.D.; Shahidi, A.; Gupta, L.A.; Sadeghi, F.; Peroulis, D. Application of ball bearing cage RF temperature sensor in high speed turbocharger. In Proceedings of the 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI), Memphis, TN, USA, 6–11 July 2014; IEEE: New York, NY, USA, 2014; pp. 1312–1313. [Google Scholar]
- Griffith, R.C.; Slaughter, S.E.; Mavrosakis, P.E. Applying Ball Bearings to the Series Turbochargers for the Caterpillar® Heavy-Duty on-Highway Truck Engines; No. 2007-01-4235l; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2007. [Google Scholar]
- Huang, R.; Ge, X.; Ma, C. Critical speed analysis on vehicle turbocharger with ball bearings. Veh. Engine 2007, 30, 72–76. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, Y.; Chen, T. Rotor dynamics analysis for ball bearing turbocharger considering the sealed construction. Zhendong Yu Chongji (J. Vib. Shock.) 2012, 31, 153–156+182. [Google Scholar]
- Huang, R.; Zhang, W.; Xing, W.; Zhang, Y. Gas excitation’s influence on dynamic behavior of a turbocharger rotor–ball bearing system. J. Vib. Shock. 2014, 33, 140–146. [Google Scholar]
- Huang, R.; Zhang, W.; Jiang, Y.; Xing, W. Influences of acceleration on dynamic characteristics of a turbocharger’s ball bearing–rotor system. J. Vib. Shock. 2014, 33, 136–140. [Google Scholar]
- Huang, R.; Zhen, S.; Zhang, W. Influences of ball bearing stiffness on transient response of a turbocharger. J. Vib. Shock. 2016, 35, 83–87. [Google Scholar]
- Ashtekar, A.; Sadeghi, F. Experimental and analytical investigation of high speed turbocharger ball bearings. J. Eng. Gas. Turbines Power 2011, 133, 122501. [Google Scholar] [CrossRef]
- Conley, B.; Sadeghi, F. Experimental and analytical investigation of turbocharger whirl and dynamics. Tribol. Trans. 2021, 64, 239–252. [Google Scholar] [CrossRef]
- Conley, B.; Sadeghi, F.; Griffith, R.C.; McCormack, J.W. Experimental investigation of the dynamic loads in a ball bearing turbocharger. J. Tribol. 2019, 141, 111101. [Google Scholar] [CrossRef]
- Conley, B.; Sadeghi, F. Impact of whirl and axial motion on ball bearing turbocharger dynamics. Tribol. Trans. 2023, 66, 338–349. [Google Scholar] [CrossRef]
- Conley, B.B. Experimental and Analytical Investigation of Ball Bearing Turbocharger Dynamics. Ph.D. Dissertation, Purdue University Graduate School, West Lafayette, IN, USA, 2022. [Google Scholar]
- Wan, H. Design and Experiment Study of Rolling Bearings of Automobile Turbocharger. Master’s Thesis, Henan University of Science and Technology, Luoyang, China, 2015. [Google Scholar]
- Lu, D. Application of collaborative simulation technology in rotor bearing systems. In Proceedings of the 12th Joint Academic Conference on Multibody Dynamics and Control, the 7th Joint Academic Conference on Aerospace Dynamics and Control, and the 15th National Joint Academic Conference on Analytical Mechanics, Shanghai, China, 13 November 2021; p. 90. [Google Scholar] [CrossRef]
- Majer, M.; Chatterton, S.; Dassi, L.; Gheller, E.; Pennacchi, P.E.L.M.; Colonna, P.; Pini, M. Mechanical design and rotordynamic analysis of the ORCHID turbine. J. Glob. Power Propuls. Soc. 2025, 9, 45–66. [Google Scholar] [CrossRef]
- Bala Murugan, S.; Behera, R.K.; Parida, P.K. Nonlinear Dynamic Analysis of Automotive Turbocharger Rotor System. In Advances in Applied Mechanical Engineering: Select Proceedings of ICAMER 2019; Springer: Singapore, 2020; pp. 443–453. [Google Scholar]
- Fang, B.; Zhang, J.; Hong, J.; Yan, K. Research on the nonlinear stiffness characteristics of double-row angular contact ball bearings under different working conditions. Lubricants 2023, 11, 44. [Google Scholar] [CrossRef]
- Desai, A. Analytical and Experimental Investigation of Effect of Cage and Shaft Flexibility on Dynamics of Bearing Shaft Systems. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 2007. [Google Scholar]
- Wensing, J.A. On the Dynamics of Ball Bearings. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 1998. [Google Scholar]
- Yao, T. Modeling and Simulation Analysis of the Rigid–Flexible Coupling Multi-Body Dynamics of the Milling Machine Spindle System. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2007. [Google Scholar]
- Yao, T. Research on Multibody Contact Dynamics of Ball Bearings. Ph.D. Dissertation, Kunming University of Science and Technology, Kunming, China, 2009. [Google Scholar]
- Yao, T.; Chi, Y.; Huang, Y. Dynamic contact analysis of ball bearing. Mech. Des. Manuf. 2007, 45, 1–3. [Google Scholar] [CrossRef]
- Yao, T.; Chi, Y.; Huang, Y.; Tan, Y. Rigid and Flexible Contact Dynamics Analysis on Rolling Bearing. China Mech. Eng. 2008, 19, 1924–1928. [Google Scholar]
- Fan, R.; Yao, T.; Liu, X.; Xiong, T. Stability analysis of angular contact ball bearing cage. Mach. Des. Res. 2017, 33, 76–81. [Google Scholar]
- Zhu, K.; Zhang, S.; Luo, Z.; Luo, F. Design of double-row angular contact ball bearings and study of their life and reliability. Mech. Eng. 2024, 56, 136–141+145. [Google Scholar]
- Li, Z.; Wang, Q.; Wang, R.; Qin, B. Dynamic Characteristics Analysis of Double Row Angular Contact Ball Bearings with Different Bearing Configurations. J. Mech. Eng. 2025, 61, 220–231. [Google Scholar]
- Deng, S.; Jia, Q.; Xue, J. Principles of Rolling Bearing Design, 2nd ed.; China Standards Press: Beijing, China, 2014. [Google Scholar]
- Yao, T.Q.; Wang, L.H.; Chi, Y.L.; Huang, Y. Research on multibody contact dynamics of ball bearings. J. Aerosp. Power 2013, 28, 1624–1637. [Google Scholar]
- Deng, S.E.; Xie, P.F.; Yang, H.S.; Gao, Y.T. Flexible-body dynamics analysis on cage of high-speed angular contact ball bearing. Acta Armamentarii 2011, 32, 625. [Google Scholar]
- Deng, S.E.; Dong, X.; Cui, Y.C.; Hu, G.C. Analysis of dynamic stiffness characteristics of double-row angular contact ball bearings. Acta Armamentarii 2015, 36, 1140. [Google Scholar]
- Gunduz, A.; Dreyer, J.T.; Singh, R. Effect of bearing preloads on the modal characteristics of a shaft-bearing assembly: Experiments on double row angular contact ball bearings. Mech. Syst. Signal Process. 2012, 31, 176–195. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, X. Load calculation for double row angular contact ball bearing based on deformation coordination. Bearing 2004, 47, 1–4. [Google Scholar] [CrossRef]
- Zhuo, Y.; Zhou, X.; Yang, C. Dynamic analysis of double-row self-aligning ball bearings due to applied loads, internal clearance, surface waviness and number of balls. J. Sound Vib. 2014, 333, 6170–6189. [Google Scholar] [CrossRef]
- Cheng, C.; Wang, J. Load analysis of double row angular contact ball bearings. Mech. Sci. Technol. Aerosp. Eng. 2014, 33, 829–833. [Google Scholar]
- Liu, Y.; Yang, M.; Su, B.; Deng, S. Simulation Analysis of the Friction Power Consumption of Double Row Angular Contact Ball Bearings for Aero-engine. J. Mech. Transm. 2021, 45, 129–135. [Google Scholar]
- Saheta, V. Dynamics of Rolling Element Bearings Using Discrete Element Method. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 2001. [Google Scholar]
- Cao, L. Dynamic Bearing Simulation Using Combined EFEM-DEM Method. Ph.D. Dissertation, Purdue University, West Lafayette, IN, USA, 2018. [Google Scholar]
- Ashtekar, A.; Sadeghi, F.; Stacke, L.E. A new approach to modeling surface defects in bearing dynamics simulations. J. Tribol. 2008, 130, 041103. [Google Scholar] [CrossRef]
- Ashtekar, A.; Sadeghi, F.; Stacke, L.E. Surface defects effects on bearing dynamics. Proc. Inst. Mech. Eng. Part. J. J. Eng. Tribol. 2010, 224, 25–35. [Google Scholar] [CrossRef]
- Doro, A.M.K. A Preliminary Study of the Impact of Material, Unbalanced Mass, and Bearing Type on Turbocharger Vibration Behavior Using ANSYS. Ph.D. Dissertation, Cleveland State University, Cleveland, OH, USA, 2024. [Google Scholar]
- Luo, Z.; Wang, J.; Han, Q.; Wang, D. Research progress on the dynamics of combined support rotor systems. Trans. Chin. Soc. Mech. Eng. 2021, 57, 44–60. [Google Scholar]
- Sawalem, M.; Aburwais, M. Analysis of Double-Row Ball Bearing Used in TACCHI FTC 100 Machine (case study). Int. J. Eng. Inf. Technol. (IJEIT) 2023, 11, 21–24. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Liu, H.; Liu, T.; Wang, Q. Modeling and Dynamic Analysis of Double-Row Angular Contact Ball Bearing–Rotor–Disk System. Lubricants 2024, 12, 441. [Google Scholar] [CrossRef]
- Wen, B.; Ma, S.; Fang, B.; Yan, K.; Zhang, X.; Zhang, J.; Hong, J. Quasi-dynamic modelling and performance analysis of double-row angular contact ball bearing considering overturning moment. Eur. J. Mech.-A/Solids 2025, 116, 105924. [Google Scholar] [CrossRef]
- Kim, K.; Ryu, K. Rotordynamic analysis of automotive turbochargers supported on ball bearings and squeeze film dampers in series: Effect of squeeze film damper design parameters and rotor imbalances. Tribol. Lubr. 2018, 34, 9–15. [Google Scholar]
- Gunter, E.J. Design of Oil and Air Squeeze Film Dampers for a Ball Bearing Turbocharger; Dyrobes: Charlottesville, VA, USA, 2023. [Google Scholar]
- Zhou, H.; Luo, G.; Chen, G.; Wang, F. Nonlinear dynamic analysis of a rotor supported on the ball bearings with squeeze film dampers. Mech. Sci. Technol. Aerosp. Eng. 2013, 32, 499–505. [Google Scholar]
- Zhou, H.L.; Luo, G.H.; Chen, G.; Wang, F. Analysis of the nonlinear dynamic response of a rotor supported on ball bearings with floating-ring squeeze film dampers. Mech. Mach. Theory 2013, 59, 65–77. [Google Scholar] [CrossRef]
- Brouwer, M. Dynamic Performance of Turbocharger Rotor-Bearing Systems. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2015. [Google Scholar]
- Gjika, K.; Costeux, A.; LaRue, G.; Wilson, J. Ball bearing turbocharger vibration management: Application on high speed balancer. Mech. Ind. 2020, 21, 619. [Google Scholar] [CrossRef]
- Heidari, H.; Ashkooh, M. The influence of asymmetry in centralizing spring of squeeze film damper on stability and bifurcation of rigid rotor response. Alex. Eng. J. 2016, 55, 3321–3330. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Y.; Yang, T.; Luo, Z.; Han, Q. Navigating the Dynamics of Squeeze Film Dampers: Unraveling Stiffness and Damping Using a Dual Lens of Reynolds Equation and Neural Network Models for Sensitivity Analysis and Predictive Insights. Mathematics 2024, 12, 771. [Google Scholar] [CrossRef]
- Groves, K.H.; Bonello, P. Improved identification of squeeze-film damper models for aeroengine vibration analysis. Tribol. Int. 2010, 43, 1639–1649. [Google Scholar] [CrossRef]
- Liu, Y. Modeling of a Dynamic Nonlinear Rotor System with a Squeeze Film Damper. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
- Wang, X.; Han, Z.; Ding, Q.; Zhang, W. Influence of fluid inertia on dynamic characteristics of elastic ring squeeze film damper-rotor system. J. Aerosp. Power 2018, 33, 2981–2990. [Google Scholar]
- He, H.; Wang, S.; Wang, L.; Ji, J.; Zhao, L. Influence of elastic ring damper on power performance of turbocharger rotor. Veh. Engine 2016, 4, 70–74. [Google Scholar]
- Nerg, J.; Jaatinen-Värri, A.; Pyrhönen, J.; Sopanen, J. Mechanical design of rotor-bearing system in a high-speed 20 kw range extender for battery electric vehicles. In Proceedings of the 12th International Conference on Vibrations in Rotating Machinery, Virtual, 14–15 October 2020; CRC Press: Boca Raton, FL, USA, 2020; pp. 511–521. [Google Scholar]
- Fan, T.; Behdinan, K. An Analytical Turbulence Model for Squeeze Film Damper Short-Bearing Analysis. Appl. Mech. 2025, 6, 48. [Google Scholar] [CrossRef]
- He, F.; Yang, T.; Ren, Y.; Zu, S.; Li, Y.; Luo, Z.; Shi, H.; Li, L.; Bai, X. Design of similarity method for rotor system with squeeze film damper. Mech. Syst. Signal Process. 2025, 240, 113423. [Google Scholar] [CrossRef]
- Luo, Z.; Sun, K.; Ge, X.; Zhou, G.; Cui, Z. Dynamic analysis of the rotor system with elastic ring squeeze film damper considering oil film temperature. Nonlinear Dyn. 2023, 111, 15981–16002. [Google Scholar] [CrossRef]
- Li, Y.; Yang, H.; Deng, S. Dynamic characteristics study of elastic ring squeeze film damper with rigid–elastic–oil coupled model. Lubricants 2023, 11, 491. [Google Scholar] [CrossRef]
- Sun, K.; Luo, Z.; Li, L.; Wu, F.; Hao, H. Mechanical and vibration characteristics investigation of the elastic ring squeeze film damper-rotor considering oil film sealing and leakage. Int. J. Non-Linear Mech. 2024, 161, 104701. [Google Scholar] [CrossRef]
- Yan, W.; Lu, J.; Pan, J.; Liu, J.; Fuyang, C.; Ye, D. Research on dynamic characteristic coefficients of integral squeeze film damper. Machines 2024, 12, 274. [Google Scholar] [CrossRef]
- Lu, Q.; Li, C.; Zhang, Y.; Fang, H.; Bin, G. Study on the vibration control method of a turboshaft engine rotor based on piezoelectric squeeze film damper oil film clearance. Mech. Sci. 2023, 14, 237–246. [Google Scholar] [CrossRef]
- Dong, H.; He, L.; Jia, X. Using integral squeeze film damper to suppress vibration of gas turbine. J. Vib. Eng. Technol. 2023, 11, 3163–3176. [Google Scholar] [CrossRef]
- Zhang, Y.; Hou, L.; Wang, S.; Zhao, K.; Zhao, L.; Li, Q. Vibration reduction characteristics analysis and experimental study of staggered-type double elastic ring squeeze film damper under complex operating conditions. Mech. Syst. Signal Process. 2025, 235, 112919. [Google Scholar] [CrossRef]
- Huang, R.; Ge, X.-B.; Ma, C.-C. Research on the critical speed of a mixed-flow turbocharger with hybrid ceramic ball bearing. J. Beijing Inst. Technol. 2009, 18, 298–303. [Google Scholar]
- Ashtekar, A.; Sadeghi, F.; Powers, G.; Mantel, K.; Griffith, R. Experimental investigation of turbocharger rotor bearing system. In Proceedings of the ASME Turbo Expo 2011: Power for Land, Sea, and Air, Vancouver, BC, Canada, 6–10 June 2011; Volume 54662, pp. 559–566. [Google Scholar]
- Zhen, S. Stiffness Characteristics of Ball Bearing Turbocharger and Influence on the Rotor Dynamic Characteristics. Master’s Thesis, Beijing Institute of Technology, Beijing, China, 2016. [Google Scholar]
- Shafiee, A.; Sadeghi, F.; Wilmer, M.G. An Integrated Finite Element and adams Modeling Approach for Analyzing Rotor-Bearing Housing Systems. J. Tribol. 2025, 147, 014303. [Google Scholar] [CrossRef]
- Li, T.; Guo, H.; Cheng, Z.; Men, R.; Li, J.; Chen, Y. Nonlinear Vibration Analysis of Turbocharger Rotor Supported on Rolling Bearing by Modified Incremental Harmonic Balance Method. Machines 2025, 13, 360. [Google Scholar] [CrossRef]
- Li, Y.; Cui, Y.; Deng, S. Research on Sudden Unbalance Response of Rigid-Elastic-Oil Coupled Ball Bearings. Lubricants 2024, 12, 161. [Google Scholar] [CrossRef]
- Huang, R.; Shang, W.T.; Zhang, W.L. Study on turbocharger transient response characteristics and its evaluation method. Chin. Intern. Combust. Engine Eng. 2014, 35, 27–35. [Google Scholar]
- Tian, X.; Mao, Y.; Xu, S.; Yao, J.; Guo, F. Heat generating analysis of high-speed hybrid ceramic ball bearing of turbocharger and efficiency. Mod. Manuf. Eng. 2011, 34, 5–9. [Google Scholar] [CrossRef]
- Zhang, N.; Burke, R.D.; Duda, T.; Brace, C.J.; Akehurst, S.; Capon, G.; Dowell, P.G.; Davies, P. Experimental and analytical investigation of implementing a ball bearing turbocharger on a production diesel engine. In Proceedings of the 11th International Conference on Turbochargers and Turbocharging, London, UK, 13–14 May 2014. [Google Scholar]
- Huang, R.; Wang, S.Q.; Wei, M.S. Mechanical loss measuring method and equipment for turbocharger. Neiranji Gongcheng/Chin. Intern. Combust. Engine Eng. 2010, 31, 92–97. [Google Scholar]
- Ozaki, M.; Yoshida, T.; Fujita, Y.; Futae, T.; Arai, T.; Yamada, Y. Development of Turbocharger for Next-generation Hybrid Electric Vehicles. Mitsubishi Heavy Ind. Tech. Rev. 2021, 58, 1. [Google Scholar]
- Faraj, S.S.; Hadi, N.H. Dynamic Stress Analysis of Turbocharger Blades under High-Velocity Impact Load. Iraqi J. Ind. Res. 2024, 11, 25–34. [Google Scholar] [CrossRef]
- An, Y.; Li, P.; Sun, C. Effect of Ball Bearing Turbo Charger on Combustion and Emissions for Heavy Duty Diesel Engine. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4778968 (accessed on 4 November 2025).
- Fasolia, V.; Hetman, M.; Staryi, A. Performance analysis of turbocharger rotor friction pairs of an automobile engine. Probl. Tribol. 2023, 28, 58–65. [Google Scholar] [CrossRef]
- Riera, P.; Macareno, L.M.; Fernandez de Bustos, I.; Aguirrebeitia, J. Hard Preloaded Duplex Ball Bearing Dynamic Model for Space Applications. Machines 2025, 13, 581. [Google Scholar] [CrossRef]
- Serrano, J.R.; Izaguirre, A.O.T.; García-Cuevas, L.M.; Usaquén, T.R.; Guillaume, M. A methodology to study oil-coking problem in small turbochargers. Int. J. Engine Res. 2020, 21, 1193–1204. [Google Scholar] [CrossRef]
- Hu, X.; Lin, J. Study on Flow Field Characteristics of High-Speed Double-Row Ball Bearings with Under-Race Lubrication. Aerospace 2025, 12, 861. [Google Scholar] [CrossRef]
- Zhou, H.; Cao, G.; Chen, X.; Zhang, Y.; Cang, Y. A study on the thermal properties of oil-film viscosity in squeeze film dampers. Lubricants 2023, 11, 163. [Google Scholar] [CrossRef]
- Tian, X.; Mao, Y.; Xu, S.; Yao, J.; Guo, F. Development of high speed hybrid ceramic bearing for tank engine turbocharger. Mech. Sci. Technol. Aerosp. Eng. 2012, 31, 1390–1394. [Google Scholar]
- Cheng, C.; Wang, J.G. Optimal design of double-row angular-contact ball bearing based on genetic algorithm. J. Mach. Des. 2015, 32, 46–50. [Google Scholar]
- Cheng, C.; Wang, J.G. Optimum Design of Double-row Angular-contact Ball Bearing with Immune Algorithm. J. Aerosp. Power 2015, 30, 2810–2816. [Google Scholar]
- Hu, Q.G.; Du, C.C.; Wu, M.Q. Optimization Design of Penalty Function Particle Swarm Optimization Algorithm for Angular Contact Ball Bearings. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2021, 40, 145–150. [Google Scholar]
- Xu, Y.; Cao, H.; Shi, J.; Pei, S.; Zhang, B.; She, K. A comprehensive multi-parameter optimization method of squeeze film damper-rotor system using hunter-prey optimization algorithm. Tribol. Int. 2024, 194, 109538. [Google Scholar] [CrossRef]
- Sharko, O.; Stepanchikov, D.; Sharko, A.; Yanenko, A. Computer diagnostics of the condition of ship rolling bearings during their operation. Sci.-Based Technol. 2024, 63, 409–418. [Google Scholar]
- Nnaji, O.E.; Nkoi, B.; Lilly, M.T.; Le-ol, A.K. Evaluating the reliability of a marine diesel engine using the Weibull distribution. J. Newviews Eng. Technol. (JNET) 2020, 2, 1–9. [Google Scholar]
- Chen, Y.; Li, J.; Chen, C. Optimization design of thin wall angular contact ball bearing based on MATLAB genetic algorithm. J. Phys. Conf. Ser. 2023, 2459, 012104. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).