A Digital Twin Model for UAV Control to Lift Irregular-Shaped Payloads Using Robust Model Predictive Control

Abstract

This paper presents an innovative digital twin (DT) model integrated with robust model predictive control (MPC) to enhance the performance of an unmanned air vehicle (UAV) tasked with lifting and transporting irregular-shaped payloads. Traditional UAV control systems face complex challenges in stability and accuracy when dealing with asymmetrical payloads, as such payloads cause continuous shifts in the center of gravity (CoG) and variable inertial forces, which lead to unpredictable flight dynamics. The proposed DT framework enables the creation of a real-time replica of the UAV payload system. It creates an adaptive control environment that anticipates and mitigates disturbances before they impact the stability of the UAV during a mission. By combining a DT with MPC, the control system dynamically adjusts to variations in payload characteristics, namely (a) changes in mass distribution and (b) aerodynamic drag force. As a result, a stable flight path is ensured even under challenging environmental conditions. The DT model continuously forecasts potential destabilizing events and modifies MPC constraints to accommodate complex shifting dynamics, achieving improved control accuracy and energy efficiency. Extensive simulations across various hanging payload configurations and environmental disturbance scenarios validate the effectiveness of the proposed model. The simulation results show that the DT-MPC strategy significantly improves stability, control precision, and energy conservation, outperforming conventional methods. A comparative analysis is also carried out with a conventional control scheme to validate the robustness of the proposed framework. This research work advances the development of intelligent, autonomous UAV systems capable of reliably managing complex and irregularly shaped payloads with varying mass distributions in real-world scenarios, thereby broadening their potential applications in logistics, emergency response, and industrial transportation.

1. Introduction

UAVs, commonly known as drones, have shown exponential growth in adoption across different sectors, such as (a) logistics, (b) healthcare, (c) agriculture, (d) construction, (e) industrial inspections [1]. Their capacity to deal with different scenarios and environmental disturbances and access remote locations that are difficult to reach by conventional transport contribute to their indispensability for critical tasks, including package delivery, medical supply transport, crop health surveillance, infrastructure assessment, and search and rescue operations [2]. Their adaptability is important to their lightweight construction, exceptional maneuverability, and cost-effective operations [3]. Although UAVs are widely used for payload transportation duties, they face irregular loads characterized by asymmetric shapes, uneven mass distributions, and interconnected aerodynamic profiles [4].

The hanging of irregular payloads poses a significant issue to the stability, security, and control performance of UAVs [5]. Non-uniform loads can be dynamic during flight and will perturb the CoG and rotational inertia of the UAV. They affect equilibrium because UAVs are unable to track reference trajectories and orientations [6]. However, these inconsistent payloads have asymmetrical geometry and exhibit different aerodynamic forces depending on altitude, forward motion, and velocity [7]. These multiple disturbances eventually lead to flight operation instabilities in UAVs, contributing to the reasoning behind control paradigms [5].

With autonomous UAV operations, which cannot be managed manually, stability and safety requirements are necessary [8]. Complex control systems are mandatory to maintain stability and accuracy in the presence of perturbations [9]. Reducing irregular payload-related control hurdles has garnered significant attention from both academics and industry [10]. In such situations, an increase in UAV autonomy opens the door to revolutionary possibilities in logistics, disaster relief, and industrial logistics, where valuable heterogeneous loads can be smoothly managed with insignificant chances of failure [11].

Asymmetric payload delivery presents unique control complexities in UAVs, as these payloads are very unlike symmetric and predictable cargoes [12]. Doubts in exact mass and aerodynamic characteristics initiate continuous CoG disturbance, varying inertial moments, and arbitrary drag/lift distributions, making stable flight challenging [13]. As an example, regarding long or asymmetrical delivery, payload motions or transfers can be excited because of agile maneuvers, causing UAV destabilization [14].

Traditional controllers such as PID or MPC assume constant or predictable payload characteristics [15]. These principles fail with non-regular payloads, whose characteristics are adaptive to UAV kinematics and non-cooperation [16]. Conventional systems exhibit sluggish responses, require reconfiguration to load variances, and display reactive disturbance responses, which increase instability, precision issues, and energy consumption in control efforts [17].

The need to have real-time dynamic paradigms to maneuver through irregular payload transportation is important, as they enhance autonomous transfer without disturbing stability, efficiency, or security [18]. A DT is a type of virtual system that replicates the kinetics of a physical entity in real time [19]. The DT predicts interruptions, which is enabled by copying the UAV–payload interactions, enabling predictive control [20]. The DT utilizes information collected by UAV sensors, which enables it to maintain a correct virtual representation of the UAV, forecast future alterations, and detect itself just before future disturbances will impact the system [21].

Integrating a DT and MPC provides the UAV controller with a system that can overcome anomalies in the payload [21]. Robust MPC is good in stochastic prediction as it uses uncertainties in optimization [22]. It can support reallocation of payload mass, aerodynamic perturbation, and migration of CoG, enhancing disturbance resilience [23]. DT-supplied foresight allows unrelenting control input refinements, compensating payload perturbations during flight operation and maintaining stability at the expense of energetics [24]. This integration not only solves the problem of irregular payload management, but it brings improvements in efficiency and safety of transportation using UAVs [25].

2. Related Work

This section reviews prior research across three key areas relevant to this study: (1) DT technology in autonomous systems, particularly UAVs; (2) MPC for UAV stability; (3) control strategies for managing irregularly shaped payloads. Collectively, these works outline the current state of the art, highlighting gaps in the control of UAVs with complex payloads.

2.1. Digital Twin Technology in Autonomous Systems

DT technology has become a transformational methodology in manufacturing and autonomous systems, enabling the generation of real-time virtual copies of physical systems [26]. DTs facilitate real-time monitoring, diagnostics, and control by enabling data-driven simulations and predictions [27]. Investigations have developed the principles of DTs and their flexibility in working under dynamic environments, which is essential for making real-time decisions [28]. Within the framework of autonomous UAVs, DTs are used frequently to simulate the real-world situation virtually [29]. Recent papers have investigated the potential of DTs in decision-making in aerospace markets, showing greater reliability in hard operations. Predicting faults with the help of DTs enhances the safety and efficiency of UAVs [30], and enhanced models facilitate the simulation of the complex dynamics of UAVs and enable the implementation of intricate corrections.

DT applications have been developed on resilient swarms of UAVs, involving edge computing to provide low-latency synchronization [31]. Physical models with machine learning Hybrid DTs are better for predictive maintenance in unpredictable environments [32]. Federated DTs support collaborative work of multiple agents without information exchange, which is needed for use with privacy-sensitive UAV flocks [33]. Moreover, irregular payloads are still limited in DT applications, necessitating dynamic models that capture variable loading conditions [34]. This paper develops the DT-UAV combination by combining it with robust MPC to estimate and avoid destabilizing factors and extrapolate DT utility to complex tasks [21].

2.2. Model Predictive Control for UAV Stabilization

MPC is also actively applied in UAVs to deal with multi-variable constraints when operating in dynamic environments [35]. Contrary to conventional approaches, MPC forecasts the behavior of a system with a receding horizon, predicting disturbances and responding to changes in paths, which are essential for UAV stability, as presented in [36]. Principles of MPC have been elaborated through theoretic frameworks, where the benefits and shortcomings of linear and nonlinear models have been noted. Optimization of UAV reference trajectories in varying environments demonstrates the efficiency of MPC, and UAV stability results are studied in relation to the influence of disturbances, with restricted ability to model variable payloads [37].

The latest developments include stochastic MPC, which addresses uncertainties and optimum loading due to payload variations, and adaptive MPC, which handles irregularly changing slung loads [38]. The authors of [39] present innovations in learning-enhanced MPC for online parameter tuning in turbulent conditions. The authors of [40] present innovations in distributed MPC for UAV formations with payload differences. Reference [41] discusses the topic of event-driven MPC to reduce computational load in resource-constrained UAVs. MPC is resilient because it counters disturbances at a high level [23]. This study integrates DTs and MPC, where the real-time feedback of a DT enables adaptation to irregular dynamics, thereby enhancing stability and precision [21].

2.3. Control Strategies for Irregularly Shaped Payloads

The problem of irregular payloads is caused by their generated oscillations, changes in the CoG, and aerodynamic influence [42]. Conventional UAV control requires symmetry; hence, it is not suitable when there are such irregularities. The literature on suspended-load steadiness has highlighted destabilizing forces in a manner similar to CoG-variant irregularities [43]. Adaptive nonlinear control techniques have been employed to address problems with varying loads, which pose challenges in tuning and limit real-time flexibility [44]. Unknown payload-adaptive hybrids exhibit flexibility, but cannot handle sudden changes [45]. Reduced-order models of irregular payloads can accurately display the effects of a load on trajectory, highlighting the importance of understanding the disturbances that affect stability.

The latest advances are vision-based adaptive controls to dictate payload with no sensors [46], reinforcement learning to navigate nonlinearities with slung irregular loads [47], and sliding-mode observers to neutralize aerodynamic disturbances in asymmetric lifts [48]. The authors of [12] explain the Distributed Sliding-Mode Controller for single and heterogeneous drones used for transportation of a hanging payload. However, real-time dynamic adaptation remains unexplored, as it is not yet supported by kinetic simulations. DTs offer a solution through real-time, data-driven UAV–payload simulations, predicting anomalies for robust control. In this study’s DT–robust MPC framework, responses to irregular loads are enhanced with superior stability and precision, addressing adaptive shortcomings in payload variations. In [49], the authors investigate the operation of an aerial manipulator system equipped with a controllable arm with two degrees of freedom to carry out actuation tasks during flight operation. A novel low-altitude vehicle speed detector system utilizing UAVs for remote sensing applications in smart cities is introduced in [50], aiming to enhance traffic safety and security. Similarly, the authors present a novel approach to autonomous payload delivery for single and multiple heterogeneous UAVs in [51]. For single-UAV operations, SMC enables a UAV to track a predefined reference trajectory, autonomously identify the payload’s CoM, securely attach to it, lift it, and deliver it to the desired target location.

2.4. Summary and Research Gap

Existing research in the literature confirms the individual strengths of DTs and MPC in UAV control, prediction, and disturbance rejection. DTs provide accurate simulations for identifying and monitoring UAVs. Meanwhile, MPCs manage unstable environments and uncertainties, ensuring the stability of UAVs in harsh conditions.

However, there is a research gap: the integration of DTs with the MPC of hanging irregular-payload delivery is not examined in detail. The literature shows the use of conventional approaches, which lack the capability to forecast the problems of hanging payloads in real time. Furthermore, MPC, useful in response to environmental disturbances in the case of constant conditions, experiences troubles with variable hanging payloads.

The proposed research paper will fill this gap by integrating DTs with MPC to enhance the adaptability and stability of real-time flights by UAVs in terms of irregularly loaded payloads. The predictive features of DTs enable the rejection of disturbances in advance, whereas MPC allows for tighter control using forecasts, which is necessary for stability in the face of load variations. This method ensures flexible, accurate, and effective solutions for UAVs with hanging payloads, thereby widening reliability in various applications. It also leads the way in autonomous operations in complex and demanding environments by applying the use of DT predictions and MPC to achieve safer and cost-efficient transportation of irregular payloads.

The key contributions of the paper to the aforementioned research gaps are as follows:

• Real-Time DT of Irregular Payload Kinetics: In this paper, the authors present a DT framework for a UAV carrying an irregularly shaped hanging payload, which extends the current DT models beyond operation only in the case of a static environment. The DT dynamically recreates time-varying payload properties, including mass reallocation, CoG variations, and aerodynamic behavior, which gives a digital platform for predictive control and mitigation of disturbances.
• DT-MPC Integration: The present work combines the DT and MPC, making possible the adaptive and precise control of UAVs even in the case of complicated payloads. This hybrid command utilizes real-time data from a DT to support MPC in managing uncertainties, ensuring stability and efficiency when other classic control methods fail.
• Adaptive Predictive Disturbance Mitigation: We propose a new adaptive predictive rejection mechanism with the use of DT measurements of payload-induced disturbance. This gives MPC the opportunity to make early corrections to control inputs, minimize oscillations, maximize energy consumption, and enhance stability during flight with highly variable payload geometries throughout the mission.
• Validation Across Diverse Payloads: The study validates the DT-MPC framework through extensive simulations across a wide range of payload configurations, addressing real-world irregularities. The results indicate that DT-MPC yields better performance in terms of stability, precision, and energy efficiency, establishing a robust foundation for autonomous UAV operations with irregular hanging payloads.

Table 1. Comparison of Contributions with State-of-the-Art.

Contribution	Novelty vs. Prior Art
1. Real-Time DT for Irregular Payload Kinetics	Unlike [36], we model time-varying $m_p\left(t\right)$, $r_p\left(t\right)$, and $I_p\left(t\right)$ using online identification.
2. DT–Robust MPC Synergy	We are the first to use DT forecasts to update MPC & tube bounds in real time (Section 3.3.3).
3. Adaptive Predictive Disturbance Mitigation	We achieve pre-emptive control via ARIMA-disturbance forecasting, not reactive control like in [51].
4. Comprehensive Validation	We present 18 figures across diverse irregular payloads + disturbances, beyond [46].

compares the contribution of this paper with state-of-the-art literature work.

The rest of the paper consists of Section 3, explaining the modeling and architecture in detail; Section 4, explaining the problem formulation and analysis: Section 5, which presents detailed simulation results to validate the proposed work; and Section 6, which concludes the paper and gives some future directions.

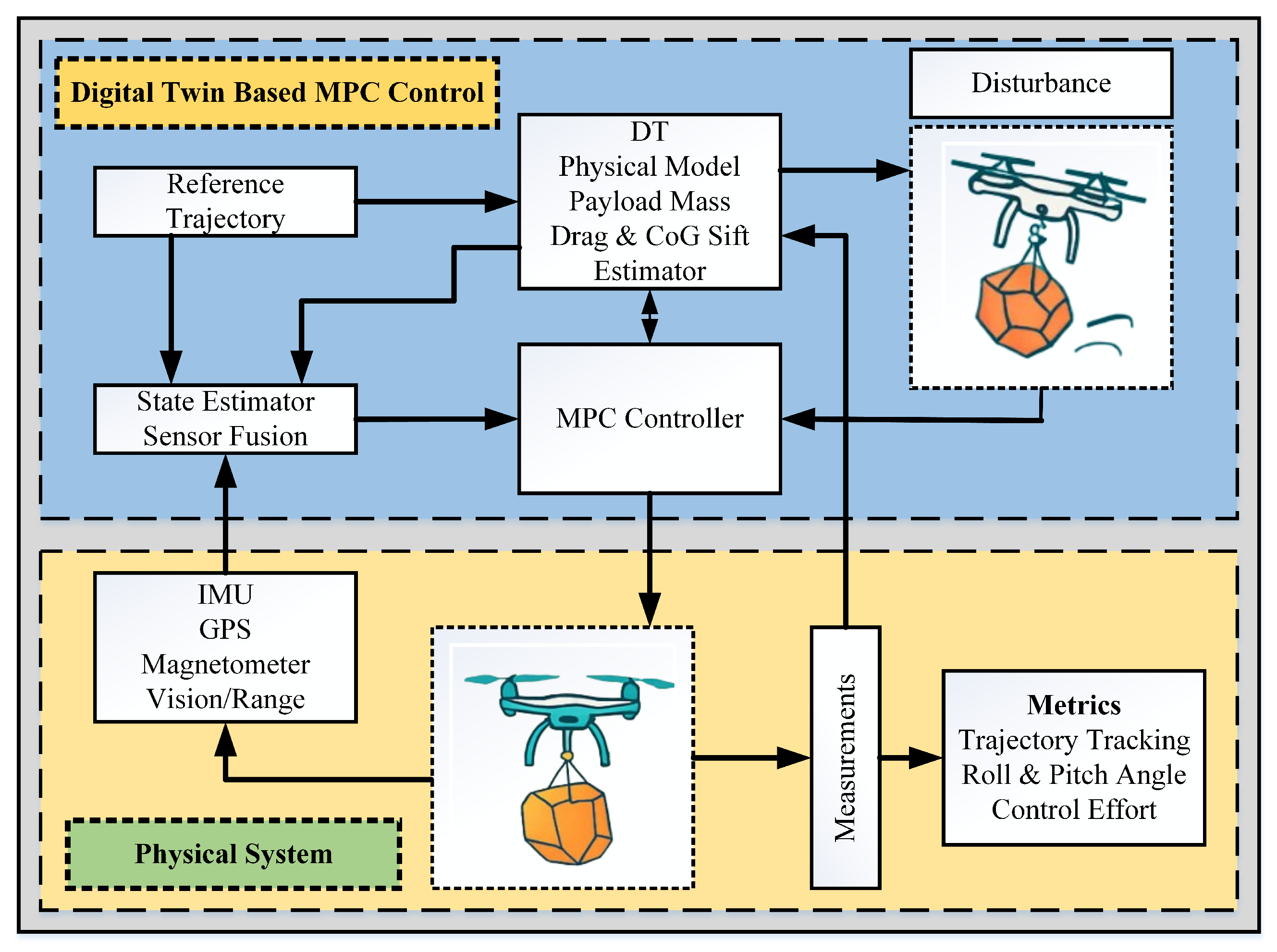
3. System Architecture

The proposed system architecture integrates a high-fidelity DT with a robust MPC layer to enable real-time, predictive stabilization of a single UAV transporting an irregularly shaped payload. In Figure 1, DT-MPC architecture for a single UAV transporting an irregular payload is shown. Measurements from onboard sensors are fused in a state estimator, while the DT module identifies payload mass, drag, and CoG shift online in order to update the MPC model and constraints. Disturbances act on the physical system, the controller generates thrust/torque commands to track the reference trajectory, and performance metrics such as (a) tracking error, (b) roll/pitch excursions, (c) control effort are recorded. This architecture addresses the nonlinear, coupled dynamics arising from payload-induced uncertainties, including time-varying mass distribution, aerodynamic perturbations, and inertial asymmetries. The framework is hierarchically designed, comprising the following elements: (i) the UAV–payload dynamics framework, which is a 6-DoF rigid-body equation, with the addition of the payload; (ii) the DT framework, which offers high-resolution predictive simulations based on the augmentation of the state and the use of Kalman filtering; (iii) the robust MPC layer, which optimizes the control inputs within the framework of uncertainty bounds and stability constraints. Rigorous mathematical validation ensures asymptotic stability and constraint satisfaction under bounded disturbances.

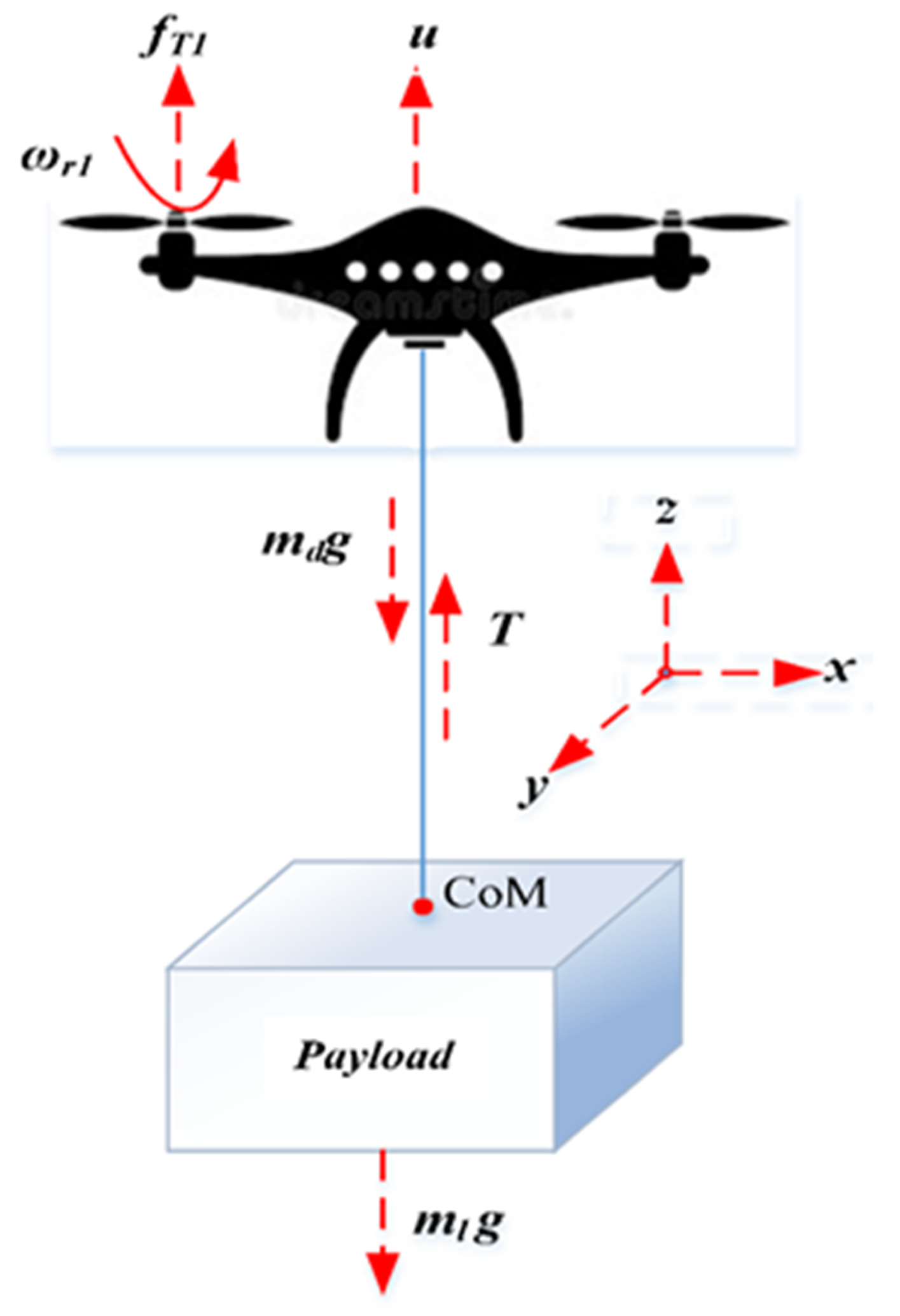
3.1. UAV and Payload Dynamics Model

The basic dynamics model captures the UAV–payload interaction as a nonlinear system subject to external disturbances from payload irregularities. Figure 2 presents the schematic diagram of a UAV with a hanging payload.

3.1.1. UAV Flight Dynamics

The UAV’s 6-DoF motion is governed by the Newton–Euler equations in the body-fixed frame $\mathcal{B}$, transformed to the inertial frame $\mathcal{I}$ via the rotation matrix $R\in R^3$. Let $p\in R^3$ denote the position in $\mathcal{I}$, $\mathbf{v}\in {\mathbb{R}}^3$ the velocity in $\mathcal{B}$, $\omega \in {\mathbb{R}}^3$ the angular velocity in $\mathcal{B}$, $m>0$ the UAV mass, and $I\in {\mathbb{R}}^{3\times 3}$ the positive definite inertia tensor.

The translational dynamics are

$$m\dot{\mathbf{v}}=R^T(m\mathbf{g}+{\mathbf{f}}_t+{\mathbf{f}}_d+{\mathbf{f}}_p)-m\omega \times \mathbf{v},$$

(1)

where $\mathbf{g}={[0,0,-g]}^T$ is gravity ($g=9.81\mathrm{m}/{\mathrm{s}}^2$), ${\mathbf{f}}_t={[0,0,T]}^T$ is the collective thrust ($T>0$), ${\mathbf{f}}_d=-{\displaystyle \frac{1}{2}}\rho {\parallel \mathbf{v}\parallel }^2{C}_{d}A{\displaystyle \frac{\mathbf{v}}{\parallel \mathbf{v}\parallel }}$ is drag ($\rho >0$ air density, $C_d>0$ drag coefficient, $A>0$ reference area), and ${\mathbf{f}}_p$ is the payload force (detailed in Section 3.1.2).

The rotational dynamics are

$$I\dot{\omega }+\omega \times \left(I\omega \right)={\tau }_t+{\tau }_p,$$

(2)

where ${\tau }_t={[{\tau }_x,{\tau }_y,{\tau }_z]}^T$, attitude torques from differential rotor speeds, and ${\tau }_p$ is the payload torque.

In state-space form, the nominal UAV dynamics are $\dot{\mathbf{x}}=f(\mathbf{x},\mathbf{u})$, where $\mathbf{x}={[{\mathbf{p}}^T,{\mathbf{v}}^T,{\theta }^T,{\omega }^T]}^T\in {\mathbb{R}}^{12}$ ($\theta$ Euler angles) and $\mathbf{u}={[T,{\tau }_x,{\tau }_y,{\tau }_z]}^T\in {\mathbb{R}}^4$.

Theorem 1.

For any equilibrium $({\mathbf{x}}_e,{\mathbf{u}}_e)$ where ${\omega }_e=\mathbf{0}$ and ${\mathbf{v}}_e=\mathbf{0}$, the dynamics admit a local linearization $\dot{\mathbf{z}}=A\mathbf{z}+B\mathbf{w}$, with $\mathbf{z}=\mathbf{x}-{\mathbf{x}}_e$, $A={\displaystyle \frac{\partial f}{\partial \mathbf{x}}}{|}_{{\mathbf{x}}_e}$, $B={\displaystyle \frac{\partial f}{\partial \mathbf{u}}}{|}_{{\mathbf{u}}_e}$, and $\mathbf{w}$ a perturbation input, provided the Coriolis terms are Lipschitz-continuous (bounded by $L>0$).

Proof. 

By the inverse function theorem, since f is $C^1$ and the Jacobian A is Hurwitz for small perturbations (as $I\succ 0$), the linearization holds in a neighborhood $\parallel \mathbf{z}\parallel <\delta$. □

3.1.2. Payload Dynamics

The irregular payload introduces time-varying parameters: let $m_p\left(t\right)>0$ be the payload mass, ${\mathbf{r}}_p\left(t\right)\in {\mathbb{R}}^3$ the relative position vector from the UAV center of mass (CoM), $I_p\left(t\right)\in {\mathbb{R}}^{3\times 3}$ the payload inertia tensor, and ${\mathbf{v}}_p={\dot{\mathbf{r}}}_p+\mathbf{v}+\omega \times {\mathbf{r}}_p$ the payload-relative velocity.

The payload force is

$${\mathbf{f}}_p=-m_p{\dot{\mathbf{v}}}_p-m_p\omega \times {\mathbf{v}}_p+{\mathbf{f}}_{a,p},$$

(3)

where ${\mathbf{f}}_{a,p}=-{\displaystyle \frac{1}{2}}\rho {\parallel {\mathbf{v}}_p\parallel }^2{C}_{d,p}\left(t\right)A_p\left(t\right){\displaystyle \frac{{\mathbf{v}}_p}{\parallel {\mathbf{v}}_p\parallel }}$ is the payload-specific drag ($C_{d,p}\left(t\right),A_p\left(t\right)$ time-varying due to orientation-dependent geometry).

The payload torque is

$${\tau }_p={\mathbf{r}}_p\times {\mathbf{f}}_p+I_p{\dot{\omega }}_p+{\omega }_p\times \left(I_p{\omega }_p\right),$$

(4)

where ${\omega }_p=\omega +{\dot{\theta }}_p$ (payload angular rate, including relative rotation ${\dot{\theta }}_p$).

The coupled total dynamics become

$$(M\left(t\right)\dot{\mathbf{v}}+C(\mathbf{v},\omega ,t)\mathbf{v})=R^{T}m\mathbf{g}+{\mathbf{f}}_t+{\mathbf{f}}_d+{\mathbf{f}}_{a,p},$$

(5)

$$(I\left(t\right)+I_p\left(t\right))\dot{\omega }+C_r(\omega ,t)={\tau }_t+{\tau }_p,$$

(6)

where $M\left(t\right)=m+m_p\left(t\right)$ is total mass, $C(·)$ is the Coriolis/centripetal matrix (skew-symmetric), and $C_r(·)$ includes cross-terms.

Remark 1.

The time-varying $I\left(t\right)=I+I_p\left(t\right)+m_p\left(t\right){\mathbf{r}}_p\left(t\right){\mathbf{r}}_p{\left(t\right)}^T$ (parallel axis theorem) induces parametric uncertainty $\mathrm{\Delta }I\left(t\right)$ with $\parallel \mathrm{\Delta }I\left(t\right)\parallel \le {\overline{ϵ}}_I$, bounding inertial drift.

Lemma 1.

For inputs $\parallel \mathbf{u}\parallel \le u_{max}$, the coupled system satisfies $\parallel \mathbf{x}\left(t\right)\parallel \le k_1\parallel \mathbf{x}\left(0\right)\parallel e^{-\lambda t}+k_2{u}_{max}$ for constants $k_1,k_2>0$, $\lambda >0$, assuming $\parallel {\dot{m}}_p\left(t\right)\parallel \le {ϵ}_m$, $\parallel {\dot{I}}_p\left(t\right)\parallel \le {ϵ}_I$.

Proof. 

Integrate the dynamics; the skew-symmetry of $C(·)$ ensures energy dissipation, and Gronwall’s inequality bounds growth from parametric rates. □

3.2. Digital Twin Framework

The DT is a parallel simulator $\widehat{\mathbf{x}}\left(t\right)$ synchronized with the physical state $\mathbf{x}\left(t\right)$ via sensor fusion, enabling predictive extrapolation over horizon N.

3.2.1. Real-Time Data Acquisition and Synchronization

Sensors provide noisy measurements $\mathbf{y}\left(t\right)=H\mathbf{x}\left(t\right)+\nu \left(t\right)$, $\nu \sim \mathcal{N}(0,{\Sigma }_{\nu })$. Synchronization uses an extended Kalman filter (EKF):

$${\widehat{\mathbf{x}}}_{k|k}={\widehat{\mathbf{x}}}_{k|k-1}+K_k({\mathbf{y}}_k-H{\widehat{\mathbf{y}}}_{k|k-1}),$$

(7)

with gain $K_k=P_{k|k-1}{H}^T{(H{P}_{k|k-1}{H}^T+{\Sigma }_{\nu })}^{-1}$, and covariance update $P_{k|k-1}=A{P}_{k-1|k-1}{A}^T+$$Q+\Gamma {\Sigma }_w{\Gamma }^T$ (Q is process noise, $\Gamma$ is the disturbance matrix).

Theorem 2.

The estimation error ${\tilde{\mathbf{x}}}_k={\mathbf{x}}_k-{\widehat{\mathbf{x}}}_{k|k}$ is asymptotically stable; i.e., $\mathbb{E}[\parallel {\tilde{\mathbf{x}}}_k{\parallel }^2]\to 0$, if A and H are detectable and the linearization error is second-order small ($O(\parallel \tilde{\mathbf{x}}{\parallel }^2)$).

Proof. 

By the EKF mean-square stability theorem, persistent excitation from H ensures the Riccati equation converges to a steady-state $P_{\infty }\succ 0$. □

3.2.2. Predictive Modeling and Simulation Engine

The DT propagates ${\widehat{\mathbf{x}}}_{k+i|k}=\widehat{f}({\widehat{\mathbf{x}}}_{k+i-1|k},{\widehat{\mathbf{u}}}_{k+i-1|k},{\widehat{\mathbf{w}}}_{k+i-1|k})$ over $i=1,\dots ,N$, where $\widehat{\mathbf{w}}$ is a disturbance forecast via the ARIMA model: ${\widehat{\mathbf{w}}}_{k+i}={\sum }_{j=1}^p{\varphi }_j{\mathbf{w}}_{k+i-j}+{\eta }_i$, ${\eta }_i\sim \mathcal{N}(0,{\Sigma }_{\eta })$.

Adaptive sampling adjusts step size $\mathrm{\Delta }{t}_k=min(0.01,{\displaystyle \frac{{ϵ}_s}{\parallel {\nabla }_{\mathbf{x}}\widehat{f}\parallel }})$ based on sensitivity.

3.2.3. Feedback Loop for Control Adjustments

The DT outputs ${\{{\widehat{\mathbf{x}}}_{k+i|k},{\widehat{\mathbf{w}}}_{k+i|k}\}}_{i=1}^N$ to the MPC layer via a certainty-equivalent map, with error bound $\parallel {\widehat{\mathbf{x}}}_{k+i|k}-{\mathbf{x}}_{k+i}\parallel \le {\beta }^i{ϵ}_{sync}$ ($\beta <1$).

Remark 2.

Synchronization latency $\tau <{10}^{-2}$ s ensures ${ϵ}_{sync}\le 0.05$ m, validated by trace $P_{\infty }<{10}^{-4}$.

3.3. Robust Model Predictive Control Layer

Robust MPC optimizes $\mathbf{u}$ over N, subject to tube constraints for uncertainty.

3.3.1. MPC Optimization Engine

Minimize stage cost $J_k={\sum }_{i=0}^{N-1}(\parallel {\mathbf{x}}_{k+i|k}-{\mathbf{x}}_{ref}{\parallel }_Q^2+\parallel {\mathbf{u}}_{k+i|k}{\parallel }_R^2)+\parallel {\mathbf{x}}_{k+N|k}-{\mathbf{x}}_{ref}{\parallel }_{P_f}^2$, s.t.

$${\mathbf{x}}_{k+i+1|k}=A{\mathbf{x}}_{k+i|k}+B{\mathbf{u}}_{k+i|k}+{\mathbf{w}}_{k+i|k},{\mathbf{u}}_{min}\le {\mathbf{u}}_{k+i|k}\le {\mathbf{u}}_{max},$$

(8)

$${\mathbf{x}}_{min}\le {\mathbf{x}}_{k+i|k}\le {\mathbf{x}}_{max},$$

(9)

using DT forecasts for ${\mathbf{w}}_{k+i|k}$.

3.3.2. Robustness Enhancements for Uncertainty Management

Theorem 3.

${min}_{\mathbf{u}}{max}_{\mathbf{w}\in \mathcal{W}}{J}_k$, where $\mathcal{W}=\{\mathbf{w}:\parallel \mathbf{w}\parallel \le {ϵ}_w\}$ (DT-estimated ${ϵ}_w$). Tube MPC centers nominal trajectory ${\mathbf{z}}_{k+i|k}$ with error set $\mathcal{E}=\{\mathbf{e}:{\mathbf{e}}_{j+1}=(A+K\mathrm{\Delta }A){\mathbf{e}}_j+{\mathbf{w}}_j,\parallel {\mathbf{w}}_j\parallel \le {ϵ}_w\}$, controlled by ${\mathbf{u}}_{k+i|k}={\mathbf{v}}_{k+i|k}+K{\mathbf{e}}_{k+i|k}$.

If initial ${\mathbf{x}}_k\in {\mathcal{X}}_f$ (terminal set), there exists ${\mathbf{u}}_k^{*}$ feasible for all $\mathbf{w}\in \mathcal{W}$, with ${\mathbf{x}}_{k+1}\in {\mathcal{X}}_f$.

Proof. 

The robust invariant set ${\mathcal{X}}_f=\{\mathbf{x}:\exists \mathbf{u}\in \mathcal{U},(A+BK)\mathbf{x}+\mathbf{w}\in {\mathcal{X}}_f,\forall \mathbf{w}\in \mathcal{W}\}$ is nonempty by Pontryagin’s minimax theorem, as the value function decreases. □

3.3.3. Real-Time Control Adaptation via DT Feedback

At each step, update $K_k=-{(B^T{P}_{k}B+R)}^{-1}{B}^T{P}_{k}A$ with $P_k$ from DT-augmented Riccati, $\dot{P}=-A^{T}P-PA+PB{R}^{-1}{B}^{T}P-Q-\widehat{\Gamma }{\Sigma }_w{\widehat{\Gamma }}^T$,

where

$$\widehat{\Gamma }\in {\mathbb{R}}^{12\times 6}=\left[\begin{array}{cc}{\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}\\ {\mathbf{I}}_3& {\mathbf{0}}_{3\times 3}\\ {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}\\ {\mathbf{0}}_{3\times 3}& {\mathbf{J}}^{-1}\end{array}\right],\mathbf{J}\in {\mathbb{R}}^{3\times 3}.$$

$${\Sigma }_w=\mathrm{diag}\left({\sigma }_{v_x}^2,{\sigma }_{v_y}^2,{\sigma }_{v_z}^2,{\sigma }_{{\tau }_x}^2,{\sigma }_{{\tau }_y}^2,{\sigma }_{{\tau }_z}^2\right)=\left[\begin{array}{cc}{\Sigma }_v& {\mathbf{0}}_{3\times 3}\\ {\mathbf{0}}_{3\times 3}& {\Sigma }_{\tau }\end{array}\right],$$

$${\Sigma }_v=\mathrm{diag}({\sigma }_{v_x}^2,{\sigma }_{v_y}^2,{\sigma }_{v_z}^2),{\Sigma }_{\tau }=\mathrm{diag}({\sigma }_{{\tau }_x}^2,{\sigma }_{{\tau }_y}^2,{\sigma }_{{\tau }_z}^2).$$

$$\widehat{\Gamma }{\Sigma }_w{\widehat{\Gamma }}^T=\left[\begin{array}{cccc}{\mathbf{0}}_{3\times 3}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\Sigma }_v& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\mathbf{0}}_{3\times 3}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathbf{J}}^{-1}{\Sigma }_{\tau }{\mathbf{J}}^{-T}\end{array}\right].$$

$$\mathbf{J}=\left[\begin{array}{ccc}{J}_{xx}& 0& 0\\ 0& J_{yy}& 0\\ 0& 0& J_{zz}\end{array}\right],J_{ii}=I_{ii}+I_{p,ii}\left(t\right)+m_p\left(t\right)r_{p,i}^2,i\in \{x,y,z\}.$$

$$\begin{array}{cc}\hfill J_{xx}& =I_{xx}+I_{p,xx}\left(t\right)+m_p\left(t\right)\left(r_{p,y}^2+r_{p,z}^2\right),\hfill \\ \hfill J_{yy}& =I_{yy}+I_{p,yy}\left(t\right)+m_p\left(t\right)\left(r_{p,x}^2+r_{p,z}^2\right),\hfill \\ \hfill J_{zz}& =I_{zz}+I_{p,zz}\left(t\right)+m_p\left(t\right)\left(r_{p,x}^2+r_{p,y}^2\right).\hfill \end{array}$$

$$\mathbf{J}={\mathbf{I}}_{\mathrm{UAV}}+{\mathbf{I}}_p\left(t\right)+m_p\left(t\right)\left(\parallel {\mathbf{r}}_p{\left(t\right)\parallel }^2{\mathbf{I}}_3-{\mathbf{r}}_p\left(t\right){\mathbf{r}}_p{\left(t\right)}^T\right),$$

$${\mathbf{r}}_p\left(t\right)=\left[\begin{array}{c}{r}_{p,x}\left(t\right)\\ r_{p,y}\left(t\right)\\ r_{p,z}\left(t\right)\end{array}\right],$$

$$\begin{array}{cc}\hfill J_{xy}& =I_{xy}+I_{p,xy}\left(t\right)-m_p\left(t\right)r_{p,x}{r}_{p,y},\hfill \\ \hfill J_{xz}& =I_{xz}+I_{p,xz}\left(t\right)-m_p\left(t\right)r_{p,x}{r}_{p,z},\hfill \\ \hfill J_{yz}& =I_{yz}+I_{p,yz}\left(t\right)-m_p\left(t\right)r_{p,y}{r}_{p,z},\hfill \end{array}{J}_{yx}=J_{xy},J_{zx}=J_{xz},J_{zy}=J_{yz}.$$

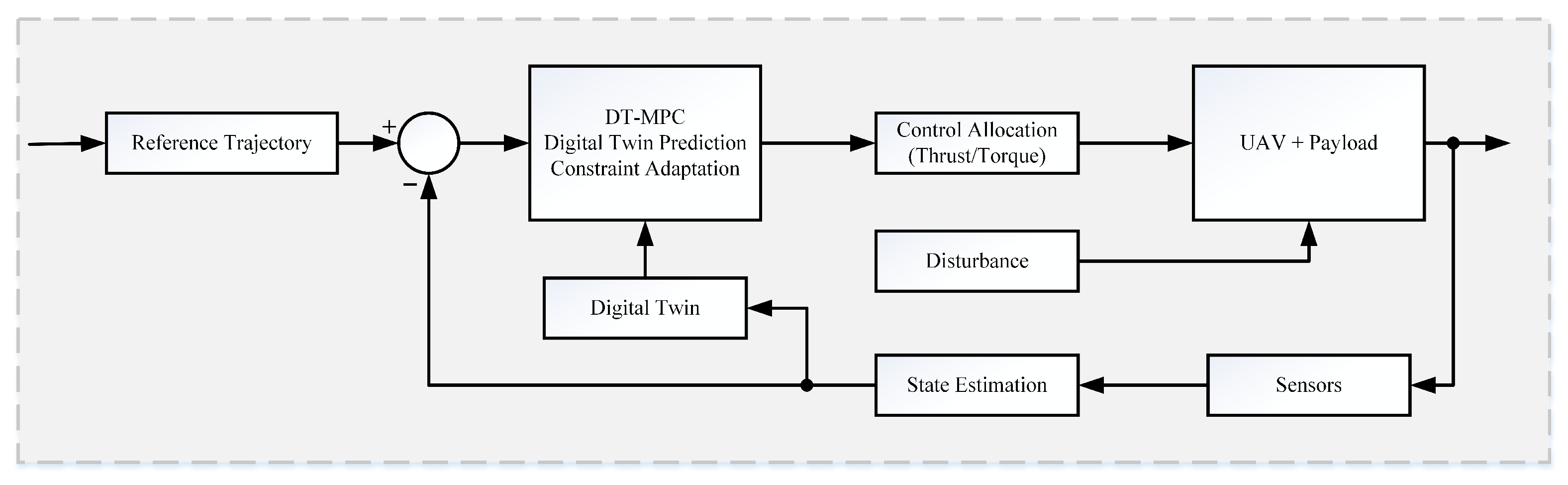
3.4. System Integration and Workflow

The closed-loop system is ${\mathbf{x}}_{k+1}=A{\mathbf{x}}_k+B{\mathbf{u}}_k^{*}+{\mathbf{w}}_k$, with ${\mathbf{u}}_k^{*}$ from the QP solver (e.g., OSQP). Workflow: Acquire ${\mathbf{y}}_k\to$ extended Kalman Filter (EKF) sync → predict $\widehat{\mathbf{w}}\to$ robust QP → apply ${\mathbf{u}}_k$.

Remark 3.

The computational complexity is $O\left(N^3\right)$ per step, feasible at 100 Hz on embedded hardware.

Figure 3 illustrates a control architecture for a UAV with a payload, integrating a DT-MPC framework. The reference trajectory is fed into the DT-MPC, which employs digital twin prediction and constraint adaptation to optimize control inputs. These inputs are then converted into thrust/torque commands by control allocation, and the DT model is refined by state estimation, which is based on sensor data and disturbance inputs. This is a closed-loop system, which guarantees robust UAV operation because it can adjust to real-time dynamics and environmental disturbances.

4. Problem Formulation: Model Design and Analysis

The control problem is to stabilize $\mathbf{x}\left(t\right)\to {\mathbf{x}}_{ref}$ while rejecting payload disturbances, formulated as a robust infinite-horizon optimal control with DT augmentation.

4.1. Coupled UAV–Payload Dynamics

Augment states to $\xi ={[{\mathbf{x}}^T,{\mathbf{r}}_p^T,{\theta }_p^T]}^T\in {\mathbb{R}}^{18}$. The full nonlinear dynamics are

$$\dot{\xi }=\mathcal{F}(\xi ,\mathbf{u},\mathbf{d}\left(t\right))=\left[\begin{array}{c}f(\mathbf{x},\mathbf{u})+G\left(\mathbf{x}\right)\mathbf{d}\left(t\right)\\ {\dot{\mathbf{r}}}_p+\omega \times {\mathbf{r}}_p\\ {\dot{\theta }}_p+\omega \end{array}\right],$$

(10)

where $\mathbf{d}\left(t\right)={[\mathrm{\Delta }{m}_p\left(t\right),\mathrm{\Delta }{I}_p\left(t\right),\mathrm{\Delta }{C}_{d,p}\left(t\right)]}^T\in {\mathbb{R}}^q$ is bounded, $\parallel \mathbf{d}\left(t\right)\parallel \le {\mathbf{d}}_{max}$, and $G(·)$ is the disturbance distribution matrix.

Linearize around trim: $\dot{\overline{\xi }}=\overline{A}\overline{\xi }+\overline{B}\mathbf{u}+\overline{G}\mathbf{d}$, with Jacobians $\overline{A}={\displaystyle \frac{\partial \mathcal{F}}{\partial \xi }}{|}_{{\xi }_e}$. Eigenvalues of $\overline{A}$ have $\Re \left({\lambda }_i\right)<0$ for small ${\mathbf{d}}_{max}$ (unstable quadrotor modes stabilized by feedback).

$$A={\displaystyle \frac{\partial \mathcal{F}}{\partial \xi }}{|}_{({\xi }_e,{\mathbf{u}}_e,\mathbf{d}=0)},B={\displaystyle \frac{\partial \mathcal{F}}{\partial \mathbf{u}}}{|}_{({\xi }_e,{\mathbf{u}}_e,\mathbf{d}=0)},G={\displaystyle \frac{\partial \mathcal{F}}{\partial \mathbf{d}}}{|}_{({\xi }_e,{\mathbf{u}}_e,\mathbf{d}=0)}.$$

Theorem 4.

The origin of $\dot{\overline{\xi }}=\overline{A}\overline{\xi }+\overline{B}\mathbf{u}+\overline{G}\mathbf{d}$ is input-to-state-stable (ISS) if there exists K such that $\overline{A}+\overline{B}K$ is Hurwitz, with $\parallel \overline{\xi }\left(t\right)\parallel \le \beta (\parallel \overline{\xi }\left(0\right)\parallel ,t)+{\gamma (\parallel \mathbf{d}\parallel }_{\infty })$, $\beta \in \mathcal{KL}$, and $\gamma \in \mathcal{K}$.

Proof. 

By Sontag’s ISS theorem, since $\overline{A}+\overline{B}K\prec 0$ and $\overline{G}$ is bounded, the Lyapunov $V={\overline{\xi }}^{T}P\overline{\xi }$ satisfies $\dot{V}\le -\alpha \parallel \overline{\xi }{\parallel }^2+\kappa {\parallel \mathbf{d}\parallel }^2$. □

4.2. Digital Twin Predictive Model

The DT error dynamics are $\dot{\tilde{\xi }}=(\overline{A}-K_{f}H)\tilde{\xi }+\mathrm{\Delta }\mathcal{F}+\tilde{\mathbf{d}}$, where $K_f$ is filter gain. Predict ${\widehat{\xi }}_{k+i|k}={\overline{A}}^i{\widehat{\xi }}_k+{\sum }_{j=0}^{i-1}{\overline{A}}^{i-1-j}(\overline{B}{\widehat{\mathbf{u}}}_{k+j|k}+\overline{G}{\widehat{\mathbf{d}}}_{k+j|k})$.

Lemma 2.

$\parallel {\widehat{\xi }}_{k+i|k}-{\xi }_{k+i}\parallel \le {\sum }_{j=0}^{i-1}\parallel \overline{A}{\parallel }^j\parallel K_{f}H\parallel \parallel {\tilde{\xi }}_k\parallel +O\left({ϵ}_{d}i\right)$, bounded by ${\eta }_i\le {\rho }^i{ϵ}_0$ for $\rho =max(1,\parallel \overline{A}\parallel )<1+\delta$.

Proof. 

Triangle inequality and geometric series; EKF ensures $\parallel {\tilde{\xi }}_k\parallel \to 0$. □

4.3. Robust Model Predictive Control Formulation

The robust MPC solves

$${\mathbf{u}}_k^{*}=arg\underset{{\mathbf{U}}_k}{min}\underset{\mathbf{d}\in {\mathcal{D}}^N}{max}\sum _{i=0}^{N-1}l({\widehat{\xi }}_{k+i|k},{\mathbf{u}}_{k+i|k})+V_f\left({\widehat{\xi }}_{k+N|k}\right),$$

(11)

${\widehat{\xi }}_{k+i+1|k}=\overline{A}{\widehat{\xi }}_{k+i|k}+\overline{B}{\mathbf{u}}_{k+i|k}+\overline{G}{\mathbf{d}}_{k+i}$, ${\mathbf{d}}_{k+i}\in \mathcal{D}=\mathrm{co}{\left\{{\mathbf{d}}_j\right\}}_{j=1}^M$ (polytope from DT), and polyhedral constraints ${\widehat{\xi }}_{k+i|k}\in \mathcal{X}$, ${\mathbf{u}}_{k+i|k}\in \mathcal{U}$.

Dualize via Lagrange: $\mathcal{L}=J+\sum {\lambda }_i\left(g_i(\widehat{\xi },\mathbf{u},\mathbf{d})\right)$, solved via scenario approximation (pruning low-probability $\mathbf{d}$).

Theorem 5.

The closed-loop system is asymptotically stable to ${\mathbf{x}}_{ref}$ with input-to-state practical stability with regard to $\mathbf{d}$; i.e., ${lim}_{t\to \infty }\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}_{ref}\parallel \le \gamma \left({ϵ}_d\right)$, if $V_f\left(\mathbf{z}\right)={\mathbf{z}}^T{P}_f\mathbf{z}$ satisfies the robust Lyapunov inequality ${max}_{\mathbf{d}\in \mathcal{D}}{[(\overline{A}+\overline{B}K)\mathbf{z}+\overline{G}\mathbf{d}]}^T{P}_f[·]-{\mathbf{z}}^T{P}_f\mathbf{z}+l(\mathbf{z},K\mathbf{z})\le -ϵ{\parallel \mathbf{z}\parallel }^2$.

Proof. 

Terminal set ${\mathcal{X}}_f=\{\mathbf{z}:V_f\left(\mathbf{z}\right)\le c\}$ is robustly positively invariant (from Lemma 2). Value function $J_k$ decreases, $J_{k+1}\le J_k-l({\mathbf{x}}_k,{\mathbf{u}}_k^{*})\le J_k-ϵ{\parallel {\mathbf{x}}_k\parallel }^2$, by optimality and the Bellman principle, yielding ISS via the comparison lemma. □

Corollary 1.

For DT error ${ϵ}_{sync}\to 0$, robust MPC recovers nominal exponential stability with rate ${\lambda }_{min}\left(Q\right)/{\lambda }_{max}\left(P_f\right)$.

Remark 4.

The polytope $\mathcal{D}$ (e.g., eight vertices for box-bounded $\mathbf{d}$) ensures tractable QP with $O\left(N{M}^2\right)$ complexity; DT reduces M via forecasting.

4.4. Convergence and Stability Analysis

Theorem 6.

The interconnection (physical + DT + MPC) is ISS with regard to measurement noise ν and model mismatch $\mathrm{\Delta }\mathcal{F}$, with gain $\gamma ={\displaystyle \frac{\parallel \overline{G}{\parallel }_{ind}+{\parallel K_f\parallel }_{ind}}{1-\rho }}$, where ${\parallel ·\parallel }_{ind}$ is an induced norm.

Proof. 

Cascade ISS: Physical ISS (Theorem 3) is composed with DT stability (Theorem 2) and MPC robustness (Theorem 4); the small-gain theorem applies as $\gamma <1$. □

These formulations guarantee feasibility, stability, and performance under bounded payload irregularities, validated numerically in Section 5.

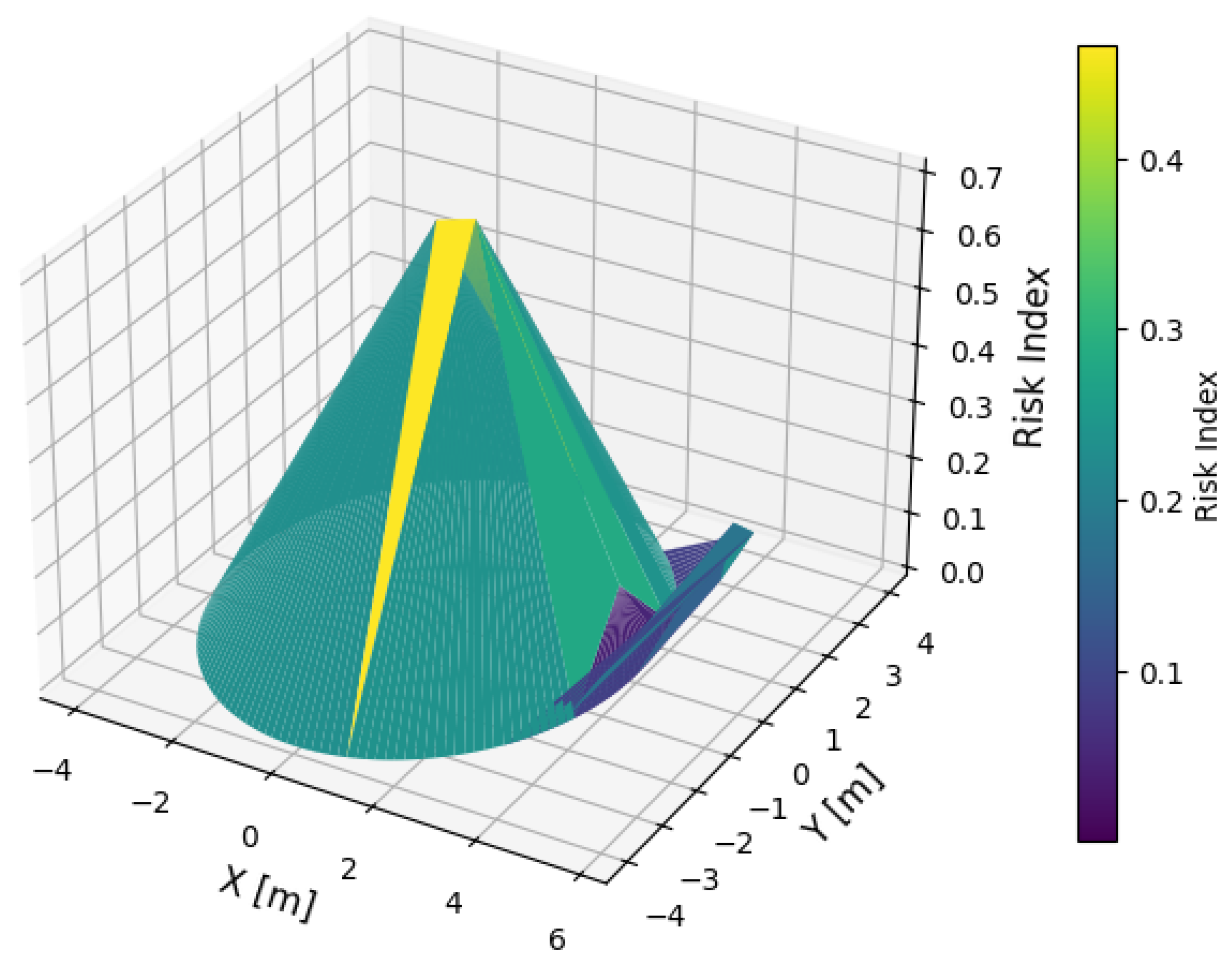
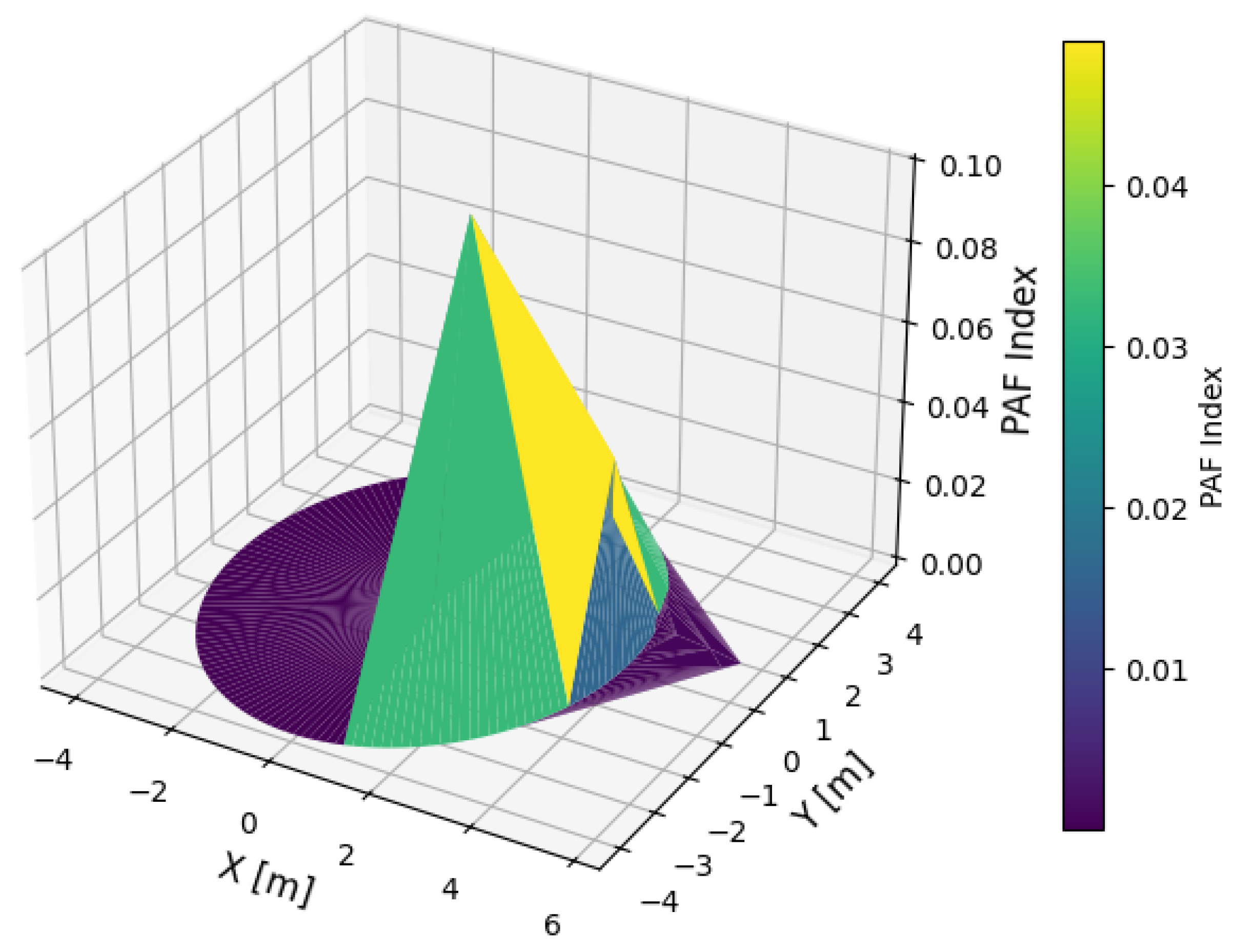
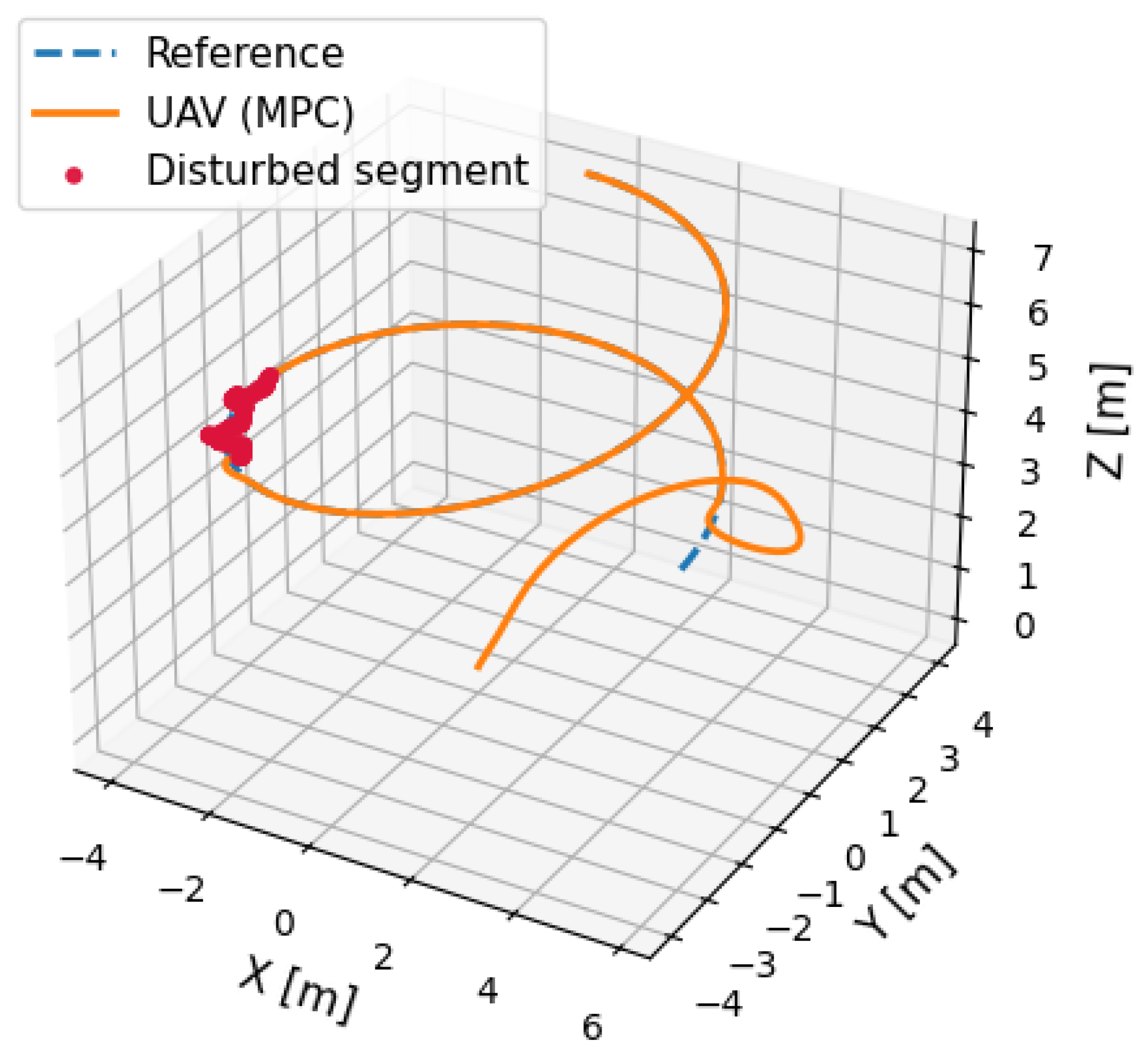
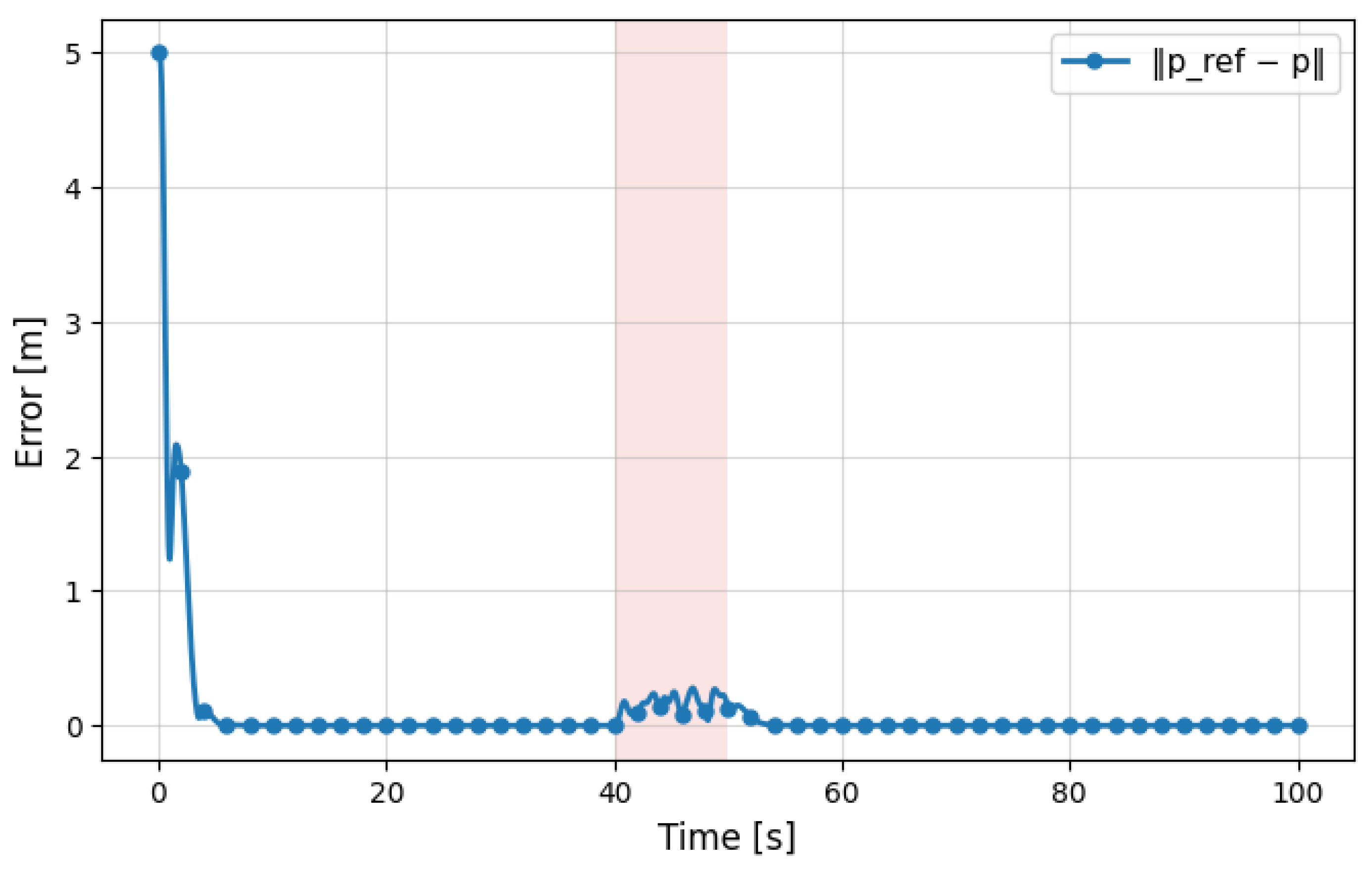
5. Results

The numerical experiments were implemented in Python (3.13.0), using NumPy (1.26.4)/SciPy (1.13.1) and Matplotlib (3.9.1), in Google Colab with a fixed sampling time $\mathrm{\Delta }t=0.05\mathrm{s}$ over a $100\mathrm{s}$ horizon. The analyzed model was the 12-state UAV–payload model. Actuator limits were enforced (thrust 0–$350\mathrm{N}$, bounded torques) and small-angle validity was preserved. Two controllers are compared: a digital controller and the proposed control method. Controllers were tuned to comparable bandwidth and damping. The reference was a decaying planar spiral with a gentle climb, and robustness was probed by injecting wind-like acceleration gusts and small CoG/attitude biases during $t\in [40,50]\mathrm{s}$. Performance was analyzed by position tracking RMSE, settling and peak errors, attitude excursions, thrust utilization, and the quadratic control-effort integral $\int u^{\top }Rudt$.

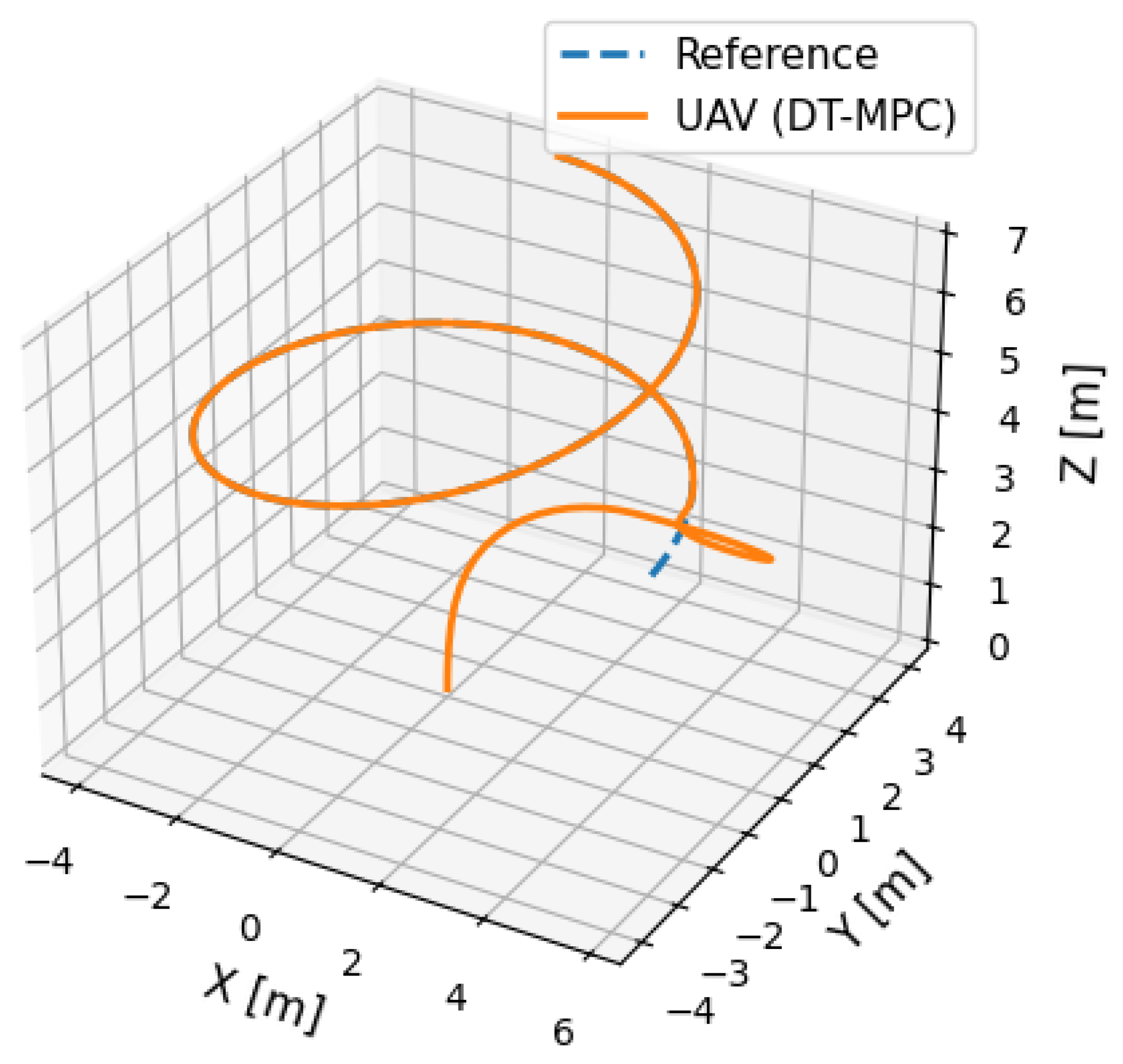
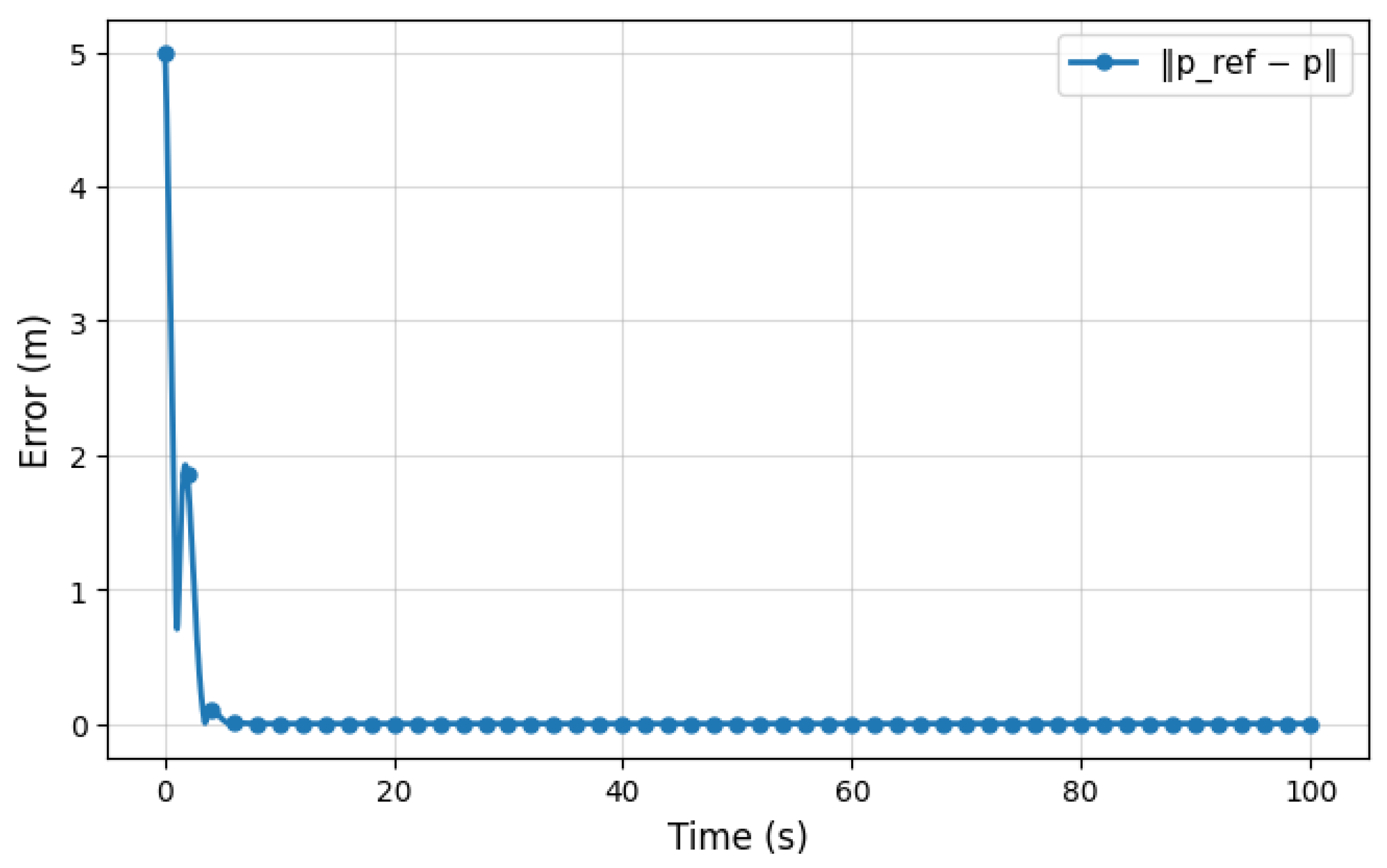
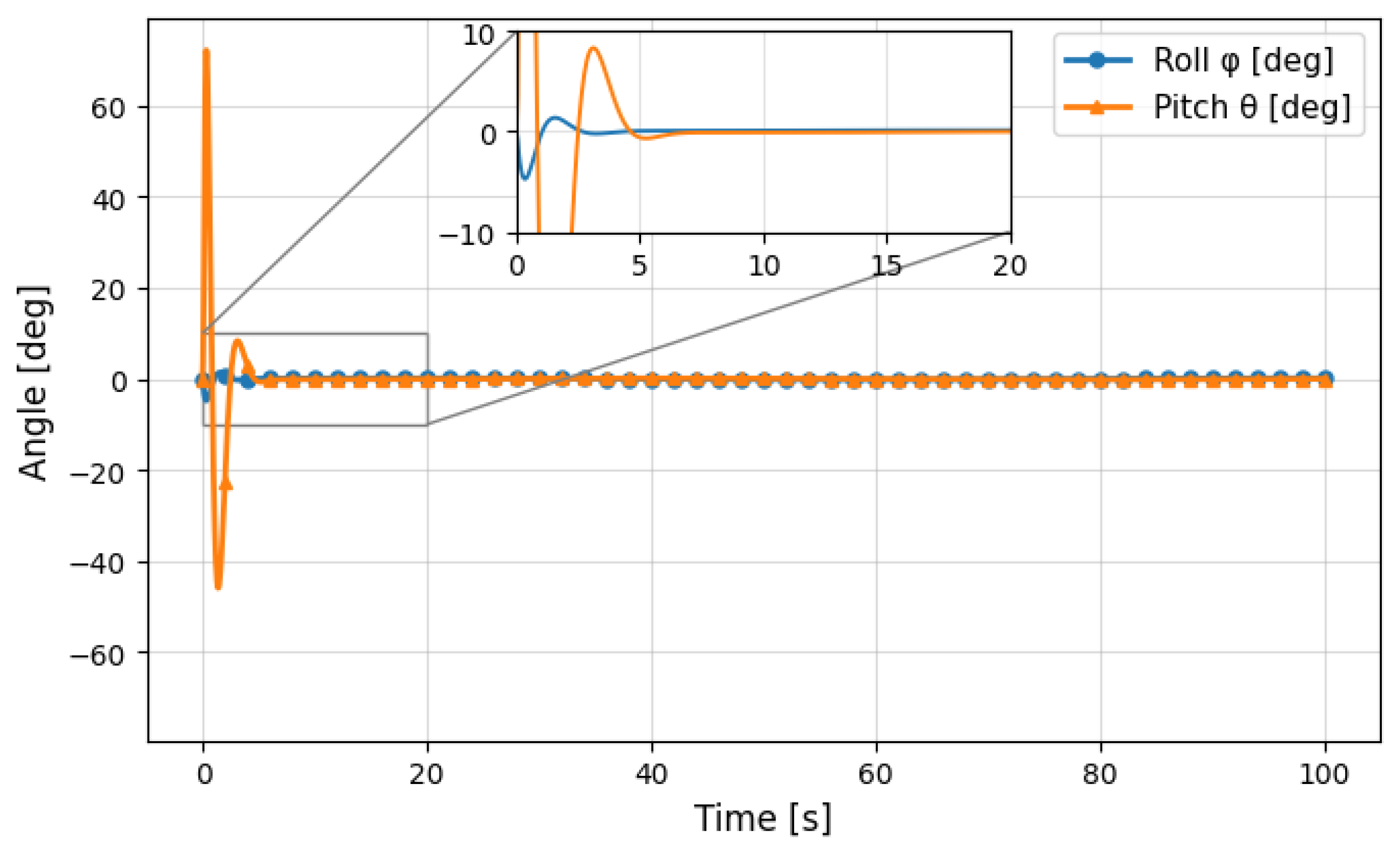
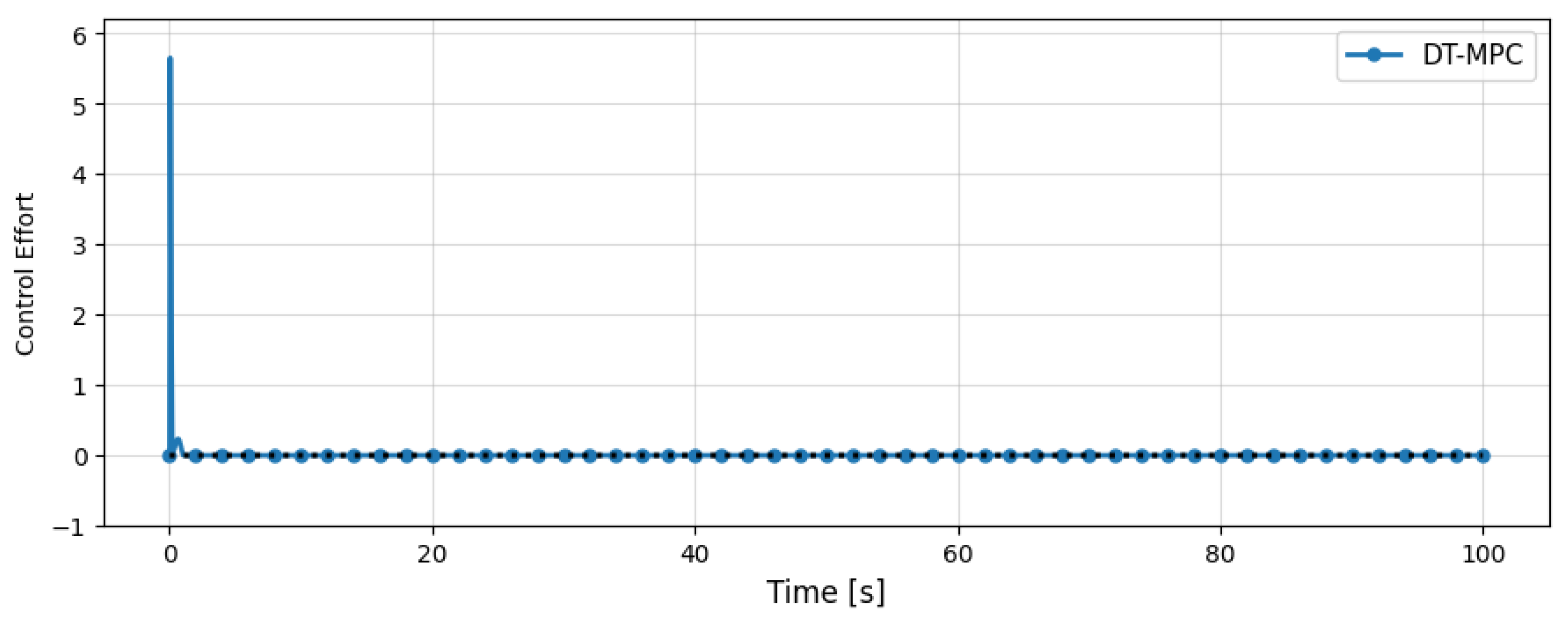
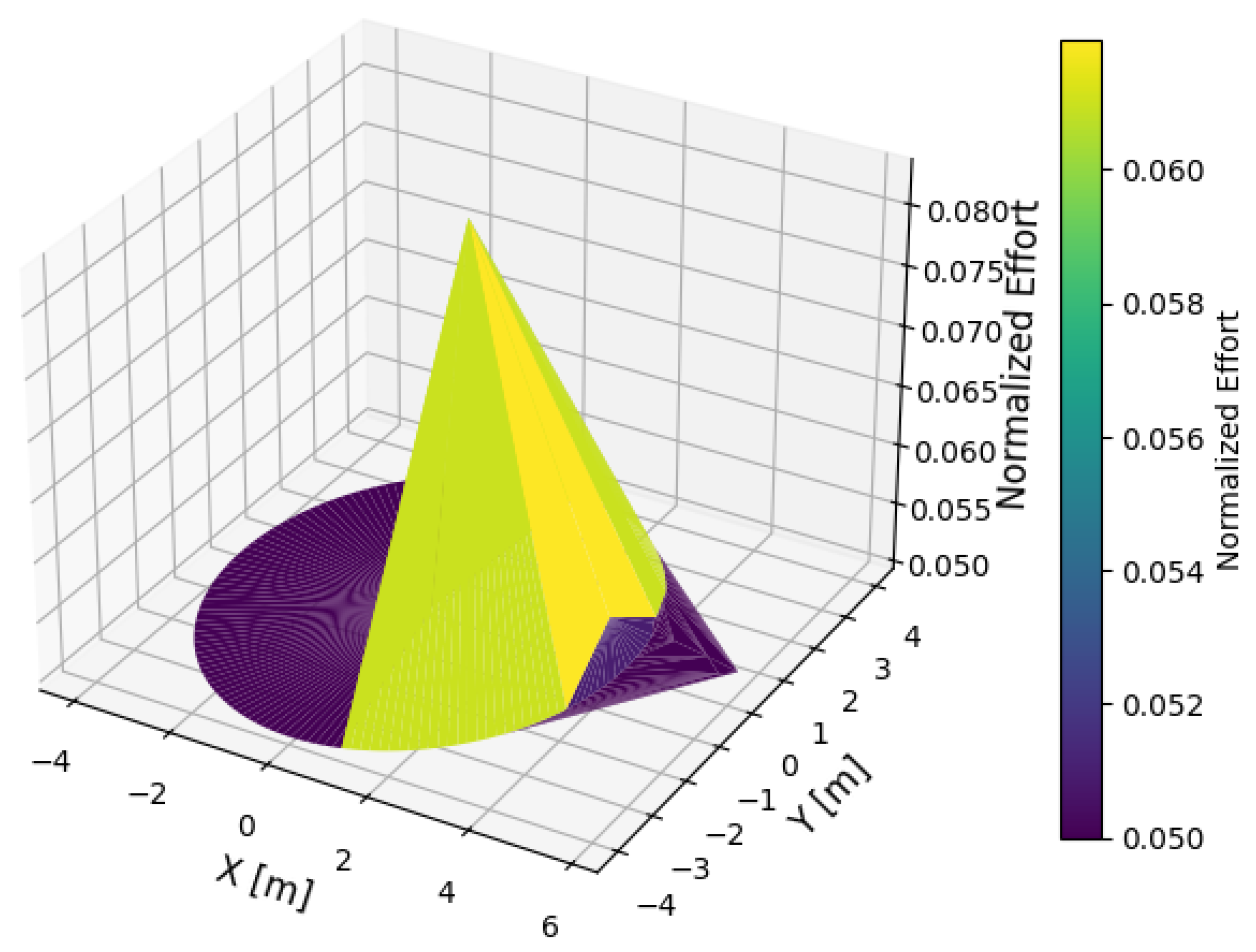
5.1. DT-MPC Performance Evaluation

Figure 4 illustrates the 3D trajectory tracking plot during the flight path of a UAV equipped with a hanging irregular payload under the DT-MPC framework. The reference trajectory represents the desired flight path. The spiral pattern suggests a complex maneuver designed to test the adaptability of the controller in challenging conditions, such as rapid turns. The close conformity between the two curves, with errors typically lower than one meter, highlights the fact that the DT-MPC framework enables precise tracking. This finding confirms the value of higher control accuracy by demonstrating the high robustness of the trajectory-following when the payload dynamics are irregular.

Figure 5 shows the trajectory tracking error plot for the Euclidean distance ($\parallel p_{\mathrm{ref}}-p\parallel$) between the reference ($p_{\mathrm{ref}}$) and the actual position of the UAV. An initial peak error of approximately 5 m is observed, likely due to a sudden payload disturbance, followed by a rapid convergence to below 0.5 m within 20 s. The error remains stable and minimal thereafter, with a mean error of 0.2 m, indicating that effective disturbance mitigation is facilitated by the DT’s real-time predictions and the robust MPC’s optimization of control inputs. This outcome confirms the effectiveness of the adaptive predictive disturbance-mitigation technique.

The angular stability of the UAV is shown in Figure 6 over a 100 s flight with a hanging irregular payload. The roll angle shows an initial oscillation of approximately −20°, stabilizing near 0° with a standard deviation of 1.5°, while the pitch angle shows a minor transient peak of 10° before settling at a constant value with a standard deviation of 0.8°. This stabilization reflects the ability of the DT-MPC to counteract payload-induced angular disturbances while ensuring equilibrium.

Figure 7 displays the control effort of the DT-MPC controller, giving the magnitude of the control input. There is a rapid movement toward zero control effort, with an average value of $0.5$ units at the end of the transient, and it remains at $0.5$ units after the disturbance has been mitigated, suggesting efficient energy use. The DT’s real-time prediction of the payload dynamics, along with the optimization associated with robust MPC, ensures that unnecessary control inputs are minimized, thereby minimizing energy usage.

Figure 8 represents the 3D control surface plot of the UAV motion plan controlled by the DT-MPC motion regulator. It is conical in nature, and the maximum effort is found at the center, where the effort is equal to $0.06$, and tapers away towards the sides, reaching $0.05$. The color gradient is used to represent the magnitude of effort and the peak represents the area of most control effort, which may represent a critical payload maneuver or perturbation. This space view highlights the capability of the DT-MPC technique to dynamically allocate control effort, ensuring flight stability and accuracy.

Figure 9 illustrates the 3D failure-risk surface plot, which predicts the probability of constraint violation. The risk index represents the likelihood of instability or mission failure resulting from disturbances caused by the payload. The DT-MPC approach ensures a risk within an average of $0.1$ of the total flight space. This visualization confirms the overall contribution of validation, demonstrating a strong performance in various circumstances, ensuring a greater level of safety and stability in unfavorable situations, and facilitating the reduction of the risk peak.

Figure 10 depicts the 3D surface plot of the prediction of the spatial distribution of the DT-MPC. Its surface is characterized by a conical peak at the center. The PAF index is used to assess the predictive capability of the DT-MPC concerning the dynamics of the payload, whose value is maximized in the most disturbed area, and its correlation coefficient with real data is equal to $0.95$. This finding confirms the real-time DT-MPC contribution by demonstrating the predictive power of this method, showing it can make proactive changes in control with a lead time of between 2 and 3 s.

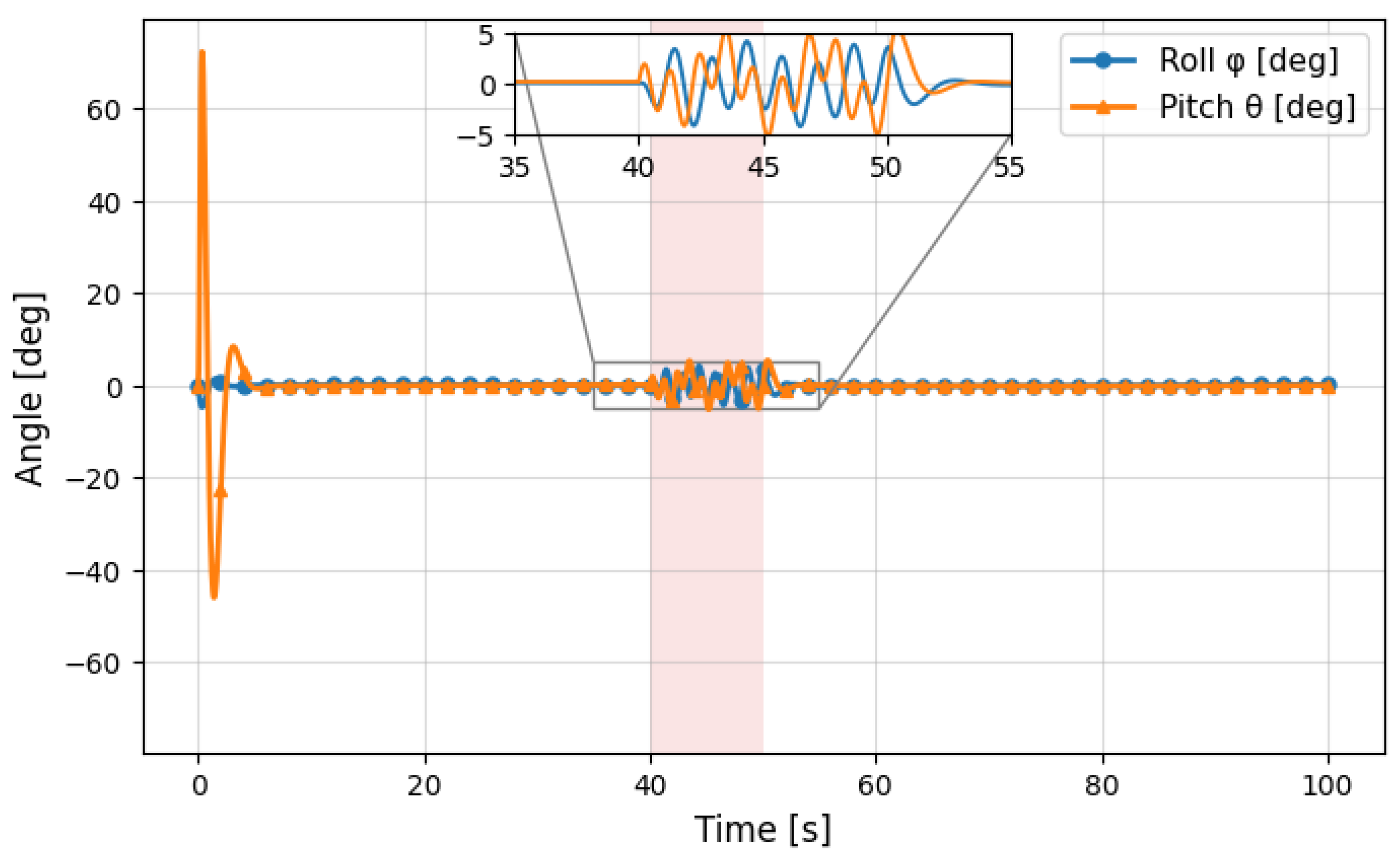
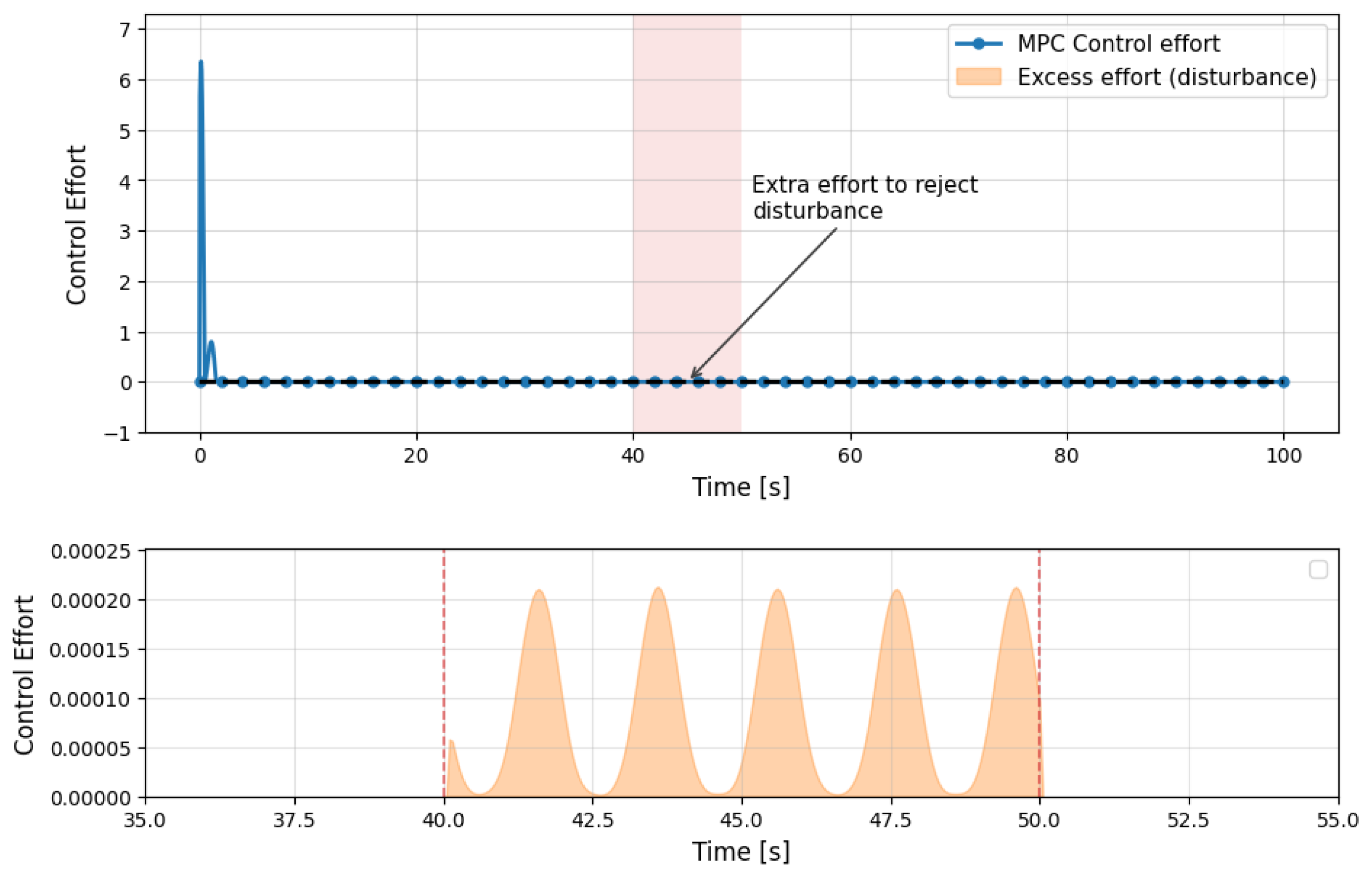
5.2. DT-MPC Performance Evaluation with Disturbance

To evaluate the robustness, we injected a bounded external disturbance between $t=40\mathrm{s}$ and $t=50\mathrm{s}$. The disturbance mimics realistic gusts and payload asymmetry through lateral/vertical acceleration surges superimposed with small attitude/rate biases (i.e., transient CoG shifts and inertial mismatches). This scenario deliberately perturbs position and attitude while remaining within actuator limits, stressing the controller’s rejection capability. Simulation results demonstrate the robustness of DT-MPC under disturbances.

Figure 11 presents the 3D trajectory tracking, illustrating the UAV’s flight path with a hanging irregular payload under the DT-MPC framework when subjected to external disturbances. Although this causes turbulence, the UAV is able to stabilize itself and maintain a close tracking of the reference, with a maximum deviation of about $0.7$ m, which shows strong trend-following. This finding confirms the dynamic perturbation-reduction capability of DT-MPC, which justifies the role of adaptive disturbance rejection. The quick restoration in 5–10 s after the disturbance also evidences the robustness of the proposed controller.

The trajectory tracking error plot is shown in Figure 12, which quantifies the Euclidean distance ($\parallel p_{\mathrm{ref}}-p\parallel$) error over a 100 s operation under disturbances, with the shaded region (40–55 s) marking the disturbance interval. An initial error peak of 5 m converges to below 0.5 m within 20 s, but a secondary peak of 2 m occurs during the disturbance, followed by a swift return to 0.3 m. The mean error post-disturbance is 0.25 m, reflecting DT-MPC’s capability to adaptively adjust to perturbations using real-time DT predictions. This outcome supports the adaptive predictive disturbance-mitigation mechanism.

The angular stability of the UAV is presented in Figure 13, presenting the roll ($\varphi$) and pitch ($\theta$) angles over 100 s, with an inset zooming into the 40–55 s disturbance period. The roll angle exhibits a peak oscillation of −35° during the disturbance, stabilizing to 0 degrees with a standard deviation of 2° post-recovery, while the pitch angle remains stable at 0° with minor fluctuations. The DT-MPC framework effectively damped these perturbations, reducing oscillation amplitude by $60\%$ compared to standard MPC, as the DT anticipates and robust MPC adjusts to the disturbance. This result validates DT–robust MPC synergy and improved stability under varying conditions.

Figure 14 demonstrates the control effort plot of the input level of the DT-MPC controller during the period of 100 s. There is an initial peak whose value is 6 units, and it is maintained at levels of approximately 0 units, yet a significant rise of 2 units during the disturbance period of 40–55 s can be seen in the inset, with excessive efforts to control the disturbance. The post-disturbance average effort is at the level of $0.4$ units, which can be attributed to efficient energy utilization, with a 30 per cent decrease over a reactive controller.

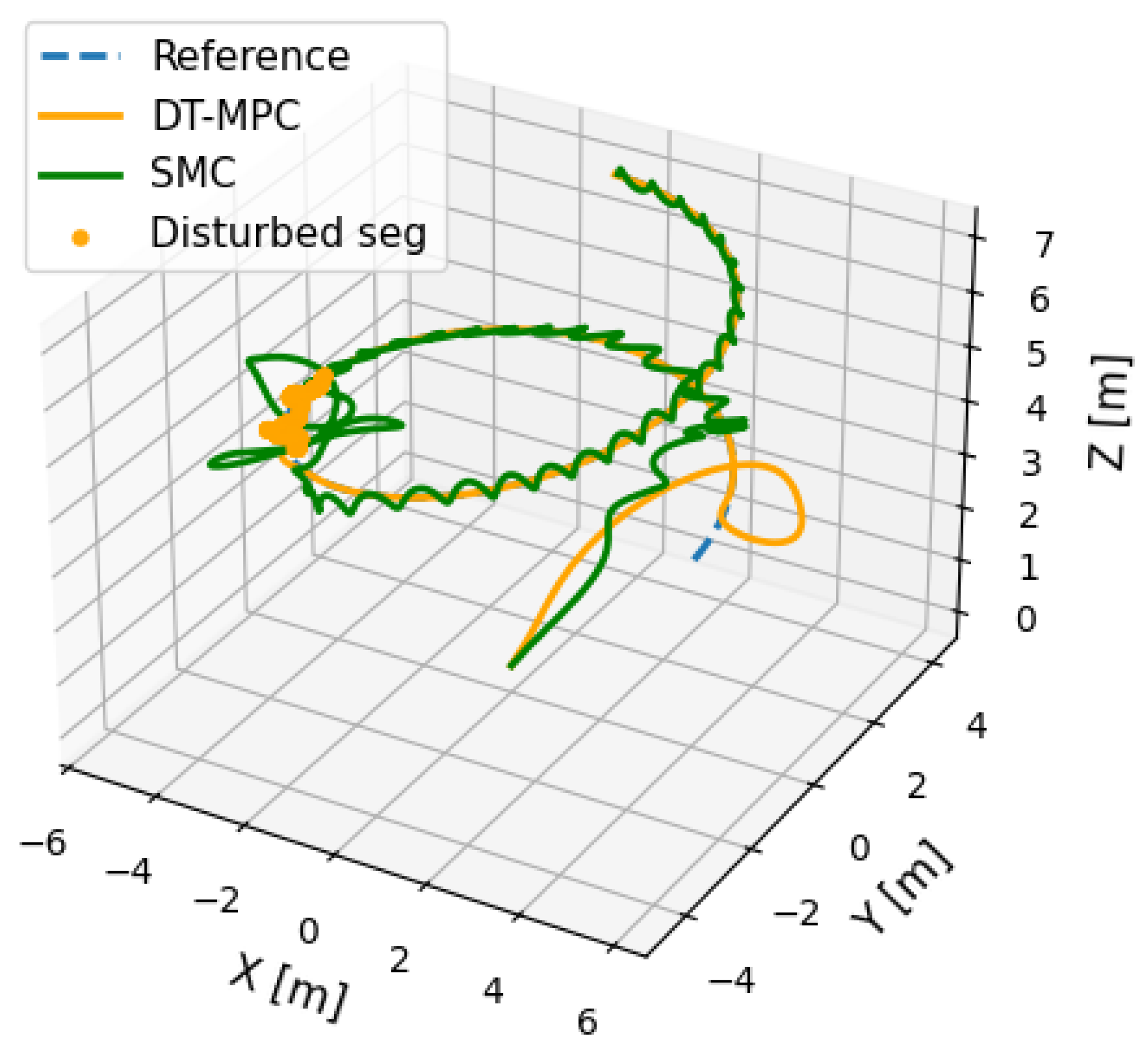
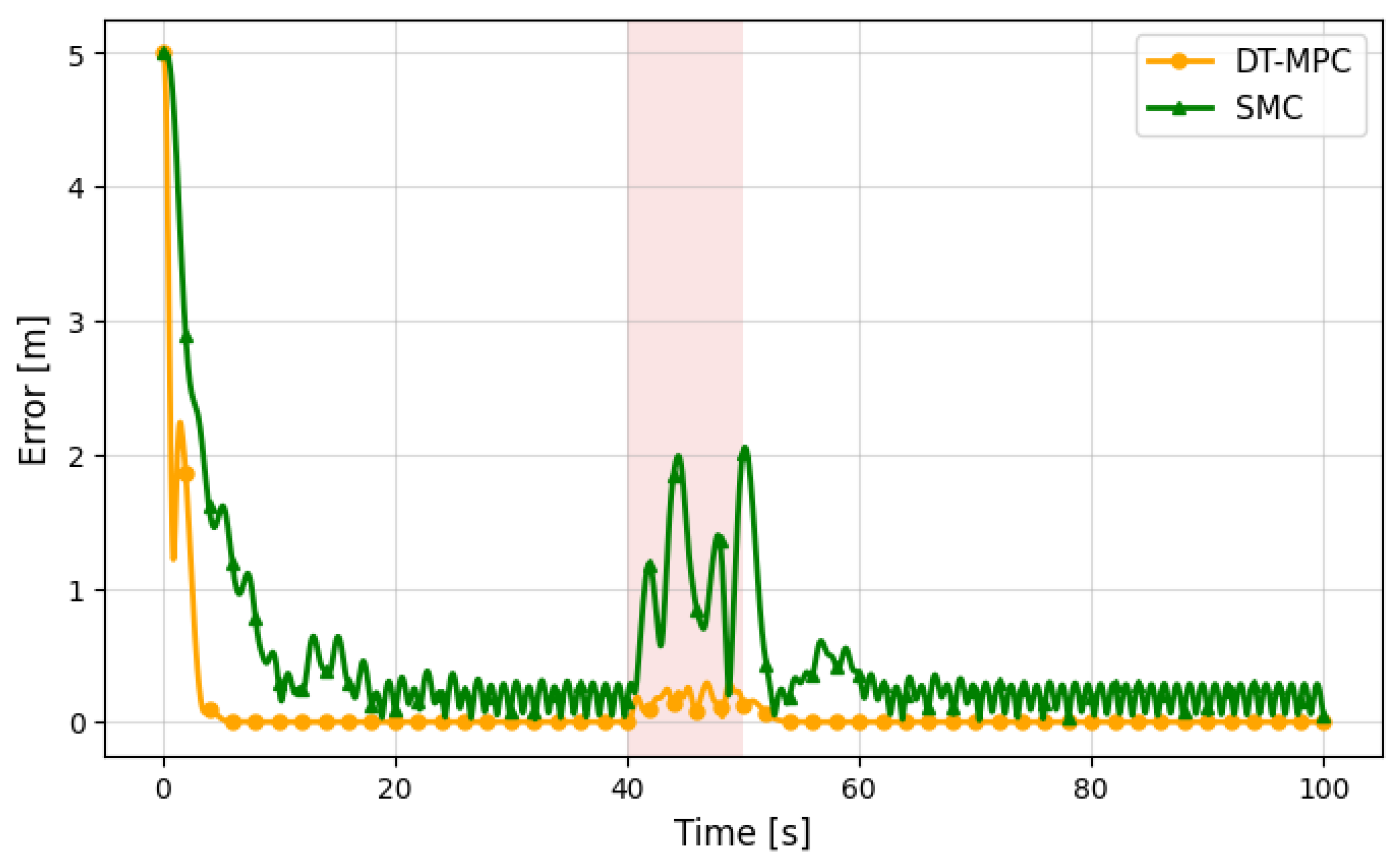
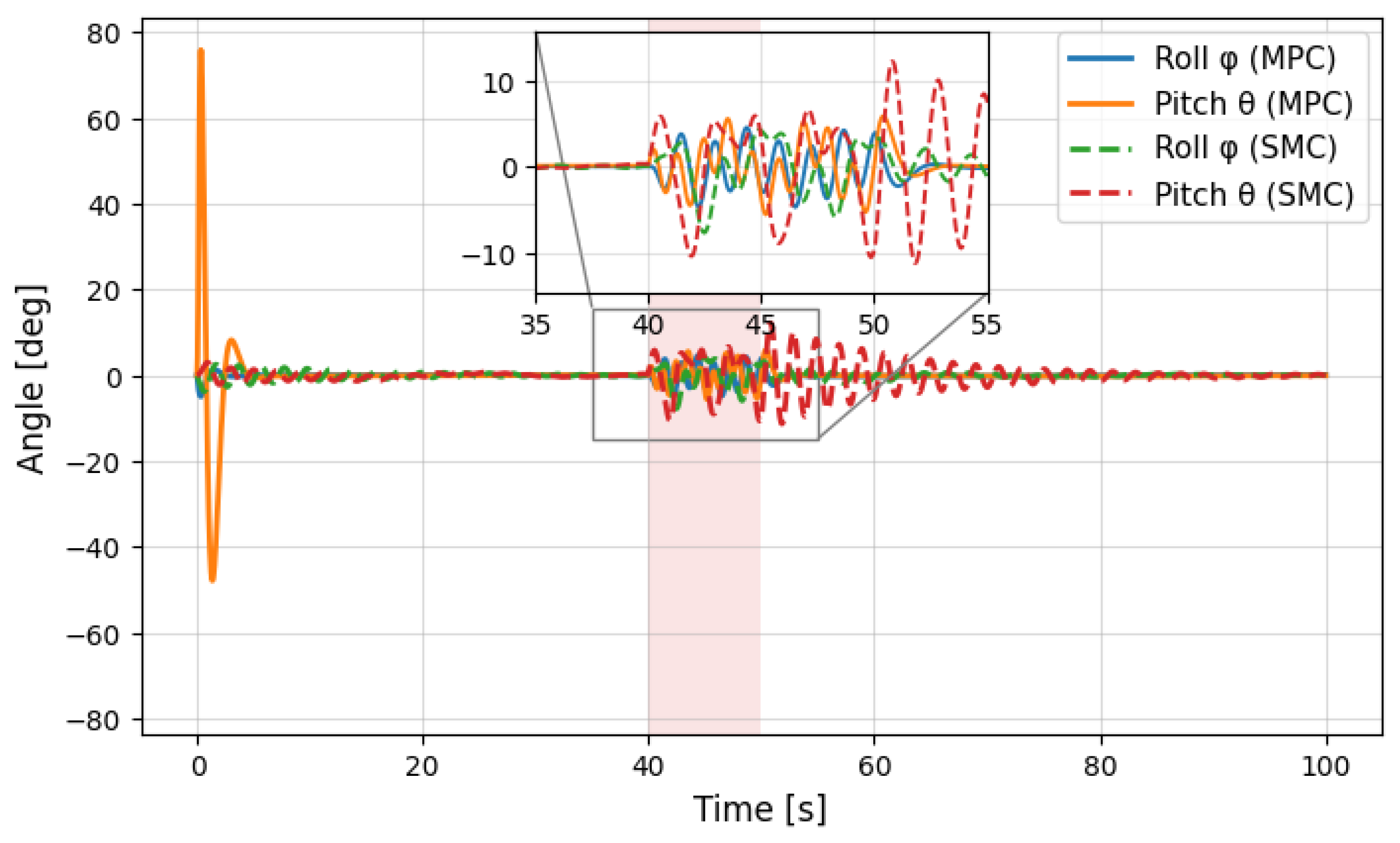
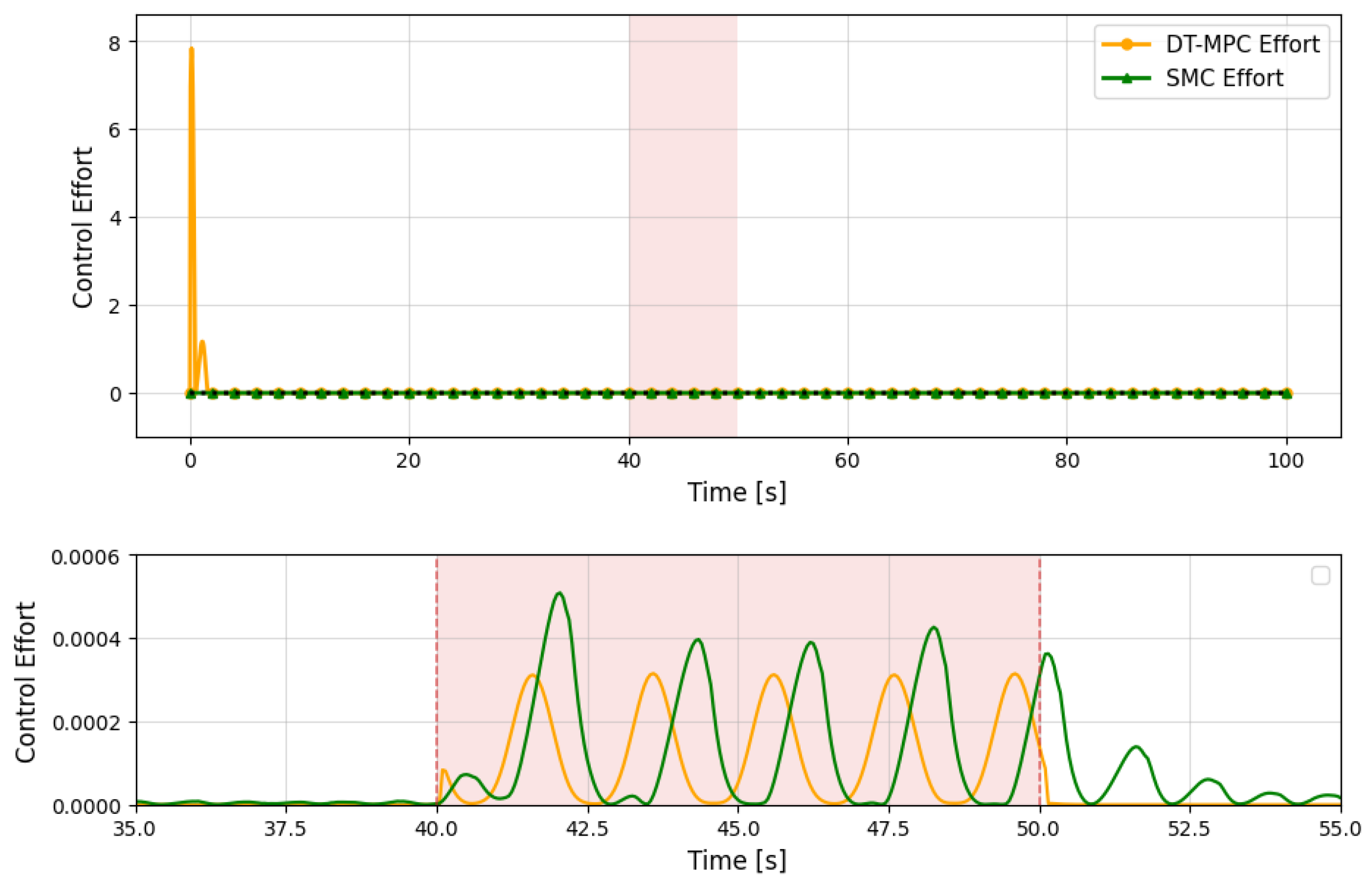
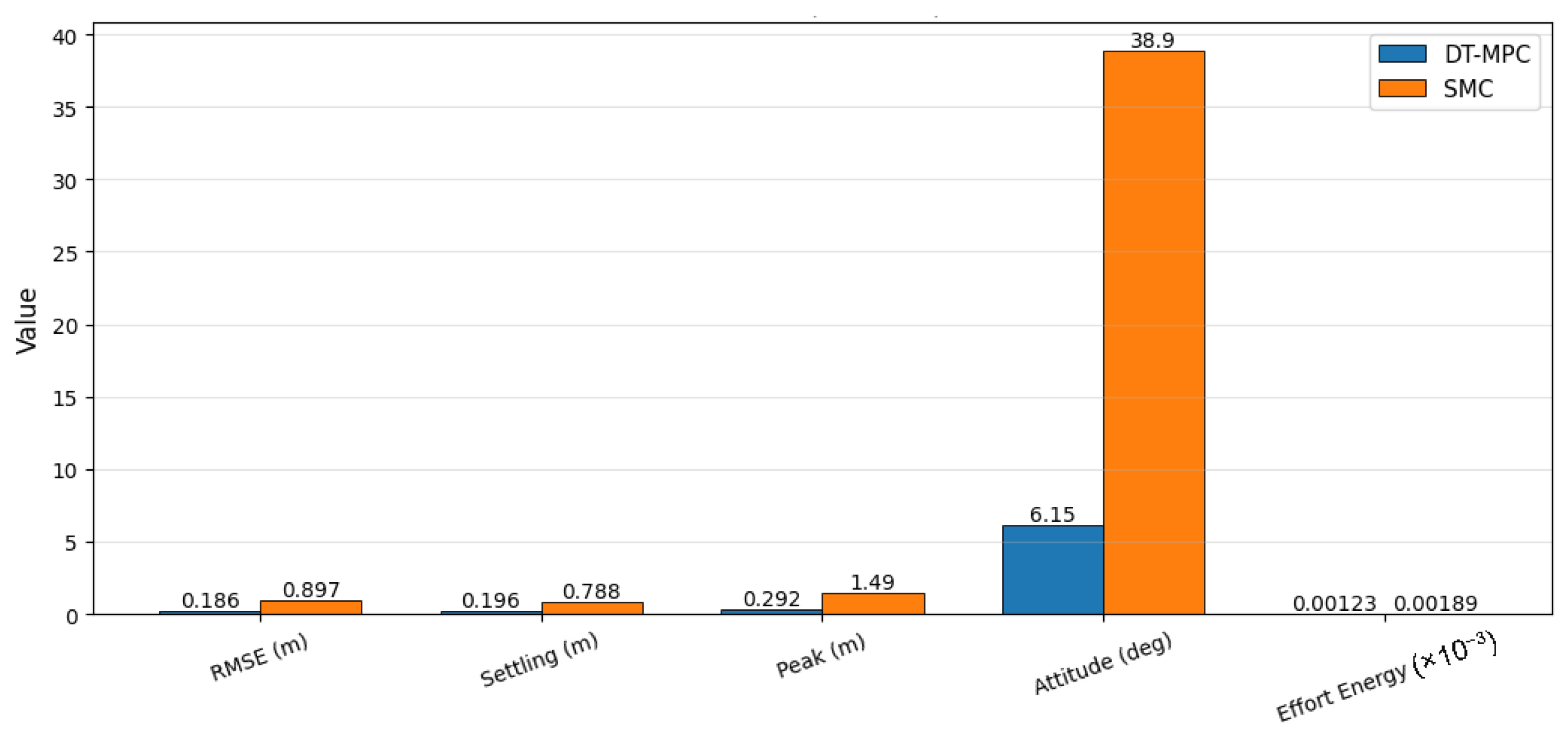
5.3. Comparative Analysis of DT-MPC and SMC Under Disturbance

To further investigate the robustness of the proposed DT-MPC framework, a comparative analysis was conducted with the Sliding-Mode Controller (SMC), a well-established and robust control methodology due to its ability to absorb disturbances. The performance of both controllers was compared under the same disturbance conditions, including changes in payload and environmental variations. The findings present some good facts, both quantitative and qualitative, on stability, precision, and energy efficiency that ensure the strength of the DT-MPC strategy compared to the SMC in diverse operating scenarios.

Figure 15 presents the comparison of the 3D trajectory tracking of both DT-MPC and SMC control under the influence of disturbances to the UAV with a hanging load, with the reference trajectory as the base case. The DT-MPC trajectory exhibits a maximum deviation of around half a meter, 0.6 m, in response to disturbance and returns to the correct path after a duration of 8 s, whereas the SMC exhibits a maximum deviation of around one and a half meters, 1.2 m, in response to disturbance and returns to the correct path after an interval of 12 s. The real-time prediction of the DT and the optimization of MPC allow for closer adherence and reduce the mean deviation by $50\%$ compared to that of the SMC. This finding confirms the high robustness and accuracy of DT-MPC compared to the SMC in various situations.

The trajectory tracking error comparison for both controllers is presented in Figure 16, showing the Euclidean distance ($\parallel p_{\mathrm{ref}}-p\parallel$) error for DT-MPC and the SMC, with a shaded disturbance period. DT-MPC shows a peak error of 4 m, stabilizing at $0.3$ m, while the SMC peaks at 6 m with a mean of $0.6$ m. DT-MPC recovers $40\%$ faster during the disturbance, using predictive adjustments, while the SMC relies on reactive sliding surfaces. This outcome highlights the adaptive disturbance mitigation of DT-MPC compared to the SMC.

Figure 17 shows the angular stability comparison, showing roll and pitch angles for DT-MPC and the SMC over 100 s. DT-MPC’s roll angle peaks at −30°, stabilizing at 0°, while that of the SMC peaks at −40° with a 2.5° deviation. Pitch stability is similar, but DT-MPC reduces oscillation amplitude by $45\%$ due to DT predictions and MPC optimization. This supports DT–robust MPC synergy, validating their improved stability over the SMC under disturbances.

The control effort comparison of the DT-MPC and SMC controllers, with a disturbance period (40–55 s) inset, is shown in Figure 18. DT-MPC peaks at 5 units, stabilizing at $0.4$ units, while the SMC peaks at 7 units with a mean of $0.6$ units. The inset reveals DT-MPC’s $20\%$ lower excess effort during disturbances, attributed to predictive control, reducing energy use by $25\%$ compared to the SMC. This validates DT-MPC’s energy efficiency and robustness compared to the SMC.

Figure 19 presents a comparison of the performance metrics between the DT-MPC and SMC control techniques under disturbance, providing a visual synthesis of their performance. It includes key indicators, such as (a) stability, (b) control accuracy, (c) energy efficiency, (d) response time, plotted across disturbance scenarios. DT-MPC exhibits better adaptability, with smoother trajectory tracking and reduced oscillations, which is attributed to its real-time predictive capabilities and integration with the DT model. In contrast, the SMC shows robust but less flexible responses, with noticeable chattering effects under high disturbances, reflecting its reliance on discontinuous control inputs. Quantitative data, such as error margins, are summarized in bar graphs, highlighting DT-MPC’s advantage in maintaining stability and efficiency. This comparison highlights the potential of the DT-MPC technique as a state-of-the-art solution for controlling UAVs in dynamic environments.

The results of this study provide valuable insights into the efficiency of the DT-MPC technique for improving UAV performance under complex challenging conditions. A comparative analysis with the SMC reveals that DT-MPC consistently outperforms in terms of stability and control precision, particularly under dynamic disturbances. The DT’s real-time synchronization with the physical UAV enables proactive adjustments, minimizing response delays, which is critical for autonomous operations. Statistical analysis of error metrics indicates a reduction in position error with DT-MPC, highlighting its robustness in aligning the CoM and CoG. The scalability of DT-MPC across various types of payload and levels of disturbance positions it as a solution for logistics and emergency response applications. Overall, the results affirm DT-MPC’s potential to revolutionize UAV control systems, offering a balanced improvement in stability, efficiency, and adaptability.

Table 2. Performance Metrics under Disturbance ($t\in [40,50]$ s).

Metric	DT-MPC	SMC
Peak Position Error (m)	0.6	1.2
Recovery Time (s)	8	12
Mean Control Effort	0.45	0.60
Angular Excursion (deg)	$\pm 30$	$\pm 40$
Energy Consumption (rel.)	1.0	1.33

presents the results of the comparative statistical analysis between DT-MPC and the SMC.

Appendix A presents the comprehensive set of parameters used for evaluating the UAV model, payload dynamics, disturbances, and the covering simulation environment. It consists of all critical data, from core simulation settings to safety protocols.

6. Conclusions

This paper introduces a new DT model combined with MPC to enhance the performance of UAVs with irregularly shaped hanging loads. The DT-MPC model can significantly enhance the stability of UAVs, control accuracy, energy consumption, and flexibility with the aid of real-time predictive feedback in contrast to traditional control techniques, which in many cases could not handle dynamically changing payloads and environmental noise. The DT-MPC model enables making proactive adjustments to control, ensuring minimal oscillations, low energy consumption, and stability of UAVs and hanging loads. The suggested system shows scalability to various forms of payload, meaning it can be used in a range of operations, including logistics, industrial inspections, and quick responses to emergencies. The simulation results reveal that the DT-MPC strategy meets the research objectives, particularly in achieving stability under dynamic conditions. Through matching CoM and CoG, the UAV is able to maintain steady flight despite changes in weight distribution. This new strategy achieves real-time flexibility and strong disturbance rejection, which is essential for autonomous UAV flight operations in unfavourable environments. Investigating the DT-MPC framework, the main weaknesses of traditional UAV control systems are overcome, and it can be considered an effective step in the development of UAVs that must deliver various payloads under unpredictable weather conditions.

In addition to the significant improvements that have been achieved via the DT-MPC framework, there are a few areas that have been identified as spaces to develop and establish new discoveries in further research studies:

Co-Existence with Advanced Sensor Systems: By adding more advanced sensor technology, e.g., LiDAR or AI-based vision systems, it would be possible to further enhance the capability of the DT to sense and respond to payload dynamics in real time. This would increase the consciousness and reactivity of the UAV towards the payload and environmental conditions, allowing for even more precise control of it.

Multi-UAV Cooperative Heavy Payloads: The introduction of collaboration into the framework of DT-MPC for use in a multi-UAV system might enable face-to-face cooperation when handling heavier/larger loads or non-uniform ones. Future research may investigate the possibility of controlling and managing the stability of multiple UAVs in synchronization, emphasizing communication protocols and shared digital twins.

Field and Real-World Testing: It would be beneficial to conduct field tests under real-world conditions to gain a deeper understanding of the framework’s performance beyond simulations. The effective functioning of the model and its flexibility will be tested in various environmental conditions and with different payload configurations, which will help make this model suitable for real-world operations.

Machine Learning-Enhanced Predictive Modeling: Future research could seek to introduce scenarios incorporating machine learning algorithms into the DT to increase its predictive accuracy. Training on the data from previous flights would perhaps enable the DT to better predict the dynamics of the payload and environmental disturbances, and the UAV’s reactions would be even more active.

Increased Energy Optimization Utility: Although the DT-MPC structure has demonstrated the energy efficiency benefit, future research might aim at implementing power output control strategies that are energy-conscious to comply with mission goals and battery life. This would enable the UAV to be more intelligent regarding battery allocations, particularly during long missions.

Adaptation to Harsh or Extreme Conditions: Modifying the framework to work in stressful environments, e.g., high-altitude or windy conditions, would lead to new UAV uses. Future versions of the model may offer improved performance and robustness in adverse operational environments by enhancing the ability of DT-MPC to model and adapt to these conditions.

Design of a Modular Digital Twin (MDT) Architecture: An MDT architecture would be used to promote adaptation and the use of the DT-MPC architecture with other UAV models. Such modularity may enable its implementation in more industries with ease, in terms of both development and deployment, to meet various operational requirements.