Rolling Contact Fatigue and Wear of Rails and Wheels: A Comprehensive Review

Abstract

Rolling contact fatigue (RCF) and wear are the primary types of damage found in rails and wheels, and these often compete with each other. This paper presents a comprehensive review of studies on RCF and wear of rails and wheels, focusing on their competition. First, RCF and wear in actual rails and wheels are discussed. Next, theory and models for RCF cracks are presented—from crack initiation, through short and long crack growth, to crack branching and branch crack growth. Then, different wear forms, wear regimes, and their theories and models are introduced. Several studies analyzing the competition between RCF and wear are discussed. Finally, current gaps or problems of the studies on RCF and wear of rails and wheels are identified, and recommendations for future work are provided. This review aims to assist researchers who investigate and address the problems associated with RCF and wear of rails and wheels.

1. Introduction

The rolling contact between wheels and rails is crucial for railway systems. Under a cyclic wheel passage, high contact pressure and tangential traction lead to the initiation of cracks known as rolling contact fatigue (RCF) and wear in both surfaces. They cause considerable damage to rails and wheels. According to the railway wheel turning data [1], most wheels were turned owing to either RCF or tread/flange wear. The cost of rail and track maintenance increases considerably with regard to the detection of RCF cracks, the installation of reinforcements, the renewal of rails and wear on curved sections of rails. In some cases, either RCF or wear dominates, making the other negligible. However, when both affect rails and wheels to a comparable degree, their competition becomes critical as measures taken to reduce one may influence the progression or mitigation of the other.

The full lifecycle of a crack in a rail can be determined by combining all the phases of crack growth. By overlaying the wear-induced reduction in crack length onto the crack growth curve, Figure 1 illustrates how wear can truncate the crack lifecycle [2]. Curve A in this figure shows crack initiation and growth by ratcheting; curve B shows the contact stress–driven growth; curve C shows the crack moving away from the heavily stressed zone near the contact and rate decreases; and curve D shows the crack driven by rail bending and residual stresses. If the wear rate is higher than the crack growth rate, then the crack will be worn away. However, a low wear rate can be detrimental as the crack can move from curve A to D. This concept can be applied to RCF and wear competition of wheels.

Based on the permitted amount of material that can be lost, an increase in wear rate will decrease the lifespan of the rail (Figure 2). The fatigue life curve in this figure is based on the variation in crack growth rates with crack length shown by curves B and C in Figure 1. The actual life of a material is the lower value of its fatigue and wear life, as indicated by the bold curve. The peak point on this curve represents the maximum lifespan that can be achieved by balancing material removal rate via natural wear and grinding; this is referred to as the “magic wear rate” [3] or optimum wear rate. Operation at the maximum life point is difficult because of variability in operating conditions. For a reduced life (dashed line) operation could be at points A or B, but B is inherently safer.

Herein, a review of the literature on RCF and wear of rails and wheels, particularly the competition between them, is presented. Section 2 and Section 3 describe various types of RCFs and wear, respectively, occurring on actual rails and wheels. Section 4 describes the initiation to eventual brittle failure of RCF cracks and the analytical and empirical models used to analyze these mechanisms. Section 5 outlines various types of wear and their models. Section 6 describes studies on RCF crack growth and wear competition in rails and wheels, aiming for the magic wear rate. Section 7 highlights the current gaps or problems of the studies related to RCF, where wear of rails and wheels was identified, and provides recommendations for future work.

In the following text, since many papers are referred to, the same letter is used with different meanings, i.e., A in Equation (7) represents the material constant, not the A in Equation (9), which represents magnification factor. In such cases, the meaning of the letter is explained in each case.

2. Field-Observed RCF

2.1. RCF of Rails

RCF damage in rails became a major problem following the appearance of fatigue cracks—known as “dark spots”—in the curves of the Sanyo Main Line of Japan around 1951. The seriousness of this issue was quickly recognized, prompting extensive research into the phenomenon. In the Tokaido Shinkansen Line, which began operation in October 1964, rail “shelling” (or squats in Europe) in the middle of the rail became noticeable around 1973. On the Sanyo Shinkansen Line between Osaka and Okayama stations, squats began to occur when the cumulative passing tonnage (an index used to evaluate the damage to the track caused by train loads, expressed as “axle weight × number of passing axles”) exceeded 150 Mt. Its increasing tendency became more pronounced when the tonnage exceeded 200 Mt.

2.1.1. Squats

Figure 3 shows a typical appearance of squats [4]. The main crack develops as a “horizontal crack,” which is a coplanar crack, in the direction of train travel at a shallow angle, and a small horizontal crack develops in the opposite direction of the train. Such horizontal cracks rapidly form in tunnels where water leaks constantly wet the top of the rail. The crack branches to form a “transverse crack,” which causes spalling of the rail surface or rail breakage.

2.1.2. Head Checks

On high rails in curved sections and even on straight sections in some cases, wheel flanges contact rail gauge corners and cause damage to gauge corners. This is because the wheel diameter difference at the contact point, unlike the top of the head, causes a large differential slip to act on it. Typical examples of damage are cracks that form continuously at regular intervals, known as “head checks.” The intervals are usually 1–3 mm, depending on the contact conditions and the material.

2.1.3. Studs

Studs are often associated with high-traction sites, such as station exits [5]. They typically initiate at 10–20° to the vertical toward the gauge on the high rail in curves, rapidly growing into the rail at an angle of approximately 20° to the rail surface. The stud fans out across the rail from the initial surface crack, developing at a substantially constant depth of 3–6 mm. If left untreated, it may extend to the opposite side of the railhead, causing a severe spall with a fracture surface characteristic of a conventional fatigue crack.

2.1.4. Belgrospi

Belgrospi refers to a “network of cracks developing on the railhead of tracks with speed exceeding 160 km/h and affected by short-pitch corrugation” [6]. This defect features crack nests between dark troughs and bright crests or near occasional crests. Corrugation and crack nests have wavelengths of >80 mm, shallow corrugation depth, and slight shelling. Shelling within each wavelength can lead to multiple rail fractures, posing a considerable risk to the safety of train operations.

2.1.5. Indentation

Surface damage can also promote the initiation of RCF cracks. Indentations, commonly observed in the field, are usually owing to hard objects from the external environment, such as dropped freight train goods (for example, minerals) or ballast stones dislodged by passing trains. When these objects enter the wheel–rail interface and crash, they cause damage to the rail and sometimes the wheel surfaces. In general, rail indentations can also contribute to the initiation of squats.

2.2. RCF of Wheels

RCF initiating at the wheel tread is related to loading between the wheel and rail. When the stress due to loading exceeds the yield stress of the material, its surface undergoes plastic deformation. Consequently, permanent deformation and ultimately fatigue cracking occur at the thin surface layer, which grows into small crack at a shallow angle that grows into the wheel. Most of these cracks grow as the vehicle operates and can cause damage. Typical RCF cracks in wheels are described in subsequent sections.

2.2.1. Spalling

Spalling is a nest-like failure, in which the surface layer separates at a depth of a few mm, almost parallel to the surface. This type of damage is caused by the arrest of thermal cracks, followed by the initiation and growth of cracks due to the occurrence of RCF parallel to the surface near the bottom of the arrested cracks (Figure 4) [7]. The adjacent cracks coalesce and cause detachment of the tread materials. Thermal crack initiation occurs owing to thermal fatigue in the tread surface layer. This fatigue results from repeated temperature changes owing to tread braking heat. The material in the layer yields in compression owing to restraint from the low temperatures of the surrounding parts. It inhibits expansion. It then progresses to tensile stress during natural cooling after the braking stops.

2.2.2. Shelling

Shelling is the damage caused by pure RCF and can occur even in the absence of thermal effects. It can occur at two points of origin—either on the tread surface where plastic flow is pronounced, or in the subsurface region with the maximum shear stress. In either case, the crack is at a shallow angle to the surface, and the cracked area is often detached.

2.2.3. Heavy Shelling

This is one of the forms of shelling. Fluid, such as snowmelt or rainwater trapped inside a surface crack, generates internal pressure. This pressure considerably affects crack growth, and the more pronounced the fluid effect, the deeper the crack tends to be. In this case, the crack consists of a main crack growing deeper inside the tread and many cracks that branch from the main crack. The branched cracks reach the surface again, resulting in detaching.

2.2.4. Flat Spalling

A wheel flat is an oval-shaped plane area created by the localized wear on the tread surface when the wheel stops rotating due to strong braking force and slides along the rail. A structure known as a white etching layer (WEL) may appear under the wheel flat. Delamination may occur if the wheel with a flat spot is used without repair. Two types of cracks can cause delamination: those within the WEL and those at the edge of the flat spot between the WEL and base metal.

3. Field-Observed Wear

3.1. Wear of Rails

Wear of rail is mainly caused by microscopic adhesion and fracture at the actual contact point of the friction surfaces. It occurs when two objects are plastically deformed due to localized high pressure at the contact point, causing one of the objects to spall from its surface and generating wear debris. Factors such as the tonnage of vehicles passing, wheel material and shape, lateral pressure, frange lubrication, materials and shapes of rails, curved alignment, gradient, track maintenance status, rail lubrication, environmental conditions, and weather affect wear.

3.1.1. Side Wear

The top and side surfaces within the gauge of rail head are worn with prolonged rail use. The wear on the head surface of straight and curved low rails is almost flat. However, the gauge corners of high rails are subjected to a large slip caused by wheel rotation under lateral force, which causes side wear (Figure 5) [8]. Rail replacement is time- and labor-intensive. Improving the wear resistance of rails can considerably reduce the maintenance cost. Head-hardened rail and lubrication are commonly used to improve the wear resistance and reduce the frictional coefficient. In Japan, HH340 rails and HH370 rails with heat-treated heads are often used for the outer rails of sharp curves.

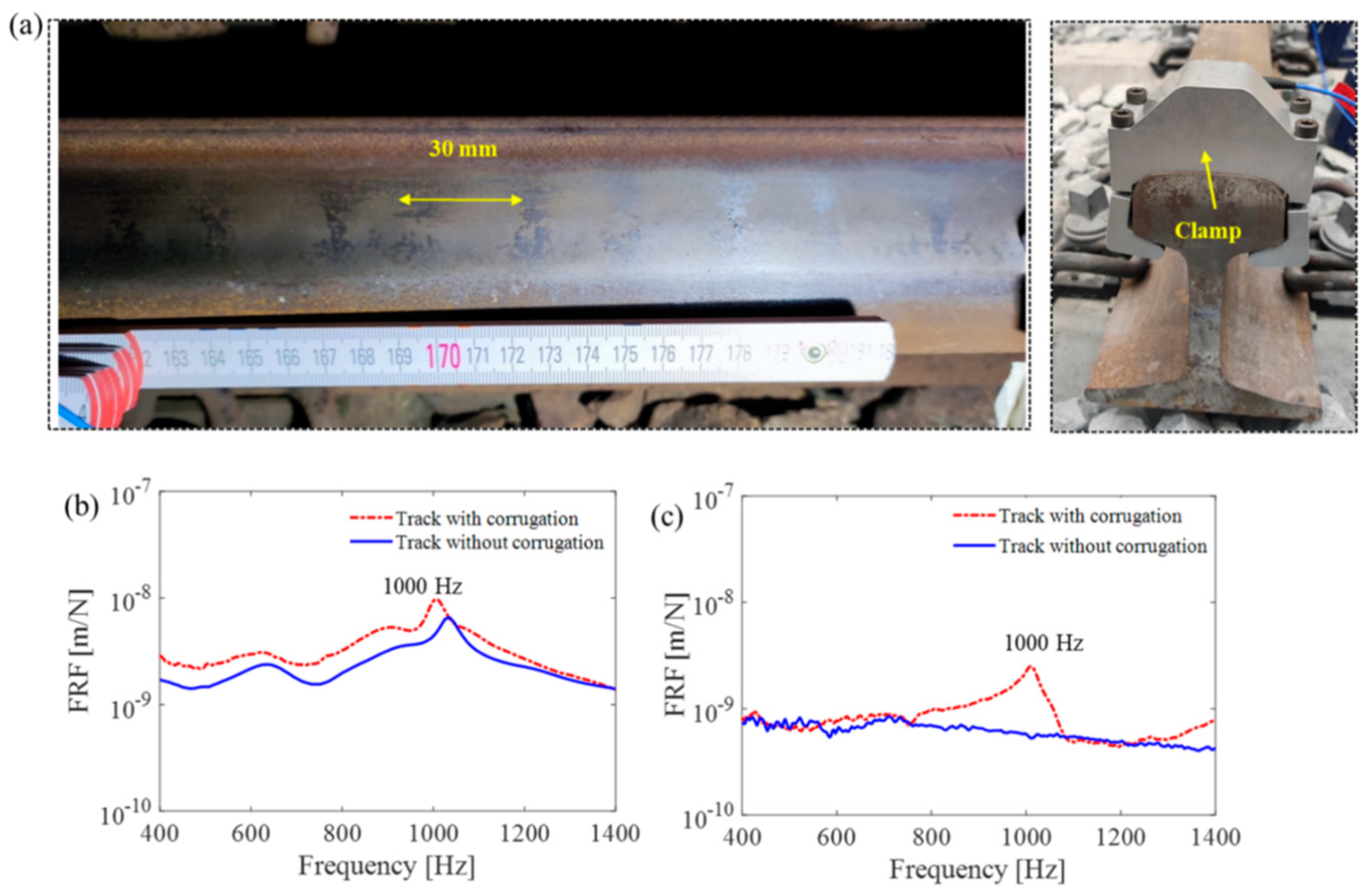
3.1.2. Corrugation

Corrugation is a phenomenon in which the top surface of a rail wears or plastically deforms in a wavy pattern at regular intervals. Figure 6 shows an example of the corrugation [9]. Corrugations on conventional railway lines can be broadly categorized into three types: corrugation with a wavelength of 30–80 mm occurring on straight sections, corrugations with a wavelength of 400–600 mm occurring mainly on the outer rails of sharp curves with a curve radius of 800 m or less, and corrugations with a wavelength of 60–150 mm occurring mainly on the inner rail of sharp curves with a curve radius of 400 m or less.

3.2. Wear of Wheels

Wear of wheel considerably impacts the performance of railway systems and increases the maintenance cost. Wheel profiles have been designed focusing on enhancing their strength and minimizing wear, as well as ensuring ride comfort and safety. Any change in the initial wheel profile can considerably impact the vehicle dynamics; therefore, such changes must be corrected, and the wheel must be restored to its original profile. However, wheel reprofiling is restricted to a predefined limit of 780 of 860 mm wheel diameter, beyond which the wheel must be replaced. Wheel reprofiling and replacement considerably add to the maintenance cost.

3.2.1. Hollow Wear and Grooving Wear

The abnormal wear in wheel tread can be classified into hollow wear and grooving wear based on the wear pattern. Hollow wear refers to the large and concave wear pattern at the center of the wheel tread, whereas grooving wear involves the formation of concave wear partially at the edge of the tread where it contacts the brake shoe. Grooving wear is caused by a complex combination of various factors, such as uneven hardness of the brake shoe.

3.2.2. Flange Vertical Wear

Flange wear occurs when (1) there are many curves or (2) the outer flange strongly contacts the rail on a curve due to high load bearing capacity on the side, high rotation resistance of the bogie, or high rigidity of the axle box support as well as during (3) wheel axle parallelism or diagonal dimension of the bogie is out of alignment.

3.2.3. Wheel Polygonal Wear

Wheel polygonal wear is a typical form of damage that occurs on the wheels of locomotives, metros, and high-speed trains. High-amplitude vibrations caused by impacts between rails and polygonal wheels accelerate train and track degradation, generating high noise levels. Severe polygonal wear threatens railway safety and reduces passenger ride comfort.

To ensure reliability, rails and wheels are regularly maintained following regulations. For example, in Japan, inspection cycles for rail squats are established, and reinforcement plates are installed depending on the length of horizontal and transverse cracks.

4. RCF Crack Models

4.1. Crack Initiation

The response of materials in the railway wheel-rail contact zone can be categorized into one of the four types, as shown in Figure 7 [10]. A perfectly elastic response (a) is rare in the contact area, as it occurs only if the yield stress is not exceeded, and plastic deformation occurs even at fairly low contact loads. Exceeding the yield stress during the initial loading cycles introduces residual stresses, and the plastically deformed material undergoes work hardening. These two effects may combine to cause the material response to stabilize in an elastic state on continued cycles. This phenomenon is called elastic shakedown (b). If the loading is more severe and the cyclic stress–strain curve becomes a stable closed loop with zero net plastic deformation, the material response is called plastic shakedown (c). When the material exhibits additional plastic deformation with each loading cycle, it is known as a ratcheting material response. The accumulation of deformation continues until the ductility of the material is exceeded and the material ruptures (d). RCF crack initiation criteria for elastic shakedown, plastic shakedown, and ratchetting material responses are explained below.

4.1.1. Elastic Shakedown

Dang Van proposed a multiaxial fatigue crack initiation criterion based on shear stress [11]. This criterion states that damage or crack initiation occurs when the combination of the shear stress amplitude τ_a(t) and the hydrostatic stress σ_h(t) satisfies one or both of the following inequalities during some portion of the stress cycle t₁ < t < t₂:

$${\tau }_a\left(t\right)+a_{DV}{\sigma }_h\left(t\right)>{\tau }_e \mathrm{or} {\tau }_a\left(t\right)-a_{DV}{\sigma }_h\left(t\right)<-{\tau }_e$$

(1)

where τ_e is the fatigue limit of the material in pure shear and a_DV is a material constant. In this case, the value of the left-hand side is calculated using the critical plane approach. Ekberg et al. [12] and Kato et al. [13] employed the Dang Van criterion to evaluate the RCF crack initiation in railway wheel treads.

4.1.2. Plastic Shakedown

Jiang and Sehitoglu [14] defined the damage parameter as follows:

$$FP=〈{\sigma }^{\max }〉{\displaystyle \frac{\Delta \epsilon }{2}}+J\Delta \tau \Delta \gamma$$

(2)

where < > is MacCauley brackets, σ^max is the maximum stress, Δε is the normal strain amplitude, Δτ is the shear stress amplitude, Δγ is the engineering shear strain amplitude, and J is a material constant. In this case, the plane with the maximum value of the damage parameter FP_max is the critical plane for crack initiation. The fatigue initiation life N_f is calculated on this plane as follows;

$$F{P}_{\max }={\left(〈{\sigma }^{\max }〉{\displaystyle \frac{\Delta \epsilon }{2}}+J\Delta \tau \Delta \gamma \right)}_{\max }={\displaystyle \frac{{\left({{\sigma }^{\prime }}_f\right)}^2}{E}}{\left(2N_f\right)}^{2b}+{{\sigma }^{\prime }}_f{{\epsilon }^{\prime }}_f{\left(2N_f\right)}^{b+c}$$

(3)

where E (Itaric) is the Young’s modulus. σ′_f and ε′_f are the axial fatigue strength and axial fatigue ductility coefficients and b and c are the fatigue strength and fatigue ductility exponents, respectively. Ringsberg [15] and Akama et al. [16] used this criterion to predict the initiation of head checks at the gauge corners of rails.

4.1.3. Ratcheting

Franklin and Kapoor [17,18,19] proposed a method for predicting the crack initiation life based on ratcheting and applied it to rails. The ferrite and pearlite grains are assumed to be hexagonal (the brick model), and the crack is assumed to initiate when the total accumulated plastic shear strain γ_n^ij in the region reaches the critical shear strain γ_c. For each load cycle and grain (i, j) in row j and column i, the strain increment Δγ^ij is calculated using the maximum value of the orthogonal shear stress τ_zx^j(max) at each depth and the effective shear yield stress k_eff^ij for each grain.

$${\gamma }_{\mathrm{n}}^{\mathrm{ij}}={\gamma }_{\mathrm{n}-1}^{\mathrm{ij}}+\Delta {\gamma }^{\mathrm{ij}}$$

(4)

$$\Delta {\gamma }^{\mathrm{ij}}=C\left[\left({\displaystyle \frac{{\tau }_{\mathrm{zx}(\max )}^{\mathrm{j}}}{k_{\mathrm{eff}}^{\mathrm{ij}}}}\right)-1\right]$$

(5)

where n is the number of load cycles and C is the ratcheting rate parameter to RCF and wear competition for the rails.

The effective shear yield stress increases as the plastic shear strain accumulates. The new value is calculated using a modified Voce equation:

$$k_{\mathrm{eff}}^{\mathrm{ij}}=k_0\max \left(1, {\beta }_s\sqrt{1-e^{-{\gamma }_{\mathrm{n}}^{\mathrm{ij}}}}\right)$$

(6)

where k₀ is the initial shear yield stress and β_s is the strain hardening ratio. Figure 8 shows how modeling indicates the distribution of failure leads to the generation of wear debris and crack-like flaws. In this figure, the black squares are the bricks where γ_n^ij reaches γ_c.

Garnham et al. [20] analyzed the microstructure of used rail samples taken from the outer rail of a curved section and rail test pieces from a twin-disc tests via scanning electron microscopy. They concluded that the nonmetallic inclusion MnS was flattened due to the accumulation of repeated stress, becoming the source of crack initiation. Akama and Kimata [21] considered crack initiation from such nonmetallic inclusions and applied this crack initiation criterion to RCF cracks in wheel treads.

4.2. Crack Growth

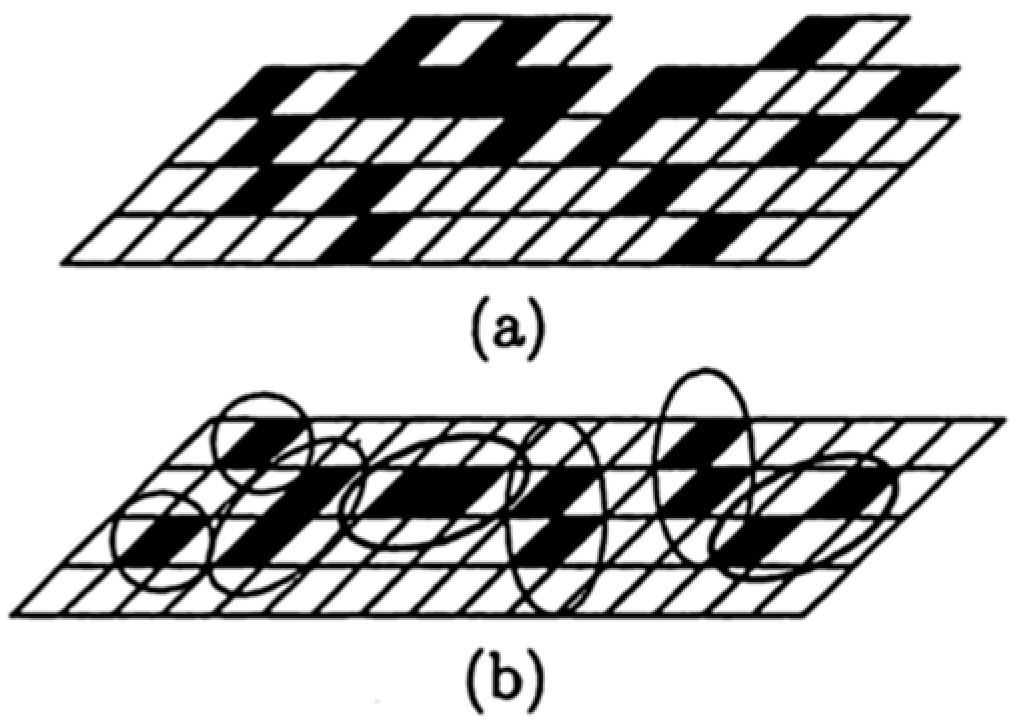
4.2.1. Short Crack

After crack initiation, “short fatigue crack” growth occurs that cannot be dealt with linear elastic fracture mechanics (LEFM) [22]. When the crack size becomes comparable to the scale of the characteristic microstructural dimensions (i.e., less than or equal to the grain size), obstacles such as grain boundaries, particle inclusions, or phase changes hinder further crack growth. These obstacles are called “barriers” that retard or even arrest crack growth. In such cases, the crack is called a “microstructurally short crack” (MSC). After overcoming these microstructural barriers, the crack may be long enough to grow based on continuum-mechanics mechanisms, whereby the crack length and applied stress or strain determine the crack growth rate. However, crack growth may occur within plastic regions, which invalidates the LEFM analyses, and the growth rate is greater than that predicted via LEFM. Such a crack is known as a “physically small crack” (PSC). When addressing the initial stages of crack growth, the characteristics of short-cracks must be considered.

(a)

MSC crack growth (Stage I)

Hoshide and Kusuura [23] and Hobson [24] proposed a crack growth equation for Stage I that described the crack growth within the first few ferrite grains, grain boundary ferrite, and ferrite within the lamellar structure of pearlite colonies. Such cracks are driven by the cyclic shear stress range on the slip planes in the ferrite grain, in the grain boundary ferrite, or on the planes parallel to the lamellae structure in the pearlite grain, depending on the point of crack initiation. The crack growth rate is influenced by the distance between the crack tip and dominant microstructural barriers. The grain boundary strength makes it a major microstructural obstacle to crack growth, and the grain boundary is therefore assumed to act as a barrier. The crack growth rate in Stage I is described as follows:

$${\displaystyle \frac{da}{dN}}=A\Delta {\tau }_{\omega }^{\alpha }\cdot \left(d-a\right)$$

(7)

where A and α are material constants, a is the crack length, N is the cycle, and Δτ_ω is the cyclic shear stress range on the slip planes.

Distinguishing between the initiation and growth of a Stage I crack is extremely difficult; these may be considered continuous phenomena.

(b)

PSC crack growth (Stage II)

When a crack is long enough to allow the crack tip to open, PSC crack growth occurs (Stage II). In this stage, the influence of the crack microstructure is disregarded, and the crack growth is described via continuum mechanics as follows:

$${\displaystyle \frac{da}{dN}}=B\Delta {{\epsilon }_{\mathrm{t}}}^{\beta }a-D$$

(8)

where Δε_t is the total normal strain perpendicular to the crack faces and B, β, and D are the experimentally determined material constants. During transition from Stage I to II, the crack length is introduced in terms of the number of grains.

(c)

Coalescence

The sudden extension of crack length must be considered during the crack growth stage because cracks may coalesce. Crack coalescence is represented by assuming that cracks combine when the crack length reaches a critical value and the tip-to-tip distance between them is less than the critical distance [25]. After coalescence, the crack length is defined by the length of the straight line between both crack tips. When multiple cracks coalesce to form a large crack, the overall crack length is determined by the maximum distance between the crack tips.

(d)

Surface roughness

Wheel and rail surfaces have microscale roughness. Instead of a smooth Hertzian contact pressure distribution, the contact between the two surfaces occurs at asperity peaks. This makes the real contact area only a fraction of the apparent contact area; thus, the pressures at these contact points are correspondingly high. Kapoor et al. [26] performed a series of twin-disc tests. They showed that even when the load was below the shakedown limit, surface roughness caused plastic deformation within a few microns. Franklin and Kapoor [18] approximated the rough contact by multiplying the orthogonal shear stress as follows:

A(1 − z) = d

(9)

where d is the affected depth, z is the distance of the depth direction and A is a magnification factor.

Donzella et al. [27] and Akama and Kimata [21] used Seabra and Berthe’s [28] approach, in which surface roughness results in pressure peaks with amplitudes that depend mainly on the perturbation amplitude A_mp and the wavelength λ. The pressure concentration factor is defined as the ratio of pressure peak P_max to the nominal maximum contact pressure P₀:

$$\mathrm{PCF}={\displaystyle \frac{P_{\max }}{P_0}}=C_1{\left({\displaystyle \frac{\lambda }{A_{\mathrm{mp}}}}\right)}^{{\alpha }_{\mathrm{p}}}{\left({\displaystyle \frac{b}{R_{\mathrm{e}}}}\right)}^{{\beta }_{\mathrm{p}}}{\left({\displaystyle \frac{\lambda }{b}}\right)}^{{\gamma }_{\mathrm{p}}}$$

(10)

where b is the half-width of the contact area, R_e is the equivalent radius of the contacting bodies, and C₁, α_p, β_p, and γ_p are the parameters of roughness characteristics.

Some studies have considered only Stage II for short RCF cracks and evaluated the driving force of crack growth using the crack tip displacement [29,30,31], J-integral [31,32,33], and configurational force [34,35,36].

4.2.2. Long Crack

LEFM is strictly applicable when the crack tip plastic zone r_p is less than 1/50 of the crack length a and the bulk stress is less than 1/3 of the yield stress σ_y. However, practically, it is often applied even when r_p/a = 1/20 or more. When the horizontal crack increases to 3 mm in length, r_p/a corresponds to 1/20 [37]. Many studies on this coplanar crack have been conducted using stress intensity factor (SIF), a typical parameter for LEFM. In this case, the K_I for the opening mode (Mode I), K_II for the in-plane shear mode (Mode II), and K_III for the out-of-plane shear mode (Mode III) at the crack tip were considered.

(a)

Role of the lubricant

Way [38] found that a lubricant is required to enable cracks to grow through the regions of residual compressive stresses on the surface of materials. Several possible mechanisms have been proposed as follows:

    (1)

Fluid lubrication mechanism

Cracks may grow in K_II driven by cyclic shear stresses with the fluid acting as a lubricant between the faces. This mechanism relies on the assumption that if a crack is subjected to a cycle of shear stress, it will grow in its own plane, along the direction of the principal shear stress. The fluid lubricates the faces of the crack so that the K_II at the crack tip increases. Keer and Bryant [39] and Bower [40] have used the dislocation distribution technique to calculate SIFs in a two-dimensional (2D) crack. These calculations predicted similar cycles of variations in K_II at the crack tip, indicating that the amplitude of these variations is sufficiently large to cause crack growth. Bogdański et al. [41] further studied mixed-mode SIFs generated during rolling–sliding contact, such as that between a rail and wheel. They performed three-dimensional (3D) simulations to predict the full cycles of K_I, K_II, and K_III variations when the crack was subjected to the passage of a contact.

    (2)

Hydraulic pressure mechanism

Fluid may be forced into the crack, prizing the faces apart and driving the crack by transferring the stress by hydraulic action and creating K_I at the tip. The body force method developed by Kaneta and Murakami et al. is widely used for calculating SIFs for RCF cracks [42,43,44,45]. They considered that the fluid in the cracks transmitted contact pressure to the crack faces via hydraulic action. The pressure was assumed to linearly decrease from the contact pressure at the crack mouth to zero at the crack tip. This represents the dynamic nature of fluid pressurization at the crack mouth and depressurization as the wheel passes over the crack. The sliding behavior of the crack faces was modified using the friction between them in regions where the crack was closed. In cases wherein the applied shear stress was insufficient to overcome this friction force, that region of the crack was assumed to be locked. This analytical model [45] is shown in Figure 9.

The elastic half-space contains a semielliptical surface-breaking crack of width 2a at the surface, and its length is denoted as d. The crack is inclined at an angle α to the surface of the semi-infinite solid, over which an elliptical Hertzian contact load with a surface traction moves along the x-direction. Figure 10 and Figure 11 show the variation in the dimensionless Mode I SIF (F_I) at the deepest point of the crack tip during a load cycle. These results are obtained by assuming that the crack faces are subjected to fluid pressure, indicated by the solid lines. The dotted lines are the results for the condition of no fluid pressure. In cases wherein the fluid pressure existed, F_I was positive in a certain region of |e/c_x| < 1. A positive value indicated that the crack tip was open, and the magnitude of the positive value of F_I induced by the fluid pressure was larger for type A than for type B.

The main results obtained from the study are summarized below:

(i)

When the surface traction is large and the crack face friction is low, shear mode crack growth occurs at the deepest point of the crack tip. The crack then extends roughly along the original crack plane.

(ii)

The directions of the surface traction, the movement of the contact pressure, and the crack inclination angle strongly control the oil seepage into the crack.

(iii)

The tensile mode fatigue crack growth is induced by the oil hydraulic action owing to oil entering the crack. In particular, the transition from a pit to a crack is primarily caused by tensile mode growth.

(iv)

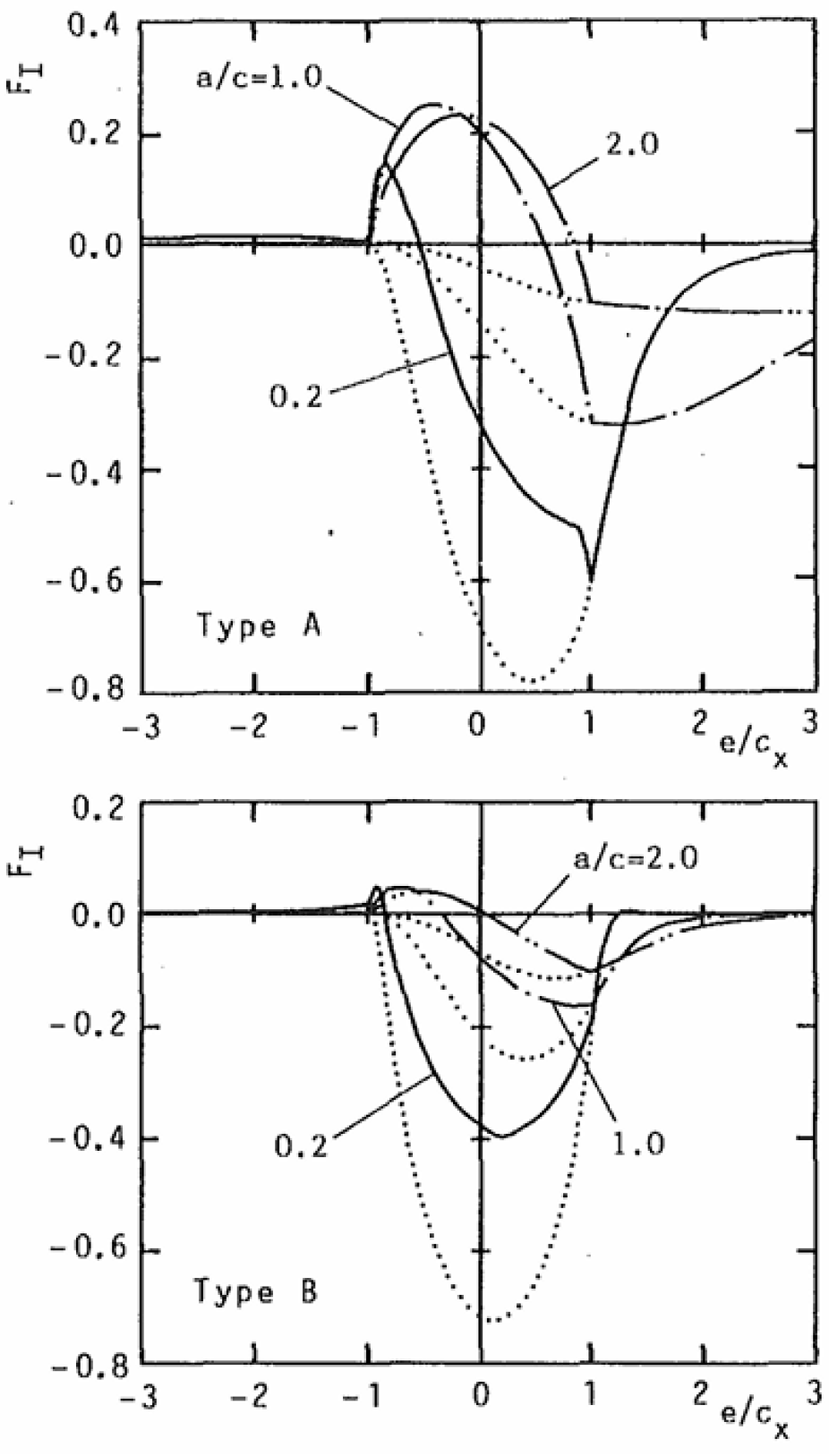
The tensile mode crack growth induced by oil hydraulic pressure is likely to occur at the deepest point of the crack when the crack is shallow compared with the width of the mouth and the crack size a/c is large. However, as the depth of the crack increases, the crack growth is most likely to occur at the tip of the mouth, which may result in an arrowhead-shaped crack.

(v)

When the major axis of the contact ellipse is in the direction of motion of the load and the ratio of the major to the minor axis is large, the possibility of the tensile mode crack growth is low.

These analytical results are consistent with the typical experimental result observed by numerous researchers. These pressure and friction distributions were also applied in the work by Fletcher and Beynon [46,47] using Green’s function approach.

Kaneta et al. [48] performed a series of experiments to reproduce the dark spot defects (squats) using a newly developed two-disk rolling/sliding contact machine. They explained the cause of occurrence of these dark spot defects. Figure 12 shows a typical dark spot defect observed in their experiments, which was very similar to those observed in actual rails.

The dark spot defects are caused by the frequent repetitions of dry and wet runnings, and the traction force plays an important role in the occurrence of the cracks. The principal crack may occur from a tiny pit formed a posteriori on the contacting surface. The second crack is formed by cracks branched from the extended principal crack. Experiments have been conducted to prove that water is capable of entering the tip of the crack. Furthermore, a possible mechanism for the dark spot cracking has been proposed on the basis of the LEFM approach.

    (3)

Fluid entrapment mechanism

Under the conditions of pure rolling, or if there is a driving traction applied to the surface, the crack is pulled open by the capillary action. When the load moves a small distance further, this fluid may be trapped inside the crack. This causes a part of the crack to be prevented from closing by fluid pressure. The fluid is assumed to be incompressible, so that the fluid pressure is determined by the condition that the volume of the crack must remain constant. As the load moves over the surface, the fluid is first forced toward the tip of the crack. Subsequently, the crack begins to reopen, until at a critical point the mouth of the crack re-opens. At this point, the fluid pressure required to keep the crack’s volume constant is greater than the contact pressure at its mouth; therefore, it is assumed that fluid must be escaping from the crack. While the fluid is escaping, the fluid pressure acting on the crack is determined from the condition that it must be just sufficient to keep the crack open near the mouth. This allows fluid to flow between its faces. It is also assumed that the faces of the crack can slip tangentially relative to each other while fluid flows between them. The study undertaken by Bower [40] is the most comprehensive examination of the mechanisms, and Akama and Mori [49] also analyzed the cycles of K_I and K_II using boundary element (BE) method. Bogdański et al. [50] performed 3D cases using finite element (FE) method to predict the full cycles of K_I, K_II and K_III when the crack was subjected to the passage of a contact.

Fletcher et al. [51] conducted full-scale track tests to investigate the fluid penetration of surface-breaking RCF cracks on a specially built test track. The tests showed that a water-based ultraviolet fluorescent marker fluid could penetrate cracks of various sizes under locomotive load and in the unloaded control sample. This evidence of crack penetration by fluid is consistent with crack growth mechanisms that depend on fluids inside the cracks. Use of a paint-based marker fluid did not reveal fluid penetration of the cracks, because the fluid simply did not penetrate as its physical properties were too different from those of water. Another possible reason is that it degraded under the wheel pressure load and became visually undetectable.

(b)

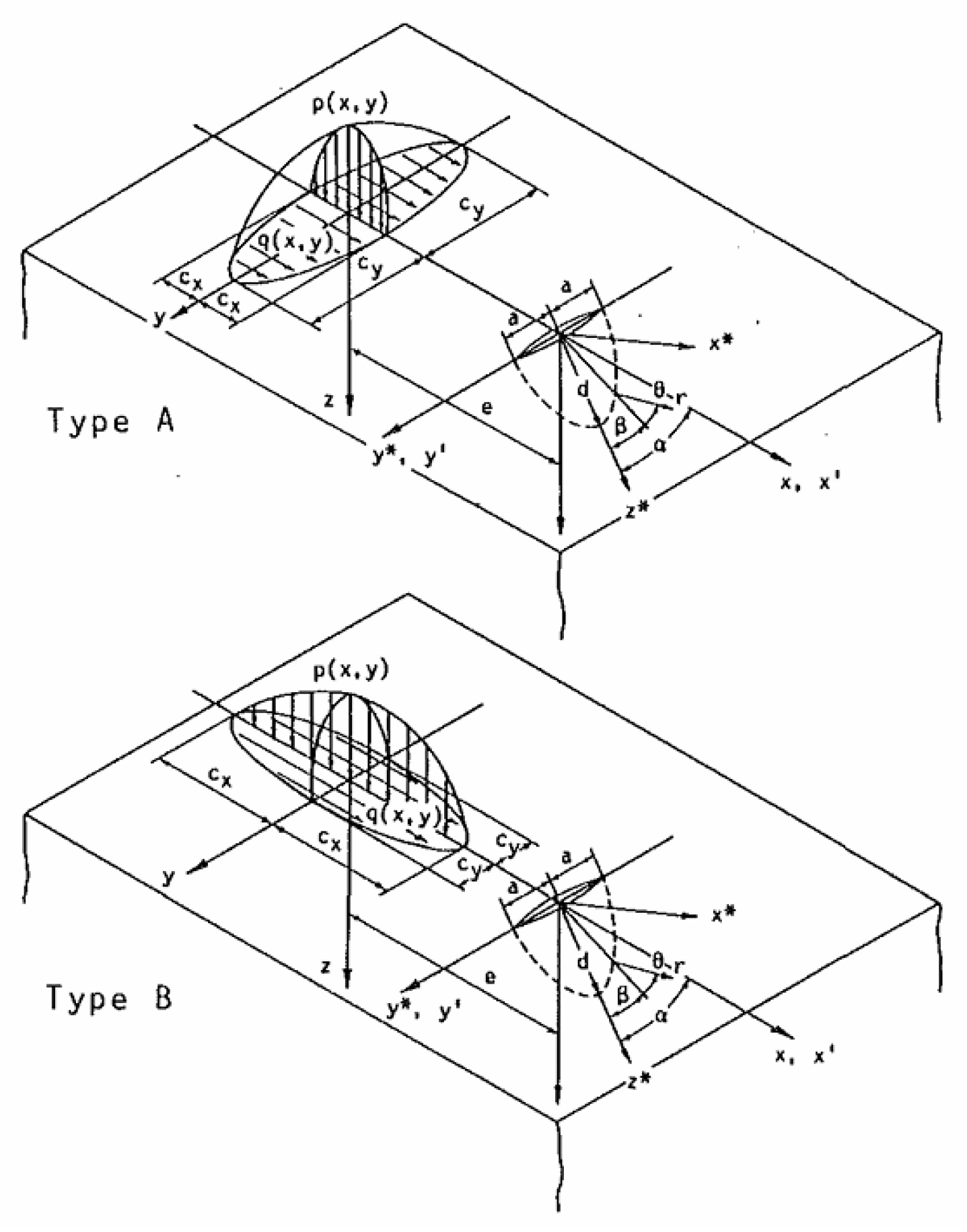
Crack growth laws

Horizontal crack growth laws were developed using loading conditions closer to those experienced in the rail. This helps account for “non-proportional” changes in Mode I and II loading that occur during the wheel passage. Bold et al. [52] developed crack growth laws for RCF cracks using biaxial fatigue specimens of normal-grade rail steel cut from the rail web. Following Equations (11) and (12) summarize their work, showing K_I and K_II ranges. ΔK_eq is an equivalent SIF range, used to combine K_I and K_II, although the peaks in the SIFs for different modes of failure were out of phase with one another during the passage of the contact. ΔK_th is the threshold SIF range.

$$\Delta K_{\mathrm{eq}}=\sqrt{\Delta K_{\mathrm{I}}^2+{\left[\left({\displaystyle \frac{614}{507}}\right)\Delta K_{\mathrm{II}}^{3.21}\right]}^{{\displaystyle \frac{2}{3.74}}}}$$

(11)

$${\displaystyle \frac{\mathrm{d}a}{\mathrm{d}N}}=0.000507\left(\Delta K_{\mathrm{eq}}^{3.74}-\Delta K_{\mathrm{th}}^{3.74}\right)$$

(12)

The stress cycles applied during the development of this law were based on predictions by Bower [40] of the stresses to which inclined RCF cracks in rail are subjected.

Horizontal cracks were subjected to non-proportional mixed-mode loading with not only superimposed K_I and K_II cycles but also K_III cycles. Akama and Matsubara [4] organized K_I, K_II and K_III in the equivalent SIF range ΔK_v proposed by Richard [53] and performed a growth analysis using the Paris law in the following equation:

$${\displaystyle \frac{ \mathrm{d}a}{\mathrm{d}N}}=3.71\times {10}^{-11}{\left(\Delta K_{\mathrm{v}}\right)}^{2.36}, \Delta K_{\mathrm{v}}={\displaystyle \frac{\Delta K_{\mathrm{I}}}{2}}+{\displaystyle \frac{1}{2}}\sqrt{\Delta K_{\mathrm{I}}^2+4{\left(1.155\Delta K_{\mathrm{II}}\right)}^2+4{\left(\Delta K_{\mathrm{III}}\right)}^2}$$

(13)

The constants in Paris law were obtained from a mixed-mode crack growth test with non-proportional K_I/K_II loading [54] and from a non-proportional K_I/K_III loading [55]. Then, the crack growth rates of rail steel were obtained for each loading.

(c)

Crack branching

Once a horizontal crack has grown to a certain length, it may begin to branch at an angle of approximately 60° to the surface. Otsuka et al. [56] assumed that crack growth may occur by whichever mode first gives a resultant SIF exceeding the material threshold. This assumption uses the theories of maximum shear stress and maximum tangential stress criteria developed by Erdogan and Sih [57], represented by Equations (14) and (15), respectively. The directions of growth are θ_σ and θ_τ for tensile and shear mode growth, respectively. K_σ and K_τ denote the equivalent SIFs for both these modes, respectively.

$$K_{\sigma }=\cos {\displaystyle \frac{{\theta }_{\sigma }}{2}}\left[K_{\mathrm{I}}{\cos }^2{\displaystyle \frac{{\theta }_{\sigma }}{2}}-{\displaystyle \frac{3}{2}}{K}_{\mathrm{II}}\sin {\theta }_{\sigma }\right]$$

(14)

$$K_{\tau }={\displaystyle \frac{1}{2}}\cos {\displaystyle \frac{{\theta }_{\tau }}{2}}\left[K_{\mathrm{I}}\sin {\theta }_{\tau }+K_{\mathrm{II}}\left(3\cos {\theta }_{\tau }-1\right)\right]$$

(15)

Kaneta et al. [42,43,44,45] applied these theories for RCF situations and showed that the value of θ_σ that corresponds to the maximum value of K_σ is given by one of the roots of the derivative of K_σ with respect to θ_σ, given by Equation (16).

$$\tan {\displaystyle \frac{{\theta }_{\sigma }}{2}}={\displaystyle \frac{\left(1\pm \sqrt{1+8{\gamma }^2}\right)}{4\gamma }},\gamma ={\displaystyle \frac{K_{\mathrm{II}}}{K_{\mathrm{I}}}}$$

(16)

Similarly the value of θ_τ which gives the maximum value of K_τ was found using one of the roots of Equation (17).

$${\tan }^3{\displaystyle \frac{{\theta }_{\tau }}{2}}-{\displaystyle \frac{1}{\gamma }}{\tan }^2{\displaystyle \frac{{\theta }_{\tau }}{2}}-{\displaystyle \frac{7}{2}}\tan {\displaystyle \frac{{\theta }_{\tau }}{2}}+{\displaystyle \frac{1}{2\gamma }}=0$$

(17)

The values of K_σ and K_τ at various instants throughout the passage of the wheel are used to calculate crack growth direction from Equations (16) and (17) evaluated at each instant. As a result, a range of values for the resultant K_σ and K_τ as well as θ_σ and θ_τ were obtained.

Dubourg and Lamacq [58] predicted the crack growth path (direction and rate) based on Hourlier and Pineau’s criterion [59] under non-proportional loading. This criterion assumed that a crack follows the easiest path available, i.e., the path along the direction θ that maximizes the growth rate at the tip of an infinitesimal segment of length s of the kinked crack da/dN (s, θ) (Figure 13).

Experimental crack growth rates under a characteristic RCF load sequence must be combined with the theoretical expressions of k₁ and k₂ to apply the aforementioned criterion. These are the local SIFs at the tip of the infinitesimal segment s inclined at an angle θ of the original crack. The expressions of k₁ and k₂ were expressed following Amestoy [60] as Equation (18) using K_I and K_II, which are SIFs of the original crack tip.

$$k_1-i{k}_2=k_1^{\left(0\right)}-i{k}_2^{\left(0\right)}+\sqrt{s}\left[k_1^{\left(1\right)}-i{k}_2^{\left(1\right)}\right]+O\left(\sqrt{s}\right)$$

(18)

where

$$\left|\begin{array}{c}{k}_1^{\left(0\right)}\\ k_2^{\left(0\right)}\end{array}\right|=\left|\begin{array}{cc}{K}_{11}^{\left(0\right)}& K_{12}^{\left(0\right)}\\ K_{21}^{\left(0\right)}& K_{22}^{\left(0\right)}\end{array}\right|·\left|\begin{array}{c}{K}_{\mathrm{I}}\\ K_{\mathrm{II}}\end{array}\right| \mathrm{and} \left|\begin{array}{c}{k}_1^{\left(0\right)}\\ k_2^{\left(0\right)}\end{array}\right|=\left|\begin{array}{cc}{K}_{11}^{\left(1\right)}& K_{12}^{\left(1\right)}\\ K_{21}^{\left(1\right)}& K_{22}^{\left(1\right)}\end{array}\right|·\left|\begin{array}{c}\sin 2\theta \left(N_1-N_2\right)\\ \cos 2\theta \left(N_1-N_2\right)\end{array}\right|$$

Here, N₁, N₂ are principal stresses and θ is the angle of first principal direction to Ox, K_ij⁽⁰⁾ and K_ij⁽¹⁾ are the coefficient files determined analytically and depending only on θ.

For example, Equations (11) and (12) are expressed at the tip of s, ∆k_l and ∆k₂ replacing ∆K_I and ∆K_II are then expressed according to Equations (18) and da/dN(s, θ) are computed.

(d)

Branch crack growth

In case of rail, after the crack has branched, it may start to grow at ~60° to the surface. The transverse cracks may lead to rail breaks if they keep on growing. The crack growth in this phase is influenced by several factors.

    (1)

Bending stress

Fatigue cracks in steel are generally observed to grow perpendicular to the maximum principal stress, in this case, transverse to the rail longitudinal axis. The cyclic stresses contributing to the growth arise from each wheel passage. The cyclic bending stresses can be calculated for the rail head by considering the rail as a beam on an elastic foundation that provides vertical, lateral and torsional restraint to deformation under the applied loads. The rail is assumed to be supported on a continuous elastic foundation. These are known as “Winkler” models.

    (2)

Contact stress

The Hertz theory assumes that the contacting surfaces are continuous and may be represented by second-degree polynomials prior to elastic deformation. However, the predicted elliptical contact deviated from the actual measurements of the contact area between wheel and rails [61]. In practice, the contact zone is adequately represented as a rectangle. The relative lateral position between the wheel and rail and the large variations between the radii of curvature at each wheel and rail location lead to the distribution of contact areas for any rail location.

    (3)

Thermal stress

Longitudinal expansion or contraction is restricted in long lengths of continuously welded rail, so longitudinal stress can develop when the temperature changes. Compressive longitudinal stress should be avoided to prevent rail buckling in hot weather. However, excessive tensile stress should also be avoided, as this can cause small cracks to become rail breaks. When continuously welded rails are subjected to a temperature rise ΔT from their equilibrium temperature T₀, the longitudinal thermal stress is nominally given by

$${\sigma }_{\mathrm{x},\mathrm{T}}=-E•{\alpha }_{\mathrm{T}}\Delta T$$

(19)

where E is a Young modulus and α_T is a coefficient of thermal expansion of rail steel.

    (4)

Residual stress

Residual stresses are introduced into rails during manufacturing, particularly during roller straightening. The residual longitudinal stress distribution in standard carbon rails without subsequent heat treatments comprises tensile stresses in the head and foot and compressive stresses in the web. Regardless of their initial form, the residual stresses are modified under the action of high contact stresses during traffic passages. Within the contact zone on the rail head, the longitudinal stresses transform into compressive stresses at a rate dependent on the magnitude of axle loads and reach their final values. The cracks developed in this region are subjected to both K_I and K_II. However, the role of K_II decreases after the cracks have branched. The fractured surfaces of the broken rails showed no evidence of shear mode. Striation patterns were present due to crack tip blunting and subsequent resharpening, which indicates that the cracks were growing in K_I.

Kashiwaya and Ishida [62] modeled such a transverse crack as a circular crack inclined at 60° to the top surface of the rail and subjected to pure K_I loading. In their model, it was assumed that the transverse crack growth occurred only by tensile stresses and the crack shape remained circular. Then, crack growth was calculated by considering stresses generated by train passage, residual stresses, and thermal stresses. The crack growth rates were obtained using compact tension specimens of 20 mm thickness to ensure plane strain conditions under K_I. The fatigue crack growth rate was strongly related to the range of SIFs, and the crack growth rate can be adequately characterized by Paris law:

$${\displaystyle \frac{da}{dN}}=C{\left(\Delta K_{\mathrm{I}}\right)}^m$$

(20)

where C and m are the material constants. Based on the results of tension–compression tests performed on a standard test specimen made of JIS 60 kg rail, the values of these constants were obtained as follows.

C = l.0 × 10⁻¹¹, m = 3

The growth rate of a transverse crack was mainly controlled by the thermal stress and increased rapidly in winter due to large tensile thermal stresses.

Fletcher et al. [63] investigated the interaction between adjacent transverse cracks (tens of mm) that are just getting started with their final stage. They performed the modeling using the FRANC3D BE Version 2 software. For the majority of runs with multiple cracks, a crack separation of 5 mm was used. This distance was representative of the crack separation observed on rails in curves. The cracks inclined at 30° below the rail surface were modeled to reasonably represent shallow RCF cracks reaching the end of contact stress–driven growth (curve C) and moving into bending stress–driven growth (curve D) in Figure 1. For 10 mm radius cracks with 5 mm separations, K_I and K_II were reduced to between 40% and 55% of the value predicted for a single crack. Using the crack growth law developed for mixed-mode loading of rail steel, this reduction in SIFs translated to a reduction in the crack growth rate to ~27% of its value for single-crack models.

Mair and Groenhout [64] proposed a method to simulate the growth of transverse fatigue cracks in the rail head. The periphery of many cracks in the rail head was adequately represented as an ellipse, and an approximate solution was obtained. The SIF for an elliptical crack under an arbitrary normal loading was determined using Shah and Kobayashi’s method [65], provided the internal pressure could be expressed in terms of a polynomial in the local axis system (m, n).

$${\sigma }_{\mathrm{x}}=-p\left(m,n\right)$$

(21)

where

$$p\left(m,n\right)={\displaystyle \sum A_{ij}{m}^i{n}^j};i+j\le 3$$

(22)

The corresponding K_I as a function of parametric angle of the defect ellipse θ can be derived as follows:

$$\begin{array}{l}{K}_{\mathrm{I}}={\displaystyle \frac{8G}{a_c{b}_c}}{\left({\displaystyle \frac{\pi }{a_c{b}_c}}\right)}^{1/2}{\left(a_c^2{\sin }^2\theta +b_c^2{\cos }^2\theta \right)}^{1/4}\times \\ \left[C_{00}+{\displaystyle \frac{C_{10}\cos \theta }{a_c}}+{\displaystyle \frac{C_{01}\sin \theta }{b_c}}-{\displaystyle \frac{4C_{20}{\cos }^2\theta }{a_c^2}}+{\displaystyle \frac{C_{11}\cos \theta \sin \theta }{a_c{b}_c}}-{\displaystyle \frac{4C_{02}{\sin }^2\theta }{b_c^2}}\cdots \right]\end{array}$$

(23)

where G is the shear modulus, a_c is the semimajor axis of elliptic crack, b_c is the semiminor axis of elliptic crack, and C_ij is the function of A_ij and the elliptic functions.

The SIF range is not the only parameter that affects the crack growth rate. Therefore, Equation (20) was modified considering the stress ratio R, the threshold SIF range ΔK_th, and the maximum K_I value K_Imax during each load cycle. With increasing K_I range, usually toward the end of component’s life, the crack growth rate increased considerably. In rails, such growth rate acceleration occurs at crack sizes around 20% of the rail head area; before this stage, the defects must be removed. Crack development at low growth rates exhibited a stronger dependence on K_Imax rather than ΔK_I, resulting in a greater influence of stress ratio R. Consequently, Equation (20) was modified for rail steels as follows:

$${\displaystyle \frac{da}{dN}}={\displaystyle \frac{{\left(1-R\right)}^2\left\{1-{\left(\frac{\Delta K_{\mathrm{th}}}{K_{\mathrm{Imax}}}\right)}^2\right\}}{\left(\frac{K_{\mathrm{Ic}}}{K_{\mathrm{Imax}}}-1\right)}}B{K}_{\mathrm{Imax}}^{mc}$$

(24)

where ΔK_th is the threshold SIF range at R = 0, B and m_c are the material constants, and K_Ic is the plane strain fracture toughness. Typical values of B and m_c are 0.53 × 10⁻¹⁰ m/cycle and 2.13, respectively.

5. Wear Models

Crack growth competes with wear during the initiation and early growth stages of cracks. Various types of wear occur depending on contact loading, materials, and environmental conditions. The subsequent sections describe the common wear mechanisms that occur in metal contacts.

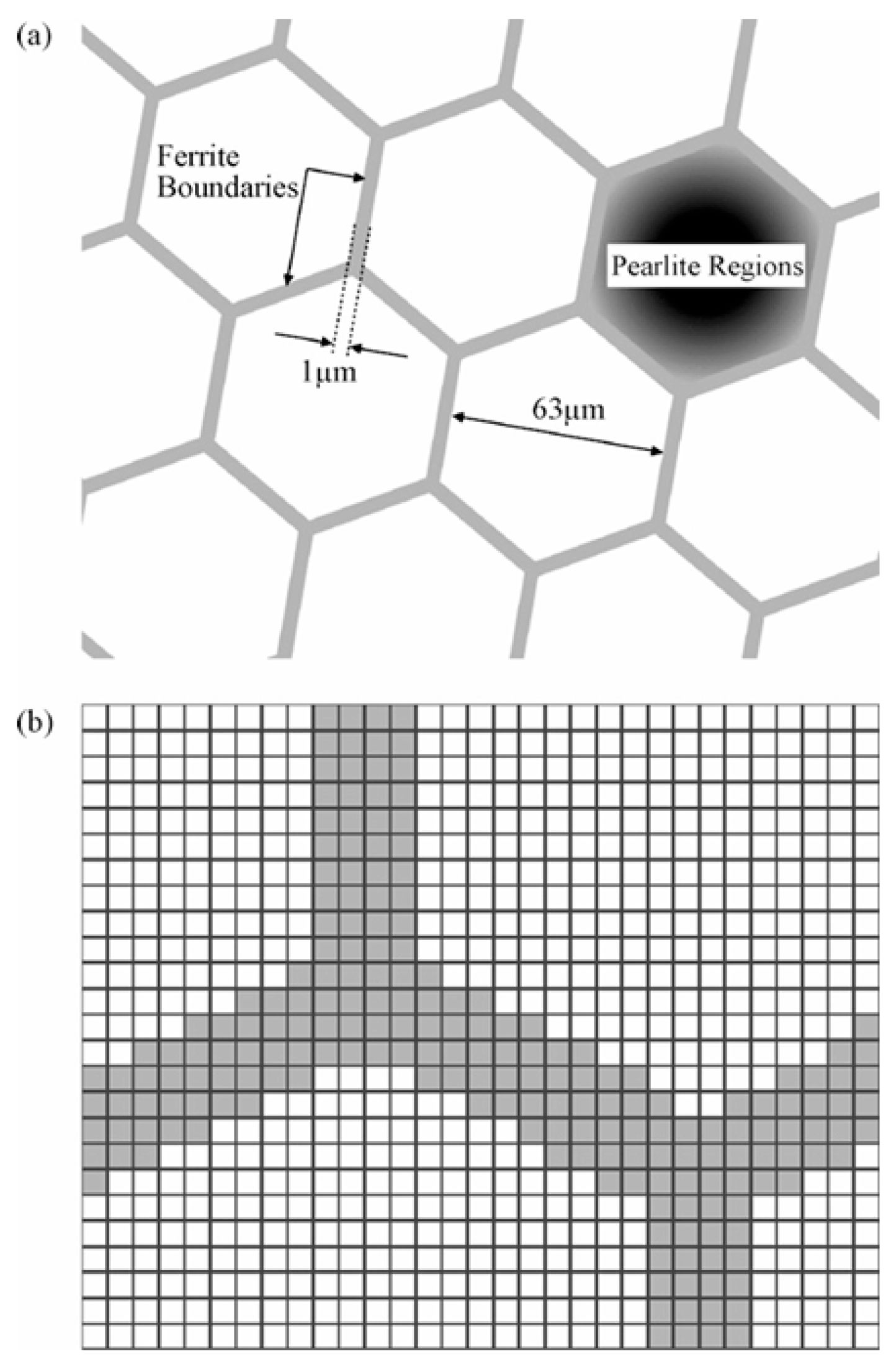
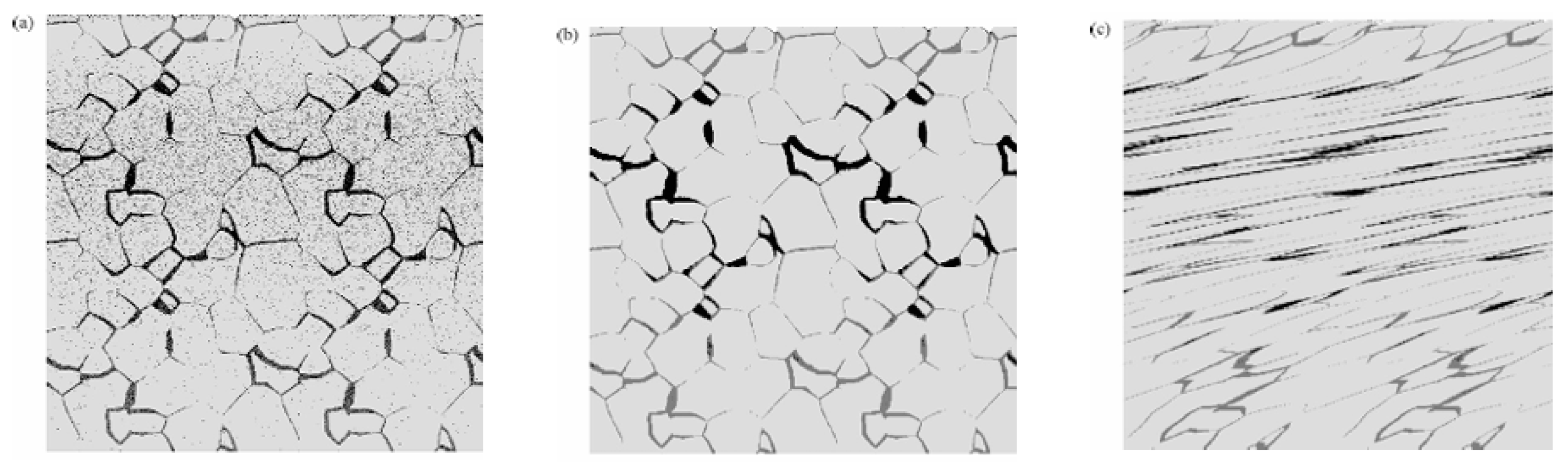
5.1. Wear Mechanisms

5.1.1. Adhesive Wear

When a metal–metal junction forms between intimately contacting surfaces is sheared by frictional motion, a small fragment known as “transfer element” is sheared from one surface and adheres onto the mating surface. This transfer element creates a new asperity on the mating surface and may form a new junction during further sliding. When the next shearing occurs, a “transfer particle” is formed due to the accumulation of transfer elements. As the process repeats, the transfer particle gradually grows to a considerable size and large particles are removed from the metal surface as wear particles. Holm [66] and Archard [67] determined the amount of wear V, as follows:

$$V=k{\displaystyle \frac{PL}{H}}$$

(25)

where P is the load, L is the sliding distance, and H is the hardness. The constant k is known as the wear coefficient. This constant is interpreted as the probability that a true contact point will form wear particles with a certain volume when it repeatedly contacts the mating surface.

5.1.2. Abrasive Wear

Abrasive wear occurs when a surface is worn by the action of hard asperities on the counterface (two-body abrasive wear) or by hard particles trapped between the contacting surfaces (three-body abrasive wear). These third-body particles contain fragments of worn surface that has oxidized or hard contaminants such as silica or quartz. The wear mechanism involves hard particles plowing through the soft surface, which causes the debris to detach. When a conical asperity with a half-apex angle θ is pressed with a load P and slid by distance L, the amount of wear is given by

$$V={\displaystyle \frac{2PL}{H\tan \theta }}$$

(26)

5.1.3. Fatigue Wear

Fatigue wear arises from cycling loading under friction. Repeated, alternating stresses lead to the formation and growth of subsurface cracks that cause surface degradation. Crack initiation begins in the region wherein strains or stresses reach the critical values. The crack initiated at this weak point grows along the direction of weak planes, thereby generating a primary crack. This primary crack matures into secondary cracks owing to stresses induced by the sliding contact at the interface. These secondary cracks formed on the material’s subsurface grow along the weaker plane toward the surface and form wear particles.

5.1.4. Corrosive Wear

Corrosive wear occurs in corrosive environments. The removal and repair of oxide films on the metal surface affects the wear rate. Such type of wear commonly occurs in water and air environments. It can also occur in oil because it contains water and oxygen. The removal of oxide film usually accelerates wear, but corrosion products can also have a lubricating effect.

5.1.5. Delamination Wear

When a surface undergoes plastic deformation under repeated cyclic loading, thin sheets of wear debris are detached from the surface. Suh [68] proposed a theory based on the behavior of dislocations at the surface, subsurface crack and void formation, and subsequent joining of cracks by shear deformation of the surface. According to this theory, the wear particles are likely to appear as thin, flake-like sheets, and the surface layer can undergo substantial plastic deformation. Kapoor et al. [69] proposed that slivers are produced by ratchetting of the surface layers and reaching a critical plastic strain; such wear is therefore called “ratchetting wear.”

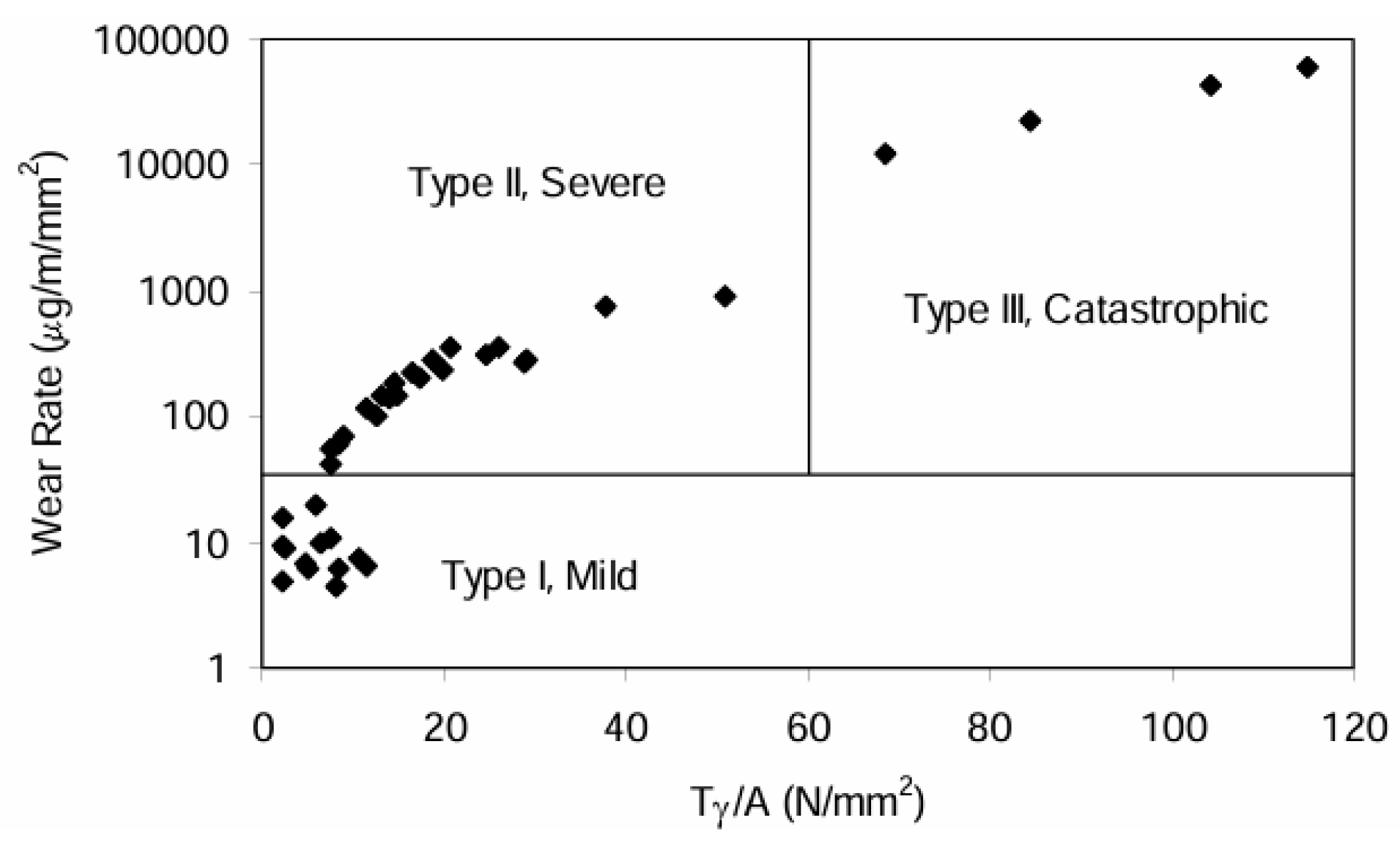
5.2. Wear Regimes

The test for studying wear is often carried out on twin-disc machines. In this test, two discs made of wheel and rail material are loaded together and rotated at varying speeds to give the required slip. Twin-disc tests were conducted to study the wear behavior of railway wheel and rail steels and identified wear regimes. Early tests [70,71,72] revealed the existence of two wear regimes: severe and mild. In severe wear, relatively large (1–100 μm) metallic wear particles are formed that cause metallic surfaces to wear. The specific wear rate is within 10⁻⁷–10⁻⁵ mm²/N in ambient air conditions. In mild wear, fine (10–100 nm) wear oxide-containing particles are generated with a specific wear rate of <10⁻⁸ mm²/N.

Olofsson and Telliskivi [73] investigated the development of the damage mechanisms of wear and plastic deformation on new and 3-year-old rails in a commuter track over two years. They concluded that different wear mechanisms affected different parts of the rail. Mild wear was the dominant wear mechanism at the rail head, whereas severe wear was the dominant mechanism at the rail edge.

However, an additional wear regime, known as the catastrophic wear regime, was identified in subsequent studies [74,75,76]. Based on the ASTM standard G40, catastrophic wear occurs rapidly and causes significant surface damage or deterioration. This wear changes the shape of the component to an extent, such that its service life is considerably reduced or its function is destroyed. Figure 14 shows the results obtained by testing the wear mechanism under various contact conditions [76]. As the contact severity increases, transitions occur between different wear regimes. The relationship between Tγ/A and wear rate breaks down, and various wear regimes emerge, namely, mild, severe, and catastrophic. Herein, T is the tractive force, γ is the slip, and A is the contact area. Wheel tread and railhead wear are generally categorized as a mild wear regime, whereas wheel flange and rail gauge corner wear are considered a severe or catastrophic regime. The first transition from mild to severe wear is associated with the onset of full sliding contact and the second to catastrophic wear is caused by surface temperature.

5.3. Wear Coefficient

Historically, the wear coefficient k in Equation (25) was defined as the probability of wear particles detaching from the junction. Owing to the absence of a standard test method, wear coefficient values reported by different investigators substantially varied, with deviations up to 1000%. To address this, Yang [77] proposed a test methodology for determining the wear coefficient more accurately, consistently, and efficiently. Based on prior wear data, the average deviation between the predicted and measured standard steady-state wear coefficient values was approximately 20%.

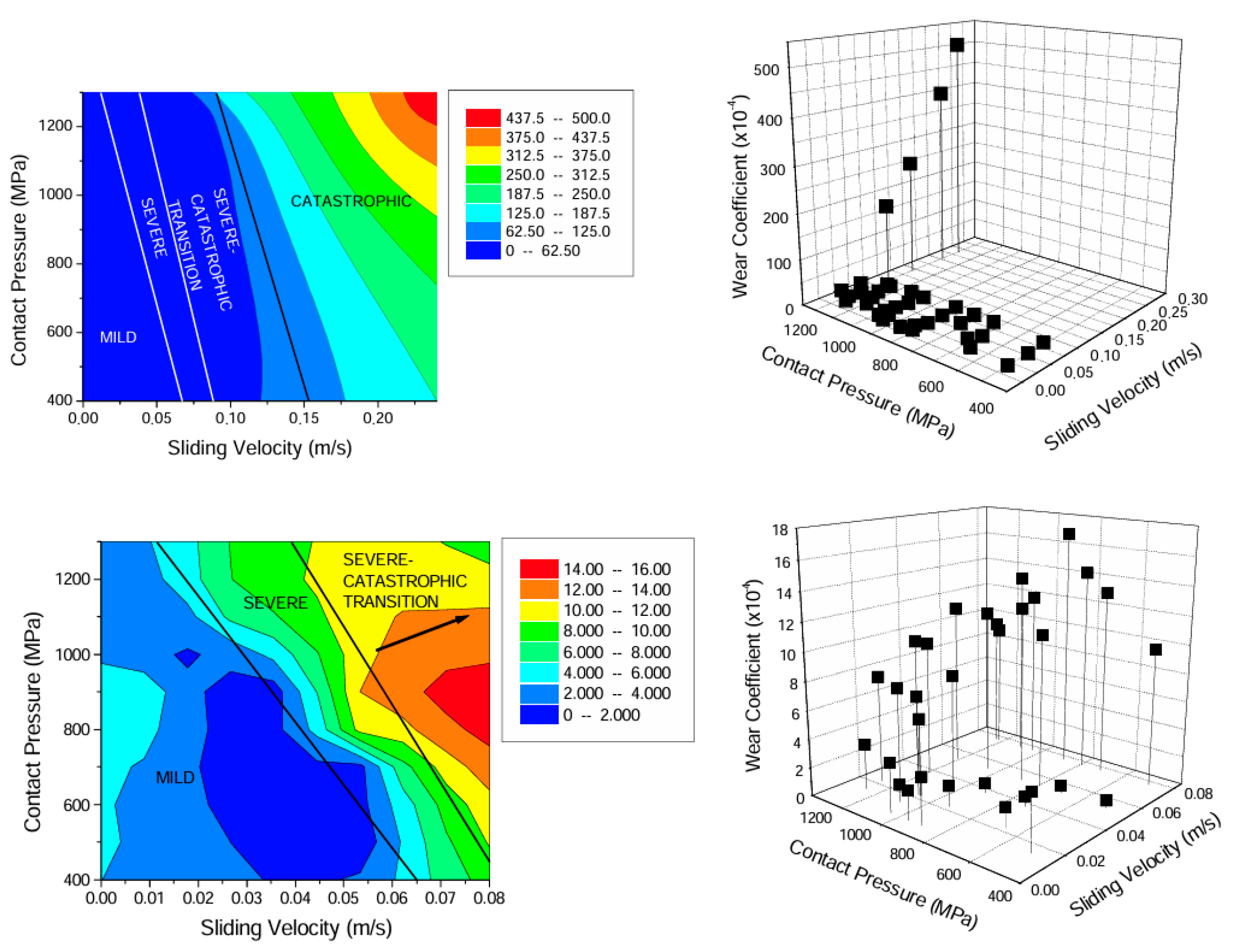
5.4. Wear Coefficient Maps

While the Tγ/A method is used for plotting wear rate data, it can easily identify wear regime transitions. It can also be used to compare different material combinations; however, it does not facilitate fully understanding the effects of different parameters, such as contact pressure and slip, on the wear rate. Therefore, a mapping method was developed for plotting wear data. Wear coefficients were also calculated from the rail steel wear data using Archard’s equation as follows:

$$k={\displaystyle \frac{VH}{NS}}$$

(27)

where V is the wear volume, N is the normal load, S is the sliding distance, and H is the material hardness. Wear coefficients were then plotted against contact pressure and sliding speed in the contact. Two types of plots were developed: contour maps and 3D point graphs. Figure 15 shows the data obtained from twin-disc testing using BS11 rail material versus Class D tire material [76].

5.5. Wear Functions

This section briefly introduces three representative wear functions and their original definitions.

5.5.1. BRR Function

This function models global wear by relating the lost material to the product Tγ, referred to as the “wear index” [72]. This relationship is based on experimental wear measurements of different materials obtained through twin-disc tests. The wear index is calculated as a single value for the entire contact patch and statistically distributed across its extent. It requires only the calculation of global tangential forces and creepages.

5.5.2. KTH Function

This function is based on Archard’s wear law defined in Equation (25) [78]. The values of k are obtained from analyses and experimental data on different materials under dry contact conditions, making the function material-independent and valid for diverse conditions. This function can be globally or locally applied; however, when Archard’s wear model is used globally, a key limitation is the inability to account for spin in calculating global sliding distance.

5.5.3. USFD Function

This function relates the wear rate to the wear index, as follows:

$$W=k_{USFD}{\displaystyle \frac{T\gamma }{A}}$$

(28)

where A denotes the contact area and k_USFD represents an empirical wear constant dependent on the contacting materials [75,76,79]. Based on this methodology, specific wear rates for different materials are obtained directly from twin-disc test results or literature data. This function can be globally and locally applied, depending on the contact parameters used.

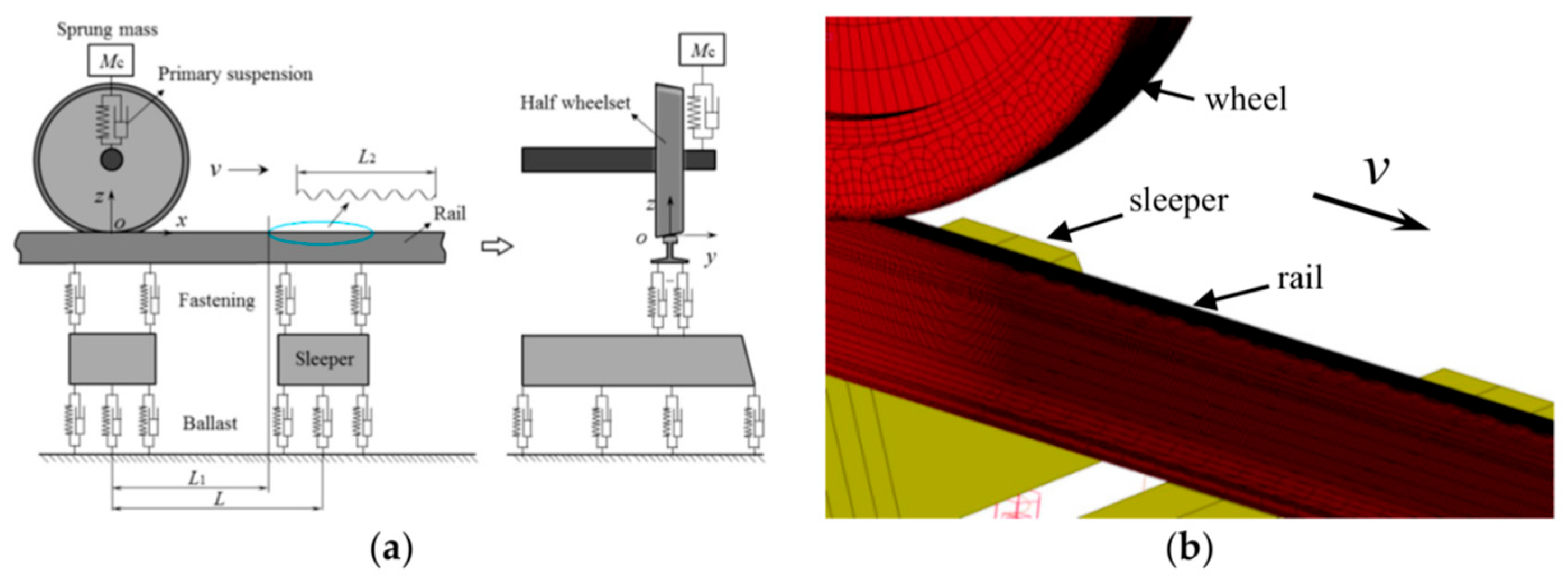
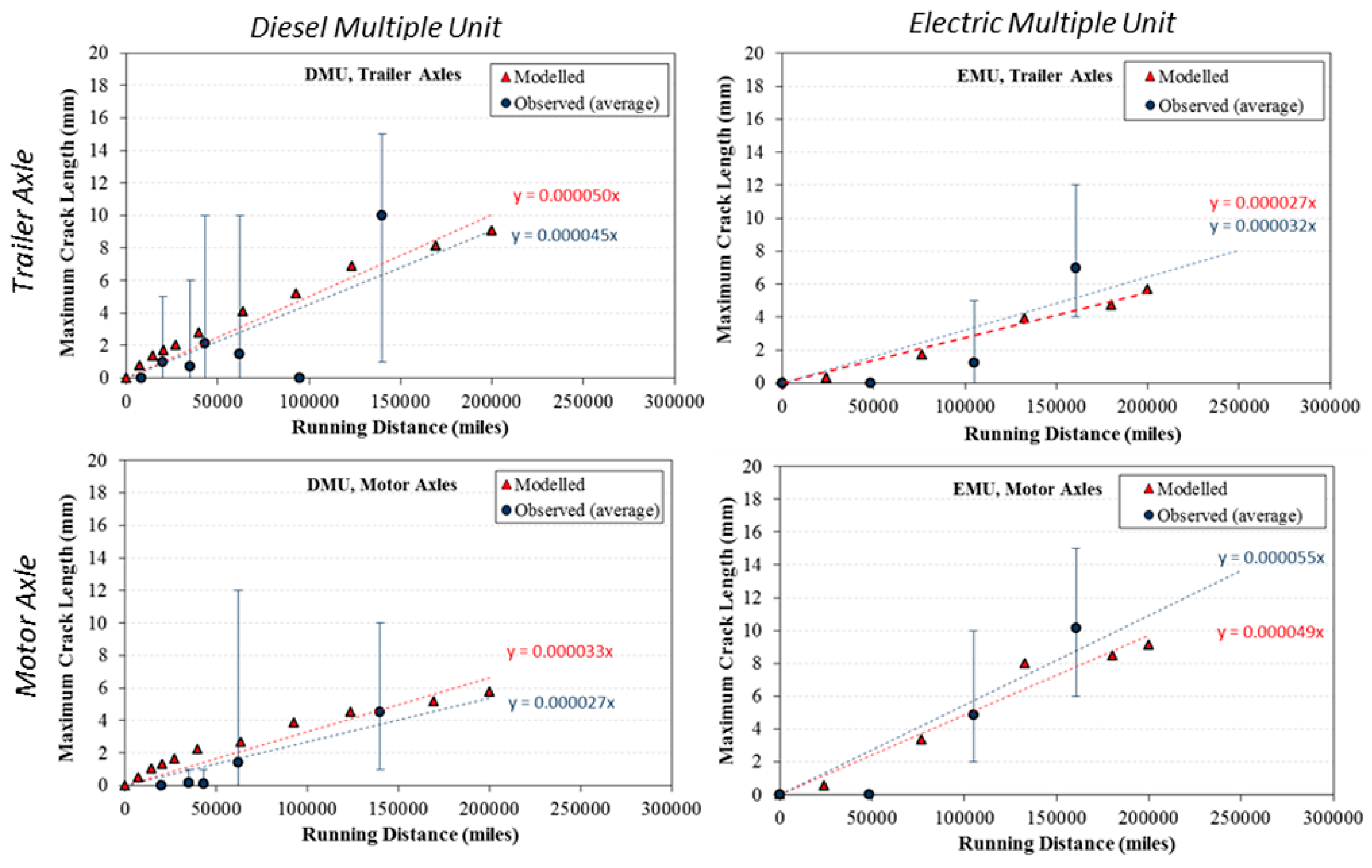
5.6. Wear Prediction

Pombo et al. [80] developed a computational tool that predicted the wear growth of wheels in realistic service conditions. It used a commercial multibody software to study the dynamic problem and a code for managing its input and output data to compute the wear evolution. In the wear prediction tool, three alternative wear functions described in Section 5.5 were implemented. The comparison of results obtained with the functions revealed a good agreement in wear prediction.

Jin et al. [81] conducted experimental research on wheel and rail wear using a large rolling–sliding contact test machine with actual profiles of wheel and rail specimens. They evaluated the effects of axle load, angle of attack, rail hardness, and lubrication on the wear behavior of the wheel flange and rail gauge corner. Based on these results, they calculated the Archard wear coefficients for Japanese railway tracks under various conditions. A wear prediction model of the rail profile was developed by considering contact stress, slip ratio at contact patch, and material hardness based on the experimental results and the wheel–rail contact analyses. The prediction results were compared with the measured values of an actual rail, and the effectiveness of wear prediction methodology was verified for application in actual railway systems.

5.7. Corrugation

Li et al. [82] developed a 3D FE dynamic frictional rolling contact model to study of short pitch corrugation. This model considers the direct and instantaneous coupling between the contact mechanics and structural dynamics in a vehicle-track system. The schematic of the FE vehicle-track model is shown in Figure 16. Herein, the authors examined the system responses in terms of vibration modes, contact forces and the resulting wear using smooth rail and corrugated rail with progressively increasing amplitude to infer the conditions for consistent corrugation initiation and growth. They assumed wear to be the damage mechanism, modeled short pitch corrugation using wavelengths from field observations of a Dutch railway. The wear of an element is as follows:

$$w\left(x,y\right)=k{W}_f\left(x,y\right)=k{\displaystyle \sum {\tau }_i\left(x,y\right)v_i\left(x,y\right)\Delta t}$$

(29)

where W_f(x, y) is the frictional work, τ_i(x, y) and v_i(x, y)are the local tangential stress and slip, respectively. N is the number of time steps Δt during which the element passes through the contact patch.

The main insights are as follows:

(1)

The longitudinal vibration modes were probably dominant in initiating short pitch corrugation;

(2)

During the evolution of short pitch corrugation, the interaction and consistency between the longitudinal and vertical modes determined its development. Once a certain severity was reached, the vertical modes became dominant.

Li et al. [83] proposed a new hypothesis for the formation process of short-pitch rail corrugation using a 3D FE model [82] with fastening models. Longitudinal compression modes were responsible for corrugation initiation with necessary initial excitation that allows flexibility for longitudinal vibration. Consistency between longitudinal compression and vertical bending eigenfrequencies of the wheel-track system was required for consistent corrugation growth, which also determines maximum corrugation amplitude. Corrugation initiated by frequency selection instead of wavelength fixing. The proposed mechanism could explain field observations, including the wavelength and periodicity of corrugation in the Netherlands. It could also explain why corrugation formed on continuously supported tracks, despite the absence of pinned-pinned resonance. Furthermore, it could explain the small variation between the corrugation wavelength and train speed.

Zhang and Li [84] investigated the development mechanism of short pitch corrugation based on extensive field observations of 105 corrugations over a 5-year period. Comprehensive field data were obtained during the 11 observations, including the corrugation photos, their geometry, and the dynamic behaviors of the tracks and vehicles. The numerical predictions of the corrugation development process in [79,80] were validated by the field observations and measurements. One of the results is shown in Figure 17. Figure 17b,c show that the longitudinal and vertical frequency response functions (FRFs) exhibit a predominant resonance peak around 1000 Hz, supporting the numerical prediction that consistency between the vertical and longitudinal modes determines corrugation growth. Furthermore, when compared with the FRFs of tracks without corrugation, the vertical resonance peak at 1000 Hz, which corresponds to the vertical pinned–pinned resonance mode, occurred at the corrugated and noncorrugated tracks. However, the longitudinal mode at 1000 Hz only appeared in tracks with corrugation. This indicates that the longitudinal vibration mode is decisive in corrugation formation.

5.8. Wheel Polygonal Wear

Wang et al. [85] conducted rolling–sliding wear tests using three wheel steels paired with two rail steels to explore the influence of the “wheel hardness (H_w)/rail hardness (H_r)” on wheel polygon wear initiation and evolution. The results showed that when paired with a softer rail, the wheel was less likely to become polygonal as H_w/H_r increased. When paired with a harder rail, polygonal initiation occurred earlier at a moderate H_w/H_r of 0.792. The largest H_w/H_r of 1.263 provided the best antipolygon condition for the wheel material. The wear mechanism for polygonal wheels was dominated by abrasive, fatigue, and oxidative wear at the crest and fatigue wear at the trough.

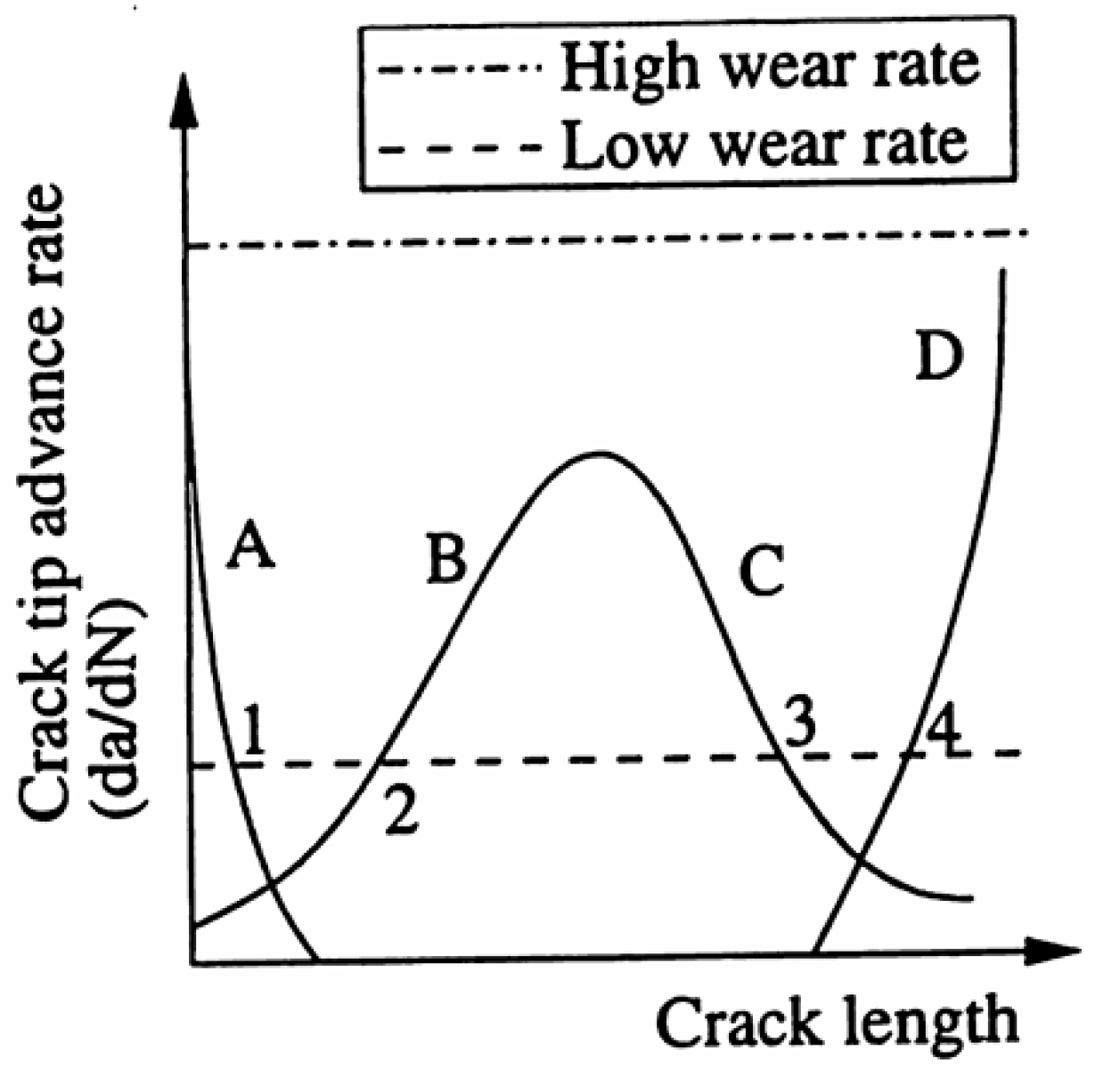
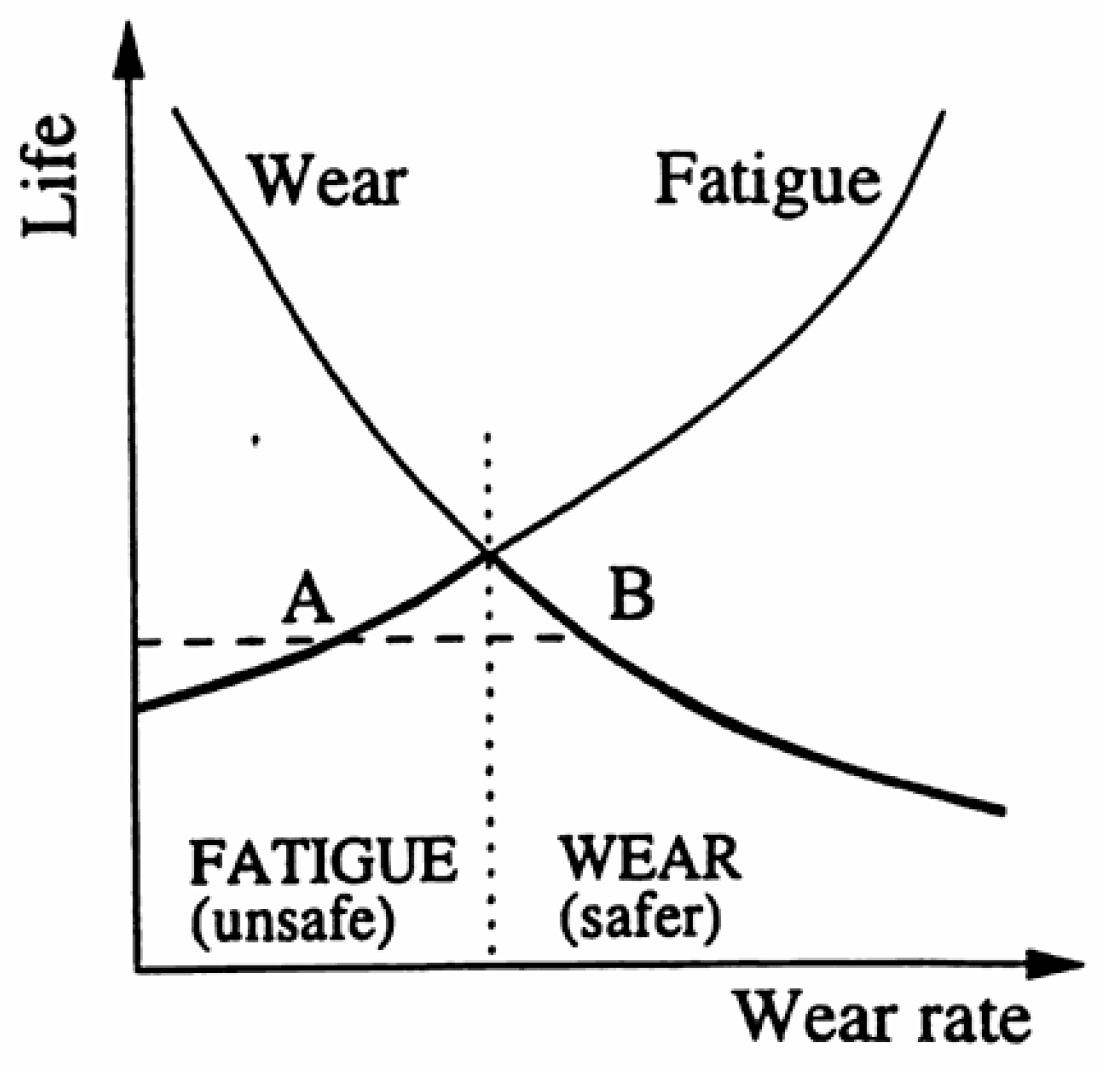
6. Competition Between RCF and Wear

6.1. Numerical Studies

The competition between RCF and wear in wheel/rail systems has been extensively elucidated in numerical studies. For instance, some studies evaluated crack growth using the Hobson rule or Paris law as well as wear using the Archard model, while others evaluated both crack growth and wear using the wear index.

A pioneering research on the competition between RCF crack growth and wear in a wheel/rail system was conducted by Franklin et al. [17,18,19], who developed a “brick model” based on incremental plasticity by ratcheting. In this model, the rail cross section is divided into various sections (or bricks). If the bricks reach their critical shear strain, they are considered to have failed and are marked as weak. Franklin et al. designed many patterns of weak and nonfailed healthy bricks as scenarios to represent failure mechanisms. These patterns helped to identify the scenarios in which bricks were removed from the rail surface as wear debris or remained within the rail as crack-like defects. Figure 18 shows a simple hexagonal representation of a standard grade rail microstructure, in which pearlite regions enclosed by proeutectoid ferrite at prior-austenite grain boundaries are treated as a single-phase material. (a) 63 μm/1 μm microstructure oriented at 10°. (b) Close-up of the 60 μm/4 μm microstructure with 1 μm × 1 μm elements.

Figure 19 shows the results of a simulation at 1800 MPa after 10,000 cycles. Figure 19a,b shows the results of simulations without and with shielding, respectively. Without shielding, greater scatter of failed elements can be observed in the proeutectoid ferrite and the relatively hard pearlite. This scatter reflects the variation in their material properties, which were sampled from a normal (Gaussian) distribution.

Burstow [86,87,88] developed a “whole life rail model” that considered the competition between RCF crack growth and wear in a rail. This model used a “damage function” that described the relationship between Tγ and the RCF crack initiation fatigue damage. The damage function comprised four regions: (i) a threshold below which RCF damage does not occur, (ii) a region where RCF damage increases linearly, (iii) a region where high wear suppresses crack growth, and (iv) a region where damaged material is entirely removed by wear.

Mazzù [89,90,91] proposed an integrated model that considers multiple interacting damage mechanisms in railway wheels. The procedure was based on models developed for wear, cyclic plasticity, and surface and subsurface fatigue cracks. These models were incorporated into an algorithm that exchanged input and output data between each failure model. Wear was assessed using the Archard model of adhesive wear. Cracks were evaluated using SIFs, threshold SIFs, and a Paris-type law.

Karttunen et al. [92,93] provided an engineering “meta-model” to predict gauge corner and flange root degradation concerning RCF and wear from measured rail, wheel, and track geometries. The impact of RCF is quantified using a dimensionless “fatigue index” (FI) [94] based on shakedown. Deterioration due to wear is quantified using Tγ.

Dirks and Enblom [95] introduced a model that could predict the wear and RCF of rails and wheels. Two existing RCF prediction models, namely the FI model and damage function model, were analyzed and compared in a parametric study. Wear was predicted using the Archard model.

Bevan et al. [1] developed a damage model to predict the deterioration rate of a wheel tread in terms of wear and RCF damage. This model used a description of a fleet’s route diagram to characterize the duty cycle of the vehicle. Several vehicle dynamics simulations were conducted using this duty cycle and a combination of the Archard and Tγ damage models to calculate the wheel and rail contact forces. Therefore, the formation of wear and RCF damage was predicted. Figure 20 shows the observed and predicted crack lengths on the motor and trailer axles of typical DMU and EMU vehicles.

Brouzoulis [96] presented a 2D FE model to simulate the growth of a single RCF crack in a rail. This model accounted for wear and allowed crack curving. The Archard wear model was used along with a Paris-type crack growth law to predict the amount of wear. The crack driving force was derived based on the concept of material forces.

Jun et al. [97] calculated the minimum crack size required for a crack to grow in a rail and defined it as the smallest crack that grows rapidly enough to avoid being removed by wear and periodic grinding. The Archard wear model and the “2.5D” fatigue crack growth model developed by Fletcher and Kapoor [98] were used for calculations.

Trummer et al. [99] developed a predictive model for RCF crack initiation at the surface of rails and wheels and referred to it as the “wedge model.” In this model, both surface RCF crack initiation and delamination wear were deemed to be governed by the growth of microscopic cracks in a severely shear-deformed layer near the rail surface.

Hiensch and Steenbergen [100] extended the concept of a “damage function” from a conventional rail to a premium pearlite rail by simulating the dynamic train–track interaction and using field observations. They derived the RCF damage index for the rails to describe the behavior of the associated “damage function.”

Akama and Kimata [21] developed a numerical simulation model to study the competition between RCF-initiated short crack growth and wear in a wheel tread. The simulation model assumed that the wheel materials were polycrystalline ferrite and pearlite and that RCF crack initiation was dependent on whether the total accumulated plastic shear strain reached the critical value. In the early crack growth simulations, Hobson’s two-stage short crack growth model was applied. The Archard model was used to determine wear mechanisms. One of the results is shown in Figure 21.

6.2. Experimental Studies

Recent studies focus on experimental investigations, elucidating the effects of hardness, microstructure, alloy, dry-to-wet time ratio, and corrosion on the RCF and wear of rails and wheels.

Hu et al. [101] investigated the wear and RCF in wheel–rail materials by varying H_w/H_r and creepages. The results revealed that with the H_w/H_r increasing from 0.927 to 1.218, the wheel wear rate considerably decreased, while the rail wear rate increased. When H_w/H_r = 1.218, the rail wear rate increased. Both the wheel and rail wear rates increased as the creepage enlarged. In addition, the fatigue damage of ER7 and CL60 wheel materials was dominated by slender multilayer cracks, whereas the fatigue cracks were short and contained abundant interlayer broken materials on the C-class wheel steel.

Zhang et al. [102] studied the wear and fatigue competition mechanism of a bainitic rail steel via RCF testing. Results showed that the damage process could be divided into initial (before 2.0 × 10⁵ cycles), middle (around 2.0 × 10⁵ cycles), and late (after 2.0 × 10⁵ cycles) stages, with wear, wear and fatigue, and fatigue as the dominant mechanisms in each stage, respectively.

Zani and Petrogalli [103] conducted experiments with a twin-disc machine to study the relationship between RCF and wear. First, they plotted the collected test data on shakedown maps to assess the cyclic response and calculate FI for predicting surface-initiated fatigue damage. They then correlated the FI and cyclic yield strength of the material with the experimental wear rate. They also developed maps to predict changes in wear rate and cyclic response under varying contact conditions, slip ratio, and extraction position of specimens. The estimated wear rate was superimposed onto the shakedown map to investigate a possible relationship between RCF and wear.

Wang et al. [104] explored the competition mechanism between wear and RCF in hypoeutectoid, eutectoid rail, and bainitic rail steels under different slip ratios. As the slip ratio increased, the wear rates of hypoeutectoid and eutectoid rail steels first increased and stabilized, whereas that of bainitic rail steels increased. Bainitic rail steels suffered catastrophic wear when the slip ratio exceeded 2%. The RCF crack growth rate of hypoeutectoid and eutectoid rail steels first increased rapidly and then slowly. The competitive relationship between wear and RCF was reflected by the variation in the rail wear form.

Zeng et al. [105] investigated the effect of vanadium microalloying on the RCF and wear behavior of railway wheel steels. Their findings demonstrated that microalloying enhances the RCF resistance of railway steels by simultaneously delaying crack initiation through increased yield strength and restricting crack growth by reducing plastic deformation capacity. Although microalloying enhances the matrix hardness of wheel steel, it diminishes its strain-hardening ability, which can compromise wear resistance. This study further identified the yield ratio—an indicator of plastic deformation capacity and strain-hardening ability—as a suitable parameter for characterization of the RCF and wear resistance of tested steels. The yield ratio was positively correlated with RCF resistance and negatively correlated with wear resistance.

Luo et al. [106] investigated the competitive relationship between wear and RCF in heavy-haul railway freight wheel steels. Wear and RCF tests were performed under dry friction and oil lubrication conditions on wheel steels with three different hardness levels: A# (329 HB), B# (341 HB), and C# (355 HB). The material used for wheel disks is commonly a medium carbon steel used for wheels in Chinese heavy-duty railway freight cars. Results indicated that wear-induced failure was the dominant mechanism in wear test, whereas RCF-related failure was the dominant mechanism in the RCF tests. A combined model comprising the Archard wear model and RCF model, as well as a competition coefficient, were proposed to describe the competition between wear and RCF. Figure 22a shows that in severely dry conditions, intense wear rapidly removes the initiated RCF cracks. Figure 22b shows that due to oil lubrication, the wear is restrained and the RCF cracks can grow further.

Tao et al. [107] conducted an on-site investigation on a metro line in China to observe the wheel tread condition and measure the wear patterns of rails and wheels. Based on the observation and measurement results collected from 23 trains, the relationship between wheel wear and RCF was analyzed. Results revealed that about 42% of wheels on this line experienced RCF in the central area of the wheel tread. Moreover, wheels with RCF generally showed groove wear, indicating wear is the main cause of RCF in the central area of the wheel tread on this line.

Wang et al. [108] conducted RCF and wear tests under dry–wet alternation conditions with varying dry–wet time ratios, contact stresses, and slip ratios. The results revealed that as the dry–wet duration ratio increased, crack propagation accelerated considerably owing to the oil wedge effect, while wear initially increased before decreasing, peaking when severe peeling occurred on the rail surface. Under RCF-dominant conditions, the rail experienced severe peeling and spalling, resulting in fatigue wear. However, under wear-dominant conditions, crack propagation was suppressed owing to the continuous removal of surface material and cracks.

Shen et al. [109] investigated the effect of microstructural changes on rolling contact damage behaviors using dry–wet contact wear tests. Compared with the pearlitic microstructure, the mixed martensite–bainite microstructure of rail steel effectively mitigates rolling contact damage and resists plastic deformation. The plastic deformation zone caused by rolling contact presented a hardening layer that effectively hindered crack propagation to increased depths. Fatigue cracking without matrix spalling was identified as the primary wear behavior on the wear surface of rail steel with high martensite content, and its crack length was reduced by 30.8% compared with the pearlitic microstructure.

He et al. [110] investigated the wear and damage behavior of wheel and rail materials under different corrosion conditions in advance using rolling friction and wear tests. The results indicated that the friction coefficient and wear rate of the precorroded wheel and rail samples were greater than those of the uncorroded samples. Surface damage to the uncorroded samples was mainly abrasive wear accompanied by surface cracks. However, precorrosion produced larger furrows and spurred wear by destroying the surface integrity of wheel and rail materials, creating a relatively loose corrosion layer. The size and depth of spalling pits on the surface of these samples after wear were larger and deeper, and the degree of surface damage was greater than that of the uncorroded samples.

7. Future Work

In this section, current gaps or problems in the studies on RCF and wear of rails and wheels are identified and recommendations for future work will be provided.

7.1. Details of Crack Initiation and MSC Growth

To obtain an accurate lifespan for RCF crack initiation, physical processes such as slip band formation and dislocation movement are required to be considered. Regarding short crack growth, most studies do not consider stage I growth, in which the microstructure affects crack growth. Crack growth and wear mainly compete with each other in the stages of crack initiation and early growth, as shown by curves A and B in Figure 1. Therefore, the details of crack initiation and MSC growth must be considered. Urashima and Nishida [111] studied the fatigue crack initiation and growth behavior of rail steels using SEM observations. They observed that slip occurred parallel to the lamella of the pearlite colony and that fatigue cracks were initiated in the very early stage of fatigue. Moreover, they observed that cracks preferentially grew along the lamella and deflected slightly when they reached the boundary of the pearlite block. Such observations should be extensively performed and incorporated into the MSC model. As the directions of the slip band and the lamella are random, it may be better to introduce statistical methods.

7.2. Three-Dimensional Analysis of Short Cracks

Cracks and microstructure are usually studied by taking cross-sections, and the real 3D nature is inferred or approximated from the 2D view. To properly model the early stages of crack growth, the whole crack in 3D is required to be considered. Bomidi et al. [112,113] developed a 3D FE model to study subsurface-initiated spalling observed in bearings. The microstructure topology was represented by randomly generated Voronoi tessellations. The elastic–plastic model coupled with continuum damage mechanics was used to predict ratcheting behavior and fatigue damage in heavily loaded contacts. Franklin et al. [114] used a 3D model of microstructure for rail steel based on convex polyhedra, generated using the Voronoi method, to model the early stages of crack growth. However, this was the first step for representing 3D structures, and a model for 3D short crack growth has yet to be developed.

7.3. Modeling for Fatigue Wear

Chawanat and Akama [31] performed twin-disc tests that combined wheel and rail discs. The wheel disc was the high-speed side and included WEL. Therefore, the initial wear amount of the rail disc was greater when the slip ratio (S_r) was 9% than when the S_r was 1%. However, when S_r was 1%, the rail disc’s wear amount increased rapidly in the subsequent cycle and became greater when S_r was 9%. This is owing to fatigue wear, wherein the wear caused by adhesive wear on the rail disc was minimal, leading to the accumulation of fatigue. This results in crack initiation, growth, and branching, ultimately causing delamination. Fatigue wear modeling of rails and wheels has hardly been done. Wang and Kato [115] proposed a model to predict fatigue wear lifespan using a simplified theoretical expression that combines the Manson–Coffin equation and the analytical solution of an elastic-perfectly plastic model. Although it is a different field of research, this may be considered a clue.

7.4. Complex Shape of Horizontal Crack Growth

Deng et al. [116] performed a 5-year continuous field monitoring study on squats induced by corrugations. A small black depression formed at the corrugation under wheel-rail dynamic forces, and then, a primary crack typically initiated on the gauge side edge of the depression. The crack then grew in a U-shape on the rail surface toward the gauge side in the traffic and opposite-traffic directions as well as into the rail toward the field side at an angle of approximately 20°. Initially, the black squat depression was elliptical in shape; then, its edge followed the U-shaped cracking path as it grew. The squats turned into a kidney-like shape, typically with a U-shaped crack. As the squats grew further, a ridge formed in the middle part of the depression and an I-shaped crack appeared at this ridge owing to the impact of the wheels. This process eventually led to two lung-shaped mature squats, typically with a Y-shaped crack. Previous numerical studies have assumed that the shape of the growing horizontal crack remains semielliptical even in 3D analyses. However, the growth shape is complex, as aforementioned, so numerical analysis must consider this.

7.5. Effects of Rolling Reversal of Wheel

Trains often operate as a shuttle service. When a train arrives at the terminal station, its direction of travel is reversed, and so is the rolling direction of the wheels. The investigation of how the crack growth and wear on the wheel tread are changed by reversing the rolling direction is important. Tyfour and Beynon [117] performed the unlubricated twin-disc tests using the wheel and rail steel and indicated that direction reversals can decrease the wear rate. The largest decrease in rail wear rate occurred with frequent reversals. They also investigated the influences of reversing direction on RCF initiation and growth of rail discs with water lubrication [118]. They noted that reversing the rolling direction increased RCF life. Akama and Takahashi [119] conducted a series of wear and fatigue tests using a twin-disc machine, supported by FE simulations. They elucidated how reversing the wheel’s rolling direction affects wear and RCF cracks on the wheel tread. In wet conditions, the wear rate increased when the rolling direction of the wheel disc was reversed in some cases. By contrast, in dry conditions, the wear rate was much higher than in wet conditions; however, it changed little before and after the reversal. The Archard model could not explain the increase in wear rate after the reversal in wet conditions because the model does not consider the delamination wear induced by the fluid. Further research is needed on this issue.

7.6. Utilization of Advanced Technology

Recently, big data analysis and artificial intelligence have rapidly advanced. Jamshidi et al. [120] assessed rail failure risks by analyzing a type of squat that was automatically detected from extensive video camera records. Vernaillen et al. [121] analyzed rail wear across the entire Belgian railway network using big data techniques. Brkić et al. [122] modeled the reliability and availability analysis using the Markov model for railway data transmission systems. These studies demonstrate that advanced technologies should be incorporated into the reliability and safety analysis for RCF and wear of rails and wheels.

8. Conclusions

This study presented a comprehensive literature review on RCF and wear of rails and wheels. The following conclusions can be obtained:

(1)

RCF and wear of actual rails and wheels were discussed. Primary RCF defects include squats, head checks, studs, indentation, and Belgrospi. The main wheel RCF defects include spalling, shelling, heavy shelling, and flat shelling. Substantial rail wear includes side wear and corrugation, whereas wheel wear includes hollow and grooving wear, flange vertical wear, and wheel polygonal wear. Each was briefly explained.

(2)

Theory and models for RCF cracks were presented, ranging from crack initiation to short crack growth, coplanar crack growth, branching, and branch crack growth. Regarding initiation, different models were described based on elastic shakedown, plastic shakedown, and ratcheting material response. During the growth of short cracks, a two-stage growth model comprising MSC and PSC was explained. For long coplanar crack growth, the influence of fluid penetrating into the crack was notable, and three primary models were described. Crack growth laws were formulated using a mixed mode combining Modes I and II, with some incorporating Mode III. For branch angle, the models based on the theories of maximum shear stress and maximum tangential stress criteria, as well as the model based on the maximum growth rate criterion, were explained. For branch crack growth, relevant factors were listed, and the Paris-type growth law employed was described.

(3)

Wear mechanisms that must be considered, such as adhesive, abrasive, fatigue, corrosive, and delamination wear, were briefly explained. In addition to the conventional wear regimes of mild and severe, the catastrophic wear regime observed in twin-disc tests was explained. Owing to the difficulty in determining the wear coefficient, a methodology for accurately, consistently, and efficiently determining it was introduced. A wear coefficient map was presented to illustrate the effects of various parameters, such as contact pressure and slip, on wear rates. Three representative wear functions—BRR, KTH, and USFD—were explained with their original definitions. Examples of research on corrugation wear and wheel polygonal wear are also presented.

(4)

The competition between RCF and wear in rails and wheels has become an important topic in recent research. Several studies addressing this competition were discussed, which were divided into numerical and experimental studies. In numerical studies, some evaluated RCF crack growth using the Hobson rule or Paris law and wear using the Archard model, whereas others assessed crack growth and wear using the wear index. By contrast, experimental studies have elucidated the effects of hardness, microstructure, alloy, dry–wet time ratio, and corrosion on RCF and wear.

(5)

Finally, current gaps or limitations in studies on RCF and wear of rails and wheels were identified, and recommendations for future work were provided. These include: details of crack initiation and MSC growth, 3D analysis of short cracks, modeling of fatigue wear, complex horizontal crack growth shapes, effects of wheel rolling reversal, and utilization of advanced technologies, such as big data analysis, artificial intelligence, and Markov model-based data communication systems.

In the future, this review can assist researchers seeking to investigate and address the problems associated with RCF and wear of rails and wheels.