A Crack Defect Detection and Segmentation Method That Incorporates Attention Mechanism and Dimensional Decoupling
Abstract
1. Introduction
2. Related Work
3. Construction of the Network Model
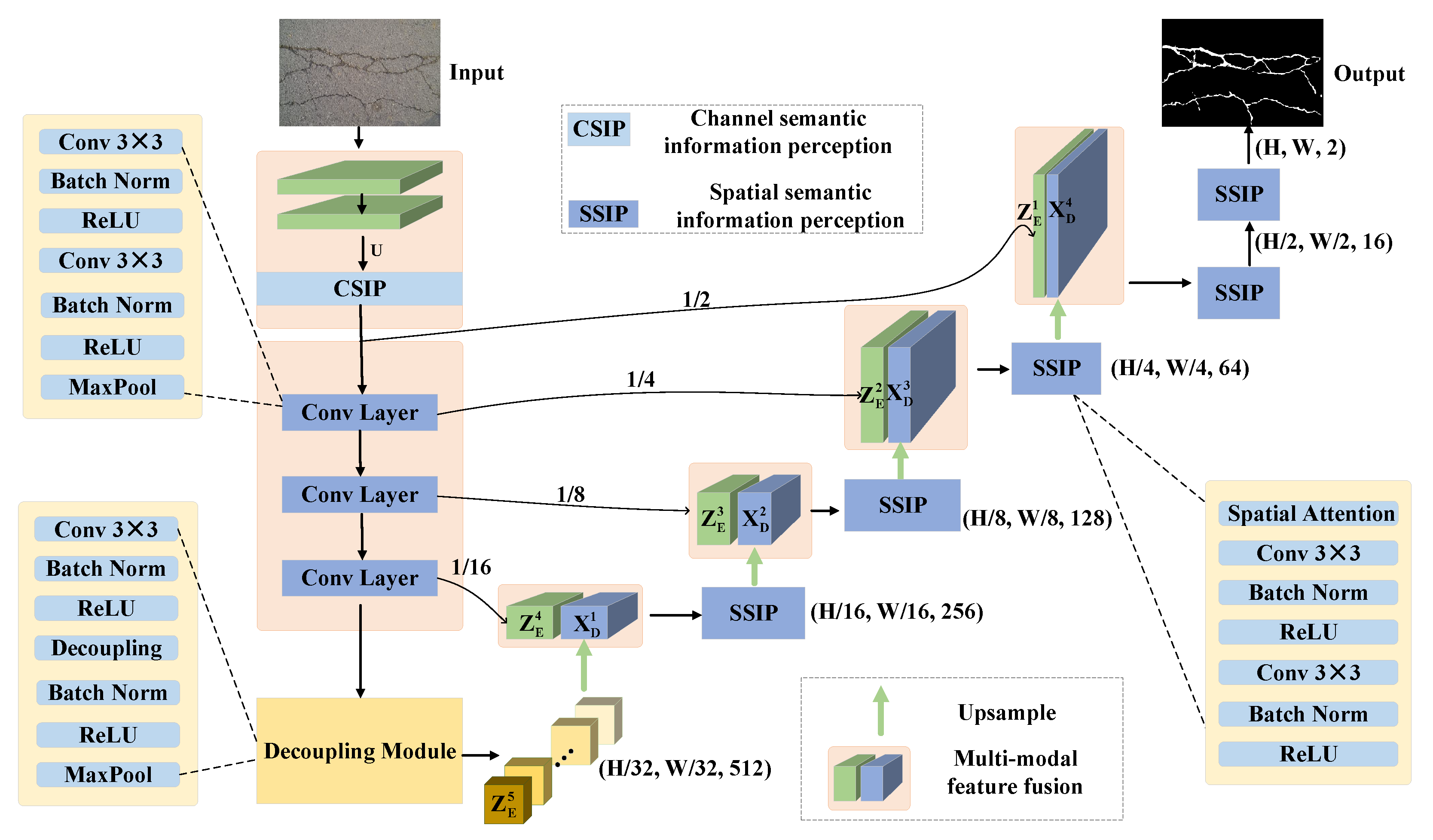
3.1. Network Model Structure
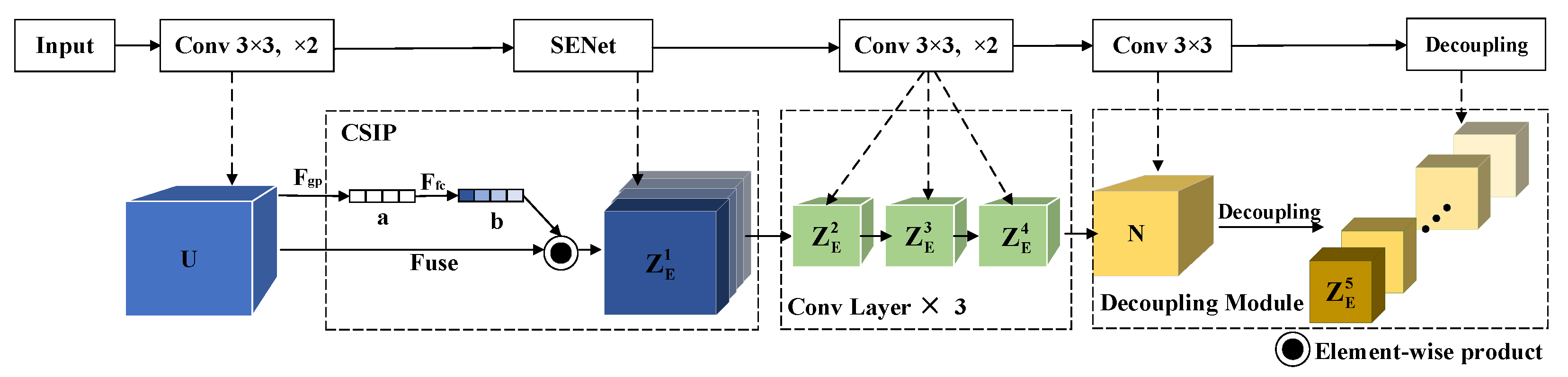
3.2. Encoder
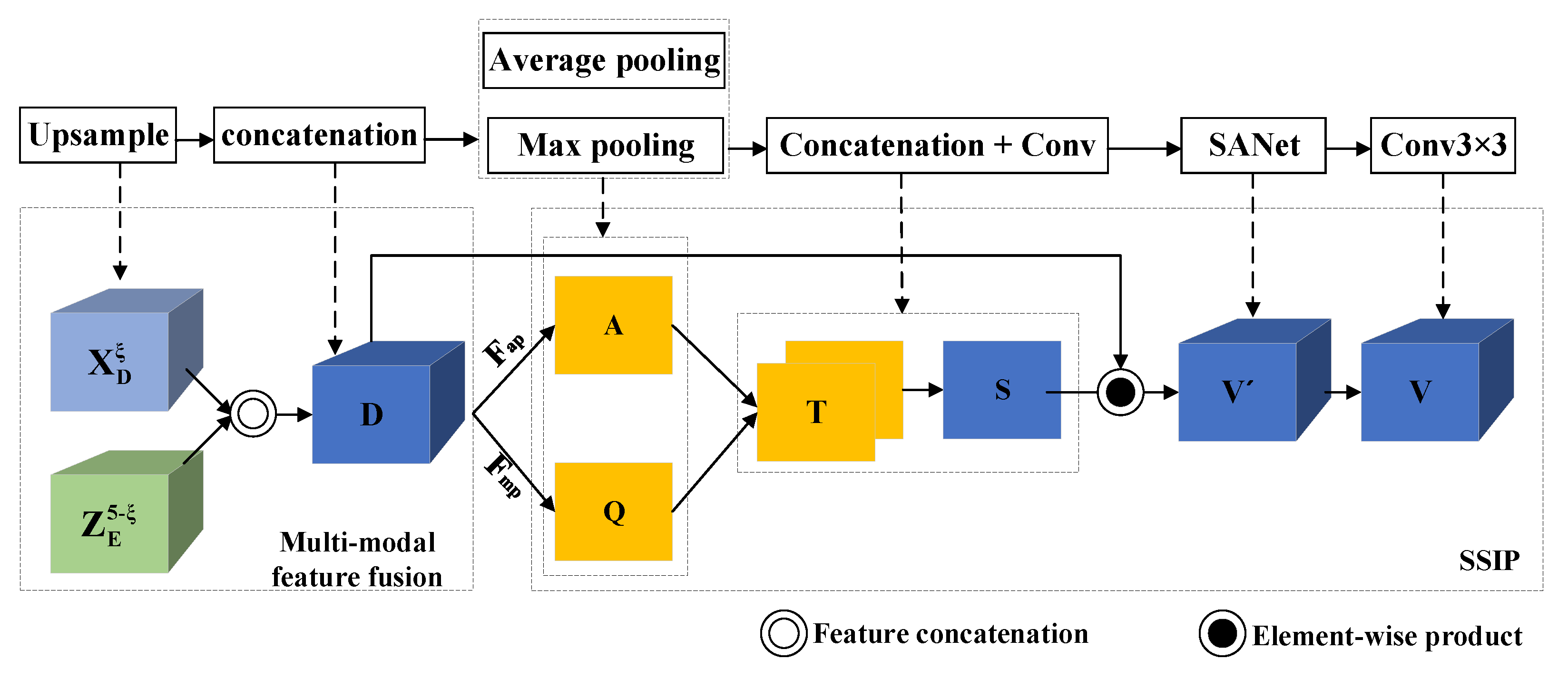
3.3. Decoder
3.4. Loss Function
4. Experiments
4.1. Experimental Environment
4.2. Datasets
4.2.1. Concrete Crack Images for Classification
- The crack samples in different backgrounds, including dry, wet, and crack samples with different textures.
- A sample with multiple cracks.
- Starting from the surface finish, select proofs with complex interference such as the large-area noise.
- Samples of cracks with different thicknesses.
- A sample where the edge of the crack is indistinguishable from the background.
4.2.2. DeepCrack
4.3. Evaluation Indicators
4.4. Classification Experiment
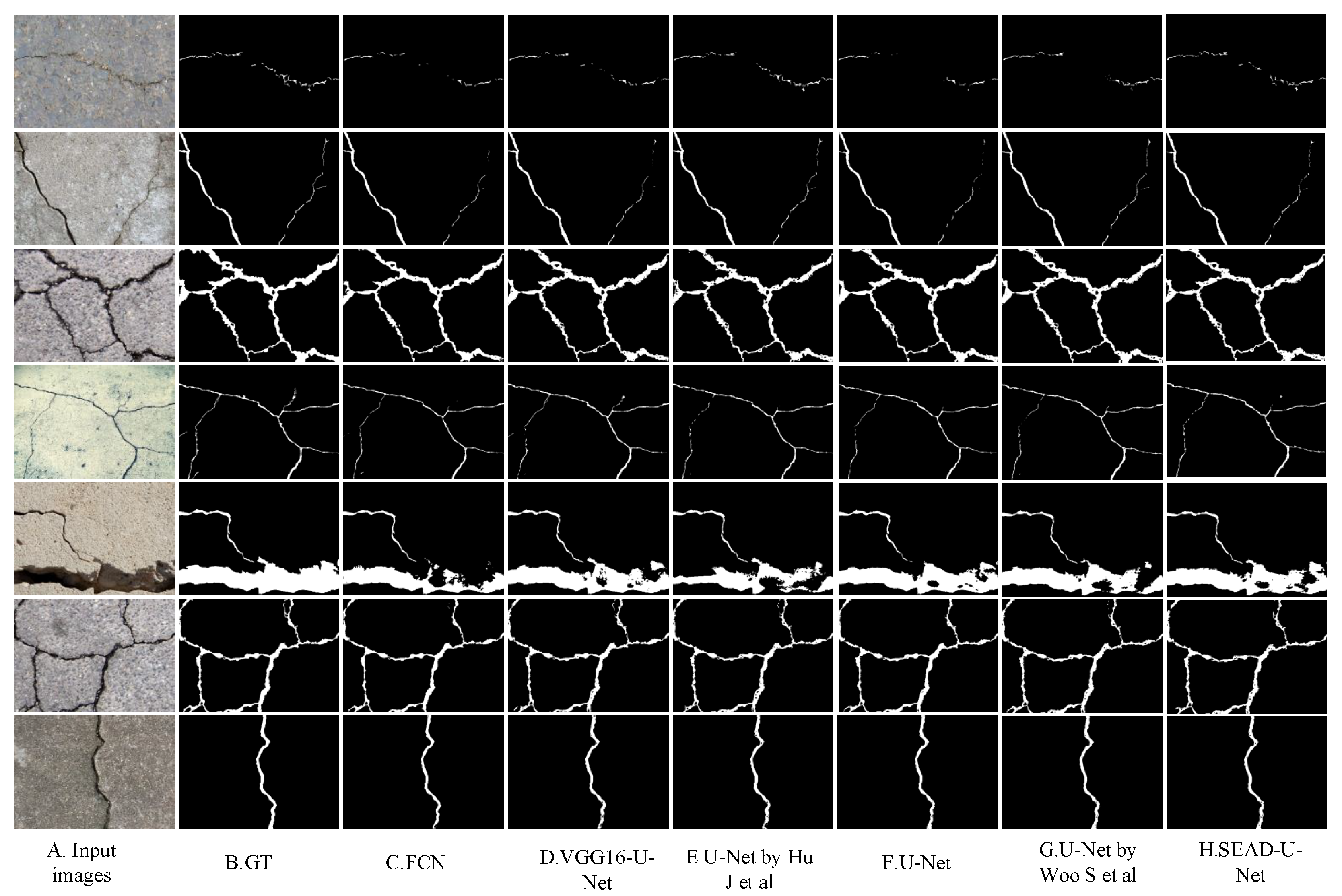
4.5. Segmentation Experiment
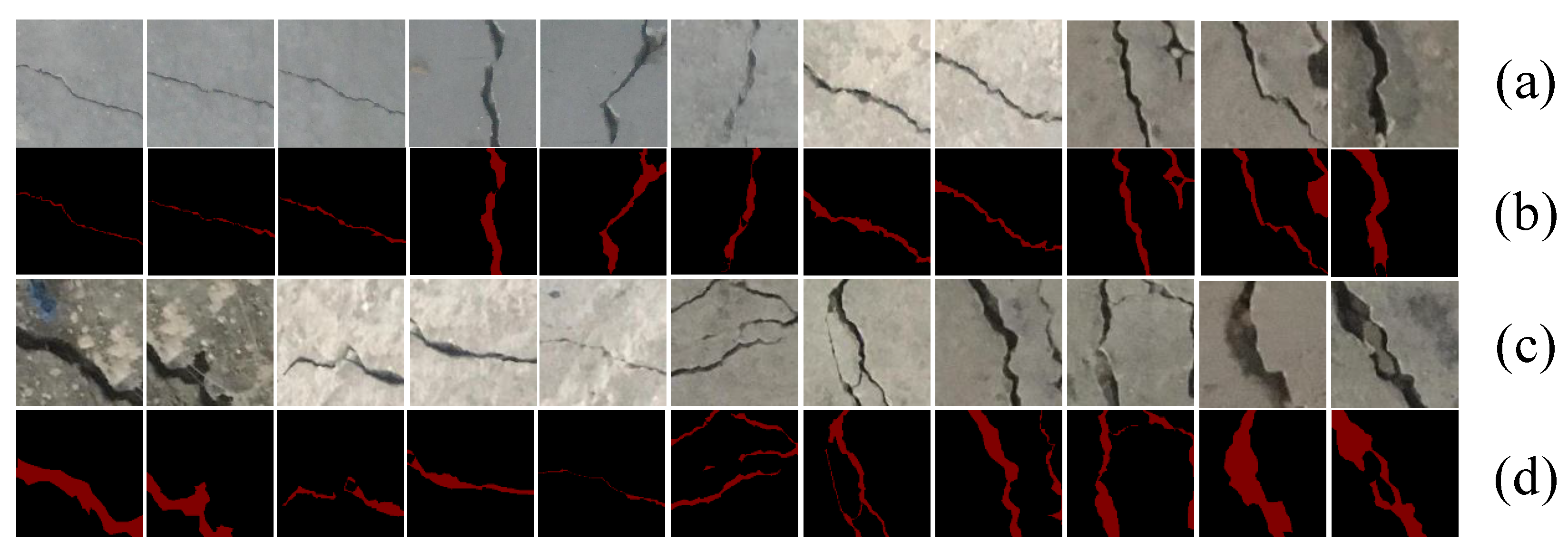
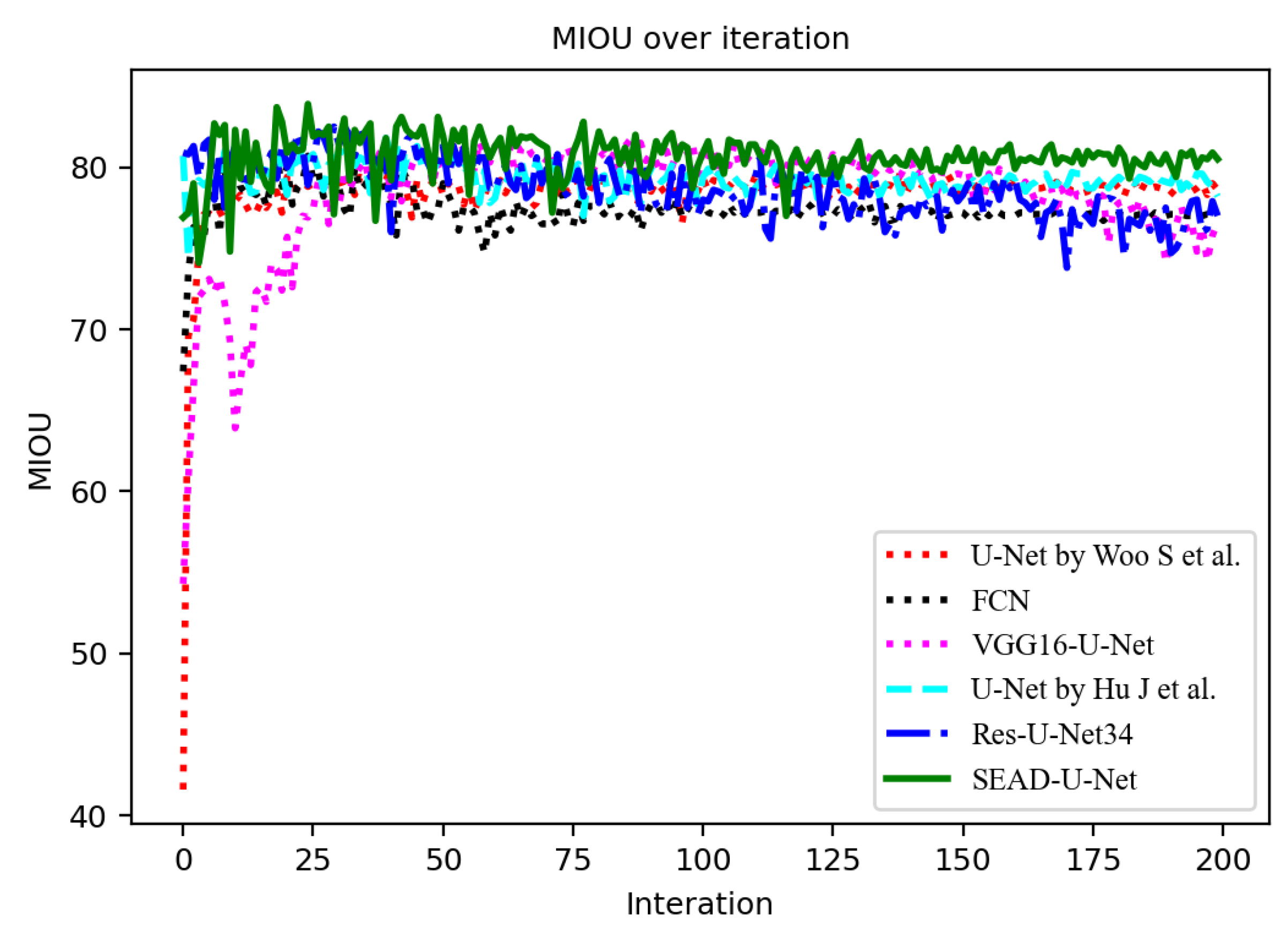
4.5.1. CCIC Dataset Experiment
4.5.2. DeepCrack Dataset Experiment
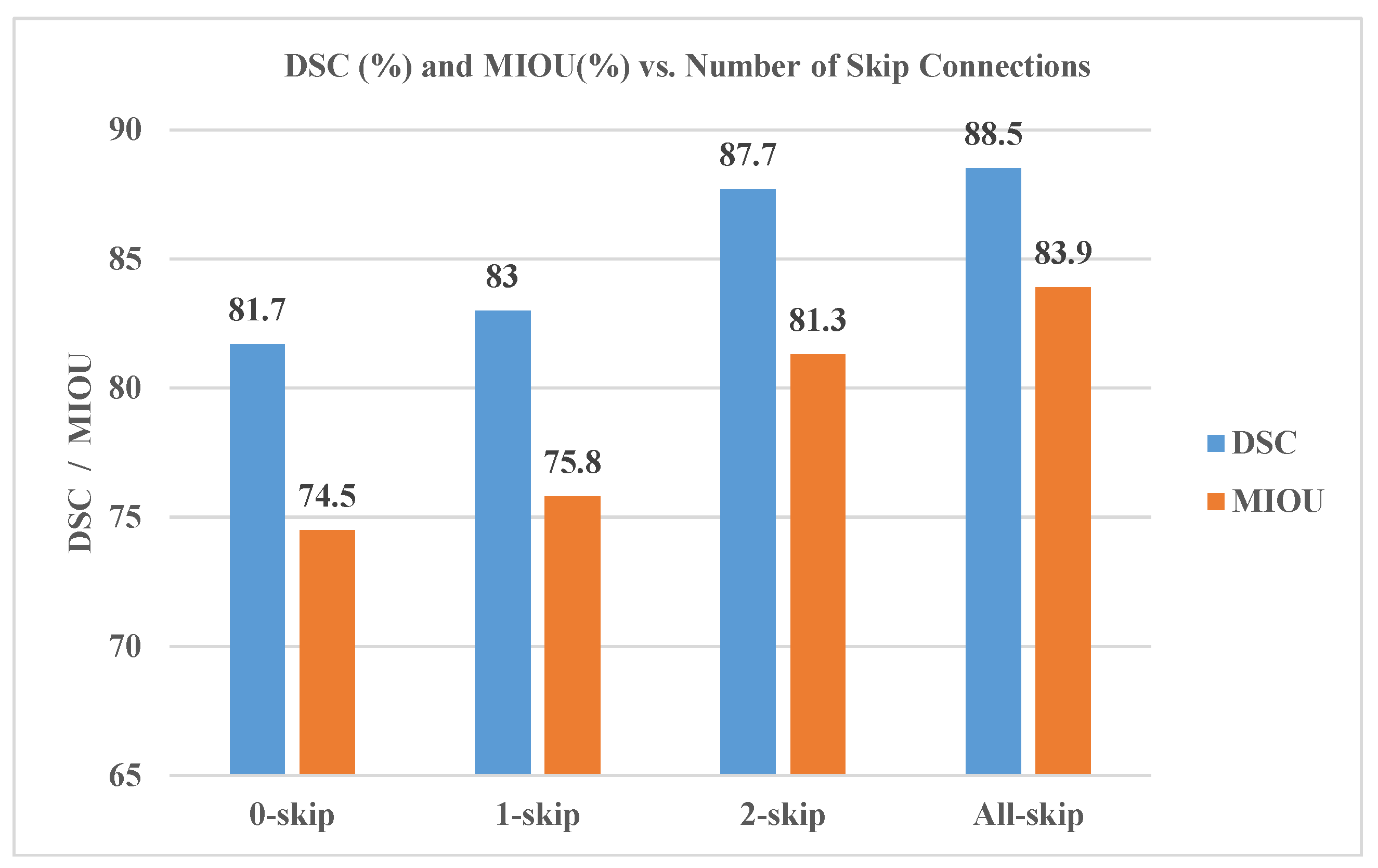
4.5.3. Ablation Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kapela, R.; Śniatała, P.; Turkot, A.; Rybarczyk, A.; Pożarycki, A.; Rydzewski, P.; Wyczałek, M.; Błoch, A. Asphalt surfaced pavement cracks detection based on histograms of oriented gradients. In Proceedings of the 2015 22nd International Conference Mixed Design of Integrated Circuits & Systems (MIXDES), Torun, Poland, 25–27 June 2015; pp. 579–584. [Google Scholar] [CrossRef]
- Ji, W.; Yu, S.; Wu, J.; Ma, K.; Bian, C.; Bi, Q.; Li, J.; Liu, H.; Cheng, L.; Zheng, Y. Learning Calibrated Medical Image Segmentation via Multi-rater Agreement Modeling. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 12336–12346. [Google Scholar] [CrossRef]
- Lu, G.; Duan, S. Deep Learning: New Engine for the Study of Material Microstructures and Physical Properties. IEEE Trans. Intell. Transp. Syst. 2019, 9, 263–276. [Google Scholar] [CrossRef]
- Silva, W.R.L.d.; Lucena, D.S.d. Concrete Cracks Detection Based on Deep Learning Image Classification. Proceedings 2018, 2, 489. [Google Scholar] [CrossRef]
- Tang, J.; Mao, Y.; Wang, J.; Wang, L. Multi-task Enhanced Dam Crack Image Detection Based on Faster R-CNN. In Proceedings of the 2019 IEEE 4th International Conference on Image, Vision and Computing (ICIVC), Xiamen, China, 5–7 July 2019; pp. 336–340. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef]
- David Jenkins, M.; Carr, T.A.; Iglesias, M.I.; Buggy, T.; Morison, G. A Deep Convolutional Neural Network for Semantic Pixel-Wise Segmentation of Road and Pavement Surface Cracks. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Roma, Italy, 3–7 September 2018; pp. 2120–2124. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Lau, S.L.H.; Chong, E.K.P.; Yang, X.; Wang, X. Automated Pavement Crack Segmentation Using U-Net-Based Convolutional Neural Network. IEEE Access 2020, 8, 114892–114899. [Google Scholar] [CrossRef]
- Choi, W.; Cha, Y.J. SDDNet: Real-Time Crack Segmentation. IEEE Trans. Ind. Electron. 2020, 67, 8016–8025. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Hu, X.; Yang, J. Selective Kernel Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 510–519. [Google Scholar] [CrossRef]
- Qin, Z.; Zhang, Z.; Chen, X.; Wang, C.; Peng, Y. Fd-Mobilenet: Improved Mobilenet with a Fast Downsampling Strategy. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 1363–1367. [Google Scholar] [CrossRef]
- Rabano, S.L.; Cabatuan, M.K.; Sybingco, E.; Dadios, E.P.; Calilung, E.J. Common Garbage Classification Using MobileNet. In Proceedings of the 2018 IEEE 10th International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment and Management (HNICEM), Baguio City, Philippines, 29 November–2 December 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Prasanna, P.; Dana, K.J.; Gucunski, N.; Basily, B.B.; La, H.M.; Lim, R.S.; Parvardeh, H. Automated Crack Detection on Concrete Bridges. IEEE Trans. Autom. Sci. Eng. 2016, 13, 591–599. [Google Scholar] [CrossRef]
- Shi, Y.; Cui, L.; Qi, Z.; Meng, F.; Chen, Z. Automatic Road Crack Detection Using Random Structured Forests. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3434–3445. [Google Scholar] [CrossRef]
- Amhaz, R.; Chambon, S.; Idier, J.; Baltazart, V. Automatic Crack Detection on Two-Dimensional Pavement Images: An Algorithm Based on Minimal Path Selection. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2718–2729. [Google Scholar] [CrossRef]
- Cord, A.; Chambon, S. Automatic road defect detection by textural pattern recognition based on AdaBoost. Comput.-Aided Civ. Infrastruct. Eng. 2012, 27, 244–259. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, F.; Daniel Zhang, Y.; Zhu, Y.J. Road crack detection using deep convolutional neural network. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 3708–3712. [Google Scholar] [CrossRef]
- Fang, F.; Li, L.; Gu, Y.; Zhu, H.; Lim, J.H. A novel hybrid approach for crack detection. Pattern Recognit. 2020, 107, 107474. [Google Scholar] [CrossRef]
- Fan, R.; Bocus, M.J.; Zhu, Y.; Jiao, J.; Wang, L.; Ma, F.; Cheng, S.; Liu, M. Road Crack Detection Using Deep Convolutional Neural Network and Adaptive Thresholding. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 474–479. [Google Scholar] [CrossRef]
- Protopapadakis, E.; Voulodimos, A.; Doulamis, A.; Doulamis, N.; Stathaki, T. Automatic crack detection for tunnel inspection using deep learning and heuristic image post-processing. Appl. Intell. 2019, 49, 2793–2806. [Google Scholar] [CrossRef]
- Zou, L.; Liu, Y.; Huang, J. Crack Detection and Classification of a Simulated Beam Using Deep Neural Network. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 7112–7117. [Google Scholar] [CrossRef]
- Kim, H.; Ahn, E.; Shin, M.; Sim, S.H. Crack and noncrack classification from concrete surface images using machine learning. Struct. Health Monit. 2019, 18, 725–738. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Zhang, L.; Yu, S.; Prokhorov, D.; Mei, X.; Ling, H. Feature Pyramid and Hierarchical Boosting Network for Pavement Crack Detection. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1525–1535. [Google Scholar] [CrossRef]
- Cui, X.; Wang, Q.; Dai, J.; Xue, Y.; Duan, Y. Intelligent crack detection based on attention mechanism in convolution neural network. Adv. Struct. Eng. 2021, 24, 1859–1868. [Google Scholar] [CrossRef]
- Ren, Y.; Huang, J.; Hong, Z.; Lu, W.; Yin, J.; Zou, L.; Shen, X. Image-based concrete crack detection in tunnels using deep fully convolutional networks. Constr. Build. Mater. 2020, 234, 117367. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Özgenel, Ç.F.; Sorguç, A.G. Performance comparison of pretrained convolutional neural networks on crack detection in buildings. In Proceedings of the International Symposium on Automation and Robotics in Construction, Berlin, Germany, 20–25 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Fu, H.; Meng, D.; Li, W.; Wang, Y. Bridge Crack Semantic Segmentation Based on Improved Deeplabv3+. J. Mar. Sci. Eng. 2021, 9, 671. [Google Scholar] [CrossRef]




| Method | Precision | Recall | |
|---|---|---|---|
| SVM | 0.8112 | 0.6734 | 0.7359 |
| Boosting | 0.7360 | 0.7587 | 0.7472 |
| CNN by Zhang L et al. [21] | 0.8696 | 0.9251 | 0.8965 |
| CNN by Fan R et al. [23] | 0.9967 | 0.9046 | 0.9484 |
| Our method | 0.9953 | 0.9993 | 0.9973 |
| Method | P | R | MIOU | #Params | Time/Image (s) | |
|---|---|---|---|---|---|---|
| ResU-Net34 [16] | 0.880 | 0.929 | 0.904 | 0.825 | 33.9M | 0.042 |
| U-Net by Woo S et al. [15] | 0.879 | 0.899 | 0.889 | 0.800 | 17.2M | 0.043 |
| U-Net by Hu J et al. [11] | 0.895 | 0.904 | 0.900 | 0.818 | 17.2M | 0.041 |
| VGG16-U-Net | 0.888 | 0.911 | 0.899 | 0.817 | 28.1M | 0.046 |
| FCN [6] | 0.898 | 0.889 | 0.893 | 0.807 | 23.9M | 0.052 |
| SEAD-U-Net | 0.919 |
| Method | P | R | MIOU | #Params | Time/Image (s) | |
|---|---|---|---|---|---|---|
| FCN [6] | 0.845 | 0.835 | 0.840 | 0.854 | 23.9M | 0.097 |
| U-Net [8] | 0.834 | 0.862 | 0.848 | 0.861 | 17.2M | 0.065 |
| VGG16-U-Net | 0.823 | 0.846 | 0.835 | 0.851 | 28.1M | 0.086 |
| U-Net by Woo S et al. [15] | 0.849 | 0.819 | 0.834 | 0.849 | 17.2M | 0.070 |
| U-Net by Hu J et al. [11] | 0.805 | 0.865 | 0.834 | 0.850 | 17.2M | 0.065 |
| SEAD-U-Net |
| Skip-Connection | P | R | MIOU | |
|---|---|---|---|---|
| 0-skip | 0.867 | 0.842 | 0.854 | 0.745 |
| 1-skip | 0.869 | 0.856 | 0.862 | 0.758 |
| 2-skip | 0.926 | 0.870 | 0.897 | 0.813 |
| All-skip | 0.906 |
| Method | P | R | MIOU | |
|---|---|---|---|---|
| DE + SE + SA | 0.859 | 0.839 | 0.849 | 0.862 |
| SE + SA | 0.865 | 0.833 | 0.849 | 0.862 |
| DE + SE | 0.854 | 0.822 | 0.837 | 0.852 |
| DE + SA | 0.827 | 0.843 | 0.835 | 0.851 |
| SEAD-U-Net | 0.851 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Liu, W.; Li, Y.; Wang, H.; Cao, S.; Zhou, C. A Crack Defect Detection and Segmentation Method That Incorporates Attention Mechanism and Dimensional Decoupling. Machines 2023, 11, 169. https://doi.org/10.3390/machines11020169
He L, Liu W, Li Y, Wang H, Cao S, Zhou C. A Crack Defect Detection and Segmentation Method That Incorporates Attention Mechanism and Dimensional Decoupling. Machines. 2023; 11(2):169. https://doi.org/10.3390/machines11020169
Chicago/Turabian StyleHe, Lixin, Wangwei Liu, Yiming Li, Handong Wang, Shenjie Cao, and Chengying Zhou. 2023. "A Crack Defect Detection and Segmentation Method That Incorporates Attention Mechanism and Dimensional Decoupling" Machines 11, no. 2: 169. https://doi.org/10.3390/machines11020169
APA StyleHe, L., Liu, W., Li, Y., Wang, H., Cao, S., & Zhou, C. (2023). A Crack Defect Detection and Segmentation Method That Incorporates Attention Mechanism and Dimensional Decoupling. Machines, 11(2), 169. https://doi.org/10.3390/machines11020169






