A Novel Investigation of Non-Periodic Snap BVP in the $\mathbb{G}$-Caputo Sense

Abstract

In the present paper, we consider a nonlinear fractional snap model with respect to a $\mathbb{G}$-Caputo derivative and subject to non-periodic boundary conditions. Some qualitative analysis of the solution, such as existence and uniqueness, are investigated in view of fixed-point theorems. Moreover, the stabilities of Ulam–Hyers and Ulam–Hyers–Rassias criterions are considered and investigated. Some numerical simulations were performed using MATLAB for understanding the theoretical results. All results in this work play an important role in understanding ocean engineering phenomena due to the huge applicability of jerk and snap in seakeeping, ride comfort, and shock response spectrum.

1. Introduction

The second derivative of the accelaration (fourth derivative of position) is a physical quantity called a snap or jounce, which can be modeled as:

$$\left\{\begin{array}{c}{\displaystyle \frac{{\mathrm{dv}}_1}{\mathsf{ὶ}}}={\mathrm{v}}_2\left(\mathsf{ὶ}\right),\hfill \\ {\displaystyle \frac{{\mathrm{dv}}_2}{\mathrm{d}\mathsf{ὶ}}}={\mathrm{v}}_3\left(\mathsf{ὶ}\right),\hfill \\ {\displaystyle \frac{{\mathrm{dv}}_3}{\mathrm{d}\mathsf{ὶ}}}={\mathrm{v}}_4\left(\mathsf{ὶ}\right),\hfill \\ {\displaystyle \frac{{\mathrm{dv}}_4}{\mathrm{d}\mathsf{ὶ}}}=\mathfrak{T}({\mathrm{v}}_1,{\mathrm{v}}_2,{\mathrm{v}}_3,{\mathrm{v}}_4).\hfill \end{array}\right.$$

(1)

It is obvious that the model (1) can be reduced to the following equation:

$${\displaystyle \frac{{\mathrm{d}}^4{\mathrm{v}}_1}{\mathrm{d}{\mathsf{ὶ}}^4}}=\mathfrak{T}\left({\mathrm{v}}_1,{\displaystyle \frac{{\mathrm{dv}}_1}{\mathrm{d}\mathsf{ὶ}}},{\displaystyle \frac{{\mathrm{d}}^2{\mathrm{v}}_1}{\mathrm{d}{\mathsf{ὶ}}^2}},{\displaystyle \frac{{\mathrm{d}}^3{\mathrm{v}}_1}{\mathrm{d}{\mathsf{ὶ}}^3}}\right).$$

(2)

In fact, the terms jerk and snap are exceptionally rare for most individuals, counting physicists and engineers. Scientists jerk and snap are the third and fourth derivatives of our position with regard to time, respectively. Equation (1) contains a 4th-order derivative of the variable ${\mathrm{v}}_1$, and it describes a 4th-order dynamical vibration model. The corresponding fractional model is achieved by using the fractional derivative (of order less than or equal 1) instead of the standard derivative $\frac{\mathrm{d}}{\mathrm{d}\mathsf{ὶ}}$. Many types of fractional derivatives can be used here, such as the Riemann–Liouville, Caputo and Hadamard. We prefer to use the generalized fractional derivative with respect to differentiable increasing function $\mathbb{G}$. Gottlie in [1] applied the method of harmonic balance to non-linear jerk equations, which involves the third order time-derivative. In 2017, Elsonbaty et al., by applying the contraction principle, investigated the following jerk system:

$$\left\{\begin{array}{c}{\displaystyle \frac{{\mathrm{dv}}_1}{\mathrm{d}\mathsf{ὶ}}}={\mathrm{v}}_2\left(\mathsf{ὶ}\right),{\displaystyle \frac{{\mathrm{dv}}_2}{\mathrm{d}\mathsf{ὶ}}}={\mathrm{v}}_3\left(\mathsf{ὶ}\right),\hfill \\ {\displaystyle \frac{{\mathrm{dv}}_3}{\mathrm{d}\mathsf{ὶ}}}=\lambda {\mathrm{v}}_1\left(\mathsf{ὶ}\right)-\beta {\mathrm{v}}_2\left(\mathsf{ὶ}\right)-{\mathrm{v}}_3\left(\mathsf{ὶ}\right)-{\mathrm{v}}_1^3\left(\mathsf{ὶ}\right),\hfill \end{array}\right.$$

in which derivatives are with respect to time, and $\lambda$ and $\beta$ denote positive parameters with $\beta \in \mathbb{R}$ [2]. In 2018, Rahman et al. [3] with the help of the modified harmonic balance method, obtained a second approximate solution for a simple nonlinear 3rd-order jerk initial problem formulated as

$$\left\{\begin{array}{c}{\displaystyle \frac{{\mathrm{d}}^3{\mathrm{v}}_1}{\mathrm{d}{\mathsf{ὶ}}^3}}+\mathcal{T}\left({\mathrm{v}}_1,{\displaystyle \frac{{\mathrm{dv}}_1}{\mathrm{d}\mathsf{ὶ}}},{\displaystyle \frac{{\mathrm{d}}^2{\mathrm{v}}_1}{\mathrm{d}{\mathsf{ὶ}}^2}}\right)=0,\hfill \\ {\mathrm{v}}_1\left(0\right)=0,{\displaystyle \frac{{\mathrm{dv}}_1}{\mathrm{d}\mathsf{ὶ}}}{|}_{\mathsf{ὶ}=0}=A,{\displaystyle \frac{{\mathrm{d}}^2{\mathrm{v}}_1}{\mathrm{d}{\mathsf{ὶ}}^2}}{|}_{\mathsf{ὶ}=0}=0.\hfill \end{array}\right.$$

Additionally, Prakash et al. in [4], introduced an extension of the jerk system to the fractional order jerk system without any equilibrium point, given as:

$$\left\{\begin{array}{c}{\mathcal{D}}_{0^{+}}^{\alpha }{\mathrm{v}}_1\left(\mathsf{ὶ}\right)={\mathrm{v}}_2\left(\mathsf{ὶ}\right),{\mathcal{D}}_{0^{+}}^{\beta }{\mathrm{v}}_2\left(\mathsf{ὶ}\right)={\mathrm{v}}_3\left(\mathsf{ὶ}\right),\hfill \\ {\mathcal{D}}_{0^{+}}^{\gamma }{\mathrm{v}}_3\left(\mathsf{ὶ}\right)=-{\mathrm{v}}_2\left(\mathsf{ὶ}\right)+3{\mathrm{v}}_2^2\left(\mathsf{ὶ}\right)-{\mathrm{v}}_1^2\left(\mathsf{ὶ}\right)-{\mathrm{v}}_1\left(\mathsf{ὶ}\right){\mathrm{v}}_3\left(\mathsf{ὶ}\right)+\beta -\mathcal{T}\left({\mathrm{v}}_1\left(\mathsf{ὶ}\right)\right){\mathrm{v}}_2\left(\mathsf{ὶ}\right),\hfill \end{array}\right.$$

where $\alpha$, $\beta$ and $\gamma \in (0,1]$ are orders of fractional type. Many researchers have investigated the sufficient conditions for a wide domain of fractional nonlinear ordinary differential equations by employing methods which include standard fixed-point theorems, iterative approaches, etc. (see [5,6,7,8,9,10,11,12,13]). However, to the best of our knowledge, limited results can be found on the existence/stability of solutions for a fractional jerk system via the generalized $\mathbb{G}$-Caputo derivative. In 2020, Liu et al., developed two iterative algorithms to determine the periods and then the periodic solutions of nonlinear jerk equations for two possible cases initial values unknown and initial values given [14]. The authors in the recent article [15] considered the $\mathbb{G}$—fractional snap model with a constant initial conditions

$$\left\{\begin{array}{cc}{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)={\mathrm{v}}_1\left(\mathsf{ὶ}\right),\hfill & \mathrm{v}\left({\tau }_1\right)={\mathrm{u}}_0,\hfill \\ {{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}{\mathrm{v}}_1\left(\mathsf{ὶ}\right)={\mathrm{v}}_2\left(\mathsf{ὶ}\right),\hfill & {\mathrm{v}}_1\left({\tau }_1\right)={\mathrm{u}}_1,\hfill \\ {{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}{\mathrm{v}}_2\left(\mathsf{ὶ}\right)={\mathrm{v}}_3\left(\mathsf{ὶ}\right),\hfill & {\mathrm{v}}_2\left({\tau }_1\right)={\mathrm{u}}_2,\hfill \\ {{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}{\mathrm{v}}_3\left(\mathsf{ὶ}\right)=\mathcal{T}(\mathsf{ὶ},\mathrm{v},{\mathrm{v}}_1,{\mathrm{v}}_2,{\mathrm{v}}_3),\hfill & {\mathrm{v}}_3\left({\tau }_1\right)={\mathrm{u}}_3,\hfill \end{array}\right.$$

(3)

where the $\mathbb{G}$-Caputo derivatives are illustrated by symbol ${}^c{\mathcal{D}}_{{\tau }_1+}^{\eta ;\mathbb{G}}$, and $\eta \in \{\alpha ,\beta ,\gamma ,\delta \}$ such that $0<\eta \le 1$; the increasing function $\mathbb{G}\in C^1[{\tau }_1,{\tau }_2]$ is such that ${\mathbb{G}}^{\prime }\left(\mathsf{ὶ}\right)\ne 0,\forall \mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$ and continuous function $\mathcal{T}\in C([{\tau }_1,{\tau }_2]\times {\mathbb{R}}^4)$ and ${\mathrm{u}}_0,{\mathrm{u}}_1,{\mathrm{u}}_2,{\mathrm{u}}_3\in \mathbb{R}$, but we here in this article shall use non-periodic boundary conditions that generalize many boundary and initial conditions. The authors in [16] studied the following coupled system of fractional differential equations:

$$\left\{\begin{array}{c}{{}_{{\tau }_1}^R\mathcal{D}}^{\alpha ;\mathbb{G}}{\mathrm{v}}_1\left(\mathsf{ὶ}\right)={\mathfrak{T}}_1\left(\mathsf{ὶ},{\mathrm{v}}_1\left(\mathsf{ὶ}\right),{\mathrm{v}}_2\left(\mathsf{ὶ}\right)\right),\hfill \\ {{}_{{\tau }_1}^R\mathcal{D}}^{\beta ;\mathbb{G}}{\mathrm{v}}_2\left(\mathsf{ὶ}\right)={\mathfrak{T}}_2\left(\mathsf{ὶ},{\mathrm{v}}_1\left(\mathsf{ὶ}\right),{\mathrm{v}}_2\left(\mathsf{ὶ}\right)\right),\hfill \end{array}\right.$$

(4)

for $\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$ equipped with the generalized fractional integral boundary conditions

$$\left\{\begin{array}{cc}{\mathrm{v}}_1\left({\delta }_1\right)=0,\hfill & {\mathrm{v}}_1\left(b\right)={{}_{{\tau }_1}\mathcal{I}}^{{\gamma }_1;\mathbb{G}}{\mathrm{v}}_1\left({\mu }_1\right),\hfill \\ {\mathrm{v}}_2\left({\delta }_2\right)=0,\hfill & {\mathrm{v}}_2\left(b\right)={{}_{{\tau }_1}\mathcal{I}}^{{\gamma }_2;\mathbb{G}}{\mathrm{v}}_2\left({\mu }_2\right),\hfill \end{array}\right.$$

(5)

where $\mathbb{G}\in (0,1]$, ${{}_{{\tau }_1}^R\mathcal{D}}^{\alpha ;\mathbb{G}}$ and ${{}_{{\tau }_1}^R\mathcal{D}}^{\beta ;\mathbb{G}}$ denote the generalized proportional fractional derivatives of Riemann–Liouville type of order $\alpha ,\beta \in (1,2]$; ${{}_{{\tau }_1}\mathcal{I}}^{{\gamma }_i;\mathbb{G}}$ denote the generalized proportional fractional integrals of order ${\gamma }_i\in (0,1)$, ${\delta }_i,{\mu }_i\in ({\tau }_1,{\tau }_2)$; and ${\mathfrak{T}}_i:[{\tau }_1,{\tau }_2]\times {\mathbb{R}}^2\to \mathbb{R}$ are continuous functions where $i=1,2$.

We consider the following problem:

$$\left\{\begin{array}{cc}{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)={\mathrm{v}}_1\left(\mathsf{ὶ}\right),{\tau }_1\le \mathsf{ὶ}\le {\tau }_2,\hfill & \mathrm{v}\left({\tau }_1\right)={\lambda }_0\mathrm{v}\left({\tau }_2\right),\hfill \\ {{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}{\mathrm{v}}_1\left(\mathsf{ὶ}\right)={\mathrm{v}}_2\left(\mathsf{ὶ}\right),\hfill & {\mathrm{v}}_1\left({\tau }_1\right)={\lambda }_1{\mathrm{v}}_1\left({\tau }_2\right),\hfill \\ {{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}{\mathrm{v}}_2\left(\mathsf{ὶ}\right)={\mathrm{v}}_3\left(\mathsf{ὶ}\right),\hfill & {\mathrm{v}}_2\left({\tau }_1\right)={\lambda }_2{\mathrm{v}}_2\left({\tau }_2\right),\hfill \\ {{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}{\mathrm{v}}_3\left(\mathsf{ὶ}\right)=\mathfrak{T}(\mathsf{ὶ},\mathrm{v},{\mathrm{v}}_1,{\mathrm{v}}_2,{\mathrm{v}}_3),\hfill & {\mathrm{v}}_3\left({\tau }_1\right)={\lambda }_3{\mathrm{v}}_3\left({\tau }_2\right),\hfill \end{array}\right.$$

(6)

where the symbol ${}^c{\mathcal{D}}_{{\tau }_1+}^{\eta ;\mathbb{G}}$, where $\eta \in \{\alpha ,\beta ,\gamma ,\delta \}$ is the $\mathbb{G}$-Caputo derivative such that $0<\eta \le 1$, the function $\mathbb{G}\in C^1[{\tau }_1,{\tau }_2]$ is increasing such that ${\mathbb{G}}^{\prime }\left(\mathsf{ὶ}\right)\ne 0,\forall \mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$, $\mathfrak{T}\in C([{\tau }_1,{\tau }_2]\times {\mathbb{R}}^4)$ and ${\lambda }_0,{\lambda }_1,{\lambda }_2,{\lambda }_3\in \mathbb{R}\backslash \left\{1\right\}$. Clearly, we can write the system as follows:

$$\left\{\begin{array}{c}{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right)\right)\hfill \\ =\mathfrak{T}\left(\mathsf{ὶ},\mathrm{v}\left(\mathsf{ὶ}\right),{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right),{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right),{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right)\right),\hfill \\ \mathrm{v}\left({\tau }_1\right)={\lambda }_0\mathrm{v}\left({\tau }_2\right),{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_1\right)={\lambda }_1{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_2\right),\hfill \\ {}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_1\right)\right)={\lambda }_2{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_2\right)\right),\hfill \\ {}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_1\right)\right)\right)={\lambda }_3{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_2\right)\right)\right),\hfill \end{array}\right.$$

(7)

where ${\mathbb{G}}^{\prime }\left(\mathsf{ὶ}\right)\ne 0,\forall \mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$, $\mathfrak{T}\in C([{\tau }_1,{\tau }_2]\times {\mathbb{R}}^4)$ and ${\lambda }_0,{\lambda }_1,{\lambda }_2,{\lambda }_3\in \mathbb{R}\backslash \left\{1\right\}$.

This paper is organized as follows: In Section 2, we present some necessary definitions of fractional calculus and useful lemmas and some theorems about the fixed–point that are needed in the subsequent sections. In Section 3, with the help of Banach and Leary–Schauder fixed-point theorem, we give the proof of the fundamental theorems to prove the existence and uniqueness of solutions for problem (7). The stability results are extensively discussed in Section 4 in the context of the Ulam–Hyers and its generalized version, along with Ulam–Hyers–Rassias and its generalized version for solutions of the fractional $\mathbb{G}$-snap problem (7). Two significant examples, along with codes and numerical results, are presented in Section 5 in which our all outcomes are guaranteed. Those numerical examples were generated using MATLAB for understanding the theoretical results. Finally, we will give some suggestions to the reader in the conclusion Section 6.

2. Preliminaries

Some primitive notions, definitions and notations, which will be utilized throughout the manuscript, are recalled here. Let $\mathbb{G}:[{\tau }_1,{\tau }_2]\to \mathbb{R}$ be increasing via ${\mathbb{G}}^{\prime }\left(\mathsf{ὶ}\right)\ne 0,\forall \mathsf{ὶ}$. We start this part by defining $\mathbb{G}$—fractional integrals and derivatives. In all notations of this section, we set

$${\partial }_{\mathbb{G}}=\frac{1}{{\mathbb{G}}^{\prime }\left(\mathsf{ὶ}\right)}\frac{\mathrm{d}}{\mathrm{d}\mathsf{ὶ}}.$$

The qth $\mathbb{G}$—integral for an integrable function $\mathrm{v}:[{\tau }_1,{\tau }_2]\to \mathbb{R}$ with respect to $\mathbb{G}$ is illustrated as follows ([17]):

$${\mathcal{I}}_{{\tau }_1^{+}}^{q;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)=\frac{1}{\mathsf{\Gamma }\left(q\right)}{\int }_{{\tau }_1}^{\mathsf{ὶ}}{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left(\xi \right))}^{q-1}{\mathbb{G}}^{\prime }\left(\xi \right)\mathrm{v}\left(\xi \right)\mathrm{d}\xi ,$$

(8)

where

$$\mathsf{\Gamma }\left(q\right)={\int }_0^{+\infty }{e}^{-\mathsf{ὶ}}{\mathsf{ὶ}}^{q-1}\mathrm{d}\mathsf{ὶ},q>0.$$

By applying the Algorithm 1, we can obtain the qth $\mathbb{G}$—integral (8).

Algorithm 1: MATLAB lines for getting the qth $\mathbb{G}$—integral of function $\mathrm{v}$.

1 function [mathcalD]= LPhiRLfractionalderivative(a, alpha, uppsi, xfunc, t) 2 syms vs. e; 3 n = floor(alpha) + 1; 4 if fix(alpha) == alpha 5   F = (eval(subs(diff(uppsi, v), {v}, {t})))^n … 6   * eval(subs(diff(xfunc, v, n), {v}, {t})); 7   E = F; 8 else 9   F = int( subs(diff(uppsi, v), {v}, {e})… 10   * ( eval(subs(uppsi, {v}, {t})) … 11   - subs(uppsi, {v}, {e}) )^(n-alpha-1)… 12   * (eval(subs(diff(uppsi, v), {v}, {e})))^n … 13   * eval(subs(diff(xfunc, v, n), {v}, {e})), a, t); 14   E = 1/gamma(n-alpha) * F; 15 end; 16 mathcalD = E; 17 end

Let $n\in \mathbb{N}$ and $\mathbb{G},\mathrm{v}\in C^n[{\tau }_1,{\tau }_2]$ be such that $\mathbb{G}$ has the same properties mentioned above. The qth-$\mathbb{G}$-fractional derivative of $\mathrm{v}$ is defined by

$$\begin{array}{cc}\hfill {\mathcal{D}}_{{\tau }_1^{+}}^{q;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)& ={\partial }_{\mathbb{G}}^{\left(n\right)}{\mathcal{I}}_{{\tau }_1^{+}}^{n-q;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\hfill \\ \hfill & =\frac{1}{\mathsf{\Gamma }(n-q)}{\partial }_{\mathbb{G}}^{\left(n\right)}{\int }_{{\tau }_1}^{\mathfrak{t}}{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left(\xi \right))}^{n-q-1}{\mathbb{G}}^{\prime }\left(\xi \right)\mathrm{v}\left(\xi \right)\mathrm{d}\xi ,\hfill \end{array}$$

in which $n=\left[q\right]+1$ [18]. The qth $\mathbb{G}$-Caputo derivative of $\mathrm{v}$ is defined by

$${}^c{\mathcal{D}}_{{\tau }_1^{+}}^{q;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)={\mathcal{I}}_{{\tau }_1^{+}}^{n-q;\mathbb{G}}{\partial }_{\mathbb{G}}^n\mathrm{v}\left(\mathsf{ὶ}\right),$$

in which $n=\left[q\right]+1$ for $q\notin \mathbb{N}$, $n=q$ for $q\in \mathbb{N}$ [19]. In other words,

$${}^c{\mathcal{D}}_{{\tau }_1^{+}}^{q;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)=\left\{\begin{array}{cc}{\partial }_{\mathbb{G}}^n\mathrm{v}\left(\mathsf{ὶ}\right),\hfill & q=n\in \mathbb{N},\hfill \\ {\displaystyle {\int }_{{\tau }_1}^{\mathsf{ὶ}}\frac{{\mathbb{G}}^{\prime }\left(\xi \right){(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left(\xi \right))}^{n-q-1}}{\mathsf{\Gamma }(n-q)}{\partial }_{\mathbb{G}}^n\mathrm{v}\left(\xi \right)\mathrm{d}\xi ,}\hfill & q\notin \mathbb{N}.\hfill \end{array}\right.$$

(9)

This derivative gives the Caputo–Hadamard derivative and the Caputo derivative when $\mathbb{G}\left(\mathsf{ὶ}\right)=ln\mathsf{ὶ}$ and $\mathbb{G}\left(\mathsf{ὶ}\right)=\mathsf{ὶ}$, respectively. The qth $\mathbb{G}$-Caputo derivative of the function $\mathrm{v}$ is specified as ([19], Theorem 3)

$${}^c{\mathcal{D}}_{{\tau }_1^{+}}^{q;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)={\mathcal{D}}_{{\tau }_1^{+}}^{q;\mathbb{G}}\left(\mathrm{v}\left(\mathsf{ὶ}\right)-\sum _{k=0}^{n-1}\frac{{\partial }_{\mathbb{G}}^k\mathrm{v}\left({\tau }_1\right)}{k!}{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^k\right).$$

By using the MATLAB function in Algoritm 2, we can get the qth $\mathbb{G}$-Caputo derivative (9).    

Algorithm 2: MATLAB lines for getting qth $\mathbb{G}$-Caputo derivative of function $\mathrm{v}$.

1 function [mathcalD]= LPhiRLfractionalderivative(a, alpha, uppsi, xfunc, t) 2 syms vs. e; 3 n = floor(alpha) + 1; 4 if fix(alpha) == alpha 5   F = (eval(subs(diff(uppsi, v), {v}, {t})))^n … 6   * eval(subs(diff(xfunc, v, n), {v}, {t})); 7   E = F; 8 else 9   F = int( subs(diff(uppsi, v), {v}, {e})… 10   * ( eval(subs(uppsi, {v}, {t})) … 11   - subs(uppsi, {v}, {e}) )^(n-alpha-1)… 12   * (eval(subs(diff(uppsi, v), {v}, {e})))^n … 13   * eval(subs(diff(xfunc, v, n), {v}, {e})), a, t); 14   E = 1/gamma(n-alpha) * F; 15 end 16 mathcalD = E; 17 end

The composition rules for the above $\mathbb{G}$-operators are recalled in this lemma.

Lemma 1

([17,20]).Let $n-1<q<n$ and $\mathrm{v}\in C^n[{\tau }_1,{\tau }_2]$. Then the following holds:

$${\mathcal{I}}_{{\tau }_1^{+}}^{q;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{q;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)=\mathrm{v}\left(\mathsf{ὶ}\right)-\sum _{k=0}^{n-1}\frac{{\partial }_{\mathbb{G}}^k\mathrm{v}\left({\tau }_1\right)}{k!}{\left[\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right)\right]}^k,$$

for all $\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$. Moreover, if $m\in \mathbb{N}$ and $\mathrm{v}\in C^{n+m}[{\tau }_1,{\tau }_2]$, then the following holds:

$$\begin{array}{cc}\hfill {\partial }_{\mathbb{G}}^m\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{q;\mathbb{G}}\mathrm{v}\right)\left(\mathsf{ὶ}\right)& ={}^c{\mathcal{D}}_{{\tau }_1^{+}}^{q+m;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)+\sum _{k=0}^{m-1}\frac{{[\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right)]}^{k+n-q-m}}{\mathsf{\Gamma }(k+n-q-m+1)}{\partial }_{\mathbb{G}}^{k+m}\mathrm{v}\left({\tau }_1\right).\hfill \end{array}$$

Observe that if ${\partial }_{\mathbb{G}}^k\mathrm{v}\left({\tau }_1\right)=0,\forall k=n,n+1,\dots ,n+m-1$, we can get the following relation:

$${\partial }_{\mathbb{G}}^m\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{q;\mathbb{G}}\mathrm{v}\right)\left(\mathsf{ὶ}\right)={}^c{\mathcal{D}}_{{\tau }_1^{+}}^{q+m;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right),\mathsf{ὶ}\in [{\tau }_1,{\tau }_2].$$

Lemma 2 

([17]).Let$q,\acute{q}>0,$and$\mathrm{v}\in C[{\tau }_1,{\tau }_2]$. Then, $\forall \mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$and by assuming${\breve{\mathbb{G}}}_{{\tau }_1}\left(\mathsf{ὶ}\right)=\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right)$, we have

1. 

${\mathcal{I}}_{{\tau }_1^{+}}^{q;\mathbb{G}}{\mathcal{I}}_{{\tau }_1^{+}}^{\acute{q};\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)={\mathcal{I}}_{{\tau }_1^{+}}^{q+\acute{q};\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)$;

2. 

${}^c{\mathcal{D}}_{{\tau }_1^{+}}^{q;\mathbb{G}}{\mathcal{I}}_{{\tau }_1^{+}}^{q;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)=\mathrm{v}\left(\mathsf{ὶ}\right)$;

3. 

${\mathcal{I}}_{{\tau }_1^{+}}^{q;\mathbb{G}}{\left({\breve{\mathbb{G}}}_{{\tau }_1}\left(\mathsf{ὶ}\right)\right)}^{\acute{q}-1}={\displaystyle \frac{\mathsf{\Gamma }\left(\acute{q}\right)}{\mathsf{\Gamma }\left(\acute{q}+q\right)}}{\left({\breve{\mathbb{G}}}_{{\tau }_1}\left(\mathsf{ὶ}\right)\right)}^{\acute{q}+q-1}$;

4. 

${}^c{\mathcal{D}}_{{\tau }_1^{+}}^{q;\mathbb{G}}{\left({\breve{\mathbb{G}}}_{{\tau }_1}\left(\mathsf{ὶ}\right)\right)}^{\acute{q}-1}={\displaystyle \frac{\mathsf{\Gamma }\left(\acute{q}\right)}{\mathsf{\Gamma }(\acute{q}-q)}}{\left({\breve{\mathbb{G}}}_{{\tau }_1}\left(\mathsf{ὶ}\right)\right)}^{\acute{q}-q-1}$;

5. 

${}^c{\mathcal{D}}_{{\tau }_1^{+}}^{q;\mathbb{G}}{\left({\breve{\mathbb{G}}}_{{\tau }_1}\left(\mathsf{ὶ}\right)\right)}^k=0,(k=0,\dots ,n-1)$, $n\in \mathbb{N},q\in (n-1,n]$.

We recall the following two fixed-point theorems.

Theorem 1 (Banach fixed-point theorem). 

Let $\mathrm{V}=(\mathrm{V},{∥·∥}_{\mathrm{V}})$ be a Banach space, and let $\mathsf{\Psi }:\mathrm{V}\to \mathrm{V}$ be a contraction mapping on a closed ball

$${\mathrm{U}}_{\varsigma }=\left\{\mathrm{v}\in \mathrm{V}:{∥\mathrm{v}-{\mathrm{v}}_0∥}_{\mathrm{V}}\le \varsigma \right\};$$

that is, there exists a positive real number $\varpi <1,$ such that

$${∥\mathsf{\Psi }\mathrm{v}-\mathsf{\Psi }\acute{\mathrm{v}}∥}_{\mathrm{V}}\le \varpi {∥\mathrm{v}-\acute{\mathrm{v}}∥}_{\mathrm{V}},$$

for all $\mathrm{v},\acute{\mathrm{v}}\in {\mathrm{U}}_{\varsigma }$. Then, Ψ admits a unique fixed point ${\mathrm{v}}^{\ast }$ provided

$${∥\mathsf{\Psi }{\mathrm{v}}_0-{\mathrm{v}}_0∥}_{\mathrm{V}}<(1-\varpi )\varsigma .$$

Theorem 2 (Leray–Schauder). 

Let $\mathrm{V}=(\mathrm{V},{∥·∥}_{\mathrm{V}})$ be a Banach space, let $\mathrm{B}$ be a closed convex bounded subset of $\mathrm{V}$ and let O be an open set contained in $\mathrm{B}$ with $0\in O$. Let $\mathsf{\Psi }:\overline{O}\to \mathrm{B}$ be a continuous and compact mapping. Then, either (i) Ψ admits a fixed point belonging to $\overline{O}$, or (ii) there exist $\mathrm{v}\in \partial O$ and $\varpi \in (0,1)$ such that $\mathrm{v}=\varpi \mathsf{\Psi }\mathrm{v}$.

3. Existence-Uniqueness Results

Here, we analyze the existence properties of solutions and their uniqueness for the proposed fractional non-periodic snap problem. We require the following lemma, which specifies the corresponding integral equation. Hereafter, we assume

(H1) 

$\mathrm{v},$${}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v},$ and

$${}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\right),{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\right)\right),{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right),$$

are continuously differentiable real-valued functions on $({\tau }_1,{\tau }_2).$

Lemma 3.

Let $\gamma ,\beta ,\alpha ,\delta \in (0,1]$, $\lambda ,\mu ,\nu ,\xi \ne 1,$ and (H1) be held. If g is a real-valued continuous function on $[{\tau }_1,{\tau }_2]$, then the solution of the linear fractional non-periodic snap problem

$$\left\{\begin{array}{c}{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right)\right)=g\left(\mathsf{ὶ}\right),\mathsf{ὶ}\in ({\tau }_1,{\tau }_2)\hfill \\ \mathrm{v}\left({\tau }_1\right)={\lambda }_0\mathrm{v}\left({\tau }_2\right),{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_1\right)={\lambda }_1{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_2\right),\hfill \\ {{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_1\right)\right)={\lambda }_2{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_2\right)\right),\hfill \\ {}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_1\right)\right)\right)={\lambda }_3{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_2\right)\right)\right),\hfill \end{array}\right.$$

(10)

is given by

$$\begin{array}{cc}\hfill \mathrm{v}\left(\mathsf{ὶ}\right)& =\frac{{\lambda }_3}{\left(1-{\lambda }_3\right)}\left[\frac{{\lambda }_0{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta +\gamma }}{\left(1-{\lambda }_0\right)}\right.\hfill \\ \hfill & \times \left(\frac{{\lambda }_1{\lambda }_2}{\left(1-{\lambda }_1\right)\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(\beta +1)}\right.\hfill \\ \hfill & +\frac{{\lambda }_1}{\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(\beta +\gamma +1)}+\frac{{\lambda }_2}{\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\alpha +\beta +1)}\hfill \\ \hfill & \left.+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\right)+\frac{{\lambda }_1{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta +\gamma }}{\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\alpha +1)}\hfill \\ \hfill & \times \left(\frac{{\lambda }_2}{\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}+\frac{1}{\mathsf{\Gamma }(\beta +\gamma +1)}\right)+{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }\hfill \\ \hfill & \left.\times \left(\frac{{\lambda }_2{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\alpha +\beta +1)}+\frac{{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\right)\right]{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)\hfill \\ \hfill & +\frac{{\lambda }_2}{1-{\lambda }_2}\left[\frac{{\lambda }_1{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta }}{\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(\beta +1)}\right.\hfill \\ \hfill & \times \left(\frac{{\lambda }_0{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }}{\left(1-{\lambda }_0\right)}+{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }\right)\hfill \\ \hfill & \left.+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +1)}\left(\frac{{\lambda }_0{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }}{\left(1-{\lambda }_0\right)}+{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }\right)\right]{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}g\left({\tau }_2\right)\hfill \\ \hfill & +\frac{{\lambda }_1}{\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\alpha +1)}\left(\frac{{\lambda }_0{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }}{1-{\lambda }_0}+{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }\right){\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\beta +\gamma ;\mathbb{G}}g\left({\tau }_2\right)\hfill \\ \hfill & +{\mathcal{I}}_{{\tau }_1^{+}}^{\alpha +\delta +\beta +\gamma ;\mathbb{G}}\left(\frac{{\lambda }_{0}g\left({\tau }_2\right)}{1-{\lambda }_0}+g\left(\mathsf{ὶ}\right)\right).\hfill \end{array}$$

(11)

Proof. 

Consider $\mathrm{v}\left(\mathsf{ὶ}\right)$ satisfying the snap problem (10). The continuity of g and

$${{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\right)\right)\right),$$

ensures that ${\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g$ and

$${\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\right)\right)\right)\right),$$

exist and are continuous. Hence, by applying the $\delta$-th integral ${\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}$ to both sides of Equation (10), by Lemma 2, we obtain

$${{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right)=c_0+{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left(\mathsf{ὶ}\right),$$

(12)

with $c_0\in \mathbb{R}$. The differentiability of ${\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g$ and

$${{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\right)\right),$$

on $({\tau }_1,{\tau }_2)$ implies (10) by operating ${{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}$ to both sides of (12). Using the boundary condition,

$${}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_1\right)\right)\right)={\lambda }_3{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_2\right)\right)\right),$$

we deduce that

$$c_0={\lambda }_3{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_2\right)\right)\right)=\frac{{\lambda }_3}{1-{\lambda }_3}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right).$$

Similarly, applying the $\gamma$-th integral operator ${\mathcal{I}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}$, we get

$${{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)=c_1+\frac{{\lambda }_3{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\left(1-{\lambda }_3\right)\mathsf{\Gamma }(\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)+{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}g\left(\mathsf{ὶ}\right).$$

The boundary condition

$${{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_1\right)\right)={\lambda }_2{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_2\right)\right),$$

gives the following:

$$\begin{array}{cc}\hfill c_1& ={\lambda }_2{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_2\right)\right)\hfill \\ \hfill & =\frac{{\lambda }_3{\lambda }_2{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\left(1-{\lambda }_3\right)\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)+\frac{{\lambda }_2}{1-{\lambda }_2}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}g\left({\tau }_2\right).\hfill \end{array}$$

Next, we apply the $\beta$-th integral operator ${\mathcal{I}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}$ to obtain

$$\begin{array}{cc}\hfill {{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)& =c_2+\frac{{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta }}{\mathsf{\Gamma }(\beta +1)}\hfill \\ \hfill & \times \left(\frac{{\lambda }_3{\lambda }_2{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\left(1-{\lambda }_3\right)\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)+\frac{{\lambda }_2}{1-{\lambda }_2}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}g\left({\tau }_2\right)\right)\hfill \\ \hfill & +\frac{{\lambda }_3{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta +\gamma }}{\left(1-{\lambda }_3\right)\mathsf{\Gamma }(\beta +\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)+{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\beta +\gamma ;\mathbb{G}}g\left(\mathsf{ὶ}\right).\hfill \end{array}$$

(13)

The boundary condition ${{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_1\right)={\lambda }_1{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_2\right),$ gives

$$\begin{array}{cc}\hfill c_2& ={\lambda }_1{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left({\tau }_2\right)=\frac{{\lambda }_1{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta }}{\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\beta +1)}\hfill \\ \hfill & \times \left(\frac{{\lambda }_3{\lambda }_2{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\left(1-{\lambda }_3\right)\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)+\frac{{\lambda }_2}{1-{\lambda }_2}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}g\left({\tau }_2\right)\right)\hfill \\ \hfill & +\frac{{\lambda }_1{\lambda }_3{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta +\gamma }}{\left(1-{\lambda }_1\right)\left(1-{\lambda }_3\right)\mathsf{\Gamma }(\beta +\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)+\frac{{\lambda }_1}{1-{\lambda }_1}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\beta +\gamma ;\mathbb{G}}g\left({\tau }_2\right).\hfill \end{array}$$

(14)

Finally, we apply the integral operator ${\mathcal{I}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}$ to obtain

$$\begin{array}{cc}\hfill \mathrm{v}\left(\mathsf{ὶ}\right)& =c_3+\frac{{\lambda }_1{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta }}{\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(\beta +1)}\hfill \\ \hfill & \times \left(\frac{{\lambda }_3{\lambda }_2{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\left(1-{\lambda }_3\right)\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)+\frac{{\lambda }_2}{1-{\lambda }_2}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}g\left({\tau }_2\right)\right)\hfill \\ \hfill & +\frac{{\lambda }_1{\lambda }_3{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta +\gamma }}{\left(1-{\lambda }_1\right)\left(1-{\lambda }_3\right)\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(\beta +\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)\hfill \\ \hfill & +\frac{{\lambda }_1{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }}{\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\alpha +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\beta +\gamma ;\mathbb{G}}g\left({\tau }_2\right)+\frac{{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }}{\mathsf{\Gamma }(\alpha +\beta +1)}\hfill \\ \hfill & \times \left(\frac{{\lambda }_3{\lambda }_2{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\left(1-{\lambda }_3\right)\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)+\frac{{\lambda }_2}{1-{\lambda }_2}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}g\left({\tau }_2\right)\right)\hfill \\ \hfill & +\frac{{\lambda }_3{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta +\gamma }}{\left(1-{\lambda }_3\right)\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)+{\mathcal{I}}_{{\tau }_1^{+}}^{\alpha +\delta +\beta +\gamma ;\mathbb{G}}g\left(\mathsf{ὶ}\right).\hfill \end{array}$$

The last boundary condition $\mathrm{v}\left({\tau }_1\right)={\lambda }_0\mathrm{v}\left({\tau }_2\right)$ can be applied to get

$$\begin{array}{cc}\hfill c_3& ={\lambda }_0\mathrm{v}\left({\tau }_2\right)=\frac{{\lambda }_0{\lambda }_1{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }}{\left(1-{\lambda }_0\right)\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(\beta +1)}\hfill \\ \hfill & \times \left(\frac{{\lambda }_3{\lambda }_2{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\left(1-{\lambda }_3\right)\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)+\frac{{\lambda }_2}{1-{\lambda }_2}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}g\left({\tau }_2\right)\right)\hfill \\ \hfill & +\frac{{\lambda }_0{\lambda }_1{\lambda }_3{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta +\gamma }}{\left(1-{\lambda }_0\right)\left(1-{\lambda }_1\right)\left(1-{\lambda }_3\right)\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(\beta +\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)\hfill \\ \hfill & +\frac{{\lambda }_0{\lambda }_1{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }}{\left(1-{\lambda }_0\right)\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\alpha +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\beta +\gamma ;\mathbb{G}}g\left({\tau }_2\right)\hfill \\ \hfill & +\frac{{\lambda }_0{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }}{\left(1-{\lambda }_0\right)\mathsf{\Gamma }(\alpha +\beta +1)}(\frac{{\lambda }_3{\lambda }_2{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\left(1-{\lambda }_3\right)\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)\hfill \\ \hfill & +\frac{{\lambda }_2}{1-{\lambda }_2}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}g\left({\tau }_2\right))+\frac{{\lambda }_0{\lambda }_3{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta +\gamma }}{\left(1-{\lambda }_0\right)\left(1-{\lambda }_3\right)\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}g\left({\tau }_2\right)\hfill \\ \hfill & +\frac{{\lambda }_0}{1-{\lambda }_0}{\mathcal{I}}_{{\tau }_1^{+}}^{\alpha +\delta +\beta +\gamma ;\mathbb{G}}g\left({\tau }_2\right).\hfill \end{array}$$

Therefore, we now see that $\mathrm{v}\left(\mathsf{ὶ}\right)$ fulfills (11), and the proof is ended. □

In the next result, our goal is to verify the unique solution of the fractional non-periodic snap problem (7) by using Banach fixed-point theorem.

Consider the space

$$\begin{array}{cc}\hfill \mathrm{V}& =\{\mathrm{v}\in C[{\tau }_1,{\tau }_2]:{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v},{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\right),\hfill \\ \hfill & {}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\right)\right)\in C[{\tau }_1,{\tau }_2]\}.\hfill \end{array}$$

Then, $\mathrm{V}$ is a Banach space via the norm

$$\begin{array}{cc}\hfill \parallel \mathrm{v}\parallel & =\underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\left|\mathrm{v}\left(\mathsf{ὶ}\right)\right|+\underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right|+\underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right|\hfill \\ \hfill & +\underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right)\right|.\hfill \end{array}$$

The following notations are useful:

$$\begin{array}{cc}\hfill A_1& ={\displaystyle \frac{{\lambda }_0}{1-{\lambda }_0}}\left[\frac{{\lambda }_1{\lambda }_2}{\left(1-{\lambda }_1\right)\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(\beta +1)}\right.\hfill \\ \hfill & +\frac{{\lambda }_1}{\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(\beta +\gamma +1)}\hfill \\ \hfill & \left.+\frac{{\lambda }_2}{\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\alpha +\beta +1)}+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\right],\hfill \\ \hfill A_2& =\frac{{\lambda }_1}{\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\alpha +1)}\left[\frac{{\lambda }_2}{\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}+\frac{1}{\mathsf{\Gamma }(\beta +\gamma +1)}\right],\hfill \\ \hfill A_3& =\frac{{\lambda }_2}{(1-{\lambda }_2)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\alpha +\beta +1)},\hfill \\ \hfill A_4& =\frac{{\lambda }_1}{(1-{\lambda }_1)\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(\beta +1)},\hfill \\ \hfill A_5& =\frac{{\lambda }_1}{(1-{\lambda }_1)\mathsf{\Gamma }(\alpha +1)}.\hfill \end{array}$$

(15)

In virtue of Lemma 3, we can use the integral solution of the fractional non-periodic snap problem (7) to define a operator $\mathsf{\Psi }:\mathrm{V}\to \mathrm{V}$ as the following.

$$\begin{array}{cc}\hfill \mathsf{\Psi }\mathrm{v}\left(\mathsf{ὶ}\right)& =\frac{{\lambda }_3}{\left(1-{\lambda }_3\right)}\left[A_1{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta +\gamma }+A_2{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta +\gamma }\right.\hfill \\ \hfill & \left.+{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }\left(A_3{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }+\frac{{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\right)\right]{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}{f}_x\left({\tau }_2\right)\hfill \\ \hfill & +\frac{{\lambda }_2}{1-{\lambda }_2}\left[A_4\left({(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta }\left(\frac{{\lambda }_0{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }}{\left(1-{\lambda }_0\right)}+{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }\right)\right)\right.\hfill \\ \hfill & \left.+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +1)}\left(\frac{{\lambda }_0{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }}{\left(1-{\lambda }_0\right)}+{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }\right)\right]{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}{\mathfrak{T}}_{\mathrm{v}}\left({\tau }_2\right)\hfill \\ \hfill & +A_5\left(\frac{{\lambda }_0{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }}{1-{\lambda }_0}+{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }\right){\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\beta +\gamma ;\mathbb{G}}{\mathfrak{T}}_{\mathrm{v}}\left({\tau }_2\right)\hfill \\ \hfill & +{\mathcal{I}}_{{\tau }_1^{+}}^{\alpha +\delta +\beta +\gamma ;\mathbb{G}}\left(\frac{{\lambda }_0{\mathfrak{T}}_{\mathrm{v}}\left({\tau }_2\right)}{1-{\lambda }_0}+{\mathfrak{T}}_{\mathrm{v}}\left(\mathsf{ὶ}\right)\right),\hfill \end{array}$$

(16)

where

$${\mathfrak{T}}_{\mathrm{v}}\left(\mathsf{ὶ}\right)=\mathfrak{T}\left(\mathsf{ὶ},\mathrm{v}\left(\mathsf{ὶ}\right),{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right),{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right),{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right)\right),$$

for $\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$.

The following hypothesis is strongly needed for the contraction principle of the operator $\mathsf{\Psi }$.

(H2) 

The function $\mathfrak{T}\in C([{\tau }_1,{\tau }_2]\times {\mathbb{R}}^4),$ and $\exists \ell >0$ such that $\forall \mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$ and $\mathrm{v},\acute{\mathrm{v}}\in {\mathrm{W}}^4$, $\mathrm{W}=C[{\tau }_1,{\tau }_2]$, $\acute{\mathrm{v}}={\left({\mathrm{v}}_j\right)}_{j\in \{1,2,3,4\}}$, $\acute{\mathrm{v}}={\left({\acute{\mathrm{v}}}_j\right)}_{j\in \{1,2,3,4\}}$,

$$\begin{array}{cc}\hfill ∥{\mathfrak{T}}_{\mathrm{v}}\left(\mathsf{ὶ}\right)-{\mathfrak{T}}_{\acute{\mathrm{v}}}\left(\mathsf{ὶ}\right)∥& \le \ell \sum _{j=1}^4∥\mathrm{v}\left(\mathsf{ὶ}\right)-\acute{\mathrm{v}}\left(\mathsf{ὶ}\right)∥,\hfill \end{array}$$

where $∥\mathrm{v}∥={\sum }_{j=1}^4∥{\mathrm{v}}_j∥$.

Theorem 3.

Let (H1) and (H2) be held. Then, the fractional non-periodic snap problem (7) admits a unique solution on $[{\tau }_1,{\tau }_2]$ if $\ell \Delta <1$, where

$$\begin{array}{cc}\hfill \Delta & =[\frac{\left|{\lambda }_3\right|}{\mathsf{\Gamma }(\delta +1)\left|1-{\lambda }_3\right|}\left(\left|A_1\right|+\left|A_2\right|+\left|A_3\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\right)\hfill \\ \hfill & +\frac{\left|{\lambda }_2\right|}{\left|(1-{\lambda }_0)(1-{\lambda }_2)\right|\mathsf{\Gamma }(\gamma +\delta +1)}\left(\left|A_4\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +1)}\right)\hfill \\ \hfill & +\frac{\left|A_5\right|}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\delta +\beta +\gamma +1)}\hfill \\ \hfill & +\frac{\left(2\left|{\lambda }_0\right|+1\right)}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\alpha +\delta +\beta +\gamma +1)}]{\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\alpha +\beta +\gamma +\delta }\hfill \\ \hfill & +{\displaystyle \frac{\left|{\lambda }_3\right|}{\left|(1-{\lambda }_3)\left(1-{\lambda }_1\right)\right|\mathsf{\Gamma }(\delta +1)}}\left(\frac{\left|{\lambda }_2\right|}{\left|1-{\lambda }_2\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}+\frac{1}{\mathsf{\Gamma }(\beta +\gamma +1)}\right)\hfill \\ \hfill & +(\frac{\left|{\lambda }_2\right|}{\left|\left(1-{\lambda }_2\right)\left(1-{\lambda }_1\right)\right|\mathsf{\Gamma }(\beta +1)\mathsf{\Gamma }(\gamma +\delta +1)}\hfill \\ \hfill & +\frac{\left(2\left|{\lambda }_1\right|+1\right)}{\left|1-{\lambda }_1\right|\mathsf{\Gamma }(\delta +\beta +\gamma +1)}){\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\beta +\gamma +\delta }\hfill \\ \hfill & +\left({\displaystyle \frac{\left|{\lambda }_3\right|}{\left|(1-{\lambda }_3)\left(1-{\lambda }_2\right)\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\delta +1)}}+\frac{2\left|{\lambda }_2\right|+1}{\left|1-{\lambda }_2\right|\mathsf{\Gamma }(\gamma +\delta +1)}\right)\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\gamma +\delta }+{\displaystyle \frac{\left(2\left|{\lambda }_3\right|+1\right)}{\left|1-{\lambda }_3\right|\mathsf{\Gamma }(\delta +1)}}{\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\delta }.\hfill \end{array}$$

(17)

Proof. 

Define the compact subset $B_{\varsigma }$ of the Banach space $\mathrm{V}$ as

$$B_{\varsigma }=\left\{\mathrm{v}\in \mathrm{V}:∥\mathrm{v}∥\le \varsigma \right\},$$

for some constant $\varsigma >0$ satisfying $\varsigma (1-\ell \Delta )\ge {\mathfrak{T}}^{\ast }\Delta$, where

$${\mathfrak{T}}^{\ast }=\underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\left|\mathfrak{T}(\mathsf{ὶ},0,0,0,0)\right|.$$

To apply the Banach Theorem, we verify that $\mathsf{\Psi }{B}_{\varsigma }\subset B_{\varsigma }$, i.e., $\mathsf{\Psi }$ maps $B_{\varsigma }$ into itself, where $\mathsf{\Psi }$ is defined by (16). For any $\mathrm{v}\in B_{\varsigma },$ we obtain

$$\begin{array}{cc}\hfill \left|\left(\mathsf{\Psi }\mathrm{v}\right)\left(\mathsf{ὶ}\right)\right|& \le \frac{\left|{\lambda }_3\right|}{\left|1-{\lambda }_3\right|}\left(\left|A_1\right|+\left|A_2\right|+\left|A_3\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\right)\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\alpha +\beta +\gamma }\left|{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}{\mathfrak{T}}_{\mathrm{v}}\left({\tau }_2\right)\right|\hfill \\ \hfill & +\frac{\left|{\lambda }_2\right|}{\left|(1-{\lambda }_0)(1-{\lambda }_2)\right|}\left(\left|A_4\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +1)}\right)\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\alpha +\beta }\left|{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}{\mathfrak{T}}_{\mathrm{v}}\left({\tau }_2\right)\right|\hfill \\ \hfill & +\frac{\left|A_5\right|}{\left|1-{\lambda }_0\right|}{\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\alpha }\left|{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\beta +\gamma ;\mathbb{G}}{\mathfrak{T}}_{\mathrm{v}}\left({\tau }_2\right)\right|\hfill \\ \hfill & +\left|{\mathcal{I}}_{{\tau }_1^{+}}^{\alpha +\delta +\beta +\gamma ;\mathbb{G}}\left(\frac{{\lambda }_0}{(1-{\lambda }_0)}{\mathfrak{T}}_{\mathrm{v}}\left({\tau }_2\right)+{\mathfrak{T}}_{\mathrm{v}}\left(\mathsf{ὶ}\right)\right)\right|\hfill \\ \hfill & \le \left[\frac{\left|{\lambda }_3\right|}{\mathsf{\Gamma }(\delta +1)\left|1-{\lambda }_3\right|}\left((\left|A_1\right|+\left|A_2\right|+\left|A_3\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\right)\right.\hfill \\ \hfill & +\frac{\left|{\lambda }_2\right|}{\left|(1-{\lambda }_0)(1-{\lambda }_2)\right|\mathsf{\Gamma }(\gamma +\delta +1)}\left(\left|A_4\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +1)}\right)\hfill \\ \hfill & \left.+\frac{\left|A_5\right|}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\delta +\beta +\gamma +1)}+\frac{\left(2\left|{\lambda }_0\right|+1\right)}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\alpha +\delta +\beta +\gamma +1)}\right]\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\alpha +\beta +\gamma +\delta }\underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\left(\right|{\mathfrak{T}}_{\mathrm{v}}\left(\mathsf{ὶ}\right)-{\mathfrak{T}}_0\left(\mathsf{ὶ}\right)|+|{\mathfrak{T}}_0\left(\mathsf{ὶ}\right)\left|\right)\hfill \\ \hfill & \le \left[\frac{\left|{\lambda }_3\right|}{\mathsf{\Gamma }(\delta +1)\left|1-{\lambda }_3\right|}\left((\left|A_1\right|+\left|A_2\right|+\left|A_3\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\right)\right.\hfill \\ \hfill & +\frac{\left|{\lambda }_2\right|}{\left|(1-{\lambda }_0)(1-{\lambda }_2)\right|\mathsf{\Gamma }(\gamma +\delta +1)}\left(\left|A_4\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +1)}\right)\hfill \\ \hfill & \left.+\frac{\left|A_5\right|}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\delta +\beta +\gamma +1)}+\frac{\left(2\left|{\lambda }_0\right|+1\right)}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\alpha +\delta +\beta +\gamma +1)}\right]\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\alpha +\beta +\gamma +\delta }\left(\ell {∥\mathrm{v}∥}_{\mathrm{V}}+{\mathfrak{T}}^{\ast }\right).\hfill \end{array}$$

In addition, by (13) and (14), we have

$$\begin{array}{cc}\hfill {{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathsf{\Psi }\mathrm{v}\left(\mathsf{ὶ}\right)& =\frac{{\lambda }_3}{\left(1-{\lambda }_3\right)}\hfill \\ \hfill & \times \left[{\displaystyle \frac{{\lambda }_1{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta +\gamma }}{\left(1-{\lambda }_1\right)}}\left(\frac{{\lambda }_2}{\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}+\frac{1}{\mathsf{\Gamma }(\beta +\gamma +1)}\right)\right.\hfill \\ \hfill & \left.+{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta }\left(\frac{{\lambda }_2{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}+\frac{{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\mathsf{\Gamma }(\beta +\gamma +1)}\right)\right]{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}{\mathfrak{T}}_{\mathrm{v}}\left({\tau }_2\right)\hfill \\ \hfill & +\frac{{\lambda }_2}{(1-{\lambda }_2)\mathsf{\Gamma }(\beta +1)}\left(\frac{{\lambda }_1{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta }}{\left(1-{\lambda }_1\right)}+{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta }\right){\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}{\mathfrak{T}}_{\mathrm{v}}\left({\tau }_2\right)\hfill \\ \hfill & +{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\beta +\gamma ;\mathbb{G}}\left(\frac{{\lambda }_1.{\mathfrak{T}}_{\mathrm{v}}\left({\tau }_2\right)}{1-{\lambda }_1}+{\mathfrak{T}}_{\mathrm{v}}\left(\mathsf{ὶ}\right)\right).\hfill \end{array}$$

Then

$$\begin{array}{cc}\hfill \left|{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathsf{\Psi }\mathrm{v}\left(\mathsf{ὶ}\right)\right|& \le \frac{\left|{\lambda }_3\right|}{\left|1-{\lambda }_3\right|}\left[\left|{\displaystyle \frac{{\lambda }_1}{\left(1-{\lambda }_1\right)}}\left(\frac{{\lambda }_2}{\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}+\frac{1}{\mathsf{\Gamma }(\beta +\gamma +1)}\right)\right|\right.\hfill \\ \hfill & +\left.\left|\frac{{\lambda }_2}{\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}+\frac{1}{\mathsf{\Gamma }(\beta +\gamma +1)}\right|\right]\hfill \\ \hfill & \times {\displaystyle \frac{{\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\beta +\gamma +\delta }}{\mathsf{\Gamma }(\delta +1)}}\underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\left(\right|{\mathfrak{T}}_{\mathrm{v}}\left(\mathsf{ὶ}\right)-{\mathfrak{T}}_0\left(\mathsf{ὶ}\right)|+|{\mathfrak{T}}_0\left(\mathsf{ὶ}\right)\left|\right)\hfill \\ \hfill & +{\displaystyle \frac{{\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\beta +\gamma +\delta }}{\mathsf{\Gamma }(\delta +\gamma +1)\mathsf{\Gamma }(\beta +1)}}\frac{\left|{\lambda }_2\right|}{\left|(1-{\lambda }_2)\left(1-{\lambda }_1\right)\right|}\underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\left(\right|{\mathfrak{T}}_{\mathrm{v}}\left(\mathsf{ὶ}\right)-{\mathfrak{T}}_0\left(\mathsf{ὶ}\right)|+|{\mathfrak{T}}_0\left(\mathsf{ὶ}\right)\left|\right)\hfill \\ \hfill & +{\displaystyle \frac{{\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\beta +\gamma +\delta }}{\mathsf{\Gamma }(\delta +\beta +\gamma +1)}}\frac{\left(2\left|{\lambda }_1\right|+1\right)}{\left|1-{\lambda }_1\right|}\underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\left(\right|{\mathfrak{T}}_{\mathrm{v}}\left(\mathsf{ὶ}\right)-{\mathfrak{T}}_0\left(\mathsf{ὶ}\right)|+|{\mathfrak{T}}_0\left(\mathsf{ὶ}\right)\left|\right)\hfill \\ \hfill & \le \left[\frac{\left|{\lambda }_3\right|}{\left|\left(1-{\lambda }_3\right)\left(1-{\lambda }_1\right)\right|\mathsf{\Gamma }(\delta +1)}\left(\frac{\left|{\lambda }_2\right|}{\left|1-{\lambda }_2\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}+\frac{1}{\mathsf{\Gamma }(\beta +\gamma +1)}\right)\right.\hfill \\ \hfill & \left.+{\displaystyle \frac{\left|{\lambda }_2\right|}{\left|(1-{\lambda }_2)\left(1-{\lambda }_1\right)\right|\mathsf{\Gamma }(\delta +\gamma +1)\mathsf{\Gamma }(\beta +1)}}+{\displaystyle \frac{\left(2\left|{\lambda }_1\right|+1\right)}{\left|1-{\lambda }_1\right|\mathsf{\Gamma }(\delta +\beta +\gamma +1)}}\right]\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\beta +\gamma +\delta }.\left(\ell {∥\mathrm{v}∥}_{\mathrm{V}}+{\mathfrak{T}}^{\ast }\right).\hfill \end{array}$$

Additionally, we have

$$\begin{array}{cc}\hfill {}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\right)\left(\mathsf{ὶ}\right)& =\frac{{\lambda }_3}{\left(1-{\lambda }_3\right)\mathsf{\Gamma }(\gamma +1)}(\frac{{\lambda }_2{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\left(1-{\lambda }_2\right)}\hfill \\ \hfill & +{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }){\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}{\mathfrak{T}}_{\mathrm{v}}\left({\tau }_2\right)+{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}\left(\frac{{\lambda }_2}{1-{\lambda }_2}{\mathfrak{T}}_{\mathrm{v}}\left({\tau }_2\right)+{\mathfrak{T}}_{\mathrm{v}}\left(\mathsf{ὶ}\right)\right).\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill \left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\right)\left(\mathsf{ὶ}\right)\right|& \le (\frac{\left|{\lambda }_3\right|}{\left|(1-{\lambda }_3)\left(1-{\lambda }_2\right)\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\delta +1)}\hfill \\ \hfill & +\frac{2\left|{\lambda }_2\right|+1}{\left|1-{\lambda }_2\right|\mathsf{\Gamma }(\gamma +\delta +1)})\times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\gamma +\delta }\left(\ell {∥\mathrm{v}∥}_{\mathrm{V}}+{\mathfrak{T}}^{\ast }\right).\hfill \end{array}$$

The last equality

$${{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right)={\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}\left(\frac{{\lambda }_3}{1-{\lambda }_3}{\mathfrak{T}}_{\mathrm{v}}\left({\tau }_2\right)+{\mathfrak{T}}_{\mathrm{v}}\left(\mathsf{ὶ}\right)\right),$$

implies that

$$\left|{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right)\right|\le \frac{\left(2\left|{\lambda }_3\right|+1\right){\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\delta }\left(\ell {∥\mathrm{v}∥}_{\mathrm{V}}+{\mathfrak{T}}^{\ast }\right)}{\left|1-{\lambda }_3\right|\mathsf{\Gamma }(\delta +1)}.$$

From the above inequalities, we obtain

$${\parallel \mathsf{\Psi }\mathrm{v}\parallel }_{\mathrm{V}}\le \Delta \left(\ell ·\varsigma +{\mathfrak{T}}^{\ast }\right).$$

This implies that ${\parallel \mathsf{\Psi }\mathrm{v}\parallel }_{\mathrm{V}}\le \varsigma ,$ which means that $\mathsf{\Psi }\mathrm{v}\in B_{\varsigma }.$ In particular, we notice that

$${\parallel \mathsf{\Psi }0\parallel }_{\mathrm{V}}={\mathfrak{T}}^{\ast }\Delta \le \left(1-\ell \Delta \right)\varsigma .$$

In the next step, the contractive property of the operator $\mathsf{\Psi }$ is investigated. Let $\mathrm{v},\acute{\mathrm{v}}\in \mathrm{V}$; then, we estimate

$$\begin{array}{cc}\hfill \left|\left(\mathsf{\Psi }\mathrm{v}\right)\left(\mathsf{ὶ}\right)\right.& \left.-\left(\mathsf{\Psi }\acute{\mathrm{v}}\right)\left(\mathsf{ὶ}\right)\right|\le \frac{\ell \left|{\lambda }_3\right|{\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\alpha +\beta +\gamma +\delta }{∥\mathrm{v}-\acute{\mathrm{v}}∥}_{\mathrm{V}}}{\mathsf{\Gamma }(\delta +1)\left|(1-{\lambda }_3)\right|}\hfill \\ \hfill & \times \left(\left|A_1\right|+\left|A_2\right|+\left|A_3\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\right)\hfill \\ \hfill & +\frac{\left|{\lambda }_2\right|}{\left|(1-{\lambda }_0)(1-{\lambda }_2)\right|\mathsf{\Gamma }(\gamma +\delta +1)}\left(\left|A_4\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +1)}\right)\hfill \\ \hfill & +\frac{\left|A_5\right|}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\delta +\beta +\gamma +1)}+\frac{\left(2\left|{\lambda }_0\right|+1\right)}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\alpha +\delta +\beta +\gamma +1)}.\hfill \end{array}$$

Additionally, we have

$$\begin{array}{cc}\hfill \left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\left(\mathsf{ὶ}\right)\right.& \left.-{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\acute{\mathrm{v}}\right)\left(\mathsf{ὶ}\right)\right|\hfill \\ \hfill & \le \left[{\displaystyle \frac{\left|{\lambda }_3\right|}{\left|(1-{\lambda }_3)\left(1-{\lambda }_1\right)\right|\mathsf{\Gamma }(\delta +1)}}\right(\frac{\left|{\lambda }_2\right|}{\left|1-{\lambda }_2\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }(\beta +\gamma +1)})+\frac{\left|{\lambda }_2\right|}{\left|\left(1-{\lambda }_2\right)\left(1-{\lambda }_1\right)\right|\mathsf{\Gamma }(\gamma +\delta +1)\mathsf{\Gamma }(\beta +1)}\hfill \\ \hfill & +\frac{\left(2\left|{\lambda }_1\right|+1\right)}{\left|1-{\lambda }_1\right|\mathsf{\Gamma }(\delta +\beta +\gamma +1)}]\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\beta +\gamma +\delta }·\ell {∥\mathrm{v}-\acute{\mathrm{v}}∥}_{\mathrm{V}}.\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\right)\left(\mathsf{ὶ}\right)-{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\acute{\mathrm{v}}\right)\right)\left(\mathsf{ὶ}\right)\right|\hfill \\ \hfill & \le \left({\displaystyle \frac{\left|{\lambda }_3\right|}{\left|(1-{\lambda }_3)\left(1-{\lambda }_2\right)\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\delta +1)}}+\frac{\left(2\left|{\lambda }_2\right|+1\right)}{\left|1-{\lambda }_2\right|\mathsf{\Gamma }(\gamma +\delta +1)}\right)\hfill \\ \hfill & \times {\left|\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right|}^{\gamma +\delta }\ell {∥\mathrm{v}-\acute{\mathrm{v}}∥}_{\mathrm{V}}.\hfill \end{array}$$

Finally,

$$\begin{array}{cc}\hfill & \left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({}^c{\mathcal{D}}_{a^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\right)\right)\left(\mathsf{ὶ}\right)-{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\acute{\mathrm{v}}\right)\right)\right)\left(\mathsf{ὶ}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{\left(2\left|{\lambda }_3\right|+1\right)}{\left|1-{\lambda }_3\right|\mathsf{\Gamma }(\delta +1)}}{\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\delta }·\ell {∥\mathrm{v}-\acute{\mathrm{v}}∥}_{\mathrm{V}}.\hfill \end{array}$$

From the above inequalities, we obtain

$$\parallel \mathsf{\Psi }\mathrm{v}-\mathsf{\Psi }\acute{\mathrm{v}}{\parallel }_{\mathrm{V}}\le \ell \Delta {\parallel \mathrm{v}-\acute{\mathrm{v}}\parallel }_{\mathrm{V}}.$$

Since $\ell \Delta <1$, $\mathsf{\Psi }$ is a contraction on $\mathrm{V}$, and Banach fixed-point theorem guarantees the existence of a unique fixed point for $\mathsf{\Psi }$, and accordingly, the existence of a unique solution for the fractional non-periodic snap problem (7) and the proof are ended. □

The next existence property for possible solutions of the fractional non-periodic snap problem (7) is checked based on hypotheses of Leary-Shauder fixed-point theorem. We assume the following hypotheses:

(H3) 

The function $\mathfrak{T}\in C([{\tau }_1,{\tau }_2]\times {\mathbb{R}}^4).$ Moreover, there exist a monotonic increasing finite real-valued function $\mathfrak{h}\in C[0,\infty )$ and a finite real-valued function $\hslash \in C[{\tau }_1,{\tau }_2]$, such that

$$\left|{\mathfrak{T}}_{\mathrm{v}}\left(\mathsf{ὶ}\right)\right|\le \hslash \left(\mathsf{ὶ}\right)\mathfrak{h}\left(∥\mathrm{v}∥\right),$$

for any $\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$, and $\mathrm{v}=({\mathrm{v}}_1,{\mathrm{v}}_2,{\mathrm{v}}_3,{\mathrm{v}}_4),{\mathrm{v}}_j\in C[{\tau }_1,{\tau }_2],j=1,2,3,4.$;

(H4) 

Let $\varsigma >0$,

$${\hslash }^{\ast }=sup\left\{\hslash \left(\mathsf{ὶ}\right):\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]\right\},$$

and $\varpi \in (0,1)$ such that

$$\varsigma \le \Delta {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)<\varsigma {\varpi }^{-1}.$$

(18)

Theorem 4.

Let (H1) , (H3) and (H4) be held. Then, there exists at least one solution for the fractional non-periodic snap problem (7) on $[{\tau }_1,{\tau }_2]$.

Proof. 

Let $\mathsf{\Psi }:\mathrm{V}\to \mathrm{V}$ be defined as in (16) and $\mathrm{B}$ be any bounded convex closed subset in $\mathrm{V}$. We show that the hypotheses of Leary–Schauder fixed-point theorem can be applied on the operator $\mathsf{\Psi }$. Hence, the proof consists of several steps.

Step 1: 

The continuity of the operator $\mathsf{\Psi }$ is obtained by applying the dominated convergence theorem and noting that the function $\mathfrak{T}$ is jointly continuous.

Step 2: 

We show that $\mathsf{\Psi }:\overline{U_{\varsigma }}\to \mathrm{B}$ is uniformly bounded, where

$$U_{\varsigma }=\left\{\mathrm{v}\in \mathrm{B}:∥\mathrm{v}∥<\varsigma \right\},$$

is an open ball with radius $\varsigma >0$. For $\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$, we easily deduce that

$$\begin{array}{cc}\hfill sup& \left\{\left|{\mathfrak{T}}_{\mathrm{v}}\left(\mathsf{ὶ}\right)\right|:\mathsf{ὶ}\in [{\tau }_1,{\tau }_2],\mathrm{v}\in {\overline{U}}_{\varsigma }\right\}\hfill \\ \hfill & \le sup\left\{\hslash \left(\mathsf{ὶ}\right)\mathfrak{h}\left(∥\mathrm{v}∥\right):\mathsf{ὶ}\in [{\tau }_1,{\tau }_2],\mathrm{v}\in {\overline{U}}_{\varsigma }\right\}\hfill \\ \hfill & \le sup\left\{\hslash \left(\mathsf{ὶ}\right):\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]\right\}·sup\left\{\mathfrak{h}\left(∥\mathrm{v}∥\right):\mathrm{v}\in {\overline{U}}_{\varsigma }\right\}\hfill \\ \hfill & \le {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right).\hfill \end{array}$$

Then, for any $\mathrm{v}\in {\overline{U}}_{\varsigma },$ and $\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$, we can obtain

$$\begin{array}{cc}\hfill \left|\left(\mathsf{\Psi }\mathrm{v}\right)\left(\mathsf{ὶ}\right)\right|& \le \left[\frac{\left|{\lambda }_3\right|}{\mathsf{\Gamma }(\delta +1)\left|1-{\lambda }_3\right|}\left(\left|A_1\right|+\left|A_2\right|+\left|A_3\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\right)\right.\hfill \\ \hfill & +\frac{\left|{\lambda }_2\right|}{\left|(1-{\lambda }_0)(1-{\lambda }_2)\right|\mathsf{\Gamma }(\gamma +\delta +1)}\left(\left|A_4\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +1)}\right)\hfill \\ \hfill & \left.+\left(\frac{\left|A_5\right|}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\delta +\beta +\gamma +1)}+\frac{\left(2\left|{\lambda }_0\right|+1\right)}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\alpha +\delta +\beta +\gamma +1)}\right)\right]\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\alpha +\beta +\gamma +\delta }{\hslash }^{\ast }\mathfrak{h}\left(\varrho \right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \left|{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathsf{\Psi }x\left(\mathsf{ὶ}\right)\right|& \le [\frac{\left|{\lambda }_3\right|}{\left|\left(1-{\lambda }_3\right)\left(1-{\lambda }_1\right)\right|\mathsf{\Gamma }(\delta +1)}\hfill \\ \hfill & \times \left(\frac{\left|{\lambda }_2\right|}{\left|1-{\lambda }_2\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}+\frac{1}{\mathsf{\Gamma }(\beta +\gamma +1)}\right)\hfill \\ \hfill & +{\displaystyle \frac{\left|{\lambda }_2\right|}{\left|(1-{\lambda }_2)\left(1-{\lambda }_1\right)\right|\mathsf{\Gamma }(\delta +\gamma +1)\mathsf{\Gamma }(\beta +1)}}\hfill \\ \hfill & +{\displaystyle \frac{\left(2\left|{\lambda }_1\right|+1\right)}{\left|1-{\lambda }_1\right|\mathsf{\Gamma }(\delta +\beta +\gamma +1)}}]{\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\beta +\gamma +\delta }{\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right).\hfill \end{array}$$

Similarly, we have

$$\begin{array}{cc}\hfill \left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\right.& \left.\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\right)\left(\mathsf{ὶ}\right)\right|\hfill \\ \hfill & \le ({\displaystyle \frac{\left|{\lambda }_3\right|}{(\left|1-{\lambda }_3)\left(1-{\lambda }_2\right)\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\delta +1)}}\hfill \\ \hfill & +\frac{\left(2\left|{\lambda }_2\right|+1\right)}{\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +\delta +1)}){\left|\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right|}^{\gamma +\delta }{\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right),\hfill \end{array}$$

and

$$\left|{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right)\right|\le {\displaystyle \frac{\left(2\left|{\lambda }_3\right|+1\right)}{\left|1-{\lambda }_3\right|\mathsf{\Gamma }(\delta +1)}}\times {\left|\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right|}^{\delta }{\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right).$$

From the above inequalities, we obtain

$${\parallel \mathsf{\Psi }\mathrm{v}\parallel }_{\mathrm{V}}\le \Delta {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right),$$

independently of the element $\mathrm{v}\in {\overline{U}}_{\varsigma }$, which implies that $\mathsf{\Psi }\left({\overline{U}}_{\varsigma }\right)\subseteq \mathrm{B}$ is uniformly bounded.

Step 3: 

Now, we show that $\mathsf{\Psi }$ is equicontinuous. Let ${\mathsf{ὶ}}_1,{\mathsf{ὶ}}_2\in [{\tau }_1,{\tau }_2],$ such that

$${\tau }_1\le {\mathsf{ὶ}}_1<{\mathsf{ὶ}}_2\le {\tau }_2,$$

and $\mathrm{v}\in {\overline{U}}_{\varsigma }$, we deduce

$$\begin{array}{cc}\hfill \left|\left(\mathsf{\Psi }\mathrm{v}\right)\left({\mathsf{ὶ}}_2\right)\right.& \left.-\left(\mathsf{\Psi }\mathrm{v}\right)\left({\mathsf{ὶ}}_1\right)\right|\hfill \\ \hfill & \le \left|\frac{{\lambda }_3}{(1-{\lambda }_3)\mathsf{\Gamma }\left(\delta +1\right)}\right|[\left|A_2\right|{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\delta +\beta +\gamma }\hfill \\ \hfill & \times \left({(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }-{(\mathbb{G}\left({\mathsf{ὶ}}_1\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }\right)+\frac{{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\delta }}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\hfill \\ \hfill & \times \left({(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta +\gamma }-{(\mathbb{G}\left({\mathsf{ὶ}}_1\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta +\gamma }\right)]{\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }(\delta +\gamma +1)}\left|\frac{{\lambda }_2}{1-{\lambda }_2}\right|[\left|A_4\right|{\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\beta +\gamma +\delta }\hfill \\ \hfill & \times \left({(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }-{(\mathbb{G}\left({\mathsf{ὶ}}_1\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }\right)+\frac{{\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\delta +\gamma }}{\mathsf{\Gamma }(\alpha +\beta +1)}\hfill \\ \hfill & \times \left({(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }-{(\mathbb{G}\left({\mathsf{ὶ}}_1\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }\right)]{\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)\hfill \\ \hfill & +\frac{\left|A_5\right|}{\mathsf{\Gamma }(\beta +\gamma +\delta +1)}{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\delta +\beta +\gamma }\hfill \\ \hfill & \times \left({(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }-{(\mathbb{G}\left({\mathsf{ὶ}}_1\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }\right){\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }(\alpha +\beta +\gamma +\delta +1)}[{(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta +\gamma +\delta }\hfill \\ \hfill & -{(\mathbb{G}\left({\mathsf{ὶ}}_1\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta +\gamma +\delta }+2{(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\mathsf{ὶ}}_1\right))}^{\delta +\beta +\gamma }]{\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \left|{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathsf{\Psi }\mathrm{v}\left({\mathsf{ὶ}}_2\right)\right.& \left.-{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathsf{\Psi }\mathrm{v}\left({\mathsf{ὶ}}_1\right)\right|\hfill \\ \hfill & \le \frac{{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\delta }}{\mathsf{\Gamma }(\delta +1)}[\frac{\left|{\lambda }_3{\lambda }_2\right|{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\left|\left(1-{\lambda }_3\right)\left(1-{\lambda }_2\right)\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}\hfill \\ \hfill & \times \left[{(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta }-{(\mathbb{G}\left({\mathsf{ὶ}}_1\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta }\right]\hfill \\ \hfill & +\frac{\left|{\lambda }_3\right|}{\left|1-{\lambda }_3\right|\mathsf{\Gamma }(\beta +\gamma +1)}\hfill \\ \hfill & \times \left[{(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta +\gamma }-{(\mathbb{G}\left({\mathsf{ὶ}}_1\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta +\gamma }\right]]{\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)\hfill \\ \hfill & +\frac{\left|{\lambda }_2\right|{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\delta +\gamma }}{\left|1-{\lambda }_2\right|\mathsf{\Gamma }(\delta +\gamma +1)\mathsf{\Gamma }(\beta +1)}\hfill \\ \hfill & \times \left[{(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta }-{(\mathbb{G}\left({\mathsf{ὶ}}_1\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta }\right]{\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }(\delta +\beta +\gamma +1)}[2{(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\mathsf{ὶ}}_1\right))}^{\delta +\beta +\gamma }\hfill \\ \hfill & +{(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\delta +\beta +\gamma }-{\left(\mathbb{G}\left({\mathsf{ὶ}}_1\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\delta +\beta +\gamma }]{\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)\hfill \end{array}$$

Similarly, we have

$$\begin{array}{cc}\hfill \left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\right)\left({\mathsf{ὶ}}_2\right)\right.& \left.-{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\right)\left({\mathsf{ὶ}}_2\right)\right|\hfill \\ \hfill & \le \frac{\left|{\lambda }_3\right|{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\delta }}{\left|1-{\lambda }_3\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\delta +1)}|{(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }\hfill \\ \hfill & -{(\mathbb{G}\left({\mathsf{ὶ}}_1\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }|{\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }(\delta +\gamma +1)}[2\left({(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\mathsf{ὶ}}_1\right))}^{\delta +\gamma }\right)\hfill \\ \hfill & +{(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\delta +\beta +\gamma }-{(\mathbb{G}\left({\mathsf{ὶ}}_1\right)-\mathbb{G}\left({\tau }_1\right))}^{\delta +\gamma }]{\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right).\hfill \end{array}$$

Additionally, we have

$$\begin{array}{cc}\hfill \left|{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\right.& \left.\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right))\left({\mathsf{ὶ}}_2\right)\right)\right)-{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right))\left({\mathsf{ὶ}}_1\right)\right)\right)\right|\hfill \\ \hfill & \le \frac{{\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)}{\mathsf{\Gamma }(\delta +1)}[2{\left(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\mathsf{ὶ}}_1\right)\right)}^{\delta +1}\hfill \\ \hfill & +{\left(\mathbb{G}\left({\mathsf{ὶ}}_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\delta +1}-{\left(\mathbb{G}\left({\mathsf{ὶ}}_1\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\delta +1}].\hfill \end{array}$$

From the above inequalities, we obtain

$$\left\{\begin{array}{c}|\left(\mathsf{\Psi }\mathrm{v}\right)\left({\mathsf{ὶ}}_2\right)-\left(\mathsf{\Psi }\mathrm{v}\right)\left({\mathsf{ὶ}}_1\right)|\to 0,\hfill \\ \left|{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\left({\mathsf{ὶ}}_2\right)-{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\left({\mathsf{ὶ}}_1\right)\right|\to 0,\hfill \\ \left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\right)\left({\mathsf{ὶ}}_2\right)-{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\right)\left({\mathsf{ὶ}}_2\right)\right|\to 0,\hfill \\ \left|{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\right)\left({\mathsf{ὶ}}_2\right)\right)-{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\left(\mathsf{\Psi }\mathrm{v}\right)\right)\left({\mathsf{ὶ}}_1\right)\right)\right|\to 0,\hfill \end{array}\right.$$

as ${\mathsf{ὶ}}_2\to {\mathsf{ὶ}}_1,$ independently of $\mathsf{ὶ}$, which implies that $\mathsf{\Psi }\left({\overline{U}}_{\varsigma }\right)$ is equicontinuous. Using the Arzelà–Ascoli theorem, we deduce that $\mathsf{\Psi }$ is compact on ${\overline{U}}_{\varsigma }$. If there exist $\mathrm{v}\in \partial U$ and $\varpi \in (0,1)$ such that $\mathrm{v}=\varpi \mathsf{\Psi }\mathrm{v}$, then

$$\mathrm{v}={∥\mathrm{v}∥}_{\mathrm{V}}=\varpi {∥\mathsf{\Psi }\mathrm{v}∥}_{\mathrm{V}}\le \varpi \Delta {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)<\varsigma ,$$

which draws a contradiction.

Therefore, by Leray–Schauder fixed-point theorem, $\mathsf{\Psi }$ admits at least one fixed point $\mathrm{v}\in {\overline{U}}_{\varsigma }$ as a solution of the fractional non-periodic snap problem (7), and this finishes the proof. □

4. Stability Criterion

We introduce in this section many stability criteria, namely, the Ulam–Hyers and Ulam–Hyers–Rassias, with their generalizations for the solutions of the fractional non-periodic snap problem (7) on $[{\tau }_1,{\tau }_2]$.

Definition 1

([21]). The fractional non-periodic snap problem (7) is Ulam–Hyers stable if there exists a positive real number ${\chi }_{\mathfrak{T}}^{\ast }$, such that for any $\epsilon >0$, and ${\mathrm{v}}^{\ast }\in \mathrm{V}$ satisfying

$$\left|{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}{\mathrm{v}}^{\ast }\left(\mathsf{ὶ}\right)\right)\right)\right)-{\mathfrak{T}}_{{\mathrm{v}}^{\ast }}\left(\mathrm{v}\right)\right|<\epsilon ,\mathsf{ὶ}\in ({\tau }_1,{\tau }_2),$$

(19)

there exists $\mathrm{v}\in \mathrm{V}$ satisfying the fractional non-periodic snap problem (7) with

$${∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}\le \epsilon {\chi }_{\mathfrak{T}}^{\ast }.$$

Definition 2.

The fractional non-periodic snap problem (7) is generalized Ulam–Hyers stable if there exists a function ${\pi }_{\mathfrak{T}}^{\ast }\in C[0,\infty )$ with ${\pi }_{\mathfrak{T}}^{\ast }\left(0\right)=0$ such that, for any $\epsilon >0$ and ${\mathrm{v}}^{\ast }\in \mathrm{V}$ satisfying the inequality (19), there exists $\mathrm{v}\in \mathrm{V}$ as a solution of the fractional non-periodic snap problem (7) with

$${∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}\le {\pi }_{\mathfrak{T}}^{\ast }\left(\epsilon \right).$$

Definition 3.

The fractional non-periodic snap problem (7) is Ulam–Hyers–Rassias stable with respect to a function $\vartheta \in C[{\tau }_1,{\tau }_2]$ if there exists a positive real number ${\chi }_{\mathfrak{T}}^{\ast }$, such that for any $\epsilon >0$, and ${\mathrm{v}}^{\ast }\in \mathrm{V}$ satisfying

$$\left|{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}{\mathrm{v}}^{\ast }\left(\mathsf{ὶ}\right)\right)\right)\right)-{\mathfrak{T}}_{{\mathrm{v}}^{\ast }}\left(\mathsf{ὶ}\right)\right|<\epsilon \vartheta \left(\mathsf{ὶ}\right),\mathsf{ὶ}\in ({\tau }_1,{\tau }_2)$$

(20)

there exists $\mathrm{v}\in \mathrm{V}$ satisfying the fractional non-periodic snap problem (7) with

$${∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}\le \epsilon {\chi }_{\mathfrak{T}}^{\ast }\underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\vartheta \left(\mathsf{ὶ}\right).$$

Definition 4.

The fractional non-periodic snap problem (7) is generalized Ulam–Hyers–Rassias stable with respect to a function $\vartheta \in C[{\tau }_1,{\tau }_2]$ if for any ${\mathrm{v}}^{\ast }\in \mathrm{V}$, satisfying

$$\left|{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}{\mathrm{v}}^{\ast }\left(\mathsf{ὶ}\right)\right)\right)\right)-{\mathfrak{T}}_{{\mathrm{v}}^{\ast }}\left(\mathsf{ὶ}\right)\right|<\vartheta \left(\mathsf{ὶ}\right),\mathsf{ὶ}\in ({\tau }_1,{\tau }_2)$$

there exists $\mathrm{v}\in \mathrm{V}$ satisfying the fractional non-periodic snap problem (7) with

$${∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}\le \underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\vartheta \left(\mathsf{ὶ}\right).$$

Remark 1.

The relationships among these kinds of stability can be summarized by the following implications:

(i) 

Definition 2 ⇒ Definition 1, if ${\pi }_{\mathfrak{T}}^{\ast }\left(\epsilon \right)=\epsilon {\chi }_{\mathfrak{T}}^{\ast }$;

(ii) 

Definition 3 ⇒ Definition 4, if ${\chi }_{\mathfrak{T}}^{\ast }$=${\epsilon }^{-1}$;

(iii) 

Definition 3 ⇒ Definition 1, if $\vartheta \left(\mathsf{ὶ}\right)=1$.

Remark 2.

Notice that ${\mathrm{v}}^{\ast }$$\in \mathrm{V}$ satisfies the inequality (19) iff there exists $\rho \in C[{\tau }_1,{\tau }_2]$ such that

(i) 

$\left|\rho \right(\mathsf{ὶ}\left)\right|<\epsilon$, $\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$,

(ii) 

${{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}{\mathrm{v}}^{\ast }\left(\mathsf{ὶ}\right)\right)\right)\right)={\mathfrak{T}}_{{\mathrm{v}}^{\ast }}\left(\mathsf{ὶ}\right)+\rho \left(\mathsf{ὶ}\right),\mathsf{ὶ}\in ({\tau }_1,{\tau }_2)$.

Remark 3.

Notice that ${\mathrm{v}}^{\ast }\in \mathrm{V}$ satisfies the inequality (20) iff there exists $\sigma \in C[{\tau }_1,{\tau }_2]$ such that

(i) 

$|\sigma \left(\mathsf{ὶ}\right)|<\epsilon \vartheta \left(\mathsf{ὶ}\right)$,

(ii) 

${{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}{x}^{\ast }\left(\mathsf{ὶ}\right)\right)\right)\right)={\mathfrak{T}}_{{\mathrm{v}}^{\ast }}\left(\mathsf{ὶ}\right)+\sigma \left(\mathsf{ὶ}\right),\mathsf{ὶ}\in ({\tau }_1,{\tau }_2)$.

The Ulam–Hyers stability of the fractional non-periodic snap problem (7) is investigated by the next result.

Theorem 5.

Let (H1) and (H2) be held; then, the fractional non-periodic snap problem (7) is Ulam–Hyers stable, and accordingly is Ulam–Hyers–Rassias stable provided that $\ell \Delta <1$.

Proof. 

For every $\epsilon >0$ and ${\mathrm{v}}^{\ast }\in \mathrm{V}$ satisfying (19), we can find a function $\rho \in C[{\tau }_1,{\tau }_2]$ satisfying

$${{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}{\mathrm{v}}^{\ast }\left(\mathsf{ὶ}\right)\right)\right)\right)={\mathfrak{T}}_{{\mathrm{v}}^{\ast }}\left(\mathsf{ὶ}\right)+\rho \left(\mathsf{ὶ}\right),\mathsf{ὶ}\in ({\tau }_1,{\tau }_2),$$

with $\left|\rho \right(\mathsf{ὶ}\left)\right|\le \epsilon$. It follows by Lemma 3 that

$$\begin{array}{cc}\hfill {\mathrm{v}}^{\ast }\left(\mathsf{ὶ}\right)& =\frac{{\lambda }_3}{\left(1-{\lambda }_3\right)}[A_1{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta +\gamma }\hfill \\ \hfill & +A_2{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta +\gamma }\hfill \\ \hfill & +{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }(A_3{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }\hfill \\ \hfill & +\frac{{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\gamma }}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\left)\right]{\mathcal{I}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}({\mathfrak{T}}_{{\mathrm{v}}^{\ast }}\left({\tau }_2\right)+\rho \left({\tau }_2\right))\hfill \\ \hfill & +\frac{{\lambda }_2}{1-{\lambda }_2}\left[A_4\right({(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\beta }(\frac{{\lambda }_0{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }}{\left(1-{\lambda }_0\right)}\hfill \\ \hfill & +{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }\left)\right)+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +1)}(\frac{{\lambda }_0{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }}{\left(1-{\lambda }_0\right)}\hfill \\ \hfill & +{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha +\beta }\left)\right]{\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\gamma ;\mathbb{G}}(f_{x^{\ast }}\left({\tau }_2\right)+\rho \left({\tau }_2\right))\hfill \\ \hfill & +\frac{{\lambda }_1}{\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\alpha +1)}(\frac{{\lambda }_0{(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }}{1-{\lambda }_0}\hfill \\ \hfill & +{(\mathbb{G}\left(\mathsf{ὶ}\right)-\mathbb{G}\left({\tau }_1\right))}^{\alpha }){\mathcal{I}}_{{\tau }_1^{+}}^{\delta +\beta +\gamma ;\mathbb{G}}({\mathfrak{T}}_{{\mathrm{v}}^{\ast }}\left({\tau }_2\right)+\rho \left({\tau }_2\right))\hfill \\ \hfill & +{\mathcal{I}}_{{\tau }_1^{+}}^{\alpha +\delta +\beta +\gamma ;\mathbb{G}}\left(\frac{{\lambda }_0}{1-{\lambda }_0}\left({\mathfrak{T}}_{{\mathrm{v}}^{\ast }}\left({\tau }_2\right)+\rho \left({\tau }_2\right)\right)+\left({\mathfrak{T}}_{{\mathrm{v}}^{\ast }}\left(\mathsf{ὶ}\right)+\rho \left(\mathsf{ὶ}\right)\right)\right).\hfill \end{array}$$

Using Theorem 3, there exists a unique solution $\mathrm{v}\in \mathrm{V}$ satisfying the fractional non-periodic snap problem (7). Then,

$$\begin{array}{cc}\hfill \left|{\mathrm{v}}^{\ast }\left(\mathsf{ὶ}\right)-\mathrm{v}\left(\mathsf{ὶ}\right)\right|& \le \frac{\left|{\lambda }_3\right|}{\mathsf{\Gamma }(\delta +1)\left|1-{\lambda }_3\right|}[\left|A_1\right|+\left|A_2\right|+\left|A_3\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\hfill \\ \hfill & +\frac{\left|{\lambda }_2\right|}{\left|(1-{\lambda }_0)(1-{\lambda }_2)\right|\mathsf{\Gamma }(\gamma +\delta +1)}\left(\left|A_4\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +1)}\right)\hfill \\ \hfill & +\frac{\left|A_5\right|}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\delta +\beta +\gamma +1)}+\frac{2\left|{\lambda }_0\right|+1}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\alpha +\delta +\beta +\gamma +1)}]\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\alpha +\beta +\gamma +\delta }\left(\ell {∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}+\epsilon \right).\hfill \end{array}$$

Additionally, we have

$$\begin{array}{cc}\hfill \left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}{\mathrm{v}}^{\ast }\left(\mathsf{ὶ}\right)\right.& \left.-{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right|\hfill \\ \hfill & \le \left[{\displaystyle \frac{\left|{\lambda }_3\right|}{\left|(1-{\lambda }_3)\left(1-{\lambda }_1\right)\right|\mathsf{\Gamma }(\delta +1)}}\right(\frac{\left|{\lambda }_2\right|}{\left|1-{\lambda }_2\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }(\beta +\gamma +1)})+\frac{\left|{\lambda }_2\right|}{\left|\left(1-{\lambda }_2\right)\left(1-{\lambda }_1\right)\right|\mathsf{\Gamma }(\gamma +\delta +1)\mathsf{\Gamma }(\beta +1)}\hfill \\ \hfill & +\frac{2\left|{\lambda }_1\right|+1}{\left|1-{\lambda }_1\right|\mathsf{\Gamma }(\delta +\beta +\gamma +1)}]\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\beta +\gamma +\delta }\left(\ell {∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}+\epsilon \right).\hfill \end{array}$$

Similarly, we have

$$\begin{array}{cc}\hfill \left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}{\mathrm{v}}^{\ast }\right)\left(\mathsf{ὶ}\right)\right.& \left.-{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\right)\left(\mathsf{ὶ}\right)\right|\hfill \\ \hfill & \le [{\displaystyle \frac{{\lambda }_3}{\left|(1-{\lambda }_3)\left(1-{\lambda }_2\right)\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\delta +1)}}\hfill \\ \hfill & +\frac{2\left|{\lambda }_2\right|+1}{\left|1-{\lambda }_2\right|\mathsf{\Gamma }(\gamma +\delta +1)}]{\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\gamma +\delta }\left(\ell {∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}+\epsilon \right).\hfill \end{array}$$

Finally,

$$\begin{array}{cc}\hfill \left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}{x}^{\ast }\right)\right)\left(\mathsf{ὶ}\right)\right.& \left.-{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\right)\left(\mathsf{ὶ}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{2\left|{\lambda }_3\right|+1}{\left|1-{\lambda }_3\right|\mathsf{\Gamma }(\delta +1)}}{\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\delta }\left(\ell {∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}+\epsilon \right).\hfill \end{array}$$

From the above inequalities, we obtain

$${∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}\le \Delta \left(\ell {∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}+\epsilon \right)\le {\displaystyle \frac{\Delta }{1-\ell \Delta }}\epsilon .$$

Since $\ell \Delta <1$, this shows the existence of a positive real

$${\chi }_{\mathfrak{T}}^{\ast }={\displaystyle \frac{\Delta }{1-\ell \Delta }}>0,$$

and hence according to Definition 1, the solution of (7) is Ulam–Hyers stable. Similarly, it shows the existence of a function ${\pi }_{\mathfrak{T}}^{\ast }\in C[0,\infty )$ with ${\pi }_{\mathfrak{T}}^{\ast }$$\left(0\right)=0$ such that

$${\pi }_{\mathfrak{T}}^{\ast }\left(\epsilon \right)={\displaystyle \frac{\Delta }{1-\ell \Delta }}\epsilon .$$

Hence, the solution of (7) is GUH stable. □

The UHR stability for the fractional non-periodic snap problem (7) is checked in the following.

Theorem 6.

Let (H1) and (H2) be held. Then, the fractional non-periodic snap problem (7) is Ulam–Hyers–Rassias stable, and accordingly, is generalized Ulam–Hyers–Rassias stable.

Proof. 

For every $\epsilon >0$ and ${\mathrm{v}}^{\ast }\in \mathrm{V}$ satisfying (20), we can find a function $\sigma \in C[{\tau }_1,{\tau }_2]$ satisfying

$${{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\delta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}{\mathrm{v}}^{\ast }\left(\mathsf{ὶ}\right)\right)\right)\right)={\mathrm{v}}_{{\mathrm{v}}^{\ast }}\left(\mathsf{ὶ}\right)+\sigma \left(\mathsf{ὶ}\right),$$

such that $|\sigma \left(\mathsf{ὶ}\right)|\le \epsilon \vartheta \left(\mathsf{ὶ}\right)$. Using Theorem 3, there exists a unique solution $\mathrm{v}\in \mathrm{V}$ satisfying the fractional non-periodic snap problem (7). It follows by Lemma 3 that

$$\begin{array}{c}\hfill \left|{\mathrm{v}}^{\ast }\left(\mathsf{ὶ}\right)-\mathrm{v}\left(\mathsf{ὶ}\right)\right|\\ \hfill & \le \frac{\left|{\lambda }_3\right|}{\mathsf{\Gamma }(\delta +1)\left|1-{\lambda }_3\right|}[\left|A_1\right|+\left|A_2\right|+\left|A_3\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\hfill \\ \hfill & +\frac{\left|{\lambda }_2\right|}{\left|(1-{\lambda }_0)(1-{\lambda }_2)\right|\mathsf{\Gamma }(\gamma +\delta +1)}\left(\left|A_4\right|+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +1)}\right)\hfill \\ \hfill & +\frac{\left|A_5\right|}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\delta +\beta +\gamma +1)}+\frac{2\left|{\lambda }_0\right|+1}{\left|1-{\lambda }_0\right|\mathsf{\Gamma }(\alpha +\delta +\beta +\gamma +1)}]\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\alpha +\beta +\gamma +\delta }\left(\ell {∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}+\epsilon \underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\vartheta \left(\mathsf{ὶ}\right)\right).\hfill \end{array}$$

Additionally, we have

$$\begin{array}{cc}\hfill \left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}{\mathrm{v}}^{\ast }\left(\mathsf{ὶ}\right)\right.& \left.-{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right|\le \hfill \\ \hfill & \le \left[{\displaystyle \frac{\left|{\lambda }_3\right|}{\left|(1-{\lambda }_3)\left(1-{\lambda }_1\right)\right|\mathsf{\Gamma }(\delta +1)}}\right(\frac{\left|{\lambda }_2\right|}{\left|1-{\lambda }_2\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }(\beta +\gamma +1)})+\frac{\left|{\lambda }_2\right|}{\left|\left(1-{\lambda }_2\right)\left(1-{\lambda }_1\right)\right|\mathsf{\Gamma }(\gamma +\delta +1)\mathsf{\Gamma }(\beta +1)}\hfill \\ \hfill & +\frac{\left(2\left|{\lambda }_1\right|+1\right)}{\left|1-{\lambda }_1\right|\mathsf{\Gamma }(\delta +\beta +\gamma +1)}]\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\beta +\gamma +\delta }\left(\ell {∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}+\epsilon \underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\vartheta \left(\mathsf{ὶ}\right)\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}{\mathrm{v}}^{\ast }\right)\left(\mathsf{ὶ}\right)\right.& \left.-{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\right)\left(\mathsf{ὶ}\right)\right|\hfill \\ \hfill & \le \left[{\displaystyle \frac{{\lambda }_3}{\left|(1-{\lambda }_3)\left(1-{\lambda }_2\right)\right|\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\delta +1)}}+\frac{2\left|{\lambda }_2\right|+1}{\left|1-{\lambda }_2\right|\mathsf{\Gamma }(\gamma +\delta +1)}\right]\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\gamma +\delta }\left(\ell {∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}+\epsilon \underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\vartheta \left(\mathsf{ὶ}\right)\right).\hfill \end{array}$$

Finally

$$\begin{array}{cc}\hfill \left|{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}{\mathrm{v}}^{\ast }\right)\right)\left(\mathsf{ὶ}\right)\right.& \left.-{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\gamma ;\mathbb{G}}\left({}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\beta ;\mathbb{G}}{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\right)\left(\mathsf{ὶ}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{2\left|{\lambda }_3\right|+1}{\left|1-{\lambda }_3\right|\mathsf{\Gamma }(\delta +1)}}\hfill \\ \hfill & \times {\left(\mathbb{G}\left({\tau }_2\right)-\mathbb{G}\left({\tau }_1\right)\right)}^{\delta }\left(\ell {∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}+\epsilon \underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\vartheta \left(\mathsf{ὶ}\right)\right).\hfill \end{array}$$

From the above inequalities, we obtain

$$\begin{array}{cc}\hfill {∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}& \le \Delta \left(\ell {∥{\mathrm{v}}^{\ast }-\mathrm{v}∥}_{\mathrm{V}}+\epsilon \underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\vartheta \left(\mathsf{ὶ}\right)\right)\hfill \\ \hfill & \le \frac{\epsilon \Delta }{1-\ell \Delta }\underset{\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]}{sup}\vartheta \left(\mathsf{ὶ}\right).\hfill \end{array}$$

Since $\ell \Delta <1$, this shows the existence of a positive real number

$${\chi }_{\mathfrak{T}}^{\ast }={\displaystyle \frac{\Delta }{1-\ell \Delta }}.$$

Hence, according to Definition 3, the solution of (7) is Ulam–Hyers–Rassias stable. Therefore, the solution of (7) is generalized Ulam–Hyers–Rassias stable. □

5. Numerical Applications

We give here some examples of the fractional non-periodic snap problem (7) based on numerical simulation to analyze their solutions. In these examples, we consider different cases of the function $\mathbb{G}$ to cover the Caputo, Caputo–Hadamard and Katugampola versions with different orders.

Example 1.

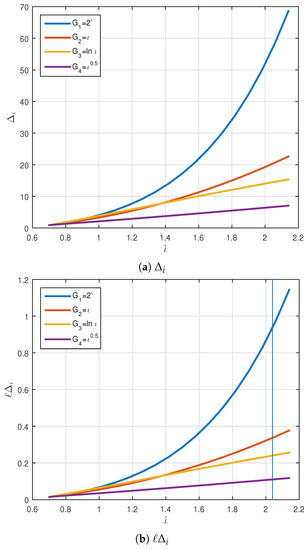
We consider a nonlinear fractional non-periodic snap problem as

$$\left\{\begin{array}{c}{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)={\mathrm{v}}_1\left(\mathsf{ὶ}\right),\hfill \\ {{}^c\mathcal{D}}_{0.7^{+}}^{0.66;\mathbb{G}}{\mathrm{v}}_1\left(\mathsf{ὶ}\right)={\mathrm{v}}_2\left(\mathsf{ὶ}\right),\hfill \\ {{}^c\mathcal{D}}_{0.7^{+}}^{0.25;\mathbb{G}}{\mathrm{v}}_2\left(\mathsf{ὶ}\right)={\mathrm{v}}_3\left(\mathsf{ὶ}\right),\hfill \\ {{}^c\mathcal{D}}_{0.7^{+}}^{0.79;\mathbb{G}}{\mathrm{v}}_3\left(\mathsf{ὶ}\right)={\displaystyle \frac{3\mathsf{ὶ}}{100(\sqrt{3}+{\mathsf{ὶ}}^2)}}+{\displaystyle \frac{{arctan}^2\left(\mathrm{v}\right)}{60\left(1+{arctan}^2\left(\mathrm{v}\right)\right)}}\hfill \\ +{\displaystyle \frac{exp\left(\right|{\mathrm{v}}_1\left|\right)}{75\left(\sqrt{3}+exp\left(\right|{\mathrm{v}}_1\left|\right)\right)}}+{\displaystyle \frac{1}{120}}arcsin{\displaystyle \frac{{\mathrm{v}}_2}{\sqrt[3]{1+{\mathrm{v}}_2}}}\hfill \\ +{\displaystyle \frac{\mathsf{ὶ}}{100}}{\displaystyle \frac{sin|{\mathrm{v}}_3|}{15+sin|{\mathrm{v}}_3|}},\hfill \end{array}\right.$$

(21)

for $\mathsf{ὶ}\in [0.7,2.1]$ and $\mathrm{v}\left(0.7\right)=-12.5\mathrm{v}\left(2.1\right)$,

$${\mathrm{v}}_1\left(0.7\right)=4.3{\mathrm{v}}_1\left(2.1\right),{\mathrm{v}}_2\left(0.7\right)=5.6{\mathrm{v}}_2\left(2.1\right),{\mathrm{v}}_3\left(0.7\right)=13.82{\mathrm{v}}_3\left(2.1\right).$$

Clearly ${\tau }_1=0.7$, ${\tau }_2=2.1$, $\alpha =0.43$, $\beta =0.66$, $\gamma =0.25$, $\delta =0.79$ and

$$\begin{array}{cc}\hfill \mathfrak{T}(\mathsf{ὶ},\mathrm{v},{\mathrm{v}}_1,{\mathrm{v}}_2,{\mathrm{v}}_3)& =\frac{3\mathsf{ὶ}}{100(\sqrt{3}+{\mathsf{ὶ}}^2)}+\frac{{arctan}^2\left(\mathrm{v}\right)}{60\left(1+{arctan}^2\left(\mathrm{v}\right)\right)}\hfill \\ \hfill & +\frac{exp\left(\right|{\mathrm{v}}_1\left|\right)}{75\left(\sqrt{3}+exp\left(\right|{\mathrm{v}}_1\left|\right)\right)}+\frac{1}{120}arcsin\frac{{\mathrm{v}}_2}{\sqrt[3]{1+{\mathrm{v}}_2}}\hfill \\ \hfill & +\frac{\mathsf{ὶ}}{100}\frac{sin|{\mathrm{v}}_3|}{15+sin|{\mathrm{v}}_3|}.\hfill \end{array}$$

Thus, we can rewrite the above system as

$$\left\{\begin{array}{c}{{}^c\mathcal{D}}_{0.7^{+}}^{0.79;\mathbb{G}}\left({}^c{\mathcal{D}}_{0.7^{+}}^{0.25;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.66;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right)\right)\hfill \\ ={\displaystyle \frac{3\mathsf{ὶ}}{100(\sqrt{3}+{\mathsf{ὶ}}^2)}}+{\displaystyle \frac{{arctan}^2\left(\mathrm{v}\left(\mathsf{ὶ}\right)\right)}{60\left(1+{arctan}^2\left(\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right)}}\hfill \\ +{\displaystyle \frac{exp\left(\left|{{}^c\mathcal{D}}_{0.7^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right|\right)}{75\left(\sqrt{3}+exp\left(\left|{{}^c\mathcal{D}}_{0.7^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right|\right)\right)}}\hfill \\ +{\displaystyle \frac{1}{120}}arcsin{\displaystyle \frac{{{}^c\mathcal{D}}_{0.7^{+}}^{0.66;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)}{\sqrt[3]{1+{{}^c\mathcal{D}}_{0.7^{+}}^{0.66;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)}}}\hfill \\ +{\displaystyle \frac{\mathsf{ὶ}}{100}}{\displaystyle \frac{sin\left|{{}^c\mathcal{D}}_{0.7^{+}}^{0.79;\mathbb{G}}\left({}^c{\mathcal{D}}_{0.7^{+}}^{0.25;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.66;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right)\right)\right|}{15+sin\left|{{}^c\mathcal{D}}_{0.7^{+}}^{0.79;\mathbb{G}}\left({}^c{\mathcal{D}}_{0.7^{+}}^{0.25;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.66;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)\right)\right)\right)\right|}},\hfill \\ \mathrm{v}\left(0.7\right)=-12.5\mathrm{v}\left(2.1\right),{}^c{\mathcal{D}}_{0.7^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(0.7\right)=4.3{}^c{\mathcal{D}}_{0.7^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(2.1\right),\hfill \\ {}^c{\mathcal{D}}_{0.7^{+}}^{0.66;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(0.7\right)\right)=5.6{}^c{\mathcal{D}}_{0.7^{+}}^{0.66;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(2.1\right)\right),\hfill \\ {}^c{\mathcal{D}}_{0.7^{+}}^{0.25;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.66;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(0.7\right)\right)\right)\hfill \\ =13.82{}^c{\mathcal{D}}_{{\tau }_1^{+}}^{0.25;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.66;\mathbb{G}}\left({{}^c\mathcal{D}}_{0.7^{+}}^{0.43;\mathbb{G}}\mathrm{v}\left(2.1\right)\right)\right).\hfill \end{array}\right.$$

(22)

At present, we have

$$\begin{array}{cc}\hfill |\mathfrak{T}& (\mathsf{ὶ},\mathrm{v}\left(\mathsf{ὶ}\right),{\mathrm{v}}_1\left(\mathsf{ὶ}\right),{\mathrm{v}}_2\left(\mathsf{ὶ}\right),{\mathrm{v}}_3\left(\mathsf{ὶ}\right))-\mathfrak{T}(\mathsf{ὶ},\acute{\mathrm{v}}\left(\mathsf{ὶ}\right),{\acute{\mathrm{v}}}_1\left(\mathsf{ὶ}\right),{\acute{\mathrm{v}}}_2\left(\mathsf{ὶ}\right),{\acute{\mathrm{v}}}_3\left(\mathsf{ὶ}\right))|\hfill \\ \hfill & =|\frac{3\mathsf{ὶ}}{100(\sqrt{3}+{\mathsf{ὶ}}^2)}+\frac{{arctan}^2\left(\mathrm{v}\right)}{60\left(1+{arctan}^2\left(\mathrm{v}\right)\right)}+\frac{exp\left(\right|{\mathrm{v}}_1\left|\right)}{75\left(\sqrt{3}+exp\left(\right|{\mathrm{v}}_1\left|\right)\right)}\hfill \\ \hfill & +\frac{1}{120}arcsin\frac{{\mathrm{v}}_2}{\sqrt[3]{1+{\mathrm{v}}_2}}+\frac{\mathsf{ὶ}}{100}\frac{sin|{\mathrm{v}}_3|}{15+sin|{\mathrm{v}}_3}\hfill \\ \hfill & -(\frac{3\mathsf{ὶ}}{100(\sqrt{3}+{\mathsf{ὶ}}^2)}+\frac{{arctan}^2\left(\acute{\mathrm{v}}\right)}{60\left(1+{arctan}^2\left(\acute{\mathrm{v}}\right)\right)}+\frac{exp\left(\right|{\acute{\mathrm{v}}}_1\left|\right)}{75\left(\sqrt{3}+exp\left(\right|{\acute{\mathrm{v}}}_1\left|\right)\right)}\hfill \\ \hfill & +\frac{1}{120}arcsin\frac{{\acute{\mathrm{v}}}_2}{\sqrt[3]{1+{\acute{\mathrm{v}}}_2}}+\frac{\mathsf{ὶ}}{100}\frac{sin|{\acute{\mathrm{v}}}_3|}{15+sin|{\acute{\mathrm{v}}}_3|}\left)\right|\hfill \\ \hfill & \le \frac{1}{60}|\frac{{arctan}^2\left(\mathrm{v}\right)}{1+{arctan}^2\left(\mathrm{v}\right)}-\frac{{arctan}^2\left(\acute{\mathrm{v}}\right)}{1+{arctan}^2\left(\mathrm{v}\right)}|\hfill \\ \hfill & +\frac{1}{75}|\frac{exp\left(\right|{\mathrm{v}}_1\left|\right)}{\sqrt{3}+exp\left(\right|{\mathrm{v}}_1\left|\right)}-\frac{exp\left(\right|{\acute{\mathrm{v}}}_1\left|\right)}{\sqrt{3}+exp\left(\right|{\acute{\mathrm{v}}}_1\left|\right)}|\hfill \\ \hfill & +\frac{1}{120}|arcsin\frac{{\mathrm{v}}_2}{\sqrt[3]{1+{\mathrm{v}}_2}}-arcsin\frac{{\acute{\mathrm{v}}}_2}{\sqrt[3]{1+{\acute{\mathrm{v}}}_2}}|\hfill \\ \hfill & +\left|\frac{\mathsf{ὶ}}{100}\right||\frac{sin|{\mathrm{v}}_3|}{15+sin|{\mathrm{v}}_3|}-\frac{sin|{\acute{\mathrm{v}}}_3|}{15+sin|{\acute{\mathrm{v}}}_3|}|\hfill \\ \hfill & \le \frac{1}{60}\sum _{j=1}^4|{\mathrm{v}}_j\left(\mathsf{ὶ}\right)-{\acute{\mathrm{v}}}_j\left(\mathsf{ὶ}\right)|.\hfill \end{array}$$

Thus, $\ell =\frac{1}{60}$. Furthermore,

$$\begin{array}{cc}\hfill {\mathfrak{T}}^{\ast }& =\underset{\mathsf{ὶ}\in [0.7,2.1]}{sup}\left|\mathfrak{T}(\mathsf{ὶ},0,0,0,0)\right|\hfill \\ \hfill & =\underset{\mathsf{ὶ}\in [0.7,2.1]}{sup}|\frac{3\mathsf{ὶ}}{100\left(\sqrt{3}+{\mathsf{ὶ}}^2\right)}+\frac{1}{75\left(\sqrt{3}+1\right)}|\hfill \\ \hfill & =0.01513.\hfill \end{array}$$

By using equations in (15), we obtain

$$\begin{array}{cc}\hfill A_1& ={\displaystyle \frac{{\lambda }_0}{1-{\lambda }_0}}\left[\frac{{\lambda }_1{\lambda }_2}{\left(1-{\lambda }_1\right)\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(\beta +1)}\right.\hfill \\ \hfill & +\frac{{\lambda }_1}{\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(\beta +\gamma +1)}\hfill \\ \hfill & \left.+\frac{{\lambda }_2}{\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\alpha +\beta +1)}+\frac{1}{\mathsf{\Gamma }(\alpha +\beta +\gamma +1)}\right]\hfill \\ \hfill & ={\displaystyle \frac{12.5}{1-12.5}}\left[\frac{4.3\times 5.6}{\left(1-4.3\right)\left(1-5.6\right)\mathsf{\Gamma }(0.25+1)\mathsf{\Gamma }(0.43+1)\mathsf{\Gamma }(0.66+1)}\right.\hfill \\ \hfill & +\frac{4.3}{\left(1-4.3\right)\mathsf{\Gamma }(0.43+1)\mathsf{\Gamma }(0.66+0.25+1)}\hfill \\ \hfill & +\frac{5.6}{\left(1-5.6\right)\mathsf{\Gamma }(0.25+1)\mathsf{\Gamma }(0.43+0.66+1)}\hfill \\ \hfill & \left.+\frac{1}{\mathsf{\Gamma }(0.43+0.66+0.25+1)}\right]\simeq -0.197948,\hfill \\ \hfill A_2& =\frac{{\lambda }_1}{\left(1-{\lambda }_1\right)\mathsf{\Gamma }(\alpha +1)}\left[\frac{{\lambda }_2}{\left(1-{\lambda }_2\right)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\beta +1)}+\frac{1}{\mathsf{\Gamma }(\beta +\gamma +1)}\right]\hfill \\ \hfill & =\frac{4.3}{\left(1-4.3\right)\mathsf{\Gamma }(0.43+1)}[\frac{5.6}{\left(1-5.6\right)\mathsf{\Gamma }(0.25+1)\mathsf{\Gamma }(0.66+1)}\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }(0.66+0.25+1)}]\simeq 0.667007,\hfill \\ \hfill A_3& =\frac{{\lambda }_2}{(1-{\lambda }_2)\mathsf{\Gamma }(\gamma +1)\mathsf{\Gamma }(\alpha +\beta +1)}\hfill \\ \hfill & =\frac{5.6}{(1-5.6)\mathsf{\Gamma }(0.25+1)\mathsf{\Gamma }(0.43+0.66+1)}\simeq -1.289645,\hfill \\ \hfill A_4& =\frac{{\lambda }_1}{(1-{\lambda }_1)\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(\beta +1)}\hfill \\ \hfill & =\frac{4.3}{(1-4.3)\mathsf{\Gamma }(0.43+1)\mathsf{\Gamma }(0.66+1)}\simeq -1.631008,\hfill \\ \hfill A_5& =\frac{{\lambda }_1}{(1-{\lambda }_1)\mathsf{\Gamma }(\alpha +1)}=\frac{4.3}{(1-4.3)\mathsf{\Gamma }(0.43+1)}\simeq -1.470628.\hfill \end{array}$$

Now, from (17), we consider four cases for $\mathbb{G}$ as ${\mathbb{G}}_1\left(\mathsf{ὶ}\right)=2^{\mathsf{ὶ}}$, ${\mathbb{G}}_2\left(\mathsf{ὶ}\right)=\mathsf{ὶ}$ (Caputo derivative), ${\mathbb{G}}_3\left(\mathsf{ὶ}\right)=ln\mathsf{ὶ}$ (Caputo–Hadamard derivative), ${\mathbb{G}}_4\left(\mathsf{ὶ}\right)=\sqrt{\mathsf{ὶ}}$ (Katugampola derivative).

Hence, we have as Equation (17)

$$\begin{array}{cc}\hfill \Delta ={\Delta }_i& =[\frac{\left|13.82\right|}{\mathsf{\Gamma }(0.79+1)\left|1-13.82\right|}\left(\left|A_1\right|+\left|A_2\right|+\left|A_3\right|+\frac{1}{\mathsf{\Gamma }(0.43+0.66+0.25+1)}\right)\hfill \\ \hfill & +\frac{\left|5.6\right|}{\left|(1+12.5)(1-5.6)\right|\mathsf{\Gamma }(0.25+0.79+1)}\left[\left|A_4\right|+\frac{1}{\mathsf{\Gamma }(0.43+0.66+1)}\right]\hfill \\ \hfill & +\frac{\left|A_5\right|}{\left|1+12.5)\right|\mathsf{\Gamma }(0.79+0.66+0.25+1)}\hfill \\ \hfill & +\frac{\left(2\left|-12.5\right|+1\right)}{\left|1+12.5)\right|\mathsf{\Gamma }(0.43+0.66+0.25+0.79+1)}]\hfill \\ \hfill & \times {\left({\mathbb{G}}_i\left({\tau }_2\right)-{\mathbb{G}}_i\left({\tau }_1\right)\right)}^{0.43+0.66+0.25+0.79}\hfill \\ \hfill & +{\displaystyle \frac{\left|13.82\right|}{\left|(1-13.82)\left(1-4.3\right)\right|\mathsf{\Gamma }(0.79+1)}}\hfill \\ \hfill & \times \left[\frac{\left|5.6\right|}{\left|1-5.6\right|\mathsf{\Gamma }(0.25+1)\mathsf{\Gamma }(0.66+1)}+\frac{1}{\mathsf{\Gamma }(0.66+0.25+1)}\right]\hfill \\ \hfill & +[\frac{\left|5.6\right|}{\left|\left(1-5.6\right)\left(1-4.3\right)\right|\mathsf{\Gamma }(0.66+1)\mathsf{\Gamma }(0.25+0.79+1)}\hfill \\ \hfill & +\frac{2\left|4.3\right|+1}{\left|1-4.3\right|\mathsf{\Gamma }(0.79+0.66+0.25+1)}]{\left({\mathbb{G}}_i\left({\tau }_2\right)-{\mathbb{G}}_i\left({\tau }_1\right)\right)}^{0.66+0.25+0.79}\hfill \\ \hfill & +[{\displaystyle \frac{\left|13.82\right|}{\left|(1-13.82)\left(1-5.6\right)\right|\mathsf{\Gamma }(0.25+1)\mathsf{\Gamma }(0.79+1)}}\hfill \\ \hfill & +\frac{2\left|5.6\right|+1}{\left|1-5.6\right|\mathsf{\Gamma }(0.25+0.79+1)}]{\left({\mathbb{G}}_i\left({\tau }_2\right)-{\mathbb{G}}_i\left({\tau }_1\right)\right)}^{0.25+0.79}\hfill \\ \hfill & +{\displaystyle \frac{\left(2\left|13.82\right|+1\right)}{\left|1-13.82\right|\mathsf{\Gamma }(0.79+1)}}{\left({\mathbb{G}}_i\left({\tau }_2\right)-{\mathbb{G}}_i\left({\tau }_1\right)\right)}^{0.79},\hfill \end{array}$$

for $i=1,2,3,4$.

In Table 1 and Table 2, one can see the numerical results of

$$\varsigma \ge \frac{{\mathfrak{T}}^{\ast }\Delta }{1-\ell \Delta },$$

which we consider the maximum level for $\mathsf{ὶ}>2.1$. These values show that for $\mathsf{ὶ}\in [0.7,2.1]$, they are not more than $\frac{{\mathfrak{T}}^{\ast }\Delta }{1-\ell \Delta }$. We define the Algorithm S1 for obtaining the values of ${\Delta }_i$ which is shown the MATLAB commands. Thus,

$$\Delta \simeq \left\{\begin{array}{cc}58.5500,\hfill & \mathbb{G}\left(\mathsf{ὶ}\right)=2^{\mathsf{ὶ}},\hfill \\ 20.6809,\hfill & \mathbb{G}\left(\mathsf{ὶ}\right)=\mathsf{ὶ},\hfill \\ 32.6116,\hfill & \mathbb{G}\left(\mathsf{ὶ}\right)=ln\mathsf{ὶ},\hfill \\ 14.6088,\hfill & \mathbb{G}\left(\mathsf{ὶ}\right)=\sqrt{\mathsf{ὶ}}.\hfill \end{array}\right.$$

One can check numerical results of ${\Delta }_i$, $\ell {\Delta }_i$ and ${\varsigma }_i$ in Table 1 and Table 2 for $i=1,2,3,4$ and $\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$, as we can see in Figure 1. Thus,

$$\ell {\Delta }_i\simeq \left\{\begin{array}{cc}0.9758,\hfill & \mathbb{G}\left(\mathsf{ὶ}\right)=2^{\mathsf{ὶ}},\hfill \\ 0.3769,\hfill & \mathbb{G}\left(\mathsf{ὶ}\right)=\mathsf{ὶ},\hfill \\ 0.3447,\hfill & \mathbb{G}\left(\mathsf{ὶ}\right)=ln\mathsf{ὶ},\hfill \\ 0.2435,\hfill & \mathbb{G}\left(\mathsf{ὶ}\right)=\sqrt{\mathsf{ὶ}},\hfill \end{array}\right\}<1.$$

Accordingly, all requirements of Theorem 3 hold, and so the fractional non-periodic snap problem (21) has one unique solution on the $[{\tau }_1,{\tau }_2]$.

Table 1. Numerical values of $\Delta ,\ell \Delta$ in Example 1 $\forall \mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$ when ${\mathbb{G}}_1=2^{\mathsf{ὶ}}$ and ${\mathbb{G}}_2=\mathsf{ὶ}$.

	${\mathbb{G}}_1\left(\mathsf{ὶ}\right)=2^{\mathsf{ὶ}}$			${\mathbb{G}}_2\left(\mathsf{ὶ}\right)=\mathsf{ὶ}$
$\mathsf{ὶ}$	$\Delta$	$\ell \Delta$	$\mathbf{\varsigma }\ge \frac{{\mathfrak{T}}^{\ast }\Delta }{\mathbf{1}-\ell \Delta }$	$\Delta$	$\ell \Delta$	$\mathbf{\varsigma }\ge \frac{{\mathfrak{T}}^{\ast }\Delta }{\mathbf{1}-\ell \Delta }$
$0.70$	$0.8883$	$0.0148$	$0.0092$	$0.8883$	$0.0148$	$0.0092$
$0.78$	$1.5676$	$0.0261$	$0.0165$	$1.4765$	$0.0246$	$0.0155$
$0.86$	$2.3236$	$0.0387$	$0.0248$	$2.0774$	$0.0346$	$0.0221$
$0.94$	$3.2366$	$0.0539$	$0.0351$	$2.7444$	$0.0457$	$0.0295$
$1.02$	$4.3417$	$0.0724$	$0.0480$	$3.4857$	$0.0581$	$0.0380$
$1.10$	$5.6729$	$0.0945$	$0.0643$	$4.3049$	$0.0717$	$0.0476$
$1.18$	$7.2671$	$0.1211$	$0.0848$	$5.2044$	$0.0867$	$0.0585$
$1.26$	$9.1651$	$0.1528$	$0.1110$	$6.1855$	$0.1031$	$0.0707$
$1.34$	$11.4127$	$0.1902$	$0.1446$	$7.2496$	$0.1208$	$0.0846$
$1.42$	$14.0615$	$0.2344$	$0.1884$	$8.3976$	$0.1400$	$0.1002$
$1.50$	$17.1699$	$0.2862$	$0.2467$	$9.6303$	$0.1605$	$0.1177$
$1.58$	$20.8036$	$0.3467$	$0.3266$	$10.9483$	$0.1825$	$0.1374$
$1.66$	$25.0369$	$0.4173$	$0.4407$	$12.3524$	$0.2059$	$0.1595$
$1.74$	$29.9538$	$0.4992$	$0.6135$	$13.8430$	$0.2307$	$0.1846$
$1.82$	$35.6494$	$0.5942$	$0.9010$	$15.4207$	$0.2570$	$0.2129$
$1.90$	$42.2306$	$0.7038$	$1.4626$	$17.0860$	$0.2848$	$0.2450$
$1.98$	$49.8186$	$0.8303$	$3.0113$	$18.8393$	$0.3140$	$0.2817$
$2.06$	$58.5500$	$0.9758$	$\boxed{24.8503}$	$20.6809$	$0.3447$	$0.3237$
$2.14$	$68.5790$	$1.1430$	$-4.9195$	$22.6114$	$0.3769$	$\boxed{0.3722}$

Table 2. Numerical values of $\Delta ,\ell \Delta$ in Example 1 $\forall \mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$ when ${\mathbb{G}}_3\left(\mathsf{ὶ}\right)=ln\mathsf{ὶ}$ and ${\mathbb{G}}_4\left(\mathsf{ὶ}\right)=\sqrt{\mathsf{ὶ}}$.

	${\mathbb{G}}_3=ln\mathsf{ὶ}$			${\mathbb{G}}_4=\sqrt{\mathsf{ὶ}}$
$\mathsf{ὶ}$	$\Delta$	$\ell \Delta$	$\mathbf{\varsigma }\ge \frac{{\mathfrak{T}}^{\ast }\Delta }{\mathbf{1}-\ell \Delta }$	$\Delta$	$\ell \Delta$	$\mathbf{\varsigma }\ge \frac{{\mathfrak{T}}^{\ast }\Delta }{\mathbf{1}-\ell \Delta }$
$0.70$	$0.8883$	$0.0148$	$0.0092$	$0.8883$	$0.0148$	$0.0092$
$0.78$	$1.6818$	$0.0280$	$0.0177$	$1.2392$	$0.0207$	$0.0130$
$0.86$	$2.4509$	$0.0408$	$0.0262$	$1.5536$	$0.0259$	$0.0164$
$0.94$	$3.2439$	$0.0541$	$0.0352$	$1.8669$	$0.0311$	$0.0198$
$1.02$	$4.0558$	$0.0676$	$0.0446$	$2.1833$	$0.0364$	$0.0232$
$1.10$	$4.8802$	$0.0813$	$0.0545$	$2.5040$	$0.0417$	$0.0268$
$1.18$	$5.7115$	$0.0952$	$0.0647$	$2.8295$	$0.0472$	$0.0305$
$1.26$	$6.5457$	$0.1091$	$0.0754$	$3.1598$	$0.0527$	$0.0342$
$1.34$	$7.3794$	$0.1230$	$0.0863$	$3.4947$	$0.0582$	$0.0381$
$1.42$	$8.2102$	$0.1368$	$0.0976$	$3.8341$	$0.0639$	$0.0420$
$1.50$	$9.0363$	$0.1506$	$0.1091$	$4.1779$	$0.0696$	$0.0461$
$1.58$	$9.8564$	$0.1643$	$0.1210$	$4.5257$	$0.0754$	$0.0502$
$1.66$	$10.6693$	$0.1778$	$0.1331$	$4.8775$	$0.0813$	$0.0545$
$1.74$	$11.4745$	$0.1912$	$0.1455$	$5.2330$	$0.0872$	$0.0588$
$1.82$	$12.2713$	$0.2045$	$0.1582$	$5.5920$	$0.0932$	$0.0633$
$1.90$	$13.0594$	$0.2177$	$0.1712$	$5.9544$	$0.0992$	$0.0678$
$1.98$	$13.8386$	$0.2306$	$0.1845$	$6.3200$	$0.1053$	$0.0725$
$2.06$	$14.6088$	$0.2435$	$0.1981$	$6.6887$	$0.1115$	$0.0772$
$2.14$	$15.3697$	$0.2562$	$\boxed{0.2119}$	$7.0603$	$0.1177$	$\boxed{0.0821}$

Figure 1. Graphical representation of ${\Delta }_i$ and $\ell {\Delta }_i$ for $\mathsf{ὶ}\in [0.7,2.1]$ in Example 1.

We check our results of Theorem 4 in the following example which in we consider

$$\mathbb{G}\left(\mathsf{ὶ}\right)=2^{\mathsf{ὶ}},\mathsf{ὶ},ln\left(\mathsf{ὶ}\right),\sqrt{\mathsf{ὶ}},$$

and in particular, $\mathbb{G}\left(\mathsf{ὶ}\right)=\mathsf{ὶ}$ (Caputo type) for three different orders ${\alpha }_1$, ${\alpha }_2$ and ${\alpha }_3$.

Example 2.

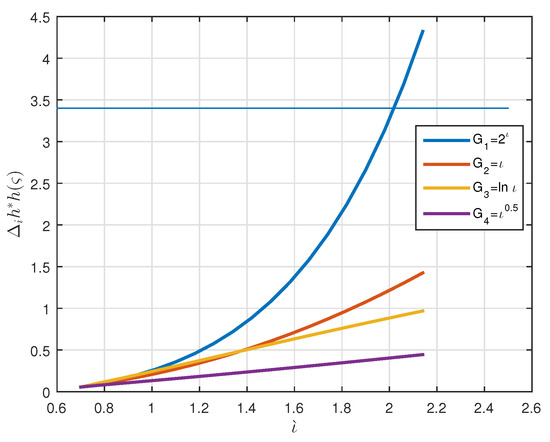
According to the system (6), we consider again a nonlinear fractional non-periodic snap problem (21). From the following inequality

$$\begin{array}{cc}\hfill |\mathfrak{T}& (\mathsf{ὶ},\mathrm{v}\left(\mathsf{ὶ}\right),{\mathrm{v}}_1\left(\mathsf{ὶ}\right),{\mathrm{v}}_2\left(\mathsf{ὶ}\right),{\mathrm{v}}_3\left(\mathsf{ὶ}\right))|\hfill \\ \hfill & =|\frac{3\mathsf{ὶ}}{100(\sqrt{3}+{\mathsf{ὶ}}^2)}+\frac{{arctan}^2\left(\mathrm{v}\right)}{60\left(1+{arctan}^2\left(\mathrm{v}\right)\right)}+\frac{exp\left(\right|{\mathrm{v}}_1\left|\right)}{75\left(\sqrt{3}+exp\left(\right|{\mathrm{v}}_1\left|\right)\right)}\hfill \\ \hfill & +\frac{1}{120}arcsin\frac{{\mathrm{v}}_2}{\sqrt[3]{1+{\mathrm{v}}_2}}+\frac{\mathsf{ὶ}}{100}\frac{sin|{\mathrm{v}}_3|}{15+sin|{\mathrm{v}}_3|}|\hfill \\ \hfill & \le \frac{6}{70}\mathsf{ὶ}\sum _{j=1}^4\left|{\mathrm{v}}_j\left(\mathsf{ὶ}\right)\right|,\hfill \end{array}$$

for $\mathsf{ὶ}\in [{\tau }_1,{\tau }_2]$. This means that, we can choose $\hslash \left(\mathsf{ὶ}\right)=\frac{6}{70}\mathsf{ὶ}$ and $\mathfrak{h}\left(\mathsf{ὶ}\right)=\mathsf{ὶ}$. Thus, for $j=1,2,3,4$,

$$\left|\mathfrak{T}(\mathsf{ὶ},\mathrm{v}\left(\mathsf{ὶ}\right),{\mathrm{v}}_1\left(\mathsf{ὶ}\right),{\mathrm{v}}_2\left(\mathsf{ὶ}\right),{\mathrm{v}}_3\left(\mathsf{ὶ}\right))\right|\le \hslash \left(\mathsf{ὶ}\right)\mathfrak{h}\left(\sum _{j=1}^4\left|{\mathrm{v}}_j\left(\mathsf{ὶ}\right)\right|\right),$$

and (H3) holds. In addition to,

$${\hslash }^{\ast }=\underset{\mathsf{ὶ}\in [0.7,2.1]}{sup}\hslash \left(\mathsf{ὶ}\right)=0.18.$$

(23)

By assuming $\varsigma =0.35>0$, $\varpi =0.1\in (0,1)$ and (23), we obtain $\varsigma {\varpi }^{-1}=3.5$ and

$$\Delta {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)\simeq \left\{\begin{array}{cc}3.138571,\hfill & \mathbb{G}\left(\mathsf{ὶ}\right)=2^{\mathsf{ὶ}},\hfill \\ 1.302899,\hfill & \mathbb{G}\left(\mathsf{ὶ}\right)=\mathsf{ὶ},\hfill \\ 0.920351,\hfill & \mathbb{G}\left(\mathsf{ὶ}\right)=ln\mathsf{ὶ},\hfill \\ 0.4213861,\hfill & \mathbb{G}\left(\mathsf{ὶ}\right)=\sqrt{\mathsf{ὶ}}\hfill \end{array}\right\}<\varsigma {\varpi }^{-1},$$

for $\mathsf{ὶ}\in [0.7,1.98]$ whenever $\mathbb{G}\left(\mathsf{ὶ}\right)=2^{\mathsf{ὶ}}$, $\mathsf{ὶ}\in [0.7,2.06]$ whenever $\mathbb{G}\left(\mathsf{ὶ}\right)=\mathsf{ὶ},ln\mathsf{ὶ},\sqrt{\mathsf{ὶ}}$. Therefore, (H4) holds. Table 3 shows the results and one can see 2D plot of $\Delta {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)$ in Figure 2. In Table 3, one can see the numerical results of suitable $\Delta {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)$, which we consider for $\mathsf{ὶ}\in [0.7,2.1]$.Now, we consider three cases for α as $\alpha \in \{{\alpha }_1=0.18,{\alpha }_2=0.49,{\alpha }_3=0.92\}$ in (21) as follows:

$$\left\{\begin{array}{c}{{}^c\mathcal{D}}_{{\tau }_1^{+}}^{\alpha ;\mathbb{G}}\mathrm{v}\left(\mathsf{ὶ}\right)={\mathrm{v}}_1\left(\mathsf{ὶ}\right),\hfill \\ {{}^c\mathcal{D}}_{0.7^{+}}^{0.66;\mathbb{G}}{\mathrm{v}}_1\left(\mathsf{ὶ}\right)={\mathrm{v}}_2\left(\mathsf{ὶ}\right),\hfill \\ {{}^c\mathcal{D}}_{0.7^{+}}^{0.25;\mathbb{G}}{\mathrm{v}}_2\left(\mathsf{ὶ}\right)={\mathrm{v}}_3\left(\mathsf{ὶ}\right),\hfill \\ {{}^c\mathcal{D}}_{0.7^{+}}^{0.79;\mathbb{G}}{\mathrm{v}}_3\left(\mathsf{ὶ}\right)={\displaystyle \frac{3\mathsf{ὶ}}{100(\sqrt{3}+{\mathsf{ὶ}}^2)}}+{\displaystyle \frac{{arctan}^2\left(\mathrm{v}\right)}{60\left(1+{arctan}^2\left(\mathrm{v}\right)\right)}}\hfill \\ +{\displaystyle \frac{exp\left(\right|{\mathrm{v}}_1\left|\right)}{75\left(\sqrt{3}+exp\left(\right|{\mathrm{v}}_1\left|\right)\right)}}+{\displaystyle \frac{1}{120}}arcsin{\displaystyle \frac{{\mathrm{v}}_2}{\sqrt[3]{1+{\mathrm{v}}_2}}}\hfill \\ +{\displaystyle \frac{\mathsf{ὶ}}{100}}{\displaystyle \frac{sin|{\mathrm{v}}_3|}{15+sin|{\mathrm{v}}_3|}}.\hfill \end{array}\right.$$

(24)

By using relations in Equation (15), applying Equation (17) in the sequel, for $\mathbb{G}\left(\mathsf{ὶ}\right)=\mathsf{ὶ}$, Caputo case, we have

$$\begin{array}{cc}\hfill \alpha =0.18:& \left\{\begin{array}{c}{A}_1=-0.16214,\hfill \\ A_2=0.63979,\hfill \\ A_3=-1.42487,\hfill \\ A_4=-1.56445,\hfill \\ A_5=-1.41062,\hfill \end{array}\right.\hfill \\ \hfill \alpha =0.49:& \left\{\begin{array}{c}{A}_1=-0.20406,\hfill \\ A_2=0.66707,\hfill \\ A_3=-1.25172,\hfill \\ A_4=-1.63117,\hfill \\ A_5=-1.47077,\hfill \end{array}\right.\hfill \\ \hfill \alpha =0.92:& \left\{\begin{array}{c}{A}_1=-0.22032,\hfill \\ A_2=0.61004,\hfill \\ A_3=-0.95360,\hfill \\ A_4=-1.49171,\hfill \\ A_5=-1.34502,\hfill \end{array}\right.\hfill \end{array}$$

and

$$\Delta =\left\{\begin{array}{cc}22.62667,\hfill & \alpha =0.18,\hfill \\ 22.55698,\hfill & \alpha =0.49,\hfill \\ 14.21049,\hfill & \alpha =0.92,\hfill \end{array}\right.\ell \Delta =\left\{\begin{array}{cc}0.37711,\hfill & \alpha =0.18,\hfill \\ 0.37594,\hfill & \alpha =0.49,\hfill \\ 0.23684,\hfill & \alpha =0.92.\hfill \end{array}\right.$$

Table 3. Numerical values of $\Delta ,\Delta {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)$ in Example 2 $\forall \mathsf{ὶ}\in [0.7,2.1]$ when $\mathbb{G}\left(\mathsf{ὶ}\right)=2^{\mathsf{ὶ}},\mathsf{ὶ},ln\mathsf{ὶ},\sqrt{\mathsf{ὶ}}$.

	${\mathbb{G}}_1=2^{\mathsf{ὶ}}$		${\mathbb{G}}_2=\mathsf{ὶ}$		${\mathbb{G}}_3=\mathsf{ὶ}$		${\mathbb{G}}_4=\sqrt{\mathsf{ὶ}}$
$\mathsf{ὶ}$	$\Delta$	$\Delta {\hslash }^{\ast }\mathfrak{h}\left(\mathbf{\varsigma }\right)$	$\Delta$	$\Delta {\hslash }^{\ast }\mathfrak{h}\left(\mathbf{\varsigma }\right)$	$\Delta$	$\Delta {\hslash }^{\ast }\mathfrak{h}\left(\mathbf{\varsigma }\right)$	$\Delta$	$\Delta {\hslash }^{\ast }\mathfrak{h}\left(\mathbf{\varsigma }\right)$
$0.70$	$0.8883$	$0.0560$	$0.8883$	$0.0560$	$0.8883$	$0.0560$	$0.8883$	$0.0560$
$0.78$	$1.5676$	$0.0988$	$1.4765$	$0.0930$	$1.6818$	$0.1060$	$1.2392$	$0.0781$
$0.86$	$2.3236$	$0.1464$	$2.0774$	$0.1309$	$2.4509$	$0.1544$	$1.5536$	$0.0979$
$0.94$	$3.2366$	$0.2039$	$2.7444$	$0.1729$	$3.2439$	$0.2044$	$1.8669$	$0.1176$
$1.02$	$4.3417$	$0.2735$	$3.4857$	$0.2196$	$4.0558$	$0.2555$	$2.1833$	$0.1375$
$1.10$	$5.6729$	$0.3574$	$4.3049$	$0.2712$	$4.8802$	$0.3075$	$2.5040$	$0.1578$
$1.18$	$7.2671$	$0.4578$	$5.2044$	$0.3279$	$5.7115$	$0.3598$	$2.8295$	$0.1783$
$1.26$	$9.1651$	$0.5774$	$6.1855$	$0.3897$	$6.5457$	$0.4124$	$3.1598$	$0.1991$
$1.34$	$11.4127$	$0.7190$	$7.2496$	$0.4567$	$7.3794$	$0.4649$	$3.4947$	$0.2202$
$1.42$	$14.0615$	$0.8859$	$8.3976$	$0.5290$	$8.2102$	$0.5172$	$3.8341$	$0.2416$
$1.50$	$17.1699$	$1.0817$	$9.6303$	$0.6067$	$9.0363$	$0.5693$	$4.1779$	$0.2632$
$1.58$	$20.8036$	$1.3106$	$10.9483$	$0.6897$	$9.8564$	$0.6210$	$4.5257$	$0.2851$
$1.66$	$25.0369$	$1.5773$	$12.3524$	$0.7782$	$10.6693$	$0.6722$	$4.8775$	$0.3073$
$1.74$	$29.9538$	$1.8871$	$13.8430$	$0.8721$	$11.4745$	$0.7229$	$5.2330$	$0.3297$
$1.82$	$35.6494$	$2.2459$	$15.4207$	$0.9715$	$12.2713$	$0.7731$	$5.5920$	$0.3523$
$1.90$	$42.2306$	$2.6605$	$17.0860$	$1.0764$	$13.0594$	$0.8227$	$5.9544$	$0.3751$
$1.98$	$49.8186$	$\boxed{3.1386}$	$18.8393$	$1.1869$	$13.8386$	$0.8718$	$6.3200$	$0.3982$
$2.06$	$58.5500$	$3.6887$	$20.6809$	$1.3029$	$14.6088$	$0.9204$	$6.6887$	$0.4214$
$2.14$	$68.5790$	$4.3205$	$22.6114$	$\boxed{1.4245}$	$15.3697$	$\boxed{0.9683}$	$7.0603$	$\boxed{0.4448}$

Figure 2. 2D graphs of $\Delta {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)$ vs. $\mathsf{ὶ}\in [0.7,2.1]$ in Example 2.

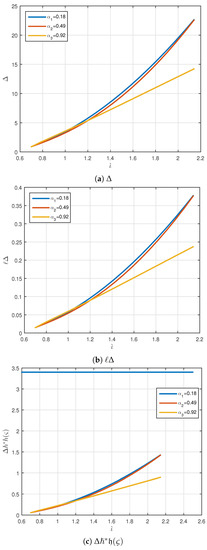
We define the Algorithm S2 for obtaining the values of $A_i$ and Δ, which is shown the MATLAB commands. Table 4, Table 5 and Table 6 show the results and one can see 2D plot of $\Delta ,\ell \Delta ,{\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)$ in Figure 3. In Table 4, Table 5 and Table 6, one can see the numerical results of $\varsigma \ge \frac{{\mathfrak{T}}^{\ast }\Delta }{1-\ell \Delta }$, which we consider maximum level for $\mathsf{ὶ}>2.1$. These values show that for $\mathsf{ὶ}\in [0.7,2.1]$, they are not more than $\frac{{\mathfrak{T}}^{\ast }\Delta }{1-\ell \Delta }$.

Table 4. Numerical values of $\Delta ,\ell \Delta$, $\Delta {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)$ in Example 2 $\forall \mathsf{ὶ}\in [0.7,2.1]$ when $\mathbb{G}=\mathsf{ὶ}$ and $\alpha =0.18$.

	$\mathit{\alpha }=0.18$
$\mathsf{ὶ}$	$\Delta$	$\ell \Delta$	$\mathbf{\varsigma }\ge \frac{{\mathfrak{T}}^{\ast }\Delta }{\mathbf{1}-\ell \Delta }$	$\Delta {\hslash }^{\ast }\mathfrak{h}\left(\mathbf{\varsigma }\right)$	$\mathbf{\varsigma }{\mathbf{\varpi }}^{-\mathbf{1}}$
$0.70$	$0.8883$	$0.0148$	$0.0092$	$0.0560$	$3.5000$
$0.78$	$1.4991$	$0.0250$	$0.0158$	$0.0944$	$3.5000$
$0.86$	$2.1459$	$0.0358$	$0.0228$	$0.1352$	$3.5000$
$0.94$	$2.8699$	$0.0478$	$0.0309$	$0.1808$	$3.5000$
$1.02$	$3.6730$	$0.0612$	$0.0401$	$0.2314$	$3.5000$
$1.10$	$4.5542$	$0.0759$	$0.0505$	$0.2869$	$3.5000$
$1.18$	$5.5123$	$0.0919$	$0.0623$	$0.3473$	$3.5000$
$1.26$	$6.5462$	$0.1091$	$0.0754$	$0.4124$	$3.5000$
$1.34$	$7.6545$	$0.1276$	$0.0900$	$0.4822$	$3.5000$
$1.42$	$8.8362$	$0.1473$	$0.1063$	$0.5567$	$3.5000$
$1.50$	$10.0903$	$0.1682$	$0.1244$	$0.6357$	$3.5000$
$1.58$	$11.4157$	$0.1903$	$0.1446$	$0.7192$	$3.5000$
$1.66$	$12.8116$	$0.2135$	$0.1671$	$0.8071$	$3.5000$
$1.74$	$14.2773$	$0.2380$	$0.1922$	$0.8995$	$3.5000$
$1.82$	$15.8119$	$0.2635$	$0.2202$	$0.9961$	$3.5000$
$1.90$	$17.4147$	$0.2902$	$0.2517$	$1.0971$	$3.5000$
$1.98$	$19.0852$	$0.3181$	$0.2871$	$1.2024$	$3.5000$
$2.06$	$20.8227$	$0.3470$	$0.3271$	$1.3118$	$3.5000$
$2.14$	$22.6267$	$0.3771$	$0.3726$	$1.4255$	$3.5000$

Table 5. Numerical values of $\Delta ,\ell \Delta$, $\Delta {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)$ in Example 2 $\forall \mathsf{ὶ}\in [0.7,2.1]$ when $\mathbb{G}=\mathsf{ὶ}$ and $\alpha =0.49$.

	$\mathit{\alpha }=0.49$
$\mathsf{ὶ}$	$\Delta$	$\ell \Delta$	$\mathbf{\varsigma }\ge \frac{{\mathfrak{T}}^{\ast }\Delta }{\mathbf{1}-\ell \Delta }$	$\Delta {\hslash }^{\ast }\mathfrak{h}\left(\mathbf{\varsigma }\right)$	$\mathbf{\varsigma }{\mathbf{\varpi }}^{-\mathbf{1}}$
$0.70$	$0.8883$	$0.0148$	$0.0092$	$0.0560$	$3.5000$
$0.78$	$1.4730$	$0.0246$	$0.0155$	$0.0928$	$3.5000$
$0.86$	$2.0654$	$0.0344$	$0.0219$	$0.1301$	$3.5000$
$0.94$	$2.7208$	$0.0453$	$0.0292$	$0.1714$	$3.5000$
$1.02$	$3.4485$	$0.0575$	$0.0375$	$0.2173$	$3.5000$
$1.10$	$4.2531$	$0.0709$	$0.0470$	$0.2679$	$3.5000$
$1.18$	$5.1377$	$0.0856$	$0.0576$	$0.3237$	$3.5000$
$1.26$	$6.1046$	$0.1017$	$0.0697$	$0.3846$	$3.5000$
$1.34$	$7.1555$	$0.1193$	$0.0833$	$0.4508$	$3.5000$
$1.42$	$8.2921$	$0.1382$	$0.0987$	$0.5224$	$3.5000$
$1.50$	$9.5156$	$0.1586$	$0.1160$	$0.5995$	$3.5000$
$1.58$	$10.8273$	$0.1805$	$0.1355$	$0.6821$	$3.5000$
$1.66$	$12.2281$	$0.2038$	$0.1575$	$0.7704$	$3.5000$
$1.74$	$13.7191$	$0.2287$	$0.1824$	$0.8643$	$3.5000$
$1.82$	$15.3013$	$0.2550$	$0.2107$	$0.9640$	$3.5000$
$1.90$	$16.9753$	$0.2829$	$0.2428$	$1.0694$	$3.5000$
$1.98$	$18.7421$	$0.3124$	$0.2796$	$1.1808$	$3.5000$
$2.06$	$20.6024$	$0.3434$	$0.3218$	$1.2980$	$3.5000$
$2.14$	$22.5570$	$0.3760$	$0.3708$	$1.4211$	$3.5000$

Table 6. Numerical values of $\Delta ,\ell \Delta$, $\Delta {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)$ in Example 2 $\forall \mathsf{ὶ}\in [0.7,2.1]$ when $\mathbb{G}=\mathsf{ὶ}$ and $\alpha =0.92$.

	$\mathit{\alpha }=0.92$
$\mathsf{ὶ}$	$\Delta$	$\ell \Delta$	$\mathbf{\varsigma }\ge \frac{{\mathfrak{T}}^{\ast }\Delta }{\mathbf{1}-\ell \Delta }$	$\Delta {\hslash }^{\ast }\mathfrak{h}\left(\mathbf{\varsigma }\right)$	$\mathbf{\varsigma }{\mathbf{\varpi }}^{-\mathbf{1}}$
$0.70$	$0.8883$	$0.0148$	$0.0092$	$0.0560$	$3.5000$
$0.78$	$1.6516$	$0.0275$	$0.0174$	$0.1041$	$3.5000$
$0.86$	$2.3473$	$0.0391$	$0.0251$	$0.1479$	$3.5000$
$0.94$	$3.0442$	$0.0507$	$0.0329$	$0.1918$	$3.5000$
$1.02$	$3.7503$	$0.0625$	$0.0410$	$0.2363$	$3.5000$
$1.10$	$4.4668$	$0.0744$	$0.0495$	$0.2814$	$3.5000$
$1.18$	$5.1931$	$0.0866$	$0.0583$	$0.3272$	$3.5000$
$1.26$	$5.9277$	$0.0988$	$0.0675$	$0.3734$	$3.5000$
$1.34$	$6.6694$	$0.1112$	$0.0770$	$0.4202$	$3.5000$
$1.42$	$7.4165$	$0.1236$	$0.0868$	$0.4672$	$3.5000$
$1.50$	$8.1678$	$0.1361$	$0.0970$	$0.5146$	$3.5000$
$1.58$	$8.9220$	$0.1487$	$0.1075$	$0.5621$	$3.5000$
$1.66$	$9.6780$	$0.1613$	$0.1184$	$0.6097$	$3.5000$
$1.74$	$10.4351$	$0.1739$	$0.1296$	$0.6574$	$3.5000$
$1.82$	$11.1923$	$0.1865$	$0.1411$	$0.7051$	$3.5000$
$1.90$	$11.9490$	$0.1992$	$0.1530$	$0.7528$	$3.5000$
$1.98$	$12.7046$	$0.2117$	$0.1653$	$0.8004$	$3.5000$
$2.06$	$13.4586$	$0.2243$	$0.1780$	$0.8479$	$3.5000$
$2.14$	$14.2105$	$0.2368$	$0.1910$	$0.8953$	$3.5000$

Figure 3. Graphical representation of $\Delta$, $\ell \Delta$ and $\Delta {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)$ for $\mathsf{ὶ}\in [0.7,2.1]$ in Example 2.

Hence (H3) holds for

$$\alpha \in \left\{{\alpha }_1=0.18,{\alpha }_2=0.49,{\alpha }_3=0.92\right\}.$$

One can see the 2D spectrum of $\Delta ,\ell \Delta$ and $\Delta {\hslash }^{\ast }\mathfrak{h}\left(\varsigma \right)$ in Figure 3. In all three cases for the order ${\alpha }_i$, we see that all requirements of Theorem 4 are fulfilled. Therefore, this guarantees that for all of three different cases by terms of the order α, the fractional non-periodic snap problem (24) admits at least a solution on the interval $[0.7,2.1]$.

6. Conclusions

In this paper, we defined a new fractional mathematical model consisting of a fractional snap equation with non-periodic boundary conditions in the framework of the generalized $\mathbb{G}$-operators. Thus, some investigations on the qualitative behaviors of its solutions, including existence, uniqueness and stability, were performed separately. To obtain the uniqueness of the solution, we used Banach contraction theorem, and for the general existence of at least one solution, we used the Shauder fixed-point theorem. Ulam–Hyers and Ulam–Hyers–Rassias with their generalizations were discussed and investigated. In the final step, we designed examples with different cases of the function $\mathbb{G}$, such as Caputo, Caputo–Hadamard and Katugampola; and with different orders of q, we obtained some numerical results concerning the fractional non-periodic snap problem.