A Self-Adaptive Algorithm for the Common Solution of the Split Minimization Problem and the Fixed Point Problem

Abstract

In this paper, a new self-adaptive step size algorithm to approximate the solution of the split minimization problem and the fixed point problem of nonexpansive mappings was constructed, which combined the proximal algorithm and a modified Mann’s iterative method with the inertial extrapolation. The strong convergence theorem was provided in the framework of Hilbert spaces and then proven under some suitable conditions. Our result improved related results in the literature. Moreover, some numerical experiments were also provided to show our algorithm’s consistency, accuracy, and performance compared to the existing algorithms in the literature.

1. Introduction

Throughout this paper, we denote two nonempty closed convex subsets of two real Hilbert spaces $H_1$ and $H_2$ by C and Q, respectively. We denote the orthogonal projections onto a set C by $P_C$ and let $A^{\ast }:H_2\to H_1$ be an adjoint operator of $A:H_1\to H_2$, where A is a bounded linear operator.

Over the past decade, inverse problems have been widely studied since they stand at the core of image reconstruction problems and signal processing. The split feasibility problem (SFP) is one of the most popular inverse problems that has attracted the attention of many researchers. Cencer and Elfving first considered the split feasibility problem (SFP) in 1994 [1]. The split feasibility problem (SFP) can mathematically be expressed as follows: find an element x with:

$$\begin{array}{c}\hfill x\in C\mathrm{such}\mathrm{that}Ax\in Q.\end{array}$$

(1)

As mentioned above, the SFP (1) has received much attention from many researchers because it can be applied to various science branches. Several practical algorithms to solve the SFP (1) presented in recent years were given in [2,3,4,5,6,7]. It is important to note that the split feasibility problem (SFP) (1) is equivalent to the following minimization formulation:

$$\begin{array}{c}\hfill \underset{x\in C}{min}{\displaystyle \frac{1}{2}}{\parallel Ax-P_{Q}Ax\parallel }^2.\end{array}$$

(2)

In 2002, Byrne [2] introduced a practical method called the CQ algorithm for solving the SFP, which is defined as follows:

$$\begin{array}{c}\hfill x_{n+1}=P_C(x_n-{\tau }_n{A}^{\ast }(A-P_{Q}A)x_n),\end{array}$$

(3)

for all $n\ge 1$ and $x_1\in H_1$ is arbitrarily chosen. They considered the step size ${\tau }_n\in (0,2/{\parallel A\parallel }^2)$. The advantage of the CQ algorithm is that there is no need to compute the inverse of a matrix because it only deals with an orthogonal projection. However, the CQ algorithm still needs to compute an operator norm of A.

A self-adaptive step size was then introduced by Yang [8] to avoid computing an operator norm of A. Yang designed the step size as follows:

$$\begin{array}{c}\hfill {\tau }_n={\displaystyle \frac{{\rho }_n}{{\parallel A^{\ast }(I-P_Q)A{x}_n\parallel }^{\prime }}}\end{array}$$

(4)

where ${\rho }_n$ is a positive sequence parameter that satisfies ${\sum }_{n=0}^{\infty }{\rho }_n=\infty$ and ${\sum }_{n=0}^{\infty }{\rho }_n^2<\infty$. Moreover, there are two additional conditions for the self-adaptive step size: (1) Q must be a bounded subset; (2) A must be a full-column-rank matrix.

After that, López [9] modified a self-adaptive step size to remove the two additional conditions of Yang [8]. López then obtained a practical self-adaptive step size given by:

$$\begin{array}{c}\hfill {\tau }_n={\displaystyle \frac{{\rho }_n\parallel (I-P_Q)A{x}_n\parallel }{{\parallel A^{\ast }(I-P_Q)A{x}_n{\parallel }^2}^{\prime }}}\end{array}$$

(5)

where ${\rho }_n$ is a positive sequence bounded below by zero and bounded above by four.

The split minimization problem is presented below. Let f and g be two proper semi-continuous and convex functions on $H_1$ and $H_2$, respectively. Moudafi and Thakur [10] considered the interesting problem called the proximal split feasibility problem. This problem is defined to find a minimizer x such that:

$$\begin{array}{c}\hfill \underset{x\in H_1}{min}\left\{f\left(x\right)+g_{\lambda }\left(Ax\right)\right\}\end{array}$$

(6)

where $\lambda >0$ and $g_{\lambda }\left(Ax\right)$ is the following Moreau–Yoshida approximate:

$$\begin{array}{c}\hfill g_{\lambda }\left(Ax\right)=\underset{y\in H_2}{min}\left\{g\left(y\right)+{\displaystyle \frac{1}{2\lambda }}{\parallel y-Ax\parallel }^2\right\}.\end{array}$$

(7)

It is fascinating to observe the case of $C\cap A^{-1}Q\ne \varnothing$. The minimization problem (6) can be reduced to the SFP (1) when we set $f={\delta }_C$ and $g={\delta }_Q$, where ${\delta }_C$ and ${\delta }_Q$ are the indicator functions of the subsets C and Q, respectively. The reader can refer to [11] for details. By using the relations (7), we can then define the proximity operator of a function g of order $\lambda$ as the following form:

$$\begin{array}{c}\hfill {\mathrm{prox}}_{\lambda g}\left(y\right)=arg\underset{\tilde{y}\in H_2}{min}\left\{g\left(\tilde{y}\right)+{\displaystyle \frac{1}{2\lambda }}{\parallel \tilde{y}-y\parallel }^2\right\}.\end{array}$$

(8)

Moreover, the subdifferential of function f at the point x is given by the following form:

$$\begin{array}{c}\hfill \partial f\left(x\right)=\left\{\widehat{x}\in H_1|f\left(x\right)+⟨\widehat{x},\overline{x}-x⟩\le f\left(\overline{x}\right),\forall \overline{x}\in H_1\right\}.\end{array}$$

(9)

Recall the following notations:

$$argminf=\{\widehat{x}\in H_1:f\left(\widehat{x}\right)\le f\left(x\right),\forall x\in H_1\}$$

and

$$argming=\{\widehat{y}\in H_2:g\left(\widehat{y}\right)\le g\left(y\right),\forall y\in H_2\}.$$

In the case of $(argminf)\cap (A^{-1}argming)\ne \varnothing$, Moudafi and Thakur [10] also considered a generalization for the minimization problem (6), named the split minimization problem (SMP), which can be expressed to find:

$$\begin{array}{c}\hfill x\in argminf\mathrm{such}\mathrm{that}Ax\in argming.\end{array}$$

(10)

Besides considering the SMP (10), they also introduced an algorithm to solve the SMP (10). It is defined as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_{n+1}={\mathrm{prox}}_{\lambda {\tau }_{n}f}(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g}A)x_n),\forall n\ge 1,\hfill \end{array}\right.\end{array}$$

(11)

where $x_1\in H_1$ is arbitrarily chosen and ${\tau }_n$ is a self-adaptive step size. In addition, Moudafi and Thakur [10] proved a weak convergence result under some suitable conditions imposed on the parameters.

Recently, Abbas [12] constructed and introduced two iterative algorithms to solve the split minimization problem (SMP) (10). These algorithms are defined as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_{n+1}={\mathrm{prox}}_{\lambda {\tau }_{n}f}((1-{ϵ}_n)-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)x_n,\forall n\ge 1,\hfill \end{array}\right.\end{array}$$

(12)

and:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_{n+1}=(1-{ϵ}_n){\mathrm{prox}}_{\lambda {\tau }_{n}f}(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)x_n,\forall n\ge 1,\hfill \end{array}\right.\end{array}$$

(13)

where $x_1$ is arbitrarily chosen, step size ${\tau }_n={\displaystyle \frac{{\rho }_n(h\left(x_n\right)+l\left(x_n\right))}{\parallel \nabla h\left(x_n\right){\parallel }^2+{\parallel \nabla l\left(x_n\right)\parallel }^2}}$ with ${\rho }_n\in (0,4)$, and functions $h,l,\nabla h$ and $\nabla l$ are defined in Section 3. Abbas [12] provided the sequences generated by the algorithms (12) and (13), which converge strongly to a solution.

Furthermore, currently, fixed point problems of a nonexpansive mapping are still extensively studied by many research works since they are at the core of several problems in the real world, such as signal processing and image recovery. One of the famous algorithms to solve the fixed point problem of a nonexpansive mapping is as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_{n+1}=(1-t_n)x_n+t_{n}S\left(x_n\right),\forall n>0,\hfill \end{array}\right.\end{array}$$

(14)

where $S:C\to C$ is a nonexpansive mapping and the initial point $x_1$ is chosen in C, $\left\{t_n\right\}\in [0,1]$. The algorithm (14) is known as Mann’s algorithm [13]. It is well known that a Mann-type algorithm gives strong convergence provided the underlying space is smooth enough. There are many works in this direction. The reader can refer to [14,15,16] for details.

Apart from studying all the above problems, speeding up the convergence rate of algorithms has been often studied by many authors. Polyak [17] introduced a helpful technique to accelerate the rate of convergence called the heavy ball method. After that, many researchers have modified the heavy ball method to use with their algorithms. Nesterov [18] modified the heavy ball method to improve the rate of convergence for the algorithms. This algorithm is known as the modified heavy ball method:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{w}_n=z_n+{\theta }_n(z_n-z_{n-1})\hfill \\ z_{n+1}=w_n-{\tau }_n\nabla f\left(w_n\right),\forall n\ge 2,\hfill \end{array}\right.\end{array}$$

(15)

where $z_1,z_2\in H_1$ are arbitrarily chosen, ${\tau }_n>0$, $0\le {\theta }_n<1$ is an extrapolation factor, and the term ${\theta }_n(z_n-x_{z-1})$ is called the inertia. For more details, the reader is directed to [19,20,21].

Based on the above ideas, the aims of this work were: (1) to construct a new self-adaptive step size algorithm combine with the proximal algorithm, the modified Mann method with the inertial extrapolation to solve the split minimization problem (SMP) (10), and the fixed point problems of a nonexpansive mapping; (2) to establish the strong convergence results for the SMP and fixed point problems using the proposed algorithm; (3) to give numerical examples for our algorithm to present its consistency, accuracy, and performance compared to the existing algorithms in the literature.

2. Preliminaries

Some notations used throughout this paper are presented in this section. For an element x in a Hilbert space, $x_n\to x$ and $x_n\rightharpoonup x$ are denoted by a strong convergence and a weak convergence, respectively.

Lemma 1.

For every u and v in a real Hilbert space H, then,

$$\begin{array}{ccc}\hfill {\parallel v-w\parallel }^2& =& {\parallel v\parallel }^2-{\parallel w\parallel }^2+2⟨w-v,w⟩,\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {\parallel v+w\parallel }^2& \le & {\parallel v\parallel }^2+2⟨w,w+v⟩,and\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill {\parallel \kappa v+(1-\kappa )w\parallel }^2& =& {\kappa \parallel v\parallel }^2+{(1-\kappa )\parallel w\parallel }^2-\kappa (1-\kappa ){\parallel v-w\parallel }^2,\hfill \end{array}$$

(18)

where $\kappa \in [0,1]$.

Proposition 1.

Let $S:C\to H_1$ be a mapping with $C\subset H_1$, where u and v are elements in C. The mapping S is called:

1. 

monotone if:

$$⟨u-v,Su-Sv⟩\ge 0;$$

2. 

ξ-inverse strongly monotone (ξ-ism) if:

$$⟨u-v,Su-Sv⟩\ge {\xi \parallel Su-Sv\parallel }^2,$$

for some constants $\xi >0$;

3. 

nonexpansive if:

$$\parallel Su-Sv\parallel \le \parallel u-v\parallel ;$$

4. 

firmly nonexpansive if:

$${\parallel Su-Sv\parallel }^2\le ⟨Su-Sv,u-v⟩.$$

It is well known that the metric projection $P_C$ of $H_1$ onto C is a nonexpansive mapping where $C\subseteq H_1$ is a nonempty closed convex, and it satisfies $\parallel P_{C}u-P_C{v\parallel }^2\le ⟨u-v,P_{C}u-P_{C}v⟩$ for all $u,v\in H_1.$ Moreover, $P_{C}u$ is characterized by the following properties:

$$\begin{array}{ccc}\hfill \parallel u-P_C{u\parallel }^2+{\parallel v-P_{C}u\parallel }^2& \le & {\parallel u-v\parallel }^2,\hfill \end{array}$$

(19)

and:

$$\begin{array}{ccc}\hfill {\parallel u-v\parallel }^2-{\parallel P_{C}u-P_{C}v\parallel }^2& \le & \parallel (u-v)-(P_{C}u-P_{C}v){\parallel }^2,\hfill \end{array}$$

(20)

for all $u\in H_1$ and $v\in C$. We denote $\mathsf{\Gamma }\left(H_2\right)$ the collection of proper convex lower semicontinuous functions on $H_2$.

Definition 1.

Refs. [22,23]: Let $g\in \mathsf{\Gamma }\left(H_2\right)$ and $x\in H_2$. Define the proximal operator of g by:

$${prox}_g\left(x\right)=arg\underset{u\in H_2}{min}\left\{g\left(u\right)+{\displaystyle \frac{1}{2}}{\parallel u-x\parallel }^2\right\}.$$

The proximal of g of order λ ($\lambda >0$) is given by:

$${prox}_{\lambda g}\left(x\right)=arg\underset{u\in H_2}{min}\left\{g\left(u\right)+{\displaystyle \frac{1}{2\lambda }}{\parallel u-x\parallel }^2\right\}.$$

Below are some of the valuable properties of the proximal operators.

Property 1.

Refs. [24,25]: Let $g\in \mathsf{\Gamma }\left(H_2\right)$, $\lambda \in (0,\infty )$, and Q be a nonempty closed convex subset of $H_2$.

1. 

If $g={\delta }_Q$ where ${\delta }_Q$ is an indicator function of Q, then the proximal operators ${prox}_{\lambda g}=P_Q$, for all $\lambda >0$;

2. 

${prox}_{\lambda g}$ is firmly nonexpansive;

3. 

${prox}_{\lambda g}={(I+\lambda \partial g)}^{-1}=J_{\lambda }^{\partial g}$, the resolvent of the subdifferential $\partial g$ of g;

4. 

$x={prox}_g(x+y)$ if and only if $y\in \partial g\left(x\right)$.

Let $g\in \mathsf{\Gamma }\left(H_2\right)$. In [26], it was shown that $Fix\left({\mathrm{prox}}_g\right)=arg{min}_{H_2}g$. Moreover, they showed that ${\mathrm{prox}}_g$ and $I-{\mathrm{prox}}_g$ are both firmly nonexpansive.

Lemma 2.

Ref. [27]: Any sequence $\left\{{\upsilon }_n\right\}$ in a Hilbert space $H_1$ satisfies Opial’s condition if ${\upsilon }_n\rightharpoonup v$ implies the following inequality:

$$\underset{n\to \infty }{lim\; inf}\parallel {\upsilon }_n-v\parallel <\underset{n\to \infty }{lim\; inf}\parallel {\upsilon }_n-z\parallel ,$$

for every $z\in H_1$ with $z\ne v$.

Lemma 3.

Ref. [28]: Any sequence of nonnegative real number $\left\{a_n\right\}$ can be written in the following relation:

$$z_{n+1}\le (1-{\beta }_n)z_n+{\beta }_n{\gamma }_n+{\zeta }_n,n\ge 0,$$

and the following three conditions hold:

1. 

$\left\{{\beta }_n\right\}\subset [0,1],\sum {\beta }_n=\infty ;$

2. 

${lim\; sup}_{n\to \infty }{\gamma }_n\le 0;$

3. 

${\zeta }_n\ge 0,\sum {\zeta }_n<\infty foralln>0.$

Then, ${lim}_{n\to \infty }{z}_n=0$.

Lemma 4.

Ref. [29]: Let a sequence $\left\{{\Lambda }_n\right\}\subseteq \mathbb{R}$ be nondecreasing at infinity in the sense that there is a subsequence $\left\{{\Lambda }_{n_j}\right\}\subseteq \left\{{\Lambda }_n\right\}$ such that $\left\{{\Lambda }_{n_j}\right\}<\left\{{\Lambda }_{n_{j+1}}\right\}$ for all $j\ge 0$. For an integer $m_0$, define the integer sequence ${\left\{\eta \left(m\right)\right\}}_{m\ge m_0}$ by:

$$\eta \left(m\right)=max\{k\le m|{\Lambda }_k\le {\Lambda }_{k+1}\}.$$

Then, a sequence ${\left\{\eta \left(m\right)\right\}}_{m\ge m_0}$ does not decrease and verifies ${lim}_{m\to \infty }\eta \left(m\right)=\infty$. Furthermore,

$$max\{{\Lambda }_{\eta \left(m\right)},{\Lambda }_m\}\le {\Lambda }_{\eta \left(m\right)+1},$$

for all $m\ge m_0.$

3. Results

This section proposes an iterative algorithm generating a sequence that strongly converges to a solution of split minimization problems (10) and fixed point problems of a nonexpansive mapping. We established the convergence theorem of the proposed algorithm under the statements as follows:

Let $S:H_1\to H_1$ be a nonexpansive mapping. Denote the set of all solutions of a split minimization (10) by $\mathsf{\Gamma }$ and the set of all fixed points of the mapping S by $Fix\left(S\right)$. Let $\mathsf{\Omega }=\mathsf{\Gamma }\cap Fix\left(S\right)$, and suppose that:

$$\begin{array}{ccc}\hfill l\left(u\right)& =& {\displaystyle \frac{1}{2}}{\parallel (I-{\mathrm{prox}}_{\lambda {\tau }_{n}f})u\parallel }^2,\hfill \\ \hfill h\left(u\right)& =& {\displaystyle \frac{1}{2}}{\parallel (I-{\mathrm{prox}}_{\lambda g})Au\parallel }^2.\hfill \end{array}$$

(21)

Then, we obtained the gradients of the functions h and l as follows:

$$\begin{array}{ccc}\hfill \nabla l\left(u\right)& =& (I-{\mathrm{prox}}_{\lambda {\tau }_{n}f})u,\hfill \\ \hfill \nabla h\left(u\right)& =& A^{\ast }(I-{\mathrm{prox}}_{\lambda g})Au.\hfill \end{array}$$

Lemma 5.

Let $h:H_2\to \mathbb{R}$ and $l:H_1\to \mathbb{R}$ be two functions that are defined as (21). Then, the gradients $\nabla h$ and $\nabla l$ are Lipschitz continuous.

Proof. 

By the notation $\nabla h\left(u\right):=A^{\ast }(I-{\mathrm{prox}}_{\lambda g})Au$, we find that:

$$\begin{array}{ccc}\hfill & & {\parallel \nabla h\left(u\right)-\nabla h\left(v\right)\parallel }^2\hfill \\ & =& ⟨A^{\ast }((I-{\mathrm{prox}}_{\lambda g})Au-(I-{\mathrm{prox}}_{\lambda g})Av),A^{\ast }((I-{\mathrm{prox}}_{\lambda g})Au-(I-{\mathrm{prox}}_{\lambda g})Av)⟩\hfill \\ & =& ⟨(I-{\mathrm{prox}}_{\lambda g})Au-(I-{\mathrm{prox}}_{\lambda g})Av,A{A}^{\ast }((I-{\mathrm{prox}}_{\lambda g})Au-(I-{\mathrm{prox}}_{\lambda g})Av)⟩\hfill \\ & \le & L\parallel (I-{\mathrm{prox}}_{\lambda g})Au-(I-{\mathrm{prox}}_{\lambda g}){Av\parallel }^2,\hfill \end{array}$$

(22)

where $L=\parallel A^{\ast }A\parallel$. On the other hand,

$$\begin{array}{ccc}\hfill ⟨\nabla h\left(u\right)-\nabla h\left(v\right),u-v⟩& =& ⟨A^{\ast }((Au-{\mathrm{prox}}_{\lambda g}Au)-(Av-{\mathrm{prox}}_{\lambda g}Av),u-v⟩\hfill \\ & =& ⟨(I-{\mathrm{prox}}_{\lambda g})Au-(I-{\mathrm{prox}}_{\lambda g})Av,Au-Av⟩\hfill \\ & \ge & \parallel (I-{\mathrm{prox}}_{\lambda g})Au-(I-{\mathrm{prox}}_{\lambda g}){Av\parallel }^2.\hfill \end{array}$$

(23)

By combining (22) with (23), we find that:

$$⟨\nabla h\left(u\right)-\nabla h\left(v\right),u-v⟩\ge {\displaystyle \frac{1}{L}}{\parallel \nabla h\left(u\right)-\nabla h\left(v\right)\parallel }^2.$$

Therefore, we obtained that $\nabla h$ is $\frac{1}{L}$-inverse strongly monotone. Moreover:

$$\parallel \nabla h\left(u\right)-\nabla h\left(v\right)\parallel \le L\parallel u-v\parallel .$$

Similarly, one can prove that $\nabla l$ is also Lipschitz continuous. This completes the proof.    □

A valuable assumption for analyzing our main theorem is given as follows.

Assumption 1.

Suppose that $\left\{{\rho }_n\right\}$, $\left\{{\theta }_n\right\}$ are positive sequences and $\left\{{\alpha }_n\right\}$, $\left\{{\delta }_n\right\}$ are sequences in interval $(0,1)$ that satisfy the following assumptions:

(A1) 

$inf{\alpha }_n(1-{\alpha }_n)>0$;

(A2) 

${lim}_{n\to \infty }{\delta }_n=0$ and ${\sum }_{n=1}^{\infty }{\delta }_n=\infty$;

(A3) 

$inf{\rho }_n(4-{\rho }_n)>0$ with $0<{\rho }_n<4$;

(A4) 

${\theta }_n\parallel x_n-x_{n-1}\parallel \to 0$ and ${\displaystyle \frac{{\theta }_n}{{\delta }_n}}\parallel x_n-x_{n-1}\parallel \to 0$ as $n\to \infty$.

Theorem 1.

Let $H_1$ and $H_2$ be two real Hilbert spaces and S be a nonexpansive mapping on $H_1$. Assume that A is a bounded linear operator from $H_1$ to $H_2$ with its adjoint operator $A^{\ast }$, and $f:H_1\to \mathbb{R}\cup \{+\infty \}$ and $g:H_2\to \mathbb{R}\cup \{+\infty \}$ are proper lower semicontinuous and convex functions. Assume that SMP (10) is consistent (that is, $\mathsf{\Omega }\ne \varnothing$), and let $x_1$ and v be in $H_1$. Then, the sequence $\left\{x_n\right\}$ in Algorithm 1 strongly converges to $z\in \mathsf{\Omega }$, where $z=P_{\mathsf{\Omega }}\left(v\right).$

Algorithm 1 A split minimization algorithm.

Initialization: Let $\lambda >0$ and $x_0,x_1\in H_1$ be arbitrarily chosen. Choose some positive sequences $\left\{{\rho }_n\right\}$, $\left\{{\delta }_n\right\}$ and $\left\{{\alpha }_n\right\}$ satisfying Assumption 1. Set $n=1$. Iterative step: Given the current iteration $x_n$, calculate the next iterations as follows: $$\begin{array}{c}\hfill \begin{array}{cc}\hfill u_n& =x_n+{\theta }_n(x_n-x_{n-1})\hfill \\ \hfill y_n& ={\mathrm{prox}}_{\lambda {\tau }_{n}f}(I-{\tau }_n{A}^{\ast }(A-{\mathrm{prox}}_{\lambda g}A))u_n\hfill \\ \hfill x_{n+1}& ={\alpha }_n{x}_n+(1-{\alpha }_n)S[{\delta }_{n}v+(1-{\delta }_n)y_n],\hfill \end{array}\end{array}$$ (24) where: $$\begin{array}{c}\hfill {\tau }_n=\left\{\begin{array}{cc}\frac{{\rho }_{n}h\left(u_n\right)}{\parallel \nabla h\left(u_n\right){\parallel }^2+{\parallel \nabla l\left(u_n\right)\parallel }^2},\hfill & \parallel \nabla h\left(u_n\right){\parallel }^2+{\parallel \nabla l\left(u_n\right)\parallel }^2\ne 0,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$ (25) Stopping criterion: If $x_{n+1}=y_n=u_n=x_n$, stop. Otherwise, put $n=n+1$, and go to Iterative step.

Proof. 

Assume that $z=P_{\mathsf{\Omega }}\left(v\right)\in \mathsf{\Omega }$. By using the firm non-expansiveness of $(I-{\mathrm{prox}}_{\lambda g})$ (see [30,31] for details), we find that:

$$\begin{array}{ccc}\hfill ⟨\nabla h\left(u_n\right),u_n-z⟩& =& ⟨\nabla h\left(u_n\right)-\nabla h\left(z\right),u_n-z⟩\hfill \\ & =& ⟨(I-{\mathrm{prox}}_{\lambda g})A{u}_n-(I-{\mathrm{prox}}_{\lambda g})Az,A{u}_n-Az⟩\hfill \\ & \ge & \parallel (I-{\mathrm{prox}}_{\lambda g})Az-(I-{\mathrm{prox}}_{\lambda g})A{u}_n{\parallel }^2\hfill \\ & =& 2h\left(u_n\right),\hfill \end{array}$$

(26)

and:

$$\begin{array}{ccc}\hfill & & \parallel y_n{-z\parallel }^2\hfill \\ & =& \parallel {\mathrm{prox}}_{\lambda {\tau }_{n}f}(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n-{\mathrm{prox}}_{\lambda {\tau }_{n}f}(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A){z\parallel }^2\hfill \\ & \le & \parallel (I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n-(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A){)z\parallel }^2\hfill \\ & & -\parallel (I-{\tau }_n)((I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n-(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)z){\parallel }^2\hfill \\ & =& \parallel u_n{-z\parallel }^2-2{\tau }_n⟨\left(A^{\ast }(I-{\mathrm{prox}}_{\lambda g})A\right)(u_n-z),u_n-p⟩\hfill \\ & & +{\tau }_n^2{\parallel \left(A^{\ast }(I-{\mathrm{prox}}_{\lambda g})A\right)(u_n-z)\parallel }^2\hfill \\ & & -\parallel (I-{\tau }_n)((I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n-(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)z){\parallel }^2\hfill \\ & =& \parallel u_n{-z\parallel }^2-2{\tau }_n⟨\nabla h\left(u_n\right)-\nabla h\left(z\right),u_n-z⟩+{\tau }_n^2{\parallel \nabla h\left(u_n\right)-\nabla h\left(z\right)\parallel }^2\hfill \\ & & -\parallel (I-{\tau }_n)((I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n-(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)z){\parallel }^2\hfill \\ & \le & {\displaystyle \parallel }{u}_n{-z\parallel }^2+{\tau }_n^2{\parallel \nabla h\left(u_n\right)\parallel }^2-4{\tau }_{n}h\left(u_n\right)\hfill \\ & & -\parallel (I-{\tau }_n)((I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n-(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)z){\parallel }^2\hfill \\ & \le & \parallel u_n{-z\parallel }^2-{\rho }_n(4-{\rho }_n){\displaystyle \frac{h^2\left(u_n\right)}{\parallel \nabla h\left(u_n\right){\parallel }^2+{\parallel \nabla l\left(u_n\right)\parallel }^2}}\hfill \\ & & -\parallel (I-{\tau }_n)(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n{\parallel }^2.\hfill \end{array}$$

(27)

This implies:

$$\begin{array}{ccc}\hfill \parallel y_n-z\parallel & \le & \parallel u_n-z\parallel .\hfill \end{array}$$

(28)

Next, we set $w_n={\delta }_{n}v+(1-{\delta }_n)y_n$. For fixed $v\in C,$ we obtain that:

$$\begin{array}{ccc}\hfill \parallel w_n-z\parallel & =& \parallel {\delta }_{n}v+(1-{\delta }_n)y_n-z+{\delta }_{n}z-{\delta }_{n}z\parallel \hfill \\ & \le & (1-{\delta }_n)\parallel y_n-z\parallel +{\delta }_n\parallel v-z\parallel \hfill \\ & \le & (1-{\delta }_n)\parallel u_n-z\parallel +{\delta }_n\parallel v-z\parallel \hfill \\ & \le & max\{\parallel u_n-z\parallel ,\parallel v-z\parallel \},\hfill \end{array}$$

(29)

and

$$\begin{array}{ccc}\hfill \parallel u_n-z\parallel & \le & {\theta }_n\parallel x_n-x_{n-1}\parallel +\parallel x_n-z\parallel .\hfill \end{array}$$

(30)

Since S is nonexpansive, we find that:

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-z\parallel & =& \parallel {\alpha }_n{x}_n+(1-{\alpha }_n)S{w}_n-z+{\alpha }_{n}z-{\alpha }_{n}z\parallel \hfill \\ & \le & (1-{\alpha }_n)\parallel w_n-z\parallel +{\alpha }_n\parallel x_n-z\parallel \hfill \\ & \le & max\{\parallel w_n-z\parallel ,\parallel x_n-z\parallel \}\hfill \\ & \le & max\{\parallel x_n-z\parallel ,\parallel v-z\parallel ,\parallel x_n-z\parallel +{\theta }_n\parallel x_n-x_{n-1}\parallel \}\hfill \\ & & ⋮\hfill \\ & \le & max\{\parallel x_0-z\parallel ,\parallel v-z\parallel ,\parallel x_0-z\parallel +{\theta }_1\parallel x_1-x_0\parallel \}.\hfill \end{array}$$

(31)

Thus, $\left\{x_n\right\}$ is bounded, and this implies that $\left\{w_n\right\},\left\{y_n\right\}$, and $\left\{u_n\right\}$ are also bounded.

Next, we observe that:

$$\begin{array}{ccc}\hfill \parallel y_n-u_n\parallel & =& \parallel {\mathrm{prox}}_{\lambda {\tau }_{n}f}(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n-u_n\parallel \hfill \\ & =& \parallel {\mathrm{prox}}_{\lambda {\tau }_{n}f}(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n-(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n\hfill \\ & & +(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n-u_n\parallel \hfill \\ & \le & \parallel {\mathrm{prox}}_{\lambda {\tau }_{n}f}(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n-(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n\parallel \hfill \\ & & +\parallel (I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n-u_n\parallel \hfill \\ & =& \parallel (I-{\mathrm{prox}}_{\lambda {\tau }_{n}f})(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n\parallel +{\tau }_n\parallel \nabla h\left(u_n\right)\parallel .\hfill \end{array}$$

(32)

Next, we claim that $\parallel x_{n+1}-x_n\parallel \to 0$ and $x_n\to z$. Consider:

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-x_n\parallel & =& \parallel {\alpha }_n{x}_n-x_n+(1-{\alpha }_n)S{w}_n\parallel \hfill \\ & =& \parallel (1-{\alpha }_n)(S{w}_n-x_n)\parallel \hfill \\ & =& (1-{\alpha }_n)\parallel S{w}_n-x_n\parallel ,\hfill \end{array}$$

(33)

and:

$$\begin{array}{ccc}\hfill \parallel u_n{-z\parallel }^2& =& \parallel x_n+{\theta }_n(x_n-x_{n+1}){-z\parallel }^2\hfill \\ & \le & 2{\theta }_n⟨x_n-x_{n-1},u_n-z⟩+{\parallel x_n-z\parallel }^2\hfill \\ & \le & 2{\theta }_n\parallel u_n-z\parallel \parallel x_n-x_{n-1}\parallel +\parallel x_n{-z\parallel }^2.\hfill \end{array}$$

(34)

Moreover, consider:

$$\begin{array}{ccc}& & \parallel x_{n+1}{-z\parallel }^2\hfill \\ & =& \parallel (1-{\alpha }_n)(S{w}_n-z)+{\alpha }_n(x_n-z){\parallel }^2\hfill \\ & \le & (1-{\alpha }_n)\parallel S{w}_n{-z\parallel }^2+{\alpha }_n\parallel x_n{-z\parallel }^2-(1-{\alpha }_n){\alpha }_n{\parallel S{w}_n-x_n\parallel }^2\hfill \\ & \le & (1-{\alpha }_n)\parallel w_n{-z\parallel }^2+{\alpha }_n\parallel x_n{-z\parallel }^2-(1-{\alpha }_n){\alpha }_n{\parallel S{w}_n-x_n\parallel }^2\hfill \\ & \le & {\alpha }_n\parallel x_n{-z\parallel }^2+(1-{\alpha }_n)(1-{\delta }_n)\parallel y_n{-z\parallel }^2+{\delta }_n{\parallel v-z\parallel }^2-(1-{\alpha }_n){\alpha }_n{\parallel S{w}_n-x_n\parallel }^2\hfill \\ & \le & {\alpha }_n\parallel x_n{-z\parallel }^2+{\delta }_n{\parallel v-z\parallel }^2-{\alpha }_n(1-{\alpha }_n)\parallel S{w}_n-x_n{\parallel }^2+(1-{\alpha }_n)[\parallel u_n{-z\parallel }^2\hfill \\ & & -{\rho }_n(4-{\rho }_n){\displaystyle \frac{h^2\left(u_n\right)}{\parallel \nabla h\left(u_n\right){\parallel }^2+{\parallel \nabla l\left(u_n\right)\parallel }^2}}-\parallel (I-{\tau }_n)(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n{\parallel }^2]\hfill \\ & \le & ({\alpha }_n+(1-{\alpha }_n))\parallel x_n{-z\parallel }^2+{\delta }_n{\parallel v-z\parallel }^2+2{\theta }_n\parallel u_n-z\parallel \parallel x_n-x_{n-1}\parallel \hfill \\ & & -(1-{\alpha }_n){\rho }_n(4-{\rho }_n){\displaystyle \frac{h^2\left(u_n\right)}{\parallel \nabla h\left(u_n\right){\parallel }^2+{\parallel \nabla l\left(u_n\right)\parallel }^2}}-{\alpha }_n(1-{\alpha }_n){\parallel S{w}_n-x_n\parallel }^2\hfill \\ & & -\parallel (I-{\tau }_n)(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n{\parallel }^2\hfill \\ & \le & \parallel x_n{-z\parallel }^2+2{\theta }_n\parallel u_n-z\parallel \parallel x_n-x_{n-1}\parallel +{\delta }_n{\parallel v-z\parallel }^2-{\alpha }_n(1-{\alpha }_n){\parallel S{w}_n-x_n\parallel }^2\hfill \\ & & -{\rho }_n(4-{\rho }_n){\displaystyle \frac{h^2\left(u_n\right)}{\parallel \nabla h\left(u_n\right){\parallel }^2+{\parallel \nabla l\left(u_n\right)\parallel }^2}}-{\parallel (I-{\tau }_n)(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n\parallel }^2.\hfill \end{array}$$

(35)

Therefore, we obtain:

$$\begin{array}{ccc}\hfill & & {\rho }_n(4-{\rho }_n){\displaystyle \frac{h^2\left(u_n\right)}{\parallel \nabla h\left(u_n\right){\parallel }^2+{\parallel \nabla l\left(u_n\right)\parallel }^2}}+(1-{\alpha }_n){\alpha }_n{\parallel x_n-S{w}_n\parallel }^2\hfill \\ & & +\parallel (I-{\tau }_n)(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n{\parallel }^2\hfill \\ & \le & \parallel x_n{-z\parallel }^2-\parallel x_{n+1}{-z\parallel }^2+2{\theta }_n\parallel u_n-z\parallel \parallel x_n-x_{n-1}\parallel +{\delta }_n{\parallel v-z\parallel }^2.\hfill \end{array}$$

(36)

We next show the sequence $\parallel x_n-z\parallel \to 0$ by dividing into two possible cases.

Case 1. Assume that $\{\parallel x_n-z{\parallel }^2\}$ is the non-increasing sequence. There exists $n_0\in \mathbb{N}$ such that $\parallel x_{n+1}{-z\parallel }^2\le {\parallel x_n-z\parallel }^2,$ for each $n\ge n_0$. Then, the sequence $\{\parallel x_n-z\parallel \}$ converges, and so:

$$\underset{n\to \infty }{lim}(\parallel x_{n+1}{-z\parallel }^2-\parallel x_n-z{\parallel }^2)=0.$$

Since ${lim}_{n\to \infty }{\delta }_n=0$, we obtain by using (36) that:

$$\underset{n\to \infty }{lim}{\rho }_n(4-{\rho }_n){\displaystyle \frac{h^2\left(u_n\right)}{\parallel \nabla h\left(u_n\right){\parallel }^2+{\parallel \nabla l\left(u_n\right)\parallel }^2}}=0,$$

$$\underset{n\to \infty }{lim}{\alpha }_n(1-{\alpha }_n)\parallel S{w}_n-x_n\parallel =0,$$

and:

$$\underset{n\to \infty }{lim}{\parallel (I-{\tau }_n)(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n\parallel }^2=0.$$

We then obtain by using $lim{\alpha }_n(1-{\alpha }_n)=0,inf{\rho }_n(4-{\rho }_n)>0,$ and $\parallel \nabla h\left(u_n\right){\parallel }^2+{\parallel \nabla l\left(u_n\right)\parallel }^2$ being bounded that:

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}h\left(u_n\right)& =& 0,\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}\parallel S{w}_n-x_n\parallel & =& 0,\hfill \end{array}$$

(38)

and:

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{\parallel (I-{\tau }_n)(I-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_n\parallel }^2=0.\end{array}$$

(39)

Thus, we obtain by using (33) that:

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel x_{n+1}-x_n\parallel =0.\end{array}$$

(40)

Moreover, it easy to see that:

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel u_n-x_n\parallel =0.\end{array}$$

(41)

By applying (36) and (39) in the Formula (32), we find that:

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel y_n-u_n\parallel =0.\end{array}$$

(42)

We next observe that:

$$\begin{array}{ccc}\hfill \parallel w_n-u_n\parallel & =& \parallel u_n-{\delta }_{n}v+(1-{\delta }_n)y_n\parallel \hfill \\ & =& {\delta }_n\parallel y_n-v\parallel +(1-{\delta }_n)\parallel y_n-u_n\parallel .\hfill \end{array}$$

(43)

By using the fact that ${\delta }_n\to 0$, we find that:

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel w_n-u_n\parallel =0.\end{array}$$

(44)

Moreover, we observe that:

$$\begin{array}{ccc}\hfill \parallel S{w}_n-w_n\parallel & \le & \parallel S{w}_n-x_n\parallel +\parallel u_n-x_n\parallel +\parallel w_n-u_n\parallel .\hfill \end{array}$$

(45)

We then obtain by using (38), (41), and (44) that:

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel S{w}_n-w_n\parallel =0.\end{array}$$

(46)

Next, we observe that:

$$\begin{array}{ccc}\hfill \parallel y_n-{\mathrm{prox}}_{\lambda {\tau }_{n}f}{y}_n\parallel & \le & \parallel u_n-{\tau }_n{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A{u}_n-y_n\parallel \hfill \\ & \le & \parallel u_n-y_n\parallel +|{\tau }_n|\parallel \nabla h\left(u_n\right)\parallel .\hfill \end{array}$$

(47)

Thus, we obtain immediately that:

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel y_n-{\mathrm{prox}}_{\lambda {\tau }_{n}f}{y}_n\parallel =0.\end{array}$$

(48)

We next show that ${lim\; sup}_{n\to \infty }⟨v-z,z-S{w}_n⟩\ge 0$, where $z=P_{\mathsf{\Omega }}\left(v\right).$ To prove this, we can choose a subsequence $\left\{w_{n_i}\right\}$ of $\left\{w_n\right\}$ with:

$$\underset{n\to \infty }{lim\; sup}⟨v-z,S{w}_n-z⟩=\underset{i\to \infty }{lim}⟨v-z,S{w}_{n_i}-z⟩.$$

Since $\left\{w_{n_i}\right\}$ is a bounded sequence, we can take a weakly convergent subsequence $\left\{w_{n_i}\right\}$ of $\left\{w_n\right\}$ that converges to $w\in H_1$, that is $w_{n_i}\rightharpoonup w$. By using the fact that $\parallel S{w}_n-w_n\parallel \to 0,$ we find that $S{w}_{n_i}\rightharpoonup w$.

We next show $w\in \mathsf{\Omega }$ in two steps. First, we show that w is a fixed point of S. By contradiction, we assume that $y\notin Fix\left(S\right)$. Since $w_{n_i}\rightharpoonup w$ and $Sw\ne w,$ by Opial’s conditions, we conclude that:

$$\begin{array}{ccc}\hfill \underset{i\to \infty }{lim\; inf}\parallel w_{n_i}-w\parallel & <& \underset{i\to \infty }{lim\; inf}\parallel w_{n_i}-Sw\parallel \hfill \\ & \le & \underset{i\to \infty }{lim\; inf}(\parallel w_{n_i}-S{w}_{n_i}\parallel +\parallel S{w}_{n_i}-Sw\parallel )\hfill \\ & \le & \underset{i\to \infty }{lim\; inf}(\parallel w_{n_i}-w\parallel ).\hfill \end{array}$$

(49)

This is a contradiction. This implies $w\in Fix\left(S\right).$ Second, we show $w\in \mathsf{\Gamma }.$ Since w is a weak limit point of $\left\{w_n\right\}$, there is a $\left\{w_{n_i}\right\}\subseteq \left\{w_n\right\}$ such that $w_{n_i}\rightharpoonup w$. Since h is lower semicontinuous, we find that:

$$0\le h\left(w\right)\le \underset{i\to \infty }{lim\; inf}h\left(w_{n_i}\right)=\underset{n\to \infty }{lim}h\left(w_n\right)=0.$$

This implies:

$$h\left(w\right)={\displaystyle \frac{1}{2}}{\parallel (I-{\mathrm{prox}}_{\lambda g})Aw\parallel }^2=0.$$

Then, $Aw={\mathrm{prox}}_{\lambda g}Aw$, and so, $0\in \partial g\left(Aw\right)$. This means that $Aw$ is a minimizer of the operator g.

Similarly, since l is lower semicontinuous, we find that:

$$0\le l\left(w\right)\le \underset{i\to \infty }{lim\; inf}l\left(w_{n_i}\right)=\underset{n\to \infty }{lim}l\left(w_n\right)=0.$$

This implies:

$$l\left(w\right)={\displaystyle \frac{1}{2}}{\parallel (I-{\mathrm{prox}}_{\lambda {\tau }_{n}f})w\parallel }^2=0.$$

Thus, w is in a fixed point set of the proximal operator ${\mathrm{prox}}_{\lambda {\tau }_{n}f}$, that is $0\in \partial f\left(w\right)$. This means that w is a minimizer of the operator f. This implies $w\in \mathsf{\Gamma }$. Therefore, we can conclude that $w\in \mathsf{\Omega }.$

According to the properties of matric projections, since $w\in \mathsf{\Omega }$ and $z=P_{\mathsf{\Omega }}\left(v\right)$, then $⟨v-P_{\mathsf{\Omega }}\left(v\right),w-P_{\mathsf{\Omega }}\left(v\right)⟩\le 0.$ Consider,

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim\; sup}⟨z-v,z-x_{n+1}⟩& =& \underset{n\to \infty }{lim\; sup}⟨z-v,z-S{w}_n⟩\hfill \\ & =& \underset{i\to \infty }{lim}⟨z-v,z-S{w}_{n_i}⟩\hfill \\ & =& ⟨z-v,z-w⟩\hfill \\ & \le & 0.\hfill \end{array}$$

(50)

In the final step, we show that the sequence $\parallel x_n-z\parallel \to 0,$ as $n\to \infty$. We observe that:

$$\begin{array}{ccc}\hfill \parallel w_n{-z\parallel }^2& =& \parallel {\delta }_n(z-v)+(1-{\delta }_n)(z-y_n){\parallel }^2\hfill \\ & \le & 2{\delta }_n⟨z-v,z-x_{n+1}⟩+(1-{\delta }_n){\parallel z-y_n\parallel }^2,\hfill \end{array}$$

(51)

and:

$$\begin{array}{ccc}\hfill \parallel x_{n+1}{-z\parallel }^2& =& ⟨(1-{\alpha }_n)(S{w}_n-z)+{\alpha }_n(x_n-z),x_{n+1}-z⟩\hfill \\ & =& {\alpha }_n⟨z-x_n,z-x_{n+1}⟩+(1-{\alpha }_n)⟨z-S{w}_n,z-x_{n+1}⟩\hfill \\ & \le & {\displaystyle \frac{{\alpha }_n}{2}}\parallel z-x_n{\parallel }^2+{\displaystyle \frac{{\alpha }_n}{2}}\parallel z-x_{n+1}{\parallel }^2+{\displaystyle \frac{(1-{\alpha }_n)}{2}}[\parallel z-w_n{\parallel }^2+\parallel z-x_{n+1}{\parallel }^2]\hfill \\ & =& {\displaystyle \frac{{\alpha }_n}{2}}\parallel z-x_n{\parallel }^2+{\displaystyle \frac{1}{2}}\parallel z-x_{n+1}{\parallel }^2+{\displaystyle \frac{(1-{\alpha }_n)}{2}}{\parallel z-w_n\parallel }^2.\hfill \end{array}$$

(52)

This implies:

$$\begin{array}{ccc}\hfill \parallel x_{n+1}{-z\parallel }^2& \le & {\alpha }_n\parallel z-x_n{\parallel }^2+(1-{\alpha }_n){\parallel z-w_n\parallel }^2.\hfill \end{array}$$

(53)

By combining (27) with (34) and (51), we find that:

$$\begin{array}{ccc}\hfill \parallel x_{n+1}{-z\parallel }^2& \le & {\alpha }_n\parallel z-x_n{\parallel }^2+(1-{\alpha }_n)[(1-{\delta }_n)\parallel z-y_n{\parallel }^2+2{\delta }_n⟨z-v,z-x_{n+1}⟩]\hfill \\ & \le & {\alpha }_n\parallel x_n{-z\parallel }^2+(1-{\delta }_n)(1-{\delta }_n){\parallel z-x_{n+1}\parallel }^2\hfill \\ & & +2{\theta }_n(1-{\alpha }_n)(1-{\delta }_n)\parallel z-u_n\parallel \parallel x_n-x_{n-1}\parallel \hfill \\ & & -{\rho }_n(4-{\rho }_n){\displaystyle \frac{h^2\left(u_n\right)}{\parallel \nabla h\left(u_n\right){\parallel }^2+{\parallel \nabla l\left(u_n\right)\parallel }^2}}+2{\delta }_n⟨v-z,x_{n+1}-z⟩\hfill \\ & \le & [1-(1-{\alpha }_n){\delta }_n]\parallel x_n-z{\parallel }^2+(1-{\alpha }_n){\delta }_n\{2⟨z-v,z-x_{n+1}⟩\hfill \\ & & +2(1-{\delta }_n){\displaystyle \frac{{\theta }_n}{{\delta }_n}}\parallel x_{n-1}-x_n\parallel \parallel z-u_n\parallel \}.\hfill \end{array}$$

(54)

Thus, we obtain by using Lemma 3, Assumption (A4), Inequality (50), and the boundedness of $\left\{u_n\right\}$ that $x_n\to z=P_{\mathsf{\Omega }}\left(v\right).$

Case 2. Assume that $\{\parallel x_n-z{\parallel }^2\}$ is increasing. By applying Assumptions (A1), (A2), and (A4) to (36), we find that $\parallel S{w}_n-x_n\parallel \to 0$. Thus, we obtain by using (33) that $\parallel x_{n+1}-x_n\parallel \to 0$.

Suppose that ${\Lambda }_n={\parallel x_n-z\parallel }^2$, and for each $n\ge n_0$ (where $n_0$ large enough), define a mapping $\eta :\mathbb{N}\to \mathbb{N}$ as follows:

$$\eta \left(n\right):=max\{k\in \mathbb{N}:{\Lambda }_k\le {\Lambda }_{k+1},k\le n\}.$$

Thus, $\eta \left(n\right)\to \infty$ when n tends to infinity, and for each $n\ge n_0$,

$$0\le {\Lambda }_{\eta \left(n\right)}\le {\Lambda }_{\eta \left(n\right)+1}.$$

We then obtain by using Inequality (36) that:

$$\begin{array}{ccc}& & {\delta }_{\eta \left(n\right)}{\parallel v-z\parallel }^2+2{\displaystyle \frac{{\theta }_{\eta \left(n\right)}}{{\delta }_{\eta \left(n\right)}}}\parallel u_{\eta \left(n\right)}-z\parallel \parallel x_{\eta \left(n\right)}-x_{\eta \left(n\right)-1}\parallel \hfill \\ & \ge & {\Lambda }_{\eta \left(n\right)}-{\Lambda }_{\eta \left(n\right)+1}+{\delta }_{\eta \left(n\right)}{\parallel z-v\parallel }^2+2{\displaystyle \frac{{\theta }_{\eta \left(n\right)}}{{\delta }_{\eta \left(n\right)}}}\parallel u_{\eta \left(n\right)}-z\parallel \parallel x_{\eta \left(n\right)}-x_{\eta \left(n\right)-1}\parallel \hfill \\ & \ge & {\Lambda }_{\eta \left(n\right)}-{\Lambda }_{\eta \left(n\right)+1}+{\delta }_{\eta \left(n\right)}{\parallel v-z\parallel }^2+2{\theta }_{\eta \left(n\right)}\parallel u_{\eta \left(n\right)}-z\parallel \parallel x_{\eta \left(n\right)}-x_{\eta \left(n\right)-1}\parallel \hfill \\ & \ge & {\rho }_{\eta \left(n\right)}(4-{\rho }_{\eta \left(n\right)}){\displaystyle \frac{h^2\left(u_{\eta \left(n\right)}\right)}{\parallel \nabla h\left(u_{\eta \left(n\right)}\right){\parallel }^2+{\parallel \nabla l\left(u_{\eta \left(n\right)}\right)\parallel }^2}}+{\alpha }_{\eta \left(n\right)}(1-{\alpha }_{\eta \left(n\right)}){\parallel S{w}_{\eta \left(n\right)}-x_{\eta \left(n\right)}\parallel }^2\hfill \\ & & +\parallel (I-{\tau }_{\eta \left(n\right)})(I-{\tau }_{\eta \left(n\right)}{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_{\eta \left(n\right)}{\parallel }^2.\hfill \end{array}$$

(55)

Since ${\delta }_{\eta \left(n\right)}\to 0$ as $n\to \infty$ and also ${\displaystyle \frac{{\theta }_{\eta \left(n\right)}}{{\delta }_{\eta \left(n\right)}}}\parallel x_{\eta \left(n\right)}-x_{\eta \left(n\right)-1}\parallel \to 0$ when n tends to infinity, we observe that:

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}h\left(u_{\eta \left(n\right)}\right)& =& 0,\hfill \end{array}$$

(56)

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}\parallel S{w}_{\eta \left(n\right)}-x_{\eta \left(n\right)}\parallel & =& 0,\hfill \end{array}$$

(57)

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}{\parallel (I-{\tau }_{\eta \left(n\right)})(I-{\tau }_{\eta \left(n\right)}{A}^{\ast }(I-{\mathrm{prox}}_{\lambda g})A)u_{\eta \left(n\right)}\parallel }^2& =& 0,\hfill \end{array}$$

(58)

and:

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim\; sup}⟨v-z,x_{\eta \left(n\right)+1}-z⟩\le 0.\end{array}$$

(59)

Moreover, we obtain that:

$$\begin{array}{ccc}\hfill {\Lambda }_{\eta \left(n\right)+1}& \le & [1-(1-{\alpha }_n){\delta }_{\eta \left(n\right)}]{\Lambda }_{\eta \left(n\right)}+(1-{\alpha }_{\eta \left(n\right)}){\delta }_{\eta \left(n\right)}\{2⟨z-v,z-x_{\eta \left(n\right)+1}⟩\hfill \\ & & +{\displaystyle \frac{2{\theta }_{\eta \left(n\right)}(1-{\delta }_{\eta \left(n\right)})}{{\delta }_{\eta \left(n\right)}}}\parallel u_{\eta \left(n\right)}-z\parallel \parallel x_{\eta \left(n\right)}-x_{\eta \left(n\right)-1}\parallel \}.\hfill \end{array}$$

(60)

This implies that:

$$\begin{array}{c}\hfill {\Lambda }_{\eta \left(n\right)}\le 2⟨v-z,x_{\eta \left(n\right)+1}-z⟩+(1-{\delta }_{\eta \left(n\right)}){\displaystyle \frac{2{\theta }_{\eta \left(n\right)}}{{\delta }_{\eta \left(n\right)}}}\parallel u_{\eta \left(n\right)}-z\parallel \parallel x_{\eta \left(n\right)}-x_{\eta \left(n\right)-1}\parallel .\end{array}$$

(61)

Thus, we obtain:

$$\underset{n\to \infty }{lim\; sup}{\Lambda }_{\eta \left(n\right)}=\underset{n\to \infty }{lim\; sup}\parallel x_{\eta \left(n\right)}-z\parallel =0.$$

We now obtain by using Lemma 4 that:

$$0\le \parallel x_n-z\parallel \le max\{\parallel x_{\eta \left(n\right)}-z\parallel ,\parallel x_n-z\parallel \}\le \parallel x_{\eta \left(n\right)+1}-z\parallel \to 0,$$

as $n\to \infty$. This implies that $x_n\to z$ and $z=P_{\mathsf{\Omega }}\left(v\right).$ The proof is complete. □

Remark 1. 

(a) 

If we put ${\theta }_n=0,S\equiv I,{\alpha }_n=0$, and ${\delta }_n=0$ for all $n\ge 2$ in our proposed algorithm, we found that the algorithm (11) of Moudafi and Thakur was obtained. Moreover, we obtained a strong convergence theorem, while Moudafi and Thakur [10] only obtained a weak convergence theorem;

(b) 

If we put $A\equiv I$, $S\equiv I,f\equiv g\equiv 0,$ and ${\delta }_n=0$ for all $n\ge 2$ in our proposed algorithm, we found that Algorithm (1.2) in [32] was obtained;

(c) 

If we put ${\theta }_n=0$, $A\equiv I$, $S\equiv I,f\equiv g\equiv 0,$ and ${\delta }_n=0$ for all $n\ge 2$ in our proposed algorithm, we found that the Mann iteration algorithm in [13] was obtained. Moreover, we obtained a strong convergence theorem, while Mann [13] only obtained a weak convergence theorem;

(d) 

As an extraordinary choice, an extrapolation factor ${\theta }_n$ in our proposed algorithm can be chosen as follows: $0\le {\theta }_n\le \overline{{\theta }_n}$,

$$\begin{array}{c}\hfill \overline{{\theta }_n}=\left\{\begin{array}{cc}min\left\{\frac{n-1}{n+\kappa -1}\frac{{ϵ}_n}{\parallel x_n-x_{n-1}}\right\},\hfill & \mathrm{if}{x}_n\ne x_{n-1},\hfill \\ \frac{n-1}{n+\kappa -1},\hfill & else,\hfill \end{array}\right.\end{array}$$

(62)

for each integer n greater than or equal to three and a positive sequence $\left\{{ϵ}_n\right\}$ with $\frac{{ϵ}_n}{{\delta }_n}\to 0$, as $n\to \infty$. This choice was recently derived in [33,34] as an inertial extrapolated step.

4. Applications and Numerical Results

This section provides the numerical experiments to illustrate the performance and compare Algorithm 1 with and without the inertial term. Moreover, we present an experiment to compare our scheme with the Abbas algorithms [12]. All code was written in MATLAB 2017b and run on a MacBook Pro 2012 with a 2.5 GHz Intel Core i5.

First, we illustrate the performance of our proposed algorithm by comparing the proposed algorithm with and without the inertial term as the following experiment:

Example 1.

Suppose $C=Q=\{x\in {\mathbb{R}}^{100}:\parallel x{\parallel }_2\le 1\}$, and let $Ax=x$. In problem (10), assume that $f={\delta }_C$ and $g={\delta }_Q$, where δ is the indicator function. Then:

$$\begin{array}{c}\hfill {prox}_{\lambda {\tau }_{n}f}\left(x\right)=P_C\left(x\right)=P_Q\left(x\right)={prox}_{\lambda g}=\left\{\begin{array}{c}{\displaystyle \frac{x}{{\parallel x\parallel }_2}},\mathrm{if}{\parallel x\parallel }_2>1\hfill \\ x,otherwise.\hfill \end{array}\right.\end{array}$$

Thus, the problem (10) becomes the SEP (1). We next took the parameters ${\rho }_n=2,{\alpha }_n={\displaystyle \frac{1}{4000}}$ and ${\delta }_n={\displaystyle \frac{1}{n+1}}$. Thus, by Algorithm 1, we obtained that:

$$\begin{array}{ccc}\hfill u_n& =& x_n+{\theta }_n(x_n-x_{n-1})\hfill \\ \hfill y_n& =& {prox}_{\lambda {\tau }_{n}f}(I-{\tau }_n{A}^{\ast }(A-{prox}_{\lambda g}A)u_n\hfill \\ \hfill x_{n+1}& =& \left({\displaystyle \frac{1}{4000}}\right)x_n+\left(1-{\displaystyle \frac{1}{4000}}\right)\left[\left({\displaystyle \frac{1}{n+1}}\right)v+\left(1-{\displaystyle \frac{1}{n+1}}\right)y_n\right].\hfill \end{array}$$

(63)

We then provide a comparison of the convergence of Algorithm 1 with:

$${\theta }_n=\left\{\begin{array}{c}0.5\mathrm{if}{x}_n-x_{n-1}=0,\hfill \\ min\left\{0.5,{\displaystyle \frac{1}{(n+1)\parallel x_n-x_{n-1}{\parallel }_2}}\right\}\mathrm{if}{x}_{n-1}-x_n\ne 0,\hfill \end{array}\right.$$

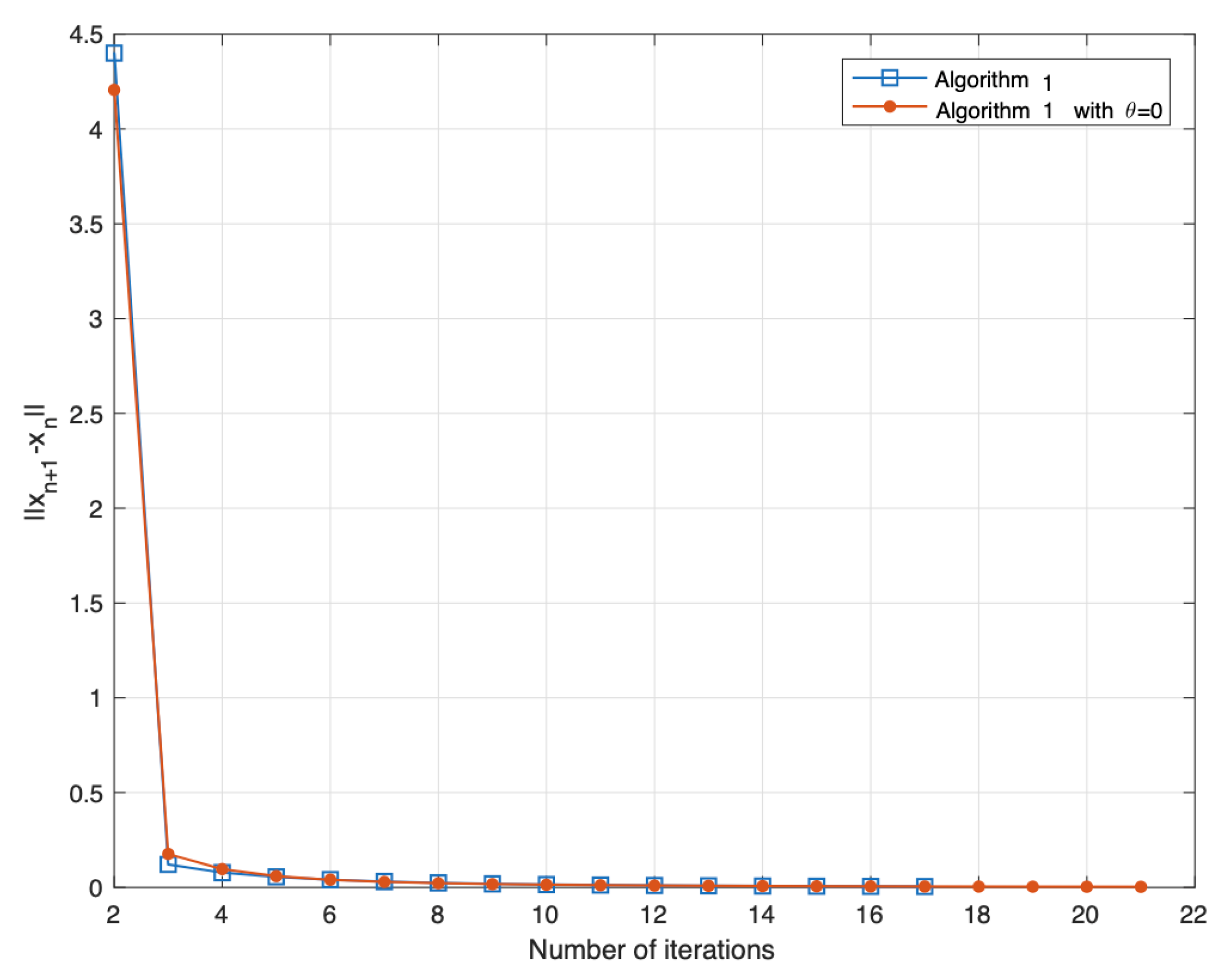
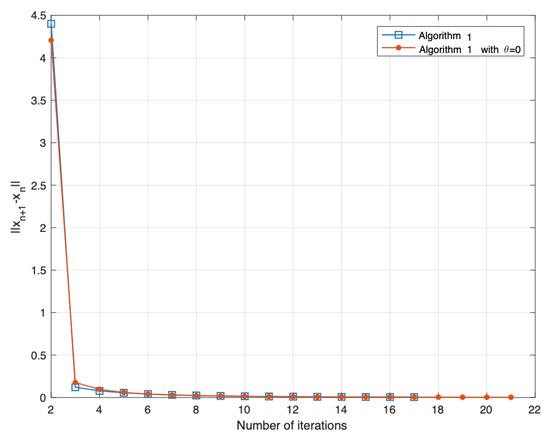
and Algorithm 1 with ${\theta }_n=0$ in terms of the number of iterations with the stopping criterion $\parallel A^{\ast }(I-P_Q){Ax\parallel }_2^2+{\parallel (I-P_C)x_n\parallel }_2^2<{10}^{-2}$. The result of this experiment is reported in Figure 1.

Figure 1. Comparing Algorithm 1 with Algorithm 1 defined without the inertial term.

Remark 2. 

By observing the result of Example 1, we found that our proposed algorithm with inertia was faster and more efficient than our proposed algorithm without inertia (${\theta }_n=0$).

Second, we used the example in Abbas [12] to show the performance of our algorithm by comparing our proposed algorithm with Algorithms (12) and (13) in terms of CPU time as the following experiment:

Example 2.

Let $H_1=H_2={\mathbb{R}}^N$ and $g={\parallel ·\parallel }_2$ be the Euclidean norm in ${\mathbb{R}}^N$. The metric projection onto the Euclidean unit ball B is defined by the following:

$$\begin{array}{c}\hfill P_B\left(x\right)=\left\{\begin{array}{c}{\displaystyle \frac{x}{{\parallel x\parallel }_2}},\mathrm{if}{\parallel x\parallel }_2>1\hfill \\ x,otherwise.\hfill \end{array}\right.\end{array}$$

Thus, the proximal operator (the block soft thresholding) [24] is given by:

$$\begin{array}{c}\hfill {prox}_g\left(x\right)=\left\{\begin{array}{cc}x-{\displaystyle \frac{x}{{\parallel x\parallel }_2}},\hfill & {\mathrm{if}\parallel x\parallel }_2\ge 1\hfill \\ 0,\hfill & otherwise..\hfill \end{array}\right.\end{array}$$

For $i=1,2,\dots ,N$, let $x_i\in \mathbb{R}$,

$$h_i\left(x_i\right):=max\left\{\right|x_i|-1,0\},$$

and:

$$f\left(x\right):=\sum _{i=1}^N{h}_i\left(x_i\right).$$

Then (see [35]),

$$\begin{array}{c}\hfill {prox}_{h_i}\left(x_i\right)=\left\{\begin{array}{cc}{x}_i,\hfill & if|x_i|<1\hfill \\ sign\left(x_i\right),\hfill & if1\le |x_i|\le 2\hfill \\ sign(x_i-1),\hfill & if|x_i|>2,\hfill \end{array}\right.\end{array}$$

and:

$${prox}_f\left(x\right)=({prox}_{h_1}\left(x_1\right),{prox}_{h_2}\left(x_2\right),\dots ,{prox}_{h_N}\left(x_N\right)),$$

for all $x\in {\mathbb{R}}^N$. Assume that $Ax=x$, and let us consider the split minimization problem (SMP) (10) as follows:

$$\begin{array}{c}\hfill z^{\ast }\in argminfandA{z}^{\ast }\in argming.\end{array}$$

(64)

It is easy to check that $x=(0,0,...,0)$ is in the set of solutions of Problem (64). We now took ${ϵ}_n={\displaystyle \frac{1}{n+1}}$ and:

$${\theta }_n=\left\{\begin{array}{cc}min\left\{{\displaystyle \frac{1}{(n+1)\parallel x_n-x_{n-1}{\parallel }_2^2}},0.5\right\},\hfill & if{x}_n\ne x_{n-1},\hfill \\ 0.5,\hfill & otherwise.,\hfill \end{array}\right.$$

for all $n\ge 1$. We next took $S\equiv I$, then we obtained by Algorithm 1 that:

$$\begin{array}{ccc}\hfill u_n& =& x_n+{\theta }_n(x_n-x_{n-1})\hfill \\ \hfill x_{n+1}& =& {prox}_{\lambda {\tau }_{n}f}(I-{\tau }_n{A}^{\ast }(I-{prox}_{\lambda g})A)u_n.\hfill \end{array}$$

(65)

The iterative schemes (12) and (13) are:

$$\begin{array}{c}\hfill x_{n+1}={prox}_{\lambda {\gamma }_{n}f}\left(\left(1-{\displaystyle \frac{1}{n+1}}\right)x_n-{\gamma }_n(I-{prox}_{\lambda g})x_n\right)\end{array}$$

(66)

and:

$$\begin{array}{c}\hfill x_{n+1}=\left(1-{\displaystyle \frac{1}{n+1}}\right){prox}_{\lambda {\gamma }_{n}f}\left((I-{\gamma }_n(I-{prox}_{\lambda g}))x_n\right),\end{array}$$

(67)

respectively, where ${\gamma }_n$ was given in [12].

We now provide a comparison of the convergence of the iterative schemes (12) and (13) in Abbas’s work [12] with our proposed algorithm with $S\equiv I$ in terms of CPU time, where initial points $x_1$, $x_2$ were randomly generated vectors in ${\mathbb{R}}^N$. We tested this experiment with different choices of N as follows: $N=100,500,1000,2000$.

We used ${\displaystyle \frac{\parallel x_{n+1}-x_n\parallel }{\parallel x_2-x_1\parallel }}<{10}^{-2}$ as the stopping criterion. The result of this experiment is reported in Table 1.

Table 1. Computation results for Example 2.

	N	100	500	1000	2000
Algorithm (12)	CPU (seconds)	0.602975	0.556099	0.603340	0.674949
Algorithm (13)	CPU (seconds)	0.222086	0.267980	0.262785	0.270231
Our proposed algorithm	CPU (seconds)	0.120814	0.228486	0.238006	0.247131

Remark 3. 

By observing the result of Example 2, we found that our proposed algorithm was more efficient than Abbas’s Algorithms (12) and (13) regarding the CPU time.

Finally, we show the average error of our algorithm as the following experiment:

Example 3.

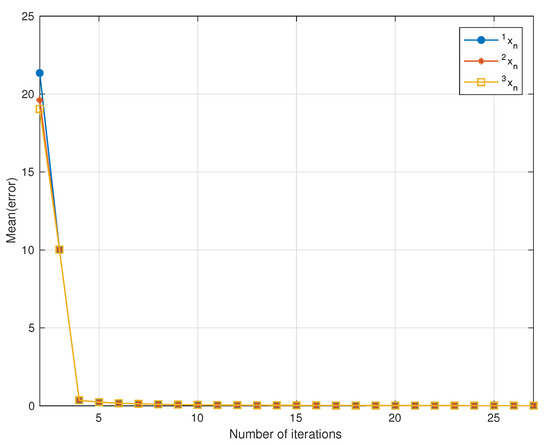
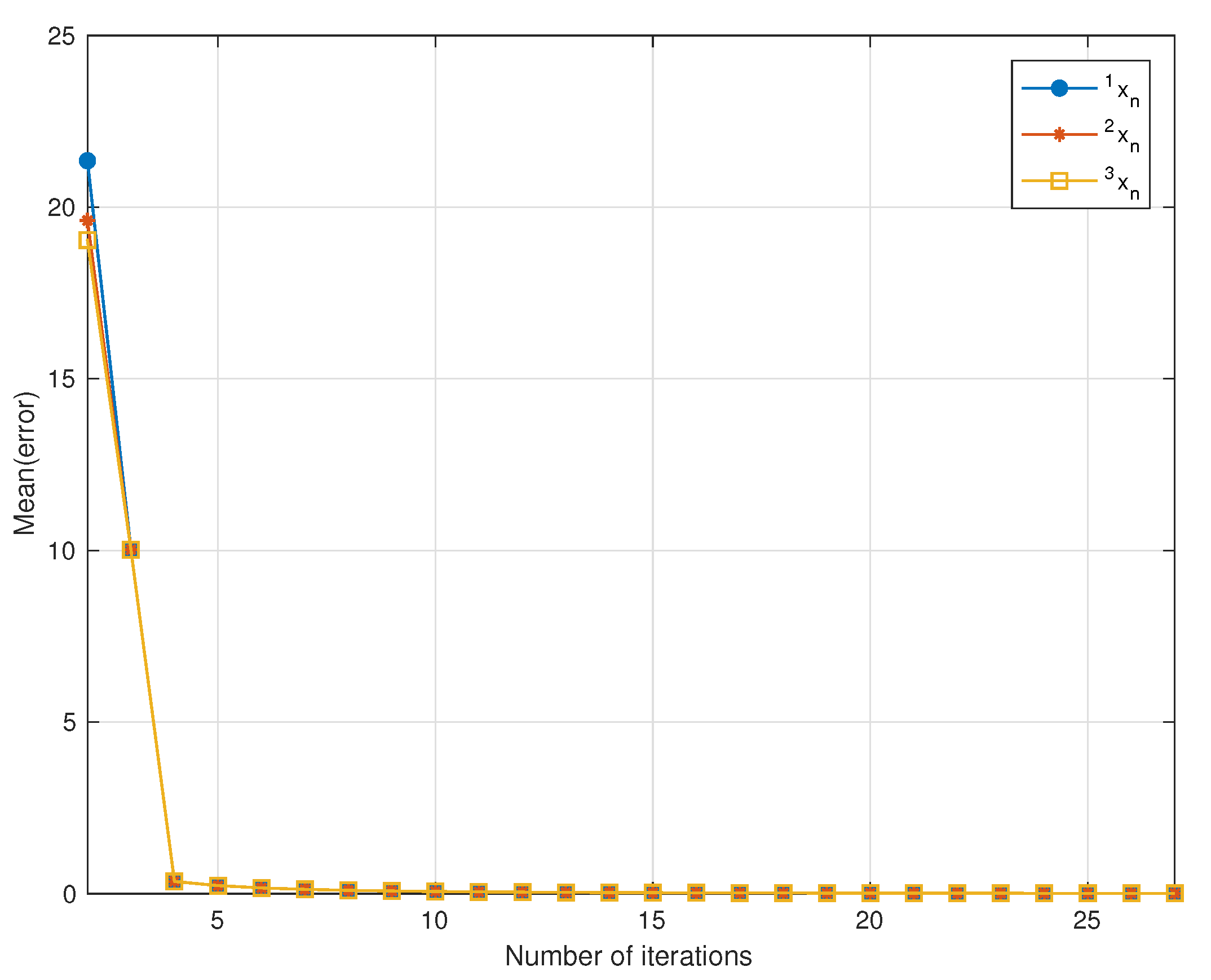
Let $H_1,H_2,g,{\mathrm{prox}}_g,f$, and ${\mathrm{prox}}_f$ be defined as in example (2). In this experiment, we took $x_1:=x_1\left(i\right)=(x_1^1\left(i\right),x_1^2\left(i\right),\dots ,x_1^{10}\left(i\right))$, where $i=1,2,\dots ,20$. Let $\left\{x_n\left(i\right)\right\}$ be a sequence generated by Algorithm 1 and the parameters ${\rho }_n=2,v=0.0025,{\alpha }_n=0.00025$, and ${\delta }_n={\displaystyle \frac{1}{n+1}}.$ The mean-error is given by:

$$\begin{array}{c}\hfill Error\left(x_n\right):={\displaystyle \frac{1}{20}}\sum _{i=1}^{20}\parallel x_{n+1}\left(i\right)-x_n\left(i\right)\parallel .\end{array}$$

(68)

We used $Error\left(x_n\right)<{10}^{-2}$ as the stopping criterion of this experiment. We then observed that the sequence $\left\{x_n\right\}$ generated by Algorithm 1 converged to a solution if $Error\left(x_n\right)$ converged to zero. Figure 2 shows the average error of our method in three groups of 20 initial points.

Figure 2. Computation results for Example 3.

Remark 4. 

By observing the result of Example 3, we found that the choice of the initial value did not affect the ability of our algorithm to achieve the solutions.

5. Conclusions

This paper discussed split minimization problems and fixed point problems of a nonexpansive mapping in the framework of Hilbert spaces. We introduced a new iterative scheme that combined the proximal algorithm and the modified Mann method with an inertial extrapolation and a self-adaptive step size. For the proposed algorithm, the main advantage was that there was no need to compute the operator norm of A. Moreover, we illustrated the performance of our proposed algorithm by comparing with other existing methods in terms of CPU time. The obtained results were improved and extended various existing results in existing pieces of literature.