Abstract
This work was devoted to the study of a relaxation limit of the so-called aggregation equation with a pointy potential in one-dimensional space. The aggregation equation is today widely used to model the dynamics of a density of individuals attracting each other through a potential. When this potential is pointy, solutions are known to blow up in final time. For this reason, measure-valued solutions have been defined. In this paper, we investigated an approximation of such measure-valued solutions thanks to a relaxation limit in the spirit of Jin and Xin. We study the convergence of this approximation and give a rigorous estimate of the speed of convergence in one dimension with the Newtonian potential. We also investigated the numerical discretization of this relaxation limit by uniformly accurate schemes.
MSC:
35L65; 65M12; 35D30
1. Introduction
The so-called aggregation equation has been widely used to model the dynamics of a population of individuals in interaction. Let , sufficiently smooth, be the interaction potential governing the population. Then, in one dimension in space, the dynamics of the density of individuals, denoted by , is governed by the following equation, for and :
Such equations appear in many applications in population dynamics: for instance, to describe the collective migration of cells by swarming, the motion of bacteria by chemotaxis, the crowd motion, the flocking of birds, or fishes school, see, e.g., [1,2,3,4,5,6,7]. From a mathematical point of view, these equations have been widely studied. When the potential W is not smooth enough, it is known that weak solutions may blow up in finite time [8,9]. Thus, the existence of weak (measure) solutions has been investigated in, e.g., [10,11].
In this paper, we consider a relaxation limit in the spirit of Jin–Xin [12] of the aggregation equation in one space dimension on . It is now well-established that such modifications allow regularizing the solutions. For a given , we introduce the system:
This system is complemented by initial data and . It is clear, at least formally, that when , the solution of system (2) converges to the one of the aggregation Equations (1) (and it is actually only true if ). We mention that the aggregation equation may also be derived thanks to a hydrodynamical limit of kinetic equations [6,7,13].
The aim of this work was to study the convergence as of the relaxation system (2) towards the aggregation equation. More precisely, we establish a precise estimate of the speed of convergence, and we also illustrate with some numerical simulations. These estimates are obtained only in the case of the Newtonian potential in one dimension . Indeed, in this particular case, we may link the aggregation equation to a scalar conservation law [14,15]. The same link holds for the relaxation system (2)—denoting:
where the notation stands for the integral with respect to the probability measure , then we verify easily that:
so that . Then, integrating (2), we deduce that is a solution to:
which is complemented with the initial data , and . Clearly, as , we expect that the solution of the above system converges to the solution of the following Burgers equation:
Introducing the quantities and , (3) is equivalent to the diagonalized system:
We will adapt the techniques developed in [16] to obtain convergence estimates for our system.
In order to illustrate this convergence result, numerical discretizations of the relaxation system (2) are investigated. The schemes we propose are such that they are uniform with respect to , that is they satisfy the so-called asymptotic preserving (AP) property [17]. Therefore, such schemes in the limit must be consistent with the aggregation equation. The numerical simulations of solutions of the aggregation equation for pointy potentials have been studied by several authors, see, e.g., [11,13,18,19,20,21,22]. In particular, some authors pay attention to recover the correct behavior of the numerical solutions after the blow-up time. To do so, particular attention must be paid to the definition of the product when is a measure.
In this article, we propose two discretizations of the relaxation system which satisfy the AP property. In a first approach, we propose a simple splitting algorithm where we split the transport part and the right hand side in system (2). It results in a numerical scheme which is very simple to implement and for which we easily verify the AP property. The second approach relies on a well-balanced discretization in the spirit of [20,23]. This scheme is more expensive to implement than the first scheme, but its numerical solution has less diffusion, as it is illustrated by our numerical results.
The outline of the paper is the following. In Section 2, after recalling some useful notations, we prove our main result: an estimation of the speed of convergence in the Wasserstein distance with respect to of the solutions of the relaxation system (2) towards the solution of the aggregation Equation (1) in the case . The numerical discretization is investigated in Section 3. Two numerical schemes verifying the AP property are proposed. The first scheme is based on a splitting algorithm, whereas the second scheme relies on a well-balanced discretization. Numerical results and comparisons are provided in Section 4.
2. Convergence Result
2.1. Notations
Before stating and proving our main results, we first recall some useful notations and results. Since we are dealing with conservation laws (in which the total mass is conserved), we will work in some space of probability measures, namely the Wasserstein space of order , which is the space of probability measures with a finite order p moment:
This space is endowed with the Wasserstein distance defined by (see, e.g., [24,25])
where is the set of measures on with marginals and , meaning that:
with , the set of continuous functions on that vanish at infinity. From a simple minimization argument, we know that in the definition of , the infimum is actually a minimum. A map that realizes the minimum in the definition (5) of is called an optimal transport plan, the set of which is denoted by .
In the one-dimensional framework, we may simplify these definitions. Indeed, any probability measure on the real line can be described in terms of its cumulative distribution function , which is a right-continuous and non-decreasing function with and . Then, we can define the generalized inverse of (or monotone rearrangement of ) by , it is a right-continuous and non-decreasing function as well, defined on . We have for every non-negative Borel map :
In particular, if and only if . Moreover, in the one-dimensional setting, there exists a unique optimal transport plan realizing the minimum in (5). More precisely, if and belong to , with monotone rearrangements and , then where is the restriction of the Lebesgue measure on . Thus, we have the explicit expression of the Wasserstein distance (see [24,26,27]):
and the map is an isometry between and the convex subset of (essentially) non-decreasing functions of .
2.2. Convergence Estimates
Let us first consider the limit for the system (3). Compactness methods were used in [28] to get convergence in space. However, in order to pass to the aggregation equation, one may want global convergence, which we prove in the following theorem, along the lines of Katsoulakis and Tzavaras [16].
Theorem 1.
Let, and set. There exists a constantsuch that, for any, denoting bythe solution to (3) with initial data, the following estimate holds:
where u is the entropy solution to the Burgers equation with initial datum.
Proof.
Denote the solution to (4), and .
So as to obtain entropy inequalities on , we need monotonicity properties on G. One can check that is decreasing with respect to and if the so-called subcharacteristic condition holds. Up to a slight modification of the nonlinear term in (3), which does not affect the value of :
the choice ensures that the subcharacteristic condition and the bound holds for all time.
Now, obtaining entropy inequalities on consists of making a comparison with constant state solutions to (4). Namely, letting , and , we have for all , and therefore is a solution to (4). Thus, the following system holds:
Multiplying (7a) by , (7b) by and summing yields:
Hence, using the monotonicity of G, we obtain the following entropy inequalities on :
We now turn to proving the entropy inequalities on . Straightforward computations yield the existence of a constant such that, for all , one has . We therefore work on the variable in the first place. Let , and such that . We have:
where verifies . Thus, we are left to control . To do so, we formally differentiate this quantity and use (4):
Integrating in space gives:
where and are positive constants which do not depend on nor on time. A Gronwall lemma then gives:
where we still denote as a constant independent of time and of .
In addition, since, , one has and therefore:
with . Differentiating (9) in time and (11) in space, and using (8) thus yields:
Then, we estimate using Kuznetsov’s doubling of variables technique (see, e.g., [29] for scalar conservation laws with viscosity and [30] for a more general formalism) in order to combine (12) with Kruzkov inequalities on the entropy solution u, that read:
Writing, respectively, (13) at point for and (12) at point for , we obtain:
Now, let and be two mollyfing kernels. Setting and testing (14a) and (14b) against and , respectively, and integrating over , we obtain on the one hand:
and on the other hand:
Now, since is even, and and , we deduce by adding (15) and (16):
Then, we write:
A triangle inequality gives for :
with , the second term appearing in (17) and for the last one we write:
and then we use the fact that is uniformely Lipschitz in with respect to . Indeed, one has with being uniformely bounded with respect to as stays in the compact set for all time. In addition, estimating can be done reusing (4) and (10):
with still independent of time and of . Hence, and . All in all, we get for :
Moreover, similarly, for :
Returning to (18), we obtain:
However, using a triangle inequality, one can show that:
and similarly:
We then bound from above the term RHS using inequality for :
Finally, we obtain:
which, after optimizing the values of and and noticing that , gives:
and this inequality, along with and (10) gives in turn the result. □
Denoting , the convergence of towards in ensures that is a probability measure. Indeed, since for all , is a non-negative distribution, so is . The Riesz–Markov theorem then ensures that can be represented by a non-negative Borel measure. In addition, almost everywhere, for , is a non-increasing function taking values in and hence converges to a certain limit when x goes to . The same holds true for the limit function . However, since , then must vanish as x goes to . Therefore, the total mass of is 1.
Then, passing to the relaxation system (2) for the aggregation Equation (1) can be done by using (6) with . As a consequence, Theorem 1 translates as follows for the aggregation.
Theorem 2.
Let, and set. There exists a constantsuch that, for any, denotingthe solution to (2) with initial data, one has:
whereis the unique solution (1) with initial datum.
3. Numerical Discretization
Hereafter, we denote the time step and we introduce a Cartesian mesh of size . We denote for and for . In this section, we extend our framework and consider the aggregation Equation (1) with arbitrary pointy potentials W, which satisfy the following conditions:
- (i)
- W is even and ;
- (ii)
- ;
- (iii)
- W is -convex, i.e., there exists such that is convex;
- (iv)
- W is -lipschitz continuous for some .
In this framework, the convergence of towards for a slightly different problem has also been studied in [7]. Adapting the argument, the convergence still holds provided the sub-characteristic condition is verified. However, for such general potentials, the authors were not able to obtain the estimates of the speed of convergence as stated in Theorem 2.
In this section, we propose some numerical schemes able to capture the limit , thus satisfying the so-called asymptotic preserving (AP) property. We consider two approaches, the first one based on a splitting algorithm, and the second one based on a well-balanced discretization.
3.1. A Splitting Algorithm
A first simple approach to discretize the system (2) is to use a splitting method. Such a method is known to be convergent and easy to implement but introduces numerical diffusion.
Notice that the system (2) rewrites, with , , as
The idea of the method is to solve in a first step on the system:
with initial data . We obtain and . Notice that this system may be solved explicitly. Indeed, by adding and subtracting the two equations, we deduce after an integration:
Then, in a second step, we discretize by a classical finite volume upwind scheme the system:
That is:
Coming back to the variables and , we obtain:
with . Then, the splitting algorithm reads:
and:
Lemma 1.
For any, if both the CFL conditionand the subcharacteristic conditionhold, then the splitting scheme (23) and (24) is-stable:
Proof.
We have:
Under the condition , in the expression of , the coefficient in front of is non-negative and the one in front of is non-positive. Similarly, in , the coefficient of is non-positive and the one in front of is non-negative. Taking the absolute value and adding up therefore yields:
It remains to remark that, provided the CFL condition is verified, (24) gives:
□
Note that similar schemes have also been studied in [31] and proved convergent at a rate of .
Let us now verify the AP property. When , we verify that the equation on (25) converges to the following Rusanov discretization of (1) (see [21] for numerical simulations using the Rusanov scheme):
This limiting scheme provides a consistent discretization of (1). Indeed, a similar scheme has been extensively studied in [11] using compactness arguments and the following convergence result was proven:
Lemma 2.
Assumeand that the stability conditionsandare satisfied. Letand suppose we initialize the scheme (27) withwhere. Then, denotingthe reconstruction given by the scheme (27), that is:
thenconverges weakly in the sense of measures ontowards the solution ρ of Equation (1), asgoes to 0.
It has been also proven in [32] that the scheme (27) converges at a rate of .
3.2. Well-Balanced Discretization
Although the splitting method provides a simple way to obtain a discretization which is uniform with respect to the parameter , the resulting scheme has strong numerical diffusion and may not have good large time behavior. Then, well-balanced schemes have been introduced. A scheme is said to be well-balanced when it conserves equilibria. The method proposed in this section comes from [20].
Let us assume that, for some , the approximation of solution of (22) is known. We construct an approximation at time using a finite volume upwind discretization of (22), with the discretization of the source terms to be prescribed right afterwards:
In order to preserve equilibria, we set:
where solve the stationary system with incoming boundary conditions, on :
In addition, in the same fashion, , where is the solution of the stationary system on :
Reporting Equations (30b) and (31a) into the discretization of the source term, we obtain and . Hence, one may rewrite the scheme (28) as
Remark that the stationary system:
is equivalent to:
Therefore, denoting and , which are constant, respectively, on and , one has:
Thus, it turns out that the scheme can be rewritten only in terms of the discretized unknowns and of :
Or equivalently:
However, solving the stationary systems (30) and (31) involves the resolution of a nonlinear and nonlocal ODE. Instead, we propose an approximation in the spirit of [20].
We replace the nonlinear term in (30a)–(30b) by , where stands for a fixed and consistent discretization of on the interval , to be specified afterwards. Similarly, we will replace the nonlinear term in (31a)–(31b) by with defined accordingly. In the following, we detail the construction for the problem (30a)–(30b) on .
Obviously, the definition of should be taken with care [11,20]. In [32], the authors showed that, when discretizing the product , if and were not evaluated at the same point, then the resulting scheme produces the wrong dynamics. To take this into account, we will split into one contribution coming from the left and one contribution coming from the right, i.e., we set and where and . This implies that and .
More precisely, we solve the two following boundary value problem, on :
We may explicitly solve these linear systems, and since and , we obtain the relations:
with:
Notice that we have:
where we denote and —the positive and negative negative part of a. Using the boundary conditions in (30), we have:
with (39) and the fact that is constant on , we obtain the following system on the unknowns :
Solving this system yields:
From which we deduce with (42):
and with (39):
(the above quantities are well-defined since and ). Injecting into (37), it gives the following scheme:
where the coefficients are defined in (40). Equivalently, for the variable , the scheme reads:
where we recall that and .
It remains to define the velocities used in (38) and in (40). We take:
However, this discretization implies the resolution of a nonlinear problem, since the quantities depends nonlinearly on .
Then, we implement a fixed point method initialized with and . Solving, on each cell , the system of ODEs (38) with these values for the velocities gives two sequences, and . Then, we assign the next value of the velocity to , which allows us to compute new values for the left and right densities, and , through (38). We iterate until and pass below a certain threshold. Notice that the velocities always remain bounded by . In practice, only a few iterations are needed.
The resulting scheme is consistent for any and stable under standard stability conditions, as shown by the following lemmas.
Lemma 3
( stability). Under the CFL condition and the subcharacteristic condition , there holds that the sequence defined by the scheme (47), verifies the following stability property:
Proof.
In each combination of (47), the first coefficient is non-negative under the CFL condition , and so is the last one since and . Moreover, under the subcharacteristic condition , it holds that so the remaining coefficient is non-positive. Thus, applying the triangle inequality and re-indexing the sums appropriately:
This concludes the proof. □
Lemma 4
(Consistency for smooth solutions). Assume that, for all , we have . Then, for any , the scheme (37) is consistent with (2) provided that the solutions are smooth enough.
Proof.
For , one has, using the Taylor expansions as :
Thus:
In particular, is clearly consistent with as long as the solution is smooth enough to perform standard consistency analysis for finite differences. This shows that (37a) is consistent with . As for the consistency of (37b) with , we write:
Using Taylor expansions, we have, for smooth solutions , , and . Along with the bound , this implies:
Clearly, and are consistent with an accuracy of and , respectively, with and . For the remaining terms, let us recall that, with the notations of (42):
Hence, . Since , and assuming that:
we deduce that is consistent with with accuracy . It follows that is consistent with , again with accuracy , and this concludes the proof. □
4. Numerical Experiments
We present some numerical illustrations for the two schemes described in the previous section. In addition to the potential , we also consider the smooth potential .
Numerical tests are conducted on the domain with the inital data , and both schemes are initialized with:
Figure 1 shows that both schemes recover the correct dynamics in the limit : for the potential , one can compute the exact velocity of both Dirac masses for the aggregation Equation (1) and see that they should be located, respectively, in and in final time .
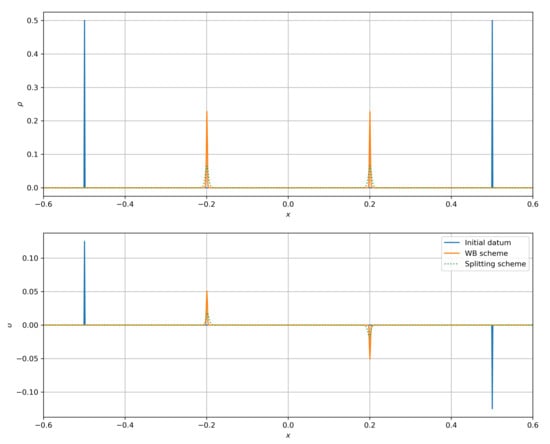
Figure 1.
Dynamics of two Dirac masses for the potential in time .
This test is set up with , on a Cartesian mesh of with 1500 cells, and the CFL . Both schemes (27) and (49) display the correct velocity for the Dirac masses, but one can notice that the Rusanov scheme (27) shows more numerical diffusion. Note that both schemes are written in conservation form, they preserve the total mass of , which is also verified numerically.
We then investigated the order of convergence when goes to 0 with fixed, in Wasserstein distance (the numerical results are the same for ).
After performing tests for several values of , it appears that the convergence rate does not depend on the size of . Therefore, as an example, we propose simulations in final time , with the same intial data and stability parameters as above, and with for Figure 2 and with for Figure 3:
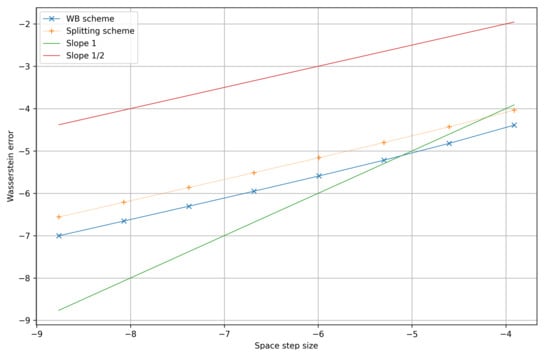
Figure 2.
Order of convergence of the splitting scheme and the well-balanced scheme for the smooth potential .
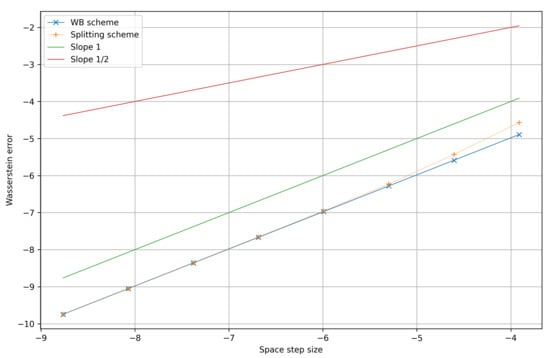
Figure 3.
Order of convergence of the splitting scheme and the well-balanced scheme for the pointy potential .
For a fixed value of , both schemes seem to converge with order with respect to for the smooth potential (see Figure 2) whereas they seem to be of order 1 for the potential (see Figure 3). This can be explained as both schemes possess some numerical diffusion which is somehow counterbalanced by the aggregation phenomenon in the case of a pointy potential, as already observed in [21]. Due to the link with the Burgers equation, this superconvergence phenomenon is directly linked to the results of Després [33], which should be rigorously extended to our case (the mere extension to the upwind scheme of [11] for the aggregation is not straightforward).
Finally, we also verified the well-balanced property of the scheme (48) by computing the distance between the approximated solution at time and the stationary solution of (2) given by
The test is conducted with , with the exact boundary conditions given by the above formula, and for several values of . As we show in Figure 4, the scheme (48) preserves well the above equilibrium for any (although we replaced the resolution of the systems (30) and (31) with linear systems, see (38)), while for the splitting scheme, we recover the linear convergence towards which is, in this case, the exact solution.
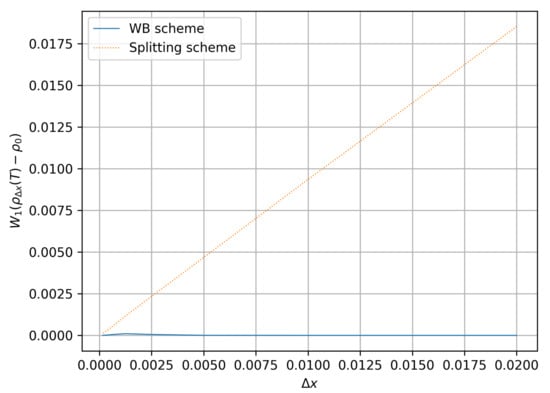
Figure 4.
Distance to the equilibrium for the splitting scheme and the well-balanced scheme and for the pointy potential .
Author Contributions
B.F., F.L., S.T.T. and N.V. contributed equally in writing this article. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of Open Access Journals |
| AS | asymptotic preserving |
References
- Morale, D.; Capasso, V.; Oelschläger, K. An interacting particle system modelling aggregation behavior: From individuals to populations. J. Math. Biol. 2005, 50, 49–66. [Google Scholar] [CrossRef]
- Burger, M.; Di Francesco, M. Large time behavior of nonlocal aggregation models with nonlinear diffusion. Netw. Heterog. Media 2008, 3, 749–785. [Google Scholar] [CrossRef]
- Burger, M.; Capasso, V.; Morale, D. On an aggregation model with long and short range interactions. Nonlinear Anal. Real World Appl. 2007, 8, 939–958. [Google Scholar] [CrossRef]
- Topaz, C.M.; Bertozzi, A.L.; Lewis, M.A. A nonlocal continuum model for biological aggregation. Bull. Math. Biol. 2006, 68, 1601–1623. [Google Scholar] [CrossRef]
- Topaz, C.M.; Bertozzi, A.L. Swarming patterns in a two-dimensional kinematic model for biological groups. SIAM J. Appl. Math. 2004, 65, 152–174. [Google Scholar] [CrossRef]
- Dolak, Y.; Schmeiser, C. Kinetic models for chemotaxis: Hydrodynamic limits and spatio-temporal mechanisms. J. Math. Biol. 2005, 51, 595–615. [Google Scholar] [CrossRef] [PubMed]
- James, F.; Vauchelet, N. Chemotaxis: From kinetic equations to aggregate dynamics. NoDEA Nonlinear Differ. Equ. Appl. 2013, 20, 101–127. [Google Scholar] [CrossRef]
- Bertozzi, A.L.; Brandman, J. Finite-time blow-up of L∞-weak solutions of an aggregation equation. Commun. Math. Sci. 2010, 8, 45–65. [Google Scholar] [CrossRef]
- Bertozzi, A.L.; Carrillo, J.A.; Laurent, T. Blow-up in multidimensional aggregation equations with mildly singular interaction kernels. Nonlinearity 2009, 22, 683–710. [Google Scholar] [CrossRef]
- Carrillo, J.A.; Difrancesco, M.; Figalli, A.; Laurent, T.; Slepčev, D. Global-in-time weak measure solutions and finite-time aggregation for nonlocal interaction equations. Duke Math. J. 2011, 156, 229–271. [Google Scholar] [CrossRef]
- Carrillo, J.A.; James, F.; Lagoutière, F.; Vauchelet, N. The Filippov characteristic flow for the aggregation equation with mildly singular potentials. J. Differ. Equ. 2016, 260, 304–338. [Google Scholar] [CrossRef]
- Jin, S.; Xin, Z. The relaxation schemes for systems of conservation laws in arbitrary space dimensions. Commun. Pure Appl. Math. 1995, 48, 235–276. [Google Scholar] [CrossRef]
- James, F.; Vauchelet, N. Numerical methods for one-dimensional aggregation equations. SIAM J. Numer. Anal. 2015, 53, 895–916. [Google Scholar] [CrossRef]
- Bonaschi, G.A.; Carrillo, J.A.; Di Francesco, M.; Peletier, M.A. Equivalence of gradient flows and entropy solutions for singular nonlocal interaction equations in 1D. ESAIM Control Optim. Calc. Var. 2015, 21, 414–441. [Google Scholar] [CrossRef]
- James, F.; Vauchelet, N. Equivalence between duality and gradient flow solutions for one-dimensional aggregation equations. Discret. Contin. Dyn. Syst. 2016, 36, 1355–1382. [Google Scholar]
- Katsoulakis, M.A.; Tzavaras, A.E. Contractive relaxation systems and the scalar multidimensional conservation law. Commun. Partial. Differ. Equ. 1997, 22, 225–267. [Google Scholar] [CrossRef]
- Jin, S. Efficient asymptotic-preserving (AP) schemes for some multiscale kinetic equations. SIAM J. Sci. Comput. 1999, 21, 441–454. [Google Scholar] [CrossRef]
- Carrillo, J.A.; Chertock, A.; Huang, Y. A finite-volume method for nonlinear nonlocal equations with a gradient flow structure. Commun. Comput. Phys. 2015, 17, 233–258. [Google Scholar] [CrossRef]
- Craig, K.; Bertozzi, A.L. A blob method for the aggregation equation. Math. Comput. 2016, 85, 1681–1717. [Google Scholar] [CrossRef]
- Gosse, L.; Vauchelet, N. Numerical High-Field Limits in Two-Stream Kinetic Models and 1D Aggregation Equations. SIAM J. Sci. Comput. 2016, 38, A412–A434. [Google Scholar] [CrossRef]
- Fabrèges, B.; Hivert, H.; Le Balc’h, K.; Martel, S.; Delarue, F.; Lagoutière, F.; Vauchelet, N. Numerical schemes for the aggregation equation with pointy potentials. ESAIM Proc. Surv. 2019. [Google Scholar] [CrossRef]
- Carrillo, J.A.; Fjordholm, U.S.; Solem, S. A second-order numerical method for the aggregation equations. Math. Comput. 2021, 90, 103–139. [Google Scholar] [CrossRef]
- Gosse, L. Computing Qualitatively Correct Approximations of Balance Laws. Exponential-Fit, Well-Balanced and Asymptotic-Preserving; Springer: Milano, Italy, 2013; Volume 2, p. 340. [Google Scholar]
- Villani, C. Topics in Optimal Transportation; American Mathematical Society (AMS): Providence, RI, USA, 2003; Volume 58, p. 370. [Google Scholar]
- Santambrogio, F. Optimal Transport for Applied Mathematicians. Calculus of Variations, PDEs, and Modeling; Birkhäuser/Springer: Cham, Switzerland, 2015; Volume 87, p. 353. [Google Scholar]
- Vallender, S.S. Calculation of the Wasserstein Distance Between Probability Distributions on the Line. Theory Probab. Appl. 1974, 18, 784–786. [Google Scholar] [CrossRef]
- Rachev, S.T.; Rüschendorf, L. Mass Transportation Problems. Vol. 1: Theory. Vol. 2: Applications; Springer: New York, NY, USA, 1998; p. 430. [Google Scholar]
- Natalini, R. Convergence to equilibrium for the relaxation approximations of conservation laws. Commun. Pure Appl. Math. 1996, 49, 795–823. [Google Scholar] [CrossRef]
- Serre, D. Systems of Conservation Laws 1: Hyperbolicity, Entropies, Shock Waves; Cambridge University Press: New York, NY, USA, 1999. [Google Scholar]
- Bouchut, F.; Perthame, B. Kružkov’s Estimates for Scalar Conservation Laws Revisited. Trans. Am. Math. Soc. 1998, 350, 2847–2870. [Google Scholar] [CrossRef]
- Liu, H.; Warnecke, G. Convergence Rates for Relaxation Schemes Approximating Conservation Laws. SIAM J. Numer. Anal. 2000, 37, 1316–1337. [Google Scholar] [CrossRef]
- Delarue, F.; Lagoutière, F.; Vauchelet, N. Convergence analysis of upwind type schemes for the aggregation equation with pointy potential. Ann. Henri Lebesgue 2020, 3, 217–260. [Google Scholar] [CrossRef]
- Després, B. Discrete Compressive Solutions of Scalar Conservation Laws. J. Hyper. Differ. Equ. 2004, 01, 493–520. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).