Abstract
Asymmetry and symmetry coexist in natural and human processes. The vital role of symmetry in art has been well demonstrated. This article highlights the complementary role of asymmetry. Further we show that the interaction of asymmetric action (recursion) and symmetric opposition (sinusoidal waves) are instrumental in generating creative features (relatively low entropy, temporal complexity, novelty (less recurrence in the data than in randomized copies and complex frequency composition). These features define Bios, a pattern found in musical compositions and in poetry, except for recurrence instead of novelty. Bios is a common pattern in many natural and human processes (quantum processes, the expansion of the universe, gravitational waves, cosmic microwave background radiation, DNA, physiological processes, animal and human populations, and economic time series). The reduction in entropy is significant, as it reveals creativity and contradicts the standard claim of unavoidable decay towards disorder. Artistic creations capture fundamental features of the world.
1. Introduction
Here we study music and poetry with mathematical methods that analyze symmetry and creativity. The relation between music and mathematics has been recognized since Pythagoras. The concept of symmetry has found many applications in science and art, but the term is given several different interpretations. Thermodynamics defines the spontaneous increase in entropy as an increase in symmetry, and, according to nineteenth century thermodynamics, natural processes tend to decay. In contrast, physics interprets symmetry as regularity, and esthetics highlights symmetry as a defining feature of beauty and art. Evolutionary theory states that natural processes are creative; human and artistic creativity thus continue natural creativity.
The term symmetry originally meant a sense of harmonious, aesthetically pleasing proportionality that embodies beauty. Soon the term symmetry acquired a more precise meaning of mathematical balance such as when one shape becomes exactly like another if you flip ("mirror" symmetry), slide, or turn it. In time, symmetry came to be defined when this internal identity could be demonstrated according to the rules of a formal system. A mathematical object is symmetric with respect to a given mathematical operation, if, when applied to the object, this operation preserves some property of the object. The set of operations that preserve a given property of the object form a group. Symmetry has been transformed in physics to mean invariance under any kind of transformation. According to Noether’s theorem, a continuous mathematical symmetry corresponds to a conserved quantity. Symmetry has come to mean any form of conservation; conversely, creation is associated with change and asymmetry. There is an ideological implication in interpreting symmetry as conservation. In this sense, it is said that most if not all laws of nature originate in symmetries [1]. Asymmetries such as the golden proportion are described as “symmetries”. This overlooks the fundamental role of asymmetry in physical and esthetic processes.
Symmetry does not exclude its opposite, asymmetry, but it is paired with it, as all opposites are. Indeed, for reasons of symmetry, symmetry itself must be paired with asymmetry. The concept of asymmetry has evolved from the mere lack of symmetry to the asymmetry of time in physics and biology, the discovery of asymmetry in biological molecules by Pasteur, and the demonstration of symmetry breaking as a core process in physical and biological evolution, from Pierre Curie to the 2008 Nobel prize winners Nambu, Kobayashi, and Maskawa. Parity symmetry is violated by phenomena that involve the weak force, and there also are violations of charge symmetry and of CP-symmetry. Asymmetry is central in natural and human processes. Asymmetry is also central to beauty and art, as illustrated by the golden proportion 1:1.618, utilized in classic architecture, renaissance and contemporary painting, books, and postcards.
Asymmetry and symmetry coexist as fundamental forms among mathematical and psychological structures. Bourbaki, a seminal group of mathematicians, described the architecture of mathematics as based on three foundations, lattices, groups and topology [2]. Lattices, groups and topology are mathematical abstractions of order, symmetry, and spatial form. The leading Swiss psychologist Jean Piaget [3] was astonished to realize that the fundamental cognitive structures he had discovered in the study of mental development corresponded to Bourbaki’s three ‘mother structures’ of mathematics.
Bourbaki’s mother forms—linear asymmetry, two-dimensional and bipolar symmetry, and vertical hierarchy as a sequence of steps—were prefigured in one of the earliest artistic archetypes: the first pyramid constructed by the prime minister and physician Imhotep (author of the first medical (and scientific) textbook, identified with Asclepius by the Greeks and the Romans), the Ziggurats built by the Sumerians, Elamites and Assyrians, and the step pyramids built by the Mayans, Mexicans and Incas (figure 1).
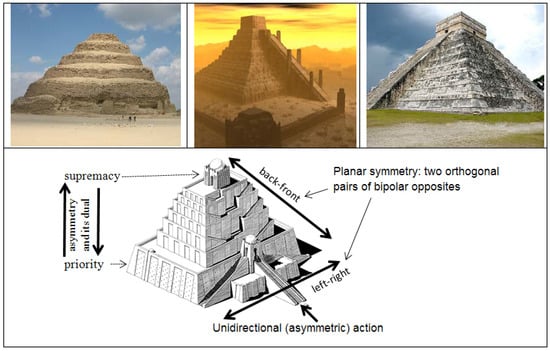
Figure 1.
Step pyramid archetype. Top: early pyramids in Egypt, Middle East, and Mexico. Bottom: Diagram illustrating how it captures asymmetry, symmetry of opposites, and transformation from simple and larger to a smaller top.
The Bourbaki forms also correspond to macroscopic features of the three dimensions of the Central Nervous System [4] that is the most complex system known: the asymmetry of sensory to motor function in its dorsal ventral axis, symmetry in its right-left axis, and the creation of complex forms from the folding of simpler ones in the vertical axis. Thus Sabelli [4,5,6] proposed that asymmetry, symmetry and continuous topological transformation from simple to complex (evolution) are the three fundamental patterns of processes, and that asymmetry and symmetry represent a primordial opposition that accounts for creativity in nature as well as in art.
Asymmetry is evident in non-stationary and non-periodic processes, both stochastic (random walks) and causal (Bios). Together, asymmetry, creativity and nonrandom causation define Bios [5], a fractal pattern generated mathematically by recursions that involve both asymmetry and symmetry (figure 2). We first identified Bios as a distinct pattern when studying heartbeat series; this led us to develop analytic methods that demonstrate causality and creativity in empirical processes. Bios is commonly found in natural and human processes: quantum processes [7], the expansion of galaxies and quasars in three surveys [8,9,10] gravitational waves [11], cosmic microwave background radiation [10], DNA [5], physiological processes [5,12,13,14,15,16,17], animal populations [18] and human populations [5], economic time series [19,20,21] and the prime numbers [22]. Levy et al [23] have already demonstrated Bios in several musical scores; we have expanded this work in this and other publications [24]. In other words, asymmetry is natural, a core property of complex and creative processes.
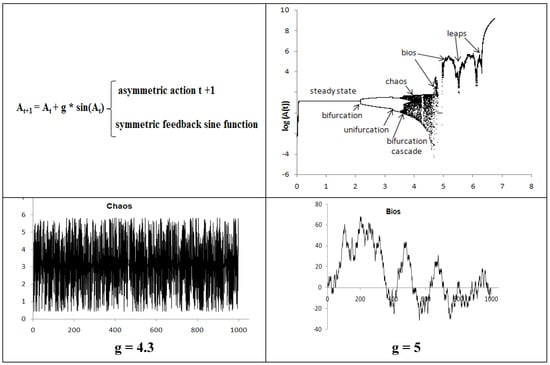
Figure 2.
Process equation. The sequence of patterns in steps of increasing complexity in the time series generated by the equation as g increases (logarithmic scale).
Causality and creativity define Bios and differentiate it from chaos and from random walks. Bios can be generated mathematically by several recursions that combine the temporal asymmetry of action and the symmetry of bipolar feedback [5,9]. The sinusoidal function provides a mathematical model for the philosophical tenet advanced by Heraclitus, Empedocles, Lao-tzu, Hegel, Darwin, and Salk that the interaction of opposites creates novel and complex processes [4]. This connects Bios with both creativity and a well-supported hypothesis regarding its generation.
To study artistic creations and archetypes in relation to natural processes is meaningful. Artistic archetypes portray fundamental patterns of nature, as highlighted by Pythagoras who found in music the mathematics of the universe. In this paper we demonstrate asymmetry, symmetry and creativity in music and poetry using mathematical techniques that measure these features in time series.
2. Methods
The data presented in the figures above are time series and therefore have no physical dimensions. We analyzed the sequence of notes in musical scores and the sequence of letters in literary texts in English and Spanish. The data were compared with mathematical models of non-periodic variations: random series, random walks, and stationary Chaos and non-stationary Bios generated by the process equation [25] (figure 2) for g = 4.3 and 5.
We measure the degree of asymmetry these musical and poetic texts and its changes in time by dividing the series into epochs and computing the middle, mean and median of each epoch. To measure symmetry and opposition we use complement plots [26] (graphs of the sine versus cosine of each term of the series) and trigonometric walks [27] (cumulative sum of the sine versus cosine of each term of the series). Complement plots omit the linearity of time but conserve temporal order (in the lines connecting successive points of the series). As sine and cosine are orthogonal to each other, this creates a 2-D plot. Sine and cosine are out of phase; one of these opposites is larger at each time and the data are plotted in a 3-D helix rather than a 2-D circle. Complement plots thus assume the priority of time, the asymmetry of opposites and the alternation of their relative size. The helix is a classic portrait of dialectic oscillation of opposites
We analyze these musical and poetic texts with recurrence methods using the Bios Data Analyzer [28]. Given a series A1, A2, …, AN, we construct the sequences (Euclidean vectors) yi of N successive members of a time series [yi = (Ai, Ai+1, Ai+2, ..., At+N)] starting with each data point Ai:. This is referred to as embedding in dimension N. Recurrence isometries are calculated by comparing the Euclidean norms of these vectors, and if the difference between them is less than a chosen cutoff radius (1%), a recurrence is plotted and counted. We have made calculations with many cutoff radii, anging from 0.1 to 50 % and the reults are similar. The quantification of recurrences at low and high embeddings allows one to consider both simple and complex patterns. Recurrence plots graph isometries as a function of time. Recurrences are colored according to their distance from red to violet. Both types of recurrence generate the same pattern in recurrence plots, but the number of isometries increases and the number of similarity recurrences decreases with the length of the vector. Isometry is the number of isometric recurrences as a percentage of the total number of possible recurrences in the sample (N x N / 2). The number of isometries (as % of the total number of possible recurrences) is computed for the original data and for a copy of the data randomized by shuffling. Novelty is defined as the increase in recurrence isometry produced by shuffling the data [29,30], and is quantified as the ratio of isometries after shuffling over isometries in the original data. Novelty is a key measure to distinguish creative from non-creative processes. Novelty is demonstrable for recurrence isometry but not for similarity recurrence. Embedding plots present the value of novelty computed with 2, 3, …, 100 embeddings.
In addition to analyzing the time series, we also analyzed the time series of difference between consecutive terms. Periodic series as well as causally generated non-periodic series (chaos, bios) show morphological and numerically quantifiable pattern in the series of differences, while random series and random walks do not show pattern (randomness) in the series of differences between consecutive terms (except at very high embeddings).
The standard deviation S.D. = √(∑ (xi-mean)2/N) of the series was recorded as a function of time. Series converging to an attractor display a decrease in S.D. with increasingly larger samples. In contrast, diversification is the increase in variance of a time series with an increase of the size of the sample (global diversification) or with increasing the embedding (local diversification): the SD is computed for sets (“embeddings”) of 2, 3, …, 100 consecutive terms of the time series, starting with each term in the series. The values obtained for each embedding are averaged for the entire series, and these averages are plotted as a function of the number of embeddings.
The power spectrum of these series was calculated using a program developed by Patel (Patel and Sabelli, 2003).
We measured entropy H with the de Moivre equation adopted by Boltzmann, and by Shannon to measure entropy, using a range of bins (N = 2, 4, 8, …), and plot the value of entropy as a function of the logarithm of the number of bins (figure 3). The values for entropy H a linear function of the logarithm of the number of bins:
where n is the number of bins used to calculate entropy [31]. The slope d (for diversity) of the entropy-bin regression line measures diversity of the data (figure 2); the slope is 0 for numerical series with two equally probable values, regardless of their temporal arrangement (random or periodic), and increases with the number of different values in the data from period 2 to period 3, 4,…, and chaos. Linearly increasing series, random series, statistical noise (random walks, pink noise), chaotic series, biotic series, and many empirical time series have a near 1 slope.
H = s + d* log2n
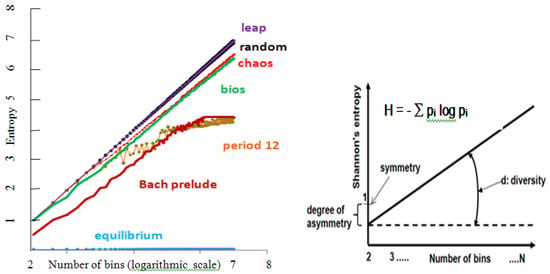
Figure 3.
Entropy-bin plot. Plot of informational entropy as defined by Shannon. It shows the calculation of the degree of symmetry (entropy at 2 bins = 1 for perfect symmetry and less than 1 for asymmetry) and diversity (slope). Many natural and human processes are highly asymmetric. Biotic series and random walks have a small degree of asymmetry, while chaos, random, and periodic series are symmetric.
The intercept s (for symmetry s) of the entropy-bin regression line at 2 bins (the least number of bins required for the calculation of entropy) is 1 for all symmetric distributions (random, sinusoidal, chaotic); asymmetry y (s < 1)is present in mathematically generated biotic series, in random walks and in empirical data (physical, biological, economic).
3. Results
3.1. Asymmetry and Symmetry
Histograms (figure 4) and Pareto histograms (figure 5) demonstrate asymmetry in the distribution of notes and letters in musical and literary texts. Statistical measures quantify asymmetry and demonstrate non-stationarity (figure 6 and Table 1).
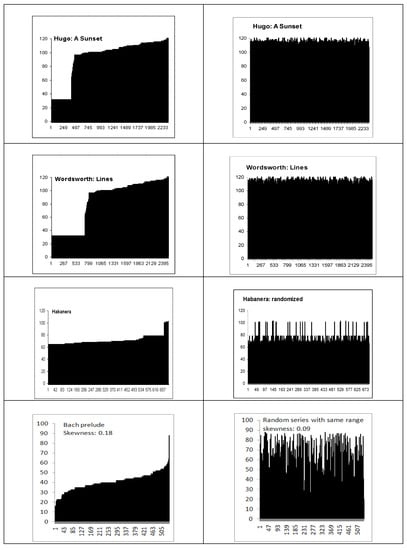
Figure 4.
Histogram showing asymmetry in the statistical distribution of letters in poetry (Hugo’s A Sunset and Wordsworth’s Lines Written as a School Exercise at Hawkshead) and musical notes (Georges Bizet’s “Habanera” from Carmen and Bach’s Prelude). Units: the number of occurences are plotted in the y-axis.
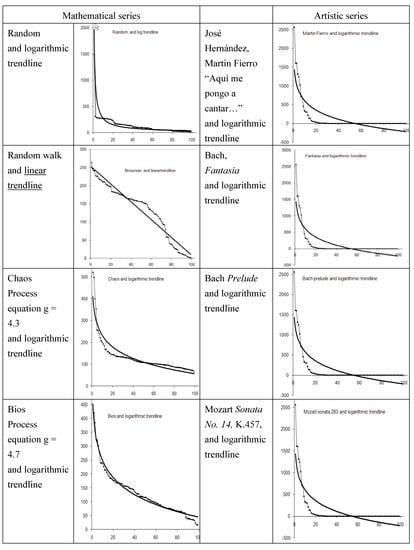
Figure 5.
Pareto histogram and logarithmic trendline (except for random walk, where a linear trendline fits).

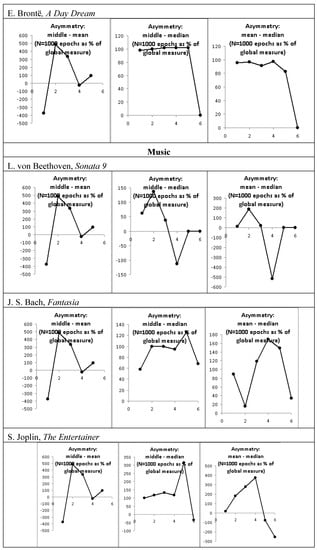
Figure 6.
Quantification of asymmetry in music and poetry.

Table 1.
Asymmetry of opposites.
Two dimensional plots (figure 7) do not show simple patterns as in chaos or bios. Trigonometric plots (figure 8) show rounded complement plots (not partial as in chaotic attractors), significant asymmetry. Table 1 presents statistical and trigonometric measures of the asymmetry of opposites.
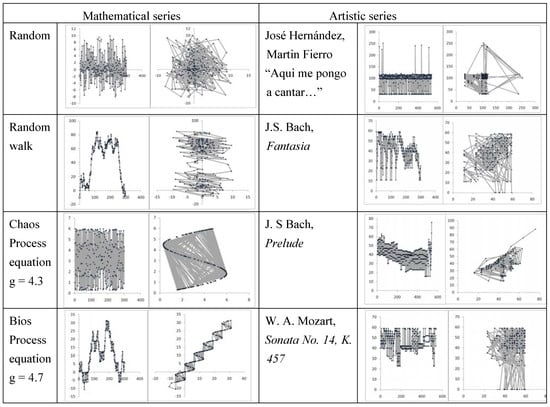
Figure 7.
Time series A(t), and twodimensional plot of A(t) vs. A(t+1).
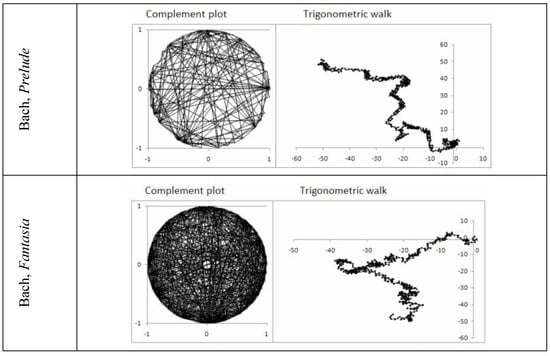
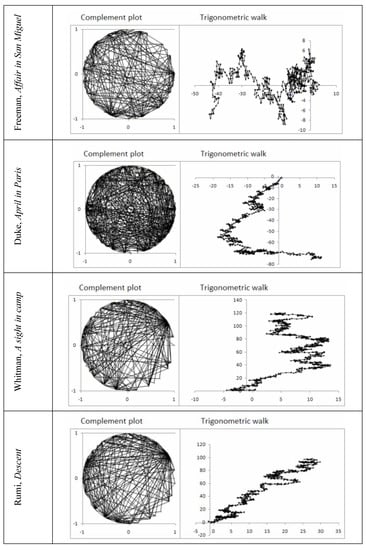
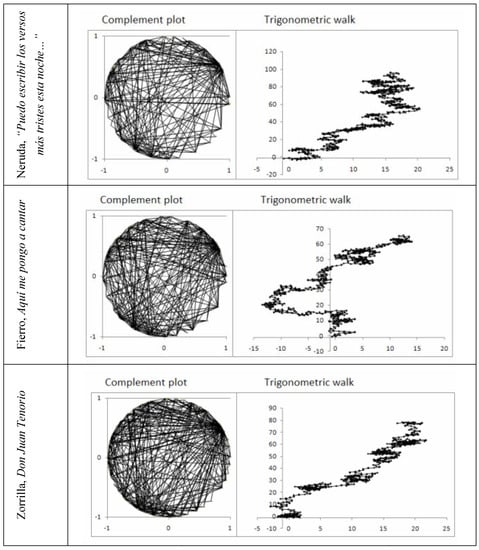
Figure 8.
Complement plots (left) and trigonometric walks (right) of musical compositions and of poems.
3.2. Entropy
Table 2 shows that maximal entropy occurs for ordered series such as a sequence of linearly increasing numbers, not for random data, as often assumed. Musical and literary texts have relatively low entropy. Figure 9 shows that this low entropy results from low symmetry rather than from decreased diversity. Both of these results are also observed in biotic series generated mathematically as well as in natural processes.

Table 2.
Low entropy of music and literary compositions.
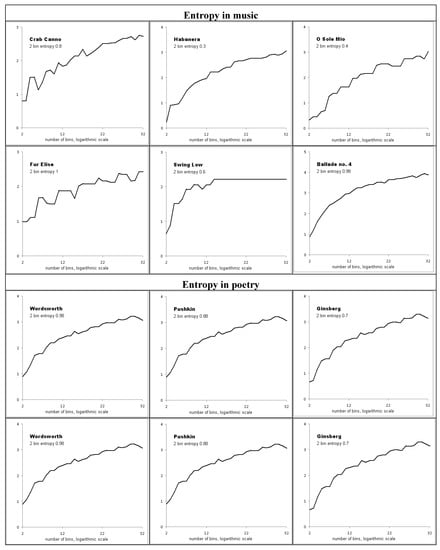
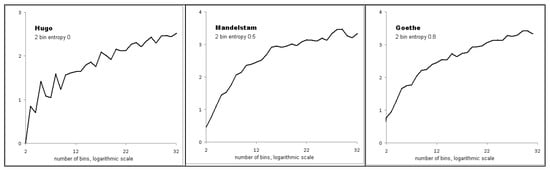
Figure 9.
Entropy of musical compositions and of literary texts as a function of the number of bins. The musical compositions analyzed include: Eduardo di Capua’s O Sole Mio, Georges Bizet’s Habanera from Carmen, Bach’s Crab Canon, Mozart’s Fur Elise, the American Spiritual Swing Low Sweet Chariot, and Chopin’s Ballade no. 4. The poems are: Wordsworth’s Lines Written as a School Exercise at Hawkshead, Pushkin’s Eugene Onegin, Ginsberg’s Howl, Hugo’s A Sunset, Mandelstam’s Tristia, and Goethe’s To Luna.
3.3. Power Spectrum Analysis
The power spectrum analysis of poems and music (Table 3) shows a broad spectrum. The slope of musical compositions is low, in the range of chaos, well below -1 (pink noise) and -1.7 (Bios generated with the process equation). There is great diversity in the slope of poems.

Table 3.
Power spectrum analysis.
3.4. Biotic Patterns in Music and Poetry
Isometry quantification (figure 10) demonstrates less recurrence (novelty) in many musical pieces, Bios, and random walks than in randomized copies, and more recurrences in many literary texts and in stationary chaos than in randomized copies.
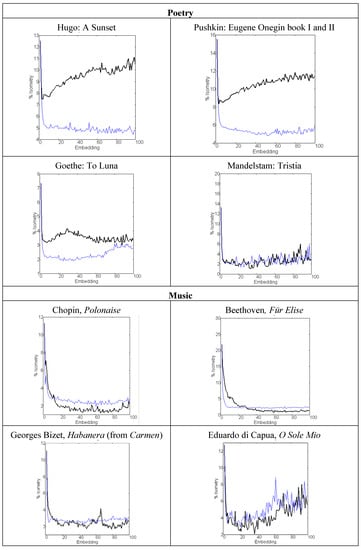
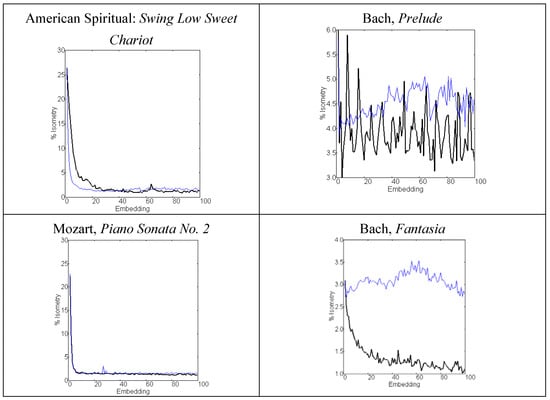
Figure 10.
Quantification of isometry as a function of the number of embeddings in musical compositions and literary texts as compared with their randomized copy (blue line).
Recurrence portraits of musical and literary (figure 11) series show changes in pattern with time (temporal complexity), as observed in mathematical Bios and in random walks; in contrast, the recurrence plots of stationary random series or chaotic attractors are uniform.
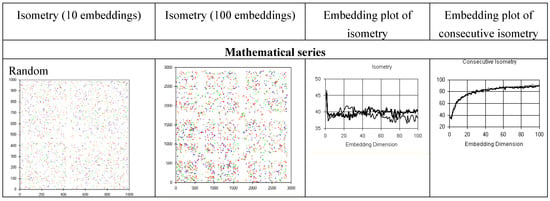
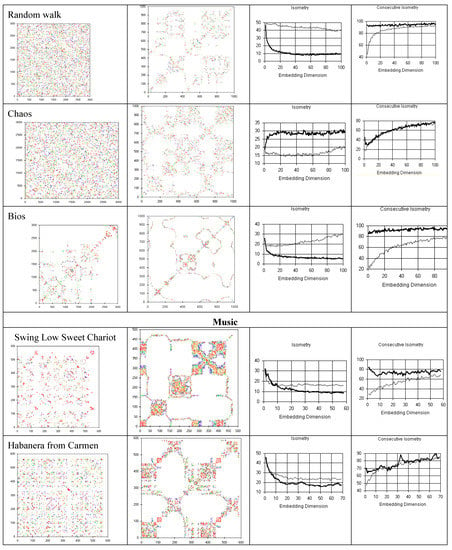
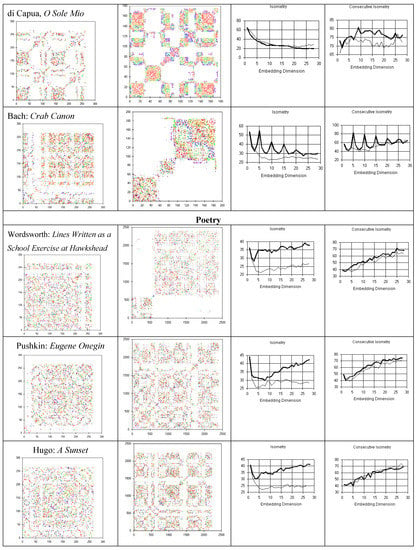
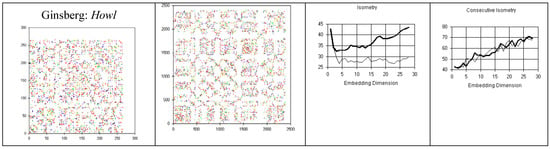
Figure 11.
Recurrence plots of musical compositions show temporal complexity. The quantification of isometries shows novelty and the quantification of consecutive isometries supports non-random causation.
Recurrence plots and quantification of the series of differences between consecutive terms (figure 12) in these data also show temporal pattern in music, chaos and Bios, indicating nonrandom causation, in contrast to random walks.
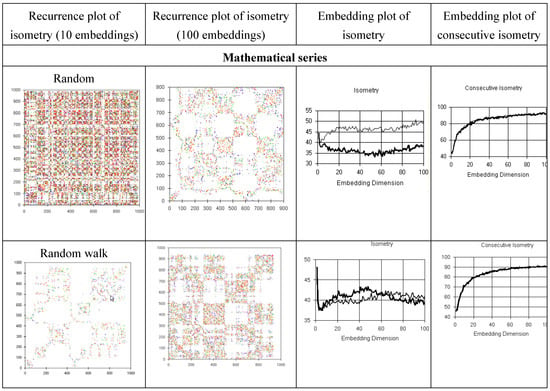
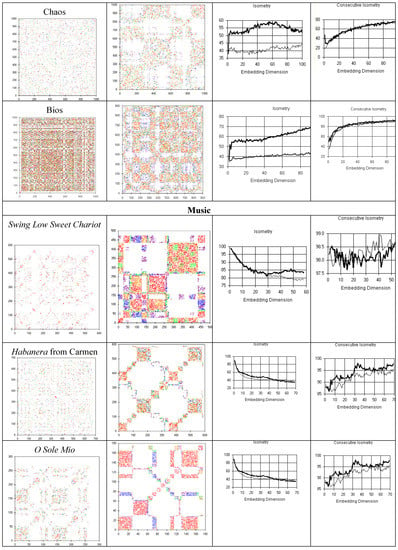
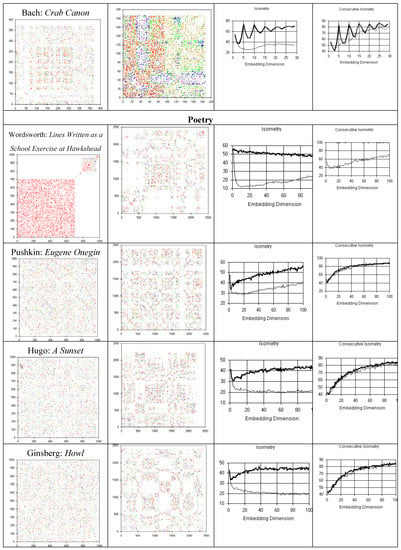
Figure 12.
Series of differences between consecutive terms Pattern in the recurrence plots and the quantification of isometry and of consecutive isometries in the show non-random causation.
Figure 13 shows temporal variation in variance, with overall increase in S.D. with embedding (local diversification) but not with time (global diversification).
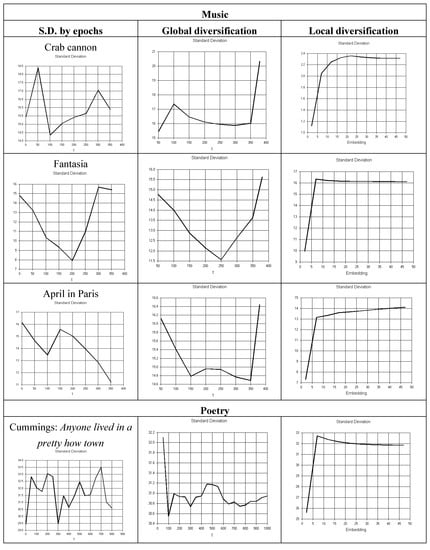
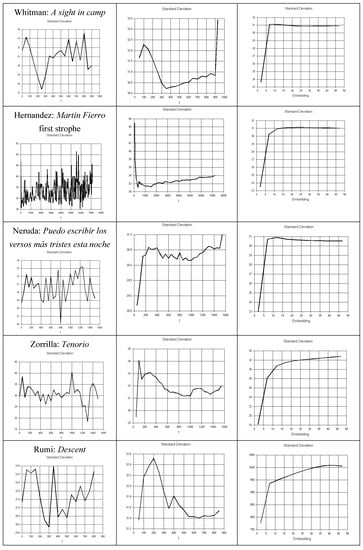
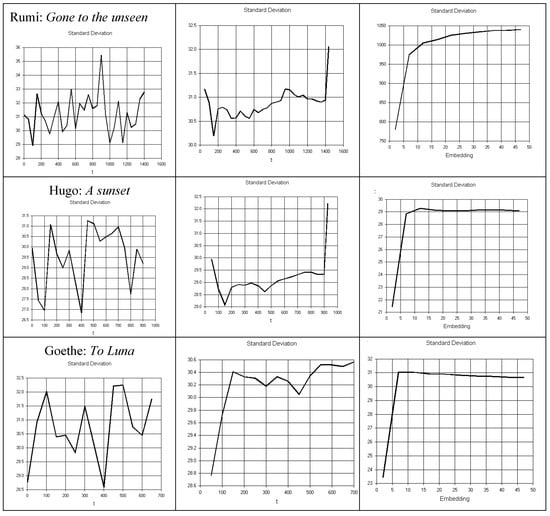
Figure 13.
Diversification. S.D. variation by epochs, global and local diversification.
4. Discussion
These results indicate that asymmetry, symmetry and creativity are evident in literary and musical series. Asymmetry is indicated by histograms (figure 4), Pareto histograms (figure 5) and the difference between middle, median and mean (figure 6). Symmetry is indicated by complement plots (figure 8).
Poems and musical scores show low entropy; low entropy indicates order and creativity just as high entropy indicates disorder and decay. Simple mathematical analyses of literary and musical series also reveal local diversification, temporal complexity, and complex frequency composition (power spectrum). Musical compositions also show novelty.
It is significant that these simple analyses demonstrate these features in artistic productions, as this validates their interpretation as indicators of creativity in natural and socioeconomic processes. This also suggests that natural and mental processes share deep similarities.
These hallmarks of creativity may be detected in series generated randomly, but they may also be generated causally. Causal (non-random) creativity defines Bios. We found empirically that fundamental physical, biological and human processes are causal and creative. Recursions such as the process equation At+1 = At + k*t* sin(At) and the diversifying equation At+1 = At + sin(k*t*At) generate a sequence of patterns as time t increases: equilibrium, periodicities, chaos, bios and leaps (figure 2).
These equations involve asymmetric action (recursion in time), bipolar opposition (sine function), and continuity (conserved term At). These three elements correspond to the defining properties of the three mother structures of mathematics (Bourbaki): lattice asymmetry, group opposition, and topological continuous transformation of spatial form. These three elementary forms are also found by Piaget in fundamental cognitive operations, in the three dimensions of the Central Nervous System [4] and in many other physical, biological and human processes as illustrated by Table 4. Some of these may be mere analogies (as between the wing of a bird and the wing of an airplane) but we as hypotheses to be tested that many of them are homologies (as between the leg of a horse and the wing of a bird). We thus conceived the idea that these three forms – unidirectional flow of energy in asymmetric time (action), bipolar opposition such as the bidirectional communication of information by bidimensional and bipolar electromagnetic radiation, and tripolar, continuous transformation of tridimensional matter-- constitute basic principles of nature [4]. This is Process theory (Table 4).

Table 4.
Asymmetry and symmetry.
The study of literary and musical creations suggests that this theory extends to art. Bourbaki’s three forms may thus provide a mathematical foundation for a theory of creative evolution and of artistic creation.
The small numbers appear to capture some important aspects of Bourbaki’s mother structures of mathematics: lattice asymmetry is unidirectional, group opposition is bidirectional, and space-like topological forms are tridimensional. We can identify these numerical forms in the three fundamental physical forces, unidirectional gravitation, bipolar and bidimensional electromagnetic force, and tri-polar nuclear forces that unite 3 quarks to form protons and neutrons and thereby construct tridimensional atomic nuclei. More generally, action (energy * time) is asymmetric, information requires the distinction between two opposite entities, and matter is tridimensional.
Asymmetry and symmetry are the defining features of lattices and groups, two of the three fundamental mathematical structures described by Bourbaki. Lattice abstracts asymmetry and thereby one-dimensional order, which is physically embodied in the sequence of time, but every lattice has a dual (a < b implies b > a). Logically and methodologically, we describe the priority of the simple and the supremacy of the complex as complementary, opposite asymmetries embodied in actual processes, a concept developed by considering the vertical organization of the Central Nervous System in the context of integrating biological, social and psychological aspects of medical diagnosis and treatment [33], and also applicable to social issues [34] and to scientific research [5].
Algebras, such as group theory, are defined by the generation of new elements by the combination of existing ones. While lattice asymmetry represents order, group opposition is regarded as abstracting symmetry. Simple reflection indicates that opposites can be perfectly symmetric (1 and -1), largely symmetric (two sides of a human body) or largely asymmetric (proton and electron, women and men, beauty and ugliness). A group is a set in which element has an inverse or symmetric opposite. Inverse elements annul each other when combining, returning to the information-less identity element. It is the combination of any other pair of elements (that are not symmetric) that generates a new element; this captures the creative interaction of opposites postulated by ancient process philosophers (Heraclitus, Empedocles, Lao-tzu) as well as by modern theorists. Many scientific disciplines, including physics, biology, sociology, and psychology, also explain the generation of complexity as resulting from the interaction of opposites.
The third fundamental structure is modeled by topology, the study of space-like forms, their formation and transformation. Material structures are tridimensional; correspondingly, topological knots are described by three ‘colors’. The human body itself shows temporal asymmetry in the dorsal-ventral axis, rough right-left symmetry, and the asymmetry of complexity in its vertical dimension. These three patterns also exist in the multiple levels of complexity that form the “vertical dimension” of nature from physical to mental processes.
A hierarchy of complexity is also evident in the sequence of patterns generated by recursions such as the logistic, the process and the diversifying equations. Indeed, symmetry and entropy decrease as the process equation enters the biotic phase.
Entropy is also relatively low in natural processes with a biotic pattern [35,36]. This may account for the development of complexity in physical and biological processes, so far justified by the local development of pockets of low entropy due to the selective intake of low entropy materials [37] and the selective excretion of high entropy waste products [37,38].
In statistics, entropy measures the degree of symmetry [39,40,41,42,43,44,45,46,47,48], while information is the degree of asymmetry [31]. According to classic thermodynamics, processes spontaneously flow towards higher entropy, i.e. from asymmetry to symmetry, and thereby towards equilibrium, and rest; actually physical and biological evolution demonstrates that processes often spontaneously flow from symmetry to asymmetry. Evolution increases information, and thereby generates complexity and beauty.
Symmetry is beautiful because it renders stability, asserts Shu-Kun Lin [49]; nevertheless, he adds, symmetry is in principle ugly because it is associated with information loss. From a different esthetic perspective, asymmetry is beautiful because it overcomes stability and drives evolution and the generation of complexity. Symmetry is beautiful because it embodies order rather than decay, disorder and rest. High entropy implies complexity, not necessarily disorder. But also asymmetry contributes to order and beauty; in fact, the mathematical definition of order is lattice asymmetry, and the asymmetric divine or golden proportion φ = 1.618… has been a cannon of beauty in architecture and painting since Phidias. While the geometric symmetry of a face often conveys beauty, in reality human faces always show a degree of mathematical asymmetry, and their asymmetry contributes to esthetic pleasure.
Mathematical modeling demonstrates that Bios is generated by recursions that involve both asymmetry and symmetry. Opposites play a major role in creative evolution, artistic creativity, and beauty, rather than annulling each other in featureless thermodynamic equilibrium.
Asymmetry and symmetry are evident contributors to beauty, which is a major component of our emotional life and of art. Both art and life also involve creative processes that transform simple forms to generate complexity. Indeed, beauty requires complexity, because it may exist in simple as well as complex patterns, but it is perceived only by relatively complex organisms (e.g. mate selection, bees and birds attraction to flowers, etc.). Here we find in art Bourbaki’s three generative forms, the asymmetry that defines lattices, the symmetry of opposites that defines groups, and the topological transformation of simple forms into complex ones.
Bourbaki’s concepts provide a way to formulate the notion of causal, non-random creativity in an exact manner. Causal creativity represents an alternative to the theological concept of creation of matter from the void, classic determinism in which causality is not creative, and the current models of random variability in theories of the early universe, quantum mechanics, biological evolution by random mutation, and stochastic markets that offer no way to understand or influence processes. In contrast to portraits of change and creativity as “noise”, the observation of Bios from quantum mechanics to music supports Pythagoras and Kepler’s perspective in which music is a model for the mathematics of the universe.
In summary, both natural and artistic creative processes display asymmetry, symmetry, and creative transformation, indicating a common, possibly fractal, process (Bios) extending from quantum entities to mental activity.
Acknowledgements
We are thankful to the Society for the Advancement of Clinical Philosophy and to Mrs. Maria McCormick for their support.
References
- Anderson, P.W. More Is Different. Science 1972, 177, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Bourbaki, N. Éléments de mathématique; Actualités Scientifiques et Industrielles: Paris, France, 1952. [Google Scholar]
- Beth, E.W.; Piaget, J. Epistémologie mathématique et psychologie; Essai sur les relations entre la logique formelle et la pensée réelle: Paris, France, 1961. [Google Scholar]
- Sabelli, H. Union of Opposites: A Comprehensive Theory of Natural and Human Processes; Brunswick Publishing: Lawrenceville, VA, USA, 1989. [Google Scholar]
- Sabelli, H. Bios: A Study of Creation; World Scientific: Singapore, 2005. [Google Scholar]
- Sabelli, H.; Carlson-Sabelli, L. As simple as one, two, three. Arithmetic: a simple, powerful, natural and dynamic logic. In Sustainable Peace in the World System and the Next Evolution of Human Consciousness, Proceeding of International Systems Society 40th meeting; Hall, M.L.W., Ed.; Louisville, KY, USA, 1996; pp. 543–554. [Google Scholar]
- Sabelli, H.; Kovacevic, L. Quantum Bios and Biotic Complexity in the Distribution of Galaxies. Complexity 2006, 11, 14–25. [Google Scholar] [CrossRef]
- Sabelli, H.; Kovacevic, L. Biotic Expansion of the Universe. In International Conference on Advances in Internet, Processing, Systems, and Interdisciplinary Research; Sveti Stefan, Montenegro, 2003; Electronic Publication IPSI-2003. [Google Scholar]
- Thomas, G.; Sabelli, H.; Kauffman, L.; Kovacevic, L. Biotic patterns in Schrödinger’s equation and the evolution of the universe. InterJournal 2006, 1787. [Google Scholar]
- Sabelli, H.; Thomas, J.; Kovacevic, L.; Horan, D. Biotic Dynamics of Galactic Distribution, Gravitational Waves, and Quantum Processes. A Causal Theory of Cosmological Evolution. In Black Holes and Galaxy Formation; Wachter, A.D., Propst, R.J., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2009. [Google Scholar]
- Sabelli, H. Complex Biotic Patterns in LIGO Recordings point to the creativity of gravitational interactions. Complexity 2010, 15, 12–24. [Google Scholar]
- Carlson-Sabelli, L.; Sabelli, H.; Zbilut, J.; Patel, M.; Messer, J.; Walthall, K.; Tom, C.; Fink, P.; Sugerman, A.; Zdanovics, O. How the heart informs about the brain. A process analysis of the electrocardiogram. In Cybernetics and Systems 94; Trappl, R., Ed.; World Scientific: Singapore, 1994. [Google Scholar]
- Carlson-Sabelli, L.; Sabelli, H.; Patel, M.; Messer, J.; Zbilut, J.; Sugerman, A.; Walthall, K.; Tom, C.; Zdanovics, O. Electropsychocardiography. Illustrating the Application of Process Methods and Chaos Theory to the Comprehensive Evaluation of Coronary Patients. Complex. Chaos Nurs. 1995, 2, 16–24. [Google Scholar]
- Carlson-Sabelli, L.; Sabelli, H.; Messer, J.; Patel, M.; Sugerman, A.; Kauffman, L.; Walthall, K. Process method: Part I. An empirical measure of novelty differentiates creative organization from static order and chaos. In Systems thinking, globalization of knowledge, and communitarian ethics, Proceeding of International Systems Society; Rhee, Y.P., Bailey, K.D., Eds.; Kwanak Press: Seoul, Korea, 1997; pp. 1072–1090. [Google Scholar]
- Sabelli, H.; Carlson-Sabelli, L.; Patel, M.; Zbilut, J.; Messer, J.; Walthall, K. Psychocardiological portraits: A clinical application of process theory. In Chaos theory in Psychology; Abraham, F.D., Gilgen, A.R., Eds.; Greenwood Publishing Group: Westport, CT, USA, 1995; pp. 107–125. [Google Scholar]
- Sabelli, H.; Carlson-Sabelli, L.; Patel, M.; Sugerman, A. Dynamics and psychodynamics: Process Foundations of Psychology. J. Mind Behav. 1997, 18, 305–334. [Google Scholar]
- Sabelli, H.; Messer, J.; Kovacevic, L.; Walthall, K. The biotic pattern of heartbeat intervals. Int. J. Cardiol. 2010, (in press). [Google Scholar] [CrossRef]
- Sabelli, H.; Kovacevic, L. Biotic Complexity of Population Dynamics. Complexity 2008, 13, 47–55. [Google Scholar] [CrossRef]
- Patel, M.; Sabelli, H. Autocorrelation and Frequency Analysis Differentiate Cardiac And Economic Bios From 1/F Noise. Kybernetes 2003, 32, 692–702. [Google Scholar] [CrossRef]
- Sabelli, H. Bios, creative organization in economic, biological, and meteorological data. In International Conference on Advances in Internet, Processing, Systems, and Interdisciplinary Research; Sveti Stefan, Montenegro, 2003; Electronic Publication IPSI-2003. [Google Scholar]
- Sabelli, H.; Sugerman, A.; Kauffman, L.; Kovacevic, L.; Carlson-Sabelli, L.; Patel, M.; Messer, J.; Konecki, J.; Walthall, K.; Kane, K. Biotic Patterns in Biological, Economic and Physical Processes. J. Appl. Syst. Stud. 2004, 5, 14–26. [Google Scholar]
- Sabelli, H. The Biotic Pattern of Prime Numbers. Cybern. Syst. J. 2008, (in press). [Google Scholar]
- Levy, A.; Alden, D.; Levy, C. Biotic patterns in music. In Society for Chaos Theory in Psychology and Life Sciences Meeting, SCTPLS2006; Johns Hopkins University: Baltimore, MD, USA, 4-6 August 2006. [Google Scholar]
- Sabelli, H. Music, Poetry, Painting, and Bipolar Illness. Nonlinear. Dynam. Psychol. Life Sci. 2010, (in press). [Google Scholar]
- Kauffman, L.; Sabelli, H. The Process equation. Cybern. Syst. 1998, 29, 345–362. [Google Scholar]
- Sabelli, H. Complement plots: Analyzing opposites reveals Mandala-like patterns in human heartbeats. Int. J. Gen. Syst. 2000, 29, 799–830. [Google Scholar] [CrossRef]
- Dekking, M.; Mendès-France, M. Uniform Distribution Modulo One. Journal für die reine und angewandte Mathematik 1981, 239, 149–153. [Google Scholar]
- Sabelli, H.; Sugerman, A.; Kovacevic, L.; Kauffman, L.; Carlson-Sabelli, L.; Patel, M.; Konecki, J. Bios Data Analyzer. Nonlinear. Dynam. Psychol. Life Sci. 2005, 9, 505–538. [Google Scholar]
- Sabelli, H. Novelty, a Measure of Creative Organization in Natural and Mathematical Time Series. Nonlinear. Dynam. Psychol. Life Sci. 2001, 5, 89–113. [Google Scholar] [CrossRef]
- Sabelli, H.; Abouzeid, A. Definition and Empirical Characterization of Creative Processes. Nonlinear. Dynam. Psychol. Life Sci. 2003, 7, 35–47. [Google Scholar] [CrossRef]
- Sabelli, H.; Patel, M.; Sugerman, A.; Kovacevic, L.; Kauffman, L. Process Entropy, a Multidimensional Measure of Diversity and Symmetry. http://creativebios.net/webjass/10Entropy.pdf.
- Sabelli, H.; Sugerman, A.; Carlson-Sabelli, L.; Patel, M.; Kauffman, L. Embedding Plots: A Tool to Measure Simplicity, Complexity and Creativity. J. Appl. Syst. Stud. 2004, 5, 159–201. [Google Scholar]
- Sabelli, H.; Carlson-Sabelli, L. Biological Priority and Psychological Supremacy, a New Integrative Paradigm Derived from Process Theory. Am. J. Psychiatry 1989, 146, 1541–1551. [Google Scholar]
- Torre, C. Chaos, Triadic Theory of Psychological Competence in the Academic Setting. In Chaos Theory in Psychology; Gilgen, A., Abraham, F., Eds.; Praeger/Greenwood Publishing: Westport, CT, USA, 1995; pp. 279–294. [Google Scholar]
- Carlson-Sabelli, L.; Sabelli, H. Phase plane of opposites: A Method to study change in complex processes, and its application to sociodynamics and psychotherapy. Social Dynam. 1992, 3, 1–6. [Google Scholar]
- Sabelli, H. Biothermodynamics. Open Cybern. Syst. J. 2009, (in press). [Google Scholar]
- Schrödinger, E. What is Life? The Physical Aspect of the Living Cell; The Macmillan Company: New York, NY, USA, 1945. [Google Scholar]
- Prigogine, I. From Being to Becoming: The New Science of Connectedness; Doubleday: New York, NY, USA, 1987. [Google Scholar]
- Prigogine, I. The End of Certainty; The Free Press: New York, NY, USA, 1997. [Google Scholar]
- Cohen, J.; Steward, I. The Collapse of Chaos; Penguin: New York, NY, USA, 1994. [Google Scholar]
- Leyton, M. Symmetry, Causality, Mind; MIT Press: Cambridge, UK, 1992. [Google Scholar]
- Petitjean, M. Order, entropy and symmetry: An awkward relation? Symmetry Cult. Sci. 2005, 16, 5–6. [Google Scholar]
- Jakulin, A. Symmetry and information theory. Symmetry Cult. Sci. 2005, 16, 7–26. [Google Scholar]
- Matsuno, K. Symmetry and Information: Symmetry as an Emergent Property of Information. Symmetry Cult. Sci. 2005, 16, 27–36. [Google Scholar]
- Smith, A. A hierarchical perspective. Symmetry Cult. Sci. 2005, 16, 37–46. [Google Scholar]
- Salthe, N. Asymmetry and self-organization. Symmetry Cult. Sci. 2005, 16, 71–90. [Google Scholar]
- Darvas, G. Order, entropy and symmetry. Symmetry Cult. Sci. 2005, 16, 91–108. [Google Scholar]
- Lin, S.K. The Nature of the Chemical Process. 1. Symmetry Evolution—Revised Information Theory, Similarity Principle and Ugly Symmetry. Int. J. Mol. Sci. 2001, 2, 10–39. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).