Abstract
From elemental particles to human beings, matter is dissymmetric with respect to mirror symmetry. In 1860, Pasteur conjectured that biomolecular handedness— homochirality—may originate from certain inherent dissymmetric forces existing in the universe. Kipping, a pioneer of organosilicon chemistry, was interested in the handedness of sodium chlorate during his early research life. Since Kipping first synthesized several Si-Si bonded oligomers bearing phenyl groups, Si-Si bonded high polymers carrying various organic groups—polysilanes—can be prepared by sodium-mediated condensation of the corresponding organodichlorosilanes. Among these polysilanes, optically active helical polysilanes with enantiomeric pairs of organic side groups may be used for testing the mirror symmetry-breaking hypothesis by weak neutral current (WNC) origin in the realm of chemistry and material science. Several theoretical studies have predicted that WNC-existing chiral molecules with stereogenic centers and/or stereogenic bonds allow for distinguishing between image and mirror image molecules. Based on several amplification mechanisms, theorists claimed that minute differences, though still very subtle, may be detectable by precise spectroscopic and physicochemical measurements if proper chiral molecular pairs were employed. The present paper reports comprehensively an inequality between six pairs of helical polysilane high polymers, presumably, detectable by (chir)optical and achiral 29Si-/13C- NMR spectra, and viscometric measurements.
1. Introduction
Why does matter dominantly exist in the universe? Why is the universe inherently chiral and asymmetric? What is the origin of biomolecular handedness in life—homochirality—on the blue planet? Several explanations have already been proposed for these questions and can be seen in many monographs and reviews [,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,]. Except for achiral glycine, the amino acids in proteins are all in their L-form. Some of these ideas rely on a matter of chance to induce the preference—an event of spontaneous symmetry breaking. Others believe that the fundamental lack of mirror image symmetry in the early Earth inevitably led to the L-preference. Although it is now established that left–right symmetry is broken at the level of interactions between subatomic particles and atomic vapor. However, detection of dissymmetry at the molecular scale remains a challenging issue.
Homochirality, though de facto, is a long-standing puzzle raising curiosity among scientists since the 19th century [,,]. In 1860, Pasteur alleged that homochirality originates from the demarcation line between the animate and inanimate worlds. He conjectured that biomolecular homochirality arises from an inherent universal dissymmetry force. He inferred the concept of broken mirror symmetry by physical origins, including circularly polarized light and a static magnetic field, although there was no theoretical or experimental evidence at that time. Most chemists and physicists believed that nature’s laws cannot distinguish between left and right in all physical properties and chemical processes.
Kipping, a pioneer of organosilicon and polysilane chemistry, and Pope assumed that biomolecular homochirality is applicable to purely inorganic substances. They examined thousands of crystals produced from achiral NaClO3 (molecular symmetry, C3v, but, crystal exists as D- and L-forms) to test the preference between left and right by mirror symmetry-breaking crystallization []. However, they did not conclude that the broken mirror symmetry crystallization occurs by the expected inherent physical origins because the events appear to be a statistical distribution—a matter of chance.
Physicists invented three discrete symmetries (C; charge, P; parity, T; time) and their combination symmetries (CP, PT, CT, and CPT) to understand nature’s laws [,,]. Physicists in the mid-20th century knew four fundamental forces (gravity, weak force, strong force, and electromagnetic force) governing matter and universe. Since the first paper describing P-symmetry conservation—the concept of the mirror symmetry—by Wigner in 1927 [,], they had long accepted this concept as being axiomatic in developing theories for explaining phenomena. However, violations of C, P, T, and CP symmetries at the levels of elemental particles and upward constitute the most fundamental concept in modern physics [,], since the broken P-symmetry at subatomic level was proven experimentally by Wu et al. in 1957 [] to verify the P-symmetry conservation, which had been questioned by Lee and Yang in 1956 [].
Nambu demonstrated the idea of "spontaneous symmetry breaking" in the 1960s [,]. His work led to the standard model in particle physics developed by Weinberg [], Salam [], and Glashow []. The standard model unifying the parity-violating (PV) weak force and parity-conserving (PC) electromagnetic force led to the idea of an electroweak (EW) force, which may not be familiar with chemists and material scientists. The existence of three massive W± and Z0 bosons along with a massless photon predicted by the model was proven by an international team at CERN in 1983 []. Scientists interested in the origin of biomolecular handedness assume that the PV-weak neutral current (WNC) mediated by massive neutral Z0 boson is intimately connected to the mirror symmetry breaking at the closed-shell biomolecular level as well as the atomic parity violation (APV) [,].
In chemistry, bioscience, and material science, left and right can interchange through a mirror. Many physical properties of materials and chemical reactions obey mirror symmetry-based physics laws. A pair of image and mirror image molecules—enantiomers—shows no differences in melting point, boiling point, and spectroscopic properties that involve electronic transition energies, vibrational frequencies, and magnetic resonance frequencies. The pair should exhibit exactly equal intensities with opposite signs in circular dichroism (CD) and optical rotation in electronic and vibrational regions due to the PC electromagnetic force in physical and chemical processes.
However, modern theoretical studies [,,,,,,,,,,,,,,,,,,,,,,,,,,] have claimed that an image and its mirror molecule are no longer enantiomers due to an energy inequality induced by the existence of PV-WNC. Due to a parity-violating energy shift (PVES) of the electronic binding energy with a positive value, +EPV, for the image molecule and a PVES with a negative value, –EPV, for the mirror image molecule, or vice versa, PVES makes the pair become a diastereomer, exhibiting subtle differences in physical properties and chemical processes. The parity-violating energy difference (PVED) between image and mirror image molecules is given as PVED = EPV – (–EPV) = 2•EPV. Numbers of theoretical studies have discussed that the occurrence of PVES may appear spectroscopically as slight differences in electronic transition energies [,,], vibrational frequencies [], ro-vibrational frequencies [,], NMR chemical shifts [], circular polarization in electronic transition and vibrational frequency regions [,], a concept hereafter called the molecular parity violation (MPV) hypothesis in this article.
Because of the extremely small PVED of ~10-19 eV and negligibly small 10–15 %ee [], PV–WNC cannot induce any observable MPV effects. In the molecules containing heavy elements, PVED may increase up to ~10-14 eV due to the heavy element effect [], yet it still remains undetectable. Thus far, several amplification models, including polymerization and crystallization [], molecules with heavier atoms [], tunneling and oscillating between left and right in a double well [], non-equilibrium autocatalytic chemical reactions [,], and second-order phase transition systems [], have been proposed.
Several experimental results testing the MPV hypothesis have been reported so far. Based on the Salam’s hypothesis describing that homochirality is the consequence of the cooperative second-order phase transition of an electron-neutron pair [], Wang et al. examined a pair of D- and L-alanine single crystals by means of Raman, NMR, neutron scattering, supersonic wave, magnetic susceptivity, and calorimeter []. She claimed the detection of subtle differences in physical properties between the D- and L-crystals below 270 K. Although these results were verified by other independent research groups, Compton and Schwerdtfeger [], and Wilson et al. [] did not agree with her claim due to a lack of reproducibility. They ascribed her results to certain impurities incorporated in non-naturally occurring alanine, crystal imperfection, and restricted motions in the solid crystals. To achieve discrete molecular systems in dilute gas phase, enabling the avoidance of molecular collisions, a few research groups are continuing to detect minute differences between images and mirror images using ultrahigh-resolution laser spectroscopy in mid-IR and far-IR regions []. More recently, Schwerdtfeger et al. predicted theoretically the large MPV effects for the chiral NWHClI molecule from relativistic density functional theory, revealing mirror symmetry breaking in N–W stretching frequency of 0.7 Hz in IR region. Because this value could be detectable by an ultrahigh-resolution CO2 laser spectrometer [], the work was highlighted as a cover picture of a chemistry journal.
In 2006, Shinitzky et al. reported the subtle differences in helix-coil transition behaviors of D- and L-oligopeptides in water, as characterized by CD and isothermal titration calorimetry experiments []. They ascribed the differences to ortho (triplet, ↑↑) and para (singlet, ↑↓) nuclear spin states of water protons and the methylene protons of amino acids. Lahav and Schurig failed to reproduce Shinitzky’s results []. Schwerdtfeger et al. claimed that several MPV-related experimental results are weakly based theoretically []. On the other hand, in 2008, Pomonis et al. reported that the α-helical motif in poly-D-glutamic acid is stable thermally, compared to that of poly-L-glutamic acid. Pomonis et al. ascribed this difference to an increased interaction of the L-species with more abundant ortho-water, in support of the Shinitzky’s claim [].
Although conclusive results using common chemical substances and apparatuses have not yet been reported, these modern MPV theories and current experimental reports, though still controversial, stimulated the author to revisit the equality and inequality of several ambidextrous artificial helical Si–Si bonded polymer–polysilanes–in solution as a function of temperature [,]. In a previous communication, the author reported preliminary testing results, implicating a possibility of detecting subtle differences in chiroptical and achiral 29Si-NMR and viscometric data for a pair of helical polysilanes []. The present paper reported comprehensively the experimental tests of an equality and an inequality observed in chiroptical, 29Si-/13Si-NMR, and viscometric measurements for six pairs of helical polysilanes carrying ambidextrous chiral side groups.
2. Results and Discussion
A family of polysilanes (Figure 1), compound 1 which is symmetrically substituted with chiral side groups, and compounds 2–6 which are asymmetrically substituted with chiral and achiral side groups, has several advantages for testing the MPV hypothesis because:
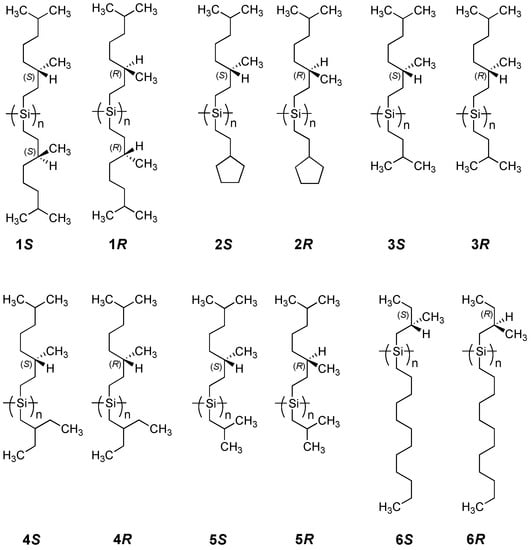
Figure 1.
Chemical structures of the six helical polysilane pairs tested in this work.
(i) The ambidextrous (S)- and (R)-3,7-dimethyloctyl moieties derive from highly pure β–citronellol available commercially from Fluka and/or Sigma-Aldrich. The use of β-citronellols allows for the ability to test the present results in any laboratory. By contrast, (R)-2-methylbutanol is not available commercially, and was obtained from custom synthesis by Chemical Soft (Kyoto, Japan) while (S)-2-methylbutanol is commercially available (TCI).
(ii) The Cotton CD signals of the helical polysilanes completely match the profiles of the corresponding Siσ–Siσ* absorptions (the electrically allowed S0–S1 transitions) in the near-UV region []. To evaluate the MPV effect induced by WNC (intrinsic chiral physical origins), excluding the effects caused by the PC electromagnetic force (conventional chiral chemical origins), we can compare the apparent dimensionless Kuhn’s dissymmetry factors between a pair of helical polysilanes in isotropic solution, which are defined as gCD = Δε/ε, where Δε and ε are the apparent CD and UV intensities [,]. The value of gCD is independent of sufficiently high molecular weight (Mw), although both Δε and ε depend somewhat on Mw []. The apparent gCD values may be directly connected to the sum and/or subtraction of the |gPV| and |gPC| terms for the helical polysilane pairs. The values of gPV and gPC are dissymmetry factors of the PV and PC terms, respectively. The difference in population between the P- (dihedral angle (θ) ~150°) and M- (θ ~210°) motifs for the polysilane pairs is directly associated with the gPV and gPC values. The gPV term, induced by ΔEPV with the same magnitude but opposite sign for the pairs, contributes to the apparent gCD value.
(iii) Helical polysilanes in a double well with a small barrier height of 2–3 kcal per Si–Si unit [] exhibit an energy splitting energy, allowing quantum tunneling between P- and M-helices []. The tunneling between P and M permits an effective mixing between weak and electromagnetic forces because outer- and inner-shell electrons have an opportunity to interact with nucleons. This is important for electrons and nucleons because weak forces mediated by massive Z0 bosons are effective only to neighbors within ultrashort-range interactions of ~10-18 m [,].
(iv) Heavier Si nuclei (natural abundance of 28Si 92.2 % (spin: 0, NMR inactive), 29Si 4.7% (spin: –1/2, NMR active), and 30Si 3.1% (spin: 0, NMR inactive) containing 14 protons and 14–16 neutrons and effective repeating numbers (Neff) of up to ~104 [] may linearly enhance ΔEpv in comparison to the C–C bonded organic small molecules. The value of ΔEpv is proportional to Neff•Z5, while Z3 is due to the WNC interaction and Z2, the spin-orbit interaction (where Z is the atomic number) [,]. A preliminary expected advantage ratio, gadv = ΔEpv/kT ~10-12 at 300 K, may sufficiently exceed the detectable PNC limit with a critical gadv of ~10-17 [,,]. By comparing 29Si-NMR spectra, the degree of main chain mobility is detectable as the difference in linewidth; the sum of the shielding and deshielding terms by inner-shell electrons of the main chain could be measurable as changes in chemical shifts [].
2.1. Chiroptical Spectral Analysis
2.1.1. Helical Polysilane Symmetrically Substituted with Chiral Side Groups in Isotropic Solution
A comparison of UV and CD spectra between 1S and 1R in isooctane below and above the helix-helix transition temperature (Tc) of –65 °C is shown in Figure 2. The negatively signed Cotton CD signal of 1S with an extremum of 3.90 eV at –68 °C is almost the inverse of the positively signed Cotton CD spectrum with an extremum of 3.85 eV at –21 °C over the whole 3.0 eV to 5.5 eV range. Conversely, the positively signed CD signal of 1R with an extremum of 3.89 eV at –76 °C is almost the inverse of the negatively signed CD signal with an extremum of 3.87 eV at –30 °C. Evidently, 1S and 1R undergo a helix-helix transition between the two temperatures.
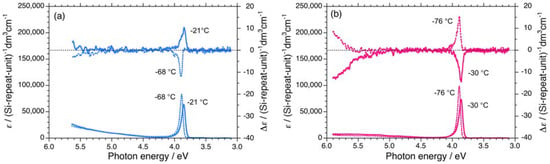
Figure 2.
UV and CD spectra in isooctane of (a) 1S (Mw = 863,000, Mn = 147,000) at –88 °C and –21°C, and (b) 1R (Mw = 394,000, Mn = 85,800) at –76 °C and –10 °C.
The magnitudes of the UV and CD signal intensities near 3.9 eV of 1S and 1R in isooctane as a function of temperature are shown in Figure 3. The UV intensities of 1S are somewhat weak compared to those of 1R in the range of –90 °C to +80 °C. However, the absolute magnitudes of the CD signals are intense in the negative CD region regardless of the side chirality and temperature.
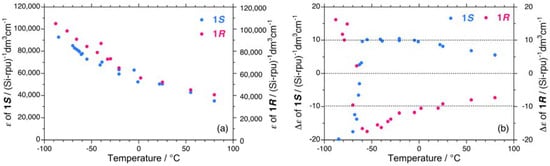
Figure 3.
The magnitudes of the (a) UV absorptivity and (b) CD signal near 3.9 eV of 1S (Mw = 863,000, Mn = 147,000) and 1R (Mw = 394,000, Mn = 85,800) in isooctane as a function of temperature.
This tendency is evident when compared to the absolute magnitudes of the apparent gCD values, |gCD|. The values of gCD near 3.9 eV for 1S and 1R in isooctane as a function of temperature are shown in Figure 4(a). Evidently, 1S and 1R undergo a cooperative, second-order helix-helix transition around –65 °C. In the range of –90 °C to –70 °C, the |gCD| values of 1S are greater than those of 1R, whereas in the range of –50 °C to +80 °C, the |gCD| values of 1S are smaller than those of 1R.
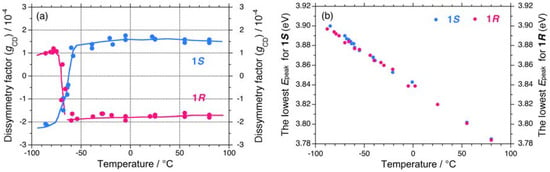
Figure 4.
(a) Apparent gCD values near 3.9 eV and (b) apparent lowest exciton peak energies of 1S (Mw = 863,000, Mn = 147,000) and 1R (Mw = 394,000, Mn = 85,800) in isooctane as a function of temperature.
The differences in the |gCD| values are possible to relate with the observable contribution from the 2•|gPV| term arising from the subtraction between the (|gPC| – |gPV|) and (|gPC| + |gPV|) terms of 1S and 1R in the range of –90 °C to –70 °C and between the (|gPC| + |gPV|) and (|gPC| – |gPV|) terms of 1S and 1R in the range of –50 °C to +80 °C. Regardless of the solution temperatures, the sign of |gPV| is negative, suggesting a preference for left-handed helicity (minus, M) rather than right-handed helicity (plus, P) in isooctane. The lowest exciton peak energies (Epeak) for 1S and 1R in isooctane as a function of temperature are not significantly different [Figure 4(b)].
2.1.2. Helical Polysilane Aggregates Dispersed in Solution
The subtle differences in the |gCD| values between 1S and 1R dissolved in isotropic isooctane are recognized. However, the significant difference in the |gCD| values between 1S and 1R when dispersed as aggregate particles in isotropic chloroform is more evident. The aggregates spontaneously form when the polymer sample solution temperature is decreased. The bisignate CD signal originates from the so-called exciton-coupling signal of the Si–Si main chain chromophore in the aggregates.
A bisignate CD signal of 1S aggregates with extrema of 3.80 eV (negative) and 3.85 eV (positive) appears at –10 °C while 1S dissolved in chloroform at 50 °C exhibits a single CD signal with an extremum of 3.82 eV (positive) [Figure 5(a)]. Similarly, the bisignate CD signal of 1R aggregates with extrema of 3.79 eV (positive) and 3.85 eV (negative) appears at –10 °C, while 1R dissolved in chloroform at 50 °C exhibits a single CD signal with an extremum of 3.81 eV (negative) [Figure 5(b)]. The |gCD| value at the first Cotton CD band near 3.8 eV of 1S and 1R in chloroform in the range of –10 °C to +50 °C is plotted in Figure 5(c). The |gCD| value of 1R at –10 °C is approximately 30-times more intense than that of 1S at –10 °C. The difference in the |gCD| values of 1S and 1R was significantly more amplified for the aggregate forms than those molecularly dissolved in solution.
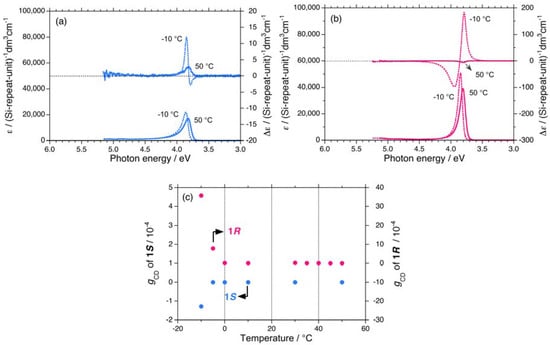
Figure 5.
UV and CD spectra in chloroform of (a) 1S (Mw = 140,000, Mn = 34,400) at –10 °C and +50 °C, and (b) 1R (Mw = 149,000, Mn = 39,500) at –10 °C and +50 °C. (c) Apparent gCD values near 3.8 eV of 1S and 1R aggregates dispersed in chloroform as a function of temperature.
2.1.3. Helical Polysilanes Asymmetrically Substituted with Chiral and Achiral Side Groups in Isotropic Solution
Three polysilanes (2S/2R, 3S/3R, 4S/4R) asymmetrically substituted with the chiral (S)-/(R)- 3,7-dimethyloctyl and the achiral cyclopentaneethyl, 3-methylpentyl, and 2-ethylbutyl side groups undergo helix-helix transitions in isooctane []. The Tcs of 2, 3, and 4 increase in the order of –33 °C, –22 °C, and –7 °C, respectively. The UV and CD spectra of 2S/2R, 3S/3R, and 4S/4R in isooctane below and above Tc are displayed in Figures 6(a)–6(b) and Appendix Figures A1(a)–1(d).
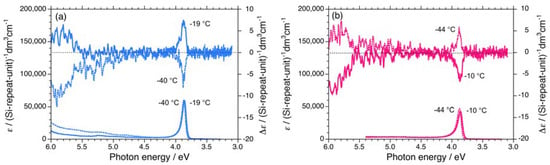
Figure 6.
UV and CD spectra in isooctane of (a) 2S (Mw = 93,100, Mn = 57,900) at –40 °C and –19 °C and (b) 2R (Mw = 51,800, Mn = 25,200) at –44 °C and –10 °C.
The apparent gCD values near 3.9 eV of 2S/2R, 3S/3R, and 4S/4R in isooctane as a function of temperature are shown in Figures 7(a)–7(c), respectively. The |gCD| values of 2, 3, and 4 are considerably more intense in the negative CD region, regardless of the side chain chirality and temperature. Above the Tcs, the |gCD| values of 2, 3, and 4 carrying the (R)-group are greater than those with the (S)-group. By contrast, below the Tcs, the |gCD| values of 2, 3, and 4 carrying the (S)-group are greater than those with the (R)-group. These features of 2, 3, and 4 are identical to those of 1.
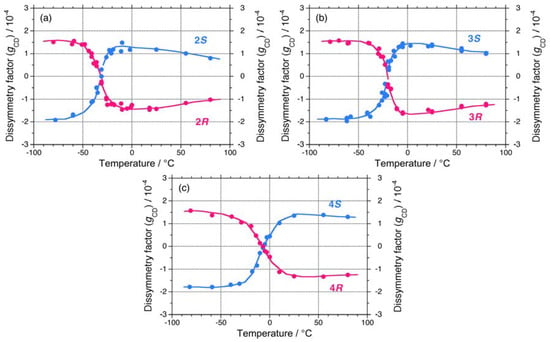
Figure 7.
Apparent gCD values near 3.9 eV in isooctane as a function of temperature of (a) 2S (Mw = 93,100, Mn = 57,900) and 2R (Mw = 51,800, Mn = 25,200), (b) 3S (Mw = 232,000, Mn = 78,900) and 3R (Mw = 156,000, Mn = 76,800), and (c) 4S (Mw = 14,500, Mn = 11,300) and 4R (Mw = 19,000, Mn = 15,200).
On the other hand, 5 and 6 do not undergo helix-helix transitions in the range of –80 °C and +80 °C. However, even the 5S/5R pair gives weak, but detectable differences in their chiroptical properties at low temperatures. The UV and CD spectra of the 5S/5R pair in isooctane at low and high temperatures are displayed in Appendix Figures A1(e)–A1(f). The |gCD| value of 5R at –80 °C is more intense than that of 5S at –80 °C (Figure 7(a)), whereas the |gCD| values of 1–4 with the (S)-group at –80 °C are more intense than those of 1–4 with the (R)-group at –80 °C. Therefore, regardless of the side chain chirality, the |gCD| values of 1–5 at –80 °C are intensely negative, preferring M-screw-sense (Table 1).

Table 1.
Chiroptical parameters (gCD, |gPC|, gPV values in 10-4) of six polysilanes in isooctane.
A non-helix-helix-transitioned pair (6S/6R) exhibited subtle differences in chiroptical properties. The UV and CD spectra of the 6S/6R pairs in isooctane at lower and higher temperatures are displayed in Appendix Figures A1(g)–A1(h). Although the |gCD| value of the negative CD band of 6R are almost identical to those of 6S in the range of –5 °C to +80 °C [Figure 8(b)], and the magnitudes of the UV and CD intensities of 6S are slightly greater than those of 6R in the range of –5 °C to +80 °C [Appendix Figure A2(a)]. The lowest Cotton CD extremum energies of 6S and 6R depend on the solution temperature in the range of –5 °C to +80 °C [Appendix Figure A2(b)].
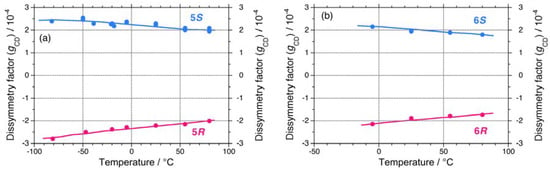
Figure 8.
Apparent gCD values near 3.9 eV in isooctane as a function of temperature of (a) 5S (Mw = 42,300, Mn = 23,500) and 5R (Mw = 36,900, Mn = 19,000) and (b) 6S (Mw = 108,000, Mn = 37,300) and 6R (Mw = 80,900, Mn = 34,600).
From the variable temperature CD/UV spectroscopic measurements and chiroptical analyses, three chiroptical parameters (|gCD|, |gPC|, and gPV) of 1–6 are summarized in Table 1. Polysilanes 1–4 having helix-helix transition ability showed detectable differences in the |gCD| values in the range of –80 °C to +80 °C, presumably, arising from considerable mixing of the gPV and gPC terms at any temperatures. Even polysilane 5, which lacks the ability to transition, appears to mix gPV with gPC terms at –80 °C. The signs of the gPV values of 1–5 are negative, potentially, due to intrinsic physical origins and regardless of the side chain chiralities (chemical origins). The ratio of |gPV| to |gPC| ranges from 0.06 to 0.17. However, polysilane 6, which lacks the ability to transition, did not markedly show this mixing in the range of –80 °C to +80 °C. Possible reasons for these differences will be discussed in the following sections along with a relationship of the sign of the CD band and helix preference.
2.2. NMR Spectral Analysis
2.2.1. 29Si–NMR Spectroscopic Features
A solution NMR spectrometer is commonly used in chemistry and biochemistry laboratories as a typical achiral physical detection system for observing nuclear spin states surrounded by multiple electrons. Considerable differences in the 29Si-NMR spectral characteristics (chemical shift and linewidth) for helix-helix-transitioned 1S/1R and 3S/3R in CDCl3 were detectable, as shown in Figures 9(a)–9(b). By contrast, very weak differences for the non-helix-helix-transitioned 5S/5R pair were observed [Figure 9(c)].
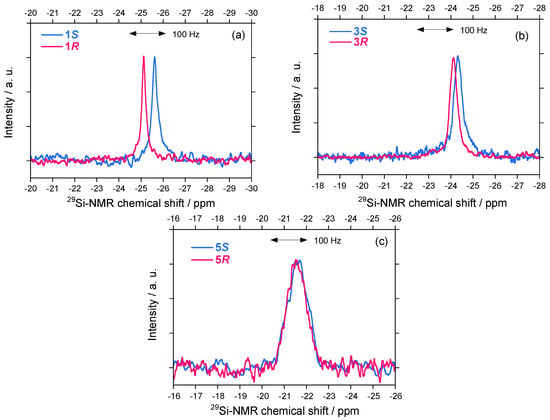
Figure 9.
29Si-NMR spectra of (a) 1S (Mw = 31,400, Mn = 17,400) and 1R (Mw = 30,100, Mn = 20,000) in CDCl3 at 40 °C (50 mg in CDCl3 0.6 mL), (b) 3S (Mw = 44,000 and Mn = 31,100) and 3R (Mw = 42,700, Mn = 29,000) in CDCl3 at 30 °C, and (c) 5S (Mw = 37,500 and Mn = 22,900) and 5R (Mw = 28,700, Mn = 17,900) in CDCl3 at 30 °C.
The 29Si-NMR linewidths, which are a measure of the main chain mobility, of symmetrically substituted 1S/1R are slightly different: 1S: 19 Hz and 1R: 13 Hz, suggesting that the main chain of 1S is less mobile than its 1R counterpart. A more clear difference is observed in the 29Si-NMR chemical shifts: 1S and 1R resonances at –25.62 and –25.11 ppm, respectively, indicating that 1S resonates by 31 Hz upfield of 1R. Asymmetrically substituted 3S/3R also gives subtle differences in the 29Si-NMR chemical shifts and linewidths [Figure 9(b)]. Because 3S and 3R resonate at –24.30 and –24.11 ppm, respectively, 3S resonates by 11.4 Hz upfield of 3R. In addition, 3S exhibit a broader linewidth (v1/2 = 28 Hz) than that of 3R (v1/2 = 24 Hz).
The differences in 29Si-NMR chemical shifts reach up to 10–30 Hz and therefore are possible to use for comparison with the theoretically predicted value of ~1 mHz for rotamers of H–El–El–H (El = O, S, Se, Te) containing heavier elements and other molecular systems [,,]. One possible explanation for polysilane highpolymers is that the 29Si-NMR chemical shift experiences an almost equal contribution in the opposite direction as a consequence of paramagnetic shielding (downfield shift) and diamagnetic shielding (upfield shift) tensors induced by electrons. By contrast, very weak differences in 29Si-NMR for 5S and 5R at –21.6 ppm with a broader linewidth of ~72 Hz are observed even though 5S had a ~5 Hz upfield resonance from that of 5R. The difference could be related to the existence of the handed WNC governing the heavier helical Si-Si main chain dynamics.
2.2.2. 13C–NMR Spectral Features
Subtle differences in 13C-NMR spectral characteristics (chemical shifts and signal intensities) for 1S/1R were observed [Figure 10(a)]. The 13C-NMR signal intensities, which are a measure of side chain mobility, were slightly different between 1S and 1R. To numerically enhance the differences in the chemical shift and signal intensities, the difference spectrum between 1S and 1R was given in Figure 10(b). Several carbons of the (S)-side chain resonate at a downfield region compared to those of the (R)-side chain. A possible explanation is that the 13C-NMR chemical shift experiences mainly as a consequence of paramagnetic shielding (downfield shift) tensors induced by electrons. This difference could infer the difference in dynamics of the side chain made of the lighter carbon atoms, influenced by the handed WNC.
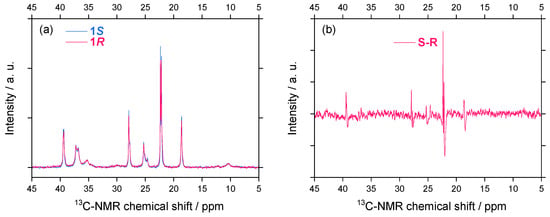
Figure 10.
(a) 13C-NMR spectra of 1S (Mw = 31,400 and Mn = 17,400) and 1R (Mw = 30,100, Mn =20,000) in CDCl3 at 40 °C and (b) the difference spectrum between 1S and 1R.
2.3. Electronic Calculation and Molecular Mechanics Calculation
A possible explanation for the differences in the |gCD| values between the 1–4 pairs may be due to a slight modification of the potential energy surface as a function of the Si–Si–Si–Si dihedral angle of 1S, isotactic (it) and syndiotactic (st) sequences of 3S, as schematically shown in Figures 11(a)–11(b). For comparison, the potential energy surfaces of the it- and st-sequences of 5S and 6S are given in Figures 11(c)–11(d).
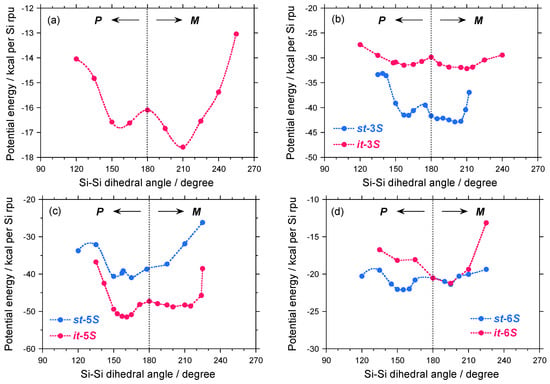
Figure 11.
The potential energy of (a) 1S with fifty Si-repeating units and hydrogen termini, (b) st- and it-3Ss with thirty Si-repeating units and hydrogen termini, and (c) st- and it-5Ss with thirty Si-repeating units and hydrogen termini, and (d) st- and it-6Ss with n-hexyl-(S)-2-methylsilane with thirty Si-repeating units and hydrogen termini calculated for simplicity. Here n-hexyl moiety was used in place of n-dodecyl group for simplicity.
As shown in Figure 11(a), although 1S has two local minima located at ~150° and ~210°, it favors M–screw-sense as the global minimum. Dihedral angles of ~150° and ~210° correspond to 73-helices with P- and M-screw-senses, respectively. The energy difference (ΔE) between the P- and M-helices is only ~1 kcal per Si–repeating unit and the EB value from the M-helix is only ~2 kcal per Si–repeating unit. These small ΔE and EB values are responsible for a thermo-driven helix-helix transition. Therefore, 1S at –80 °C preferentially adopts M-screw-sense, providing negative Cotton CD signals.
In the case of 3S, due to asymmetrically substituted side groups, the it- and st-sequences should be considered. Although both the it- and st-sequences have two local minima located at ~150° and ~210°, they slightly favor M-screw-sense as the global minimum. With global minima between it- and st-sequences, the st-sequence with M–screw-sense is the most stable of the four possible helices. Therefore, M-st-3S is assumed to be the global minimum. The value of ΔE between the P- and M-helices is only ~1 kcal per Si–repeating unit and the EB value of M-helix is only ~3 kcal per Si–repeating unit. Similar to 1S, the small ΔE and EB values of M-st-3S are responsible for the thermo-driven helix-helix transition. Therefore, 3S at –80 °C preferentially adopts M-screw-sense, providing the negative CD signal.
In case of 5S, the st-sequence has a single minimum located at ~195°, while the it-sequence has two local minima located at ~150° and ~195°. Among the three minima, the it-sequence with P-screw-sense may be a global minimum, suggesting that 5S at –80 °C may prefer P-screw-sense, thereby yielding a positive CD signal.
When the relationship between the CD sign and P-/M-preference for 1, 3, and 5 with the S-chiral group was compared, the helix-helix transition polysilanes carrying the S-chiral group favor M-screw-sense, thus exhibiting a negative CD band. Conversely, the non-helix-helix transition polysilane carrying the same S-chiral group favors P-screw-sense and exhibits a positive CD band. These ideas are consistent with the experimental results [Figures 4(a), 7(a)–7(c), and 8(a)].
The potential energy curves for models of 1S and 1R with fifty Si repeating units with uncorrected and corrected PV terms are schematically shown in Figure 12. Although commercial molecular mechanics packages do not include any parity violation effects and high level ab initio techniques using the PV Hamiltonian is needed in future, the small positive Epv bias of +0.5 kcal for the P-motif and a small negative Epv of –0.5 kcal for the M-motif were added for explanation purpose only, regardless of the side chain chirality in which helix induction is governed by the PC electromagnetic force origin. Note that these values are not exact and merely hypothetically.
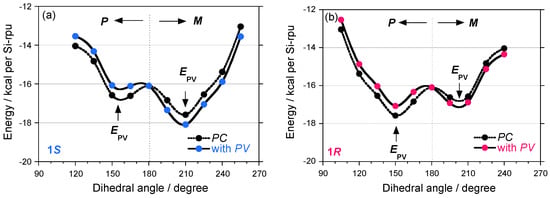
Figure 12.
The potential energy of (a) 1S and (b) 1R with hypothetical corrections of EPV of +0.5 kcal for P- and –0.5 kcal for M-screw-senses for explanation purpose only.
Before the PV term addition, 1S and 1R were classified into classical mirror images of helical polymers because of an almost degenerate asymmetric double well. If the EPV bias effectively allow for the induction of inequality to the potential energy by exp(2•EPV/kT), the double-well potential curves do not keep the mirror image relationship. In the images and mirror images of helical polymers 1–5, the absolute gCD values of the negative CD signals at –80 °C, possibly due to their M-screw-sense preference, are greater than those for the corresponding P-one, regardless of the side chain chirality and temperature. These observations suggest that the sign of gPV may be negative for the 1–5 pairs and that their preferential screw-sense is M rather than P because the P-helix should give a positive CD signal.
In the case of 6S carrying an (S)-2-methylbutyl moiety, the it-sequence has a single minimum located at ~195°, while the st-sequence has two local minima located at ~150° and ~195°. Among the three minima, the P-st-sequence may be a global minimum, suggesting that 6S at –80 °C may preferentially adopt a P-screw-sense, thus yielding positive CD signals, which are consistent with the experimental results [Figure 8(b)].
From these molecular mechanics calculations, the potential energy in the almost degenerate double well with small ΔE and EB values is responsible for the thermo-driven helix–helix transition ability due to the flexible helical main chain. These features are assumed to be important for detecting subtle differences by the PV-force origin for helical polymers. By contrast, the potential energy in the almost single well with the large ΔE and EB values cannot afford the subtle differences due to a very rigid helical structure. The helical main chain flexibility in a double well with small ΔE and EB values, leading to quantum tunneling oscillation, is important for testing the MPV hypothesis.
To further confirm the relationship between the screw-sense, absolute magnitude of gCD, and CD sign, Gaussian03 calculations (TD-DFT, B3LYP, 3-21G basis set) of the parent oligosilane, H-(SiH2)13-H, as a model of a polysilane were performed []. The simulated UV and CD spectra of oligosilane with a dihedral angle of 140° are shown in Figure 13(a). The spectral shape of the CD signals completely matches the corresponding UV spectrum, which is distinct for helical polysilanes. Based on the spectral characteristics, the gCD values of the parent polysilane monotonically increase from zero to +8 × 10-4 as the dihedral angle changes from 180° to 125° [Figure 13(b)]. The gCD values change the sign from positive to negative at a dihedral angle of less than ~75° and the absolute magnitude markedly increases to –1.7×10-2 as the dihedral angle changes from 100° to 60°.
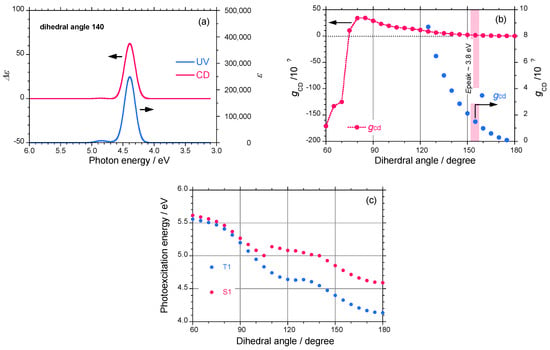
Figure 13.
(a) Simulated UV and CD spectra of (SiH2)13 with a dihedral angle of P-140°, (b) simulated gCD as a function of the dihedral angle in H-(SiH2)13-H, (c) photoexcitation energies (singlet and triplet states) of H-(SiH2)13-H as a function of the dihedral angle.
When the dihedral angle changes from 180° to 60°, the electrically allowed transition energy between the singlet-singlet (S0–S1) states monotonically increases from 4.6 eV to 5.6 eV. Similarly, the electrically forbidden transition energy between the singlet-triplet (S0–T1) states, though the oscillator strength is zero, monotonically increases from 4.2 eV to 5.5 eV (Figure 12(c)). The gCD value of a 73-helix with a dihedral angle of 155° was calculated to be +1.4×10-4, which is in good agreement with the observed gCD values of ~2.5×10-4 for 5 and 6 bearing (S)-chiral side groups. The molecular mechanics and Gaussian calculations suggest that the P-screw-sense of polysilane gives a positive CD band when the dihedral angle is between 75° and 180°.
2.4. Viscometric Measurements
Slight differences were also observed in the viscometric data (κ and α) in the Kuhn-Mark-Houwink-Sakurada plots ([η] = κ ∙ Mα [], where [η] is intrinsic viscosity, M is molecular weight, κ is a constant, and α is viscosity index) between the four pairs of 1, 2, 3, 5, and 6 in chloroform at 30 °C, in tetrahydrofuran (THF) at 40 °C, and in toluene at 70 °C. The viscometric measurement is well-established as a physico-chemical method to characterize floppy chain-like polymers in dilute solution. Based on the MPV hypothesis, the degree of chain coiling mediated by handed inner-shell electrons interacting with the massive nucleus may result in subtle differences in the value of α over a wide range of molecular masses between the polysilane pairs.
According to measurements and analyses by TRC and the NTT R&D center [1996/03/06 (report no. T113613), 1998/09/25 (report no. T215754), 1999/03/05 (report no. T218558), 1999/05/19 (report no. T218904)], subtle differences in the α values of the unfractionated polymer samples were observed experimentally. These features could be associated with differences in the main chain stiffness of the polysilane pairs in solution: for 1 (chloroform at 30 °C), 1S, α = 1.13, 1R, α = 1.26; for 1 (toluene, 70 °C), 1S, α = 1.70, 1R, α = 1.57; for 2 (THF, 30 °C), 2S, α = 0.91, 2R, α = 0.97; for 3 (toluene, 70 °C), 3S, α = 1.47, 3R, α = 1.32; for 3 (THF, 30 °C), 3S, α = 1.47, 3R, α = 1.32; for 5 (toluene, 70 °C), 5S,α = 1.49, 5R, α = 1.36; for 5 (THF, 30 °C), 5S, α = 1.29, 5R, α = 1.22; for 6 (toluene, 70 °C), 6S, α = 1.21, 6R, α = 1.49; for 6 (THF, 30 °C), 6S, α = 0.93, 6R, α = 0.88.
3. Experimental Section
3.1. Measurements
All CD and UV absorption spectra were recorded simultaneously on a JASCO J-720 spectropolarimeter equipped with a liquid nitrogen-controlled quartz cell with a path length of 5 mm in a cryostat ranging from +23 °C to –90 °C and a Peltier-controlled quartz cell with a path length of 10 mm ranging from +90 °C to –10 °C. This temperature range assured that isooctane was sufficiently fluid because the melting and boiling points of isooctane are –100 °C and +100 °C, respectively. The scanning conditions were as follows: scanning rate of 50 nm per min, band width of 1 nm, response time of 1 sec, and twice or single accumulations. The solution temperature in the cryostat was monitored by directly immersing a thermocouple into the solution, while the solution temperature in the Peltier-controlled cell was considered to be the same as the aluminum block cell housing. The sample concentration was 2×10-5 (Si-repeat-unit)-1•dm-3 for UV and CD measurements. The 13C- (75.43 MHz) and 29Si- (59.59 MHz) NMR spectra were taken in CDCl3 at 30 °C or 40 °C with a Varian Unity 300 MHz NMR spectrometer using tetramethylsilane as an internal standard. Optical rotation at the Na-D line was measured with a JASCO DIP-370 polarimeter using a synthetic quartz (SQ) cell with a path length of 10 mm at room temperature (24 °C). The weight-average molecular weight (Mw) and number-average molecular weight of the polymers (Mn) were evaluated using gel permeation chromatography (Shimadzu A10 instruments, Shodex KF-806M column, and HPLC-grade tetrahydrofuran as eluent at 30 °C) based on calibration with polystyrene standards (Tohso). The intrinsic viscosity–molecular weight relationship was investigated at the Toray Research Center (TRC, Shiga, Japan) using a Waters 1500 GPC apparatus with a Viscotec H502a viscometer.
3.2. Monomer Synthesis
The Toray Research Center (TRC) and Nippon Telegraph and Telephone Corporation (NTT) R&D center [reported on 1998/03/11 (report no. T216669), 1998/06/29 (report no. T217117), 1998/08/17 (report no. T217601)] analyzed the enantiopurities of the starting materials and intermediates. These materials were used to prepare chiral organodichlorosilanes as follows (in %ee) by a Grignard coupling reaction of the corresponding alkylbromide with alkyltrichlorisilanes by means of a chiral GC technique (β-DEX225 and β-DEX325, Spelco): (S)-(+)-/(R)-(–)-citronellol = 97.4/97.9, (S)-(+)-β-/(R)- (–)-β-citronellol = 97.4/97.9, (S)-(–)-/(R)-(+)-3,7-dimethyloctanol = 95.9/95.7, (S)-(–)-/(R)-(+)-3,7- dimethylbromide = 95.0/96.6, (S)-(–)-/(R)-(+)-2-methylbutanol = 99.7/100.0. (See, Appendix, Figure A3 and A4).
A typical synthetic scheme of 1S and 1R is given in the Appendix, Scheme A1. The Grignard reagent obtained from 41.3 g (0.186 mol) of (R)-(–)-3,7-dimethyloctylbromide ([α]24D = –5.96° (neat), 96.0 %ee) was added to a solution of 13.3 g (7.82 mmol) of tetrachlorosilane (Shin-Etsu) in dry diethylether at room temperature to produce bis{(R)-(–)-3,7-dimethyloctyl}dichlorosilane. The bromide was prepared at Chemical Soft (Kyoto, Japan) by bromination of (R)-(+)-3,7-dimethyloctanol ([α]24D = +3.90° (neat), 95.7 % ee) with PPh3 and Br2 in CCl4, followed by hydrogenation of (R)-(d)- (+)-β-citronellol (Fluka, [α]24D = +4.46° (neat), 97.9 % ee). Filtration of the reaction mixture and vacuum distillation of the filtrate produced pure alcohol. Colorless liquid. Yield 11.0 g (37 %). bp 142–146 °C/0.18 Torr, [α]24D = –2.57° (neat), 29Si-NMR (CDCl3, 30 °C, ppm) 34.75, 13C-NMR (CDCl3, 30 °C, ppm) 17.36, 19.10, 22.62, 22.71, 24.74, 27.96, 29.13, 34.79, 36.46, 39.30.
Bis{(S)-(+)-3,7-dimethyloctyldichlorosilane} was synthesized in a similar way using (S)-(+)-3,7-dimethyloctylbromide ([α]24D = +6.05° (neat), 96.2 %ee, Chemical Soft) from (S)-(-)-3,7- dimethyloctanol ([α]24D = –4.22° (neat), 95.9 %ee) and (S)-(l)-(-)-β-citronellol (Fluka, [α]24D = –4.55° (neat), 97.4 %ee) as the starting material. Colorless liquid. bp 142–144 °C/0.52 Torr, [α]24D = +2.35° (neat), 29Si-NMR (CDCl3, 30 °C, ppm) 34.74, 13C-NMR (CDCl3, 30 °C, ppm) 17.35, 19.10, 22.62, 22.71, 24.73, 27.96, 29.13, 34.79, 36.45, 39.29.
The enantiopurity of the starting materials and intermediates was determined at TRC by chiral gas chromatography (Spelco, β-DEX-325 and β-DEX-225, 30 m × 0.25 mm ID, oven temperature of 70 °C–95 °C, He carrier with 1.2 mL/min; β-DEX-225 at 90 °C for citronellol, β-DEX-225 at 82 °C for 3,7-dimethyloctanol, and β-DEX-325 at 70 °C for 3,7-dimethylbromide). The author concluded that the image and mirror image starting materials and intermediates and the corresponding organodichlorosilanes had sufficiently high enantiopurity with almost identical ees. However, the chiral GC analysis at TRC indicated that the enantiopurity of (S)-(l)-(–)-β-3,7-citronellol (Merck, [α]24D = –3.11° (neat)) was only 64.8 %ee and of (S)-(–)-3,7-dimethyloctanol (Chemical Soft, using Merck’s product, (S)-(l)-(–)-β-3,7-citronellol) was 66.4 %ee. Therefore, the author used Fluka products as starting materials for the TRC analysis.
(R)-(–)-3,7-dimethyloctyl-2-methylpropyldichlorosilane, bp 86–92 °C/0.45 Torr, [α]24D = –1.77° (neat), 29Si-NMR (CDCl3, 30 °C, ppm) 33.21, 13C-NMR (CDCl3, 30 °C, ppm) 18.37, 19.04, 22.56, 22.66, 24.14, 24.67, 25.55, 27.91, 29.10, 30.25, 34.73, 36.40, 39.24.
(S)-(+)-3,7-dimethyloctyl-2-methylpropyldichlorosilane, bp 89–93 °C/0.60 Torr, [α]24D = +1.81° (neat), 29Si-NMR (CDCl3, 30 °C, ppm) 33.34, 13C-NMR (CDCl3, 30 °C, ppm) 18.43, 19.09, 22.61, 22.70, 24.20, 24.72, 25.60, 27.96, 29.16, 30.31, 34.78, 36.45, 39.29.
(R)-(–)-3,7-dimethyloctyl-3-methylbutyldichlorosilane, bp 104–105 °C/0.50 Torr, [α]24D = -1.61° (neat), 29Si-NMR (CDCl3, 30 °C, ppm) 34.65, 13C-NMR (CDCl3, 30 °C, ppm) 17.36, 17.89, 19.11, 21.98, 22.63, 22.72, 24.74, 27.98, 29.12, 30.18, 31.16, 34.79, 36.47, 39.31.
(S)-(+)-3,7-dimethyloctyl-3-methylbutyldichlorosilane, bp 122 –127 °C/1.5 Torr, [α]24D = +1.61° (neat), 29Si-NMR (CDCl3, 30 °C, ppm) 34.67, 13C-NMR (CDCl3, 30 °C, ppm) 17.35, 17.88, 19.10, 21.97, 22.62, 22.71, 24.73, 27.97, 29.12, 30.17, 31.15, 34.78, 36.46, 39.30.
(R)-(–)-3,7-dimethyloctyl-3-cyclopentylethyldichlorosilane, bp 131–133 °C/0.80 Torr, [α]24D = +1.40° (neat), 29Si-NMR (CDCl3, 30 °C, ppm) 34.27, 13C-NMR (CDCl3, 30 °C, ppm) 17.38, 19.11, 19.36, 22.63, 22.71, 24.74, 25.25, 27.98, 28.52, 29.12, 32.26, 34.79, 36.46, 39.31, 42.42.
(S)-(+)-3,7-dimethyloctyl-3-cyclopentylethyldichlorosilane, bp 115–118 °C/0.35 Torr, [α]24D = +1.52° (neat), 29Si-NMR (CDCl3, 30 °C, ppm) 34.31, 13C-NMR (CDCl3, 30 °C, ppm) 17.38, 19.10, 19.34, 22.62, 22.70, 24.73, 25.24, 27.97, 28.51, 29.11, 32.25, 34.78, 36.45, 39.29, 42.41.
(R)-(–)-3,7-dimethyloctyl-2-ethylbutyldichlorosilane, bp 80–81°C/0.55 Torr, [α]24D = –1.63° (neat), 29Si-NMR (CDCl3, 30 °C, ppm) 34.23, 13C-NMR (CDCl3, 30 °C, ppm) 10.56, 18.42, 19.11, 22.63, 22.71, 24.69, 24.76, 27.75, 27.99, 29.23, 34.83, 35.97, 36.51, 39.33.
(S)-(+)-3,7-dimethyloctyl-2-ethylbutyldichlorosilane, bp 123–124 °C/2.2 Torr, [α]24D = +1.73° (neat), 29Si-NMR (CDCl3, 30 °C, ppm) 34.15, 13C-NMR (CDCl3, 30 °C, ppm) 10.50, 18.36, 19.06, 22.57, 22.66, 24.62, 24.70, 27.69, 27.93, 29.17, 34.76, 35.90, 36.44, 39.26.
(R)-(+)-2-methylbutyl-n-dodecyldichlorosilane, bp 128–135 °C/0.60 Torr, [α]24D = –6.22° (neat), 29Si-NMR (CDCl3, 30 °C, ppm) 33.18, 13C-NMR (CDCl3, 30 °C, ppm) 11.21, 14.11, 21.35, 21.85, 22.47, 22.72, 28.15, 29.15, 29.38, 29.48, 29.67, 30.27, 31.96, 32.38, 32.52.
(S)-(+)-2-methylbutyl-n-dodecyldichlorosilane, bp 148–151 °C/0.35 Torr, [α]24D = +6.27° (neat), 29Si-NMR (CDCl3, 30 °C, ppm) 33.18, 13C-NMR (CDCl3, 30 °C, ppm) 11.23, 14.14, 21.33, 21.84, 22.45, 22.72, 28.08, 29.15, 29.39, 29.48, 29.37, 30.24, 31.95, 32.37, 32.52.
3.3. Polymer Preparation
A typical synthetic procedure is described for 1S as follows. To a mixture of 12 mL of dry toluene (Kanto), 0.75 g (33 mmol) of sodium (Wako), and 0.06 g (0.23 mmol) of 18-crown-6 (Wako), 4.0 g (11 mmol) of diorganodichlorosilane was added dropwise in an argon atmosphere. The mixture was stirred slowly at 110 °C. After 3 hours, 200 mL of dry toluene was added to reduce the solution viscosity, and the mixture was stirred continuously for an additional 30 minutes. The hot reaction mixture slurry was passed immediately through a 5-μm PTFE filter under argon gas pressure. To the clear filtrate, the precipitating solvents isopropanol and ethanol were carefully added. Several portions of the white precipitates were collected by centrifugation and dried at 120 ˚C under vacuum overnight.
The weight-average molecular weight (Mw) and number-average molecular weight (Mn) of the polymers were evaluated using gel permeation chromatography (Shimadzu A10 instrument, Shodex KF806M column, and HPLC-grade tetrahydrofuran as eluent at 30 °C), based on calibration with polystyrene standards as follows. For the purpose of chiroptical measurements, 1S, Mw = 863,000, Mn = 147,000 and Mw = 140,000, Mn = 34,400; 1R, Mw = 394,000, Mn = 85,800 and Mw = 149,000, Mn = 39,500; 2S, Mw = 93,100, Mn = 57,900; 2R, Mw = 51,800, Mn = 25,200, 3S, Mw = 232,000, Mn = 78,900; 3R, Mw = 156,000, Mn = 76,800, 4S, Mw = 14,500, Mn = 11,300; 4R, Mw = 19,000, Mn = 15,200, 5S, Mw = 42,300, Mn = 23,500; 5R, Mw = 36,900, Mn = 19,000, 6S, Mw = 108,000, Mn = 37,300; 6R, Mw = 80,900, Mn = 34,600.
For NMR measurements, lower molecular mass samples with an almost equal Mw value were used: 1S, Mw = 31,400 and Mn = 17,400; 1R, Mw = 30,100, Mn =20,000; 3S, Mw = 44,000 and Mn = 31,100; 3R, Mw = 42,700, Mn = 29,000; 5S, Mw = 37,500 and Mn = 22,900; 5R, Mw = 28,700, Mn = 17,900.
3.4. Molecular Mechanics Calculations
Molecular mechanics calculations were achieved using Molecular Simulation Inc. (MSI), the Discover 3 module, Ver. 4.00 on a Silicon Graphics Indigo II XZ computer based on standard parameters (default) with an Si-Si bond length of 2.34 Å, an Si–Si–Si bond angle of 111°, and the MSI pcff force field suitable for polymers. For this calculation, the MSI built-in functions of simple-minimize (default condition is dihedral angle restraints, steepest descents for the first derivative, iteration limit of 1000, movement limit of 0.2, and derivative for 1.0) and simple-dynamics (conditions of constant volume and temperature, initial temperature of 300 K, direct velocity scaling with a time step of 1 fs, integration, initial velocity of random velocities from the Boltzmann distribution) were used with the set-up parameters.
3.5. Electronic State Calculation using Gaussian03 []
Electronic state calculations including the parent polysilane, H-(HSiH2)13-H, as a model of the present polysilanes, was employed using the time-dependent (TD)–density function DFT Gaussian03 program (TD-DFT, B3LYP, 3-21G basis sets) running on an Apple iMac (IntelCoreDuo2, 2.0 GHz, 4GB memory, MacOS ver.10.4.11). For the calculations, the geometries of the parent polysilane with dihedral angles varying from 80° to 180° with 5° and 10° intervals were optimized by the PM3-MM level of Gaussian03 using initial standard parameters (default) with an Si–Si bond length of 2.34 Å and an Si-Si-Si bond angle of 111°.
4. Conclusions
The experimental data in the absolutely artificial helical polysilanes may not provide conclusive proof to support the MPV hypothesis and the inherent physical origin of homochirality on Earth. Subtle differences in enantiopurity, tacticity, molecular weight, and molecular weight distribution of the polysilanes used in this work may have affected the chiroptical properties and the achiral NMR (29Si and 13C) as well as achiral viscometric data. Nevertheless, the author believed that the differences demonstrated here may infer the emergence of a preference between left and right at the polysilane level in isotropic solutions by certain inherent physical origins such as WNC, though the present experiments do not unequivocally support the MPV hypothesis. The subtle left-right asymmetry may appear in four pairs of helix-helix transition polysilanes (1–4), whereas two pairs of non-helix-helix transition polysilanes (5, 6) are not evident. If the MPV hypothesis is correct, a real enantiomer of the helical polysilane with M-screw-sense may be an anti-polysilane with M-screw-sense made of anti-atoms, which is possible to exist in the anti-matter world [,,,], in the framework of the CPT conservation theorem by the indication of recent CP–symmetry breaking of the B-meson decay experiments and theory [,,].
5. Acknowledgements
The major part of the present work was carried out from 1995 to 2001 when the author worked for NTT Basic Research Laboratory where Hiromi Tamoto–Takigawa (worked for NTT-AT) and Masao Motonaga (worked for CREST-JST) measured and analyzed the variable temperature UV/CD spectra of the polysilanes in solution. The author synthesized the polysilanes and characterized by NMR and GPC. The potential energy surface (MSI, Discover 3) and electronic state (Gaussian03) were calculated at NTT (FY 1998–FY2000) and NAIST (FY 2009), respectively.
The author gratefully acknowledges Profs. Julian R. Koe (International Christian University (International Christian University), Kyozaburo Takeda (Waseda University), Hiroyuki Teramae (Jousei University), Nobuo Matsumoto (Shonan Institute of University), Masaie Fujino (Gunma National College of Technology), Kazuaki Furukawa (NTT), Takahiro Sato (Osaka University), Noriyuki Hatakenaka (Hiroshima University), the late Akio Teramoto (Osaka University, Emeritus), Masaki Hasegawa (University of Tokyo, Emeritus), Hideki Sakurai (Tohoku University, Emeritus), Toyoki Kunitake (Kyushu University, Emeritus), Junji Watanabe (Tokyo Institute of Technology), Kento Okoshi (Tokyo Institute of Technology), Masashi Kunitake (Kumamoto University), Zhang-Biao Zhang (Tianjin Normal University), Yong-Gang Yang (Soochow University), Eiji Yashima (Nagoya University), Yoshihisa Inoue (Osaka University), Hiroshi Masuhara (NAIST), Teruki Sugiyama (NAIST), Yoshio Okamoto (Nagoya University, Emeritus), Kenso Soai (Tokyo Science of University), and Wei Zhang (Soochow University) for their intuitive insights on helical polysilanes, entropy driven transitions, and chiroptical analysis from the early stage of this work until now. MF is also thankful to Drs. Hiroshi Nakashima (NTT), Osamu Niwa (AIST), Hong-Zhi Tang (Afton Chemicals), Anubhav Saxena (Momentive), Roopali Rai (Momentive), Akihiro Ohira (AIST), Masaaki Ishikawa (JASCO), Takayoshi Kawasaki (Tokyo Institute of Technology), Kenji Gomi (Kodansha Scientific), Masao Morita (NTT-AT), Masanobu Naito (NAIST), and Hisanari Onouchi (Nitto Denko) for fruitful discussions. The author wishes to thank his students at NAIST, Yoshihiro Kimura, Fumiko Ichiyanagi, Dr. Yoko Nakano (Eindhoven University of Technology), Takashi Mori, Satoshi Fukao, Jalilah Binti Abd Jalil, Yoshifumi Kawagoe, Ayako Nakao, and Makoto Taguchi for stimulating discussions. The author is grateful for fund from CREST-JST (FY1998–FY2003), Grant-in-Aid for Scientific Research for Exploratory Research from MEXT (16655046, FY2004–FY2006), the NAIST Foundation (FY2009), the SEKISUI Chemical Grant Program for Research on Manufacturing Based on Learning from Nature (FY2010), and Grant-in-Aid for Scientific Research (B) from MEXT (22350052, FY2010–FY2013). The author is particularly grateful to Profs. Martin Quack (ETH), Robert Compton (University of Tennessee), Robert West (University of Wisconsin), Leo W. Jenneskens (University of Utrecht), and Victor Borovkov (Osaka University) for stimulating discussions at international symposiums and domestic conferences. Finally, the author acknowledges Prof. David B. Cline (University of California, LA) for giving the author an opportunity to describe this unpublished work in the special issue of Symmetry of Life and Homochirality.
6. References
- Kipping, F.S.; Pope, W.J. Enantiomorphism. J. Chem. Soc. 1898, 73, 606–617. [Google Scholar] [CrossRef]
- Frank, F.C. On spontaneous asymmetric synthesis. Biochim. Biophys. Acta 1953, 11, 459–463. [Google Scholar] [CrossRef]
- Wald, G. The origin of optical activity. Ann. N.Y. Acad. Sci. 1957, 69, 352–368. [Google Scholar] [CrossRef] [PubMed]
- Ulbricht, T.L.V.; Vester, F. Attempts to induce optical activity with polarized β-radiation. Tetrahedron 1962, 18, 629–637. [Google Scholar] [CrossRef]
- Yamagata, Y. A hypothesis for the asymmetric appearance of biomolecules on Earth. J. Theoret. Biol. 1966, 11, 495–498. [Google Scholar] [CrossRef]
- Thiemann, W.; Darge, W. Experimental attempts for the study of the origin of optical activity on earth. Orig. Life 1974, 5, 263–283. [Google Scholar] [CrossRef] [PubMed]
- Rein, D. Some remarks on parity violating effects of intramolecular interactions. J. Mol. Evol. 1974, 4, 15–22. [Google Scholar] [CrossRef]
- Letokhov, V.S. On difference of energy levels of left and right molecules due to weak interactions. Phys. Lett. 1975, 53A, 275–276. [Google Scholar] [CrossRef]
- Zel’dovich, B.Ya.; Saakyan, D.B.; Sobel’man, I.I. Energy difference between right- and left-hand molecules, due to parity nonconservation in weak interactions of electrons with nuclei. Sov. Phys. JETP. Lett. 1977, 25, 94–97. [Google Scholar]
- Keszthelyi, L. Origin of the asymmetry of biomolecules and weak interaction. Orig. Life 1977, 8, 299–340. [Google Scholar] [CrossRef]
- Harris, R.A.; Stodolsky, L. Quantum beats in optical activity and weak interactions. Phys. Lett. 1978, 78B, 313–317. [Google Scholar] [CrossRef]
- Hegstrom, R.A.; Rein, D.W.; Sandars, P.G.H. Calculation of the parity nonconserving energy difference between mirror-image molecules. J. Chem. Phys. 1980, 73, 2329–2341. [Google Scholar] [CrossRef]
- Mason, S.F. Origins of biomolecular handedness. Nature 1984, 311, 19–23. [Google Scholar] [CrossRef] [PubMed]
- Hegstrom, R.A. Weak neutral current and β radiolysis effects on the origin of the biomolecular chirality. Nature 1985, 315, 749–750. [Google Scholar] [CrossRef]
- Kondepudi, D.K.; Nelson, G.W. Weak neutral currents and the origin of biomolecular chirality. Nature 1985, 314, 438–441. [Google Scholar] [CrossRef]
- Mason, S.F.; Tranter, G.E. The electroweak origin of biomolecular handedness. Proc. R. Soc. Lond. 1985, A397, 45–65. [Google Scholar] [CrossRef]
- Quack, M. On the measurement of the parity violating energy difference between enantiomers. Chem. Phys. Lett. 1986, 132, 147–153. [Google Scholar] [CrossRef]
- Barron, L.D. Symmetry and molecular chirality. Chem. Soc. Rev. 1986, 15, 189–223. [Google Scholar] [CrossRef]
- Applequist, J. Optical activity: Biot’s bequest. Amer. Sci. 1987, 75, 59–68. [Google Scholar]
- Wiesenfeld, L. Effect of atomic number on parity-violating energy differences between enantiomers, O, S, Se, Te. Mol. Phys. 1988, 64, 739–745. [Google Scholar] [CrossRef]
- Barra, A.L.; Robert, J.B.; Wiesenfeld, L. Possible observation of parity nonconservation by high-resolution NMR. Europhys. Lett. 1988, 5, 217–222. [Google Scholar] [CrossRef]
- Avetisov, V.A.; Goldanskii, V.I.; Kuz’min, V.V. Handedness, origin of life and evolution. Phys. Today 1991, 33–41. [Google Scholar] [CrossRef]
- Latel, H. Parity Violation in Atomic Physics. In Chirality - From Weak Bosons to the α-Helix; Janoschek, R., Ed.; Springer: Berlin, Germany, 1992; Chapter 1; pp. 1–17. [Google Scholar]
- Gardner, M. The new ambidextrous universe - Symmetry and asymmetry from mirror reflections to superstrings, 3rd ed.; Freeman: New York, NY, USA, 1990. [Google Scholar]
- Bonner, W.A. Terrestrial and extraterrestrial sources of molecular homochirality. Orig. Life Evol. Biosph. 1991, 21, 407–420. [Google Scholar] [CrossRef]
- Salam, A. The role of chirality in the origin of life. J. Mol. Evol. 1991, 33, 105–113. [Google Scholar] [CrossRef]
- Orgel, L. Molecular replication. Nature 1992, 358, 203–209. [Google Scholar] [CrossRef] [PubMed]
- Kikuchi, O.; Kiyonaga, H. Parity-violating energy shift of helical n-alkane. J. Mol. Struct. 1994, 312, 271–274. [Google Scholar] [CrossRef]
- Bada, J.L. Origins of homochirality. Nature 1995, 374, 594–595. [Google Scholar] [CrossRef]
- Cline, D.B. Physical Origin of Homochirality in Life; AIP Conference Proceedings 379; AIP Press: Woodbury, NY, USA, 1996. [Google Scholar]
- Avalos, M.; Babiano, R.; Cintas, P.; Jiménez, J.; Palacios, J.; Barron, L.D. Absolute asymmetric synthesis under physical fields: Facts and fictions. Chem. Rev. 1998, 98, 2845–2874. [Google Scholar] [CrossRef]
- Bailey, J.; Chrysostomou, A.; Hough, J.H.; Gledhill, T.M.; McCall, A.; Clark, S.; Ménard, F.; Tamura, M. Circular polarization in star-formation regions: Implications for biomolecular homochirality. Science 1998, 281, 672–674. [Google Scholar] [CrossRef]
- Pályi, G.; Zucchi, C.; Caglioti, L. Advances in Biochemistry; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Szabó-Nagy, A.; Keszthelyi, L. Demonstration of the parity-violating energy difference between enantiomers. Proc. Natl. Acad. Sci. USA 1999, 96, 4252–4255. [Google Scholar] [CrossRef]
- Feringa, B.L.; van Delden, R.A. Absolute asymmetric synthesis: the origin, control, and amplification of chirality. Angew. Chem. Int. Ed. 1999, 38, 3418–3438. [Google Scholar] [CrossRef]
- Avalos, M.; Babiano, R.; Cintas, P.; Jiménez, J.; Palacios, J. From parity to chirality: Chemical implications revisited. Tetrahedron Assym. 2000, 11, 2991–2404. [Google Scholar] [CrossRef]
- MacDermott, A.J. The ascent of parity-violation: Exochirality in the solar system and beyond. Enantiomer 2000, 5, 153–168. [Google Scholar] [PubMed]
- Avalos, M.; Babiano, R.; Cintas, P.; Jiménez, J.L.; Palacios, J.C. Chiral autocatalysis: Where stereochemistry meets the origin of life. Chem. Commun. 2000, 887–892. [Google Scholar] [CrossRef]
- Frank, P.; Bonner, W.A.; Zare, R. On One Hand But Not the Other: The Challenge of the Origin and Survival of Homochirality in Prebiotic Chemistry. In Chemistry for the 21st Century; Keinan, E., Schechter, E., Eds.; Wiley-VCH: Weinheim, German, 2001; Chapter 11; pp. 175–208. [Google Scholar]
- Lough, L.W.; Wainer, I.W. Chirality in Natural and Applied Science; Blackwell: Oxford, UK, 2002. [Google Scholar]
- Quack, M. How important is parity violation for molecular and biomolecular chirality? Angew. Chem. Int. Ed. 2002, 41, 4618–4630. [Google Scholar] [CrossRef] [PubMed]
- Shinitzky, M.; Nudelman, F.; Barda, Y.; Haimovitz, R.; Chen, E.; Deamer, D.W. Unexpected differences between D- and L-tyrosine lead to chiral enhancement in racemic mixtures. Orig. Life Evol. Biosph. 2002, 32, 285–297. [Google Scholar] [CrossRef] [PubMed]
- Crassous, J.; Chardonnet, C.; Saue, T.; Schwerdtfeger, P. Recent experimental and theoretical developments towards the observation of parity violation (PV) effects in molecules by spectroscopy. Org. Biomol. Chem. 2005, 3, 2218–2224. [Google Scholar] [CrossRef] [PubMed]
- Wagniére, G.H. On Chirality and the Universal Asymmetry—Reflections in Image and Mirror Image; Wiley-VCH: Weinheim, German, 2007. [Google Scholar]
- Soai, K.; Kawasaki, T. Asymmetric autocatalysis with amplification of chirality. Top. Curr. Chem. 2008, 284, 1–33. [Google Scholar]
- Guijarro, A.; Yus, M. The Origin of Chirality in The Molecules of Life; RSC: London, UK, 2009. [Google Scholar]
- Fujiki, M. Mirror symmetry breaking of silicon polymers—From weak bosons to artificial helix. Chem. Rec. 2009, 9, 271–298. [Google Scholar] [CrossRef]
- Sozzi, M.S. Discrete symmetries and CP violation: From experiment to theory; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Wigner, E. Einige folgerungen aus der schroedingerschen theorie fur die termstrukturen. Z. Phys. 1927, 43, 624–652. [Google Scholar] [CrossRef]
- Wigner, E.P. Symmetries and Reflections: Scientific Essays; MIT Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Wigner, E.P. Violations of symmetry in physics. Sci. Am. 1965, 213, 28–36. [Google Scholar] [CrossRef]
- Adair, R.K. A flaw in a universal mirror. Sci. Am. 1988, 258, 30–36. [Google Scholar] [CrossRef]
- Wu, C.S.; Ambler, E.; Hayward, R.W.; Hoppes, D.D.; Hudson, R.P. Experimental test of parity conservation in beta decay. Phys. Rev. 1957, 105, 1413–1415. [Google Scholar] [CrossRef]
- Lee, T.D.; Yang, C.N. Question of parity conservation in weak interactions. Phys. Rev. 1956, 105, 254–258. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical model of elementary particles based on an analogy with superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical model of elementary particles based on an analogy with superconductivity. II. Phys. Rev. 1961, 124, 246–254. [Google Scholar] [CrossRef]
- Weinberg, S. Conceptual foundations of the unified theory of weak and electromagnetic interactions. Rev. Mod. Phys. 1980, 52, 515–523. [Google Scholar] [CrossRef]
- Salam, A. Gauge unification of fundamental forces. Rev. Mod. Phys. 1980, 52, 525–538. [Google Scholar] [CrossRef]
- Glashow, S.L. Towards a unified theory: Threads in a tapestry. Rev. Mod. Phys. 1980, 52, 539–543. [Google Scholar] [CrossRef]
- Rubbia, C. Experimental observation of the intermediate vector bosons W+, W-, and Z0. Rev. Mod. Phys. 1985, 57, 699–722. [Google Scholar] [CrossRef]
- Bouchiat, M.A.; Pottier, L. Optical experiments and weak interactions. Science 1986, 234, 1203–1210. [Google Scholar] [CrossRef] [PubMed]
- Frois, B.; Bouchiat, M.A. Parity violation in atoms and polarized electron scattering; World Scientific: London, UK, 1999. [Google Scholar]
- Wang, W.; Yi, F.; Ni, Y.; Zhao, Z.; Jin, X.; Tang, Y. Parity violation of electroweak force in phase transitions of single crystals of D- and L-alanine and valine. J Biol. Phys. 2000, 26, 51–65. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, R.; Pyda, M.; Pak, J.; Wunderlich, B.; Thompson, J.R.; Pagni, R.; Pan, H.; Barnes, C.; Schwerdtfeger, P.; Compton, R. Search for electroweak interactions in amino acid crystals. II. The Salam hypothesis. J. Phys. Chem. A 2003, 107, 6674–6680. [Google Scholar] [CrossRef]
- Wilson, C.C.; Myles, D.; Ghosh, M.; Johnson, L.N.; Wang, W. Neutron diffraction investigations of L- and D-alanine at different temperatures: The search for structural evidence for parity violation. New J. Chem. 2005, 29, 1318–1322. [Google Scholar] [CrossRef]
- Figgen, D.; Koers, A.; Schwerdtfeger, P. NWHClI: A small and compact chiral molecule with large parity-violation effects in the vibrational spectrum. Angew. Chem. Int. Ed. 2010, 49, 2941–2943. [Google Scholar] [CrossRef] [PubMed]
- Scolnik, Y.; Portnaya, I.; Cogan, U.; Tal, S.; Haimovitz, R.; Fridkin, M.; Elitzur, A.C.; Deamer, D.W.; Shinitzky, M. Subtle differences in structural transitions between poly-L- and poly-D-amino acids of equal length in water. Phys. Chem. Chem. Phys. 2006, 8, 333–339. [Google Scholar] [CrossRef] [PubMed]
- Lahav, M.; Weissbuch, I.; Shavit, E.; Reiner, C.; Nicholson, G.J.; Schurig, V. Parity violating energetic difference and enantiomorphous crystals-caveats; Reinvestigation of tyrosine crystallization. Orig. Life Evol. Biosph. 2006, 36, 151–170. [Google Scholar] [CrossRef] [PubMed]
- Figgen, D.; Schwerdtfeger, P. Structures, inversion barriers, and parity violation effects in chiral SeOXY molecules (X,Y=H, F, Cl, Br, or I). J. Chem. Phys. 2009, 130, 054306. [Google Scholar] [CrossRef]
- Kodona, E.K.; Alexopoulos, C.; Panou-Pomonis, E.; Pomonis, P.J. Chirality and helix stability of polyglutamic acid enantiomers. J. Colloid Interf. Sci. 2008, 319, 71–80. [Google Scholar] [CrossRef]
- Fujiki, M.; Koe, J.R.; Terao, K.; Sato, T.; Teramoto, A.; Watanabe, J. Optically active polysilanes. Ten years of progress and new polymer twist for nanoscience and nanotechnology. Polym. J. 2003, 35, 297–344. [Google Scholar] [CrossRef]
- Fujiki, M. Switching handedness in optically active polysilanes. J. Organomet. Chem. 2003, 685, 15–34. [Google Scholar] [CrossRef]
- Fujiki, M. Experimental tests of parity violation at helical polysilylene level. Macromol. Rapid Commun. 2001, 22, 669–674. [Google Scholar] [CrossRef]
- Dekkers, H.P.J.M. Circularly Polarized Luminescence: A probe for Chirality in the Excited State. In Circular Dichroism: Principles and Applications, 2nd ed.; Berova, N., Nakanishi, K., Woody, R.W., Eds.; Wiley-VCH: New York, NY, USA, 2000; Chapter 7. [Google Scholar]
- Sato, T.; Terao, K.; Teramoto, A.; Fujiki, M. Molecular properties of helical polysilylenes in solution. Polymer 2003, 44, 5477–5495. [Google Scholar] [CrossRef]
- Laubender, G.; Berger, R. Ab initio calculation of parity-violating chemical shifts in NMR spectra of chiral molecules. ChemPhysChem 2003, 4, 395–399. [Google Scholar] [CrossRef] [PubMed]
- Weijo, V.; Manninen, P.; Vaara, J. Perturbational calculations of parity-violating effects in nuclear-magnetic-resonance parameters. J. Chem. Phys. 2005, 123, 054501. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; Millam, J.M.; Iyengar, S.S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G.A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J.E.; Hratchian, H.P.; Cross, J.B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R.E.; Yazyev, O.; Austin, A.J.; Cammi, R.; Pomelli, C.; Ochterski, J.W.; Ayala, P.Y.; Morokuma, K.; Voth, G.A.; Salvador, P.; Dannenberg, J.J.; Zakrzewski, V.G.; Dapprich, S.; Daniels, A.D.; Strain, M.C.; Farkas, O.; Malick, D.K.; Rabuck, A.D.; Raghavachari, K.; Foresman, J.B.; Ortiz, J.V.; Cui, Q.; Baboul, A.G.; Clifford, S.; Cioslowski, J.; Stefanov, B.B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R.L.; Fox, D.J.; Keith, T.; Al-Laham, M.A.; Peng, C.Y.; Nanayakkara, A.; Challacombe, M.; Gill, P.M.W.; Johnson, B.; Chen, W.; Wong, M.W.; Gonzalez, C.; Pople, J.A. Gaussian 03, revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Kamide, K.; Kataoka, A. Theoretical relationships between parameters in the Kuhn-Mark- Houwink-Sakurada equation. Macromol. Chem. Phys. 2003, 128, 217–228. [Google Scholar] [CrossRef]
- Carter, A.B.; Sanda, A.I. CP violation in B-meson decays. Phys. Rev. D 1981, 23, 1567–1579. [Google Scholar] [CrossRef]
- Aubert, B.; Boutigny, D.; Gaillard, J.M.; Hicheur, A.; Karyotakis, Y.; Lees, J.P.; Robbe, P.; Tisserand, V.; Palano, A.; Chen, G.P.; Chen, J.C.; Qi, N.D.; Rong, G.; et al. Observation of CP violation in the B0 meson system. Phys. Rev. Lett. 2001, 87, 091801. [Google Scholar] [CrossRef]
- Abe, K.; Abe, R.; Adachi, I.; Aihara, H.; Akatsu, M.; Alimonti, G.; Asai, K.; Asai, M.; Asano, Y.; Aso, T.; Aulchenko, V.; et al. Observation of large CP violation in the neutral B meson system. Phys. Rev. Lett. 2001, 87, 091802. [Google Scholar] [CrossRef]
7. Appendix
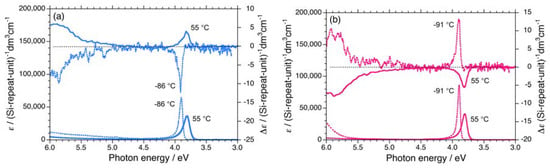
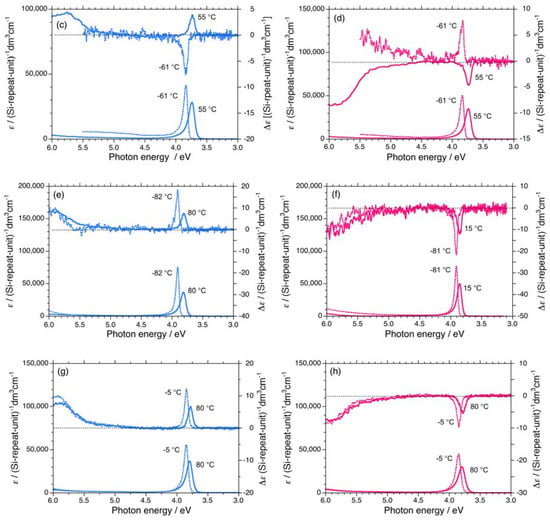
Figure A1.
UV and CD spectra in isooctane of (a) 3S (Mw = 232,000, Mn = 78,900) at –86 °C and +55 °C, (b) 3R (Mw = 156,000, Mn = 76,800) at –91 °C and +55 °C, (c) 4S (Mw = 14,500, Mn = 11,300) at –61 °C and +55 °C, (d) 4R (Mw = 19,000, Mn = 15,200) at –61 °C and +55 °C, (e) 5S (Mw = 42,300, Mn = 23,500) at –82 °C and +80°C, (f) 5R (Mw = 36,900, Mn = 19,000) at –81 °C and +15 °C, (g) 6S (Mw = 108,000, Mn = 37,300) at –5 °C and +80 °C, and (h) 6R (Mw = 80,900, Mn = 34,600) at –5 °C and +80 °C.
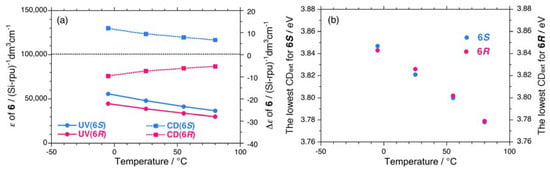
Figure A2.
(a) Absorptivity (ε) and CD signal (Δε), and (b) apparent CD extrema near 3.9 eV of 6S (Mw = 108,000, Mn = 37,300) and 6R (Mw = 80,900, Mn = 34,600) in isooctane as a function of temperature.
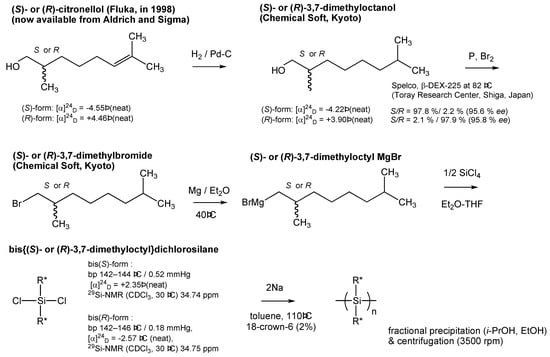
Scheme A1.
Synthetic scheme of 1S and 1R. For 2S/2R, 3S/3R, 4S/4R, and 5S/5R, the corresponding organotrichlorosilane (Shin-Etsu) was used. For synthesis of 6S/6R, n-dodecyltrichlorosilane (Shin-Etsu), (S)-2-methylchloride (TCI), and (R)-2-methyl- chloride (synthesized by Chemical Soft, Kyoto, Japan) were used as starting materials.
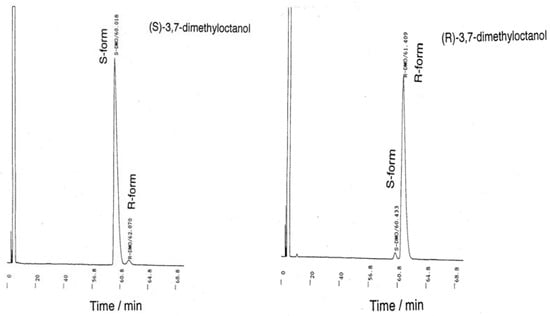
Figure A3.
Gas chromatography (GC) charts of (S)-(–)-3,7-dimethyloctanol and (R)-(+)-3,7- dimethyloctanol. Measurement and analysis were carried out at TRC (Shiga, Japan) by the chiral GC method (Supelco, β-DEX-225, 30 m x 0.25 mm ID, column oven 82 °C, He carrier with 1.2 mL/min).
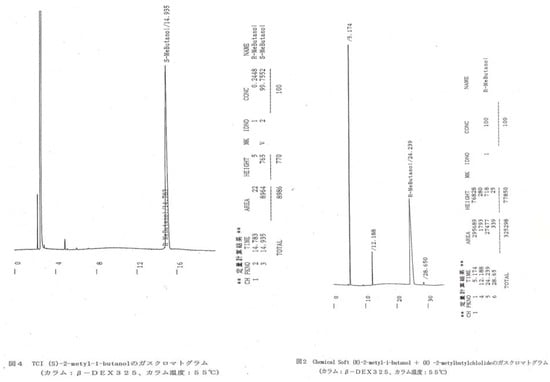
Figure A4.
GC charts of (S)-(+)-2-methylbutanol and (R)-(+)-2-methylbutanol. Measurement and analysis were done by TRC with the chiral GC method (Supelco, β-DEX-325, 30 m x 0.25 mm ID, column oven 55 °C, He carrier with 1.2 mL/min).
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).