Integral and Numerical Formulations for Seeking the Period of Non-Conservative Nonlinear Oscillator With/Without the First Integral

Abstract

For a non-conservative nonlinear oscillator (NCNO) having a periodic solution, the existence of the first integral is a certain symmetry of the nonlinear dynamical system, which signifies the balance of kinetic energy and potential energy. A first-order nonlinear ordinary differential equation (ODE) is used to derive the first integral, which, equipped with a right-end boundary condition, can determine an implicit potential function for computing the period by an exact integral formula. However, the integrand is singular, which renders a less accurate value of the period. A generalized integral conservation law endowed with a weight function is constructed, which is proved to be equivalent to the exact integral formula. Minimizing the error to satisfy the periodicity conditions, the optimal initial value of the weight function is determined. Two non-iterative methods are developed by integrating three first-order ODEs or two first-order ODEs to compute the period. Very accurate value of the period can be observed upon testing five examples. For the NCNO without having the first integral, the integral-type period formula is derived. Four examples belong to the Liénard equation, involving the van der Pol equation, are evaluated by the proposed iterative method to determine the oscillatory amplitude and period. For the case with one or more limit cycles, the amplitude and period can be estimated very accurately. For the NCNO of a broad type with or without having the first integral, the present paper features a solid theoretical foundation and contributes integral-type formulations for the determination of the oscillatory period. The development of new numerical algorithms and extensive validation across a diverse set of examples is given.

1. Introduction

A considerable attention was devoted to the semi-analytical and analytical solutions for non-conservative nonlinear oscillators (NCNOs), because they are greatly important in our real world to tackle the nonlinear dynamical phenomena. Actually, the research on the periodic motion of the NCNO with/without a forcing term was a mature subject [1]. We can observe ubiquitous periodic motions in a lot of areas of mechanics and engineering applications, which are in practice the NCNO systems.

Seeking the periods and periodic solutions of NCNOs are a crucial periodic problem in nonlinear dynamical systems. When the period and oscillatory amplitude are unknown values, the periodic problem is a difficult task. Therefore, a lot of numerical methods were developed to solve the periodic problems of NCNO systems, like the differential transform method [2], the collocation method and high dimensional harmonic balance method [3], the time domain collocation method [4], and the shape function iteration method [5]. In addition, there are many analytic methods such as the parameter-expanding method [6], the linearized Lindstedt-Poincaré method [7], the harmonic balance method [8,9,10,11], the variational iteration method [12,13], and the homotopy perturbation method [14,15]. Viswanath [16] developed a method to compute high-precision periodic orbits of nonlinear dynamical systems based on the linearized Lindstedt-Poincaré method.

We must emphasize the importance of studying oscillations in general nonlinear dynamical systems. The development of oscillation theory is vital, as it represents a fundamental mathematical tool in analyzing the dynamic behavior of these systems. For example the study on the periodic motion of the second-order nonlinear ODE without delay effects has a lot of applications. The neutral differential equations are a class of differential equations that involve derivatives of an unknown function with delay effects, where the highest derivative of the function appears in both its current and delayed values within the same equation. These equations are important in scientific and engineering applications [17,18,19].

A second-order NCNO is modeled by

$$\left\{\begin{array}{c}\ddot{x}+f(x,\dot{x})=0,\hfill \\ x\left(0\right)=A, \dot{x}\left(0\right)=0,\hfill \end{array}\right.$$

(1)

where the amplitude $A>0$ is a constant. The function $f(x,\dot{x})\in \mathcal{C}\left({\mathbb{R}}^2\right)$ is a continuous function of $(x,\dot{x})$, and satisfies the Lipschitz condition for the uniqueness of the solution of Equation (1) [20].

Let $\dot{x}=y$. The Bendixson-Dulac Theorem [1] reveals that a necessary condition for the existence of a periodic motion in a simply connected region $\Omega \subset {\mathbb{R}}^2$ is that $\partial f(x,y)/\partial y$ must change its sign inside $\Omega$.

In terms of first-order ODEs, Equation (1) can be written as

$$\left\{\begin{array}{c}\dot{x}=y,\hfill \\ \dot{y}=-f(x,y).\hfill \end{array}\right.$$

(2)

The divergence of the vector field is

$$\mathrm{Div}(y,-f(x,y))=-{\displaystyle \frac{\partial f(x,y)}{\partial y}}.$$

(3)

If $\mathrm{Div}(y,-f(x,y\left)\right)=0$, i.e., $\partial f(x,y)/\partial y=0$, then the dynamical system in Equation (1) is conservative; otherwise, it is a non-conservative nonlinear oscillator (NCNO).

For Equation (1) the period T is the smallest positive real number that satisfies the periodicity conditions:

$$x\left(0\right)=x\left(T\right)=A, \dot{x}\left(0\right)=\dot{x}\left(T\right)=0.$$

(4)

In general, the period $T>0$ of a periodic orbit, which is a simple closed curve in the phase plane, of the system is an unknown constant; however, the periodicity conditions in time can be used to determine T. Seeking T to allow a periodic solution is termed a periodic problem.

He and Garcia [21] derived a sufficient and necessary condition for Equation (1) existing a periodic solution. If and only if a function $\varphi \left(x\right)$ satisfies

$$\dot{x}=\varphi \left(x\right)\in {\mathcal{C}}^1\left(\mathbb{R}\right),$$

(5)

$${\displaystyle \frac{d\varphi \left(x\right)}{dx}}=-{\displaystyle \frac{f(x,\varphi (x\left)\right)}{\varphi \left(x\right)}}, \varphi \left(A\right)=0$$

(6)

Equation (1) possesses a periodic solution [21].

The explicit forms of $f(x,\dot{x})$ and $\varphi \left(x\right)$ are different for different problems to be solved. For example a tapered beam has the following

$$f(x,\dot{x})={\displaystyle \frac{x+ax{\dot{x}}^2+b{x}^3}{1+a{x}^2}},$$

(7)

where $a>0$ and $b>0$ are constants. Its first integral can be derived as follows [22]:

$$\dot{x}=\varphi \left(x\right)=\sqrt{{\displaystyle \frac{2(A^2-x^2)+b(A^4-x^4)}{2(1+a{x}^2)}}}.$$

(8)

In general the explicit form of $\varphi$ is not available, unless one can solve the ODE in Equation (6) explicitly. $\varphi \left(x\right)$ can be deemed as a potential function of the dynamical system and ${\varphi }^2\left(x\right)$ signifies the potential energy.

Equation (5) is indeed the first integral of Equation (1), from which we can derive an exact integral formula to compute the period:

$$T=4{\int }_0^A{\displaystyle \frac{dx}{\varphi \left(x\right)}}.$$

(9)

The first integral is a certain symmetry of the nonlinear dynamical system. It signifies the conservation of kinetic energy and potential energy of the dynamical system, that is, ${\dot{x}}^2={\varphi }^2\left(x\right)$.

There are three types of second-order nonlinear dynamical systems: conservative system, non-conservative system having the first integral and non-conservative system without having the first integral. For the first two types of systems the integral-type frequency formulas are well developed in [22]. However, for the last type of system, the integral-type period formula is not yet available. Mainly, we are concerned with the integral-type period formula for the dissipative nonlinear dynamical system.

The relationship between the period and vibration amplitude is a crucial property of NCNOs. By improving the precision of the relationship, there were many modifications of He’s frequency formula [23,24,25,26]. The modifications of He’s frequency-amplitude formulation were summarized in [27,28], and the discussions of the frequency-amplitude formulas were conducted in [29].

Speaking roughly, the methods for solving the periodic problems of NCNO can be classified into three types: exact methods, analytically approximate methods, and purely numerical methods. Hereon we propose the fourth type method as a combination of the exact method and the numerical method, shortened as exact-numerical method. We are going to derive the integral-type formula for NCNO, which is exact in the sense that when the exact solution is inserted into the integral formula the exact value of the period can be obtained [22]. For most NCNO the exact solution is not available; hence, we employ the numerical integration method to realize the integral-type formula. It would be clear that the proposed exact-numerical method is very effective and accurate in computing the unknown amplitude and period. This method outperforms the methods that appeared in the above literature from the aspect of accuracy and efficiency.

A limit cycle is a closed orbit in the phase plane of a nonlinear dynamical system, where at least one other trajectory spirals into or out of it. Essentially, it is a stable and repeating pattern of behavior in a nonlinear dynamical system, and nearby orbits eventually settling into this repeating cycle. A typical example of the limit cycle is the van der Pol equation, which is a self-sustaining oscillation [1]. Many applications of the limit cycle can be seen in the biological oscillation and aeroelastic oscillation [30,31].

For the non-conservative Liénard equation without having the first integral, the present paper will propose an integral-type period formula and derive an iteration method to determine both the unknown values of period and oscillation amplitude.

The innovation points of the present paper are coined as follows:

1.

A first-order nonlinear ODE is used to derive the first integral, which, equipped with a right-end boundary condition, can determine, in general, an implicit function for computing the period by an exact integral formula.

2.

A novel integral-type period formula involved a weight function and its initial value for the NCNO having the first integral is derived, which is equivalent to the exact integral formula. To meet the periodicity conditions to determine the initial value, a very accurate period can be obtained.

3.

Based on the integral-type period formula, two non-iterative numerical methods are developed, which save the computational cost.

4.

For the NCNO without having the first integral a supplementary variable is introduced, which helps derive an integral-type period formula for the non-conservative Liénard equation in the dimensionless time domain.

5.

An iterative type numerical method is developed to compute the oscillatory amplitude and period of the Liénard equation.

2. A New Approach of the Period for NCNO

Under the existence condition of Bendixson-Dulac we discuss the period for a periodic solution of Equation (1), which must satisfy the periodicity conditions in Equation (4). After inserting $\dot{x}=\varphi \left(x\right)$, Equation (1) can be deemed as a nonlinear oscillator of conservative type:

$$\ddot{x}+f(x,\varphi \left(x\right))=0,$$

(10)

$$x\left(0\right)=A, \dot{x}\left(0\right)=0.$$

(11)

As noticed in [21], from Equations (5) and (6) it follows that

$$\ddot{x}={\displaystyle \frac{d\varphi }{dx}}\dot{x}=-{\displaystyle \frac{f(x,\varphi )}{\varphi }}\varphi =-f(x,\varphi ).$$

Therefore, Equations (5) and (6) are sufficient conditions to derive Equation (10) from Equation (1), which is in fact a conservative nonlinear oscillator [32].

Equation (6) was further explored in [33] to provide an upper bound for the number of periodic orbits in planar systems, and in [34] to derive the homotopy-first integral method for NCNO.

According to $xf(x,\varphi )>0$, $f(x,\varphi )>0$ in the range $x\in [0, A]$, to compute T, we only need to consider the periodic orbit in the first quadrant in the phase plane with $x\ge 0$ and $\dot{x}\ge 0$; hence $\varphi \left(x\right)\ge 0, x\in [0, A]$ via Equation (5). Based on these conditions, an exact integral-type period formula of Equation (1) is [35]:

$$T=2\sqrt{2}{\int }_0^A{\displaystyle \frac{dx}{\sqrt{{\int }_x^{A}f(s,\varphi \left(s\right))ds}}}.$$

(12)

The reason that Equation (12) may lose its accuracy for satisfying the periodicity conditions (4) is that the integrand is singular at $x=A$ owing to ${\int }_A^{A}f(x,\varphi \left(x\right))dx=0$. Upon giving $f(x,\varphi (x\left)\right)$ and A there exists no room in Equation (12) to improve the accuracy of T, and the limiting value of T is convergent slowly. Therefore, we propose a new approach that can modify Equation (12), such that the period can precisely satisfy the periodicity conditions (4).

By the integration of Equation (6), we have

$${\varphi }^2\left(x\right)=2{\int }_x^{A}f(s,\varphi \left(s\right))ds\ge 0, 0\le x\le A,$$

(13)

where the right-end boundary condition $\varphi \left(A\right)=0$ was used. When $\varphi \left(x\right)$ is determined from Equation (13) implicitly, we can use Equation (9) to compute T. However, this integral formula is hard to realize because $\varphi \left(A\right)=0$ and $\varphi \left(x\right)$ is an implicit function of x.

At the same time, as the period for the nonlinear oscillator in Equations (10) and (11), Equation (9) is equivalent to Equation (12), which can be seen by inserting Equation (13) into Equation (12):

$$T=2\sqrt{2}{\int }_0^A{\displaystyle \frac{dx}{\frac{\varphi \left(x\right)}{\sqrt{2}}}}=4{\int }_0^A{\displaystyle \frac{dx}{\varphi \left(x\right)}}.$$

In order to derive an integral-type period formula we introduce a weight function $W\left(x\right)>0$, such that the strong form ODE in Equation (10) can be transformed into an integral-type equation, which satisfies Equation (10) in a weak sense. The theoretical background of the following results is the Galerkin method, where $W\left(x\right)>0$ is also called the test function.

Let $W\left(x\right)>0$ be a differentiable weight function. Multiplying Equation (10) by $W\left(x\right)$ and integrating it from $t=0$ to $t=T$ generates

$${\int }_0^{T}W\left(x\left(t\right)\right)\ddot{x}\left(t\right)dt+{\int }_0^{T}f(x\left(t\right),\varphi \left(x\left(t\right)\right))W\left(x\left(t\right)\right)dt=0.$$

(14)

When the first integral term is integrated by parts and using the periodicity condition $W\left(x\left(T\right)\right)\dot{x}\left(T\right)=W\left(x\left(0\right)\right)\dot{x}\left(0\right)$ due to $x\left(T\right)=x\left(0\right)$ and $\dot{x}\left(T\right)=\dot{x}\left(0\right)$ specified in Equation (4), it becomes

$${\int }_0^{T}W\left(x\left(t\right)\right)\ddot{x}\left(t\right)dt=-{\int }_0^T\dot{W}\left(x\left(t\right)\right)\dot{x}\left(t\right)dt;$$

(15)

moreover, using $\dot{W}\left(x\left(t\right)\right)=W^{\prime }\left(x\left(t\right)\right)\dot{x}$ where $W^{\prime }\left(x\right)=dW\left(x\right)/dx$, we have

$${\int }_0^{T}W\left(x\left(t\right)\right)\ddot{x}\left(t\right)dt=-{\int }_0^T{W}^{\prime }\left(x\left(t\right)\right){\dot{x}}^2\left(t\right)dt.$$

(16)

Hence, Equation (14) is transformed to

$${\int }_0^T{W}^{\prime }\left(x\left(t\right)\right){\dot{x}}^2\left(t\right)dt={\int }_0^{T}f(x\left(t\right),\varphi \left(x\left(t\right)\right))W\left(x\left(t\right)\right)dt,$$

(17)

which is a generalized integral conservation law for the nonlinear oscillator in Equation (10). While the left side signifies a generalized kinetic energy within one period, the right side is a generalized work performed by the oscillator within one period.

Remark 1.

As a special case of Equation (17) with $W\left(x\right)=x$, we have

$${\int }_0^T{\dot{x}}^2\left(t\right)dt={\int }_0^{T}f(x\left(t\right),\varphi \left(x\left(t\right)\right))x\left(t\right)dt.$$

(18)

While the left side is the kinetic energy of the oscillator within one period, the right side is a work $f\left(x\right(t),\varphi (x\left(t\right)\left)\right)x\left(t\right)$ engaged by the oscillator within one period. Therefore, we call Equation (17) a generalized integral conservation law for the nonlinear oscillator in Equation (10). It is a weak form of the conservation law for the nonlinear oscillator in Equation (10).

Shaping Equation (17) to be the integral with respect to x yields

$${\int }_0^A{W}^{\prime }\left(x\left(t\right)\right){\dot{x}}^2\left(t\right){\displaystyle \frac{dt}{dx}}dx={\int }_0^{A}f(x\left(t\right),\varphi \left(x\left(t\right)\right))W\left(x\left(t\right)\right){\displaystyle \frac{dt}{dx}}dx.$$

(19)

In the range from $x=0$ to $x=A$, we have $\dot{x}\ge 0$, and by means of Equation (5), Equation (19) can be recast to

$${\int }_0^A{W}^{\prime }\left(x\right)\varphi \left(x\right)dx={\int }_0^A{\displaystyle \frac{f(x,\varphi (x\left)\right)W\left(x\right)}{\varphi \left(x\right)}}dx.$$

(20)

This is a generalized integral conservation law for the nonlinear oscillator in Equation (10) in the spatial domain $x\in [0,A]$.

We consider the following first-order ordinary differential equations (ODEs):

$$W^{\prime }\left(x\right)={\displaystyle \frac{2}{{\varphi }^2\left(x\right)}}, W\left(0\right)=W_0,$$

(21)

$$V^{\prime }\left(x\right)={\displaystyle \frac{2f(x,\varphi (x\left)\right)W\left(x\right)}{\varphi \left(x\right)}}, V\left(0\right)=0,$$

(22)

where $W_0$ is a parameter.

The left-hand side of Equation (20) with the aid of Equations (9) and (21) is changed to

$${\int }_0^A{W}^{\prime }\left(x\right)\varphi \left(x\right)dx=2{\int }_0^A{\displaystyle \frac{dx}{\varphi \left(x\right)}}={\displaystyle \frac{T}{2}},$$

(23)

which, by equating to the right side of Equation (20), reduces to

$$T=2{\int }_0^A{\displaystyle \frac{f(x,\varphi (x\left)\right)W\left(x\right)}{\varphi \left(x\right)}}dx.$$

(24)

Because W is governed by the first-order ODE in Equation (21), an initial value $W\left(0\right)$ must be specified for the unique solution of $W\left(x\right)$, if $\varphi \left(x\right)$ is available from Equation (6). The reason for introducing the first-order ODE in Equation (21) is that we can derive Equation (23), such that the period T can be obtained via the integral of $W^{\prime }\left(x\right)\varphi \left(x\right)$. More reason for setting the above two first-order ODEs in Equations (21) and (22) would be clearly shown in Theorems 1 and 2 as follows.

By means of Equations (22) and (24), we can obtain

$$T={\int }_0^A{V}^{\prime }\left(x\right)dx=V\left(A\right).$$

(25)

Through the integration of Equations (21) and (22) from $x=0$ to $x=A$ and with $W\left(0\right)=W_0$ and $V\left(0\right)=0$, one can obtain the period by $T=V\left(A\right)$. This is a non-iterative method to compute the period T for the NCNO in Equation (1) by using $\dot{x}=\varphi \left(x\right)$.

Theorem 1.

For the nonlinear oscillator in Equations (10) and (11) the two integral Formulas (9) and (24) for the period are identical, i.e.,

$$2{\int }_0^A{\displaystyle \frac{f(x,\varphi (x\left)\right)W\left(x\right)}{\varphi \left(x\right)}}dx=4{\int }_0^A{\displaystyle \frac{dx}{\varphi \left(x\right)}}=T,$$

(26)

if $W^{\prime }\left(x\right)$ is given by Equation (21) and $W\left(0\right)=W_0=0$ is the given initial value of $W\left(x\right)$.

Proof. 

By means of Equation (6) with $f(x,\varphi (x\left)\right)/\varphi \left(x\right)$ being replaced by $-d\varphi \left(x\right)/dx$, the left-hand side of Equation (26) becomes

$$2{\int }_0^A{\displaystyle \frac{f(x,\varphi (x\left)\right)W\left(x\right)}{\varphi \left(x\right)}}dx=-2{\int }_0^{A}W\left(x\right){\displaystyle \frac{d\varphi \left(x\right)}{dx}}dx;$$

(27)

integrating by part and using Equation (21) renders

$$\begin{array}{c}2{\int }_0^A{\displaystyle \frac{f(x,\varphi (x\left)\right)W\left(x\right)}{\varphi \left(x\right)}}dx=-{\left.2W\left(x\right)\varphi \left(x\right)\right|}_0^A+2{\int }_0^A\varphi \left(x\right)W^{\prime }\left(x\right)dx\hfill \\ =-2W\left(A\right)\varphi \left(A\right)+2W\left(0\right)\varphi \left(0\right)+2{\int }_0^A{\displaystyle \frac{2}{\varphi \left(x\right)}}dx\hfill \\ =2W\left(0\right)\varphi \left(0\right)+{\int }_0^A{\displaystyle \frac{4}{\varphi \left(x\right)}}dx,\hfill \end{array}$$

(28)

where $\varphi \left(A\right)=0$ was used. If $W\left(0\right)=W_0=0$, Equation (28) reduces to Equation (26). □

Theorem 2.

For the nonlinear oscillator in Equations (10) and (11) the period of the periodic orbit can be computed by

$$T=2\sqrt{2}W\left(0\right){\left({\int }_0^{A}f(x,\varphi \left(x\right))dx\right)}^{1/2}+{\int }_0^A{\displaystyle \frac{2\sqrt{2}}{\sqrt{{\int }_x^{A}f(s,\varphi \left(s\right))ds}}}dx.$$

(29)

Proof. 

In view of Equation (26) the period for the nonlinear oscillator in Equations (10) and (11) is equivalent to that in Equation (24), which with the aid of Equation (28) becomes

$$T=2W\left(0\right)\varphi \left(0\right)+{\int }_0^A{\displaystyle \frac{4}{\varphi \left(x\right)}}dx.$$

(30)

Inserting Equation (13) for $\varphi \left(x\right)$ and taking $W\left(0\right)=W_0$ into the above equation we can derive Equation (29). □

Either we can integrate Equations (21) and (22) by subjecting them to the initial values $W\left(0\right)=W_0$ and $V\left(0\right)=0$ to compute the period by $T=V\left(A\right)$ in Equation (25), or simply we use the new theoretical formula (30) to compute the period. No matter which formulation is undertaken, $W_0$ can be determined by minimizing the $L_2$ error to satisfy the periodicity conditions (4):

$$\underset{W_0}{min}\sqrt{{[x\left(T\right)-A]}^2+{\dot{x}}^2\left(T\right)}.$$

(31)

In the minimization problem in Equation (31) with a single parameter $W_0$, we can adopt the so-called interval reduction method (IRM) to find the optimal value of $W_0$. First we select a large interval and list the data of $\sqrt{{[x\left(T\right)-A]}^2+{\dot{x}}^2\left(T\right)}$ in the computer; we can observe where the minimal point locates; then we reduce the interval to a smaller one to involve that minimal point. Carrying out the same procedure a few times by the computer, we can find a quite accurate value of $W_0$, which leads to the minimal value of $\sqrt{{[x\left(T\right)-A]}^2+{\dot{x}}^2\left(T\right)}$. If each interval is divided into 100 points, and the times for interval reduction is 10, then in the IRM we need to apply the RK4 to integrate the ODEs 1000 times.

Examples will be given later to show that Equation (25) or Equation (30) is more accurate than Equation (12) to satisfy the periodicity conditions (4). The reason that Equation (12) loses its accuracy to satisfy the periodicity conditions (4) is that ${\int }_A^{A}f(x,\varphi \left(x\right))dx={\varphi }^2\left(A\right)/2=0$, which is a singular integral formula. $W_0=W\left(0\right)$ in Equation (29) plays a main role in adjusting and correcting the period to satisfy the periodicity conditions (4). $2\sqrt{2}{W}_0{\left({\int }_0^{A}f(x,\varphi \left(x\right))dx\right)}^{1/2}=2W\left(0\right)\varphi \left(0\right)$ is a compensated term to remedy the shortcoming of the singularity that appeared in the integrand in Equation (12).

Remark 2.

For a conservative system

$$\ddot{x}\left(t\right)+f\left(x\right)=0,$$

(32)

the following integral formula is well-known [1]:

$$T=2\sqrt{2}{\int }_0^A{\displaystyle \frac{dx}{\sqrt{{\int }_x^{A}f\left(s\right)ds}}}.$$

(33)

Theorems 1 and 2 are crucial. We can also derive other exact integral formulas in Equations (26) and (29) for the NCNO having the first integral. These formulas are equivalent to that in Equations (9) and (12). Therefore, we can transform these integral formulas into a numerical integration problem without any iteration to quickly compute the exact value of the period as shown below. These findings are sound and have a great influence on remedying the singularity exhibited in the original integral formula in Equation (9).

3. Seeking the Period by Two Non-Iterative Methods

In view of Equations (6), (21) and (22), we have three first-order ODEs to compute T. First, we transform Equation (6) to an initial value problem by introducing

$$\xi =A-x, \phi \left(\xi \right)={\varphi }^2\left(x\right),$$

(34)

such that

$${\displaystyle \frac{d\phi \left(\xi \right)}{d\xi }}=2f(A-\xi ,\sqrt{\phi \left(\xi \right)}), \phi \left(0\right)=0,$$

(35)

where $\phi \left(0\right)={\varphi }^2\left(A\right)=0$. Integrating the above ODE from $\xi =0$ to $\xi =A$ yields the initial value ${\varphi }_0:=\varphi \left(0\right)=\sqrt{\phi \left(A\right)}$. Then, Equation (6) is transformed to an initial value problem:

$${\displaystyle \frac{d\varphi \left(x\right)}{dx}}=-{\displaystyle \frac{f(x,\varphi (x\left)\right)}{\varphi \left(x\right)}}, \varphi \left(0\right)={\varphi }_0.$$

(36)

We must emphasize that the transformation (34) is a crucial step to obtain the initial value ${\varphi }_0:=\varphi \left(0\right)=\sqrt{\phi \left(A\right)}$ by numerically integrating Equation (35). Such that we can transform the periodic problem to an initial value problem as shown below.

3.1. First Method

The algorithm begins by computing the initial value ${\varphi }_0=\varphi \left(0\right)=\sqrt{\phi \left(A\right)}$ by numerically integrating Equation (35). Let $z_1=\varphi$, $z_2=W$ and $z_3=V$. Equations (36), (21) and (22) generate three first-order ODEs:

$$z_1^{\prime }\left(x\right)=-{\displaystyle \frac{f(x,z_1)}{z_1}}, z_1\left(0\right)={\varphi }_0,$$

(37)

$$z_2^{\prime }\left(x\right)={\displaystyle \frac{2}{z_1^2}}, z_2\left(0\right)=W_0,$$

(38)

$$z_3^{\prime }\left(x\right)={\displaystyle \frac{2f(x,z_1)z_2}{z_1}}, z_3\left(0\right)=0.$$

(39)

The processes for determining T: (i) Compute ${\varphi }_0$, and give $W_0$ and $\Delta x=A/N$ with N given; (ii) Apply the fourth-order Runge-Kutta method (RK4) to integrate Equations (37)–(39) with N steps from $x=0$ to $x=A$, and take

$$T=z_3\left(A\right).$$

(40)

We can choose the best value of $W_0$, such that Equation (31) is satisfied. This is a non-iterative method to determine T; we name it the first method.

3.2. Second Method

The algorithm begins by computing the initial value ${\varphi }_0=\varphi \left(0\right)=\sqrt{\phi \left(A\right)}$ by numerically integrating Equation (35). Based on Theorem 2 a simpler non-iterative method can be derived as follows. Let $y_1=\varphi$, and

$$y_2\left(x\right)={\int }_0^x{\displaystyle \frac{4}{\varphi \left(s\right)}}ds.$$

(41)

Equations (36) and (41) yield two first-order ODEs:

$$y_1^{\prime }\left(x\right)=-{\displaystyle \frac{f(x,y_1)}{y_1}}, y_1\left(0\right)={\varphi }_0,$$

(42)

$$y_2^{\prime }\left(x\right)={\displaystyle \frac{4}{y_1}}, y_2\left(0\right)=0.$$

(43)

Instead of Equations (37)–(39), a simpler non-iterative method for determining T is given as follows. (i) Compute ${\varphi }_0$, and give $w_0$ (to distinguish it from $W_0$ used in the first method), and $\Delta x=A/N$. (ii) Applying the RK4 to integrate Equations (42) and (43) up to $x=A$, and by means of Equation (30), one has

$$T=y_2\left(A\right)+2{\varphi }_0{w}_0.$$

(44)

We can choose the best value of $w_0$, such that Equation (31) is satisfied. This non-iterative method is named the second method.

Both the first method and the second method are suitable for the second-order NCNO which has the first integral.

3.3. An Iterative Method

For comparing purpose we list an iteration method in [36] for a conservative system to find the period T. Let $\tau :=t/T$, $\mathbf{x}:={(x,y)}^T$ and $\mathbf{f}:={(y,-f(x,y))}^T$.

(i)

Give ${\mathbf{x}}^0={(A,0)}^T$, $T_0$, $\nu$, $\Delta \xi$, $\epsilon$, and N

(ii)

For $k=0,1,\dots$, with N steps from $\tau =0$ to $\tau =1$, apply the RK4 to integrate

$${\mathbf{x}}^{\prime }\left(\tau \right)=T\mathbf{f}\left(\mathbf{x}\right),$$

(45)

where $T=T_K$ and $\mathbf{x}\left(0\right)={\mathbf{x}}^0$. Take

$${\mathbf{c}}^{k+1}=\mathbf{x}\left(1\right), F\left(T_k\right)=\parallel {\mathbf{c}}^{k+1}-{\mathbf{x}}^0\parallel , T_{k+1}=T_k+{\displaystyle \frac{\nu \Delta \xi }{1+{\xi }_k}}F\left(T_k\right).$$

(46)

If ${\mathbf{c}}^{k+1}$ converges with

$$F\left(T_k\right)<\epsilon ,$$

then stop; otherwise, go to step (ii).

The above iteration process to determine T is basically to solve the nonlinear equation $F=\sqrt{{[x\left(T\right)-A]}^2+y^2\left(T\right)}=0$, which is the periodicity condition in the phase plane. The disadvantage of this iterative method is that it converges slowly and an extra parameter $\nu$ is needed. Upon comparing it to the non-iterative methods, one can appreciate the advantage of the first method in Section 3.1 and the second method in Section 3.2.

4. Analysis of Examples

4.1. Example 1: Mickens’ Oscillator

We consider the Mickens’ oscillator [37]:

$$\ddot{x}+x(1+{\dot{x}}^2)=0, x\left(0\right)=A, \dot{x}\left(0\right)=0.$$

(47)

In [37] the following exact integral formula was derived:

$$T=4A{\int }_0^1{\displaystyle \frac{dx}{\sqrt{exp\left[A^2(1-x^2)\right]-1}}}.$$

(48)

For this example,

$$\varphi \left(x\right)=\sqrt{exp(A^2-x^2)-1}$$

(49)

was derived in [21], which being inserted into Equation (9) can derive Equation (48).

In Equation (48) we divide the integral interval $[0, 1]$ into $N_0$ sub-intervals, and in practice we compute the integral of Equation (48) by applying the three-point Gaussian quadrature to each sub-interval. In Table 1, the periods computed from Equation (48) with different $N_0$ are compared, and the errors of periodicity conditions measured by $\sqrt{{[x\left(T\right)-A]}^2+{\dot{x}}^2\left(T\right)}$ are listed. When $N_0$ is increased, the error is reduced and T tends to a limiting value. However, it is hard to compute the limiting value because when $N_0$ is increased to a large value the computation cost is also more expensive. Even up to $N_0$ = 500,000 the error of periodicity conditions is still in the order of $9.97\times {10}^{-4}$, which is not very accurate. As mentioned, the loss of accuracy is due to the singularity of the integrand at $x=A$. So for saving the computational time, we will fix $N_0=2000$ in the computation of the period by using the exact integral formula.

Table 1. Comparing the periods with different values of $N_0$ for Equation (47) with $A=1$.

${\mathit{N}}_0$	500	1000	2000	5000	10,000	100,000	500,000
T	5.49569	5.50492	5.51144	5.51723	5.52015	5.52497	5.52620
Error	$3.15\times {10}^{-2}$	$2.23\times {10}^{-2}$	$1.58\times {10}^{-2}$	$9.97\times {10}^{-3}$	$7.05\times {10}^{-3}$	$2.23\times {10}^{-3}$	$9.97\times {10}^{-4}$

As shown in Equation (49) the exact value of $\varphi \left(0\right)$ is

$${\varphi }_e\left(0\right)=\sqrt{exp\left(A^2\right)-1}.$$

(50)

Table 2 compares the numerical value obtained by ${\varphi }_0=\varphi \left(0\right)=\sqrt{\phi \left(A\right)}$ by numerically integrating Equation (35) to that in Equation (50) for different N with $A=1$. $N=1000$ is sufficient for the high accuracy of ${\varphi }_0$.

Table 2. Comparing numerical and exact values of $\varphi \left(0\right)$ with $A=1$.

N	200	400	600	1000	2000
${\varphi }_0$	1.3108324944	1.3108324944	1.3108324944	1.3108324944	1.3108324944
$|{\varphi }_e\left(0\right)-{\varphi }_0|$	$2.88\times {10}^{-11}$	$1.80\times {10}^{-12}$	$3.54\times {10}^{-13}$	$4.60\times {10}^{-14}$	$4.89\times {10}^{-15}$

In Table 3, Err1 denotes the error of periodicity conditions for Equation (40) of the first method, Err2 denotes the error of periodicity conditions for Equation (44) of the second method, and Err3 denotes the error of periodicity conditions for Equation (48). Here we fix $N=1000$. It can be seen that the preservation of periodicity conditions is poor by using the exact period in Equation (48); however, the present methods in Section 3 with the optimal value of $W_0$ determined by Equation (31) for the first method, and $w_0$ for the second method can make significant improvements to the accuracy of periodicity conditions about seven to eight orders.

Table 3. Comparing the periods with different values of A for Equation (47).

A	0.5	1.0	1.5	2.0
$W_0$	0.14566546	0.056728558	0.024090724	0.0090669521
Equation (40)	6.08844891	5.52719985	4.69024721	3.76133883
Err1	$2.17\times {10}^{-10}$	$3.74\times {10}^{-10}$	$1.34\times {10}^{-9}$	$1.05\times {10}^{-9}$
$w_0$	0.01855325487	0.00754468288	0.00339580682	0.00135200508
Equation (44)	6.088448909	5.527199848	4.690247206	3.761338831
Err2	$7.93\times {10}^{-12}$	$2.89\times {10}^{-13}$	$3.82\times {10}^{-12}$	$1.15\times {10}^{-10}$
Equation (48)	6.07269167	5.51144258	4.67448989	3.74558144
Err3	$7.88\times {10}^{-3}$	$1.58\times {10}^{-2}$	$2.36\times {10}^{-2}$	$3.15\times {10}^{-2}$

By using Equation (48) to compute the period with fourth-order accuracy, as shown in the last column of Table 1, we need $N_0=500,000$, and in the Gaussian quadrature for each sub-interval we need three evaluations of functions. Therefore the total number of evaluations of functions is 1,500,000. By applying the interval reduction method (IRM) to find the optimal value of $W_0$, we need to apply the RK4 to integrate the ODEs approximately 1000 times as that estimated below Equation (31). For three ODEs in the first method, we need 3000 evaluations of functions if we take $N=1000$. Therefore, the total number of evaluations of functions for the first method is $3,000,000$. By applying the interval reduction method (IRM) to find the optimal value of $w_0$, we need to apply the RK4 to integrate the ODEs approximately 1000 times. For ODEs in the second method we need 2000 evaluations of functions if we take $N=1000$. Therefore, the total number of evaluations of functions for the second method is $2,000,000$. The computational cost for both methods is larger than that using Equation (48) to compute the period. However, it is deserved because the accuracy of the period can be raised from ${10}^{-4}$ to ${10}^{-10}$ for the first method and to ${10}^{-13}$ for the second method as shown in Table 3.

4.2. Example 2: Tapered Beam’s Oscillator

The free vibration of a tapered beam is governed by [38]:

$$\ddot{x}+{\displaystyle \frac{x+ax{\dot{x}}^2+b{x}^3}{1+a{x}^2}}=0, x\left(0\right)=A, \dot{x}\left(0\right)=0,$$

(51)

where $a>0$ and $b>0$ are constants.

By using He’s frequency-amplitude formula [38], one has

$$\omega =\sqrt{{\displaystyle \frac{4+3b{A}^2}{4+2a{A}^2}}}, T={\displaystyle \frac{2\pi }{\omega }}=2\pi \sqrt{{\displaystyle \frac{4+2a{A}^2}{4+3b{A}^2}}}.$$

(52)

Table 4 compares the errors of periodicity conditions obtained from Equations (40), (44) and (52). Here, we fix $N=1000$. It can be seen that the preservation of periodicity conditions is poor by using the period in Equation (52); however, the present methods in Section 3 with the optimal values of $W_0$ and $w_0$ determined by Equation (31) can make significant improvements to the accuracy of periodicity conditions approximately nine to ten orders.

Table 4. Comparing the periods with different values of A for Equation (51) with $a=b=1$.

A	0.5	1.0	1.5	2.0
$W_0$	0.1466520859	0.061884537568	0.033935975395	0.021119643912
Equation (40)	6.10956696	5.76252391	5.44617179	5.21048263
Err1	$6.40\times {10}^{-12}$	$8.31\times {10}^{-13}$	$6.49\times {10}^{-12}$	$6.38\times {10}^{-11}$
$w_0$	0.01864432055	0.00807389617	0.00452252842	0.00285479213
Equation (44)	6.109566963	5.762523908	5.446171795	5.210482627
Err2	$2.37\times {10}^{-12}$	$5.75\times {10}^{-13}$	$6.49\times {10}^{-12}$	$6.37\times {10}^{-11}$
Equation (52)	6.11560350	5.81709925	5.58708269	5.44139809
Err3	$3.02\times {10}^{-3}$	$5.46\times {10}^{-2}$	$2.12\times {10}^{-1}$	$4.68\times {10}^{-1}$

By means of Equation (8) the exact value of $\varphi \left(0\right)$ is

$${\varphi }_e\left(0\right)=\sqrt{A^2+{\displaystyle \frac{b{A}^4}{2}}}.$$

(53)

Table 5 compares the numerical value obtained by ${\varphi }_0=\varphi \left(0\right)=\sqrt{\phi \left(A\right)}$ by numerically integrating Equation (35) to Equation (53) for different N with $A=1$ and $a=b=1$. $N=1000$ is sufficient for the high accuracy of ${\varphi }_0$.

Table 5. Comparing numerical and exact values of $\varphi \left(0\right)$ with $A=1$ and $a=b=1$.

N	200	400	600	1000	2000
${\varphi }_0$	1.2247448713	1.2247448713	1.2247448713	1.2247448713	1.2247448713
$|{\varphi }_e\left(0\right)-{\varphi }_0|$	$4.55\times {10}^{-12}$	$2.85\times {10}^{-13}$	$5.60\times {10}^{-14}$	$7.33\times {10}^{-15}$	$1.11\times {10}^{-15}$

To test the sensitivity to the initial value $w_0$, we compare the period computed by Equation (44) of the second method for different values of $w_0$ in Table 6, where we fix $N=1000$, $A=1$, and $a=b=1$. It shows that these periods are not accurate upon comparing to the accurate one $T=5.762523908$ in Table 4. It is better to use the optimal value of $w_0$ determined by Equation (31) to compute the period. In general a trial and error method cannot obtain an accurate period.

Table 6. Comparing numerical and exact values of $\varphi \left(0\right)$ with $A=1$ and $a=b=1$.

${\mathit{w}}_0$	0	0.0001	0.001	0.01	0.1
Equation (44)	5.7427469821	5.7429919311	5.7451964719	5.7672418796	5.9876959564

4.3. Example 3

We consider a damped nonlinear oscillator [39]:

$$\ddot{x}+{\displaystyle \frac{kx}{1+c{\dot{x}}^2}}+bx=0, x\left(0\right)=A, \dot{x}\left(0\right)=0,$$

(54)

where k, c, and b are some constants. We fix $k=c=b=1$.

The following formula was derived in [39]:

$$\omega =\sqrt{{\displaystyle \frac{bc{A}^2-4+\sqrt{{(bc{A}^2-4)}^2+16c{A}^2(b+k)}}{2c{A}^2}}}, T={\displaystyle \frac{2\pi }{\omega }},$$

(55)

which is the same to that obtained by the homotopy perturbation method [40].

Table 7 compares the errors of periodicity conditions obtained from Equations (40), (44) and (55). Here, we fix $N=1000$. It can be seen that the preservation of periodicity conditions is poor by using the period in Equation (55); however, the present methods in Section 3 with the optimal values of $W_0$ and $w_0$ can make significant improvements to the accuracy of periodicity conditions approximately eight orders.

Table 7. Comparing the periods with different values of A for Equation (54) with $k=b=c=1$.

A	0.5	1.0	1.5	2.0
$W_0$	0.08379665879	0.04611492534864	0.0332632374835999	0.02650146305
Equation (40)	4.556823013	4.761520952	4.950289407	5.106510051
Err1	$4.63\times {10}^{-11}$	$1.82\times {10}^{-11}$	$4.27\times {10}^{-9}$	$1.60\times {10}^{-9}$
$w_0$	0.01036419015	0.00555505229	0.00390180798	0.00303558286
Equation (44)	4.556823013	4.761520952	4.950289408	5.106510052
Err2	$2.17\times {10}^{-13}$	$3.56\times {10}^{-12}$	$7.73\times {10}^{-13}$	$1.60\times {10}^{-12}$
Equation (55)	4.56533883	4.81677061	5.06904073	5.28350800
Err3	$8.52\times {10}^{-3}$	$1.10\times {10}^{-1}$	$3.49\times {10}^{-1}$	$6.61\times {10}^{-1}$

As shown in Section 3.1 and Section 3.2 the second method is simpler than the first method. Both methods need to compute ${\varphi }_0=\varphi \left(0\right)=\sqrt{\phi \left(A\right)}$ by numerically integrating Equation (35), and determine $W_0$ and $w_0$ by Equation (31). The computational cost is quite saving because the iteration is not required for both methods. Most time is spent to find $W_0$ and $w_0$ by Equation (31), which is carried out by the interval reduction method (IRM). Through approximately a seven-to-ten-times reduction of the interval, very precise values of $W_0$ and $w_0$ can be obtained. In the RK4 we take $N=1000$ such that the error of integration is in the order of ${10}^{-12}$, which is sufficient to obtain highly accurate period. Moreover, as shown in Table 3, Table 4 and Table 7 for examples 1–3, the second method is more accurate than the first method. For these two reasons we prefer the second method rather than the first method. For the next two examples we only apply the second method to compute the period.

4.4. Example 4: A Restrained Cantilever Beam’s Oscillator

The oscillation of a restrained cantilever beam is governed by [41]:

$$\ddot{x}+x+{\displaystyle \frac{(x+2x^3){\dot{x}}^2}{1+x^2+x^4}}=0, x\left(0\right)=A, \dot{x}\left(0\right)=0.$$

(56)

By using the harmonic balance method [42], one has

$$T={\displaystyle \frac{2\pi }{\omega }}=2\pi \sqrt{{\displaystyle \frac{8+4A^2+3A^4}{8+6A^2+5A^4}}}.$$

(57)

Table 8 compares the errors of periodicity conditions obtained from Equations (44) and (57). It can be seen that the preservation of periodicity conditions is poor by using the period in Equation (57) when A is large; however, the second method in Section 3.2 with the optimal value of $w_0$ determined by Equation (31) can make a significant improvement of the accuracy of periodicity conditions about ten orders.

Table 8. Comparing the periods with different values of A for Equation (56).

A	0.5	0.9	1.0
$w_0$	0.461949308	0.524118214	0.178196230
Equation (44)	6.070975486	5.591743766	5.449380849
Err1	$3.6\times {10}^{-13}$	$2.19\times {10}^{-13}$	$2.72\times {10}^{-13}$
Equation (57)	6.07979183	5.68387919	5.58275665
Err2	$4.62\times {10}^{-3}$	$8.31\times {10}^{-2}$	$1.34\times {10}^{-1}$

4.5. Example 5

We consider [43]:

$$\ddot{x}+{\displaystyle \frac{\kappa x{\dot{x}}^2+x^3-x}{1+\kappa x^2}}=0, x\left(0\right)=A, \dot{x}\left(0\right)=0,$$

(58)

where $\kappa >0$ is a constant.

Under the assumption $A>2/\sqrt{3}$, one has [43]

$$T={\displaystyle \frac{2\pi }{\omega }}=2\pi \sqrt{{\displaystyle \frac{4+2\kappa A^2}{3A^2-4}}}.$$

(59)

Table 9 compares the errors of periodicity conditions obtained from Equations (44) and (59). It can be seen that the preservation of periodicity conditions is poor by using the period in Equation (59) when A is large; however, the second method in Section 3.2 with the optimal value of $w_0$ determined by Equation (31) can make a significant improvement of the accuracy of periodicity conditions about ten orders.

Table 9. Comparing the periods with different values of A for Equation (58) with $\kappa =2$.

A	1.5	2.0	2.5
$w_0$	0.039116137	0.008564667	0.003914656
Equation (44)	14.34770077	9.337913851	7.951851408
Err1	$2.58\times {10}^{-12}$	$1.75\times {10}^{-10}$	$5.13\times {10}^{-9}$
Equation (59)	13.6610851	9.93458827	8.67587976
Err2	$2.41\times {10}^{-1}$	$4.15\times {10}^{-1}$	$8.07\times {10}^{-1}$

5. The Oscillation Amplitude and Period for the Liénard Equation

We consider the Liénard equation [1]:

$$\left\{\begin{array}{c}\ddot{x}+g\left(x\right)\dot{x}+h\left(x\right)=0,\hfill \\ x\left(0\right)=A, \dot{x}\left(0\right)=0, x\left(T\right)=A, \dot{x}\left(T\right)=0,\hfill \end{array}\right.$$

(60)

where $A>0$ and $T>0$ are both unknown constants. Equation (60) constitutes a special type boundary value problem with an unknown endpoint T of a time interval $[0,T]$, and also an unknown initial value A.

Inserting $f(x,\varphi )=g\varphi +h$ into Equation (6) yields

$${\displaystyle \frac{d\varphi \left(x\right)}{dx}}=-g\left(x\right)-{\displaystyle \frac{h\left(x\right)}{\varphi \left(x\right)}}, \varphi \left(A\right)=0.$$

(61)

It is a singular first-order ODE in the interval $x\in [0,A]$, because of $\varphi \left(A\right)=0$. The existence of $\varphi \left(x\right)$ cannot be guaranteed, such that the method in Section 3 is not applicable for seeking the period of the Liénard equation. Moreover, because A and T are two unknown constants, this periodic problem is more difficult than that in Section 2.

We introduce a dimensionless time $\eta$ and a dimensionless displacement z by

$$\eta ={\displaystyle \frac{t}{T}},$$

(62)

$$x^{\prime }\left(\eta \right)=T\dot{x}, x^{″}\left(\eta \right)=T^2\ddot{x},$$

(63)

$$\begin{array}{c}z\left(\eta \right)={\displaystyle \frac{x\left(\eta \right)}{A}}, z^{\prime }\left(\eta \right)={\displaystyle \frac{x^{\prime }\left(\eta \right)}{A}}={\displaystyle \frac{T\dot{x}}{A}}, z^{″}\left(\eta \right)={\displaystyle \frac{x^{″}\left(\eta \right)}{A}}={\displaystyle \frac{T^2\ddot{x}}{A}},\hfill \end{array}$$

(64)

where $x^{\prime }\left(\eta \right)=dx\left(\eta \right)/d\eta$, $x^{″}\left(\eta \right)=d^{2}x\left(\eta \right)/d{\eta }^2$, $z^{\prime }\left(\eta \right)=dz\left(\eta \right)/d\eta$, and $z^{″}\left(\eta \right)=d^{2}z\left(\eta \right)/d{\eta }^2$.

So far, Equation (60) changes to

$$\left\{\begin{array}{c}{z}^{″}\left(\eta \right)+Tg\left(Az\right)z^{\prime }\left(\eta \right)+T^2{\displaystyle \frac{h\left(Az\right)}{A}}=0,\hfill \\ z\left(0\right)=1, z^{\prime }\left(0\right)=0, z\left(1\right)=1, z^{\prime }\left(1\right)=0.\hfill \end{array}\right.$$

(65)

Theorem 3.

For the Liénard Equation (60) the period of the periodic orbit can be computed by

$$T=\sqrt{{\displaystyle \frac{{\int }_0^1{z}^{\prime }{\left(\eta \right)}^{2}d\eta }{{\int }_0^{1}z\left(\eta \right)\frac{h\left(Az\right(\eta \left)\right)}{A}d\eta }}}.$$

(66)

Proof. 

It is obvious that

$$z\left(\eta \right)z^{″}\left(\eta \right)={\left[z\left(\eta \right)z^{\prime }\left(\eta \right)\right]}^{\prime }-z^{\prime }{\left(\eta \right)}^2;$$

(67)

taking the product of $z\left(\eta \right)$ to the first one in Equation (65) and using Equation (67) yields

$${\left[z\left(\eta \right)z^{\prime }\left(\eta \right)\right]}^{\prime }-z^{\prime }{\left(\eta \right)}^2+Tz\left(\eta \right)g\left(Az\left(\eta \right)\right)z^{\prime }\left(\eta \right)+T^{2}z\left(\eta \right){\displaystyle \frac{h\left(Az\right(\eta \left)\right)}{A}}=0.$$

(68)

Integrating it with respect to $\eta$ from $\eta =0$ to $\eta =1$, considering the second one in Equation (65), and noting that

$$T{\int }_0^{1}z\left(\eta \right)g\left(Az\left(\eta \right)\right)z^{\prime }\left(\eta \right)d\eta =T{\int }_1^{1}z\left(\eta \right)g\left(Az\left(\eta \right)\right)dz\left(\eta \right)=0,$$

renders Equation (66).

By the Levinson-Smith theorem [44] for the existence of a non-constant periodic solution of Equation (60), one of the necessary conditions is $xh\left(x\right)>0, \forall x\ne 0$. By this way, the above T is always existent. As shown by Equation (66) the damping term $g\left(x\right)\dot{x}$ gives no explicit influence on the value of T. However, z and $z^{\prime }\left(\eta \right)$ are influenced by g. □

Equation (66) in Theorem 3 implies that T is an implicit function of A. Let $v_1=z$, $v_2=z^{\prime }$, and

$$\begin{array}{c}{v}_3\left(\eta \right):={\int }_0^{\eta }{z}^{\prime }{\left(\xi \right)}^{2}d\xi ,\hfill \end{array}$$

(69)

$$\begin{array}{c}{v}_4\left(\eta \right):={\int }_0^{\eta }z\left(\xi \right){\displaystyle \frac{h\left(Az\right(\xi \left)\right)}{A}}d\xi .\hfill \end{array}$$

(70)

Then, the period T derived in Equation (66) for Equation (60) can be written as

$$T=\sqrt{{\displaystyle \frac{v_3\left(1\right)}{v_4\left(1\right)}}}.$$

(71)

By means of $v_1\left(\eta \right)=z\left(\eta \right)$, $v_2\left(\eta \right)=z^{\prime }\left(\eta \right)$ and from Equations (65), (69) and (70), we have four first-order ODEs:

$$\begin{array}{c}{v}_1^{\prime }=v_2, v_1\left(0\right)=1,\hfill \\ v_2^{\prime }=-Tg\left(A{v}_1\right)v_2-T^2{\displaystyle \frac{h\left(A{v}_1\right)}{A}}, v_2\left(0\right)=0,\hfill \\ v_3^{\prime }=v_2^2, v_3\left(0\right)=0,\hfill \\ v_4^{\prime }={\displaystyle \frac{v_{1}h\left(A{v}_1\right)}{A}}, v_4\left(0\right)=0,\hfill \end{array}$$

(72)

which can be deemed as an initial value problem (IVP) for $v_k, k=1,\dots ,4$.

Consequently, the iteration method is (i) giving A, $T_0$, $ϵ$, and $\Delta \eta =1/N$; (ii) for $k=0,1,2,\dots$, RK4 integrating Equation (72) with $T=T_k$ up to $\eta =1$, and taking

$$T_{k+1}=\sqrt{{\displaystyle \frac{v_3\left(1\right)}{v_4\left(1\right)}}}.$$

(73)

If the sequence of $T_{k+1}$ converges,

$$|T_{k+1}-T_k|<ϵ,$$

(74)

then stop; otherwise, go to step (ii).

The above process is carrying out for each A in a range $A\in [a_0,b_0]$ and we update $T_0=T_k$ obtained in the previous step, and then we pick up the optimal value of A by

$$\underset{A\in [a_0,b_0]}{min}\sqrt{{[x\left(T\right)-A]}^2+{\dot{x}}^2\left(T\right)},$$

(75)

where x and $\dot{x}$ are obtained by integrating Equation (60) with

$$\dot{x}=y, \dot{y}=-h\left(x\right)-g\left(x\right)y, x\left(0\right)=A, y\left(0\right)=0.$$

(76)

The interval reduction method (IRM) is adopted to select a suitable range of $[a_0,b_0]$ in Equation (75).

Remark 3.

The integral formula in Equation (66) for the Liénard Equation (60) was derived at the first time, which is exact in the sense that when the exact solution is inserted into the integral formula the exact value of the period can be obtained. For the Liénard Equation (60) the exact solution is in general not available; hence, we employ the numerical integration method in Equations (72)–(75) to realize the integral-type formula. The iteration is convergent fast because they are based on the exact integral formula in Equation (66).

6. Examples Testing for the Liénard Equation

In this section we apply the above iteration method to determine the oscillation amplitude and period for some examples of Equation (60).

6.1. Example 6

We consider [45]:

$$\ddot{x}+x+\mu (x^2-1)\dot{x}=0, x\left(0\right)=A, \dot{x}\left(0\right)=0,$$

(77)

where A is an unknown constant. According to [45], $A=2.01989$ for $\mu =2$.

In Equation (74), we take $ϵ={10}^{-8}$ as the convergence criterion. With $[a_0,b_0]=[2.01988872,2.01988873]$, we divide the interval into 100 sub-intervals. For each A in the sub-interval we carry out the iterations in Equations (72)–(74) to compute T. Then, we save the minimal one according to Equation (75). The convergence is very fast with ten iterations at the first sub-interval, and in the sequential sub-intervals it converges with one iteration. Because $T_0$ is updated, the subsequent iteration converges very fast with one iteration.

By using the iteration method we obtain $A=2.0198887241$ and $T=7.62988181$. Figure 1 plots the periodic orbit of the van der Pol equation with the absolute error $2.74\times {10}^{-6}$ of periodicity conditions.

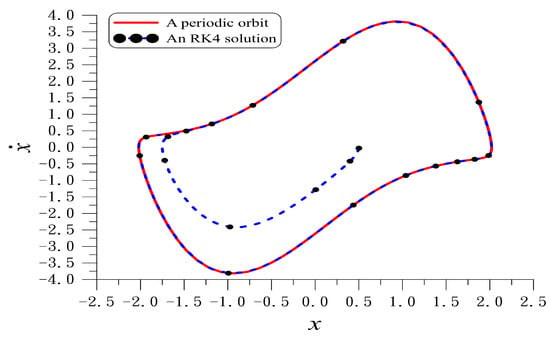
Figure 1. For example 6 of the van der Pol equation showing a periodic orbit and comparing the periodic solution with that computed by RK4 to the limit cycle.

Most researchers in the discussion of the Liénard equation adopt the following system [45,46]:

$$\dot{x}=y-F\left(x\right), \dot{y}=-h\left(x\right), x\left(0\right)=A, y\left(0\right)=0,$$

(78)

where

$$F\left(x\right)={\int }_0^{x}g\left(s\right)ds.$$

(79)

For the van der Pol equation $F\left(x\right)=\mu (x^3/3-x)$, and we have

$$\dot{x}=y-\mu \left({\displaystyle \frac{x^3}{3}}-x\right), \dot{y}=-x, x\left(0\right)=A, y\left(0\right)=0.$$

(80)

For this system we must check the following condition to determine A and T:

$$\underset{A\in [a_0,b_0]}{min}\sqrt{{[x\left(T\right)-A]}^2+y^2\left(T\right)},$$

(81)

where x and y are obtained by integrating Equation (80).

By using the iteration method we obtain $A=1.813672$ and $T=7.63514388$. Figure 2 plots the periodic orbit of the van der Pol equation with the absolute error $8.93\times {10}^{-3}$ of periodicity conditions. Two drawbacks of the second formulation are that A is not the maximum amplitude and the error of periodicity conditions is increased.

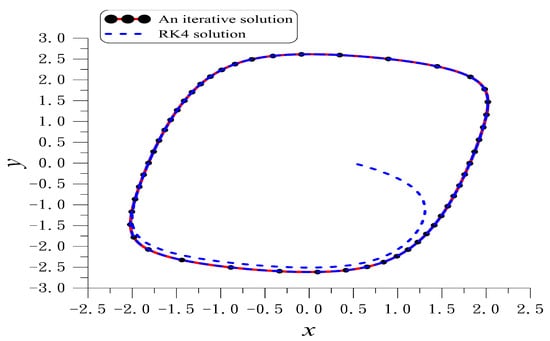
Figure 2. For example 6 of the van der Pol equation showing a periodic orbit for the second system and comparing it with that computed by RK4 to the limit cycle.

6.2. Example 7

We consider [46]:

$$\ddot{x}+x+(0.8-4x^2+1.6x^4)\dot{x}=0, x\left(0\right)=A, \dot{x}\left(0\right)=0,$$

(82)

where A is an unknown constant.

By using the iteration method we obtain $A=1.9992596$ and $T=6.80510034$. Figure 3 plots the periodic orbit with the absolute error $1.6\times {10}^{-6}$ of periodicity conditions. A smaller periodic orbit is also plotted with $A=1.0033976$, $T=6.47573456$, and the absolute error of periodicity conditions is $1.6\times {10}^{-5}$.

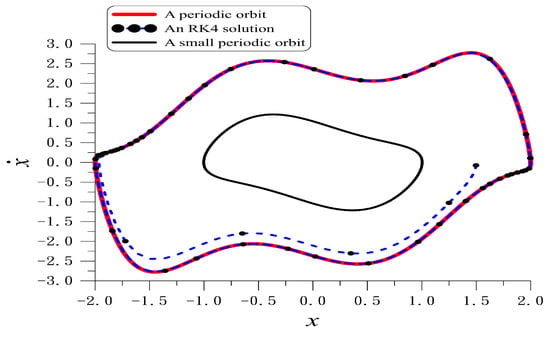
Figure 3. For example 7 showing a periodic orbit and comparing the periodic solution with that computed by RK4 to the limit cycle, and a smaller periodic orbit.

6.3. Example 8

We consider [46]:

$$\ddot{x}+x+(5x^4-3\mu x^2+1)\dot{x}=0, x\left(0\right)=A, \dot{x}\left(0\right)=0,$$

(83)

where A is an unknown constant. When $\mu >2.5$, there exist two limit cycles [47]. We take $\mu =2.6$.

By using the iteration method we obtain $A=1.571265$ and $T=6.97206374$. Figure 4a plots the periodic orbit with the absolute error $1.54\times {10}^{-4}$ of periodicity conditions.

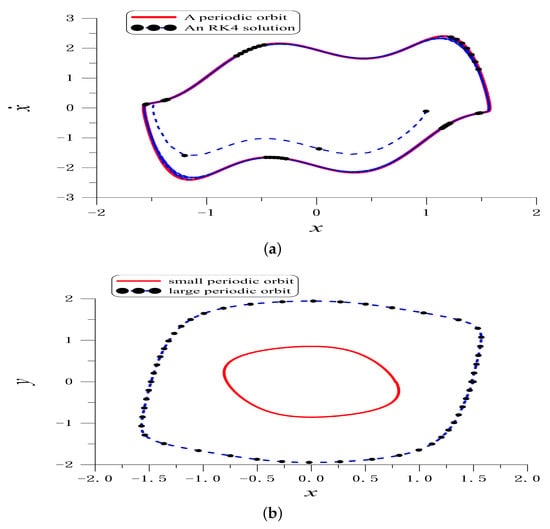
Figure 4. For example 8 showing (a) a periodic orbit and comparing the periodic solution with that computed by RK4 to the limit cycle, and (b) two periodic orbits in the second system.

Equation (83) is recast to the second system by

$$\left\{\begin{array}{c}\dot{x}=y-x^5+\mu x^3-x,\hfill \\ \dot{y}=-x,\hfill \\ x\left(0\right)=A, y\left(0\right)=0.\hfill \end{array}\right.$$

(84)

Figure 4b plots two periodic orbits with $A=1.5$ and $T=6.97318909$ for larger one, and $A=0.7828$ and $T=6.6$ for smaller one.

6.4. Example 9

We consider

$$\left\{\begin{array}{c}\dot{x}=y-{\displaystyle \frac{8}{25}}{x}^5+{\displaystyle \frac{4}{3}}{x}^3+{\displaystyle \frac{4}{5}}x,\hfill \\ \dot{y}=-x,\hfill \\ x\left(0\right)=A, y\left(0\right)=0.\hfill \end{array}\right.$$

(85)

By using the iteration method we obtain $A=2.176061524$ and $T=10.14155437$. Figure 5 plots the periodic orbit with the absolute error $1.42\times {10}^{-4}$ of periodicity conditions. The RK4 solution is starting from $x\left(0\right)=-2$ and $y\left(0\right)=7$, and it fast tends to the limit cycle with the maximum value of x to be $maxx=2.4515651228$.

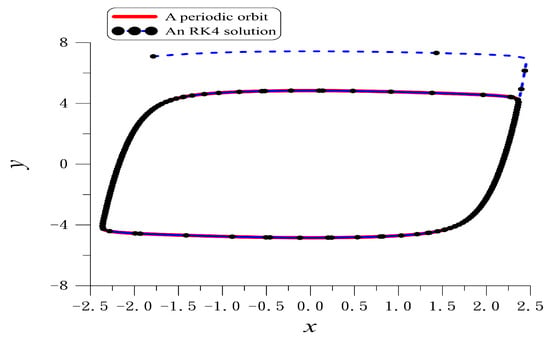
Figure 5. For example 9 showing a periodic orbit and comparing the periodic solution with that computed by RK4 to the limit cycle.

7. Conclusions

A theoretical foundation of the integral-type formula was set up for the NCNO, which has the first integral. A weight function was introduced so that a generalized integral conservation law was derived for an integral-type formula of the period in Equation (24). Correspondingly, we derived two non-iterative numerical methods for quickly computing the period. Five examples exhibited high accuracy of the proposed methods.

We demonstrated the non-existence of the first integral for the Liénard equation. Then, we turned to the periodic problem of the Liénard equation, involving the van der Pol equation, and derived the integral formula of period for the limit cycle in terms of a dimensionless displacement in the dimensionless time domain in Equation (66). An iterative numerical method was developed with four examples for testing the accuracy of the proposed method to compute both the unknown values of oscillation amplitude and period.

In summary, the present paper is equipped with several novelties and significant contributions, which are highlighted below.

1.

We have transformed the first-order nonlinear ODE used to derive the potential function $\varphi \left(x\right)$ to an initial value problem. The initial value $\varphi \left(0\right)$ can be determined very accurately.

2.

A novel integral-type period formula involved a weight function and its initial value for the NCNO having the first integral was derived, which is equivalent to the exact integral formula. The initial value of weight function was determined to meet the periodicity conditions and a very accurate period can be obtained.

3.

The derivation of two non-iterative methods through the integration of two or three first-order ODEs is mathematically sound and reduces computational complexity.

4.

To improve the singularities and minimization of error via weight function adjustment is both innovative and well-justified.

5.

For the NCNO without having the first integral, we derived an integral-type period formula for the non-conservative Liénard equation in the dimensionless time domain.

6.

An iterative numerical method was developed to compute the amplitude and period of the Liénard equation. Even for the problem with multiple limit cycles the amplitude and period can be computed very fast.

7.

Results showed strong agreement with known amplitudes and periods, even for systems with one or two limit cycles, confirming the method’s accuracy and applicability.

8.

The periodic problem for the third-order NCNO and more complex dynamical systems may be pursued in the near future by developing the corresponding integral-type and iterative method to determine the period.

Our results obtained are not applicable to the systems of Equation (1) of a general form, when the existence of a periodic solution is not guaranteed. The numerical methods in Section 3.1 and Section 3.2 are restricted to the systems with periodic solutions, which satisfy Equation (1) and exist the first-integral. The numerical method in Section 5 is restricted to the Liénard equation. For other dynamical systems with periodic solutions and limit cycles, the integral-type and iterative method to depict the oscillatory behavior will be pursued in the future.