Numerical Study of Asymmetry in Blast Pressure Propagation and Rock Damage Under Eccentric Decoupled Charges

Abstract

The eccentric decoupled charge (EDC) is widely used in blasting engineering, but the combined effects of decoupling ratio, coupling medium, and explosive position (eccentricity coefficient) on blast pressure propagation and rock damage remain insufficiently understood. In this study, the RHT material model in LS-DYNA is calibrated using fracture patterns from laboratory tests, and a series of cubic single-hole numerical models is established to examine the influence of charging parameters on pressure evolution and rock damage. The results show that EDC blasting generates a clear eccentricity effect in pressure propagation: the coupled side exhibits a higher peak pressure and faster loading, while the decoupled side experiences delayed wave arrival and lower peak pressure. This asymmetry intensifies with increasing decoupling ratio and eccentricity coefficient. Pressure decay follows a nonlinear power function, with attenuation in the axial direction being greater than in the radial direction. The total damage volume decreases with increasing decoupling ratio, but the eccentricity of the damage pattern becomes more evident, especially in the crushed zone. Different coupling media influence this effect: air/sand coupling readily produces eccentricity effects, while water coupling requires a larger decoupling ratio to do so. From an energy perspective, the evolving asymmetry in fracture behavior is closely linked to the redistribution of internal energy between the coupled and decoupled sides, as governed by the charging configuration.

1. Introduction

The drilling and blasting method is widely employed in slope excavation, tunnel construction, and other blasting applications due to its cost-effectiveness and operational efficiency [1,2,3,4]. However, this method often leads to damage in the surrounding rock, resulting in both over-excavation and under-excavation [5]. Such damage compromises the mechanical integrity and stability of the rock mass, thereby increasing support costs and extending the construction period [6]. To control blasting-induced damage and achieve a smoother excavation profile, controlled blasting techniques such as smooth blasting are commonly adopted [7,8]. Among these techniques, radial decoupled charges using air, sand, or water as the coupling medium are frequently applied. However, under the influence of gravity, the explosive column tends to shift from the center of the borehole and attach to one side of the borehole wall. This phenomenon is referred to as the eccentric decoupled charge (EDC) condition [9]. Detonation under EDC conditions causes an uneven distribution of explosive energy around the borehole, weakening the effectiveness of contour control, increasing the risks of over- and under-excavation, and potentially leading to excessive damage to the reserved rock mass, ultimately threatening its overall stability [10]. Therefore, investigating the blasting behavior under EDC conditions is of great significance for improving the performance and reliability of blasting operations.

Under EDC conditions, variations in the distance between the borehole wall and the center of the charge lead to significant differences in pressure distribution, with the high-pressure region shifting toward the eccentric side of the explosive [11]. Previous studies [12,13] have demonstrated that an increase in decoupling ratio results in an exponential rise in the maximum-to-minimum pressure ratio along the borehole wall, indicating potential for directional crack control. Follow-up research [14,15] further confirmed that EDC-induced fractures exhibit pronounced asymmetry, with the crushed zone markedly concentrated on the eccentric side of the charge. Moreover, increasing the decoupling coefficient effectively reduces the extent of both the crack and crushed zones. In summary, compared with traditional concentric loading, EDC offers notable advantages in promoting directional fracture control and improving excavation efficiency [16]. However, it should be noted that most of the above studies have primarily focused on air as the coupling medium, without adequately considering commonly used alternatives such as sand and water, nor accounting for the influence of decoupling ratio when these media are involved.

The decoupling ratio and coupling medium are two critical factors influencing the performance of decoupled charge blasting [17]. Among them, air, sand, and water are the most commonly used filling media in engineering practice. Air, due to its high compressibility and low wave impedance, leads to low efficiency in transferring explosive energy to the surrounding rock. Consequently, air coupling is effective in reducing excessive fragmentation near the blast hole and mitigating damage to the reserved rock mass [18,19]. In contrast, sand is a porous material whose compressive strength increases markedly with volumetric strain. When subjected to explosive loading, the sand undergoes rapid compaction and forms a consolidated layer that adheres to the borehole wall, thereby enhancing its ability to transmit stress from the detonation products [20]. Compared with air and sand, water coupling causes less energy dissipation, enabling more efficient energy transfer to the rock, which results in more uniform fragmentation and a larger damage zone [21,22,23]. Based on these differences, Li et al. [23] proposed a fracture control blasting method utilizing dual air–water coupling to take advantage of the distinct energy transmission characteristics of different coupling media. These physical differences suggest that the selection of coupling medium should correspond to specific engineering objectives, such as maximizing rock fragmentation or minimizing blast-induced damage. Nevertheless, most existing studies have not concurrently examined the effects of decoupling ratio and coupling medium in their analyses.

To address this gap, some researchers have attempted to simultaneously investigate the effects of decoupling ratio and coupling medium on blasting performance. For example, Chi et al. [24] examined how the decoupling ratio influences fragment size in physical experiments using water and air as coupling media, and found that smaller decoupling ratios combined with water coupling significantly reduced fragment size. In contrast, Yang et al. [25] integrated LS-DYNA simulations with field tests to compare stress attenuation patterns using air and rubber media under varying coupling coefficients, revealing the critical role of wave impedance differences in energy transfer. Huo et al. [26] further investigated initial borehole wall pressure characteristics and confirmed that both peak pressure and loading rate decrease with increasing decoupling ratio, and that both values are significantly higher under water coupling than under air coupling. However, most of the above studies relied on simplified two-dimensional models or concentric uncoupled charge assumptions. These simplifications fail to capture the effects of explosive position, charge length, and stemming conditions in realistic three-dimensional blasting scenarios. Li et al. [27] emphasized that two-dimensional models are inadequate for accurately reproducing the dynamic fracture processes and damage patterns in rock masses under blasting loads, indicating the necessity of three-dimensional analysis. In practice, the eccentricity coefficient, decoupling ratio, and coupling medium jointly govern the spatial distribution of explosive energy and the resulting fracture asymmetry. For instance, the same eccentricity can lead to very different pressure and damage patterns depending on the decoupling ratio and the coupling medium. Therefore, it is necessary to consider these factors together rather than separately. At the same time, only a limited number of works have explicitly focused on eccentric decoupled charges, and even those studies noted that research in this area remains relatively scarce compared with conventional concentric blasting [11,28]. Existing investigations have usually treated decoupling ratio, coupling medium, and eccentricity separately, whereas in practice these factors jointly govern the spatial distribution of explosive energy and the resulting fracture asymmetry.

Recently, Xu et al. [11] investigated the effects of different coupling media on the damage characteristics of EDC at a specific decoupling ratio (20/7) through field experiments and three-dimensional numerical simulations, and found that sand coupling produced the most pronounced directional damage effect under the given conditions. Building upon these findings, the present study develops a validated three-dimensional LS-DYNA model to systematically investigate how decoupling ratio, coupling medium (air, sand, water), and explosive eccentricity together affect pressure evolution and rock damage. An additional energy-based analysis is carried out to interpret the mechanism of fracture asymmetry. The results are expected to provide a clearer understanding of asymmetric blasting behavior and offer references for improving contour control and reducing unwanted damage in engineering practice. In particular, this study provides practical guidance on selecting appropriate decoupling ratios and coupling media, as well as optimizing explosive placement to achieve efficient excavation while minimizing damage to the reserved rock mass.

2. Numerical Model and Numerical Calibration

2.1. Blasting Tests

In the blasting test, a rectangular concrete block measuring 250 mm × 250 mm × 150 mm was used, with a centrally drilled borehole of 20 mm diameter and 150 mm depth. The specimen had a density of 2162 kg·m⁻³, a Poisson’s ratio of 0.28, a longitudinal wave velocity of 3525 m·s⁻¹, a transverse wave velocity of 1911 m·s⁻¹, a uniaxial compressive strength of 26.85 MPa, a tensile strength of 2.59 MPa, and an elastic modulus of 21.3 GPa. The charge, with a radius of 7 mm and a length of 20 mm, corresponded to a decoupling ratio of 20/7. Air/sand/water served as the coupling media in separate tests. Both the top and bottom of the borehole were sealed with 40 mm of soil, as illustrated in Figure 1. After blasting, blast-induced cracks on the top surface of the specimen under EDC conditions with different coupling media were extracted using image recognition techniques, as shown in Figure 2.

2.2. Numerical Model

To ensure the reliability of the simulation results, a three-dimensional finite element model replicating the geometry of the test specimen was developed to reproduce the crack patterns observed after the physical explosion test, as shown in Figure 3. Due to the close contact between the explosive and the surrounding rock in the EDC configuration, generating a stable mesh was challenging. As a result, the explosive was modeled using the initial volume fraction method [29,30], which defined the explosive via the keyword *INITIAL_VOLUME_FRACTION_GEOMETRY, with the coupling media serving as the background material. Stress-free boundaries were applied to replicate the laboratory setup, where the concrete specimens were also tested under free surfaces. All simulations employed eight-node hexahedral solid elements with reduced integration (Solid 164), which are widely used in blasting and impact simulations. The rock and stemming were modeled using the Lagrangian algorithm, while the explosive, coupling medium, and air domain were modeled using the Arbitrary Lagrange Euler (ALE) algorithm to avoid large deformation [31]. The fluid–solid interaction was implemented using the command CONSTRAINED_LAGRANGE_IN_SOLID. The total simulation time for each blasting case was set to 240 μs, which was sufficient for the pressure propagation and fracture patterns to fully develop and stabilize. For subsequent analyses, the model was divided into two parts by the YZ plane (x = 0), with x > 0 defined as the coupled side and x < 0 as the decoupled side. The material parameters for the rock, explosive, coupling media, and stemming are summarized below.

2.2.1. Material Model for Rock

LS-DYNA provides a widely used constitutive model known as the RHT model for simulating the behavior of rock under explosive loading. Compared with the HJC model, the RHT model incorporates three distinct limit surfaces: the elastic limit surface, the failure surface, and the residual strength surface [32,33]. It is classified as a tensile–compressive damage model [34]. Previous studies have shown that the RHT model can effectively simulate the full response process of rock, concrete, and similar materials under explosive loading [35,36,37]. This includes the elastic stage, damage evolution, and final failure under blast conditions. Therefore, the RHT model is well suited for studying the dynamic response of concrete under explosive loading and provides more accurate simulation results.

The RHT model consists of a p-α equation of state and an intrinsic constitutive equation, and includes 38 parameters. The density ρ_r = 2162 kg·m⁻³, uniaxial compressive strength f_c = 26.85 MPa, and tensile strength f_t = 2.59 MPa were obtained from laboratory tests. The shear modulus was calculated based on elastic wave theory using the expression $G=E/\left[2\right(1+\mathsf{\nu }\left)\right]$, in which Young’s modulus E was 21.3 GPa, and ν is Poisson’s ratio. The remaining parameters were determined through theoretical calculations or obtained from the published literature, as detailed below.

Strain Rate Parameters

Strain rate is a crucial indicator that affects the strength of rock. In the RHT model, the strain rate dependence is given by

$$F_{\mathrm{r}}({\dot{\epsilon }}_{\mathrm{p}})=\left\{\begin{array}{ccc}({\dot{\epsilon }}_{\mathrm{p}}/{\dot{\epsilon }}_0^{\mathrm{t}}{)}^{{\beta }_{\mathrm{t}}}& & P\le -f_{\mathrm{t}}/3\\ {\displaystyle \frac{P+f_{\mathrm{t}}/3}{f_{\mathrm{c}}/3+f_t/3}}({\dot{\epsilon }}_{\mathrm{p}}/{\dot{\epsilon }}_0^{\mathrm{c}}{)}^{{\beta }_{\mathrm{c}}}-& {\displaystyle \frac{P-f_{\mathrm{t}}/3}{f_{\mathrm{c}}/3+f_{\mathrm{t}}/3}}({\dot{\epsilon }}_{\mathrm{p}}/{\dot{\epsilon }}_0^{\mathrm{c}}{)}^{{\beta }_{\mathrm{t}}}& -{\displaystyle \frac{f_{\mathrm{t}}}{3}}<P<{\displaystyle \frac{f_{\mathrm{t}}}{3}}\\ ({\dot{\epsilon }}_{\mathrm{p}}/{\dot{\epsilon }}_0^{\mathrm{c}}{)}^{{\beta }_{\mathrm{c}}}& & P\ge f_{\mathrm{t}}/3\end{array}\right.$$

(1)

where F_r($\dot{{\epsilon }_p}$) denotes the strain strength factor; $\dot{{\epsilon }_{\mathrm{p}}}$ is the strain rate, and P is the pressure, defined as $P=({\sigma }_1+{\sigma }_2+{\sigma }_3)/3$. The reference strain rates for compression and tension are $\dot{{\epsilon }_{\mathrm{c}}^0}$ = 3.0 × 10⁻⁵ s⁻¹ and $\dot{{\epsilon }_{\mathrm{t}}^0}$ = 3.0 × 10⁻⁶ s⁻¹, respectively. The material constants β_c and β_t, corresponding to compression and tension, respectively, are used in the following equations [33]:

$${\beta }_{\mathrm{c}}={\displaystyle \frac{4}{20+3f_{\mathrm{c}}}},{\beta }_{\mathrm{t}}={\displaystyle \frac{2}{20+f_{\mathrm{c}}}}$$

(2)

The values of β_c and β_t are set to 0.04 and 0.043, respectively.

Failure Surface Parameters

The failure surface parameters A and N can be determined by the following equation:

$${\sigma }_{\mathrm{f}}^{*}(P^{*},F_{\mathrm{r}})=A{\left(P^{*}-F_{\mathrm{r}}/3+(A/F_{\mathrm{r}}{)}^{-1/N}\right)}^N,\hspace{1em}3P^{*}\ge F_{\mathrm{r}}$$

(3)

where ${\sigma }_{\mathrm{f}}^{*}(P^{*},F_{\mathrm{r}})$ is the normalized strength relative to the compressive strength, ${\sigma }_{\mathrm{f}}^{*}={\displaystyle \frac{{\sigma }_{\mathrm{f}}}{f_{\mathrm{c}}}}$; $P^{*}$ is the normalized pressure, $P^{*}={\displaystyle \frac{P}{f_{\mathrm{c}}}}$; and A and N are the failure surface parameters. In the study, the parameters of A = 2.506 and N = 0.702 are obtained from [38].

Damage Parameters

The damage variable D, which is accumulated with plastic strain, is given as

$$D=\sum {\displaystyle \frac{\mathsf{\Delta }{\epsilon }_{\mathrm{P}}}{{\epsilon }_{\mathrm{P}}^{\mathrm{f}}}}$$

(4)

where $\mathsf{\Delta }{\epsilon }_{\mathrm{P}}$ is the effective plastic strain increment, ${\epsilon }_{\mathrm{P}}^{\mathrm{f}}$ is the plastic strain to failure under pressure P and expressed as

$${\epsilon }_{\mathrm{P}}^{\mathrm{f}}=D_1(P^{*}-(1-D)P_{\mathrm{t}}^{*}{)}^{D_2}$$

(5)

where D₁ and D₂ are two damage constants, and $P_{\mathrm{t}}^{*}$ is the failure cut-off pressure. In the study, the parameters of D₁ = 0.04 and D₂ = 1.0 are obtained from [20].

P-α Compaction EOS Parameters

In the RHT model, the p-α equation of state (EOS) is defined as follows:

$$\begin{array}{cc}{P}_R={\displaystyle \frac{1}{{\alpha }_0}}\left[(B_0+B_1{\mu }_0){\alpha }_0{\rho }_{0}e+A_1{\mu }_0+A_2{\mu }_0^2+A_3{\mu }_0^3\right],& {\mu }_0>0\end{array}$$

(6)

B₀ and B₁ are material constants; α₀ and ρ₀ represent the initial porosity and density, respectively; e is the internal energy; μ₀ is the volumetric strain; and A₁, A₂, and A₃ are Hugoniot polynomial coefficients, which are calculated using the equations provided in [35]:

$$A_1={\alpha }_0{\rho }_0{c}^2$$

(7a)

$$A_2={\alpha }_0{\rho }_0{c}^2(2s-1)$$

(7b)

$$A_3={\alpha }_0{\rho }_0{c}^2\left[(3s-1)(s-1)\right]$$

(7c)

c is the wave velocity, and s is a material constant, which is set to 1.061 in this study [26,37,38]. The initial compaction pressure P_crush is defined as 2/3 of the uniaxial compressive strength, corresponding to 17.9 MPa. Added to that, when the material is under tension, A₁ = T₁ and T₂ = 0, where T₁ and T₂ are also polynomial EOS parameters.

Other modeling parameters used in this study are found to have negligible influence on the numerical results, and additional relevant parameters are adopted from reference [35,38]. In addition, the remained parameters use the defaults, and the used parameters for used concrete are presented in

Table 1. RHT parameters for the used concrete.

Parameter	Value	Parameter	Value	Parameter	Value
ρr (kg·m−3)	2162	B	0.0105	D2	1.0
G (GPa)	8.32	T2	0.0	${\epsilon }_{\mathrm{m}}^{\mathrm{p}}$	0.01
ONEMPA	1.0 × 106	$\dot{{\epsilon }_{\mathrm{c}}^0}$(s−1)	3.0 × 10−5	Af	1.6
EPSF	2.0	$\dot{{\epsilon }_{\mathrm{t}}^0}$(s−1)	3.0 × 10−6	Nf	0.61
B0	1.22	EC (s−1)	3.0 × 1025	GAMMA	0.0
B1	1.22	ET (s−1)	3.0 × 1025	A1 (GPa)	27.21
T1 (GPa)	27.21	βc	0.04	A2 (GPa)	30.53
A	2.506	βt	0.043	A3 (GPa)	3.63
N	0.702	ξ	0.001	Pcrush (MPa)	17.9
fc (MPa)	26.85	Gc*	0.53	Plock (GPa)	6.0
fs*	0.18	Gt*	0.70	NP	3.0
ft*	0.1	XI	0.50	α0	1.013
Q0	0.68	D1	0.04

.

2.2.2. Material Model for Explosive

In LS-DYNA, explosives are modeled using the *MAT_HIGH_EXPLOSIVE_BURN material model in combination with the Jones-Wilkins-Lee (JWL) equation of state (EOS) [39,40,41], which defines the pressure P_J generated by the expansion of detonation products.

$$P_{\mathrm{J}}=A_{\mathrm{J}}\left(1-{\displaystyle \frac{\omega }{R_{1}V}}\right)e^{-R_{1}V}+B_{\mathrm{J}}\left(1-{\displaystyle \frac{\omega }{R_{2}V}}\right)e^{-R_{2}V}+{\displaystyle \frac{\omega E_{\mathrm{J}}}{V}}$$

(8)

Here, A_J, B_J, R₁, R₂, and ω are material constants; V is the relative volume of the detonation products; and E_J is the initial specific internal energy. In general, explosive parameters are determined according to the manufacturer’s specifications. The explosive parameters used in this study for blasting simulations are listed in

Table 2. Parameters for explosive material. Reproduced from Xu, Y.Q.; Tao, M.; Liu, Y.L.; Hong, Z.X.; Wu, C.Q. Cracking behavior of brittle materials under eccentric decoupled charge blasting. Eng. Fail. Anal. 2024, 163, 108536, with permission from Elsevier, 2024 [11].

ρe (kg·m−3)	De (m·s−1)	PCJ (GPa)	AJ (GPa)	BJ (GPa)	R1	R2	ω	EJ (J·m−3)
1200	6246	12.57	575.2	19	6.16	1.85	0.28	2.9 × 109

.

2.2.3. Material Model for Air

The air is modeled by combining Mat_Null and Linear_Polynomial EOS. This pressure in air P_a, under dynamic loading, is expressed as follows:

$$P_a=C_0+C_1{\delta }_a+C_2{{\delta }_a}^2+C_3{{\delta }_a}^3+\left(C_4+C_5{\delta }_a+C_6{{\delta }_a}^2\right)e_1$$

(9)

where P_a is the pressure; e₁ is the internal energy per volume; δ_a is the dynamic viscosity coefficient; C₀, C₁, C₂, C₃, C₄, C₅, and C₆ are material constants. The parameters for air are well documented with previous experimental calibrations and are listed in

Table 3. Parameters for the air medium. Reproduced from Li, X.D.; Liu, K.W.; Qiu, T.; Sha, Y.Y.; Yang, J.C.; Song, R.T. Numerical study on fracture control blasting using air-water coupling. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 29, Springer Nature, 2023, licensed under CC BY 4.0 (http://creativecommons.org/licenses/by/4.0/) [20].

ρa (kg·m−3)	C0	C1	C2	C3	C4	C5	C6	Ea (J·m−3)
1.29	0	0	0	0	0.4	0.4	0	2.5 × 106

.

2.2.4. Material Model for Sand

The *MAT_SOIL_AND_FOAM model is employed to simulate the mechanical response of sand, and its deviatoric perfectly plastic yield function ϕ is expressed as [20]:

$$\varphi =J_2-\left(\begin{array}{c}{a}_0+a_1{P}_{\mathrm{s}}+a_2{P}_{\mathrm{s}}^2\end{array}\right)$$

(10)

where J₂ is the second invariant; and P_s is the pressure of sand; a₀, a₁, and a₂ are the yield function constants for the plastic yield function, respectively. The volumetric strain of sand is given by the natural log of relative volume and is negative in compression, that is, $-\mathrm{l}\mathrm{n}(V_{\mathrm{s}}/V_{\mathrm{s}0})$, where V_s and V_s0 are the current volume and initial volume of sand, respectively. The material parameters for sand are listed in

Table 4. Parameters for the sand medium. Reproduced from Zhou, Z.L.; Wang, Z.; Cheng, R.S.; Wang, J.M. Experimental and numerical study on blast-induced rock damage and fragmentation under low temperatures. Eng. Fail. Anal. 2025, 174, 109497, Elsevier, 2025, licensed under CC BY 4.0 (http://creativecommons.org/licenses/by/4.0/) [42].

ρs (kg·m−3)	Gs (MPa)	Bs (GPa)	a0	a1	a2	PC(Pa)	EPS1	EPS2
1800	63.85	1.26	3.4 × 107	6.387 × 103	0.3	−6.9 × 103	0	−0.104
EPS3	EPS4	EPS5	EPS6	EPS7	EPS8	EPS9	EPS10	P1 (MPa)
−0.161	−0.192	−0.224	−0.246	−0.271	−0.283	−0.29	−0.4	0
P2 (MPa)	P3 MPa)	P4 (MPa)	P5 (MPa)	P6 (MPa)	P7 (MPa)	P8 (MPa)	P9 (MPa)	P10 (MPa)
20	40	60	120	200	400	600	800	4100

The value of EPS1–EPS10 can be determined by the volumetric strain of the sand.

.

2.2.5. Material Model for Water

Water is modeled by the material type of Mat_Null together with the Gruneisen EOS:

$$P_{\mathrm{w}}={\displaystyle \frac{{\rho }_{\mathrm{w}}{C_{\mathrm{w}}}^2{\nu }_{\mathrm{w}}\left[1+\left(1-\frac{\gamma }{2}\right){\nu }_{\mathrm{w}}-\frac{{\alpha }_w}{2}{{\nu }_{\mathrm{w}}}^2\right]}{{\left[1-(S_1-1){\nu }_{\mathrm{w}}-S_2\frac{{{\nu }_{\mathrm{w}}}^2}{{\nu }_{\mathrm{w}}+1}-S_3\frac{{\nu }_{\mathrm{w}}}{{\left({\nu }_{\mathrm{w}}+1\right)}^2}\right]}^2}}+(\gamma +{\alpha }_{\mathrm{w}}{\nu }_{\mathrm{w}})E_{\mathrm{w}}$$

(11)

where P_w is water pressure; ρ_w is initial density of water; C_w is intercept of the shear-compression wave velocity curve; ν_w is Poisson’s ratio; γ is GRUNEISEN constant; α_w is initial volume correction factor; S₁, S₂, and S₃ are slope factors of the shear–compression wave velocity curve; and E_w is initial energy per unit volume of water. The material parameters of water are well documented with previous experimental calibrations, and the parameters for water are set by referring to [20] and listed in

Table 5. Parameters for the water medium.

ρw (kg·m−3)	Cw (m·s−1)	γ	S1	S2	S3	Ew (J·m−3)
1000	1480	0.35	2.56	−1.986	1.2268	1.89 × 106

.

2.2.6. Material Model for Stemming Material

Soil was used as the stemming material in the blasting tests. In the numerical model, the *MAT_SOIL_AND_FOAM model was also used to simulate the dynamic response of soil under impact loading. The material parameters are provided in

Table 6. Parameters for stemming 16.

ρst (kg·m−3)	νst	Gst (MPa)	Cst (MPa)	μst	φst (°)
1680	0.35	16	0.018	9.5	37

.

2.3. Numerical Calibration

Using the aforementioned materials and finite element models, the crack patterns observed in physical tests of EDC blasting under different coupling media were successfully reproduced. To balance computational accuracy and efficiency, a mesh sensitivity analysis was carried out using the EDC blasting model with sand as the coupling medium to determine an appropriate mesh resolution. Three progressively refined mesh sizes (1 mm × 1 mm × 2 mm, 1.5 mm × 1.5 mm × 2 mm, and 2 mm × 2 mm × 2 mm) were selected based on existing recommendations [43,44], and their effects on peak pressure, PPV, and fracture network development were analyzed.

Figure 4 presents the peak pressure and PPV at various nodal locations along the OA direction for different mesh sizes. The position is defined by the ratio R_M/R₀, where R_M is the distance from a node to the borehole center O, and R₀ is the borehole radius. The results show that peak pressure and PPV at the same positions remain nearly consistent across mesh sizes, except in regions immediately adjacent to the borehole wall (distance < 2R₀). Differences among mesh sizes diminish progressively as the distance from the borehole center increases.

As illustrated in Figure 5, increasing the mesh size leads to a reduction in the number and length of microcracks near the borehole wall. While main radial cracks tend to appear coarser, the extent of the overall damage zone and the length of major cracks remain largely unchanged across mesh sizes. These findings indicate that within the tested range, the evolution of blast-induced damage is not highly sensitive to mesh refinement. The numerical results exhibit good convergence, and even relatively coarse meshes can reproduce the overall damage pattern. It is worth noting that although the 1 mm mesh offers greater accuracy in capturing the fracture network, it significantly increases computational cost. Therefore, a 2 mm × 2 mm × 2 mm mesh size is considered suitable for EDC blasting simulations in subsequent analyses.

Subsequently, EDC blasting tests under air and water coupling conditions were simulated using a mesh size of 2 mm × 2 mm × 2 mm, and the resulting surface fracture networks of the corresponding specimens were obtained, as shown in Figure 6. It is worth noting that the rock fracture simulation method adopted in this study differs from the traditional element erosion method [45,46]. The current method identifies fracture initiation by concealing rock elements that exceed a critical damage threshold and comparing the simulated crack patterns with those from physical tests. In LS-PrePost, rock damage is represented by a scalar damage variable D (0 ≤ D ≤ 1), where D = 0 (blue) corresponds to intact rock and D = 1 (red) indicates complete failure. The critical damage value is determined based on the observed crack patterns on the specimen surface, and D = 0.4 is finally selected as the threshold for crack formation. The numerical results show that, under sand coupling, four primary radial cracks are generated on the specimen surface, effectively segmenting it into four parts. Several short microcracks also appear near the borehole wall. In contrast, water coupling results in more fully developed radial cracks, which is consistent with the physical test observations. For air coupling, six cracks are generated in the specimen, although several do not fully penetrate the specimen in the simulation. This discrepancy may be attributed to the explosive modeling approach using the volume fraction method and the difference in detonation timing between the numerical simulation (simultaneous detonation) and laboratory tests (asynchronous detonation). Nevertheless, the cracks predicted by the current numerical model generally agree well with those observed in the experiments, indicating that the model can effectively capture the fracture propagation and pressure evolution processes, thereby providing a reliable basis for subsequent EDC simulations.

3. Numerical Simulation of EDC Blasting

3.1. Computational Model

A numerical model was developed based on the geometry presented in Figure 3. In addition to the decoupling ratio K of 20/7 and three coupling media (air, sand, and water), six additional decoupling ratios (20/10, 20/9, 20/8, 20/6, 20/5, and 20/4) were introduced. The explosive position was also considered. The model was discretized into approximately 1.28 million hexahedral elements, with a mesh size of 2 mm × 2 mm × 2 mm for the rock and 0.5 mm × 0.5 mm × 2 mm for both the coupling media and the stemming. The explosive diameter was defined according to the decoupling ratio, and both the diameter and explosive position were adjusted using the parameters of the *INITIAL_VOLUME_FRACTION_GEOMETRY keyword. All other modeling settings were consistent with those described in Section 2.2. During the simulations, pressure histories at target points A (10, 0, 120) mm on the coupled side and B (−10, 0, 120) mm on the decoupled side were recorded to analyze the pressure attenuation characteristics in the rock under EDC blasting.

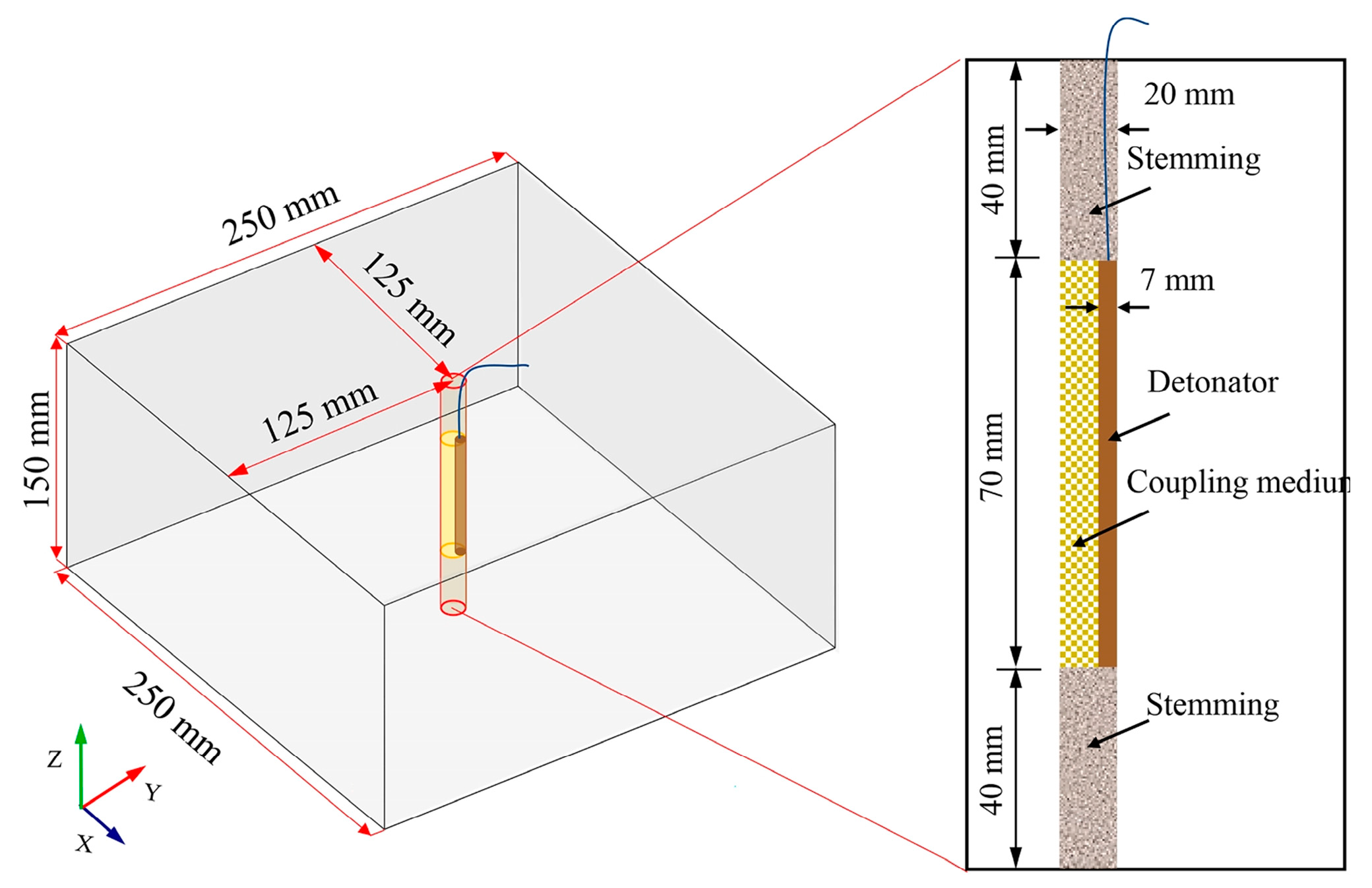
3.2. Effect of Decoupling Ratio and Coupling Media on EDC Blasting

Following the calibration of the material model, numerical simulations were conducted to examine the EDC blasting process under various decoupling ratios and coupling media conditions. The corresponding patterns of pressure propagation and damage evolution are illustrated in Figure 7. After detonation, the explosive products rapidly expand and exert strong compression on the coupling medium within the borehole, generating a distinct high-pressure zone. At T = 6 μs, the coupled side exhibits a broader high-pressure zone under the minimum decoupling ratio (K = 20/10). Moreover, the type of coupling medium has a significant effect on pressure distribution. The water medium yields the widest high-pressure region, while the air medium produces the narrowest. As the pressure continues to propagate, the air and sand media exhibit notable asymmetry in the pressure field, leading to the emergence of a pressure eccentricity effect. In contrast, the water medium shows a more uniform distribution due to its lower compressibility. Under shock wave loading, the borehole wall rock initially undergoes compression and crushing, forming a crushed zone (0.8 ≤ D ≤ 1). As energy dissipates, the radial compressive stress becomes insufficient to cause additional failure, while the circumferential tensile stress remains above the rock’s tensile strength, promoting the extension of radial cracks from the edge of the crushed zone. In addition, wave reflection at the free surface generates radial tensile stresses that initiate circumferential cracks, ultimately producing a complete damage zone. The simulation results indicate that the final damage pattern differs significantly depending on the coupling medium. Under water coupling, the cracks are densely and uniformly distributed, with bilateral expansion of the damage zone. By contrast, under air or sand coupling, the damage zone is clearly biased toward the coupled side, while the decoupled side exhibits a more asymmetric damage pattern due to uneven pressure loading.

Figure 8 presents the damage patterns and associated fracture networks of the rock mass under EDC blasting conditions. Both the charge diameter and the type of coupling medium significantly influence the resulting damage pattern. Although radial cracks emanating from the blast center are observed under three coupling media, under air and sand coupling conditions, the fracture networks appear more sparse and asymmetric, with most cracks concentrated on the side closer to the explosive charge, as shown in Figure 8a,b. In contrast, water coupling generates a dense and intersecting fracture network on both the coupled and decoupled sides, due to its higher energy transfer efficiency, as shown in Figure 8c. Moreover, as the decoupling ratio increases, the extent of energy dissipation becomes more substantial, leading to a marked decrease in both the number and length of cracks observed on the specimen surface.

To quantitatively assess the extent of blast-induced rock damage and the asymmetry in the fracture pattern, the volume ratios of the crushed zone (V_cru/V_r), crack zone (V_cra/V_r), and total damage zone (V_d/V_r) around the borehole were calculated. As shown in Figure 9, the damage zone includes both the crushed and cracked zones [47]. Additionally, the fracture eccentricity δ was defined as the volume ratio between the coupled side and the decoupled side for each damage region. Specifically, δ_cru, δ_cra, and δ_d represent the eccentricity of the crushed zone, crack zone, and total damage zone, respectively. A value of δ > 1 indicates that the damage is concentrated on the coupled side, reflecting the presence of a damage eccentricity effect.

Under identical coupling media, increasing the decoupling ratio K from 20/10 to 20/4 led to a marked decrease in the volume ratios of all three damage regions. This reduction is primarily due to the decreased charge diameter and increased thickness of the coupling layer, which together enhance energy dissipation and reduce the intensity of the stress wave. Among the three media, water coupling consistently produced the largest damage volumes, followed by sand and then air, indicating that water provides the highest energy transmission efficiency and greatest rock-breaking capacity. Regarding the eccentricity effect, the values of δ in all damage zones increased with K under both air and sand coupling. Notably, at K = 20/4, δ_cru > 20 for both media, as the transmitted stress on the decoupled side was too weak to form a significant crushed zone, resulting in an extreme disparity. Additionally, δ_d > 1 across all K values for both air and sand coupling, confirming the consistent presence of a damage eccentricity effect. The decoupling ratio K = 20/5 was identified as the threshold where the dominance of the eccentricity effect transitions: below this value, air coupling exhibits a more pronounced effect; above it, sand coupling becomes more dominant, as shown in Figure 9c. In contrast, water coupling did not display a damage eccentricity effect when K < 20/8. The effect only emerged at larger decoupling ratios, suggesting that eccentric damage under water coupling conditions requires high levels of decoupling. At lower K values, most of the explosive energy on the coupled side is consumed in forming the crushed zone, while the decoupled side experiences primarily crack initiation and extension. As K increases, the energy on the coupled side becomes increasingly directed toward crack development and eventually exceeds that on the decoupled side, leading to the onset of the eccentricity effect.

These findings indicate that the degree of rock damage and the corresponding eccentricity effect under EDC blasting are jointly governed by the decoupling ratio K and the coupling medium. For engineering applications, the decoupling ratio K and the coupling medium should be selected based on the excavation requirements: If the goal is to enhance the damage eccentricity effect, air or sand coupling is recommended. When K < 20/5, air coupling exhibits the most pronounced eccentricity effect, with the lowest damage on the decoupled side, making it ideal for protecting the surrounding rock. When K ≥ 20/5, sand coupling produces a stronger eccentricity effect, and the rock-breaking capacity on the coupled side is enhanced. Notably, even under high K values, air coupling still results in the least damage on the decoupled side, making it suitable for scenarios requiring the preservation of rock integrity on the decoupled side. When both eccentric damage and overall crushing efficiency are desired, water coupling is a suitable choice, although a higher decoupling ratio should be used to minimize energy transfer to the decoupled side.

To further investigate the pressure propagation behavior within the rock under EDC conditions, pressure–time histories at target points A and B were plotted for decoupling ratios K = 20/9, 20/7, and 20/5, as shown in Figure 10. On the coupled side, the borehole wall is first subjected to the incident shock wave, resulting in a rapid rise to peak pressure followed by sharp attenuation. This behavior is primarily influenced by the energy absorption of the crushed zone. Multiple stress wave reflections at the borehole interface generate secondary local peaks, thereby extending the duration of pressure loading.

On the decoupled side, the pressure rise is significantly delayed compared with the coupled side, and the delay increases with larger decoupling ratios. This is attributed to the thickening of the coupling medium layer, which increases the travel path of the stress wave, reduces its propagation speed, and delays the arrival time. As a result, both the peak pressure and loading rate decrease markedly. Among the three media, air exhibits the lowest peak pressure, the most pronounced delay, and the least energy transfer efficiency. The pressure difference between the coupled and decoupled sides is greatest under air coupling, leading to an apparent asymmetry in the resulting damage, as shown in Figure 10a. By contrast, water coupling exhibits the highest peak pressure, fastest propagation speed, and shortest arrival time. The smallest pressure difference between the two sides is observed in this case, suggesting a more uniform pressure distribution, as shown in Figure 10c. This facilitates the development of a coherent and evenly distributed crack network, enhancing overall crushing efficiency. Moreover, the pressure duration on the decoupled side increases in the order: air < sand < water. Liu et al. [20] attributed this trend to differences in wave reflection frequency and attenuation characteristics at the borehole wall. The degree of stress wave attenuation is closely related to the porosity of the coupling medium—higher porosity in air leads to greater attenuation. Regardless of the medium, increasing the decoupling ratio reduces the charge diameter and total explosive energy, which in turn lowers the peak pressures on both sides of the borehole and shortens the overall pressure duration.

In summary, the peak borehole wall pressure, loading rate, and pressure duration are jointly governed by the decoupling ratio and the physical characteristics of the coupling medium. As the decoupling ratio K increases or as the medium porosity becomes higher, the pressure distribution along the borehole wall becomes increasingly uneven. This leads to greater differences in pressure response between the coupled and decoupled sides, which in turn amplifies the disparity in damage extent across the borehole. These findings are consistent with the damage pattern observations discussed in the preceding section.

According to the numerical simulation results of EDC blasting, a clear distinction in peak pressure attenuation behavior was observed between the coupled and decoupled sides. To quantitatively describe the attenuation of peak borehole wall pressure along the radial and axial directions of the unloaded section, a power function was used to fit the peak pressure data under various EDC configurations [25,37,48,49]. The fitting results are presented in Figure 11 and

Table 7. Attenuation indexes of the fitting curves for EDC blasting with different decoupling ratios.

Coupling Medium	K	The Radial			The Axial
		αC	R2	αD	R2	αC	R2	αD	R2
Air	20/10	1.68	0.998	0.976	0.928	4.733	0.97	1.217	0.981
	20/9	1.778	0.998	0.954	0.921	5.13	0.976	1.266	0.992
	20/8	1.885	0.998	0.993	0.937	5.26	0.981	1.287	0.992
	20/7	2.02	0.998	0.995	0.955	5.693	0.983	1.312	0.992
	20/6	2.175	0.997	0.985	0.948	6.23	0.986	1.279	0.977
	20/5	2.374	0.996	0.966	0.934	7.016	0.987	1.134	0.977
	20/4	2.563	0.996	0.942	0.947	7.477	0.985	0.902	0.988
Sand	20/10	1.434	0.993	1.281	0.991	2.197	0.973	2.204	0.98
	20/9	1.498	0.994	1.280	0.99	2.408	0.986	2.119	0.973
	20/8	1.531	0.995	1.244	0.993	2.591	0.988	1.916	0.956
	20/7	1.608	0.997	1.256	0.996	2.928	0.993	1.314	0.973
	20/6	1.697	0.998	1.331	0.978	3.537	0.985	1.363	0.975
	20/5	1.818	0.999	1.495	0.959	4.33	0.974	1.402	0.949
	20/4	1.931	0.999	1.629	0.961	5.382	0.972	1.459	0.92
Water	20/10	1.403	0.991	0.996	0.895	1.592	0.968	1.241	0.909
	20/9	1.466	0.994	0.999	0.892	1.737	0.982	1.253	0.907
	20/8	1.5	0.994	1.012	0.892	1.868	0.989	1.285	0.914
	20/7	1.578	0.996	1.032	0.902	2.035	0.993	1.325	0.923
	20/6	1.664	0.997	1.053	0.911	2.269	0.995	1.386	0.942
	20/5	1.745	0.998	1.071	0.916	2.471	0.993	1.435	0.952
	20/4	1.859	0.998	1.088	0.923	3.162	0.98	1.48	0.962

.

$$P_{\mathrm{M}}=P_{\mathrm{b}}(R_{\mathrm{M}}/R_0{)}^{-\alpha }$$

(12a)

$$P_{\mathrm{M}}=P_{\mathrm{b}}(L_{\mathrm{M}}/L_0{)}^{-\alpha }$$

(12b)

where P_M is the peak pressure at the measurement point, P_b is the initial peak pressure at the borehole wall, R_M is the distance from the measurement point to the borehole center O, and R₀ is the borehole radius. L_M denotes the perpendicular distance from the measurement point to the explosive center O_e, and L₀ represents half the length of the charge. α is the pressure attenuation index.

From the coefficient of determination R² in Table 7, it can be seen that the fitting performance is generally better on the coupled side. The R² values in the radial direction are mostly above 0.99, and those in the axial direction exceed 0.96. In contrast, the R² values on the decoupled side are relatively lower, particularly under water coupling at low K values, where the value in the radial direction approaches 0.90. This deviation is likely caused by enhanced reflected waves under low-K water conditions, which locally increase pressure and result in slight deviations from the power function trend, as illustrated in Figure 11c,f. Nevertheless, the current fitting curves adequately describe the overall pressure decay characteristics. The variation in the attenuation index α with respect to the decoupling ratio K is shown in Figure 12. On the coupled side, both the radial direction and axial direction attenuation indices increase with K for three media, indicating stronger stress wave attenuation as the charge diameter decreases and the coupling layer thickens. Among them, air coupling exhibits the most significant attenuation, with α increasing from 1.68 to 2.563 in the radial direction and from 4.733 to 7.477 in the axial direction. This suggests that explosive pressure attenuates rapidly in the near-field borehole wall region and that axial propagation is severely limited, as shown in Figure 11a,d. Sand coupling follows, with α increasing from 1.434 to 1.931 in the radial direction and from 2.197 to 5.382 in the axial direction. Water coupling shows the slowest attenuation, with α increasing from 1.403 to 1.859 in the radial direction and from 1.592 to 3.162 in the axial direction, demonstrating superior far-field pressure transmission capabilities, as shown in Figure 11c,f.

Compared with the coupled side, the pressure decay rate on the decoupled side is lower, less influenced by the decoupling ratio K, and more sensitive to the coupling medium. Under air coupling, the attenuation index α remains relatively stable in both the radial and axial directions, ranging from 0.942 to 0.995 and from 0.902 to 1.312, respectively. This can be attributed to the lower peak pressure on the decoupled side, resulting in a smaller crushed zone, as shown in Figure 11a,d. In contrast, sand medium exhibits greater fluctuations in the attenuation index α, with values ranging from 1.244 to 1.629 in the radial direction and from 1.459 to 2.204 in the axial direction. Water coupling yields the most consistent attenuation behavior, with the attenuation index α increasing from 0.996 to 1.088 in the radial direction and from 1.241 to 1.480 in the axial direction. These results suggest that water coupling maintains better long-range pressure transmission characteristics even on the decoupled side.

Furthermore, the attenuation index in the axial direction is generally higher than that in the radial direction, indicating that the pressure decays more rapidly along the axial path. These findings demonstrate that selecting an appropriate combination of decoupling ratio K and coupling medium can effectively regulate the propagation range of the pressure wave, mitigate the impact on non-target areas, and ultimately contribute to a more controllable and efficient blasting outcome.

3.3. Effect of Eccentricity Coefficient on EDC Blasting

Building on the previous analysis, the influence of explosive position on blast pressure distribution and damage pattern under different coupling medium conditions was further investigated. To quantitatively describe the explosive position within the borehole, the eccentricity coefficient E_e was defined as the ratio of the distance from the charge center to the borehole center to the difference between the borehole diameter and the charge diameter. Four representative values were selected, 0, 1/3, 2/3, and 1, corresponding to a progression from concentric placement to full contact with the borehole wall. Figure 13 illustrates the pressure evolution and crack propagation process for different eccentricity coefficients under the condition of K = 20/5. At the onset of detonation, the blast pressure wave exhibits an ellipsoidal, outward-expanding pattern. When E_e = 0 (concentric loading), both the explosion pressure field and the resulting damage zone are symmetrically distributed around the borehole center. As E_e increases, the center of gravity of the pressure and damage distributions shifts progressively toward the eccentric side. This is manifested as an enlarged pressure field and an expanded damage zone on the coupled side of the borehole.

The corresponding blast-induced fracture networks are shown in Figure 14. When E_e = 0, symmetric damage zones are observed on the top surfaces of the rock specimens for all coupling media. Notably, under air coupling, the specimen surface exhibits no visible crushed zone and only a few short radial cracks, primarily due to the high compressibility of air, as previously discussed. As the eccentricity coefficient E_e increases, the difference in damage between the two sides of the specimen becomes more apparent. Under air and water coupling, the asymmetry is relatively minor, whereas sand coupling displays a pronounced eccentric damage pattern characterized by dense cracking on the coupled side and sparse cracking on the decoupled side.

Figure 15 presents the volume ratios and fracture eccentricity δ for each damage pattern region under different eccentricity coefficients. It is evident that the explosive position significantly affects the degree of damage eccentricity, while the overall damage volume remains relatively constant. Combined with the pressure–time histories at the monitoring points in Figure 16, it can be seen that when E_e = 0, the pressure responses on both sides are nearly identical, resulting in no observable eccentricity in the damage distribution. As E_e increases, the coupled side experiences more rapid stress loading, higher peak pressure, and a longer duration, leading to an expanded damage zone. In contrast, the decoupled side exhibits delayed pressure transfer, lower peak pressure, and a more limited damage extent. This disparity leads to a continuous increase in the fracture eccentricity δ. Furthermore, the choice of coupling medium modulates the magnitude of the eccentricity effect. Under water coupling, even moderate eccentricity coefficients (E_e = 1/3 − 2/3) may result in a reversed eccentricity distribution, thereby weakening the damage asymmetry associated with explosive position. By contrast, air and sand coupling exhibit more prominent eccentricity effects. Among them, air coupling produces stronger asymmetry at lower eccentricity coefficients (E_e ≤ 1/3), though the growth of E_e tends to level off at higher values. In sand coupling, the eccentric damage increases more steeply beyond E_e > 1/3, with a marked rise in the eccentricity of the total damage zone δ_d.

The same Equation (12) was employed to fit the decay trend of peak pressure with distance along the radial and axial directions at various eccentricity coefficients. As shown in Figure 17, the current equation provides a good fit to the pressure attenuation behavior at different explosive positions.

As shown in

Table 8. Attenuation indexes of the fitting curves for EDC blasting with different eccentricity coefficients.

Coupling Medium	Ee	The Radial				The Axial
		αC	R2	αD	R2	αC	R2	αD	R2
Air	0	1.084	0.911	1.084	0.912	1.513	0.981	1.517	0.981
	1/3	1.179	0.944	1.058	0.918	1.69	0.986	1.389	0.985
	2/3	1.373	0.982	1.182	0.917	1.852	0.976	1.057	0.98
	1	2.374	0.996	0.966	0.934	7.016	0.987	1.134	0.977
Sand	0	1.149	0.956	1.15	0.956	1.889	0.977	1.889	0.977
	1/3	1.37	0.974	0.974	0.951	2.662	0.992	1.192	0.98
	2/3	1.589	0.992	1.023	0.94	2.814	0.974	0.969	0.945
	1	1.818	0.999	1.495	0.959	4.33	0.974	1.402	0.949
Water	0	1.178	0.947	1.178	0.947	1.646	0.987	1.647	0.988
	1/3	1.288	0.97	1.099	0.929	1.787	0.992	1.521	0.979
	2/3	1.465	0.985	1.046	0.91	2.04	0.994	1.411	0.958
	1	1.745	0.998	1.071	0.916	2.471	0.993	1.435	0.952

and Figure 18, when the eccentricity coefficient E_e gradually increases from 0 to 1 (the explosive shifts closer to the borehole wall), the distribution of the explosion pressure field begins to exhibit a clear and intensifying eccentricity effect. This pressure decay behavior closely resembles the trend observed under increasing decoupling ratio K. On the coupled side, the attenuation indices in both radial and axial directions increase significantly with the eccentricity coefficient E_e. This indicates that near-field pressure decays more rapidly, while attenuation in the far field becomes more gradual. As shown in Figure 17, most of the explosive energy is directed toward the side where the charge is positioned. Among three coupling media, air coupling shows the most pronounced increase, with the attenuation index α rising from 1.084 to 2.374 in the radial direction and jumping from 1.513 to 7.016 in the axial direction—indicating sharp stress concentration and limited long-range propagation. Sand coupling follows with a moderate rise: the attenuation index α increases from 1.149 to 1.818 in the radial direction, and from 1.889 to 4.330 in the axial direction. In contrast, water coupling remains the most stable, with the attenuation index α changing only from 1.178 to 1.745 in the radial direction and from 1.646 to 2.471 in the axial direction. These results suggest that water as a coupling medium is more favorable for maintaining far-field pressure transmission under eccentric loading.

Compared with the coupled side, the pressure decay rate on the decoupled side is generally lower and shows limited sensitivity to increasing the eccentricity coefficient E_e. Instead, it is more strongly influenced by the properties of the coupling medium. Across all media, the attenuation indices on the decoupled side exhibit relatively small variations, and the coefficients of determination R² are, in most cases, lower than those of the coupled side. For instance, under air coupling, the attenuation index α ranges from 0.996 to 1.182 in the radial direction, while α ranges from 1.057 to 1.517 in the axial direction. In the case of sand coupling, the radial and axial attenuation indices range from 0.974 to 1.495 and from 0.969 to 1.889, respectively. Water coupling shows the narrowest variation, with the attenuation index α varying between 1.046 and 1.178 in the radial direction and between 1.411 and 1.646 in the axial direction. These results suggest that water as a coupling medium is more favorable for maintaining stable and efficient far-field pressure transmission on the decoupled side under eccentric loading.

4. Discussion

The numerical simulation results reveal that the spatial distribution of explosion pressure and the extent of rock damage during EDC blasting exhibit distinct eccentric characteristics. This behavior is not solely attributed to the explosive position (the eccentricity coefficient E_e), but is also strongly influenced by the charge diameter (the decoupling ratio K) and the physical properties of the coupling medium.

4.1. Energy-Based Interpretation of Eccentric Damage

The observed eccentric damage phenomenon can be explained from the perspective of energy distribution. The energy released by the explosive is primarily transferred to the rock as internal energy (IE) and kinetic energy (KE). In LS-DYNA, the internal energy includes contributions from strain, crack surface formation, and internal fracturing, as well as plastic dissipation, and is mainly consumed during the creation of new fractures [50]. Kinetic energy corresponds to the motion and ejection of fractured rock fragments. The absolute magnitude of internal energy determines the overall extent of rock damage, while the ratio δ_IE between the coupled and decoupled sides reflects the degree of damage asymmetry. Similarly, the total kinetic energy reflects the overall intensity of fragment motion, whereas δ_KE characterizes the asymmetry of fragment throw. Here, δ_IE and δ_KE are defined as the internal energy and kinetic energy on the coupled side (x > 0) divided by those on the decoupled side (x < 0), i.e., ${\delta }_{IE}={\mathrm{I}\mathrm{E}}_{\mathrm{c}}/{\mathrm{I}\mathrm{E}}_{\mathrm{D}}$ and ${\delta }_{KE}={\mathrm{K}\mathrm{E}}_{\mathrm{c}}/{\mathrm{K}\mathrm{E}}_{\mathrm{D}}$. As shown in Figure 19, energy evolution curves under different influencing factors are illustrated. As shown in Figure 19a, for the case of K = 20/5 and sand coupling, internal energy on both sides increases rapidly and then stabilizes, indicating the rapid formation of a crack network within the rock. When the eccentricity coefficient E_e = 0, internal energy, kinetic energy, δ_IE, and δ_KE are nearly equal on both sides, suggesting symmetrical damage zones and balanced energy input. As E_e increases and the explosive moves closer to the coupled side, internal energy on that side rises while that on the decoupled side decreases, resulting in a higher δ_IE. Meanwhile, δ_KE also increases, indicating that fragment throw becomes more asymmetric. This explains why both damage and fragment motion asymmetry grow stronger when the explosive approaches the borehole wall.

As shown in Figure 19b, when the explosive is fully offset toward the borehole wall (E_e = 1), increasing the charge diameter (decreasing K) leads to a general increase in internal and kinetic energy on both sides. However, δ_IE decreases, meaning that although the total fracture energy increases, it is distributed more evenly, resulting in a weaker eccentricity of damage. Similarly, δ_KE decreases, showing that fragment motion also becomes more balanced. This corresponds to the expansion of the overall fracture zone and the inward shift in the damage center toward the borehole axis, as shown in Figure 8b. As shown in Figure 19c, after increasing the charge diameter by 10 mm, the transition from sand coupling to air/water coupling results in a gradual decrease/increase in both the internal energy magnitude and its growth rate on each side. Correspondingly, the internal energy ratio δ_IE and the kinetic energy ratio δ_KE increase/decrease, suggesting that under the same charge diameter, the extent of the fracture zone becomes smaller/larger and the eccentricity effect is strengthened/weakened. This phenomenon can be attributed to the different attenuation characteristics of stress waves in various coupling media, as illustrated in Figure 10, Figure 11, Figure 12, Figure 16, Figure 17 and Figure 18. Air coupling, due to its high compressibility, produces the lowest internal energy but the largest δ_IE, thereby amplifying damage asymmetry. Sand shows intermediate behavior. At K = 20/5, the δ_IE value under sand coupling exceeds that of air coupling, which explains why K = 20/5 serves as the critical threshold distinguishing the strength of the eccentric damage effect between air and sand coupling, as shown in Figure 9c. In contrast, water coupling delivers the highest internal energy and kinetic energy, but a large portion of internal energy is dissipated in local crushing rather than in directional crack propagation, while kinetic energy is distributed more evenly between the two sides. Because water is incompressible, it prolongs the loading duration and facilitates more uniform pressure transmission, which suppresses damage asymmetry and produces smaller and more symmetric fracture zones. Under low K conditions, this may even cause reverse eccentricity. This observation is consistent with the results reported by Xu et al. [11].

In summary, the eccentricity coefficient E_e, decoupling ratio K, and coupling medium jointly influence the development of the eccentricity effect during the damage evolution of the rock mass. Among these factors, the position of the explosive primarily determines the direction of damage asymmetry, while the decoupling ratio/coupling medium governs the degree of eccentricity by controlling the loading intensity/energy transfer efficiency. In practical applications of controlled blasting, it is recommended to place explosives close to the borehole wall on the excavation side to improve energy transfer from the detonation products to the surrounding rock. This arrangement facilitates the initiation and propagation of cracks on that side. Meanwhile, increasing the thickness of the coupling medium between the explosive and the borehole wall on the retention side can significantly mitigate peripheral rock damage. To ensure effective fragmentation of the excavation-side rock while preserving the structural stability of the retained rock mass, air/sand coupling is recommended for smooth blasting holes. For production blasting, water coupling is preferable, as it helps reduce the eccentricity effect, enhances rock-breaking efficiency, and limits the generation of oversized fragments.

4.2. Limitations and Future Work

The findings of this study are based on several simplifying assumptions: the numerical model was calibrated against a single laboratory test, material parameters were mainly derived from literature and theoretical formulations, and the rock mass was assumed to be smooth and homogeneous with a single-hole charge, which facilitated isolating the effects of decoupling ratio, eccentricity, and coupling medium. However, this assumption does not reflect the inherent heterogeneity, joints, and scale effects of real rock masses, and therefore represents a limitation of the current model. The validation scope remains narrow, natural heterogeneity and jointed structures were not considered, and uncertainties are also associated with the explosive equation of state and constitutive parameters of the rock. The explosive charge itself was modeled using the initial volume fraction method with the coupling medium as the background material. While this approach facilitates stable meshing, it may not fully represent the complex detonation process and gas–rock interactions, which should be considered when interpreting the results. These assumptions allowed the model to capture the primary mechanisms of eccentric decoupled charge blasting, but also introduced limitations.

Moreover, the internal energy in LS-DYNA cannot be further decomposed into elastic, plastic, and fracture components, which represents an additional simplification of the current framework. In addition, the use of stress-free boundaries inevitably introduces reflected waves, which influence fracture development, particularly under water coupling at low decoupling ratios. While this effect is consistent with laboratory tests conducted under free surfaces, it may be amplified in finite-size numerical models compared with larger-scale rock masses. Although the mesh sensitivity analysis (1–2 mm element sizes) confirmed that peak pressure, PPV, and overall fracture patterns converged well, the finite element framework remains inherently mesh-dependent. Nevertheless, as with all finite element models, the results remain mesh-dependent to some extent, which represents a limitation of the current approach. Recent studies have further shown that advanced approaches such as ALE-based adaptive fracture modeling [51] and meshless formulations like the Element-Free Galerkin (EFG) method [52] can effectively reduce mesh dependency and improve computational efficiency in complex fracture problems, highlighting their potential as valuable alternatives to traditional FEM frameworks. Moreover, the present analysis focused on an idealized single-hole model, which does not reflect the complexity of multi-hole blasting or in situ stress conditions.

Future work should therefore proceed in three directions: (i) conduct broader experimental validation under diverse rock types, charging conditions, and confinement pressures; (ii) incorporate advanced numerical approaches such as adaptive ALE formulations and meshless methods (e.g., EFG), which have recently shown strong potential for simulating complex fracture processes without mesh dependency; and (iii) extend the framework to multi-hole and heterogeneous rock mass models to assess the combined effects of joints, anisotropy, and stress fields. Coupled with large-scale experiments and field monitoring, these developments will contribute to establishing a more robust predictive framework for eccentric decoupled charge blasting in engineering practice.

5. Conclusions

This study investigates the behavior of the EDC structure by establishing a three-dimensional numerical model calibrated against laboratory tests. The effects of varying decoupling ratios, coupling media, and explosive positions on blast pressure distribution and rock damage are systematically analyzed.

(1)

Eccentric positioning of the charge leads to clear asymmetry in both pressure propagation and rock damage. With increasing eccentricity coefficient E_e, the coupled side experiences faster wave arrival and higher peak pressure, while the decoupled side shows delayed arrival and lower peak pressure. This disparity produces increasingly asymmetric fracture patterns. From an energy perspective, the ratios of internal energy (δ_IE) and kinetic energy (δ_KE) between the coupled and decoupled sides confirm that more energy is directed toward the coupled side, thereby reinforcing fracture asymmetry.

(2)

Both the decoupling ratio K and the coupling medium strongly affect energy transfer and damage evolution. Larger decoupling ratios reduce the overall damage volume but accentuate the disparity between the coupled and decoupled sides, particularly in the crushed zone. Air and sand couplings tend to promote stronger eccentricity effects, whereas water coupling produces more balanced distributions at low decoupling ratios and shows eccentric behavior only beyond a threshold, owing to its incompressibility and the dissipation of energy in crushing.

(3)

The decay of peak explosion pressure with distance follows a power-law relationship. Attenuation on the decoupled side is slower and less correlated than on the coupled side. This decay is more sensitive to the type of coupling medium than to variations in K or E_e, and in all cases, pressure decreases more rapidly in the axial direction than in the radial direction. These findings indicate that medium properties dominate pressure dissipation, while geometric parameters primarily regulate the degree of asymmetry.

(4)

The results provide indicative insights for field practice, suggesting that eccentric placement and coupling medium selection may be used to adjust energy distribution and control fracture patterns. For instance, air and sand promote stronger eccentricity effects, while water tends to suppress asymmetry and enhance crushing efficiency. However, these conclusions are derived from an idealized single-hole model in a homogeneous medium. Multi-hole interactions, rock discontinuities, and heterogeneity were not considered. Therefore, the findings should be interpreted within these constraints, and further experimental and numerical studies are required before direct application in field blasting design.