Abstract
Predicting short-term buy and sell signals in financial markets remains a significant challenge for algorithmic trading. This difficulty stems from the data’s inherent volatility and noise, which often leads to spurious signals and poor trading performance. This paper presents a novel algorithmic trading model for silver that combines fine-tuned Convolutional Neural Networks (CNNs) with a decision filter based on the Relative Strength Index (RSI). The technique allows for the prediction of buy and sell points by turning time series data into chart images. Daily silver price per ounce data were turned into chart images using technical analysis indicators. Four pre-trained CNNs, namely AlexNet, VGG16, GoogLeNet, and ResNet-50, were fine-tuned using the generated image dataset to find the best architecture based on classification and financial performance. The models were evaluated using walk-forward validation with an expanding window. This validation method made the tests more realistic and the performance evaluation more robust under different market conditions. Fine-tuned VGG16 with the RSI filter had the best cost-adjusted profitability, with a cumulative return of 115.03% over five years. This was nearly double the 61.62% return of a buy-and-hold strategy. This outperformance is especially impressive because the evaluation period was mostly upward, which makes it harder to beat passive benchmarks. Adding the RSI filter also helped models make more disciplined decisions. This reduced transactions with low confidence. In general, the results show that pre-trained CNNs fine-tuned on visual representations, when supplemented with domain-specific heuristics, can provide strong and cost-effective solutions for algorithmic trading, even when realistic cost assumptions are used.
1. Introduction
Financial time series forecasting is one of the most common applications of artificial intelligence (AI) in finance. Financial markets have a non-linear and complex structure that is affected by many variables such as investor psychology, political developments, news flows, and economic indicators. This dynamic and chaotic structure causes markets to have high volatility and makes it difficult to predict future price movements [1]. Algorithmic trading methodologies developed for correct buy–sell decisions aim to minimize human intervention while producing trading strategies within the framework of certain rules. These methodologies aim to buy and sell financial assets at the most appropriate points by analyzing past price movements, market indicators, and investor behavior [2,3,4,5]. However, the non-linear character of financial markets has made traditional methods insufficient [6]. Obviously, the dynamic nature of markets is an obstacle to the generalizability of these models in financial time series forecasting [7]. In this context, price charts often display visual symmetry—for instance, a mirrored pattern may convert a rising peak into a falling trough. Nevertheless, the economic implications of upward versus downward movements are fundamentally asymmetric. This interplay between visual symmetry and functional asymmetry is a core element that our algorithmic silver trading model aims to capture.
Traditional mathematical and statistical methods, which are frequently used in financial time series analysis, can capture certain patterns in short-term data, but they are inadequate in modeling complex relationships on long-term data [8,9,10]. These shortcomings have led to the increased adoption of machine learning and deep learning-based approaches by researchers in financial forecasting processes.
As machine learning models are preferred more in financial time series forecasting compared to mathematical and statistical methods, studies using methods such as Extreme Gradient Boosting (XGBoost), Random Forest (RF), Support Vector Machine (SVM) and Artificial Neural Network (ANN) have increased; of course, the success of traditional machine learning models also depends on the features used. Determining the correct features is an almost impossible task [11]. On the other hand, Long Short-Term Memory (LSTM), Recurrent Neural Network (RNN), and Transformer-based deep learning models can make more accurate predictions by learning complex relationships in time series [12,13,14].
While the use of deep learning in financial forecasting is becoming widespread, Convolutional Neural Networks (CNNs) have opened a new field in financial analysis, especially through image-based data representations [15,16,17,18]. CNN models can extract visuals of price movements and patterns necessary for forecasting, as well as technical indicators, from this visual data. This method supports the decision-making process by modeling visual patterns and technical analysis indicators in financial markets, unlike traditional time series analysis.
In this study, due to the limitations of statistical and traditional machine learning models in capturing the complex dynamics of financial markets, we propose to adapt pre-trained CNN models with transfer learning for financial time series forecasting. The core motivation for our visual-based approach is rooted in an analogy to human expertise. A technical analyst, for example, first learns to recognize a wide array of patterns and shapes in the real world. This general-purpose visual intelligence is then applied to the abstract task of interpreting financial charts, leading them to a categorical decision, such as buy or sell. Similarly, we hypothesize that CNNs pre-trained on vast visual datasets like ImageNet have acquired a powerful ability to extract and process visual features. By applying transfer learning, we aim to leverage this pre-existing visual intelligence and fine-tune it for the specialized task of image classification—classifying chart images as a predictive signal for a price increase or decrease. This approach treats financial forecasting as a problem of visual classification, a perspective that is central to our study.
The objective of the proposed model is to predict the direction of silver price movement (up or down) on the next trading day (t + 1) using only the data available up to day t. This short-term forecasting objective is compatible with real-world algorithmic trading systems where decisions need to be made based on up-to-date information to take action before the next trading day begins. Unlike models that rely on manually engineered features or raw time series, to implement this approach, we generate image-based representations derived from the past 15 days of silver closing prices and technical indicators. These images serve as model inputs for forecasting the next day’s movement direction. The model produces a binary output labeled as “up” or “down” for the next trading day. If the prediction is “up”, silver is bought; if it is “down”, the current holding is sold. Furthermore, we incorporate a Relative Strength Index (RSI) filter as a decision-layer refinement mechanism, improving prediction reliability and reducing false trading signals. Our empirical results demonstrate that this strategy significantly outperforms common heuristics. The proposed model achieved up to a 115.03% return, which is nearly double the buy-and-hold strategy’s return over the five-year test period. These findings highlight the practical value and competitive edge of combining deep visual learning with domain-specific heuristics in algorithmic trading. The main contributions of the proposed model are as follows:
- Visualization of financial time series data using technical analysis indicators and forecasting with CNN models: This method makes it possible to better capture complex patterns in financial markets and allows technical analysis indicators to be learned directly by the model;
- A pre-trained CNN model is fine-tuned using the transfer learning technique: This method addresses the data shortage in CNN-based financial forecasting studies and allows the model to learn more efficiently;
- Using the RSI filter to optimize the investing strategy and enhance the model’s decision-making mechanism: The RSI filter has made it less likely for the model to provide erroneous buy and sell signals, resulting in more consistent and trustworthy investing choices;
- Comparative analysis of the proposed model with traditional investment strategies and evaluation of profitability performance: In this context, the applicability of the model for investors was investigated by carrying out long-term profitability analysis under real market conditions;
- Performance comparisons of well-known pre-trained CNN models: AlexNet [19], VGG16 [20], GoogLeNet [21], and ResNet-50 [22] for algorithmic silver trading are made.
The rest of this paper is structured as follows: The literature is reviewed in Section 2, the technical details of the suggested model are presented in Section 3, the experimental results and performance analysis are covered in Section 4, and a general evaluation and recommendations for further research are given in Section 5 and Section 6.
2. Related Work
Financial time series forecasting has been a key research area in the academic literature, with approaches from different disciplines offering various solutions. Related works were examined in three main categories: (i) traditional statistical methods, (ii) machine learning and deep learning-based methods, and (iii) CNN-based methods. In this section, the strengths and weaknesses of each method are discussed, and the position of the proposed study in the literature is explained.
2.1. Traditional Methods and Their Limitations
The most commonly used traditional approaches in the analysis of financial time series are Auto Regressive Integrated Moving Average (ARIMA) and Generalized Autoregressive Conditional Heteroskedasticity (GARCH) models. While ARIMA produces estimates based on past values, it struggles to model sudden fluctuations in the market due to its stationarity assumption. Khashei et al. examined how the ARIMA model can be used in time series forecasting and how it can be improved with AI-based techniques [23]. However, in the proposed model, the parameters (p, d, q) must be manually selected, making it difficult to determine the optimal combination. Dadhich et al. made a stock market index forecast using the ARIMA model, and a structure supported by stochastic processes and regression analysis was developed to increase the accuracy of the model [24]. However, errors in long-term forecasts made with this proposed model grow significantly. The reason for this is that it shows low performance in the face of large economic fluctuations. The GARCH model, developed to model volatility in financial markets, has emerged as a powerful tool for volatility estimation. However, since it assumes that volatility changes gradually over time, it may fail to capture sudden fluctuations. Xing et al. stated that the GARCH model alone is not sufficient to predict returns and prices in financial price collapses and proposed a new non-linear GARCH model [25]. However, the unpredictability limitation experienced in large datasets is also present here. Li et al. claimed with their results that the Kalman Filter and its derivatives (KFDA) give better results compared to neural networks in time series estimation [26]. However, the study does not account for the chaotic nature of financial time series.
2.2. Machine Learning and Deep Learning Approaches
In order to overcome situations where traditional methods are inadequate, machine learning and deep learning-based models are preferred more in financial forecasting processes. Kurani et al. comparatively examined the effectiveness of ANN and SVM algorithms in stock market forecasting [27]. The authors stated that simple SVM models can work with small datasets without the risk of over-learning, but they are not applicable to large datasets. However, they stated that the prediction performance increases when SVM works as a hybrid with RF or Genetic Algorithm, but the same problem persists for large datasets. In the same study, it was emphasized that ANN models are powerful in large datasets, but the risk of over-learning is common. Since profitability analysis was not performed in the study, a clear decision could not be reached on whether the accuracy rates of the models work or not. Basak et al. tried to predict the direction of stock market prices using RFs and XGBoost [28]. The study achieves high accuracy rates for medium and long-term forecasts using technical indicators. Especially, On-Balance Volume (OBV) and Moving Average Convergence Divergence (MACD) indicators gave strong signals in the forecast. However, RF and XGBoost have a tendency to over-learn. Although this situation is not analyzed in the article, this situation is evident in the results obtained from short-term datasets. Hu et al. applied RF, logistic regression, XGBoost, SVM, and ANN to predict the bankruptcy of US financial institutions from 2001 to 2023 [29]. In this study, it was seen that the RF method gave better results than the others. However, this study did not focus on the detection of peaks and valleys of time series.
Deep learning models such as LSTM, Gated Recurrent Unit (GRU), and Transformer are widely used in financial forecasting thanks to their ability to learn long-term dependencies in time series. Lu and Li made an electricity price forecast by comparing LSTM, CNN-GRU, and Transformer-based models [30]. The authors have shown the superiority of Transformer models over traditional LSTM and ANN models. Dai et al. proposed a unique segmentation-based approach (SALSTM) for long-term forecasting by combining Transformer and LSTM models [31]. Although the proposed model achieves high performance, it is unclear how it will work in high-volatility markets such as foreign exchange markets or cryptocurrency markets due to the limited dataset used. Chen et al. developed a non-stationary Transformer model for forecasting financial time series on carbon prices [32]. The authors tested the success of Transformer for non-stationary data and found that it performs better than traditional methods. However, while Transformer models work well on very large datasets, the risk of overfitting is high on small datasets. Furthermore, a detailed analysis of how the model will work in real-world applications is lacking.
2.3. CNN-Based Financial Forecasting Models
In recent years, CNN has emerged as a new approach to financial forecasting problems. CNN-based systems can detect patterns in price movements. Yilmaz et al. created six different graph-based models (Pearson, Spearman, Euclidean, etc.) from financial time series images of DOW30 stocks and trained them with CNNs [33]. In the study, the success of the model was demonstrated using financial performance measures such as annual return, Sharpe ratio, and win ratio. Temur et al. developed a visual data-based decision support model to make buy–sell decisions in the stock market [34]. In the study, buy–sell points were determined using 2D candlestick charts, and patterns in price movements were detected with CNN-based object recognition algorithms. YoloV3, YoloV4, Faster R-CNN, and single-shot multibox detector algorithms were run separately on real market data, and profitability analysis was performed. Pala and Sefer predicted Non-Fungible Token (NFT) prices and sales dynamics using a CNN-based transfer learning model [35]. The authors did not directly process the time series data in the study; they only performed visual-based learning. Bakai et al. created a customized dataset to detect patterns in candlestick charts and proposed a CNN model and achieved high performance [36]. Balamohan and Khanaa made stock predictions using CNN and LSTM models together in their study [37]. In the study, CNN was used to capture visual formations, and LSTM was used to learn time series dependencies. However, this model, which requires training two separate deep learning networks, requires high computational power for large data sets.
While CNNs have been employed in various financial forecasting studies, our work introduces a unique approach to this field. Unlike studies that use CNNs on one-dimensional time series data or transform it into images with different methodologies, our goal is to leverage the CNN’s core strength in spatial pattern recognition for a specific and well-established purpose. We do this by visually encoding key technical indicators into chart images, where their intersections create distinct spatial relationships. This deliberate design allows the network to identify established trading signals, such as the Golden Cross and Death Cross, by interpreting their visual form. This methodology is a novel way of integrating domain-specific knowledge into a deep learning model, setting our work apart from the existing literature.
In our previous research, we examined the use of deep learning-based image classification methods for financial time series forecasting. In [11], historical price data were converted into graphical representations that could be used to predict the daily direction of gold prices using candlestick charts and technical analysis indicators. The study demonstrated that converting financial time series into images could boost profitability, in contrast to more traditional trading strategies like buy-and-hold and RSI. Likewise, pre-trained CNN architectures such as AlexNet, GoogLeNet, and ResNet-50 were refined to forecast the BIST100 index’s direction in [38]. The findings demonstrated the potential of deep learning in stock market index forecasting, as all three CNN models outperformed a naive baseline method in classification accuracy.
The current study expands on these earlier studies by applying image-based CNN modeling to the silver market, which has a different volatility structure than stock and gold markets. To further increase decision reliability and profitability, the suggested model additionally incorporates an RSI-guided filtering step, which is in contrast to earlier research that either used a single model or did not include decision refinement mechanisms. As a result, this study not only confirms that the CNN-based strategy works for a variety of commodities but it also suggests a brand-new hybrid decision mechanism that greatly enhances trading results.
Unlike the literature, this proposed study offers an innovative contribution to the CNN-based prediction method by using the well-known pre-trained CNN models AlexNet, VGG16, GoogLeNet, and ResNet-50 for financial prediction. In addition, with the integration of the RSI filter, transaction decisions are made more reliably during the buying and selling process in the model.
3. Materials and Methods
3.1. Dataset
Within the scope of this study, 15 years of daily silver price per ounce data denominated in US dollars, covering the open market dates from 1 January 2010 to 31 December 2024, were used. The data were downloaded from www.investing.com and consist of 3907 records. The dataset’s key statistical properties for the closing prices over this period are as follows: minimum price of 11.98, maximum price of 48.45, mean price of 22.03, and a standard deviation of 6.33. The dataset was sourced and used in its raw form. No data preprocessing steps (e.g., scaling, differencing) or imputation of missing values were performed. The model’s ability to extract meaningful features from this raw, noisy data is a key aspect of our methodology.
To assess the generalization ability of the proposed model and to avoid overestimating performance due to fortuitous predictions, we adopted a walk-forward validation strategy with an expanding window approach. In the initial step of the walk-forward procedure, data from 2010 to 2019 (10 years) were used for training. The year 2020 was reserved as the first test set. In each subsequent iteration, the training window was expanded by one year: 2010–2020 for predicting 2021, 2010–2021 for 2022, and so on. This process was repeated five times, resulting in five disjoint out-of-sample test periods totaling 1302 trading days for robust model evaluation. The daily silver price per ounce chart and expanding window frames used in this study are shown in Figure 1.
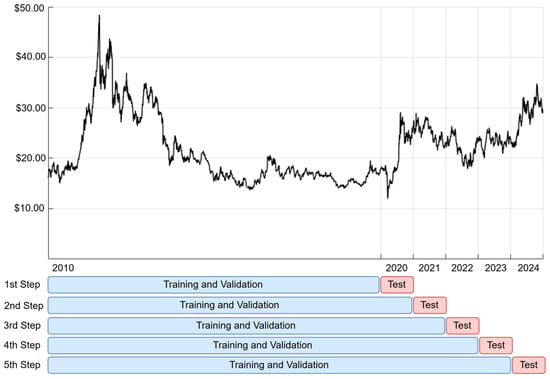
Figure 1.
Daily silver price per ounce chart and expanding window frames.
3.2. Data Labeling
The algorithmic silver trading model proposed within the scope of the study generates buy–sell signals based on price direction prediction. In order to make short-term silver price direction predictions, the data points are labeled as “Up” and “Down”. The labeling process is performed by comparing the closing price of each day with the closing price of the next day. The data are labeled as “Up” if the closing price increases the next day, and “Down” if it decreases the next day. If closing price of a given day is equal to that of the next day, the label of next day is assigned. Additionally, in order to label the data of the last transaction day, one day of data dated 1 January 2025 was included in the dataset. The data labeling procedure was carried out according to Equation (1).
where and represent the label of the tth and (t + 1)th day, respectively; and represent the closing prices of the tth and (t + 1)th days, respectively.
3.3. Creating Image Representations of Data
To convert time series data into graphical images, the closing prices along with the technical analysis indicators, simple moving average (SMA) and Bollinger bands, were used. SMA was calculated for 10-, 20-, 30-, 40-, and 50-day periods.
SMA is one of the most commonly used moving average (MA) types. In simple terms, it is the average of the closing prices of a financial asset within a specified period [39]. SMA is calculated according to Equation (2).
Here, t represents the tth day SMA is calculated, and m represents the number of days SMA will be calculated for. , represents the closing price of the nth day.
Bollinger bands are volatility bands placed above and below the MA. The middle band is the n-period MA. The upper and lower bands are calculated by adding and subtracting m times the standard deviation of the n-period price to the n-period MA, respectively [39]. Bollinger bands are calculated according to Equations (3)–(5).
Here, n represents the number of periods for which Bollinger bands are calculated, and m represents the number of standard deviations to be added or subtracted. MA(n) represents the n-period MA, and σ(n) represents the n-period price standard deviation. In this study, Bollinger bands were calculated for the SMA in the 20-day period, and the m value was set to 2.
Each image was generated over a 15-day window, ending at time t. The choice of a 15-day look-back window for our visual representations was not arbitrary. It was informed by a series of preliminary empirical analyses conducted during the model’s development. These experiments consistently demonstrated that the 15-day window size provided an optimal balance for capturing meaningful chart patterns predictive of price movements. Furthermore, this selection aligns with common practices in technical analysis, where similar timeframes are frequently used for identifying key chart patterns. While a comprehensive sensitivity analysis on window size could offer further insights, our decision is grounded in these initial findings.
For each of the 15 days within this window (from t − 14 to t), we calculated 10-, 20-, 30-, 40-, and 50-day SMAs and Bollinger bands. To compute the 50-day SMA for the earliest day in the window (t − 14), access to price data from t − 63 onwards is required. Consequently, a total of 64 consecutive past days (from t − 63 to t) were used to construct each image. Since 50-day SMA needed to be calculated for each day, in order to create the graphical image of 1 January 2010, 63 days of data between 6 October 2009 and 31 December 2009 were included in the dataset. The goal was to predict the direction of the price movement on day t + 1 using only past data, thereby ensuring a strictly causal structure and eliminating any risk of data leakage.
To visually encode these technical patterns, each chart was constructed using solid lines. All visualizations were rendered on a white background to ensure high contrast and consistency across samples. To preserve visual priority and enable the detection of key chart structures, such as short-term SMAs crossing long-term ones or the narrowing of indicator bands, the plotted lines were drawn in a deliberate order: the upper and lower Bollinger bands were rendered first, followed by the 50-, 40-, 30-, 20-, and 10-day SMAs, with the closing price placed last. We would like to note that the middle Bollinger band was not explicitly drawn, as it is mathematically equivalent to the 20-day SMA. Each line was assigned a unique hexadecimal color code: #404BE3 for the upper Bollinger band, #217B7E for the lower Bollinger band, #EDA323 for the 50-day SMA, #8DA8DF for the 40-day SMA, #FD4299 for the 30-day SMA, #C06DF8 for the 20-day SMA, #87AEDC for the 10-day SMA, and #741B47 for the closing price. These colors were selected carefully to ensure that all RGB channels contained nonzero values. While the specific color choices were not semantically meaningful, they were intended to distribute visual variation across channels and prevent any channel from being empty or redundant. All colors and line placements were applied consistently across all samples to ensure visual coherence and reproducibility.
Furthermore, this visual format, which consistently applied color, order, and line style, was intentionally designed to support spatial feature learning by convolutional layers. It preserved key visual relationships among indicators, such as MA crossovers and Bollinger band contractions, which are the types of structural patterns CNNs are particularly adept at learning, especially when provided with uniform input formatting. Preliminary experiments also suggested that excessively thick lines could obscure the precise structure of intersections or edge transitions between indicators. Therefore, a 4-pixel line width was chosen to balance visual clarity and the model’s ability to extract relevant spatial features from overlapping elements. The image generation process is illustrated in Figure 2.
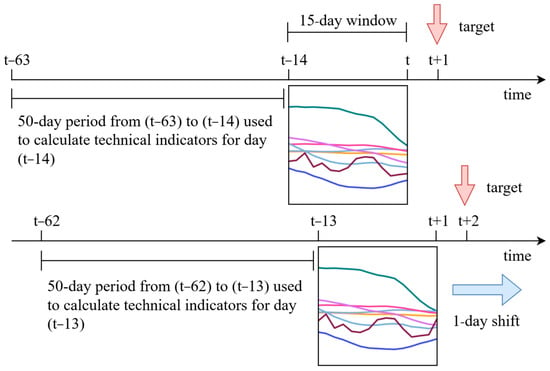
Figure 2.
The image generation process.
The created image dataset consists of a total of 3907 images, 1893 of which belong to the down class and 2014 of which belong to the up class. The graphical images with a resolution of 626 × 626 pixels obtained using technical analysis indicators were saved as separate files in PNG format. The input image size of AlexNet, one of the pre-trained CNN architectures used in this study, is 227 × 227 pixels; Since the input image size of VGG16, GoogLeNet, and ResNet-50 CNN architectures is 224 × 224 pixels, the generated graphic images are resized to 227 × 227 and 224 × 224 pixels resolutions. Sample images from the generated image dataset are shown in Figure 3.
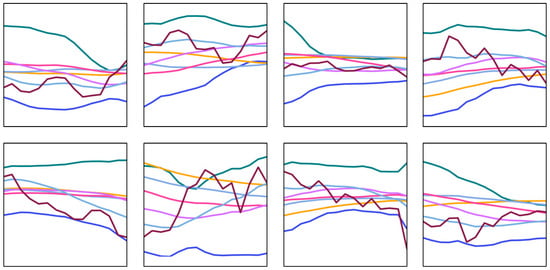
Figure 3.
Sample images from the generated image dataset, with ‘Up’ class samples shown in the top row and ‘Down’ class samples in the bottom row.
3.4. Proposed Prediction Model
CNN is a deep learning architecture that learns spatial dependencies within the data automatically across network layers. It can be applied to 1D (time series), 2D (image), or 3D (video) data [40]. The success of AlexNet, one of the pioneering CNN architectures, in the ImageNet competition led the computer vision community to turn to this field entirely [40]. Interest in CNN architectures is not limited to the computer vision community. Researchers from different fields, such as natural language processing and time series analysis, have also adapted CNN architectures to their own problems [41]. CNN architectures have been used alone or as part of a solution in hybrid models for financial time series forecasting, and the use of CNNs in this field continues with increasing interest. When the studies using CNN in financial time series forecasting in the literature are examined, it is seen that the models used are low-complexity models. In this study, an algorithmic silver trading model based on pre-trained CNN models and a transfer learning approach is proposed, motivated by the hypothesis that high-complexity models can achieve superior performance due to the complex nature of the problem. There are several reasons for using pre-trained CNN models: (i) Pre-trained CNN models have proven to be successful in image classification problems, having effectively addressed the 1000-class challenge posed by the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) [42]. (ii) Pre-trained CNN models have high complexity. (iii) Pre-trained CNN models can be adapted to similar but distinct problems with limited data [43]. (iv) They converge more rapidly during training compared to models trained from scratch. Thus, model training is completed in a shorter time [43,44].
Within the scope of this study, four pre-trained CNN architectures (AlexNet, VGG16, GoogLeNet, and ResNet-50) were fine-tuned and adapted to the problem, and their classification and profitability performances were compared. These architectures are briefly described as follows:
- AlexNet is a pioneering CNN architecture that won the ILSVRC 2012 competition by a significant margin and marked a breakthrough in deep learning. The network consists of eight layers. Three of these layers are fully connected, and five are convolutional. Thanks to the deep structure and relative simplicity of image data, more efficient feature extraction is possible;
- VGG16 is a deep CNN architecture that stands out with its consistent architecture pattern and the use of small (3 × 3) convolutional filters. Its 16 weight layers enable it to learn complex hierarchical representations. Despite having a large number of parameters (approximately 138 million), VGG16 has strong feature extraction capabilities, making it highly effective for transfer learning tasks;
- GoogLeNet is the first architecture to include the Inception module, which integrates multiple convolutional operations to facilitate multi-scale feature extraction in a single layer. Despite its depth of 22 layers, GoogLeNet maintains computational efficiency through the use of Inception modules, which incorporate 1 × 1 convolutions to reduce dimensionality. GoogLeNet is well known for finding a balance between depth and computational cost;
- ResNet-50 was built as a 50-layer deep residual network to address the vanishing gradient problem in very deep networks. The network can learn identity mappings, and training convergence is significantly improved by using residual connections, also known as skip connections. ResNet-50 is one of the most widely used transfer learning architectures because it combines significant depth with manageable computational complexity.
Before generating the final buy–sell signals, RSI [45], a technical analysis indicator commonly used by traders, was integrated into our forecasting model in order to minimize the risks arising from incorrect predictions. RSI is used by traders to identify overbought and oversold conditions and to generate potential buy–sell signals. RSI has been integrated into our model as a filter to prevent the fine-tuned models from generating buy signals under overbought conditions and sell signals under oversold conditions. The average of positive closes obtained in Equation (6) and the average of negative closes obtained in Equation (7) are the basis for calculating the RSI value in Equation (8).
In Equation (6), p represents the number of positive closes in the considered time period. In Equation (7), n represents the number of negative closes in the considered time period. (n + p) denotes the number of samples used for RSI and generally covers the last 14 time periods. Ki denotes the closing price in the current time period, while Ki−1 denotes the closing price of the previous day. The RSI is calculated according to Equation (8) and takes values between 0 and 100. In general, values above 50 suggest bullish momentum, while values below 50 indicate bearish momentum. RSI is also commonly used for generating trading signals. When the RSI falls below 30, it is interpreted as an oversold condition and may signal a potential buying opportunity. Conversely, RSI values above 70 indicate overbought conditions and may suggest a potential selling signal.
While RSI values of 30 and 70 are commonly used to identify extreme oversold and overbought conditions, our model employs a more conservative filtering approach based on the 50-level. The primary objective is not to pinpoint extreme reversal points but to ensure that the CNN’s buy signals are executed only during a period of bearish momentum (RSI < 50) and sell signals during bullish momentum (RSI > 50). This filtering strategy aims to validate the model’s directional prediction within the broader market trend, thereby reducing spurious signals and enhancing risk management. This approach acts as a simple yet effective heuristic layer, combining the visual pattern recognition of the CNN with a directional market momentum check.
In our proposed algorithmic silver trading model, the RSI is used to support the forecasts made by fine-tuned CNN models, thus improving profitability by eliminating erroneous forecasts. In this study, the final buy–sell signal forecasts of proposed algorithmic silver trading model were generated according to Algorithm 1. The overall schematic of the proposed model is shown in Figure 4.
| Algorithm 1. Final buy–sell decision. | |
| 1 | Function FinalDecision() |
| 2 | model_prediction ← Prediction obtained from the fine-tuned CNN model |
| 3 | rsi ← RSI calculated over the last 14 time periods |
| 4 | if model_prediction == “Up” and rsi < 50 then |
| 5 | return “Buy” |
| 6 | else if model_prediction == “Down” and rsi > 50 then |
| 7 | return “Sell” |
| 8 | else |
| 9 | return “Hold” |
| 10 | End Function |
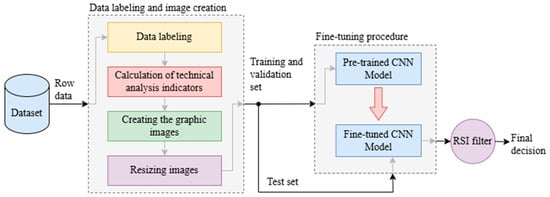
Figure 4.
Overall schematic of the proposed algorithmic silver trading model.
3.5. Experimental Setup
To assess the proposed model’s generalization ability and prevent overestimating performance from lucky predictions, we used a walk-forward validation strategy with an expanding window approach. This method offers a more realistic evaluation of the model’s long-term predictive power. We chose an expanding window over a rolling window approach because a rolling window would discard early, trend-rich data. This is particularly important given the strong upward trend observed in the first two years of the dataset, which could otherwise lead to underfitting. The expanding window, however, retains long-term patterns while gradually adding more recent information.
For the initial walk-forward step, we used data from 2010 to 2019 (10 years) for training, with 2020 as the first test set. We also set aside 20% of the training data as a randomly selected validation set. This random selection avoided underfitting by preventing the validation set from overrepresenting a particular trend period. The validation set was not used for hyperparameter tuning, but only for early halting and overfitting control. We extended the training window by one year in each subsequent iteration (for example, 2010–2020 for 2021 prediction, 2010–2021 for 2022 prediction, and so on). This procedure was carried out five times, resulting in five different out-of-sample test periods for a comprehensive assessment of the model.
To account for the stochastic nature of deep learning training, each model was trained three times. The instance whose validation accuracy was closest to the mean of the three runs was selected for testing. This approach ensures an objective evaluation by avoiding the practice of selecting models based on positive test results.
The use of early stopping served as a regularization technique. Training was stopped if no improvement was seen for five consecutive epochs after the model was assessed on the validation set at each epoch. By avoiding needless training time, this criterion made sure the model did not overfit to the training set.
Data leakage was carefully prevented at all stages of the workflow. Only historical data were used during image generation and model tuning. The test dataset was never seen during the tuning and model selection processes. The validation set was drawn solely from the training data and was never used to guide decisions about test performance. This separation ensured that no information from the test periods influenced model tuning or evaluation. Therefore, model selection, tuning, and performance reporting were performed without exposure to test results, thus eliminating the possibility of cherry-picking.
4. Model Evaluation
4.1. Classification Metrics
The classification performance of the proposed CNN models was evaluated using accuracy, precision, recall, and F1-score. The mathematical definitions of these metrics are presented below.
In these equations, TP (true positives), TN (true negatives), FP (false positives), and FN (false negatives) are derived from the confusion matrix. In binary classification, one class is designated as the positive class and the other as the negative class. In this study, the “Down” class was treated as the positive class, and the “Up” class as the negative class. Accordingly, TP refers to correctly predicted instances of the down class. TN refers to correctly predicted instances of the up class. FP refers to up instances incorrectly predicted as down. FN refers to down instances incorrectly predicted as up.
4.2. Backtesting Protocol and Profitability Analysis
The main objective of algorithmic trading is to generate accurate buy and sell signals that capitalize on price fluctuations to maximize profitability. While financial time series forecasting is traditionally approached as a regression task, it is frequently reformulated as a classification problem, particularly when the focus is on directional movement or signal generation. However, a model’s classification performance by itself does not fully reflect its financial profitability. A model with high prediction accuracy may have low profitability or even loss outcomes due to the asymmetric structure of financial markets, where not every transaction contributes equally to profitability. To show this inconsistency, Matsubara et al. [46] reported a scenario in which a model achieved above 60% classification accuracy but suffered a 22% cost loss. Li and Baston [47] pointed out that just one-third of the examined research contained profitability analyses, indicating a serious gap in evaluation methods. To address this, we employed a walk-forward validation approach using an expanding window over a five-year out-of-sample period (1 January 2020–31 December 2024). Unlike a static holdout, this method retrains the model annually with increasing historical data, better reflecting real-world application scenarios. In particular, a distinct model was trained using data from 2010 to y − 1 for each year y ∈ {2020, 2021, …, 2024}, and projections were only produced for year y. As a result, five distinct models were produced, each of which was assessed using a non-overlapping test set. This allowed for the evaluation of financial performance on an annual basis as well as temporal robustness.
In the backtesting protocol, each model was subjected to a realistic market simulation. Trading began with an initial capital of USD 10,000, and operations followed a full-position trading strategy: the entire capital was allocated upon the first buy signal and liquidated at the first subsequent sell signal. Only the first signal was processed if several successive signals of the same type were created; all further identical signals were ignored until the position was reversed. Transaction expenses were incorporated into the backtesting process in order to replicate actual trading circumstances. Commission and slippage expenses were taken into consideration. The commission was set at 0.1% for each transaction, which reflects a realistic rate commonly observed in actual financial markets. Slippage was modeled as 0.1%, representing the price difference that may occur between the time a trade signal is generated and the time the trade is actually executed. It is portrayed as a negative adjustment to reflect more realistic trading conditions, even though slippage can lead to either positive or negative price changes. To prevent overly optimistic forecasts and make sure that performance results more accurately represent actual trading situations, these settings are applied to all models.
Profitability was evaluated using a range of financial performance metrics, including Sharpe ratio [48], cumulative return, average annual return, maximum drawdown [49], number of transactions, and a cumulative return curve. The profitability metrics used in this study are defined as Equations (13)–(16).
where is the average annual return of the model, is the standard deviation of annual returns, and is the annual risk-free rate. In this study, correspond to the average yields of 1-year U.S. Treasury securities, which were obtained from the Federal Reserve Economic Data series “GS1.” For the years 2020 through 2024, the rates were 1.53%, 0.10%, 0.55%, 4.69%, and 4.79%, respectively. These values ensure consistency between the evaluation horizon and the maturity of the risk-free benchmark.
where is the starting capital, and is the final capital value at the end of the backtesting period. Cumulative return represents the overall percentage gain or loss over the evaluation period.
where denotes the return achieved in year , and is the number of years in the evaluation period. This metric gives the arithmetic average of annual returns.
where denotes the capital value at time , and represents the highest capital value observed up to time . The drawdown at any time is defined as the percentage decline from the historical peak. The maximum drawdown (Max DD) is the largest of these drawdown values across the entire investment horizon . It captures the worst-case peak-to-trough decline in capital.
4.3. Benchmark Strategies
In order to place the proposed model in a broader context, its outcomes were analyzed alongside three benchmark strategies: the buy-and-hold method, a rule-based approach based on the RSI, and a naive predictor. Each method operated under identical historical test conditions and assumed transaction costs, ensuring that performance metrics remained directly comparable.
The buy-and-hold method, widely used to represent passive investment behavior, involves taking a position at the beginning of the evaluation period and keeping it unchanged until the end. It was used as a baseline strategy, as it is frequently adopted as a benchmark in algorithmic trading studies. Although simple in implementation, this strategy tends to mirror the broader movement of the market and serves as a common point of reference in comparative performance analyses.
The RSI-based strategy [45] responds to short-term fluctuations by observing recent price momentum. In this study, the index was computed using a 14-day period, a common configuration in the financial literature. Instances where the RSI dropped below the threshold of 30 were taken as indicative of potentially undervalued conditions, whereas readings above 70 were viewed as signs of possible overvaluation. Despite its simplicity and widespread use, the method can produce unreliable signals, particularly in markets with sharp reversals or irregular price behavior.
The naive predictor serves as a baseline reference by assuming that the price movement will repeat the previous one. Despite its simplicity, such models are frequently used in financial time series forecasting studies to establish a lower-bound benchmark for evaluating predictive performance. Despite its simplicity, the naive predictor is widely accepted as a minimum performance baseline in the financial time series forecasting literature.
Deep learning models like LSTM and Transformer are often used in financial time series forecasting. However, in this study, they were not included in the benchmarking comparisons. The literature reports divergent results regarding their relative effectiveness. For example, Sezer and Ozbayoglu [15] reported that CNN outperforms LSTM and other deep learning models, while Tsantekidis and Tefas [50] found the opposite, with LSTM outperforming CNN. These discrepancies highlight the methodological difficulty of making robust comparisons between model types, given their sensitivity to hyperparameters and training protocols. In the absence of a standardized evaluation framework, such comparisons risk leading to imprecise or misleading interpretations.
Furthermore, although benchmark strategies such as buy-and-hold, RSI-based rules, and a naive predictor are included in this study for comparative purposes, direct quantitative comparison with related work is not attempted. This is due to substantial differences in financial instruments (e.g., equities, cryptocurrencies, precious metals), training data horizons, forecasting windows, and non-overlapping test periods. Such heterogeneity makes cross-study performance comparisons unreliable and potentially misleading. Notably, even the same model can produce varying results across different test periods, emphasizing the challenges of establishing consistent benchmarks in financial forecasting.
Therefore, rather than attempting to establish superiority over other deep learning models, the current study focuses on demonstrating the effectiveness of CNN-based architectures within a controlled visual representation framework. This approach is intended to contribute to methodological diversity in financial forecasting, emphasizing the potential value of technical indicator-based visual inputs.
5. Experimental Results
5.1. Training Dynamics and Validation Trends
Labeling of historical silver price data, calculation of technical analysis indicators, generation of image representations, fine-tuning of CNN models, final buy–sell signal generation, and profitability analyses were performed in the MATLAB (R2020b) environment. The computer used in this study was equipped with a 2.6 GHz i5 processor, 512 GB SSD hard disk, 8 GB DDR4 RAM, and 4 GB graphics card.
Stochastic gradient descent with momentum (SGDM) was used as the fine-tuning procedure for the CNN architectures used in this study. The stochastic gradient descent (SGD) algorithm can oscillate across the steepest descent path while approaching the optimum. Adding a momentum term to the parameter updates is a common technique to reduce these oscillations and accelerate convergence [51].
The hyperparameter values used for fine-tuning the CNN models were set as follows: The last fully connected layers of the models were replaced with a fully connected layer with two outputs. The maximum epoch number was set to 100, the mini-batch size to 32, and the learning rate was set to 10−4.
The definitions of the CNN architectural components used in this study, the number of training completion steps, the time elapsed for training, and the average validation accuracy, along with the corresponding standard deviation, are presented in Table 1.

Table 1.
Architectural properties and training outcomes of the fine-tuned CNN models.
5.2. Classification Results
A walk-forward validation strategy with an expanding window was applied over a five-year period, with each year using a separate out-of-sample evaluation window, and four different CNN architectures were tested. The performance of these models was measured on metrics such as classification accuracy and ability to identify positive–negative classes, etc. The results, including mean and standard deviation values, are presented in Table 2. These figures are based on a total of 1302 out-of-sample trading days obtained through five walk-forward validation cycles.

Table 2.
Confusion matrix and classification performance results.
In general, the models’ categorization accuracy results were not very impressive. It is not surprising that historical price patterns rarely offer reliable indicators of future movements, given the erratic and poorly linked nature of financial time series. The majority of accuracy scores fell between 48.5% and 58.8%, and in certain test years, they even fell below that.
Beyond classification accuracy, the differences between the models became more apparent when looking at how well they handled class imbalance. VGG16 and ResNet-50 demonstrated superior balance across the four architectures, exhibiting less variation from year to year and sustaining consistent F1 scores. These models imply that, possibly as a result of variations in the way they extract and process characteristics, both models are more stable in the face of shifting market conditions.
Model architecture clearly played a role in shaping these results. Deeper or more structured networks appeared to handle volatility and asymmetry more effectively, especially when rare events had to be distinguished from dominant trends. In contrast, AlexNet’s performance was closer to random guessing. Across the five test years, its average accuracy was 50.00 ± 1.73%. The corresponding precision, recall, and F1 score values were 47.81 ± 3.94%, 41.05 ± 6.15%, and 44.06 ± 4.79%, respectively. While the F1 score indicated that some meaningful discrimination was made (especially in detecting less frequent outcomes), the wide variability in recall highlights an underlying instability. To put it another way, the model’s capacity to capture minority class cases seemed to fluctuate greatly throughout the year, which raises questions about how reliable it will be in shifting circumstances.
5.3. Profitability Analysis Results
The profitability analysis outcomes for the proposed model and benchmark strategies are presented in Table 3, including the Sharpe ratio, average annual return, maximum drawdown, cumulative return, and transaction count. All metrics were computed based on transaction cost-adjusted results, with the exception of the cost-free cumulative return column, which is provided exclusively to demonstrate the effect of transaction costs on profitability. The profitability metrics indicate model performance over 1302 trading days during the five-year out-of-sample testing period.

Table 3.
Profitability and risk metrics for all compared strategies (2020–2024).
When the test results are examined, it is seen that the most successful performance was achieved when the VGG16 model was combined with RSI filtering. This structure attracted attention with a total return of 115.03% and a Sharpe ratio of 0.68, while a low standard deviation value of 0.29 revealed that the model exhibited stable performance on an annual basis. Similarly, ResNet-50 and GoogLeNet models also produced stable results when supported with the RSI filter; although they did not provide high profits, they limited volatility and reduced maximum losses, offering a more balanced risk-return profile.
As the weak link of the model, AlexNet, which was used without any filtering, produced the weakest result. It ended the period with a loss of 8.39%, a negative Sharpe ratio (−0.26), and the steepest decline observed (48.67%). This suggests that generating a large number of signals offers little advantage unless accompanied by a mechanism to weed out the unreliable ones.
The buy-and-hold strategy provided a total return of 61.62% but was subject to significant fluctuations, especially during downturns, with a maximum peak loss of 38.77%. In contrast, the classic RSI rule performed more consistently. Although it did not produce high gains, it showed a balanced stance that would be suitable for risk-averse investor profiles.
The inclusion of transaction costs has a significant impact on the cumulative returns of the evaluated strategies. While classification-based studies often overlook such real-world frictions, our results indicate that transaction costs can critically alter a strategy’s profitability profile. For example, although the AlexNet model yields a cumulative return of 59.83% in the absence of transaction costs, this drops to –8.39% when costs are included. A similar pattern is observed across most strategies. This reinforces the importance of incorporating realistic market conditions, such as commissions and slippage, into backtesting frameworks. Without such considerations, the perceived performance of an algorithm may be overly optimistic and practically misleading.
Figure 5 presents the cumulative return curves obtained from the profitability analysis, comparing the capital growth achieved by each model over time.
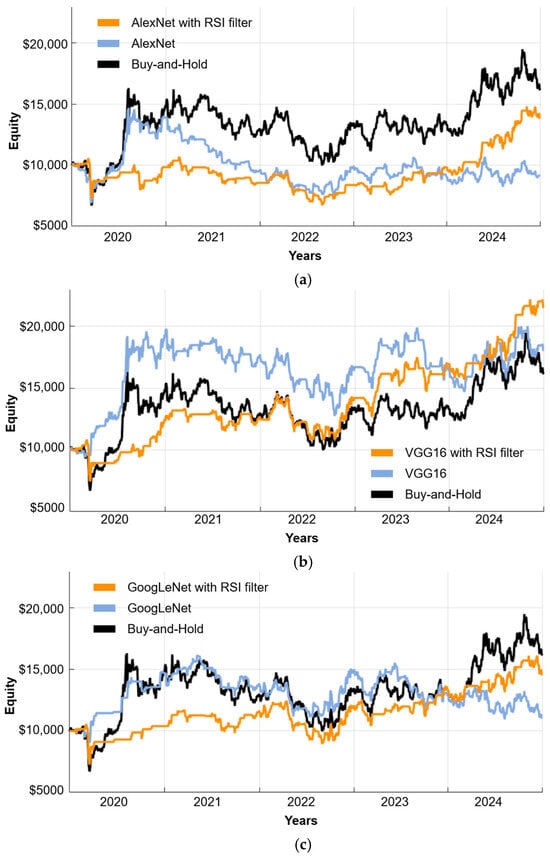
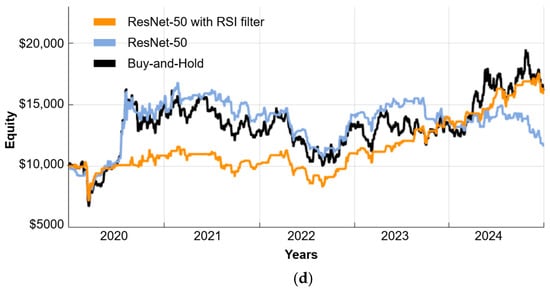
Figure 5.
Cumulative return curve of the proposed algorithmic trading model based on the AlexNet (a), VGG16 (b), GoogLeNet (c), and ResNet-50 (d) CNN architectures, along with the buy-and-hold investment strategy used for comparison.
5.4. Correlation Between Classification Performance and Profitability
In this study, to examine the relationship between classification performance and financial returns, the classification accuracy of each model with an RSI-filtering mechanism over a five-year period was statistically compared with the corresponding annual percentage capital changes. For this purpose, the Pearson correlation coefficient (to assess linear association) and the Spearman rank correlation coefficient (to assess monotonic relationships) were calculated for each model [52]. The resulting correlation coefficients are presented in Table 4.

Table 4.
Correlations between classification performance and financial profitability.
The findings indicate that none of the four models exhibited a consistent or statistically strong correlation between classification accuracy and profitability. For instance, the AlexNet model showed a negative correlation, while VGG16 and GoogLeNet yielded positive but weak correlations. In the case of ResNet50, the Spearman correlation was exactly zero. These results suggest that increases in classification accuracy do not necessarily lead to improved financial outcomes, and that there is no strong relationship between these two metrics across the tested models.
6. Discussion
This study proposes a novel algorithmic trading model for silver that combines fine-tuned CNNs with a decision filter based on RSI. By converting time series data into image representations based on technical analysis indicators, the model enables spatial extraction of buy and sell signals. This design leverages the natural pattern recognition capabilities of CNNs and has produced promising results, particularly in terms of profitability after accounting for transaction costs.
The findings indicate that classification accuracy alone is insufficient to explain financial performance. Statistical analyses conducted as part of this study reveal a weak or inconsistent relationship between classification performance and financial returns. This can be attributed to the asymmetric nature of financial outcomes: incorrect trading signals can result in disproportionately large losses compared to the limited gains from correct signals. While some previous studies place substantial emphasis on prediction accuracy in financial modeling, our results show that high accuracy rates do not guarantee economic gains. Therefore, model evaluation based solely on accuracy must be complemented by an economic impact analysis, particularly in real-world trading contexts.
The divergence between high accuracy and low profitability is further explained by two core reasons: trading signal frequency and cost sensitivity. A high-accuracy model that generates frequent trading signals can still be unprofitable, as the cumulative drag of transaction costs from many trades can outweigh the profits from successful predictions. This phenomenon, which we observed in our higher-frequency models, highlights the critical role of cost sensitivity. Conversely, a less accurate model that makes fewer, more strategic trades can achieve higher profitability and better risk-adjusted returns by minimizing these costs. This demonstrates that for real-world trading, model evaluation must extend beyond accuracy metrics to include an in-depth analysis of signal frequency and cost sensitivity.
Transaction costs emerged as a critical factor affecting the feasibility of the strategy. For instance, while the AlexNet model delivered relatively high returns when transaction costs were excluded, its profitability dropped to negative levels once costs were included. High-frequency models such as ResNet-50 and AlexNet caused significant capital erosion, in some cases exceeding 80% of the cost-free gains. The outperformance of our proposed model relative to the buy-and-hold strategy is particularly noteworthy, especially considering the predominantly upward market trend during the evaluation period. In a rising market, the buy-and-hold strategy consistently gains from the market’s natural appreciation while incurring minimal transaction costs. An active trading strategy, on the other hand, must generate returns strong enough to overcome the cumulative drag of transaction costs, which can quickly erode profits from successful trades. Our model’s ability to more than double the returns of the passive benchmark thus highlights its robustness; its trading signals were not only accurate but also powerful enough to consistently generate alpha even after accounting for the significant hurdle of transaction costs in an upward-trending market. In contrast, the VGG16 model, especially when paired with the RSI filter, exhibited a more selective and efficient trading behavior, significantly reducing unnecessary trades and preserving profitability.
Notably, although the RSI indicator alone did not yield a profitable strategy (Sharpe ratio: 0.08; Avg. annual return: 1.72%), integrating the RSI as a filter with CNN-based models consistently improved key performance metrics. For instance, the VGG16 model’s Sharpe ratio increased from 0.34 to 0.68, and the cumulative return improved from 80.63% to 115.03% when RSI filtering was applied. Similarly, other CNN architectures showed increased Sharpe ratios and reduced drawdowns with RSI integration (see Table 3). These quantitative results provide clear empirical evidence that RSI filtering helps reduce erroneous trade signals, enhancing the overall robustness and profitability of the proposed model.
Methodologically, the use of a 15-day window played a key role in stabilizing model decisions. Models like VGG16 and GoogLeNet avoided reacting to short-term market noise and instead waited for more stable and structured chart patterns before executing trades. This suggests that visual encodings not only offer alternative forms of data representation but may also serve as a natural time series smoothing mechanism.
Finally, when the model’s performance was compared with both a naive predictor strategy and traditional approaches such as buy-and-hold and RSI, it became evident once again that profitability should be evaluated not only in terms of technical accuracy but also economic significance. Despite its simplicity, the naive strategy’s poor financial performance underscored the importance of informed signal generation.
This study presents a holistic approach that incorporates not only classification accuracy but also strategic and economic viability. It provides a novel contribution to the algorithmic trading literature by demonstrating the utility of decision support based on visual representations. Naturally, certain limitations exist. The model was tested solely in the silver market; therefore, the generalizability of these results to asset classes with different volatility regimes may be limited. Furthermore, the visual representations depend on specific encoding choices (e.g., different timeframes, indicator combinations, or chart types), which may yield varying results. These aspects warrant more detailed investigation in future research.
7. Conclusions
This study proposes a novel algorithmic trading model that transforms visual representations based on technical indicators into buy and sell decisions by employing a fine-tuned CNN combined with an RSI-based filter. The proposed VGG16-based model achieved a cumulative return of 115.03% in a five-year out-of-sample test period, nearly doubling the 61.62% return delivered by the buy-and-hold strategy over the same period.
This finding directly challenges a widely accepted assumption in the literature that algorithmic models tend to underperform passive strategies, particularly during upward market trends. In contrast, the results of this study demonstrate that well-structured deep learning models can outperform passive benchmarks even in trend-following market conditions. These results underline the potential of visually driven deep learning systems to deliver not only technically sound but also economically viable trading strategies—especially when enriched with decision-filtering techniques.
Key findings of the study are as follows: (i) There is no strong relationship between predictive accuracy and financial performance. Therefore, financial models should be evaluated not only in terms of statistical precision but also economic impact. (ii) Transaction costs are a critical determinant of strategy profitability. Even if gross returns appear favorable, realistic cost assumptions can reverse profitability. Thus, transaction costs must be treated as a core dimension in model evaluation. (iii) The integration of domain-specific indicators (e.g., RSI) has led to more disciplined and efficient trading behavior. This underscores the practical value of hybrid systems that combine expert knowledge with AI. (iv) The 15-day window enabled the recognition of chart patterns commonly used in technical analysis, helping models produce fewer but more meaningful signals.
The proposed model has several potential applications in real-world trading and investment contexts: (i) The model’s ability to generate trading signals directly from financial charts makes it suitable for use in decision support systems. (ii) It can serve as an interpretive aid in semi-automated investment decision systems. (iii) It can function as a core signal-generation module in fully automated algorithmic trading systems. (iv) Eventually, it could become a key component of robo-advisor platforms capable of recognizing visual financial patterns.
Several directions for future research can be identified to enhance and extend the findings of this study: (i) Testing the model on different asset classes is essential for evaluating its generalizability. (ii) Considering that different CNN architectures are capable of capturing different feature sets, ensemble models that combine multiple CNNs may offer further performance improvements. (iii) Most importantly, there is a critical need to develop standardized evaluation protocols in financial AI that account for both predictive performance and economic outcomes.
Author Contributions
Conceptualization, Y.A. and A.F.K.; methodology, Y.A. and A.F.K.; software, Y.A.; validation, Y.A., F.O. and A.F.K.; formal analysis, Y.A.; investigation, Y.A.; resources, Y.A.; data curation, Y.A.; writing—original draft preparation, Y.A.; writing—review and editing, Y.A., F.O., and A.F.K.; visualization, Y.A.; supervision, F.O. and A.F.K. All authors have read and agreed to the published version of the manuscript.
Funding
This study was conducted as part of Y.A.’s doctoral dissertation and received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fameliti, S.P.; Skintzi, V.D. Uncertainty indices and stock market volatility predictability during the global pandemic: Evidence from G7 countries. Appl. Econ. 2024, 56, 2315–2336. [Google Scholar] [CrossRef]
- Hasbrouck, J.; Saar, G. Low-latency trading. J. Financ. Mark. 2013, 16, 646–679. [Google Scholar] [CrossRef]
- Jones, C.M. What Do We Know About High-Frequency Trading? SSRN Electron. J. 2013. [Google Scholar] [CrossRef]
- Hendershott, T.; Jones, C.M.; Menkveld, A.J. Does algorithmic trading improve liquidity? J. Financ. 2011, 66, 1–33. [Google Scholar] [CrossRef]
- Tang, Y.; Song, Z.; Zhu, Y.; Yuan, H.; Hou, M.; Ji, J.; Tang, C.; Li, J. A survey on machine learning models for financial time series forecasting. Neurocomputing 2022, 512, 363–380. [Google Scholar] [CrossRef]
- Lim, K.P.; Brooks, R.D. Why do emerging stock markets experience more persistent price deviations from a random walk over time? A country-level analysis. Macroecon. Dyn. 2010, 14, 3–41. [Google Scholar] [CrossRef]
- Clements, M.P.; Franses, P.H.; Swanson, N.R. Forecasting economic and financial time-series with non-linear models. Int. J. Forecast. 2004, 20, 169–183. [Google Scholar] [CrossRef]
- Wang, H.; Song, S.; Zhang, G.; Ayantoboc, O.O. Predicting daily streamflow with a novel multi-regime switching ARIMA-MS-GARCH model. J. Hydrol. Reg. Stud. 2023, 47, 101374. [Google Scholar] [CrossRef]
- Li, T.; Zhong, J.; Huang, Z. Potential Dependence of Financial Cycles between Emerging and Developed Countries: Based on ARIMA-GARCH Copula Model. Emerg. Mark. Financ. Trade 2020, 56, 1237–1250. [Google Scholar] [CrossRef]
- Zolfaghari, M.; Gholami, S. A hybrid approach of adaptive wavelet transform, long short-term memory and ARIMA-GARCH family models for the stock index prediction. Expert Syst. Appl. 2021, 182, 115149. [Google Scholar] [CrossRef]
- Altuntaş, Y.; Okumuş, F.; Kocamaz, A.F. Evrişimsel Sinir Ağları ve Transfer Öğrenme Yaklaşımı Kullanılarak Altın Fiyat Yönünün Tahmini. Comput. Sci. 2022, 7, 124–131. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, P.; Kumar, Y. Analysis of Financial Time Series Forecasting using Deep Learning Model. In Proceedings of the 2021 11th International Conference on Cloud Computing, Data Science & Engineering, Noida, India, 28–29 January 2021; pp. 877–881. [Google Scholar]
- Mehtab, S.; Sen, J. Analysis and Forecasting of Financial Time Series Using CNN and LSTM-Based Deep Learning Models. In Proceedings of the ICADCML 2021, Bhubaneswar, India, 15–16 January 2021; Springer: Singapore, 2022; pp. 405–423. [Google Scholar]
- Aldhyani, T.H.H.; Alzahrani, A. Framework for Predicting and Modeling Stock Market Prices Based on Deep Learning Algorithms. Electronics 2022, 11, 3149. [Google Scholar] [CrossRef]
- Sezer, O.B.; Ozbayoglu, A.M. Algorithmic financial trading with deep convolutional neural networks: Time series to image conversion approach. Appl. Soft Comput. 2018, 70, 525–538. [Google Scholar] [CrossRef]
- Khodaee, P.; Esfahanipour, A.; Taheri, H.M. Forecasting turning points in stock price by applying a novel hybrid CNN-LSTM-ResNet model fed by 2D segmented images. Eng. Appl. Artif. Intell. 2022, 116, 105464. [Google Scholar] [CrossRef]
- Ren, X.; Jiang, W.; Ji, Q.; Zhai, P. Seeing is believing: Forecasting crude oil price trend from the perspective of images. J. Forecast. 2024, 43, 2809–2821. [Google Scholar] [CrossRef]
- Thakkar, A.; Chaudhari, K. A comprehensive survey on deep neural networks for stock market: The need, challenges, and future directions. Expert Syst. Appl. 2021, 177, 114800. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Khashei, M.; Bijari, M.; Hejazi, S.R. Combining seasonal ARIMA models with computational intelligence techniques for time series forecasting. Soft Comput. 2012, 16, 1091–1105. [Google Scholar] [CrossRef]
- Dadhich, M.; Pahwa, M.S.; Jain, V.; Doshi, R. Predictive Models for Stock Market Index Using Stochastic Time Series ARIMA Modeling in Emerging Economy. In Lecture Notes in Mechanical Engineering, Proceedings of the CAMSE 2020, Virtual, 28–30 December 2020; Springer: Berlin/Heidelberg, Germany, 2021; pp. 281–290. [Google Scholar]
- Xing, D.Z.; Li, H.F.; Li, J.C.; Long, C. Forecasting price of financial market crash via a new nonlinear potential GARCH model. Phys. A Stat. Mech. Its Appl. 2021, 566, 125649. [Google Scholar] [CrossRef]
- Li, X.; Feng, S.; Hou, N.; Li, H.; Zhang, S.; Jian, Z.; Zi, Q. Applications of Kalman Filtering in Time Series Prediction. In Lecture Notes in Mechanical Engineering, Proceedings of the ICIRA 2022, Harbin, China, 1–3 August 2022; Springer: Berlin/Heidelberg, Germany, 2022; Volume 13457 LNAI, pp. 520–531. [Google Scholar]
- Kurani, A.; Doshi, P.; Vakharia, A.; Shah, M. A Comprehensive Comparative Study of Artificial Neural Network (ANN) and Support Vector Machines (SVM) on Stock Forecasting. Ann. Data Sci. 2023, 10, 183–208. [Google Scholar] [CrossRef]
- Basak, S.; Kar, S.; Saha, S.; Khaidem, L.; Dey, S.R. Predicting the direction of stock market prices using tree-based classifiers. N. Am. J. Econ. Financ. 2019, 47, 552–567. [Google Scholar] [CrossRef]
- Hu, W.; Shao, C.; Zhang, W. Predicting U.S. bank failures and stress testing with machine learning algorithms. Financ. Res. Lett. 2025, 75, 106802. [Google Scholar] [CrossRef]
- Lu, E.; Li, M. Electricity Price Forecasting Enhancement Using Combined Model. In Proceedings of the 2024 56th North American Power Symposium (NAPS), El Paso, TX, USA, 13–15 October 2024. [Google Scholar]
- Dai, Z.Q.; Li, J.; Cao, Y.J.; Zhang, Y.X. SALSTM: Segmented self-attention long short-term memory for long-term forecasting. J. Supercomput. 2025, 81, 115. [Google Scholar] [CrossRef]
- Chen, Y.; Ye, N.; Zhang, W.; Fan, J.; Mumtaz, S.; Li, X. Meta-LSTR: Meta-Learning with Long Short-Term Transformer for futures volatility prediction. Expert Syst. Appl. 2025, 265, 125926. [Google Scholar] [CrossRef]
- Yilmaz, M.; Keskin, M.M.; Ozbayoglu, A.M. Algorithmic stock trading based on ensemble deep neural networks trained with time graph. Appl. Soft Comput. 2024, 163, 111847. [Google Scholar] [CrossRef]
- Temur, G.; Birogul, S.; Kose, U. Comparison of Stock ‘Trading’ Decision Support Systems Based on Object Recognition Algorithms on Candlestick Charts. IEEE Access 2024, 12, 83551–83562. [Google Scholar] [CrossRef]
- Pala, M.; Sefer, E. NFT price and sales characteristics prediction by transfer learning of visual attributes. J. Financ. Data Sci. 2024, 10, 100148. [Google Scholar] [CrossRef]
- El Bakai, M.; Boutyour, Y.; Idrissi, A. Creating a Customized Dataset for Financial Pattern Recognition in Deep Learning. Stud. Comput. Intell. 2024, 1166, 99–117. [Google Scholar] [CrossRef]
- Balamohan, S.; Khanaa, V. Revolutionizing Stock Market Prediction: Harnessing the Power of LSTM and CNN Hybrid Approach. SN Comput. Sci. 2024, 5, 919. [Google Scholar] [CrossRef]
- Altuntaş, Y.; Kocamaz, A.F. Derin Öğrenme Tabanlı Görüntü Sınıflandırma Yaklaşımı ile Borsa İstanbul 100 Endeks Yönünün Tahmini. Comput. Sci. 2023, 8, 93–101. [Google Scholar] [CrossRef]
- Achelis, S.B. Technical Analysis from A to Z; McGraw Hill: New York, NY, USA, 2001. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 7553. [Google Scholar] [CrossRef]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Kornblith, S.; Shlens, J.; Le, Q.V. Do better imagenet models transfer better? In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 2661–2671. [Google Scholar]
- He, K.; Girshick, R.; Dollar, P. Rethinking imagenet pre-training. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4918–4927. [Google Scholar]
- Wilder, J.W. New Concepts in Technical Trading Systems; Trend Research: Greensboro, NC, USA, 1978. [Google Scholar]
- Matsubara, T.; Akita, R.; Uehara, K. Stock Price Prediction by Deep Neural Generative Model of News Articles. IEICE Trans. Inf. Syst. 2018, E101.D, 901–908. [Google Scholar] [CrossRef]
- Li, A.W.; Bastos, G.S. Stock market forecasting using deep learning and technical analysis: A systematic review. IEEE Access 2020, 8, 185232–185242. [Google Scholar] [CrossRef]
- Sharpe, W.F. The Sharpe Ratio. J. Portf. Manag. 1994, 21, 49–58. [Google Scholar] [CrossRef]
- Bacon, C.R. Practical Risk-Adjusted Performance Measurement; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Tsantekidis, A.; Tefas, A. Transferring trading strategy knowledge to deep learning models. Knowl. Inf. Syst. 2021, 63, 87–104. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Hauke, J.; Kossowski, T. Comparison of values of Pearson’s and Spearman’s correlation coefficients on the same sets of data. Quaest. Geogr. 2011, 30, 87–93. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).