Abstract
In welding applications, line-structured-light vision is widely used for seam tracking, but intense noise from arc glow, spatter, smoke, and reflections makes reliable laser-stripe segmentation difficult. To address these challenges, we propose EUFNet, an uncertainty-driven symmetrical two-stage segmentation network for precise stripe extraction under real-world welding conditions. In the first stage, a lightweight backbone generates a coarse stripe mask and a pixel-wise uncertainty map; in the second stage, a functionally mirrored refinement network uses this uncertainty map to symmetrically guide fine-tuning of the same image regions, thereby preserving stripe continuity. We further employ an uncertainty-weighted loss that treats ambiguous pixels and their corresponding evidence in a one-to-one, symmetric manner. Evaluated on a large-scale dataset of 3100 annotated welding images, EUFNet achieves a mean IoU of 89.3% and a mean accuracy of 95.9% at 236.7 FPS (compared to U-Net’s 82.5% mean IoU and 90.2% mean accuracy), significantly outperforming existing approaches in both accuracy and real-time performance. Moreover, EUFNet generalizes effectively to the public WLSD benchmark, surpassing state-of-the-art baselines in both accuracy and speed. These results confirm that a structurally and functionally symmetric, uncertainty-driven two-stage refinement strategy—combined with targeted loss design and efficient feature integration—yields high-precision, real-time performance for automated welding vision.
1. Introduction
With the welding manufacturing industry advancing towards higher precision, greater efficiency, and enhanced intelligence, welding automation has emerged as one of its cornerstone technologies. It is widely applied in various industrial sectors, including automotive manufacturing, shipbuilding, aerospace, and others. However, constrained by both objective factors (e.g., harsh welding environments) and subjective limitations in technical expertise, traditional manual welding methods are no longer sufficient to meet the demands of modern manufacturing. In light of rapid advancements in robotics and artificial intelligence, intelligent welding has become a critically important innovation in industrial production. Under this trend, intelligent welding robots have arisen as powerful enablers, significantly improving weld quality and operational efficiency [1].
Equipped with visual sensing technology, intelligent welding robots achieve fully automated, intelligent, and unattended welding [2]. Among various vision-based sensing methods, active vision technologies based on laser structured light have become predominant in welding applications due to their non-contact operation, high energy density, and exceptional accuracy [3]. The schematic diagram illustrating the welding work process is presented in Figure 1. The principle of this approach involves projecting a laser line pattern onto the workpiece surface, capturing the deformed pattern with a camera, and then applying laser triangulation techniques to accurately locate and reconstruct the geometrical parameters of the target [4].
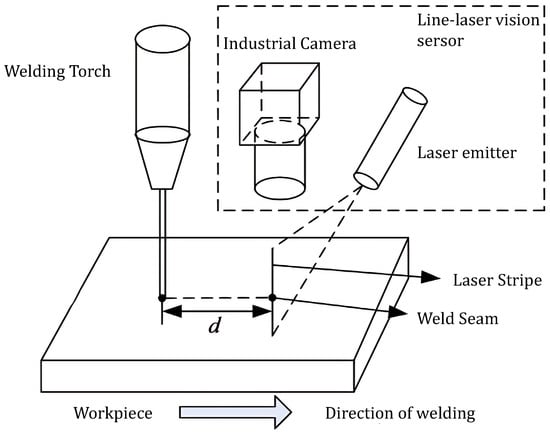
Figure 1.
Schematic diagram of the welding process: the welding torch and the laser stripe must maintain a fixed distance dd, and this relative distance remains constant during robot motion.
Within such systems, laser-line extraction serves as the foundational step for subsequent tasks, including seam tracking, groove recognition, and precise positioning. Welding environments differ markedly from other industrial settings: persistent and severe interference noise—such as arc light, spatter, slag, smoke, intense reflections, and rapid dynamic changes—renders laser-line extraction particularly challenging, constituting the primary bottleneck in system robustness and accuracy [5]. Additionally, given the real-time requirements of welding tasks, algorithmic processing speed and computational resource constraints are critical considerations [6].
Extensive research has focused on developing advanced laser-stripe segmentation techniques for complex welding scenarios [7,8,9]. These techniques can be broadly categorized into traditional methods and deep-learning-based approaches. Traditional segmentation workflows typically consist of three sequential stages. First, optical hardware optimizations and filter design are employed to physically suppress strong arc light and spatter interference (e.g., installing specialized optical filters on the camera [10]). Second, image denoising procedures customized to the welding environment remove residual noise, yielding a cleaner laser image (e.g., scene-specific filters and morphological operations). Finally, region-based segmentation separates the laser stripe from the background (e.g., thresholding or Otsu’s method for maximizing inter-class variance [11]). Ye et al. [12] reviewed an image preprocessing-based denoising pipeline that employs morphological opening followed by Otsu’s thresholding to remove spurious noise and produce a binarized image, thereby enhancing the laser-stripe features in V-groove weld images. Wu et al. [13] conducted a comparative study of three filters—Gaussian, median, and Wiener—and demonstrated that the median filter offers superior feature enhancement for laser-stripe extraction. Zhang et al. [14] proposed an image restoration algorithm that combines vector quantization (VQ) with a synthetic fractal-noise model, maintaining stripe continuity and subpixel accuracy even under severe noise conditions. Liu et al. [15] installed a narrowband band-pass filter matched to the laser wavelength on a CCD camera to physically suppress arc light and stray reflections. Zeng et al. [16] employed an LED array light source with a diffusing enclosure and custom top-and-bottom apertures to project uniform illumination onto the workpiece surface, effectively overcoming strong specular reflections. Gu et al. [17] modified a binocular camera system for synchronous image capture and added a 650 nm cut-off filter and welding-specific protective glass to the lenses; by using short-exposure triggering, they successfully suppressed intense arc-light interference.
Although traditional segmentation workflows can achieve acceptable results under limited noise conditions, they depend heavily on expert-tuned parameters—such as denoising filter settings and binarization thresholds—that must be recalibrated for each new welding setup. As a result, their performance degrades markedly when faced with unseen arc intensities, spatter distributions, or material reflectivities, leading to poor generalization and unstable operation in complex, dynamic welding environments.
In recent years, to effectively address these limitations, deep-learning-based image-segmentation techniques, such as UNet [18] and SegNet [19], have been increasingly utilized in laser-stripe segmentation tasks to enhance robustness in challenging welding environments. By leveraging the advanced learning and inference capabilities of neural networks, these methods significantly improve segmentation accuracy. For instance, Yang et al. [20] proposed a weld-image denoising network that exploits the contextual feature-learning capacity of a deep convolutional neural network (DCNN) to recover laser stripes from heavy noise interference. Zhao et al. [21] employed ERFNet [22] to extract laser stripes under strong background noise and subsequently derived the centerline and its corresponding feature points. Wang et al. [23] introduced WFENet, a semantic segmentation network enhanced with channel-attention mechanisms, achieving both rapid and accurate segmentation of laser-weld features. Chen et al. [24] presented DSNet, an efficient hybrid architecture combining convolutional neural networks and Transformers for real-time seam segmentation. Despite their promising results, these approaches still face an inherent trade-off between segmentation speed and accuracy. In practical welding applications, where image processing is typically conducted on embedded devices with limited computational resources and memory, it is essential to jointly optimize precision, real-time performance, and overall network efficiency.
Existing laser-vision welding systems often rely on off-the-shelf sensors whose optical configurations are not optimized for the severe interferences encountered in real welding (e.g., arc glow, spatter). Consequently, they exhibit unstable stripe capture under high-intensity noise. To address this, we design a custom line-laser vision sensor (Section 2) that integrates a band-pass filter and optimized projection geometry, ensuring robust, hardware-level suppression of environmental noise. Moreover, existing public datasets for laser-stripe segmentation are limited in size and noise diversity, hindering generalization to complex welding scenarios. We therefore collect and annotate a novel dataset of 3100 real-weld images encompassing multiple noise types (arc glow, spatter, slag, smoke, specular reflection), detailed in Section 4.1.
The primary contributions of this work are summarized as follows:
- (a)
- We design a custom laser-structured-light vision sensor that ensures hardware-level reliability for weld-stripe image acquisition in complex welding environments.
- (b)
- We collect and curate a novel weld-stripe image dataset, captured under real-world welding conditions and encompassing multiple types of noise (arc glow, spatter, slag, smoke, and specular reflection).
- (c)
- We propose a real-time two-stage evidential fine-tuning network for laser-stripe segmentation. By modeling evidential uncertainty and introducing a targeted optimization mechanism, our single-branch, reduced-channel architecture achieves a well-balanced trade-off between segmentation accuracy and inference speed.
The remainder of this paper is organized as follows. Section 2 elaborates on the design of the line-laser vision welding system. Section 3 presents the architecture and training strategy of the Laser Stripe Segmentation Network. Section 4 provides details regarding the construction of our Weld Seam Laser Image Dataset and evaluates our method through comparative experiments and ablation studies. Section 5 discusses the impact of uncertainty modeling and structural symmetry on segmentation performance. Finally, Section 6 concludes the paper and outlines potential directions for future research.
2. Line-Laser Vision Welding System
As shown in Figure 2, The line-laser vision sensor mounted on an intelligent welding robot system serves as the “eye” of the robot, precisely detecting and measuring the three-dimensional coordinates and geometric parameters of the weld seam. The sensor assembly comprises a laser generator, an industrial fixed-focus camera, a controller, and actuation components, all rigidly affixed to the front of a crawling welding robot. As a non-contact device, it maintains a fixed offset from the welding torch, thereby eliminating interference from external reference points on the workpiece.
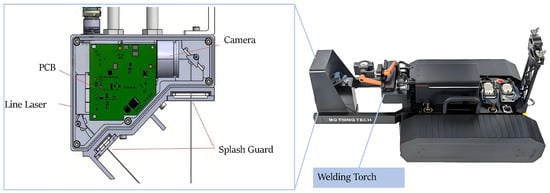
Figure 2.
Line-laser vision sensor: the sensor is rigidly mounted to both the robot and welding torch; an industrial camera and laser projector serve as the core components, with their relative positions fixed and the angle between the camera’s optical axis and the laser line maintained constant.
To meet the stringent requirements of harsh welding environments, the optical design of the sensor must mitigate specular reflections while ensuring clear visibility of workpiece features. To achieve this, we utilize an MV-CB016-10GM-S industrial camera coupled with a custom AZURE-1280MAC+BP635 fixed-focus lens (both produced by HIKVISION in Hangzhou, China) which incorporates a 635 nm band-pass filter, as well as a specialized JBP6520Z-052 laser generator (produced by Laser-tech in Zhuhai, China). This hardware configuration effectively filters out environmental noise and reliably captures laser-stripe images, even under high-intensity and high-interference welding conditions, thus providing robust input for subsequent image processing and 3D weld reconstruction.
The operation of a laser-sensor–based weld-tracking system is described as follows [25]: The projected laser stripe undergoes deformation (e.g., bending or indentation) when it encounters the weld groove. The camera captures these deformed stripe images, and image-processing algorithms extract key feature points along the stripe. Subsequently, by mapping these points to a mathematical model, the system determines the spatial position, profile shape, width, and height of the weld. The Schematic diagram of coordinate transformation is shown in Figure 3.
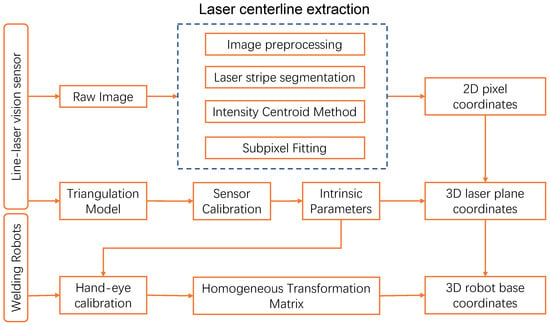
Figure 3.
The Schematic diagram of coordinate transformation: Through camera calibration, laser-plane calibration, and hand–eye calibration algorithms, pixel coordinates in the laser-stripe image are transformed into three-dimensional points in the robot’s base coordinate frame.
3. Laser Stripe Segmentation Network
To enhance the detectability of laser-stripe regions in noisy welding environments, this study formulates the task of laser-stripe regions extraction as a semantic segmentation problem. By leveraging the pixel-level classification capability of a segmentation network, each image pixel is accurately mapped to its corresponding class mask.
3.1. Network Architecture
As illustrated in Figure 4, we present a symmetrically structured, two-stage semantic segmentation framework that integrates evidential uncertainty modeling with a specialized fine-tuning module. In Stage I, a training-only Transformer branch runs in parallel with a lightweight CNN to extract coarse features; at inference, this branch is pruned so that only the CNN remains, ensuring maximum throughput. The Evidential Uncertainty Head then applies a 1 × 1 convolution and ReLU to produce nonnegative “evidence” vectors for each pixel, parameterizing a Dirichlet distribution and yielding both a coarse seed mask and its paired uncertainty map—two outputs that are inherently one-to-one and spatially symmetric. In Stage II, a mirror-image fine-tuning network uses the uncertainty map to guide symmetric refinement of the same pixel regions, preserving stripe continuity while correcting errors identified in Stage I. This explicit correspondence between uncertainty estimation and targeted refinement embodies the architectural symmetry at the heart of our design.
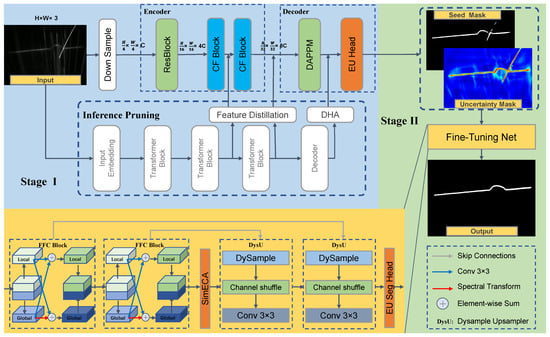
Figure 4.
Architecture of EUFNet: a two-stage network in which Stage I performs evidential uncertainty quantification to generate a seed mask and an uncertainty mask, and Stage II uses these masks as inputs to a lightweight fine-tuning network that focuses optimization on high-uncertainty regions.
The Fine-tuning Network is specifically designed for detailed correction. Fast Fourier Convolutions (FFC) [26] extract frequency-domain features to capture stripe continuity and noise characteristics. An enhanced lightweight dual-branch SimECA module, guided by the uncertainty mask, selectively suppresses errors in high-uncertainty regions while reinforcing coherent textures in low-uncertainty areas.
3.2. Stage I: Fast Segmentation Network
In Stage I, the raw laser-stripe image is initially processed by a single-branch convolutional neural network for coarse stripe extraction. To expedite inference, we utilize a multi-layer stacked CNN backbone inspired by SCTNet [27]. Additionally, to enrich semantic representations, we introduce a training-only Transformer branch that captures high-quality contextual features. An enhanced Conv-Former Block (CFBlock) integrates these semantic features back into the CNN branch, resulting in a lightweight, real-time segmentation network that combines efficient convolutional processing with rich Transformer-derived semantics, the backbone begins with two successive 3 × 3 convolution–batch norm–ReLU layers that increase the channel dimension from 3 to 32, followed by a 1 × 1 convolution that raises it to 64. This is followed by two residual blocks, each comprising two 3 × 3 convolution–batch norm–ReLU layers with skip connections, and then two Conv-Former blocks that project features to 128 channels, process them through a four-head Transformer encoder, and project back to 64 channels. The decoder is a Deep Aggregation Pyramid Pooling Module that fuses features from four parallel 3 × 3 convolutions and concludes with a 1 × 1 convolution. The segmentation head consists of one 3 × 3 convolution reducing channels to 32 and a final 1 × 1 convolution producing the 2 output classes.
Specifically, the network begins with an initial downsampling block comprising two stacked 3 × 3 standard 2D convolutions followed by a 1 × 1 convolutional bottleneck, which increases channel depth while reducing spatial resolution. Four consecutive residual blocks subsequently perform feature extraction: the first two blocks employ convolutional layer stacks with skip connections to efficiently capture local details within a limited receptive field, whereas the latter two are carefully designed CFBlocks that emulate Transformer behavior to capture long-range dependencies and semantic context.
For multi-scale feature fusion, we adopt the Deep Aggregation Pyramid Pooling Module (DAPPM) [28] as the decoder. DAPPM hierarchically aggregates contextual information across different scales through multiple 3 × 3 convolutions in a residual manner, concatenates all scale-specific feature maps, and compresses the channel dimension using a final 1 × 1 convolution. Since this aggregation operates at low resolution, it introduces negligible inference overhead. A lightweight segmentation head then generates the coarse mask output of Stage I.
3.3. Evidential Uncertainty Head
Currently, our segmentation network generates only a deterministic mask and lacks the capability to quantify its confidence in that prediction. In classification tasks, it is common practice to apply a softmax function at the final layer to map network outputs to class-probability distributions; however, these probabilities do not accurately reflect the model’s true confidence in its predictions. To obtain genuinely reliable confidence estimates, the prevailing approach involves introducing Bayesian inference [29], such as constructing a Bayesian Neural Network (BNN) [30] or employing Monte Carlo Dropout (MC Dropout) [31] during inference to approximate Bayesian sampling. Nevertheless, BNNs typically entail prohibitively high training and computational costs, while MC Dropout’s requirement for multiple forward passes imposes significant demands on memory and compute resources—limitations that impede their practical adoption in real-world systems.
To introduce uncertainty estimation more efficiently, and inspired by evidential deep learning (EDL) [32], we augment the backbone’s feature map with an Evidential Uncertainty Head (EUHead). For each pixel, EUHead predicts nonnegative “evidence” values for each class via a Softplus activation ( ), ensuring both numerical stability and strictly positive evidence required to parameterize the Dirichlet concentration parameters ( ). These evidence values are subsequently transformed into the concentration parameters of a Dirichlet distribution according to , assuming a uniform prior of 1 for all classes. Consequently, each pixel is associated with a Dirichlet parameter vector .
We quantify epistemic uncertainty at each pixel using the “vacuity” metric, which is defined as:
where K indicates the number of classes, and S represents the cumulative total of mass evidence. A larger vacuity value indicates less accumulated evidence and thus greater model uncertainty. The resulting per-pixel vacuity heatmap provides a direct visualization of the network’s confidence in its semantic predictions. Since vacuity heatmaps may vary in scale across different samples, we apply per-image min–max normalization to map vacuity values into a fixed range. This ensures consistent numeric scales for subsequent processing. During the stage II training, the normalized uncertainty map is incorporated as a pixel-wise weighting factor in the loss function. By assigning higher weights to pixels with greater vacuity, the network is encouraged to focus on uncertain or noisy regions while mitigating the influence of unreliable areas. Consequently, this enhances the robustness and reliability of the final segmentation.
3.4. Stage II: Fine-Tuning Network
In this stage, the seed segmentation mask is fused with the normalized evidential uncertainty map to generate a high-confidence, fine-grained segmentation. To enhance both confidence and the continuity of the laser stripe, we leverage principles from evidential deep learning to design a Refine Network that iteratively optimizes the seed mask using uncertainty cues, it is composed of two Fast Fourier Convolution (FFC) blocks and SimECA modules interleaved. Each FFC block splits its input (64 channels) into a local branch (32 channels with two 3 × 3 Conv–BN–ReLU layers) and a spectral branch (32 channels processed via Real 2D FFT, 1 × 1 Conv, inverse FFT), then merges via channel shuffle. Following each FFC, a SimECA attention module applies a 1D-Conv channel attention (C = 64) and a spatial–channel energy map. Finally, a Dynamic Sampling UpSampler (DySample) restores the feature map across two upsampling stages to the full 512 × 256 resolution, and the output layer consists of a 3 × 3 Conv → 1 channel plus Softplus activation for evidence generation.
The Refine Network is intentionally lightweight, employing fewer channels and a Fast Fourier Convolution (FFC)-based backbone for feature extraction. The structure of Fast Fourier Convolution is illustrated in Figure 5. By integrating FFC in the early layers, the network captures global context, thereby compensating for any long-range dependencies potentially overlooked in the stage I. A specially designed lightweight attention module, combined with an uncertainty-weighted loss function, guides the network to focus on regions of high vacuity while imposing minimal additional computational burden. After multiple layers of FFC and attention refinement, a Dynamic Sampling UpSampler (DySample) [33] performs progressive upsampling. The final convolutional layer is followed by a Softplus activation to guarantee nonnegative outputs, which are used as evidence values in our uncertainty-guided loss function. It dynamically adjusts interpolation weights based on pixel-wise uncertainty and gradually restores the feature map to the original image resolution, producing the final refined segmentation.
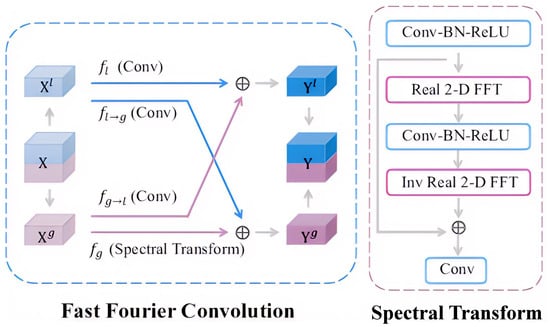
Figure 5.
Architecture of FFC: the local branch (top) captures fine-grained semantics and edge cues, while the spectral branch (bottom) extracts global contextual features. The input is first transformed via FFT, followed by point-wise convolution in the frequency domain, and then mapped back to the spatial domain via inverse FFT.
To more effectively leverage global context for uncertainty-driven refinement, we substitute traditional convolutional layers in the backbone with Fast Fourier Convolutions (FFC). Since FFC is fully differentiable, it can be seamlessly integrated into existing deep-learning architectures without requiring significant redesign.
In each FFC operation, the input feature map is first partitioned along the channel dimension into a local branch and a spectral branch. The local branch utilizes standard convolutional blocks (e.g., 3 × 3 Conv–BN–ReLU–3 × 3 Conv) to capture local semantics and edge details. Simultaneously, the spectral branch applies a real 2D fast Fourier transform (Real 2D FFT) to its input , performs point-wise or lightweight convolutions in the frequency domain, and subsequently maps the result back to the spatial domain via an inverse real 2D FFT (Inv Real 2D FFT), thereby extracting global context features. Information exchange between the two branches is facilitated through learnable mappings and , which promote feature sharing and fusion across local and global representations.
A SimECA module is subsequently integrated after the feature extraction stage to further mitigate background interference and enhance boundary and detail responses, effectively addressing residual edge blurring and noise misclassification. The structure of SimECA is illustrated in Figure 6. The dual-branch architecture of SimECA consists of a channel-attention path [34] and a spatial-attention path [35]. Channel-Attention Branch: The input feature map undergoes global average pooling to generate a descriptor of size . A one-dimensional convolution with an adaptive kernel size captures local inter-channel dependencies, followed by a sigmoid activation function that produces channel weights of shape . These weights are broadcasted to and applied to the feature map, thereby emphasizing channels pertinent to the laser stripe while suppressing irrelevant background channels. Spatial–Channel Joint Branch: For the same input features, per-pixel and per-channel de-meaned squared activations are computed, where and represent the channel-wise mean and variance, respectively. An energy map is constructed by normalizing these activations with and a regularization term , which is then passed through a sigmoid function to produce a three-dimensional attention map of size . This map evaluates each neuron simultaneously in both spatial and channel dimensions, significantly enhancing sensitivity to fine stripe-edge details.
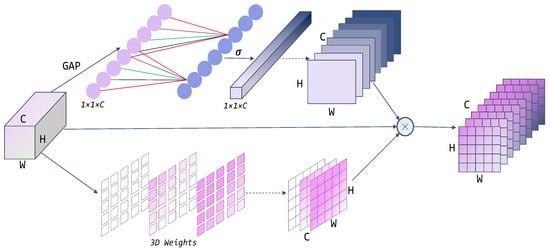
Figure 6.
Architecture of SimECA: a parallel dual-branch module comprising achannel-attention branch (top) and aspatial–channel joint branch (bottom). Their outputs are fused with the input feature map to perform feature recalibration.
The two attention maps are fused with the original feature map to recalibrate important pixels at a fine granularity. Given that SimECA introduces only a limited number of one-dimensional convolutional parameters in the channel branch, it incurs negligible computational overhead while substantially improving segmentation accuracy.
Finally, the EUSeg head generates pixel-wise class probabilities. Unlike conventional Softmax, which merely outputs normalized scores, the Dirichlet-based evidential learning framework explicitly models epistemic uncertainty. As previously discussed, the Softmax layer tends to assign overly confident probabilities to erroneous predictions and lacks a mechanism for quantifying the model’s “ignorance”. In the evidential network, nonnegative evidence is produced through a Softplus activation function and utilized to parameterize a Dirichlet distribution, from which the predictive class probabilities are subsequently derived:
Here, denotes the Dirichlet concentration parameter for class K (with K total classes), S represents the total accumulated evidence, and signifies the predictive probability for class K.
Consequently, the pixel-wise class probabilities generated by this method more accurately reflect the model’s confidence, particularly in unknown or ambiguous regions, thereby producing predictions that are not only more interpretable but also of higher epistemic reliability. The EUSeg Head thus provides segmentation outputs accompanied by meaningful and well-calibrated confidence estimates.
3.5. Loss Function
Since the two stages reflect distinct design philosophies and emphasize complementary aspects, we utilize separate loss functions in each stage to leverage their respective strengths.
In Stage I, we formulate the task as a binary classification problem and accordingly employ the weighted binary cross-entropy loss. Given the significant imbalance between the laser-stripe class (positive) and the background class (negative), the network is prone to prematurely converge toward the dominant background class. To address this issue, we incorporate a weighting factor w for the positive class. Through extensive experimentation, we have found that setting achieves optimal performance. The loss function for Stage I, denoted as , is defined as follows:
Here, N denotes the total number of pixels, and w represents the weighting factor for positive samples (set to in our experiments). is the ground-truth binary label for the i th pixel, and is the network’s predicted probability that the i th pixel belongs to the positive class (laser stripe). When (i.e., a positive sample), the corresponding loss term becomes , which enhances the network’s emphasis on stripe pixels and effectively mitigates premature convergence toward the background class.
In Stage II, the Refine network is explicitly designed to focus on regions with low confidence and high uncertainty. To further enhance supervision for pixels exhibiting greater uncertainty, we employ an uncertainty-weighted Focal Loss:
Here, and are two coefficients, set to 2 and 0.5, respectively. Specifically, denotes the uncertainty threshold, represents the uncertainty factor, and signifies the maximum additional weight. Consequently, pixels with high uncertainty ( large) receive enhanced supervision during training. This uncertainty-driven weighting mechanism dynamically allocates pixel-level attention: regions of high confidence (low uncertainty) are emphasized, while regions of low confidence (high uncertainty) are appropriately down-weighted, thereby preventing noisy or “suspicious” pixels from disproportionately influencing the gradient updates.
The focal-loss exponent was set to 2 following the original formulation of Focal Loss, which balances the down-weighting of easy examples against stable training. The uncertainty threshold was determined empirically by examining the normalized vacuity distribution on our validation set: setting = 0.5 roughly splits pixels into equal low and high uncertainty groups, ensuring that refinement focus is neither too narrow nor too broad. The maximum additional weight was likewise chosen via a small grid search (values in [1.0, 2.0, 3.0]), with = 1.5 yielding the best mIoU on validation without destabilizing training. All hyperparameter settings are fixed for all experiments and result in robust, reproducible performance.
During training, the two stages are optimized in a cascaded and end-to-end manner. Consequently, the overall loss function is formally defined as:
Here, the balancing coefficients and are initialized to 1 and 0, respectively. As training progresses across epochs, is gradually decayed while is linearly increased, thereby enhancing the effectiveness of the refinement stage. If the Stage I loss has already converged, the Stage I network is frozen (i.e., its parameters are no longer updated) and further optimization is conducted exclusively for Stage II, with an enlarged used for fine-tuning.
4. Experiments and Results
In this section, we carry out a comprehensive series of experiments on our Weld Seam Laser Image dataset to rigorously validate the effectiveness of the proposed method. In Section 4.2, we detail the experimental design and implementation specifics. In Section 4.3, we conduct comparisons of our approach against various baselines to objectively quantify its segmentation performance. Finally, in Section 4.4, we undertake ablation studies to systematically analyze the contributions of our framework and its individual components.
4.1. Weld Seam Laser Image Dataset
The dataset was collected in a real welding environment at the construction site of a large container ship. During welding operations, the line-laser vision sensor mounted on the welding robot continuously acquired grayscale images of the laser stripe on the weld seam. The dataset consists of 3100 laser-stripe images and their corresponding segmentation masks, which were manually annotated using LabelMe (version:5.2.1). These images and labels were randomly divided into training, validation, and test sets following an 8:1:1 ratio.
To capture the diversity of real-world welding tasks, the dataset encompasses weld seams of various sizes and shapes, covering multiple seam types—primarily butt and fillet welds—produced through a complex multilayer, multipass welding process (including root pass, fill, and cap). Additionally, the collected images illustrate typical noise sources encountered in welding scenarios, including arc light and spatter, ambient illumination, specular reflections, slag interference, variable exposure, and particulate matter, as depicted in Figure 7.
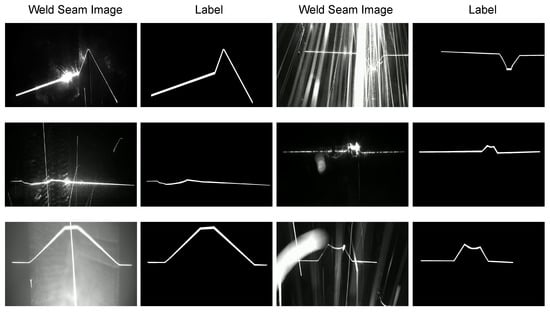
Figure 7.
Weld Seam Laser image dataset(WSLI): comprising raw laser-stripe images captured by the line-laser vision sensor and their corresponding annotations generated with the Labelme tool, encompassing a variety of noise types encountered in real welding environments.
Each image in our dataset contains a single, continuous laser stripe that delineates the weld seam and provides the essential geometric cues required for precise seam localization. By accurately isolating this stripe, one can infer critical measurements such as groove width, height, and alignment relative to the welding torch. The continuity of the stripe is particularly important: any breaks or discontinuities in the segmented output directly translate into errors in downstream geometric reconstruction and path-planning algorithms.
However, achieving robust segmentation of the laser stripe is nontrivial in real-world welding scenarios. The welding environment introduces a multitude of confounding factors—intense arc glow, erratic spatter, drifting smoke, and specular reflections—that manifest as high-frequency noise and false positives in captured images. Variations in surface finish, material reflectivity, and ambient illumination further exacerbate the segmentation task by altering stripe contrast and edge definition. Consequently, an effective segmentation framework must not only discriminate the true laser stripe from heterogeneous background disturbances but also preserve its spatial continuity under widely varying conditions.
4.2. Implementation Details
Prior to model training, all annotated images underwent a standardized preprocessing pipeline to ensure spatial consistency and fair comparison across methods. Specifically, every model used the same steps: resize to 512 × 256 pixels, histogram equalization for contrast normalization, and random horizontal flips for data augmentation. This guarantees that differences in performance arise solely from model architectures and not from disparate input preprocessing. Optimization was performed using the AdamW algorithm, initialized with a learning rate of 4 × and a weight-decay coefficient of 1.25 × to regularize model complexity. To avoid premature convergence to the dominant background class or entrapment in suboptimal local minima, we adopted the SGDR (Stochastic Gradient Descent with Warm Restarts) protocol for cosine-annealing learning-rate scheduling [36], which periodically resets the learning rate to its initial value and then decays it along a cosine curve. The full training schedule comprised 100 epochs, with a mini-batch size of 2 images, implemented in PyTorch (version:1.10.0) and executed on a single NVIDIA GeForce RTX 3090 GPU (Santa Clara, CA, USA).
For empirical validation, we conducted a comprehensive benchmark of our proposed network against a diverse selection of state-of-the-art segmentation architectures. General semantic-segmentation baselines included U-Net [18] and SegFormer [37], while high-efficiency, real-time models such as ERFNet [22] and SCTNet [26] served as additional comparators. Furthermore, we evaluated two domain-specific methods—WFENet [23] and DSNet [24]—which were explicitly designed for laser-stripe segmentation tasks. Model performance was assessed along two axes: segmentation fidelity and real-time inference capability. Segmentation accuracy metrics comprised mean intersection-over-union (mIoU) and mean pixel accuracy (mAcc), both derived from the confusion-matrix elements of true positives (TP), false positives (FP), false negatives (FN), and true negatives (TN). Real-time suitability was quantified by measuring frames per second (FPS), total parameter count (Params), and computational complexity in giga-floating-point operations per second (GFLOPs). This rigorous evaluation protocol underscores the relative trade-offs between accuracy, model size, and inference speed across contemporary approaches.
4.3. Benchmark Results
Table 1 compares our proposed method against both classical segmentation networks and real-time semantic segmentation architectures, reporting mIoU, mAcc, FPS, GFLOPs, and parameter count. Figure 8 illustrates qualitative results for the laser-stripe extraction task and juxtaposes our outputs with those of competing methods. As shown in Table 1, our approach achieves superior accuracy while maintaining the fastest inference speed: it attains an mIoU of 89.31%, approximately one percentage point higher than the nearest competitor, and operates at 236.73 FPS, outperforming all baselines in terms of real-time throughput. In Figure 8, we present side-by-side comparisons of segmentation results produced by WFENet and DSNet, the two most directly comparable models specifically designed for laser-stripe extraction. Compared to these methods, our network delivers cleaner removal of background noise and more continuous stripe delineation. These advantages can be attributed to our uncertainty modeling and optimization strategy, as well as the specialized stage II refinement network.

Table 1.
Comparisons with other methods on the WSLI dataset. The best results are highlighted in bold. FPS refers to frames per second; Params refers to the number of parameters.
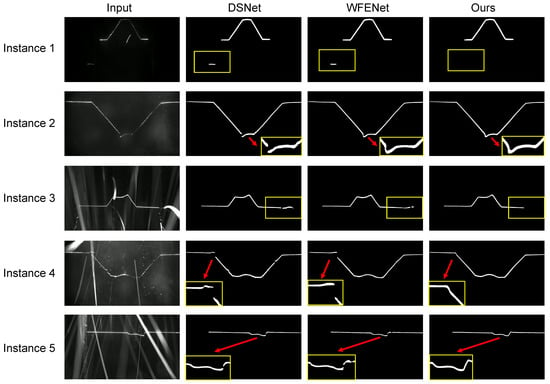
Figure 8.
Comparison of segmentation results: compared to DSNet and WFENet, EUFNet produces masks with finer detail (e.g., Instance 5) and better preserves the continuity of the laser stripe (e.g., Instance 4).
To compare the performance of these segmentation models with our proposed EUFNet across different datasets, we additionally evaluated all methods on WLSD [38]. The results, summarized in Table 2, demonstrate that EUFNet achieves robust accuracy on both our custom dataset and WLSD, significantly outperforming competing approaches in terms of generalization capability. This superiority can be attributed to our uncertainty-driven training framework: Fast Fourier Convolution blocks serve as the backbone, enabling the extraction of rich contextual information at shallow network stages with a reduced channel count, while the proposed dual-branch SimECA module refines critical details with fine-grained precision.

Table 2.
Comparative experiments on WLSD test set against other methods.The best results are highlighted in bold.
4.4. Ablation Study
To validate the effectiveness of our proposed architecture and its components, we conducted ablation studies, with the results presented in Table 3 and Table 4.

Table 3.
Ablation study on the architecture. ✓ indicates the use of this module.

Table 4.
Ablation Study on component.
As shown in Table 3, incorporating the Transformer branch during training enhances semantic representation, resulting in an increase of 0.75% in mIoU and 0.66% in mAcc. At inference time, only the single-branch CNN is retained, thereby preserving real-time performance. With the integration of evidential uncertainty modeling and optimization, segmentation accuracy improves significantly. Our fine-tuning Network, which is specifically designed to fine-tune low-confidence regions, further boosts performance, achieving a 1.17% gain in mIoU and a 0.61% gain in mAcc. Finally, the EUHead module, which quantifies pixel-level uncertainty, contributes an additional 1.02% gain in mIoU and 1.83% gain in mAcc.
We assessed the impact of the components introduced in Table 4. Our baseline architecture replaces the standard residual convolution blocks with Fast Fourier Convolutions (FFC) but excludes any attention mechanism. Replacing traditional residual units with FFC results in a 0.85% increase in mIoU. Subsequently, we integrate the lightweight, dual-branch SimECA module. This addition further enhances mIoU by 1.27%, with minimal impact on inference speed.
Figure 9 illustrates the segmentation results at different stages. In Figure 9a, we present three laser-stripe images of varying shapes captured at distinct time points during welding: (i) a laser image during the root pass of a fillet weld, (ii) a laser image during the fill pass of a butt weld, and (iii) a laser image with backing material. Figure 9b displays the corresponding evidential uncertainty masks generated by the EUHead, where regions with strong noise interference and along stripe edges exhibit very high uncertainty—indicating that the model lacks confidence in these areas. As a result, the coarse segmentation outputs from Stage I (Figure 9c) contain defects in these uncertain regions. After refinement, the Refine Network leverages uncertainty quantification to optimize these areas, producing high-confidence segmentation maps as shown in Figure 9d.

Figure 9.
Comparison of the segmentation results of Stage I and Stage II: (a) Input Images; (b) Evidential Uncertainty Quantitative Mask; (c) Seed Mask from Stage I; (d) Segmentation Results from Stage II. The subtle differences are shown within the yellow box.
4.5. Comprehensive Analysis
To achieve efficient performance on embedded devices with limited computational and memory resources, our method meticulously balances accuracy and real-time requirements. After training the model on an NVIDIA GeForce RTX 3090 GPU, we deployed it to an embedded system. Experimental results demonstrate that, when the seam-tracking laser software is fixed at 65 FPS, our approach can reliably extract laser stripes even in highly disturbed environments, fully satisfying the real-time demands of welding applications.
5. Discussion
The experimental results demonstrate that EUFNet’s uncertainty-guided two-stage framework substantially outperforms single-stage and uniform-refinement baselines on both our custom WSLI dataset and the public WLSD benchmark. By generating pixel-wise vacuity maps in Stage I and using them to weight the loss and guide the fine-tuning network, EUFNet concentrates its learning capacity on the most ambiguous stripe regions—such as boundary edges corrupted by arc glow, spatter, or specular reflections—thereby reducing both false positives and false negatives. This targeted supervision corrects coarse-stage errors more effectively than simply increasing model depth or channel counts, as evidenced by the +1.7% mIoU gain over DSNet and improved stripe continuity in heavily noisy areas (Figure 8).
In the welding scenario, achieving a balance between high frame rate and high precision is a major challenge. DSNet achieved high-speed inference at 100 FPS by significantly compressing the model size (reducing the number of parameters by 54 times), but this compact design limited its expressive power. In contrast, EUFNet, by leveraging multi-scale feature fusion and uncertainty assessment techniques, has significantly enhanced the segmentation accuracy even with a slight increase in parameters and computational load. Experiments show that EUFNet is significantly superior to DSNet in terms of weld seam positioning accuracy, while still meeting the real-time processing requirements. We also recognize that DSNet has fewer parameters and higher efficiency. In the future, we can further optimize EUFNet by combining the lightweight strategy of DSNet.
To provide further insight into EUFNet’s superiority, Table 5 compares Precision, Recall, and F1-score across models. EUFNet achieves the highest Recall (94.65%) and the best F1-score (90.82%), indicating its balanced capability to detect true stripe pixels while minimizing false alarms. In contrast, baseline methods like UNet and WFENet exhibit lower F1-scores (88.55% and 88.24%, respectively), reflecting their difficulty in maintaining both high precision and recall under challenging noise conditions.

Table 5.
Comparison of segmentation methods on the WSLI dataset, reporting Precision, Recall, and F1-score for each model. The best results are highlighted in bold.
Beyond loss weighting, the integration of Fast Fourier Convolutions and the dual-branch SimECA module in Stage II enables EUFNet to capture global stripe structure and selectively enhance salient features while maintaining real-time performance. FFC blocks efficiently encode long-range dependencies that help preserve stripe continuity across the image, and SimECA’s lightweight channel–spatial attention further suppresses background interference with minimal computational overhead. Together, these components allow EUFNet to achieve 236 FPS on an RTX 3090—faster than DSNet—despite its added uncertainty mechanisms, confirming that intelligent architectural choices can reconcile high accuracy with low latency.
6. Conclusions
In this work, to address the severe noise interference encountered in real-world welding environments, we propose EUFNet, a symmetrically structured two-stage real-time semantic segmentation network grounded in evidential deep learning (EDL). Our framework adopts a mirror-image “coarse segmentation–uncertainty quantification–fine-tuning” paradigm in which Stage I and Stage II form a functionally and structurally symmetric pair: the uncertainty map and coarse segmentation mask are produced in one-to-one correspondence, and then symmetrically refined in the second stage. By integrating self-distillation, Fast Fourier Convolution (FFC), and the SimECA module, EUFNet efficiently extracts multi-scale features and generates high-confidence laser-stripe maps in real time. This explicit architectural and operational symmetry not only enhances robustness against extreme noise but also ensures precise groove recognition and localization for automated robotic welding systems.
Moreover, we have constructed and publicly released a shipyard-scale weld-stripe image dataset consisting of 3100 grayscale images with varying stripe shapes and sizes. Each image is manually annotated and exhibits common welding interferences such as arc glow, spatter, slag, smoke, and specular reflections. This dataset serves as a comprehensive benchmark for training and evaluating segmentation models under realistic conditions.
Extensive experiments demonstrate that EUFNet, empowered by evidential uncertainty modeling and its targeted optimization mechanism, successfully harmonizes self-distillation, FFC, and SimECA to achieve simultaneous improvements in accuracy and inference speed—establishing a new standard for real-time laser-stripe extraction. While EUFNet delivers exceptional performance and runtime efficiency on our dataset, its reliance on a Transformer branch during training imposes significant demands on computational resources and memory. Future work will focus on further parameter reduction to better accommodate resource-constrained embedded platforms.
Author Contributions
Conceptualization, C.S., D.W., C.Z. (Chun Zhang), J.Y., C.Z. (Changsheng Zhu) and X.F.; methodology, D.W.; software, J.Y.; validation, D.W. and X.Z.; formal analysis, D.W.; investigation, D.W.; resources, C.Z. (Chun Zhang); data curation, D.W., J.Y. and X.Z.; writing—original draft preparation, D.W.; writing—review and editing, D.W.; visualization, D.W.; supervision, C.S., C.Z. (Chun Zhang) and C.Z. (Changsheng Zhu).; project administration, C.S. and C.Z. (Chun Zhang); funding acquisition, C.S. and X.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Projects of Scientific and Technological Innovation in Daiyue District, Tai’an City, grant number CXXM–2021006.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Acknowledgments
Thanks to Beijing Botsing Technology Co., Ltd. for providing the laser sensors experimental equipment and welding test.
Conflicts of Interest
Author Jia Yan was employed by the company Beijing Botsing Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Ali, R.; El-Betar, A.; Magdy, M. A review on optimization of autonomous welding parameters for robotics applications. Int. J. Adv. Manuf. Technol. 2024, 134, 5065–5086. [Google Scholar] [CrossRef]
- Wang, J.; Li, L.; Xu, P. Visual sensing and depth perception for welding robots and their industrial applications. Sensors 2023, 23, 9700. [Google Scholar] [CrossRef]
- Karmoua, J.; Kovács, B. A review of structured light sensing techniques for welding robot. Acad. J. Manuf. Eng. 2021, 19, 3. [Google Scholar]
- Guo, J.; Zhu, Z.; Sun, B.; Yu, Y. Principle of an innovative visual sensor based on combined laser structured lights and its experimental verification. Opt. Laser Technol. 2019, 111, 35–44. [Google Scholar] [CrossRef]
- Wang, N.; Zhong, K.; Shi, X.; Zhang, X. A robust weld seam recognition method under heavy noise based on structured-light vision. Robot. Comput.-Integr. Manuf. 2020, 61, 101821. [Google Scholar] [CrossRef]
- Smith, J.; Liu, C. A Review of Machine Vision Systems for Real-Time Weld Seam Tracking in Robotic Environments. 2024. Available online: https://easychair.org/publications/preprint/LgNn/open (accessed on 31 July 2025).
- Song, L.; He, J.; Li, Y. Center extraction method for reflected metallic surface fringes based on line structured light. J. Opt. Soc. Am. A 2024, 41, 550–559. [Google Scholar] [CrossRef] [PubMed]
- Zou, Y.; Zeng, G. Light-weight segmentation network based on SOLOv2 for weld seam feature extraction. Measurement 2023, 208, 112492. [Google Scholar] [CrossRef]
- Dai, C.; Wang, C.; Zhou, Z.; Wang, Z.; Liu, D. WeldNet: An ultra fast measurement algorithm for precision laser stripe extraction in robotic welding. Measurement 2025, 242, 116219. [Google Scholar] [CrossRef]
- You, D.; Gao, X.; Katayama, S. Review of laser welding monitoring. Sci. Technol. Weld. Join. 2014, 19, 181–201. [Google Scholar] [CrossRef]
- Shi, Y.H.; Wang, G.R.; Li, G.J. Adaptive robotic welding system using laser vision sensing for underwater engineering. In Proceedings of the 2007 IEEE International Conference on Control and Automation, Guangzhou, China, 30 May–1 June 2007; pp. 1213–1218. [Google Scholar]
- Ye, H.; Liu, Y.; Liu, W. Weld seam tracking based on laser imaging binary image preprocessing. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; pp. 756–760. [Google Scholar]
- Wu, Q.Q.; Lee, J.P.; Park, M.H.; Park, C.K.; Kim, I.S. A study on development of optimal noise filter algorithm for laser vision system in GMA welding. Procedia Eng. 2014, 97, 819–827. [Google Scholar] [CrossRef][Green Version]
- Zhang, T.; Zhu, M.; Zou, Y. Image restoration based on vector quantization for robotic automatic welding. Eng. Appl. Artif. Intell. 2024, 129, 107577. [Google Scholar] [CrossRef]
- Liu, J.; Fan, Z.; Olsen, S.I.; Christensen, K.H.; Kristensen, J.K. A real-time passive vision system for robotic arc welding. In Proceedings of the 2015 IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, 24–28 August 2015; pp. 389–394. [Google Scholar]
- Zeng, J.; Chang, B.; Du, D.; Hong, Y.; Chang, S.; Zou, Y. A precise visual method for narrow butt detection in specular reflection workpiece welding. Sensors 2016, 16, 1480. [Google Scholar] [CrossRef]
- Gu, Z.; Chen, J.; Wu, C. Three-dimensional reconstruction of welding pool surface by binocular vision. Chin. J. Mech. Eng. 2021, 34, 47. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Yang, L.; Fan, J.; Huo, B.; Li, E.; Liu, Y. Image denoising of seam images with deep learning for laser vision seam tracking. IEEE Sens. J. 2022, 22, 6098–6107. [Google Scholar] [CrossRef]
- Zhao, Z.; Luo, J.; Wang, Y.; Bai, L.; Han, J. Additive seam tracking technology based on laser vision. Int. J. Adv. Manuf. Technol. 2021, 116, 197–211. [Google Scholar] [CrossRef]
- Romera, E.; Alvarez, J.M.; Bergasa, L.M.; Arroyo, R. Erfnet: Efficient residual factorized convnet for real-time semantic segmentation. IEEE Trans. Intell. Transp. Syst. 2017, 19, 263–272. [Google Scholar] [CrossRef]
- Wang, B.; Li, F.; Lu, R.; Ni, X.; Zhu, W. Weld Feature Extraction Based on Semantic Segmentation Network. Sensors 2022, 22, 4130. [Google Scholar] [CrossRef]
- Chen, J.; Wang, C.; Shi, F.; Kaaniche, M.; Zhao, M.; Jing, Y.; Chen, S. DSNet: A dynamic squeeze network for real-time weld seam image segmentation. Eng. Appl. Artif. Intell. 2024, 133, 108278. [Google Scholar] [CrossRef]
- Yin, Z.; Ma, X.; Zhen, X.; Li, W.; Cheng, W. Welding seam detection and tracking based on laser vision for robotic arc welding. J. Phys. Conf. Ser. 2020, 1650, 022030. [Google Scholar] [CrossRef]
- Chi, L.; Jiang, B.; Mu, Y. Fast fourier convolution. Adv. Neural Inf. Process. Syst. 2020, 33, 4479–4488. [Google Scholar]
- Xu, Z.; Wu, D.; Yu, C.; Chu, X.; Sang, N.; Gao, C. Sctnet: Single-branch cnn with transformer semantic information for real-time segmentation. In Proceedings of the AAAI conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 6378–6386. [Google Scholar]
- Hong, Y.; Pan, H.; Sun, W.; Jia, Y. Deep dual-resolution networks for real-time and accurate semantic segmentation of road scenes. arXiv 2021, arXiv:2101.06085. [Google Scholar]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight uncertainty in neural network. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 1613–1622. [Google Scholar]
- Neal, R.M. Bayesian learning for Neural Networks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 118. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- Sensoy, M.; Kaplan, L.; Kandemir, M. Evidential deep learning to quantify classification uncertainty. Adv. Neural Inf. Process. Syst. 2018, 31, 3179–3189. [Google Scholar]
- Liu, W.; Lu, H.; Fu, H.; Cao, Z. Learning to upsample by learning to sample. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 6027–6037. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient channel attention for deep convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 11534–11542. [Google Scholar]
- Yang, L.; Zhang, R.Y.; Li, L.; Xie, X. Simam: A simple, parameter-free attention module for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Online, 18–24 July 2021; pp. 11863–11874. [Google Scholar]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and efficient design for semantic segmentation with transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 12077–12090. [Google Scholar]
- Dai, Y.; Chen, S.; Sun, T.; Fan, Z.; Zhang, C.; Feng, X.; Wang, G. Uncertainty-Aware Laser Stripe Segmentation with Non-Local Mechanisms for Welding Robots. IEEE Trans. Instrum. Meas. 2025, 74, 5016212. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).