Abstract
This paper comprehensively reviews how operations research and optimization procedures are applied to address challenges in wireless network communications. Key challenges such as network topology design, dynamic task scheduling, and multi-objective resource allocation are examined and systematically categorized. The revision focuses on literature published between 2023 and 2025, and covers topics such as flow optimization and routing, resource allocation and scheduling, mobile and wireless network management, network resilience and robustness, and energy efficiency. The works are selected using a methodological approach ranging from the exact optimization methods, such as mixed-integer programming, to heuristic/metaheuristic strategies and machine-learning-based techniques. It is reported a comparative analysis in terms of computational efficiency, scalability, and practical applicability. The main contribution is to highlight current research gaps and open challenges, with particular emphasis on the integration of operations research and artificial intelligence, especially in problems modeled using graphs and network structures.
1. Introduction
Operations research (OR) is a mature field that accomplishes both nonlinear and linear programming techniques using continuous and/or discrete variables. As such, it plays a key role in supporting decision-making processes and optimizing the performance of complex networks, particularly in engineering domains such as logistics, telecommunications, healthcare and security, to name a few.
Network science addresses the analysis of complex systems, which are typically modeled as graphs where nodes represent entities (nodes) such as base stations in a wireless network, for example. The edges denote their interactions, links, or relationships between nodes. As such, these modeling techniques are crucial to designing efficient telecommunication infrastructures for digital communication networks.
During the past three decades, global telecommunication policies have primarily aimed to improve economic efficiency by reducing government control, thus mitigating risks related to conflict of interest and corruption [1]. However, recent trends show a reversal with governments that are increasingly influencing through direct ownership of networks, thus expanding regulatory oversight to cover the broader digital economy and politicizing issues such as content distribution and the use of novel technologies.
Notice that even when there is an increasing number of works dealing with optimization in wireless networks, a well-structured comparative review that bridges classical operations research (OR) techniques with recent AI-based methods is still lacking, particularly in the context of 6G and beyond. Furthermore, most of the existing surveys focus on learning-based methods, without connecting them to classical optimization foundations or discussing their integration. This paper helps fill this gap by categorizing recent advances (2023–2025) in network optimization from both perspectives (OR and AI), highlighting synergies, trade-offs, and future opportunities.
Similarly, OR offers powerful mathematical programming techniques to address optimization challenges: optimal routing and design of the required infrastructure and location placement, which are critical to improving efficiency and minimizing operational costs. For example, other technologies such as cyberphysical systems (CPS) and the Internet of Things (IoT) have significantly transformed transportation systems (ITS), enabling real-time vehicle-to-infrastructure (V2I) communication, which, in turn, improves traffic management. However, these innovations still lack novel infrastructures to deal with the huge demand using the new technologies.
This paper provides a comprehensive survey of recent contributions that apply OR and optimization methods to the domain of network communications, particularly in the context of 5G, 5G+, and emerging 6G technologies. The article reviews applications of operations research and optimization methods applied in wireless network communications. Key challenges such as network topology design, resource allocation, optimal routing, and wireless network optimization for wireless networks using current and future 5G, 5G+, and 6G technologies are reviewed from 2023 to 2025, including flow optimization and routing, resilience and robustness, resource allocation and scheduling, wireless and mobile network optimization, and energy efficiency. Furthermore, the papers reviewed are categorized based on exact methods such as mixed integer programming, heuristic approximations, and machine learning-based techniques. Finally, a comparative analysis is provided in terms of efficiency, scalability, and real-world applicability. This review’s main contribution is to identify research gaps and open challenges, emphasizing the integration of operations research and artificial intelligence methods in modern networks and between operations research jointly applied with classical graph optimization problems.
Consequently, this work presents a structured literature review that combines comparative taxonomy and domain-specific analysis. Based on a systematic selection of recent papers from 2023 to 2025, we position this contribution as a structured survey of optimization techniques for modern wireless network design, particularly within the context of 6G and beyond.
The structure of the paper is as follows. In Section 2, the motivation for integrating operations research and optimization in network communications is presented, and the methodology used to select relevant literature from 2023 to 2025 is presented. Section 3 introduces the theoretical foundations of optimization in network science. The latter includes classical OR models, heuristic and metaheuristic algorithms, and recent advances in machine learning-based methods. In Section 4, the comparative insights and the limitations observed are outlined. In addition, this section briefly attempts to draw insight and identify methodological gaps based on existing reviewed material. Section 5 identifies open challenges and future research directions, especially in bridging the OR-based and AI-based approaches. Finally, Section 6 addresses benchmarking inconsistencies in reviewed studies and proposes suggestions for standard evaluation practices. Lastly, it concludes the paper and offers future perspectives on the convergence of OR and network sciences in next-generation networks.
2. Motivation and Importance of Operations Research in Wireless Networks
Network optimization has become a hot research field due to the growing demand for efficient resource allocation and high-performance devices such as laptops, mobile phones, computers, and so on. Rapid data traffic requirements and the emergence of new technologies such as 5G, 5G+, and 6G have prompted researchers to explore several optimization techniques, including mathematical programming, heuristic algorithms, and machine learning approaches. These methods can help improve network efficiency, minimize interference, reduce delays, and optimize energy consumption altogether. Another relevant problem in network optimization is designing new infrastructures. The examples in Figure 1 should be considered for user-varying positions and high data rate demands scenarios.
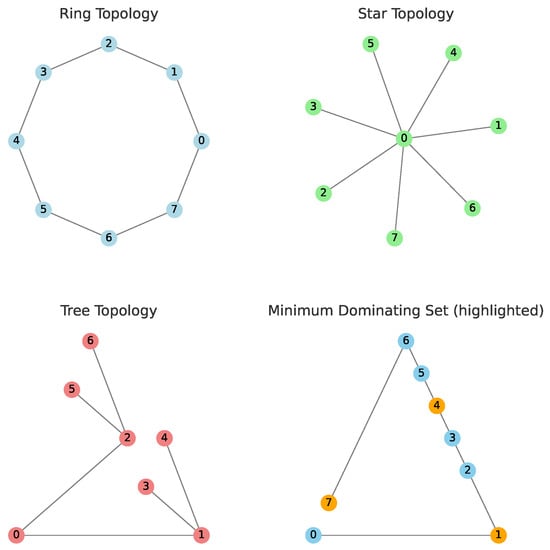
Figure 1.
Network graphs graph topologies, from left to right: a ring, a star, and a minimum dominating set topology, respectively.
Effective models ensure that users can be connected to the best network nodes at different time slots, avoiding congestion and improving reliability. Robust optimization is required to manage connectivity failures and fluctuations under uncertainty. Tools such as [2] Mininet [3] plays a key role that is essential to simulate real-world scenarios and validate optimization solutions. Particular attention has been paid to artificial intelligence. For example, neural networks have been shown to have great potential to enhance decision-making processes. However, mathematical models must be carefully designed to balance computational costs and solution quality. A promising approach is the combination of deep learning with classical optimization techniques. Moreover, integer linear programming appears to be an excellent technique for problems related to base station location and frequency assignment problems. Thus, research on network optimization is expected to continue to evolve while integrating novel emerging technologies such as quantum computing and autonomous systems. These advances will certainly improve metrics such as the efficiency, scalability, and resilience of modern communication networks.
Figure 2 presents a conceptual road showing how classical OR models continue to support modern network communications. The diagram maps the relationship between application domains such as wireless/mobile networks, routing, and resource scheduling, and the foundational OR models often used to model these problems (e.g. facility location, shortest path, knapsack). These models are then connected to core optimization techniques, including exact methods (for example, MILP), metaheuristics (for example, PSO, GA), graph-based models, and dynamic programming. From there, the framework links to modern techniques such as deep reinforcement learning (DRL), neural networks, federated learning, and graph neural networks (GNNs), which are now essential for solving large-scale, uncertain, or real-time optimization challenges in 5G/6G and IoT networks. This figure is useful because it highlights the continuity between classical theory and emerging computational methods.
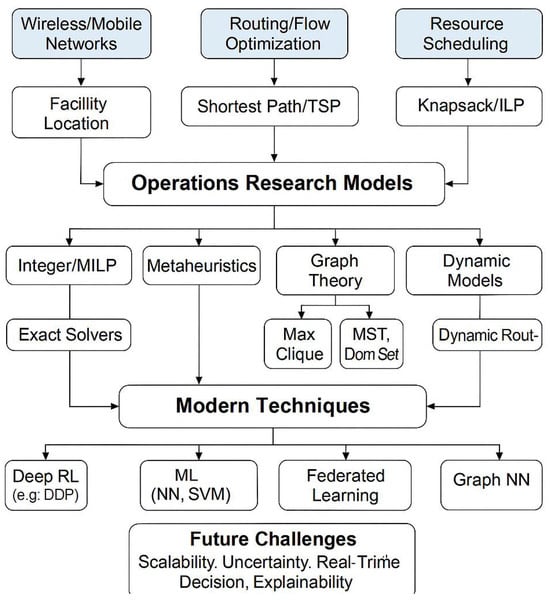
Figure 2.
Conceptual framework linking classic operations research (OR) models to modern network optimization problems and solution methods.
Consequently, it allows researchers to establish a bridge for researchers looking to apply rigorous mathematical modeling while incorporating scalable, intelligent solution approaches. It also emphasizes how future challenges, including scalability, uncertainty, and explainability, can benefit from this combined perspective.
Methodology for Selecting Papers
To review the important literature on network optimization addressed with operations research techniques, we mainly focus on research published between the years 2023 to 2025. The selection process is carried out taking into account specific criteria while ensuring high-quality and relevant journal articles. For this purpose, we search the well-known academic journals of IEEE Xplore with up to around 60 papers containing the topics mentioned above. These sources provided peer-reviewed articles from leading academic universities. The search we did includes papers on mathematical programming, heuristic algorithms, and machine learning applied to network optimization. More precisely, we recall our selection used categories, including routing and flow optimization, resource allocation and scheduling in networks, resilience and robustness optimization, wireless and mobile network optimization, and energy efficiency in wireless networks. Articles presenting experimental results and simulations were also considered to validate the findings of operations research techniques. As such, we collect some of the most relevant and up-to-date research, with the aim of providing a comprehensive overview of optimization techniques in network science. Finally, we mention that we prioritized papers published in high-impact journals related to operations research, wireless networks, machine learning, and artificial intelligence.
To improve methodological transparency, we clarify that the search was performed with the following primary keywords: (“network optimization” OR “resource allocation” OR “routing”) AND (“5G” OR “6G”) and (“machine learning” OR “reinforcement learning” OR “operations research”, “Classical Graph optimization problems in 5 and 6G”) for the period 2023–2025. Inclusion criteria required: (1) peer reviewed journal or conference paper; (2) optimization applied to wireless/mobile networks; (3) presence of methodological contribution (algorithm or model). The excluded criteria were: (1) tutorial or editorial; (2) contributions purely theoretical or hardware layer with no optimization aspect; (3) duplicate results or short abstracts. A total of 60 papers were selected after applying these filters. (See the self-explained Figure 3).
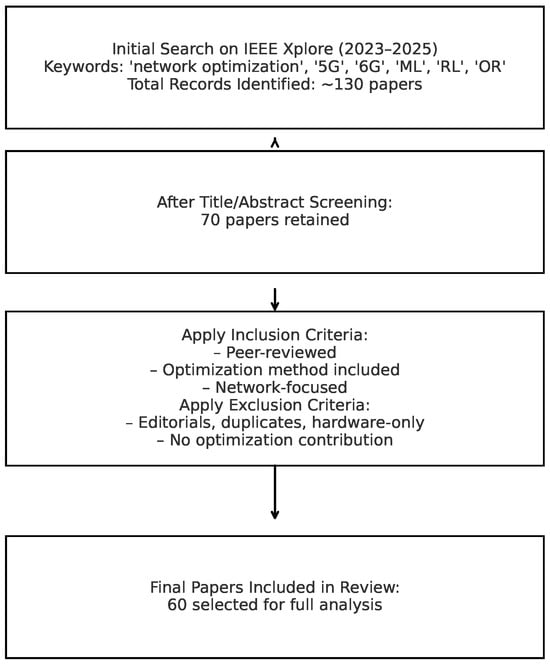
Figure 3.
Flow chart of including and excluding criteria of the structure review paper.
In Table 1, Table 2, Table 3 and Table 4, we present all articles that we reviewed in this article related to the categories mentioned above. More precisely, in column 1, we put the reference of each paper, in columns 2 and 3, we summarize the highlights of each paper and the solving methods. Then, from columns 4 to 8, we report with a mark if the content of each article is related to a specific category in each column.

Table 1.
Comparison and summary of related categories.

Table 2.
Continuation of comparison and summary of related categories.

Table 3.
Continuation of comparison and summary of related categories.

Table 4.
Continuation of comparison and summary of related categories.
Table 5 and Table 6 summarize key performance metrics explicitly reported by selected articles in our review. These include improvements in latency, energy efficiency, coverage, and robustness under different network types. Furthermore, we identify whether each study builds on classical graph-based optimization models. Although many works incorporate graphs for modeling and solution design, several rely solely on data-driven or heuristic approaches without clear topological formulations. This table helps to highlight trends, such as the increasing use of reinforcement learning in routing and scheduling, and the lack of consistent benchmarking across papers.

Table 5.
Quantitative summary of selected papers and graph-based relevance (Part 1).

Table 6.
Quantitative summary of selected papers and graph-based relevance (Part 2).
In the following, we discuss and explain the related theoretical background concerning the different categories of each article reported in Table 1, Table 2, Table 3 and Table 4. Subsequently, this study focuses on the operations research background. Finally, we discuss future gaps between reported papers regarding classic operations research models that can be incorporated and adapted, which can be addressed as future research.
3. Basics of Optimization in Network Research
Optimization is an important tool that improves the efficiency and performance of wireless networks, transportation, and computer networks, just to name a few [58] (see the references in the tables reported above). The main goal here is to find the best solution that maximizes or minimizes the objective function in an optimization problem. An example can be when optimizing a routing problem; in this case, it is possible to determine the most efficient path for data to traverse the network, avoiding congestion and delays.
Another important concept corresponds to the topic of resource allocation. Networks often have limited resources, typically in terms of bandwidth capacity and power. Therefore, optimizing resource allocation undoubtedly helps in efficiently assigning resources to meet the user demands. This is very important in modern networks (5G, 5G+, and 6G), where the number of user devices and the amount of data to be transmitted grow rapidly.
Scheduling is another area of optimization. Tasks or data flows must be efficiently scheduled to ensure that resources are used to avoid conflicts on many networks. For example, consider a cloud computing network where tasks must be scheduled on available servers in such a way that the waiting times are minimized and the throughputs are simultaneously maximized. Network optimization usually involves the use of mathematical formulations and algorithms to solve these types of models. These procedures commonly include linear programming, integer programming, and heuristic methods that have an inherent computational cost to solve them optimally or nearly optimally. This allows researchers and decision makers to develop models that can represent the complex behavior of networks. In particular, the basics of optimization in network research deal with improving network performance. Consequently, minimizing delays, maximizing throughput, or managing resources efficiently is part of the game. Since networks continuously grow and become more and more complex, it is clear that optimization approaches, including modeling and solution procedures, play a key role while ensuring that these systems work under optimal conditions.
3.1. Commonly Used Approaches of Optimization Techniques in Network Communications
Optimization is essential in a variety of fields in communications, and there are multiple approaches to solving complex network problems. In this subsection, we discuss several domains in which optimization and network sciences have been applied together. Linear and integer programming help address problems with linear constraints and integer variables. In addition, metaheuristics such as genetic algorithms (GA), particle swarm optimization (PSO), tabu search, and simulated annealing, among others, aim to approximate suboptimal solutions [59,60]. Similarly, machine learning-based optimization is an emerging approach that combines the power of machine learning with optimization to solve problems in several engineering domains. We further discuss graph-based network representations for routing, flow optimization, resource allocation and scheduling in networks, bandwidth allocation in communication networks, task scheduling in cloud networks, resilience and robustness optimization, wireless and mobile networks, and energy efficiency in wireless communications.
3.1.1. Linear and Integer Programming
A linear program is a mathematical modeling approach that is used to optimize (maximize or minimize) a linear objective function subject to linear constraints. In general, a linear programming problem can be formulated as follows [61]:
where is the decision vector of the variables and are the coefficients of the objective function. The entries in the input matrix and for all and in this particular example represent the constraint coefficients. Notice that integer programming is a nonconvex variant of a linear programming problem in which some or all of the variables are constrained to take integer values. This is utilized in many situations where the decision variables cannot be equal to fractional values. For example, when buying countable objects such as two or three televisions or laptop computers. The mathematical formulation of a mixed integer linear programming problem is similar to that of the model (1)–(4), but with the additional condition that
Notice that these constraints transform the model (1)–(4), (5) into a nonconvex problem hard to solve. This can be easily proven by the discrete nature of the feasible space.
3.1.2. Quantum-Inspired Optimization in Network Communications
Quantum computing is also another interesting approach that offers methods to solve combinatorial optimization problems emerging in 6G networks. A first example algorithm is the quantum approximate optimization algorithm (QAOA), which solves problems such as max-cut, routing, and resource allocation by encoding them as Hamiltonians on qubits. Secondly, variable quantum eigensolvers (VQEs) also optimize energy functions in network flow formulations. Similarly, Quantum annealing, implemented in platforms like D-Wave, has also been applied for facility location and graph partitioning problems, taking advantage of its capability to explore large solution spaces more efficiently than classical heuristics. Although these techniques are still in the early stages of being applied to communication networks, these hybrid quantum-classical algorithms have gained increased attention. In particular, to solve resource allocation problems restricted in dense and dynamic 6G edge environments [62,63,64].
3.1.3. Metaheuristics
Metaheuristics are suboptimal optimization techniques used to deal with complex feasible set search and optimization problems where the exact solutions are prohibitive to find in a reasonable CPU time due to the high dimensionality, linearity, or nonlinearity of the optimization problems. Unlike classic methods, such as linear or integer programming, metaheuristics do not guarantee that an optimal solution will always be obtained. However, they do offer good quality approximate solutions in significantly less computational effort. Some classic metaheuristic algorithms can be described as follows.
- Genetic algorithms: This algorithm is based on the evolution of natural selection. GA simulates a biological evolutionary process that includes selection, crossover, and mutation. These algorithms start and work on the search using a population of solutions initially that evolve during execution time to improve the quality of the solution obtained so far. In many cases, GA allows for the obtaining of optimal or near-optimal solutions, which makes them a good candidate to consider for real network problems.
- Particle swarm optimization: Similarly to GA, PSO is bioinspired by the social behavior of birds or fish. More precisely, this algorithm optimizes a set of interacting solutions, which are called particles that move around the search space to find the best possible solution. Each particle adjusts its position based on its experience and that of its neighbors.
- Taboo search: This algorithm utilizes a memory of recent past solutions and avoids visiting them again to avoid repetitions. The memory used is usually known as the “Taboo List” and is used to efficiently guide the search space, with the hope of finding better solutions within each iteration.
- Simulated annealing: It is based on the physical process of decreasing the temperature during the execution time of some material. The algorithm explores the solution space, allowing, from time to time, the acceptance of a worse current solution to escape from local optimal solutions.
Each of these procedures can be adapted to the nature of particular optimization problems for different areas of application. In Algorithms 1–4, we depict the pseudocode of a generic GA, PSO, taboo search, and simulated annealing, respectively.
| Algorithm 1: Genetic algorithm. |
 |
Analogously to GA, the particle swarm optimization procedure simulates the social behavior of birds to explore the solution space. Using this approach, each particle represents, at the beginning, a solution point, which is adjusted while taking into account its history and the history of the complete swarm.
Taboo search is another efficient metaheuristic that keeps a record of previously explored solutions, marking them as Taboo to avoid revisiting them. This allows focus on promising areas.
| Algorithm 2: Particle swarm optimization. |
 |
| Algorithm 3: Tabu search. |
 |
Simulated annealing is also a bioinspired algorithm based on the physical process of cooling a metal. Here, the system is allowed to change to worse solutions with a probability that gradually decreases over time.
| Algorithm 4: Simulated annealing. |
 |
3.1.4. Machine-Learning-Based Optimization
Machine learning using optimization mixes novel optimization techniques with machine learning formulations to solve complex problems in dynamic and uncertain environments. Traditional optimization procedures are usually not as effective in adapting when changing rapidly or handling large, high-dimensional amounts of data, making ML-based procedures attractive to incorporate. Consequently, the joint use of neural networks and optimization, and also support vector machines (SVM), can help substantially in these two independent approaches. These learning methods can be used to find patterns in the data and provide the necessary solutions for problems that are too complex for classic techniques. In the following, a basic structure of the algorithms used in machine learning-based optimization is presented [65,66].
Recent advances have also shown the potential of reinforcement learning techniques in highly dynamic environments such as edge computing and multiaccess edge computing networks (MECNs) [67]. In these settings, network nodes must make decentralized and latency-sensitive decisions for allocating heterogeneous resources, such as CPU cycles, memory, and bandwidth, under uncertainty and high mobility. DRL-based frameworks have been proposed to dynamically load tasks, optimize service latency between distributed nodes, and manage energy consumption. Techniques such as proximal policy optimization (PPO) and deep Q-networks (DQN) are increasingly used to model resource allocation as a sequential decision-making problem in MEC [68]. The ability of RL agents to learn optimal policies in time without requiring full knowledge of the system is useful for scalability and adaptive resource management in edge-based architectures.
3.2. Taxonomy of Optimization Approaches in Network Communications
To better understand how optimization techniques are being applied in modern network communication problems, we built a taxonomy based on the papers reviewed in this article. This taxonomy classifies each paper according to:
- The type of network problem being addressed (e.g., routing, scheduling, and energy efficiency).
- Procedures used to solve the problems: exact methods like classical optimization (e.g., MILP), or suboptimal approximation methods such as heuristics/metaheuristics (e.g., genetic algorithms), or machine learning and reinforcement learning techniques.
Our aim here is to provide the reader with a clear view of what types of techniques are most common for each problem type and to identify areas that are either well studied or underexplored. Table 7 summarizes these findings.

Table 7.
Taxonomy of optimization approaches by problem category and solution technique.
From Table 7, we can observe some interesting patterns: Table 7 reports several important trends. Firstly, traditional optimization techniques (e.g., linear or integer programming) are still preferably used in problems related to routing and infrastructure design. For example, p-median or flow-based models. However, metaheuristic approaches are preferred in areas such as energy-efficient routing and wireless sensor networks, especially when exact methods are too computationally intensive. On the other hand, machine learning and reinforcement learning techniques are preferable for dynamic settings in 6G networks, resource allocation with uncertainty, and edge computing domains.
It is also worth mentioning that resilience optimization and energy-aware systems remain relatively underexplored using classical OR methods. This highlights future opportunities for research. In summary, the taxonomy in Figure 4 constitutes a useful example bridge between well-established OR models and emerging AI-based strategies. The latter offers valuable guidance for new researchers to address modern network optimization challenges.
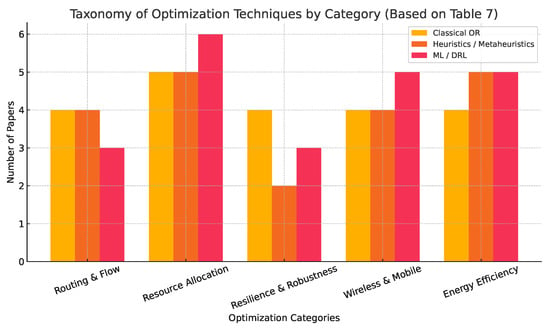
Figure 4.
Visual taxonomy of optimization techniques by category, summarizing the number of papers applying classical OR, heuristics, and ML/DRL methods as classified in Table 7.
Based on the taxonomy summarized in Table 7, the following sections focus on hybrid learning optimization frameworks that illustrate how these techniques are applied in real-world network scenarios.
3.3. Predict-And-Optimize
A generic algorithm to predict and take the best decision, optimizing simultaneously, can be explained as follows. Of course, with this algorithm, it is possible to observe real outcomes, update the dataset, and retrain the predict-and-optimize Algorithm 5 using Algorithm 6 to improve future predictions. In particular, Neural networks are machine learning models that can learn from non-linear data and optimize solutions through an iterative process of weight tuning. Training a neural network (NN) involves minimizing a loss function to find the optimal weights, as shown in Algorithm 6.
Support vector machines are a supervised approach to classification and regression that seeks to find an optimal hyperplane that separates classes with maximum margin. In the context of optimization, SVMs seek the optimal class separation margin in the feature space. Here, a generic algorithm is presented in Algorithm 7 to perform each of the required steps within SVM.
| Algorithm 5: Predict-and-optimize. |
 |
| Algorithm 6: Optimization with NN. |
 |
| Algorithm 7: Optimizing with SVM. |
 |
Notice that the NN approach iteratively adjusts the weights using methods such as gradient descent, while in backpropagation, the weights are adjusted to minimize the loss function. On the other hand, the SVM approach is first used for classification and regression, and then it is optimized to find the position of a hyperplane while maximizing the margin of separation between different classes. In optimization, the goal is thus to find the hyperplane that best divides the data with the largest possible margin.
3.4. Types of Network Models
Networks are fundamental to optimizing and analyzing real complex systems. Usually, these studies are represented by using graphs composed of vertices and links that connect some of the nodes. In turn, this allows one to facilitate the analysis and optimization of networks. Depending on the structural evolution of networks over time, they can be classified as static, where the structure remains unchanged, or dynamic, where nodes and connections change over time. In general, in terms of optimization, there are centralized and distributed approaches, where a single node or entity makes global decisions, or where multiple nodes cooperate to find local solutions that optimize the system as a whole. Network models play a key role in optimizing and analyzing real complex systems. The representation of networks using graphs allows the modeling of various real-world problems in different domains such as communication, transportation, and social networks. Several fundamental optimization problems in graph theory are highly relevant to network science and operations research. In the following, we present and describe some key models and their mathematical formulations, which could be easily adapted to 5G, 5G+, and 6G technologies to further contribute to the domain of future network sciences [59,61].
- Maximum Clique Problem
Given a graph , with a set of vertices V and a set of links E, the maximum clique problem consists of finding the largest subset of vertices such that all vertices in S are pairwise connected. Its mathematical formulation is as follows.
where is a binary decision variable equal to 1 if node is selected as part of the clique and 0 otherwise.
- Maximum Independent or Stable Set Problem
The maximum independent set problem consists of finding the largest subset of vertices such that no two vertices in S are adjacent. In this formulation, is a binary variable equal to 1 if node i is included in the independent set and 0 otherwise. Its formulation is as follows.
Notice that there exists a strong relationship between the two optimization problems: the maximum clique and the maximum independent set problems. The first one finds the maximal clique over all possible cliques in the graph. The second one finds the maximal independent set among all independent sets of the same graph. Surprisingly, finding a maximal clique is equivalent to finding a maximal clique in the same complement graph. Both problems have proven to be NP-hard.
- p-Median Problem
This is another interesting classic graph optimization problem. It can be described as follows: given a graph with demand points V and p candidate facility locations, and a set of edges E, the p-median problem aims to find optimal locations to place or install p facilities out of to minimize the total weighted distance between demand points and customers to each facility. The formulation can be written as follows:
In problem (12)–(16), (12) minimizes the total distances between customer and facility . The latter is performed using the binary variable and the symmetric distance matrix for all and . In this model, is a binary variable equal to 1 if the client node i is assigned to the facility j, and is 1 if the facility j is opened. Then, the constraints (13) ensure that each customer is assigned to a unique facility node. Similarly, constraints (14) impose that a customer can only be assigned to a unique and open facility node . Next, the constraint (15) guarantees that the sum of facilities should be equal to p. Finally, the constraints (16) denote the domain of the decision variables.
- Facility Location Problem
This problem appears as a variant of the p-median problem by introducing a fixed cost for all , i.e., for the open facility at location j. The rest of the variables and parameters retain the same meaning as in the p-median model, including and . Then, the goal is to minimize the total installation and assignment cost without specifying a fixed number of facilities. The formulation is as follows:
In model (17)–(20), the objective function (17) minimizes the installation cost and the total distance between customers and open facilities. The only difference from the p-median problem is that model (17)–(20) does not impose a fixed input parameter p of the facilities. The rest is analogous to the p-median and thus self-explanatory.
- Minimum Spanning Tree
The Minimum Spanning Tree (MST) problem aims to connect all nodes in a connected graph with the minimum total edge weight without forming cycles in the output solution of the problem. Given an input connected graph . In this model, is a binary variable equal to 1 if the edge is selected in the spanning tree and 0 otherwise. The parameter represents the cost or weight associated with the edge . The term denotes the subset of edges whose both endpoints lie within the subset of nodes . One of its formulations can be written as [61]:
This is an exponential formulation due to the exponential number of subtour elimination constraints in (23). The objective function (21) minimizes the total connectivity costs of the output solution tree. Finally, the constraints (23) avoid cycles in the tree solution obtained. Another related problem is known in graph optimization as the traveling salesman problem (TSP).
- Traveling Salesman Problem (TSP)
The TSP aims to find a Hamiltonian cycle consisting of the largest cycle that unites all nodes of the input connected network. The Hamiltonian cycle should be the shortest route that visits each node of the graph exactly once and returns to the starting point. Similarly to MST, there are several equivalent formulations in the literature [61]. The problem requires an input graph where A denotes a set of arcs instead of edges. Consequently, for each edge in E, we replace each edge by the two arcs and in A. In this model, is a binary variable equal to 1 if the arc is part of the tour and 0 otherwise. The parameter represents the travel cost or distance from node i to node j. The set corresponds to the arcs whose endpoints are both within a subset . To be coherent, in the following we also present an exponential formulation.
In model (25)–(29), the objective function (25) minimizes the total cost of connectivity. Constraints (26) and (27) ensure that each node has one incoming and one outgoing arc. Constraints (28) avoid cycles except for the size cycle , thus forming the Hamiltonian cycle.
Notice that all these formulations are classic graph optimization models from the operations research domain. Consequently, they provide many opportunities to construct new novel modeling approaches for the generic field of network science. In particular, for future wireless communication networks. They can be adapted to problems in the domains of 5G, 5G+ and 6G communications, transportation networks, logistics, and supply chain management. The maximum clique and maximum independent set are classic models that can be used and adapted for all the above-mentioned infrastructures required in social networks, bioinformatics, and so on. Similarly, p-median and facility location problems are key models to enrich the domains of optimizing infrastructures in wireless networks. The minimum spanning tree has been used and can be used for many other modern network design topologies for communication and energy optimization problems. Finally, TSP is a fundamental problem for ring infrastructures in communications, logistics, and planning.
Recently, advances in graph neural networks (GNNs) have offered powerful tools for dynamic network modeling in 6G environments [69]. Despite static graph optimization, GNNs enable the learning of node and edge representations over time, allowing real-time adaptations to changing topologies, device mobility, and stochastic interference. Many architectures, such as graph attention networks (GATs), spatial-temporal GNNs, and message passing neural networks (MPNNs), have been applied to predict routing, resource allocation, and user association in mobile networks. Similarly, processing network graphs under uncertainty, such as fluctuating connectivity or unreliable links, can benefit from probabilistic graph models, robust GNN training, and Bayesian graph learning techniques. These methods complement traditional OR models by providing learning-based adaptability in dynamic and uncertain 6G scenarios [70,71,72,73].
- Static Versus Dynamic Networks
In general, networks can be categorized as static or dynamic. In the former case, this occurs when the topology remains constant over time. In the latter case, the nodes and edges evolve, which directly influences the optimization strategies. Examples of both types of networks include mobile telecommunications networks, social networks online, autonomous vehicle systems, and many others. Below, we present two classic mathematical formulations to better illustrate how the time dimension can be incorporated in operations research problems involving networks: the dynamic shortest path problem and another one for the dynamic facility location problem.
- Dynamic Shortest Path Problem (DSPP)
The dynamic shortest path problem consists of finding the shortest path in a network where the edge weights change over time. Formally, given a graph with time-dependent edge costs , the main goal is to minimize the travel cost between a source s and a destination d. In this formulation, is a binary variable equal to 1 if the arc is selected in the path and 0 otherwise. The parameter denotes the time-dependent cost of arc traversing at time t. The node s represents the source and d the destination. The set A is the set of directed arcs derived from the network topology. The model can be written as follows:
where the objective function (30) minimizes the changing costs. The remaining constraints are static and determine the flow to be directed in such a way that the shortest path is obtained [59,61].
3.5. Centralized and Distributed Optimization
Observe that network optimization using graph theory allows us to deal with the fundamental problems in communications. Notice that over time, networks can be static, which means that the topology remains fixed or dynamic due to mobility, failures, or network movements. In addition, note that network optimization can be used in a centralized or distributed manner. In centralized optimization, a single global entity makes decisions with full access to the data, guaranteeing that the optimal solution will be obtained, although it can be computationally expensive and not easily scalable.
Distributed optimization, on the other hand, allows us to make decisions from multiple agents cooperating simultaneously, making the network more robust and scalable. Although it may require efficient communication between nodes. An example of a more dynamic network can be represented with a time-indexed graph , where and change their coordinates and connection links at each time step t. Following the idea of a typical dynamic shortest path problem, it can be formulated as follows.
In this dynamic formulation, is a binary variable equal to 1 if arc is used at time t and 0 otherwise. The cost function represents the time-dependent cost of traversing the arc at time t, and denotes the set of available arcs at time t. Similarly, is the set of active nodes at time t, and is the net flow demand at node i at time t. Optimization is performed on a finite time horizon T.
- Distributed Optimization
Distributed optimization uses many nodes to update their decisions on time using local information and communication with their neighbors. A distributed problem for resource allocation can be formulated as follows.
where the variable is the decision at node i, is the neighborhood of i, and denotes the communication weights in a cooperative algorithm. The input parameter can be a non-linear function related to the cost of installation, depending on the decision variable x. Similarly, can be associated with resource allocation costs depending on the decision variables and . Next, denotes the communication weight used in the consensus constraint. A consensus approach is a distributed method in which local nodes make decisions based on communication with their neighbors, useful in decentralized networks such as blockchain. or software-defined networks (SDN).
3.6. Lessons Learned and Technique Limitations
Several important lessons and limitations can be observed from optimization techniques based on the reviewed work.
For example, classical optimization approaches such as linear and integer programming are still commonly used for structured problems, including routing and facility location, since these methods offer solid mathematical foundations and guarantee optimal solutions. However, they do not scale to large networks and often require long computational efforts in terms of CPU time to be solved optimally.
Metaheuristic methods such as genetic algorithms (GA), particle swarm optimization (PSO), and tabu search are commonly used when exact methods are too slow. These methods are more flexible and provide good quality solutions in complex environments like wireless sensor networks in reasonable CPU time efforts. However, they do not guarantee optimality and their performance often depends on careful parameter tuning.
Machine learning (ML) and deep reinforcement learning (DRL) techniques are increasingly popular for problems that involve uncertainty, high-dimensional data, and dynamic conditions, such as those found in 6G, IoT, and edge computing. These techniques can adapt in real time and learn from data. However, they require large training datasets, high computational resources, and often lack interpretability.
In general, we observe that classical methods are underused in areas like resilience and robustness optimization. This suggests a research opportunity that combines the theoretical strength of operations research with the adaptability of modern AI methods. In summary, each family of techniques has its own strengths and weaknesses. Understanding these trade-offs is key to selecting the best method for each network optimization problem.
3.7. Observed Gaps in Benchmarking and Poor Consistency Across Reviewed Works
Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 present a solid classification of recent works using OR and AI techniques. However, an important limitation observed is the lack of standardized benchmarking and consistent evaluation procedures. For example, several works report significant improvements in latency and energy efficiency. However, these metrics are measured using different numbers of nodes in the networks considered, different traffic models, or simulation environments. Consequently, individual works such as [4,11,23] claim performance gains using reinforcement learning or deep learning; their results are not directly comparable due to differing experimental settings and baseline experiments. Moreover, some works rely on established classical formulations (e.g. MILP or ILP) as benchmarks [5,8], but many others do not report comparisons with standard baselines. The latter makes it difficult to assess the true advantages of the proposed approaches. To address this gap, we suggest the potential use of a minimal comparative framework in future studies, perhaps including:
- Same network topologies (for example, ring, tree, random graphs with 100 to 500 nodes).
- Standardized metrics (e.g., end-to-end delay in ms, energy per bit in J, task drop rate %).
- Clear reporting of computational cost (e.g., run-time, number of iterations).
- Baseline algorithms (e.g., MILP from [59], PSO from [60] or rule-based heuristics).
Although the scope of this review is not to enforce a benchmarking standard, we emphasize that such a framework would be highly beneficial for reproducibility and to evaluate the progress of hybrid OR-AI techniques in various applications related to 6G. Finally, public simulation platforms such as Mininet [3] or solver tools such as CPLEX [2] can also contribute to comparable experiments, provided that their use is clearly documented. Shared datasets and open code repositories would also support the transition from theoretical modeling to practical, scalable deployment in next-generation networks.
As illustrated in Figure 5, even when similar metrics, such as latency improvement, are reported in recent studies, the lack of standardized conditions, such as network size, baseline methods and traffic models, prevents a meaningful comparison. This further reinforces the urgent need for a shared benchmarking framework to support reproducibility, fair evaluation, and methodological transparency in the field of network optimization.
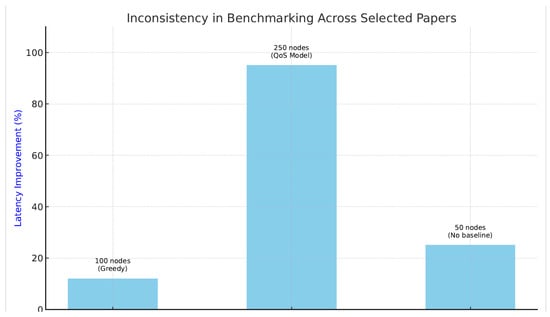
Figure 5.
Illustrative comparison of latency improvement metrics across three selected papers [4,10,23], highlighting inconsistency in benchmark settings (e.g., network size and baseline type). This visual supports the argument regarding the need for standardized evaluation.
To support future comparative studies, we propose the following minimal benchmarking framework for optimization in wireless networks.
- Network topologies: Use standard graphs such as ring, tree, and random topologies with sizes ranging from 100 to 500 nodes.
- Evaluation metrics: Report latency (ms), energy per bit (J), and task drop rate (%) using consistent baselines.
- Computational reporting: Include CPU time, iteration counts, and convergence thresholds.
- Baseline methods: Compare against classical models (e.g., MILP, PSO) and simple heuristics.
These elements can help promote reproducibility and fair comparison among AI and OR-based optimization methods, as shown in Table 8.

Table 8.
Proposed benchmarking elements for future comparative studies.
3.8. Resource Allocation and Scheduling in Networks
Resource allocation and scheduling in networks are important problems in distributed systems. In particular, telecommunications, cloud computing, and sensor networks aim to efficiently distribute bandwidth, power, and processing times among several nodes, minimizing costs, and maximizing network bit rates.
- Bandwidth Resource Allocation in Communication Networks
Let represent a network with a set of nodes V and a set of user edges E representing links with limited bandwidth . The goal of the optimization problem is to assign the bandwidth where the variable represents the amount of bandwidth allocated to the link , and is the minimum bandwidth demand for node i, thus ensuring the required capacity constraints. In this model, is a binary variable that indicates whether node i is active or not. The parameter denotes the total capacity of the link in the network graph. A generic model can then be written as
The variables in this model can be defined as
- : Binary variable for each node i. if the node i is activated or selected. if the node i is not active.
- : Non-negative variable for each edge . Represents the flow or allocation from node i to node j, which is bounded from above by .
Finally, the objective function maximizes the maximum number of active nodes. The constraints for all ensure the minimum demand for each activated node. Next, the constraints for all ensure that the links are not saturated.
- Task Scheduling in a Cloud Network
The set of tasks T needs to be assigned to a set of servers S to minimize the overall completion time in a cloud computing system. Consider that the processing times for tasks on the server s are limited by the amount of capacity of each server. Then, a mathematical formulation can be written as follows.
In this model, is a binary variable equal to 1 if the task is assigned to the server . Generic models of this type can provide a solid reference for solving real-world resource allocation and scheduling problems in networked systems. In particular, this model minimizes the worst bandwidth allocation while ensuring that each user’s demand is met within the network’s capabilities. Another example is a model that minimizes the total task completion time by efficiently distributing tasks across servers with limited capacity in a cloud task scheduling situation. In particular, in this model, the binary variable indicates if the task is assigned to server or not. The parameter represents the weight or cost of allocating the task t to the server s, and is the maximum capacity of the server s. The objective function goal is thus to minimize the worst charge accumulated among all servers. This can be expressed as . The first constraint ensures that each task t is assigned to a unique server. The second ensures that the sum of the weights of the tasks assigned to a server does not exceed the capacity .
- Resilience and Robustness Optimization
Resilience and robustness optimization in networks focus on designing optimal infrastructures capable of dealing with failures and attacks while simultaneously ensuring service. Resilience is the quality of the network’s ability to recover from disruptions. At the same time, robustness guarantees the capacity to maintain network operation under difficult conditions. As such, graph-based models help optimize these relevant aspects by minimizing the impact of failures against strategic attacks, connectivity, and functionality.
- Resilient Network Design
The following model ensures that the network remains operational after the failure of a subset of critical connections. In this model, is a binary variable equal to 1 if the link is included in the resilient design.
where represents the set of all possible connection failures, ensuring that at least one path remains in good condition. The variable for all equals one if the edge is still operating; otherwise it equals zero. The input matrix denotes the cost of choosing the edge . Constraints (34) ensure that any subset is considered. Finally, constraints (35) are domain constraints for the decision variables.
- Robust Network Design Against Attacks
This model minimizes the worst-case connectivity loss when an adversary removes a set of critical nodes. In this robust optimization model, is a binary variable equal to 1 if node i remains functional under attack and 0 otherwise. The parameter k represents the minimum number of nodes that must fail for a subset S to be considered compromised. The set contains all vulnerable or critical subsets that are evaluated under attack scenarios. The model is
where denotes all possible attack scenarios. The idea in this model is to simply maximize the total number of remaining nodes while in an attack , k nodes have been removed. This is achieved by the constraints (37). Finally, the constraints (38) define the domain of the decision variables. These models provide a structured framework to make the network resilient and robust against failures and strategic attacks.
3.9. A Practical Framework Connecting Classical OR Models with 5G/6G Networks
Classical optimization models, including the p-median, facility location, and spanning tree, have been widely studied in OR. As can be observed, their adaptation to 6G networks requires a clear bridge between theory and modern challenges. In this subsection, a simple and effective framework is proposed that allows researchers to connect classic OR problems with practical applications in modern wireless networks.
This framework consists of three main layers. The first is concerned with classical OR models, including classical formulations such as the minimum spanning tree, the maximum clique, the location of the facility, and p-median problems. Assume that these models represent the mathematical foundation and structure. Subsequently, in the second layer, consider 5G/6G network problems together with their real-world specific requirements and constraints, such as ultralow latency, dynamic mobility, stochastic channel behavior, massive device density, and energy efficiency. These key specific elements of future technologies enrich traditional OR models with more realistic assumptions. Finally, layer three corresponds to the modern solution techniques for solving the novel formulations. They can be deep reinforcement learning (DRL), graph neural networks (GNNs), federated learning, and/or digital twin simulations, among others. As such, it is possible to complement OR models by improving scalability, learning capabilities, and real-time adaptation. Consequently, this three-layer structure helps to clearly understand how classical OR tools are still very useful for modern network design and optimization. Figure 6 visually summarizes this idea. This figure below indicates to researchers the new paradigm for reusing and adapting existing OR techniques in combination with modern AI and learning tools to address the new requirements of 5G/6G systems.

Figure 6.
The three layers approach to connect classical OR modeling with 5G/6G network optimization.
It also helps practitioners see the value of classical models in new contexts while staying open to hybrid and data-driven approaches.
3.10. Wireless and Mobile Networks Optimization
The optimization of wireless and mobile networks is highly relevant for improving the efficiency and performance of real-time communications. Since users are constantly moving and signal conditions vary, these aspects pose challenges in terms of coverage, resource allocation, and interference management. Since mathematical formulations consider dynamic user locations, frequency assignments, and network management, they play a key role in ensuring the quality of service. In addition, the network infrastructure, such as the location of the base station or the routing of the data transmission route, is also crucial in the performance of mobile and 6G networks.
- Power Control in Wireless Networks
Power control in wireless networks seeks to determine the optimal transmission power for each node to minimize interference while maintaining communication quality. In this formulation, denotes the transmission power of node i. The parameter models the level of interference caused by node i on node j, while represents the gain or attenuation factor of the channel between i and j. The value is the minimum signal threshold required at the receiver node j to maintain acceptable quality. The power for each node is limited between and . It is stated as
In model (39)–(41), the objective is to minimize the power interaction between each pair of nodes . Here, the parameter denotes the channel gain between each pair of nodes. Constraints (40) ensure that a minimum power is required for each node . Finally, the constraints (41) indicate that each power node for each should be between parameters and .
- Base Station Location Problem
In the base station location problem, the goal is to optimize the location of base stations while providing user coverage to mobile users. It also considers the constraints for maintaining available resources and coverage areas. In this formulation, is a binary variable equal to 1 if a base station is installed at candidate location , and is equal to 1 if the user is served by the station i. The parameter denotes the installation cost on site i. The set V contains potential base station sites, and U represents the set of users requiring service. It is stated as
In model (42)–(46), the objective function is to minimize the installation costs for each , which is achieved using the binary variable for all . All users must be assigned to a particular and unique facility . All of this is ensured by the remaining constraints, which are equal to the facility location problem previously explained. Thus, we omitted the detailed explanation of each of the constraints here.
3.11. Energy Efficiency in Wireless Networks
Since data traffic and connectivity demands increase, it is essential to design algorithms and models that minimize energy consumption while maintaining the quality of service. In the following, we present two examples of modeling power allocation in wireless networks and network resource allocation, respectively.
- Resource Power Allocation in Wireless Networks
In wireless networks, power allocation is essential to improve efficiency while maintaining the quality of service at high levels. The problem can be formulated as an optimization problem to minimize total power consumption. In this model, is the transmission power of node , where N is the set of transmitting nodes. The variable represents the signal-to-noise ratio at node i, and is the minimum required SNR threshold for reliable communication. The parameter denotes the channel gain between node i and its receiver. Consequently, the following optimization problem can be stated.
where the total power consumption is minimized in the objective (47). Next, constraints (48) ensure that the signal-to-noise ratio of each node must be greater than or equal to a predefined threshold . Then, the constraints (49) indicate that the power of each node can be calculated as shown in the ratio formula where denotes channel gain. Finally, each power must be nonnegative, which is achieved by the constraints (50).
- Network Resource Allocation
This model considers the problem of resource allocation in a multicell wireless network where the goal is to maximize energy efficiency by assigning bandwidth and power to users, also ensuring fair distribution. In this model, denotes the transmission rate of node , and is its associated transmission power. The objective is to maximize global energy efficiency, defined as the total rate per unit of power. The function maps each rate to its required power, typically based on channel characteristics or modulation schemes. The parameter B is the total available bandwidth or the aggregate rate budget for the network. The model is stated as
The objective function (51) maximizes the sum of the total capacities over the sum of the total powers of each node . Next, constraints (52) limit that the sum of the total capacity should not exceed the value B, which is the total available bandwidth in the network. The generic constraints (53) illustrate the relationship between capacity and power. Finally, the constraints (54) ensure that the capacity and power variables must be nonnegative.
3.12. Practical Limitations in the Revised Optimization Techniques
However, we notice that many works report high-level performance metrics for latency, energy efficiency, and throughput. It is relevant to take into account real-world deployment scenarios, which often impose important limitations that are not always consistently addressed in the literature. It was already mentioned above that exact optimization approaches, including MILP and ILP, although mathematically rigorous, are known to suffer from poor scalability [5,59]. These methods are computationally expensive and become intractable for large-sized instances, making them difficult to apply for a real large-scale 6G topology involving hundreds of nodes and dynamic user profiles. Secondly, metaheuristic and AI-based methods are often trained in simulated environments with fixed assumptions. Even when they outperform classical methods in several benchmarks [11,57], they also require extensive computational resources, in particular during training steps, and may lack generalization, taking into account different network conditions or hardware constraints. Finally, transferability remains an open issue. Optimization models consider specific network configurations such as star, mesh, or dynamic edge networks and rarely include a sensitivity analysis to test their robustness across varying topologies or failure scenarios.
As a consequence, these limitations underscore the need for hybrid approaches to balance model tractability and learning flexibility, and for benchmarking protocols that account for both solution quality and computational costs.
4. Comparative Insights and Observed Limitations
Although the paper successfully compiles a wide range of recent research efforts in network optimization, covering routing, scheduling, energy efficiency, and robustness, the comparative analysis of these works remains limited. This section attempts to gain insight and identify methodological gaps based on the existing reviewed material (see Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6).
4.1. Technique Comparison by Category
An inspection of Table 1, Table 2, Table 3 and Table 4 reveals that deep reinforcement learning (DRL) is a recurring technique, particularly in energy sensitive scheduling and resource allocation tasks (e.g., [11,23,34,42]). In contrast, classical mixed-integer linear programming (MILP) is primarily used in early-stage topology design and routing problems (e.g. [5,8]). However, no explicit performance comparison is offered across these approaches. Consequently, this limits our understanding of when a method is preferable in practice.
4.2. Benchmarking and Reproducibility
Again, even when several of the revised papers report percentage improvements (e.g., 12% latency reduction in [4], or 95% improvement in processing time in [10]), few provide details on instance sizes or computational times. The absence of shared benchmark data sets or standardized simulation environments hinders reproducibility and fair comparison between existing methods. Moreover, some methods reduce their analytical clarity as they rely only on simulation or machine learning frameworks without any formal formulation [22,39,43].
4.3. Gaps in Methodological Transparency
Despite the strong relevance of data-driven approaches, several articles do not report parameter sensitivity, training time, or limitations. DRL-based works, in particular, tend to lack interpretability or convergence analysis. On the other hand, while classical OR models (e.g., p-median, MST, TSP) offer provable guarantees, they are often dismissed in large-scale dynamic settings without evaluation of their hybrid potential with learning-based methods.
4.4. Implications
Clearly, these gaps pose opportunities and future challenges in integrating classical optimization models with modern AI techniques using an intelligent framework while simultaneously preserving interpretability and scalability. In addition, creating a unified benchmarking framework would also enhance the comparability and practical applicability of future research works.
Although the previous sections presented a comparative analysis of methods and limitations, we now shift the focus to open research questions and future directions, particularly how operations research can be extended and hybridized to meet emerging 6G demands.
A close review of the algorithm side reveals several particularities. For example, particle swarm optimization (PSO) often struggles in high-dimensional search spaces or highly constrained problems, whereas genetic algorithms (GA) or tabu search offer better diversity preservation and constraint satisfaction. Deep-reinforcement learning (DRL) methods, while powerful, suffer from training instability due to delayed rewards, non-stationarity of the environment, and sparse feedback in long-horizon tasks. These issues are particularly relevant in network scheduling and routing. Although recent advances have been made, DRL frameworks often require significant tuning, large training sets, and lack the formal guarantees offered by mixed integer linear programming (MILP) in terms of optimality. In scenarios involving hard constraints (e.g., capacity limits, integer assignments), MILP remains preferable due to its exactness, interpretability, and robustness. In particular, when used in offline or deterministic settings.
5. Open Challenges and Future Research for Modeling and Solving Methods: Joining Network Science and Operations Research
In this section, the opportunities of combining network science with classic OR problems in the form of open challenges and future research directions for novel formulations and solving approaches are discussed. In particular, recent articles from 2023 to 2025 on each related topic of energy efficiency in wireless networks, routing and flow optimization, resilience and robustness optimization, resource allocation and scheduling, wireless and mobile network optimization, and methods for solving these problems are discussed and referenced in the recent literature (see Table 1, Table 2, Table 3 and Table 4).
5.1. Energy Efficiency in Wireless Networks
The revised papers in this domain deal with several relevant topics in wireless networks, the Internet of Things, optimizing energy and resources, and the application of advanced techniques such as machine learning to solve complex problems. Many of these topics are related directly to classic problems in operations research, offering great opportunities to develop novel formulations and solution approaches to use traditional and modern knowledge.
Reduction of energy consumption is one of the main goals in several works [20,22,23,42,52,56]. In references [42], the authors formulate minimization energy problems in a distributed manner. Reference [20] focuses on minimizing the expected total energy consumption in the long term in wireless networks. For this purpose, the authors consider models for efficient batteries that vary in time. Ref. [56] addresses the assignment of resources and handles the optimization of tasks in computing continuum environments, taking into account failed tasks and the necessary resources using explicit heuristic algorithms, which are classic for the well-known approximation bin-packing problem [56]. Energy efficiency and age of information (AoI) are also studied jointly in wireless personal communication networks (WPCNs) [23].
These assignment and resource problems can be aligned directly with classic allocation of resources, such as bin packing, which consists of assigning tasks or user resources with limited capacities, or with scheduling problems, which allow determining the sequence order and execution time of tasks on different machines. Similarly, optimizing power and bandwidth assignment [52] or with aggregation of frames to minimize energy usage [22]. These problems also fall into this category of classifications.
Reference [24] is devoted to the deployment of relays to ensure connectivity and improve the energetic efficiency and useful life of energy-based wireless sensor networks (EH-WSN) while discussing the optimal location of relays [24]. This is related to facility location problems, such as base station installations, relays, chargers, or access points. On the other hand, the covering problem or the dominating classic set of structures consists of selecting a minimum set of nodes to cover and monitor a predefined area or set of nodes of the network. The requirement of WSN scalable architectures highlights the relevance of these models and deployments [49]. Reference [21] addresses the mobile charging problem while simultaneously focusing on optimizing the routes to ensure the robustness of the system. The work mentions the heuristics of the TSP as related to routing optimization.
Notice that recall of aerial vehicle (UAV) data [26] or mobile charging [44] inherently involves routing problems similar to TSP or more general vehicle routing problems (VRP), where the objective might be to minimize the distance traveled, maximize the energy collected or the data collected, or ensure that all nodes are visited before their batteries run out.
Networks are often modeled using graph theory. Refs. [14,26] proposes a scheduling methodology that takes advantage of the directional characteristics of beams in mmWave networks to avoid interference, using graph theory for beam scheduling and intercell interference avoidance. Problems such as interference avoidance or user clustering in wireless networks can be formulated as graph coloring, maximum clique, or maximum independent set problems, where nodes (users, beams) are clustered or selected based on their compatibility (or incompatibility, in the case of interference).
The paper by [57] provides a systematic review of how ML is applied to solve optimization problems in 6G wireless networks. Techniques such as deep reinforcement learning (DRL) are used for stochastic optimization, graph neural networks (GNNs) for structured optimization, and federated learning for distributed optimization. Ref. [56] also mentions the use of DRL for energy-efficient optimization in edge inference.
Here lies a key combination point: classical IoT models (such as TSP, facility location, bin packing, and graph problems) can provide the mathematical structure to define a problem (e.g., finding the optimal route, best placement, most efficient assignment). Then, modern ML and optimization techniques (such as DRL, distributed algorithms, approximation algorithms, or the specific scheduling and resource allocation techniques presented in the other papers) can be used as solution methods, especially for large-scale, dynamic, or uncertain problems, where exact classical methods might be computationally prohibitive. For example, a DRL algorithm could learn a routing policy for a mobile charger (by solving a dynamic VRP/TSP instance) based on the current state of the sensor batteries, or a GNN could optimize beam assignment (by solving a graph problem) in real time.
The reviewed articles address fundamental problems in wireless networks, IoT, and energy system operations, such as energy optimization, resource allocation, infrastructure deployment, and mobility management. These problems have a natural anchor in classical operations research models, including facility location, TSP, bin packing, and graph-theory problems. The advanced techniques discussed, particularly distributed optimization and machine learning-based approaches, not only address the limitations of classical methods in complex and dynamic environments but also offer powerful new tools for solving underlying IoT formulations, paving the way for more efficient and intelligent management of future networks.
5.2. Routing and Flow Optimization
Beyond energy-related challenges, another central pillar in modern networks is efficient routing and flow optimization, which is deeply rooted in classical combinatorial problems and has gained renewed interest with the rise of AI-based solvers. The investigated articles in Table 1, Table 2, Table 3 and Table 4 cover a variety of topics related to communication networks, transportation, supply chain management, and physical systems design, with an emphasis on the optimization and the use of advanced procedures, including artificial intelligence and machine learning [4,19,30,37,39,57]. Many of these papers focus on routing, resource allocation, and location problems, which are key topics in operations research. This includes routing in wireless and wired communication networks [5,6,20,29], sensors networks [21,24,44], and in the physical design of integrated circuits (global routing) [31]. Multi-commodity flow routing [7] and low-latency constrained routing [5] are also discussed as problems. These topics have a direct connection to classical OR models. In particular, with the shortest path problem, which can be solved optimally by algorithms such as Dijkstra and A*, and network flow problems, including multi-commodity flow [31,44]. The formulation of these problems usually adopts the form of pure integer linear programming (ILP) or mixed integer linear programming (MILP), which are standard OR tools [5,8,31].
In the context of transportation systems, problems such as network flow management [53], vehicle routing [30,54], and the interaction between energy and transportation networks [28] are considered. Vehicle routing with simultaneous pickup and delivery with time windows (VRPSPDTW) [54] is an example closely related to the TSP and its generalizations, such as the VRP. The management of electric vehicle demand and the optimization of charging also fit this field [28,44]. The placement of distributed processing units (DU) in xHaul networks [5], the deployment of relay nodes in sensor networks [24], and the movement of cells in the physical layout of circuits to improve routing [31] are also studied. These problems are analogous to facility location problems or variants of the p-median problem, where the objective is to select the best location for a set of facilities to satisfy demand locations, often minimizing costs or distances. Various techniques are used, from ILP/MILP-based methods [5,8,31] and LP relaxation [7] to heuristics [5] and metaheuristics, such as genetic algorithms [54] and particle swarm optimization [37]. The use of AI/ML is promising, being applied for optimization [4,19,57], demand prediction [37], traffic classification [39], or to guide heuristic algorithms [30]. Similarly, bilevel optimization is also used to model complex interactions [28,53]. The integration of these areas with classical OR models is clear. Notice that routing and flow problems are direct extensions of shortest-path, max/min flow, and multicommodity flow problems. Other classic graph- and set-OR models can offer complementary modeling approaches, such as the minimum-spreading tree. Although not explicitly mentioned for network construction, cable length optimization [31] is related to minimization of the total connection of the MST. It could be relevant for designing low-cost networks that guarantee connectivity between points. The problems of maximum clique and maximum independent set can also be useful for identifying groups of entities, such as nodes, links, or tasks that are either completely compatible (clique) or completely incompatible (independent set). The latter can serve as an information decision in resource allocation or route planning to avoid interference or conflicts. Finally, the dominating set problem, facility location, or coverage optimization problems allow finding a minimal set of nodes that dominates or covers all other nodes (e.g., a minimal set of charging points or relays for network coverage) could be modeled as a dominating set problem.
Notice that many of these works demonstrate how complex problems in networks, transportation, and physical systems are addressed by a variety of optimization approaches, usually formulated as OR problems (ILP, MILP) or solved with algorithms (heuristics, ML-based). Many of them have deep roots in classical OR models such as network flow, TSP, VRP, and facility location. AI and ML are emerging powerful tools to improve the solution of these problems, either by predicting key parameters or by developing more efficient optimization methods for large-scale and dynamic environments. The connection to graph models such as MST, clique, independent set, and dominating set, although not always explicit in the authors’ terminology, underlines the combinatorial nature of these problems and the potential to apply or adapt these classical analytical frameworks.
5.3. Resource Allocation and Scheduling in Networks
The references in this topic discuss technologies such as 5G, 6G, mmWave, WSN, and IoT, as well as transport systems and logistics. They also consider the theoretical design of very large-scale integration (VLSI) systems. In general, common topics include the optimization of resource allocation, routing, and planning in complex static and dynamic networks. Not surprisingly, we notice that many of these problems have a correlation with classic operations research models.
In the domain of wireless networks, several works focus on the efficient allocation of resources such as spectrum, power, and time. For example, co-existence problems of different services in 5G are studied, optimizing the allocation of resource blocks and power [35]. Link scheduling in device-to-device (D2D) communications [33] or user- and beam scheduling in mmWave networks [14] aims to maximize objectives such as data rate or minimize transmitted power, while simultaneously handling interference. These problems can often be modeled using concepts from graph theory. For example, user scheduling in a wireless network can be viewed as selecting a set of feasible transmissions that do not interfere with each other. If we represent transmissions as nodes and an edge between two nodes indicates interference, then the problem of finding the maximum set of simultaneous compatible transmissions is directly related to the problem of finding a maximum independent set in the interference graph [33]. Analogously, if the goal is to select a subset of links to maximize some value, such as the total rate subject to constraints, this is close to variants of the knapsack problem. In addition, infrastructure placement, such as baseband units (BBUs) [8] or relay nodes in sensor networks [24], is a clear example of facility location problems, which allow one to determine the best locations for a limited number of resources to efficiently serve demand, usually minimizing costs or latency. Routing is crucial for the Internet of Things. Multi-commodity routing and flow problems are also addressed, including variants [7]. These problems are directly related to the models of maximum flow and multi-commodity flow. Optimization of routing in coupled power and transport networks (CPTNs) [28] or network flow management considering traveler behavior [53] are modern extensions that add complexity to traffic assignment problems in transport networks.
Vehicle routing problems, such as the vehicle routing problem with simultaneous pickup and delivery and time windows (VRPSPDTW) [54] or drone routing for delivery and pickup [30], are direct variants of the classic traveling salesman problem and the vehicle routing problem, extended to include real-world complexity including time windows and simultaneous loading and unloading operations. The routing of the shortest path is another fundamental classic graph problem for the IoT [27].
In VLSI physical design, cell routing and location are critical operations [31]. The routing is often modeled as a 3D graph where the nodes represent regions with limited capacity and the edges represent possible connections between regions [31]. The problem of routing connections between pins while avoiding capacity violations and optimizing the goal of wiring length, while maintaining the legality of cell placement, is explicitly formulated as an integer linear programming problem [31]. This demonstrates a straightforward, modern application of operations research formulations for solving complex design problems. Similarly, references on chain supply management consider the coordination of a complex network of entities [37]. On the other hand, demand forecasting uses machine learning techniques to optimize components such as inventory management, transportation, and production planning [37]. Optimization of resource allocation in [37] using particle swarm optimization is an example of how optimization techniques are applied to problems traditionally addressed with OR models.
Several classic and important problems in graph optimization can be described as the minimum spanning tree, which can be very useful in the domain of low-cost network infrastructure design and to guarantee connectivity in networks [25,44]. Similarly, the vertex cover related to the maximum independent set problem can be relevant for detecting the minimum number of nodes, that is, base stations or access points. The dominating set problem is also related to finding a dominant subset that covers all nodes of the network. This allows controlling the whole network and making the network robust against failures [9]. Continuing, the problem of maximum clique can be useful in detecting groups of users or links while operating simultaneously without interference. It is also important to note that while the problems are based on classic OR models, the solutions proposed in the sources often incorporate advanced techniques due to the large scale and dynamism of modern networks, for example, ILP [5,8,31], bilevel programming [28,53], convex programming [14,57], genetic algorithms [24,54], particle swarm optimization [37,54], ant colony-based algorithms [37,54], routing heuristics [5,30,54], and graph-based solving methods [31]. The integration of artificial intelligence for the tasks of recognizing interference patterns [33], network optimization [13,19,55], and routing policy learning [55] is also crucial. The application of transfer learning to accelerate optimization in routing problems [30,57] is also studied.
In summary, current research on networks and systems, as presented in the references, considers complex planning, routing, and resource allocation problems that have a strong conceptual connection with classic operations research models. The main distinction lies in the scale, dynamic nature of the problems, and the application of advanced computational techniques, including artificial intelligence, machine learning, and metaheuristics, to find feasible and efficient solutions. Operations research provides the fundamental modeling language and theoretical basis for understanding and formulating these modern challenges.
5.4. Resilience and Robustness Optimization
Concerning the topics of routing and flow problems, the references explore optimization formulations to determine efficient routes. For example, reference [7] focuses on multicommodity flow problems, detailing linear programming-based approaches, procedures concerning multiplicative weight update and permutation routing, and rounding techniques. highlighting the applicability of flexible packing frameworks for scenarios where flows are divided into a few routes or links [7]. The adjustment of routes through optimization considers factors such as signal range and congestion [29]. The latter allows for path splitting while minimizing routing cost and maximizing throughput in software-defined networks [9].
Designing and network planning include decisions related to component location and capacity allocation. Reference [5] formulates a processing unit (DU) location and flow routing problem as an integer optimization problem to minimize costs, using a path selection sub-problem. Ref. [5] addresses the design of a resilient power grid using nonlinear mixed-integer programming, focusing on ecological robustness and the inherent ability to tolerate disturbances. In reference [17], the robust resilience of systems against disturbances is addressed. In particular, Ref. [17] investigates the improvement of resilience in power grid emergencies. Although [15] proposes a dynamic technique to achieve resilience in complex systems, including recognition of network components. For energy systems, integrated resilience is also studied using optimization [16].
Reference [33] addresses D2D link scheduling, mentioning approaches based on support vector machines with graph kernels and fuzzy logic, as well as graph neural networks and reinforcement learning. Ref. [14] proposes a generalized methodology for scheduling in mmWave networks, jointly designing user, beam, and power allocation scheduling in multiple domains [14]. Resource allocation in NFV and cloud environments is addressed in [13] using RL-based approaches to balance resource utilization and reduce requirement blocking. The schedule of loads in rechargeable wireless sensor networks is also considered [44]. The sources show applications of GNN and RL for link scheduling [33]; neural networks (LSTM, CNN, attention) for traffic classification [39]; and RL for data routing and task allocation [4], cloud resource scheduling [13] and computational offloading [34]. Ref. [41] addresses collaborative learning in distributed networks. The combination of LSTM for demand forecasting and particle swarm optimization for resource allocation in resilient supply chain management is presented in [37].
Scheduling or allocation of wireless resources can be viewed as finding a maximum independent set of links in an interference graph [33]. However, subsets of mutually enhancing nodes can be related to the maximum coupling. Network resilience and vulnerability are inherently analyzed using graph theory for connectivity [15], or fault propagation [17]. Observe that, for protection purposes, the detection of critical infrastructures involves finding dominating sets. However, multi-commodity flow problems [7] can help balance the flow of data through the network. Next, shortest-path algorithms, such as Dijkstra or A*, mentioned in [44], are essential for many routing decisions. Finally, route planning for mobile agents, such as chargers in sensor networks [21], or data collection [26], can be formulated as variants of the travel salesman problem or vehicle routing problems.
The network topology design, or its resilient version [17], has similar fundamental components to the minimum tree construction to ensure connectivity at the lowest cost. However, future problems frequently involve capacities and flows that require more complex network models. Artificial intelligence and machine learning models can help improve the OR approaches. The machine learning approach can help improve the accuracy of the input data for optimization models [37]. However, metaheuristics [8] can help in finding near-optimal solutions. In addition, the reinforcement learning approach is particularly efficient for dynamic scheduling and routing problems where optimal policies and predictions must be learned through interaction with the environment [4,13,34]. Notice that the combination of machine learning predictions with OR models serves as a platform for powerful frameworks for data-driven decision making.
In summary, research relies heavily on mathematical and algorithmic formulations, frequently formulated as optimization problems having forms that are close to the classic OR. In addition, integration with artificial intelligence and machine learning can be seen as essential new tools for handling the data scale, uncertainty, and dynamic nature of future networks. The latter suggests that the synergy between robust theoretical OR frameworks and predictive and learning capabilities will be essential and fundamental to address resilience, efficiency, and optimization challenges.
5.5. Wireless and Mobile Networks Optimization
The references collected related to the topic of wireless and mobile network optimization explore several factors of resource optimization and management in modern and future wireless networks, including 5G, wireless sensor networks, mobile ad hoc networks, vehicular networks, and satellite networks. A frequent topic is to efficiently assign resources such as spectrum, power, and designing optimal strategies for tasks such as scheduling and routing, subject to several constraints and objectives. Examples of both are energy efficiency, low latency, high reliability, and throughput maximization [14,20,22,23,32,35,42,56].
Current articles show a trend towards modeling these problems as mathematical optimization models [5,8,35]. On the other hand, there is growing interest in mixing machine learning, deep learning, and deep reinforcement learning techniques to deal with the complexity and dynamic nature of these problems [4,19,33,35,36,39,55,57].
As many network problems are combinatorial and can be represented using graph theory [4,14,41,55], it turns out that the connection between the topics considered in the reviewed articles and the classic OR models is profound.
Problems such as the placement of distributed processing units in 5G networks [5] or the placement of relays in wireless sensor networks [24] fit directly into the framework of facility location or p-median problems. These classic models seek to find the optimal locations for a set of facilities to serve a set of clients by minimizing connection, or operation costs, and/or maximizing coverage and connectivity. The papers formulate these problems as optimization, which aligns with the OR approach. Similarly, data or flow routing is a central topic [4,5,6,24,26,27,29]. In WSNs, distributed node data collection can be modeled as an efficient routing problem that could involve variations of the travel salesman problem for a mobile entity (such as a charger [21,44] or data collector) or the construction of a minimum spanning tree for energy-efficient data aggregation [24]. Finding the lowest-cost or lowest-latency path [5,27] is a classical shortest-path problem (e.g., Dijkstra’s algorithm [27,44]).
Link scheduling and interference management in wireless networks [14,33] are strongly related to the problem of a maximum independent set. If links are modeled as vertices of a graph and an edge is added between two vertices if the corresponding links interfere, then selecting a set of links that do not interfere simultaneously is equivalent to finding an independent set in this graph. The goal of maximizing throughput might involve finding a weighted minimum independent set. The maximum clique problem identifies groups of links that interfere with each other. In sensor networks or IoT, selecting a minimal subset of nodes to monitor or control the rest of the network can be modeled as the dominant set problem. This can be relevant for the design of energy-efficient clustering protocols. Similarly, machine learning and reinforcement techniques are not only used to solve optimization problems such as resource allocation or routing that would traditionally be addressed by IoT [19,35,55], but they can also predict key parameters for an IoT model, i.e., link quality [33] or traffic demand [39]. Finally, learning high-performance heuristics for large-scale IoT problems where exact solvers are computationally prohibitive [8] can be adapted in real time to changing network conditions, something static IoT models are not designed to do.
A relevant direction for wireless and mobile 6G networks is to use reinforcement learning in edge computing environments. As such, multi-access edge computing networks (MECNs) demand low-latency, real-time decisions over heterogeneous resources, taking into account computation, memory, and bandwidth. (See, for example, [42,43]) that have explored DRL-based task offloading and scheduling strategies under these conditions. These approaches allow distributed learning agents to dynamically allocate tasks, optimize latency and throughput, and respond to network congestion and device mobility, while preserving energy efficiency. As such, reinforcement learning provides an adaptable and scalable toolset for heterogeneous resource coordination in edge-based network infrastructures.
5.6. Connecting Optimization Techniques to 6G Challenges
Our review covers a wide range of optimization approaches, highlighting the importance of 5G/6G as a guiding force for future networks. Some key 5G/6G technologies are only softly addressed. For example, the digital twin and multi-agent reinforcement-learning approaches discussed in [19] relate to user-base station interactions and dynamic environments, which are relevant for large-scale mobile optimization and potentially for massive MIMO systems. Similarly, edge computing and resource scheduling, including uncertainty, are discussed in [42]. Although federated learning in wireless aggregation is discussed in [43]. These works are promising for 6G paradigms, yet technologies such as ultra-reliable low-latency communication (URLLC), reconfigurable intelligent surfaces (RIS), and scalable multi-antenna (massive MIMO) optimization models are not analyzed in depth. These areas remain essential for future research, especially when bridging OR with emerging AI-based optimization in the 6G context.
6. Conclusions and Future Research
This review has analyzed more than 50 recent works that consider optimization challenges for modern network communications. Specifically, we focus on the intersection between classical operations research techniques and emerging artificial intelligence methods. We have mainly observed that through a brief taxonomy-based classification and comparative tables, classical OR approaches, like mixed integer programming, remain strong for infrastructure design and routing, whereas metaheuristics and deep learning-based methods dominate in dynamic, data-intensive and real-time scenarios typical of 5G/6G networks.
Key findings show a growing shift toward reinforcement learning and hybrid predictive optimization models, particularly in wireless resource allocation and energy-aware applications. However, there are persistent gaps, such as limited integration of classic models (e.g., facility location, MST) in the latest AI-driven frameworks and a lack of unified benchmarks across studies.
Concluding the article, they can be highlighted several promising research areas can be highlighted.
- Integration of classic graph-based optimization modeling approaches with deep-reinforcement-learning in federated or decentralized settings;
- Improving interpretability and robustness of AI-based methods subject to uncertainty;
- Developing standard evaluation benchmarks for reproducibility and crossing-comparisons;
- Exploring hybrid optimization frameworks combining learning with exact solvers in a scalable and explainable manner.
To conclude, we observe that the bridge between traditional OR and modern AI in network sciences is not only viable but necessary for the optimal management and complexity of next-generation communication systems. Consequently, we believe that future research should try to combine the theoretical rigor of OR with the adaptability and scalability of AI to develop robust, efficient, and intelligent networks.
Although this review collects and organizes performance metrics from several recent works, we do not include our reproducible benchmarks or experimental replications. In future work, we plan to build comparative visualizations and test selected methods under the same conditions to better evaluate their strengths and limitations. This would help validate the insights discussed and support more solid conclusions.
Several other novel technologies still merit greater attention in future research, in addition to the topics discussed previously. Graph neural networks (GNNs) constitute a powerful example of structured network data learning and appear promising for routing, clustering, and topology inference. Similarly, federated learning (FL) has become relevant for decentralized optimization in privacy-sensitive or bandwidth-limited situations. Thus, enabling collaborative model training without central data aggregation. Finally, explainable AI techniques are critical to interpret complex model decisions. Integrating these directions into future 6G architectures may improve both performance and transparency.
Author Contributions
Conceptualization, P.A., A.D.F., and E.S.J.; methodology, P.A. and A.D.F.; formal analysis, P.A. and A.D.F.; investigation, P.A., A.D.F., and E.S.J.; resources, P.A. and A.D.F.; data curation, P.A. and A.D.F.; writing—original draft preparation, P.A. and A.D.F.; writing—review and editing, P.A., A.D.F., and E.S.J.; visualization, P.A., A.D.F., and E.S.J.; supervision, P.A. and A.D.F.; project administration, P.A. and A.D.F.; funding acquisition, P.A. and A.D.F. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the financial support from Projects Dicyt 062313AS, ANID FONDECYT Iniciación No. 11230129, and Cost center No: 02030402-999, Department of Electricity, Universidad Tecnológica Metropolitana.
Acknowledgments
The authors acknowledge the support of the Vicerrectoría de Investigación, Innovación y Creación (VRIIC) of the Universidad de Santiago de Chile.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript.
| RL/DRL | (Deep) reinforcement learning |
| MARL | Multi-agent reinforcement learning |
| SI | Swarm intelligence |
| MIP/MILP | (Mixed-integer) linear programming |
| Heur. | Heuristic/meta-heuristic algorithm |
| Convex Opt. | Convex optimization |
| Multi-obj. opt. | Multi-objective optimization |
| Reg. Opt. | Regularised optimisation |
| Lyap. | Lyapunov-based control/optimisation |
| DOT-ADMM | Distributed online tracking–ADMM |
| PSO/GA | Particle swarm/genetic algorithm |
| TES | Two-stage exhaustive search (paper-specific) |
| STAR | Robust converter optimization (paper-acronym) |
| DT/DT-SimNet | Digital twin/its simulator variant |
| AO Opt. | Alternating optimization |
| Transfer Opt. | Transfer-learning-based optimization |
| IBNN | Information bottleneck neural network |
| Fuzzy DRL | DRL enhanced with fuzzy-logic rules |
| DLDQN | Double-layer deep Q-network |
| AEE | Age-energy efficiency metric |
| ISAC | Integrated sensing and communication |
| QoE/QoS | Quality of experience/service |
| BW | Bandwidth |
| BS | Base station |
| FL | Federated learning |
| MAC | Medium-access control |
| IoT/IIoT/IIoE | (Industrial) Internet of Things/Everything |
| CPS | Cyber-physical system |
| WSN/EH-WSN | (Energy-harvesting) wireless sensor network |
| WPCN | Wireless-powered communication network |
| MEC/RMECN | (Rechargeable) Multi-access edge computing network |
| 5G Xhaul | 5G packet fronthaul/backhaul |
| SAGIN | Space–air–ground integrated network |
| TSN | Time-sensitive network |
| LEO | Low-earth-orbit satellite network |
| CPTN | Coupled power–transportation network |
| MANET | Mobile ad-hoc network |
| UAV | Unmanned aerial vehicle network |
| VLSI | Very-large-scale integration (chip routing) |
| IoV | Internet of Vehicles |
| SCN/SWN | (Semantic) communication/wireless network |
| SCM | Supply-chain management |
| THz/RIS-VR | Terahertz band with reconfigurable intelligent surface for VR |
| PLC | Power-line communication |
| 6G | Sixth-generation wireless networks |
References
- Howell, B.; González, F.H.; Serentschy, G.; Jamison, M.; Potgieter, P.; Layton, R.; García, Í.H. Perspectives on political influences on changes in telecommunications and internet economy markets. Telecommun. Policy 2025, 49, 102901. [Google Scholar] [CrossRef]
- IBM ILOG CPLEX Optimization Studio. IBM. Available online: https://www.ibm.com/products/ilog-cplex-optimization-studio (accessed on 1 July 2025).
- Lantz, B.; Heller, B.; McKeown, N. A network in a laptop: Rapid prototyping for software-defined networks. In Proceedings of the 9th ACM SIGCOMM Workshop Hot Topics in Networks (HotNets-IX), Monterey, CA, USA, 20–21 October 2010; pp. 1–6. [Google Scholar]
- Ghanimi, H.M.; Sengan, S.; Prakash, K.B.; Alharbi, M.; Alroobaea, R.; Algarni, S.; Baqasah, A.M. Optimizing the cyber-physical intelligent transportation system network using enhanced models for data routing and task scheduling. Digit. Commun. Netw. 2025, in press. [CrossRef]
- Mroziński, D.; Klinkowski, M.; Walkowiak, K. Cost-Aware du Placement and Flow Routing in 5g Packet Xhaul Networks. IEEE Access 2023, 11, 12710–12726. [Google Scholar] [CrossRef]
- Liu, H.; Lai, J.; Zhu, J.; Gan, L.; Chang, Z. Enabling High-Throughput Routing for LEO Satellite Broadband Networks: A Flow-Centric Deep Reinforcement Learning Approach. IEEE Internet Things J. 2024, 11, 28705–28720. [Google Scholar] [CrossRef]
- Chaturvedi, A.; Chekuri, C.; Liu, M.; Richa, A.W.; Rost, M.; Schmid, S.; Weber, J. Improved Throughput for All-or-Nothing Multicommodity Flows with Arbitrary Demands. IEEE/ACM Trans. Netw. 2024, 32, 1435–1450. [Google Scholar] [CrossRef]
- Klinkowski, M. Optimized Planning of DU/CU Placement and Flow Routing in 5G Packet Xhaul Networks. IEEE Trans. Netw. Serv. Manag. 2024, 21, 232–248. [Google Scholar] [CrossRef]
- Ji, L.; He, S.; Gu, C.; Shi, Z.; Chen, J. Routing and Scheduling for Low Latency and Reliability in Time-Sensitive Software-Defined IIoT. IEEE Internet Things J. 2024, 11, 12929–12940. [Google Scholar] [CrossRef]
- Panayiotou, T.; Ellinas, G. Balancing Efficiency and Fairness in Resource Allocation for Optical Networks. IEEE Trans. Netw. Serv. Manag. 2024, 21, 389–401. [Google Scholar] [CrossRef]
- Fan, K.; Feng, B.; Zhang, X.; Zhang, Q. Demand-Driven Task Scheduling and Resource Allocation in Space-Air-Ground Integrated Network: A Deep Reinforcement Learning Approach. IEEE Trans. Wirel. Commun. 2024, 23, 13053–13067. [Google Scholar] [CrossRef]
- Seo, D.; Jung, K.; Roh, H.; Kim, S.; Oh, S. High-Efficiency Resource Allocation Scheme Introducing the Concept of Resource Sharing Paths in Industrial IoT. IEEE Access 2023, 11, 63821–63833. [Google Scholar] [CrossRef]
- Wei, W.; Gu, H.; Wang, K.; Li, J.; Zhang, X.; Wang, N. Multi-Dimensional Resource Allocation in Distributed Data Centers Using Deep Reinforcement Learning. IEEE Trans. Netw. Serv. Manag. 2023, 20, 1817–1829. [Google Scholar] [CrossRef]
- Sha, Z.; Ming, Y.; Sun, C.; Wang, Z. Versatile Resource Management for Millimeter-Wave Cellular Network: Near Interference-Free Scheduling Methodology. IEEE Trans. Veh. Technol. 2023, 72, 7942–7957. [Google Scholar] [CrossRef]
- Wang, H.; Pan, X.; Liu, Z.; Dang, Y.; Hong, D. A Framework for the Network-Based Assessment of System Dynamic Resilience. IEEE Trans. Reliab. 2025, 74, 2448–2458. [Google Scholar] [CrossRef]
- Lu, S.; Li, Y.; Ding, S.; Gu, W.; Xu, Y.; Song, M. Combined Electrical and Heat Load Restoration Based on Bi-Objective Distributionally Robust Optimization. IEEE Trans. Ind. Inform. 2023, 19, 9239–9252. [Google Scholar] [CrossRef]
- Huang, H.; Mao, Z.; Panyam, V.; Layton, A.; Davis, K.R. Ecological Robustness-Oriented Grid Network Design for Resilience Against Multiple Hazards. IEEE Trans. Power Syst. 2024, 39, 416–428. [Google Scholar] [CrossRef]
- Lin, F.; Li, X.; Zhang, X.; Ma, H. STAR: One-Stop Optimization for Dual-Active-Bridge Converter with Robustness to Operational Diversity. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 2758–2773. [Google Scholar] [CrossRef]
- Liu, H.; Li, T.; Jiang, F.; Su, W.; Wang, Z. Coverage Optimization for Large-Scale Mobile Networks with Digital Twin and Multi-Agent Reinforcement Learning. IEEE Trans. Wirel. Commun. 2024, 23, 18316–18330. [Google Scholar] [CrossRef]
- Li, G.-J.; Jin, S.; Yu, W.; Liang, L.; Nie, X.; Liu, H. Online Energy Consumption Optimization in WPCNs with Time-Varying Energy Storage Efficiency. IEEE Trans. Commun. 2023, 71, 1771–1784. [Google Scholar] [CrossRef]
- Yang, W.; Lin, C.; Dai, H.; Wang, P.; Ren, J.; Wang, L.; Wu, G.; Zhang, Q. Robust Wireless Rechargeable Sensor Networks. IEEE/ACM Trans. Netw. 2023, 31, 949–964. [Google Scholar] [CrossRef]
- Selvaraj, J.; Nakeeb, N.A.; Cho, J.; Easwaramoorthy, S.V. Enhancing Next-Generation Wireless Networks Using Preemptive Energy Conservation Technique. IEEE Access 2024, 12, 169328–169343. [Google Scholar] [CrossRef]
- Zheng, H.; Xiong, K.; Sun, M.; Wu, H.; Zhong, Z.; Shen, X. Maximizing Age-Energy Efficiency in Wireless Powered Industrial IoE Networks: A Dual-Layer DQN-Based Approach. IEEE Trans. Wirel. Commun. 2024, 23, 1276–1292. [Google Scholar] [CrossRef]
- Li, M.; Wang, K.; He, S. Maximizing Energy Efficiency by Optimizing Relay Deployment in EH-WSNs for Smart Grid. IEEE Commun. Lett. 2023, 27, 625–629. [Google Scholar] [CrossRef]
- Abdoulaye, I.; Belleudy, C.; Rodriguez, L.; Miramond, B. Semi-Decentralized Prediction Method for Energy-Efficient Wireless Sensor Networks. IEEE Sens. Lett. 2024, 8, 1–4. [Google Scholar] [CrossRef]
- Guo, H.; Wu, R.; Ma, Y.; Sun, S.; Wang, Y.; Qi, B.; Gao, J.; Xu, C. Synergy-Payoff-Maximization-Based Rechargeable Adaptive Energy-Efficient Dual-Mode Data Gathering Using Renewable Energy Sources. IEEE Internet Things J. 2024, 11, 35292–35305. [Google Scholar] [CrossRef]
- Zenati, D.; Maimon, T.; Cohen, K. RRO: A Regularized Routing Optimization Algorithm for Enhanced Throughput and Low Latency With Efficient Complexity. IEEE J. Sel. Areas Commun. 2025, 43, 437–447. [Google Scholar] [CrossRef]
- Cao, Z.; Han, Y.; Zhao, Q.; Wang, J.; Li, Y.; Zhao, S. Traffic and Power Flow Optimization of Coupled Power-Transportation Networks Considering Environment-Aware User Behavior. IEEE Trans. Transp. Electrif. 2023, 10, 3940–3955. [Google Scholar] [CrossRef]
- Chu, Z.; Hu, F.; Bentley, E.; Kumar, S. Intelligent Routing in Directional Ad Hoc Networks Through Predictive Directional Heat Map From Spatio-Temporal Deep Learning. IEEE Trans. Mob. Comput. 2024, 23, 2639–2656. [Google Scholar] [CrossRef]
- Wen, X.; Wu, G.; Liu, J.; Ong, Y.-S. Transfer Optimization for Heterogeneous Drone Delivery and Pickup Problem. IEEE Trans. Emerg. Top. Comput. Intell. 2025, 9, 347–364. [Google Scholar] [CrossRef]
- Fontana, T.A.; Aghaeekiasaraee, E.; Netto, R.; Almeida, S.F.; Gandhi, U.; Behjat, L.; Güntzel, J.L. ILPGRC: ILP-Based Global Routing Optimization With Cell Movements. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2024, 43, 352–365. [Google Scholar] [CrossRef]
- Liu, C.; Xia, M.; Zhao, J.; Li, H.; Gong, Y. Optimal Resource Allocation for Integrated Sensing and Communications in Internet of Vehicles: A Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2025, 74, 3028–3038. [Google Scholar] [CrossRef]
- Abbasalizadeh, M.; Vellamchety, K.; Rayavaram, P.; Narain, S. Dynamic Link Scheduling in Wireless Networks Through Fuzzy-Enhanced Deep Learning. IEEE Open J. Commun. Soc. 2024, 5, 6832–6848. [Google Scholar] [CrossRef]
- Zhou, Y.; Feng, L.; Jiang, X.; Li, W.; Zhou, F. Predictable Wireless Networked Scheduling for Bridging Hybrid Time-Sensitive and Real-Time Services. IEEE Trans. Commun. 2024, 72, 3664–3680. [Google Scholar] [CrossRef]
- Alqwider, W.; Abdalla, A.S.; Rahman, T.F.; Marojevic, V. Intelligent Dynamic Resource Allocation and Puncturing for Next-Generation Wireless Networks. IEEE Internet Things J. 2024, 11, 31438–31452. [Google Scholar] [CrossRef]
- Wang, L.; Wu, W.; Zhou, F.; Yang, Z.; Qin, Z.; Wu, Q. Adaptive Resource Allocation for Semantic Communication Networks. IEEE Trans. Commun. 2024, 72, 6900–6916. [Google Scholar] [CrossRef]
- Xu, J.; Bo, L. Optimizing Supply Chain Resilience Using Advanced Analytics and Computational Intelligence Techniques. IEEE Access 2025, 13, 18063–18078. [Google Scholar] [CrossRef]
- Bendrick, A.; Sperling, N.; Ernst, R. Large Data Transfer Optimization for Improved Robustness in Real-Time V2X-Communication. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2024, 43, 3515–3526. [Google Scholar] [CrossRef]
- Lin, W.; Chen, Y. Robust Network Traffic Classification Based on Information Bottleneck Neural Network. IEEE Access 2024, 12, 150169–150179. [Google Scholar] [CrossRef]
- Odeyomi, O.T.; Ude, B.; Roy, K. Online Decentralized Multi-Agents Meta-Learning With Byzantine Resiliency. IEEE Access 2023, 11, 68286–68300. [Google Scholar] [CrossRef]
- Bastianello, N.; Deplano, D.; Franceschelli, M.; Johansson, K.H. Robust Online Learning Over Networks. IEEE Trans. Autom. Control 2025, 70, 933–946. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.-B.; Zeng, C.; Chen, Y.; Yu, H.; Pan, Y. Joint Optimization of Transmission and Computation Resources for Rechargeable Multi-Access Edge Computing Networks. IEEE Trans. Green Commun. Netw. 2024, 8, 1259–1272. [Google Scholar] [CrossRef]
- Wang, J.; Liang, B.; Dong, M.; Boudreau, G.; Abou-Zeid, H. Joint Online Optimization of Model Training and Analog Aggregation for Wireless Edge Learning. IEEE/ACM Trans. Netw. 2024, 32, 1212–1228. [Google Scholar] [CrossRef]
- Wang, K.; Shen, Z. Minimizing Sensor Failures in Wireless Rechargeable Sensor Networks With Obstacles Through Fresnel Diffraction Model. IEEE J. Electron Devices Soc. 2024, 12, 796–807. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhou, Z.; Zhou, J.; Qin, C.; Tang, W.; Cai, Z.; Zhai, D.; Zhang, R. Coverage Maximization for Air-and-Ground Cooperative Networks. IEEE Wirel. Commun. Lett. 2023, 12, 2113–2117. [Google Scholar] [CrossRef]
- Ma, Y.; Ota, K.; Dong, M. QoE Optimization for Virtual Reality Services in Multi-RIS-Assisted Terahertz Wireless Networks. IEEE J. Sel. Areas Commun. 2024, 42, 538–551. [Google Scholar] [CrossRef]
- Taneja, A.; Rani, S. Energy Efficient Digital Twin Enabled Massive IoT Network with Use Case in Consumer Health. IEEE Trans. Consum. Electron. 2024, 70, 2099–2106. [Google Scholar] [CrossRef]
- Poposka, M.; Suraweera, H.A.; Karagiannidis, G.K.; Hadzi-Velkov, Z. Semantic Wireless Networks With Minimal Energy Consumption. IEEE Commun. Lett. 2024, 28, 1894–1898. [Google Scholar] [CrossRef]
- Varanasi, L.N.S.; Jonnalagadda, A.R.; Karri, S.P.K. Smart Edge Device Utilizing Power Line Communication for Energy Management and Control of Electrical Appliances. IEEE Access 2024, 12, 37207–37218. [Google Scholar] [CrossRef]
- Tolani, M.; Biabani, S.A.A.; Kumar, P. Energy-Efficient Deviation Aware Adaptive Bit-Mapping Medium Access Control Protocol for Wireless Sensor Network. IEEE Access 2024, 12, 94424–94435. [Google Scholar] [CrossRef]
- Zhao, C.; Tang, B.; Huang, Y.; Fu, H. Multilayer Joint Optimization of Packet Size and Adaptive Transmission Scheduling of Wireless Sensor Networks for Mechanical Vibration Monitoring. IEEE Internet Things J. 2023, 10, 6444–6455. [Google Scholar] [CrossRef]
- Tang, K.; Zheng, B.; Jiao, F.; Liu, X.; Feng, W.; Che, W.; Xue, Q. Joint Resource Allocation for Maximizing Energy Efficiency in mmWave-Based Wireless-Powered Communication Networks. IEEE Trans. Veh. Technol. 2024, 73, 8514–8528. [Google Scholar] [CrossRef]
- Li, S.; Zhou, B.; Xu, M.; Dong, X. A Bi-Level Optimization Approach to Network Flow Management Incorporating Travelers’ Herd Effect. Mathematics 2024, 12, 3923. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, W.; He, J.; Zhang, J.; Wang, J.; Li, S.; Sun, Y.; Ren, X. A New Hybrid Algorithm for Vehicle Routing Optimization. Sustainability 2023, 15, 10982. [Google Scholar] [CrossRef]
- Shao, Z.; Ding, Q.; Meng, L.; Yang, T.; Chen, S.; Li, Y. A Resource Allocation Algorithm for Cloud-Network Collaborative Satellite Networks with Differentiated QoS Requirements. Electronics 2024, 13, 3843. [Google Scholar] [CrossRef]
- Mihaiu, M.; Mocanu, B.-C.; Negru, C.; Petrescu-Nița, A.; Pop, F. Resource Allocation Optimization Model for Computing Continuum. Mathematics 2025, 13, 431. [Google Scholar] [CrossRef]
- Shi, Y.; Lian, L.; Shi, Y.; Wang, Z.; Zhou, Y.; Fu, L.; Bai, L.; Zhang, J.; Zhang, W. Machine Learning for Large-Scale Optimization in 6G Wireless Networks. IEEE Commun. Surv. Tutor. 2023, 25, 2088–2132. [Google Scholar] [CrossRef]
- Kennington, J.L. Wireless Network Design: Optimization Models and Solution Algorithms; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Wolsey, L.A. Integer Programming; Wiley-Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Glover, F.; Kochenberger, G.A. Handbook of Metaheuristics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Nemhauser, G.L.; Wolsey, L.A. Integer and Combinatorial Optimization; Wiley-Interscience: Hoboken, NJ, USA, 1988. [Google Scholar]
- Shi, J.; Zhao, R.-X.; Wang, W.; Zhang, S.; Li, X. QSAN: A Near-Term Achievable Quantum Self-Attention Network. IEEE Trans. Neural Netw. Learn. Syst. 2024, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.-X.; Li, Z.-T.; Yu, X.-T.; Zhang, Z.-C. Quantum Circuit Architecture Optimization for Variational Quantum Eigensolver via Monto Carlo Tree Search. IEEE Trans. Quantum Eng. 2021, 2, 3103910. [Google Scholar] [CrossRef]
- Wang, B.; Hu, F.; Wang, C. Optimization of quantum computing models inspired by D-wave quantum annealing. Tsinghua Sci. Technol. 2020, 25, 508–515. [Google Scholar] [CrossRef]
- Leon, F.; Hulea, M.; Gavrilescu, M. Advances in Artificial Intelligence: Models, Optimization, and Machine Learning; MDPI-Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2020. [Google Scholar] [CrossRef]
- Bertsimas, D.; Dunn, J. Machine Learning Under a Modern Optimization Lens; Dynamic Ideas LLC: Waltham, MA, USA, 2018. [Google Scholar]
- Sethu Subramanian, N.; Krishnan, P.; Jain, K.; Aneesh Kumar, K.B.; Pandey, T.; Buyya, R. Blockchain and RL-Based Secured Task Offloading Framework for Software-Defined 5G Edge Networks. IEEE Access 2025, 13, 56820–56842. [Google Scholar] [CrossRef]
- Fu, S.; Wei, W.; Feng, X.; Yin, L. Average Sum Rate Optimization in RIS-Assisted NOMA Satellite Network: A Deep Reinforcement Learning Approach. IEEE Wirel. Commun. Lett. 2025, 14, 1772–1776. [Google Scholar] [CrossRef]
- Yu, P.; Zhang, J.; Fang, H.; Li, W.; Feng, L.; Zhou, F.; Xiao, P.; Guo, S. Digital Twin Driven Service Self-Healing With Graph Neural Networks in 6G Edge Networks. IEEE J. Sel. Areas Commun. 2023, 41, 3607–3623. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, T.; Li, Z.; Dai, Y.; Zhou, X. Multimodal Knowledge Graph Embedding with Self-Attention Graph Neural Network. IEEE Trans. Comput. Soc. Syst. 2025, 1–14. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, J.; Min, G.; Zhao, Z.; Chang, Z.; Wang, Z. Spatial-Temporal Cellular Traffic Prediction for 5G and Beyond: A Graph Neural Networks-Based Approach. IEEE Trans. Ind. Inform. 2023, 19, 5722–5731. [Google Scholar] [CrossRef]
- Ji, S.; Feng, Y.; Di, D.; Ying, S.; Gao, Y. Mode Hypergraph Neural Network. IEEE Trans. Neural Netw. Learn. Syst. 2025, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Xiang, X.; Yan, C.; Xu, H.; Zhou, H. Density-Based Probabilistic Graphical Models for Adaptive Multi-Target Encirclement of AAV Swarm. IEEE Robot. Autom. Lett. 2025, 10, 8228–8235. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).