Abstract
In classical physics, the traditional way to handle dynamics is to work with initial value problems: Specifying all variables and their time-derivatives at a certain time will, together with the equations of motion, give the state of the system at any time. In this paper, it is questioned whether this is the right way to treat cosmology. The main reason is that cosmology, as opposed to almost all other parts of physics, deals with genuinely global problems. The main example in this paper will be the accelerating expansion. It is not claimed that the model studied here gives any kind of final explanation of this phenomenon. Nevertheless, it shows that what is commonly interpreted as the result of some dark energy, could instead be the result of a global condition for the universe. This model cannot be treated as a classical initial value problem. But an interesting additional property is that it can explain why the rate of acceleration now seems to be decreasing with time.
1. Introduction
Ever since the days of Isaac Newton, the most central method in physics has looked essentially as follows:
- Identify the forces involved.
- Write down the equations of motion.
- Solve these with appropriate initial conditions.
As a general rule, the equations of motion are differential equations of order two, and giving the initial conditions means specifying all variables and their time-derivatives at a certain time .
This method, which I will in the following refer to as the initial value approach, has been remarkably successful; in fact, it is probably the most successful method that has ever been designed in science.
But is it also the right way forwards in cosmology? There are obvious problems with applying the initial value approach to the very early history of our universe. It is extremely difficult to know not only the initial conditions, but also the form which the laws of nature take under these extreme circumstances. A radical approach has been suggested within the so-called cosmological bootstrap project: Rather than trying to study the detailed development of the equations of motion, one can start from just very basic principles and use, e.g., symmetry to predict consequences that can be compared with observations of the present universe (see, e.g., [1]).
Although the cosmological bootstrap avoids the explicit use of the equations of motion, they still, in general, underlie the development. In this paper, I try a different approach: It could be that some cosmological problems, including the accelerating expansion (see [2,3]), can be better understood if we give up the initial value perspective. Needless to say, this does not mean that the initial value approach would not be applicable to almost all problems in ordinary physics, in particular to problems on scales which are small in comparison with the size of the universe itself. But it may be worth asking if it could be that cosmology is different from other areas within science. And if so, why and in what way?
The answer, which I want to investigate in this paper, is that in most areas of physics, the equations of motion are generally treated from a local perspective, as is of course very natural when we deal with differential equations. But in cosmology, we inevitably have to deal with the global situation. And this could make it necessary to use conditions other than initial conditions. And it may not always be possible to include these in the local perspective in a natural way.
To illustrate what I mean, let us consider the following: Assuming the initial value approach, a very obvious way of treating cosmology (and in fact one which is very close to how cosmology has usually been treated) is to start from the present state of the universe, and then study the field equations from now, backwards and forwards, to the end points (the Big Bang and the Big Crunch; or possibly indefinitely into the future in the case of an open universe).
It goes without saying that this is a huge task, even when using shortcuts like the cosmological bootstrap or when using the perhaps somewhat simplifying assumption that the macroscopic equations we need are completely deterministic. We are in fact still far from being able to follow the development of our universe all the way back to the Big Bang, not to mention the corresponding development into the future. But an optimistic advocate of the initial value approach would probably argue that it is still possible in principle.
One of the purposes of this paper is to argue that this approach is based on hidden assumptions, which may be decisive. The method of argumentation here is to construct a model for cosmology where the usual initial value approach would fail, but where the development of our universe can still be understood in terms of different additional conditions.
In particular, this model has the property that no dark energy is needed to drive the accelerating expansion. And in addition, it predicts in a natural way that the acceleration should be slowing down. This is possibly in agreement with new observational findings (see [4]), although it may still be too early to draw firm conclusions.
2. A Possible Global Approach to Cosmology
What would a global approach to cosmology, which would not be based on the initial value approach, look like? There could of course be many such approaches. But a very natural choice, which is furthermore firmly rooted in the traditions of physics, is to start from the principle of least action.
This principle is often attributed to Maupertuis, who, in 1744, actually formulated it as a “principle of ultimate economy” (see [5]). However, in modern physics it has mainly been reduced to an algorithm for computing the equations of motion.
My suggestion in this paper is to return to the original meaning of the principle. And one of the main reasons for this is that using it as a minimizing principle we have access to a much wider range of additional conditions, which includes initial conditions and boundary conditions, but also other conditions. Needless to say, not all of these are interesting from a physical point of view, although some of them may in fact be very natural and interesting conditions. One important point which I want to make is that they, in a certain sense, are out of reach for the initial value approach.
It should perhaps be stressed that I make no claim that the view of the principle of least action in cosmology in this paper should be applied also to all other areas of physics where this principle plays an important role. Nevertheless, I think that science would profit from an open discussion about how these views should be united.
3. The Condition of Constant Four-Volume as an Example
In this section, I consider the special case of the condition of constant four-volume of the whole universe. On the one hand, this condition has been studied by many authors including, e.g., Hawking [6], and in various different contexts. On the other hand, it is obviously not compatible with the initial value approach: If we believe that we can determine the form of the whole universe, starting from given initial conditions at a certain time and solving the field equations backwards and forwards from these data, then we simply have to accept the (possibly infinite) value of the total four-volume that these computations lead to.
Reversing the logic, this can also be expressed by saying that if we believe that the condition of constant volume has a physical significance, then we cannot at the same time believe in the initial value approach.
So what is the physical background for the condition of constant four-volume? There can of course be many different points of view, but a very natural one stems from the idea that space-time is built out of some kind of elementary constituents. From such a perspective, it is not far fetched to identify the total volume with the number of such constituents. The condition of constant volume then becomes similar to other constants in physics, like, e.g., the constancy of the hadron number or the conservation of mass–energy to name two. However, it should of course be kept in mind that this is a condition in four dimensions, so it is not a question of something being preserved under the flow of time.
4. Possible Minimizing Principles
In the early history of the principle of least action, the idea of minimizing was essential. However, already Euler knew that in some examples, although perhaps somewhat artificial ones, the actual paths would not be minimizing but just stationary (or even maximizing in a certain restricted sense).
At the time of the birth of general relativity, the idea of actual minimizing had, for various reasons, more or less given way to the more general concept of stationarity. The first, and historically most important, action principle in general relativity is the Einstein–Hilbert action principle (see [7,8]), with the action integral
which makes little sense as a minimizing principle. Here R denotes the scalar curvature and denotes the invariant four-dimensional volume measure on space-time. For further details, see [9]. The action principle indeed makes sense as a tool for deducing field equations, and it gives equations of order two, and hence in principal can be used, together with standard initial conditions specifying the metric and its time-derivative at a certain time, to predict the full development, both in the future and in the past. But (1), is not the only possible choice. In fact, it was already known to Eddington [10] that there are infinitely many action integrals which will all reproduce the standard field equations in vacuum.
In the next section, I give an example of an action principle which in a certain (non-standard) sense reproduces the field equations in vacuum.
It is argued that this action principle also has the following properties:
- The field equations of this action principle, together with the metric and its time-derivative at a certain time, are not enough to determine the full development of the universe.
- This action principle could give a phase of accelerating expansion in a closed universe.
5. The Least-Curvature Universe
In this section, I investigate the condition of least scalar curvature, as defined by minimizing the integral
in a closed universe U. It should be noted right away that this is not an admissible action integral for general relativity in the usual sense: For example, it is obvious that any metric with everywhere will be stationary for I, which means that the set of stationary solutions would contain a lot of junk solutions with no physical relevance.
There is however a different perspective, according to which (2) implies the usual field equations, and in a way which is in fact closer to quantum mechanics:
Claim 1.
If we consider the multiple-histories ensemble of all possible metrics on U with a very natural ensemble measure (based on the central limit theorem), then in the limit of a very large universe, the metrics which are very close to satisfying the field equations will carry practically all the probability mass.
In essence, this says that with probability limiting to certainty, the field equations will be satisfied. This is a statement very much of the same type as when it is claimed in statistical mechanics that, e.g., a gas in a container will be distributed so that the pressure will be equal in all parts of the container (gravity neglected). As a general reference for the use of ensembles in statistical mechanics, the reader may consult [11].
To give a stringent treatment of this claim is a huge task, and a mathematically complete proof is far out of reach. For a more intuitive approach, using a less stringent, but nevertheless hopefully still clarifying, treatment using the concepts of classical statistical mechanics, see appendix A of [12] and also [13]. In this paper, no further discussion of this claim is undertaken, and the reader is simply invited to a discussion about the consequences of (2) in cosmology.
6. The Form of the Least-Curvature Universe
If we now pass from the local theory to the global theory: What would be the form of a closed universe which minimizes the scalar curvature as in (2) above?
It should be noted that the starting point here is not the field equations of general relativity. Rather, the field equations are viewed as a consequence of the minimizing of (scalar) curvature, as in Section 5. We know that mass gives rise to curvature, so for simplicity it makes sense to start from the simplest case, where there is no mass at all.
Is it possible to have a closed universe with zero scalar curvature everywhere (the Big Bang and the Big Crunch excepted)? Perhaps somewhat unexpectedly, the answer turns out to be yes: A direct computation shows that the compact, homogeneous, isotropic universe with the following metric in spatial, spherical coordinates (see [9]),
will have if we let , where and correspond to the Big Bang and the Big Crunch (see Figure 1).
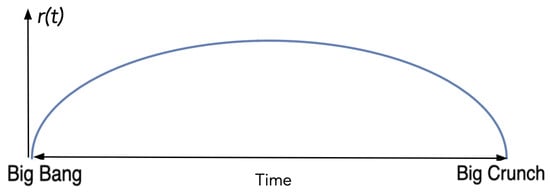
Figure 1.
The massless universe.
It should be emphasized that the Ricci tensor does not vanish and that this is not an Einstein manifold in the usual sense. Only the scalar curvature vanishes, so from the perspective of ordinary general relativity, this is not the kind of object that is usually studied.
Remark 1.
Can it still be a relevant model for cosmology? The integral in (2) now represents an action integral, the minimizing of which gives the curve in Figure 1, and with the minimal value zero. In a very big universe (but with finite volume), the Ricci tensor will appear extremely small to a local observer, in fact, locally negligible in comparison to the effects of mass to be introduced below, but with global consequences. It should perhaps also be noted that the minimizing of the integral in (2) leads to invariant equations of motion, although in general not of order two; see further below.
So what happens when we add mass to this model? Let me first give a very simple intuitive argument: Adding mass means adding something attractive, which tends to pull the universe together. And the attraction is obviously strongest where the density is high, i.e., close to the Big Bang and the Big Crunch. But if there is a contraction near the ends in Figure 1, then, under the condition of constant four-volume, this must somehow be compensated by an expansion in between, which would give something like the curve in Figure 2 below.
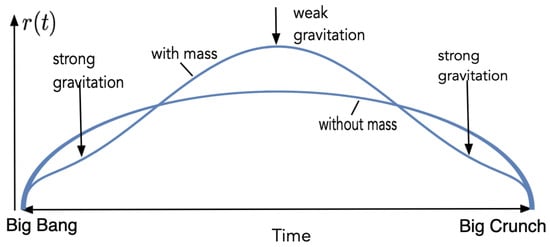
Figure 2.
The effect of mass on the radius , compared to the case without mass.
This is of course just a very intuitive argument, without any real physical or mathematical significance. But the point is that we can now try to derive the same result in a strict mathematical way, essentially using the minimizing principle (2).
A full treatment of this question is a very complicated task, and cannot be given here. In this paper, I will only describe an approach to the highly simplified case of a universe only inhabited by an evenly distributed homogeneous gas, and where its only contribution to the Lagrangian comes from its potential energy, very much in the sense of classical Newtonian physics. This is obviously something which has to be improved in many respects before this model can attempt to be compared to reality. Here, the purpose is just to illustrate a mechanism which could explain the accelerating expansion.
To make this more concrete, we now write for the geometrical part of the action
which, due to the homogeneity and isotropy assumptions, can be simplified (by integrating first over the space variables) to
To this action integral, we now, very much in the spirit of classical mechanics, simply add the contribution to the action from mass, which is (except for an unimportant constant which can be dropped out) given by the classical potential energy. In the case of a homogeneous gas, as described above, this simply becomes one over the (average) distance between the particles at the given moment of time t. Hence,
for some suitable constant .
The problem is now to minimize
under the condition of constant four-volume:
where is a fixed number. What does the solution to this minimizing problem look like? The traditional method of attack is to look at the Euler–Lagrange equation for the functional
The scalar curvature for the metric in (3), after a not too long computation, becomes
From this we obtain
Recall that for the problem of finding the minimum of a functional of the form
where is some sufficiently regular function, the Euler–Lagrange equation (see [14]) is given by
Using Mathematica we can compute the Euler–Lagrange equation associated with the functional in (9), and obtain (after multiplying with and slightly rearranging the terms)
For more details, see [12,13].) There are good mathematical reasons to expect there to be a more or less unique solution to the minimizing problem. But how do we find it?
represents the total mass and should be given. on the other hand should be determined from the total four-volume. But since this is a fourth-order equation, four more conditions are also needed to determine the solution. The situation can be somewhat simplified by assuming that the universe is time-symmetric. This appears to be a reasonable assumption for the large-scale form of a closed universe only inhabited by the simple kind of gas discussed here. Under more realistic assumptions, this assumption would have to be modified, but in the present case it simplifies the treatment since it readily gives that ( will be an even function, symmetric around ). To find the solution, we may now eliminate from the volume condition, leaving us with solutions depending only on and . To find the values of these parameters which minimize the integral in (2) turns out to be a very complicated problem due to the large number of solutions to (14). An example of such a solution (which is actually the one drawn in Figure 2), is given by choosing , , , and , giving the total volume of the universe . The real solution to the problem requires a more detailed study of the behavior of the curve near the end points and (which are dynamical, i.e., not given beforehand). Note, however, the phase of accelerating expansion in Figure 2, i.e., the phase where the graph is convex.
Although I cannot prove that this particular solution is globally minimizing, it seems clear that the solution is actually minimizing with respect to variations with small support, which in the classical theory of the calculus of variation can be seen as a first step towards finding a global minimum (compare Legendre’s condition [15]).
Remark 2.
The mass term used in the calculations above is of course just a very crude estimate without any ambitions even to be close to something numerically reasonable: Its purpose is just to illustrate a possible mechanism behind the accelerating expansion.
Could it be improved to something better? Hopefully the answer is yes. This may not be an easy task, but here are a few points to be considered in such an attempt:
- It would of course be better to use general relativity rather than simple Newtonian mechanics for the potential energy term in (6). But the real challenge would be to express this term just in terms of curvature. Obviously, the presence of mass is closely related to the presence of non-zero curvature, but how to express this more precisely still has to be clarified.
- To consider the matter in the universe as a more or less ideal gas may not be so bad during a limited period in the early universe. It may perhaps also be reasonable, as a coarse estimate, to consider a similar phase later on, when galaxies have already formed. But the size of the constant β in (6) may be different. Thus, more accurate estimates of the (potential) energy will be needed.
- The graph in Figure 2 seems to indicate that the universe should be time-symmetric. As remarked above, this is very helpful when computing the graph, and it may be reasonable as a first approximation to the global geometry; but it is not the belief of the author that this would be a fully realistic assumption in a more realistic model. Although theories predicting a symmetric behavior at the Big Bang and the Big Crunch have been discussed by several authors (starting from Gold’s paper [16]), nowadays few cosmologists would support this claim.
7. Conclusions
The field equations of general relativity have a long history and with roots which go far back in time. To Einstein, the most important property was invariance: In modern language this means that it should be possible to express their essence in a coordinate-free fashion.
But at the same time, Einstein, as well as all his contemporaries, were all parts of the Newtonian tradition, and in particular the belief in the traditional concept of forces as well as in the initial value approach was very strong, and has continued to be so up to this very day. In particular, this belief has led us to concepts like dark energy in order to explain the accelerating expansion.
From the point of view of the author of this paper, it is quite possible that this traditional way of thinking may still lead to an acceptable explanation: Perhaps we will find a natural source for the accelerating expansion in terms of something very traditional. But, as it is, we have been waiting for this to happen for 25 years. So perhaps it is time to turn over every stone to look for alternative explanations?
In this paper, I have suggested that a possible way forward could be to give up the traditional idea of an initial value problem in favor of a minimizing principle. This should be considered as an example of an alternative approach rather than as a final answer.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares that there are no conflicts of interest.
References
- Baumann, D.; Green, D.; Joyce, A.; Pajer, E.; Pimentel, G.L.; Sleight, C.; Taronna, M. Snowmass White Paper: The Cosmological Bootstrap. arXiv 2022. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009D38. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565D86. [Google Scholar] [CrossRef]
- Available online: https://data.desi.lbl.gov/doc/papers/ (accessed on 10 May 2025).
- Maupertuis, P. Accord de Differentes Lois de la Nature qui Avaient Jusqu’ici Paru Incompatibles; Histore Acad. Sci.: Paris, France, 1744. [Google Scholar]
- Hawking, S. General Relativity; an Einstein Centenary Survey; Cambridge University Press: Cambridge, UK, 1980; ISBN 9780521299282. [Google Scholar]
- Einstein, A. Zum Kosmologischen Problem der Allgemeinen Relativitätstheorie, Sitzungs; König. Preuss. Akad., 1931; pp. 235–237. Available online: https://echo-old.mpiwg-berlin.mpg.de/ECHOdocuView?url=/permanent/echo/einstein/sitzungsberichte/R583HGCS/index.meta&pn=1 (accessed on 10 May 2025).
- Hilbert, D. Die Grundlagen der Physik (Erste Mitteilung); Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, 1915; Mathematisch-physikalische Klasse; pp. 395–407. Available online: https://eudml.org/doc/58946 (accessed on 10 May 2025).
- Misner, C.M.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman and Company: San Fransisco, CA, USA, 1973. [Google Scholar]
- Eddington, A.S. Relativitätstheorie in Mathematischer Behandlung; Springer: Berlin/Heidelberg, Germany, 1925. [Google Scholar]
- Huang, K. Statistical Mechanics, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Tamm, M. Newton’s First Law and the Grand Unification. Symmetry 2024, 16, 1694. [Google Scholar] [CrossRef]
- Tamm, M. Natural Lagrangians. Universe 2021, 7, 74. [Google Scholar] [CrossRef]
- Gelfand, I. Calculus of Variations; Dover: New York, NY, USA, 1963. [Google Scholar]
- Bliss, G.A. Lectures on the Calculus of Variations; Chicago Univ. Press: Chicago, IL, USA, 1947. [Google Scholar]
- Gold, T. The Arrow of Time. Am. J. Phys. 1962, 30, 403. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).