Abstract
Wigner’s little groups are the subgroups of the Poincaré group whose transformations leave the four-momentum of a relativistic particle invariant. The little group for a massive particle is SO(3)-like, whereas for a massless particle, it is E(2)-like. Multiple approaches to group contractions are discussed. It is shown that the Lie algebra of the E(2)-like little group for massless particles can be obtained from the SO(3) and from the SO(2, 1) group by boosting to the infinite-momentum limit. It is also shown that it is possible to obtain the generators of the E(2)-like and cylindrical groups from those of SO(3) as well as from those of SO(2, 1) by using the squeeze transformation. The contraction of the Lorentz group SO(3, 2) to the Poincaré group is revisited. As physical examples, two applications are chosen from classical optics. The first shows the contraction of a light ray from a spherical transparent surface to a straight line. The second shows that the focusing of the image in a camera can be formulated by the implementation of the focal condition to the [ABCD] matrix of paraxial optics, which can be regarded as a limiting procedure.
1. Introduction
This paper deals with group contractions, mainly the contraction of one Lie group into another. In physics, we are quite familiar with the proper rotation group , which is a Lie group. The Lorentz and Poincaré (inhomogeneous Lorentz) groups are Lie groups. The Lorentz group, which serves as the foundational framework for Einstein’s special theory of relativity, can also be considered as an effective mathematical instrument in quantum mechanics. For example, Mukunda et al. [1] studied the symmetrical behavior of quantized classical equations of motion. Sprung et al. [2] used the Lorentz transform and the Dirac spinor in 2 + 1 dimensions to give a geometrical interpretation of the action of the transfer matrix on a scattering wave function, and then an analogy between this action and a Lorentz transform on the unit hyperboloid in 2 + 1 dimensions was developed. Blasiak et al. [3] investigated classical mechanics as related to their quantum analogues, where they illustrated their approach to defining a one-dimensional harmonic oscillator by means of generalized coherent states.
The Lorentz group serves as well in optical sciences, both in the classical and quantum domains. In the classical domain, Simon and Mukunda [4] considered both coherent and partially coherent beams in first-order optics. Bastiaans and Alieva [5] found the eigenfunctions of combinations of a magnifier, a lens, and a shearing operator to determine propagation through a first-order optical system. Nazarathy and Shamir [6] studied the canonical transformation to find relations between the operator representation of wave optics and geometric ray optics. In the quantum domain, Mandel and Wolf [7], first treated the broad area that deals with the coherence and fluctuation of light; then, they discussed the nonclassical states of light, higher-order squeezing, and quantum effects of down-conversion.
The promising field of quantum computations and information is not exempt from relying on the symmetries generated by , which is the double cover of the proper Lorentz group. Generally, they turn out to be very effective in dealing with ideas like entanglement. For qubit systems, is regarded as the invariance group. For n-qubits, it becomes . Then, as shown in Ðoković and Osterloh [8], it is possible to construct polynomial invariants for several qubits in order to classify a set of measures of multipartite entanglement. In Heydari [9], after defining a multilocal Lorentz-group invariant of , the properties of measures of entanglement were studied. As another example, Teodorescu-Frumosu and Jaeger [10] showed how the natural quantum Lorentz-group invariant group length can be used to study an arbitrary number of qubits. Additionally, they showed that this invariant length can be utilized to describe entanglement.
Entangled states have also been studied within a similar context. Başkal et al. [11] showed that in the Lorentz-covariant world, two coupled harmonic oscillators can be transferred to the concept of entanglement. Likewise, Rangamani and Takayanagi [12] discussed a situation in which holographic entanglement entropy computations respect AdS (anti-de Sitter) isometries and examined how conformal symmetry (including those within ) shapes entanglement structures in quantum field theory.
In this paper, a larger Lorentz group, , is also studied. Applications of this group are numerous. For instance, is involved in the extensions of squeezed states [13,14]. Arvind and Mukunda and Colas et al. [15,16] investigated the two- and four-mode symmetries of squeezed states using the or the locally isomorphic group. Since this group contains two coupled harmonic oscillators, can serve as a physical basis for symmetry decomposition. Furthermore, they also discussed coupled harmonic oscillators in the context of coupled Hamiltonians, as did Fring and Tenney [17], and in the description of the decoherence process as a symmetry transformation in the space. The decoherence of two beams of light can be represented by the density matrix, the Poincaré sphere, and the Stokes parameters. The Stokes parameters under various optical transformations can form a Minkowski four-vector, resulting in a two-by-two representation of the Lorentz group. A geometric presentation of the Lorentz group is given by the Poincaré sphere. The Lorentz group preserves the determinant of the density matrix and therefore cannot accommodate the decaying of the off-diagonal elements of the density matrix. This decay results in a decrease in the determinant. The group contains two Lorentz subgroups. As a consequence, the change in determinant of one Lorentz group is compensated by the change in the other group [18].
When Einstein formulated his theory of special relativity, he was interested in point particles without internal space-time structures. The focus later shifted to understanding how moving observers perceive internal spacetime structures. To address this question, in 1939, Wigner [19] considered the subgroups of the inhomogeneous Lorentz group whose transformations leave the momentum of a relativistic particle invariant. These little groups constitute the irreducible representations of the Poincaré group. They transform the internal spacetime structure of the particles. For instance, electrons can have, in addition to energy and momentum, spin degrees of freedom, and photons have helicity and gauge degrees of freedom.
Another interesting manifestation of irreducible representations of the Poincaré group using little groups has recently been introduced through the study of continuous spin particles [20]. These massless particle states are characterized by a real parameter, often referred to as the continuous spin parameter. They encompass infinitely many helicity states that mix under Lorentz transformations. This mixing reflects the nontrivial action of the Lorentz group on the helicity states. This property distinguishes continuous spin particles from ordinary massless particles of fixed helicity. When the continuous spin parameter is set to zero, the helicity states decouple from one another, reducing to a set of standard massless states in which each helicity appears exactly once [21,22]. For a review on this subject, see Bekaert et al. [23].
In studying the Lorentz group, it is often convenient to transform a given group into a simpler group. For instance, the surface of Earth, because the radius is very large, appears to be flat when we cover short distances, but we know that it is basically spherical when traveling in an airplane. The rotation group applies to spheres, while the two-dimensional Euclidean group operates on flat surfaces. The motions on the plane of can be reconciled with those on the spherical surface when we transform one group into another, using a technique called group contraction. Inönü and Wigner [24] first introduced the method of group contraction as a limiting procedure.
Later on, several contraction schemes were introduced from a range of viewpoints for different purposes. For instance, the infinite momentum limit received some considerations from the view point of high-energy particle physics [25]. We can note [26,27,28,29], where the infinite momentum has been significant from a group-theoretical perspective. Another proposal by Cattaneo and Wreszubski [30] includes a complex Hilbert space, where a theory of contractions of Lie algebra representations is applied to (the proper rotation group in two dimensions) into the (the three-dimensional Heisenberg group), which has simultaneously yielded to the analysis of the limit of a quantum system of N identical two-level particles. In Khan [31], the author contracted the conformal algebra, which is larger than the Poincaré group, to the continuous spin representation of the Poincaré group by compactifying the third transverse direction to a circle of radius R. Continuous spin representations can also arise from the five-dimensional Poincaré group through a combination of group contraction and Kaluza–Klein radius of the fifth dimension as the contraction parameter [32]. Contractions of the de Sitter (i.e., Lorentz) group were examined by Evans in [33] and also by Enayati el al. in [34], where they were studied within the conceptual structure of cosmology.
The formulation of Wigner’s little groups relies on two-by-two matrices, a structure also fundamental to classical ray optics, making the mathematical connection readily apparent. In that context, we discuss the Lie group for the two-by-two representation of the little groups. The principles governing relativistic particles and classical optics may appear to be unrelated, yet the theory of Lie groups and Lie algebras offers a good start for analogous calculations, elucidating the underlying symmetries and transformations that govern both fields.
Before we start the main body of the paper, we make a few definitions that will be useful as we continue. We take unless it is explicitly stated. A Lie group [35], is defined as a smooth manifold, where group operations, such as multiplications and inversions, are both smooth maps. The properties of Lie groups are determined by a closed set of generators which is known as the Lie algebra of the group.
Locally, the transformations corresponding to a Lie group can be obtained by exponentiating the generators of its Lie algebra, as explained below. We consider any complex valued square matrix such as X; then, we have
From this, the correspondence to any parameter can be derived from
Then, the algebra of a particular Lie group can be obtained by differentiation as
In this paper, we shall consider the four-dimensional spacetime manifold with coordinates
Then, Lorentz transformations are conventionally defined to be the group that preserves the inner product , with , where the Minkowski metric is taken to be . Specifically, we have
where stands for the components of the transformation matrix. This group is called the proper, orthochronous Lorentz group when the Lorentz transformations are restricted to the condition that det , i.e., no space reflections, and to , i.e., no time inversion.
Our main focus is to illustrate how squeeze transformations appear in the scene as a relatively recent approach to contractions. We are also interested in constructing the covariant four-momentum generators of Einstein’s by contracting the group. To this end, we organize the paper as follows.
Section 2 gives the generators of the Lorentz group and gives the matrix representation of which is the two-by-two covering group of the Lorentz group. Section 3 gives an introduction to Wigner’s little groups. Section 4 gives the two-by-two representation of the little groups. In Section 5, we give a contraction scheme by using a very large R. In Section 6, we give an infinite-momentum/small-mass limit of massive and imaginary mass particles to a massless particle. Section 7 gives an introduction to squeeze transformations. We contract the two-dimensional representation of the Minkowski vector as well as the rotation matrix on a plane as examples. In Section 8, a plane and a cylinder tangent to a sphere are considered. We then formulate how the and groups can be contracted into the two-dimensional Euclidean group and into the cylindrical group. In Section 9, we contract the Lorentz group to the Poincaré group.
In Section 10, we discuss an application to geometric optics in the form of the contraction of a ray going through a transparent spherical surface to a straight line and develop the lens maker’s formula. In Section 11, we look at the matrix of paraxial optics and inquire how we can use this to formulate Wigner’s little groups, namely, -like, -like, and -like, from optical elements. Indeed, we can represent those three little groups using one convex lens. Section 12 contains conclusions. Appendix A gives a table of the generators for the Lorentz group .
2. Generators of the Lorentz Group
The Lorentz group is a six-parameter Lie group where the generators form the Lie algebra. We start with the generators of rotations in the matrix form [36,37]:
In this formulation, is the generator of rotation around the x-axis, is the generator of rotation around the y-axis, and is the generator of rotation around the z-axis. These three rotation generators satisfy the commutation relations
which form the Lie algebra of the familiar rotation group.
The matrices which perform Lorentz boosts are
Then,
In this formulation, is the generator of boosts along the x-axis. and are boosts along the y-axis and along the z-axis, respectively. Note that these generators alone do not form the Lie algebra for a group. However, these boost generators, together with the rotation generators from Equation (6), do form a group. These six generators form the Lie algebra for the Lorentz group . There are therefore six generators of the Lorentz group, and they satisfy the commutation relations given in Equations (7) and (9). The rotation generators are anti-symmetric, while the boost generators are symmetric. Hence, there are two possible four-by-four representations of the Lorentz group: one with and the other with .
The Lie algebra of , which is the double cover of the Lorentz group, can be constructed from the three Pauli matrices [38,39,40], where the Pauli matrices are written as
We define
The explicit forms of the operators in Equation (11) are
These two-by-two matrices satisfy the following commutation relations:
Apart from an imaginary i, they are like those given in Equations (7) and (9). We note that in the complex representation of the Lorentz group generators given by Weinberg [36] and others [37,41], these commutation relations take the same form. If the signs of the generators in Equation (13) are changed, the commutation relations remain the same, that is, the commutation relations are invariant. This group, known as , is the covering group for the Lorentz group, that is, it is homomorphic (onto, but not one-to-one) to the Lorentz group. For one group to be homomorphic to another group, there must be at least two sets of generators of the one group that correspond to one set of generators of the other group. For further details about homomorphism, see Carmeli [42]. In the present case, since the proper rotation generators are anti-symmetric, but the boost generators are symmetric, there are least two sets of generators in that correspond to a given set of generators. For the proper Lorentz group, the sign of the boost generators is unambiguously defined in terms of the time and space variables. This is not the case for ; both signs must be considered.
3. Introduction to Wigner’s Little Groups
In 1939, Wigner [19] studied the inhomogeneous Lorentz (or Poincaré) group. In that paper, Wigner considered those subgroups of the inhomogeneous Lorentz group that leave the four-momentum invariant. He identified three such groups, which he named little groups. The study and applications of little groups have been effective in several domains of physics [43,44].
3.1. SO(3)-like Little Group for Massive Particles
For a particle that has a positive mass, a Lorentz frame can be identified in which the particle is at rest. The four-momentum of the particle is proportional to
The Equation (14) remains invariant under rotations. Thus, we see that the little group for a massive particle at rest is indeed the three-dimensional rotation group.
From before, the three generators of rotation group are and , and they satisfy the Lie algebra of Equation (7). These anti-symmetric operators associated with the dynamical variables represent the particle spins.
If the system is boosted along the z-axis, the boost matrix given by
can be used. Applying this matrix to the four-momentum of Equation (14) results in
The generators are transformed as
Here, remains invariant under this boost operation, but and become
The generators , although they satisfy the same Lie algebra as , are not the same. Thus, the operators are known as the generators of the -like little group for the massive particle with a nonzero momentum.
3.2. E(2)-like Little Group for Massless Particles
The four-momentum for a massless particle is proportional to
As can be seen, this expression is invariant under z-axis rotations. Additionally, Wigner [19] notes that Equation (19) is invariant under the transformation
with
where the four-by-four matrices of , , , and are given explicitly in Equations (6) and (8). As a consequence,
The generators , and form the Lie algebra of the -like little group and satisfy the following commutation relations:
Wigner also noted that the two-dimensional Euclidean group has the same Lie algebra, with
Here, and generate translations in the directions of x and y, respectively, while generates rotations. They can be written as
Furthermore, the following operators were considered by Kim and Wigner [45]:
where is constant. These operators, on the surface of a circular cylinder, generate translations along the z direction. They satisfy the following commutation relations:
This is, indeed, the Lie algebra for the cylindrical group. We illustrate in Figure 1 why the cylindrical group is isomorphic (onto and one-to-one) to the Euclidean group. They both are based on the surfaces that are tangential to a sphere.
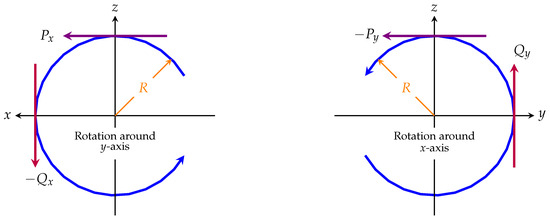
Figure 1.
This figure shows the geometry of both the Euclidean and cylindrical groups. In addition to a plane tangential at the north pole of a given sphere, there can be as well a cylinder that is tangential to the equatorial belt. The up–down translation on this cylindrical surface corresponds to the gauge transformation. Reprinted from [45] with the permission of AIP Publishing.
Now, we consider a photon having a momentum along the z direction; then, the four-potential for a plane wave is
Applying the Lorentz condition, , where the four-momentum of a massless particle is , we have . Thus, the four-potential becomes
By applying the of Equation (22) to , we have
resulting in
The transformation matrix leaves the transverse components and invariant but provides an addition to . This is, therefore, a cylindrical transformation. acts on given in Equation (29), affecting the vectorial part of the potential, which results in mixing the components. Thus, we can write . Since is the little group for massless particles, remains invariant, and is transformed as in Equation (31); thus, we have .
Although the rotation generator of the -like little group was known to correspond to the helicity of the massless particle, the physical interpretation of the translation generators was not given by Wigner in his 1939 paper [19]. Einstein’s photoelectric effect leads to regarding the massless photon as the particle manifestation of the electromagnetic wave. The photon in the quantum world has helicity or angular momentum that is aligned parallel or anti-parallel to the direction of the momentum. The question then becomes, how can we translate photon helicity to the electric and magnetic fields which are perpendicular to the direction of propagation? We solve this problem, we consider that massive and massless particles have, as defined in Wigner’s little groups [19], internal spacetime symmetries.
Although it was much debated in the literature whether operators corresponding to group transformations, when acting on the four-potential, actually implement gauge transformations, this issue was later settled in subsequent papers [36,46,47]. Presently, there is much interest in quantum electrodynamics as it relates to gauge fields and continuous spin particles [48,49,50]. In the same manner as we are still seeking spin-1/2 massless particles, we are also seeking integer and half-integer massless continuous spin particles.
3.3. SO(2,1)-like Little Group for Imaginary Mass Particles
We now examine particles with a four-momentum proportional to
Here, is a negative number; that means the particle mass is imaginary, and the particle (known as a tachyon) moves faster than light. Even though these are imaginary mass particles, the mathematics of this little group has found application in many branches of physics.
The transformations that leave the four-vector of Equation (32) invariant consist of Lorentz boosts along the x- and y-axes and rotations in the -plane. Consider, for example, the Lorentz boost along the y direction, with
This is generated by . Hence, the commutation relations are
This is the Lie algebra of the Lorentz group applicable to two space and one time dimensions. This group is known in the literature as .
If we boost the four-momentum of Equation (32) along the z direction, it becomes
Then, remains invariant, while and become
The generators , and satisfy the same Lie algebra as that of Equation (34). This is the -like little group.
Here, the Lorentz group is applicable to the coordinates. The rotation around the z-axis, while also leaving the four-momenta invariant, will extend the representation to the full space. Calculations in high-energy physics that involve Lorentz transformations are mostly based on [40]. Additionally, this group is one of the basic languages in classical and quantum optics [51,52]. Furthermore, if becomes very large, the generators of the little groups become the same, and the four-momentum for the massive, massless, and imaginary mass particles takes the same form.
4. Two-by-Two Representation of Little Groups
In order to see that matrices belonging to actually perform Lorentz transformations, the two-by-two Minkowski coordinate matrix is considered as [53]
whose determinant is . The group elements act on X through the following transformation:
Since W and are unimodular, the quadratic form is preserved. An matrix performs Lorentz transformations by way of Equation (38) on the form of Equation (37).
Similarly, the momentum four-vector can be expressed by a two-by-two matrix as
whose determinant is
and is equal to , or , depending on the nature of the mass of the particle. If a massive particle moves only along the direction, this matrix becomes
This matrix takes the form
when the particle is at rest. On the other hand, for massless particles, while for tachyon particles [54,55,56], the mass is imaginary. Thus, for all these masses, there are three distinct two-by-two matrix representations proportional to
where m is conveniently factored out. These matrices are collectively called Wigner four-momentum matrices and are denoted by . For all matrices,
satisfies
More generally, consider the matrices that leave the four-momentum invariant:
Internal spacetime symmetries of relativistic particles are dictated by these W matrices. They constitute Wigner’s little group. In particular, they transform four-momentum matrices of Equation (43) by
rendering to remain invariant. Corresponding Wigner matrices are
These matrices are unimodular with real elements; thus, they fall within the group.
5. Contraction with Large Radius Limit
New Lie algebras can be constructed from existing ones through a limiting process known as contraction. Even if the process turns out to be singular, it may converge to a well-defined limit [35]. This idea is not new and dates back to the pioneering work of Inönü and Wigner [24]. Contraction of to can be exemplified by means of a simple geometric configuration consisting of a small neighborhood that appears to be flat on the surface of a very large sphere. For this purpose, we examine a spherical surface with radius R and then consider when z is large and approximately equal to the radius of the sphere as
The column vector on the left-hand side is for , and the vector on the right-hand side is for the space where is applicable. Also, the region around the north pole is taken to be small, which appears like a flat surface [35,45]. The matrix on the right-hand side is denoted as and is to be employed for the contraction. Consider the following operations on the rotation generators of Equation (6):
where
Here, R is interpreted as the radius of a sphere in three dimensions, which becomes very large during the process. The change in the algebraic structure of the Lie group can be seen from the commutation relations
where , which is a similarity transformation and does not affect the above relation. In view of this, we consider [35]
So in the limit , the above commutation relation vanishes, while becomes , and becomes . Finally, we have the following:
Together with , these generators satisfy the commutation relations of Equation (24). Hence, they are the generators of the Lie algebra of the group.
6. Boosting of Massive and Imaginary Mass Particles to Their Massless Limits
Einstein’s formula, , shows that in the large-momentum or zero-mass limit the energy–momentum relation for massive particles becomes that for massless particles. In accordance with this line of reasoning, it has been suggested that the internal symmetry of massive particles becomes that of massless particles in the same limit [45].
The group generated by , , and given in Equation (6) is the little group for a massive particle at rest. Should this massive particle move along the z direction comparable to the speed of light, we know that remains invariant, and the eigenvalue is the helicity. On the other hand, it is to be expected that in the infinite-momentum limit, and will go through certain changes.
We saw in Section 3.2 that the generators, , , and , form the Lie algebra for the -like little group for massless particles moving along the z direction and that values have the form
and thus are related to rotation and boost generators. The four-momentum of massless particles remains invariant under transformations generated by the , , and operators, where generates rotations and the translation-like generators, while and generate gauge transformations [46,47,57].
If a massive particle is at rest, the little group is , which is generated by . When this particle is boosted along the z direction, its four-momentum becomes , where the boost matrix is [58]
Under this boost operation, remains invariant as
However, the boosted and become
It is apparent that the Lorentz boosts in Equations (58) and (59) are similarity transformations; therefore, the commutation relations will still be satisfied by the operators as
In order to obtain contractions, we again resort to Einstein’s equation: . The right-hand side of this equation goes to zero for massless particles, thereby causing the values of E and to approach each other. Thus, while approaches to one, approaches to infinity. This suggests that we follow a similar limiting procedure of Section 5, where the quantity now serves a function analogous to the radius of the sphere. Therefore, in the same sprit, we rewrite Equation (51) as
These give the same result as in Equation (56). This process is similar to the group contraction process described in Section 5, where in the present case, an group for a massive particle is contracted to become an -like group for a massless particle. In passing by, we note that here the contraction parameter goes to one, while the common practice takes it in such a way that it either goes to zero or infinity. However, tending to a finite limit is a strategy that has been discussed long ago by Suskind [59], where the parameter is and approaches one as the speed of the particle becomes close to that of light.
Let us now consider the boost matrix of Equation (15). As noted in Section 3.3, this will transform the four-momentum , of an imaginary mass particle, along the z direction, which becomes . This vector, normalized with , approaches its massless counterpart as . In fact, the same is true for the massive case, with approaching through the same scheme.
As for the generators, when boosted, remains invariant, while and become as in Equation (36). The generators , and satisfy the same Lie algebra as that of Equation (34), which is an -like little group.
It is possible to use contraction matrices with different parameters in the components. For instance, we can implement this boost matrix to obtain another -like group from . Within the same line of approach as above we simply formulate as follows:
The matrices and take the same form as in Equation (21) in Section 3.2 and, together with , satisfy the commutation relations as in Equation (23) for the and the -like little groups.
7. Contraction with Squeeze Transformations
Although rotations and translations are familiar to us with respect to the -plane, the concept of squeeze transformations is newer. In a squeeze transformation, the product remains the same because when the x-axis is expanded, the y-axis is contracted. Hence, a squeeze transformation is one that preserves the area.
The squeeze transformation matrix takes the form of a boost transformation:
where is the inverse.
When a squeeze matrix is applied to the two-by-two representation of the Lorentz group given in Equation (37), this equation transforms as . Explicitly,
When the limit of large is taken, this matrix becomes
Then, the inverse transformation is performed
This means that , and because a space-like hypersurface is needed, we choose and then .
If the X matrix is written as a column vector, we obtain
The changed vector on the right is now called the contracted vector.
As another example, the squeeze transformation is applied to the rotation matrix. The rotation, in this two-dimensional space, is generated by . The rotation matrix is
When the squeeze matrix of Equation (65) is applied to , we have
Applying the inverse of the squeeze transformation, the result becomes
The resulting transformation matrix is
As can be seen, this matrix is the contracted rotation matrix.
Now, this contracted matrix is applied to the vector ) to obtain
The y variable remains invariant, but the x direction translation now depends on the y variable. This is a shear transformation [11].
8. Contraction of SO(3) and SO(2,1) to E(2) and the Cylindrical Group
Let us start with the familiar three-dimensional sphere. Then, we shall consider both a tangent plane at the north pole and a cylindrical surface touching the equatorial belt. The transformation group on these tangential surfaces will be obtained using the squeeze procedure introduced in Section 7.
We refer to Figure 2 to compare two contraction schemes with equivalent outcomes in terms of their transformation matrices. The figure on the left represents the spherical surface of the earth. A flat plane tangent at the north pole can be achieved by using the limiting process of Section 5. Additionally, a cylindrical surface tangent to the equatorial belt can be produced [44]. As with the figure on the right, it can be seen that a planar surface can also be obtained by shrinking the z-axis and expanding the area on the -plane by implementing squeeze operators. To achieve a cylindrical configuration whose axis is along the z direction, this squeeze process can be used to expand the z-axis while shrinking the area on the -plane.
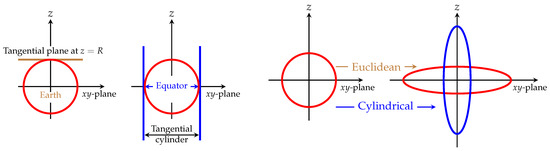
Figure 2.
We can consider a flat plane tangent at any point on the surface of a very large sphere, like the earth, and choose the north pole. We also can consider a cylindrical surface tangent to the equatorial belt. Reprinted with permission from IOP [44]. We illustrate at the right how squeezing is used to obtain a flat plane by contracting the z-axis while expanding the -plane. To obtain the cylindrical surface, squeezing expands the z-axis while at the same time contracting the radius of the -plane. Reprinted with permission from IOP [44].
It is possible to construct symmetry properties on these surfaces contracting the rotation group to . The Lie algebra of the rotation group was given in Equation (7), and the generators were defined explicitly in Equation (6).
On the tangential plane at the north pole, we generate transformations by rotations around the z direction using the generator . Translations are then generated along the x and y directions using the translation generators in Equation (25), which represent translations in the x- and y-axes. The commutation relations of these three generators, which form the Lie algebra for , were given in Equation (24).
We now use a squeeze matrix similar to the one in Section 7:
and we proceed in the following manner:
The generators and have been given in Equations (6) and (55).
We can apply the same technique as in Equation (76) to . This group is generated by the , , and values that were given explicitly in Equations (6) and (8). Of course, remains the same, and the resulting forms of and are similar to those given in Equation (55).
We can write the transformation matrix for either or in exponential form as
For , the matrix for that result has the form
while for , the result is
When either the matrix in Equation (78) or (79) acts on the vector , in the space where is applicable, the form that results is indeed an transformation.
We now consider a cylindrical plane attached to the equator. As can be seen in Figure 2, we can accomplish this by expanding the z-axis while, at the same time, the radius of the circle, , becomes very small. The inverse of above procedure can be used to obtain explicit forms for and as
We find as before that remains invariant, but , and , where they are defined as
As can be seen, this is again the same algebra as for given in Equation (55).
For the cylindrical contraction of , we use the same technique as in Equation (80). Then,
This set of generators also has the same form as that given in Equation (81) for contracting the rotation group to the cylindrical group. The transformations for these two groups are illustrated in Figure 3.
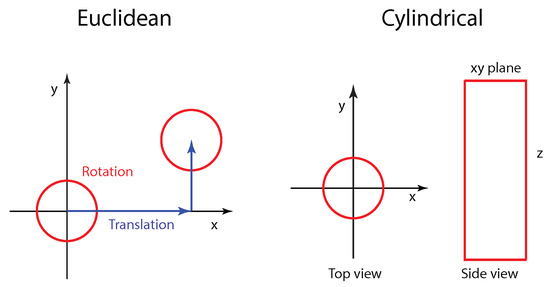
Figure 3.
For the Euclidean group, we can make rotations around the z-axis and translations along the x and y-axes. However, we make translations up and down along the z-axis and rotations in the -plane for the cylindrical group. Reprinted with permission from IOP [44].
9. Contraction of SO(3, 2) to the Poincaré Group
The Lorentz group consists of three space dimensions and two time dimensions. They act on coordinates given as , where the Minkowski metric on this coordinate space is chosen to be . We explicitly give the five-by-five matrices representing the ten generators of the group in Table A1. From the table, it can be seen that the six and matrices, generating rotations and boosts in the space, contain only zero elements in their first rows and columns. Thus, with respect to them, the s coordinate remains invariant. This indicates that the the generators and constitute the familiar four-by-four matrices of the Lorentz group operating in Minkowski space. The remaining three boost generators, , produce boosts with respect to the s variable. Additionally, the matrix generates rotations between the two time variables t and s. These four matrices have elements only in the first row and column. Here, our goal is converting the and generators into the translation generators and which can be applied to homogeneous Lorentz group, of the space with , represented by the six generators and to enlarge it into the Poincaré group.
In this section, we intend to obtain the translation-like generators of the Poincaré group by using the procedure introduced in Section 5. For this purpose, a five-by-five contraction matrix will be employed, where R is replaced by . We could as well have employed a five-by-five squeeze matrix for the contractions; however, since here we are only interested in obtaining the translation-like generators, the form of the contraction matrix we use here is sufficiently simple for our purpose. This is illustrated in Figure 4.
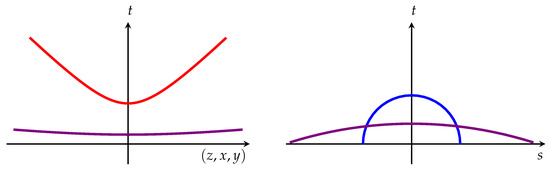
Figure 4.
Applying the contraction matrix, the hyperbola on the left is straightened to become a horizontal line on the axis. Similarly, the same process is applied to the circular curve on the right [60].
The form of the five-by-five contraction matrix is
We note that this matrix and the inverse leave the last four columns and rows invariant. This results in the invariance of the four-dimensional Minkowski subspace of . For the generators and , this is not true.
The explicit five-by-five matrix for and , the translation matrices, as obtained from and , have the following forms:
We notice that these translation generators have zero elements in the first rows.
Now, the contraction procedure can be formulated as
These four contracted generators lead to the five-by-five transformation matrix
performing translations
in the four-dimensional Minkowski space. This means that the group becomes the inhomogeneous Lorentz group governing the Poincaré symmetry for quantum mechanics and quantum field theory. In quantum mechanics, the four-momentum operator is
Thus, we can translate the matrix in Equation (88) into the language of differential operators as
This contraction procedure produces four translation generators corresponding to the energy-momentum four-vector in the Lorentzian system. The on-shell condition leads to
which is widely known as Einstein’s .
10. Physical Example I: Contraction of Convex Spherical Surface
We studied group contraction using an approximation of a spherical surface to a flat one ( to /cylindrical). Many branches of physics and engineering employ this procedure. Here, we take an example from geometric optics. Although a lens surface is approximately spherical, if the light rays could be expressed as a linear function, that would be useful. Let us examine that possibility.
The equation for a straight line in the -coordinate system can be written as
For a given x variable, the line is completely determined by the y variable and the slope. Thus, the column vector
completely specifies the line. To move from one coordinate point to another, the transformation can be represented as
The right-hand side matrix above is known as the ray transfer matrix in classical optics [61,62]. It has the same triangular form as the ray transfer matrix given in Equation (103).
Figure 5 illustrates a convex spherical surface of a transparent material that has a radius R and an index of refraction n.
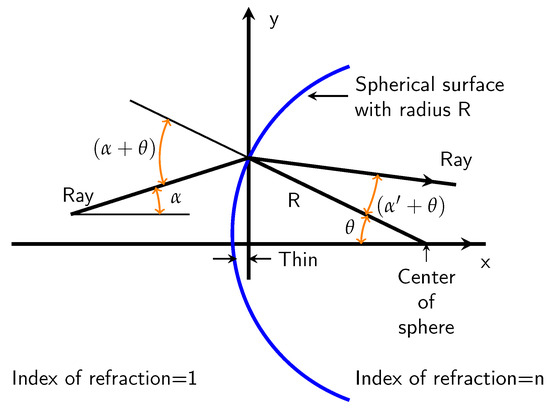
Figure 5.
The distance of a ray from the axis, together with a linear approximation of the relation with the slope of the ray, results in matrix optics. The surface of the transparent convex material is either spherical or is composed of any curved surface considered as an approximation to a spherical surface near the y-axis [40].
Here, the angle of the ray to the axis of the surface will be assumed to be very small. Furthermore, the radius of the spherical surface is assumed to be much larger than the distance from the ray to the y-axis. Then, from Snell’s law,
where air is assumed to have an index of refraction of 1. Since all the angles are small in the expression above,
and
Although there is no change in y, the slope changes through
The rays thus have the slopes a and , where a is in air, and is in the refractive material. We ignore, in the spirit of the already discussed group contraction, the variation in the x coordinate that is of order [63]. Thus, we can represent the relation between a and by the matrix
Suppose now that we have another convex surface of refractive material that has a radius of curvature and that faces in the opposite direction. If the ray comes out from this refractive surface, the applicable matrix is
These two convex surfaces, if the distance between them is small, constitute a thin lens. If we now multiply the matrix of Equation (99) from the left by the matrix of Equation (100), the net effect is the matrix
where
The expression in Equation (102) is known as the lens maker’s formula, and f is the focal length of the thin lens. The matrix of Equation (101) and the translation matrix of Equation (94) are considered to be the basic building blocks comprising a group theoretical approach for modern geometrical optics [61,64].
11. Physical Example II: Camera Optics and Little Groups
By way of this example, we aim to show that the two-by-two representation of the little groups in this paper coincides with the matrix representation of the one-lens system. It will then be shown that the focal condition corresponds to the transition from one little group to another. However, the transition from one little group to another is a singular transformation. The transition between little groups will be made possible by considering the correspondence between different little groups. In this way, an analytic transformation of computations on a hyperbolic surface to a spherical surface can be achieved, and the parameters of the lens system with those of the little groups can be formulated.
The simplest lens system consists of the lens matrix and the ray transfer matrix [61]:
where f is the focal length, and d is the separation distance between the two reference planes. Here, we take the focal length to be positive. If the object and image are and from the lens, respectively, the optical system is described by
The image becomes focused when the upper-right element of this matrix vanishes with
The diagonal elements are dimensionless; however, the presence of nondimensionless off-diagonal elements renders the matrix intractable. Nonetheless, it can be decomposed into
with
In the camera configuration, both the image and object distances are larger than the focal length, and both and are negative. Thus, we start with the negative of the middle matrix of Equation (106):
This matrix can further be renormalized so that the two diagonal elements become equal. To this end, it can be written as
with
Then, the core matrix becomes
with
where the latter is written in terms of the and x variables.
Now, our main concern is the core matrix C of Equation (112), which contains all the parameters of the system, and its upper-right element will vanish when the focal condition is satisfied. This form of the core matrix can be seen to be effective in cavity optics when the power of the matrix, which is composed of two mirrors, has to be evaluated [64]. This form can also be examined in relation to the Lorentz group and Wigner rotations.
Now that we have an equi-diagonal matrix with dimensionless components, we can equate it to (a) squeezed rotation , (b) an -like transformation (like in Equation (49)), and (c) a squeezed boost , with specific constraints defined below:
where the range of the angle variable is between 0 and , and is positive. The expressions given in the right-hand side of Equations (114)–(116) take the same mathematical forms as those of the representations of the -, -, and -like little groups. The two-by-two forms of Wigner’s little groups are given in Equations (48) and (49). Equations (114) and (116) are the squeezed (boosted) forms of the transformation matrices and of Equation (48), respectively. Equation (115) is like Equation (49), which is the little group transformation for a massless particle.
The left-hand sides of Equations (114)–(116) have components such that all the parameters are determined from , and f of the lens optics, and if we gradually increase the value of x, the upper-right element becomes zero, and then it should become positive. The right-hand side of the above expression cannot accommodate this transition, since the transition from one form to another form is a singular transformation. On the other hand, the core matrix of Equation (112) is analytic in the x and variables when both and are greater than 1.
Therefore, we seek another form of a little group matrix whose components are analytically well behaved. For this purpose, we consider , where the rotation and the boost matrices are taken from Equation (48). This is the two-by-two representation of a transformation that preserves the momentum of a relativistic particle traveling in the minus z direction [44]. These little groups can be equated under certain restrictions:
The relations between the parameters of these groups are found to be as follows:
For Equation (117), the relations are
For Equation (118), it is
For Equation (119), they are
Let us note that the quantity , while changing sign from minus to plus, it has to pass through zero. This process is analytic with the parameters and .
Therefore, the matrix in the left-hand side of Equations (117)–(119) will provide the means to define those transformation parameters in terms of the lens parameters of Equation (112), meanwhile circumventing the singularity problem and emerging from the limiting nature of the contraction procedure. Thus, one can establish a correspondence between lens optics and the transformations of the little groups. Furthermore, transformations from one little group to another can be achieved by adjusting focal conditions.
In terms of these parameters, the core matrix can be written as
Here, both sides have upper-right elements which are analytic as they go through zero. The parameters are now related by
and finally by
Therefore, we have the Lorentz transformation parameters and expressed in terms of the parameters of the one-lens system.
Here, we have shown how the physical lens parameters are related to the parameters of the group. The upper-right component of the matrix governs the focal condition. The lens parameters are adjusted to satisfy the focal condition, causing this component to become zero. Thus, it is the realization of this condition that makes the transition from one little group to another possible.
12. Conclusions
In this paper, we discussed a range of approaches to contraction procedures within the context of Wigner’s little groups. We started by introducing the well-known scheme of group contraction using an approximation of a spherical surface to a flat one. We then considered Einstein’s , which shows that in the large-momentum/zero-mass limit, the massive particle becomes a massless particle. Therefore, the limiting procedure is illustrated by converting massive and imaginary mass particles to a massless particle using the infinite-momentum limit.
Our main focus was on the contraction procedure based on squeeze transformations. This approach is relatively recent compared to old-standing limiting procedures. Moreover, as illustrated in Figure 2, the squeeze transformation offers the advantage of providing a geometric picture comparable to the one with a tangent plane at the north pole of a very large sphere and a tangent cylinder around the equator. In this case, a planar surface can be achieved by shrinking along the z-axis and expanding the circular area on the -plane. Conversely, a cylindrical configuration can be obtained, whose axis is along the z direction, by expanding along the z-axis while shrinking the area on the -plane. With this new approach, we contracted Wigner’s little group to both the and the cylindrical group. Similarly, Wigner’s little group, the Lorentz group , was contracted to these same two groups.
As a further example of group contraction, the group was contracted into the Poincaré group, and the result was shown to lead to Einstein’s widely known .
Finally, two physical examples were presented. The first concerned a ray that emanates from a transparent spherical surface into a straight line, wherein we derived the lens maker’s formula. The second physical example illustrates how camera optics can be used to realize Wigner’s little groups from optical elements. It is seen that little groups corresponding to massive, massless, and imaginary mass particles can be transformed from one to another through the focusing condition of the image in a camera.
Despite the fact that laws governing relativistic particles differ significantly from the principles of classical optics, the theory of Lie groups and Lie algebras offers valuable analogous computations that can improve our understanding of symmetries and transformations in both fields.
Although it is a reappraisal of our earlier work, this paper is written from a fresh viewpoint that has not been previously presented.
Author Contributions
Conceptualization, S.B., Y.S.K. and M.E.N.; writing—original draft preparation, S.B., Y.S.K. and M.E.N.; writing—review editing, S.B., Y.S.K. and M.E.N.; visualization, S.B., Y.S.K. and M.E.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable.
Acknowledgments
We would like to thank Gerald Q. Maguire of KTH Royal institute of Technology for an improved redrawing of most of the figures.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Generators for the Lie algebra of written in five-by-five matrix form.The coordinate system is , with the Minkowski metric . The generators are responsible for the rotations among the three space coordinates. generates rotations between the two time-like components. generates boosts with the second time-like component, while are for the boosts with the first time-like component.
Table A1.
Generators for the Lie algebra of written in five-by-five matrix form.The coordinate system is , with the Minkowski metric . The generators are responsible for the rotations among the three space coordinates. generates rotations between the two time-like components. generates boosts with the second time-like component, while are for the boosts with the first time-like component.
| Rotation generators in 5 × 5 matrix form | |
| , | |
| , | |
| Boost generators in 5 × 5 matrix form | |
| , | |
| , | |
| , | |
References
- Mukunda, N.; Balachandran, A.P.; Nilsson, J.S.; Sudarshan, E.C.G.; Zaccaria, F. Evolution, symmetry, and canonical structure in dynamics. Phys. Rev. D 1981, 23, 2189–2200. [Google Scholar] [CrossRef]
- Sprung, D.W.L.; Morozov, G.V.; Martorell, J. Geometrical approach to scattering in one dimension. J. Phys. A Math. Gen. 2004, 37, 1861–1880. [Google Scholar] [CrossRef]
- Błasiak, P.; Horzela, A.; Kapuścik, E. Alternative Hamiltonians and Wigner quantization. J. Opt. B Quantum Semiclassical Opt. 2003, 5, S245. [Google Scholar] [CrossRef]
- Simon, R.; Mukunda, N. Iwasawa decomposition in first-order optics: Universal treatment of shape-invariant propagation for coherent and partially coherent beams. J. Opt. Soc. Am. A 1998, 15, 2146. [Google Scholar] [CrossRef]
- Bastiaans, M.J.; Alieva, T. Classification of lossless first-order optical systems and the linear canonical transformation. J. Opt. Soc. Am. A 2007, 24, 1053–1062. [Google Scholar] [CrossRef][Green Version]
- Nazarathy, M.; Shamir, J. First-order optics—A canonical operator representation: Lossless systems. J. Opt. Soc. Am. 1982, 72, 356–364. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Reprinted with Corrections ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA; Melbourne, Australia; Madrid, Spain; Cape Town, South Africa; Singapore; São Paulo, Brazil; Delhi, India, 2008. [Google Scholar]
- Ðoković, D.Ž.; Osterloh, A. On polynomial invariants of several qubits. J. Math. Phys. 2009, 50, 033509. [Google Scholar] [CrossRef]
- Heydari, H. Quantum relative phase, m-tangle, and multi-local Lorentz-group invariant. Quantum Inf. Process. 2010, 9, 233–238. [Google Scholar] [CrossRef]
- Teodorescu-Frumosu, M.; Jaeger, G. Quantum Lorentz-group invariants of n-qubit systems. Phys. Rev. A 2003, 67, 052305. [Google Scholar] [CrossRef]
- Başkal, S.; Kim, Y.S.; Noz, M.E. Entangled Harmonic Oscillators and Space-Time Entanglement. Symmetry 2016, 8, 55–80. [Google Scholar] [CrossRef]
- Rangamani, M.; Takayanagi, T. Holographic Entanglement Entropy; Lecture Notes in Physics; Springer International Publishing: Cham, Switzerland, 2017; Volume 931. [Google Scholar] [CrossRef]
- Cerveró, J.M.; Lejarreta, J.D. Generalized two-mode harmonic oscillator: Dynamical group and squeezed states. J. Phys. A Math. Gen. 1996, 29, 7545. [Google Scholar] [CrossRef]
- Hasebe, K. Spin-entangled squeezed state on a Bloch four-hyperboloid. J. Phys. A Math. Theor. 2021, 54, 245303. [Google Scholar] [CrossRef]
- Arvind, B.; Mukunda, N. Non-classical photon statistics for two-mode optical fields. J. Phys. A Math. Gen. 1996, 29, 5855–5872. [Google Scholar] [CrossRef][Green Version]
- Colas, T.; Grain, J.; Vennin, V. Four-mode squeezed states: Two-field quantum systems and the symplectic group Sp(4,R). Eur. Phys. J. C 2022, 82, 6. [Google Scholar] [CrossRef]
- Fring, A.; Tenney, R. Lewis—Riesenfeld invariants for PT-symmetrically coupled oscillators from two-dimensional point transformations and Lie algebraic expansions. J. Math. Phys. 2022, 63, 123509. [Google Scholar] [CrossRef]
- Başkal, S.; Kim, Y.S. de Sitter group as a symmetry for optical decoherence. J. Phys. A Math. Gen. 2006, 39, 7775–7788. [Google Scholar] [CrossRef]
- Wigner, E.P. On Unitary Representations of the Inhomogeneous Lorentz Group. Ann. Math. 1939, 40, 149–204. [Google Scholar] [CrossRef]
- Bekaert, X.; Najafizadeh, M.; Setare, M. A gauge field theory of fermionic continuous-spin particles. Phys. Lett. B 2016, 760, 320–323. [Google Scholar] [CrossRef]
- Rivelles, V.O. Gauge theory formulations for continuous and higher spin fields. Phys. Rev. D 2015, 91, 125035. [Google Scholar] [CrossRef]
- Schuster, P.; Toro, N. On the theory of continuous-spin particles: Wavefunctions and soft-factor scattering amplitudes. J. High Energy Phys. 2013, 2013, 104. [Google Scholar] [CrossRef]
- Bekaert, X.; Skvortsov, E.D. Elementary particles with continuous spin. Int. J. Mod. Phys. A 2017, 32, 1730019. [Google Scholar] [CrossRef]
- Inönü, E.; Wigner, E.P. On the Contraction of Groups and Their Representations. Proc. Natl. Acad. Sci. USA 1953, 39, 510–524. [Google Scholar] [CrossRef] [PubMed]
- Misra, S.P.; Maharana, J. Diffraction scattering and group contraction. Phys. Rev. D 1976, 14, 133–139. [Google Scholar] [CrossRef]
- Bacry, H.; Chang, N. Kinematics at infinite momentum. Ann. Phys. 1968, 47, 407–423. [Google Scholar] [CrossRef]
- Tóth, K. On the group-structure of theories in the infinite momentum frame. Nucl. Phys. B 1975, 92, 524–540. [Google Scholar] [CrossRef]
- Beckers, J.; Jaspers, M. Representations of the poincaré algebra, spin algebras and the infinite-momentum frame. Phys. A Stat. Mech. Its Appl. 1975, 79, 338–349. [Google Scholar] [CrossRef]
- Bagchi, A.; Nachiketh, M.; Soni, P. Anatomy of null contractions. J. High Energy Phys. 2024, 2024, 141. [Google Scholar] [CrossRef]
- Cattaneo, U.; Wreszinski, W.F. Contractions of lie algebra representations. Rev. Math. Phys. 1999, 11, 1179–1207. [Google Scholar] [CrossRef]
- Khan, A.M. Continuous spin representation from contraction of the conformal algebra. J. Math. Phys. 2021, 62, 032305. [Google Scholar] [CrossRef]
- Khan, A.M.; Ramond, P. Continuous spin representations from group contraction. J. Math. Phys. 2005, 46, 053515. [Google Scholar] [CrossRef]
- Evans, N.T. Discrete Series for the Universal Covering Group of the 3 + 2 de Sitter Group. J. Math. Phys. 1967, 8, 170–184. [Google Scholar] [CrossRef]
- Enayati, M.; Gazeau, J.P.; Pejhan, H.; Wang, A. The de Sitter (dS) Group and Its Representations: An Introduction to Elementary Systems and Modeling the Dark Energy Universe; Synthesis Lectures on Mathematics & Statistics; Springer International Publishing: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Gilmore, R. Lie Groups, Lie Algebras, and Some of Their Applications; Dover Publications: Mineola, NY, USA, 2005. [Google Scholar]
- Weinberg, S. The Quantum Theory of Fields; Paperback ed.; 10. print ed.; Volume 1 Foundations; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; p. 609. [Google Scholar]
- Schwartz, M.D. Quantum Field Theory and the Standard Model; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Dirac, P.A.M. Application of Quaternions to Lorentz Transformations. Proc. R. Ir. Acad. Sect. A Math. Phys. Sci. 1945, 50, 261–270. [Google Scholar]
- Naimark, M. Linear Representation of the Lorentz Group. Usp. Mat. Nauk 1954, 9, 19–93. [Google Scholar]
- Başkal, S.; Kim, Y.S.; Noz, M.E. Theory and Applications of the Poincaré Group, 2nd ed.; 2024 ed.; Springer Nature Switzerland: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Zee, A. Group Theory in a Nutshell for Physicists; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]
- Carmeli, M.; Malin, S. Representations of the Rotation and Lorentz Groups: An Introduction; Lecture Notes in Pure and Applied Mathematics; No. 16; M. Dekker: New York, NY, USA, 1976. [Google Scholar]
- Lévy-Leblond, J.M. Une nouvelle limite non-raelativiste du groupe de Poincaré. Ann. L’institut Henri Poincaré. Sect. A Phys. Théor. 1965, 3, 1–12. [Google Scholar]
- Başkal, S.; Kim, Y.S.; Noz, M.E. Physics of the Lorentz Group (Second Edition): Beyond High-Energy Physics and Optics; IOP Publishing: Bristol, UK, 2021. [Google Scholar] [CrossRef]
- Kim, Y.S.; Wigner, E.P. Cylindrical group and massless particles. J. Math. Phys. 1987, 28, 1175–1179. [Google Scholar] [CrossRef]
- Kim, Y.S.; Wigner, E.P. Space-time geometry of relativistic particles. J. Math. Phys. 1990, 31, 55–60. [Google Scholar] [CrossRef]
- Kupersztych, J. Is there a link between gauge invariance, relativistic invariance and electron spin? Il Nuovo C. B Ser. 11 1976, 31, 1–11. [Google Scholar] [CrossRef]
- Schuster, P.; Toro, N. Quantum electrodynamics mediated by a photon with generalized (continuous) spin. arXiv 2023, arXiv:2308.16218. [Google Scholar]
- Schuster, P.; Toro, N.; Zhou, K. Interactions of particles with “continuous spin” fields. J. High Energy Phys. 2023, 2023, 10. [Google Scholar] [CrossRef]
- Schuster, P.; Toro, N. Quantum electrodynamics mediated by a photon with continuous spin. Phys. Rev. D 2024, 109, 096008. [Google Scholar] [CrossRef]
- Gerry, C.C. Remarks on the use of group theory in quantum optics. Opt. Express 2001, 8, 76–85. [Google Scholar] [CrossRef] [PubMed]
- Wünsche, A. Symplectic groups in quantum optics. J. Opt. B Quantum Semiclassical Opt. 2000, 2, 73. [Google Scholar] [CrossRef]
- Weyl, H. The Theory of Groups and Quantum Mechanics; Nachdr. ed.; Dover Books on Mathematics; Dover Publications: Mineola, NY, USA, 2009. [Google Scholar]
- Feinberg, G. Possibility of Faster-Than-Light Particles. Phys. Rev. 1967, 159, 1089–1105. [Google Scholar] [CrossRef]
- Van Dam, H.; Ng, Y.J.; Biedenharn, L.C. A comment on fermionic tachyons and poincaré representations. Phys. Lett. B 1985, 158, 227–230. [Google Scholar] [CrossRef]
- Barci, D.G.; Bollini, C.G.; Rocca, M. Quantization of a six-dimensional Wess-Zumino model. Il Nuovo C. A 1995, 108, 797–808. [Google Scholar] [CrossRef]
- Hamada, Y.; Seo, M.S.; Shiu, G. Large gauge transformations and little group for soft photons. Phys. Rev. D 2017, 96, 105013. [Google Scholar] [CrossRef]
- Han, D.; Kim, Y.S.; Noz, M.E.; Son, D. Internal space-time symmetries of massive and massless particles. Am. J. Phys. 1984, 52, 1037–1043. [Google Scholar] [CrossRef]
- Susskind, L. Model of Self-Induced Strong Interactions. Phys. Rev. 1968, 165, 1535–1546. [Google Scholar] [CrossRef]
- Başkal, S.; Kim, Y.S.; Noz, M.E. Einstein’s E =mc2 Derivable from Heisenberg’s Uncertainty Relations. Quantum Rep. 2019, 1, 236–251. [Google Scholar] [CrossRef]
- Blaker, J.W. Geometric Optics—The Matrix Theory; Marcel Decker: New York, NY, USA, 1971. [Google Scholar]
- Hecht, E. Optics, 5th ed.; Pearson Education, Inc.: Boston, MA, USA, 2017. [Google Scholar]
- Dereniak, E.L.; Dereniak, T.D. Geometrical and Trigonometric Optics; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2008. [Google Scholar]
- Başkal, S.; Kim, Y.; Noz, M. Mathematical Devices for Optical Sciences; IOP Publishing: Bristol, UK, 2019; OCLC: 1034620988. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).