Abstract
In the digital era, secure data sharing has become a core requirement for enabling cross-domain collaboration, cloud computing, and Internet of Things (IoT) applications, as well as a critical measure for safeguarding privacy and defending against malicious attacks. In light of the risks of data leakage and misuse in open environments, achieving efficient, controllable, and privacy-preserving data sharing has emerged as a key research focus. This paper first provides a systematic review of the prevailing secure data sharing technologies, including proxy re-encryption, searchable encryption, key agreement and distribution, and attribute-based encryption, summarizing their design principles and application features. Subsequently, game-theoretic modeling based on incentive theory is introduced to construct a strategic interaction framework between data owners and data users, aiming to analyze and optimize benefit allocation mechanisms. Furthermore, the paper explores the integration of game theory with secure sharing mechanisms to enhance the sustainability and stability of the data sharing ecosystem. Finally, it outlines the critical challenges currently faced in secure data sharing and discusses future research directions, offering theoretical insights and technical references for building a more comprehensive data sharing framework.
1. Introduction
Cybersecurity focuses on safeguarding cyberspace against unauthorized access, malicious disruptions, and interference [1]. As an interdisciplinary research domain, cybersecurity investigations extend beyond developing protective technologies, to encompass the examination of security- and privacy-related incidents, as well as human-centered processes [2,3]. Recent advancements have broadened the data sources for cybersecurity research, incorporating network/application tracing, database and information system activities, along with user behavioral patterns [4]. Notably, government agencies, commercial entities, and nonprofit organizations now systematically aggregate cybersecurity-related information that holds significant potential for research applications [5].
Data play a pivotal role in cybersecurity research. As threats continually evolve with increasing sophistication and detection challenges, researchers require access to more comprehensive datasets, to maintain predictive capabilities against potential risks and devise adaptive solutions within dynamic environments [6,7]. Mitigating emerging forms of malware, ransomware, and phishing attacks necessitates a proactive collaborative cybersecurity paradigm involving real-time knowledge exchange, data sharing, and technological interoperability [8]. However, organizational silos persist in cybersecurity operations, where corporations and research teams frequently operate in isolation, exhibiting reluctance to disclose sensitive information, even for collective security enhancement—a practice that substantially constrains the scope and efficacy of research [9]. Data serve as a multifaceted digital commodity, enabling intra-organizational optimization, enrichment of existing products/services, knowledge acquisition, and commercial monetization. Fundamentally, data sharing entails transferring datasets or granting access rights for algorithmic training purposes, thereby provisioning third parties with resources to achieve specific objectives (e.g., value creation or process optimization) [10,11]. This practice simultaneously facilitates novel inter-organizational collaborative–competitive dynamics through complementary data integration. Nevertheless, persistent concerns regarding privacy vulnerabilities and operational barriers continue to deter organizations and research teams from engaging in data sharing initiatives [12,13].
The imperative for data sharing has reached heightened urgency in the contemporary landscape, where sensor technologies and ubiquitous digitalization continuously generate real-world process data. A European Commission study [14] revealed that 80% of industrial data remain untapped, underscoring a substantial underutilization of digital assets. Complementing this finding, PwC research [15] identified corporate data sharing practices as primarily customer-centric, followed by supplier-oriented and external entity engagements, while predicting the increasing importance of cross-scale data exchanges between large enterprises and SMEs in coming years. Within the European Union, the evolving significance of inter-organizational data governance has crystallized through legislative advancements. Beyond the foundational General Data Protection Regulation (GDPR), emerging frameworks including the Data Governance Act (DGA) and Data Act (DA) systematically supplement legal infrastructure for secure data sharing. These regulatory innovations are projected to stimulate additional GDP growth of up to EUR 270 billion by 2028 through optimized data circulation [14,15,16].
Recently, there have been calls to provide cybersecurity data to broader academic communities, but these calls have not received timely responses. This is partly because, in practical processes, data sharing usually requires the participants to consume a certain amount of resources and involves costs. Under the absence of effective participant incentive mechanisms, it is difficult to balance multi-party interests. Therefore, most companies and research teams are unwilling to proactively share data or forward messages [17]. Thus, to improve data sharing willingness, the key lies in formulating effective incentive mechanisms. Simultaneously, a reward–punishment combination strategy should be adopted. These incentive mechanisms can motivate all participants to contribute high-quality services and effectively reduce the possibilities of data leaks and tampering, while avoiding vicious competition and improper resource consumption [18].
As a novel technology, cloud computing facilitates the integration of storage and computational resources in the era of big data, enabling continuous aggregation of data resources and unleashing immense potential value. With the rapid advancement of Internet technologies, cloud computing has emerged as a mainstream data-sharing paradigm [19], due to its cost-effectiveness, high performance, and rapid accessibility, effectively addressing the issue of ‘data silos’. A viable solution involves constructing secure and efficient data storage and sharing frameworks through cloud computing, where users and organizations frequently delegate their data to cloud servers with superior computational and storage capabilities for storage and sharing [20]. However, while enabling data sharing, cloud servers pose increasing security risks, as outsourced data becomes physically separated from direct user management, rendering it vulnerable to theft and tampering. To protect data privacy and prevent leakage of outsourced data [21,22], users typically encrypt their data prior to cloud uploads [23]. This encryption mechanism ensures that neither cloud servers nor other adversaries can access sensitive information, thereby preserving data confidentiality and user privacy. In recent years, achieving secure data sharing has become a focal point of domestic and international research efforts.
Among various data-intensive domains, the healthcare sector has emerged as a key focus of data sharing research, due to the highly sensitive nature of personal health information involved. Medical data encompass not only structured information such as electronic medical records, imaging data, and prescription histories, but also real-time physiological signals and behavioral traces collected by wearable devices. These data hold significant value for disease prediction, personalized treatment, and public health response.
To enhance the utility of medical data, while preserving patient privacy, recent research has called for the establishment of cross-institutional sharing platforms and collaborative mechanisms. However, in practice, data sharing among hospitals, research institutions, and third-party platforms remains limited. This is primarily due to the absence of effective incentive mechanisms, insufficient security safeguards, and a lack of mutual trust. The high commercial value and legal risks associated with medical data further prompt data holders to adopt conservative management approaches, thereby exacerbating the problem of ‘data silos’. The key terms and their definitions relevant to this study are presented in Table 1.

Table 1.
Glossary of key terms.
The motivation for this study stemmed from the pressing challenges of privacy protection and security in data sharing within the digital era. Although existing research has proposed various encryption and sharing schemes—such as searchable encryption, proxy re-encryption, and attribute-based encryption—there remain significant technical and theoretical gaps in effectively balancing security and sharing efficiency in practical applications. The novelty of this paper lies in providing a comprehensive survey of mainstream data security sharing technologies, and in introducing game-theoretic models to address critical issues such as insufficient incentives and privacy leakage. This offers new perspectives and potential solutions for secure and efficient data sharing.
The remainder of this paper is organized as follows: Section 2 provides an overview of the fundamental models and key components of secure data sharing, clarifying the roles and interactions of the various stakeholders involved in the sharing process. Section 3 presents a systematic review of the foundational theories and core technologies closely related to secure sharing, offering theoretical support for the subsequent analysis. Section 4 examines and compares four mainstream secure data sharing approaches from a technical perspective, and further introduces game-theoretic incentive mechanisms to explore strategy evolution and optimal design under bounded rationality. Finally, Section 5 concludes the paper and, in light of current research bottlenecks, outlines potential future research directions. This study conducted a classified and comprehensive review of the key technologies underpinning secure data sharing based on a systematic literature search and screening process.
2. Data Security Sharing Model
2.1. Initial System Model
A data secure sharing system model can be summarized as shown in Figure 1, comprising three entities: cloud servers, data owners, and data users. In the healthcare data sharing ecosystem, the data owner refers to the legitimate holder of medical data, typically the patient, who possesses individual health-related records such as electronic medical records. Encryption methods adopt searchable encryption (SE), proxy re-encryption (PRE), attribute-based encryption (ABE), or key agreement. A cloud server, acting as a third-party data custodian, is responsible for the unified integration, centralized management, and access control of the collected medical data. The data user represents the ultimate recipient of the medical data, such as research institutions, who obtain access to the data through legitimate authorization for the purposes of scientific research or technological development. In this model, the data owner stores the plaintext data and, in order to ensure secure data sharing, encrypts the data before uploading it to the cloud server. The cloud server provides services such as storage and retrieval for secure data sharing. It stores the encrypted data uploaded by the data owner. When a data user requests the encrypted data from the cloud server, the server returns the encrypted data to the user. Once the data user determines which data to download from the data owner, they download the encrypted data from the cloud server, decrypt it, and obtain the plaintext data.

Figure 1.
Data security sharing system model.
2.2. Threat Model
In the data security sharing system, data move through seven stages from the data owner to the data user: generation, encryption, transmission, storage, sharing, decryption, and destruction. In this process, data security faces multiple threats, including key attacks [24], data leakage [25], identity impersonation [26], data theft [27], data tampering [28], data corruption [29], and data misuse [30]. It is important to emphasize that the term ‘data corruption’ as used in this paper not only refers to the alteration of ciphertext in transit, but also includes the compromising of auxiliary elements such as associated indexes, integrity tags, and re-encryption keys cached on the server side. The destruction of any of these components may render the data undecryptable or cause distorted decryption results, thereby threatening the system’s availability and integrity. To better illustrate the real-world impact of these threats in secure data sharing scenarios, this paper presents the following representative cases:
(1) Key Attacks: In 2023, the U.S.-based password management company LastPass experienced a significant security breach. Attackers exploited vulnerabilities on an employee’s computer and leveraged key leakage to successfully steal encrypted backups containing customers’ sensitive data. This incident revealed weaknesses in key management processes and highlighted the critical importance of key security and protective measures.
(2) Data Tampering and Leakage: In 2022, the Australian telecommunications operator Optus suffered a cyberattack in which hackers infiltrated the company’s database, tampered with and exfiltrated sensitive information from nearly 10 million users, including names, dates of birth, and passport numbers. This breach exposed the serious risks of large-scale data tampering and leakage.
(3) Identity Impersonation and Data Misuse: In early 2023, the South African branch of the global credit reporting agency TransUnion experienced a massive data breach. Hackers impersonated legitimate users to bypass access controls and illegally accessed sensitive data of approximately 54 million South African citizens, including social identity information and credit records. This led to long-term misuse of user data and a heightened risk of financial fraud.
(4) Data Corruption: In 2022, Microsoft’s cloud platform Azure experienced a global storage outage, resulting in data corruption and loss for numerous customers. For some, critical business data were permanently damaged, significantly impacting business operations.
These cases demonstrate that the threats encountered during secure data sharing are not only persistent but also involve increasingly broad and complex data management scenarios. As such, it is imperative to continuously strengthen security measures and risk control mechanisms in the design of data sharing systems. The corresponding threat model is illustrated in Figure 2.
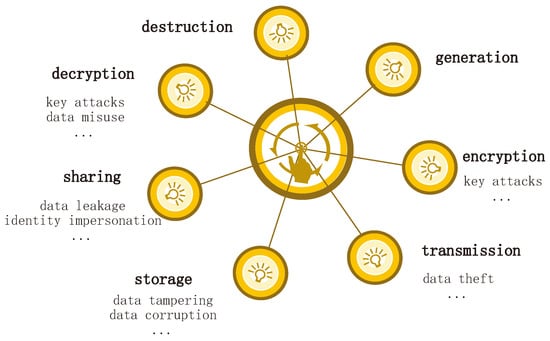
Figure 2.
Threat model of data.
Most threat models in existing schemes assume the following:
(1) Cloud servers are considered to be semi-honest in the context of data security sharing. While cloud servers store encrypted data and are capable of honestly performing retrieval operations, they are inherently curious about the encrypted data. This curiosity introduces potential risks, such as data leakage, data tampering, data corruption, and the possibility of attackers impersonating authorized identities.
(2) A maliciously authorized external attacker, leveraging a legitimate identity, may download encrypted data from the cloud server and attempt to decrypt it.
(3) A malicious unauthorized external attacker may eavesdrop on the key exchange process between the data owner and the data user, attempting to exploit key attack techniques to steal the shared encryption key. During the transmission of encrypted data over the network, network attacks may result in data loss or leakage, exposing sensitive information to unauthorized parties. Additionally, an attacker may impersonate a legitimate identity, download encrypted data from the cloud server, and attempt to decrypt the data using stolen or forged credentials.
In the field of information system security design, the STRIDE model proposed by Microsoft’s Security Development Lifecycle (SDL) has become one of the most widely adopted threat modeling frameworks in the industry [31]. STRIDE systematically enumerates potential threats through a checklist of six high-level categories—Spoofing, Tampering, Repudiation, Information Disclosure, Denial of Service, and Elevation of Privilege—to assist researchers in identifying risks at the architectural stage and developing targeted mitigation strategies. For scenarios involving intensive personal data, the LINDDUN framework [32] provides a complementary perspective by focusing on privacy threats. It categorizes risks into Linkability, Identifiability, Non-repudiation, Detectability, Disclosure, Unawareness, and Non-compliance. When combined with Data Flow Diagram (DFD) analysis, LINDDUN enables early detection of issues such as identity linkages, information leakage, and regulatory compliance, offering a quantitative basis for selecting technologies like differential privacy, minimal recognizable sets, and lawful auditing mechanisms. In practice, these two models are often used in combination: STRIDE is first applied to address traditional security concerns, covering CIA+A (Confidentiality, Integrity, Availability, and Auditability), while LINDDUN is then used to delve deeper into privacy-specific risks. This dual-layered checklist—‘security + privacy’—is particularly well suited for cross-domain applications centered around sensitive data, such as secure data sharing.
2.3. Security Requirements
The security requirements for data secure sharing and the cryptographic primitives that ensure these requirements can be summarized as shown in Table 2.

Table 2.
Security requirements and associated cryptographic primitives.
In addressing the aforementioned security requirements, cryptographic primitives such as encryption, signatures, authentication, and key exchange play a critical role. For instance, signatures are used to verify the authenticity of transformed keys and ciphertexts, preventing forgery; attribute-based encryption and key management ensure legitimate delegation of transformation rights; encryption techniques safeguard data confidentiality; auditing protocols verify data integrity; and the combined application of multiple cryptographic primitives, such as encryption with unintentional storage and homomorphic techniques, effectively protects privacy.
3. Relevant Knowledge
3.1. Bilinear Mapping
Given that and are cyclic multiplicative groups of order p, where p is a prime, and the bilinear map satisfies the following properties:
(1) bilinear: For any and , there exists .
(2) non-degenerate: There exist such that , where denotes the identity element of the group .
(3) computable: For any , there exists a probabilistic polynomial-time algorithm to compute .
Let and be cyclic multiplicative groups of prime order p. A bilinear map is said to satisfy the following properties:
(1) Bilinearity: For all and , the mapping satisfies .
(2) Non-degeneracy: There exist such that , where denotes the identity element of group .
(3) Computability: For any , there exists a probabilistic polynomial-time algorithm that efficiently computes .
3.2. Shamir Secret Sharing Scheme
Secret sharing schemes are typically based on mathematical principles such as polynomial interpolation, linear algebra, and others. The core idea of these schemes is to divide a secret S into n shares according to a specific rule and distribute these shares among n participants. These shares possess the following properties:
(1) A single share, or a subset of shares, does not reveal any information about the secret S.
(2) When a sufficient number of shares (reaching the threshold) have been collected, the original secret S can be accurately reconstructed through a specific algorithm or computation process.
The Shamir Secret Sharing Scheme is as follows:
(1) Construction Process: Let the secret be denoted by S, with a threshold value k, and let p be a prime number such that . All arithmetic operations—addition, multiplication, and inversion—are performed over the finite field . A random polynomial of degree over is constructed as
where is the secret, and the remaining coefficients () are randomly selected from . For each participant i (), their individual share is computed as , where is a unique non-zero value serving as the identifier for participant i. Thus, each participant i holds a secret share represented as the pair .
(2) Reconstruction Process: When k participants want to reconstruct the secret, they need to collect their secret shares . Using the Lagrange interpolation formula, the original polynomial can be constructed as
By substituting into , the secret value S is obtained:
This scheme ensures that the secret can only be reconstructed when k or more participants collaborate. Fewer than k participants have no information about the secret. To prove the existence of the Lagrange interpolation polynomial, we construct it as follows:
It is easy to verify that the polynomial constructed in this manner satisfies all the given interpolation points . Specifically, when , we have
In this expression, for the term where , the numerator and denominator are equal, so the fraction equals 1 and the term becomes . For all , the numerator contains the factor , so those terms vanish. Hence,
Therefore, the constructed polynomial satisfies all the interpolation conditions. This proves that the Lagrange interpolation polynomial exists.
3.3. Searchable Encryption Technology
Searchable encryption is a cryptographic mechanism that enables keyword or condition-based searches to be performed directly over encrypted data, without requiring decryption. Only the ciphertexts or results corresponding to matching entries are returned. Throughout the entire process, the cloud server or search engine remains unaware of the underlying plaintext content and the user’s search intent.
3.3.1. Public Key Searchable Encryption
The formal definition of Public Key Searchable Encryption (PKSE) typically involves several key steps: key generation, data encryption, index construction, trapdoor generation, search, and result retrieval. It is defined as a tuple of six probabilistic polynomial-time algorithms:
The definitions of these algorithms are as follows:
(1) Key Generation Algorithm : Given a security parameter , this algorithm generates a public–private key pair . The public key is used to encrypt data and construct searchable indexes, while the secret key is securely held by the data owner for decrypting search results and performing related operations.
(2) Data Encryption Algorithm : Given a public key , a plaintext message M, and a random value r, the data owner uses this algorithm to produce a ciphertext C encrypting M.
(3) Index Generation Algorithm : Given the public key and a keyword set extracted from the message M, this algorithm outputs an index set associated with the ciphertext C. Both I and C are stored on the cloud server.
(4) Trapdoor Generation Algorithm : Given the secret key and a query keyword , the data user uses this algorithm to generate a trapdoor T.
(5) Search Algorithm : Given the public key and trapdoor T, the cloud server performs a search over the stored index set I. If the keyword matches (i.e., ), it returns the corresponding ciphertext C; otherwise, the search fails.
(6) Decryption Algorithm : Given a ciphertext C and the secret key , this algorithm outputs the original plaintext message M.
3.3.2. Symmetric Searchable Encryption
Unlike Public Key Searchable Encryption, Symmetric Searchable Encryption (SSE) utilizes symmetric keys to encrypt data and construct indexes, enabling efficient search operations over ciphertexts, while ensuring data confidentiality. The SSE scheme comprises five primary steps, defined as a tuple of five probabilistic polynomial-time algorithms:
The definitions of these algorithms are as follows:
(1) Key Generation Algorithm : Given a security parameter , this algorithm generates a symmetric key K. The key K is used for encrypting data, generating verifiable indexes, and decrypting data.
(2) Encryption Algorithm : Given the symmetric key K and plaintext data M, the data owner uses this algorithm to produce a ciphertext C and a corresponding searchable index I.
(3) Trapdoor Generation Algorithm : Given the symmetric key K and a search keyword , this algorithm outputs a trapdoor T.
(4) Search Algorithm : Given the searchable index I and trapdoor T, the cloud server performs a search operation over the stored index collection. If the keyword matches (i.e., ), the corresponding ciphertext C is returned; otherwise, the search fails.
(5) Decryption Algorithm : Given the symmetric key K and ciphertext C, this algorithm returns the original plaintext message M.
3.4. Proxy Re-Encryption
Proxy Re-Encryption (PRE) is a public key cryptographic technique that enables a proxy server to convert a ciphertext encrypted under User A’s public key into a ciphertext under User B’s public key without learning the underlying plaintext. This mechanism allows secure data sharing between User A and User B without requiring either party to reveal their private keys. The algorithm for secure data sharing from User A to User B proceeds as follows:
(1) Key Generation Algorithm : Given a security parameter , this algorithm generates a key pair for each user. Let denote User A’s public and private keys, and denote User B’s public and private keys.
(2) Re-Encryption Key Generation Algorithm : User A inputs their private key and User B’s public key , and this algorithm outputs a re-encryption key .
(3) Encryption Algorithm : Given User A’s public key and the plaintext message M, the algorithm outputs a ciphertext C encrypted under . User A then sends the ciphertext C and the re-encryption key to the proxy server.
(4) Re-Encryption Algorithm : The proxy server takes the re-encryption key and the ciphertext C as inputs and outputs a re-encrypted ciphertext under User B’s public key .
(5) Decryption Algorithm : User B inputs their private key and the re-encrypted ciphertext , and the algorithm outputs the original plaintext M.
4. Data Security Sharing Schemes
At present, numerous researchers both domestically and internationally have conducted in-depth studies on various data security sharing schemes, achieving a series of notable results. From a technical perspective, these results have mainly focused on four key areas: proxy re-encryption, searchable encryption, key agreement and distribution, and attribute-based encryption. In addition, leveraging the decentralized, tamper-resistant, and transparent nature of blockchain technology, many existing solutions have integrated blockchain to enhance the security and trustworthiness of the data sharing process.
A well-designed incentive mechanism not only effectively motivates data owners to provide high-quality data services but also serves as a driving force in building a secure and sustainable data sharing ecosystem. To further explore the synergistic mechanisms between data security sharing technologies and incentive mechanisms, this study systematically reviews and summarizes recent representative cases in this field.
Blockchain-based data sharing features decentralization, tamper resistance, and strong auditability, which significantly enhance the transparency and trustworthiness of data transmission. This makes it particularly suitable for multi-party collaboration scenarios lacking a strong trust foundation. Additionally, smart contracts enable automated incentive distribution and access control. However, such systems also face challenges, including high system complexity, substantial on-chain storage and computation costs, and relatively high processing latency. In contrast, non-blockchain data sharing models rely on centralized platforms, such as cloud servers, for data hosting and access management. These approaches offer advantages such as simplified deployment, fast response times, and lower computational overhead. Nonetheless, they are more vulnerable to issues such as centralized trust dependency, difficulty in tracing data tampering, and heightened risks of privacy breaches. As a result, a trade-off exists between security and efficiency, and the appropriate technological choice should be made based on the specific requirements of the application scenario.
In the context of healthcare data sharing, a regional medical consortium adopted a blockchain-plus-Attribute-Based Encryption (ABE) scheme to enable cross-institutional sharing of patients’ electronic medical records (EMRs). In this system, patients—as data owners—define access policies, and medical institutions obtain data access only after permission verification via the blockchain. However, during deployment, issues such as policy abuse, metadata leakage on the blockchain, and insufficient revocation mechanisms in ABE emerged. These problems prompted deeper reflection on the design of privacy-preserving mechanisms. This case highlights the practical challenges that theoretical solutions may encounter and suggests that future research should focus on revocation mechanisms, encrypted metadata, and dynamic authorization strategies.
4.1. Searchable Encryption and Secure Data Sharing
The application of Searchable Encryption (SE) technology in secure data sharing models is illustrated in Figure 3, aiming to enable encrypted data to be searched without requiring decryption on the cloud server side. This model involves four key entities: a Trusted third party, Data owner, Data user, and Cloud server. First, the trusted third party is responsible for generating and securely distributing the cryptographic keys required for the search, ensuring confidentiality and integrity during key transmission. The data owner uses the system’s keys to encrypt the original data, producing ciphertexts, and simultaneously constructs secure searchable indexes (also encrypted). Both the ciphertext and the encrypted index are uploaded to the cloud server for storage. When a data user wishes to retrieve specific information, they use the keys obtained from the trusted third party to convert a keyword into an encrypted form known as a search trapdoor. This trapdoor is submitted to the cloud server, which then locally performs a matching operation against the encrypted index, without decrypting the underlying data. Once matching entries have been identified, the server returns the corresponding ciphertexts to the data user, who then decrypts them using their own private key to recover the original information. This model effectively balances data confidentiality and search efficiency, making it well suited for cloud-based data sharing environments with stringent privacy requirements. A comparison of related studies is shown in Table 3.

Figure 3.
Searchable encryption technology and data security sharing model.

Table 3.
Comparison table of searchable encryption techniques.
(1) Without Blockchain Integration
In research on searchable encryption (SE), early work by D. Song, D. Wagner, and A. Perrig [36] first proposed an efficient searchable encryption scheme based on symmetric encryption. This allowed keyword searches of encrypted data without the need for decryption, offering a balance between privacy protection and practicality in data sharing scenarios. It enabled users to securely store encrypted data with third parties (e.g., cloud servers), while still supporting controlled query operations, laying the foundation for secure data sharing and fostering further developments in SE technology. Cui et al. [33] combined SE with key aggregation, allowing users to search across multiple documents using a single key. However, their solution did not address cloud server load issues and relied on a trusted third party (TTP) to generate system parameters. Zhou et al. [49] supported cross-domain search by multiple data owners, enabling users to access data from different owners using a single aggregated key. Nevertheless, it lacked computational efficiency, as all search requests had to be handled by the cloud server. Oh et al. [34] extended traditional Key-Aggregate Searchable Encryption (KASE), enabling users to generate keyword trapdoors using a single aggregate key to retrieve only target data rather than all documents. They introduced fog nodes to pre-verify keywords, reducing cloud server workload (traditional KASE relies entirely on the cloud for verification). Data owners could generate aggregated keys directly without TTP involvement, realizing fully decentralized access control. Li et al. [50] supported enterprise-level data sharing and monitoring via hierarchical keyword search, suitable for multi-user scenarios. However, the computational overhead increased with user numbers, and the single-key exposure issue remained unresolved. Curtmola et al. [37] proposed the first sub-linear SSE scheme, enhancing medical data retrieval efficiency, but lacking dynamic update capabilities. Stefanov et al. [38] introduced dynamic SSE with support for incremental data updates, but required significant client storage. Zhang et al. [51] conducted a systematic classification and technical comparison of SE for medical cloud data sharing, highlighting dynamic updates, verification mechanisms, and complex queries as core directions for future optimization. Popa and Zeldovich [39] introduced Multi-Key SSE (MKSE), allowing users to search shared documents using individual keys. However, their solution did not support revocation and had a weak security model vulnerable to insider attacks. Patel et al. [40] proposed a dynamic document sharing and revocation scheme, addressing the inefficiency of traditional multi-user SSE in revoking access. They introduced a cross-user leakage graph to quantify leakage via graph component analysis, offering a novel approach to privacy evaluation in multi-user scenarios. Curtimola et al. [37] extended SE to multi-user settings, but only supported single-owner authorization for multiple users and failed to handle bidirectional authorization where users act as both data owners and searchers. Tang [41] proposed a multi-party SE scheme featuring both worst-case and average-case security models to address scenarios involving server–user collusion and partial user trust, respectively. By separating searchable content between data owners and authorized users within indexes, this avoided the search pattern leakage seen in Popa-Zeldovich’s model. A Follow algorithm was introduced to allow users to distribute tokens via public channels, enabling search permission delegation without interaction, solving the key distribution scalability issue present in the Popa-Zeldovich scheme. Niu et al. [52,53] combined PRE and SE to enable multi-keyword search, but their proposal lacked dynamic revocation, preventing patients from withdrawing previously granted access. Costa et al. [54] constructed encrypted indexes, allowing healthcare professionals to perform private keyword searches over patient data without decrypting it. Shao et al. [55] were the first to integrate Proxy Re-Encryption (PRE) with SE, enabling keyword-searchable ciphertext conversion, though their approach relied on a centralized cloud server, lacked access control, and was vulnerable to single-point failure. Ateniese et al. [56] designed a unidirectional PRE scheme resistant to collusion attacks but that did not support keyword search, thus failing to enable ciphertext retrieval. Li et al. [25] combined blockchain with SE, using B+ tree indexes and dynamic access control to enhance the security, efficiency, and flexibility of data sharing. Their solution used a consortium blockchain and IPFS for cloud-chain cooperation, balancing storage and security, while optimizing retrieval efficiency through B+ trees. The scheme of Trivedi et al. [26] used attribute tokens for multi-user authentication, but only supported single-keyword search and incurred high computational overhead. Li et al. [57] combined KP-ABE and CP-ABE for access control, though key management complexity increased significantly with the number of users. Lee et al. [35] improved decentralization and reduced reliance on TTP: KASE keys were generated directly by data owners, removing the need for TTP, and supporting efficient key management, enabling a single key to decrypt multiple files and mitigating the key explosion problem.
(2) With Blockchain Integration
Hu et al. [58] implemented decentralized privacy-preserving search on Ethereum, using smart contracts to manage keyword indexes. Yang [45] introduced DCC-SE, which utilized a consensus committee for more efficient key distribution and dynamic management, avoiding the high latency of smart contracts. Ali et al. [59] stored encrypted indexes on the blockchain and verified access rights, but their approach relied on Attribute-Based Encryption (ABE) and a trust value model, limiting patients’ control over their data. Iqbal et al. [60] used the BGV fully homomorphic encryption scheme to protect audio medical data and integrated blockchain for audit tracing, but their solution did not support multi-keyword search. Wang et al. [46] proposed a consortium blockchain-based medical data sharing scheme, combining Conditional Proxy Re-Encryption (CPRE) with Searchable Encryption (SE). They used keywords as re-encryption conditions to support keyword search and access control, but the scheme failed to address retrieval efficiency for large-scale data, due to the use of a globally ordered index, which led to high complexity. Feng et al. [47] designed a binary-search-based index structure, but in the face of massive data, the size of the balanced binary tree caused high search overhead. The scheme only supported static access control, though it enabled fine-grained permission management. Zhang et al. [42] combined Ciphertext-Policy Attribute-Based Keyword Search (CP-ABKS) with blockchain to support data auditing and integrity verification. However, it only supported single-keyword search and did not address key management efficiency. Li et al. [43] implemented symmetric searchable encryption on the blockchain, but the search results were imprecise and inefficient. Zhang et al. [61] leveraged blockchain to enable verifiability of the search process, but did not address access control in multi-institution data sharing scenarios. Niu et al. [29] optimized the index structure using polynomial equations to improve search efficiency and supported attribute-based access control. By integrating ABE with blockchain, they enabled cross-institution fine-grained access management and proposed a complete architecture combining ‘blockchain-based index storage + cloud-based ciphertext storage’, which reduced on-chain storage pressure.
Liu et al. [44] employed the KASE-CQ scheme, which leverages the DCDH (Decisional Co-Diffie-Hellman) assumption to demonstrate resistance against Inside Trapdoor Attacks (ITA). The core of this scheme lies in the trapdoor structure, which ensures that an adversary cannot recover from T2, thereby preventing derivation of the aggregate key. To enhance multi-keyword search efficiency, users submit a single aggregate trapdoor Tr = {T1,T2,T3}, where T3 denotes the set of keyword fields. The server directly evaluates the conjunctive expression without generating multiple trapdoors. The trapdoor size—comprising two group elements plus keyword field indices—and the search time are both independent of the number of keywords. Only one bilinear pairing computation is required during the testing phase, significantly improving efficiency. In the healthcare domain, data sharing is essential for delivering high-quality medical services. However, the sensitivity of medical data demands strong security and privacy protection. Blockchain-based searchable encryption technologies offer a promising solution to this challenge. For instance, Niu et al. [28] proposed a blockchain-based key aggregate searchable encryption scheme that is resilient to key leakage. This scheme stores key update records and ciphertext metadata on the blockchain to prevent unauthorized decryption in the event of key compromise. Moreover, it employs smart contracts to enable dynamic key management, thereby enhancing the security and efficiency of data sharing. Another example is the scheme developed by Costa et al. [54], who constructed an encrypted index that allows healthcare practitioners to perform private searches of patient data using encrypted keywords. This approach preserves patient privacy, while ensuring the accessibility of medical data. These pilot studies and implementation cases demonstrate the practical applicability of combining blockchain and searchable encryption technologies in healthcare data sharing. However, several challenges remain, including the computational overhead, storage requirements, and protection of user privacy. These issues call for further optimization and resolution in future research. Zhang et al. [48] proposed a searchable encryption scheme with an enhanced access control mechanism. The protocol unfolds through the following stages: (1) A trusted authorization authority initializes the system by generating and distributing public and private keys to both data owners and data users. (2) The data owner encrypts the data and outsources the ciphertext to the cloud server for secure storage. (3) When a data user intends to search for specific content, they generate a search token based on the query keywords and send a data access request, along with the token, to the cloud server. (4) Upon receiving the request, the data owner performs a trust evaluation of the requesting user. If the user is deemed trustworthy, the data owner generates a corresponding authorization trapdoor and forwards it to the cloud server. (5) The cloud server then executes the search over the encrypted index using the trapdoor and returns the matching results to the data user. To further enhance security, the scheme incorporates an Authorized Label Private Set Intersection (AL-PSI) protocol, which reduces leakage from Keyword Pattern Reveal Property (KPRP) to the more restrictive Whole Result Pattern (WRP); i.e., only the number of matched documents is revealed. The use of authorization trapdoors enforces owner-enforced access control, ensuring that only authorized users can generate valid search tokens. For multi-keyword search optimization, the protocol shifts the application of PSI from the initial stage of the search (as in LSE) to a later stage, thereby preserving the combined query capability of OXT. In this setting, the data owner encrypts the index entries (xtag) using the public key, and the data user generates a corresponding search token (XTAG). The AL-PSI protocol is then used to compute the intersection between the encrypted index and the search token, avoiding the need for per-keyword verification and significantly improving efficiency. These pilot studies and implementation cases demonstrate the practical applicability of combining blockchain and searchable encryption technologies in healthcare data sharing. However, several challenges remain, including computational overhead, storage requirements, and the protection of user privacy. These issues call for further optimization and resolution in future research.
4.2. Proxy Re-Encryption and Secure Data Sharing
Proxy re-encryption (PRE) plays a pivotal role in secure data sharing models. A typical architecture, as illustrated in Figure 4, involves four key entities: the Trusted third party, Data owner, Proxy server, and Data user. The Trusted third party acts as the trust anchor of the system, responsible for generating and securely distributing key pairs. It provides public keys to both data owners and data users, while securely managing the associated private keys. The Data owner uses their public key to encrypt sensitive data, producing an initial ciphertext that is then uploaded to the Proxy Server. Based on predefined access control policies, the Proxy server performs a proxy re-encryption operation on the ciphertext, transforming it into a re-encrypted ciphertext that is decryptable by the intended Data user. Finally, the Data user applies their private key to decrypt the re-encrypted ciphertext and securely access the original data. This approach enables efficient and fine-grained data sharing, while preserving security and control over access. A comparison of various proxy re-encryption schemes is presented in Table 4.
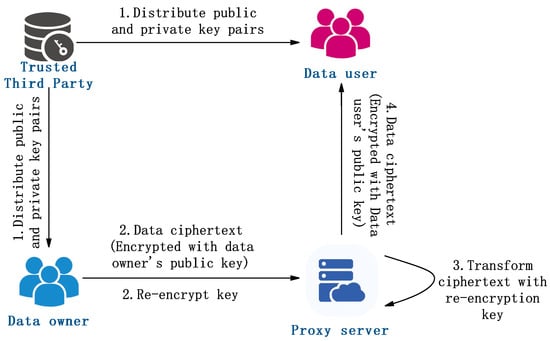
Figure 4.
Proxy re-encryption technology and data security sharing model.

Table 4.
Comparison of proxy re-encryption (PRE) schemes and blockchain integration.
(1) Identity-Based Proxy Re-Encryption (IBPRE)
Identity-Based Encryption (IBE) derives cryptographic keys directly from users’ identities. In 2007, Green and Ateniese [70] introduced the concept of identity-based proxy re-encryption. Since then, various PRE schemes with distinct security properties have been proposed for different application scenarios.
Wei et al. [27] proposed a Revocable-Storage IBE (RS-IBE) scheme that supports both forward and backward secrecy. The ciphertext update process in their design relies solely on public information, and the additional computational and storage overhead introduced by forward secrecy is upper bounded. However, Lee [71] identified correctness issues in Wei et al.’s RS-IBE scheme and presented corresponding improvements. To address fuzzy user data sharing in cloud computing environments, Meshram et al. [72] introduced a subtree-based forward-secure IBE scheme, achieving forward security for data contributors with relatively low computational costs.
In the domain of electronic healthcare, Sudarsono [73] proposed a secure data sharing scheme that integrates identity-based encryption (IBE) and digital signatures within electronic medical systems. The scheme adopts a hybrid security architecture combining IBE, BLS short signatures, and AES symmetric encryption. In this framework, the sender uses the receiver’s unique identity to perform IBE encryption on a temporary symmetric key , resulting in the encrypted key component . The health data M are then encrypted using to generate the ciphertext , and a BLS signature is applied to produce the authentication tag . The receiver (e.g., a physician) authenticates their identity with the electronic medical server to obtain the corresponding private key . After verifying the signature , the receiver decrypts to recover , and finally decrypts to retrieve the original medical data. This scheme ensures data confidentiality, integrity, and authenticity, and is particularly well suited for secure and fine-grained access control in privacy-sensitive healthcare data sharing scenarios. The scheme was verified to be computationally efficient across different devices, making it suitable for embedded and mobile platforms. Zhang et al. [62] developed an IBE-based authorized searchable encryption scheme for mobile cloud-assisted electronic health information systems. This scheme supports keyword search of encrypted data and delegated upload functionality. By using signature-based authorization certificates generated by doctors, a trusted assistant handles the uploading of encrypted data, ensuring secure sharing of diagnostic data, while alleviating the processing burden on medical professionals. In the context of the Internet of Things (IoT), Sun et al. [63] proposed a practical and efficient Revocable IBE (RIBE) scheme based on SM9 cryptography, tailored for IoT applications. Their scheme offers reduced storage and bandwidth overhead. Unal et al. [74] presented a secure and efficient IoT cloud encryption scheme based on Identity-Based Cryptography (IBC), named the Secure Cloud Storage System (SCSS). Aimed at ensuring data security in cloud storage and supporting forensic investigations, the SCSS employs Type-3 pairings in its SAKKE-IBE construction, achieving significant improvements in both security and efficiency compared to traditional Type-1 pairing-based IBE schemes.
(2) Certificateless Proxy Re-Encryption (CLPRE)
Sur et al. [75] extended proxy re-encryption (PRE) into the domain of certificateless public key cryptography (CLPKC) and introduced the concept of certificateless proxy re-encryption (CLPRE). In their model, each user constructs a private key by combining a self-selected secret value. Following Sur’s work, a variety of CLPRE schemes have emerged. Liu et al. [76] proposed a CLPRE scheme that is secure under the IND-CCA2 model, benefiting from the simplified certificate management inherent to certificateless public key encryption. Despite its advantages, the application of CLPRE has remained limited to public cloud environments. To address this, Eltayieb et al. [77] proposed a CLPRE scheme equipped with an encrypted reverse firewall. This added component resists data exfiltration attacks, prevents information leakage by trusted third parties, and protects against ciphertext forgery, thereby enhancing overall data security.
Hundera et al. [64] introduced a novel approach that integrates certificateless cryptography (CLC) with identity-based cryptography (IBC) to create a heterogeneous secure communication environment for vehicular networks. Their scheme enables vehicular nodes in a CLC setting, to avoid certificate and key escrow management issues, while allowing authorized users in the IBC setting to circumvent public key certificate management problems. The proposed solution demonstrates significant advantages in computational overhead, communication cost, and ciphertext size, making it particularly suitable for cloud-assisted vehicular network environments. Feng et al. [65] proposed a certificateless threshold proxy re-encryption scheme supporting keyword search for industrial data sharing, based on a multi-cloud and multi-chain collaborative storage model. The scheme builds a cooperative data storage and sharing architecture that combines the concept of digital envelopes: industrial data ciphertext is stored in private enterprise clouds, while ciphertext metadata are categorized and stored across different blockchains, achieving effective data isolation. Their innovative certificateless threshold PRE scheme addresses the challenges of ciphertext retrieval and enhances system efficiency and correctness.
In practical applications, NuCypher, a decentralized key management system, launched its public testnet in 2019 and released the test results at the 2020 World Blockchain Conference. More than 2000 nodes participated in the testnet, with over 350,000 ETH staked, spanning regions across North America, Europe, and Asia. Its core technology, the Umbral protocol, enables ciphertext transformation through proxy re-encryption, supporting use cases such as medical data sharing and access control for IoT devices. For instance, in healthcare scenarios, patients can dynamically authorize doctors to access encrypted medical records via smart contracts, while token-based incentives (NKMS) ensure compliant node behavior. Test reports indicated that the network achieved a throughput of up to 200 transactions per second with latency kept under 500 ms, meeting the requirements of real-time applications [78].
(3) Attribute-Based Proxy Re-Encryption (ABPRE)
Attribute-based encryption (ABE) is a critical technique for enhancing the security of data sharing. Attribute-based proxy re-encryption (ABPRE) enables data owners to encrypt data under a set of attributes, ensuring that only users possessing the corresponding attributes can decrypt the content. This mechanism provides fine-grained access control and robust data protection. To secure cloud-stored data, Liang et al. [79] combined Key-Policy ABE (KP-ABE) with proxy re-encryption. However, due to the use of a lazy re-encryption strategy, their protocol exhibited certain security vulnerabilities. To address privacy and energy efficiency concerns in mobile social networks, He et al. [80] proposed an efficient and privacy-preserving content sharing scheme. While the scheme supports secure and fine-grained data sharing, it lacks mechanisms for secure data propagation.
In the context of cloud computing, Ge et al. [66] introduced a Verifiable and Fair Attribute-Based Proxy Re-Encryption (VF-ABPRE) scheme, and formally defined the VF-ABPRE model. This model considers both the verifiability and fairness of attribute-based encrypted data sharing in cloud environments. In this scheme, data recipients can verify the correctness of re-encrypted ciphertexts, while servers are protected from malicious accusations. For cross-blockchain data sharing, Duan et al. [67] proposed a multi-authority attribute-based proxy re-encryption scheme. This approach allows data owners to flexibly update cross-chain access policies without re-encrypting data multiple times, thereby improving the efficiency and flexibility of data sharing. By leveraging relay-chain technology, the scheme constructs a trusted and decentralized sharing environment. The use of smart contracts ensures fair profit distribution, while hybrid encryption and decentralized storage platforms significantly alleviate the storage burden on blockchains.
(4) Key-Aggregate Proxy Re-Encryption (KAPRE)
In their seminal work [81], Chen et al. were the first to integrate key-aggregate methods into proxy re-encryption schemes, thereby formulating the concept of Key-Aggregate Proxy Re-Encryption (KAPRE). To address the issues of high computational overhead, complex key management, and vulnerability to trapdoor attacks in existing searchable encryption schemes, Wang et al. [24] proposed an Efficient and Verifiable Keyword-Aggregate Searchable Encryption (EVKAKSE) scheme. In this design, the data owner first generates a public key and a master secret key , and constructs a secure index . During file encryption, a symmetric key and a keyword ciphertext are generated for each file, while a verification tag is stored on an auxiliary server. To allow access to a file set S, the data owner assigns the user a single aggregate key . The user then generates a single trapdoor and submits it to the cloud. The cloud, assisted by an auxiliary server that provides parameters such as , verifies the correctness of the keyword ciphertext via the pairing equation , and returns the encrypted files. Finally, the user computes to decrypt the files and compares the received verification tag with the stored to ensure data integrity. This scheme effectively improves the efficiency and security of searchable encryption, while enabling verifiable access control in encrypted cloud data sharing. Subsequently, Pareek et al. [30] also employed key-aggregate proxy re-encryption for secure cloud data sharing. In their scheme, data owners encrypt data using public keys and generate fixed-size re-encryption keys, allowing for the re-encryption of multiple ciphertexts for a single user. This approach significantly reduces the storage and communication overheads associated with re-encryption keys.
Although the KAPRE framework demonstrates significant advantages in enhancing data confidentiality and computational efficiency in cloud environments, it faces several limitations that constrain its practicality and security. Firstly, the re-encryption process demands a larger number of keys. Secondly, KAPRE is inherently non-interactive, as re-encryption keys are generated solely by the delegator, without requiring any involvement from the delegatee. Lastly, most existing KAPRE schemes exhibit limited resistance to collusion attacks, posing further security concerns.
(5) Broadcast Proxy Re-Encryption (BPRE)
Broadcast Proxy Re-Encryption (BPRE) is one of the most effective approaches for ensuring secure data sharing, and its conceptual foundation was inspired by broadcast encryption, originally introduced by Fiat and Naor in [82]. In a BPRE framework, a data owner can perform a single encryption operation to encrypt data and disseminate it to multiple recipients. Subsequently, a proxy can re-encrypt the data for each recipient individually, without having to know the identities of the recipients.
In the context of cloud-based email systems, Xu et al. [68] introduced the concept of Conditional Identity-Based Broadcast Proxy Re-Encryption (CIBPRE) and proposed a corresponding scheme. Compared to traditional methods, their solution demonstrates advantages in communication efficiency and user experience. However, its applicability is limited to the domain of cloud email systems, restricting its broader deployment.
To address data-sharing scenarios more broadly, Sun et al. [69] proposed the concept of Proxy Broadcast Re-Encryption (PBRE) and developed a corresponding scheme. They proved its CCA security under the decisional n-BDHE assumption in the random oracle model. Notably, this scheme exhibits collusion resistance, enabling the proxy to transform the delegator’s ciphertext into ciphertexts for a group of recipients. Experimental results indicated that the re-encryption time cost of their scheme outperformed several existing methods.
4.3. Attribute-Based Encryption and Secure Data Sharing
Attribute-Based Encryption (ABE) is a form of public key encryption that enables decryption rights to be defined through sets of attributes or access policies. ABE-based data sharing schemes associate data access permissions with user attributes, offering a flexible and efficient solution for secure data distribution. The two main security models include Ciphertext-Policy ABE (CP-ABE) and Key-Policy ABE (KP-ABE). These models play significant roles across various application domains, ensuring both data security and privacy preservation in shared environments. The fundamental difference between Ciphertext-Policy Attribute-Based Encryption (CP-ABE) and Key-Policy Attribute-Based Encryption (KP-ABE) lies in the embedding position of the access policy, the authority over access control, and the directionality of the operational logic. In CP-ABE, the access policy, which may include complex logical expressions such as (Doctor AND Cardiology) OR Director, is embedded directly into the ciphertext by the data owner, who thus retains full control over the definition and enforcement of access rules. The user’s private key is associated with a set of attributes, and decryption is only possible if these attributes satisfy the policy specified in the ciphertext. This data-centric model enables fine-grained and dynamic access control, making it suitable for use cases like governmental hierarchical document sharing. However, it poses the risk of semantic leakage, as access policies in plaintext may reveal sensitive business logic (e.g., indicating that ‘directors can access this data’). Moreover, the computational burden of policy evaluation is shifted to the user side, potentially leading to higher decryption latency on resource-constrained devices such as mobile terminals. In contrast, KP-ABE embeds the access policy directly into the private key, such as (Position = Manager AND Department = R&D) OR Clearance ≥ 5, which is managed by a central authority. The ciphertext in this case only contains a lightweight set of attributes (e.g., {Department: R&D, Classification: High}). Successful decryption requires that the attributes in the ciphertext satisfy the policy hardcoded into the key. This authority-centric approach is particularly suitable for role-based access control in enterprise environments, where permissions are predefined and centrally distributed (e.g., a policy that ‘all R&D managers can access highly classified files’). KP-ABE supports efficient key management, but its flexibility is limited: once a policy has been embedded in the private key, the addition of new attributes or roles typically requires re-issuing keys or reconfiguring system-wide strategies. In summary, both CP-ABE and KP-ABE offer fine-grained access control, but with distinct trade-offs. CP-ABE favors dynamic, data owner-driven policy specification, at the cost of higher user-end computation and possible policy exposure, while KP-ABE prioritizes centralized policy enforcement and efficiency but lacks policy adaptability. The choice between the two should be informed by the rate of evolution of access requirements and the computational constraints of user devices in the target application scenario. A summary of attribute-based encryption techniques is presented in Table 5.

Table 5.
Table of attribute-based encryption (ABE) techniques.
(1) CP-ABE and Data Sharing
The application of Ciphertext-Policy Attribute-Based Encryption (CP-ABE) in the data security sharing model is illustrated in Figure 5, involving four key entities: the Trusted third party, Data owner, Cloud server, and Data user. Initially, during the system setup phase, the Trusted third party generates and distributes the necessary system parameters to the data owner (used for encryption), and issues private keys bound to attribute sets to authorized data users—these keys and associated parameters must be kept confidential. Subsequently, the data owner defines an access policy (e.g., (A AND B) OR C) and uses the system parameters to encrypt the plaintext data accordingly, embedding the policy directly into the resulting ciphertext. The ciphertext is then outsourced to the cloud server for storage. When a data user requests access to the encrypted data, the system performs policy verification by comparing the user’s embedded attributes (contained in their private key) against the access structure encoded in the ciphertext. If the attribute set satisfies the policy, the user is able to successfully decrypt and access the data. Otherwise, the access attempt is denied. This model enables fine-grained access control and significantly enhances both the security and flexibility of data sharing, especially in environments where sensitive information must be selectively disclosed based on user roles or qualifications.

Figure 5.
CP-ABE technology and data security sharing model.
Ciphertext-Policy Attribute-Based Encryption (CP-ABE) is a type of attribute-based encryption technique initially proposed by Bethencourt et al. in 2007 [90]. In this model, data owners define access policies and embed them into the ciphertext, allowing users to decrypt the ciphertext only if their attributes satisfy the specified policy. Yang et al. [91] proposed an efficient data access control scheme for multi-authority cloud storage systems, constructing a novel multi-authority CP-ABE framework, in which the main decryption operations are outsourced to the server. Distinct from works such as [83,84,92], Liu et al. [93] introduced a new CP-ABE model with partially hidden access structures. This model extends the expressiveness of the access structures, enabling the handling of any Linear Secret Sharing Scheme (LSSS)-representable structures and offering greater flexibility and expressiveness. Zhang et al. [94] effectively addressed data security and user privacy issues in s-health applications by introducing the PASH framework. Leveraging the decentralized nature of blockchain, Wang et al. [95] proposed a secure cloud storage access control framework based on blockchain technology. By incorporating Ethereum smart contracts, they transformed traditional CP-ABE algorithms and established distributed access control between data owner nodes and data user nodes, thereby mitigating the risk of single points of failure. Wei et al. [96] presented a blockchain-based data sharing architecture for the Internet of Things (IoT), building a multi-centric trusted environment that eliminates data silos in IoT systems and facilitates collaboration among heterogeneous IoT platforms. Qin et al. [97] proposed a blockchain-based multi-authority access control scheme, where data access logs are recorded on the blockchain, addressing issues such as single-point failures and high computational and communication costs on the user side. Wang et al. [88] developed a fine-grained electronic health record sharing scheme based on the CP-ABE model, embedding access policies into the blockchain to ensure the integrity of query results during medical service delivery. To prevent Economic Denial of Sustainability (EDoS) attacks, Zhang et al. [89] designed a fine-grained access control mechanism using the CP-ABE model. By validating whether data owners possess legitimate access rights through blockchain verification, the scheme effectively defends against collusion between semi-trusted cloud service providers and malicious users. In the context of the metaverse, Zhang et al. [98] integrated non-interactive zero-knowledge proofs into CP-ABE, achieving fine-grained access control, while ensuring data confidentiality during user information exchanges.
(2) KP-ABE and Data Sharing
The application of Key-Policy Attribute-Based Encryption (KP-ABE) in the data security sharing model is illustrated in Figure 6, involving four critical entities: the Trusted third party, Data owner, Cloud server, and Data user. In this framework, the Trusted third party—often referred to as the Key Generation Center—is responsible for generating the global system parameters and the master secret key. The system parameters are securely distributed to the data owner for data encryption, while the private key issued to each data user is embedded within an access structure, representing the user’s decryption policy. The data owner encrypts plaintext data by associating it with a set of descriptive attributes (e.g., ‘Type: Research Report’, ‘Confidentiality: High’) using the system parameters, and uploads the resulting ciphertext to the cloud server. Notably, the cloud server serves solely as a storage provider, without engaging in access control decisions or key management, thereby maintaining a separation of duties and reducing trust assumptions. When a data user retrieves ciphertext from the cloud, they attempt to decrypt it using their attribute-based private key. Decryption is successful only if the attribute set embedded in the ciphertext satisfies the access structure encoded within the user’s key (e.g., ‘Department = R&D AND Role = Supervisor’). Otherwise, the decryption attempt fails, and access to the data is denied. This model achieves fine-grained and flexible access control by embedding access policies directly into the users’ private keys, thus allowing centralized management of access privileges, while ensuring that sensitive data remain confidential and securely managed within the cloud environment.
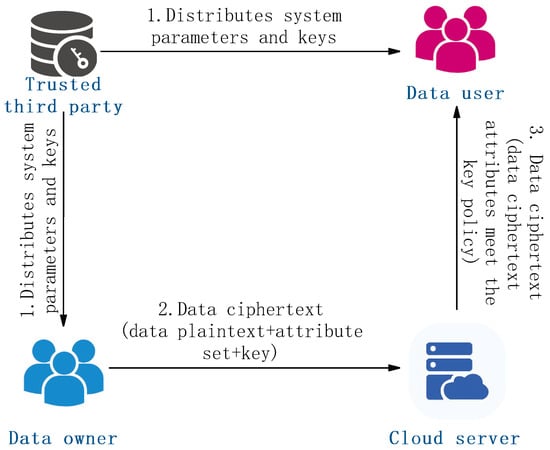
Figure 6.
KP-ABE technology and data security sharing model.
In 2006, Goyal et al. [99] introduced KP-ABE (Key-Policy Attribute-Based Encryption), in which the ciphertext is associated with a set of attributes, and the user’s secret key embeds the access policy. A user can decrypt a message only if the attribute set satisfies the access policy. The access policy is typically represented as an access tree, where the leaf nodes are labeled with attributes, and the internal nodes are threshold gates of the form , meaning that at least m out of n attributes must be satisfied for decryption to succeed. In 2017, Ma et al. [85] proposed a directly revocable and verifiable large-universe KP-ABE scheme, which supports a large attribute universe, without requiring enumeration during the setup phase. In 2020, Ye et al. [86] introduced a traceable unbounded KP-ABE scheme that maintained a fixed ciphertext size, enhancing scalability and accountability. In 2021, Ji et al. [100] presented an efficient construction method for CP-ABE based on the SM9 standard, enabling SM9 to support fine-grained access control and better serve scheduling and control in cloud environments. Building upon this, in 2024, Liu et al. [87] developed two novel KP-ABE schemes based on SM9. The first scheme, SM9-S.ABE, is optimized for small attribute domains, while the second, SM9-L.ABE, targets large attribute domains. Both schemes adopt a secret key and ciphertext structure similar to the original SM9 identity-based encryption algorithm, allowing seamless integration into SM9-based information systems, such as cloud servers and blockchain platforms.
4.4. Key Agreement and Secure Data Sharing
Key agreement refers to the process by which communicating parties (typically two or more) jointly compute and ultimately derive a shared session key through a series of interactive protocols, without relying on any pre-distributed secret keys. Each party uses their own private parameters (such as private keys or random numbers) to participate in this process. In 1976, Diffie and Hellman proposed the first public key agreement protocol [101], which addressed the key distribution problem and enabled two parties to exchange public information over an insecure channel, while establishing a shared secret key. This work laid the foundation for public-key cryptography. However, the original protocol lacked authentication mechanisms, making it vulnerable to man-in-the-middle attacks, and it did not support multi-user scenarios. Subsequently, to enhance the efficiency and security of group key agreement protocols, researchers have developed various schemes based on tree structures, identity-based cryptography, and lattice-based cryptography. In 2004, Amir et al. [102] introduced the Tree-based Group Diffie–Hellman (TGDH) protocol, which was the first to leverage tree structures to optimize communication and computation in group key agreement. Since then, group key agreement protocols have continued to evolve. In 2020, Luo et al. [103] proposed a cross-domain certificate-authenticated group key agreement (GKA) protocol tailored for 5G network slicing, enabling dynamic group membership management. Rawat et al. [104] proposed the GKAP algorithm, which combines tree structures with elliptic curve cryptography. By employing a divide-and-conquer strategy, the group is partitioned into smaller subgroups that form a hierarchical tree structure. The algorithm is resilient against passive attacks, collusion attacks, forward secrecy, backward secrecy, and man-in-the-middle attacks. An example of the group key agreement process is illustrated in Figure 7. In this example, a group of size eight is divided using the divide-and-conquer strategy. Subsequently, the Elliptic Curve Diffie–Hellman (ECDH) protocol is applied to the leaf nodes or participants , and of the tree. Participants , and sequentially share their public keys , , , and with , and , respectively. Likewise, participants , and share their public keys , , , and with , and , respectively. Then, the subgroups of size 2 (i.e., tree nodes with level ), such as , , , and , each compute a shared group key based on their corresponding scalar multiplications: , , , and , respectively. These resulting group keys correspond to common generator points represented as , , , and . In 2021, Gan et al. [105] proposed an asymmetric group key agreement protocol based on attribute thresholds. In this scheme, users can participate in mutual authentication and key negotiation with the key generation center by satisfying a sufficient number of attributes, without disclosing personal information. Chen et al. [106] introduced a group authentication and key agreement scheme for medical Internet of Things (IoMT) applications, leveraging extended chaotic maps to address challenges related to energy consumption, privacy, and security. In 2022, Braeken et al. [107] proposed a single-round lightweight elliptic curve-based alternative scheme, where group members achieve self-authentication through QuVanstone certificates. Wang et al. [108] presented a two-round dynamic authenticated group key agreement protocol based on the Learning With Errors (LWE) problem and proved its security under the standard model. In 2023, Zhang et al. [109] proposed a single-round dynamic authenticated asymmetric group key agreement protocol with sender non-repudiation and privacy preservation. The protocol was shown to resist chosen ciphertext attacks (CCA) under the hardness assumptions of the Computational Diffie–Hellman (CDH) and the k-bilinear Diffie–Hellman Exponent (BDHE) problems. In the same year, Zhang et al. [110] also introduced a Threshold Authentication Group Key Agreement (TAGKA) protocol, which effectively addresses the problem of group key recovery after member disconnection. Yang et al. [111] proposed a dynamic contributory group key agreement protocol (GKA-SS) based on short signatures. The protocol utilizes bilinear pairings to support the signing and verification processes, and provides rigorous security proofs ensuring resistance against both active and passive attacks. In 2024, Cui et al. [112] designed a dynamic group authentication and key agreement protocol for C-V2X environments (V2X-GKA), which integrates Elliptic Curve Discrete Logarithm (ECDL) and Decisional Bilinear Diffie–Hellman (DBDH) assumptions. This protocol effectively mitigates the risks of certificate forgery and key compromise, while enabling dynamic member management and secure key updates. Cao et al. [113] proposed a conditionally private and efficient dynamic group key agreement protocol (SC-AGKA) based on a self-certified encryption system, aiming to address security issues in Vehicular Ad Hoc Networks (VANETs).
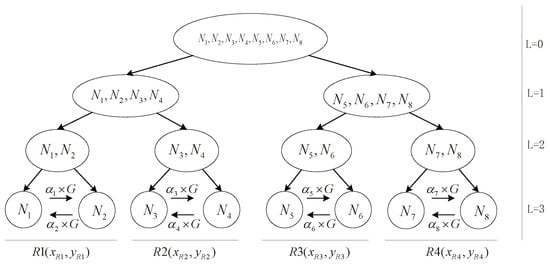
Figure 7.
Group key agreement.
Meanwhile, blockchain-based group key agreement protocols have also seen significant advancements. Due to its decentralized nature, immutability, and transparency, blockchain technology has been widely adopted to enhance the security and trustworthiness of key agreement processes. In 2020, Zhang et al. [114] proposed a blockchain-based asymmetric group key agreement protocol that protects user privacy through anonymous authentication and optimizes both computational and communication overheads. In the same year, Xu et al. [115] introduced a blockchain-based identity authentication and dynamic group key agreement scheme, which improves efficiency by simplifying the authentication process. In 2021, Chen et al. [116] introduced a novel entity called the ‘device manager’ and proposed a blockchain-based authenticated group key agreement protocol to bridge IoT devices with blockchain networks. In 2022, Naresh et al. [117] proposed a blockchain-based two-party elliptic curve Diffie–Hellman protocol, while Wang et al. [118] designed a pairing-free authenticated group key agreement scheme based on blockchain, tailored for smart grid environments, with improved computational efficiency and security. In 2023, Xu et al. [119] proposed an anonymous authentication dynamic group key agreement scheme based on blockchain and a token mechanism, significantly reducing computational and transmission costs. In the same year, Chhikara et al. [120] proposed a novel blockchain-based group key agreement protocol that employs roadside units (RSUs) as semi-trusted entities to reduce latency and operational cost. In 2024, Pérez-García et al. [121] introduced a group communication key management protocol designed for IoT environments. This protocol leverages distributed blockchain infrastructure and smart contract technology to ensure anonymity and automated key revocation. During the key agreement phase, the service provider (SP) distributes keying material to group members via the blockchain, enabling each member to locally derive the group key. Initially, each node receives a pseudonym and corresponding certificate generated by the service provider to preserve anonymity within the group. The service provider then records the keying material, including member-specific key shares, onto the blockchain. Upon retrieving this information, each group member can locally compute the group key and verify its validity. A comparison of the relevant literature is presented in Table 6.

Table 6.
Comparison table of group key distribution methods.
4.5. Key Distribution and Secure Data Sharing
Key distribution refers to the process in communication systems whereby session keys or symmetric keys are securely delivered to communicating parties via one or more trusted entities (such as a Key Distribution Center (KDC) or a Certificate Authority (CA)). In this process, the KDC typically shares a long-term key with each communicating party in advance, which is then used to encrypt, sign, or authenticate the newly distributed session key to ensure that only legitimate entities can obtain and use the key. In 2020, Yıldız et al. [122] proposed a lightweight group authentication and key distribution protocol that integrates Physical Unclonable Functions (PUFs), factorial trees, and the Chinese Remainder Theorem (CRT). The PUFs enable lightweight identity authentication and key distribution for group members, while the factorial tree and CRT effectively reduce node storage overhead and the number of communication messages during key updates. In the same year, Kumar et al. [123] proposed a more efficient centralized group key distribution protocol that significantly reduces the computational burden on the key server during the key update phase and balances the computational cost among member nodes during key recovery. They further extended this work by introducing a cluster-tree-based enhanced CGKD protocol, which effectively addresses the scalability issues caused by dynamic group membership changes. In 2021, Harn et al. [124] introduced a novel group key distribution scheme whose underlying protocol relies solely on logical XOR operations, thereby greatly simplifying the computational complexity of protocol implementation. In 2022, Hougaard et al. [125] were the first to design a balanced-tree group key exchange protocol based on the supersingular isogeny Diffie–Hellman (SIDH) scheme, achieving linear communication and storage complexity. That same year, Taurshia et al. [126] proposed a group key management scheme for resource-constrained IoT devices, utilizing a Software-Defined Networking (SDN)-assisted trusted key management server as the central authority, improving the practicality of group key management in IoT environments. Also in 2022, Harn et al. [127] introduced the first lightweight authenticated group key distribution scheme that involves only logical operations and is compatible with various authenticated pairwise key distribution mechanisms. In parallel, Gebremichael et al. [128] proposed a novel one-way function based on lattice cryptography, leveraging well-designed lattice trapdoors for inversion. By coupling multiple private keys into a single public key for group message encryption, the scheme demonstrates potential quantum resistance. In 2023, Luo et al. [129] proposed an information-theoretically secure (ITS) group authentication scheme that reduces key consumption in quantum key distribution (QKD) networks. Through the collaboration of multiple QKD nodes, group authentication tasks can be completed with significantly reduced key usage. In 2024, Cheng et al. [130] introduced an anonymous identity authentication and group key distribution scheme based on quantum random numbers. In this scheme, vehicles generate anonymous certificates by combining quantum randomness with parameters provided by a trusted authority (TA), and mutual authentication with roadside units (RSUs) is performed via zero-knowledge proofs, preserving vehicle identity privacy. For key distribution, a joint key generation mechanism is employed, in which the TA and RSUs collaboratively generate the group key. Specifically, the TA first generates a parameter using a quantum random number generator and encrypts it with a pre-distributed quantum key to ensure secure transmission of keying materials. The RSU computes another key parameter by processing the anonymous credentials of authenticated vehicles. These parameters are then broadcast to group members, who compute the final group session key locally using the received and the TA-sent . This method enhances key distribution efficiency, reduces computational and communication overheads, and guarantees both forward and backward secrecy during key updates. In the same year, Al-Mohammed et al. [131] addressed the security needs of constrained IoT devices in high-speed train (HST) environments by proposing a quantum key distribution solution tailored for high-speed space transmission systems. Their approach leverages free-space optical (FSO) communication to establish a high-speed, quantum-resistant data channel.
In the field of blockchain-based group key distribution protocols, several advances have been made to address challenges in dynamic and resource-constrained environments. In 2019, Li et al. [132] proposed a blockchain-based mutual recovery group key distribution scheme for unmanned aerial ad hoc networks (UAANETs), aimed at addressing the problem of the group key loss caused by unstable wireless channels and highly dynamic network topologies. The scheme utilizes a private blockchain maintained by the ground control station (GCS) to record and manage group key broadcasts. Through the longest-chain mechanism, nodes can effectively recover lost group keys from neighboring nodes. In 2022, Heo et al. [133] proposed a hierarchical blockchain-based group and subgroup key management scheme for urban computing scenarios. The upper-layer blockchain is used by unmanned aerial vehicles (UAVs) to monitor and record the mobility and density of IoT nodes, while the lower-layer blockchain, maintained by base stations (BSS), is responsible for tracking the mobility information of grouped IoT nodes. In 2023, Shawky et al. [134] introduced a key-based group signature method to meet the security and privacy requirements of vehicular ad hoc networks (VANETs). In the same year, Al-Mohammed et al. [135] implemented an Asynchronous Ratcheting Tree (ART) protocol based on blockchain. This protocol leverages smart contracts for distributed certificate creation and incorporates a reputation mechanism to address the heterogeneity of IoT devices in terms of resource capabilities.
4.6. Incentive Mechanisms and Secure Data Sharing
Figure 8 illustrates data sharing based on a third-party platform (e.g., cloud server). Typically, data users publish their data requests on a cloud server, which then recruits data owners to share their data. The cloud server verifies the data uploaded by data owners and, upon validation, forwards it to the data users. After receiving the data, the data users reward both the cloud server and the data owners accordingly. In data sharing models, the data owner serves as the principal rights holder of the data asset, possessing full ownership over the data. The cloud server acts as an intermediary for data transactions, responsible for collecting, storing, and auditing the data uploaded by the data owner. The data user represents the ultimate consumer of the data, employing technical means to extract the latent value of the data and thereby fully realize its potential worth. From a game-theoretic perspective, all parties may act dishonestly in pursuit of maximizing their own interests.
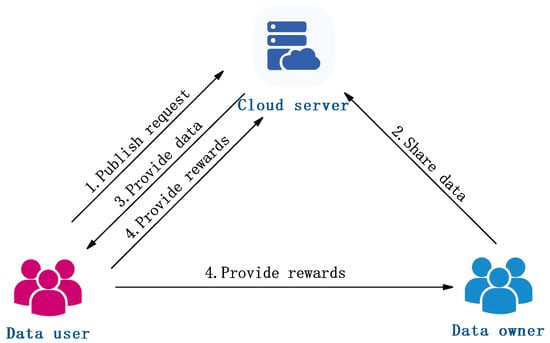
Figure 8.
Incentive mechanism and data security sharing model.
In constructing a sustainable data sharing ecosystem, the Shapley value, Stackelberg game, auction theory, contract theory, and evolutionary game models provide theoretical support from different perspectives, including fairness, incentive mechanism design, resource allocation efficiency, incentive compatibility, and dynamic adaptability. Specifically, the Shapley value model focuses on fair revenue distribution based on marginal contributions within a cooperative game framework, thereby fostering trust and sustained collaboration among participants. The Stackelberg game, through its leader–follower decision structure, effectively addresses information asymmetry and conflicts of interest, enabling strategic guidance and incentive constraints; it is particularly suitable for platform-driven data sharing mechanism design. Auction theory emphasizes efficient resource allocation and price discovery through bidding mechanisms, enhancing the economic efficiency of the system. Contract theory concerns itself with incentive compatibility and constraint mechanisms to resolve multi-party incentive coordination problems under information asymmetry. Evolutionary game models introduce temporal dynamics and bounded rationality to characterize the adaptive evolution of participants’ strategies in response to environmental feedback, thus better reflecting the behavioral changes of users and the stability of the ecosystem in real-world systems. Table 7 summarizes the game-theoretic models relevant to data sharing, while Table 8 presents a comparative analysis of these models.

Table 7.
Game-theoretic models in data sharing.

Table 8.
Comparison of game-theoretic models in data sharing.
(1) Without Blockchain Integration
Cai et al. [136] employed the Shapley value in wireless mobile ad hoc networks to promote cooperative behavior and designed an incentive mechanism based on individual contributions to motivate service providers. Ali et al. [144] examined online data sharing in social networks from a game-theoretic standpoint, demonstrating that when blacklisting is used as a trigger strategy, sharing conditions tend to stabilize. Kantarcioglu et al. [145] proposed a game-theoretic mechanism to incentivize truthful data sharing in distributed data mining. Yassine et al. [146] introduced a game-theoretic model to balance the benefits of data utilization and individual privacy in deregulated smart grids. Kamhoua et al. [147] applied a game-theoretic approach (a zero-sum Markov game model) to help online social network (OSN) users determine optimal data sharing strategies. Xiao et al. [148] proposed a game-theoretic method for data sharing in vehicular ad hoc networks (VANETs), where the platform’s payment strategy is guided by reinforcement learning. Tosh et al. [137] developed an evolutionary game-theoretic framework to study the economic implications of cybersecurity information sharing and its incentives, aiming to foster inter-organizational threat intelligence sharing. Lu et al. [138] adopted contract theory to model incentive mechanisms for cooperative spectrum sharing in cognitive IoT networks under OFDM, especially under conditions of incomplete information in real-world scenarios. An et al. [149] combined network Data Envelopment Analysis (DEA) with the Shapley value method to explore resource sharing and revenue allocation in a three-stage system. In [150], two social-aware incentive mechanisms—a one-hop-based social-aware incentive mechanism (OSIM) and a relay-based social-aware incentive mechanism (RSIM)—were proposed to address resource sharing issues in the Industrial Internet of Things (IIoT) that are constrained by social and local factors. Yi et al. [151] analyzed and modeled a novel information diffusion process driven by service incentives, describing the dynamic evolution of device interactions in IIoT. This model aims to address the challenge of information dissemination in industrial IoT applications when diverse service demands require incentive-driven communication. To facilitate data transactions and achieve a fair evaluation of data value, while balancing the interests of multiple stakeholders, Zhu et al. [139] proposed a data trading approach that integrates a data valuation mechanism with a three-stage Stackelberg game. This method aims to guide the strategic choices of all participants and optimize their utilities through game-theoretic modeling. Yu et al. [140] introduced a tripartite incentive mechanism incorporating social relationships, which models the interactions among data requesters, service providers, and mobile users using a three-stage Stackelberg game. The approach comprehensively considers data quality, reputation, and social utility to better align incentives.
(2) Blockchain-Based Approach
Blockchain-based data sharing typically involves data users, data owners, the blockchain network, and smart contracts. Data users publish data requests on the blockchain network, while data owners provide the requested data, which data users can then access. Transaction records are immutably stored on the blockchain. Once the data have been received by the data users, the data owners are rewarded accordingly. The blockchain ensures the security of the model-sharing process, enables the identification of malicious participants, and protects the overall quality of the model. Smart contracts guarantee fair benefit distribution through automatic execution. Chen et al. [141] proposed a quality-driven auction-based incentive mechanism built on a consortium blockchain, to encourage user participation in data collection and sharing. Xuan et al. [152] introduced a blockchain smart-contract-based data sharing incentive model based on evolutionary game theory to address the issue of low user participation during data sharing. The model dynamically adjusts incentives and participation costs to maintain user engagement, although its incentive dimensions are relatively limited. Shen et al. [142] developed a data sharing model integrating blockchain and the Shapley value involving three types of participants, aiming to ensure data sharing is secure, trustworthy, and fairly incentivized. Wang et al. [153] proposed a new blockchain-based federated learning data sharing framework and an incentive mechanism based on reputation scores and the Shapley value to improve the sustainability of the federated learning system and ensure fair incentives for trusted participation and data sharing. Chen et al. [154] introduced a dynamic incentive model for federated learning (DIM-DS) based on smart contracts and evolutionary game theory. The model incorporates both reputation and monetary incentives by introducing a cryptocurrency called ‘Reputation Coin’, and analyzes the stability of user strategies using evolutionary game theory. Smart contracts are used to dynamically adjust user rewards on the blockchain, promoting frequent and stable user participation and improving the accuracy of federated learning models. Liu et al. [155] proposed a data sharing solution that integrates federated learning and blockchain to address endpoint heterogeneity and limited resources. A game-based two-stage incentive mechanism is incorporated to address privacy concerns and encourage broader participation. However, this scheme lacks consideration of complex real-world scenarios, suggesting the need for further refinement of incentive models. Li et al. [143] proposed a novel peer-to-peer electronic medical record (EMR) data management and transaction system based on consortium blockchain technology. To balance the supply and demand of EMR data, a Stackelberg pricing model was developed to evaluate the interaction between EMR data owners and consumers. Zhang et al. [156] constructed a multi-stage game theory model to investigate the interaction between blockchain adoption and information-sharing strategies, demonstrating that blockchain adoption can alleviate the bilateral marginalization effect and conditionally improve product quality. However, the study lacked effective simulation of the analytical process. Gan et al. [157] proposed a healthcare blockchain data sharing method based on asynchronous federated learning. To analyze the conflicts of interest among publishing nodes, committee nodes, and participating nodes, the study introduced a tripartite evolutionary game model, offering a theoretical framework that promotes sustainable data sharing.
5. Conclusions and Outlook
This paper described technical solutions for secure data sharing from four perspectives: proxy re-encryption, searchable encryption, key agreement and distribution, and attribute-based encryption. On the one hand, Attribute-Based Encryption (ABE) faces scalability challenges in large-scale scenarios. Future research may consider integrating ABE with blockchain technology to design decentralized attribute management and authorization mechanisms, thereby reducing reliance on centralized trust and improving the efficiency of key updates. On the other hand, Searchable Encryption (SE) lacks efficient revocation mechanisms in dynamic environments. A promising direction is to combine proxy re-encryption with revocable access control, enabling dynamic updates of ciphertext indexes and synchronized revocation of user permissions.
According to current domestic and international research developments, secure data sharing has attracted widespread attention from scholars around the world. Each of these four technologies has its own characteristics and is suitable for different secure data sharing scenarios, as shown in Table 9. To address the conflicts and contradictions between data privacy protection and data security, this paper also provided a detailed review of related literature based on game theory. By leveraging game-theoretic approaches, all parties can reach an equilibrium state during the process of interaction. This equilibrium ensures that, while each party pursues their own interests, they does not harm those of others, thereby enabling stable and sustainable data sharing.

Table 9.
Comparison of secure data sharing technologies.
However, modern encryption and decryption algorithms mainly rely on computational complexity. This high computational complexity ensures that eavesdroppers, without access to the encryption key, cannot feasibly perform the extensive calculations required to break the encryption within a limited timeframe, thus ensuring data security. At the same time, cryptographic keys must be updated regularly. As computational power continues to increase, traditional public–private key encryption methods based on large-number factorization are becoming less viable. In contrast, elliptic curve algorithms based on the discrete logarithm problem offer better computational efficiency. Nevertheless, with the advent of quantum computers, even these conventional encryption methods face significant security challenges.
Quantum Key Distribution (QKD) is based on fundamental principles of quantum mechanics—specifically, Heisenberg’s uncertainty principle and the no-cloning theorem. Unlike traditional encryption methods, QKD does not rely on assumptions about computational complexity and can provide users with unconditionally secure keys. This ensures the secure transmission of private information and effectively resists attacks by quantum computers. In Quantum Key Distribution (QKD), a secure quantum key is shared between the sender (Alice) and the receiver (Bob), following the process illustrated in Figure 9. Alice and Bob transmit quantum states via a quantum channel, while simultaneously using a public classical channel to compare measurement bases and auxiliary information. As a result, both parties securely obtain the same shared key, which is stored in their respective key management devices. If an eavesdropper (Eve) attempts to measure the quantum states using any basis, the original quantum information is necessarily disturbed, resulting in a significantly elevated error rate. To detect any potential eavesdropping, Alice and Bob sacrifice a subset of their key bits for comparison over the classical channel; if the observed error rate exceeds a predefined threshold, they conclude that the quantum channel has been compromised.
Figure 9.
Quantum key distribution process.
Although Quantum Key Distribution (QKD) theoretically provides information-theoretic security, it still faces multiple technical and non-technical limitations in real-world applications. Due to the limited efficiency of single-photon detectors, the key generation rate over long distances remains at the kbps level. For example, the ‘Micius’ satellite achieved a 1200 km satellite-to-ground QKD link, generating a key rate of 1.1 kbps. On fiber links over 1000 km, the key generation rate can be as low as bits per pulse. The satellite-based quantum decoy-state source transmits 250 million signal photons per second on average and extracts keys in real-time through combined uplink and downlink optical communication. A single orbital pass can generate approximately 250 kbits to 1 Mbit of secure key, with an average key rate of 3 kbps. QKD in fiber faces exponential signal attenuation caused by photon absorption and scattering. Ultra-long-distance commercial systems require intermediate relay nodes, and if such a node is physically compromised, the entire link could collapse. In addition, QKD devices are expensive and may be unaffordable for small and medium-sized organizations. Large-scale deployment of independent QKD systems over existing optical infrastructure incurs high retrofitting and operational costs, and suffers from poor scalability and flexibility.
Quantum keys generated via QKD can be used with classical cryptographic algorithms such as the one-time pad or AES to encrypt and decrypt classical data. QKD-based secure data sharing mainly includes the following two scenarios:
(1) When the data owner and the data user are located at either end of a QKD link, a symmetric quantum key is established via the quantum channel. Encrypted information is transmitted over a classical channel to achieve secure data sharing. However, due to the low key generation rate of QKD, it is difficult to encrypt large-volume data in real time.
(2) Under the scenario described in (1), only short- to medium-range, small-scale data sharing is feasible. To support high-security, high-volume, cross-domain, and multi-party collaborative data sharing with lower costs, a quantum key pool can be used to pre-store keys. Highly random quantum keys can then be distributed via classical means to users without QKD capabilities, enabling secure data sharing across multiple users.
Therefore, it is imperative to integrate quantum key distribution networks with classical communication infrastructure, to provide a secure foundation for scalable data sharing.
Author Contributions
Formal analysis, Y.L.; Investigation, H.Z. and Y.C.; Writing—original draft, D.Z. and Z.Z. (Zhiqiang Zhou); Writing—review & editing, Z.Z. (Zilong Zhao) and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Key Research and Development Program of China under Grant 2023YFC3305404, the Education Department of Jilin Province with grants No. JJKH20251102KJ, the Science and Technology Department of Jilin Province with grants No. 20250102045JC.
Data Availability Statement
No new data were generated during this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kemmerer, R.A. Cybersecurity. In Proceedings of the 25th International Conference on Software Engineering, 2003, Proceedings, Portland, OR, USA, 3–10 May 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 705–715. [Google Scholar]
- Dunn Cavelty, M. Cybersecurity research meets science and technology studies. Politics Gov. 2018, 6, 22–30. [Google Scholar] [CrossRef]
- Craigen, D.; Diakun-Thibault, N.; Purse, R. Defining Cybersecurity. Technol. Innov. Manag. Rev. 2014, 4, 13–21. [Google Scholar] [CrossRef]
- Sarker, I.H.; Kayes, A.; Badsha, S.; Alqahtani, H.; Watters, P.; Ng, A. Cybersecurity data science: An overview from machine learning perspective. J. Big Data 2020, 7, 41. [Google Scholar] [CrossRef]
- Choucri, N.; Madnick, S.; Koepke, P. Institutions for Cybersecurity: International Responses and Data Sharing Initiatives; Cybersecurity Interdisciplinary Systems Laboratory (CISL), Sloan School of Management, Massachusetts Institute of Technology, Room E62-422: Cambridge, MA, USA, 2018; Available online: https://cams.mit.edu/wp-content/uploads/2017-06.pdf (accessed on 10 July 2025).
- Linger, R.; Goldrich, L.; Bishop, M.; Dark, M. Agile Research for Cybersecurity: Creating Authoritative, Actionable Knowledge When Speed Matters; IEEE: Los Alamitos, CA, USA, 2017. [Google Scholar]
- Walton, S.; Wheeler, P.R.; Zhang, Y.; Zhao, X. An integrative review and analysis of cybersecurity research: Current state and future directions. J. Inf. Syst. 2021, 35, 155–186. [Google Scholar] [CrossRef]
- Sebastian, G. Could incorporating cybersecurity reporting into SOX have prevented most data breaches at US publicly traded companies? An exploratory study. Int. Cybersecur. Law Rev. 2022, 3, 367–383. [Google Scholar] [CrossRef]
- Camp, J.; Cranor, L.; Feamster, N.; Feigenbaum, J.; Forrest, S.; Kotz, D.; Lee, W.; Lincoln, P.; Paxson, V.; Reiter, M.; et al. Data for Cybersecurity Research: Process and ‘Wish List’; 2009. Available online: https://digitalcommons.dartmouth.edu/cgi/viewcontent.cgi?article=1003&context=faculty_other (accessed on 10 July 2025).
- Vesselkov, A.; Hämmäinen, H.; Töyli, J. Design and governance of mHealth data sharing. Commun. Assoc. Inf. Syst. 2019, 45, 299–321. [Google Scholar] [CrossRef]
- Gregory, R.W.; Henfridsson, O.; Kaganer, E.; Kyriakou, H. Data network effects: Key conditions, shared data, and the data value duality. Acad. Manag. Rev. 2022, 47, 189–192. [Google Scholar] [CrossRef]
- Gelhaar, J.; Gürpinar, T.; Henke, M.; Otto, B. Towards a taxonomy of incentive mechanisms for data sharing in data ecosystems. In Proceedings of the PACIS, Dubai, United Arab Emirates, 12–14 July 2021; p. 121. [Google Scholar]
- Fassnacht, M.; Benz, C.; Heinz, D.; Leimstoll, J.; Satzger, G. Barriers to data sharing among private sector organizations. In Proceedings of the 56th Hawaii International Conference on Systems Sciences, Maui, HI, USA, 3–6 January 2023. [Google Scholar]
- Bahrke, J.; Manoury, C. Data Act: Commission Proposes Measures for a Fair and Inno-Vative Data Economy, 2022. Available online: https://ec.europa.eu/commission/presscorner/detail/en/ip_22_1113 (accessed on 10 July 2025).
- Pauer, A.; Nagel, L.; Fedkenhauser, T.; Fritzsche-Sterr, Y.; Resetko, A. Data Exchange as a First Step Towards Data Economy. 2018. Available online: https://www.pwc.de/en/digitale-transformation/data-exchange-as-a-first-step-towards-data-economy.pdf (accessed on 10 July 2025).
- Mildebrath, H. Data Governance Act: Briefing-EU Legislation in Progress. 2021. Available online: https://www.europarl.europa.eu/RegData/etudes/BRIE/2021/690674/EPRS_BRI(2021)690674_EN.pdf (accessed on 10 July 2025).
- Cai, T.; Lin, H.; Chen, W.; Zheng, Z.; Yu, Y. Efficient Blockchain-Empowered Data Sharing Incentive Scheme for Internet of Things. Int. J. Softw. Inform. 2021, 11, 287–313. [Google Scholar] [CrossRef]
- Zhao, R.; Yang, L.T.; Liu, D.; Deng, X.; Mo, Y. A tensor-based truthful incentive mechanism for blockchain-enabled space-air-ground integrated vehicular crowdsensing. IEEE Trans. Intell. Transp. Syst. 2022, 23, 2853–2862. [Google Scholar] [CrossRef]
- Liu, S.; Yu, J.; Chen, L.; Chai, B. Blockchain-assisted comprehensive key management in CP-ABE for cloud-stored data. IEEE Trans. Netw. Serv. Manag. 2022, 20, 1745–1758. [Google Scholar] [CrossRef]
- Li, J.; Fan, Y.; Bian, X.; Yuan, Q. Online/offline MA-CP-ABE with cryptographic reverse firewalls for IoT. Entropy 2023, 25, 616. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Zheng, X.; Rong, C.; Guo, W. Efficient traceable authorization search system for secure cloud storage. IEEE Trans. Cloud Comput. 2018, 8, 819–832. [Google Scholar] [CrossRef]
- Yang, H.; Wang, X.; Yang, C.; Cong, X.; Zhang, Y. Securing content-centric networks with content-based encryption. J. Netw. Comput. Appl. 2019, 128, 21–32. [Google Scholar] [CrossRef]
- Jung, T.; Mao, X.; Li, X.Y.; Tang, S.J.; Gong, W.; Zhang, L. Privacy-preserving data aggregation without secure channel: Multivariate polynomial evaluation. In Proceedings of the 2013 IEEE INFOCOM, Turin, Italy, 14–19 April 2013; pp. 2634–2642. [Google Scholar]
- Wang, X.; Cheng, X.; Xie, Y. Efficient verifiable key-aggregate keyword searchable encryption for data sharing in outsourcing storage. IEEE Access 2019, 8, 11732–11742. [Google Scholar] [CrossRef]
- Li, C.; Tang, J. Searchable proxy re-encryption data sharing scheme based on consortium chain. In Proceedings of the 2023 3rd International Conference on Computer Science and Blockchain (CCSB), Shenzhen, China, 17–19 November 2023; pp. 121–132. [Google Scholar]
- Trivedi, H.S.; Patel, S.J. Key-aggregate searchable encryption with multi-user authorization and keyword untraceability for distributed IoT healthcare systems. Trans. Emerg. Telecommun. Technol. 2023, 34, e4734. [Google Scholar] [CrossRef]
- Wei, J.; Liu, W.; Hu, X. Secure data sharing in cloud computing using revocable-storage identity-based encryption. IEEE Trans. Cloud Comput. 2016, 6, 1136–1148. [Google Scholar] [CrossRef]
- Niu, J.; Li, X.; Gao, J.; Han, Y. Blockchain-based anti-key-leakage key aggregation searchable encryption for IoT. IEEE Internet Things J. 2019, 7, 1502–1518. [Google Scholar] [CrossRef]
- Niu, S.; Chen, L.; Wang, J.; Yu, F. Electronic health record sharing scheme with searchable attribute-based encryption on blockchain. IEEE Access 2019, 8, 7195–7204. [Google Scholar] [CrossRef]
- Pareek, G.; Purushothama, B. KAPRE: Key-aggregate proxy re-encryption for secure and flexible data sharing in cloud storage. J. Inf. Secur. Appl. 2021, 63, 103009. [Google Scholar] [CrossRef]
- Howard, M.; LeBlanc, D. Writing Secure Code; Pearson Education, 2003. Available online: https://ptgmedia.pearsoncmg.com/images/9780735617223/samplepages/9780735617223.pdf (accessed on 10 July 2025).
- Deng, M.; Wuyts, K.; Scandariato, R.; Preneel, B.; Joosen, W. A privacy threat analysis framework: Supporting the elicitation and fulfillment of privacy requirements. Requir. Eng. 2011, 16, 3–32. [Google Scholar] [CrossRef]
- Cui, B.; Liu, Z.; Wang, L. Key-aggregate searchable encryption (KASE) for group data sharing via cloud storage. IEEE Trans. Comput. 2015, 65, 2374–2385. [Google Scholar] [CrossRef]
- Oh, J.; Lee, J.; Kim, M.; Park, Y.; Park, K.; Noh, S. A secure data sharing based on key aggregate searchable encryption in fog-enabled IoT environment. IEEE Trans. Netw. Sci. Eng. 2022, 9, 4468–4481. [Google Scholar] [CrossRef]
- Lee, J.; Oh, J.; Kwon, D.; Kim, M.; Kim, K.; Park, Y. Blockchain-Enabled Key Aggregate Searchable Encryption Scheme for Personal Health Record Sharing with Multidelegation. IEEE Internet Things J. 2024, 11, 17482–17494. [Google Scholar] [CrossRef]
- Song, D.X.; Wagner, D.; Perrig, A. Practical techniques for searches on encrypted data. In Proceedings of the 2000 IEEE Symposium on Security and Privacy, S&P 2000, Berkeley, CA, USA, 14–17 May 2000; pp. 44–55. [Google Scholar]
- Curtmola, R.; Garay, J.; Kamara, S.; Ostrovsky, R. Searchable symmetric encryption: Improved definitions and efficient constructions. In Proceedings of the 13th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; pp. 79–88. [Google Scholar]
- Stefanov, E.; Papamanthou, C.; Shi, E. Practical Dynamic Searchable Encryption with Small Leakage. Cryptology ePrint Archive 2013. Available online: https://eprint.iacr.org/2013/832 (accessed on 10 July 2025).
- Popa, R.A.; Zeldovich, N. Multi-key searchable encryption. Cryptology ePrint Archive 2013. Available online: https://eprint.iacr.org/2013/508 (accessed on 10 July 2025).
- Patel, S.; Persiano, G.; Yeo, K. Symmetric searchable encryption with sharing and unsharing. In Proceedings of the 23rd European Symposium on Research in Computer Security, Barcelona, Spain, 3–7 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 207–227. [Google Scholar]
- Tang, Q. Nothing is for free: Security in searching shared and encrypted data. IEEE Trans. Inf. Forensics Secur. 2014, 9, 1943–1952. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Y.; Liu, X.; Ma, J. An efficient blockchain-based hierarchical data sharing for healthcare internet of things. IEEE Trans. Ind. Inform. 2022, 18, 7139–7150. [Google Scholar] [CrossRef]
- Li, H.; Tian, H.; Zhang, F.; He, J. Blockchain-based searchable symmetric encryption scheme. Comput. Electr. Eng. 2019, 73, 32–45. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, B.; Qin, J.; Hou, X.; Ma, J. Key-aggregate searchable encryption supporting conjunctive queries for flexible data sharing in the cloud. Inf. Sci. 2023, 645, 119336. [Google Scholar] [CrossRef]
- Yang, N.; Tang, C.; Zhou, Q.; He, D. Dynamic consensus committee-based for secure data sharing with authorized multi-receiver searchable encryption. IEEE Trans. Inf. Forensics Secur. 2023, 18, 5186–5199. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, A.; Zhang, P.; Wang, H. Cloud-assisted EHR sharing with security and privacy preservation via consortium blockchain. IEEE Access 2019, 7, 136704–136719. [Google Scholar] [CrossRef]
- Feng, T.; Pei, H.; Xie, P.; Feng, X. Blockchain data sharing scheme based on searchable agent re-encryption. Int. J. Netw. Secur. 2021, 23, 535–544. [Google Scholar]
- Zhang, K.; Hu, B.; Ning, J.; Gong, J.; Qian, H. Pattern Hiding and Authorized Searchable Encryption for Data Sharing in Cloud Storage. IEEE Trans. Knowl. Data Eng. 2025, 37, 2802–2815. [Google Scholar] [CrossRef]
- Zhou, R.; Zhang, X.; Wang, X.; Yang, G.; Wang, H.; Wu, Y. Privacy-preserving data search with fine-grained dynamic search right management in fog-assisted Internet of Things. Inf. Sci. 2019, 491, 251–264. [Google Scholar] [CrossRef]
- Li, M.; Jia, C.; Du, R.; Shao, W.; Ha, G. Dse-rb: A privacy-preserving dynamic searchable encryption framework on redactable blockchain. IEEE Trans. Cloud Comput. 2022, 11, 2856–2872. [Google Scholar] [CrossRef]
- Zhang, R.; Xue, R.; Liu, L. Searchable encryption for healthcare clouds: A survey. IEEE Trans. Serv. Comput. 2017, 11, 978–996. [Google Scholar] [CrossRef]
- Niu, S.; Liu, W.; Han, S.; Fang, L. A data-sharing scheme that supports multi-keyword search for electronic medical records. PLoS ONE 2021, 16, e0244979. [Google Scholar] [CrossRef]
- Niu, S.; Yu, F.; Song, M.; Han, S.; Wang, C. Specified keywords search scheme for EHR sharing. Soft Comput. 2022, 26, 8949–8960. [Google Scholar] [CrossRef]
- Costa, I.; Amorim, I.; Maia, E.; Barbosa, P.; Praca, I. S3PHER: Secure and Searchable System for Patient-driven HEalth data shaRing. arXiv 2024, arXiv:2404.11372. [Google Scholar]
- Shao, J.; Cao, Z.; Liang, X.; Lin, H. Proxy re-encryption with keyword search. Inf. Sci. 2010, 180, 2576–2587. [Google Scholar] [CrossRef]
- Ateniese, G.; Fu, K.; Green, M.; Hohenberger, S. Improved proxy re-encryption schemes with applications to secure distributed storage. ACM Trans. Inf. Syst. Secur. (TISSEC) 2006, 9, 1–30. [Google Scholar] [CrossRef]
- Li, M.; Yu, S.; Zheng, Y.; Ren, K.; Lou, W. Scalable and secure sharing of personal health records in cloud computing using attribute-based encryption. IEEE Trans. Parallel Distrib. Syst. 2012, 24, 131–143. [Google Scholar] [CrossRef]
- Hu, S.; Cai, C.; Wang, Q.; Wang, C.; Luo, X.; Ren, K. Searching an encrypted cloud meets blockchain: A decentralized, reliable and fair realization. In Proceedings of the IEEE INFOCOM 2018-IEEE Conference on Computer Communications, Honolulu, HI, USA, 16–19 April 2018; pp. 792–800. [Google Scholar]
- Ali, A.; Masud, M.; Chen, C.; AlZain, M.A.; Ali, J. An Effective Blockchain Based Secure Searchable Encryption System. Intell. Autom. Soft Comput. 2022, 33, 1183–1195. [Google Scholar] [CrossRef]
- Iqbal, Y.; Tahir, S.; Tahir, H.; Khan, F.; Saeed, S.; Almuhaideb, A.M.; Syed, A.M. A novel homomorphic approach for preserving privacy of patient data in telemedicine. Sensors 2022, 22, 4432. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, R.H.; Shu, J.; Yang, K.; Zheng, D. TKSE: Trustworthy keyword search over encrypted data with two-side verifiability via blockchain. IEEE Access 2018, 6, 31077–31087. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, Y.; Cao, S.; Huang, C.; Zheng, S. Enabling identity-based authorized encrypted diagnostic data sharing for cloud-assisted E-health information systems. J. Inf. Secur. Appl. 2020, 54, 102568. [Google Scholar] [CrossRef]
- Sun, Y.; Chatterjee, P.; Chen, Y.; Zhang, Y. Efficient identity-based encryption with revocation for data privacy in internet of things. IEEE Internet Things J. 2021, 9, 2734–2743. [Google Scholar] [CrossRef]
- Hundera, N.W.; Aftab, M.U.; Mesfin, D.; Dioubi, F.; Xu, H.; Zhu, X. An efficient heterogeneous online/offline anonymous certificateless signcryption with proxy re-encryption for Internet of Vehicles. Veh. Commun. 2024, 49, 100811. [Google Scholar] [CrossRef]
- Feng, J.; Li, Y.; Wang, T.; Liu, S. A Certificateless Threshold Proxy Re-Encrypted Data Sharing Scheme With Cloud-Chain Collaboration in Industrial Internet Environments. IEEE Internet Things J. 2024, 11, 33247–33268. [Google Scholar] [CrossRef]
- Ge, C.; Susilo, W.; Baek, J.; Liu, Z.; Xia, J.; Fang, L. A verifiable and fair attribute-based proxy re-encryption scheme for data sharing in clouds. IEEE Trans. Dependable Secur. Comput. 2021, 19, 2907–2919. [Google Scholar] [CrossRef]
- Duan, P.; Ma, Z.; Gao, H.; Tian, T.; Zhang, Y. Multi-Authority Attribute-Based Encryption Scheme With Access Delegation for Cross Blockchain Data Sharing. IEEE Trans. Inf. Forensics Secur. 2024, 20, 323–337. [Google Scholar] [CrossRef]
- Xu, P.; Jiao, T.; Wu, Q.; Wang, W.; Jin, H. Conditional identity-based broadcast proxy re-encryption and its application to cloud email. IEEE Trans. Comput. 2015, 65, 66–79. [Google Scholar] [CrossRef]
- Sun, M.; Ge, C.; Fang, L.; Wang, J. A proxy broadcast re-encryption for cloud data sharing. Multimed. Tools Appl. 2018, 77, 10455–10469. [Google Scholar] [CrossRef]
- Green, M.; Ateniese, G. Identity-based proxy re-encryption. In Applied Cryptography and Network Security, Proceedings of the 5th International Conference, ACNS 2007, Zhuhai, China, 5–8 June 2007; Proceedings 5; Springer: Berlin/Heidelberg, Germany, 2007; pp. 288–306. [Google Scholar]
- Lee, K. Comments on “Secure data sharing in cloud computing using revocable-storage identity-based encryption”. IEEE Trans. Cloud Comput. 2020, 8, 1299–1300. [Google Scholar] [CrossRef]
- Meshram, C.; Lee, C.C.; Meshram, S.G.; Khan, M.K. An identity-based encryption technique using subtree for fuzzy user data sharing under cloud computing environment. Soft Comput. 2019, 23, 13127–13138. [Google Scholar] [CrossRef]
- Sudarsono, A.; Yuliana, M.; Darwito, H.A. A secure data sharing using identity-based encryption scheme for e-healthcare system. In Proceedings of the 2017 3rd International Conference on Science in Information Technology (ICSITech), Bandung, Indonesia, 25–26 October 2017; pp. 429–434. [Google Scholar]
- Unal, D.; Al-Ali, A.; Catak, F.O.; Hammoudeh, M. A secure and efficient Internet of Things cloud encryption scheme with forensics investigation compatibility based on identity-based encryption. Future Gener. Comput. Syst. 2021, 125, 433–445. [Google Scholar] [CrossRef]
- Sur, C.; Jung, C.D.; Park, Y.; Rhee, K.H. Chosen-ciphertext secure certificateless proxy re-encryption. In Communications and Multimedia Security, Proceedings of the 11th IFIP TC 6/TC 11 International Conference, CMS 2010, Linz, Austria, 31 May–2 June 2010; Proceedings 11; Springer: Berlin/Heidelberg, Germany, 2010; pp. 214–232. [Google Scholar]
- Liu, Y.; Wang, H.; Wang, C. Efficient and secure certificateless proxy re-encryption. KSII Trans. Internet Inf. Syst. (TIIS) 2017, 11, 2254–2275. [Google Scholar]
- Eltayieb, N.; Elhabob, R.; Abdelgader, A.M.; Liao, Y.; Li, F.; Zhou, S. Certificateless Proxy Re-encryption with Cryptographic Reverse Firewalls for Secure Cloud Data Sharing. Future Gener. Comput. Syst. 2025, 162, 107478. [Google Scholar] [CrossRef]
- Nunez, D. Umbral: A Threshold Proxy Re-Encryption Scheme; NuCypher Inc. and NICS Lab, University of Malaga: Malaga, Spain, 2018. [Google Scholar]
- Liang, K.; Au, M.H.; Liu, J.K.; Susilo, W.; Wong, D.S.; Yang, G.; Yu, Y.; Yang, A. A secure and efficient ciphertext-policy attribute-based proxy re-encryption for cloud data sharing. Future Gener. Comput. Syst. 2015, 52, 95–108. [Google Scholar] [CrossRef]
- He, Z.; Cai, Z.; Han, Q.; Tong, W.; Sun, L.; Li, Y. An energy efficient privacy-preserving content sharing scheme in mobile social networks. Pers. Ubiquitous Comput. 2016, 20, 833–846. [Google Scholar] [CrossRef]
- Chen, W.H.; Fan, C.I.; Tseng, Y.F. Efficient key-aggregate proxy re-encryption for secure data sharing in clouds. In Proceedings of the 2018 IEEE Conference on Dependable and Secure Computing (DSC), Kaohsiung, Taiwan, 10–13 December 2018; pp. 1–4. [Google Scholar]
- Fiat, A.; Naor, M. Broadcast encryption. In Advances in Cryptology—CRYPTO’93, Proceedings of the 13th Annual International Cryptology Conference, Santa Barbara, CA, USA, 22–26 August 1993; Proceedings 13; Springer: Berlin/Heidelberg, Germany, 1994; pp. 480–491. [Google Scholar]
- Nishide, T.; Yoneyama, K.; Ohta, K. Attribute-based encryption with partially hidden encryptor-specified access structures. In Applied Cryptography and Network Security, Proceedings of the 6th International Conference, ACNS 2008, New York, NY, USA, 3–6 June 2008; Proceedings 6; Springer: Berlin/Heidelberg, Germany, 2008; pp. 111–129. [Google Scholar]
- Li, J.; Ren, K.; Zhu, B.; Wan, Z. Privacy-aware attribute-based encryption with user accountability. In Information Security, Proceedings of the 12th International Conference, ISC 2009, Pisa, Italy, 7–9 September 2009; Proceedings 12; Springer: Berlin/Heidelberg, Germany, 2009; pp. 347–362. [Google Scholar]
- Ma, H.; Peng, T.; Liu, Z. Directly Revocable and Verifiable Key-Policy Attribute-based Encryption for Large Universe. Int. J. Netw. Secur. 2017, 19, 272–284. [Google Scholar]
- Ye, Y.; Cao, Z.; Shen, J. Unbounded key-policy attribute-based encryption with black-box traceability. In Proceedings of the 2020 IEEE 19th International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Guangzhou, China, 29 December 2020–1 January 2021; pp. 1655–1663. [Google Scholar]
- Liu, X.H.; Huang, X.Y.; Wu, W.; Ning, J.T. Key-Policy Attribute-Based Encryption Based on SM9. J. Comput. Sci. Technol. 2025, 40, 267–282. [Google Scholar] [CrossRef]
- Wang, M.; Guo, Y.; Zhang, C.; Wang, C.; Huang, H.; Jia, X. MedShare: A privacy-preserving medical data sharing system by using blockchain. IEEE Trans. Serv. Comput. 2021, 16, 438–451. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.; Zhong, H.; Gu, C.; Cui, J. Revocable and efficient blockchain-based fine-grained access control against EDoS attacks in cloud storage. IEEE Trans. Comput. 2024, 73, 2012–2024. [Google Scholar] [CrossRef]
- Bethencourt, J.; Sahai, A.; Waters, B. Ciphertext-policy attribute-based encryption. In Proceedings of the 2007 IEEE symposium on security and privacy (SP’07), Berkeley, CA, USA, 20–23 May 2007; pp. 321–334. [Google Scholar]
- Yang, K.; Jia, X.; Ren, K.; Zhang, B.; Xie, R. DAC-MACS: Effective data access control for multiauthority cloud storage systems. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1790–1801. [Google Scholar] [CrossRef]
- Lai, J.; Deng, R.H.; Li, Y. Fully secure cipertext-policy hiding CP-ABE. In Information Security Practice and Experience, Proceedings of the 7th International Conference, ISPEC 2011, Guangzhou, China, 30 May–1 June 2011; Proceedings 7; Springer: Berlin/Heidelberg, Germany, 2011; pp. 24–39. [Google Scholar]
- Liu, L.; Lai, J.; Deng, R.H.; Li, Y. Ciphertext-policy attribute-based encryption with partially hidden access structure and its application to privacy-preserving electronic medical record system in cloud environment. Secur. Commun. Netw. 2016, 9, 4897–4913. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, D.; Deng, R.H. Security and privacy in smart health: Efficient policy-hiding attribute-based access control. IEEE Internet Things J. 2018, 5, 2130–2145. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Zhang, Y. A secure cloud storage framework with access control based on blockchain. IEEE Access 2019, 7, 112713–112725. [Google Scholar] [CrossRef]
- Wei, X.; Yan, Y.; Guo, S.; Qiu, X.; Qi, F. Secure data sharing: Blockchain-enabled data access control framework for IoT. IEEE Internet Things J. 2021, 9, 8143–8153. [Google Scholar] [CrossRef]
- Qin, X.; Huang, Y.; Yang, Z.; Li, X. A blockchain-based access control scheme with multiple attribute authorities for secure cloud data sharing. J. Syst. Archit. 2021, 112, 101854. [Google Scholar] [CrossRef]
- Zhang, L.; Ou, Z.; Hu, C.; Kan, H.; Zhang, J. Data sharing in the metaverse with key abuse resistance based on decentralized CP-ABE. IEEE Trans. Comput. 2024, 74, 901–914. [Google Scholar] [CrossRef]
- Goyal, V.; Pandey, O.; Sahai, A.; Waters, B. Attribute-based encryption for fine-grained access control of encrypted data. In Proceedings of the 13th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; pp. 89–98. [Google Scholar]
- Ji, H.; Zhang, H.; Shao, L.; He, D.; Luo, M. An efficient attribute-based encryption scheme based on SM9 encryption algorithm for dispatching and control cloud. Connect. Sci. 2021, 33, 1094–1115. [Google Scholar] [CrossRef]
- Johnson, J. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef]
- Amir, Y.; Kim, Y.; Nita-Rotaru, C.; Schultz, J.L.; Stanton, J.; Tsudik, G. Secure group communication using robust contributory key agreement. IEEE Trans. Parallel Distrib. Syst. 2004, 15, 468–480. [Google Scholar] [CrossRef]
- Luo, M.; Wu, J.; Li, X. Cross-domain certificateless authenticated group key agreement protocol for 5G network slicings. Telecommun. Syst. 2020, 74, 437–449. [Google Scholar] [CrossRef]
- Rawat, A.; Deshmukh, M. Tree and elliptic curve based efficient and secure group key agreement protocol. J. Inf. Secur. Appl. 2020, 55, 102599. [Google Scholar] [CrossRef]
- Gan, Y.; Wang, B.; Zhuang, Y.; Gao, Y.; Li, Z.; Zhang, Q. An asymmetric group key agreement protocol based on attribute threshold for Internet of Things. Trans. Emerg. Telecommun. Technol. 2021, 32, e4179. [Google Scholar] [CrossRef]
- Chen, M.; Lee, T.F. Anonymous group-oriented time-bound key agreement for internet of medical things in telemonitoring using chaotic maps. IEEE Internet Things J. 2021, 8, 13939–13949. [Google Scholar] [CrossRef]
- Braeken, A. Pairing free asymmetric group key agreement protocol. Comput. Commun. 2022, 181, 267–273. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, Z.; Li, F. A two rounds dynamic authenticated group key agreement protocol based on LWE. J. Syst. Archit. 2022, 133, 102756. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, L.; Choo, K.K.R.; Chen, T. Dynamic authenticated asymmetric group key agreement with sender non-repudiation and privacy for group-oriented applications. IEEE Trans. Dependable Secur. Comput. 2021, 20, 492–505. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Wang, Y.; Miao, Y.; Liu, X.; Weng, J.; Deng, R.H. TAGKA: Threshold authenticated group key agreement protocol against member disconnect for UANET. IEEE Trans. Veh. Technol. 2023, 72, 14987–15001. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Z.; Qiu, F.; Li, F. A group key agreement protocol based on ecdh and short signature. J. Inf. Secur. Appl. 2023, 72, 103388. [Google Scholar] [CrossRef]
- Cui, B.; He, W.; Cui, Y. A dynamic C-V2X anonymous authentication and group key agreement protocol. Int. J. Inf. Secur. 2024, 23, 2977–2989. [Google Scholar] [CrossRef]
- Cao, X.; Dang, L.; Fan, K.; Zhao, X.; Fu, Y.; Luan, Y. A Dynamic and Efficient Self-Certified Authenticated Group Key Agreement Protocol for VANET. IEEE Internet Things J. 2024, 11, 29146–29156. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.; Wang, R.; Li, J.; Gan, Y.; Zhang, Y.; Yu, X. Blockchain-based asymmetric group key agreement protocol for internet of vehicles. Comput. Electr. Eng. 2020, 86, 106713. [Google Scholar] [CrossRef]
- Xu, Z.; Li, F.; Deng, H.; Tan, M.; Zhang, J.; Xu, J. A blockchain-based authentication and dynamic group key agreement protocol. Sensors 2020, 20, 4835. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.M.; Deng, X.; Gan, W.; Chen, J.; Islam, S.H. A secure blockchain-based group key agreement protocol for IoT. J. Supercomput. 2021, 77, 9046–9068. [Google Scholar] [CrossRef]
- Naresh, V.S.; Allavarpu, V.D.; Reddi, S. Provably secure blockchain privacy-preserving smart contract centric dynamic group key agreement for large WSN. J. Supercomput. 2022, 78, 8708–8732. [Google Scholar] [CrossRef]
- Wang, Z.; Huo, R.; Wang, S. A lightweight certificateless group key agreement method without pairing based on blockchain for smart grid. Future Internet 2022, 14, 119. [Google Scholar] [CrossRef]
- Xu, Z.; Liang, W.; Li, K.C.; Xu, J.; Zomaya, A.Y.; Zhang, J. A time-sensitive token-based anonymous authentication and dynamic group key agreement scheme for industry 5.0. IEEE Trans. Ind. Inform. 2021, 18, 7118–7127. [Google Scholar] [CrossRef]
- Chhikara, D.; Rana, S.; Singh, G.; Mishra, D.; Kumar, N. Blockchain-based partial group key agreement protocol for intelligent transportation systems. IEEE Trans. Veh. Technol. 2023, 72, 16701–16710. [Google Scholar] [CrossRef]
- Pérez-García, J.C.; Braeken, A.; Benslimane, A. Blockchain-based group key management scheme for iot with anonymity of group members. IEEE Trans. Inf. Forensics Secur. 2024, 19, 6709–6721. [Google Scholar] [CrossRef]
- Yıldız, H.; Cenk, M.; Onur, E. PLGAKD: A PUF-based lightweight group authentication and key distribution protocol. IEEE Internet Things J. 2020, 8, 5682–5696. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, R.; Pandey, S.K. A computationally efficient centralized group key distribution protocol for secure multicast communications based upon RSA public key cryptosystem. J. King Saud Univ.-Comput. Inf. Sci. 2020, 32, 1081–1094. [Google Scholar] [CrossRef]
- Harn, L.; Hsu, C.; Xia, Z. Lightweight and flexible key distribution schemes for secure group communications. Wirel. Netw. 2021, 27, 129–136. [Google Scholar] [CrossRef]
- Hougaard, H.B.; Miyaji, A. Authenticated logarithmic-order supersingular isogeny group key exchange. Int. J. Inf. Secur. 2022, 21, 207–221. [Google Scholar] [CrossRef]
- Taurshia, A.; Kathrine, G.J.W.; Souri, A.; Vinodh, S.; Vimal, S.; Li, K.C.; Ilango, S.S. Software-defined network aided lightweight group key management for resource-constrained Internet of Things devices. Sustain. Comput. Inform. Syst. 2022, 36, 100807. [Google Scholar] [CrossRef]
- Harn, L.; Hsu, C.; Xia, Z. General logic-operation-based lightweight group-key distribution schemes for Internet of Vehicles. Veh. Commun. 2022, 34, 100457. [Google Scholar] [CrossRef]
- Gebremichael, T.; Gidlund, M.; Hancke, G.P.; Jennehag, U. Quantum-safe group key establishment protocol from lattice trapdoors. Sensors 2022, 22, 4148. [Google Scholar] [CrossRef]
- Luo, Y.; Mao, H.K.; Li, Q.; Chen, N. An information-theoretic secure group authentication scheme for quantum key distribution networks. IEEE Trans. Commun. 2023, 71, 5420–5431. [Google Scholar] [CrossRef]
- Cheng, T.; Liu, Q.; Shi, Q.; Yang, Z.; Wang, C.; Zhang, X.; Xu, P. Efficient anonymous authentication and group key distribution scheme based on quantum random numbers for vanets. IEEE Internet Things J. 2024, 11, 23544–23560. [Google Scholar] [CrossRef]
- Al-Mohammed, H.A.; Yaacoub, E.; Abualsaud, K.; Al-Maadeed, S.A. Using quantum key distribution with free space optics to secure communications in high-speed trains. IEEE Access 2024, 12, 43560–43574. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Vijayakumar, P.; He, D.; Kumar, N.; Ma, J. Blockchain-based mutual-healing group key distribution scheme in unmanned aerial vehicles ad-hoc network. IEEE Trans. Veh. Technol. 2019, 68, 11309–11322. [Google Scholar] [CrossRef]
- Heo, G.; Chae, K.; Doh, I. Hierarchical blockchain-based group and group key management scheme exploiting unmanned aerial vehicles for urban computing. IEEE Access 2022, 10, 27990–28003. [Google Scholar] [CrossRef]
- Shawky, M.A.; Jabbar, A.; Usman, M.; Imran, M.; Abbasi, Q.H.; Ansari, S.; Taha, A. Efficient blockchain-based group key distribution for secure authentication in VANETs. IEEE Netw. Lett. 2023, 5, 64–68. [Google Scholar] [CrossRef]
- Abdmeziem, M.R.; Nacer, A.A.; Deroues, N.M. Group key management in the Internet of Things: Handling asynchronicity. Future Gener. Comput. Syst. 2024, 152, 273–287. [Google Scholar] [CrossRef]
- Cai, J.; Pooch, U. Allocate fair payoff for cooperation in wireless ad hoc networks using shapley value. In Proceedings of the 18th International Parallel and Distributed Processing Symposium, Santa Fe, NM, USA, 26–30 April 2004; p. 219. [Google Scholar]
- Tosh, D.; Sengupta, S.; Kamhoua, C.A.; Kwiat, K.A. Establishing evolutionary game models for cyber security information exchange (cybex). J. Comput. Syst. Sci. 2018, 98, 27–52. [Google Scholar] [CrossRef]
- Lu, W.; Hu, S.; Liu, X.; He, C.; Gong, Y. Incentive mechanism based cooperative spectrum sharing for OFDM cognitive IoT network. IEEE Trans. Netw. Sci. Eng. 2019, 7, 662–672. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, Z.; Wang, B.; Shao, K.; Hetu, Z.; Wang, X. FDTA: A Value-Guaranteed Fair Data Trading Approach With A Three-Stage Stackelberg Game. IEEE Internet Things J. 2025, 12, 9965–9977. [Google Scholar] [CrossRef]
- Yu, H.; Li, P.; Huang, W.; Du, R.; Xu, Q.; Nie, L.; Bao, H.; Liu, Q. Social-Aware Incentive Mechanism for Data Quality in Mobile Crowdsensing: A Three-Stage Stackelberg Game Approach. IEEE Internet Things J. 2025, 12, 7980–7994. [Google Scholar] [CrossRef]
- Chen, W.; Chen, Y.; Chen, X.; Zheng, Z. Toward secure data sharing for the IoV: A quality-driven incentive mechanism with on-chain and off-chain guarantees. IEEE Internet Things J. 2019, 7, 1625–1640. [Google Scholar] [CrossRef]
- Shen, M.; Duan, J.; Zhu, L.; Zhang, J.; Du, X.; Guizani, M. Blockchain-based incentives for secure and collaborative data sharing in multiple clouds. IEEE J. Sel. Areas Commun. 2020, 38, 1229–1241. [Google Scholar] [CrossRef]
- Li, C.; Dong, M.; Li, J.; Xu, G.; Chen, X.; Ota, K. Healthchain: Secure EMRs management and trading in distributed healthcare service system. IEEE Internet Things J. 2020, 8, 7192–7202. [Google Scholar] [CrossRef]
- Ali, B.; Maheswaran, M. A game theoretic analysis of blacklisting in online data storage systems. In Proceedings of the GLOBECOM 2009—2009 IEEE Global Telecommunications Conference, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–7. [Google Scholar]
- Kantarcioglu, M.; Nix, R. Incentive compatible distributed data mining. In Proceedings of the 2010 IEEE Second International Conference on Social Computing, Indianapolis, IN, USA, 30 November–3 December 2010; pp. 735–742. [Google Scholar]
- Yassine, A.; Shirehjini, A.A.N.; Shirmohammadi, S. Smart meters big data: Game theoretic model for fair data sharing in deregulated smart grids. IEEE Access 2015, 3, 2743–2754. [Google Scholar] [CrossRef]
- Kamhoua, C.A.; Kwiat, K.A.; Park, J.S. A game theoretic approach for modeling optimal data sharing on online social networks. In Proceedings of the 2012 9th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 26–28 September 2012; pp. 1–6. [Google Scholar]
- Xiao, L.; Chen, T.; Xie, C.; Dai, H.; Poor, H.V. Mobile crowdsensing games in vehicular networks. IEEE Trans. Veh. Technol. 2017, 67, 1535–1545. [Google Scholar] [CrossRef]
- An, Q.; Wen, Y.; Ding, T.; Li, Y. Resource sharing and payoff allocation in a three-stage system: Integrating network DEA with the Shapley value method. Omega 2019, 85, 16–25. [Google Scholar] [CrossRef]
- Sun, W.; Liu, J.; Yue, Y.; Jiang, Y. Social-aware incentive mechanisms for D2D resource sharing in IIoT. IEEE Trans. Ind. Inform. 2019, 16, 5517–5526. [Google Scholar] [CrossRef]
- Yi, Y.; Yang, Y.; Cheng, K.; Wu, Y.; Wang, X. Information dissemination with service-oriented incentive mechanism in industrial Internet of Things. IEEE Internet Things J. 2022, 9, 16897–16907. [Google Scholar] [CrossRef]
- Xuan, S.; Zheng, L.; Chung, I.; Wang, W.; Man, D.; Du, X.; Yang, W.; Guizani, M. An incentive mechanism for data sharing based on blockchain with smart contracts. Comput. Electr. Eng. 2020, 83, 106587. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, B.; Dong, A. Blockchain empowered federated learning for data sharing incentive mechanism. Procedia Comput. Sci. 2022, 202, 348–353. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Wang, S.; Wang, F.; Li, Y.; Jiang, Y.; Chen, L.; Guo, B. Dim-ds: Dynamic incentive model for data sharing in federated learning based on smart contracts and evolutionary game theory. IEEE Internet Things J. 2022, 9, 24572–24584. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, P.; Jing, W.; Song, H.H. Pd2s: A privacy-preserving differentiated data sharing scheme based on blockchain and federated learning. IEEE Internet Things J. 2023, 10, 21489–21501. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, Y.; Ren, X. Quality decision and demand information sharing: The role of blockchain adoption. Comput. Ind. Eng. 2024, 189, 109991. [Google Scholar] [CrossRef]
- Gan, C.; Xiao, X.; Zhang, Y.; Zhu, Q.; Bi, J.; Jain, D.K.; Saini, A. An asynchronous federated learning-assisted data sharing method for medical blockchain. Appl. Intell. 2025, 55, 208. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).