Graph Convolutional Network with Multi-View Topology for Lightweight Skeleton-Based Action Recognition
Abstract
1. Introduction
- We propose a multi-view topology modeling strategy that captures dynamic joint relationships via a novel pairwise interaction mechanism, while preserving original skeletal connectivity through a complementary static view.
- We propose a novel MultiScale Temporal Convolutional Network that employs depthwise separable convolutions with larger kernels for temporal feature extraction. By incorporating a pooling module and a branch preserving input information, it captures richer feature representations. The proposed temporal module achieves a lightweight design while maintaining high accuracy.
- We propose a novel Gated Channel-wise Temporal Topology (GCTT) that further improves temporal feature extraction on top of the lightweight design. Extensive experiments demonstrate that each component of our model achieves remarkable performance, and the overall model surpasses many state-of-the-art methods. Furthermore, our results highlight the importance of simultaneously leveraging dynamic and static topology information.
2. Related Work
2.1. Skeleton-Based Action Recognition
2.2. Relative Position Encoding
2.3. Lightweight Temporal Convolutional Networks
2.4. Symmetric Topology Modeling
3. Methods
3.1. Preliminaries
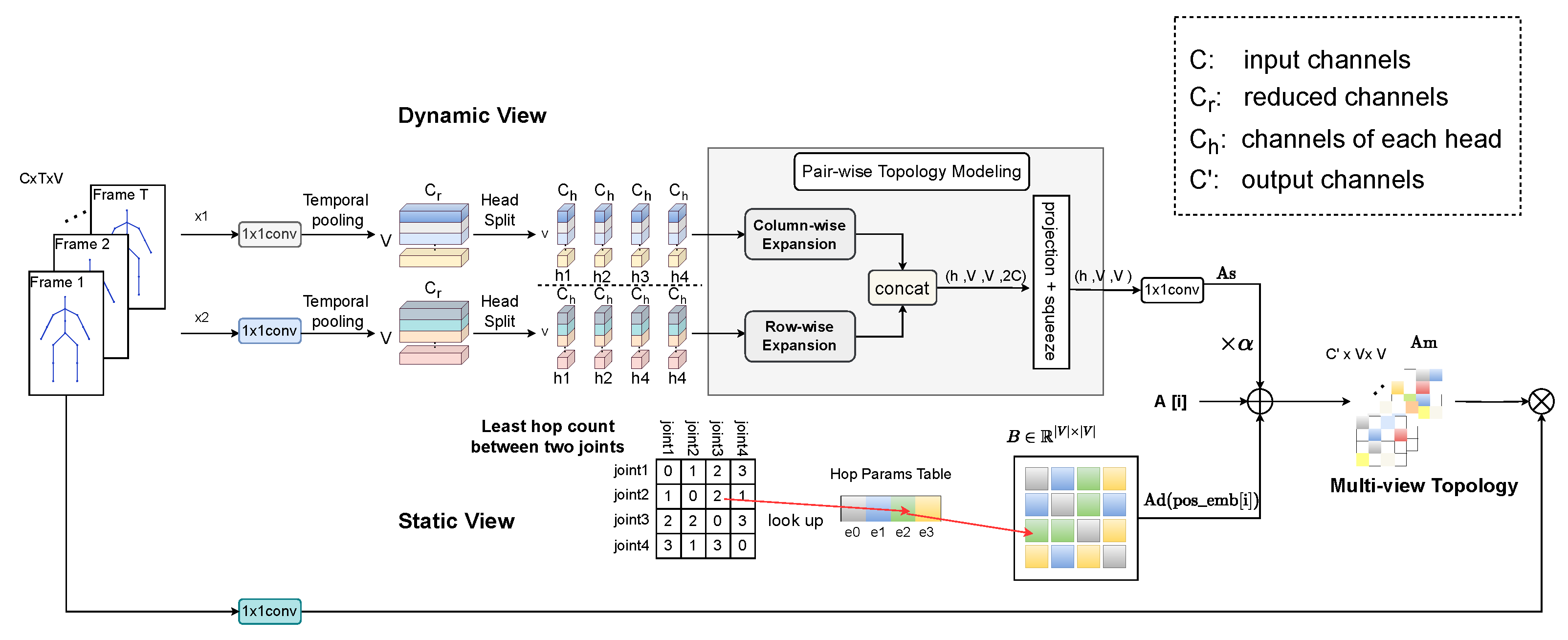
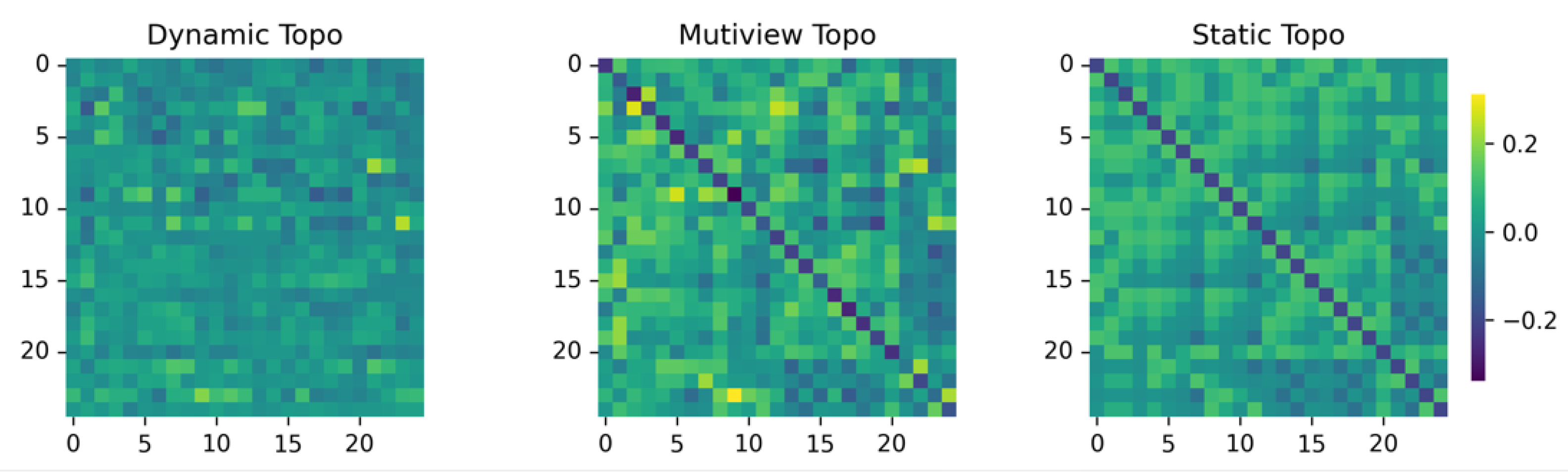
3.2. Multi-View Topology Refinement Graph Convolution
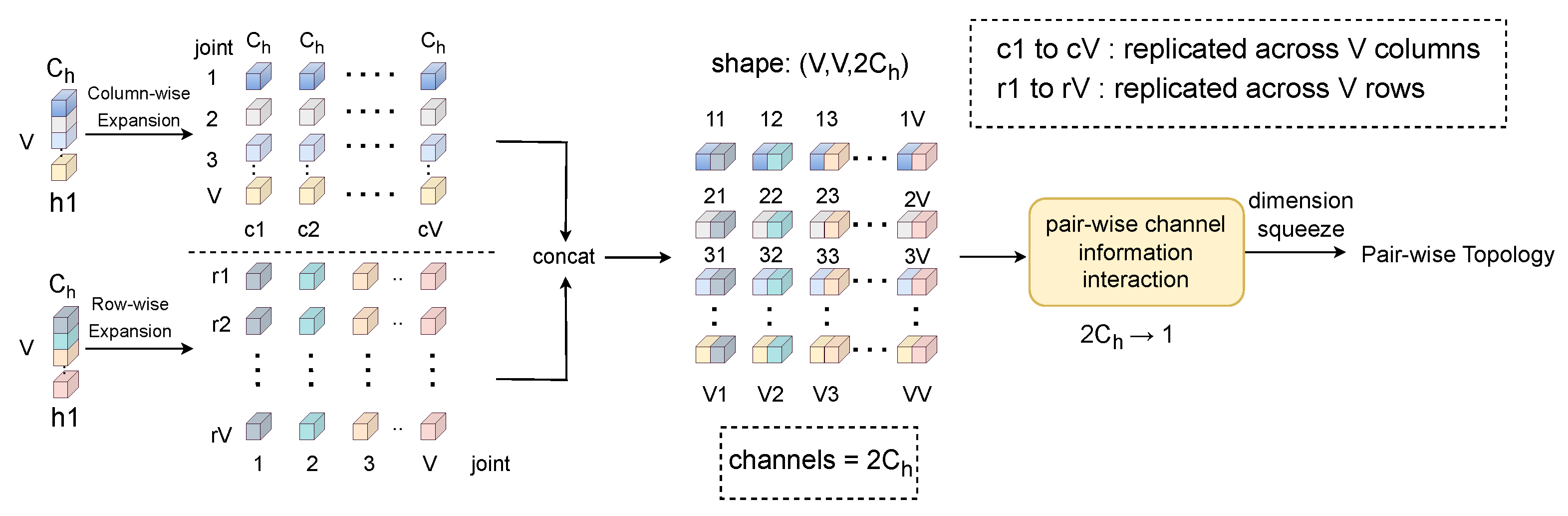
3.2.1. Dynamic View
3.2.2. Static View
3.2.3. Multi-View
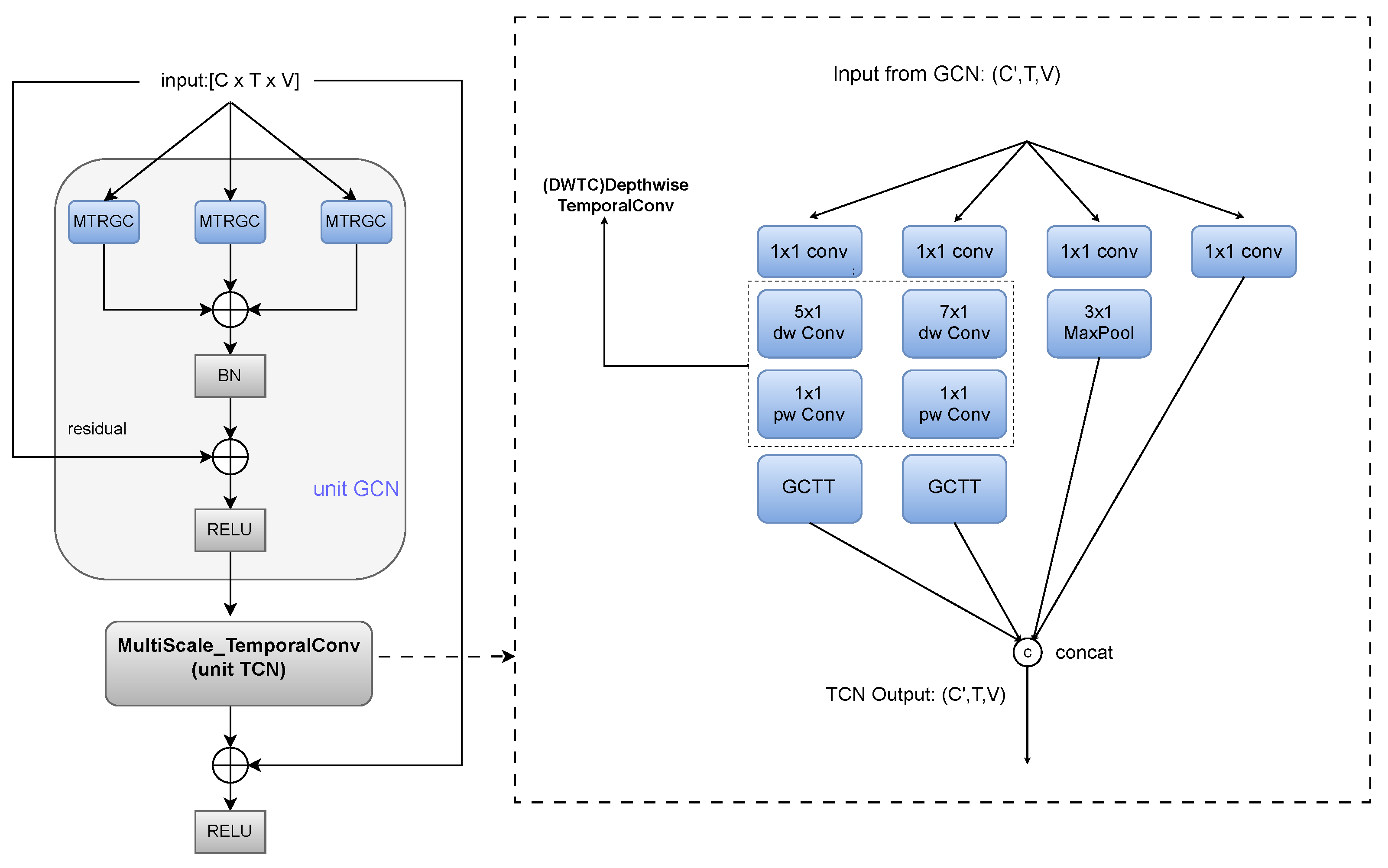
3.3. MultiScale Temporal Convolutional Network (MSTC)
3.3.1. Lightweight Implementation
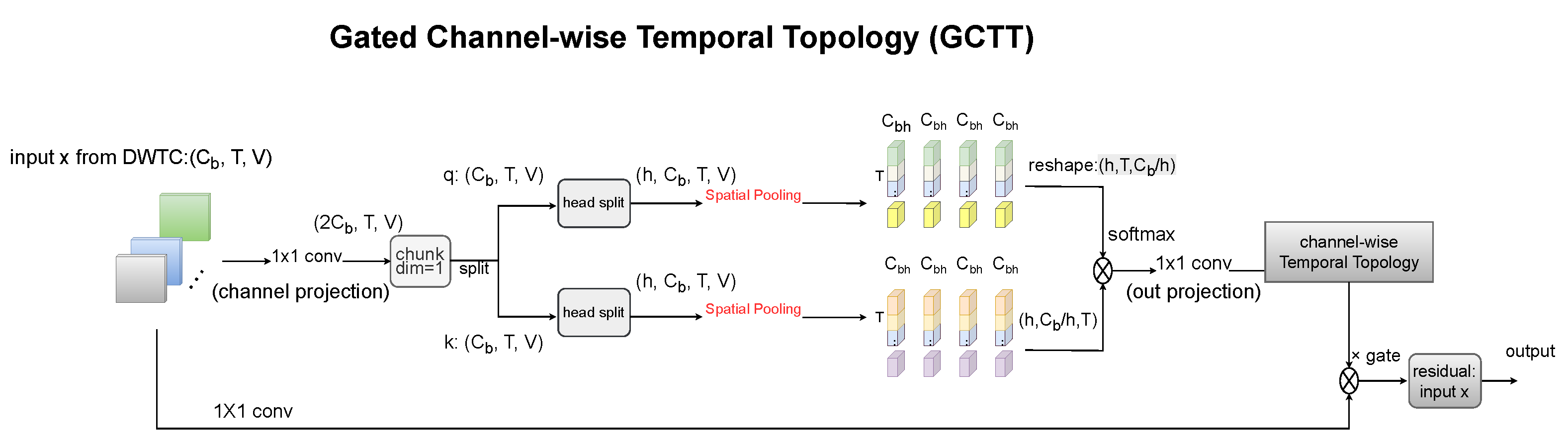
3.3.2. Gated Channel-Wise Temporal Topology Representation
3.4. Model Architecture

4. Experiments
4.1. Datasets
4.2. Implementation Details
4.3. Ablation Study
- Adding only the dynamic topology on top of the baseline improves the accuracy by 0.4%, demonstrating that our pairwise modeling strategy for dynamically capturing spatial joint relationships is highly effective.
- Adding only the static topology improves the accuracy by 0.3%, indicating that modeling the skeletal topology based on the distance between joints can effectively preserve static connection information.
- Incorporating the multi-view topology leads to a 1.1% improvement in accuracy, which exceeds the combined gains from 1 and 2. This result proves that the two views are not merely additive but synergistic, validating both the necessity and effectiveness of multi-view topology modeling, as well as the generalizability and universality of the static topology.
- After introducing the MSTC module, the accuracy slightly drops by 0.1%; however, the model size is reduced by 44% (0.99 M parameters), and FLOPs decrease by 39% (0.99 G), demonstrating the lightweight nature of the proposed design.
- Finally, with the addition of the GCTT module, the accuracy improves by 1.5% compared to the baseline, proving that our channel-wise temporal topology modeling effectively captures the relationships between different temporal frames, further enriching temporal feature extraction based on MSTC.
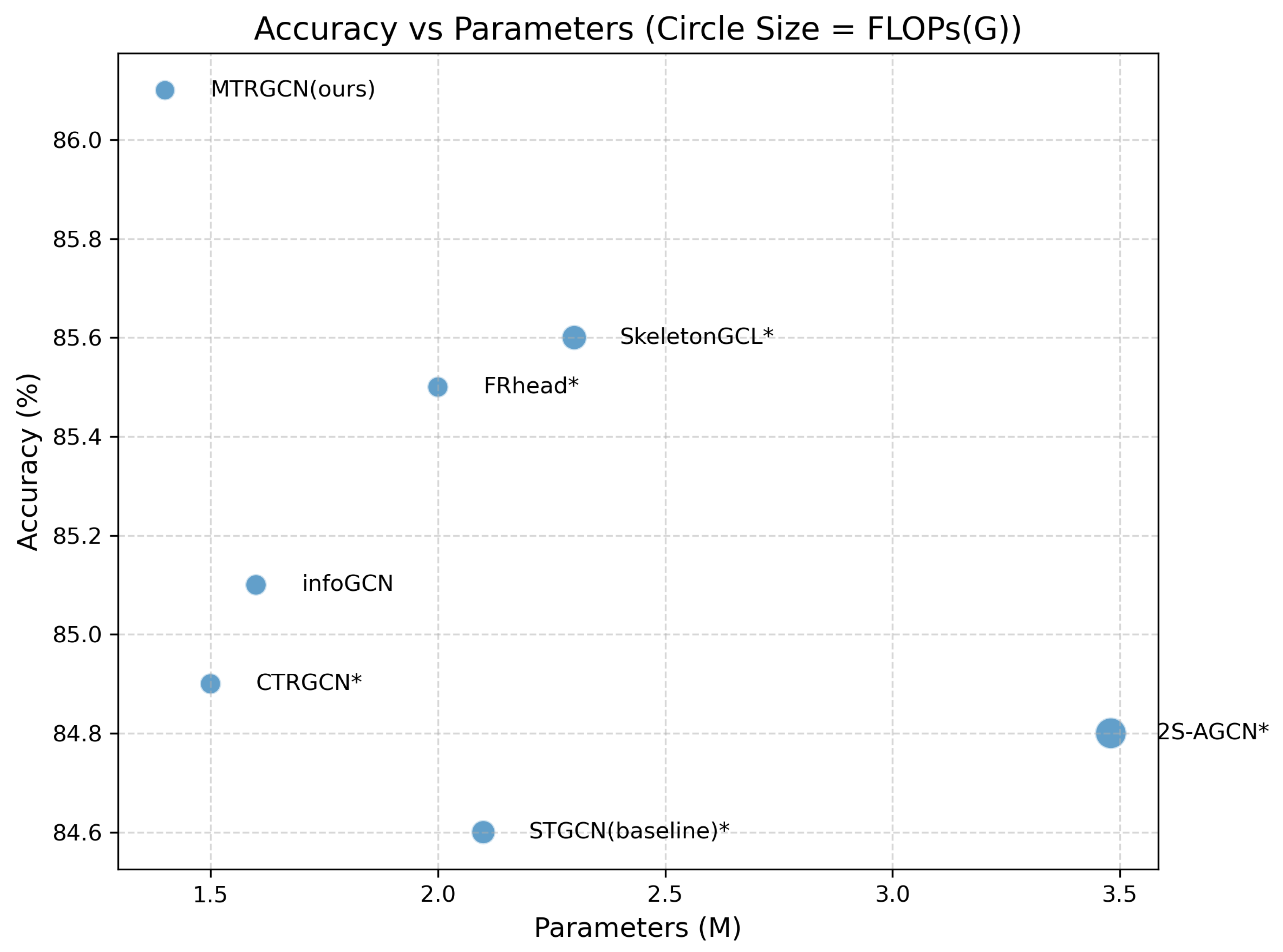
4.4. Comparison with State-of-the-Art
5. Conclusions
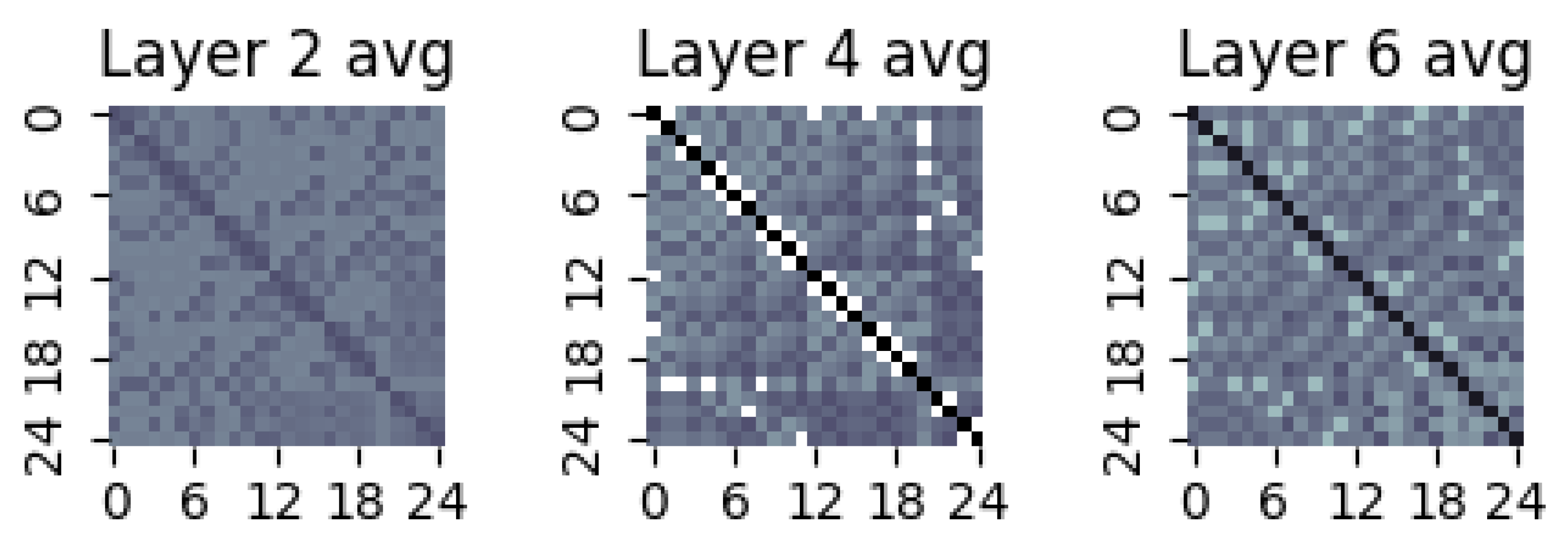
6. Visualization
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
| Acronym | Full Form |
|---|---|
| GCN | Graph Convolutional Network |
| TCN | Temporal Conbolutional Nwtwork |
| MTRGC | Multi-view Topology Refinement Graph Convolution |
| MSTC | MutiScale Temporal Convolution |
| GCTT | Gated Channel-wise Temporal Topology |
References
- Karpathy, A.; Toderici, G.; Shetty, S.; Leung, T.; Sukthankar, R.; Fei-Fei, L. Large-scale video classification with convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 1725–1732. [Google Scholar]
- Simonyan, K.; Zisserman, A. Two-stream convolutional networks for action recognition in videos. Adv. Neural Inf. Process. Syst. 2014, 27, 568–576. [Google Scholar]
- Feichtenhofer, C.; Fan, H.; Malik, J.; He, K. SlowFast networks for video recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6202–6211. [Google Scholar]
- Do, J.; Kim, M. Skateformer: Skeletal-temporal transformer for human action recognition. In Proceedings of the European Conference on Computer Vision (ECCV), Milan, Italy, 29 September–October 4; pp. 401–420.
- Ray, A.; Raj, A.; Kolekar, M.H. Autoregressive Adaptive Hypergraph Transformer for Skeleton-based Activity Recognition. In Proceedings of the 2025 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 26 February–6 March 2025; pp. 9690–9699. [Google Scholar]
- Liu, Q.; Wu, Y.; Li, B.; Ma, Y.; Li, H.; Yu, Y. SHoTGCN: Spatial high-order temporal GCN for skeleton-based action recognition. Neurocomputing 2025, 632, 129697. [Google Scholar] [CrossRef]
- Ni, B.; Wang, G.; Moulin, P. RGBD-HuDaAct: A color-depth video database for human daily activity recognition. In Proceedings of the 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 6–13 November 2011; pp. 1147–1153. [Google Scholar]
- Gao, C.; Du, Y.; Liu, J.; Lv, J.; Yang, L.; Meng, D.; Hauptmann, A.G. INFAR Dataset: Infrared action recognition at different times. Neurocomputing 2016, 212, 36–47. [Google Scholar] [CrossRef]
- Hussein, M.E.; Torki, M.; Gowayyed, M.A.; El-Saban, M. Human action recognition using a temporal hierarchy of covariance descriptors on 3D joint locations. In Proceedings of the 23rd International Joint Conference on Artificial Intelligence (IJCAI), Beijing, China, 3–9 August 2013; pp. 2466–2472. [Google Scholar]
- Wang, H.; Wang, L. Modeling temporal dynamics and spatial configurations of actions using two-stream recurrent neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 499–508. [Google Scholar]
- Liu, J.; Shahroudy, A.; Xu, D.; Wang, G. Spatio-temporal LSTM with trust gates for 3D human action recognition. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 September 2016; pp. 816–833. [Google Scholar]
- Li, C.; Zhong, Q.; Xie, D.; Pu, S. Skeleton-based action recognition with convolutional neural networks. In Proceedings of the 2017 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), Hong Kong, China, 10–14 July 2017; pp. 597–600. [Google Scholar]
- Shi, L.; Zhang, Y.; Cheng, J.; Lu, H. Skeleton-based action recognition with directed graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 7912–7921. [Google Scholar]
- Yan, S.; Xiong, Y.; Lin, D. Spatial temporal graph convolutional networks for skeleton-based action recognition. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. No. 1. [Google Scholar]
- Shi, L.; Zhang, Y.; Cheng, J.; Lu, H. Two-stream adaptive graph convolutional networks for skeleton-based action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 12026–12035. [Google Scholar]
- Chen, Y.; Zhang, Z.; Yuan, C.; Li, B.; Deng, Y.; Hu, W. Channel-wise topology refinement graph convolution for skeleton-based action recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 13359–13368. [Google Scholar]
- Zhou, Y.; Yan, X.; Cheng, Z.Q.; Yan, Y.; Dai, Q.; Hua, X.S. BlockGCN: Redefine topology awareness for skeleton-based action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 17–21 June 2024; pp. 2049–2058. [Google Scholar]
- Zhou, H.; Liu, Q.; Wang, Y. Learning discriminative representations for skeleton-based action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 10608–10617. [Google Scholar]
- Song, Y.F.; Zhang, Z.; Shan, C.; Wang, L. Constructing stronger and faster baselines for skeleton-based action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 1474–1488. [Google Scholar] [CrossRef]
- Chen, Z.; Li, S.; Yang, B.; Li, Q.; Liu, H. Multi-scale spatial temporal graph convolutional network for skeleton-based action recognition. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 2–9 February 2021; Volume 35, No. 2. pp. 1113–1122. [Google Scholar]
- Shahroudy, A.; Liu, J.; Ng, T.T.; Wang, G. NTU RGB+D: A large scale dataset for 3D human activity analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1010–1019. [Google Scholar]
- Liu, J.; Shahroudy, A.; Perez, M.; Wang, G.; Duan, L.Y.; Kot, A.C. NTU RGB+D 120: A large-scale benchmark for 3D human activity understanding. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2684–2701. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Nie, X.; Xia, Y.; Wu, Y.; Zhu, S.C. Cross-view action modeling, learning and recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 2649–2656. [Google Scholar]
- Chi, H.G.; Ha, M.H.; Chi, S.; Lee, S.W.; Huang, Q.; Ramani, K. InfoGCN: Representation learning for human skeleton-based action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 20186–20196. [Google Scholar]
- Wu, Z.; Sun, P.; Chen, X.; Tang, K.; Xu, T.; Zou, L.; Weise, T. SelfGCN: Graph convolution network with self-attention for skeleton-based action recognition. IEEE Trans. Image Process. 2024, 33, 4391–4403. [Google Scholar] [CrossRef]
- Wang, X.; Xu, X.; Mu, Y. Neural Koopman Pooling: Control-inspired temporal dynamics encoding for skeleton-based action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 10597–10607. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar] [CrossRef]
- Liu, D.; Chen, P.; Yao, M.; Lu, Y.; Cai, Z.; Tian, Y. TSGCNeXt: Dynamic-static multi-graph convolution for efficient skeleton-based action recognition with long-term learning potential. arXiv 2023, arXiv:2304.11631. [Google Scholar]
- Liu, Z.; Zhang, H.; Chen, Z.; Wang, Z.; Ouyang, W. Disentangling and unifying graph convolutions for skeleton-based action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 143–152. [Google Scholar]
- Cheng, K.; Zhang, Y.; He, X.; Chen, W.; Cheng, J.; Lu, H. Skeleton-based action recognition with shift graph convolutional network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 183–192. [Google Scholar]
- Zhang, P.; Lan, C.; Zeng, W.; Xing, J.; Xue, J.; Zheng, N. Semantics-guided neural networks for efficient skeleton-based human action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 1112–1121. [Google Scholar]
- Li, M.; Chen, S.; Chen, X.; Zhang, Y.; Wang, Y.; Tian, Q. Actional-structural graph convolutional networks for skeleton-based action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 3595–3603. [Google Scholar]
- Ye, F.; Pu, S.; Zhong, Q.; Li, C.; Xie, D.; Tang, H. Dynamic GCN: Context-enriched topology learning for skeleton-based action recognition. In Proceedings of the 28th ACM International Conference on Multimedia (ACM MM), Seattle, WA, USA, 12–16 October 2020; pp. 55–63. [Google Scholar]
- Veeriah, V.; Zhuang, N.; Qi, G.J. Differential recurrent neural networks for action recognition. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 4041–4049. [Google Scholar]
- Du, Y.; Wang, W.; Wang, L. Hierarchical recurrent neural network for skeleton-based action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1110–1118. [Google Scholar]
- Wang, J.; Liu, Z.; Wu, Y.; Yuan, J. Learning actionlet ensemble for 3D human action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 914–927. [Google Scholar] [CrossRef] [PubMed]
- Lee, I.; Kim, D.; Kang, S.; Lee, S. Ensemble deep learning for skeleton-based action recognition using temporal sliding LSTM networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1012–1020. [Google Scholar]
- Si, C.; Chen, W.; Wang, W.; Wang, L.; Tan, T. An attention enhanced graph convolutional LSTM network for skeleton-based action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 1227–1236. [Google Scholar]
- Cheng, K.; Zhang, Y.; Cao, C.; Shi, L.; Cheng, J.; Lu, H. Decoupling GCN with DropGraph module for skeleton-based action recognition. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 536–553. [Google Scholar]

| Model | Multi-View | MSTC | GCTT | Params | Flops | Acc(%) | |
|---|---|---|---|---|---|---|---|
| Dynamic | Static | ||||||
| STGCN (baseline) | - | - | - | - | 2.09 M | 2.34 G | 84.6 |
| + dynamic only | ✓ | - | - | - | 2.25 M | 2.54 G | 85.0 (↑0.4) |
| + static only | - | ✓ | - | - | 2.09 M | 2.34 G | 84.9 (↑0.3) |
| + Multi-view | ✓ | ✓ | - | - | 2.26 M | 2.54 G | 85.7 (↑1.1) |
| + MSTC | ✓ | ✓ | ✓ | - | 1.27 M | 1.55 G | 85.6 |
| Whole model | ✓ | ✓ | ✓ | ✓ | 1.37 M | 1.65 G | 86.1 (↑1.5) |
| Kernel Size 1 | Kernel Size 2 | Acc (%) |
|---|---|---|
| 5 | 5 | 85.7 |
| 5 | 7 | 86.1 |
| 7 | 7 | 85.2 |
| 7 | 9 | 85.6 |
| 9 | 9 | 85.5 |
| Methods | NTU60-XSub | NTU60-XView | NTU120-XSub | NTU120-XSet |
|---|---|---|---|---|
| STGCN [14] | 81.5 | 88.3 | – | – |
| SGN [31] | 89.0 | 94.5 | 79.2 | 81.5 |
| AS-GCN [32] | 86.8 | 94.2 | – | – |
| 2s-AGCN [15] | 88.5 | 95.1 | – | – |
| DGNN [13] | 89.9 | 96.1 | – | – |
| Shift-GCN [30] | 90.7 | 96.5 | 85.9 | 87.6 |
| MS-G3D [29] | 91.5 | 96.2 | 86.9 | 88.4 |
| Dynamic-GCN [33] | 91.5 | 96.0 | 87.3 | 88.6 |
| MST-GCN [20] | 91.5 | 96.6 | 87.5 | 88.8 |
| CTRGCN [16] | 92.4 | 96.8 | 88.9 | 90.6 |
| InfoGCN (4S) [24] | – | – | 89.4 | 90.7 |
| Efficient-G4 [19] | 92.1 | – | 88.7 | 88.9 |
| FRhead [18] | 92.8 | 96.8 | 89.5 | 90.9 |
| MTR-GCN (2S) | 92.3 | 96.4 | 89.2 | 90.4 |
| MTR-GCN (4S) | 92.8 | 96.8 | 89.6 | 90.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhang, X.; Zhang, C. Graph Convolutional Network with Multi-View Topology for Lightweight Skeleton-Based Action Recognition. Symmetry 2025, 17, 1235. https://doi.org/10.3390/sym17081235
Wang L, Zhang X, Zhang C. Graph Convolutional Network with Multi-View Topology for Lightweight Skeleton-Based Action Recognition. Symmetry. 2025; 17(8):1235. https://doi.org/10.3390/sym17081235
Chicago/Turabian StyleWang, Liangliang, Xu Zhang, and Chuang Zhang. 2025. "Graph Convolutional Network with Multi-View Topology for Lightweight Skeleton-Based Action Recognition" Symmetry 17, no. 8: 1235. https://doi.org/10.3390/sym17081235
APA StyleWang, L., Zhang, X., & Zhang, C. (2025). Graph Convolutional Network with Multi-View Topology for Lightweight Skeleton-Based Action Recognition. Symmetry, 17(8), 1235. https://doi.org/10.3390/sym17081235




