Study on Mechanism and Constitutive Modelling of Secondary Anisotropy of Surrounding Rock of Deep Tunnels
Abstract
1. Introduction
2. Capture and Verification of Secondary Anisotropy Induced by Axial-Displacement Constraint
2.1. True Triaxial Test Under Hybrid Stress–Strain Controlled Loading
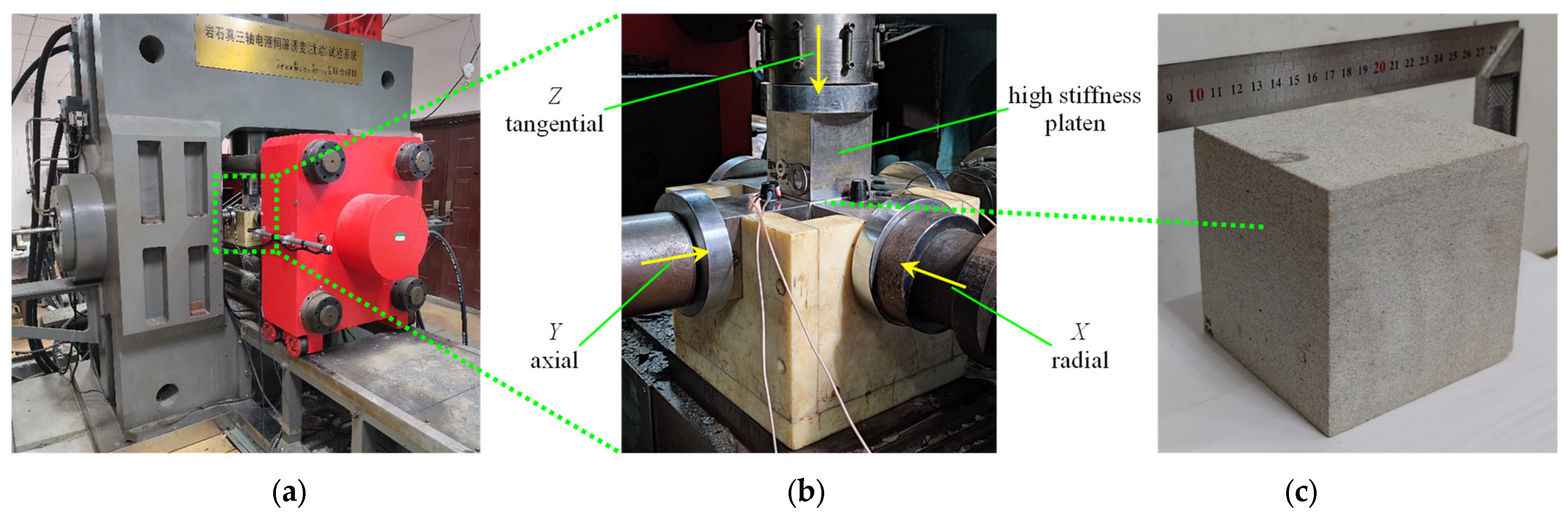
2.1.1. Testing Machine and Rock Specimen Preparation
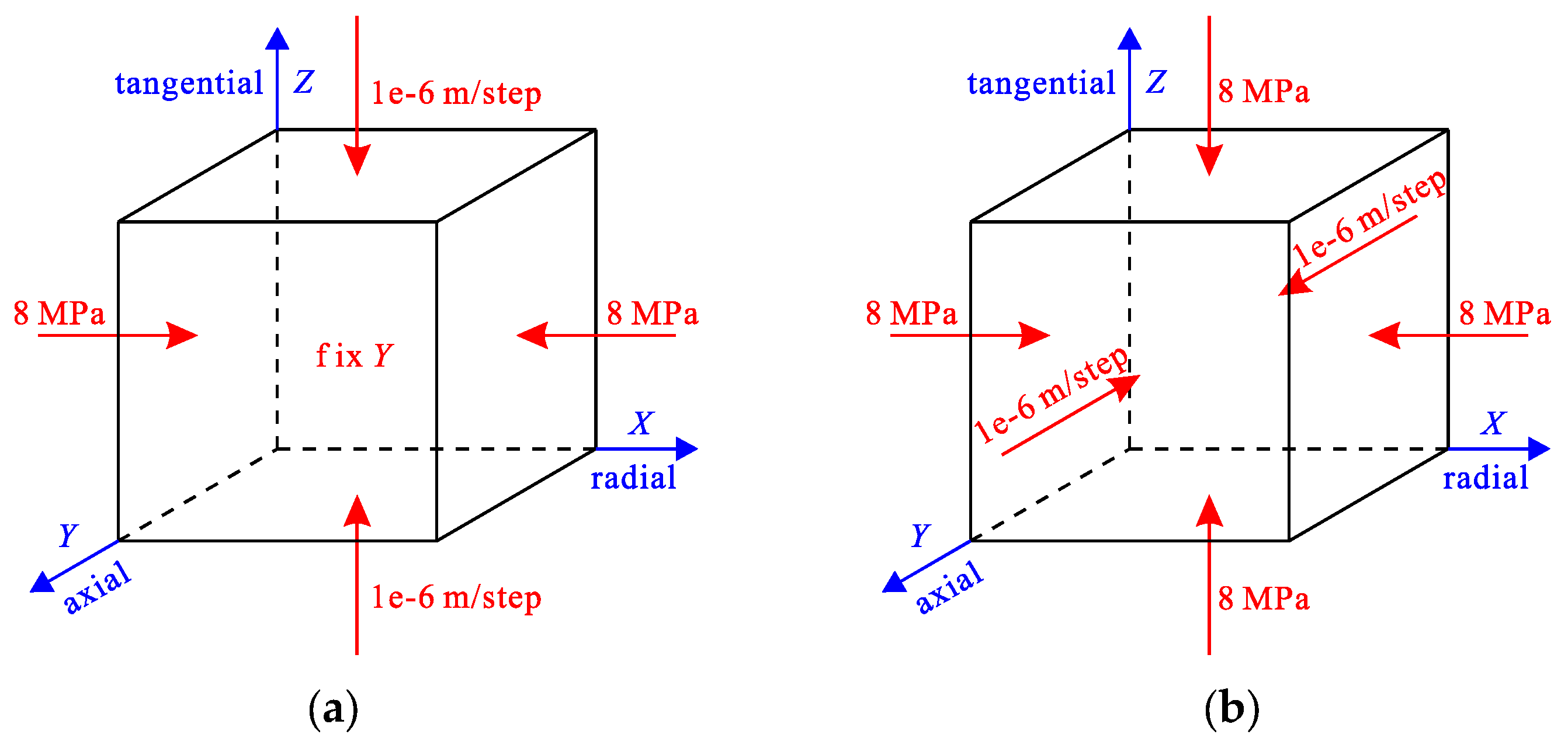
2.1.2. Testing Scheme
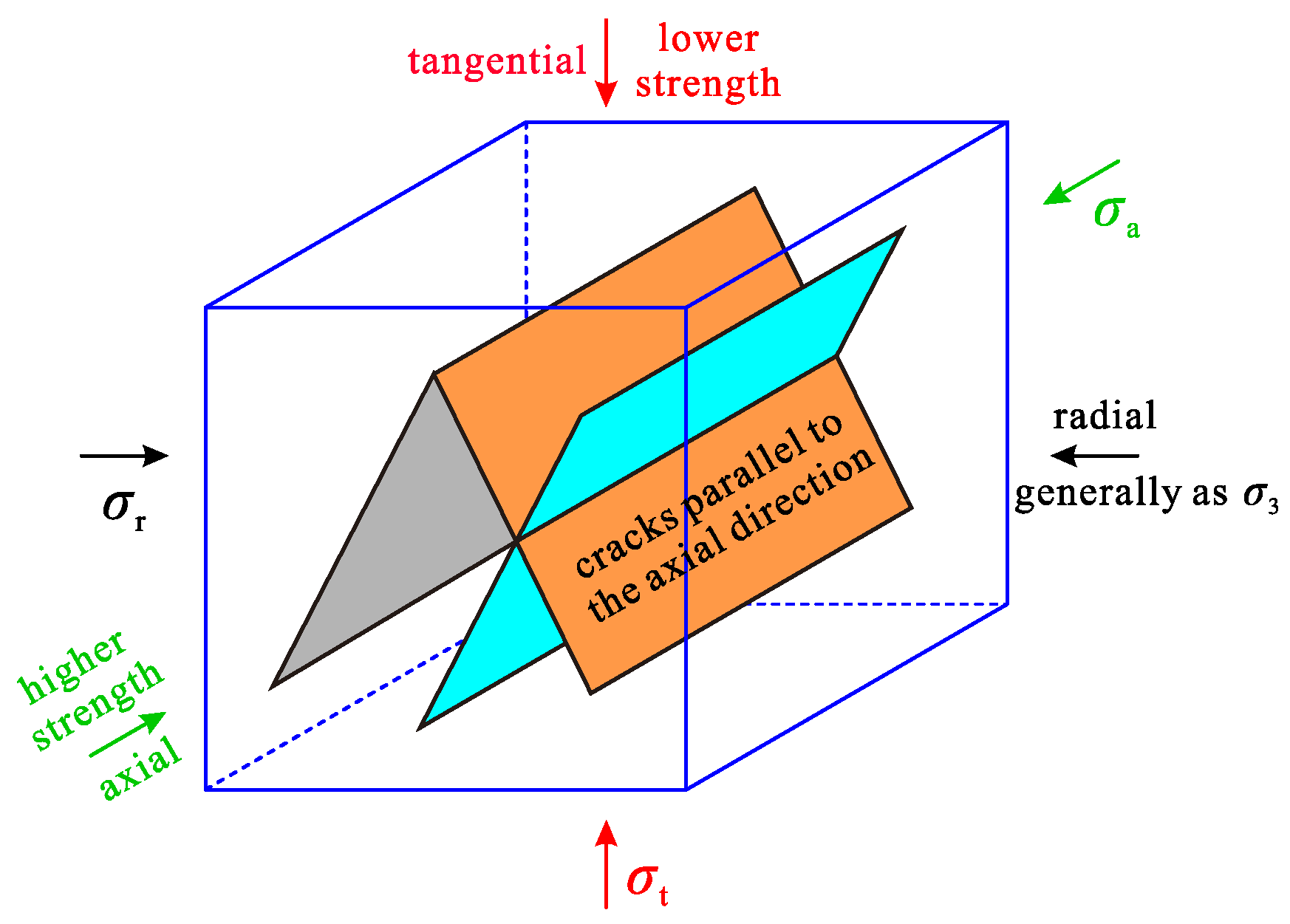
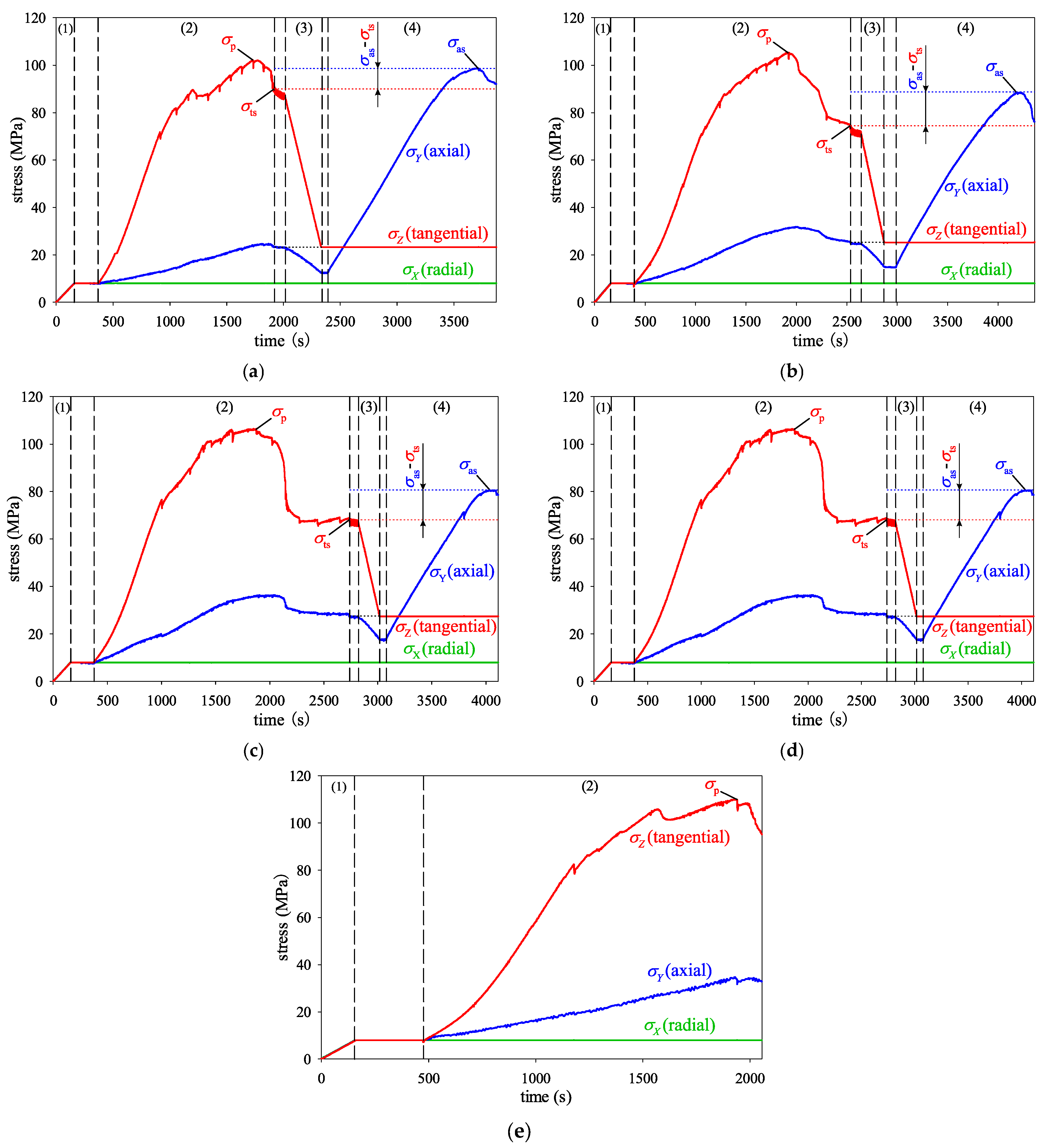
2.1.3. Testing Results and Analysis
2.2. Numerical Simulation of Heterogeneous Rock Specimen
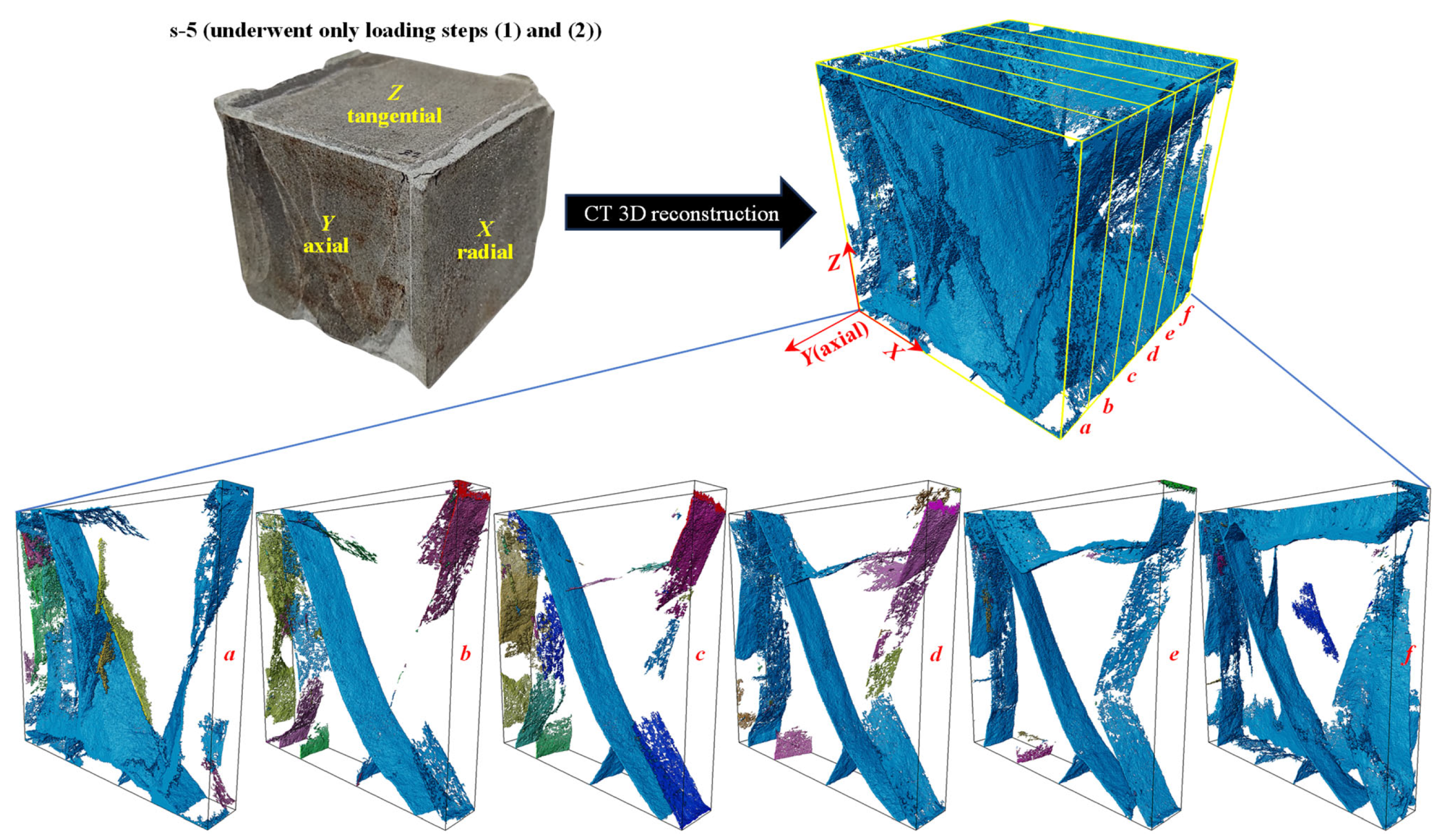
2.3. Field Borehole TV Image
3. A Novel Secondary Anisotropy Model for the Deep Tunnel Surrounding Rock
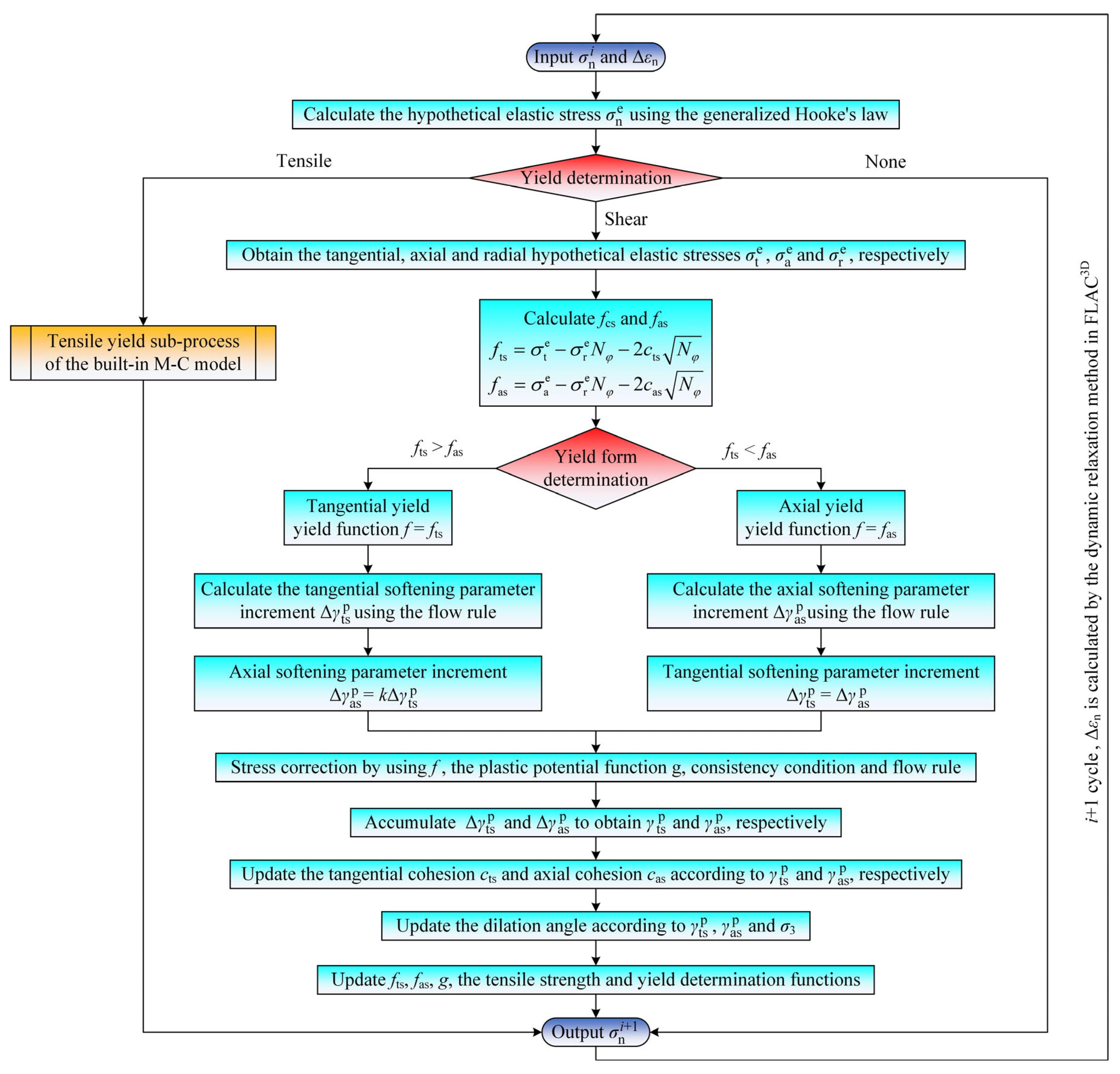
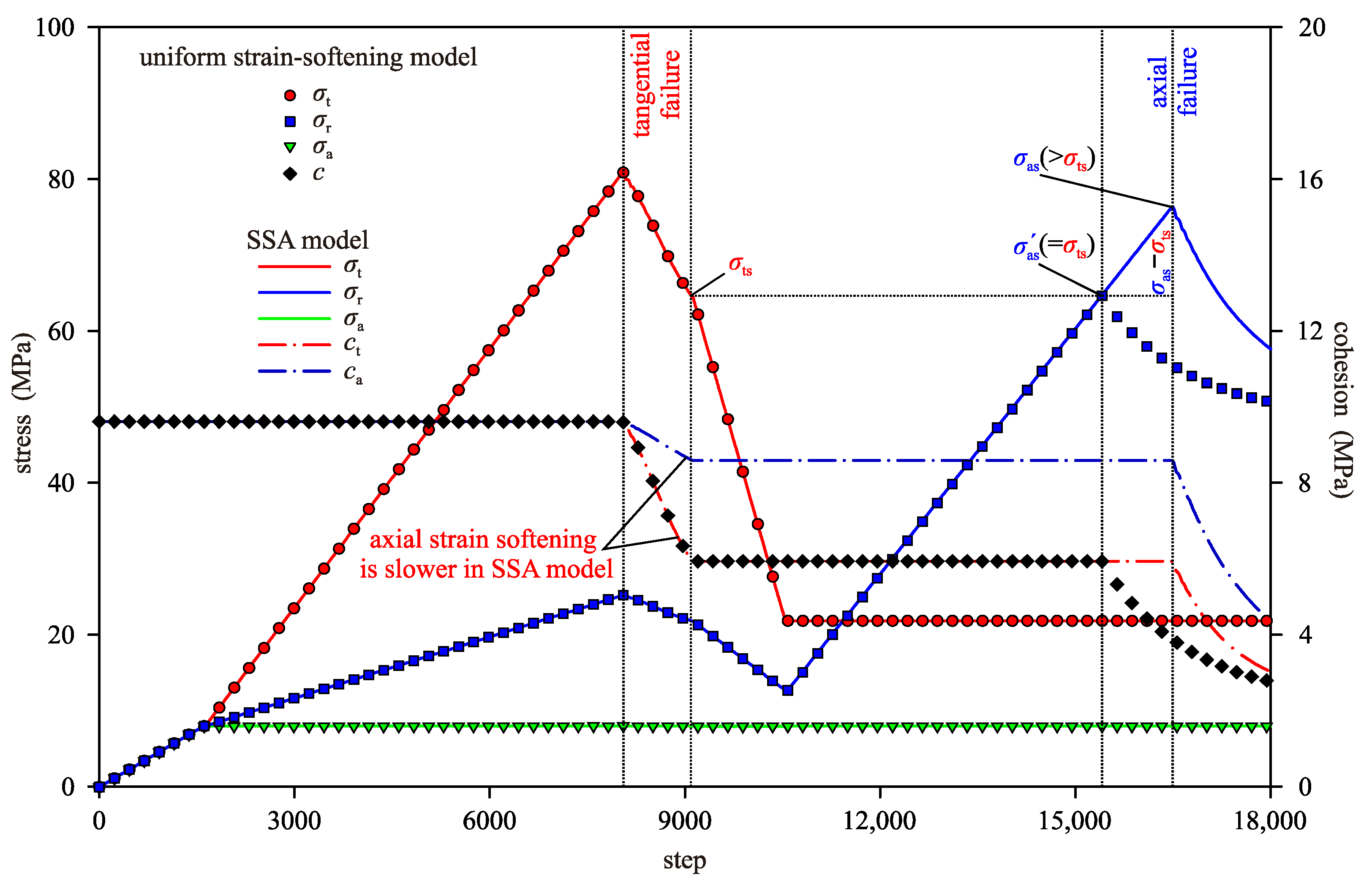
3.1. Numerical Implementation of the Secondary Anisotropy
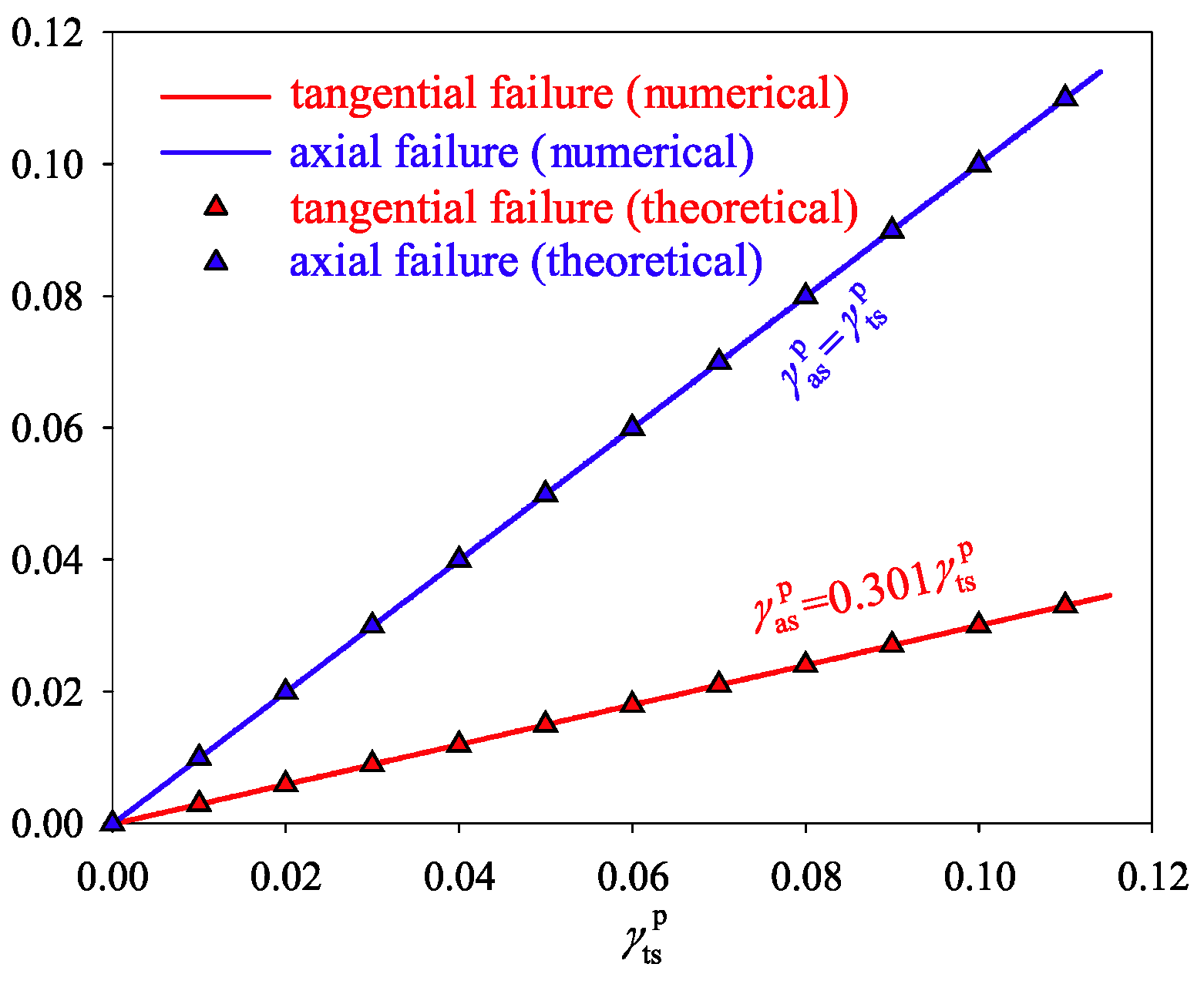
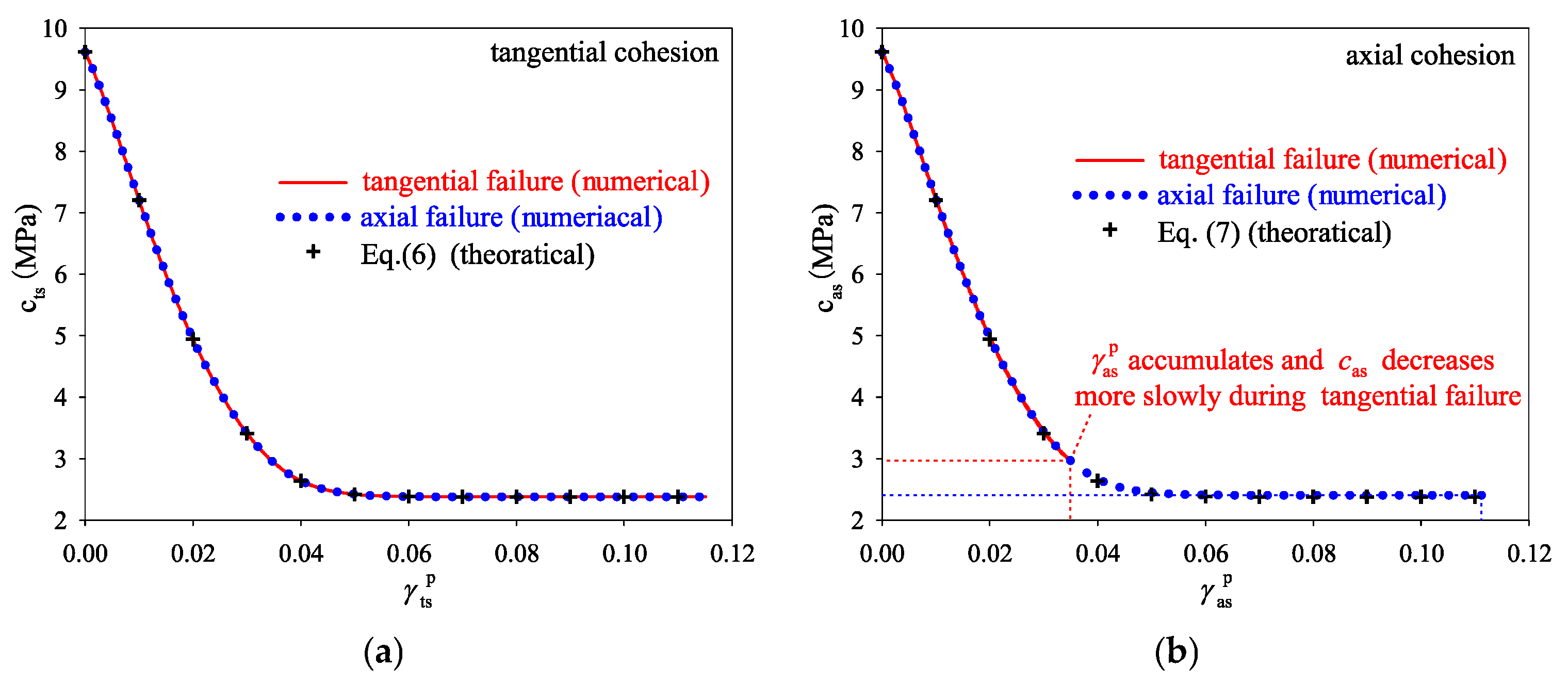
3.2. Determination of k
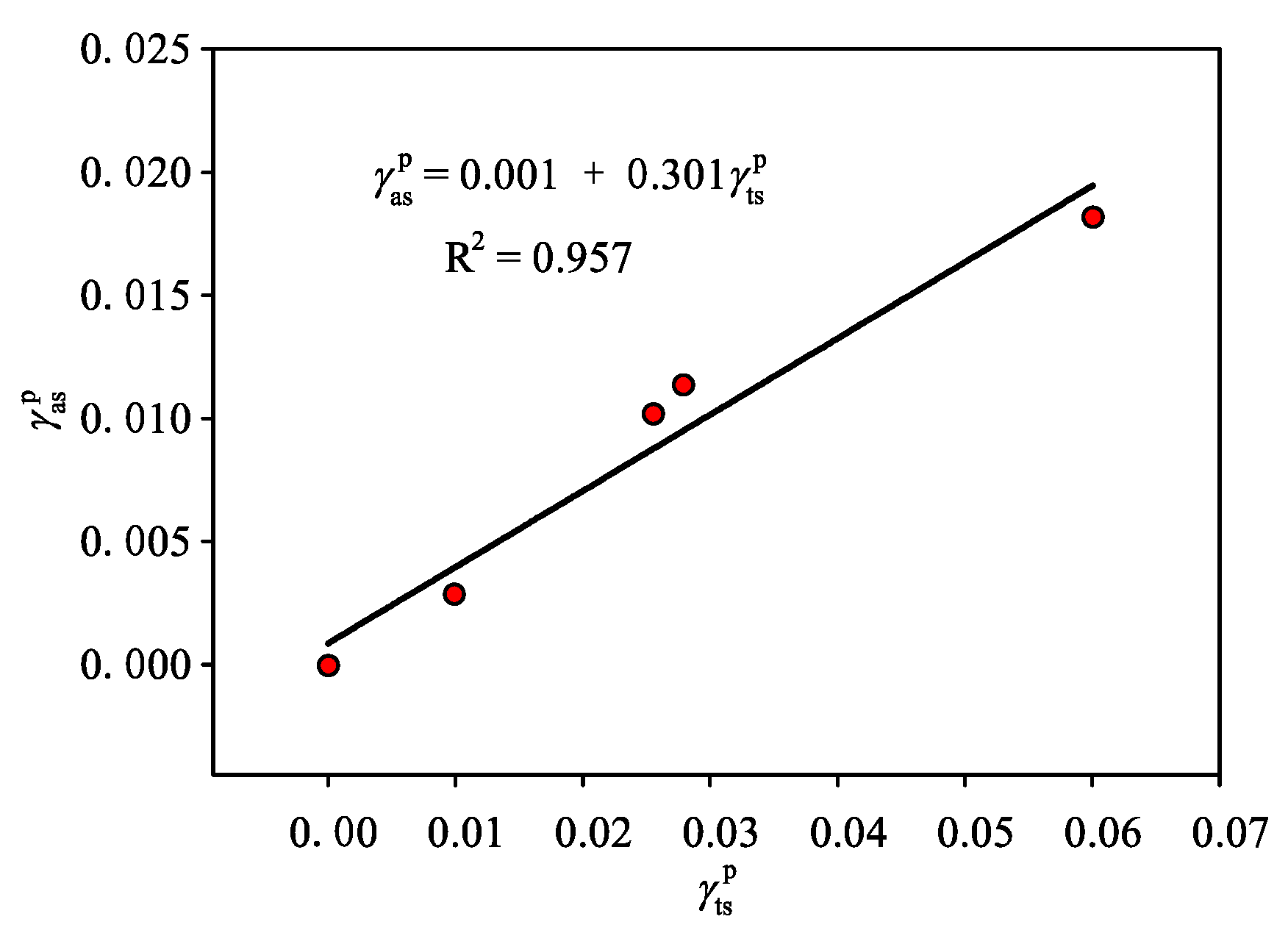
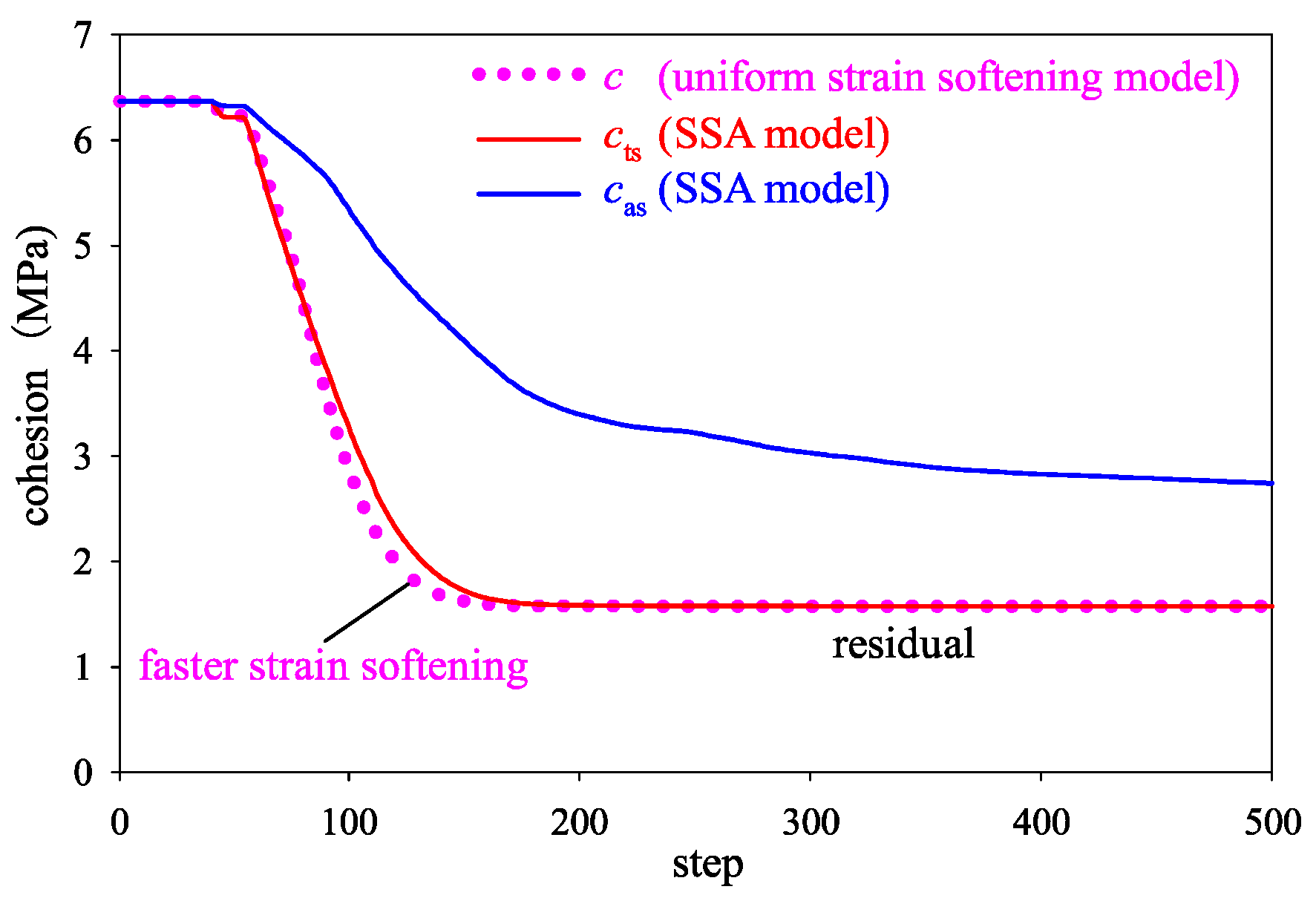
3.3. Model Verification
3.3.1. Verification of the Key Parameters
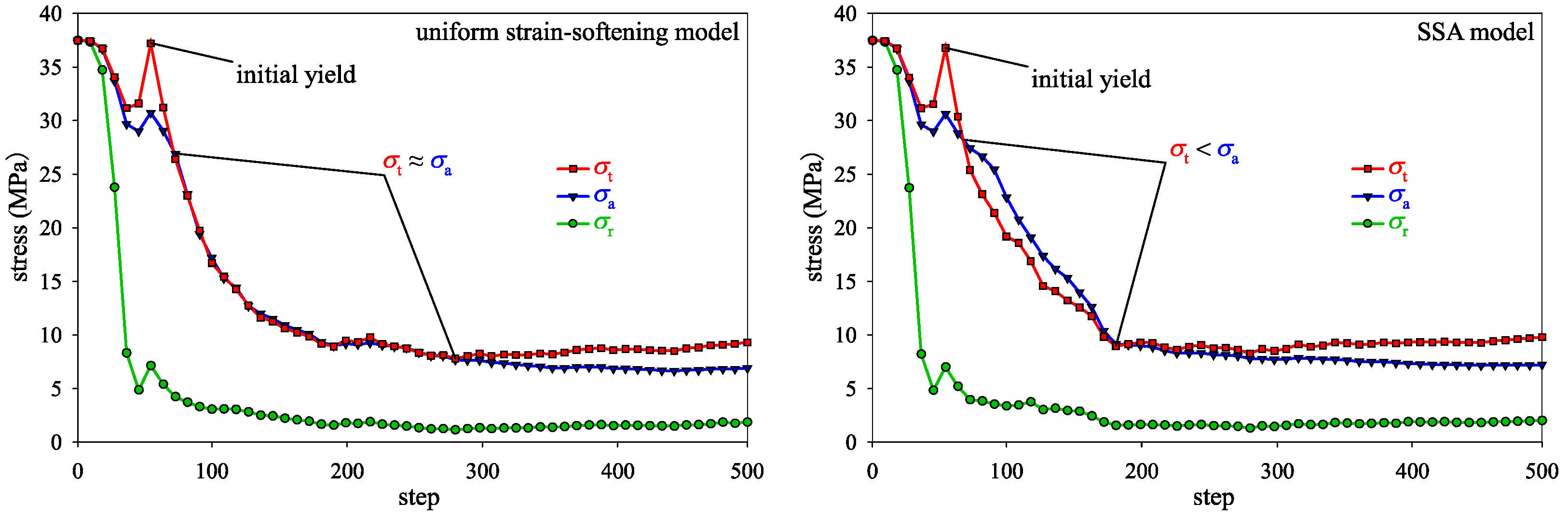
3.3.2. Verification of the Secondary Anisotropy
4. Effects of the Secondary Anisotropy on the Deformation and Failure of a Deep Tunnel Surrounding Rock
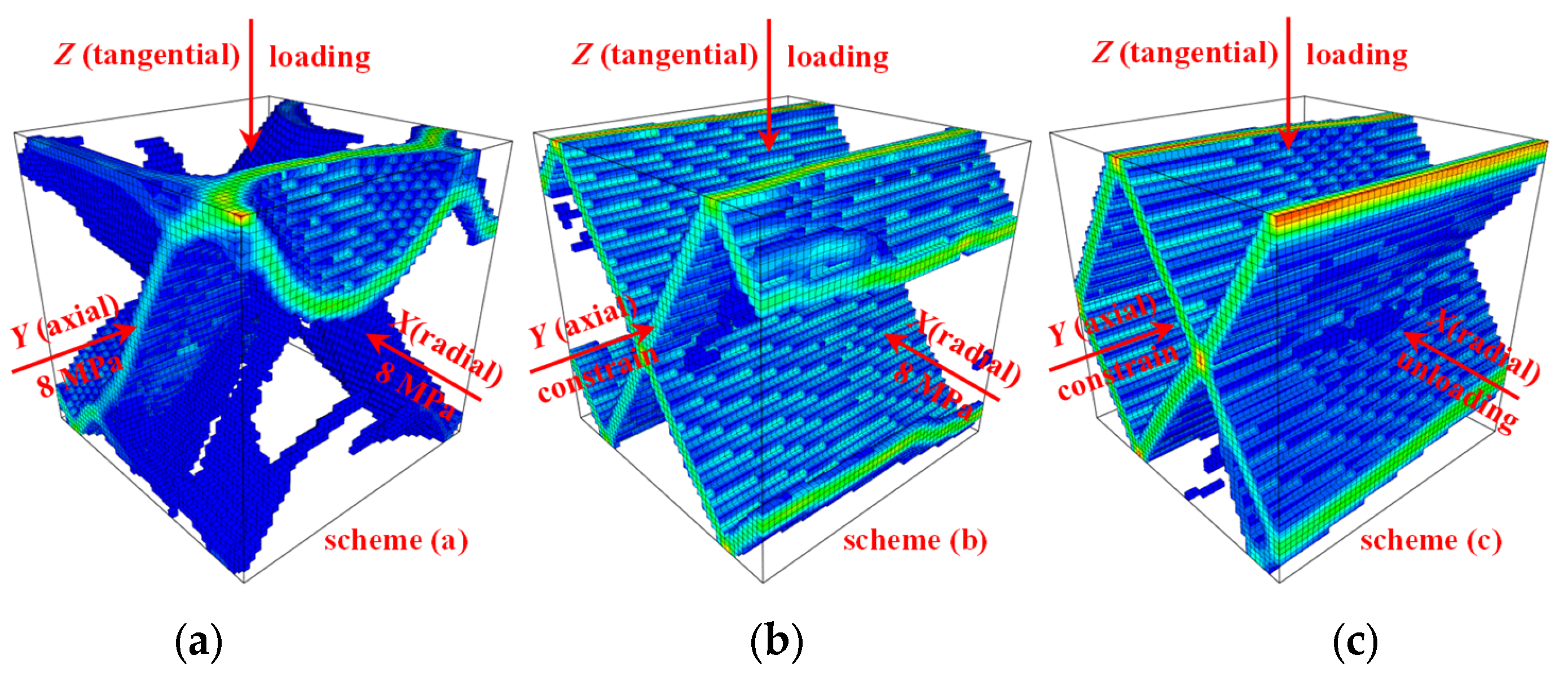
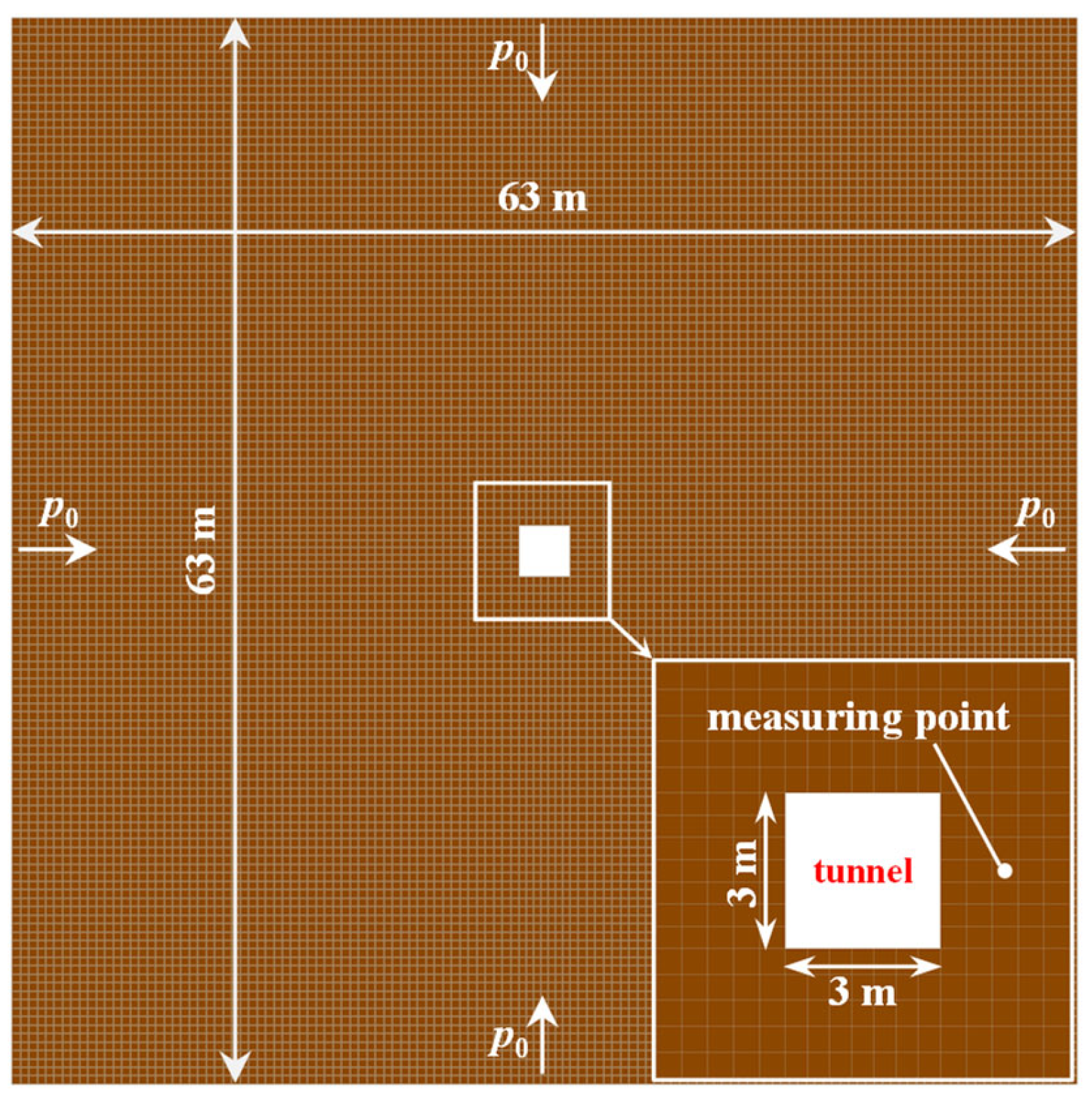
4.1. Modelling and Schemes
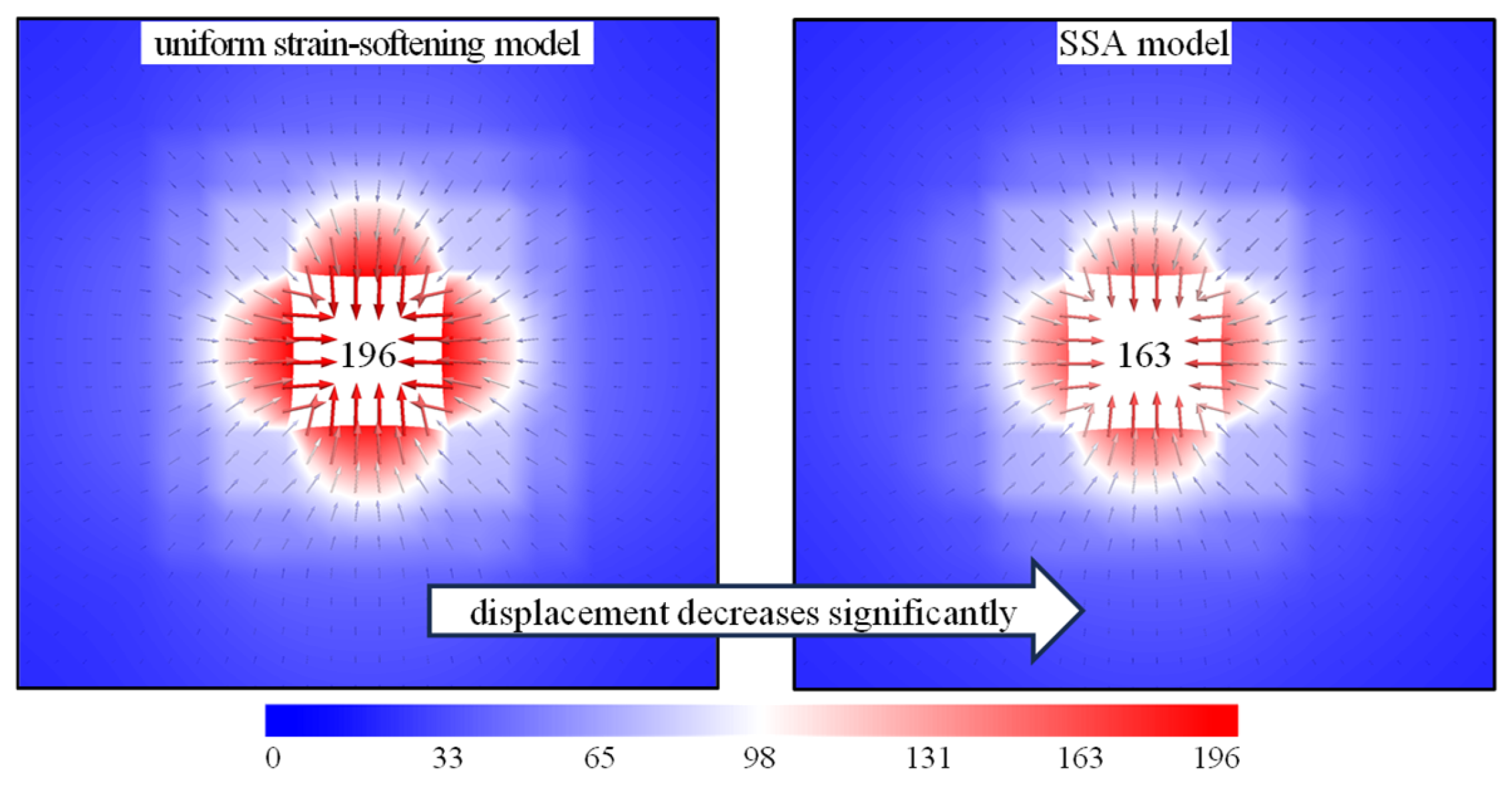
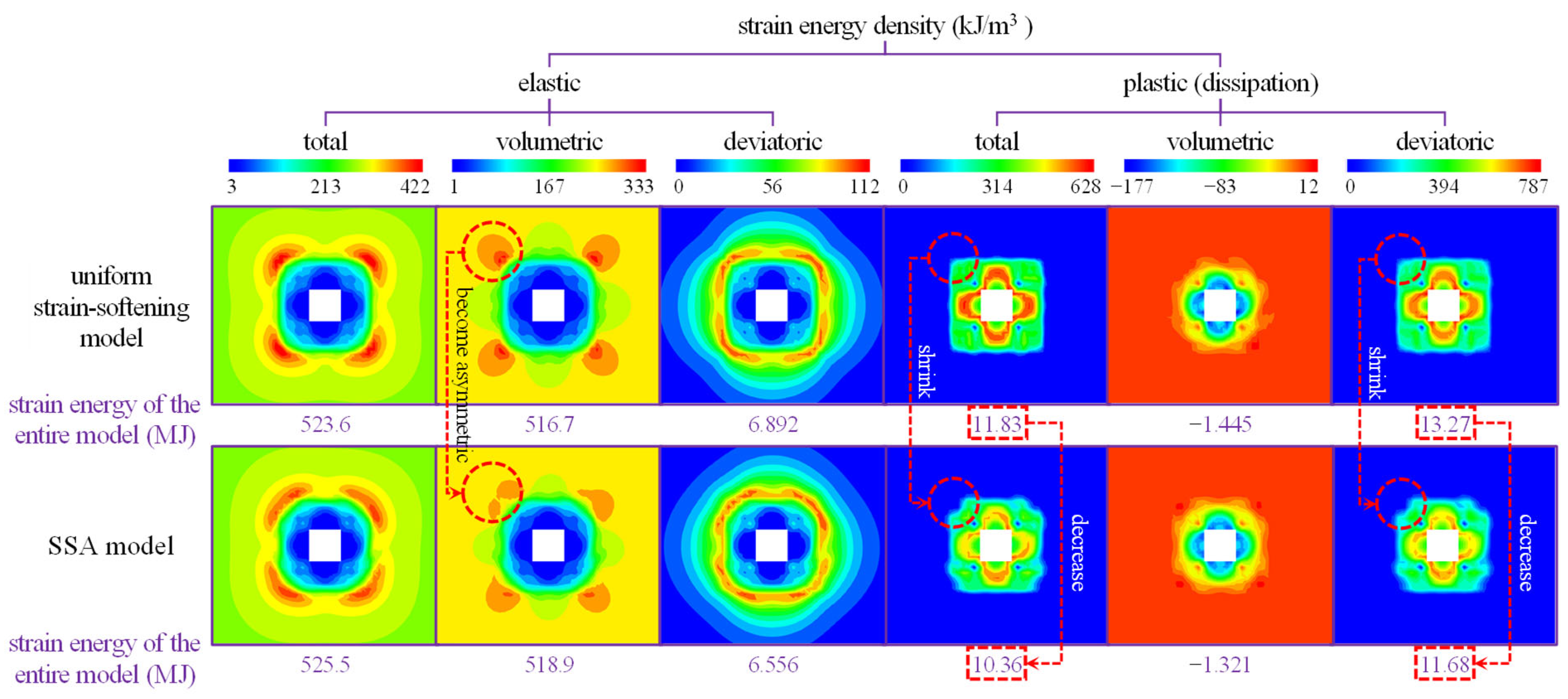
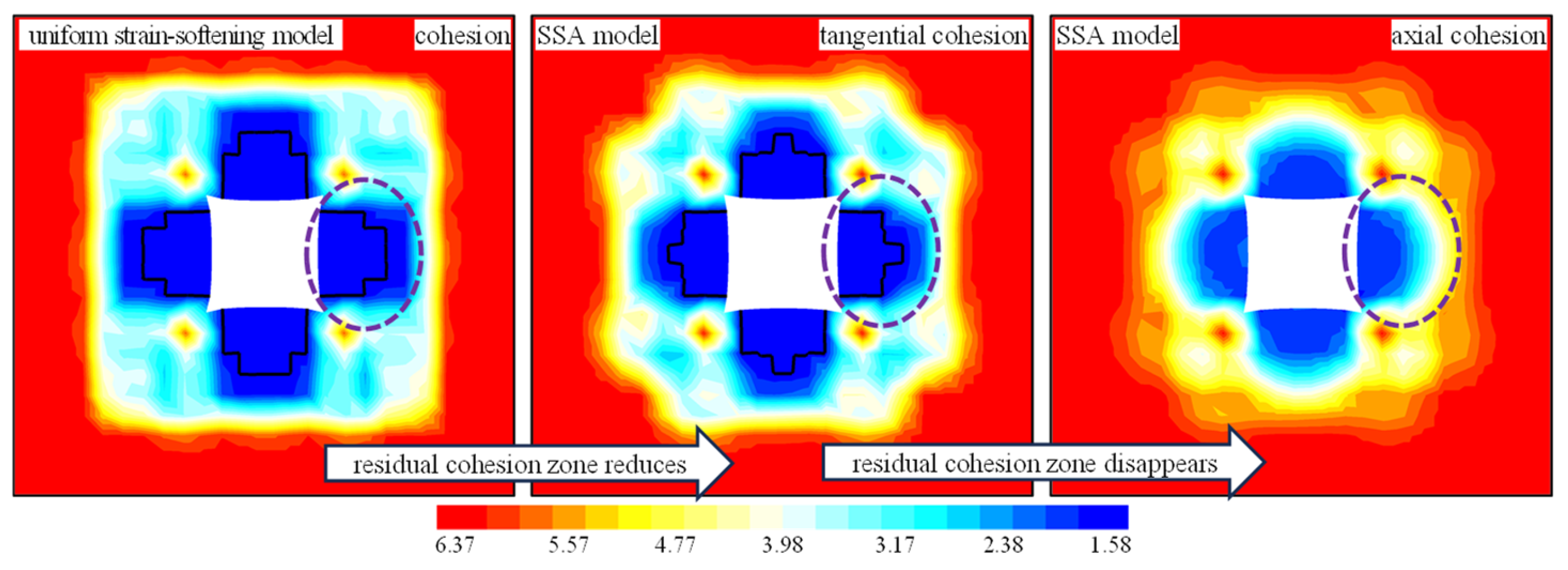
4.2. Numerical Simulation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CT 3D | Computed tomography three-dimensional |
| TV | Television |
| SSA | Strain-softening and secondary anisotropy |
| FLAC3D | Fast Lagrangian Analysis of Continua in 3 Dimensions |
References
- Kang, H.P.; Gao, F.Q.; Xu, G.; Ren, H.W. Mechanical behaviors of coal measures and ground control technologies for China’s deep coal mines—A review. J. Rock Mech. Geotech. 2023, 15, 37–65. [Google Scholar] [CrossRef]
- Xie, S.R.; Li, H.; Chen, D.D.; Feng, S.H.; Yang, J.H.; Ma, X.; Jiang, Z.S.; Xing, S.K. Research on the Control Technology and Key Parameters of External Anchor-Internal Unloading of Surrounding Rock During Gob-Side Entry Driving Under Severe Mining of 1000-m-Deep Mine. Rock Mech. Rock Eng. 2024, 57, 2913–2932. [Google Scholar] [CrossRef]
- Zhou, J.L.; Pan, J.F.; Xia, Y.X.; Du, T.T.; Liu, W.A.; Zhang, C.Y. Mechanism and prevention of coal bursts in gob-side roadway floor under thick and hard roof in the deep mining area of Ordos. Int. J. Coal Sci. Technol. 2024, 11, 80. [Google Scholar] [CrossRef]
- Jain, H.; Kumar, J. Displacements and stresses around a circular tunnel in an elastic medium with pseudo-static horizontal earthquake body forces. Comput. Geotech. 2023, 162, 105663. [Google Scholar] [CrossRef]
- Yin, S.F.; Zheng, X.J.; Wang, E.; Kang, Q.T.; Zhang, X.M. Non-uniform failure and differential pressure relief technology of roadway under irregular goafs in deep close-distance coal seams. Sci. Rep. 2023, 13, 18527. [Google Scholar] [CrossRef]
- Meng, N.K.; Bai, J.B.; Yoo, C. Failure mechanism and control technology of deep soft-rock roadways: Numerical simulation and field study. Undergr. Space 2023, 12, 1–17. [Google Scholar] [CrossRef]
- Ma, L.; Xing, L.; Liu, C.; Cui, T.; Qiao, X.; Miao, W.; Kong, P. Research on the Instability Mechanism and Control Technology of Gob-Side Entry in Deep Mines with Soft Rock. Buildings 2025, 15, 19. [Google Scholar] [CrossRef]
- Yang, S.Q.; Chen, M.; Jing, H.W.; Chen, K.F.; Meng, B. A case study on large deformation failure mechanism of deep soft rock roadway in Xin’An coal mine, China. Eng. Geol. 2017, 217, 89–101. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Practical estimates of rock mass strength. Int. J. Rock Mech. Min. Sci. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]
- Pardoen, B.; Besuelle, P.; Dal Pont, S.; Cosenza, P.; Desrues, J. Accounting for Small-Scale Heterogeneity and Variability of Clay Rock in Homogenised Numerical Micromechanical Response and Microcracking. Rock Mech. Rock Eng. 2020, 53, 2727–2746. [Google Scholar] [CrossRef]
- Xie, S.R.; Wu, Y.Y.; Chen, D.D.; Liu, R.P.; Han, X.T.; Ye, Q.C. Failure analysis and control technology of intersections of large-scale variable cross-section roadways in deep soft rock. Int. J. Coal Sci. Technol. 2022, 9, 19. [Google Scholar] [CrossRef]
- Xin, X.K.; Meng, Q.B.; Pu, H.; Wu, J.Y. Theoretical analysis and numerical simulation analysis of energy distribution characteristics of surrounding rocks of roadways. Tunn. Undergr. Space Technol. 2024, 147, 105747. [Google Scholar] [CrossRef]
- Zheng, K.Y.; Shi, C.H.; Lou, Y.L.; Jia, C.J.; Lei, M.F.; Yang, Y. A computational method for tunnel energy evolution in strain-softening rock mass during excavation unloading based on triaxial stress paths. Comput. Geotech. 2024, 169, 106212. [Google Scholar] [CrossRef]
- Cao, D.; Fan, L.; Huang, R.; Guo, C. Investigation of the Mechanical Properties of Reinforced Calcareous Sand Using a Permeable Polyurethane Polymer Adhesive. Materials 2024, 17, 5277. [Google Scholar] [CrossRef]
- Lu, A.Z.; Xu, G.S.; Sun, F.; Sun, W.Q. Elasto-plastic analysis of a circular tunnel including the effect of the axial in situ stress. Int. J. Rock Mech. Min. Sci. 2010, 47, 50–59. [Google Scholar] [CrossRef]
- Guan, K.; Zhu, W.C.; Wei, J.; Liu, X.G.; Niu, L.L.; Wang, X.R. A finite strain numerical procedure for a circular tunnel in strain-softening rock mass with large deformation. Int. J. Rock Mech. Min. Sci. 2018, 112, 266–280. [Google Scholar] [CrossRef]
- Zou, J.F.; Liu, L.; Xia, M.Y. Simple approach for solution of the quasi-plane-strain problem in a circular tunnel in a strain-softening rock mass considering the out-of-plane stress effect. Undergr. Space 2020, 5, 339–353. [Google Scholar] [CrossRef]
- Zou, J.F.; Yang, T.; Ling, W.; Guo, W.J.; Huang, F.L. A numerical stepwise approach for cavity expansion problem in strain-softening rock or soil mass. Geomech. Eng. 2019, 18, 225–234. [Google Scholar] [CrossRef]
- Yi, K.; Liu, Z.H.; Lu, Z.G.; Zhang, J.W.; Dong, S.Y. Effect of Axial In-Situ Stress in Deep Tunnel Analysis Considering Strain Softening and Dilatancy. Energies 2020, 13, 1502. [Google Scholar] [CrossRef]
- Pourhosseini, O.; Shabanimashcool, M. Development of an elasto-plastic constitutive model for intact rocks. Int. J. Rock Mech. Min. Sci. 2014, 66, 1–12. [Google Scholar] [CrossRef]
- Wu, J.Y.; Li, J.; Faria, R. An energy release rate-based plastic-damage model for concrete. Int. J. Solids Struct. 2006, 43, 583–612. [Google Scholar] [CrossRef]
- Yazdani, S.; Schreyer, H.L. An anisotropic damage model with dilatation for concrete. Mech. Mater. 1988, 7, 231–244. [Google Scholar] [CrossRef]
- Jaeger, J.C. Shear Failure of Anistropic Rocks. Geol. Mag. 1960, 97, 65–72. [Google Scholar] [CrossRef]
- Renani, H.R.; Martin, C.D.; Cai, M. An analytical model for strength of jointed rock masses. Tunn. Undergr. Space Technol. 2019, 94, 103159. [Google Scholar] [CrossRef]
- Shen, J.Y.; Shu, Z.; Cai, M.; Du, S.G. A shear strength model for anisotropic blocky rock masses with persistent joints. Int. J. Rock Mech. Min. Sci. 2020, 134, 104430. [Google Scholar] [CrossRef]
- Li, W.Q.; Hu, H.S. Seismic Sources in Stress-Induced Anisotropic Media. J. Geophys. Res-Solid. Earth 2022, 127, e2021JB023915. [Google Scholar] [CrossRef]
- Li, X.B.; Du, K.; Li, D.Y. True Triaxial Strength and Failure Modes of Cubic Rock Specimens with Unloading the Minor Principal Stress. Rock Mech. Rock Eng. 2015, 48, 2185–2196. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, Z.; Zhu, S.; Wu, J. A Case Study on Tunnel Excavation Stability of Columnar Jointed Rock Masses with Different Dip Angles in the Baihetan Diversion Tunnel. Symmetry 2023, 15, 1232. [Google Scholar] [CrossRef]
- Deng, P.H.; Liu, Q.S.; Lu, H.F. FDEM numerical study on the mechanical characteristics and failure behavior of heterogeneous rock based on the Weibull distribution of mechanical parameters. Comput. Geotech. 2023, 154, 105138. [Google Scholar] [CrossRef]
- Itasca Inc. FLAC3D: Fast Lagrangian Analysis of Continua in 3 Dimension, Version 5.01; Itasca Inc.: Minneapolis, MN, USA, 2012.
- Yi, K.; Kang, H.P.; Ju, W.J.; Liu, Y.D.; Lu, Z.G. Synergistic effect of strain softening and dilatancy in deep tunnel analysis. Tunn. Undergr. Space Technol. 2020, 97, 103280. [Google Scholar] [CrossRef]
- Li, P.F.; Wei, Y.J.; Zhang, M.J.; Huang, Q.F.; Wang, F. Influence of non-associated flow rule on passive face instability for shallow shield tunnels. Tunn. Undergr. Space Technol. 2022, 119, 104202. [Google Scholar] [CrossRef]
- Zhang, M.J.; Di, Q.G.; Li, P.F.; Wei, Y.J.; Wang, F. Influence of non-associated flow rule on face stability for tunnels in cohesive-frictional soils. Tunn. Undergr. Space Technol. 2022, 121, 104320. [Google Scholar] [CrossRef]
- Ban, L.R.; Du, W.S.; Jin, T.W.; Qi, C.Z.; Li, X.Z. A roughness parameter considering joint material properties and peak shear strength model for rock joints. Int. J. Min. Sci. Technol. 2021, 31, 413–420. [Google Scholar] [CrossRef]
- Chen, S.-L.; Hsu, K.-J.; Tang, C.-W.; Zhang, X.-L.; Lai, C.-H. Numerical Analysis of the Crown Displacements Caused by Tunnel Excavation with Rock Bolts. Symmetry 2022, 14, 1508. [Google Scholar] [CrossRef]
- Maina, D.; Konietzky, H. The effect of the intermediate principal stress on pillar strength. Int. J. Coal Sci. Technol. 2025, 12, 8. [Google Scholar] [CrossRef]
- Schwartzkopff, A.K.; Sainoki, A.; Bruning, T.; Karakus, M. A conceptual three-dimensional frictional model to predict the effect of the intermediate principal stress based on the Mohr-Coulomb and Hoek-Brown failure criteria. Int. J. Rock Mech. Min. Sci. 2023, 172, 105605. [Google Scholar] [CrossRef]
- Zhao, X.B.; Chen, H.; Lv, J.; He, X.H.; Qin, Y.W.; Sun, K.M. Triaxial Creep Damage Model for Salt Rock Based on Fractional Derivative. Sustainability 2023, 15, 10369. [Google Scholar] [CrossRef]
- Mahetaji, M.; Brahma, J.; Vij, R.K. A new extended Mohr-Coulomb criterion in the space of three-dimensional stresses on the in-situ rock. Geomech. Eng. 2023, 32, 49–68. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, R.H.; Zhang, Q.; Huang, X.H.; Wang, W.; Huang, S.L. Mechanical parameter evolutions and deterioration constitutive model for ductile-brittle failure of surrounding rock in high-stress underground engineering. Undergr. Space 2024, 15, 131–152. [Google Scholar] [CrossRef]
- Yi, K.; Liu, Z.H.; Lu, Z.G.; Zhang, J.W.; Sun, Z.Y. Transfer and dissipation of strain energy in surrounding rock of deep roadway considering strain softening and dilatancy. Energy Sci. Eng. 2021, 9, 27–39. [Google Scholar] [CrossRef]
- Kang, H.; Yi, K. Simulation study on dilatant and rheologic properties of soft rocks surrounding deep roadway and its application. J. China Coal Soc. 2023, 48, 15–33. [Google Scholar] [CrossRef]
- Kang, H.; Yi, B.; Gao, F.; Lu, H. Database and characteristics of underground in-situ stress distribution in Chinese coal mines. J. China Coal Soc. 2019, 44, 23–33. [Google Scholar] [CrossRef]
- Lu, Z.; Ju, W.; Gao, F.; Du, T. Numerical analysis on the factors affecting post-peak characteristics of coal under uniaxial compression. Int. J. Coal Sci. Technol. 2024, 11, 2. [Google Scholar] [CrossRef]
- Lv, H.; Yang, X.; Yu, Y.; Liu, W. Research on Rock Energy Constitutive Model Based on Functional Principle. Symmetry 2024, 16, 1250. [Google Scholar] [CrossRef]




| Young’s Modulus /GPa | Poisson’s Ratio | UCS /MPa | Tensile Strength /MPa | Cohesion /MPa | Friction Angle /(°) | Density /g·cm−3 |
|---|---|---|---|---|---|---|
| 4.31 | 0.22 | 39.71 | 2.32 | 9.62 | 41 | 2.37 |
| Specimen No. | Reach Peak Stress in Z Direction (Tangential) | Stop Loading in Z Direction (Tangential) | Reach Peak Stress in Y Direction (Axial) | σas–σts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z (σts) | X | Y (σas) | Z | ||
| s-1 | 8.001 | 24.143 | 102.245 | 8.002 | 23.495 | 90.302 | 7.999 | 98.671 | 23.497 | 8.369 |
| s-2 | 8.000 | 31.440 | 105.311 | 8.000 | 25.205 | 74.583 | 8.001 | 88.558 | 25.205 | 13.975 |
| s-3 | 7.999 | 30.588 | 110.604 | 7.998 | 25.582 | 75.801 | 8.000 | 91.897 | 25.580 | 16.096 |
| s-4 | 8.001 | 36.092 | 106.012 | 8.000 | 27.513 | 67.972 | 7.998 | 80.621 | 27.511 | 12.649 |
| s-5 | 7.998 | 34.590 | 110.060 | did not undergo these loading steps | ||||||
| Specimen No. | Reach Peak Stress in Z Direction (Tangential) | Stop Loading in Z Direction (Tangential) | Reach Peak Stress in Y Direction (Axial) | |||
|---|---|---|---|---|---|---|
| c0/MPa | cts/MPa | /10−3 | cas/MPa | /10−3 | ||
| s-1 | 9.919 | 0 | 7.459 | 9.91 | 9.289 | 2.88 |
| s-2 | 9.028 | 0 | 3.766 | 25.52 | 6.713 | 10.21 |
| s-3 | 10.317 | 0 | 3.953 | 27.87 | 7.351 | 11.39 |
| s-4 | 8.360 | 0 | 2.081 | 60.05 | 4.610 | 18.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, K.; Gong, P.; Lu, Z.; Su, C.; Duan, K. Study on Mechanism and Constitutive Modelling of Secondary Anisotropy of Surrounding Rock of Deep Tunnels. Symmetry 2025, 17, 1234. https://doi.org/10.3390/sym17081234
Yi K, Gong P, Lu Z, Su C, Duan K. Study on Mechanism and Constitutive Modelling of Secondary Anisotropy of Surrounding Rock of Deep Tunnels. Symmetry. 2025; 17(8):1234. https://doi.org/10.3390/sym17081234
Chicago/Turabian StyleYi, Kang, Peilin Gong, Zhiguo Lu, Chao Su, and Kaijie Duan. 2025. "Study on Mechanism and Constitutive Modelling of Secondary Anisotropy of Surrounding Rock of Deep Tunnels" Symmetry 17, no. 8: 1234. https://doi.org/10.3390/sym17081234
APA StyleYi, K., Gong, P., Lu, Z., Su, C., & Duan, K. (2025). Study on Mechanism and Constitutive Modelling of Secondary Anisotropy of Surrounding Rock of Deep Tunnels. Symmetry, 17(8), 1234. https://doi.org/10.3390/sym17081234






