Reusable Fuzzy Extractor from Isogeny-Based Assumptions

Abstract

A fuzzy extractor is a foundational cryptographic component that enables the extraction of reproducible and uniformly random strings from sources with inherent noise, such as biometric traits. Reusable fuzzy extractor guarantees the security of multiple extractions from the same noisy source. In addition, although isogeny-based cryptography has become an important branch in post-quantum cryptography, the study of fuzzy extractors based on isogeny assumptions is still in its early stages and holds much room for improvement. In this paper, we give two reusable fuzzy extractor schemes derived from isogeny-based assumptions: one is based on the linear hidden shift assumption over group actions, while the other is built upon the group-action decisional Diffie–Hellman assumption within the isogeny framework. Both proposed constructions achieve post-quantum security and are capable of correcting a linear proportion of errors. They rely solely on fundamental cryptographic primitives, which ensure simplicity and efficiency. Additionally, the second construction is based on restricted effective group action, which is weaker than the effective group action used in the first construction, thereby offering greater practical applicability.

1. Introduction

In cryptography, many cryptographic primitives, whether in symmetric or asymmetric cryptography, rely on keys that are uniformly random and exactly reproducible to ensure security. Nonetheless, generating such keys is a challenging task. Additionally, despite the fact that numerous noisy sources are available, they are usually unsuitable for direct use due to the noise. Since we aim to derive the same secret key in each generation phase, we ideally expect a symmetric process. However, due to the presence of noise, the reconstruction must handle an inherent asymmetry in the input data, ultimately achieving a goal that appears symmetric in effect. In view of this situation, the term of fuzzy extractor (FE) was initially articulated by Dodis et al. [1] in 2004, which offers a solution to the problem of how to reliably generate and accurately reproduce a uniformly random cryptographic key from noisy sources, such as biometric features [2,3] (e.g., fingerprints and iris scans), physical unclonable functions (PUFS) [4], and quantum information [5].

1.1. Fuzzy Extractor and Reusable Fuzzy Extractor

1.1.1. Fuzzy Extractor

The core of an FE consists of two procedures. One is the generation function Gen($w$), which receives a reading $w$ of the noisy source and produces a string R along with a public help string P; the other is the reproduction function Rep($w^{\prime }$, P), which takes a new reading $w^{\prime }$ and P as input. The security of the FE ensures that if $w$ has sufficient entropy, the output string R remains uniformly random from the adversary’s perspective, even if the public help string P is accessible to the adversary. Moreover, as long as $\mathrm{dis}(w,w^{\prime })<t$, Rep($w^{\prime }$, P) will output R with overwhelming probability. Then, its correctness is guaranteed.

1.1.2. Reusable Fuzzy Extractor

Nevertheless, the original FE can merely guarantee the security of a single extraction. Repeated extraction of the same noisy source will compromise security. Hence, Boyen [6] put forward the idea of reusable fuzzy extractor (RFE), which can overcome the aforementioned drawbacks and significantly enhance security. Specifically, RFE ensures such security by invoking fuzzy extractor’s generation algorithm Gen($w_j$) to generate multiple pairs of ${\{{\mathrm{P}}_j,{\mathrm{R}}_j\}}_{j\in \left[\rho \right]}$ for different readings ${\left\{w_j\right\}}_{j\in \left[\rho \right]}$ from the same noisy source; even if any other multiple pairs of ${\{{\mathrm{P}}_j,{\mathrm{R}}_j\}}_{j\ne i}$ and ${\mathrm{P}}_i$ are exposed to the adversary, ${\mathrm{R}}_i$ still remains pseudo-random from the perspective of the adversary.

In 2016, Canetti et al. [7] introduced an RFE designed for low-entropy distributions, which is based on digital lockers and capable of handling binary strings with Hamming noise. Nonetheless, their construction can only withstand a sublinear proportion of errors and relies on a non-standard assumption.

In 2018, Wen et al. [8] presented the first strongly RFE from the DDH assumption. Later, they [9] constructed another RFE built upon the LWE assumption, which is capable of withstanding a linear proportion of errors. Subsequently, they first formalized the notion of a robustly reusable fuzzy extractor (RRFE) and constructed the first RRFE under the DDH assumption and DLIN assumption over pairing groups [10]. In 2019, they [11] proposed another two RRFEs from LWE and DDH in groups without pairings, respectively.

In 2020, Li et al. [12] presented another RFE based on the LPN assumption. Their construction serves as a post-quantum secure RFE and is more efficient than previous work.

Recently, Zhou et al. proposed the first RRFE [13] and the first RFE [14] from isogeny, both of which rely on the weak pseudo-randomness of CSI-FiSh [15]. Their constructions also support the linear fraction of errors.

1.2. Isogeny-Based Cryptography and Isogeny-Based Assumptions

Advances in quantum computing have greatly promoted the rise of post-quantum cryptography [16,17]. Lattice-based hard assumptions [18,19] are a promising class of quantum-resistant problems, and lattice-based cryptographic research [20] dominates a significant portion of post-quantum cryptography. This makes post-quantum cryptography lack sufficient diversity [13,21]. Isogeny-based cryptography represents another viable non-lattice-based alternative for post-quantum secure cryptosystems [22,23]. One of the most famous protocols based on isogeny is Supersingular Isogeny Diffie–Hellman (SIDH), proposed by Jao and De Feo [24]. However, SIDH is vulnerable to certain quantum attacks [25,26], and its efficiency and security continue to be areas of active research [27]. In 2018, Castryck et al. [28] introduced Commutative Supersingular Isogeny Diffie–Hellman (CSIDH), which simplifies the SIDH protocol and provides a more efficient key exchange mechanism. Building on the CSIDH protocol, CSI-FiSh was proposed as a signature scheme by Beullens et al. [15] in 2019. Later, Alamati et al. [21] established a novel framework built on group actions, allowing for the straightforward usage of various isogeny-based assumptions.

1.2.1. Linear Hidden Shift Assumption

The linear hidden offset (LHS) problem over group actions was first proposed by Alamati et al. in [21], where they formally defined the LHS assumption and analyzed its security. They imply that the LHS assumption is secure in (restricted) effective group action (e.g., CSIDH and CSI-Fish, which are based on supersingular elliptic curves). In addition, they showed that the LHS assumption enables the realization of many cryptographic applications, including symmetric KDM-CPA secure encryption, trapdoor functions, and designated-verifier non-interactive zero-knowledge (NIZK) proofs. Later, Alamati et al. [29] constructed the new trapdoor claw-free functions (TCFS) based on the LHS assumption, which is the first post-quantum secure candidate that operates independently of lattice-related problems. Recently, Alamati et al. [30] designed another two cryptographic primitives with hinting properties from the LHS assumption, including hinting pseudo-random generators (PRGS) and hinting weak pseudo-random functions (WPRFS).

1.2.2. Group Action Decisional Diffie–Hellman Assumption

Similar to the DDH assumption, the GA-DDH assumption is the corresponding hard problem over isogeny-based group actions, which makes its first formal appearance in Stolbunov’s PhD thesis [31] and has attracted widespread research interest in recent years. In 2020, Castryck et al. [32] proposed an efficient attack to break the GA-DDH assumption for all supersingular elliptic curves over ${\mathcal{F}}_p$ with $p\equiv 1 mod 4$. However, this attack does not extend to the case where $p\equiv 3 mod 4$, which is precisely the setting used in CSIDH. Hence, it is generally accepted that the GA-DDH assumption holds for CSIDH [28,33]. So far, many cryptographic primitives based on it have emerged, including verifiable random functions (VRF) [34], oblivious pseudo-random functions (OPRF) [35], key encapsulation mechanisms (KEM) [36], etc.

From our perspective, the application of the LHS assumption or GA-DDH assumption in constructing post-quantum secure cryptographic schemes in the isogeny setting exhibits considerable potential and academic merits. In addition, as far as we know, no reusable fuzzy extractor built upon LHS or GA-DDH assumptions has been constructed. Inspired by the above process, an obvious question comes to mind:

Is it feasible to construct an RFE utilizing either the LHS assumption or the GA-DDH assumption?

1.3. Our Contributions

In this work, we provide a confirmed answer to the aforementioned question. The principal contributions of our work are as follows:

–

First, we extend the ${\mathrm{LHS}}_n^l$ assumption to the ${\mathrm{LHS}}_n^{\rho l}$ assumption via a hybrid argument. Similar to [13], we redefine the reusable fuzzy extractor and introduce an extra initialization algorithm to make it more adaptable to isogeny-based assumptions.

–

We give two constructions of RFE from isogeny-based assumptions. Our first construction is the first reusable fuzzy extractor based on the LHS assumption over isogeny-based group actions. Our second construction is the first reusable fuzzy extractor built upon the GA-DDH assumption. Furthermore, we instantiate both constructions based on specific instances of the underlying building blocks.

–

Both of our constructions are straightforward and resilient to the linear proportion of errors. In addition, compared with some previous works on reusable fuzzy extractor, our constructions impose no additional requirements (i.e., homomorphism or key-offset security) on the building blocks.

In Table 1, we present a comparison between our constructions and existing reusable fuzzy extractor schemes.

Table 1. Comparison with some existing reusable fuzzy extractor constructions. “*” is used to distinguish different works with the same abbreviation. “weak” means that any PPT adversary cannot distinguish $R_i$ from uniform strings when given the ${\left\{P_i\right\}}_{i\in \left[\rho \right]}$. “strong” means that any PPT adversary cannot distinguish $R_i$ from uniform strings, even when given the ${\left\{P_j\right\}}_{j\in \left[\rho \right]}$ and ${\left\{R_j\right\}}_{j\ne i,j\in \left[\rho \right]}$. “linear” and “sublinear” represent the ability to correct the linear fraction of errors and sublinear fraction of errors, respectively. “IT” denotes Information-theoretic. “H-KS-Free” represents whether reusability does not rely on the homomorphism or key-shift security of the building blocks. “Src. Entropy” denotes the entropy requirement of the fuzzy source. “Comp.Cost” refers to the computational cost of RFE.Gen and RFE.Rep, primarily involving modular exponentiations and group actions (exp, ★). Here, $t:=\left|w\right|/log{p}^{\prime }$ (where $\left|w\right|$ is the bit-length of the input and $p^{\prime }$ is the order of $\widehat{\mathcal{G}}$, as defined in [10]), and l and n are dimensions of the sampled matrix in Scheme 1. “PQ-Res.” indicates post-quantum resistance.

Constructions	Reuse	Err. Rate	Assump.	H -KS -Free	Src. Entropy	Comp. Cost	PQ -Res.
WLG191 [11]	strong		LWE	✗	$H_{\infty }\left(W\right)\ge m$	–	✔
CFPRS16 [7]	strong	sublinear	Strong DDH	✔	${\tilde{H}}_{\infty }(W_{j_1},\dots ,W_{j_k}$ $\mid j_1,\dots ,j_k)\ge \alpha$	–	✗
ACEK17 [37]	strong		LWE	✔	$W_i\sim \chi$	–	✔
Boy04 [6]	weak		IT	✔	${\tilde{H}}_{\infty }(W_i\mid \Delta W_{i,j})$ $={\tilde{H}}_{\infty }\left(W_i\right)$	–	✔
WL18 [9]	strong		LWE	✗	$H_{\infty }\left(W\right)\ge m$	–	✔
WL18 * [10]	strong		DDH +DLIN	✗	$H_{\infty }\left(W\right)\ge m$	$(2n^2+3)exp$	✗
WLH18 [8]	strong		DDH	✗	${\tilde{H}}_{\infty }(W_i\mid \Delta W_{i,j})$ $\ge m$	–	✗
WLG192 [11]	strong	linear	DDH	✗	$H_{\infty }\left(W\right)\ge m$	$6exp$	✗
LLGC20 [12]	strong		LPN	✗	$H_{\infty }\left(W\right)\ge m$	–	✔
ZLH24 [13]	strong		EGA -WPR	✔	$H_{\infty }\left(W\right)\ge m$	$4exp+ 4 ★$	✔
ZLH24 * [14]	strong		EGA -WPR	✗	$H_{\infty }\left(W\right)\ge m$	$3exp+ 2 ★$	✔
our scheme 1	strong		LHS	✔	$H_{\infty }\left(W\right)\ge m$	$\left[l\right(n+1\left)\right]exp$ $+(l+2) ★$	✔
our scheme 2	strong		GA -DDH	✔	$H_{\infty }\left(W\right)\ge m$	$1exp+ 3 ★$	✔

1.4. Challenges and Our Approaches

As we all know, the reusability of many mainstream RFEs relies heavily on the homomorphic property of the underlying cryptographic primitives or the hardness assumptions that have properties similar to key-shift security [8,9,12,14]. Nevertheless, in the context of isogeny, either the set $\mathcal{X}$ has no operations (as discussed in [13]), or the same operations are not defined in the same domain (e.g., the “+” in the LHS assumption, $\mathbf{M}(\mathbf{k}+\Delta )\ne \mathbf{M}\mathbf{k}+\mathbf{M}\Delta$, “+” on the left is over ${\mathcal{F}}_2$, and the right is in group $\mathcal{G}$), which makes it difficult to construct reusable fuzzy extractors or fuzzy extractors with stronger security (i.e., robustly reusable fuzzy extractors) from isogeny by conventional means.

To facilitate the use of isogeny assumptions and minimize the requirements on the underlying building blocks, we adopt the approach proposed in [13] and redefine reusable fuzzy extractor. Our modification introduces only an initialization algorithm while preserving the core structure of the traditional RFE. In our construction, the overhead of this initialization algorithm is minimal, as each user invokes it only once, requiring just a single additional execution of the secure sketch generation procedure $\mathrm{SS}.\mathrm{Gen}$.

1.4.1. Construction 1: RFE from LHS Assumption

For the first construction, we just utilize a secure sketch, universal hash functions, and an effective group action (EGA) as the key components. In RFE.Config, we incorporate the uniformly random selected hash function ${\mathrm{H}}_i$ along with certain public parameters of the EGA into crs (public and unmodifiable). During the phase of RFE.Init, $\mathrm{SS}.\mathrm{Gen}$ will produce a $s$, which is stored in the public help string ${\mathrm{P}}_{\mathrm{init}}$ and enables the recovery of $w$ in subsequent algorithms. In the RFE.Gen, we first use the sketch $s$ to recover $w$ as long as the new reading $w^{\prime }$ satisfies $\mathrm{dis}(w,w^{\prime })<t$. Later, ${\mathrm{H}}_i$ will take $w$ as input. The generated $\mathbf{k}$ (${\mathrm{H}}_i(w)$) will serve as a crucial component of the LHS assumption. Subsequently, we uniformly and randomly sample $\mathbf{M}$ from ${\mathcal{G}}^{l\times n}$ and $\mathbf{x}$ from the set ${\mathcal{X}}^l$. The EGA and its regularity property guarantee the efficiency of this sampling process. Next, $\mathbf{M}$ and $\mathbf{x}$ are put into the public help string P. Under the LHS hypothesis, $\mathbf{m}$ cannot be distinguished from uniformly random elements in ${\mathcal{X}}^l$, which is crucial for ensuring reusability. Similar to RFE.Gen, by relying on the correctness of the security sketch and some public parameters, the RFE.Rep algorithm can always regenerate R.

1.4.2. Construction 2: RFE from GA-DDH Assumption

Our second construction follows the same framework as construction 1, making the overall process somewhat similar. However, there are notable differences in the details. First, by leveraging restricted effective group action (REGA, where the GA-DDH assumption is conjectured to hold), construction 2 achieves greater practicality compared to construction 1 (EGA is more powerful than REGA). Furthermore, in our specific construction, we employ a secure sketch, an average-case strong extractor, and a family of universal hash functions. The combination of the latter two primitives, along with the special leftover hash lemma, is the key to our reusability. The detailed information is presented in $\mathrm{Section}$Section 3.3.

2. Preliminaries

This section is organized as follows. We first introduce the notational conventions used throughout the paper, followed by the definitions of cryptographic primitives and security notions that form the basis of our constructions and security proofs.

2.1. Basic Notation

In our notation, normal, bold, and capital bold letters, like x, $\mathbf{x}$, and $\mathbf{X}$, are used to represent an element, column vector, and matrix, respectively. Let $\lambda$ be the security parameter. For a column vector x, let ${\mathbf{x}}_i$ denote the i-th element of x. Given a matrix $\mathbf{M}$, let ${\mathbf{M}}^{\top }$ denote the transpose of $\mathbf{M}$. For a $l_1\times n$ matrix ${\mathbf{M}}_1$ and a $l_2\times n$ matrix ${\mathbf{M}}_2$, we use [${\mathbf{M}}_1$, ${\mathbf{M}}_2$] to denote the $(l_1+l_2)\times n$ matrix ${\left[{\mathbf{M}}_1^{\top }{\mathbf{M}}_2^{\top }\right]}^{\top }$. Let $\left[\rho \right]$ denote the set $\{1,2,\dots ,\rho \}$. The interval $[m,n]$ refers to the set $\{m,m+1,\dots ,n\}$. Let $x\leftarrow X$ indicate that x is drawn from the distribution X. For two random variables, X and Y, $X{\stackrel{\epsilon }{\approx }}_{s\left(c\right)}Y$ signifies that these two random variables are statistically (computationally) indistinguishable, with a maximum distinguishing advantage of $\epsilon$, if $\epsilon =0$; the notation can be simplified as $X{\approx }_{s\left(c\right)}Y$. For a set $\mathcal{X}$, we write $x\stackrel{\$}{\leftarrow }\mathcal{X}$ to indicate that x is selected uniformly from $\mathcal{X}$. $\left|\mathcal{X}\right|$ refers to the size of the set. PPT stands for probabilistic polynomial-time. $\mathrm{Let} {log}_2(·) \mathrm{be} \mathrm{denoted} \mathrm{by} log(·)$. Our security proof follows a game-based approach. Here, G⇒ 1 signifies that the outcome of game G is 1.

Considering a cryptographic primitive XX and its corresponding security requirement YY, we denote by ${\mathrm{Exp}}_{\mathrm{XX},\mathcal{A}}^{\mathrm{YY}}\left(1^{\lambda }\right)\Rightarrow 1$ that the security experiment returns 1 after the interaction with the adversary $\mathcal{A}$. The term ${\mathrm{Adv}}_{\mathrm{XX},\mathcal{A}}^{\mathrm{YY}}\left(1^{\lambda }\right)$ denotes adversary $\mathcal{A}$’s advantage within the context of this security experiment, that is, ${\mathrm{Adv}}_{\mathrm{XX}}^{\mathrm{YY}}\left(1^{\lambda }\right):={max}_{\mathrm{PPT} \mathcal{A}}{\mathrm{Adv}}_{\mathrm{XX},\mathcal{A}}^{\mathrm{YY}}\left(1^{\lambda }\right)$.

2.2. Metric Spaces

Definition 1 

(Metric spaces [1]). A metric space consists of a set $\mathcal{M}$, along with a distance function $\mathrm{dis}:\mathcal{M}\times \mathcal{M}\to {\mathcal{R}}^{+}\cup \left\{0\right\},$ which defines the distance between its elements (e.g., the Hamming distance, which denotes the number of positions at which two strings of equal length differ).

2.3. Min-Entropy and Statistical Distance

Definition 2 

(Min-entropy [1]). Let X be a discrete random variable; the min-entropy of X is defined as $H_{\infty }\left(X\right)=-log\left({max}_{x\in \mathcal{X}}Pr[X=x]\right).$

Definition 3 

(Average min-entropy [1]). Considering two discrete random variables X and Z, the average min-entropy of X given Z is defined as

$${\tilde{H}}_{\infty }\left(X\right|Z)=-log\left[{\mathbb{E}}_{z\leftarrow Z}(\underset{x\in \mathcal{X}}{max}Pr\left[X=x\mid Z=z\right])\right].$$

Definition 4 

(Statistical distance [1]). Considering X, Y be two random variables defined over a set $\mathcal{M}$, the statistical distance of X and Y is given by $\mathrm{SD}(X,Y)={\displaystyle \frac{1}{2}}{\sum }_{w\in \mathcal{M}}|Pr\left[X=w\right]-Pr\left[Y=w\right]|.$

2.4. Universal Hashing

Definition 5 

(Universal hash functions [1]). A family of hash functions $\mathcal{H}=\{{\mathrm{H}}_i:\mathcal{X}\to \mathcal{Y} | i\in \mathcal{I}\}$ is called universal if for all/any distinct inputs $x_1,x_2\in \mathcal{X}$, we have ${Pr}_{i\stackrel{\$}{\leftarrow }\mathcal{I}}\left[{\mathrm{H}}_i\left(x_1\right)={\mathrm{H}}_i\left(x_2\right)\right]\le {\displaystyle \frac{1}{\left|\mathcal{Y}\right|}}.$

Lemma 1 

(Generalized leftover hash lemma [1]). If $\mathcal{H}=\{{\mathrm{H}}_i:\mathcal{X}\to \mathcal{Y} | i\in \mathcal{I}\}$ is a family of universal hash functions, then for any random variable W taking values in $\mathcal{X}$ and any random variable Z, we have

$$\mathrm{SD}(({\mathrm{H}}_I\left(W\right),I,Z),(U,I,Z))\le {\displaystyle \frac{1}{2}}\sqrt{2^{-{\tilde{H}}_{\infty }\left(W\right|Z)}\left|\mathcal{Y}\right|},$$

where I and U follow uniform distributions over the sets $\mathcal{I}$ and $\mathcal{Y}$.

Here, we introduce the following special case of a leftover hash lemma [21,30], with its proof provided in [38].

Lemma 2. 

Let $\mathcal{G}$ be an abelian group under addition with the order $\left|\mathcal{G}\right|={\lambda }^{\omega \left(1\right)}$, and let $n\in \mathbb{Z}$ such that $n>log\left|\mathcal{G}\right|+\omega (log\lambda )$. If $\mathbf{r}\stackrel{\$}{\leftarrow }{\mathcal{G}}^n$, $\mathbf{t}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$, and $u\stackrel{\$}{\leftarrow }\mathcal{G}$, it is evident that $(\mathbf{r},{\sum }_{i=1}^n{\mathbf{t}}_i{\mathbf{r}}_i){\stackrel{{\epsilon }^{\prime }}{\approx }}_s(\mathbf{r},u)$, where ${\epsilon }^{\prime }=\sqrt{\left|\mathcal{G}\right|/2^n}\le 2^{-\omega (log\lambda )}$.

2.5. Secure Sketch and Average-Case Strong Extractor

Definition 6 

(Secure sketch [1]). An $(\mathcal{M},m,\widehat{m},t)$-secure sketch $\left(\mathbf{SS}\right)$ consists of two $\mathrm{PPT}$ algorithms $(\mathrm{SS}.\mathrm{Gen},\mathrm{SS}.\mathrm{Rec})$ with the following specifications.

–

$\mathrm{SS}.\mathrm{Gen}(w)$ takes $w\in \mathcal{M}$ as input and outputs a sketch $s\in \mathcal{S}$;

–

$\mathrm{SS}.\mathrm{Rec}(w^{\prime },s)$ takes $w^{\prime }\in \mathcal{M}$ and a sketch $s$ as input and outputs $\tilde{w}$.

It also satisfies the following properties:

–

Correctness: If $\mathrm{dis}(w,w^{\prime })\le t$, then

$$w=\mathrm{SS}.\mathrm{Rec}(w^{\prime },\mathrm{SS}.\mathrm{Gen}(w))=\tilde{w}.$$

–

Security: For any distribution W over $\mathcal{M}$,

$${\tilde{H}}_{\infty }(W\mid \mathrm{SS}.\mathrm{Gen}\left(W\right))>\widehat{m} \mathrm{if} H_{\infty }\left(W\right)>m.$$

An instantiation of SS was introduced in [1], which achieves information-theoretic security. For completeness, we restate it in $\mathrm{Section}$Section 4.1.

Definition 7 

(Average-case strong extractor [1]). A function $\mathrm{Ext}:\mathcal{M}\times \mathcal{K}\to \mathcal{T}$ is an average-case $(\mathcal{M},m,\mathcal{T},{\epsilon }_{ext})$-strong extractor with seed $K\in \mathcal{K}$ if for any variable W over $\mathcal{M}$ and variable Y such that ${\tilde{H}}_{\infty }\left(W\right|Y)>m$, we have $\mathrm{SD}((\mathrm{Ext}(W,K),K,Y),(U,K,Y))\le {\epsilon }_{ext},$ where K and U are uniformly distributed over $\mathcal{K}$ and $\mathcal{T}$, respectively.

2.6. Group Action, LHS Assumption, and GA-DDH Assumption

For the sake of clarity and abstraction, prior research has resorted to modeling certain isogeny-based constructions through group actions [21,29,30]. In the following, we provide a brief overview of cryptographic group actions and isogeny assumptions.

Definition 8 

(Group action [21]). Let $(\mathcal{G},+)$ be a group that acts on $\mathcal{X}$, with a mapping from $\mathcal{G}\times \mathcal{X}$ to $\mathcal{X}$ satisfying the following conditions:

1. 

Identity: For the identity element e of $\mathcal{G}$, $e★x=x$ for all $x\in \mathcal{X}$;

2. 

Compatibility: For all $g,h\in \mathcal{G}$ and $x\in \mathcal{X}$, we have $(g+h)★x=g★(h★x)$.

According to [30], it is reasonable to use the symbol + to represent the binary operation in $\mathcal{G}$ within this paper. Here, we concentrate on group actions that are both abelian and regular $\left(\mathrm{both} \mathrm{free} \mathrm{and} \mathrm{transitive}\right)$, as considered in prior works [13,30]. More precisely, we have the following:

1. 

Abelian: The group $\mathcal{G}$ is abelian;

2. 

Transitive: For any $x_1,x_2\in \mathcal{X}$, there is a group element $g\in \mathcal{G}$ satisfying $x_2=g★x_1$;

3. 

Free: A group element $g\in \mathcal{G}$ is the identity element if $x=g★x$ for some $x\in \mathcal{X}$.

Remark 1. 

For a regular group action, the map $f_x:g\mapsto g★x$ creates a bijection between $\mathcal{G}$ and $\mathcal{X}$ for any $x\in \mathcal{X}$.

Definition 9 

(Effective group action [21,30]). An effective group action $\mathrm{EGA}$$(\mathcal{G},\mathcal{X},★,\tilde{x})$ is a group action that satisfies some properties described below:

1. 

$\mathcal{G}$ is a finite group, and efficient algorithms are available for membership testing, equality testing, random sampling, group operation, and inversion;

2. 

$\mathcal{X}$ is a finite set, and known algorithms efficiently handle membership testing and compute the unique bit-string representation for every element in $\mathcal{X}$;

3. 

There is a distinguished element $\tilde{x}\in \mathcal{X}$, known as the origin, whose bit-string representation is available;

4. 

For any $g\in \mathcal{G}$ and $x\in \mathcal{X}$, efficient algorithms can compute $g★x$.

As stated in [13], we can obtain a regular and abelian EGA from CSI-FiSh [15].

Definition 10 

(Linear hidden shift assumption [21,29,30]). For an $\mathrm{EGA}$$(\mathcal{G},\mathcal{X},★,\tilde{x})$, and let $n\in \mathbb{Z}$ such that $n>log\left|\mathcal{G}\right|+\omega (log\lambda )$. The ${\mathrm{LHS}}_n^l$ assumption is ${ϵ}_1$-hard if for any $\mathrm{PPT}$ adversary $\mathcal{A}$ and any $l=poly\left(\lambda \right)$, it holds that,

$$\begin{array}{cc}\hfill {\mathrm{Adv}}_{\mathrm{LHS},\mathcal{A}}^{l,n}\left(1^{\lambda }\right):= & |Pr\left[\mathcal{A}(\mathbf{x},\mathbf{M},\mathbf{Mk}★\mathbf{x})\Rightarrow 1\right]-Pr\left[\mathcal{A}(\mathbf{x},\mathbf{M},\mathbf{u})\Rightarrow 1\right]|\le {ϵ}_1,\hfill \end{array}$$

where $\mathbf{x}\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$, $\mathbf{M}\stackrel{\$}{\leftarrow }{\mathcal{G}}^{l\times n}$, $\mathbf{k}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$ and $\mathbf{u}\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$.

By using a hybrid argument, we have the following lemma.

Lemma 3. 

For an $\mathrm{EGA}$$(\mathcal{G},\mathcal{X},★,\tilde{x})$, and let $n\in \mathbb{Z}$ such that $n>log\left|\mathcal{G}\right|+\omega (log\lambda )$, $l=\mathrm{poly}\left(\lambda \right)$. If the ${\mathrm{LHS}}_n^l$ assumption is ${ϵ}_1$-hard over the EGA, then the ${\mathrm{LHS}}_n^{\rho l}$ assumption is $\rho {ϵ}_1$-hard. More precisely, for every $\mathrm{PPT}$ adversary $\mathcal{A}$,

$$\begin{array}{cc}\hfill {\mathrm{Adv}}_{\mathrm{LHS},\mathcal{A}}^{\rho l,n}\left(1^{\lambda }\right):= & |Pr\left[\mathcal{A}(\mathbf{x},\mathbf{M},\mathbf{Mk}★\mathbf{x})\Rightarrow 1\right]-Pr\left[\mathcal{A}(\mathbf{x},\mathbf{M},\mathbf{u})\Rightarrow 1\right]|\le \rho {ϵ}_1,\hfill \end{array}$$

where $\mathbf{x}\stackrel{\$}{\leftarrow }{\mathcal{X}}^{\rho l}$, $\mathbf{M}\stackrel{\$}{\leftarrow }{\mathcal{G}}^{\rho l\times n}$, $\mathbf{k}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$ and $\mathbf{u}\stackrel{\$}{\leftarrow }{\mathcal{X}}^{\rho l}$.

Proof. 

Let $\mathbf{M}=[{\mathbf{M}}_1,{\mathbf{M}}_2,\dots ,{\mathbf{M}}_{\rho }]$, $\mathbf{x}=[{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_{\rho }]$, and $\mathbf{u}=[{\mathbf{u}}_1,{\mathbf{u}}_2,\dots ,{\mathbf{u}}_{\rho }]$, where ${\mathbf{x}}_i\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$, ${\mathbf{M}}_i\stackrel{\$}{\leftarrow }{\mathcal{G}}^{l\times n}$, and ${\mathbf{u}}_i\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$ for $i\in \left[\rho \right]$. Let

$$\begin{array}{cc}\hfill {\mathbf{Z}}_{\rho }& =(\mathbf{x},\mathbf{M},[{\mathbf{M}}_1\mathbf{k}★{\mathbf{x}}_1,{\mathbf{M}}_2\mathbf{k}★{\mathbf{x}}_2,\dots ,{\mathbf{M}}_{\rho }\mathbf{k}★{\mathbf{x}}_{\rho }]),\hfill \\ \hfill {\mathbf{Z}}_{\rho -1}& =\left(\mathbf{x},\mathbf{M},[{\mathbf{M}}_1\mathbf{k}★{\mathbf{x}}_1, {\mathbf{M}}_2\mathbf{k}★{\mathbf{x}}_2, \dots ,{\mathbf{M}}_{\rho -1}\mathbf{k}★{\mathbf{x}}_{\rho -1}, {\mathbf{u}}_{\rho }]\right),\hfill \\ \hfill & \dots \dots \hfill \\ \hfill {\mathbf{Z}}_i& =\left(\mathbf{x},\mathbf{M},[{\mathbf{M}}_1\mathbf{k}★{\mathbf{x}}_1, {\mathbf{M}}_2\mathbf{k}★{\mathbf{x}}_2, \dots , {\mathbf{M}}_i\mathbf{k}★{\mathbf{x}}_i, {\mathbf{u}}_{i+1}, \dots , {\mathbf{u}}_{\rho }]\right),\hfill \\ \hfill & \dots \dots \hfill \\ \hfill {\mathbf{Z}}_1& =\left(\mathbf{x},\mathbf{M},[{\mathbf{M}}_1\mathbf{k}★{\mathbf{x}}_1, {\mathbf{u}}_2, \dots , {\mathbf{u}}_{\rho }]\right),\hfill \\ \hfill {\mathbf{Z}}_0& =\left(\mathbf{x},\mathbf{M},[{\mathbf{u}}_1, {\mathbf{u}}_2, \dots , {\mathbf{u}}_{\rho }]\right).\hfill \end{array}$$

Then, we get

$$\begin{array}{cc}\hfill |& Pr\left[\mathcal{A}(\mathbf{x},\mathbf{M},\mathbf{Mk}★\mathbf{x})\Rightarrow 1\right]-Pr\left[\mathcal{A}(\mathbf{x},\mathbf{M},\mathbf{u})\Rightarrow 1\right]|\hfill \\ \hfill =& |Pr\left[\mathcal{A}\left({\mathbf{Z}}_{\rho }\right)\Rightarrow 1\right]-Pr\left[\mathcal{A}\left({\mathbf{Z}}_0\right)\Rightarrow 1\right]|\hfill \\ \hfill \le & {\sum }_{i=0}^{\rho -1}|Pr\left[\mathcal{A}\left({\mathbf{Z}}_{i+1}\right)\Rightarrow 1\right]-Pr\left[\mathcal{A}\left({\mathbf{Z}}_i\right)\Rightarrow 1\right]|\le \rho {ϵ}_1.\hfill \end{array}$$

□

While an EGA serves as a useful abstraction, it may sometimes be too powerful compared to what is practically achievable. A restricted effective group action (REGA) can be seen as a more limited form of an EGA.

Definition 11 

(Restricted effective group action [21,33]). A restricted effective group action $\mathrm{REGA}$$(\mathcal{G},\mathcal{X},★,\tilde{x})$ is a group action that satisfies the following properties:

1. 

The finite group $\mathcal{G}$ is generated by a set $\{g_1,\dots ,g_n\}$, and $n=\mathrm{poly}(log|\mathcal{G}\left|\right)$;

2. 

The set $\mathcal{X}$ is finite, and known algorithms efficiently handle membership testing and compute the unique bit-string representation for every element in $\mathcal{X}$;

3. 

There exists a distinguished element $\tilde{x}\in \mathcal{X}$ called the origin whose bit-string representation is known;

4. 

There exists an efficient algorithm that, when given $g_i$ in the generating set and any $x\in \mathcal{X}$, outputs $g_i★x$ and $g_i^{-1}★x$ where $i\in \left[n\right]$.

Remark 2. 

REGA can be instantiated through isogeny-based group actions, such as CSIDH [28]. Additionally, its generator set enables approximate uniform sampling over the group $\mathcal{G}$. Furthermore, due to the regularity of the group action $(\mathcal{G},\mathcal{X},★,\tilde{x})$, an efficient algorithm exists for drawing elements $x\stackrel{\$}{\leftarrow }\mathcal{X}$ [33].

Definition 12 

(GA-DDH assumption [33,39,40]). Given a REGA $(\mathcal{G},\mathcal{X},★,\tilde{x})$, the GA-DDH assumption is ${ϵ}_2$-hard if for all $\mathrm{PPT}$ adversary $\mathcal{A}$, the distinguishing advantage satisfies

$$\begin{array}{cc}\hfill | Pr\left[\mathcal{A}\left(x, a★x, b★x, (a+b)★x\right)\Rightarrow 1\right]-Pr\left[\mathcal{A}\left(x, a★x, b★x, c★x\right)\Rightarrow 1\right] | & \le {ϵ}_2,\hfill \end{array}$$

where $(\mathcal{G},\mathcal{X},★,\tilde{x})\leftarrow \mathrm{REGA}.\mathrm{Setup}\left(1^{\lambda }\right),a,b,c\stackrel{\$}{\leftarrow }\mathcal{G},x\stackrel{\$}{\leftarrow }\mathcal{X}$.

Remark 3. 

GA-DDH is considered to be applicable to particular group actions derived from isogeny, such as CSIDH [28,33], which is the typical instance of REGA. We stress that our second construction in $\mathrm{Section}$Section 3.3 is built upon the GA-DDH assumption, which is fundamentally different from the weak pseudo-randomness (WPR) assumption adopted in prior works [13,14]. Not only are the underlying assumptions distinct, but the settings are also different; the WPR assumption is considered over EGA (instantiated via CSI-FiSh), whereas GA-DDH is known not to hold in EGA, as comprehensively analyzed in [13].

3. Reusable Fuzzy Extractor

3.1. Definition of Reusable Fuzzy Extractor

Similar to [13], we introduce a modified version of the reusable fuzzy extractor RFE that incorporates an additional initialization algorithm RFE.Init, which generates the initial public string ${\mathrm{P}}_{\mathrm{init}}$. Notably, RFE.Init is invoked only once per user. The generated ${\mathrm{P}}_{\mathrm{init}}$ serves as input for the remaining algorithms.

Definition 13 

(Reusable fuzzy extractor). An $(\mathcal{M},m,\mathcal{R},t,\epsilon )$-reusable fuzzy extractor for the metric space $\mathcal{M}$ consists of four $\mathrm{PPT}$ algorithms ($\mathrm{RFE}.\mathrm{Config}$, $\mathrm{RFE}.\mathrm{Init}$, $\mathrm{RFE}.\mathrm{Gen}$, $\mathrm{RFE}.\mathrm{Rep}$$):$

–

$\mathrm{RFE}.\mathrm{Config}\left(1^{\lambda }\right)$ inputs the security parameter λ and generates a $\mathrm{crs}$;

–

$\mathrm{RFE}.\mathrm{Init}(\mathrm{crs},w)$ takes $\mathrm{crs}$ and an element $w$ from the set $\mathcal{M}$ as input, and then generates the initial public string ${\mathrm{P}}_{\mathrm{init}}$;

–

$\mathrm{RFE}.\mathrm{Gen}(\mathrm{crs},{\mathrm{P}}_{\mathrm{init}},w^{\prime })$ takes $\mathrm{crs}$, ${\mathrm{P}}_{\mathrm{init}}$, and $w^{\prime }\in \mathcal{M}$ as input and generates a public helper string $\mathrm{P}$ and an extracted string $\mathrm{R}\in \mathcal{R}$;

–

$\mathrm{RFE}.\mathrm{Rep}(\mathrm{crs},\mathrm{P},{\mathrm{P}}_{\mathrm{init}},w^{\prime \prime })$ takes the $\mathrm{crs}$, $\mathrm{P}$, ${\mathrm{P}}_{\mathrm{init}}$, and $w^{\prime \prime }\in \mathcal{M}$ as input, and then returns $\tilde{\mathrm{R}}$.

In addition, it meets the following properties:

–

$\mathrm{Correctness}:$ For $w,w^{\prime },w^{\prime \prime }\in \mathcal{M}$ with $\mathrm{dis}(w,w^{\prime })\le \mathrm{t}$, $\mathrm{dis}(w,w^{\prime \prime })\le \mathrm{t}$, if $\mathrm{crs}\leftarrow \mathrm{RFE}.\mathrm{Config}\left(1^{\lambda }\right)$, ${\mathrm{P}}_{\mathrm{init}}\leftarrow \mathrm{RFE}.\mathrm{Init}(\mathrm{crs},w)$, $(\mathrm{P},\mathrm{R})\leftarrow \mathrm{RFE}.\mathrm{Gen}(\mathrm{crs},{\mathrm{P}}_{\mathrm{init}},w^{\prime })$, $\tilde{\mathrm{R}}\leftarrow \mathrm{RFE}.\mathrm{Rep}(\mathrm{crs},\mathrm{P},{\mathrm{P}}_{\mathrm{init}},w^{\prime \prime })$, then $\tilde{\mathrm{R}}=\mathrm{R}$;

–

$\mathrm{Reusability}:$ For any distribution W over metric space $\mathcal{M}$ satisfying $H_{\infty }\left(W\right)\ge m,$ and for any $\mathrm{PPT}$ adversary $\mathcal{A}$, the following holds

$${\mathrm{Adv}}_{\mathrm{r}\mathrm{F}\mathrm{E},\mathcal{A}}^{\mathrm{r}\mathrm{e}\mathrm{u}}\left(1^{\lambda }\right):=|Pr[{\mathrm{Exp}}_{\mathrm{r}\mathrm{F}\mathrm{E},\mathcal{A}}^{\mathrm{r}\mathrm{e}\mathrm{u}}\left(1^{\lambda }\right)\Rightarrow 1]-{\displaystyle \frac{1}{2}}|\le \epsilon ,$$

where ${\mathrm{Exp}}_{\mathrm{RFE},\mathcal{A}}^{\mathrm{reu}}\left(1^{\lambda }\right)$, as shown in $\mathrm{Figure}$Figure 1, describes the reusability experiment conducted between a challenger $\mathcal{C}$ and an adversary $\mathcal{A}$.

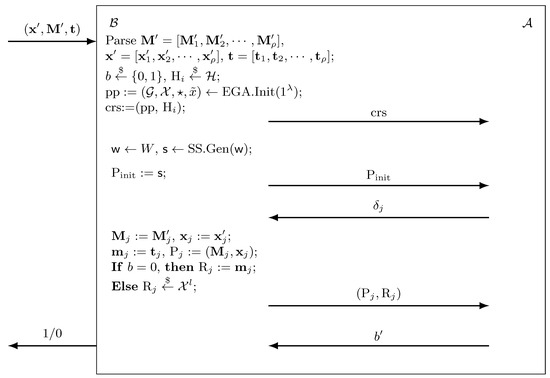
Figure 1. The reusability experiment ${\mathrm{Exp}}_{\mathrm{RFE},\mathcal{A}}^{\mathrm{reu}}\left(1^{\lambda }\right)$.

Remark 4. 

The goal of the experiment depicted in $\mathrm{Figure}$Figure 1 is to show that, when adversary $\mathcal{A}$ is given the public parameters $crs$ and ${\mathrm{P}}_{\mathrm{init}}$ and further obtains multiple pairs $({\mathrm{P}}_{\mathrm{i}},{\mathrm{R}}_{\mathrm{i}})$ from oracle queries, $\mathcal{A}$ still cannot distinguish whether the challenge response ${\mathrm{R}}_j$$(j\ne i)$ was generated via the RFE.Gen algorithm or sampled uniformly at random from the output space $\mathcal{R}$, even when ${\mathrm{P}}_j$ is known. In other words, even if the same noisy source is used multiple times (n times), and the adversary $\mathcal{A}$ learns the first $(n-1)$ pairs $({\mathrm{P}}_{\mathrm{i}},{\mathrm{R}}_{\mathrm{i}})$, as well as the final helper string ${\mathrm{P}}_n$, the output ${\mathrm{R}}_n$ still appears uniformly random to $\mathcal{A}$. Our security notion focuses on the indistinguishability of ${\mathrm{R}}_i$ from a uniformly random string. The ${\mathrm{P}}_i$ values, being public helper strings generated alongside each ${\mathrm{R}}_i$, are inherently meant to be public. ${\mathrm{P}}_{\mathrm{init}}$ is initialized only once per user when the user runs the fuzzy extractor scheme for the first time.

3.2. Construction of RFE from LHS Assumption

The detailed design of RFE = (RFE.Config, REF.Init, REF.Gen, REF.Rep) from the LHS assumption is depicted in Figure 2, which is composed of the following building blocks:

Figure 2. Design of reusable fuzzy extractor from LHS.

–

An $(\mathcal{M},m,\widehat{m},t)$-secure sketch SS = $(\mathrm{SS}.\mathrm{Gen},\mathrm{SS}.\mathrm{Rec})$, where $\mathcal{M}={\{0,1\}}^{l^{\prime }}$.

–

An EGA equipped with $\mathrm{EGA}.\mathrm{Setup}\left(1^{\lambda }\right)$, which outputs $(\mathcal{G},\mathcal{X},★,\tilde{x})$.

–

A family of universal hash functions $\mathcal{H}=\{{\mathrm{H}}_i:{\{0,1\}}^{l^{\prime }}\to {\{0,1\}}^n | i\in \mathcal{I}\}$, as defined in Equation (3). Let $n\in \mathbb{Z}$ such that $n>log\left|\mathcal{G}\right|+\omega (log\lambda )$.

Theorem 1. 

If $\mathrm{SS}$ is a $({\{0,1\}}^{l^{\prime }},m,\widehat{m},t)$-secure sketch, $\widehat{m}-n\ge \omega \left(\log \lambda \right)$, $\mathcal{H}$ is a family of universal hash functions $\mathcal{H}=\{{\mathrm{H}}_i:{\{0,1\}}^{l^{\prime }}\to {\{0,1\}}^n | i\in \mathcal{I}\}$. The ${\mathrm{LHS}}_n^l$ is ${ϵ}_1$-hard over the EGA $(\mathcal{G},\mathcal{X},★,\tilde{x})$; then, $\mathrm{RFE}$ in $Figure$Figure 2 is a $({\{0,1\}}^{l^{\prime }},m,{\mathcal{X}}^l,t,\epsilon )$-reusable fuzzy extractor, where $\epsilon \le 2^{-\omega (log\lambda )}+\rho {ϵ}_1.$

Proof. 

First, we verify the correctness of the construction in Figure 2. If dis($w$, $w^{\prime }$) ≤ t, dis($w$, $w^{\prime \prime }$) ≤ t, and $s\leftarrow \mathrm{SS}.\mathrm{Gen}(w)$, then, by the correctness of SS, we have $\widehat{w}=\tilde{w}=w$, where $\tilde{w}$← SS.Rec($w^{\prime }$, $s$) and $\widehat{w}=\mathrm{SS}.\mathrm{Rec}(w^{\prime \prime },s).$ Consequently, $\widehat{\mathbf{k}}=\mathbf{k}$. Then, $\widehat{\mathbf{m}}$ can be computed correctly, i.e., $\widehat{\mathbf{m}}$=$\mathbf{m}$, and RFE can always reproduce R.

Next, we demonstrate its reusability by presenting a sequence of games and proving the indistinguishability of adjacent ones. The differences between adjacent games are highlighted with underlined text.

Game ${\mathbf{G}}_0$: Game ${\mathbf{G}}_0$ can be viewed as ${\mathrm{Exp}}_{\mathrm{RFE},\mathcal{A}}^{\mathrm{reu}}\left(1^{\lambda }\right)$. More specifically, it can be viewed as the following:

• Challenger $\mathcal{C}$ selects $b\stackrel{\$}{\leftarrow }\{0,1\}$, samples ${\mathrm{H}}_i\stackrel{\$}{\leftarrow }\mathcal{H}$, and then calls $\mathrm{EGA}.\mathrm{Setup}\left(1^{\lambda }\right)$ to generate $\mathrm{pp}=(\mathcal{G},\mathcal{X},★,\tilde{x})$ and sets crs:=(pp, ${\mathrm{H}}_i$); it sends $\mathrm{crs}$ to $\mathcal{A}$.
• $\mathcal{C}$ selects $w$ according to W, calculates $s\leftarrow \mathrm{SS}.\mathrm{Gen}(w)$, and then sets ${\mathrm{P}}_{\mathrm{init}}:=s$, returning ${\mathrm{P}}_{\mathrm{init}}$ to $\mathcal{A}$.
• $\mathcal{A}$ may request up to $\rho$ queries from the generation oracle. Upon obtaining an offset ${\delta }_j\in \mathcal{M}$ satisfying $\mathrm{dis}\left({\delta }_j\right)\le t$ for $j\in \left[\rho \right]$, $\mathcal{C}$ calculates ${\tilde{w}}_j:=\mathrm{SS}.\mathrm{Rec}(w+{\delta }_j,s)$, ${\mathbf{k}}_j\leftarrow {\mathrm{H}}_i\left({\tilde{w}}_j\right)$, and then samples ${\mathbf{M}}_j\stackrel{\$}{\leftarrow }{\mathcal{G}}^{l\times n}$, ${\mathbf{x}}_j\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$; it calculates ${\mathbf{m}}_j={\mathbf{M}}_j{\mathbf{k}}_j★{\mathbf{x}}_j$ and sets ${\mathrm{P}}_j:=({\mathbf{M}}_j,{\mathbf{x}}_j)$; if $b=0$, ${\mathrm{R}}_j:={\mathbf{m}}_j$; otherwise, ${\mathrm{R}}_j\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$, and it returns $({\mathrm{P}}_j,{\mathrm{R}}_j)$ to $\mathcal{A}$.
• $\mathcal{A}$ finally outputs a guessing bit $b^{\prime }$; when $b^{\prime }=b$, the game outputs 1; otherwise, it outputs 0.

Obviously, we have

$$\begin{array}{c}\hfill Pr\left[{\mathbf{G}}_0\Rightarrow 1\right]=Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathrm{r}\mathrm{F}\mathrm{E},\mathcal{A}}^{\mathrm{r}\mathrm{e}\mathrm{u}}\left(1^{\lambda }\right)\Rightarrow 1\right].\end{array}$$

(1)

Game ${\mathbf{G}}_1$:${\mathbf{G}}_1$ is identical to ${\mathbf{G}}_0$, c:

2.

$\mathcal{C}$ chooses $w$ according to W, calculates $s\leftarrow \mathrm{SS}.\mathrm{Gen}(w)$, $\mathbf{k}:={\mathrm{H}}_i(w)$, and then sets ${\mathrm{P}}_{\mathrm{init}}:=s$, returning ${\mathrm{P}}_{\mathrm{init}}$ to $\mathcal{A}$.

3.

$\mathcal{A}$ may request up to $\rho$ queries from the generation oracle. Upon obtaining an offset ${\delta }_j\in \mathcal{M}$ satisfying $\mathrm{dis}\left({\delta }_j\right)\le t$ for $j\in \left[\rho \right]$, $\mathcal{C}$ sets ${\mathbf{k}}_j=\mathbf{k}$, and then samples ${\mathbf{M}}_j\stackrel{\$}{\leftarrow }{\mathcal{G}}^{l\times n}$, ${\mathbf{x}}_j\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$, calculates ${\mathbf{m}}_j={\mathbf{M}}_j{\mathbf{k}}_j★{\mathbf{x}}_j$, and sets ${\mathrm{P}}_j:=({\mathbf{M}}_j,{\mathbf{x}}_j)$; if $b=0$, ${\mathrm{R}}_j:={\mathbf{m}}_j$; otherwise, ${\mathrm{R}}_j\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$, and it returns $({\mathrm{P}}_j,{\mathrm{R}}_j)$ to $\mathcal{A}$.

□

Lemma 4. 

$Pr[{\mathbf{G}}_0\Rightarrow 1]=Pr[{\mathbf{G}}_1\Rightarrow 1].$

Proof. 

Due to the correctness of the secure sketch and $\mathrm{dis}\left({\delta }_j\right)\le t$, we deduce that

$${\tilde{w}}_j=\mathrm{SS}.\mathrm{Rec}(w+{\delta }_j,s)=w.$$

Furthermore, we can get ${\mathbf{k}}_j={\mathrm{H}}_i\left({\tilde{w}}_j\right)={\mathrm{H}}_i(w)=\mathbf{k}.$ Hence, we conclude that $Pr[{\mathbf{G}}_0\Rightarrow 1]=Pr[{\mathbf{G}}_1\Rightarrow 1].$ The lemma follows. □

Game ${\mathbf{G}}_2$:${\mathbf{G}}_2$ is equivalent to ${\mathbf{G}}_1$, with the difference that $\mathbf{k}:={\mathrm{H}}_i(w)$ is replaced by $\mathbf{k}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$. More specifically, we have the following:

2.

$\mathcal{C}$ chooses $w$ according to W, calculates $s\leftarrow \mathrm{SS}.\mathrm{Gen}(w)$, $\mathbf{k}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$, and then sets ${\mathrm{P}}_{\mathrm{init}}:=s$, returning ${\mathrm{P}}_{\mathrm{init}}$ to $\mathcal{A}$.

Lemma 5. 

$|Pr[{\mathbf{G}}_1\Rightarrow 1]-Pr[{\mathbf{G}}_2\Rightarrow 1]|\le 2^{-\omega (log\lambda )}.$

Proof. 

We prove this lemma using an argument based on information theory. Note that $w$ only appears in the second step to calculate $s\leftarrow \mathrm{SS}.\mathrm{Gen}(w)$ both in ${\mathbf{G}}_1$ and ${\mathbf{G}}_2$; thus, $s$ is all the information about W that is revealed to $\mathcal{A}$. Since our SS is an $(\mathcal{M}={\{0,1\}}^{l^{\prime }},m,\widehat{m},t)$-secure sketch and $H_{\infty }\left(W\right)\ge m$, we have

$${\tilde{H}}_{\infty }\left(W\right|\mathrm{SS}.\mathrm{Gen}\left(W\right))\ge \widehat{m}.$$

Due to Lemma 1 and the fact that $\widehat{m}-n\ge \omega \left(\log \lambda \right)$, the statistical distance between $\mathbf{k}$ and $\mathbf{u}$ is at most $2^{-\omega (log\lambda )}$, where $\mathbf{k}\leftarrow {\mathrm{H}}_i(w)$ and $\mathbf{u}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$. More precisely, we have the following:

$$\begin{array}{cc}\hfill \mathrm{SD}((\mathbf{k},{\mathrm{H}}_i,s), (\mathbf{u},{\mathrm{H}}_i,s)) & \le {\displaystyle \frac{1}{2}}\sqrt{2^{-\tilde{H}(w | s)}·2^n}\hfill \\ \hfill & \le {\displaystyle \frac{1}{2}}\sqrt{2^{-\widehat{m}}·2^n}\hfill \\ \hfill & \le 2^{-\omega (log\lambda )}.\hfill \end{array}$$

We now define a powerful algorithm $\mathcal{B}$ and show that if an adversary is capable of distinguishing between ${\mathbf{G}}_1$ and ${\mathbf{G}}_2$ with a non-negligible advantage, then $\mathcal{B}$ can also distinguish $(\mathbf{k},{\mathrm{H}}_i,s)$ and $(\mathbf{u},{\mathrm{H}}_i,s)$ with the same advantage. Assume $\mathcal{B}$ receives $(\mathbf{y},{\mathrm{H}}_i,s)$, where $\mathbf{y}$ is either $\mathbf{k}={\mathrm{H}}_i(w)$ or a uniform element $\mathbf{u}$. The goal of $\mathcal{B}$ is to identify which case it is. The algorithm $\mathcal{B}$ operates as follows:

• Algorithm $\mathcal{B}$ samples $b\stackrel{\$}{\leftarrow }\{0,1\}$, calls $\mathrm{EGA}.\mathrm{Setup}\left(1^{\lambda }\right)$ to generate $\mathrm{pp}=(\mathcal{G},\mathcal{X},★,\tilde{x})$, sets crs:=(pp, ${\mathrm{H}}_i$), and returns $\mathrm{crs}$ to $\mathcal{A}$.
• $\mathcal{B}$ sets $\mathbf{k}:=\mathbf{y}$ and ${\mathrm{P}}_{\mathrm{init}}:=s$ and sends ${\mathrm{P}}_{\mathrm{init}}$ to $\mathcal{A}$.
• $\mathcal{A}$ may request up to $\rho$ queries from the generation oracle. Upon obtaining an offset ${\delta }_j\in \mathcal{M}$ satisfying $\mathrm{dis}\left({\delta }_j\right)\le t$ for $j\in \left[\rho \right]$, $\mathcal{B}$ sets ${\mathbf{k}}_j=\mathbf{k}$, samples ${\mathbf{M}}_j\stackrel{\$}{\leftarrow }{\mathcal{G}}^{l\times n}$, ${\mathbf{x}}_j\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$, calculates ${\mathbf{m}}_j={\mathbf{M}}_j{\mathbf{k}}_j★{\mathbf{x}}_j$, and sets ${\mathrm{P}}_j:=({\mathbf{M}}_j,{\mathbf{x}}_j)$ if $b=0$, ${\mathrm{R}}_j:={\mathbf{m}}_j$; otherwise, ${\mathrm{R}}_j\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$, and it returns $({\mathrm{P}}_j,{\mathrm{R}}_j)$ to $\mathcal{A}$.
• $\mathcal{A}$ finally outputs a guessing bit $b^{\prime }$; when $b^{\prime }=b$, the game outputs 1; otherwise, it outputs 0.

If $\mathcal{B}$ is given the tuple $(\mathbf{y}=\mathbf{k},{\mathrm{H}}_i,s)$, where $\mathbf{k}$ is derived from ${\mathrm{H}}_i(w)$ and $s$ is generated via $\mathrm{SS}.\mathrm{Gen}(w)$, it will be able to simulate the game ${\mathbf{G}}_1$ for $\mathcal{A}$ perfectly. On the other hand, if $\mathcal{B}$ is given $(\mathbf{y}=\mathbf{u},{\mathrm{H}}_{\alpha },s)$, where $\mathbf{u}$ is randomly chosen from ${\{0,1\}}^n$, it will simulate the game ${\mathbf{G}}_2$ for $\mathcal{A}$ flawlessly. Therefore, we can conclude that $|Pr[{\mathbf{G}}_1\Rightarrow 1]-Pr[{\mathbf{G}}_2\Rightarrow 1]|\le 2^{-\omega (log\lambda )}.$ The lemma follows. □

Game ${\mathbf{G}}_3$:${\mathbf{G}}_3$ is equivalent to ${\mathbf{G}}_2$, with the difference that ${\mathbf{m}}_j={\mathbf{M}}_j{\mathbf{k}}_j★{\mathbf{x}}_j$ is changed to ${\mathbf{m}}_j={\widehat{\mathbf{u}}}_j$, where ${\widehat{\mathbf{u}}}_j\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$. More specifically, we have the following:

3.

$\mathcal{A}$ may request up to $\rho$ queries from the generation oracle. Upon obtaining an offset ${\delta }_j\in \mathcal{M}$ satisfying $\mathrm{dis}\left({\delta }_j\right)\le t$ for $j\in \left[\rho \right]$.,$\mathcal{C}$ sets ${\mathbf{k}}_j=\mathbf{k}$, samples ${\mathbf{M}}_j\stackrel{\$}{\leftarrow }{\mathcal{G}}^{l\times n}$, ${\mathbf{x}}_j\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$, and ${\widehat{\mathbf{u}}}_j\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$, sets ${\mathbf{m}}_j={\widehat{\mathbf{u}}}_j$, and sets ${\mathrm{P}}_j:=({\mathbf{M}}_j,{\mathbf{x}}_j)$; if $b=0$, ${\mathrm{R}}_j:={\mathbf{m}}_j$; otherwise, ${\mathrm{R}}_j\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$, and it returns $({\mathrm{P}}_j,{\mathrm{R}}_j)$ to $\mathcal{A}$.

Lemma 6. 

$|Pr[{\mathbf{G}}_2\Rightarrow 1]-Pr[{\mathbf{G}}_3\Rightarrow 1]|\le \rho {ϵ}_1.$

Proof. 

We aim to demonstrate that if a PPT adversary $\mathcal{A}$ can distinguish between ${\mathbf{G}}_2$ and ${\mathbf{G}}_3$ with a significant advantage, then it is possible to construct a PPT algorithm $\mathcal{B}$ that can solve the ${\mathrm{LHS}}_n^{\rho l}$ assumption with the same advantage. Suppose $\mathcal{B}$ is given an LHS tuple $({\mathbf{x}}^{\prime },{\mathbf{M}}^{\prime },\mathbf{t})$, where $\mathbf{t}$ is either ${\mathbf{M}}^{\prime }\mathbf{k}★{\mathbf{x}}^{\prime }$ or $\widehat{\mathbf{u}}$, and ${\mathbf{M}}^{\prime }\stackrel{\$}{\leftarrow }{\mathcal{G}}^{\rho l\times n}$, $\mathbf{k}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$, ${\mathbf{x}}^{\prime }\stackrel{\$}{\leftarrow }{\mathcal{X}}^{\rho l}$, $\widehat{\mathbf{u}}\stackrel{\$}{\leftarrow }{\mathcal{X}}^{\rho l}$. The goal of $\mathcal{B}$ is to determine which scenario holds. $\mathcal{B}$ operates as follows, and the entire interaction is illustrated in $\mathrm{Figure}$ Figure 3:

Figure 3. The entire interaction of Lemma 6.

• Algorithm $\mathcal{B}$ parses ${\mathbf{M}}^{\prime }=[{\mathbf{M}}_1^{\prime },{\mathbf{M}}_2^{\prime },\dots ,{\mathbf{M}}_{\rho }^{\prime }]$, ${\mathbf{x}}^{\prime }=[{\mathbf{x}}_1^{\prime },{\mathbf{x}}_2^{\prime },\dots ,{\mathbf{x}}_{\rho }^{\prime }]$ and $\mathbf{t}=[{\mathbf{t}}_1,{\mathbf{t}}_2,\dots ,{\mathbf{t}}_{\rho }]$, selects $b\stackrel{\$}{\leftarrow }\{0,1\}$, samples ${\mathrm{H}}_i\stackrel{\$}{\leftarrow }\mathcal{H}$, and then calls $\mathrm{EGA}.\mathrm{Setup}\left(1^{\lambda }\right)$ to generate $\mathrm{pp}=(\mathcal{G},\mathcal{X},★,\tilde{x})$, setting crs:=(pp, ${\mathrm{H}}_i$) and sending $\mathrm{crs}$ to $\mathcal{A}$.
• $\mathcal{B}$ chooses $w$ according to W, calculates $s\leftarrow \mathrm{SS}.\mathrm{Gen}(w)$, and then sets ${\mathrm{P}}_{\mathrm{init}}:=s$, returning ${\mathrm{P}}_{\mathrm{init}}$ to $\mathcal{A}$.
• $\mathcal{A}$ may request up to $\rho$ queries from the generation oracle. Upon obtaining an offset ${\delta }_j\in \mathcal{M}$ satisfying $\mathrm{dis}\left({\delta }_j\right)\le t$ for $j\in \left[\rho \right]$, $\mathcal{B}$ sets ${\mathbf{M}}_j={\mathbf{M}}_j^{\prime }$ and ${\mathbf{x}}_j={\mathbf{x}}_j^{\prime }$, ${\mathbf{m}}_j={\mathbf{t}}_j$, and sets ${\mathrm{P}}_j:=({\mathbf{M}}_j,{\mathbf{x}}_j)$; if $b=0$, ${\mathrm{R}}_j:={\mathbf{m}}_j$; otherwise, ${\mathrm{R}}_j\stackrel{\$}{\leftarrow }{\mathcal{X}}^l$, returning $({\mathrm{P}}_j,{\mathrm{R}}_j)$ to $\mathcal{A}$.
• $\mathcal{A}$ finally outputs a guessing bit $b^{\prime }$; when $b^{\prime }=b$, the game outputs 1; otherwise, it outputs 0.

If $\mathbf{t}={\mathbf{M}}^{\prime }\mathbf{k}★{\mathbf{x}}^{\prime }$, where ${\mathbf{M}}^{\prime }\stackrel{\$}{\leftarrow }{\mathcal{G}}^{\rho l\times n}$, $\mathbf{k}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$, ${\mathbf{x}}^{\prime }\stackrel{\$}{\leftarrow }{\mathcal{X}}^{\rho l}$, then $\mathcal{B}$ will accurately simulate game ${\mathbf{G}}_2$ for $\mathcal{A}$. Conversely, if $\mathbf{t}=\widehat{\mathbf{u}}$, where $\widehat{\mathbf{u}}\stackrel{\$}{\leftarrow }{\mathcal{X}}^{\rho l}$, then $\mathcal{B}$ perfectly simulates game ${\mathbf{G}}_3$ for $\mathcal{A}$. Hence, we deduce that

$$|Pr[{\mathbf{G}}_2\Rightarrow 1]-Pr[{\mathbf{G}}_3\Rightarrow 1]|\le {\mathrm{Adv}}_{\mathrm{LHS},\mathcal{A}}^{\rho l,n}\left(1^{\lambda }\right)\le \rho {ϵ}_1.$$

The lemma follows. □

Lemma 7. 

$Pr[{\mathbf{G}}_3\Rightarrow 1]=1/2.$

Proof. 

In ${\mathbf{G}}_3$, no matter whether $b=0$ or 1, ${\mathbf{m}}_j$ is always selected uniformly at random from ${\mathcal{X}}^l$; then, the adversary $\mathcal{A}$’s probability of making a correct guess is $1/2$. The lemma follows. □

By putting Equation (1) and Lemma 4–7 together, we obtain that $\epsilon \le 2^{-\omega (log\lambda )}+\rho {ϵ}_1.$ Theorem 1 follows.

3.3. Construction of RFE from GA-DDH Assumption

The detailed design of RFE = (RFE.Config, REF.Init, REF.Gen, REF.Rep) from the GA-DDH assumption is depicted in Figure 4, which is composed of the following building blocks:

Figure 4. Design of reusable fuzzy extractor from GA-DDH.

–

An $({\{0,1\}}^{l^{\prime }},m,\widehat{m},t)$-secure sketch SS = $(\mathrm{SS}.\mathrm{Gen},\mathrm{SS}.\mathrm{R}\mathrm{ec})$.

–

A REGA equipped with $\mathrm{REGA}.\mathrm{Setup}\left(1^{\lambda }\right)$, which outputs $(\mathcal{G},\mathcal{X},★,\tilde{x})$ with order $\left|\mathcal{G}\right|={\lambda }^{\omega \left(1\right)}$.

–

An average-case $({\{0,1\}}^{l^{\prime }},\widehat{m},{\{0,1\}}^n,{\epsilon }_{ext})$-strong extractor. Let $n\in \mathbb{Z}$ such that $n>log\left|\mathcal{G}\right|+\omega (log\lambda )$.

–

A family of universal hash functions $\mathcal{H}=\{{\mathrm{H}}_i:{\{0,1\}}^n\to \mathcal{G} | {\mathrm{H}}_i\left(x\right)={\sum }_{q=1}^n{x}_q{i}_q,i\in {\mathcal{G}}^n\}$ (While our GA-DDH-based construction requires the seed of the universal hash function to be sampled with high min-entropy (ideally uniformly at random), the design is tolerant to minor imperfections due to the entropy gap between the source and the output. However, for practical implementations, we recommend using a cryptographically secure pseudo-random number generator or high-entropy physical source to ensure robust security).

Theorem 2. 

If $\mathrm{SS}$ is a $({\{0,1\}}^{l^{\prime }},m,\widehat{m},t)$-secure sketch, $\mathcal{H}$ is a family of universal hash functions $\mathcal{H}=\{{\mathrm{H}}_i:{\{0,1\}}^n\to \mathcal{G} | i\in {\mathcal{G}}^n\}$. The GA-DDH assumption is ${ϵ}_2$-hard over the REGA $(\mathcal{G},\mathcal{X},★,\tilde{x})$; then, $\mathrm{RFE}$ in $Figure$Figure 4 is a $({\{0,1\}}^{l^{\prime }},m,\mathcal{X},t,\epsilon )$-reusable fuzzy extractor, where $\epsilon \le {\epsilon }_{ext}+\rho {ϵ}_2+2^{-\omega (log\lambda )}.$

Proof. 

First, the correctness of the RFE in Figure 4 follows from the correctness of the secure sketch SS. Similar to the proof of Theorem 1, we also use game-based proof to verify reusability. Adjacent games’ differences are highlighted with underlined text.

Game ${\mathbf{G}}_0$: Game ${\mathbf{G}}_0$ can be viewed as ${\mathrm{Exp}}_{\mathrm{RFE},\mathcal{A}}^{\mathrm{reu}}\left(1^{\lambda }\right)$. More specifically, we have the following:

• Challenger $\mathcal{C}$ selects $b\stackrel{\$}{\leftarrow }\{0,1\}$, samples ${\mathrm{H}}_i\stackrel{\$}{\leftarrow }\mathcal{H}$, and then calls $\mathrm{REGA}.\mathrm{Setup}\left(1^{\lambda }\right)$ to generate $\mathrm{pp}=(\mathcal{G},\mathcal{X},★,\tilde{x})$, selecting $k\stackrel{\$}{\leftarrow }\mathcal{K}$, $x\stackrel{\$}{\leftarrow }\mathcal{X}$, setting crs:=(pp, k, x, ${\mathrm{H}}_i$), and returning $\mathrm{crs}$ to $\mathcal{A}$.
• $\mathcal{C}$ chooses $w$ according to W, calculates $s\leftarrow \mathrm{SS}.\mathrm{Gen}(w)$, and then sets ${\mathrm{P}}_{\mathrm{init}}:=s$, returning ${\mathrm{P}}_{\mathrm{init}}$ to $\mathcal{A}$.
• $\mathcal{A}$ may request up to $\rho$ queries from the generation oracle. Upon obtaining an offset ${\delta }_j\in \mathcal{M}$ satisfying $\mathrm{dis}\left({\delta }_j\right)\le t$ for $j\in \left[\rho \right]$, $\mathcal{C}$ computes ${\tilde{w}}_j:=\mathrm{SS}.\mathrm{Rec}(w+{\delta }_j,s)$, ${\mathbf{t}}_j\leftarrow \mathrm{Ext}({\tilde{w}}_j,k)$, and $y_j\leftarrow {\mathrm{H}}_i\left({\mathbf{t}}_j\right)$, samples $r_j\stackrel{\$}{\leftarrow }\mathcal{G}$, computes $c_j=r_j★x$, and then calculates $v_j=y_j★c_j$, setting ${\mathrm{P}}_j:=c_j$; if $b=0$, ${\mathrm{R}}_j:=v_j$; otherwise, ${\mathrm{R}}_j\stackrel{\$}{\leftarrow }\mathcal{X}$, and it returns $({\mathrm{P}}_j,{\mathrm{R}}_j)$ to $\mathcal{A}$.
• $\mathcal{A}$ finally outputs a guessing bit $b^{\prime }$; when $b^{\prime }=b$, the game outputs 1; otherwise, it outputs 0.

Obviously, we deduce that

$$\begin{array}{c}\hfill Pr\left[{\mathbf{G}}_0\Rightarrow 1\right]=Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathrm{r}\mathrm{F}\mathrm{E},\mathcal{A}}^{\mathrm{r}\mathrm{e}\mathrm{u}}\left(1^{\lambda }\right)\Rightarrow 1\right].\end{array}$$

(2)

Game ${\mathbf{G}}_1$:${\mathbf{G}}_1$ is equivalent to ${\mathbf{G}}_0$, aside from some conceptual differences:

2.

$\mathcal{C}$ chooses $w$ according to W, calculates $s\leftarrow \mathrm{SS}.\mathrm{Gen}(w)$, $\mathbf{t}\leftarrow \mathrm{Ext}(w,k)$, $y\leftarrow {\mathrm{H}}_i\left(\mathbf{t}\right)$, and then sets ${\mathrm{P}}_{\mathrm{init}}:=s$, returning ${\mathrm{P}}_{\mathrm{init}}$ to $\mathcal{A}$.

3.

$\mathcal{A}$ may request up to $\rho$ queries from the generation oracle. Upon obtaining an offset ${\delta }_j\in \mathcal{M}$ satisfying $\mathrm{dis}\left({\delta }_j\right)\le t$ for $j\in \left[\rho \right]$, $\mathcal{C}$ sets ${\mathbf{t}}_j=\mathbf{t}$, $y_j=y$, samples $r_j\stackrel{\$}{\leftarrow }\mathcal{G}$, computes $c_j=r_j★x$, and then calculates $v_j=y_j★c_j$, setting ${\mathrm{P}}_j:=c_j$; if $b=0$, ${\mathrm{R}}_j:=v_j$; otherwise, ${\mathrm{R}}_j\stackrel{\$}{\leftarrow }\mathcal{X}$, returning $({\mathrm{P}}_j,{\mathrm{R}}_j)$ to $\mathcal{A}$.

□

Lemma 8. 

$Pr[{\mathbf{G}}_0\Rightarrow 1]=Pr[{\mathbf{G}}_1\Rightarrow 1].$

Proof. 

Due to the correctness of the secure sketch and $\mathrm{dis}\left({\delta }_j\right)\le t$, we have

$${\tilde{w}}_j=\mathrm{SS}.\mathrm{Rec}(w+{\delta }_j,s)=w.$$

Furthermore, we can get

$${\mathbf{t}}_j=\mathrm{Ext}({\tilde{w}}_j,k)=\mathrm{Ext}(w,k)=\mathbf{t}, y_j={\mathrm{H}}_i\left({\mathbf{t}}_j\right)={\mathrm{H}}_i\left(\mathbf{t}\right)=y.$$

Hence, we have $Pr[{\mathbf{G}}_0\Rightarrow 1]=Pr[{\mathbf{G}}_1\Rightarrow 1].$ The lemma follows. □

Game ${\mathbf{G}}_2$:${\mathbf{G}}_2$ is identical to ${\mathbf{G}}_1$, with the difference that $\mathbf{t}\leftarrow \mathrm{Ext}(w,k)$ is changed to $\mathbf{t}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$. More specifically, we have the following:

2.

$\mathcal{C}$ chooses $w$ according to W, calculates $s\leftarrow \mathrm{SS}.\mathrm{Gen}(w)$, $\mathbf{t}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$, $y\leftarrow {\mathrm{H}}_i\left(\mathbf{t}\right)$, and then sets ${\mathrm{P}}_{\mathrm{init}}:=s$, returning ${\mathrm{P}}_{\mathrm{init}}$ to $\mathcal{A}$.

Lemma 9. 

$|Pr[{\mathbf{G}}_1\Rightarrow 1]-Pr[{\mathbf{G}}_2\Rightarrow 1]|\le {\epsilon }_{ext}.$

Proof. 

Note that $w$ only appears in the second step to compute $s\leftarrow \mathrm{SS}.\mathrm{Gen}(w)$ both in ${\mathbf{G}}_1$ and ${\mathbf{G}}_2$; thus, $s$ is all the information about W that is revealed to $\mathcal{A}$. Meanwhile, since our SS is an $(\mathcal{M}={\{0,1\}}^{l^{\prime }},m,\widehat{m},t)$-secure sketch and $H_{\infty }\left(W\right)\ge m$, we have ${\tilde{H}}_{\infty }\left(W\right|\mathrm{SS}.\mathrm{Gen}\left(W\right))\ge \widehat{m}.$

We now present an algorithm $\mathcal{B}$ and prove that if an adversary exists that can distinguish ${\mathbf{G}}_1$ from ${\mathbf{G}}_2$ with a non-negligible advantage, then $\mathcal{B}$ can distinguish between $\left(\mathrm{Ext}\right(w,k)=\mathbf{t},k,s)$ and $(\mathbf{u},k,s)$ with the same advantage. Let $\mathcal{B}$ receive $(\mathbf{d},k,s)$, where $\mathbf{d}$ is either $\mathbf{t}=\mathrm{Ext}(w,k)$ or a uniformly chosen element $\mathbf{u}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$. The task of $\mathcal{B}$ is to identify which case is given. Algorithm $\mathcal{B}$ operates as follows:

• Algorithm $\mathcal{B}$ selects $b\stackrel{\$}{\leftarrow }\{0,1\}$, samples ${\mathrm{H}}_i\stackrel{\$}{\leftarrow }\mathcal{H}$, and then calls $\mathrm{REGA}.\mathrm{Setup}\left(1^{\lambda }\right)$ to generate $\mathrm{pp}=(\mathcal{G},\mathcal{X},★,\tilde{x})$; it samples $x\stackrel{\$}{\leftarrow }\mathcal{X}$, sets crs:=(pp, k, x, ${\mathrm{H}}_i$), and returns $\mathrm{crs}$ to $\mathcal{A}$.
• $\mathcal{B}$ sets $\mathbf{t}:=\mathbf{d}$, $y\leftarrow {\mathrm{H}}_i\left(\mathbf{t}\right)$, ${\mathrm{P}}_{\mathrm{init}}:=s$, and returns ${\mathrm{P}}_{\mathrm{init}}$ to $\mathcal{A}$.
• $\mathcal{A}$ may request up to $\rho$ queries from the generation oracle. Upon obtaining an offset ${\delta }_j\in \mathcal{M}$ satisfying $\mathrm{dis}\left({\delta }_j\right)\le t$ for $j\in \left[\rho \right]$, $\mathcal{B}$ sets ${\mathbf{t}}_j=\mathbf{t}$, $y_j=y$, samples $r_j\stackrel{\$}{\leftarrow }\mathcal{G}$, computes $c_j=r_j★x$, $v_j=y_j★c_j$, and sets ${\mathrm{P}}_j:=c_j$; if $b=0$, ${\mathrm{R}}_j:=v_j$; otherwise, ${\mathrm{R}}_j\stackrel{\$}{\leftarrow }\mathcal{X}$, returning $({\mathrm{P}}_j,{\mathrm{R}}_j)$ to $\mathcal{A}$.
• $\mathcal{A}$ finally outputs a guessing bit $b^{\prime }$; when $b^{\prime }=b$, the game outputs 1; otherwise, it outputs 0.

Assuming that $\mathcal{B}$ is given the tuple $(\mathbf{d}=\mathbf{t},k,s)$, where $\mathbf{t}$ is generated by $\mathrm{Ext}(w,k)$, k is sampled from $\mathcal{K}$, and $s$ is created via $\mathrm{SS}.\mathrm{Gen}(w)$, $\mathcal{B}$ will successfully simulate game ${\mathbf{G}}_1$ for $\mathcal{A}$. On the other hand, if $\mathcal{B}$ is provided with the tuple $(\mathbf{d}=\mathbf{u},k,s)$, where $\mathbf{u}$ is randomly chosen from ${\{0,1\}}^n$, $\mathcal{B}$ will simulate game ${\mathbf{G}}_2$ for $\mathcal{A}$ perfectly. Consequently, we conclude that

$$\begin{array}{cc}\hfill | & Pr\left[{\mathbf{G}}_1\Rightarrow 1\right]-Pr\left[{\mathbf{G}}_2\Rightarrow 1\right] |\le \mathrm{SD}\left(\left(\mathrm{Ext}(w,k), k, s\right), \left(\mathbf{u}, k, s\right)\right)\le {\epsilon }_{\mathrm{ext}}.\hfill \end{array}$$

The lemma follows. □

Game ${\mathbf{G}}_3$:${\mathbf{G}}_3$ is identical to ${\mathbf{G}}_2$, with the difference that $y\leftarrow {\mathrm{H}}_i\left(\mathbf{t}\right)$ is changed to $y\stackrel{\$}{\leftarrow }\mathcal{G}$. More specifically, we have the following:

2.

$\mathcal{C}$ chooses $w$ according to W, calculates $s\leftarrow \mathrm{SS}.\mathrm{Gen}(w)$, $\mathbf{t}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$, $y\stackrel{\$}{\leftarrow }\mathcal{G}$, and then sets ${\mathrm{P}}_{\mathrm{init}}:=s$, returning ${\mathrm{P}}_{\mathrm{init}}$ to $\mathcal{A}$.

Lemma 10. 

$|Pr[{\mathbf{G}}_2\Rightarrow 1]-Pr[{\mathbf{G}}_3\Rightarrow 1]|\le 2^{-\omega (log\lambda )}.$

Proof. 

Recall that in ${\mathbf{G}}_2$, $\mathbf{t}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$, ${\mathrm{H}}_i\stackrel{\$}{\leftarrow }\mathcal{H}$ (i.e., $i\stackrel{\$}{\leftarrow }{\mathcal{G}}^n$), and ${\mathrm{H}}_i$ are public in crs. According to Lemma 2, we have $(i,{\sum }_{q=1}^n{\mathbf{t}}_q{i}_q){\stackrel{{\epsilon }^{\prime }}{\approx }}_s(i,u),$ where ${\sum }_{q=1}^n{\mathbf{t}}_q{i}_q={\mathrm{H}}_i\left(\mathbf{t}\right)$, $u\stackrel{\$}{\leftarrow }\mathcal{G}$, and ${\epsilon }^{\prime }=\sqrt{\mathcal{G}/2^n}\le 2^{-\omega (log\lambda )}$. Thus, y is statistically indistinguishable in ${\mathbf{G}}_2$ and ${\mathbf{G}}_3$. This proof follows similarly to that of Lemma 5, and can thus be easily derived. The lemma follows. □

Game ${\mathbf{G}}_4$:${\mathbf{G}}_4$ is equivalent to ${\mathbf{G}}_3$, with the difference that $v_j=y_j★c_j$ is changed to $v_j=u_j^{\prime }★x$, where $u_j^{\prime }\stackrel{\$}{\leftarrow }\mathcal{G}$. More specifically, we have the following:

3.

$\mathcal{A}$ may request up to $\rho$ queries from the generation oracle. Upon obtaining an offset ${\delta }_j\in \mathcal{M}$ satisfying $\mathrm{dis}\left({\delta }_j\right)\le t$ for $j\in \left[\rho \right]$, $\mathcal{C}$ sets ${\mathbf{t}}_j=\mathbf{t}$, $y_j:=y$, samples $r_j\stackrel{\$}{\leftarrow }\mathcal{G}$, computes $c_j=r_j★x$, samples $u_j^{\prime }\stackrel{\$}{\leftarrow }\mathcal{G}$, and then calculates $v_j=u_j^{\prime }★x$, setting ${\mathrm{P}}_j:=c_j$; if $b=0$, ${\mathrm{R}}_j:=v_j$; otherwise, ${\mathrm{R}}_j\stackrel{\$}{\leftarrow }\mathcal{X}$, returning $({\mathrm{P}}_j,{\mathrm{R}}_j)$ to $\mathcal{A}$.

Lemma 11. 

$|Pr[{\mathbf{G}}_3\Rightarrow 1]-Pr[{\mathbf{G}}_4\Rightarrow 1]|\le \rho {ϵ}_2.$

Proof. 

We prove this lemma through a series of games ${\mathbf{G}}_{3.\alpha }$, where $\alpha \in [0,\rho ]$. The specific description of ${\mathbf{G}}_{3.\alpha }$ is provided below.

• Challenger $\mathcal{C}$ selects $b\stackrel{\$}{\leftarrow }\{0,1\}$, samples ${\mathrm{H}}_i\stackrel{\$}{\leftarrow }\mathcal{H}$, and then calls $\mathrm{REGA}.\mathrm{Setup}\left(1^{\lambda }\right)$ to generate $\mathrm{pp}=(\mathcal{G},\mathcal{X},★,\tilde{x})$, selecting $k\stackrel{\$}{\leftarrow }\mathcal{K}$ and $x\stackrel{\$}{\leftarrow }\mathcal{X}$; then, it sets crs:=(pp, k, x, ${\mathrm{H}}_i$) and returns $\mathrm{crs}$ to $\mathcal{A}$.
• $\mathcal{C}$ chooses $w$ according to W, calculates $s\leftarrow \mathrm{SS}.\mathrm{Gen}(w)$, $\mathbf{t}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$, $y\stackrel{\$}{\leftarrow }\mathcal{G}$, sets ${\mathrm{P}}_{\mathrm{init}}:=s$, and returns ${\mathrm{P}}_{\mathrm{init}}$ to $\mathcal{A}$.
• $\mathcal{A}$ may request up to $\rho$ queries from the generation oracle. Upon obtaining an offset ${\delta }_j\in \mathcal{M}$ satisfying $\mathrm{dis}\left({\delta }_j\right)\le t$ for $j\in \left[\rho \right]$, $\mathcal{C}$ sets ${\mathbf{t}}_j=\mathbf{t}$, $y_j=y$, samples $r_j\stackrel{\$}{\leftarrow }\mathcal{G}$, computes $c_j=r_j★x$. If $j\le \alpha$, samples $u_j^{\prime }\stackrel{\$}{\leftarrow }\mathcal{G}$, and then sets $v_j=u_j^{\prime }★x$; otherwise, it sets $v_j=y_j★c_j$. Then, it sets ${\mathrm{P}}_j:=c_j$; if $b=0$, ${\mathrm{R}}_j:=v_j$; otherwise, ${\mathrm{R}}_j\stackrel{\$}{\leftarrow }\mathcal{X}$, returning $({\mathrm{P}}_j,{\mathrm{R}}_j)$ to $\mathcal{A}$.
• $\mathcal{A}$ finally outputs a guessing bit $b^{\prime }$; when $b^{\prime }=b$, the game outputs 1; otherwise, the outputs 0.

Obviously, we have ${\mathbf{G}}_{3.0}$, which is identical to ${\mathbf{G}}_3$, and ${\mathbf{G}}_{3.\rho }$ is equivalent to ${\mathbf{G}}_4$. Before proving this lemma, let us first prove the following proposition. □

Proposition 1. 

$|Pr[{\mathbf{G}}_{3.(\alpha -1)}\Rightarrow 1]-Pr[{\mathbf{G}}_{3.\alpha }\Rightarrow 1]|\le {ϵ}_2, \alpha \in \left[\rho \right].$

Proof. 

We will show that if there exists an adversary $\mathcal{A}$ that can distinguish ${\mathbf{G}}_{3.(\alpha -1)}$ and ${\mathbf{G}}_{3.\alpha }$ with a non-negligible advantage, then there exists a PPT algorithm $\mathcal{B}$ that can solve the GA-DDH problem with the same advantage. Assume that $\mathcal{B}$ is provided with a tuple $(x,r^{\prime }★x,y^{\prime }★x,d^{\prime }★x)$, where $r^{\prime },y^{\prime }\stackrel{\$}{\leftarrow }\mathcal{G}$ and $x\stackrel{\$}{\leftarrow }\mathcal{X}$, and $d^{\prime }$ is either $r^{\prime }+y^{\prime }$ or a random element $u^{\prime }$ from $\mathcal{G}$. The goal of $\mathcal{B}$ is to determine which case holds. Algorithm $\mathcal{B}$ operates as follows:

• Algorithm $\mathcal{B}$ selects $b\stackrel{\$}{\leftarrow }\{0,1\}$, samples ${\mathrm{H}}_i\stackrel{\$}{\leftarrow }\mathcal{H}$, and then calls $\mathrm{REGA}.\mathrm{Setup}\left(1^{\lambda }\right)$ to generate $\mathrm{pp}=(\mathcal{G},\mathcal{X},★,\tilde{x})$; it samples $k\stackrel{\$}{\leftarrow }\mathcal{K}$, sets crs:=(pp, k, x, ${\mathrm{H}}_i$), and sends $\mathrm{crs}$ to $\mathcal{A}$.
• $\mathcal{B}$ chooses $w$ according to W, calculates $s\leftarrow \mathrm{SS}.\mathrm{Gen}(w)$ and $\mathbf{t}\stackrel{\$}{\leftarrow }{\{0,1\}}^n$, implicitly sets $y=y^{\prime }$, and then sets ${\mathrm{P}}_{\mathrm{init}}:=s$, returning ${\mathrm{P}}_{\mathrm{init}}$ to $\mathcal{A}$.
• $\mathcal{A}$ may request up to $\rho$ queries from the generation oracle. Upon obtaining an offset ${\delta }_j\in \mathcal{M}$ satisfying $\mathrm{dis}\left({\delta }_j\right)\le t$ for $j\in \left[\rho \right]$, $\mathcal{B}$ sets ${\mathbf{t}}_j=\mathbf{t}$, implicitly sets $y_j=y$, samples $r_j\stackrel{\$}{\leftarrow }\mathcal{G}$, and computes $c_j=r_j★x$. If $j<\alpha$, it samples $u_j^{\prime }\stackrel{\$}{\leftarrow }\mathcal{G}$ and sets $v_j=u_j^{\prime }★x$; if $j=\alpha$, it sets $c_j=r^{\prime }★x$, $v_j=d^{\prime }★x$; if $j>\alpha$, it sets $v_j=r_j★(y^{\prime }★x)$. Then, it sets ${\mathrm{P}}_j:=c_j$; if $b=0$, ${\mathrm{R}}_j:=v_j$; otherwise, ${\mathrm{R}}_j\stackrel{\$}{\leftarrow }\mathcal{X}$, returning $({\mathrm{P}}_j,{\mathrm{R}}_j)$ to $\mathcal{A}$.
• $\mathcal{A}$ finally outputs a guessing bit $b^{\prime }$; when $b^{\prime }=b$, the game outputs 1; otherwise, it outputs 0.

If $d^{\prime }=r^{\prime }+y^{\prime }$, then $\mathcal{B}$ accurately simulates game ${\mathbf{G}}_{3.\alpha -1}$ for $\mathcal{A}$; if $d^{\prime }=u^{\prime }$, then $\mathcal{B}$ perfectly simulates game ${\mathbf{G}}_{3.\alpha }$ for $\mathcal{A}$. Hence, we conclude that

$$|Pr[{\mathbf{G}}_{3.(\alpha -1)}\Rightarrow 1]-Pr[{\mathbf{G}}_{3.\alpha }\Rightarrow 1]|\le {ϵ}_2.$$

The proposition follows. □

Therefore, by using Proposition 1 $\rho$ times, we obtain $|Pr[{\mathbf{G}}_3\Rightarrow 1]-Pr[{\mathbf{G}}_4\Rightarrow 1]|\le \rho {ϵ}_2.$ The lemma follows.

Game ${\mathbf{G}}_5$:${\mathbf{G}}_5$ is identical to ${\mathbf{G}}_4$, except that $v_j=u_j^{\prime }★x$ is changed to $v_j={\tilde{u}}_j$, where ${\tilde{u}}_j\stackrel{\$}{\leftarrow }\mathcal{X}$. More specifically, we have the following:

3.

$\mathcal{A}$ may request up to $\rho$ queries from the generation oracle. Upon obtaining an offset ${\delta }_j\in \mathcal{M}$ satisfying $\mathrm{dis}\left({\delta }_j\right)\le t$ for $j\in \left[\rho \right]$, $\mathcal{C}$ sets ${\mathbf{t}}_j=\mathbf{t}$ and $y_j:=y$, samples $r_j\stackrel{\$}{\leftarrow }\mathcal{G}$, computes $c_j=r_j★x$, samples ${\tilde{u}}_j\stackrel{\$}{\leftarrow }\mathcal{X}$, and then sets $v_j={\tilde{u}}_j$, setting ${\mathrm{P}}_j:=c_j$; if $b=0$, ${\mathrm{R}}_j:=v_j$; otherwise, ${\mathrm{R}}_j\stackrel{\$}{\leftarrow }\mathcal{X}$, returning $({\mathrm{P}}_j,{\mathrm{R}}_j)$ to $\mathcal{A}$.

Lemma 12. 

$Pr[{\mathbf{G}}_4\Rightarrow 1]=Pr[{\mathbf{G}}_5\Rightarrow 1].$

Proof. 

Note that in ${\mathbf{G}}_4$, $v_j=u_j^{\prime }★x$, $u_j^{\prime }\stackrel{\$}{\leftarrow }\mathcal{G}$. Since the group action is regular, according to Remark 1 and Remark 2, $v_j$ is uniformly distributed over $\mathcal{X}$ in ${\mathbf{G}}_4$ in the REGA setting. Thus, the distributions of $v_j$ in ${\mathbf{G}}_4$ and ${\mathbf{G}}_5$ are identical. The lemma follows. □

Lemma 13. 

$Pr[{\mathbf{G}}_5\Rightarrow 1]=1/2.$

Proof. 

The proof is similar to that of Lemma 7 and is omitted for brevity. □

Putting Equation (2) and Lemmas 8–13 together, we obtain that $\epsilon \le {\epsilon }_{ext}+\rho {ϵ}_2+2^{-\omega (log\lambda )}.$ Theorem 2 follows.

4. Instantiation

4.1. Instantiation of Building Blocks

4.1.1. Syndrome-Based Secure Sketch

Considering a linear error-correcting code $\mathcal{E}$ that is ${[n,k,2t+1]}_{\mathcal{F}}$ and lies within the space ${\mathcal{F}}^n$. Specifically, $\mathcal{E}=\{w\in {\mathcal{F}}^n\mid \mathbf{H}w=0\}$, where $\mathbf{H}$ is an $(n-k)\times n$ parity-check matrix. As proposed in [1], a syndrome-based secure sketch can be constructed using an efficient ${[n,k,2t+1]}_{\mathcal{F}}$-linear error-correcting code, and the construction can be summarized as follows:

–

$\mathrm{SS}.\mathrm{Gen}(w):=\mathrm{syn}(w)=\mathbf{H}w=s$;

–

$\mathrm{SS}.\mathrm{Rec}(w^{\prime },s):=w^{\prime }-\mathrm{Decode}(\mathrm{syn}\left(w^{\prime }\right)-s)=w^{\prime }-\mathbf{e}$.

Lemma 14. 

Given an ${[n,k,2t+1]}_{\mathcal{F}}$ error-correcting code, it is feasible to construct an $({\mathcal{F}}^n,m,m-(n-k)|\mathcal{F}|,t)$ secure sketch, which is efficient if encoding and decoding are efficient.

As there are efficient ${[n,k,2t+1]}_{\mathcal{F}}$-linear error-correcting codes where $t=O\left(n\right)$, the syndrome-based secure sketch can handle a linear proportion of errors.

4.1.2. Universal Hash Functions and Strong Extractor

In our construction 1, we use the following commonly used family of universal hash functions [8,14].

$$\mathcal{H}=\{{\mathrm{H}}_i:{\{0,1\}}^{l^{\prime }}\to {\{0,1\}}^n | \mathrm{H}\left(x\right)=i·x\},$$

(3)

where $i\in {\{0,1\}}^{l^{\prime }+n-1}$, symbol “·” represents matrix-vector multiplication in ${\mathcal{F}}_2$, and i is interpreted as an $n\times l^{\prime }$ Toeplitz matrix.

In our construction 2, we use the universal hash function presented in Lemma 2. More precisely, we have the following:

$$\mathcal{H}=\{{\mathrm{H}}_i:{\{0,1\}}^n\to \mathcal{G} | {\mathrm{H}}_i\left(x\right)=\sum _{q=1}^n{x}_q{i}_q,i\in {\mathcal{G}}^n\}.$$

(4)

The leftover hash lemma (Lemma 1) implies that universal hash functions are good (average-case strong) extractors. The construction of universal hash functions in Equation (3) is a good instance.

4.1.3. (Restricted) Effective Group Action

• EGA from CSI-FiSh. As stated in [13], we can derive a regular and abelian effective group action (EGA) from isogeny via CSI-FiSh, which precomputes the group structure $Cl\left(\mathbb{Z}\left[{\pi }_p\right]\right)$ of CSIDH-512 (to optimize sampling from the ideal class group $\mathcal{G}$, one can precompute its group structure, typically making $\mathcal{G}$ cyclic. Uniform sampling from $\mathcal{G}$ then becomes efficient. Sampling from $\mathcal{G}$ can be realized by applying a random group element to a fixed representative, leveraging the regularity of the group action. This strategy is used in prior isogeny-based works such as CSI-FiSh.).

• $(p,N,\left[g\right],E_0)\leftarrow \mathrm{CSI}.\mathrm{Setup}$, where p specifies the prime field, N denotes the order of the ideal class group $Cl\left(\mathbb{Z}\left[{\pi }_p\right]\right)$, $\left[g\right]$ is a generator of $Cl\left(\mathbb{Z}\left[{\pi }_p\right]\right)$, and $E_0$ is the base elliptic curve defined by $y^2=x^3+x$.
• Define $\mathcal{G}:=Cl\left(\mathbb{Z}\left[{\pi }_p\right]\right)$, $\mathcal{X}:={Ell}_p\left(\mathbb{Z}\left[{\pi }_p\right]\right)$, and set the origin $\tilde{x}:=E_0$. The group $Cl\left(\mathbb{Z}\left[{\pi }_p\right]\right)\cong ({\mathbb{Z}}_N,+)$ supports efficient group operations, including equality checking, random sampling, addition, and inversion.

• REGA from CSIDH. As stated in [41], let p be a large prime of the form $p=4·{\ell }_1\dots {\ell }_n-1$, where each ${\ell }_i$ is a small distinct odd prime. We consider the elliptic curve $E_0:y^2=x^3+x$ over ${\mathbb{F}}_p$, which is supersingular. The endomorphism ring of this curve over ${\mathbb{F}}_p$ is $\mathcal{O}=\mathbb{Z}\left[\pi \right]$, where $\pi$ is the Frobenius endomorphism. $\mathcal{E}l{l}_p\left(\mathcal{O}\right)$ is the set of elliptic curves defined over ${\mathbb{F}}_p$ whose endomorphism ring is $\mathcal{O}$. The ideal class group $Cl\left(\mathcal{O}\right)$ acts on this set, which is formalized by a map.

  $$★:Cl\left(\mathcal{O}\right)\times \mathcal{E}l{l}_p\left(\mathcal{O}\right)\to \mathcal{E}l{l}_p\left(\mathcal{O}\right),$$

  $$\left(\right[\mathfrak{a}],E)\mapsto \left[\mathfrak{a}\right]★E.$$

We abstract the generation process of (R)EGA as an algorithm called $\left(\mathrm{R}\right)\mathrm{EGA}.\mathrm{Setup}\left(1^{\lambda }\right)$, which outputs the description of (R)EGA.

4.2. Instantiations of Our Construction 1 and Construction 2

Based on concrete instantiations of the aforementioned building blocks, Figure 5 and Figure 6 illustrate the complete instantiations of our reusable fuzzy extractors under the LHS assumption and the GA-DDH assumption, respectively.

Figure 5. Instantiation of reusable fuzzy extractor from LHS.

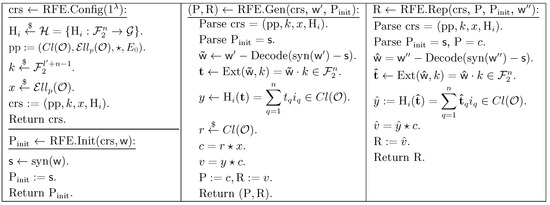
Figure 6. Instantiation of reusable fuzzy extractor from GA-DDH.

5. Conclusions

In this work, we present two constructions of RFE under isogeny-based assumptions and rigorously prove their security. Indeed, our motivation stems from the observation that existing post-quantum secure FE schemes (whether reusable or robust) are predominantly based on lattice-based hardness assumptions, such as the LWE assumption. Excessive dependence on lattice assumptions has led to a lack of diversity in post-quantum FE constructions. If significant progress were to be made in solving lattice problems, the security of these lattice-based fuzzy extractors would be at serious risk.

Moreover, we note that fuzzy extractors based on isogeny assumptions are still rare. To the best of our knowledge, only two such constructions [13,14] exist, both published last year and relying on the WPR assumption, a specific isogeny-based hardness assumption. In contrast, other cryptographic primitives based on isogeny assumptions, such as key exchange protocols [28] and digital signatures [15], have seen rapid development. This disparity suggests that adapting isogeny-based assumptions to the fuzzy extractor setting is non-trivial and that constructing reusable or robust fuzzy extractors using conventional techniques is far from straightforward—a challenge also noted in [13]. Therefore, inspired by the refinement of the RRFE security model in [13], we propose a similar modification to the security model of RFE. This refinement eliminates the need to rely on the key-shift security of underlying primitives or assumptions in the security proof. Based on the optimized model, we construct two reusable fuzzy extractors under the LHS assumption and the GA-DDH assumption, respectively. Compared to the construction in [13,14], our first scheme is able to extract longer uniform strings (l-times longer), albeit at a higher computational cost. Moreover, our second construction achieves the same output length as the schemes in [13,14] while incurring a lower computational cost than [13] and nearly matching the efficiency of [14].

Our constructions utilize only some fundamental cryptographic primitives: secure sketches for fuzzy error correction, and hash functions or strong extractors to extract uniform randomness, which can be further employed in other cryptographic applications, such as serving as keys for symmetric or asymmetric encryption schemes. On the one hand, we achieve the reusability of FE, ensuring security across multiple extractions from the same noisy source. On the other hand, we recognize that robustness is also a crucial component of fuzzy extractor security; it protects against active attacks on the public helper string. However, we have not yet identified an effective or satisfactory method for achieving robustness in our setting. In particular, achieving both robustness and reusability in a single fuzzy extractor remains an open challenge, which we leave for future investigation.

In addition, an interesting open direction for future research is to investigate the applicability of our framework to multi-factor fuzzy sources, such as combinations of voice and facial biometrics. This would require addressing challenges in feature fusion, noise modeling, and entropy extraction beyond the single-source setting considered in this work. Another promising direction for future work is to investigate the practical deployment of our constructions on resource-constrained edge systems, as well as to evaluate their robustness under real-world noise patterns. Meanwhile, it is important to explore the integration of our reusable fuzzy extractor constructions with other post-quantum cryptographic protocols, such as key exchange, authentication, and secure enrollment schemes. In particular, combining our techniques with post-quantum primitives (e.g., isogeny-based or lattice-based protocols) may yield end-to-end secure systems that are resilient against quantum adversaries and robust to input noise.