Dynamic Modeling and Modal Analysis of Rectangular Plates with Edge Symmetric Periodic Acoustic Black Holes

Abstract

The vibration noise of plate structures in engineering is strongly related to the modal resonance, and modal design is the key to improve the dynamic characteristics of plate structures and avoid structural resonance. This paper investigates the dynamic and mode characteristics for an edge periodic acoustic black hole plate structure to provide a new approach to vibration and sound attenuation in plate structures. Firstly, based on the principles of symmetry and periodicity, this work presents the geometrical modeling and mathematical description of a rectangular plate with symmetrical periodic acoustic black holes at its edge. Then, it presents the dynamic modeling of a rectangular plate with periodic acoustic black holes at its edge via the “remove-and-fill” substitution method, which reveals the effects of the structural parameters and period distribution, etc., on the modal characteristics of vibration. The study indicates that the power law index, radius, number and configuration (e.g., semicircular, rectangular block shape) of the edge periodic acoustic black holes significantly affect the modal frequency of the rectangular plate, and increasing the radius of the acoustic black holes or the number of the black holes results in a decrease in the modal frequency of the rectangular plate. Moreover, the four-side symmetric layout achieves broader modal frequency modulation, while semicircular acoustic black holes can achieve a lower modal frequency compared with the rectangular wedge-shaped acoustic black hole. The theoretical model is verified by finite element simulation (FEM) and experiments, in which the errors of the first six modal frequencies are within 2%. The research in this paper provides a theoretical basis for the realization of modal frequency control in plate structures and the suppression of structural resonance through the design of edge periodic acoustic black hole structures.

1. Introduction

Plate structures, as fundamental components that are widely employed in engineering, also serve as the primary source of vibration and noise in machinery and equipment. As the critical interface between such structures and external constraints, the edge region of a plate structure not only influences its functional performance, strength, and reliability but also significantly impacts its vibration modes and dynamic characteristics owing to varying edge configurations and boundary conditions. For commonly used rectangular plate structures, their installation and fixation are typically established via boundary conditions—such as fixed supports, simple supports, free edges, and elastic connections—which vary with the specific engineering application scenario. Such boundary treatment methods can satisfy engineering application requirements, yet they often entail dynamic risks. Specifically, when the excitation frequency matches or approximates the structural modal frequencies under periodic dynamic excitation, modal resonance may be induced. This resonance can disrupt the normal operation of the structure and generate significant vibration and sound radiation. Although the modal frequencies can be adjusted by configuring boundary conditions under specific scenarios, the scope and magnitude of such adjustments are often constrained by operational requirements. This constraint typically renders it challenging to effectively avoid overlapping with excitation frequencies. Therefore, in this study, by investigating the dynamic modeling and modal characteristics of periodic rectangular plates with symmetric edge conditions—starting from their edge regions—the edge structure and boundary constraints are accurately designed and adjusted to effectively solve the modal resonance issue in such plate structures.

Acoustic black holes (ABHs), as novel structures designed to manipulate wave propagation and energy concentration, have garnered significant attention in vibration and noise control research recently. Their operational principle originates from geometric acoustics’ waveguide theory. Specifically, by tailoring the geometric parameters—such as the thickness and cross-sectional profiles—of materials or structures to exhibit a power law gradient, the propagation speed of sound waves gradually decreases with distance. This causes acoustic energy to concentrate in a targeted region, endowing ABHs with unique advantages in vibration control. This characteristic inspires a new strategy for the control of vibration in plate structures: periodically placing ABHs along the plate edges can regulate vibrational wave propagation. Moreover, the gradient geometry of these ABHs offers a new way to design the modal properties of plate structures with ABHs at their edges. In recent decades, numerous scholars have conducted experimental and theoretical investigations into the application of ABHs for vibration and noise mitigation.

Mironov [1] first showed theoretically that bending waves propagate non-reflectively in plate structures when the thickness decreases quadratically. This work revealed an exponential attenuation law for both the phase velocity and energy density. Subsequently, Mironov et al. [2] extended this idea to aerodynamics. They proposed a model where the sound velocity gradually drops to zero via the graded design of waveguide wall acoustic admittance. The physical mechanism of this model is highly similar to shear wave propagation in seafloor sediments. Feurtado et al. [3] further conducted a quantitative analysis of how the thickness gradient index influences microwave absorption performance. They found that, while a high gradient index enhances the absorption efficiency, it requires balancing with the smoothness assumption—thereby providing a theoretical foundation for the optimization of structural parameters.

In vibration control applications, the Krylov research group [4,5,6] was the first to propose an ABH damper based on a power law wedge structure. This design effectively suppresses resonant bending vibrations in thin plates by optimizing the thickness gradient index (m ≥ 2) and integrating a surface damping layer. Experimental results demonstrate that, compared with traditional uniform-thickness plates, this structure reduces the resonance peaks by over 15 dB. Subsequently, Krylov et al. [7] systematically reviewed the theoretical advancements and engineering applications of ABHs. They clarified how ABHs achieve the near-complete absorption of bending waves via thickness gradients and compared their characteristics with those of optical black holes. This team also experimentally verified their effectiveness in thin plate damping and discussed their potential in two key areas: air sound absorption and super-acoustic Lamb wave non-reflective terminals. Georgiev et al. [8] further extended ABHs’ applications to beam and elliptical plate structures, achieving the efficient dissipation of high-frequency vibration energy via wave-focusing effects and the optimization of vibration-absorbing film parameters. Through modal analysis, Denis et al. [9] revealed the micro-mechanism by which ABHs enhance high-frequency damping: they increase the modal density and the overlap factor, thereby improving the energy dissipation efficiency. Jae Yeon Lee et al. [10] creatively proposed an Archimedes spiral ABH design to address space constraints. Experimental results demonstrated that, in the medium-to-high-frequency band, its vibration-damping performance improved significantly with increasing arc lengths, all while maintaining the benefits of a light weight.

For theoretical modeling, Wonju Jeon et al. [11] first obtained an exact analytical solution for ABH structures by transforming the Euler–Bernoulli equation into a generalized hypergeometric equation. Their work systematically clarified the wave absorption mechanisms for different power law exponents. Li Cheng et al. [12] proposed a semi-analytical model based on Mexican Hat wavelet decomposition, effectively characterizing the coupling effect between ABH structures and damping layers. This model revealed the critical role of the damping layer quality in determining the performance of truncated regions. Yuhang Wang et al. [13] proposed a Rayleigh–Ritz energy model to accurately calculate the power flow and structural strength in ABH beams. This model reveals the spatial–frequency distribution law of energy within these structures. Jie Deng et al. [14,15] systematically investigated the formation mechanism of low-frequency band gaps in periodic ABHs using the K(ω) method. Jie Deng’s team proposed an elliptical ABH lens that overcame traditional structural thickness limitations and achieved the controllable focusing of bending wave energy. Jingtao Du et al. [16] developed a semi-analytical dynamic model for the ABH coupling plate system using the Rayleigh–Ritz method, employing a modified Fourier series to characterize transverse and in-plane vibration displacement fields. They studied the model’s convergence and verified its accuracy via finite element analysis and experiments, proving that the ABH coupling plate exhibits excellent vibration attenuation performance.

In expanding engineering applications, Ouahabi et al. [17] integrated the ABH effect into aeroacoustics, achieving efficient sound wave absorption in the 100–1000 Hz frequency band via a quasi-periodic rib waveguide structure. Guasch et al. [18] systematically analyzed the noise reduction performance of pipeline-based ABHs using the transfer matrix method and proposed an optimal design approach based on finite ring numbers and damping parameters. Xiaoqi Zhang et al. [19] proposed an innovative combination of ABHs and microperforated plates to achieve low-frequency broadband sound absorption with sub-wavelength thickness in circular pipes. Subsequently, Zhang et al. [20] used finite element simulations and impedance tube experiments to clarify the low-frequency broadband absorption mechanism of finite inner-ring ABH structures in pipes: cavity resonance near the ring wall generates high-pressure gradient energy dissipation zones, while wave delay effects promote the transition from single-peak resonance to multi-peak broadband responses and lower the resonance frequency. Feng Zheng et al. [21] demonstrated 5–18 dB vibration attenuation in ABH thin plates across the 200–3000 Hz frequency band via composite material structure design. Jiakai Yuan et al. [22] designed structures embedded with single ABH and ABH arrays, using the method of vibration power flow analysis to investigate the energy propagation characteristics in composite plate structures with ABHs at medium and low frequencies. This work also analyzed the energy-focusing effects of two-dimensional ABHs on low-frequency bending waves in composite plates. Ruilei Ma et al. [23] designed a pressure plate structure for underwater vehicles that exhibited broadband vibration reduction across 50 Hz to 10 kHz. Haoming Liang et al. [24] optimized the energy-focusing effects of two-dimensional ABH arrays using orthogonal testing, finding that transversely arranged double ABH structures exhibited optimal performance.

Recent studies highlight two distinct trends in ABH research. First, periodic structural designs have overcome traditional ABHs’ frequency limitations—take Liling Tang et al. [25]’s tunnel double-layer plate structure, for example, which achieves low-frequency sound radiation suppression. Second, the energy dissipation efficiency is enhanced via coupled optimization across multiple physical fields. For instance, the concave ABH structure designed by Wonju Jeon et al. [26] retains excellent vibration-damping performance with a 50% weight reduction. Pislyak et al. [27] conducted experimental comparisons of two ABH models: rigid disk arrays and density gradient media. Their work validated the synergistic effects of trace microwave-absorbing materials. Pelat et al. [28] systematically reviewed the damping mechanisms of ABHs in thin-walled structures. Chenhui Zhao et al. [29] summarized their applications in vibration suppression, noise control, and energy recovery. Xiaoran Wang et al. [30] used a disk-boundary ABH design to mitigate the boundary reflections of acoustic emission waves and improve the signal-to-noise ratio.

The existing research demonstrates that ABHs [31,32,33] have achieved significant progress in structural vibration and noise control. However, studies on edge-mounted ABH structures—especially periodic configurations in edge regions—remain unexplored, offering a new approach to solving vibration and noise issues in rectangular plates. This paper mainly focuses on the influence mechanism of the modal frequency of the edge periodic ABH plate structure based on the theoretical method, revealing the influence law of the ABH structural parameters on the modal frequency and providing a theoretical basis for the dynamic design and performance regulation of the ABH boundary plate structure. As the ABH has a variable cross-section structure, actual engineering applications may encounter stress concentration, strength issues, and other problems. Considering the specific application objectives and situation, the structural strength and stress can be set as the constraints; based on this, the modal design and optimization of the ABH boundary plate structure can be performed to ensure that it meets the requirements of the engineering application to improve its dynamic performance.

Specifically, the dynamical modeling equations of a rectangular plate with a periodic ABH distribution along the edges are developed in Section 2 of this article by combining the Gaussian expansion method with the energy method, and the theoretical method is verified by simulations and experiments. In Section 3, the influence of key parameters such as the power law exponents, number of ABHs, and ABH configuration on the modal frequencies and the shape of the plate are investigated, and, in Section 4, the article is summarized.

2. Dynamic Model of Acoustic Black Hole Symmetric Periodic Boundary Rectangular Plate

In this subsection, a geometrical description of the ABH rectangular plate with periodic semicircular, rectangular wedge-shaped edges is firstly presented, followed by the establishment of the corresponding dynamical model. The verification of the theoretical model is finally conducted in conjunction with finite element simulations and experiments.

2.1. Geometric Configuration and Mathematical Description of the Edge of a Rectangular Plate Periodic ABH

(1)

A rectangular plate on the edge of a semicircular annular ABH

Figure 1 illustrates the structure of a rectangular plate with periodically arranged semicircular annular ABHs along all four edges. The central region of the plate is a uniform-thickness structure with thickness h, and its dimensions are 2a and 2b in the x- and y-directions, respectively. Along the x- and y-direction boundaries, p and q non-uniform-thickness ABHs are uniformly distributed, respectively.

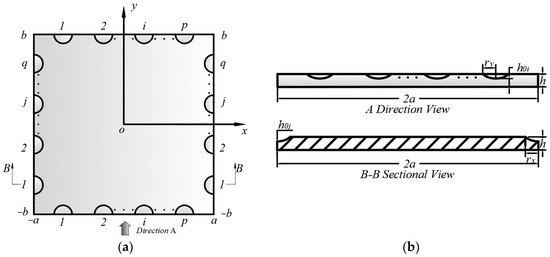
Figure 1. Schematic of a rectangular plate with periodic semicircular ABHs at the edges: (a) top view showing semicircular ABHs periodically distributed along the plate boundary; (b) cross-sectional view of the ABH region in the plate boundary.

Let the center coordinates of the $i^{th}$ semicircular annular ABH along the x-direction be $\left(X_i,Y_i\right)$ with radius $r_y$. Similarly, let the center coordinates of the $j^{th}$ semicircular ABH along the y-direction be $\left(X_j,Y_j\right)$ with radius $r_x$. The thickness model of the ABHs is then defined as

$$\left\{\begin{array}{c}{h}_i\left(x,y\right)={\epsilon }_i{\left[{\left(x-X_i\right)}^2+{\left(y-Y\right)}^2\right]}^{{\displaystyle \frac{m_i}{2}}}+h_{0i}\\ h_j\left(x,y\right)={\epsilon }_j{\left[{\left(x-X_j\right)}^2+{\left(y-Y_j\right)}^2\right]}^{{\displaystyle \frac{m_j}{2}}}+h_{0j}\end{array}\right.$$

(1)

where $h_{0i}$ and $h_{0j}$ represent the residual thicknesses, $m_i$ and $m_j$ denote the power law orders, and ${\epsilon }_i$ and ${\epsilon }_j$ signify the smoothing parameters, respectively.

For periodic ABHs along the $y=\pm b$ edges of a rectangular plate, the center coordinates $\left(X_i,Y_i\right)$ of the $i^{th}$ ABH are given by $\left(-a+r_x+\left(2i-1\right)\times {\displaystyle \frac{a-r_x}{p}},\pm b\right), (i=\mathrm{1,2},\cdots ,p)$. Similarly, for ABHs along the $x=\pm a$ edges, the center coordinates $\left(X_j,Y_j\right)$ of the $j^{th}$ ABH are $\left(\pm a,-b+r_y+\left(2j-1\right)\times {\displaystyle \frac{b-r_y}{q}}\right), (j=\mathrm{1,2},\cdots ,q)$. Here, $r_x$ and $r_y$ denote the radii of the ABHs parallel to the y-axis and x-axis, respectively.

(2)

A rectangular plate on the edge of a rectangular block-shaped ABH

For the rectangular prism-shaped ABHs, see Figure 2.

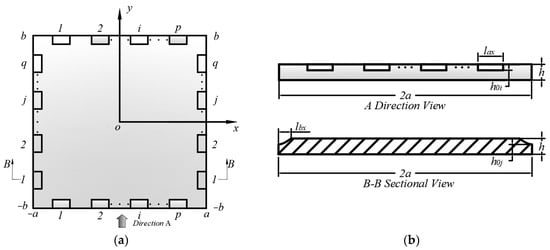
Figure 2. Schematic of a rectangular plate with periodic block-shaped ABHs at the edges: (a) top view showing rectangular ABHs periodically distributed along the plate boundary; (b) cross-sectional view of the ABH region in the plate boundary with a periodically rectangular ABH distribution.

For block-shaped periodic ABHs along the $y=\pm b$ edges of a rectangular plate, the center coordinates of the $i^{th}$ ABHs are $\left(X_i,Y_i\right)$, where the dimensions parallel to the x- and y-axes are $l_{bx}$ and $l_{by}$, respectively. Similarly, for ABHs along the $x=\pm a$ edges, the center coordinates of the $j^{th}$ ABHs are $\left(X_j,Y_j\right)$, with the dimensions parallel to the x- and y-axes denoted as $l_{ax}$ and $l_{ay}$, respectively. The ABH is the thinnest at the plate edge, with a corresponding residual thickness of $h_{0,i}$. The thickness expression for the block-shaped ABH is

$$h_i\left(x,y\right)=\left\{\begin{array}{c}{\epsilon }_i{\left(b+y\right)}^{m_i}+h_{0i} y=-b\\ {\epsilon }_i{\left(b-y\right)}^{m_i}+h_{0i} y=b\end{array}\right.$$

(2)

$$h_j\left(x,y\right)=\left\{\begin{array}{c}{\epsilon }_j{\left(a+x\right)}^{m_j}+h_{0j} x=-a\\ {\epsilon }_j{\left(a-x\right)}^{m_j}+h_{0j} x=a\end{array}\right.$$

(3)

For periodic ABHs along the $y=\pm b$ edges, the center coordinates $\left(X_i,Y_i\right)$ of the $i^{th}$ ABH are given by $\left(-a+l_{ax}+\left(2i-1\right){\displaystyle \frac{a-l_{ax}}{p}};\pm b\right), (i=\mathrm{1,2},\cdots p)$. Similarly, for ABHs along the $x=\pm a$ edges, the center coordinates $\left(X_j,Y_j\right)$ of the $j^{th}$ ABH are $\left(\pm a,-b+l_{by}+\left(2j-1\right){\displaystyle \frac{b-l_{by}}{q}};\right), (j=\mathrm{1,2},\cdots q)$.

Here, the interval range of the $i^{th}$ edge ABH along $y=\pm b$ is

$$\mathrm{When} y=-b,\left\{\begin{array}{c}{X}_i-{\displaystyle \frac{l_{bx}}{2}}\le x\le X_i+{\displaystyle \frac{l_{bx}}{2}}\\ -b\le y\le l_{by}\end{array}\right.$$

(4)

$$\mathrm{When} y=b,\left\{\begin{array}{c}{X}_i-{\displaystyle \frac{l_{bx}}{2}}\le x\le X_i+{\displaystyle \frac{l_{bx}}{2}}\\ b-l_{by}\le y\le b\end{array}\right.$$

(5)

Here, the interval range of the $j^{th}$ edge ABH along $x=\pm a$ is

$$\mathrm{When} x=-a,\left\{\begin{array}{c}-a\le x\le {-a+l}_{ax}\\ Y_j-{\displaystyle \frac{l_{ay}}{2}}\le y\le Y_j-{\displaystyle \frac{l_{ay}}{2}}\end{array}\right.$$

(6)

$$\mathrm{When} x=a,\left\{\begin{array}{c}a-l_{ax}\le x\le a\\ Y_j-{\displaystyle \frac{l_{ay}}{2}}\le y\le Y_j-{\displaystyle \frac{l_{ay}}{2}}\end{array}\right.$$

(7)

2.2. Dynamic Model of Rectangular Plate with Periodic ABH Boundary

Based on the Kirchhoff–Love theory, the in-plane displacements $u$ and $v$ of a rectangular thin plate with periodic ABH distributions at the boundaries, as shown in Figure 1 and Figure 2, can be expressed in terms of the out-of-plane displacement $w$. The displacement vector is given by

$${\left[u v w\right]}^T={\left[-z{\displaystyle \frac{\mathsf{\partial }W}{\mathsf{\partial }x}} -z{\displaystyle \frac{\mathsf{\partial }W}{\mathsf{\partial }y}} w\left(x,y,t\right)\right]}^T$$

(8)

The out-of-plane displacement $w$ in Equation (8) can be expressed as a combination of the basis function ${\phi }_i(x,y)$ and the weight coefficient $a_i\left(t\right)$:

$$w\left(x,y,t\right)=\sum _i{a}_i\left(t\right){\phi }_i\left(x,y\right)=\sum _{k=1}^m\sum _{r=1}^n{a}_{kr}\left(t\right){\alpha }_k^j\left(x\right){\beta }_r^s\left(y\right)$$

(9)

For a plate structure with ABHs at the edges, compared with other shape functions, such as polynomial functions, the Gaussian function can capture the rapid changes in the ABH region with fewer terms, which significantly reduces the computational degrees of freedom and improves the computational efficiency. Moreover, its fast-decaying property reduces the numerical oscillations at the ABH edges and improves the stability of the solution. Therefore, we choose the Gaussian function as the shape function in this study. Additionally, if the Gaussian function is chosen as the admissible shape function, the basis functions in the x- and y-directions in Equation (9) can be expressed as

$${\alpha }_k^j\left(x\right)=2^{{\displaystyle \frac{j}{2}}}exp\left[-{\displaystyle \frac{{\left(2^{j}x-k\right)}^2}{2}}\right]$$

(10)

$${\beta }_r^s\left(y\right)=2^{{\displaystyle \frac{s}{2}}}exp\left[-{\displaystyle \frac{{\left(2^{s}x-r\right)}^2}{2}}\right]$$

(11)

In Equations (10) and (11), $j$ and $s$ are the scaling parameters in the x- and y-directions, respectively. They represent the stretching or compression of the original Gaussian function, which is related to the dimensions of the rectangular plate [34].

The rectangular plate with periodically distributed ABHs studied in this paper is shown in Figure 3. In the periodic edge ABH regions, the thickness function is defined as $h(x, y)$, while the remaining area of the plate is a homogeneous structure with uniform thickness h. The Lagrangian function of the plate with periodic edge ABHs can be expressed as

$$\mathrm{L}=E_k-E_p+W$$

(12)

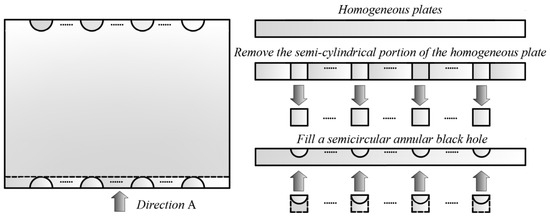
Figure 3. Solution of periodic edge ABH energy.

For a rectangular plate with periodic ABHs at the edges—where the edge regions feature non-uniform-thickness structures—this paper adopts the “remove-and-fill” replacement method to construct an equivalent energy model. The basic concept of this method is illustrated in Figure 3.

For a rectangular plate with four simply supported edges and periodic ABHs at the edges, the kinetic and potential energies are derived as follows:

$$E_k=E_{k-plate}-E_{k-cylinder edge}+E_{k-black hole edge}$$

(13)

$$E_p=E_{p-plate}-E_{p-cylinder edge}+E_{p-black hole edge}$$

(14)

In this formula, $E_{k-plate}$ and $E_{p-plate}$ denote the kinetic and potential energies of a homogeneous rectangular plate. $E_{k-cylinder edge}$ and $E_{p-cylinder edge}$ represent the kinetic and potential energies of a cylindrical region with the same thickness as the plate, which replaces the removed ABH area. $E_{k-black hole edge}$ and $E_{p-black hole edge}$ signify the kinetic and potential energies of the edge-mounted ABH region, respectively.

For a rectangular plate with periodically distributed semicircular ABHs at the edges, the kinetic energy expressions for each component are

$$E_{k-plate}={\displaystyle \frac{1}{2}}{\int }_{-b}^b{\int }_{-a}^a\rho h{\left({\displaystyle \frac{\mathsf{\partial }w}{\mathsf{\partial }t}}\right)}^{2}dxdy$$

(15)

$$\begin{gathered} E_{k-cylinder edge}=\sum _{i=1}^p{\displaystyle \frac{1}{2}}{\int }_{-b}^{{-b+r}_y}{\int }_{X_i-\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}^{X_i+\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}\rho h{\left({\displaystyle \frac{\mathsf{\partial }w}{\mathsf{\partial }t}}\right)}^{2}dxdy \\ +\sum _{i=1}^p{\displaystyle \frac{1}{2}}{\int }_{b-r_y}^b{\int }_{X_i-\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}^{X_i+\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}\rho h{\left({\displaystyle \frac{\mathsf{\partial }w}{\mathsf{\partial }t}}\right)}^{2}dxdy \\ +\sum _{j=1}^q{\displaystyle \frac{1}{2}}{\int }_{-a}^{-a+r_x}{\int }_{Y_j-\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}^{Y_j+\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}\rho h{\left({\displaystyle \frac{\mathsf{\partial }w}{\mathsf{\partial }t}}\right)}^{2}dxdy \\ +\sum _{j=1}^q{\displaystyle \frac{1}{2}}{\int }_{a-r_x}^a{\int }_{Y_j-\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}^{Y_j+\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}\rho h{\left({\displaystyle \frac{\mathsf{\partial }w}{\mathsf{\partial }t}}\right)}^{2}dxdy \end{gathered}$$

(16)

$$\begin{gathered} E_{k-black hole edge}=\sum _{i=1}^p{\displaystyle \frac{1}{2}}{\int }_{-b}^{{-b+r}_y}{\int }_{X_i-\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}^{X_i+\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}\rho h\left(x,y\right){\left({\displaystyle \frac{\mathsf{\partial }w}{\mathsf{\partial }t}}\right)}^{2}dxdy \\ +\sum _{i=1}^p{\displaystyle \frac{1}{2}}{\int }_{b-r_y}^b{\int }_{X_i-\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}^{X_i+\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}\rho h\left(x,y\right){\left({\displaystyle \frac{\mathsf{\partial }w}{\mathsf{\partial }t}}\right)}^{2}dxdy \\ +\sum _{j=1}^q{\displaystyle \frac{1}{2}}{\int }_{-a}^{-a+r_x}{\int }_{Y_j-\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}^{Y_j+\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}\rho h(x,y){\left({\displaystyle \frac{\mathsf{\partial }w}{\mathsf{\partial }t}}\right)}^{2}dxdy \\ +\sum _{j=1}^q{\displaystyle \frac{1}{2}}{\int }_{a-r_x}^a{\int }_{Y_j-\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}^{Y_j+\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}\rho h\left(x,y\right){\left({\displaystyle \frac{\mathsf{\partial }w}{\mathsf{\partial }t}}\right)}^{2}dxdy \end{gathered}$$

(17)

where (16) and (17) lead to

$$X_i=-a+r_x+\left(2i-1\right)\times {\displaystyle \frac{a-r_x}{p}}, Y_i=-a+r_y+\left(2j-1\right)\times {\displaystyle \frac{a-r_y}{q}}$$

Considering the elastic boundary support, the potential energy of each component of the rectangular plate with ABH edges is derived in Equation (14) using the replacement method. The potential energy of a homogeneous rectangular plate with a uniform thickness is given by

$$E_{p-plate}={\displaystyle \frac{1}{2}}{\int }_{-b}^b{\int }_{-a}^{a}D\left[\begin{array}{c}{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}\right)}^2+{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}\right)}^2+\\ 2\nu {\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}{\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}+2\left(1-\nu \right){\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }x\mathsf{\partial }y}}\right)}^2\end{array}\right]dxdy$$

(18)

The potential energies of the uniform-thickness cylindrical replacement region in the ABH edge area and the ABH edge itself are given by

$$\begin{gathered} E_{p-cylinder edge}=\sum _{i=1}^p{\displaystyle \frac{1}{2}}{\int }_{-b}^{{-b+r}_y}{\int }_{X_i-\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}^{X_i+\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}D\left[\begin{array}{c}{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}\right)}^2+{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}\right)}^2+\\ 2\nu {\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}{\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}+2\left(1-\nu \right){\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }x\mathsf{\partial }y}}\right)}^2\end{array}\right]dxdy \\ +\sum _{i=1}^p{\displaystyle \frac{1}{2}}{\int }_{b-r_y}^b{\int }_{X_i-\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}^{X_i+\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}D\left[\begin{array}{c}{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}\right)}^2+{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}\right)}^2+\\ 2\nu {\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}{\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}+2\left(1-\nu \right){\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }x\mathsf{\partial }y}}\right)}^2\end{array}\right]dxdy \\ +\sum _{j=1}^q{\displaystyle \frac{1}{2}}{\int }_{-a}^{-a+r_x}{\int }_{Y_j-\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}^{Y_j+\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}D\left[\begin{array}{c}{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}\right)}^2+{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}\right)}^2+\\ 2\nu {\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}{\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}+2\left(1-\nu \right){\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }x\mathsf{\partial }y}}\right)}^2\end{array}\right]dxdy \\ +\sum _{j=1}^q{\displaystyle \frac{1}{2}}{\int }_{a-r_x}^a{\int }_{Y_j-\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}^{Y_j+\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}D\left[\begin{array}{c}{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}\right)}^2+{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}\right)}^2+\\ 2\nu {\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}{\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}+2\left(1-\nu \right){\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }x\mathsf{\partial }y}}\right)}^2\end{array}\right]dxdy \end{gathered}$$

(19)

$$\begin{gathered} E_{p-black hole edge}=\sum _{i=1}^p{\displaystyle \frac{1}{2}}{\int }_{-b}^{{-b+r}_y}{\int }_{X_i-\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}^{X_i+\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}D\left(x,y\right)\left[\begin{array}{c}{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}\right)}^2+{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}\right)}^2+\\ 2\nu {\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}{\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}+2\left(1-\nu \right){\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }x\mathsf{\partial }y}}\right)}^2\end{array}\right]dxdy \\ +\sum _{i=1}^p{\displaystyle \frac{1}{2}}{\int }_{b-r_y}^b{\int }_{X_i-\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}^{X_i+\sqrt{{r_y}^2-{\left(y-Y_i\right)}^2}}D\left(x,y\right)\left[\begin{array}{c}{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}\right)}^2+{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}\right)}^2+\\ 2\nu {\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}{\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}+2\left(1-\nu \right){\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }x\mathsf{\partial }y}}\right)}^2\end{array}\right]dxdy \\ +\sum _{j=1}^q{\displaystyle \frac{1}{2}}{\int }_{-a}^{-a+r_x}{\int }_{Y_j-\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}^{Y_j+\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}D\left(x,y\right)\left[\begin{array}{c}{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}\right)}^2+{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}\right)}^2+\\ 2\nu {\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}{\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}+2\left(1-\nu \right){\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }x\mathsf{\partial }y}}\right)}^2\end{array}\right]dxdy \\ +\sum _{j=1}^q{\displaystyle \frac{1}{2}}{\int }_{a-r_x}^a{\int }_{Y_j-\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}^{Y_j+\sqrt{{r_x}^2-{\left(y-X_i\right)}^2}}D\left(x,y\right)\left[\begin{array}{c}{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}\right)}^2+{\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}\right)}^2+\\ 2\nu {\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}}{\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}}+2\left(1-\nu \right){\left({\displaystyle \frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }x\mathsf{\partial }y}}\right)}^2\end{array}\right]dxdy \end{gathered}$$

(20)

Here, the bending stiffness of a homogeneous rectangular plate is defined as $D={\displaystyle \frac{E^{*}{h}^3}{12\left(1-{\nu }^2\right)}}$, that of the ABH region is $D\left(x,y\right)={\displaystyle \frac{E^{*}h{\left(x,y\right)}^3}{12\left(1-{\nu }^2\right)}}$, and the complex Young’s modulus is $E^{*}=E\left(1+i\eta \right)$. In these expressions, $v$ denotes Poisson’s ratio, and $\eta$ represents the damping loss factor.

Using a similar approach, and combining Equations (2)–(7), the kinetic and potential energies of a rectangular plate with periodically distributed quadrangular block-shaped ABHs at the edges can be derived, and, for brevity, these derivations are not repeated here.

Assuming that the external excitation force acting on the plate is $f\left(t\right)$, the work done by this force is given by

$$W={\int }_{-b}^b{\int }_{-a}^{a}f\left(t\right)w\left(x,y,t\right)dxdy$$

(21)

By substituting Equations (13)–(22) into Equation (12) and inserting the Lagrangian $L$ into the Euler–Lagrange equation, the governing dynamic equation of the rectangular plate with periodically distributed ABHs is derived as follows:

$$\mathit{M}\ddot{a}\left(t\right)+\mathit{K}a\left(t\right)=f\left(t\right)$$

(22)

Assuming that the external excitation force is harmonic, the excitation and response vectors can be expressed as

$$f\left(t\right)=\widehat{F}{e}^{i\omega t}$$

(23)

$$a\left(t\right)=\widehat{A}{e}^{i\omega t}$$

(24)

In Equation (23), $\widehat{F}$ denotes the external force amplitude vector, and, in Equation (24), $\widehat{A}$ represents the response amplitude vector. Substituting Equations (23) and (24) into Equation (22) yields

$$\left(\mathit{K}-{\omega }^2\mathit{M}\right)\widehat{A}=\widehat{F}$$

(25)

Setting $\widehat{F}=0$, Equation (25) reduces to a generalized eigenvalue problem:

$$\left(\mathit{K}-{\omega }^2\mathit{M}\right)\widehat{A}=0$$

(26)

Setting the determinant of the coefficient matrix to zero yields the frequency equation, which is given by

$$\Delta =\left|\mathit{K}-{\omega }^2\mathit{M}\right|=0$$

(27)

From Equations (26) and (27), the natural frequency ${\omega }_n$ and the corresponding eigenvector ${\widehat{A}}_n$ of the rectangular plate with periodically distributed ABHs can be obtained.

2.3. Model Validation

To validate the theoretical model developed in this study, FEM simulations and experimental tests are used. Moreover, two verification samples are designed for a rectangular plate with periodically distributed semicircular ABHs at the edges. Their geometric and material parameters are listed in Table 1.

Table 1. Geometric and material parameters of model validation sample.

Geometric Parameters			Material Parameters
Length and width of plate a × b	0.16 m × 0.16 m	0.40 m × 0.30 m	Steel
Thickness of plate $h_{uni}$	2 mm	5 mm	ρ1 = 7800 kg/m3
Number of black holes, long side p, short side q	p = 1, q = 1	p = 4, q = 2	E1 = 210 GPa
Power law exponent of black hole m	2	2
Radius of black hole $r_{abh}$	10 mm	20 mm	ν1 = 0.3
Boundary condition	Quadrilateral freedom	Quadrilateral freedom

Using a prototype with the geometric and material parameters given in the left column of Table 1, both a numerical analysis model and a finite element simulation model are developed based on the theoretical framework derived in this section. The finite element simulation model is obtained using the COMSOL Multiphysics 6.3 software. Figure 4 displays the FEM modeling geometry and the meshing.

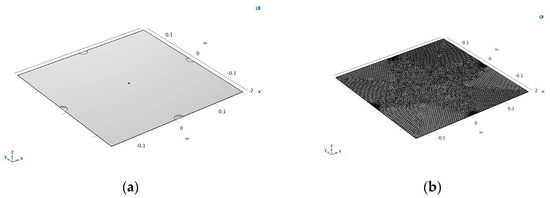
Figure 4. Finite element simulation: (a) finite element geometric model; (b) finite element meshing.

The first six modal frequencies obtained through finite element simulation calculations versus the theoretical calculations are shown in Table 2.

Table 2. The first six characteristic frequencies obtained from the theoretical model and finite element model.

Modal Order	Theory ft (Hz)	Simulation fs (Hz)	Relative Error a (%)
(1,1)	25.75	25.83	0.31
(1,2)	79.61	80.27	0.83
(2,2)	150.53	153.24	1.80
(1,3)	160.36	161.57	0.75
(2,3)	221.81	220.78	0.46
(1,4)	259.45	260.46	0.39

a relative error calculation formula: ${\displaystyle \frac{\left|f_s-f_t\right|}{f_t}}\times 100\%.$

As shown in Table 2, the numerical results from the theoretical model agree well with those from the finite element simulations, with the errors in the first six modal frequencies all within 2%.

Given that Sample 1 is a square plate with an ABH on each of its four edges, to ensure generality and universality, an experimental specimen with semicircular ABH cell boundaries for a rectangular plate with dimensions of 0.4 m × 0.3 m was fabricated, with the geometric and material parameters given in the right column of Table 1; this is called Sample 2. Modal tests are performed on Sample 2 using the LMS dynamic test system. The LMS dynamic test system includes hardware such as the SC316 data acquisition frontend, an ICP accelerometer, and an ICP-equipped multi-type hammer, as well as TestLab 2021 software modules for impact testing and modal analysis.

The tests employ the single-point excitation multiple-point response (SIMO) hammering method, i.e., fixing the hammering point and having all the acceleration sensors located on the sample under test, so as to measure the transfer function for the experimental modal analysis or the transfer path analysis. In this case, the test equipment uses the LMS test system, where a force hammer (LMS 086c03) is used to acquire the excitation signal and a PCB acceleration three-way transducer (ICP 365A25 series) is used to acquire the acceleration signals at multiple measurement points. In this test, the specimen panel is divided into 6 × 5 sections to organize the measurement points for the modal test. The detailed test equipment, the sample, and the procedure are shown in Figure 5.

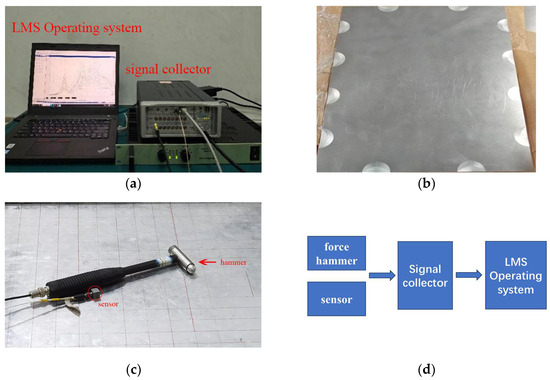
Figure 5. Vibration mode test system and ABH plate experimental sample: (a) experimental signal processing system; (b) experimental sample of semicircular ABH plate; (c) experimental excitation unit and sensors; (d) schematic diagram of experimental flow.

The first five modal frequencies obtained from the experimental modal testing and finite element modal analysis of Sample 2 are listed in Table 3, and the comparison results show that the errors are within 2%, which indicates good agreement. Combined with the previous validation and comparison results of the finite element simulation and the theoretical solution for Sample 1, the correctness of the dynamic model developed in this section for rectangular plates with periodically distributed ABHs at the edges can be confirmed.

Table 3. The first five characteristic frequencies obtained from the experimental model and the finite element model.

Modal Order	Experiment ft (Hz)	Simulation fs (Hz)	Relative Error a (%)
(1,1)	137.23	139.05	1.01
(2,1)	164.14	166.46	1.41
(1,2)	310.31	312.19	0.61
(3,1)	325.88	328.79	0.89
(2,2)	481.21	485.84	0.96

3. Modal Characteristics of Rectangular Plate with Periodic Boundary of ABHs

To explore the inherent properties of rectangular plates featuring periodic edge-mounted ABHs, this study focuses on the ABH-integrated plate structure depicted in Figure 1. This study systematically analyzes how the power law index, ABH radius, number of holes, and geometric configuration at the plate edge affect the modal frequencies and mode shape characteristics. These findings offer a theoretical framework for the tailoring of the dynamic properties of plate structures via edge-mounted ABHs, enabling the precise regulation of their intrinsic behavior.

3.1. Influence of Power Law Exponent m of ABH on Modal Frequency of Rectangular Plate

In this section, the rectangular plate with semicircular periodic ABHs is studied. It has four ABHs symmetrically distributed in a periodic pattern on the two edges parallel to the x-axis and two ABHs on the two edges parallel to the y-axis. All ABHs on the plate’s four edges have identical geometric dimensions. The rectangular plate has dimensions of 0.40 m × 0.30 m, a thickness of 2 mm, and a radius $r_{abh}$ of 20 mm and is simply supported on all four sides. Table 1 displays the material parameters. Assuming that the black hole power exponent m is 2, 2.5, and 3.0, respectively, Table 4 displays the first six modal frequencies of rectangular plates with periodic edges of ABHs. The first, third, and fifth modal modes of rectangular plates with periodic ABH boundaries are depicted in Figure 6 and correspond to the various power law exponents listed in Table 4.

Table 4. First six modal frequencies (Hz) of rectangular plates with periodic edges of ABHs with different power law exponents.

Modal Order	Power Law Exponent m	2.5	3.0
	2
(1,1)	84.50	84.42	84.35
(2,1)	176.08	175.90	175.73
(1,2)	248.93	248.65	248.48
(3,1)	330.33	329.99	429.69
(2,2)	339.48	338.97	338.55
(3,2)	492.61	491.75	490.96

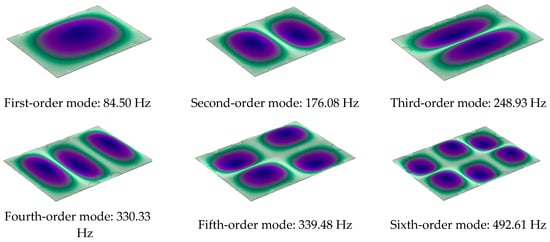
Figure 6. Modal shapes of rectangular plates with periodic boundaries of ABHs (m = 2).

For the rectangular plate with semicircular periodic ABHs distributed at a 4:2 ratio along the x- and y-axes, Table 4 shows that, for the first-order mode, as the ABH power law exponent m increases from 2 to 3.0, the modal frequency of the plate decreases gradually from 84.50 Hz to 84.35 Hz, exhibiting an overall downward trend—although the reduction is minimal. Similar trends are observed in the second-order and higher-order modal frequencies. This behavior arises because edge-mounted ABHs reduce the overall stiffness of the rectangular plate, thereby lowering its modal frequency to some extent. However, for a 2-mm-thick thin plate, when the residual thickness of the edge ABHs remains constant, variations in the power law exponent m have a negligible effect on the plate’s bending stiffness and mass, leading to only minor changes in its modal frequency. Regarding the mode shapes, Figure 6 indicates that the ABH-edged rectangular plate and the uniform rectangular plate exhibit similar vibration patterns.

3.2. Influence of Radius of ABH $r_{abh}$ on Modal Frequency of Rectangular Plate

In order to investigate how the dimensions of ABHs affect the modal properties of rectangular plates, three configurations of ABHs are considered in this work for plates with fixed dimensions of 400 mm × 300 mm and power law exponent m = 2. The configurations feature long-to-short-side ABHs with number ratios of p:q = 0:4, 4:0, and 4:2. Specifically, ABHs are symmetrically and periodically distributed on both short edges only, both long edges only, or all four edges. In each case, the edge-mounted ABHs have identical geometric dimensions. Figure 7 plots the relationship between the ABH radius and the plate’s first four modal frequencies.

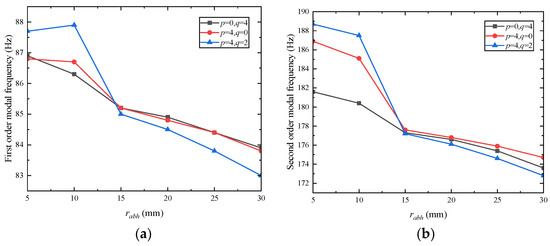
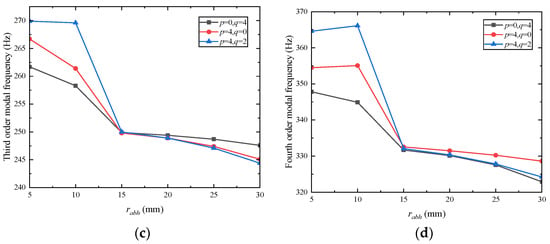
Figure 7. Relationship between ABH radius and modal frequency: (a) The relationship between ABH radius and first-order modal frequency; (b) The relationship between ABH radius and second-order modal frequency; (c) The relationship between ABH radius and third-order modal frequency; (d) The relationship between ABH radius and fourth-order modal frequency.

As shown in Figure 7, the first- to fourth-order modal frequencies of periodic rectangular plates with these three ABH configurations (edge distributions of 0:4, 4:0, and 4:2) generally exhibit a gradual downward trend as the ABH radius increases. When the radius ranges from 5 mm to 15 mm, the modal frequencies are highly sensitive to radius changes, decreasing rapidly with an increasing radius. However, as the radius continues to increase from 15 mm to 30 mm, the rate of decrease in the modal frequencies slows significantly. This slowdown becomes more pronounced for higher-order modes, indicating that larger ABH radii have a diminishing effect on modal frequency reduction, particularly for higher vibration modes. These results highlight the nonlinear relationship between the ABH size and plate modal characteristics, with the sensitivity being most pronounced in the moderate radius range before plateauing at larger sizes. For a smaller ABH ratio (specifically 5 mm and 10 mm), the modal frequencies of the rectangular plate with ABHs on all four edges are higher than those of the plate with symmetrically arranged ABHs on two opposite edges. However, when the radius exceeds 15 mm, the modal frequencies of the all-four-edge ABH plate become lower than those of the two-opposite-edge configuration. For configurations with the same number of ABHs, the modal frequencies of rectangular plates with symmetric periodic ABHs on the two long edges are higher than those of plates with symmetric ABHs on the two short edges. At relatively small ABH radii (5 mm and 10 mm), the modal frequencies of the rectangular plate are sensitive to the ABH configuration—whether the ABHs are arranged symmetrically on two opposite edges or all four edges. This sensitivity enables modal frequency tuning through different ABH layouts, offering a novel approach to controlling the vibrational mode states via ABH design. When the ABH radius is 15 mm, the modal frequencies of the rectangular plate with periodically distributed ABHs exhibit minimal sensitivity to variations in the ABH layout. Thus, for engineering applications requiring stable modal frequencies, an ABH radius of 15 mm is recommended.

As shown in Figure 7, the intrinsic reason lies in the fact that, when the ABH is embedded in the plate structure, owing to the variable cross-section of the ABH structure, the ABHs embedded in the plate will change the bending stiffness of the plate structure, thus affecting its modal frequency. For the ABHs laid out at the edge of the rectangular plate, when its radius increases, the overall bending stiffness of the plate decreases, which leads to a decrease in its modal frequency.

3.3. Influence of Combination of ABH Number and Black Hole Radius on Modal Frequency of Rectangular Plate

Figure 7 and Figure 8, respectively, illustrate the variations in the modal frequencies of two types of rectangular ABH plates—one with long-side symmetry and the other with four-side symmetry—as functions of the modal number. In these figures, the black curve represents the first-order modal frequency when the black hole radius is 10 mm, while the red curve corresponds to the first-order modal frequency at a black hole radius of 25 mm.

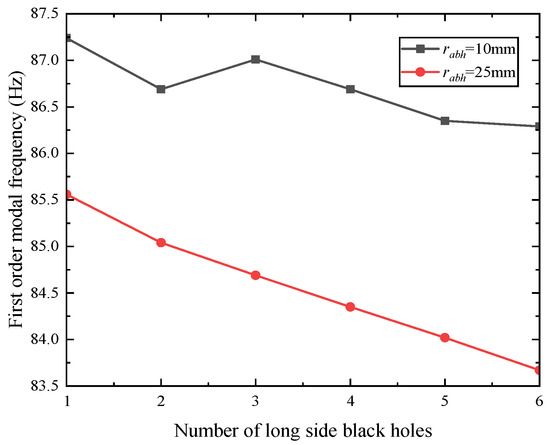
Figure 8. Relationship between the number of ABHs and the modal frequency of two long-side symmetric rectangular plates (short side with no black holes, q = 0).

An analysis of Figure 7 and Figure 8 reveals two key trends in modal frequency variation with the number of ABHs. First, when $r_{abh}$ = 25 mm, the modal frequency decreases linearly as the number of black holes increases; for the same count, a rectangular plate with symmetric periodic ABHs on two long sides exhibits a higher modal frequency than one with four-side symmetric configurations. Second, at identical black hole numbers, the first-order modal frequency for $r_{abh}$ = 10 mm is significantly higher than that for $r_{abh}$ = 25 mm, showing a slow, fluctuating decline as the number of ABHs rises.

Figure 9 and Figure 10 present three-dimensional graphs plotting the ABH radius, number of ABHs, and modal frequency.

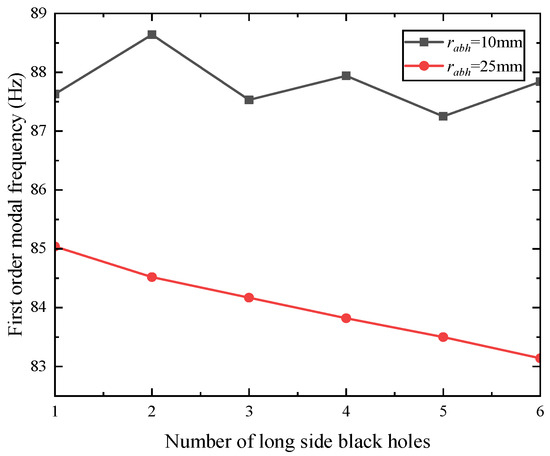
Figure 9. Relationship between ABH number and modal frequency of rectangular plates with four symmetrical sides (short-side black hole number q = 2).

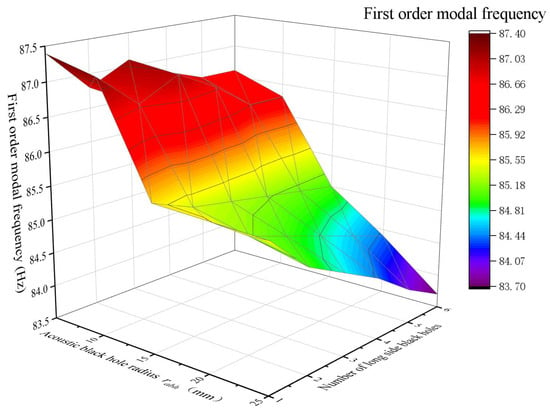
Figure 10. Relationship between the radius of black holes, the number of black holes, and the modal frequency of a rectangular plate with long-side symmetric periodic ABHs.

As shown in Figure 9 and Figure 10, for both rectangular plates with two long-side symmetric periodic ABHs and those with four-side symmetric periodic ABHs, the first-order modal frequency increases as the ABH radius decreases and the number of ABHs reduces; conversely, larger ABH radii and greater ABH numbers correspond to lower first-order modal frequencies. When the ABH radii are small, the first-order modal frequency decreases gradually with an increase in the number of ABHs; when the ABH radii are relatively large (such as 25 mm), this frequency declines rapidly as the number of ABHs increases. For rectangular plates of the same dimensions, the first-order modal frequency can be effectively adjusted over a broad range by appropriately designing the ABH radius and quantity. For instance, in a rectangular plate with dimensions of 400 mm × 300 mm × 2 mm, the first-order modal frequency varies from 83 Hz to 90 Hz.

3.4. Influence of ABH Configuration on Modal Frequency of Rectangular Plate

Any cross-section conforming to the power law function curve can be defined as an ABH. This section analyzes the modal frequency characteristics of rectangular plates incorporating periodic ABHs with three edge configurations: semicircular, rectangular 1, and rectangular 2 cross-sections. For a comparative analysis, the three ABHs are designed with approximately equal cross-sectional areas. Their geometric parameters are listed in Table 5, with the material parameters consistent with those in Table 1.

Table 5. Geometric parameters of ABHs with three configurations.

Geometric Parameter	Semicircular Section	Rectangular Section 1	Rectangular Section 2
m	2.5	2.5	2.5
h	2 mm	2 mm	2 mm
a	400 mm	400 mm	400 mm
b	300 mm	300 mm	300 mm
$h_0$	0.5 mm	0.5 mm	0.5 mm
$r_{abh}$	20 mm	-	-
$l_{ax}$	-	40 mm	16 mm
$l_{by}$	-	16 mm	40 mm
$\epsilon 1$	4.87481/m	4.87481/m	4.87481/m

It should be noted that, although the two rectangular cross-section ABH configurations (denoted as rectangular 1 and rectangular 2) in Table 5 share identical geometric parameters, their layout orientations at the rectangular plate edges differ, resulting in distinct directions for the black hole power law curves. Specifically, the power law curve of the rectangular 1 configuration—with periodic ABH boundaries—extends along the x-axis direction, whereas that of the rectangular 2 configuration propagates along the y-axis direction.

Figure 11, Figure 12, Figure 13 and Figure 14 illustrate the relationship between the ratio of the long-side to short-side black hole numbers and the modal frequencies of rectangular plates featuring three distinct ABH types with different boundary distribution patterns.

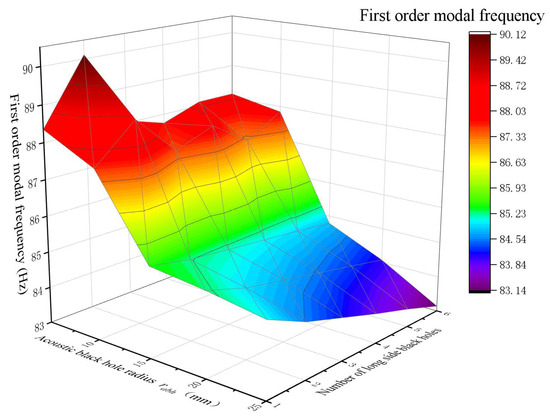
Figure 11. Relationship between the radius of black holes, the number of black holes, and the modal frequency of a rectangular plate with four symmetrical periodic ABHs.

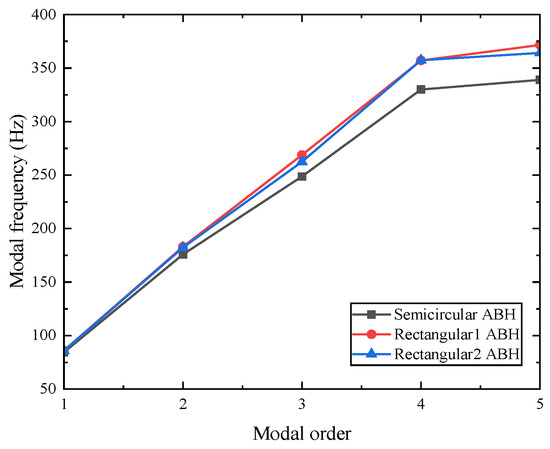
Figure 12. Modal frequencies of rectangular plates with periodic ABHs of different configurations (p = 4, q = 2).

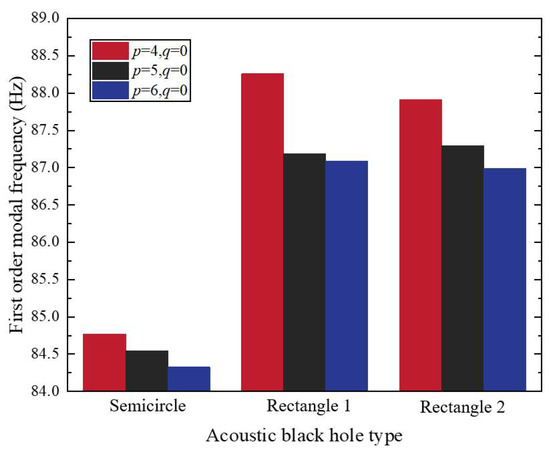
Figure 13. The relationship between the type of ABH and the first-order modal frequency of a rectangular plate.

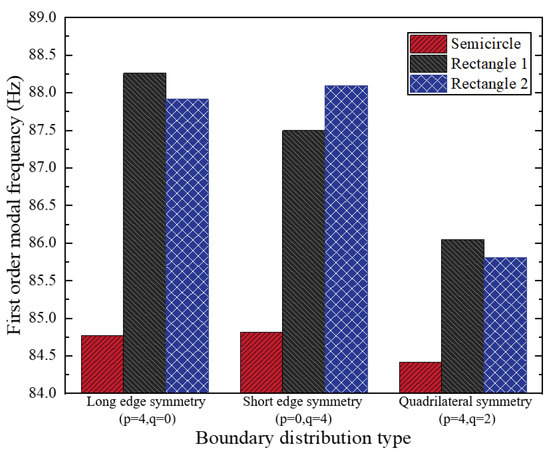
Figure 14. Relationship between boundary distribution types of periodic ABHs and modal frequencies of rectangular plates.

As depicted in Figure 12, the first five modal frequencies of the rectangular plates with the rectangular 1 and rectangular 2 cross-section configurations are comparable to those of the semicircular cross-section ABH, yet they are consistently higher than the corresponding modal frequencies of the semicircular ABH plate. Notably, the discrepancy in the modal frequencies widens with increasing modal order, while the first four modal frequencies rise sharply as the order increases. Figure 13 presents the first-order modal frequencies of long-side symmetric periodic ABH rectangular plates for the three configurations. Among the three types, the semicircular ABH plate exhibits the lowest first-order modal frequency, whereas the rectangular 1 configuration shows the highest. For the same ABH type, an increase in the black hole number correlates with a decrease in the first-order modal frequency. According to Figure 14, which illustrates the relationship between the boundary type and modal frequency, the rectangular plate with four-side symmetry has the lowest first-order modal frequency. Additionally, the semicircular ABH configuration yields lower modal frequencies than the rectangular ABH configurations. Figure 15 demonstrates that, for four-side symmetric rectangular plates, as the ratio of the long-side to short-side black hole numbers decreases—with the long-side black hole count held constant and the short-side count increasing—the first-order modal frequencies of all three ABH configurations exhibit a downward trend.

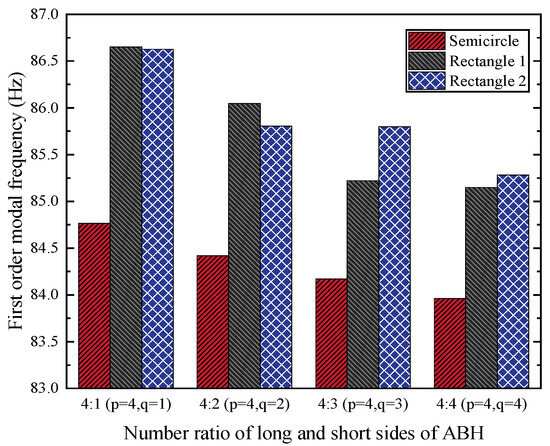
Figure 15. Relationship between the number ratio of long and short periodic ABHs with four symmetrical sides and the modal frequency of the rectangular plate.

Summarizing the above, for the two types of ABH configurations with approximately equal ABH areas studied in this paper, the modal frequency of the semicircular ABH with the same area is lower than that of the rectangular wedge-shaped ABH when the ABH cycle is arranged at the edge of the rectangular plate. This indicates that the overall bending stiffness of the rectangular plate with the semicircular ABH at the edge is relatively small compared with the rectangular wedge-shaped ABH, making it suitable for the design and regulation of the modes of the low frequency. If the modal frequency that needs to be controlled is high, rectangular wedge-shaped ABHs are available. In practice, the type of black hole can be selected according to the distribution range of the modal frequencies.

4. Conclusions

This paper mainly investigates the dynamic modeling of a rectangular plate at the boundary of a periodic ABH. It reveals the relationship between the edge parameters of the rectangular plate of a periodic ABH and the modal characteristics, aiming to provide a theoretical basis for the modulation of the modal characteristics of the rectangular plate via the design of the edges of the ABH. The main conclusions are as follows:

(1)

The “remove-and-fill” substitution method proposed in this paper can effectively resolve the dynamic modeling problems of the rectangular plate with a variable cross-section in the edge ABH by constructing a local energy model of the rectangular plate in the edge ABH. Through selecting the Gaussian function as the shape function, the rapid changes in the ABH region can be captured with fewer terms, which significantly reduces the computational degrees of freedom and improves the computational efficiency and stability of the solution.

(2)

The edge parameters of the periodic ABHs, including the radii of the edge ABHs, the number of ABHs, and the periodic distribution of the ABHs, directly affect the overall bending stiffness of the plate structure and significantly influence its modal frequency, which is a key parameter in the regulation of the dynamic properties of the structure. In addition, the configuration of the ABH also has an important effect on the modal frequency of the plate structure, and the modal frequency of the semicircular ABHs is relatively low compared with that of the rectangular wedge-shaped ABHs. The modal frequencies of rectangular plates with four-side symmetric periodic ABHs are lower than those of two-side symmetric rectangular plates.

(3)

Without changing the main structure, the design and regulation of the structural modal frequency can be realized only through boundary structure design, which has significant engineering value and application prospects in the vibration and noise control of aerospace panels, automobile base plates, and body structures, etc.

This research work considers the structural properties of ABHs; another important property of ABHs is the energy aggregation effect based on wave characteristics. The next step will be to further investigate the energy aggregation properties of edge periodic ABHs, as well as their applications in vibration control. The related research results will be discussed in detail separately.