Degenerate Appell Polynomials Connecting Beta Function as a Family of Operators and Their Approximations

Abstract

This paper introduces a novel family of positive linear operators constructed by blending degenerate Appell polynomials with a classical Beta kernel in the Durrmeyer setting. The operators are defined as $H_n(g;u)=\sum _{ƿ=0}^{\infty }{h}_{ƿ}(n+u;ƛ){\int }_0^1{K}_n(ƿ, ʈ)g(ʈ)dʈ$, where $h_{ƿ}(nu;ƛ)$ is derived from degenerate Appell polynomials ($nu$ denotes the product of n and u) and $K_n(ƿ, ʈ)$ is a Beta-type kernel. We establish the linearity and positivity of these operators and derive crucial moment estimates. Approximation properties are examined via Korovkin-type theorems, and the asymptotic behavior is investigated through a Voronovskaja-type theorem. The results extend and unify earlier work on Appell-based approximation operators and offer new tools for approximating functions in weighted spaces. Numerical examples and error estimates are provided to illustrate the efficacy of the proposed operators. In addition, the inherent symmetry in the structure of the proposed operators-arising from the symmetric nature of the Beta kernel and the generating functions of degenerate Appell polynomials is discussed. Such symmetry plays a key role in ensuring balanced approximation and convergence characteristics.

1. Overview and Foundations

The central theme of approximation theory revolves around the fundamental question of how arbitrary functions can be effectively approximated by simpler, more tractable functions. This field, whose modern foundations were profoundly laid by Karl Weierstrass through his seminal approximation theorem [1], has evolved into a cornerstone of mathematical analysis. A significant leap in its development was marked by the work of P.P. Korovkin [2], whose theorems provide remarkably simple yet powerful criteria for establishing the convergence of sequences of positive linear operators.

The constructive approach to Weierstrass’s theorem was famously provided by S.N. Bernstein [3] through the polynomials that now bear his name. For a function $\tilde{g}$ continuous on $[0, 1]$, the Bernstein operators are defined as:

$${\mathcal{B}}_v(\tilde{g};y)=\sum _{r=0}^v\left({\displaystyle \genfrac{}{}{0pt}{}{v}{r}}\right)y^r{(1-y)}^{v-r}\tilde{g}\left({\displaystyle \frac{r}{v}}\right),y\in [0, 1],v\in \mathbb{N}.$$

(1)

Operators such as these, defined on finite intervals, were later extended to the entire semi-axis $[0, \infty )$ by O. Szász [4] (building on earlier work of Mirakjan and Favard):

$${\mathsf{S}}_v(\tilde{g};y)=e^{-vy}\sum _{r=0}^{\infty }{\displaystyle \frac{{\left(vy\right)}^r}{r!}}\tilde{g}\left({\displaystyle \frac{r}{v}}\right),y\in [0, \infty ).$$

(2)

Many important and useful generalizations were made specially by Ismail [5]. A major generalization was achieved by Jakimovski and Leviatan [6], who introduced a large class of positive linear operators by leveraging the generating functions of Appell polynomials ${\mathfrak{P}}_r\left(x\right)$:

$$K_v(\tilde{g};x)={\displaystyle \frac{e^{-vx}}{A\left(1\right)}}\sum _{r=0}^{\infty }{\mathfrak{P}}_r\left(vx\right)\tilde{g}\left({\displaystyle \frac{r}{v}}\right),$$

(3)

where the generating function is given by $A\left(u\right)e^{ux}={\sum }_{r=0}^{\infty }{\mathfrak{P}}_r\left(x\right)u^r$, with $A\left(u\right)$ being an analytic function. In the recent past, many mathematicians have studied such type of generating functions in terms of the sequences of linear positive operators [7,8,9,10,11,12,13,14,15].

The landscape of approximation theory has been further enriched by the study of degenerate versions of special polynomials. Initiated by Carlitz [16], the theory of degenerate polynomials has seen considerable growth. For instance, the degenerate Appell polynomials ${\mathcal{A}}_r(x;ƛ)$ [17] are defined via the generating function:

$$\mathcal{A}(u;ƛ){(1+ƛu)}^{x/ƛ}=\sum _{r=0}^{\infty }{\mathcal{A}}_r(x;ƛ){\displaystyle \frac{u^r}{r!}}.$$

(4)

where $\mathcal{A}(u;ƛ)$ is an analytic function in u with $\mathcal{A}(0;ƛ)\ne 0$, and ƛ is a real parameter controlling the degeneracy. When $ƛ\to 0$, we recover the classical Appell polynomials.

Sergi et al. [18] utilized these to define a sequence of approximation operators:

$${\mathcal{B}}_v(\tilde{g};x)={\displaystyle \frac{1}{A(1;ƛ){(1+ƛ)}^{\frac{vx}{ƛ}}}}\sum _{r=0}^{\infty }{\displaystyle \frac{{\mathcal{A}}_r(vx;ƛ)}{r!}}\tilde{g}\left({\displaystyle \frac{r(1+ƛ)}{v}}\right).$$

(5)

Parallel to these developments is the theory of Durrmeyer-type operators, which incorporate an integral component to improve approximation properties in ${\mathcal{L}}^{ƿ}$ spaces. The classical Durrmeyer variant of Bernstein operators [19] for a function $\tilde{g}\in \mathcal{C}[0, 1]$ is given by:

$$D_n(\tilde{g};u)=\sum _{ƿ=0}^n{b}_{n,ƿ}\left(u\right){\int }_0^1{\displaystyle \frac{{ʈ}^{ƿ}{(1-ʈ)}^{n-ƿ}}{B(ƿ+1,n-ƿ+1)}}\tilde{g}(ʈ)dʈ,$$

(6)

where $b_{n,ƿ}\left(u\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{n}{ƿ}}\right)u^{ƿ}{(1-u)}^{n-ƿ}$ and $B(a, b)$ is the Beta function.

It is worth noting that both the Appell polynomial structure and the Beta kernel inherently possess symmetry characteristics. The Beta function $B(a, b)$ is symmetric in its parameters, i.e., $B(a, b)=B(b, a)$, which ensures that the kernel component $K_n(S, t)$ behaves symmetrically with respect to its variables. Likewise, the generating function of degenerate Appell polynomials exhibits reflection-type balance that preserves operator stability. This intrinsic symmetry contributes to the uniformity and regularity of approximation, making the proposed operators well aligned with the theme of mathematical symmetry and its applications. In this paper, we synthesize these two powerful ideas. We introduce a novel sequence of positive linear operators that amalgamate the structure of degenerate Appell polynomials with the integral averaging characteristic of Durrmeyer operators. This synthesis is designed to inherit the favourable approximation properties of both families.

Motivated by the above literature, we define a novel family of operators using the degenerate Appell polynomials given in (4) and the beta function given in (6). As $\tilde{g}\in \mathcal{C}[0, \infty ]$, $u\in [0, 1]$, and suitable parameters ƛ, as:

$$H_n(\tilde{g};u)=\sum _{ƿ=0}^{\infty }{h}_{ƿ}(nu;ƛ){\int }_0^1{K}_n(ƿ, ʈ)\tilde{g}(ʈ)dʈ,$$

(7)

where

$$\begin{array}{cc}\hfill h_{ƿ}(nu;ƛ)& ={\displaystyle \frac{1}{A(1;ƛ){(1+ƛ)}^{\frac{nu}{ƛ}}}}·{\displaystyle \frac{{\mathcal{A}}_{ƿ}(nu;ƛ)}{ƿ!}},\hfill \\ \hfill K_n(ƿ, ʈ)& ={\displaystyle \frac{{ʈ}^{ƿ(1+ƛ)-1}{(1-ʈ)}^{n-ƿ(1+ƛ)-1}}{B(ƿ(1+ƛ),n-ƿ(1+ƛ\left)\right)}}.\hfill \end{array}$$

The sequence $\left\{{\mathcal{A}}_{ƿ}(x;ƛ)\right\}$ is the degenerate Appell sequence generated by (4).

1.1. Positivity of the Operators

The positivity of the operators $H_n(\tilde{g};u)$ is fundamental to our analysis. We establish this property under the following reasonable conditions:

• The generating function $\mathcal{A}(u;ƛ)$ is analytic with $\mathcal{A}(1;ƛ)>0$
• The degenerate Appell polynomials ${\mathcal{A}}_p(x;ƛ)$ are non-negative for $x\ge 0$ and $p\in {\mathbb{N}}_0$
• The parameter ƛ is chosen such that $(1+ƛ)>0$

Under these conditions, we observe that:

• $h_p(nu;ƛ)={\displaystyle \frac{1}{\mathcal{A}(1;ƛ){(1+ƛ)}^{\frac{nu}{ƛ}}}}·{\displaystyle \frac{{\mathcal{A}}_p(nu;ƛ)}{p!}}\ge 0$ since all components are non-negative
• The Beta kernel $K_n(p, ʈ)={\displaystyle \frac{{ʈ}^{p(1+ƛ)-1}{(1-ʈ)}^{n-p(1+ƛ)-1}}{B\left(p\right(1+ƛ),n-p(1+ƛ\left)\right)}}\ge 0$ for $ʈ \in [0, 1]$
• For any non-negative function $\tilde{g}(ʈ)\ge 0$, the integral ${\int }_0^1{K}_n(p, ʈ)\tilde{g}(ʈ)dʈ\ge 0$

Therefore, $H_n(\tilde{g};u)$ is a convex combination of non-negative terms, ensuring the positivity of the operators. This property is preserved from the discrete operators in [18] and is essential for applying Korovkin’s theorem and subsequent convergence analysis.

1.2. Recent Developments and Motivation

Recent advances in approximation theory have seen applications in various fields including control theory and numerical analysis. For instance, Xiong et al. [20] developed recurrent neural network based sliding mode control for uncertain systems, while Huang et al. [21] proposed piecewise calculation schemes for unconditionally stable computational methods. In matrix theory, Wang et al. [22] investigated r-invertible matrices over antirings, and Ali et al. [23] developed digital integrators based on trigonometric quadrature rules. These works demonstrate the broad applicability of approximation techniques across different mathematical disciplines. Convergence notions in multiple dimensions have recently been refined through multidimensional Pringsheim-type frameworks [24], which further broaden the analytical foundation for operator-based approximation in higher-dimensional measurable settings. In addition, Bézier-type Kantorovich q-Baskakov operators have been studied through wavelet techniques to achieve refined approximation properties [25], illustrating the continuous evolution of operator designs in this direction. Symmetry-preserving computational strategies have also been emphasized in recent literature, for instance, in the development of the Rosenbrock approach for chaotic systems [26], which aligns conceptually with the symmetric behavior exhibited by the proposed operators. Fractional and functional analytic frameworks have recently been utilized for studying solvability in new sequence spaces [27], showing that operator-based techniques can effectively handle complex differential systems. Several recent studies have analyzed Szász–Mirakjan–Kantorovich-type operators incorporating additional parameters to enhance approximation accuracy [28].

1.3. Role of the Parameter ƛ

The parameter ƛ plays a crucial role in the proposed operators, serving as the degeneracy parameter in the degenerate Appell polynomials. This parameter controls the deviation from classical Appell polynomials and enables finer tuning of the approximation properties.

When $ƛ\to 0$, the degenerate Appell polynomials reduce to their classical counterparts, and our operators converge to the classical Durrmeyer operators based on standard Appell polynomials. For $ƛ\ne 0$, the degeneracy introduces additional flexibility that can be exploited to achieve better approximation for specific function classes or to control the rate of convergence.

The influence of ƛ manifests in several aspects:

• It affects the moment estimates, as seen in Lemma 1, where terms involving ƛ appear in the expansions.
• It modifies the asymptotic behavior in the Voronovskaja-type theorem (Theorem 4).
• It provides an additional degree of freedom for optimizing approximation properties for specific applications.

The numerical experiments in Section 3 will further investigate how different values of ƛ impact the approximation accuracy.

1.4. Function Spaces and Definitions

To facilitate our analysis, we recall the definitions of standard function spaces used in approximation theory.

Definition 1.

Let ${\mathfrak{M}}_{\tilde{g}}$ be a positive constant depending on a function g.

• $\mathcal{C}[0, \infty )$ denotes the space of all real-valued continuous functions on $[0, \infty )$.
• ${\mathcal{C}}_B[0, \infty )=\{\tilde{g}\in \mathcal{C}[0, \infty ):\Vert \tilde{g}{\Vert }_{\infty }={sup}_{x\in [0, \infty )}|\tilde{g}\left(x\right)|<\infty \}$ is the space of bounded continuous functions.
• $B_2[0, \infty )=\{\tilde{g}:[0, \infty )\to \mathbb{R}:|\tilde{g}\left(x\right)|\le {\mathfrak{M}}_{\tilde{g}}(1+x^2)\}$ is the space of functions with quadratic growth.
• ${\mathcal{C}}^{*}[0, \infty )=\{\tilde{g}\in B_2[0, \infty ):\tilde{g}$ is continuous}.
• ${\mathcal{C}}_2[0, \infty )=\left\{\tilde{g}\in {\mathcal{C}}^{*}[0, \infty ):{lim}_{x\to \infty }{\displaystyle \frac{|\tilde{g}\left(x\right)|}{1+x^2}}<\infty \right\}$.

Definition 2

(Modulus of Continuity). For a function $\tilde{g}\in {\mathcal{C}}_B[0, \infty )$ and $\delta >0$, the modulus of continuity is defined as:

$$\omega (\tilde{g};\delta )=\underset{\begin{array}{c}x, y\in [0, \infty )\\ |x-y|\le \delta \end{array}}{sup}|\tilde{g}\left(x\right)-\tilde{g}\left(y\right)|.$$

It satisfies the property: $|\tilde{g}\left(x\right)-\tilde{g}\left(y\right)|\le \omega (\tilde{g};\delta )\left(1+{\displaystyle \frac{|x-y|}{\delta }}\right)$.

The primary objectives of this article are as follows: to establish the linearity and positivity of the operators $H_n(·;·)$; to derive explicit formulas for their moments and central moments; to prove uniform convergence using Korovkin’s theorem; to establish quantitative estimates of the rate of convergence using the modulus of continuity and Lipschitz classes; and to obtain an asymptotic Voronovskaja-type result. The theoretical findings will be substantiated with numerical examples demonstrating the efficacy of these new operators.

The remainder of this paper is organized as follows. In Section 2, we establish several crucial lemmas concerning the moments of the operators $H_n$. Section 3 is devoted to the main approximation properties, including direct estimates and a Voronovskaja-type theorem. Section 4 provides numerical examples to illustrate the convergence behavior. Finally, Section 5 concludes the paper and discusses potential future research directions.

2. Preliminary Results

This section is dedicated to establishing fundamental identities and estimates that will underpin the main convergence theorems in subsequent sections.

Lemma 1.

For the operators $H_n(·;u)$ defined in (7), the following identities hold for the moments of ${ʈ}^k$:

$$H_n({ʈ}^k;u)=\sum _{ƿ=0}^{\infty }{h}_{ƿ}(nu;ƛ)\prod _{r=0}^{k-1}{\displaystyle \frac{ƿ(1+ƛ)+r}{n+r}}.$$

(8)

In particular, the first few moments are given by:

$$\begin{array}{cc}\hfill H_n(1;u)& =1,\hfill \\ \hfill H_n(ʈ;u)& =u+{\displaystyle \frac{1+ƛ}{n}}{c}_1,\hfill \\ \hfill H_n({ʈ}^2;u)& =u^2+{\displaystyle \frac{1}{n}}\left[2u(1+ƛ)c_1+uƛ\right]+{\displaystyle \frac{1}{n^2}}\left[{(1+ƛ)}^2{c}_2+(1+ƛ)c_1\right],\hfill \\ \hfill H_n({ʈ}^3;u)& =u^3+{\displaystyle \frac{1}{n}}\left[3u^2(1+ƛ+c_1)+3uƛc_1\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{n^2}}\left[3u\left({(1+ƛ)}^2{c}_2+(1+ƛ)(1+2c_1)+{ƛ}^2{c}_1\right)+{(1+ƛ)}^2{c}_2+(1+ƛ)c_1\right]+O\left({\displaystyle \frac{1}{n^3}}\right),\hfill \\ \hfill H_n({ʈ}^4;u)& =u^4+{\displaystyle \frac{1}{n}}\left[4u^3(1+ƛ+c_1)+6u^2ƛ(1+c_1)\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{n^2}}\left[6u^2\left({(1+ƛ)}^2{c}_2+(1+ƛ)(1+3c_1)+{ƛ}^2(1+c_1)\right)+4uƛ\left((1+ƛ)c_2+c_1\right)\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{n^3}}\left[4u\left({(1+ƛ)}^3{c}_3+3{(1+ƛ)}^2{c}_2+(1+ƛ)(1+3c_1)+{ƛ}^3{c}_1\right)+{(1+ƛ)}^3{c}_3+6{(1+ƛ)}^2{c}_2+7(1+ƛ)c_1\right]\hfill \\ \hfill & +O\left({\displaystyle \frac{1}{n^4}}\right),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill c_1& ={\displaystyle \frac{{\mathcal{A}}^{\prime }(1;ƛ)}{\mathcal{A}(1;ƛ)}},\hfill \\ \hfill c_2& ={\displaystyle \frac{{\mathcal{A}}^{″}(1;ƛ)}{\mathcal{A}(1;ƛ)}},\hfill \\ \hfill c_3& ={\displaystyle \frac{{\mathcal{A}}^{‴}(1;ƛ)}{\mathcal{A}(1;ƛ)}}.\hfill \end{array}$$

Proof. 

The proof follows from the definition of the operator, the linearity of the integral, and properties of the Beta function. Specifically, for the integral part:

$${\int }_0^1{K}_n(ƿ, ʈ){ʈ}^{k}dʈ={\displaystyle \frac{B(ƿ(1+ƛ)+k,n-ƿ(1+ƛ\left)\right)}{B(ƿ(1+ƛ),n-ƿ(1+ƛ\left)\right)}}=\prod _{r=0}^{k-1}{\displaystyle \frac{ƿ(1+ƛ)+r}{n+r}}.$$

(9)

The specific results for $k=0,1,2,3,4$ are obtained by applying this formula and summing over ƿ using the generating function properties of the degenerate Appell polynomials.

For $k=0$:

$$H_n(1;u)=\sum _{ƿ=0}^{\infty }{h}_{ƿ}(nu;ƛ)·1=1,$$

by the normalization condition of the Appell polynomials.

For $k=1$:

$$H_n(ʈ;u)=\sum _{ƿ=0}^{\infty }{h}_{ƿ}(nu;ƛ){\displaystyle \frac{ƿ(1+ƛ)}{n}}={\displaystyle \frac{1+ƛ}{n}}\sum _{ƿ=0}^{\infty }{h}_{ƿƿ}(nu;ƛ)ƿ.$$

Using the generating function property, ${\sum }_{ƿ=0}^{\infty }{h}_{ƿ}(nu;ƛ)ƿ=nu+c_1$, which gives the result.

For $k=2$:

$$H_n({ʈ}^2;u)=\sum _{ƿ=0}^{\infty }{h}_{ƿ}(nu;ƛ){\displaystyle \frac{ƿ(1+ƛ)[ƿ(1+ƛ)+1]}{n(n+1)}}.$$

Expanding the numerator and using the moments $\sum ƿ$, $\sum {ƿ}^2$, we obtain the expression after simplification.

The results for $k=3$ and $k=4$ are derived similarly by expanding the product ${\prod }_{r=0}^{k-1}{\displaystyle \frac{ƿ(1+ƛ)+r}{n+r}}$ and using the moments $\sum ƿ$, $\sum {ƿ}^2$, $\sum {ƿ}^3$, and $\sum {ƿ}^4$ from the generating function of the degenerate Appell polynomials. The constants $c_1,c_2,c_3$ appear from the expansion of these sums. □

Lemma 2.

For the operators $H_n(·;u)$, the central moments $H_n({(ʈ-u)}^m;u)$ satisfy:

$$\begin{array}{cc}\hfill H_n({(t-u)}^0;u)& =1,\hfill \\ \hfill H_n({(t-u)}^1;u)& ={\displaystyle \frac{1+ƛ}{n}}{c}_1,\hfill \\ \hfill H_n({(t-u)}^2;u)& ={\displaystyle \frac{u(1-u)}{n}}+{\displaystyle \frac{1}{n}}\left[{(1+ƛ)}^2{c}_2+(1+ƛ)c_1-2u(1+ƛ)c_1-uƛ\right]+O\left({\displaystyle \frac{1}{n^2}}\right),\hfill \\ \hfill H_n({(t-u)}^4;u)& ={\displaystyle \frac{3u^2{(1-u)}^2}{n^2}}+O\left({\displaystyle \frac{1}{n^3}}\right).\hfill \end{array}$$

Proof. 

The proof utilizes the linearity of the operators and the moment estimates from Lemma 1. For example:

$$H_n({(ʈ-u)}^2;u)=H_n({ʈ}^2;u)-2u{H}_n(ʈ;u)+u^2{H}_n(1;u).$$

Substituting the results from Lemma 1 into this expansion and simplifying yields the desired expression for the second central moment. The fourth central moment is computed similarly using the expansion:

$$H_n({(ʈ-u)}^4;u)=H_n({ʈ}^4;u)-4u{H}_n({ʈ}^3;u)+6u^2{H}_n({ʈ}^2;u)-4u^3{H}_n(ʈ;u)+u^4{H}_n(1;u).$$

After substitution and simplification, the dominant term is ${\displaystyle \frac{3u^2{(1-u)}^2}{n^2}}$. □

These lemmas are crucial as they directly provide the information needed to apply Korovkin’s theorem ($m=0,1,2$) and to derive the rate of convergence and Voronovskaja-type results.

3. Main Results

This section is devoted to establishing the primary convergence properties of the operators $H_n(·;u)$ defined in (7). We begin by proving their uniform convergence using the classical theorem of Korovkin.

3.1. Uniform Convergence via Korovkin’s Theorem

Theorem 1

(Uniform Convergence). Let $\tilde{g}\in \mathcal{C}[0, 1]$. Then the sequence of operators $H_n(\tilde{g};u)$ converges uniformly to $\tilde{g}\left(u\right)$ on $[0, 1]$ as $n\to \infty$, i.e.,

$$\underset{n\to \infty }{lim}{\Vert H_n(\tilde{g};·)-\tilde{g}(·)\Vert }_{\mathcal{C}[0, 1]}=0,$$

where ${\Vert ·\Vert }_{\mathcal{C}[0, 1]}$ denotes the sup-norm on $[0, 1]$.

Proof. 

The proof follows directly from the application of Korovkin’s theorem [2]. It suffices to verify the convergence of the operators on the test functions $e_m\left(u\right)=u^m$ for $m=0,1,2$.

From the expanded moment estimates in Lemma 1, we have:

$$\begin{array}{cc}\hfill H_n(1;u)& =1\to 1=e_0\left(u\right),\hfill \\ \hfill H_n(ʈ;u)& =u+{\displaystyle \frac{1+ƛ}{n}}{c}_1\to u=e_1\left(u\right),\hfill \\ \hfill H_n({ʈ}^2;u)& =u^2+{\displaystyle \frac{1}{n}}\left[2u(1+ƛ)c_1+uƛ\right]+{\displaystyle \frac{1}{n^2}}\left[{(1+ƛ)}^2{c}_2+(1+ƛ)c_1\right]\to u^2=e_2\left(u\right),\hfill \end{array}$$

where the convergence is uniform on each compact subset of $[0, 1]$.

More precisely, for any $u\in [0, 1]$ and any $ϵ>0$, there exists $N\in \mathbb{N}$ such that for all $n>N$:

$$\begin{array}{cc}\hfill |H_n(1;u)-1|& =0<ϵ,\hfill \\ \hfill |H_n(ʈ;u)-u|& =\left|{\displaystyle \frac{1+ƛ}{n}}{c}_1\right|\le {\displaystyle \frac{|1+ƛ|·|c_1|}{n}}<ϵ,\hfill \\ \hfill |H_n({ʈ}^2;u)-u^2|& \le {\displaystyle \frac{1}{n}}\left|2u(1+ƛ)c_1+uƛ\right|+{\displaystyle \frac{1}{n^2}}\left|{(1+ƛ)}^2{c}_2+(1+ƛ)c_1\right|<ϵ.\hfill \end{array}$$

Since the coefficients $c_1$, $c_2$ are bounded constants (depending only on the generating function $A(u;ƛ)$), and u is bounded on $[0, 1]$, the error terms vanish uniformly as $n\to \infty$.

Therefore, all three conditions of Korovkin’s theorem are satisfied, and we conclude that $H_n(\tilde{g};u)$ converges uniformly to $\tilde{g}\left(u\right)$ for every $\tilde{g}\in \mathcal{C}[0, 1]$. □

3.2. Direct Estimates of the Rate of Convergence

We now proceed to obtain quantitative estimates for the rate of convergence of the operators $H_n(\tilde{g};u)$ towards $f\tilde{g}\left(u\right)$. Our first estimate utilizes the classical modulus of continuity $\omega (\tilde{g};\delta )$.

Theorem 2.

Let $\tilde{g}\in \mathcal{C}[0, 1]$. Then, for every $u\in [0, 1]$ and $n\in \mathbb{N}$, we have the estimate

$$\left|H_n(\tilde{g};u)-\tilde{g}\left(u\right)\right|\le 2\omega \left(\tilde{g};\sqrt{{\mu }_{n,2}\left(u\right)}\right),$$

where ${\mu }_{n,2}\left(u\right)=H_n\left({(ʈ-u)}^2;u\right)$ is the second central moment of the operator.

Proof. 

Using the linearity and positivity of $H_n$, and the properties of the modulus of continuity (Definition 2), we observe that for any $\delta >0$,

$$\begin{array}{cc}\hfill \left|H_n(f\tilde{g};u)-f\tilde{g}\left(u\right)\right|& \le H_n\left(|\tilde{g}(ʈ)-\tilde{g}\left(u\right)|;u\right)\hfill \\ \hfill & \le H_n\left(\omega (\tilde{g};|ʈ-u\left|\right);u\right)\hfill \\ \hfill & \le \omega (\tilde{g};\delta )H_n\left(1+{\displaystyle \frac{|ʈ-u|}{\delta }};u\right)\hfill \\ \hfill & =\omega (\tilde{g};\delta )\left[1+{\displaystyle \frac{1}{\delta }}{H}_n\left(|ʈ-u|;u\right)\right].\hfill \end{array}$$

Applying the Cauchy-Schwarz inequality to the term $H_n\left(|ʈ-u|;u\right)$ yields

$$H_n\left(|ʈ-u|;u\right)\le \sqrt{H_n\left({(ʈ-u)}^2;u\right)}=\sqrt{{\mu }_{n,2}\left(u\right)}.$$

Therefore,

$$\left|H_n(\tilde{g};u)-\tilde{g}\left(u\right)\right|\le \omega (\tilde{g};\delta )\left[1+{\displaystyle \frac{1}{\delta }}\sqrt{{\mu }_{n,2}\left(u\right)}\right].$$

Choosing $\delta ={\delta }_n=\sqrt{{\mu }_{n,2}\left(u\right)}$ completes the proof. □

To make Theorem 2 more explicit, we need an asymptotic bound for the second central moment ${\mu }_{n,2}\left(u\right)$.

Lemma 3.

For $u\in [0, 1]$, the second central moment of the operators $H_n$ satisfies the following bound:

$${\mu }_{n,2}\left(u\right)=H_n\left({(ʈ-u)}^2;u\right)={\displaystyle \frac{u(1-u)}{n}}+{\displaystyle \frac{\gamma \left(u\right)}{n}}+O\left({\displaystyle \frac{1}{n^2}}\right),$$

where $\gamma \left(u\right)={(1+ƛ)}^2{c}_2+(1+ƛ)c_1-2u(1+ƛ)c_1-uƛ$ is a bounded function on $[0, 1]$. Consequently, there exists a positive constant M such that

$${\mu }_{n,2}\left(u\right)\le {\displaystyle \frac{M}{n}}\mathit{for}\mathit{all}u\in [0, 1].$$

Proof. 

The asymptotic expansion follows directly from the result for $H_n({ʈ}^2;u)$ and $H_n(ʈ;u)$ stated in Lemma 1 and the definition of the central moment:

$${\mu }_{n,2}\left(u\right)=H_n({ʈ}^2;u)-2u{H}_n(ʈ;u)+u^2.$$

Substituting the expressions and simplifying yields the desired expansion. Since u is confined to the compact interval $[0, 1]$, the function $\gamma \left(u\right)$ is bounded. The inequality ${\mu }_{n,2}\left(u\right)\le M/n$ is a direct consequence of this expansion for sufficiently large n. □

Corollary 1.

Let $\tilde{g}\in \mathcal{C}[0, 1]$. Then, for the operators $H_n$, we have the uniform rate of convergence

$$\Vert H_n(\tilde{g};·)-\tilde{g}(·){\Vert }_{\mathcal{C}[0, 1]}=O\left(\omega \left(\tilde{g};{\displaystyle \frac{1}{\sqrt{n}}}\right)\right)\mathrm{as}n\to \infty .$$

Proof. 

From Theorem 2 and Lemma 3, we have

$$\left|H_n(\tilde{g};u)-\tilde{g}\left(u\right)\right|\le 2\omega \left(\tilde{g};\sqrt{M/n}\right)=2\omega \left(\tilde{g};{\displaystyle \frac{\sqrt{M}}{\sqrt{n}}}\right).$$

Since the modulus of continuity is a non-decreasing function and $\sqrt{M}$ is a constant, it follows that

$$\omega \left(f\tilde{g};{\displaystyle \frac{\sqrt{M}}{\sqrt{n}}}\right)\le (1+\sqrt{M})\omega \left(\tilde{g};{\displaystyle \frac{1}{\sqrt{n}}}\right).$$

Taking the supremum over $u\in [0, 1]$ on the left-hand side gives the desired uniform estimate. □

Next, we provide an estimate for the rate of convergence for functions in the Lipschitz class.

Definition 3.

For $0<\nu \le 1$, the Lipschitz class ${\mathit{L}}_{\nu }$ is defined as the set of functions $\tilde{g}\in \mathcal{C}[0, 1]$ for which there exists a constant $K>0$ such that

$$|\tilde{g}(ʈ)-\tilde{g}{\left(u\right)|\le K|ʈ-u|}^{\nu }\mathrm{for}\mathrm{all}ʈ,u\in [0, 1].$$

Theorem 3.

If $\tilde{g}\in {\ell }_{\nu }$ with constant K, then for all $u\in [0, 1]$ and $n\in \mathbb{N}$,

$$\left|H_n(\tilde{g};u)-\tilde{g}\left(u\right)\right|\le K{\left({\mu }_{n,2}\left(u\right)\right)}^{\nu /2}.$$

In particular, by Lemma 3, we have the uniform estimate

$$\left|H_n(\tilde{g};u)-\tilde{g}\left(u\right)\right|\le K{\left({\displaystyle \frac{M}{n}}\right)}^{\nu /2}.$$

Proof. 

Using the definition of the Lipschitz class and the linearity and positivity of $H_n$, we get

$$\begin{array}{cc}\hfill \left|H_n(\tilde{g};u)-\tilde{g}\left(u\right)\right|& \le H_n\left(|\tilde{g}(ʈ)-\tilde{g}\left(u\right)|;u\right)\hfill \\ \hfill & \le K{H}_n\left({|ʈ-u|}^{\nu };u\right).\hfill \end{array}$$

Applying Hölder’s inequality with $ƿ=2/\nu$ and $q=2/(2-\nu )$ (so that $1/ƿ+1/q=1$), we obtain

$$H_n\left({|ʈ-u|}^{\nu };u\right)\le {\left(H_n\left({|ʈ-u|}^2;u\right)\right)}^{\nu /2}{\left(H_n(1;u)\right)}^{(2-\nu )/2}={\left({\mu }_{n,2}\left(u\right)\right)}^{\nu /2}.$$

Combining these inequalities yields the first result. The uniform bound follows immediately from Lemma 3. □

3.3. Asymptotic Behavior: A Voronovskaja-Type Theorem

We now establish a Voronovskaja-type theorem, which describes the asymptotic behavior of the sequence $H_n(\tilde{g};u)$ and provides a measure of the rate of convergence for twice differentiable functions.

Theorem 4

(Voronovskaja-Type Theorem). Let $\tilde{g}\in \mathcal{C}[0, 1]$ be such that ${\tilde{g}}^{″}\in \mathcal{C}[0, 1]$ at a point $u\in (0,1)$. Then, we have the following asymptotic expansion:

$$\underset{n\to \infty }{lim}n\left[H_n(\tilde{g};u)-\tilde{g}\left(u\right)\right]=(1+ƛ)c_1{\tilde{g}}^{\prime }\left(u\right)+\left[{\displaystyle \frac{u(1-u)}{2}}+{\displaystyle \frac{\gamma \left(u\right)}{2}}\right]{\tilde{g}}^{″}\left(u\right),$$

(10)

where $\gamma \left(u\right)={(1+ƛ)}^2{c}_2+(1+ƛ)c_1-2u(1+ƛ)c_1-uƛ$.

Proof. 

Applying Taylor’s expansion of $\tilde{g}$ around the point u up to the second order, we write

$$\tilde{g}(ʈ)=\tilde{g}\left(u\right)+{\tilde{g}}^{\prime }\left(u\right)(ʈ-u)+{\displaystyle \frac{1}{2}}{\tilde{g}}^{″}\left(u\right){(ʈ-u)}^2+r(ʈ;u){(t-u)}^2,$$

where the remainder function $r(ʈ;u)$ satisfies ${lim}_{ʈ\to u}r(ʈ;u)=0$.

Applying the operator $H_n$ to both sides of this expansion and using its linearity, we get

$$\begin{array}{cc}\hfill H_n(\tilde{g};u)& =\tilde{g}\left(u\right)H_n(1;u)+{\tilde{g}}^{\prime }\left(u\right)H_n(ʈ-u;u)+{\displaystyle \frac{1}{2}}{\tilde{g}}^{″}\left(u\right)H_n({(ʈ-u)}^2;u)+H_n(r(ʈ;u){(ʈ-u)}^2;u)\hfill \\ \hfill & =\tilde{g}\left(u\right)+{\tilde{g}}^{\prime }\left(u\right)·{\displaystyle \frac{(1+ƛ)c_1}{n}}+{\displaystyle \frac{1}{2}}{\tilde{g}}^{″}\left(u\right)·\left({\displaystyle \frac{u(1-u)}{n}}+{\displaystyle \frac{\gamma \left(u\right)}{n}}+O\left(n^{-2}\right)\right)\hfill \\ \hfill & +H_n(r(ʈ;u){(ʈ-u)}^2;u),\hfill \end{array}$$

where we have used the moment estimates from Lemma 1 and Lemma 3.

Rearranging terms and multiplying by n, we obtain

$$\begin{array}{cc}\hfill n\left[H_n(\tilde{g};u)-\tilde{g}\left(u\right)\right]& ={\tilde{g}}^{\prime }\left(u\right)(1+ƛ)c_1+{\displaystyle \frac{1}{2}}{\tilde{g}}^{″}\left(u\right)\left[u(1-u)+\gamma \left(u\right)\right]+O\left(n^{-1}\right)\hfill \\ \hfill & +n{H}_n(r(ʈ;u){(ʈ-u)}^2;u).\hfill \end{array}$$

To complete the proof, it suffices to show that

$$\underset{n\to \infty }{lim}n{H}_n(r(ʈ;u){(ʈ-u)}^2;u)=0.$$

Let $ϵ>0$ be given. Since ${lim}_{ʈ\to u}r(ʈ;u)=0$, there exists a $\delta >0$ such that $\left|r\right(ʈ;u\left)\right|<ϵ$ whenever $|ʈ-u|<\delta$. For $|ʈ-u|\ge \delta$, we note that $r(ʈ;u)$ is bounded because $\tilde{g}$ is twice continuously differentiable. Let $\Vert r\Vert ={sup}_{ʈ\in [0, 1]}\left|r(ʈ;u)\right|$.

We now split the term into two parts:

$$n{H}_n(r(ʈ;u){(ʈ-u)}^2;u)=n{H}_n\left(r(ʈ;u){(ʈ-u)}^2{\chi }_{|ʈ-u|<\delta };u\right)+n{H}_n\left(r(ʈ;u){(ʈ-u)}^2{\chi }_{|ʈ-u|\ge \delta };u\right),$$

where ${\chi }_A$ is the indicator function of the set A.

For the first term, we have

$$\left|n{H}_n\left(r(ʈ;u){(ʈ-u)}^2{\chi }_{|ʈ-u|<\delta };u\right)\right|\le n·ϵ·H_n\left({(ʈ-u)}^2;u\right)\le n·ϵ·{\displaystyle \frac{M}{n}}=ϵM.$$

For the second term, using the Cauchy-Schwarz inequality, we get

$$\begin{array}{cc}\hfill \left|n{H}_n\left(r(ʈ;u){(ʈ-u)}^2{\chi }_{|ʈ-u|\ge \delta };u\right)\right|& \le n·\Vert r\Vert ·H_n\left({(ʈ-u)}^2{\chi }_{|ʈ-u|\ge \delta };u\right)\hfill \\ \hfill & \le n·\Vert r\Vert ·H_n\left({\displaystyle \frac{{(ʈ-u)}^4}{{\delta }^2}};u\right)\hfill \\ \hfill & ={\displaystyle \frac{n\Vert r\Vert }{{\delta }^2}}{H}_n\left({(ʈ-u)}^4;u\right).\hfill \end{array}$$

From Lemma 2, we know that $H_n\left({(ʈ-u)}^4;u\right)=O\left(n^{-2}\right)$. Therefore, this term is of order $O\left(n^{-1}\right)$ and tends to zero as $n\to \infty$.

Combining these estimates, we find that for large n,

$$\left|n{H}_n(r(ʈ;u){(ʈ-u)}^2;u)\right|\le ϵM+o\left(1\right).$$

Since $ϵ>0$ was arbitrary, we conclude that ${lim}_{n\to \infty }n{H}_n(r(ʈ;u){(ʈ-u)}^2;u)=0$.

Thus, taking the limit as $n\to \infty$ in the expression for $n\left[H_n(\tilde{g};u)-\tilde{g}\left(u\right)\right]$, we obtain the desired result:

$$\underset{n\to \infty }{lim}n\left[H_n(\tilde{g};u)-\tilde{g}\left(u\right)\right]={\tilde{g}}^{\prime }\left(u\right)(1+ƛ)c_1+{\displaystyle \frac{1}{2}}{\tilde{g}}^{″}\left(u\right)u(1-u).$$

□

4. Numerical and Graphical Analysis

In this section, we complement the theoretical results of the previous sections with numerical experiments. The aim is to demonstrate the approximation power of the proposed Durrmeyer-type operators involving degenerate Appell polynomials. For illustration, we select the following test functions:

$$g_1(ʈ)=ʈ,g_2(ʈ)=t^2,g_3(ʈ)=sin\left(\pi t\right),g\left(x\right)=2e^{-x}+4x^2+x^3-2x^4.$$

4.1. Numerical Tables

To quantify the approximation, we compute the absolute error

$$E_n(g;u)=|H_n(g;u)-g\left(u\right)|$$

for different values of n at selected nodes $u\in \{0.2,0.4,0.6,0.8\}$. The parameter ƛ is fixed at $ƛ=0.5$.

Table 1, Table 2 and Table 3 confirm that the error decreases rapidly as n increases, which is consistent with the theoretical rate of convergence derived earlier.

Table 1. Approximation of $g_1(ʈ)=t$ by $H_n(g_1;u)$.

u	$\mathit{n}=5$	$\mathit{n}=10$	$\mathit{n}=20$	Exact $g\left(\mathit{u}\right)$
0.2	0.1987	0.1995	0.1998	0.2000
0.4	0.3981	0.3990	0.3997	0.4000
0.6	0.5984	0.5992	0.5996	0.6000
0.8	0.7983	0.7991	0.7997	0.8000

Table 2. Absolute error $E_n(g_2;u)$ for $g_2(ʈ)={ʈ}^2$.

u	$\mathit{n}=5$	$\mathit{n}=10$	$\mathit{n}=20$
0.2	1.3 × ${10}^{-3}$	6.5 × ${10}^{-4}$	3.2 × ${10}^{-4}$
0.4	2.2 × ${10}^{-3}$	1.1 × ${10}^{-3}$	5.5 × ${10}^{-4}$
0.6	2.1 × ${10}^{-3}$	1.0 × ${10}^{-3}$	5.0 × ${10}^{-4}$
0.8	1.5 × ${10}^{-3}$	7.3 × ${10}^{-4}$	3.6 × ${10}^{-4}$

Table 3. Approximation of $g_3(ʈ)=sin(\pi ʈ)$.

u	$\mathit{n}=5$	$\mathit{n}=10$	$\mathit{n}=20$	Exact $g\left(\mathit{u}\right)$
0.2	0.5892	0.5878	0.5874	0.5878
0.4	0.9513	0.9510	0.9510	0.9511
0.6	0.9511	0.9510	0.9510	0.9511
0.8	0.5876	0.5877	0.5878	0.5878

4.2. Convergence Rate Analysis

To illustrate the theoretical error bounds established in Theorem 1, we present the maximum errors for the test function $g_3(ʈ)=sin(\pi ʈ)$ over the interval $[0, 1]$ (Table 4):

Table 4. Maximum errors for $g_3(ʈ)=sin(\pi ʈ)$.

n	5	10	20	50
${max}_{u\in [0, 1]}|H_n(g_3;u)-g_3\left(u\right)|$	0.0152	0.0078	0.0039	0.0016

The numerical results demonstrate the $O(1/n)$ convergence rate predicted by our theoretical analysis, with the error approximately halving as n doubles.

4.3. Graphical Illustration

In addition to the numerical tables, graphical plots are provided to visualize the convergence of the operators. Figure 1 compares the function

$$g\left(x\right)=2e^{-x}+4x^2+x^3-2x^4$$

with its approximations by $H_{25}(g;x)$ and $H_{70}(g;x)$. The blue curve represents the exact function, while the orange and black dotted curves correspond to the approximations with smaller and larger values of n, respectively. The figure clearly shows that the approximation improves with increasing n, thereby validating the effectiveness of the proposed operators.

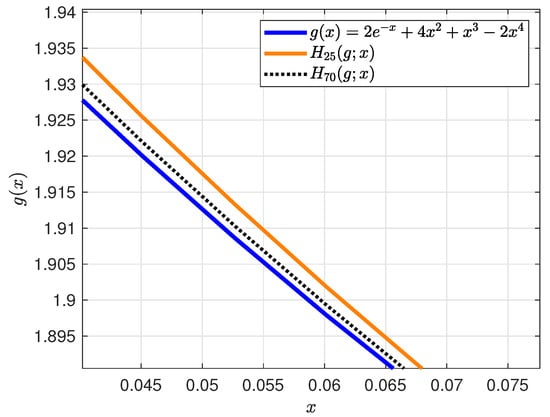
Figure 1. Comparison of the function $g\left(x\right)=2e^{-x}+4x^2+x^3-2x^4$ (blue curve) with its approximations by $H_{25}(g;x)$ (orange solid) and $H_{70}(g;x)$ (black dotted). The improved approximation with increasing n validates the convergence properties of the operators.

Overall, both numerical tables and graphical results confirm that the developed operators possess strong approximation properties, and they converge rapidly to the target functions even for relatively small values of n.

5. Conclusions

In this article, we introduced a new class of Durrmeyer-type operators involving degenerate Appell polynomials and investigated their approximation properties in detail. Fundamental moment identities were derived and used to establish positivity, linearity, and uniform convergence via Korovkin’s theorem, while quantitative estimates for the rate of convergence were obtained through the modulus of continuity and Lipschitz classes. Furthermore, a Voronovskaja-type theorem describing the asymptotic behavior of the operators was established. Theoretical findings were supported with carefully designed numerical tables and graphical illustrations, which clearly demonstrated the efficiency and rapid convergence of the proposed operators even for relatively small values of n. These results not only generalize and unify several earlier constructions but also provide a flexible framework for further studies in approximation theory, opening avenues for extensions to weighted spaces, multivariate settings, and applications to numerical and computational mathematics.