A Tripartite Analytical Framework for Nonlinear (1+1)-Dimensional Field Equations: Painlevé Analysis, Classical Symmetry Reduction, and Exact Soliton Solutions

Abstract

This study presents a tripartite analytical framework for the (1+1)-dimensional nonlinear Klein–Fock–Gordon equation, a key model for spinless particles in relativistic quantum mechanics. The investigation begins with a Painlevé analysis showing that the equation is completely integrable via the Painlevé test by using Maple. Subsequently, classical Lie symmetry analysis is employed to derive the infinitesimal generators of the equation. A Lagrangian formulation is constructed for these generators, from which similarity variables are systematically obtained. This framework enables a complete similarity reduction, transforming the complex nonlinear partial differential equation into a more tractable ordinary differential equation. To solve this reduced ordinary differential equation and to obtain a spectrum of soliton solutions, we implement the new generalized exponential differential rational function method. This advanced technique utilizes a rational trial function based on the $ith$ derivatives of exponentials, generating a diverse spectrum of closed-form soliton solutions through strategic choices of arbitrary constants. The novelty of this approach provides a unified framework for handling higher-order nonlinearities, yielding solutions such as multi-peakons and lump solitons, which are vividly characterized using Mathematica-generated 3D, 2D, and contour plots. These findings provide significant insights into nonlinear wave dynamics with potential applications in quantum field theory, nonlinear optics, plasma physics, etc.

1. Introduction

The ability of nonlinear partial differential equations (NLPDEs) to model complex physical phenomena has captured the attention of researchers in various fields during recent decades. These equations offer a basic framework for examining dynamical systems with nonlinearity, making it possible to interpret and model the complex multidimensional behaviors in a variety of scientific and engineering fields. These fields include mathematical fluid dynamics, circuit analysis, plasma physics, population dynamics, gas dynamics, nonlinear optical fibers, celestial mechanics, nanobiosciences, birefringent fibers within nonlinear science, etc. These NLPDEs help us deeply to understand the complex physical systems and predict how they will evolve with time and space. Researchers have carefully studied many nonlinear models in many fields as discussed above, like the generalized Bogoyavlensky–Konopelchenko equation [1], the (4+1)-dimensional Davey–Stewartson–Kadomtsev–Petviashvili equation (DSKPE) [2], TFESWW (2+1)-dim shallow water wave [3], the Fractional Reaction-Duffing model [4], the Einstein vacuum field model [5], the mKdV model [6], Biswas–Milovic equations [7], the Riemann wave model [8], BBMP equations [9], (2+1)-dimensional variable coefficients graphene sheets equation [10], and many more models [11,12,13,14,15,16,17,18]. Solving nonlinear models precisely is still challenging. Solitons are unique, localized wave packets that retain their shape and speed throughout time because of a fine balance between nonlinearity and dispersion. As a result, the study of soliton analysis has been essential to the research of NLPDEs. Advanced soliton theory has given rise to many powerful methods, such as the unified Riccati expansion method [19], the Sardar sub-equation method [20], Kudryashov variants [21,22,23], bifurcation analysis [24], the modified Jacobi elliptic expansion method [25], the Riccati–Bernoulli sub-optimal differential equation approach [26], and many more [18,27,28,29,30,31,32,33,34].

The basic purpose of this research is to examine the (1+1)-dimensional nonlinear wave equation with mass and self-interaction terms known as the Klein--Fock–Gordon extension [35], a nonlinear framework with broad applications in quantum mechanics and high energy physics. In 1926, Oskar Klein and Walter Gordon proposed this equation, as it describes relativistic electrons. In the same year, some other scientists, Louis de Broglie, Johann Kudar, Theophile de Donder, Frans-H. van den Dungen, and Vladimir Fock, have claimed the same relativistic equation; therefore, this equation was named after these scientists [36]. Later on, it turned out that the spinning electrons are described well by the Dirac equation, and the Klein–Fock–Gordon (KFG) equation correctly describes the spinless pions and is supposed to be the relativistic version of the Schrodinger equation. The KFG equation is utilized in applied physical sciences, quantum field theory, relativistic physics, dispersive wave phenomena, plasma physics, and nonlinear optics. Numerous research works have already examined its variants for modeling the elementary particles [37,38,39,40,41,42]. We start our study by using the following form of the KFG equation:

$$u_{tt}+\alpha u_{xx}+\beta u+\delta u^3=0,$$

(1)

where $u=u(x,t)$ is the wave profile of the particle and $\alpha$, $\beta$, and $\delta$ are real constants. The third and the fourth terms of Equation (1) represent the particle’s mass and nonlinearity, which introduce self-interaction, respectively. The main reason for the selection of this model is its foundational importance in the fields of theoretical physics, specially in the field of quantum field theory. The literature review of this model inspired us to add work on such an important equation because of its ability to model a wide range of physical phenomena in various fields such as, in particle physics, it describes the scalar fields to model the Higgs mechanism. In nonlinear optics, it also helps, as the third order term in our equation expresses the third order dispersion, which is important in understanding the propagation of ultrashort pulses in optical fibers. It also describes many other phenomena, such as a splay wave’s propagation along a lied membrane, the unified theory for elementary particles, the propagation of magnetic flux on a Josephson line, the Blochwall motion of magnetic crystals, the propagation of dislocations within crystals, etc. [43]. This nonlinear model has been solved successfully by many skilled researchers by using a range of multiple advanced techniques such as, in 2018, M. S. Islam et al. [44] have applied the improved F-expansion method to obtain the solutions of the KFG equation in the form of hyperbolic, trigonometric, and rational function structures. In 2019, Ghazala et al. [45] studied the time-fractional KFG equation using an effective technique known as the generalized projective Riccati equation method. In 2021, M. N. Alam et al. [46] utilized the modified $\left({\displaystyle \frac{G^{\prime }}{G}}\right)$ expansion method and the generalized Kudryashov method to obtain stable and functional solutions in the form of various soliton profiles, including kink-type shape, bright and dark lump shape, bright and dark singular kinky shape, periodic bright and dark lump shape, multiple bright and dark lump shape, lump with rough wave shape, rough wave shape, and kinky shape. In 2022, H. U. Rehman et al. [47] derived analytical solutions of the KFG equation via the Sardar sub-equation approach. First, the equation was solved to obtain solitary wave solutions in the form of bright, singular, dark, periodic singular, combined dark-bright, and combined dark-singular solitons. Then, by using the modulation instability process, the stability of the solutions was discussed. In 2024, M. Iqbal et al. [48] used the auxiliary equation technique to produce more generic and wide-ranging soliton solutions in the form of hyperbolic functions. This technique has explored various forms of solitons, such as dark soliton, brilliant soliton, mixed bright and dark solitons, and other sorts of solitons, by varying the values of constant parameters appearing in the technique. In 2025, M. M. Tariq et al. [49] applied traveling wave transformation to convert the KFG model into ordinary differential equation form and then improved the modified Sardar sub-equation, and modified Khater methods were applied to obtain advanced analytical solutions. Further, by using the Galilean transformation, phase portraits of the equilibrium points were examined to convert the equation into a planar dynamical system along with the chaotic behaviour. Similar to above, many other effective methods [50,51,52] also have been applied successfully to obtain soliton solutions.

Motivated by earlier studies and acknowledging the importance of the nonlinear model (1), the present manuscript aims to conduct a detailed study on the KFG equation; as per the best of our knowledge, only the soliton solutions of this equation are determined so far. For this, we introduce two important integrable aspects in this study to investigate Equation (1) that involve the Painlevé analysis and the Lie symmetry analysis. To check its integrability and solvability, we can identify the specific resonance points for this model by applying the Painlevé test. After checking solvability using the one-parameter Lie symmetry approach, we find the invariant transformations of the same model, which helps to reduce the complexity of the nonlinear model by reducing their dimensions or converting the partial differential equation to an ordinary differential equation. Further, novelty occurs in this study because of the utilization of an innovative analytical method: the new generalized exponential differential rational function method (NGEDRFM). This method offers a valuable advantage by constructing exact analytical solutions, particularly multi-peakon waves for high-dimensional nonlinear equations, which are otherwise challenging to solve. NGEDRFM stands apart from prior methods by unifying exponential, differential, and rational function approaches into a single adaptable framework, allowing it to capture a broader range of wave dynamics, such as amplitudes, interactions, velocities, phase profiles, and evolution of waves, with fewer computational steps. This enhances its applicability across complex systems and higher-dimensional systems, providing precise solutions where traditional techniques may struggle or require simplification.

The remaining manuscript is organized as follows: In Section 2, the Painlevé analysis is studied. In Section 3, the Lie symmetry analysis is applied to obtain infinitesimal generators. In Section 4, the nonlinear partial differential equation is reduced to an analytically nonlinear ordinary differential equation by utilizing the general linear combination of infinitesimal generators. In Section 5, we implement the NGEDRFM to derive exact closed-form solutions. In Section 6, the graphical interpretation is discussed. In the last Section 7, conclusions and results of the model are discussed.

2. Painlevé Analysis (PA) of Equation (1)

In this section, we will move with the Painlevé integrability of the KFG equation by using the WTC algorithm [53] for testing PDEs for the Painlevé property. The Painlevé test is performed on the general Equation (1). However, for the sake of clarity and to avoid unnecessarily lengthy expressions in the subsequent expansions, we illustrate the procedure using the specific parameter set $\alpha =\beta =\delta =1$. We emphasize that this choice is for presentation purposes only; the key outcomes of the test, namely the leading-order exponent and the resonance values, are independent of the specific values of $\alpha$, $\beta$, and $\delta$. The analysis with arbitrary parameters confirms the same integrability structure. Based on the ARS hypothesis [54], the ordinary differential equation resulting from the symmetric reduction of a completely integrable partial differential equation exhibits the Painlevé property. A PDE is deemed to satisfy the Painlevé test if its general solution remains single-valued in the vicinity of every movable singular manifold. The Painlevé test comprises three principal phases: the leading-order analysis, resonance determination, and the compatibility verifications [55]. By using the Painlevé property [55], it is supposed that Equation (1) has a Laurent expansion solution of the following form:

$$u=u(x,t)=\sum _{j=0}^{\infty }{u}_j(x,t)g{(x,t)}^{j+p}.$$

(2)

Here, $g(x,t)$ is an analytic function that defines the singular manifold $g(x,t)=0$, around which the expansion is performed, and the coefficients $u_j(x,t)(j=0,1,2\dots )$ are analytic functions of x and t, in the neighborhood of this manifold, where p is an integer with minimum one exponent.

$\mathbf{Step}\mathbf{1}$ The leading order behavior (LOB): The LOB (most dominant terms) and coefficients will be determined by assuming following ansatz of the form:

$$u(x,t)=\mathcal{X}g{(x,t)}^p,$$

(3)

where $\mathcal{X}$ is an analytical function of x and t and p denotes the dominant behavior and we will assess it at first. For this, we put Equation (3) in Equation (1), and equating the most dominant terms yields $p=$−1.

Now we suppose ansatz of the form:

$$u(x,t)=u_0(x,t)g{(x,t)}^{-1}.$$

(4)

After finding all the required derivatives of Equation (4) occurring in Equation (1) and following LOB terms step, we find

$$u_0(x,t)=\pm \sqrt{-2{\left(g_x(x,t)\right)}^2-2{\left(g_t(x,t)\right)}^2}.$$

(5)

The positive value will be taken in next to complete analysis.

$\mathbf{Step}\mathbf{2}$ Determination of resonance Values (RVs): Now we find RVs (i.e., js) associated with the LOB with reference to Equation (2) along with the values calculated in step 1. Taking the following ansatz

$$u(x,t)=u_0(x,t)g{(x,t)}^{-1}+u_j(x,t)g{(x,t)}^{j-1}.$$

(6)

Using Equations (6) and (5) in Equation (1) and holding the coefficients of dominant terms ($g^{j-3}(x,t)$) equal to zero yields the following characteristic equation of resonance:

$$(j^2-3j-4)g_t^4+(j^2-3j-4)g_x^4+2(j^2-3j-4)g_t^2{g}_t^2=0.$$

(7)

The solution of Equation (7) results in these resonance values: $j_1=-1$ and $j_2=4$. It is to be noted that this step calculated two RVs as a result of the second order of the specimen Equation (1), which justifies the smooth conduct of the Painlevé test. As customary, the resonance at $j_1$ (called universal resonance) embodies the arbitrariness intrinsic to the movable singular manifold g(x,t) = 0.

$\mathbf{Step}\mathbf{3}$ Verification of Compatibility Conditions (CCs): In the last step, we will find at first find the constant of integration to check CCs. With reference to Equation (2) and having $j_{max}$ = 4, we have a Laurent series of the following form:

$$u(x,t)=g{(x,t)}^{-1}\sum _{j=0}^4{u}_j(x,t)g{(x,t)}^j.$$

(8)

The expansion of Equation (8) yields:

$$u(x,t)=u_0(x,t)g{(x,t)}^{-1}+u_1(x,t)+u_2(x,t)g(x,t)+u_3(x,t)g{(x,t)}^2+u_4(x,t)g{(x,t)}^3.$$

(9)

After substituting Equation (9) in Equation (1), we pull out the groups of the same power of g(x,t). At different levels of j, we take out the coefficients of $g^{j-3}(x,t)$ to calculate $u_j(j=1,2,3$ and $4)$. For instance, at level j = 1, we take the coefficients of $g^{-2}(x,t)$ equal to zero, which yields $u_1(x,t)$ and so on. Thus, at level j = 1, we get:

$$u_1(x,t)={\displaystyle \frac{\left(3(g_t^2+g_x^2)g_{tt}\right)+(g_t^2+3g_x^2)\left(g_{xx}\right)+4\left(g_{tx}\right)\left(g_t\right)\left(g_x\right)}{\left(\sqrt{-2g_x^2-2g_t^2}\right)(3g_t^2+3g_x^2)}}.$$

(10)

Similarly at level j = 2, we get:

$$\begin{array}{c}\hfill u_2(x,t)=-{\displaystyle \frac{1}{3\left(\sqrt{-2g_x^2-2g_t^2}\right){\left(g_x^2+g_t^2\right)}^4}}\left({\mathcal{G}}_1+{\mathcal{G}}_2+{\mathcal{G}}_3+{\mathcal{G}}_4+{\mathcal{G}}_5+{\mathcal{G}}_6+{\mathcal{G}}_7\right).\end{array}$$

(11)

where all ${\mathcal{G}}_i^{\prime }s={\mathcal{G}}_i{(x,t)}^{\prime }s(i=1,2\dots 7)$ are sub-values of $u_2$ enlisted in the following set:

$$\left.\begin{array}{ccc}{\mathcal{G}}_1\hfill & =\hfill & \left(g_t{\left(g_x^2+g_t^2\right)}^3\right)g_{ttt},\hfill \\ {\mathcal{G}}_2\hfill & =\hfill & \left(g_t{\left(g_x^2+g_t^2\right)}^3\right)g_{txx},\hfill \\ {\mathcal{G}}_3\hfill & =\hfill & \left(g_x{\left(g_x^2+g_t^2\right)}^3\right)g_{xxx},\hfill \\ {\mathcal{G}}_4\hfill & =\hfill & \left(g_x\left(g_t^6+3g_t^4{g}_x^2+g_x^6\right)g_{ttx}\right),\hfill \\ {\mathcal{G}}_5\hfill & =\hfill & \left(-{\displaystyle \frac{7\left(g_x^4{g}_t^2\right)}{6}}-{\displaystyle \frac{3\left(g_t^4{g}_x^2\right)}{2}}+{\displaystyle \frac{5\left(g_x^6\right)}{6}}-{\displaystyle \frac{3\left(g_t^6\right)}{2}}\right)g_{tt}^2,\hfill \\ {\mathcal{G}}_6\hfill & =\hfill & \left(\left(\left(g_t^4+{\displaystyle \frac{10\left(g_t^2{g}_x^2\right)}{3}}\right)+g_x^4\right)g_{xx}+6g_x\left(g_t^2+{\displaystyle \frac{5g_x^2}{9}}\right)g_t{g}_{tx}\right)\left(g_x^2+g_t^2\right)g_{tt},\hfill \\ {\mathcal{G}}_7\hfill & =\hfill & \left(\left({\displaystyle \frac{5g_t^4}{6}}-{\displaystyle \frac{3g_x^4}{2}}\right)g_{xx}^2+\left(-{\displaystyle \frac{10g_t^3{g}_x}{3}}-6g_t{g}_x^3\right)g_{tx}{g}_{xx}+\left(g_t^4-{\displaystyle \frac{2g_t^2{g}_x^2}{3}}+g_x^4\right)g_{tx}^2+{\left(g_x^2+g_t^2\right)}^3\right)\left(g_x^2+g_t^2\right).\hfill \end{array}\right\}$$

(12)

The values of the set of Equation (12) appearing in Equation (11) underscore the considerable complexity of the expression of $u_2(x,t)$.

Analogously, at level $j=3$, we derive an explicit expression in the form of $u_3$; however, its length prevents direct presentation here. But at level $j=4$

$$u_4(x,t)=u_4(x,t).$$

(13)

Thus, it is verified that resonance at value $j=4$ occurs arbitrarily about the manifold, so $u_4(x,t)$ is an arbitrary function which fulfills the CCs. Consequently, Equation (1) is adjudged Painlevé-integrable.

3. Lie Symmetry Analysis (LSA) and Infinitesimal Generators of Equation (1)

In this section, our aim is to apply LSA on the KFG equation. The general algorithm for the LSA for PDE’s solution is discussed in [56]. Initially, we considered the Lie group of transformations with infinitesimal parameter ($\epsilon$) acting on independent and dependent variables for Equation (1) as follows:

$$\left.\begin{array}{c}{t}^{*}=t+\epsilon \tau (x,t,u)+O\left({\epsilon }^2\right),\hfill \\ x^{*}=x+\epsilon \xi (x,t,u)+O\left({\epsilon }^2\right),\hfill \\ u^{*}=u+\epsilon \varphi (x,t,u)+O\left({\epsilon }^2\right).\hfill \end{array}\right\}$$

(14)

where $\epsilon <1$ is a small parameter, with $\tau$, $\xi ,$ and $\varphi$ as the infinitesimals of the transformation depending on the x, t, and u in Equation (14), which are to be found. The corresponding vector field associated with the above group of transformations will be enlisted as

$$\mathcal{J}=\tau {\displaystyle \frac{\partial }{\partial t}}+\xi {\displaystyle \frac{\partial }{\partial x}}+\varphi {\displaystyle \frac{\partial }{\partial u}}.$$

(15)

The symmetry group of Equation (1) is generated by the vector field of the form (15) by applying a second prolongation to Equation (1), written as

$${\mathcal{J}}^{\left[2\right]}=\mathcal{J}+{\varphi }^t{\displaystyle \frac{\partial }{\partial u_t}}+{\varphi }^{tt}{\displaystyle \frac{\partial }{\partial u_{tt}}}+{\varphi }^x{\displaystyle \frac{\partial }{\partial u_x}}+{\varphi }^{xx}{\displaystyle \frac{\partial }{\partial u_{xx}}}+{\varphi }^{xt}{\displaystyle \frac{\partial }{\partial u_{xt}}}.$$

(16)

where ${\varphi }^t$, ${\varphi }^{tt}$, ${\varphi }^x$, ${\varphi }^{xx}$, and ${\varphi }^{xt}$ are the coefficients of ${\mathcal{J}}^{\left[2\right]}$ called extended infinitesimals needing to be solved. The values of these coefficients are given as

$$\left.\begin{array}{c}{\varphi }^t={\mathcal{D}}_t\varphi -u_x{\mathcal{D}}_t\xi -u_t{\mathcal{D}}_t\tau ,\hfill \\ {\varphi }^{tt}={\mathcal{D}}_t{\varphi }^t-u_{xt}{\mathcal{D}}_t\xi -u_{tt}{\mathcal{D}}_t\tau ,\hfill \\ {\varphi }^x={\mathcal{D}}_x\varphi -u_x{\mathcal{D}}_x\xi -u_t{\mathcal{D}}_x\tau ,\hfill \\ {\varphi }^{xx}={\mathcal{D}}_x{\varphi }^x-u_{xx}{\mathcal{D}}_x\xi -u_{xt}{\mathcal{D}}_x\tau ,\hfill \\ {\varphi }^{xt}={\mathcal{D}}_t{\varphi }^x-u_{xx}{\mathcal{D}}_t\xi -u_{xt}{\mathcal{D}}_t\tau .\hfill \end{array}\right\}$$

(17)

where ${\mathcal{D}}_t$ and ${\mathcal{D}}_x$ are the total derivatives, expressed as:

$$\left.\begin{array}{c}{\mathcal{D}}_t={\displaystyle \frac{\partial }{\partial t}}+u_t{\displaystyle \frac{\partial }{\partial u}}+u_{tt}{\displaystyle \frac{\partial }{\partial u_t}}+u_{xt}{\displaystyle \frac{\partial }{\partial u_x}},\hfill \\ {\mathcal{D}}_x={\displaystyle \frac{\partial }{\partial x}}+u_x{\displaystyle \frac{\partial }{\partial u}}+u_{xx}{\displaystyle \frac{\partial }{\partial u_x}}+u_{xt}{\displaystyle \frac{\partial }{\partial u_t}}.\hfill \end{array}\right\}$$

(18)

By applying the invariance condition

$${\mathcal{J}}^{\left[2\right]}{\left(\mathcal{M}\right)}_{\left|Equation\right(1)=0}=0.$$

(19)

where $\mathcal{M}=u_{tt}+\alpha u_{xx}+\beta u+\delta u^3.$ To obtain an overdetermined system of PDEs, we use Equation (19), and we find that coefficients $\xi (x,t,u)$, $\tau (x,t,u)$, and $\varphi (x,t,u)$ must fulfill the symmetry condition

$${\varphi }^{tt}+\alpha {\varphi }^{xx}+(\beta +3\delta u^2)\varphi =0.$$

(20)

On putting the values of appeared terms in Equation (20) from the expressions of (17) by utilizing (18) and setting the coefficients of various monomials in the partial derivative of u with respect to x and t to zero, we obtain an undetermined system of partial differential equations as follows

$$\left.\begin{array}{c}-\alpha {\tau }_{xx}-{\tau }_{tt}+2{\varphi }_{tu}=0,-\alpha {\xi }_{xx}+2\alpha {\varphi }_{xu}-{\xi }_{tt}=0,-2{\tau }_{tu}+{\varphi }_{uu}=0,{\varphi }_u-2{\tau }_t=0,\hfill \\ -2\alpha {\tau }_x-2{\xi }_t=0,-\alpha {\tau }_u=0,-2\alpha {\tau }_{xu}-2{\xi }_{tu}=0,-2\alpha {\xi }_{xu}+\alpha {\varphi }_{uu}=0,-{\tau }_{uu}=0,\hfill \\ -\alpha {\xi }_{uu}=0,-2\alpha {\xi }_x+\alpha {\varphi }_u=0,-\alpha {\tau }_{uu}=0,-2\alpha {\tau }_u=0,-3\alpha {\xi }_u=0,-{\xi }_u=0,-2{\xi }_u=0,\hfill \\ 3\delta \varphi =0,-3{\tau }_u=0,-{\xi }_{uu}=0,\alpha {\varphi }_{xx}+\beta \varphi +{\varphi }_{tt}=0.\hfill \end{array}\right\}$$

(21)

After solving system (21), it yields a symmetry group of Equation (1) in the form

$$\tau =C_2,\xi =C_{3}and\varphi =0.$$

(22)

Theorem 1.

The Generator of Equation (1). Equation (22) exhibits two-dimensional Lie algebra explained by the two generators as:

$${\mathcal{J}}_1={\displaystyle \frac{\partial }{\partial t}},{\mathcal{J}}_2={\displaystyle \frac{\partial }{\partial x}}.$$

(23)

Applying the definition of Lie Bracket/Commutator, denoted by $[{\mathcal{J}}_p,{\mathcal{J}}_q]$ = ${\mathcal{J}}_p{\mathcal{J}}_q-{\mathcal{J}}_q{\mathcal{J}}_p$, while expanding, we can write the commutators as:

$$\begin{array}{c}\hfill [{\mathcal{J}}_p,{\mathcal{J}}_q]=[{\mathcal{J}}_q,{\mathcal{J}}_p]=0,p,q=1,2.\end{array}$$

(24)

Theorem 2.

Assume ${\mathcal{A}}_{*}$ is the most general symmetry generator of Equation (1). We can construct a general linear combination of two generators, ${\mathcal{J}}_1$ and ${\mathcal{J}}_2$, which provides the following:

$${\mathcal{A}}_1={\mathcal{J}}_1{\mathcal{A}}_2={\mathcal{J}}_2{\mathcal{A}}_{*}={\mathcal{J}}_1+\omega {\mathcal{J}}_2,\omega \ne 0.$$

(25)

Proof. 

Let $\mathcal{J}$ be a random member such as ${\mathcal{J}}_1\epsilon {\mathcal{A}}_{*}$. Then, we may write the following;

$$\mathcal{J}={\kappa }_1{\mathcal{J}}_1+{\kappa }_2{\mathcal{J}}_2.$$

where ${\kappa }_1$ and ${\kappa }_2$ are free contestants. We investigate the possibility of eliminating one of the two free constants.

Set 1: ${\kappa }_1$ = 0 and ${\kappa }_2$ = 1, which lead to space-independent solutions.

$$\begin{array}{c}\hfill \mathcal{J}={\mathcal{J}}_2\\ \hfill {\mathcal{A}}_2={\mathcal{J}}_2.\end{array}$$

Set 2: ${\kappa }_1$ = 1 and ${\kappa }_2$ = 0, which lead to time-independent solutions.

$$\begin{array}{c}\hfill \mathcal{J}={\mathcal{J}}_1\\ \hfill {\mathcal{A}}_1={\mathcal{J}}_1.\end{array}$$

Set 3: ${\kappa }_1$ = 1 and ${\kappa }_2\ne$ 0, which lead to traveling wave type solutions.

$$\begin{array}{c}\hfill \mathcal{J}={\mathcal{J}}_1+{\kappa }_2{\mathcal{J}}_2\\ \hfill Let{\kappa }_2=\omega \ne 0,\\ \hfill {\mathcal{A}}_{*}={\mathcal{J}}_1+\omega {\mathcal{J}}_2.\end{array}$$

□

4. The Similarity Reduction for Equation (1)

To obtain reduction equations for the set of Equation (25), it is needed to resolve the associated characteristic equation, which is stated in general as follows:

$${\displaystyle \frac{dx}{\xi }}={\displaystyle \frac{dt}{\tau }}={\displaystyle \frac{du}{\varphi }}.$$

(26)

Case 1: For infinitesimal generator ${\mathcal{J}}_1$, we have the following characteristic equation

$${\displaystyle \frac{dx}{0}}={\displaystyle \frac{dt}{1}}={\displaystyle \frac{du}{0}}.$$

Our aim is to find invariants ${\mathcal{I}}_1$ and ${\mathcal{I}}_2$ such that;

$${\mathcal{J}}_1\left({\mathcal{I}}_1\right)=0,and{\mathcal{J}}_1\left({\mathcal{I}}_2\right)=0.$$

On solving the above characteristic equation, we get:

$$u={\mathcal{I}}_2=\mathcal{U}\left({\mathcal{I}}_1\right),{\mathcal{I}}_1=x.$$

(27)

The verification of invariance for ${\mathcal{J}}_1$:

$${\mathcal{J}}_1\left({\mathcal{I}}_1\right)={\displaystyle \frac{\partial }{\partial t}}\left(x\right)=0;{\mathcal{J}}_1\left({\mathcal{I}}_2\right)={\displaystyle \frac{\partial }{\partial t}}\left(u\right)=0whichholdstrue.$$

In the next section, we will use Equation (27) in Equation (1) to get the following ODE reduction of Equation (1):

$$\alpha {\mathcal{U}}^{″}+\beta \mathcal{U}+\delta {\mathcal{U}}^3=0.$$

(28)

where ′ shows a derivative with respect to x only which justifies the time-independent solutions’ statement of $\mathit{Set}\mathbf{2}$.

Case 2: For infinitesimal generator ${\mathcal{J}}_2$, we have the following characteristic equation

$${\displaystyle \frac{dx}{1}}={\displaystyle \frac{dt}{0}}={\displaystyle \frac{du}{0}}.$$

The solution of the above provides;

$$u=\mathcal{U}\left({\mathcal{I}}_1\right),{\mathcal{I}}_1=t.$$

(29)

It is obvious from Equation (29) the verification of invariance holds for ${\mathcal{J}}_2$. Using Equation (29) in Equation (1), we get the following ODE reduction of Equation (1):

$${\mathcal{U}}^{″}+\beta \mathcal{U}+\delta {\mathcal{U}}^3=0.$$

(30)

where ′ shows a derivative with respect to t only, which justifies the space-independent solutions statement of $\mathit{Set}\mathbf{1}$.

Case 3: For infinitesimal generator composed of a linear combination of ${\mathcal{J}}_1$ and ${\mathcal{J}}_2$ as in Equation (25), we have

$${\displaystyle \frac{dx}{\omega }}={\displaystyle \frac{dt}{1}}={\displaystyle \frac{du}{0}}.$$

Solution of the above provides;

$$u=\mathcal{U}\left({\mathcal{I}}_1\right),{\mathcal{I}}_1=x-\omega t.$$

(31)

It is obvious from Equation (29) that the verification of invariance holds for ${\mathcal{A}}^{**}$ too. Using Equation (31) in Equation (1), we get the following ODE reduction of Equation (1):

$$\delta {\mathcal{U}}^3+({\omega }^2+\alpha ){\mathcal{U}}^{″}+\beta \mathcal{U}=0.$$

(32)

where ′ indicates the derivative with respect to ${\mathcal{I}}_1({\mathcal{I}}_1=x-\omega t.)$ appearing in Equation (31) and hence $\mathit{Set}\mathbf{3}$’s statement justified.

5. The New Generalized Exponential Differential Rational Function Method (NGEDRFM)

In this portion, our interest is to apply the newly proposed NGEDRFM methodology [57] to Equation (32) to get a highly accurate variety of solutions. For this, we presume that the trial solution of Equation (32) adopts the form

$$\mathcal{U}\left({\mathcal{I}}_1\right)=F_0+\sum _{j=1}^S{F}_j{\left({\displaystyle \frac{d^j}{d{\mathcal{I}}_1^j}}\mathcal{Y}\left({\mathcal{I}}_1\right)\right)}^j+\sum _{j=1}^S{G}_j{\left({\displaystyle \frac{d^j}{d{\mathcal{I}}_1^j}}\mathcal{Y}\left({\mathcal{I}}_1\right)\right)}^{-j},$$

(33)

where the exponential rational function (ERF) $\mathcal{Y}\left({\mathcal{I}}_1\right)$ is expressed as

$$\mathcal{Y}\left({\mathcal{I}}_1\right)={\displaystyle \frac{p_{1}exp\left(s_1{\mathcal{I}}_1\right)+p_{2}exp\left(s_2{\mathcal{I}}_1\right)}{p_{3}exp(s_3{\mathcal{I}}_1)+p_{4}exp\left(s_4{\mathcal{I}}_1\right)}}.$$

(34)

To fix the ERF and to determine the constants $F_j,(j=0,1,2\dots S)$ and $G_j,(j=1,2\dots S)$, we choose the various values of parameters $p_i,s_i,(1\le i\le 4)$ in the coming fragments of this section. The required value S in Equation (33) is calculated by applying the homogeneous balancing principle to Equation (32).

After finding S, embedding Equation (33) along with Equation (34) into Equation (32) yields a polynomial equation. Then, equating various powers of appearing functions in this polynomial results in a system of algebraic equations. On careful calculations of this system via the computer software Mathematica, we get various coefficients and constants appearing in Equation (33), which finally provide us precise solutions to Equation (32).

5.1. Application of Novel Methodology

By the implementation of the homogeneous method to Equation (32), we get $S=1$, and by Equation (33), we have:

$$\mathcal{U}\left({\mathcal{I}}_1\right)=F_0+F_1\left({\displaystyle \frac{d\mathcal{Y}\left({\mathcal{I}}_1\right)}{d{\mathcal{I}}_1}}\right)+{\displaystyle \frac{G_1}{\left(\frac{d\mathcal{Y}\left({\mathcal{I}}_1\right)}{d{\mathcal{I}}_1}\right)}}.$$

(35)

To get the soliton profile for Equation (1), we look forward with the steps as described in the general description of NGEDRFM. By setting different values of $p_i,s_i,(1\le i\le 4)$ one by one and using Mathematica, we get a spectrum of solutions.

Family of Solutions

$\mathbf{Set}\mathbf{1}:\mathbf{For}[\mathbf{p}\mathbf{1},\mathbf{p}\mathbf{2},\mathbf{p}\mathbf{3},\mathbf{p}\mathbf{4}]=[\mathbf{1},-\mathbf{1},\mathbf{i},\mathbf{i}]\mathbf{and}[\mathbf{s}\mathbf{1},\mathbf{s}\mathbf{2},\mathbf{s}\mathbf{3},\mathbf{s}\mathbf{4}]=[\mathbf{i},-\mathbf{i},\mathbf{0},\mathbf{0}].$

The substitution of the above set yields the following ERF:

$$\mathcal{Y}\left({\mathcal{I}}_1\right)=sin\left({\mathcal{I}}_1\right),and{\mathcal{I}}_1=x-\omega t.$$

(36)

Considering the Equations (36) and (35), the solution of Equation (32) is derived as:

$\mathit{Case}\mathbf{1.1}:$

$$\beta =0;\delta =0;\alpha =-{\omega }^2;F_0\ne 0;F_1\ne 0;G_1\ne 0,$$

(37)

Using (37), the solution of Equation (32) is:

$$\mathcal{U}\left({\mathcal{I}}_1\right)=F_0+F_{1}cos\left({\mathcal{I}}_1\right)+G_{1}sec\left({\mathcal{I}}_1\right).$$

(38)

As a result, the newly generated solution of Equation (1) is

$$u_1(x,t)=F_0+F_{1}cos(x-\omega t)+G_{1}sec(x-\omega t),where\omega =\pm \sqrt{\alpha }.$$

(39)

$\mathbf{Set}\mathbf{2}:\mathbf{For}[{\mathbf{p}}_{\mathbf{1}},{\mathbf{p}}_{\mathbf{2}},{\mathbf{p}}_{\mathbf{3}},{\mathbf{p}}_{\mathbf{4}}]=[\mathbf{1},\mathbf{1},\mathbf{1},\mathbf{1}]\mathbf{and}[{\mathbf{s}}_{\mathbf{1}},{\mathbf{s}}_{\mathbf{2}},{\mathbf{s}}_{\mathbf{3}},{\mathbf{s}}_{\mathbf{4}}]=[\mathbf{i},-\mathbf{i},\mathbf{0},\mathbf{0}].$

The substitution of the above yields the following ERF:

$$\mathcal{Y}\left({\mathcal{I}}_1\right)=cos\left({\mathcal{I}}_1\right),and{\mathcal{I}}_1=x-\omega t.$$

(40)

Following the preceding technique, the following sets are found by embedding Equation (40) in Equation (35) and then using the result in Equation (32).

$\mathit{Case}\mathbf{2.1}:$

$$\beta =0;\delta =0;\alpha =-{\omega }^2;F_0\ne 0;F_1\ne 0;G_1\ne 0.$$

(41)

Using (41), the solution of Equation (32) is:

$$\mathcal{U}\left({\mathcal{I}}_1\right)=F_0-F_{1}sin\left({\mathcal{I}}_1\right)-G_{1}cosec\left({\mathcal{I}}_1\right).$$

(42)

As a result, the newly generated solution of Equation (1) is

$$u_2(x,t)=F_0-F_{1}sin(x-\omega t)-G_{1}cosec(x-\omega t),where\omega =\pm \sqrt{\alpha }.$$

(43)

$\mathbf{Set}\mathbf{3}:\mathbf{For}[{\mathbf{p}}_{\mathbf{1}},{\mathbf{p}}_{\mathbf{2}},{\mathbf{p}}_{\mathbf{3}},{\mathbf{p}}_{\mathbf{4}}]=[\mathbf{1},-\mathbf{1},\mathbf{i},\mathbf{i}]\mathbf{and}[{\mathbf{s}}_{\mathbf{1}},{\mathbf{s}}_{\mathbf{2}},{\mathbf{s}}_{\mathbf{3}},{\mathbf{s}}_{\mathbf{4}}]=[\mathbf{i},-\mathbf{i},\mathbf{i},-\mathbf{i}].$ The substitution of the above yields the following ERF:

$$\mathcal{Y}\left({\mathcal{I}}_1\right)=tan\left({\mathcal{I}}_1\right),and{\mathcal{I}}_1=x-\omega t.$$

(44)

By putting Equation (44) in Equation (35) and then using the result in Equation (32), we get the following:

$\mathit{Case}\mathbf{3.1}:$

$$\beta =0;\delta =0;\alpha =-{\omega }^2;F_0\ne 0;F_1\ne 0;G_1\ne 0.$$

(45)

Using (45), the solution of Equation (32) is:

$$\mathcal{U}\left({\mathcal{I}}_1\right)=F_0+F_{1}se{c}^2\left({\mathcal{I}}_1\right)+G_{1}co{s}^2\left({\mathcal{I}}_1\right).$$

(46)

As a result, the newly generated solution of Equation (1) is

$$u_3(x,t)=F_0+F_{1}se{c}^2(x-\omega t)+G_{1}co{s}^2(x-\omega t),where\omega =\pm \sqrt{\alpha }.$$

(47)

$\mathbf{Set}\mathbf{4}:\mathbf{For}[{\mathbf{p}}_{\mathbf{1}},{\mathbf{p}}_{\mathbf{2}},{\mathbf{p}}_{\mathbf{3}},{\mathbf{p}}_{\mathbf{4}}]=[\mathbf{i},\mathbf{i},\mathbf{1},-\mathbf{1}]\mathbf{and}[{\mathbf{s}}_{\mathbf{1}},{\mathbf{s}}_{\mathbf{2}},{\mathbf{s}}_{\mathbf{3}},{\mathbf{s}}_{\mathbf{4}}]=[\mathbf{i},-\mathbf{i},\mathbf{i},-\mathbf{i}].$ The above yields the following ERF:

$$\mathcal{Y}\left({\mathcal{I}}_1\right)=cot\left({\mathcal{I}}_1\right),and{\mathcal{I}}_1=x-\omega t.$$

(48)

Using Equation (48) along with Equation (35) and then using the result in Equation (32), we get the following solution:

$\mathit{Case}\mathbf{4.1}:$

$$\beta =0;\delta =0;\alpha =-{\omega }^2;F_0\ne 0;F_1\ne 0;G_1\ne 0.$$

(49)

Using (49), the solution of Equation (32) is:

$$\mathcal{U}\left({\mathcal{I}}_1\right)=F_0-F_{1}cose{c}^2\left({\mathcal{I}}_1\right)-G_{1}si{n}^2\left({\mathcal{I}}_1\right).$$

(50)

As a result, the newly generated solution of Equation (1) is

$$u_4(x,t)=F_0-F_{1}cose{c}^2(x-\omega t)-G_{1}si{n}^2(x-\omega t),where\omega =\pm \sqrt{\alpha }.$$

(51)

$\mathbf{Set}\mathbf{5}:\mathbf{For}[{\mathbf{p}}_{\mathbf{1}},{\mathbf{p}}_{\mathbf{2}},{\mathbf{p}}_{\mathbf{3}},{\mathbf{p}}_{\mathbf{4}}]=[\mathbf{i},-\mathbf{i},\mathbf{i},\mathbf{i}]\mathbf{and}[{\mathbf{s}}_{\mathbf{1}},{\mathbf{s}}_{\mathbf{2}},{\mathbf{s}}_{\mathbf{3}},{\mathbf{s}}_{\mathbf{4}}]=[\mathbf{1},-\mathbf{1},\mathbf{0},\mathbf{0}].$ The above yields the following ERF:

$$\mathcal{Y}\left({\mathcal{I}}_1\right)=sinh\left({\mathcal{I}}_1\right),and{\mathcal{I}}_1=x-\omega t.$$

(52)

On embedding Equation (52) into Equation (35), we get:

$\mathit{Case}\mathbf{5.1}:$

$$\beta =0;\delta =0;\alpha =-{\omega }^2;F_0\ne 0;F_1\ne 0;G_1\ne 0.$$

(53)

Using (53), the solution of Equation (32) is:

$$\mathcal{U}\left({\mathcal{I}}_1\right)=F_0+F_{1}cosh\left({\mathcal{I}}_1\right)+G_{1}sech\left({\mathcal{I}}_1\right).$$

(54)

As a result, the newly generated solution of Equation (1) is

$$u_5(x,t)=F_0+F_{1}cosh(x-\omega t)+G_{1}sech(x-\omega t),where\omega =\pm \sqrt{\alpha }.$$

(55)

$\mathbf{Set}\mathbf{6}:\mathbf{For}[{\mathbf{p}}_{\mathbf{1}},{\mathbf{p}}_{\mathbf{2}},{\mathbf{p}}_{\mathbf{3}},{\mathbf{p}}_{\mathbf{4}}]=[\mathbf{i},\mathbf{i},\mathbf{i},\mathbf{i}]\mathbf{and}[{\mathbf{s}}_{\mathbf{1}},{\mathbf{s}}_{\mathbf{2}},{\mathbf{s}}_{\mathbf{3}},{\mathbf{s}}_{\mathbf{4}}]=[\mathbf{1},-\mathbf{1},\mathbf{0},\mathbf{0}].$

The above yields the following ERF:

$$\mathcal{Y}\left({\mathcal{I}}_1\right)=cosh\left({\mathcal{I}}_1\right),and{\mathcal{I}}_1=x-\omega t.$$

(56)

Using Equations (56) and (35) and then using the result in Equation (32), we get the following:

$\mathit{Case}\mathbf{6.1}:$

$$\beta =0;\delta =0;\alpha =-{\omega }^2;F_0\ne 0;F_1\ne 0;G_1\ne 0.$$

(57)

Using (57), the solution of Equation (32) is

$$\mathcal{U}\left({\mathcal{I}}_1\right)=F_0+F_{1}sinh\left({\mathcal{I}}_1\right)+G_{1}cosech\left({\mathcal{I}}_1\right).$$

(58)

As a result, the newly generated solution of Equation (1) is

$$u_6(x,t)=F_0+F_{1}sinh(x-\omega t)+G_{1}cosech(x-\omega t),where\omega =\pm \sqrt{\alpha }.$$

(59)

$\mathbf{Set}\mathbf{7}:\mathbf{For}[{\mathbf{p}}_{\mathbf{1}},{\mathbf{p}}_{\mathbf{2}},{\mathbf{p}}_{\mathbf{3}},{\mathbf{p}}_{\mathbf{4}}]=[\mathbf{i},-\mathbf{i},\mathbf{i},\mathbf{i}]\mathbf{and}[{\mathbf{s}}_{\mathbf{1}},{\mathbf{s}}_{\mathbf{2}},{\mathbf{s}}_{\mathbf{3}},{\mathbf{s}}_{\mathbf{4}}]=[\mathbf{1},-\mathbf{1},\mathbf{1},-\mathbf{1}].$

The above yields the following ERF:

$$\mathcal{Y}\left({\mathcal{I}}_1\right)=tanh\left({\mathcal{I}}_1\right),and{\mathcal{I}}_1=x-\omega t.$$

(60)

By using Equation (60) in Equation (35) and then using the result in Equation (32), we get the following:

$\mathit{Case}\mathbf{7.1}:$

$$\beta =0;\delta =0;\alpha =-{\omega }^2;F_0\ne 0;F_1\ne 0;G_1\ne 0.$$

(61)

Using (61), the solution of Equation (32) is:

$$\mathcal{U}\left({\mathcal{I}}_1\right)=F_0+F_{1}sec{h}^2\left({\mathcal{I}}_1\right)+G_{1}cos{h}^2\left({\mathcal{I}}_1\right).$$

(62)

As a result, the newly generated solution of Equation (1) is

$$u_7(x,t)=F_0+F_{1}sec{h}^2(x-\omega t)+G_{1}cos{h}^2(x-\omega t),where\omega =\pm \sqrt{\alpha }.$$

(63)

$\mathbf{Set}\mathbf{8}:\mathbf{For}[{\mathbf{p}}_{\mathbf{1}},{\mathbf{p}}_{\mathbf{2}},{\mathbf{p}}_{\mathbf{3}},{\mathbf{p}}_{\mathbf{4}}]=[\mathbf{1},\mathbf{1},\mathbf{1},-\mathbf{1}]\mathbf{and}[{\mathbf{s}}_{\mathbf{1}},{\mathbf{s}}_{\mathbf{2}},{\mathbf{s}}_{\mathbf{3}},{\mathbf{s}}_{\mathbf{4}}]=[\mathbf{1},-\mathbf{1},\mathbf{1},-\mathbf{1}].$

The above yields the following ERF:

$$\mathcal{Y}\left({\mathcal{I}}_1\right)=coth\left({\mathcal{I}}_1\right),and{\mathcal{I}}_1=x-\omega t.$$

(64)

Using Equations (64) and (35) and then using the result in Equation (32), we get the following:

$\mathit{Case}\mathbf{8.1}:$

$$\beta =0;\delta =0;\alpha =-{\omega }^2;F_0\ne 0;F_1\ne 0;G_1\ne 0.$$

(65)

Using (65), the solution of Equation (32) is:

$$\mathcal{U}\left({\mathcal{I}}_1\right)=F_0-F_{1}cosec{h}^2\left({\mathcal{I}}_1\right)-G_{1}sin{h}^2\left({\mathcal{I}}_1\right).$$

(66)

As a result, the newly generated solution of Equation (1) is

$$u_8(x,t)=F_0-F_{1}cosec{h}^2(x-\omega t)-G_{1}sin{h}^2(x-\omega t),where\omega =\pm \sqrt{\alpha }.$$

(67)

6. Graphical Interpretation

In this section, we perform a graphical study of the soliton solutions derived for the KFG equation using the NGEDRFM. For this, a detailed summary of the parameter values is listed in Table 1 below. The real, imaginary, and finally absolute parts of each solution are explored separately through 3D, 2D, and contour plots, as our solutions consist of trigonometric functions, and these functions have further expansions in terms of exponential functions, which may involve real and imaginary parts. The real components of each solution show how shape and polarity change with space and time and how they change with the real axis. Meanwhile, the imaginary components of each solution show similar localized peaks with the phase shift $\pi /2$ as compared to the real parts of the solutions. The absolute values involve both real and imaginary parts of the respective solutions, which represent the intensity or the physical amplitude of the respective soliton waves. These plots Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show multi-peakons, which are multi-soliton solutions, and they are of significant importance, as these are observed in many physical phenomena, such as in wave dynamics in studying shallow water waves, in nonlinear optical dynamics, etc.

Table 1. Parameter values for the graphical explanation of the solutions of the KFG equation.

Figure	Solution	Parameter Values
Figure 1	$u_1(x,t)$	$\beta =0,\alpha =-0.5929,\delta =0,F_0=-0.3i,F_1=-0.01i,G_1=-0.1i$, $\omega =-0.77i,{\mathcal{I}}_1=x-\omega t$.
Figure 2	$u_2(x,t)$	$\beta =0,\alpha =-0.01,\delta =0,F_0=0.2i,F_1=0.5,G_1=0.5i,$$\omega =-0.1i,{\mathcal{I}}_1=x-\omega t$.
Figure 3	$u_3(x,t)$	$\beta =0,\alpha =1,\delta =0,F_0=0,F_1=-0.03i,G_1=-0.01i$, $\omega =-i,{\mathcal{I}}_1=x-\omega t$.
Figure 4	$u_4(x,t)$	$\beta =0,\alpha =2.25,\delta =0,F_0=0,F_1=-0.03i,G_1=-0.0001i,$$\omega =-1.5i,{\mathcal{I}}_1=x-\omega t$.
Figure 5	$u_5(x,t)$	$\beta =0,\alpha =6.25,\delta =0,F_0=0.5,F_1=-0.03i,G_1=-1i,$$\omega =-2.5i,{\mathcal{I}}_1=x-\omega t$.
Figure 6	$u_6(x,t)$	$\beta =0,\alpha =6.25,\delta =0,F_0=0.5,F_1=-0.03i,G_1=-1i,$$\omega =-2.5i,{\mathcal{I}}_1=x-\omega t$.
Figure 7	$u_7(x,t)$	$\beta =0,\alpha =12.25,\delta =0,F_0=0.5,F_1=-0.003i,G_1=0.0001i,$$\omega =-3.5i,{\mathcal{I}}_1=x-\omega t$.
Figure 8	$u_8(x,t)$	$\beta =0,\alpha =0.25,\delta =0,F_0=i,F_1=0.005i,G_1=-0.005i,$$\omega =0.5i,{\mathcal{I}}_1=x-\omega t$.

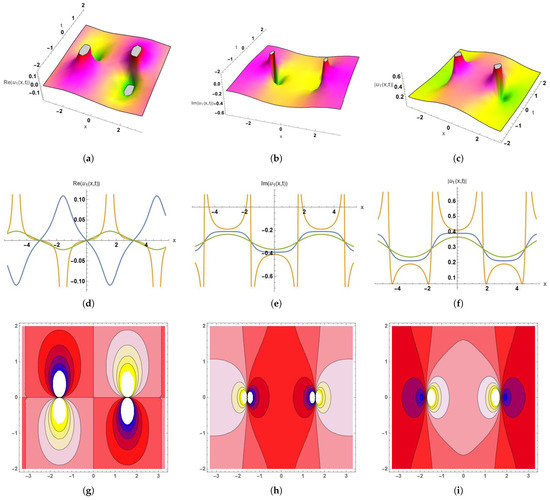
Figure 1. Dynamic graphical visualization of the obtained solution (39), (a–c) 3D surface plot of the real part, imaginary part, and absolute part of $u_1(x,t)$, (d–f) 2D surface plot of the real part, imaginary part, and absolute part of $u_1(x,t)$, (g–i) contour plots of the real part, imaginary part, and absolute part of $u_1(x,t)$ with the parameters $\beta =0,\alpha =-0.5929,\delta =0,F_0=-0.3i,F_1=-0.01i,G_1=-0.1i,\omega =-0.77i,{\mathcal{I}}_1=x-\omega t$. (a) 3D Plot-Re($u_1(x,t)$), with $-3.3\le x\le 3.3$, and $-2\le t\le 2$. (b) 3D Plot-Im($u_1(x,t)$), with $-3.3\le x\le 3.3$, and $-2\le t\le 2$. (c) 3D Plot-$|u_1(x,t)|$, with $-3.3\le x\le 3.3$, and $-2\le t\le 2$. (d) 2D Plot- Re($u_1(x,t)$). Here, the blue curve occurs at t = −1, orange at t = 0.1, and green at t = 2, with $-5.3\le x\le 5.3$. (e) 2D Plot-Im($u_1(x,t)$). Here, the blue curve occurs at t = −1, orange at t = 0.1, and green at t = 2, with $-5.3\le x\le 5.3$. (f) 2D Plot-$|u_1(x,t)|$. Here, the blue curve occurs at t = −1, orange at t = 0.1, and green at t = 2, with $-5.3\le x\le 5.3$. (g) Contour Plot-Re($u_1(x,t)$), with $-3.3\le x\le 3.3$, and $-2\le t\le 2$. (h) Contour Plot-Im($u_1(x,t)$), with $-3.3\le x\le 3.3$, and $-2\le t\le 2$. (i) Contour Plot-$|u_1(x,t)|$, with $-3.3\le x\le 3.3$, and $-2\le t\le 2$.

Figure 2. Dynamic graphical visualization of the obtained solution (43), (a–c) 3D surface plot of the real part, imaginary part, and absolute part of $u_2(x,t)$, (d–f) 2D surface plot of the real part, imaginary part, and absolute part of $u_2(x,t)$, (g–i) contour plots of the real part, imaginary part, and absolute part of $u_2(x,t)$ with the parameters $\beta =0,\alpha =-0.01,\delta =0,F_0=0.2i,F_1=0.5,G_1=0.5i,\omega =-0.1i,{\mathcal{I}}_1=x-\omega t$. (a) 3D Plot-Re($u_2(x,t)$), with $-0.001\le x\le 0.001$, and $-0.1\le t\le 0.1$. (b) 3D Plot-Im($u_2(x,t)$), with $-0.001\le x\le 0.001$, and $-0.1\le t\le 0.1$. (c) 3D Plot-$|u_2(x,t)|$, with $-0.001\le x\le 0.001$, and $-0.1\le t\le 0.1$. (d) 2D Plot-Re($u_2(x,t)$), Here, the blue curve occurs at t = −1, orange at t = 0.1, and green at t = 1, with $-5\le x\le 5$. (e) 2D Plot-Im($u_2(x,t)$), Here, the blue curve occurs at t = −1, orange at t = 0, and green at t = 2, with $-5\le x\le 5$. (f) 2D Plot-$|u_2(x,t)|$, Here, the blue curve occurs at t = −1, orange at t = 0, and green at t = 2, with $-5\le x\le 5$. (g) Contour Plot-Re($u_2(x,t)$), with $-4\le x\le 4$, and $-5\le t\le 5$. (h) Contour Plot-Im($u_2(x,t)$), with $-4\le x\le 4$, and $-5\le t\le 5$. (i) Contour Plot-$|u_2(x,t)|$, with $-4\le x\le 4$, and $-5\le t\le 5$.

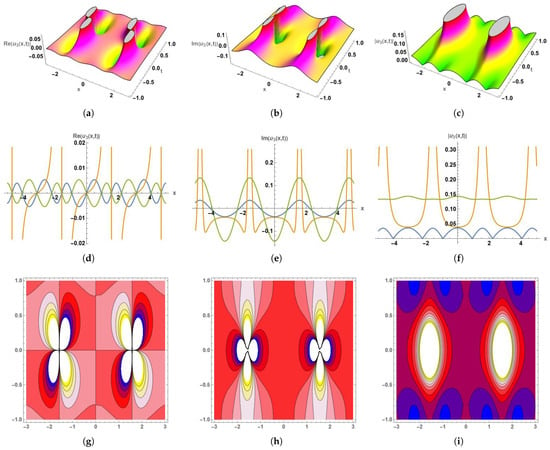
Figure 3. Dynamic graphical visualization of the obtained solution (47), (a–c) 3D surface plot of the real part, imaginary part, and absolute part of $u_3(x,t)$, (d–f) 2D surface plot of the real part, imaginary part, and absolute part of $u_3(x,t)$, (g–i) contour plots of the real part, imaginary part, and absolute part of $u_3(x,t)$ with the parameter values $\beta =0,\alpha =1,\delta =0,F_0=0,F_1=-0.03i,G_1=-0.01i,\omega =-i,{\mathcal{I}}_1=x-\omega t$. (a) 3D Plot-Re($u_3(x,t)$), with $-3\le x\le 3$, and $-1\le t\le 1$. (b) 3D Plot-Im($u_3(x,t)$), with $-3\le x\le 3$, and $-1\le t\le 1$. (c) 3D Plot-$|u_3(x,t)|$, with $-3\le x\le 3$, and $-1\le t\le 1$. (d) 2D Plot-Re($u_3(x,t)$), Here, the blue curve occurs at t = −1, orange at t = 0.1, and green at t = 1, with $-5\le x\le 5$. (e) 2D Plot-Im($u_3(x,t)$), Here, the blue curve occurs at t = −1, orange at t = 0.2, and green at t = 2, with $-5\le x\le 5$. (f) 2D Plot-$|u_3(x,t)|$, Here, the blue curve occurs at t = −1, orange at t = 0.2, and green at t = 2, with $-5\le x\le 5$. (g) Contour Plot-Re($u_3(x,t)$), with $-3\le x\le 3$, and $-1\le t\le 1$. (h) Contour Plot-Im($u_3(x,t)$), with $-3\le x\le 3$, and $-1\le t\le 1$. (i) Contour Plot-$|u_3(x,t)|$, with $-3\le x\le 3$, and $-1\le t\le 1$.

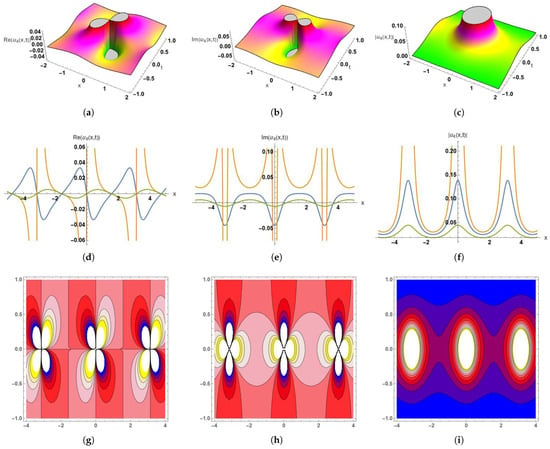
Figure 4. Dynamic graphical visualization of the obtained solution (51), (a–c) 3D surface plot of the real part, imaginary part, and absolute part of $u_4(x,t)$, (d–f) 2D surface plot of the real part, imaginary part, and absolute part of $u_4(x,t)$, (g–i) contour plots of the real part, imaginary part, and absolute part of $u_4(x,t)$ with the parameter values $\beta =0,\alpha =2.25,\delta =0,F_0=0,F_1=-0.03i,G_1=-0.0001i,\omega =-1.5i,{\mathcal{I}}_1=x-\omega t$. (a) 3D Plot-Re($u_4(x,t)$), with $-2\le x\le 2$, and $-1\le t\le 1$. (b) 3D Plot-Im($u_4(x,t)$), with $-2\le x\le 2$, and $-1\le t\le 1$). (c) 3D Plot-$|u_4(x,t)|$, with $-2\le x\le 2$, and $-1\le t\le 1$. (d) 2D Plot-Re($u_4(x,t)$), Here, the blue curve occurs at t = −0.5, orange at t = 0.1, and green at t = 1, with $-5\le x\le 5$. (e) 2D Plot-Im($u_4(x,t)$), Here, the blue curve occurs at t = −0.5, orange at t = 0.1, and green at t = 1, with $-5\le x\le 5$. (f) 2D Plot-$|u_4(x,t)|$, Here, the blue curve occurs at t = −0.3, orange at t = 0, and green at t = 0.5, with $-5\le x\le 5$. (g) Contour Plot-Re($u_4(x,t)$), with $-4\le x\le 4$, and $-1\le t\le 1.$ (h) Contour Plot-Im($u_4(x,t)$), with $-4\le x\le 4$, and $-1\le t\le 1.$ (i) Contour Plot-$|u_4(x,t)|$, with $-4\le x\le 4$, and $-1\le t\le 1$.

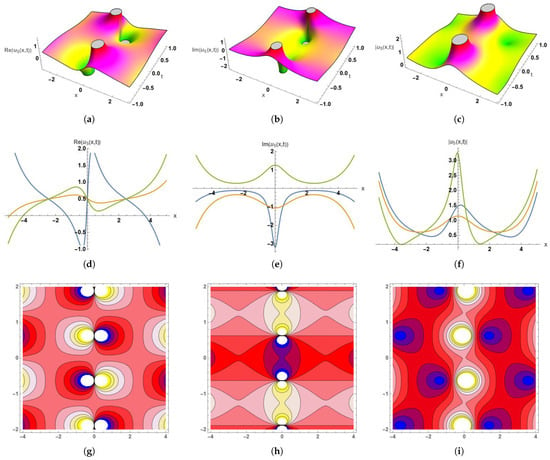
Figure 5. Dynamic graphical visualization of the obtained solution (55), gives bright soliton solutions; (a–c) 3D surface plot of the real part, imaginary part, and absolute part of $u_5(x,t)$, (d–f) 2D surface plot of the real part, imaginary part, and absolute part of $u_5(x,t)$, (g–i) contour plots of the real part, imaginary part, and absolute part of $u_5(x,t)$ with the parameter values $\beta =0,\alpha =6.25,\delta =0,F_0=0.5,F_1=-0.03i,G_1=-1i,\omega =-2.5i,{\mathcal{I}}_1=x-\omega t$. (a) 3D Plot-Re($u_5(x,t)$), with $-3\le x\le 3$, and $-1\le t\le 1$). (b) 3D Plot-Im($u_5(x,t)$), with $-3\le x\le 3$, and $-1\le t\le 1$). (c) 3D Plot-$|u_5(x,t)|$, with $-3\le x\le 3$, and $-1\le t\le 1$. (d) 2D Plot-Re($u_5(x,t)$), Here, the blue curve occurs at t = −0.5, orange at t = 0.1, and green at t = 1, with $-5\le x\le 5$. (e) 2D Plot-Im($u_5(x,t)$), Here, the blue curve occurs at t = −0.5, orange at t = 0.1, and green at t = 1, with $-5\le x\le 5$. (f) 2D Plot-$|u_5(x,t)|$, Here, the blue curve occurs at t = −0.3, orange at t = 0, and green at t = 0.5, with $-5\le x\le 5$. (g) Contour Plot-Re($u_5(x,t)$), with $-4\le x\le 4$, and $-2\le t\le 2.$ (h) Contour Plot-Im($u_5(x,t)$), with $-4\le x\le 4$, and $-2\le t\le 2.$ (i) Contour Plot-$|u_5(x,t)|$, with $-4\le x\le 4$, and $-2\le t\le 2$.

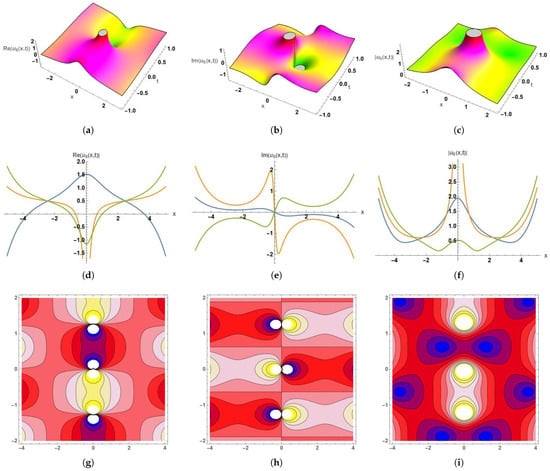
Figure 6. Dynamic graphical visualization of the obtained solution (59), gives bright soliton solutions; (a–c) 3D surface plot of the real part, imaginary part, and absolute part of $u_6(x,t)$, (d–f) 2D surface plot of the real part, imaginary part, and absolute part of $u_6(x,t)$, (g–i) contour plots of the real part, imaginary part, and absolute part of $u_6(x,t)$ with the parameter values $\beta =0,\alpha =6.25,\delta =0,F_0=0.5,F_1=-0.03i,G_1=-1i,\omega =-2.5i,{\mathcal{I}}_1=x-\omega t$. (a) 3D Plot-Re($u_6(x,t)$), with $-3\le x\le 3$, and $-1\le t\le 1$. (b) 3D Plot-Im($u_6(x,t)$), with $-3\le x\le 3$, and $-1\le t\le 1$. (c) 3D Plot-$|u_6(x,t)|$, with $-3\le x\le 3$, and $-1\le t\le 1$. (d) 2D Plot-Re($u_6(x,t)$), Here, the blue curve occurs at t = −0.5, orange at t = 0.1, and green at t = 1, with $-5\le x\le 5$. (e) 2D Plot-Im($u_6(x,t)$), Here, the blue curve occurs at t = −0.5, orange at t = 0.1, and green at t = 1, with $-5\le x\le 5$. (f) 2D Plot-$|u_6(x,t)|$, Here, the blue curve occurs at t = −0.3, orange at t = 0, and green at t = 0.5, with $-5\le x\le 5$. (g) Contour Plot-Re($u_6(x,t)$), with $-4\le x\le 4$, and $-1\le t\le 1.$ (h) Contour Plot-Im($u_6(x,t)$), with $-4\le x\le 4$, and $-1\le t\le 1.$ (i) Contour Plot-$|u_6(x,t)|$, with $-4\le x\le 4$, and $-1\le t\le 1$.

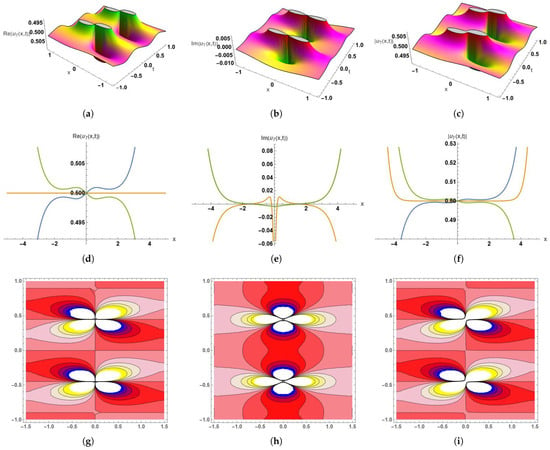
Figure 7. Dynamic graphical visualization of the obtained solution (63), (a–c) 3D surface plot of the real part, imaginary part, and absolute part of $u_7(x,t)$, (d–f) 2D surface plot of the real part, imaginary part, and absolute part of $u_7(x,t)$, (g–i) contour plots of the real part, imaginary part, and absolute part of $u_7(x,t)$ with the parameter values $\beta =0,\alpha =12.25,\delta =0,F_0=0.5,F_1=-0.003i,G_1=0.0001i,\omega =-3.5i,{\mathcal{I}}_1=x-\omega t$. (a) 3D Plot-Re($u_7(x,t)$), with $-1.2\le x\le 1.2$, and $-1\le t\le 1$.) (b) 3D Plot-Im($u_7(x,t)$), with $-1.2\le x\le 1.2$, and $-1\le t\le 1$. (c) 3D Plot-$|u_7(x,t)|$, with $-1.2\le x\le 1.2$, and $-1\le t\le 1$. (d) 2D Plot-Re($u_7(x,t)$), Here, the blue curve occurs at t = −1, orange at t = 0, and green at t = 1, with $-5\le x\le 5$. (e) 2D Plot-Im($u_7(x,t)$), Here, the blue curve occurs at t = −1, orange at t = 0.5, and green at t = 1, with $-5\le x\le 5$. (f) 2D Plot-$|u_7(x,t)|$, Here, the blue curve occurs at t = −1, orange at t = 0, and green at t = 1, with $-5\le x\le 5$. (g) Contour Plot-Re($u_7(x,t)$), with $-1.5\le x\le 1.5$, and $-1\le t\le 1.$ (h) Contour Plot-Im($u_7(x,t)$), with $-1.5\le x\le 1.5$, and $-1\le t\le 1.$ (i) Contour Plot-$|u_7(x,t)|$, with $-1.5\le x\le 1.5$, and $-1\le t\le 1$.

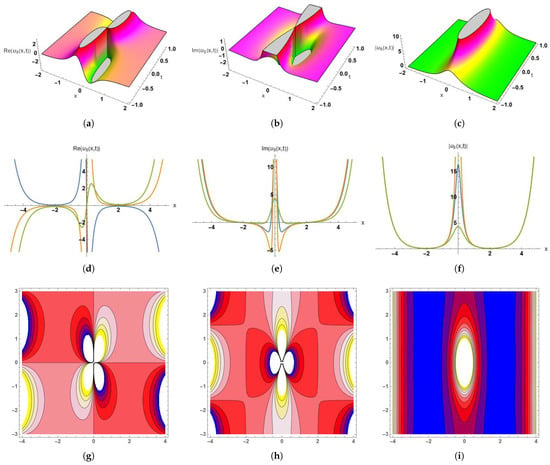
Figure 8. Dynamic graphical visualization of the obtained solution (67), (a–c) 3D surface plot of the real part, imaginary part, and absolute part of $u_8(x,t)$, (d–f) 2D surface plot of the real part, imaginary part, and absolute part of $u_8(x,t)$, (g–i) contour plots of the real part, imaginary part, and absolute part of $u_8(x,t)$ with the parameter values $\beta =0,\alpha =0.25,\delta =0,F_0=i,F_1=0.005i,G_1=-0.005i,\omega =0.5i,{\mathcal{I}}_1=x-\omega t$. (a) 3D Plot-Re($u_8(x,t)$), with $-2\le x\le 2$, and $-1\le t\le 1.$ (b) 3D Plot-Im($u_8(x,t)$), with $-2\le x\le 2$, and $-1\le t\le 1.$ (c) 3D Plot-$|u_8(x,t)|$, with $-2\le x\le 2$, and $-1\le t\le 1.$ (d) 2D Plot-Re($u_8(x,t)$), here, the blue curve occurs at t = −0.5, orange at t = 0.3, and green at t = 1, with $-5\le x\le 5$. (e) 2D Plot-Im($u_8(x,t)$), here, the blue curve occurs at t = −0.5, orange at t = 0.3, and green at t = 1, with $-5\le x\le 5$. (f) 2D Plot-$|u_8(x,t)|$, here, the blue curve occurs at t = −0.5, orange at t = 0.3, and green at t = 1, with $-5\le x\le 5$. (g) Contour Plot-Re($u_8(x,t)$), with $-4\le x\le 4$, and $-3\le t\le 3$. (h) Contour Plot-Im($u_8(x,t)$), with $-4\le x\le 4$, and $-3\le t\le 3$. (i) Contour Plot-$|u_8(x,t)|$, with $-4\le x\le 4$, and $-3\le t\le 3$.

These diverse structures, including the lump solitons and interactions visible in other figures, demonstrate the model’s rich nonlinear behavior, which has potential applications in understanding wave dynamics in fields like nonlinear optics and plasma physics.

7. Conclusions

In this manuscript, the (1+1)-dimensional nonlinear Klein–Fock–Gordon (KFG) partial differential equation has been studied using a three-layered analytical approach: the Painlevé integrability test, the classical symmetry analysis, and finally, the soliton profile solutions have been extracted using a novel technique. First, the Painlevé integrability of the model has been examined, and the KFG equation has successfully passed the full Painlevé test, establishing its analytic solvability. This shows that the model can be further discussed in the future, as its integrability has proved that the model is completely solvable by some integration schemes, and the new research could be conducted using this model in the future. Then, the infinitesimal symmetry generators have been derived by establishing a group of transformations using the infinitesimal parameters. Through the similarity variables, we have obtained the reduction equations in three categories: space-dependent, time-dependent, and finally (space+time)-dependent ordinary differential equations. The reduction equations in the forms of space-dependent only and time-dependent only may lack in explaining the complete dynamics of the KFG model because the space-dependent form may provide us a static or stationary solution, ignoring the time evolution part of the original partial differential equation. Similarly, the time-dependent form describes a timely evolved system where the field is constant at every point in the space, providing a spatially homogeneous solution. Therefore, that one ordinary differential equation has been further examined, which involved a similarity variable involving both the time- and space-dependent variables. Finally, by applying the NGEDRFM in the reduced equation, we have derived the new closed-form soliton solutions of the KFG model, including hyperbolic, trigonometric, and exponential solutions, by incorporating general arbitrary function selection, a novel contribution not documented for this model in prior works. To explicitly demonstrate the novelty and advantage of the NGEDRFM, we provide a comparative analysis of our solutions with the solutions obtained by established methods such as the F-expansion [44] and Sardar sub-equation [47] approaches, etc. in the Table 2.

Table 2. Comparison of solutions obtained by the NGEDRFM with known results from the literature.

Our Solutions	Known Solution from Literature	Advantages of Our Solution
Equation (39) $u_1(x,t)$	$u(x,t)=Asec\left(\xi \right)$ or $u(x,t)=Acos\left(\xi \right)$ By F-Expansion [44], Sardar sub-equation [47]	Our solution combines trigonometric and secant functions into a single, more complex structure not previously reported.
Equation (47) $u_3(x,t)$	$u(x,t)=Ase{c}^2\left(\xi \right)$ By Generalized Kudryashov [46]	We can recover known periodic solutions from Equation (47) as a special case ($F_0=G_1=0$), but our case offers a wider spectrum of solutions with the new arbitrary constants.
Equation (55) $u_5(x,t)$	$u(x,t)=Asech\left(\xi \right)$ bright soliton By Kudryashov [46], Auxiliary Equation [48]	Represents a novel combination of a bright soliton and a kink-type profile, enabling new wave interaction models.
Equation (63) $u_7(x,t)$	Not found as per the best of our knowledge	This specific multi-peakon and lump-soliton profile might not have been documented for the KFG equation in prior studies, as per the best of our knowledge.

We have visualized these analytical solutions through two-dimensional, three-dimensional, and contour plots by using Mathematica, revealing soliton-like pulses. These plots have shown interesting features in the solutions, like lumps, multi-peakon solitons, and interactions between solitons and waves. These solutions have wide-ranging applications, offering valuable insights into physical phenomena. For example, in quantum field theory, the solutions of this equation explain the interaction of particles within fields with a nonlinearity term. Similarly, it has wide use in engineering problems, mathematical modeling, and nonlinear dynamics. These findings can have practical implications in various real-world scenarios. Looking ahead, further exploration of the practical applications of these solutions in the mentioned fields presents an exciting avenue for future research. By continuing to investigate and apply these findings, we can unlock even greater potential for addressing complex problems and fostering innovation in diverse areas of research.