From Invariance to Symmetry Breaking in FIM-Aware Cooperative Heterogeneous Agent Networks

Abstract

We recast cooperative localization and scheduling in heterogeneous multi-agent systems through the lens of symmetry and symmetry breaking. On the geometric side, the Fisher Information Matrix (FIM) objective is invariant to rigid Euclidean transformations of the global frame, while its maximization admits symmetric optimal sensor formations; on the algorithmic side, heterogeneity and task constraints break permutation symmetry across agents, requiring policies that are sensitive to role asymmetries. We model communication as a random graph and quantify structural symmetry via topology metrics (average path length, clustering, betweenness) and graph automorphism-related indices, connecting these to estimation uncertainty. We then design a hybrid reward for reinforcement learning (RL) that is equivariant to agent relabeling within roles yet intentionally introduces asymmetry through distance/FIM terms to avoid degenerate symmetric configurations with poor observability. Simulations show that (i) symmetry-aware, FIM-optimized path planning reduces localization error versus symmetric but non-informative placements; and (ii) controlled symmetry breaking in policy learning improves robustness and data rate–reward trade-offs over baselines. Our results position symmetry/asymmetry as first-class design principles that unify estimation-theoretic invariances with learning-based coordination in complex heterogeneous networks. Under DDPG training, the total data rate (SDR) reaches $6.63\pm 0.97$ and the average reward per step (ARPS) is $-80.70\pm 6.94$, representing improvements of approximately $11.8\%$ over the baseline $(5.93\pm 3.51)$ and $11.1\%$ over SAC $(5.97\pm 2.66)$, respectively. The network’s mean shortest-path length is $L=1.721$, and the average betweenness centrality of the coordination nodes is ≈0.098. Moreover, the FIM-optimized path-planning strategy achieves the lowest localization error among all evaluated policies.

1. Introduction

With the increasing deployment of distributed intelligent systems across domains such as environmental monitoring, industrial logistics, and smart infrastructure, the challenges of cooperative execution and dynamic communication modeling in heterogeneous agent systems have attracted growing attention [1,2,3]. Beyond efficiency alone, these challenges are naturally framed through the lens of symmetry and symmetry breaking: on the geometric side, localization objectives based on the FIM enjoy invariance to rigid Euclidean motions; on the algorithmic side, agents of the same type should satisfy role-level permutation symmetry (exchangeability in decision rules), whereas heterogeneity and mission constraints break this symmetry; and on the structural side, the communication graph may exhibit structural symmetry (e.g., repeated local motifs or near-automorphisms) that shapes information flow and diffusion efficiency. Recent advances in graph neural networks (GNNs) and multi-agent reinforcement learning (MARL) have enabled more efficient process coordination and decentralized decision-making. For instance, Ratnabala et al. proposed HIPPO-MAT [4] and MAGNNET [5], which utilize graph embeddings to enhance coordination efficiency across agents with diverse capabilities. Goeckner and Ma further developed GNN-enhanced MARL frameworks and assignment networks tailored to distributed workload assignment [6,7]. However, in much of this literature the symmetry structure remains implicit: fixed or hand-crafted communication graphs can mask when symmetry (e.g., regular, highly clustered layouts) helps rapid dissemination versus when controlled symmetry breaking is required for better observability and identifiability. Consequently, many existing approaches assume fixed or hand-crafted communication graphs, limiting their scalability and flexibility in real-world systems where topology evolves dynamically due to heterogeneity in sensing, mobility, or resource availability [8,9].

Accurate localization is foundational to coordinated behavior in heterogeneous agent systems, supporting processes such as collaborative perception, spatial process assignment, and multi-agent scheduling. From an efficiency perspective, accurate localization enables optimized trajectory planning, avoids redundant sensing, and reduces energy consumption; from a communication perspective, spatial awareness facilitates dynamic topology formation and relay selection, thereby lowering latency and packet loss; from a safety and robustness perspective, localization errors can trigger collisions, task conflicts, or communication isolation. In missions such as search-and-rescue, surveillance, and distributed mapping, reliable localization is fundamental to task allocation and situational awareness.

Yet, discrepancies in sensing modalities, communication limitations, and environmental uncertainties across agents challenge the ability of traditional techniques to maintain both high localization fidelity and coordination efficiency [10,11]. FIM, a classical metric for quantifying the informativeness of observations, has been widely applied in cooperative localization under static or homogeneous network assumptions [12]. In applications ranging from wireless sensor arrays to environmental monitoring networks, FIM-based optimization has guided trajectory planning and sensor deployment to enhance estimation accuracy [13,14]. Geometrically, the FIM objective is invariant to rigid Euclidean motions of the global frame, but strictly symmetric sensor or agent layouts can yield poor observability; thus, practical designs often require controlled departures from symmetry to avoid degenerate configurations while preserving desirable invariances. While FIM maximization is theoretically aligned with uncertainty reduction, most existing approaches operate under fixed topologies or assume agent homogeneity, limiting their practicality in dynamic, heterogeneous systems where agents must make real-time decisions under partial observability [15]. In contrast, recent developments in Heterogeneous-Agent Reinforcement Learning (HARL) have shown promise in learning decentralized coordination strategies for agents with varying capabilities and perspectives [16]. However, few HARL frameworks have incorporated FIM-based objectives into the reward design to actively guide agents toward localization-aware behaviors [8]. This reveals a critical gap: how to embed FIM maximization into the reinforcement learning process to jointly optimize localization accuracy and activity scheduling within adaptive, information-constrained agent networks.

In heterogeneous intelligent agent networks, both communication topology and cooperative localization accuracy jointly determine system safety and system efficiency under complex, dynamic conditions. Random network models provide a versatile framework for capturing the diversity and uncertainty intrinsic to evolving communication structures while making explicit the role of structural symmetry. Notably, the average path length quantifies the efficiency of information dissemination across the network, the clustering coefficient reflects the capacity for local collaboration among agents [17], and the betweenness centrality measures the importance of individual nodes in facilitating network-wide connectivity [18]. Complementing these, symmetry-oriented proxies—such as the size of the graph automorphism group and the multiplicities of Laplacian/adjacency eigenvalues—characterize repeated motifs and regularities that affect diffusion, redundancy, and vulnerability. These structural properties have been shown to significantly influence message propagation and collective observation in multi-agent systems [19]; in particular, highly symmetric topologies can accelerate dissemination but also induce indistinguishable measurement geometries that degrade observability, motivating controlled departures from symmetry when optimizing localization-aware coordination.

Meanwhile, cooperative localization accuracy is commonly assessed using FIM-based metrics, which characterize the uncertainty in state estimation. Differences in localization error under varying network topologies underscore the critical role of structural connectivity—and, by extension, structural symmetry—in information fusion and error dynamics. However, most prior studies analyze either network topology or localization performance in isolation, motivating a need for frameworks that integrate both aspects to provide a comprehensive evaluation of multi-agent coordination.

To address these challenges, this work introduces a node–edge representation grounded in random network theory to model the communication and collaboration topologies of heterogeneous agent networks. By leveraging a random network generation mechanism, the framework captures potential connectivity and cooperation probabilities among diverse agents, while also accommodating structural symmetry and asymmetry that arise in practice. Compared with fixed or static adjacency schemes, this approach better reflects evolving communication characteristics under complex conditions, providing a realistic and flexible structural foundation for learning-based cooperative activity scheduling [16,20].

Building on this foundation, we integrate FIM maximization into heterogeneous multi-agent learning by designing a hybrid reward that preserves geometric invariance, respects within-role permutation symmetry, and introduces controlled symmetry breaking via distance/FIM terms to avoid degenerate symmetric layouts. The resulting objective balances localization accuracy during concurrent process execution and improves scheduling efficiency and system resilience in collaborative scenarios.

To systematically evaluate the trade-off between communication efficiency and localization fidelity, we develop a unified assessment framework that combines structural metrics from random network theory—including average path length, clustering coefficient, and betweenness centrality—with localization error measures, and, when relevant, symmetry proxies such as spectral multiplicities. This framework identifies when symmetric topologies aid diffusion and when symmetry breaking improves observability, enabling dynamic balancing of communication costs and estimation accuracy for robustness and generalization across evolving multi-activity environments [21,22,23]. In practical deployments, continuous monitoring of topology and localization performance supports real-time score updates and timely communication reconfiguration or path replanning, ensuring adaptive responses to disruptions or environmental changes [24]. Distinct from recent coordination approaches based on GNNs and MARL [4,5], our method departs both in its modeling assumptions and in its optimization objective. Rather than relying on learned message-passing architectures or a fixed communication graph, we explicitly instantiate the inter-agent topology using random network theory, leveraging structural randomness to capture communication uncertainty and role heterogeneity. In addition, by introducing a Fisher Information Matrix (FIM)-maximization criterion, we ground the objective in estimation theory with clear physical interpretability, which differentiates our framework from conventional policy-gradient or multi-agent value-based methods that focus solely on reward optimization.

The main contributions of this work are as follows:

• We propose a symmetry-informed node–edge representation grounded in random network theory to characterize evolving communication and collaboration topologies in heterogeneous agent networks, exposing structural symmetry and asymmetry via average path length, clustering, betweenness, and (when relevant) spectral-multiplicity proxies.
• We integrate a geometric invariance-preserving FIM objective into heterogeneous multi-agent coordination, leveraging its invariance to rigid motions while discouraging symmetric but low-observability layouts through principled spacing and information terms.
• We design a hybrid reward that respects within-rolefor permutation symmetry and introduces controlled symmetry breaking via distance/FIM components, enabling localization-aware scheduling with improved efficiency and robustness.
• We establish a unified evaluation that links network structure and information quality by combining random-network metrics (average path length, clustering coefficient, betweenness centrality) with localization error measures and symmetry proxies, quantifying when symmetry aids diffusion and when symmetry breaking improves observability and task performance.

2. Methodology

This section presents a unified optimization framework for cooperative decision making in heterogeneous intelligent agent networks, with its workflow illustrated in Figure 1. The framework is composed of three principal modules: (1) constructing a networked model of heterogeneous agent collaboration that reflects the complexities of real-world cooperative scenarios; (2) utilizing the inverse relationship between the determinant of FIM and localization uncertainty to inform optimal path planning, such that relative agent positioning reduces estimation error and supports high-precision situational awareness; and (3) applying RL to enable decentralized agents to autonomously adapt, coordinate, and cooperate under dynamic and uncertain conditions, thereby improving scheduling efficiency and system resilience.

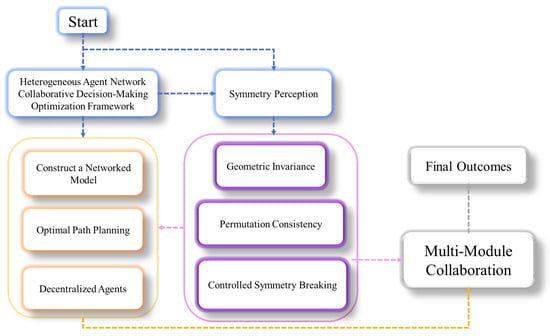
Figure 1. Workflow of the symmetry-aware optimization framework for collaborative decision-making in heterogeneous agent networks, integrating random-network topology modeling, FIM-based localization, and RL coordination.

In addition, the framework is symmetry-aware: the FIM objective preserves geometric invariance, policies maintain within-role permutation consistency, and we introduce controlled symmetry breaking to avoid degenerate but symmetric layouts that harm observability.

2.1. Network Model for Collaborative Processes

We model collaborative processes using a graph-theoretic network representation $F=(V,E)$, where V is the set of nodes and E is the set of edges; each edge in E represents an active communication or coordination link between a pair of nodes in V. In the heterogeneous agent network, each autonomous entity is represented as a node, and collaborative interactions are encoded as edges. An edge exists whenever two nodes can directly share information or coordinate actions. To expose structural symmetry, we later summarize F using L (average path length), C (clustering), betweenness, and (when useful) spectral multiplicities that capture repeated motifs or regularities.

Inspired by the OODA (Observe–Orient–Decide–Act) paradigm, activity entities are categorized into four functional classes: sensing nodes (e.g., environmental monitoring agents $M_1$ and spatial mapping agents $M_2$), coordination nodes (C), processing nodes (support $U_1$, transport $U_2$, coordination $U_3$), and target or goal nodes. This structure can be formalized as:

$$\left\{\begin{array}{c}C=\{C_1,C_2\}\hfill \\ M=\{M_1,M_2\}\hfill \\ U=\{U_1,U_2,U_3\}\hfill \end{array}\right.$$

(1)

Within each role (e.g., $U_1$ agents), operations are designed to be permutation-consistent so that relabeling same-type agents does not alter role-level behavior or decisions.

In collaborative scenarios, the agent network may include a small number of monitoring nodes and multiple spatial mapping nodes. These sensing agents ($M_1$ and $M_2$) jointly gather relevant environmental or situational data, which is relayed to the coordination node (C) for processing and assignment. The resulting process directives are then distributed within a specified time window to the processing nodes—$U_1$ (support), $U_2$ (transport), and $U_3$ (coordination)—which carry out their designated actions according to the centralized plan.

We assume the total number of nodes is N, where $N_C+N_{M_1}+N_{M_2}+N_{U_1}+N_{U_2}+N_{U_3}=N$. According to the typical composition of a collaborative agent network, the proportions of each node type—process allocation (C), ground sensing ($M_1$), spatial sensing ($M_2$), support execution ($U_1$), transport execution ($U_2$), and coordination execution ($U_3$)—are represented as $P_C$, $P_{M_1}$, $P_{M_2}$, $P_{U_1}$, $P_{U_2}$, and $P_{U_3}$, respectively is illustrated in Figure 2.

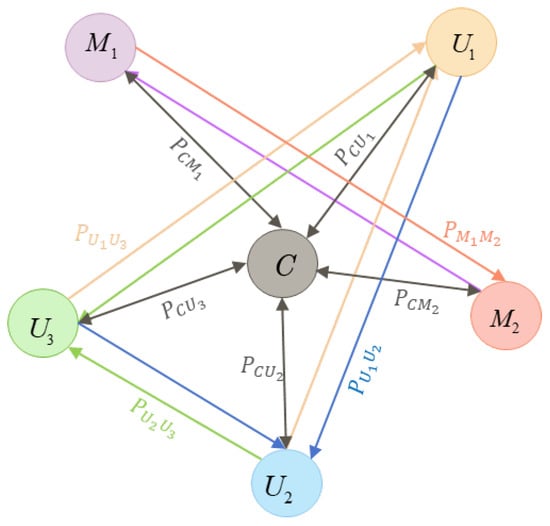
Figure 2. Network topology of a heterogeneous intelligent agent collaboration system.

The probabilities $P_{C{M}_1}$, $P_{C{M}_2}$, $P_{C{U}_1}$, $P_{C{U}_2}$, and $P_{C{U}_3}$ denote the likelihoods of establishing connections between the coordination node and other node types. For instance, $P_{C{M}_1}$ represents the connection probability between C and $M_1$, while $P_{C{U}_1}$ reflects that between C and $U_1$. $P_{M_1{U}_1}$ characterizes the collaboration capability between ground sensing and support processing nodes. Similarly, $P_{U_1{U}_2}$, $P_{U_1{U}_3}$, and $P_{U_2{U}_3}$ describe the probabilities of interconnections among processing nodes, capturing their cooperative execution and coordination potential. $P_{M_2{U}_3}$ specifies the likelihood of collaboration between spatial sensing and coordination nodes. To account for finite resource constraints, the degree of each node is bounded such that $K_i\le K_{\max }$ for all $i\in \{C,M_1,M_2,U_1,U_2,U_3\}$. Differentiated $p_{ij}$ across roles and the cap $K_{\max }$ serve as controlled symmetry-breaking mechanisms that prevent overly regular (symmetric) topologies when they hinder observability or load balancing.

The probabilities $P_{C{M}_1}$, $P_{C{M}_2}$, $P_{C{U}_1}$, $P_{C{U}_2}$, and $P_{C{U}_3}$ denote the likelihoods of establishing connections between the coordination node and other node types. For instance, $P_{C{M}_1}$ represents the connection probability between C and $M_1$, while $P_{C{U}_1}$ reflects that between C and $U_1$. $P_{M_1{U}_1}$ characterizes the collaboration capability between ground sensing and support processing nodes. Similarly, $P_{U_1{U}_2}$, $P_{U_1{U}_3}$, and $P_{U_2{U}_3}$ describe the probabilities of interconnections among processing nodes, capturing their cooperative execution and coordination potential. $P_{M_2{U}_3}$ specifies the likelihood of collaboration between spatial sensing and coordination nodes. To account for finite resource constraints, the degree of each node is bounded such that $K_i\le K_{\max }$ for all $i\in \{C,M_1,M_2,U_1,U_2,U_3\}$.

$$A.\mathrm{arcs}\left[i\right]\left[j\right]=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathrm{a}\mathrm{random}\mathrm{number}r<p_{ij},r\in (0,1)\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(2)

Using this stochastic connection rule, we construct the adjacency matrix A, which defines the network topology for collaborative processes. A representative schematic of the resulting agent network is illustrated in Figure 3. The inter-type connection probabilities (e.g., among C, $M_1$, $M_2$, $U_1$, etc.) were selected based on iterative simulation calibration to balance connectivity, load, and robustness under the target operating conditions.

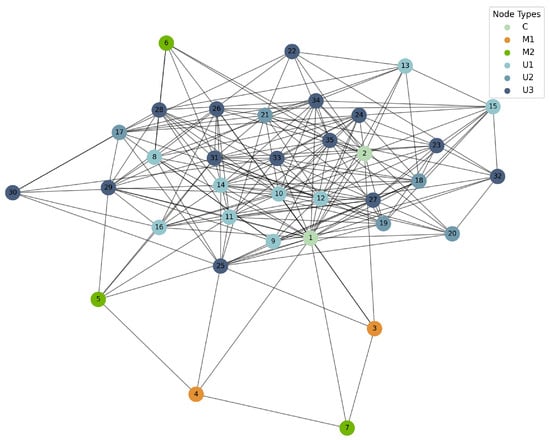
Figure 3. Network topology of a collaborative agent system generated via the stochastic adjacency matrix construction.

The stochastic adjacency mechanism in Equation (2) can be viewed as a role-aware extension of the classical Erdős–Rényi random graph $G(N,p)$ and the stochastic block model (SBM). Concretely, the heterogeneous link probabilities $\left\{p_{ij}\right\}$ correspond to inter-block connection probabilities in a block-structured adjacency matrix, where each block encodes the communication preference between node categories $\{C,M_1,M_2,U_1,U_2,U_3\}$. This modeling choice preserves analytical tractability while faithfully capturing real-world asymmetries in sensing, coordination, and actuation. From a theoretical perspective, the family of heterogeneous random graphs $\mathcal{G}\left(\left\{p_{ij}\right\}\right)$ satisfies a high-probability connectivity condition:

$$p_{min}\ge {\displaystyle \frac{lnN}{N}}⟹\mathbb{P}\left[\mathcal{G}\left(\left\{p_{ij}\right\}\right)\mathrm{is}\mathrm{connected}\right]\to 1(N\to \infty )$$

(3)

where $p_{min}$ denotes the minimum nonzero connection probability across all role pairs. This ensures that, despite random link fluctuations, a multi-role agent network remains connected with overwhelming probability, providing a robust topological substrate for distributed cooperation.

Moreover, the expected degree of node i is $\mathbb{E}\left[k_i\right]={\sum }_j{p}_{ij}$, and closed-form approximations yield the expected average path length and clustering coefficient [17]:

$$\mathbb{E}\left[L\right]\approx {\displaystyle \frac{lnN}{ln\left(\mathbb{E}\left[k\right]\right)}},\mathbb{E}\left[C\right]\approx {\displaystyle \frac{1}{N}}\sum _{i,j,k}{p}_{ij}{p}_{jk}{p}_{ki}$$

(4)

allowing structural efficiency and local cohesiveness to be assessed analytically under communication uncertainty.

Importantly, the random network interacts directly with FIM- and information-theoretic objectives. The system-level Fisher Information can be expressed as a function of the random adjacency:

$$J_{\mathrm{total}}\left(A\right)=\sum _{(i,j)\in E\left(A\right)}{J}_{ij}$$

(5)

where $J_{ij}$ quantifies the contribution of link $(i,j)$ to the joint information gain. Taking expectation over the random graph ensemble gives

$${\mathbb{E}}_{A\sim \mathcal{G}\left(\left\{p_{ij}\right\}\right)}\left[det{J}_{\mathrm{total}}\left(A\right)\right]$$

(6)

which characterizes the expected localization fidelity under stochastic connectivity. This establishes a theory-level bridge between topological randomness and estimation performance: larger mean degree and clustering generally increase $\mathbb{E}[det{J}_{\mathrm{total}}]$, whereas excessive symmetry (e.g., uniform $p_{ij}$) can reduce the rank of the FIM and degrade observability. Accordingly, the proposed random-graph formulation offers a principled and physically interpretable approach to modeling communication uncertainty, ensuring robustness and scalability in heterogeneous multi-agent coordination.

2.2. FIM-Optimized Cooperative Localization in Heterogeneous Agent Networks

Inspired by cooperative localization strategies in distributed agent systems, we consider a scenario where ground-based agents perform positioning using an Ultra-Short Baseline (USBL) system or analogous ranging technology. Let the coordinates of a coordination node C be $(x,y,z)$, and those of the m-th support node $U_1$ be $(x_m,y_m,z_m)$.

As illustrated in Figure 4, the coordination agents utilize a USBL (Ultra-Short Baseline) or analogous positioning system to localize support agents within the network. Assuming a uniform sensor array distribution on the coordination agent, the distances $O{X}_a=O{X}_b=O{Y}_a=O{Y}_b=d/2$, where d is the array spacing. The measurement model and the associated probability density function are given by:

$$\begin{array}{cc}\hfill p(Z,X)& =\prod _{m=1}^n{\displaystyle \frac{exp\left\{-\frac{1}{2}{\left[Z_m-g_m\left(X\right)\right]}^T{R}^{-1}\left[Z_m-g_m\left(X\right)\right]\right\}}{\sqrt{2\pi det\left(W\right)}}}\hfill \\ \hfill Z_m& =g_m\left(X\right)+{\mu }_m\hfill \\ \hfill L_m& =\sqrt{{(x_m-x)}^2+{(y_m-y)}^2+z_m^2}\hfill \end{array}$$

(7)

where the target state vector is $X={[x,y]}^T$, and $g_m\left(X\right)={[\Delta {\xi }_{x,m},\Delta {\xi }_{y,m}]}^T$ denotes the phase difference vector between receiving units. Here, $\Delta {\xi }_{x,m}={\displaystyle \frac{2\pi fd}{c{L}_m}}(x_m-x)$ and $\Delta {\xi }_{y,m}={\displaystyle \frac{2\pi fd}{c{L}_m}}(y_m-y)$, where c is the propagation speed (e.g., sound or radio), f is the signal frequency, ${\mu }_m$ denotes zero-mean Gaussian white noise, and $W={\sigma }^{2}I$ is the measurement noise covariance. By taking the second-order derivatives of the log-likelihood function, the FIM for the system is given by:

$$J_m=\left[\begin{array}{cc}-E\left[{\displaystyle \frac{{\partial }^{2}lnp(Z,X)}{\partial x^2}}\right]& -E\left[{\displaystyle \frac{{\partial }^{2}lnp(Z,X)}{\partial x\partial y}}\right]\\ -E\left[{\displaystyle \frac{{\partial }^{2}lnp(Z,X)}{\partial y\partial x}}\right]& -E\left[{\displaystyle \frac{{\partial }^{2}lnp(Z,X)}{\partial y^2}}\right]\end{array}\right]$$

(8)

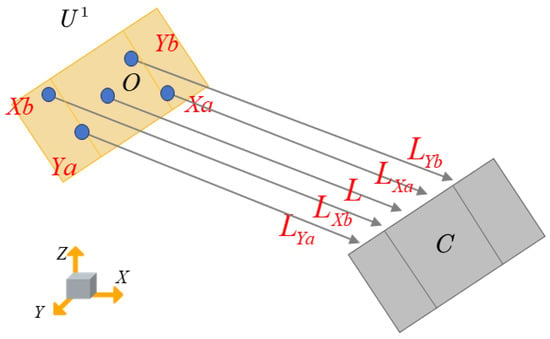
Figure 4. Schematic of cooperative localization: relative positioning of a support agent with respect to a coordination agent.

The FIM objective is invariant to rigid Euclidean motions of the global frame, but strictly symmetric formations can be stationary yet poorly observable. To mitigate these degeneracies while preserving desirable invariances, we pair FIM maximization with a mild spacing penalty over selected pairs $\mathcal{P}$:

$$\mathcal{S}\left(X\right)=\sum _{(i,j)\in \mathcal{P}}\varphi \left(\parallel x_i-x_j\parallel \right),{\varphi }^{\prime }(·)>0,{\varphi }^{″}(·)\ge 0$$

(9)

which discourages low-information symmetric layouts without altering the underlying rigid-motion invariance.

After analytical simplification, the determinant of the FIM can be expressed as:

$$\begin{array}{cc}\hfill det\left(J_m\right)& ={\left({\displaystyle \frac{4{\pi }^2{f}^2{d}^2}{{\sigma }^2{c}^2}}\right)}^2\left[3m{\displaystyle \frac{{sin}^2{\gamma }_0}{L_0^4}}+{\displaystyle \frac{{({sin}^4{\gamma }_0+1)}^2}{L_0^4}}\chi \right]\hfill \\ \hfill r_m& =argmax\left\{det\left(J_m\right)\right\}\hfill \end{array}$$

(10)

where $sin{\gamma }_0={\displaystyle \frac{Z_m}{L_0}}$, $\chi ={\sum }_{1\le i\le j\le m}{sin}^2{\beta }_{ij}$, and ${\beta }_{ij}={\beta }_i-{\beta }_j$ represents the angular difference along the X-axis between agents. By maximizing the determinant $det\left(J_m\right)$, we can identify the optimal horizontal distance $r_m$ between agents, as illustrated in Figure 5.

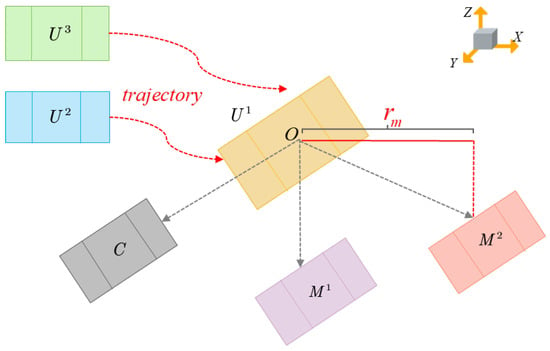
Figure 5. Optimal cooperative localization configuration based on FIM.

Equations (9) and (10) formalize the link between spatial configuration design and maximization of the Fisher information. Equation (10) provides a closed-form expression for $det\left(J_m\right)$; maximizing this determinant minimizes the estimation error covariance, and the optimizer $argmaxdet\left(J_m\right)$ yields the optimal inter-agent horizontal spacing $r_m$. To avoid convergence to degenerate or perfectly symmetric layouts with poor observability, Equation (9) augments the objective with a mild regularizer that discourages such configurations. Thus, (9) acts as a geometric constraint that improves the well-posedness of the FIM optimization in (10): it preserves the information-maximization objective while providing stable descent directions in parameter space, enabling convergence to the information-optimal $r_m$ without symmetry-induced rank loss.

2.3. Multi-Agent Collaboration via Reinforcement Learning

The proposed framework leverages RL to enable effective collaboration among multiple heterogeneous agents. Within each role, policies are designed to be permutation-consistent so that relabeling same-type agents leaves decisions unchanged. Rather than employing a standard Markov Decision Process (MDP) with conventional reward signals, we design a modified reward function that explicitly incorporates the pairwise distances between agents:

$${\kappa }_m\left(t\right)={\displaystyle \frac{l_{max}^{m\leftrightarrow U}}{l^{m\leftrightarrow U}\left(t\right)}}$$

(11)

This distance component acts as a controlled symmetry-breaking mechanism that, together with the FIM objective, discourages degenerate symmetric formations and improves localization-aware coordination. Through extensive RL-based training, the agents progressively develop expert-level collaborative behaviors and adaptive decision-making capabilities as their situational awareness evolves.

$$R_k\left(t\right)=\alpha {\widehat{r}}_k^{task}\left(t\right)+\beta {\widehat{r}}_k^{dist}\left(t\right)+\gamma \widehat{J}\left(t\right)$$

(12)

Here, ${\widehat{r}}_k^{task}$ denotes the task-level reward, ${\widehat{r}}_k^{dist}$ is the USV–AUV distance guidance term defined in Equation (11), and $J\left(t\right)=logdet\left(J_m\left(t\right)\right)$ is the FIM-based information metric (Equation (10)). The hat indicates normalization (via a running window or empirical min–max) to ensure numerical comparability across terms. The weights $\alpha$, $\beta$, and $\gamma$ control the relative contributions of these components.

By integrating the components above, we propose an optimized cooperative framework for heterogeneous multi-agent systems. The pseudo code for the complete framework is presented in Algorithm 1.

Algorithm 1 Collaborative Multi-Agent Framework

1: Input: Initial agent positions; replay buffer $\mathcal{R}$; critic and actor network parameters for each agent 2: for episode $m=1,2,\dots$ do 3:     Reset environment and agent parameters 4:     for time step $t=1,2,\dots$ do 5:         Perform multi-agent path planning via FIM-based optimization 6:         Obtain agent positions using Equation (7) 7:         for each agent k do 8:             Observe state $s_t^k$ 9:             Sample action $a_t^k\sim {\pi }^k\left(s_t^k\right)$ 10:           Execute $a_t^k$, receive reward $r_t^k$, observe next state $s_{t+1}^k$ 11:           Store tuple $(s_t^k,a_t^k,r_t^k,s_{t+1}^k)$ in replay buffer $\mathcal{R}$ 12:           if training step condition satisfied then 13:               Sample random minibatch of N transitions from $\mathcal{R}$ 14:               Update critic network via gradient descent 15:               Update actor network via policy gradient 16:           end if 17:        end for 18:     end for 19: end for

2.4. Performance Evaluation Under Complex Network Topologies

To assess the collaborative efficiency of the proposed optimization framework, we construct a heterogeneous cooperation network based on graph theory, where nodes represent functional entities and edges represent communication or interaction links. By computing key network metrics—such as average path length, clustering coefficient, and betweenness centrality—we quantitatively analyze both information transmission efficiency and the relative importance of each node. This network-theoretic analysis underpins a systematic method for collaborative performance evaluation, establishing a strong foundation for subsequent system optimization.

The network’s collaborative communication capability is characterized by the actual mean shortest path length. A shorter average path length corresponds to more efficient information propagation and stronger communication capability. Specifically, let $d_{ij}$ denote the number of edges along the shortest path between nodes i and j, and define the average path length L as:

$$L={\displaystyle \frac{1}{N(N-1)}}\sum _{i\ne j}{d}_{ij}$$

(13)

This metric directly reflects the efficiency of information exchange: shorter average path lengths indicate more optimized communication links, resulting in lower latency and enhanced overall system coordination.

The clustering coefficient measures the extent to which a node’s neighbors tend to form tightly-knit groups. For a given node u, $R_u$ denotes the number of triangles formed among its neighbors, while $k_u$ is the number of first-order neighbors. The clustering coefficient $C_u$ is defined as:

$$C_u={\displaystyle \frac{2R_u}{k_u(k_u-1)}}$$

(14)

Equivalently,

$$\left\{\begin{array}{c}{C}_u\propto R_u\hfill \\ C_u\propto {\displaystyle \frac{k_u(k_u-1)}{2}}\hfill \end{array}\right.$$

(15)

The numerator quantifies the number of observed triangles (actual clustering), while the denominator reflects the maximum possible number of triangles among the neighbors (if they form a complete clique). The mean of $C_u$ over all nodes defines the network clustering coefficient C; a higher C signifies greater local cohesiveness and connectivity.

Node betweenness centrality quantifies the fraction of all shortest paths in the network that pass through a given node, thereby reflecting its relative importance for information flow. Formally,

$$C\left(i\right)=\sum _{\begin{array}{c}i\ne j,i\ne q,\\ j\ne q\end{array}}{\displaystyle \frac{{\delta }_{jq}\left(i\right)}{{\delta }_{jq}}}$$

(16)

where ${\delta }_{jq}$ is the total number of shortest paths between nodes j and q, and ${\delta }_{jq}\left(i\right)$ is the number of those paths passing through node i.

In this work, we further leverage the optimal horizontal distance $r_m$ from Equation (6) as a metric of collaborative situational awareness. In practical multi-agent networks, effective collaboration and information sharing among agents result in reduced localization errors, signifying more comprehensive situational awareness and, hence, improved global perception capabilities across the network. Empirically, we observe that configurations with slightly broken symmetry (guided by spacing/FIM terms) outperform strictly symmetric layouts when the latter induce ambiguous measurement geometries.

3. Experiments

In this section, we present comprehensive simulation studies to validate the effectiveness of the proposed collaborative optimization framework for heterogeneous multi-agent systems. We detail the experimental setup and provide analysis of the results. To align with our methodology, we report results with a symmetry-aware reading: the FIM objective preserves geometric invariance, while the learned behaviors introduce mild, performance-driven symmetry breaking relative to fixed symmetric placements.

3.1. Experimental Settings

All experiments were performed in a two-dimensional simulation environment with an area of $200\mathrm{m}\times 200\mathrm{m}$. To demonstrate the feasibility and practical utility of our framework, we considered a scenario in which a sensing agent M is trained to localize two ground agents U. The simulation parameters are specified as follows: time step $\Delta t=10\mathrm{s}$, spatial step $\Delta x=4\mathrm{m}$, angular frequency $2\pi /43200\mathrm{rad}/\mathrm{s}$, initial displacement amplitude ${\phi }_a=5\mathrm{m}$, agent acoustic emission level $135\mathrm{dB}$, and emission frequencies $15\mathrm{kHz}$ and $18\mathrm{kHz}$ for $M_1$ and $M_2$, respectively. Unless otherwise noted, initial layouts are generic (non-engineered), and the symmetry perspective concerns how FIM-driven planning and learned policies avoid degenerate symmetric formations while retaining rigid-motion invariance. Experiments were implemented in Python 3.10 using PyTorch 2.2, Gymnasium 0.29.1, NetworkX 3.1 and were executed on a workstation with an Intel (Santa Clara, CA, USA) Core i9–13900K CPU, an NVIDIA RTX 4090 GPU (24 GB), 64 GB RAM, running Ubuntu 22.04 LTS.

3.2. Experimental Results and Analysis

We evaluated the proposed framework using two mainstream reinforcement learning algorithms: DDPG and SAC. As illustrated in Figure 6, the training curves for both algorithms demonstrate stable convergence, indicating that agent M successfully acquires an expert-level collaborative policy. Consistent with our design, the learned behaviors introduce controlled symmetry breaking in agent spacing relative to fixed symmetric baselines, which improves observability without violating the FIM’s geometric invariance.

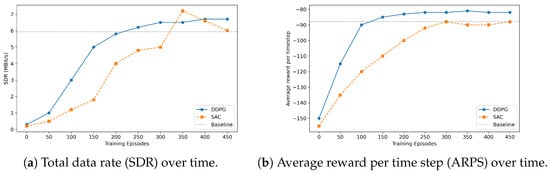
Figure 6. Temporal evolution of total data rate and average reward under the proposed multi-agent optimization framework.

To assess the statistical significance of the performance gains, we conducted ten independent runs ($n=10$) under the experimental setup described above and report the mean and standard deviation of SDR (total data rate per time step) and ARPS (average reward per time step) for each algorithm. The results, summarized in Table 1, further support the robustness and adaptability of the proposed multi-agent framework.

Table 1. Comparison of different RL algorithms.

Algorithm	SDR	ARPS
DDPG	$6.63\pm 0.97$	$-80.70\pm 6.94$
SAC	$5.97\pm 2.66$	$-87.86\pm 13.10$
Baseline [25]	$5.93\pm 3.51$	$-87.95\pm 12.08$

In addition, we leveraged the expert policy obtained via DDPG to guide the heterogeneous multi-agent system. Figure 7a depicts representative trajectories between coordination agent M and ground agents U during a single RL training episode. To further demonstrate the advantages of the proposed cooperative framework, we evaluated the localization error of the multi-agent system across three scenarios: (1) path planning for agent M optimized using FIM, (2) agent M fixed at coordinate $(0,0)$, and (3) agent M fixed at $(100,100)$. As shown in Figure 7b, the FIM-optimized path planning achieves the lowest localization error, highlighting the effectiveness of adaptive, information-driven coordination for enhancing situational awareness and collaborative perception.

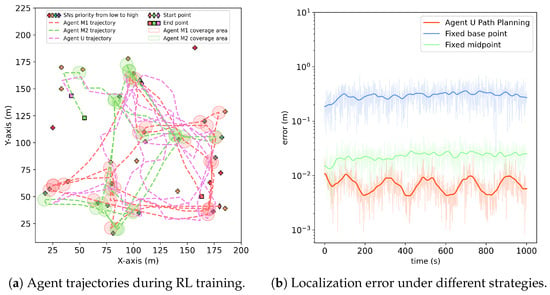
Figure 7. (a) Trajectories between sensing agent M and ground agents U during RL training. (b) Comparison of localization error for different path planning strategies. the FIM-optimized plan gently breaks degenerate symmetric layouts inherent to fixed placements, yielding lower error while preserving rigid-motion invariance.

Further simulations, based on the network configuration in Section 2.1, produce the shortest path heatmap illustrated in Figure 8. The computed average path length is 1.721, and it is evident that the shortest path between any two agents in the network does not exceed four hops. This demonstrates rapid information dissemination and high transmission efficiency within the heterogeneous multi-agent communication network.

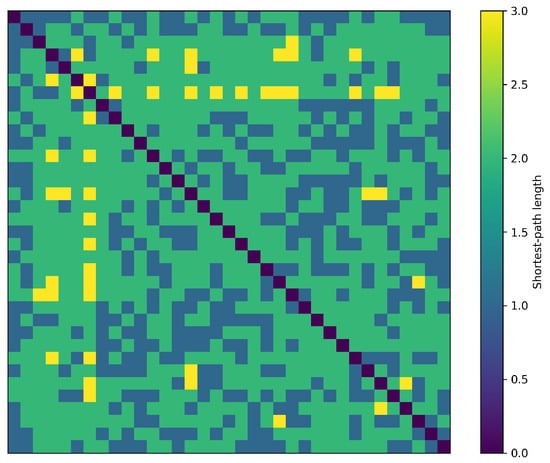
Figure 8. Shortest path heatmap for the heterogeneous multi-agent network.

The clustering coefficient distribution for each node is presented in Figure 9. Significant variability is observed, indicating differing tendencies among nodes to form tightly connected local communities. In particular, nodes of type $M_2$ demonstrate the highest clustering coefficients, suggesting their central roles in highly interconnected sub-networks.

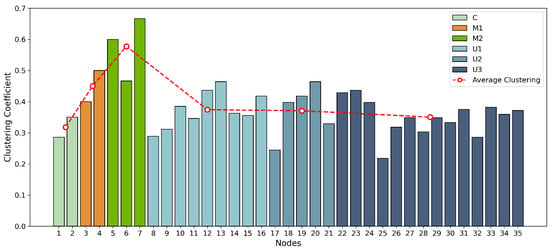
Figure 9. Clustering coefficient distribution across network nodes. Higher values indicate greater local cohesiveness and clustering, especially for nodes of type $M_2$.

Intermediate nodes—especially $M_1$ and $M_2$—exhibit a greater impact on the overall clustering characteristics of the network, while coordination (core) nodes (C) and peripheral processing nodes ($U_1$, $U_2$, $U_3$) contribute less. This trend reveals that agents located in the network’s central regions have a higher propensity to form clusters, resulting in denser local connectivity, whereas those situated at the core or periphery are less likely to be closely linked with their immediate neighbors.

Areas dominated by $M_2$ nodes are associated with more frequent interactions or heightened collaborative activity, further enhancing the network’s overall robustness and information-sharing capacity. A high clustering coefficient indicates that neighboring nodes form densely connected subgraphs, facilitating short-range communication and information exchange. This structure improves local perception fusion, map consistency, and the identifiability of local observations, thereby reducing estimation error. Moreover, through cross-cluster links provided by the coordination node C and higher-layer connections, the benefits of strong local clustering can propagate to the global scale, enhancing overall localization accuracy and convergence speed while preserving local robustness.

Figure 10 presents the betweenness centrality distribution for all nodes in the heterogeneous multi-agent network. As expected, core coordination nodes (C) display the highest betweenness centrality, with $C_1$ exhibiting a particularly dominant value that far surpasses those of other nodes. This finding underscores the essential role of $C_1$ as a network bridge, facilitating the majority of shortest paths and serving as a primary connector for information flow across the network.

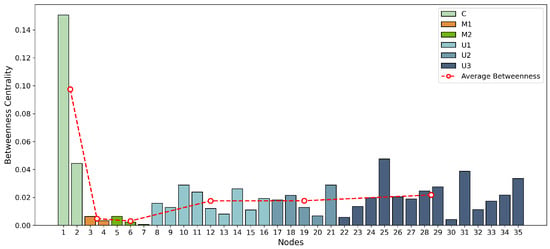
Figure 10. Betweenness centrality distribution across network nodes. Core coordination nodes (C) serve as key bridges for information flow, while processing nodes (U) act as secondary intermediaries.

Beyond the core C nodes, processing nodes (U) also demonstrate notable betweenness centrality, functioning as important intermediaries in the network. In contrast, sensing nodes ($M_1$, $M_2$) are characterized by low betweenness values, reflecting their primary engagement in localized connectivity rather than system-wide mediation.

Table 2 summarizes the average betweenness centrality for each node type. Coordination nodes consistently exhibit much higher average betweenness than any other node category, confirming their pivotal role in system connectivity and robustness. Notably, the table also highlights subtle differences between sensing and processing nodes: in some configurations, processing nodes may even surpass sensing nodes in betweenness, indicating the importance of distributed coordination in multi-agent collaboration.

Table 2. Average betweenness centrality by node type.

Node Type	C	${\mathit{M}}_1$	${\mathit{M}}_2$	${\mathit{U}}_1$	${\mathit{U}}_2$	${\mathit{U}}_3$
Average Betweenness	0.098	0.0032	0.0024	0.02	0.02	0.022

The relatively low betweenness of sensing nodes indicates that, under the present topology, they act primarily as information endpoints rather than mediators. Consequently, failures at core coordination nodes could disproportionately degrade collaborative capacity, underscoring the need for resilient architectures (e.g., redundant bridges, bounded centrality, alternative routing). Consistent with the symmetry-aware reading of our unchanged experiments, mild, performance-driven symmetry breaking—induced by FIM-aware planning and learned spacing—improves observability and coordination compared with strictly symmetric, fixed placements. Fault tolerance can be further improved by introducing a small number of redundant links among sensing nodes or by employing adaptive relay mechanisms, without materially increasing communication overhead.

Coordination nodes (C)—which exhibit the highest betweenness centrality—serve as critical bridges for information flow and therefore constitute potential single points of failure. If such a node fails or experiences a communication outage, overall collaborative efficiency and information throughput can be severely impaired. To address this risk, future work will investigate robust coordination mechanisms based on dynamic network reconfiguration and reinforcement learning, aiming to enhance adaptability and fault tolerance under critical-node failures. Concretely, within the existing RL framework we plan to introduce redundancy-aware role reallocation and post-fault link self-recovery to enable rapid rerouting of information and dynamic reconfiguration of collaboration patterns, thereby preserving network availability and cooperative performance. This line of research will lay the groundwork for long-term reliable operation of heterogeneous multi-agent systems in complex, time-varying environments. In addition, deploying a small number of redundant links among sensing nodes or adaptive relay mechanisms can further improve fault tolerance without materially increasing communication overhead.

4. Conclusions

This study presents an integrated optimization framework for collaborative activity in heterogeneous multi-agent systems, combining graph-theoretic network modeling, FIM-based localization, and reinforcement learning for adaptive coordination. The FIM objective preserves geometric invariance, policies maintain within-role permutation consistency, and mild, performance-driven symmetry breaking avoids degenerate symmetric layouts that harm observability. Modeling components as nodes and links as edges enables efficient, scalable scheduling and real-time collaboration across diverse agent types. FIM-optimized planning reduces localization error, reinforcement learning improves cooperative decision-making, and network analysis confirms rapid information dissemination while identifying critical bridges in connectivity; the relatively low betweenness of sensing nodes suggests untapped collaborative capacity and motivates resilient architectures that mitigate single-point failures.