Generalized Fibonacci Polynomials and Their Properties

Abstract

This study presents a unified framework for the simultaneous analysis of generalized Fibonacci numbers and their associated polynomial extensions, both of which play a significant role in combinatorial analysis and discrete mathematics. The generalized Fibonacci polynomials have been extended to four new families of polynomials, each defined through systematic extensions of the generalized Fibonacci polynomials $U_{kl}\left(\varsigma \right)$ and $V_{kl}\left(\varsigma \right)$. In addition, we explore further generalizations involving the extended Humbert-type polynomials $U_{kl,m}^{\left(r\right)}\left(\varsigma \right)$ and $V_{kl,m}^{\left(r\right)}\left(\varsigma \right).$ Based on the algebraic structure and generating functions of these newly defined polynomial families, several algebraic identities that reveal their rich mathematical properties have been derived. Additionally, we aim to present the graphical representations of a family of polynomials, analyze their roots, examine the distribution of the roots, and investigate the correlations among the largest roots. Finally, to gain a deeper understanding of the structural properties of the polynomials, the root magnitude distribution and the density distribution of root values are also examined.

1. Introduction

The $(\mathcal{P},\mathcal{Q})$-Fibonacci and $(\mathcal{P},\mathcal{Q})$-Lucas polynomials are generalizations of the classical Fibonacci and Lucas sequences. These polynomials extend the well-known recurrence relations and combinatorial interpretations into a broader algebraic framework through the use of $(\mathcal{P},\mathcal{Q})$-polynomials, allowing for the exploration of richer mathematical structures. When $\mathcal{P}=\mathcal{Q}=1$, the classical sequences are obtained as special cases, making these polynomials both a general and inclusive approach. The $(\mathcal{P},\mathcal{Q})$-generalizations play an important role in various areas of mathematics, including quantum calculus, number theory, combinatorics, and the study of special functions. In the literature, numerous studies have been devoted to investigating the structural properties of these polynomials.

Horadam [1] defined the following polynomial sequence $\left\{W_n\left(\zeta \right)\right\}$ as

$$W_n\left(\zeta \right)=\mathcal{P}\left(\zeta \right)W_{n-1}\left(\zeta \right)+\mathcal{Q}\left(\zeta \right)W_{n-2}\left(\zeta \right)\mathrm{for}n\ge 2,$$

with $W_0\left(\zeta \right)=c_0$ and $W_1\left(\zeta \right)=c_1{\zeta }^d$. Nalli and Haukkanen [2] introduced the $h\left(\zeta \right)$-Fibonacci polynomials $h\left(\zeta \right)$-Lucas polynomials, which encompass the Fibonacci, Pell, Lucas, and Pell–Lucas polynomials as particular cases.

Let $\mathcal{P}\left(\varsigma \right)$ and $\mathcal{Q}\left(\varsigma \right)$ be real coefficients polynomials. For a fixed integer $m\ge 2,$ the generalized $(\mathcal{P},\mathcal{Q})$-Fibonacci and Lucas polynomials $U_{l,m}\left(\varsigma \right)$ and $V_{l,m}\left(\varsigma \right)$ [3] are shown that for $l\ge m,$

$$U_{l,m}\left(\varsigma \right)=\mathcal{P}\left(\varsigma \right)U_{l-1,m}\left(\varsigma \right)+\mathcal{Q}\left(\varsigma \right)U_{l-m,m}\left(\varsigma \right)$$

(1)

with $U_{0,m}\left(\varsigma \right)=0,U_{1,m}\left(\varsigma \right)=1,U_{2,m}\left(\varsigma \right)=\mathcal{P}\left(\varsigma \right),\dots ,U_{m-1,m}\left(\varsigma \right)={\mathcal{P}}^{m-2}\left(\varsigma \right)$ and

$$V_{l,m}\left(\varsigma \right)=\mathcal{P}\left(\varsigma \right)V_{l-1,m}\left(\varsigma \right)+\mathcal{Q}\left(\varsigma \right)V_{l-m,m}\left(\varsigma \right)$$

(2)

with $V_{0,m}\left(\varsigma \right)=2,V_{1,m}\left(\varsigma \right)=\mathcal{P}\left(\varsigma \right),V_{2,m}\left(\varsigma \right)={\mathcal{P}}^2\left(\varsigma \right),\dots ,V_{m-1,m}\left(\varsigma \right)={\mathcal{P}}^{m-1}\left(\varsigma \right).$ Specially, when $m=2,$$U_{l,2}\left(\varsigma \right)=U_l\left(\varsigma \right)$ and $V_{l,2}\left(\varsigma \right)=V_l\left(\varsigma \right)$ are the $(\mathcal{P},\mathcal{Q})$-Fibonacci and Lucas polynomials, respectively.

In 1965, Gould introduced the Humbert polynomials defined by $P_l(m,\varsigma ,y,r,c),$ and investigated their explicit expressions, recurrence relations, and higher-order derivatives. By assigning specific values to the parameters $m,\varsigma ,y,r,c,$ these polynomials reduce to certain well-known ones, such as Fibonacci, Chebyshev and Legendre polynomials. In recent years, numerous studies have been conducted on Humbert polynomials. In particular, many of these studies have focused on special polynomials and explored them from various perspectives [4].

Gould [5] introduced the generating function of the Humbert-Gould polynomials $P_l(m,\varsigma ,y,r,c)$

$$\sum _{l=0}^{\infty }{P}_l(m,\varsigma ,y,r,c)t^l={\left(c-m\varsigma t+y{t}^m\right)}^r,$$

where m is a positive integer and other parameters are unrestricted in general.

For each complex number $r,$ Wang et al. [4] defined the generalized Humbert polynomials $U_{l,m}^{\left(r\right)}\left(\varsigma \right)$ as convolutions of $U_{l,m}\left(\varsigma \right)$ by the generating function

$$\sum _{l=0}^{\infty }{U}_{l+1,m}^{\left(r\right)}\left(\varsigma \right)t^l={\left(1-\mathcal{P}\left(\varsigma \right)t-\mathcal{Q}\left(\varsigma \right)t^m\right)}^{-r}.$$

(3)

Note that when $r=1,$ $U_{l,m}^{\left(1\right)}\left(\varsigma \right)=U_{l,m}\left(\varsigma \right)$ are generalized $\left(\mathcal{P},\mathcal{Q}\right)$-Fibonacci polynomials. The explicit expression of $U_l^{\left(r\right)}\left(\varsigma \right)$ is given by

$$U_{l+1}^{\left(r\right)}\left(\varsigma \right)=\sum _{k=0}^{\left[l/2\right]}\left({\displaystyle \genfrac{}{}{0pt}{}{r+k-1}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{r+l-k-1}{l-2k}}\right){\mathcal{P}}^{l-2k}\left(\varsigma \right){\mathcal{Q}}^k\left(\varsigma \right).$$

Pathan and Khan [6] aimed to present a unified framework for a class of generalized Humbert polynomials encompassing well-known families such as Gegenbauer, Legendre, Hermite, and Laguerre polynomials, along with several related generating functions and hypergeometric representations in their work. Also, Alam et al. [7] presented several expansions of the Humbert–Hermite polynomials, particularly those expressed in terms of Hermite–Gegenbauer (ultraspherical) and Hermite–Chebyshev polynomials. This study not only unifies prior findings but also broadens the theoretical framework of Humbert’s polynomials, paving the way for future research and applications across various areas of mathematics. In [3,7], the generating function of $V_{l,m}^{\left(r\right)}\left(\varsigma \right)$ is given by

$$\sum _{l=0}^{\infty }{V}_{l,m}^{\left(r\right)}\left(\varsigma \right)t^l={\left({\displaystyle \frac{2-\mathcal{P}\left(\varsigma \right)t}{1-\mathcal{P}\left(\varsigma \right)t-\mathcal{Q}\left(\varsigma \right)t^m}}\right)}^r.$$

(4)

Cvijović showed that

$${\left(\sum _{l=1}^{\infty }{f}_l{t}^l\right)}^r=\sum _{l=r}^{\infty }{g}_l\left(r\right)t^l,$$

where the numbers $f_l$ are the coefficients of the powers of t

$$g_r\left(r\right)=f_1^r\mathrm{and}{g}_l\left(r\right)={\displaystyle \frac{1}{(l-r)f_1}}\sum _{j=1}^{l-r}\left[\left(j+1\right)\left(r+1\right)-\left(l+1\right)\right]f_{j+1}{g}_{l-j}\left(r\right)$$

(5)

for a fixed positive integer r and $l\ge r+1$ [8].

In mathematical analysis, the exponential and natural logarithm functions are often represented through their power series expansions, which serve as foundational tools in both theoretical and applied contexts. Specifically, the exponential function $e^t$ is given by the infinite series

$$e^t=\sum _{l=0}^{\infty }{\displaystyle \frac{t^l}{l!}}$$

which converges for all real and complex values of $t.$ Logarithm function $ln(1-t)$ can be expressed as a power series expansion around $t=0,$ valid for $\left|t\right|<1,$ as follows

$$ln(1-t)=-\sum _{l=1}^{\infty }{\displaystyle \frac{t^l}{l}}.$$

(6)

The Stirling numbers are widely recognized for their fundamental role in combinatorial analysis. In [9,10], the Stirling numbers of the first kind $S_1\left(l,k\right)$ are usually defined as the coefficients of the powers of t in $t^{\underline{l}}$ where

$$t^{\underline{l}}=t\left(t+1\right)\dots \left(t+l-1\right)=\sum _{k=0}^l{S}_1\left(l,k\right)t^k$$

in which for $l\ge 0,$ $S_1\left(l,0\right)={\delta }_{l,0},$ ${\delta }_{l,k}$ is the Kronecker delta. The generating function of $S_1\left(l,k\right)$ is given by

$${\displaystyle \frac{{\left(ln\left(1+t\right)\right)}^k}{k!}}=\sum _{l=k}^{\infty }{S}_1\left(l,k\right){\displaystyle \frac{t^l}{l!}}\mathrm{for}k\in \mathbb{N}.$$

(7)

The Daehee numbers of the first kind of order $r,D_l^r$ [11], are defined by the generating functions to be

$${\left({\displaystyle \frac{ln\left(1+t\right)}{t}}\right)}^r=\sum _{l=0}^{\infty }{D}_l^r{\displaystyle \frac{t^l}{l!}}.$$

(8)

For $r=1,D_l^1=D_l$ are called Daehee numbers.

Cauchy numbers play an important role in various fields such as combinatorics, numerical analysis, and special functions. The Cauchy numbers of the first kind $C_n$ [9] have the generating function

$${\displaystyle \frac{t}{ln(1+t)}}=\sum _{l=0}^{\infty }{C}_l{\displaystyle \frac{t^l}{l!}}.$$

(9)

Although extensive studies have been conducted on classical Fibonacci and Lucas polynomials in recent years, research on their generalizations continues to progress. In this paper, we go beyond these generalizations by extending the generalized Fibonacci and Lucas polynomials into four new families. The main aim of this study is to introduce a new family of polynomials into the literature, to investigate their algebraic and combinatorial structures in detail, to derive new algebraic identities, and to explore their numerical properties comprehensively with potential applications in analysis, applied mathematics, and engineering. Furthermore, it goes beyond the existing references by providing both theoretical studies and their applications.

This paper follows the steps below:

• Generalized Fibonacci polynomials are defined, and using these polynomials, extended Humbert-type polynomials are examined.
• By means of the newly defined generalized Fibonacci polynomials, the study is systematically extended to four new polynomial families.
• Some algebraic identities involving these four new polynomials and the generalized Humbert-type polynomials are presented.
• For a specific polynomial family, graphs are provided. The roots of certain polynomials are computed and their root distributions are examined. Afterwards, correlations among the largest roots are investigated.
• Finally, in order to gain a deeper understanding of the structural properties of the polynomials, the magnitude distribution and density distribution of the roots are systematically studied.

2. Generalized Fibonacci Polynomials and Their Properties

In this section, we focus on the simultaneous treatment of generalized Fibonacci numbers [12] and their associated polynomial extensions, which constitute two central constructs in combinatorial analysis and discrete mathematics. Specifically, we introduce and analyze four families of polynomials denoted by $M_E(k,l,\varsigma ), M_L(k,l,\varsigma ), N_E(k,l,\varsigma )$ and $N_L(k,l,\varsigma )$, each of which is constructed based on extensions of classical Fibonacci sequences and polynomials. There are some identities involving these polynomials.

The generalized second order sequences $\left\{U_l\right\}$ and $\left\{V_l\right\}$ [13], are defined for $l>0$ and nonzero integer number p by

$$U_{l+1}=p{U}_l+U_{l-1}\mathrm{and}{V}_{l+1}=p{V}_l+V_{l-1}$$

in which $U_0=0,$$U_1=1$ and $V_0=2,$$V_1=p$, respectively.

Kılıç and Stanica [14] derived the following recurrence relations for the sequences $\left\{U_{kl}\right\}$ and $\left\{V_{kl}\right\}$ for $k\ge 0$, $l>0$. It is clearly that

$$U_{k\left(l+1\right)}=V_k{U}_{kl}+{\left(-1\right)}^{k+1}{U}_{k\left(l-1\right)}\mathrm{and}{V}_{k\left(l+1\right)}=V_k{V}_{kl}+{\left(-1\right)}^{k+1}{V}_{k\left(l-1\right)},$$

where the initial conditions are $0,$$U_k$ and $2,$$V_k,$ respectively.

Now, we will define the generalized Fibonacci and Lucas polynomials.

Definition 1.

For any positive integers $l,k,$ the generalized Fibonacci and Lucas polynomials are defined by

$$\begin{array}{ccc}\hfill U_{kl}\left(\varsigma \right)& =& \varsigma V_k{U}_{k(l-1)}\left(\varsigma \right)+{\left(-1\right)}^{k+1}{U}_{k(l-2)}\left(\varsigma \right),\hfill \\ \hfill V_{kl}\left(\varsigma \right)& =& \varsigma V_k{V}_{k(l-1)}\left(\varsigma \right)+{\left(-1\right)}^{k+1}{V}_{k(l-2)}\left(\varsigma \right),\hfill \end{array}$$

(10)

with initial conditions $0,$ $U_k$ and $2,$ $\varsigma V_k,$ respectively, where $U_l$ is l-th generalized Fibonacci number and $V_l$ is l-th. generalized Lucas number.

Clearly, Binet forms of $\left\{U_{kl}\left(\varsigma \right)\right\}$ and $\left\{V_{kl}\left(\varsigma \right)\right\}$ are given by

$$U_{kl}\left(\varsigma \right)=U_k{\displaystyle \frac{{\left({\alpha }_k\left(\varsigma \right)\right)}^l-{\left({\beta }_k\left(\varsigma \right)\right)}^l}{{\alpha }_k\left(\varsigma \right)-{\beta }_k\left(\varsigma \right)}}\mathrm{and}{V}_{kl}\left(\varsigma \right)={\left({\alpha }_k\left(\varsigma \right)\right)}^l+{\left({\beta }_k\left(\varsigma \right)\right)}^l,$$

where ${\alpha }_k\left(\varsigma \right)=\left(\varsigma V_k+\sqrt{{\varsigma }^2{V}_k^2+4{(-1)}^{k+1}}\right)/2$ and ${\beta }_k\left(\varsigma \right)=\left(\varsigma V_k-\sqrt{{\varsigma }^2{V}_k^2+4{(-1)}^{k+1}}\right)/2.$ Note that $U_{-kl}\left(\varsigma \right)={\left(-1\right)}^{kl+l+1}{U}_{kl}\left(\varsigma \right).$

Lemma 1.

For any positive integer $k,$ we have

$$\sum _{l=0}^{\infty }{U}_{kl}\left(\varsigma \right)t^l={\displaystyle \frac{U_{k}t}{1-\varsigma V_{k}t+{(-1)}^k{t}^2}}\mathit{and}\sum _{l=0}^{\infty }{V}_{kl}\left(\varsigma \right)t^l={\displaystyle \frac{2-\varsigma V_{k}t}{1-\varsigma V_{k}t+{(-1)}^k{t}^2}}.$$

(11)

Proof. 

Consider that

$$\begin{array}{ccc}& & \left(1-\varsigma V_{k}t+{(-1)}^k{t}^2\right)\sum _{l=0}^{\infty }{U}_{kl}\left(\varsigma \right)t^l\hfill \\ & =& \sum _{l=0}^{\infty }{U}_{kl}\left(\varsigma \right)t^l-\varsigma V_k\sum _{l=1}^{\infty }{U}_{k(l-1)}\left(\varsigma \right)t^l+{(-1)}^k\sum _{l=2}^{\infty }{U}_{k(l-2)}\left(\varsigma \right)t^l\hfill \\ & =& U_{k}t+\sum _{l=2}^{\infty }\left(U_{kl}\left(\varsigma \right)-\varsigma V_k{U}_{k(l-1)}\left(\varsigma \right)+{(-1)}^k{U}_{k(l-2)}\left(\varsigma \right)\right)t^l=U_{k}t\hfill \end{array}$$

with (10). Similarly, the generating function of $V_{kl}\left(\varsigma \right)$ is obtained.    □

Now, from (1) and (2), Definition 2 can be given as follows:

Definition 2.

For any positive integers $l,m,k,$ the generalized $({\mathcal{P}}_k,{\mathcal{Q}}_k)$-Fibonacci polynomials $U_{kl,m}\left(\varsigma \right)$ and the generalized $({\mathcal{P}}_k,{\mathcal{Q}}_k)$-Lucas polynomials $V_{kl,m}\left(\varsigma \right)$ [3] are defined by for $l\ge m,$

$$U_{kl,m}\left(\varsigma \right)=\varsigma V_k{U}_{k(l-1),m}\left(\varsigma \right)+{\left(-1\right)}^{k+1}{U}_{k(l-m),m}\left(\varsigma \right)$$

with the initial conditions $U_{0,m}\left(\varsigma \right)=0, U_{k,m}\left(\varsigma \right)=U_k, U_{2k,m}\left(\varsigma \right)=\varsigma V_k,\dots ,U_{k(m-1),m}\left(\varsigma \right)={\varsigma }^{m-2}{V}_k^{m-2}$ and

$$V_{kl,m}\left(\varsigma \right)=\varsigma V_k{V}_{k(l-1),m}\left(\varsigma \right)+{\left(-1\right)}^{k+1}{V}_{k(l-m),m}\left(\varsigma \right)$$

with the initial conditions $V_{0,m}\left(\varsigma \right)=2, V_{k,m}\left(\varsigma \right)=\varsigma V_k, V_{2k,m}\left(\varsigma \right)={\varsigma }^2{V}_k^2,\dots ,V_{k(m-1),m}\left(\varsigma \right)={\varsigma }^{m-1}{V}_k^{m-1}.$

Taking $\mathcal{P}\left(\varsigma \right)=\varsigma V_k$ and $\mathcal{Q}\left(\varsigma \right)={\left(-1\right)}^{k+1}$ in (3) and (4), the generating functions of the generalized Humbert polynomial $U_{kl,m}^{\left(r\right)}\left(\varsigma \right)$ and polynomial $V_{kl,m}^{\left(r\right)}\left(\varsigma \right)$ are given by

$$\sum _{l=0}^{\infty }{U}_{k(l+1),m}^{\left(r\right)}\left(\varsigma \right)t^l={\left(1-\varsigma V_{k}t+{(-1)}^k{t}^m\right)}^{-r},$$

(12)

and

$$\sum _{l=0}^{\infty }{V}_{kl,m}^{\left(r\right)}\left(\varsigma \right)t^l={\left({\displaystyle \frac{2-\varsigma V_{k}t}{1-\varsigma V_{k}t+{(-1)}^k{t}^m}}\right)}^r.$$

(13)

Now, the finite sums involving the generalized Fibonacci and Lucas polynomials are defined as follows:

$$\begin{array}{ccc}\hfill \sum _{i=0}^l{\displaystyle \frac{{\varsigma }^i}{i!}}{U}_{k(l-i)}\left(\varsigma \right)& =& M_E(k,l,\varsigma )\mathrm{and}\sum _{i=1}^l{\displaystyle \frac{{\varsigma }^i}{i}}{U}_{k(l-i)}\left(\varsigma \right)=M_L(k,l,\varsigma ),\hfill \\ \hfill \sum _{i=0}^l{\displaystyle \frac{{\varsigma }^i}{i!}}{V}_{k(l-i)}\left(\varsigma \right)& =& N_E(k,l,\varsigma )\mathrm{and}\sum _{i=1}^l{\displaystyle \frac{{\varsigma }^i}{i}}{V}_{k(l-i)}\left(\varsigma \right)=N_L(k,l,\varsigma ).\hfill \end{array}$$

(14)

These sums are called as M-type polynomials and N-type polynomials (

Table 1. The few terms of M-type polynomials.

l	${\mathit{M}}_{\mathit{E}}(\mathit{k},\mathit{l},\mathit{\varsigma })$	${\mathit{M}}_{\mathit{L}}(\mathit{k},\mathit{l},\mathit{\varsigma })$
0	0
1	$U_k$	0
2	$\varsigma U_k\left(V_k+1\right)$	$\varsigma U_k$
3	$U_k\left({\varsigma }^2\left(V_k^2+V_k+{\displaystyle \frac{1}{2}}\right)+{\left(-1\right)}^{k+1}\right)$	${\varsigma }^2{U}_k\left(V_k+{\displaystyle \frac{1}{2}}\right)$
⋮	⋮	⋮

and

Table 2. The few terms of N-type polynomials.

l	${\mathit{N}}_{\mathit{E}}(\mathit{k},\mathit{l},\mathit{\varsigma })$	${\mathit{N}}_{\mathit{L}}(\mathit{k},\mathit{l},\mathit{\varsigma })$
0	2
1	$\varsigma (V_k+2)$	$2\varsigma$
2	${\varsigma }^2\left(V_k^2+V_k+1\right)+2{\left(-1\right)}^{k+1}$	${\varsigma }^2\left(V_k+1\right)$
3	${\varsigma }^3\left(V_k^3+V_k^2+{\displaystyle \frac{1}{2}}{V}_k+{\displaystyle \frac{1}{3}}\right)+{(-1)}^{k+1}\varsigma (3V_k+2)$	${\varsigma }^3\left(V_k^2+{\displaystyle \frac{V_k}{2}}+{\displaystyle \frac{2}{3}}\right)+2\varsigma {(-1)}^{k+1}$
⋮	⋮	⋮

). The graphical representations of these polynomials obtained for the values $k=p=2$ and $l=5$ are presented in Figure 1.

While $M_E(k,l,\varsigma )$ and $M_L(k,l,\varsigma )$ are smoother and less oscillatory functions, $N_E(k,l,\varsigma )$ and $N_L(k,l,\varsigma )$ are more oscillatory and complex. Moreover, all functions except $M_E(k,l,\varsigma )$ pass through the origin.

Now, the following recurrence relations characterize the behavior of $M_E(k,l,\varsigma ),$$M_L(k,l,\varsigma ),$$N_E(k,l,\varsigma )$ and $N_L(k,l,\varsigma )$. These relations involve the parameter k and variable $\varsigma$, and hold for all integer $l\ge 1$.

Lemma 2.

For any positive integers $l,k,$ we have

$$\begin{array}{ccc}\hfill M_E(k,l+1,\varsigma )-\varsigma V_k{M}_E(k,l,\varsigma )+{(-1)}^k{M}_E(k,l-1,\varsigma )& =& {\displaystyle \frac{{\varsigma }^l}{l!}}{U}_k,\hfill \\ \hfill N_E(k,l+1,\varsigma )-\varsigma V_k{N}_E(k,l,\varsigma )+{(-1)}^k{N}_E(k,l-1,\varsigma )& =& {\displaystyle \frac{{\varsigma }^{l+1}}{l!}}\left({\displaystyle \frac{2}{l+1}}-V_k\right),\hfill \\ \hfill M_L(k,l+1,\varsigma )-\varsigma V_k{M}_L(k,l,\varsigma )+{(-1)}^k{M}_L(k,l-1,\varsigma )& =& {\displaystyle \frac{{\varsigma }^l}{l}}{U}_k,\hfill \\ \hfill N_L(k,l+1,\varsigma )-\varsigma V_k{N}_L(k,l,\varsigma )+{(-1)}^k{N}_L(k,l-1,\varsigma )& =& {\varsigma }^{l+1}\left({\displaystyle \frac{2}{l+1}}-{\displaystyle \frac{V_k}{l}}\right).\hfill \end{array}$$

Proof. 

From (14), we can write

$$\begin{array}{ccc}\hfill \varsigma V_k{M}_E(k,l,\varsigma )-{(-1)}^k{M}_E(k,l-1,\varsigma )& =& \sum _{i=0}^l{\displaystyle \frac{{\varsigma }^i}{i!}}\varsigma V_k{U}_{k(l-i)}\left(\varsigma \right)-{(-1)}^k\sum _{i=0}^{l-1}{\displaystyle \frac{{\varsigma }^i}{i!}}{U}_{k(l-1-i)}\left(\varsigma \right)\hfill \\ & =& \sum _{i=0}^{l-1}{\displaystyle \frac{{\varsigma }^i}{i!}}\left(\varsigma V_k{U}_{k(l-i)}\left(\varsigma \right)-{(-1)}^k{U}_{k(l-1-i)}\left(\varsigma \right)\right)\hfill \\ & =& \sum _{i=0}^{l-1}{\displaystyle \frac{{\varsigma }^i}{i!}}{U}_{k(l+1-i)}\left(\varsigma \right)\hfill \\ & =& M_E(k,l+1,\varsigma )-{\displaystyle \frac{{\varsigma }^l}{l!}}{U}_k,\hfill \end{array}$$

as claimed. Similarly, the other recurrence relations can be given.    □

Lemma 3.

For any positive integers $l,k,$ the generating functions of $M_E(k,l,\varsigma ), M_L(k,l,\varsigma ),$$N_E(k,l,\varsigma )$ and $N_L(k,l,\varsigma )$ are given by

$$\begin{array}{ccc}\hfill \sum _{l=0}^{\infty }{M}_E(k,l,\varsigma )t^l& =& {\displaystyle \frac{U_{k}t}{1-\varsigma V_{k}t+{(-1)}^k{t}^2}}{e}^{\varsigma t},\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill \sum _{l=1}^{\infty }{M}_L(k,l,\varsigma )t^l& =& -{\displaystyle \frac{U_{k}t}{1-\varsigma V_{k}t+{(-1)}^k{t}^2}}ln(1-\varsigma t),\hfill \\ \hfill \sum _{l=0}^{\infty }{N}_E(k,l,\varsigma )t^l& =& {\displaystyle \frac{2-\varsigma V_{k}t}{1-\varsigma V_{k}t+{(-1)}^k{t}^2}}{e}^{\varsigma t},\hfill \\ \hfill \sum _{l=1}^{\infty }{N}_L(k,l,\varsigma )t^l& =& -{\displaystyle \frac{2-\varsigma V_{k}t}{1-\varsigma V_{k}t+{(-1)}^k{t}^2}}ln(1-\varsigma t).\hfill \end{array}$$

(16)

Proof. 

By Lemma 1, consider that

$$\begin{array}{ccc}\hfill \sum _{l=0}^{\infty }{M}_E(k,l,\varsigma )t^l& =& \sum _{l=0}^{\infty }\sum _{i=0}^l{\displaystyle \frac{{\varsigma }^i}{i!}}{U}_{k(l-i)}\left(\varsigma \right)t^l\hfill \\ & =& \sum _{l=0}^{\infty }{\displaystyle \frac{{\varsigma }^l}{l!}}{t}^l\sum _{l=0}^{\infty }{U}_{kl}\left(\varsigma \right)t^l={\displaystyle \frac{U_{k}t}{1-\varsigma V_{k}t+{(-1)}^k{t}^2}}{e}^{\varsigma t}.\hfill \end{array}$$

Similarly, the other generating functions are obtained.    □

In Theorems 1 and 2, various identities are presented in detail, involving the four newly defined polynomial families, the generalized Humbert polynomial $U_{kl,m}^{\left(r\right)}\left(\varsigma \right)$, the polynomial $V_{kl,m}^{\left(r\right)}\left(\varsigma \right)$, and the Cauchy numbers of the first kind. These identities not only reveal the underlying algebraic structures but also provide a framework for exploring the combinatorial properties of the polynomials.

Theorem 1.

For any positive integers $l,k,r,$ we have

$$\begin{array}{ccc}\hfill U_k{U}_{kl,2}^{\left(r\right)}\left(\varsigma \right)& =& \sum _{j=0}^l\sum _{i=0}^j{M}_E(k,l-j,\varsigma )U_{k(j-i+1),2}^{(r-1)}\left(\varsigma \right){\displaystyle \frac{{\left(-\varsigma \right)}^i}{i!}},\hfill \\ & =& {\displaystyle \frac{1}{\varsigma }}\sum _{j=0}^l\sum _{i=0}^j{(-\varsigma )}^i{\displaystyle \frac{C_i}{i!}}{U}_{k(j-i+1),2}^{(r-1)}\left(\varsigma \right)M_L(k,l-j+1,\varsigma ).\hfill \end{array}$$

Proof. 

By (12) and (15), we can write

$$\begin{array}{ccc}\hfill \sum _{l=0}^{\infty }{U}_{kl,2}^{\left(r\right)}\left(\varsigma \right)t^l& =& {\displaystyle \frac{t{e}^{\varsigma t}}{1-\varsigma V_{k}t+{\left(-1\right)}^k{t}^2}}{\displaystyle \frac{1}{{\left(1-\varsigma V_{k}t+{\left(-1\right)}^k{t}^2\right)}^{r-1}}}{e}^{-\varsigma t}\hfill \\ & =& {\displaystyle \frac{1}{U_k}}\sum _{l=0}^{\infty }{M}_E(k,l,\varsigma )t^l\sum _{l=0}^{\infty }{U}_{k(l+1),2}^{(r-1)}\left(\varsigma \right)t^l\sum _{l=0}^{\infty }{\left(-\varsigma \right)}^l{\displaystyle \frac{t^l}{l!}}\hfill \\ & =& {\displaystyle \frac{1}{U_k}}\sum _{l=0}^{\infty }{M}_E(k,l,\varsigma )t^l\sum _{l=0}^{\infty }\sum _{i=0}^l{\left(-\varsigma \right)}^i{U}_{k(l-i+1),2}^{(r-1)}\left(\varsigma \right){\displaystyle \frac{t^l}{i!}}\hfill \\ & =& {\displaystyle \frac{1}{U_k}}\sum _{l=0}^{\infty }\sum _{j=0}^l\sum _{i=0}^j{\left(-\varsigma \right)}^i{M}_E(k,l-j,\varsigma )U_{k(j-i+1),2}^{(r-1)}\left(\varsigma \right){\displaystyle \frac{t^l}{i!}}\hfill \end{array}$$

from the product of the generating functions. Thus, the first equality is given. Similarly, with the help of (9), using product of generating functions, we have the second equality.    □

Theorem 2.

For any positive integers $l,k,r,$ we have

$$\begin{array}{ccc}\hfill V_{kl,2}^{\left(r\right)}\left(\varsigma \right)& =& \sum _{j=0}^l\sum _{i=0}^j{N}_E(k,l-j,\varsigma )V_{k(j-i),2}^{(r-1)}\left(\varsigma \right){\displaystyle \frac{{\left(-\varsigma \right)}^i}{i!}}\hfill \\ & =& {\displaystyle \frac{1}{\varsigma }}\sum _{j=0}^l\sum _{i=0}^j{N}_L(k,l-j+1,\varsigma )V_{k(j-i),2}^{(r-1)}\left(\varsigma \right)C_i{\displaystyle \frac{{\left(-\varsigma \right)}^i}{i!}}.\hfill \end{array}$$

Proof. 

From Lemma 3, (9) and (13), the proof is complete.    □

The polynomials $g_l\left(r\right)$ and $f_l\left(r\right)$, which are expressed by recurrence relations, are represented in closed form by means of the generalized Humbert polynomial $U_{kl,m}^{\left(r\right)}\left(\varsigma \right)$, the polynomial $V_{kl,m}^{\left(r\right)}\left(\varsigma \right)$ and (8).

Theorem 3.

For any positive integers $l,k$ and $r,$ we have

$$g_l\left(r\right)=U_k^r\sum _{i=0}^{l-r}{U}_{k(l-r-i+1),2}^{\left(r\right)}\left(\varsigma \right){\displaystyle \frac{r^i{\varsigma }^i}{i!}}\mathit{and}{f}_l\left(r\right)=\sum _{i=0}^{l-r}{V}_{k(l-r-i),2}^{\left(r\right)}\left(\varsigma \right)D_i^r{\displaystyle \frac{{\left(-\varsigma \right)}^{i+r}}{i!}},$$

where as shown in (5), for $l\ge r+1$

$$\begin{array}{ccc}\hfill g_r\left(r\right)& =& U_k^r,g_l\left(r\right)={\displaystyle \frac{1}{(l-r)U_k}}\sum _{j=1}^{l-r}\left[\left(j+1\right)\left(r+1\right)-\left(l+1\right)\right]M_E(k,j+1,\varsigma )g_{l-j}\left(r\right),\hfill \\ \hfill f_r\left(r\right)& =& {\left(2\varsigma \right)}^r,f_l\left(r\right)={\displaystyle \frac{1}{2\varsigma (l-r)}}\sum _{j=1}^{l-r}\left(\left(j+1\right)\left(r+1\right)-\left(l+1\right)\right)N_L(k,j+1,\varsigma )f_{l-j}\left(r\right).\hfill \end{array}$$

Proof. 

By (12), we have   

$$\begin{array}{ccc}\hfill \sum _{l=r}^{\infty }{g}_l\left(r\right)t^l& =& {\left(\sum _{l=1}^{\infty }{M}_E(k,l,\varsigma )t^l\right)}^r=U_k^r\sum _{l=0}^{\infty }{U}_{k(l+1),2}^{\left(r\right)}\left(\varsigma \right)t^l\sum _{l=0}^{\infty }{\left(r\varsigma \right)}^l{\displaystyle \frac{t^l}{l!}}\hfill \\ & =& U_k^r\sum _{l=r}^{\infty }\sum _{i=0}^{l-r}{U}_{k(l-r-i+1),2}^{\left(r\right)}\left(\varsigma \right){\displaystyle \frac{{\left(r\varsigma \right)}^i}{i!}}{t}^l,\hfill \end{array}$$

as claimed. Similarly, the other identity is obtained.    □

In the following theorem, the polynomials $M_E(k,l,\varsigma )$ and $M_L(k,l,\varsigma )$ are expressed in closed form involving the generalized Fibonacci and Lucas polynomials.

Theorem 4.

For any positive integers $l,k,$ we have

$$M_L(k,l,\varsigma )=\sum _{j=0}^{l-2}\sum _{i=1}^{l-j-1}{\displaystyle \frac{{\varsigma }^{l-j-1}{V}_k^{l-j-i-1}}{i}}\left(U_k{V}_{kj}\left(\varsigma \right)-U_{k(j+1)}\left(\varsigma \right)\right),$$

and

$$\begin{array}{ccc}& & N_L(k,l,\varsigma )+{\left(-1\right)}^k{\varsigma }^{l+2}{V}_k^{l+2}\sum _{i=1}^l{\displaystyle \frac{1}{i{V}_k^i}}\hfill \\ & =& \sum _{j=1}^l\sum _{i=1}^j{\varsigma }^j{V}_k^{j-i}{\displaystyle \frac{1}{i}}\left({\displaystyle \frac{{\varsigma }^2{V}_k^2}{U_k}}{U}_{k(l-j-1)}\left(\varsigma \right)-{\displaystyle \frac{2\varsigma V_k}{U_k}}{U}_{k(l-j)}\left(\varsigma \right)+V_{k(l-j)}\left(\varsigma \right)\right).\hfill \end{array}$$

Proof. 

By (6) and (16), consider that

$$\begin{array}{ccc}\hfill \sum _{l=1}^{\infty }{M}_L(k,l,\varsigma )t^l& =& -U_k{\displaystyle \frac{tln(1-\varsigma t)}{1-\varsigma V_{k}t}}{\displaystyle \frac{1-\varsigma V_{k}t}{1-\varsigma V_{k}t+{(-1)}^k{t}^2}}\hfill \\ & =& -U_k{\displaystyle \frac{tln(1-\varsigma t)}{1-\varsigma V_{k}t}}\left({\displaystyle \frac{2-\varsigma V_{k}t}{1-\varsigma V_{k}t+{(-1)}^k{t}^2}}-{\displaystyle \frac{1}{U_k}}{\displaystyle \frac{U_k}{1-\varsigma V_{k}t+{(-1)}^k{t}^2}}\right)\hfill \\ & =& -U_k{\displaystyle \frac{tln(1-\varsigma t)}{1-\varsigma V_{k}t}}\left(\sum _{i=0}^{\infty }{V}_{ki}\left(\varsigma \right)t^i-{\displaystyle \frac{1}{U_k}}\sum _{i=0}^{\infty }{U}_{k\left(i+1\right)}\left(\varsigma \right)t^i\right)\hfill \\ & =& U_k\sum _{l=2}^{\infty }\sum _{i=1}^{l-1}{\displaystyle \frac{{\varsigma }^{l-1}{V}_k^{l-i-1}}{i}}{t}^l\sum _{i=0}^{\infty }\left(V_{ki}\left(\varsigma \right)-{\displaystyle \frac{1}{U_k}}{U}_{k(i+1)}\left(\varsigma \right)\right)t^i\hfill \end{array}$$

and then, equals

$$U_k\sum _{l=2}^{\infty }\sum _{j=0}^{l-2}\sum _{i=1}^{l-j-1}{\displaystyle \frac{{\varsigma }^{l-j-1}{V}_k^{l-j-i-1}}{i}}\left(V_{kj}\left(\varsigma \right)-{\displaystyle \frac{1}{U_k}}{U}_{k(j+1)}\left(\varsigma \right)\right)t^l$$

with product of the generating functions, the first sum is obtained. Similarly, by Lemma 3, the other sum is given. Thus, we have the proof.    □

The following theorem clearly reveals the relationship between the polynomials $M_E(k,l,\varsigma )$ and $M_L(k,l,\varsigma ).$

Theorem 5.

For any positive integers $l,k,$ we have

$$M_L(k,l,\varsigma )=\sum _{j=1}^l\sum _{i=1}^j{\left(-1\right)}^{j-i}{\displaystyle \frac{{\varsigma }^j}{i(j-i)!}}{M}_E(k,l-j,\varsigma ).$$

Proof. 

By (6), (11) and (14), we have   

$$\begin{array}{ccc}\hfill \sum _{l=1}^{\infty }{M}_L(k,l,\varsigma )t^l& =& -{\displaystyle \frac{U_{k}t}{1-\varsigma V_{k}t+{(-1)}^k{t}^2}}ln(1-\varsigma t)=-ln(1-\varsigma t)e^{-\varsigma t}\sum _{l=0}^{\infty }{M}_E(k,l,\varsigma )t^l\hfill \\ & =& \sum _{l=1}^{\infty }{\displaystyle \frac{{\varsigma }^l{t}^l}{l}}\sum _{l=0}^{\infty }{\displaystyle \frac{{\left(-\varsigma \right)}^l{t}^l}{l!}}\sum _{l=0}^{\infty }{M}_E(k,l,\varsigma )t^l\hfill \\ & =& \sum _{l=1}^{\infty }\sum _{i=1}^l{\displaystyle \frac{{\varsigma }^l}{i}}{\displaystyle \frac{{\left(-1\right)}^{l-i}}{(l-i)!}}{t}^l\sum _{l=0}^{\infty }{M}_E(k,l,\varsigma )t^l\hfill \\ & =& \sum _{l=1}^{\infty }\sum _{j=1}^l\sum _{i=1}^j{\displaystyle \frac{{\varsigma }^j}{i}}{\displaystyle \frac{{\left(-1\right)}^{j-i}}{(j-i)!}}{M}_E(k,l-j,\varsigma )t^l,\hfill \end{array}$$

as claimed.    □

The following theorem establishes a fundamental identity between the newly defined $M_E(k,j,\varsigma )$ polynomial family and the generalized Fibonacci polynomials $U_{kl}\left(\varsigma \right)$, formulated through the Stirling numbers of the first kind $S_1(i,j)$.

Theorem 6.

For any positive integers $l,k,$ we have

$$\sum _{i=0}^l\sum _{j=0}^i{\displaystyle \frac{j!{(-1)}^{j+i}}{i!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\varsigma }{l-i}}\right)U_{kj}\left(\varsigma \right)S_1(i,j)={\displaystyle \frac{{(-1)}^l}{l!}}\sum _{j=0}^l{\left(-1\right)}^{j}j!M_E(k,j,\varsigma )S_1(l,j).$$

Proof. 

From (7) and (11), we obtain that

$$\begin{array}{ccc}& & {\displaystyle \frac{U_{k}ln(1-t)e^{\varsigma ln(1-t)}}{1-\varsigma V_{k}ln(1-t)+{(-1)}^{k}ln{(1-t)}^2}}\hfill \\ & =& {(1-t)}^{\varsigma }\sum _{l=0}^{\infty }{U}_{kl}\left(\varsigma \right){(ln(1-t))}^l\hfill \\ & =& {(1-t)}^{\varsigma }\sum _{l=0}^{\infty }{\left(-1\right)}^{l}l!U_{kl}\left(\varsigma \right)\sum _{i=l}^{\infty }{S}_1(i,l){\displaystyle \frac{t^i}{i!}}\hfill \\ & =& \sum _{l=0}^{\infty }\left({\displaystyle \genfrac{}{}{0pt}{}{\varsigma }{l}}\right){(-1)}^l{t}^l\sum _{i=0}^{\infty }\sum _{l=0}^i{\left(-1\right)}^l{U}_{kl}\left(\varsigma \right)l!S_1(i,l){\displaystyle \frac{t^i}{i!}}\hfill \\ & =& \sum _{j=0}^{\infty }\sum _{i=0}^j\sum _{l=0}^i{(-1)}^{l+j-i}{U}_{kl}\left(\varsigma \right)S_1(i,l){\displaystyle \frac{l!}{i!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\varsigma }{j-i}}\right)t^j\hfill \end{array}$$

(17)

and by (7), (14)

$$\begin{array}{ccc}\hfill \sum _{l=0}^{\infty }{M}_E(k,l,\varsigma ){(ln(1-t))}^l& =& \sum _{l=0}^{\infty }{\left(-1\right)}^{l}l!M_E(k,l,\varsigma )\sum _{i=l}^{\infty }{S}_1(i,l){\displaystyle \frac{t^i}{i!}}\hfill \\ & =& \sum _{l=0}^{\infty }\sum _{j=0}^l{\left(-1\right)}^j{M}_E(k,j,\varsigma )j!S_1(l,j){\displaystyle \frac{t^l}{l!}}.\hfill \end{array}$$

(18)

Thus, combining (17) and (18), we have the proof.    □

3. Numerical Investigation of Root Properties of the Generalized Fibonacci Polynomials

In this section, we present the graphical representations of the polynomials, analyze their zeros [15], examine the distribution of roots, explore the correlations among the largest roots, and investigate both the root magnitude distribution and the root density distribution. The study of root structures arises from the need to observe the fundamental mathematical properties of these generalized polynomial families [16]. While root distribution patterns reveal structural relationships between different types of polynomials, the correlation analysis among the largest roots provides insights into their asymptotic behavior. Moreover, the density distribution analysis helps to characterize how these polynomials partition the complex plane and offers implications for special cases. In this paper, all data analysis and visualization processes were carried out using Python 3.12.4 [17] in the Jupyter Notebook [18] environment within the Anaconda distribution.

Now, the initial terms of the M-type and N-type polynomials are shown in

Table 3. A few of M-type polynomials for $k=2,3$ with $1\le l\le 6$.

l	${\mathit{M}}_{\mathit{E}}(2,\mathit{l},\mathit{\varsigma })$	${\mathit{M}}_{\mathit{L}}(3,\mathit{l},\mathit{\varsigma })$
1	2	0
2	$4\varsigma$	$2\varsigma$
3	${\displaystyle \frac{25}{2}}{\varsigma }^2-1$	$9{\varsigma }^2$
4	${\displaystyle \frac{1}{3}}(113{\varsigma }^3-21\varsigma )$	${\displaystyle \frac{2}{3}}\left(55{\varsigma }^3+3\varsigma \right)$
5	${\displaystyle \frac{2713}{24}}{\varsigma }^4-{\displaystyle \frac{67}{2}}{\varsigma }^2+1$	${\displaystyle \frac{1}{6}}\left(883{\varsigma }^4+102{\varsigma }^2\right)$
6	${\displaystyle \frac{1}{30}}\left(10174{\varsigma }^5-4145{\varsigma }^3+300\varsigma \right)$	${\displaystyle \frac{2}{15}}\left(4418{\varsigma }^5+785{\varsigma }^3+15\varsigma \right)$

and

Table 4. A few of N-type polynomials for $k=2,3$ with $1\le l\le 6$.

l	${\mathit{N}}_{\mathit{E}}(4,\mathit{l},\mathit{\varsigma })$	${\mathit{N}}_{\mathit{L}}(5,\mathit{l},\mathit{\varsigma })$
1	$9\varsigma$	$2\varsigma$
2	$57{\varsigma }^2-2$	$12{\varsigma }^2$
3	${\displaystyle \frac{1}{6}}\left(2375{\varsigma }^3-138\varsigma \right)$	${\displaystyle \frac{1}{6}}\left(763{\varsigma }^3+12\varsigma \right)$
4	${\displaystyle \frac{11079}{4}}{\varsigma }^4-218{\varsigma }^2+2$	${\displaystyle \frac{1}{3}}\left(4187{\varsigma }^4+102{\varsigma }^2\right)$
5	${\displaystyle \frac{1}{120}}\left(2326557{\varsigma }^5-230620{\varsigma }^3+4440\varsigma \right)$	${\displaystyle \frac{1}{60}}\left(920999{\varsigma }^5+30070{\varsigma }^3+120\varsigma \right)$
6	${\displaystyle \frac{48857677}{360}}{\varsigma }^6-{\displaystyle \frac{194671}{12}}{\varsigma }^4+477{\varsigma }^2-2$	${\displaystyle \frac{1}{20}}\left(3376959{\varsigma }^6+138170{\varsigma }^4+1120{\varsigma }^2\right)$

.

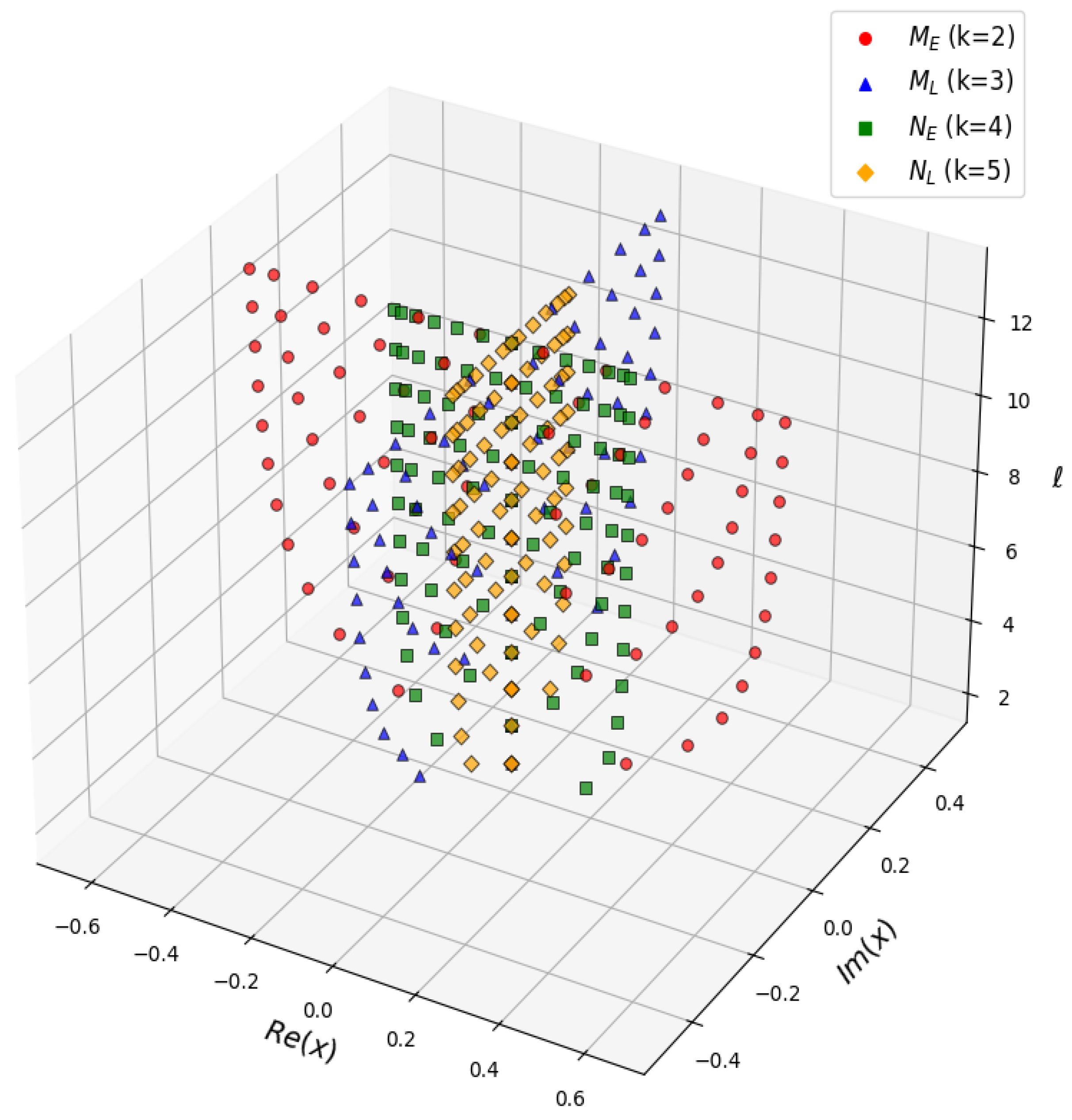
For each pairwise polynomial of degrees $2\le l\le 13$, the roots of $M_E\left(2,l,\varsigma \right)=0$ and $M_L\left(3,l,\varsigma \right)=0$ are distributed in a simpler, ring-like pattern, while the roots of $N_E\left(4,l,\varsigma \right)=0$ and $N_L\left(5,l,\varsigma \right)=0$ exhibit a denser and more complex structure near the center (

Table 5. Approximate solutions of $M_E\left(2,l,\varsigma \right)=0$ and $M_L\left(3,l,\varsigma \right)=0$.

Degree l	$\mathit{\varsigma }$ Solutions of ${\mathit{M}}_{\mathit{E}}\left(2,\mathit{l},\mathit{\varsigma }\right)=0$	$\mathit{\varsigma }$ Solutions of ${\mathit{M}}_{\mathit{L}}\left(3,\mathit{l},\mathit{\varsigma }\right)=0$
2	0	0
3	±0.2828	0
4	$0,\pm$0.4311	0, ±$0.2860i$
5	±0.5125, ±0.1835	0, ±$0.3399i$
6	0, ±$0.5597$, ±$0.3068$	0, ±$0.3948i$, ±$0.1476i$
7	±0.5888, ±0.3916, ±0.1360	0, ±$0.4263i$, ±$0.2416i$
8	0, ±0.6076, ±0.4514, ±0.2379	0, ±$0.4457i$, ±$0.3039i$, ±$0.1075i$

and

Table 6. Approximate solutions of $N_E\left(4,l,\varsigma \right)=0$ and $N_L\left(5,l,\varsigma \right)=0$.

Degree l	$\mathit{\varsigma }$ Solutions of ${\mathit{N}}_{\mathit{E}}\left(4,\mathit{l},\mathit{\varsigma }\right)=0$	$\mathit{\varsigma }$ Solutions of ${\mathit{N}}_{\mathit{L}}\left(5,\mathit{l},\mathit{\varsigma }\right)=0$
2	±0.1873	0
3	0, ±$0.2411$	0, ±$0.1254i$
4	±0.2610, ±$0.1030$	0, ±$0.1561i$
5	0, ±0.2701, ±$0.1617$	0, ±$0.1673i$, ±$0.0682i$
6	±0.2750, ±0.1972, ±$0.0708$	0, ±$0.1726i$, ±$0.1055i$
7	0, ±0.2780, ±0.2198, ±$0.1199$	0, ±$0.1754i$, ±$0.1275i$, ±$0.0440i$
8	±0.2798, ±0.2349, ± 0.1548, ±$0.0539$	0, ±$0.1771i$, ±$0.1414i$, ±$0.0780i$

). All roots are symmetric with respect to the real axis, and as l increases, the roots spread vertically, forming layered distributions. Among them, $N_L\left(5,l,\varsigma \right)$ shows the most complex root behavior, whereas $M_E\left(2,l,\varsigma \right)$ remains the simplest.

In Figure 2, each color represents a different value of k, and the roots illustrate their distribution on the complex plane. The fact that the roots form vertical layers as l increases indicates that there are characteristic ranges of root magnitudes for each degree. The symmetric distribution of all roots with respect to the real axis is a consequence of the polynomials having real coefficients. The tendency of the roots to cluster closer to the origin as k increases demonstrates the systematic influence of the parameter k on root magnitudes. The differences in the observed root distribution patterns between the polynomials $M_E\left(2,l,\varsigma \right)$ and $N_L\left(5,l,\varsigma \right)$ reflect the fundamental distinction between the generalized Fibonacci polynomials $U_{kl}\left(\varsigma \right)$ and the generalized Lucas polynomials $V_{kl}\left(\varsigma \right)$ used in their definitions. Although these polynomials have the same recurrence relations, they possess different initial conditions, which contribute to the differing root behaviors observed in the visualizations. The formation of vertical layers by the roots as l increases further confirms the presence of characteristic ranges of root magnitudes for each degree. More specifically, this difference can be explained by how the initial values propagate through the recurrence relations. The M-type polynomials, which originate from initial values of $U_0\left(\varsigma \right)=0$. This allows for the possibility of roots at the origin ($\varsigma =0$) for certain degrees, contributing to their simpler, ring-like patterns. In contrast, the N-type polynomials start from initial values of $V_0\left(\varsigma \right)=2$. The nonzero constant term ‘2’ in their definition generally results in a non-zero value at $\varsigma =0$, preventing a root at the origin and contributing to the denser and more complex root distributions observed for the $N_E\left(k,l,\varsigma \right)$ and $N_L\left(k,l,\varsigma \right)$ polynomials.

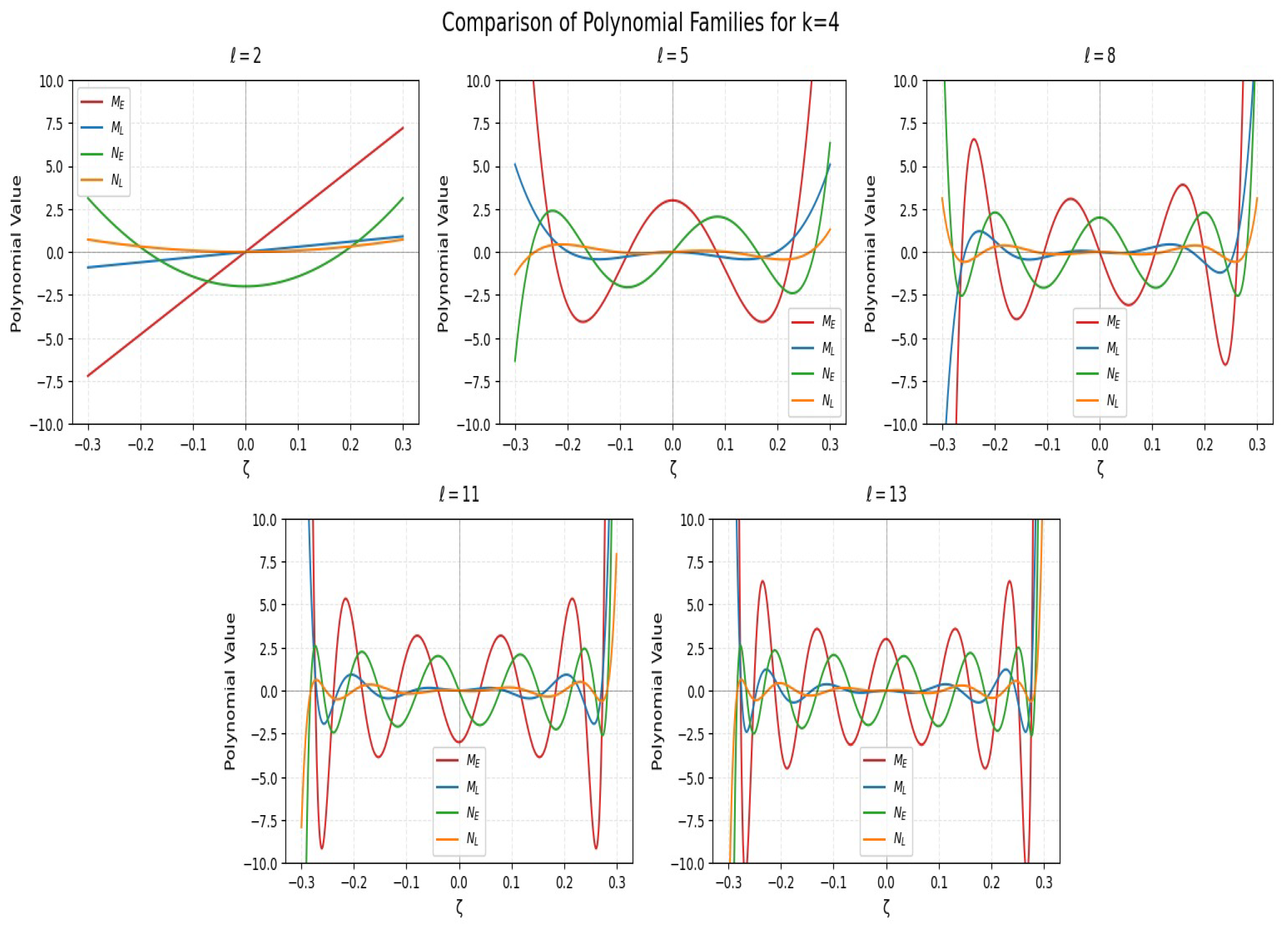
The Figure 3 clearly demonstrate how each polynomial family evolves with increasing degree. While M-type polynomials exhibit relatively smoother oscillatory behavior, N-type polynomials display more pronounced fluctuations, reflecting the different initial conditions in their recurrence relations. Notably, despite these visual differences in oscillation patterns, as l increases, the maximum root magnitudes across all families converge toward similar values and exhibit proportional growth rates.

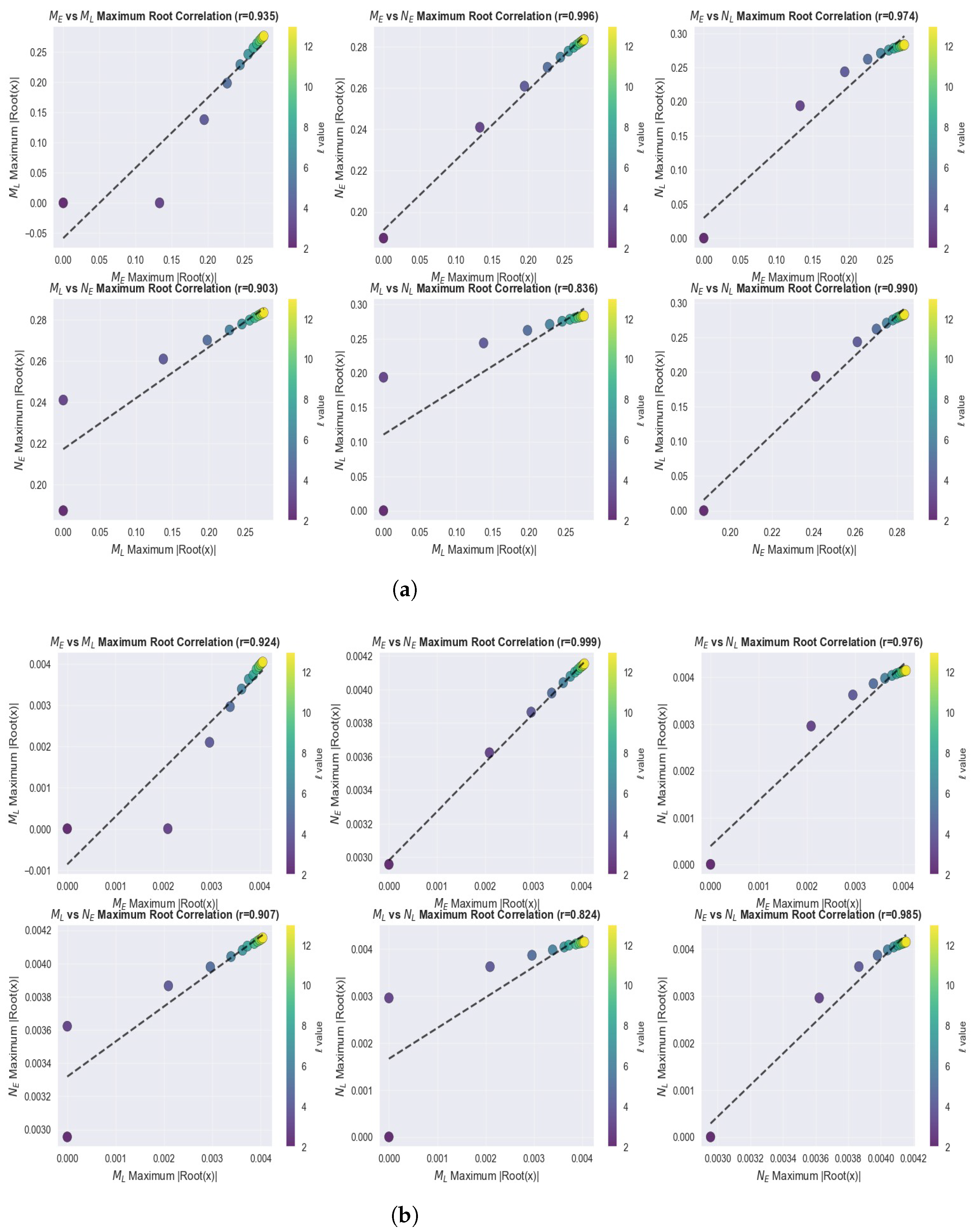
In Figure 4, high correlation values $(r>0.8)$ indicate that the polynomial families exhibit similar behavior for different values of k. As expected from the visual analysis in Figure 4, as l increases (lighter-colored points), the maximum root values display a stronger linear relationship. The minimal influence of changes in the parameter k on correlation values demonstrates that these relationships are fundamental properties independent of the choice of k. As illustrated in Figure 3 and Figure 4, the consistency of these behavioral patterns across different polynomial types reinforces the fundamental mathematical relationships underlying these generalized Fibonacci-based polynomial families. While the newly introduced polynomial families are not orthogonal in the classical sense, they are defined by recurrence relations. For high degrees, the leading-order behavior of solutions to such recurrences tends to dominate, overriding the influence of initial conditions or lower-order terms. This is the likely reason why the largest roots follow a similar, predictable pattern across the different families, explaining the high correlation observed.

In some correlation plots, particularly for lower-order polynomials ($l=2,3$, represented by dark-colored points), slight deviations of a few data points from the overall linear trend can be observed. These potential outliers correspond to cases where the recurrence relations have not yet converged to their asymptotic behavior. However, when the value of l exceeds 5, all polynomial families exhibit strong correlations, indicating that the linear relationships between the maximum roots become increasingly robust for higher-order polynomials. This observation is consistent with the expectation that, for sufficiently large degrees, the dominant terms in the recurrence relations govern the behavior, minimizing the influence of initial conditions that may cause deviations at lower degrees. Therefore, although outliers appear for small l values, they do not affect the general conclusion regarding the strong correlation patterns observed among the polynomial families.

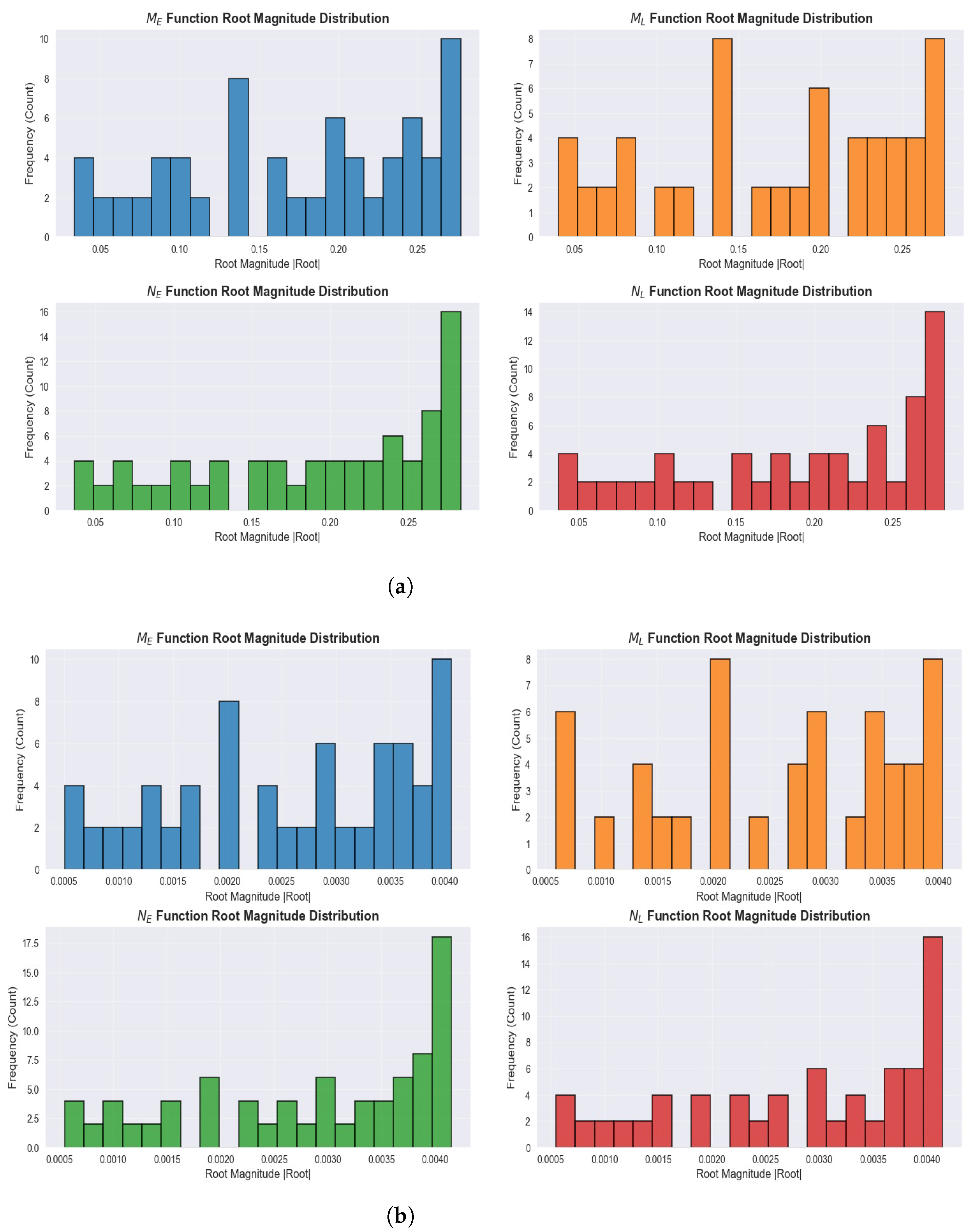
Figure 5 histograms reveal that the root magnitudes of different polynomial families exhibit distinct patterns. The $M_E\left(4,l,\varsigma \right)$ polynomial shows a relatively balanced distribution—that is, the histogram bars remain at comparable heights across different magnitude intervals—and contains roots spread over a wider range compared to the other families. The roots of each $M_L\left(4,l,\varsigma \right)$ polynomial tend to cluster at smaller values—as evidenced by the higher frequency counts concentrated on the left side of the histogram—and exhibit a narrower distribution range—illustrated by the compressed width of the non-zero bins. The $N_E\left(4,l,\varsigma \right)$ polynomial displays a pronounced accumulation of roots at larger magnitudes—observable as progressively taller bars toward the right side of the histogram—reflecting the nature of Lucas polynomials. The $N_L\left(4,l,\varsigma \right)$ polynomial shows the most dramatic behavior, with the majority of its roots concentrated in the highest-density interval—as indicated by the dominant peak in the rightmost bins containing significantly more roots than other intervals.

The increase of the k value from 4 to 7 leads to a general rise in density values for all polynomials; this is an expected outcome due to the direct influence of the k parameter on polynomial coefficients. Notably, the characteristic shape of each polynomial’s distribution is preserved—the relative pattern of bar heights and the location of concentration regions remain qualitatively similar despite the scale change. This indicates that the observed distribution patterns arise from the intrinsic structural properties of the polynomial families and are independent of the k value.

The clustering of large-magnitude roots in the $N_L\left(4,l,\varsigma \right)$ polynomial—referring to the accumulation in high-magnitude bins—supports the correlation analysis shown in Figure 4. The systematic behavior of these large roots arises from the fact that, as the polynomial degree increases, the largest roots dominate the overall behavior of the polynomial. The “maximum roots” compared in Figure 4 originate from this dense region—the area corresponding to the highest bars in the histogram. While the M-type polynomials $M_E\left(4,l,\varsigma \right)$ and $M_L\left(4,l,\varsigma \right)$, which include generalized Fibonacci polynomials, exhibit a more uniform distribution—with roots spread over multiple bins without any interval dominating the frequency count—the N-type polynomials $N_E\left(4,l,\varsigma \right)$ and $N_L\left(4,l,\varsigma \right)$, which include generalized Lucas polynomials, show concentration at extreme values—appearing as pronounced peaks at the high-magnitude end of the histograms. This distinction highlights the different mathematical characteristics of the two groups.

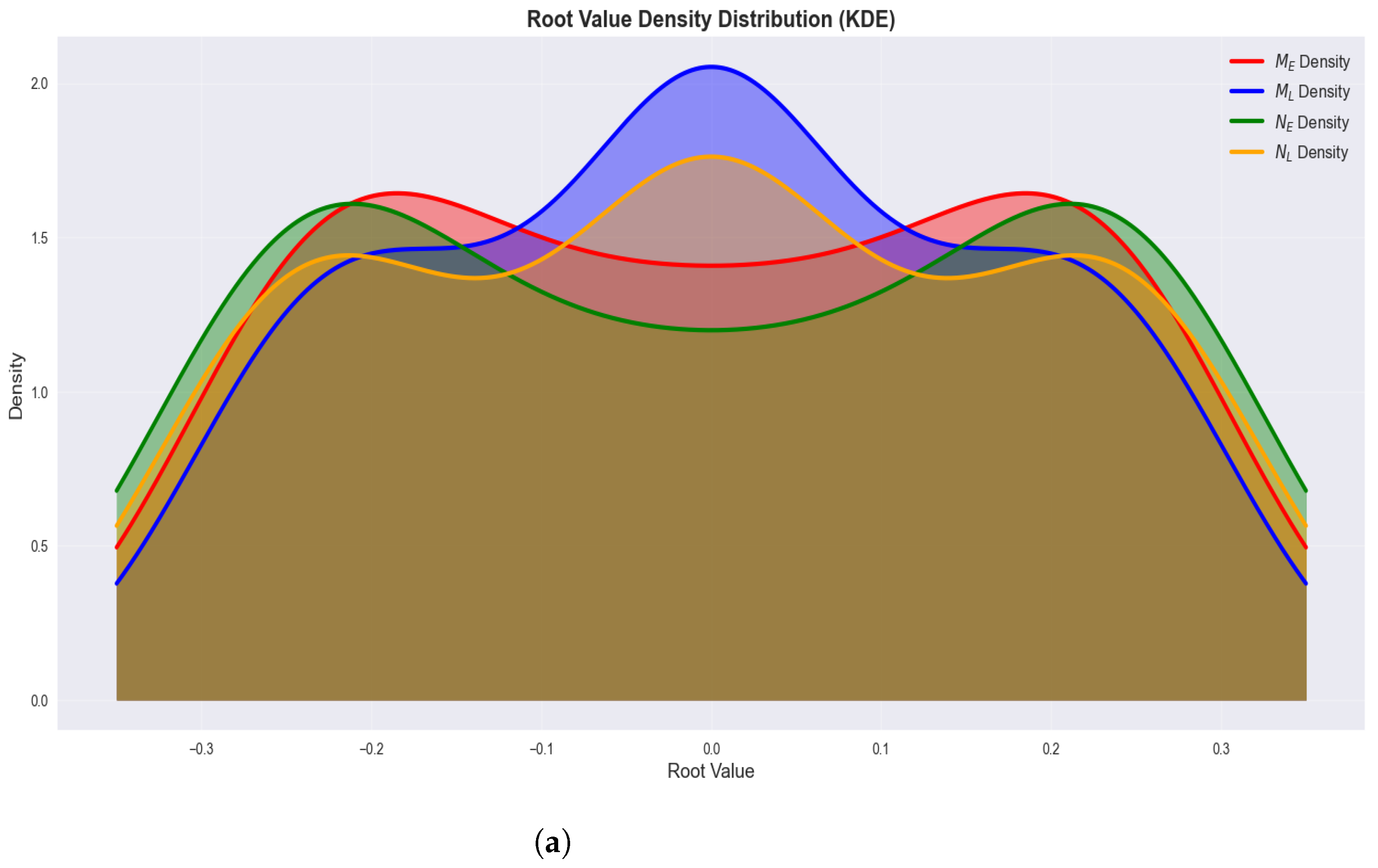
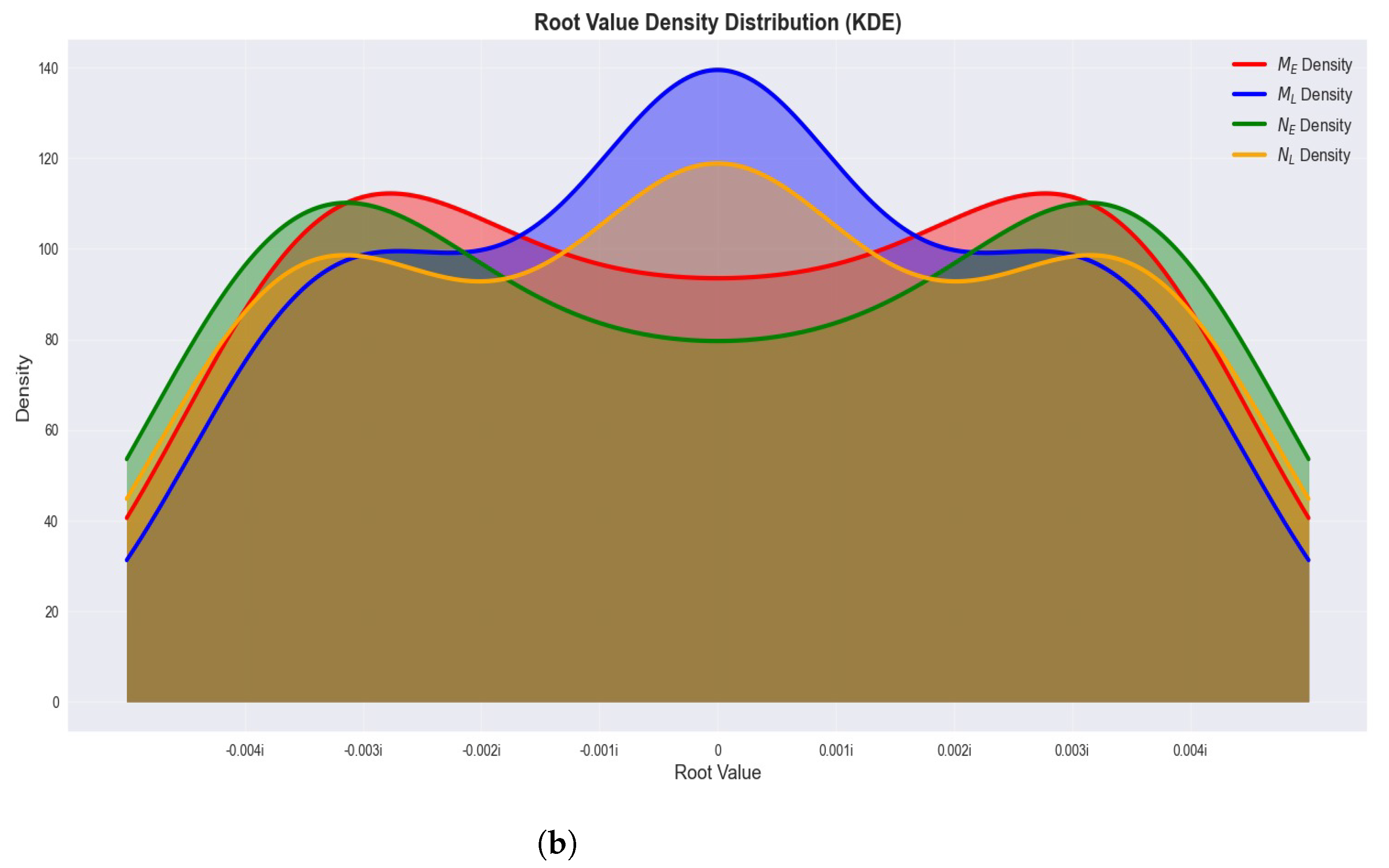
In Figure 6, the kernel density estimation (KDE) provides a detailed view of how the root values of each polynomial family are distributed along the real axis. To obtain smooth probability density estimates from discrete root samples, we employ Gaussian kernel density estimation using scipy.stats.gaussian_kde. The KDE method approximates the underlying continuous probability density function as:

$$\widehat{f}\left(x\right)={\displaystyle \frac{1}{nh}}\sum _{i=1}^{n}K\left({\displaystyle \frac{x-x_i}{h}}\right)$$

where K is the Gaussian kernel function $K\left(u\right)={\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{1}{2}}{u}^2}$, n is the total number of root samples across all degrees ($2\le l\le 13$), h is the bandwidth parameter automatically selected using Scott’s rule $h=n^{-1/(d+4)}\sigma$ (with $d=1$ denoting the dimensionality and $\sigma$ the standard deviation of the root data), and $x_i$ are the observed root values. The density curves are computed over 1000 equally spaced points in the interval $[-0.35,0.35]$.

The $M_L(4,l,\varsigma )$ polynomial (blue) exhibits a sharp, high peak centered around zero, indicating that most of its roots are concentrated near the origin. In contrast, the $M_E(4,l,\varsigma )$ polynomial (red) shows a bimodal distribution with peaks in two distinct regions, reflecting a tendency for roots to cluster in certain symmetric areas.

The $N_E(4,l,\varsigma )$ (green) and $N_L(4,l,\varsigma )$ (orange) polynomials display broader and more uniform distributions; however, $N_E(4,l,\varsigma )$ also exhibits a slight bimodal characteristic similar to $M_E(4,l,\varsigma )$. When the value of k increases from 4 to 7, the overall shapes of the distributions remain preserved, with only a scaling factor changing. This consistency confirms that the characteristic root distribution patterns of each polynomial family are intrinsic structural features, independent of the k parameter.

4. Conclusions

This study introduces a unified framework for the simultaneous investigation of generalized Fibonacci numbers and their associated polynomial extensions. Four novel families of polynomials—$M_E(k,l,\varsigma )$, $M_L(k,l,\varsigma )$, $N_E(k,l,\varsigma )$, and $N_L(k,l,\varsigma )$—have been defined through systematic extensions of the generalized Fibonacci polynomials $U_{kl}\left(\varsigma \right)$ and $V_{kl}\left(\varsigma \right)$. Furthermore, broader generalizations have been explored via the extended Humbert-type polynomials $U_{kl,m}^{\left(r\right)}\left(\varsigma \right)$ and $V_{kl,m}^{\left(r\right)}\left(\varsigma \right)$.

Based on the algebraic structures and generating functions of these newly introduced polynomial families, several original algebraic and combinatorial identities have been derived. In addition, graphical representations of selected polynomial families were presented, their roots were analyzed, the distribution of root values was examined, and the correlations among the largest roots were investigated. The root magnitude distribution and root value density distribution were also evaluated, contributing to a deeper understanding of the underlying structural properties of these polynomial sequences.

In future research, several directions can be pursued. These include investigating the combinatorial interpretations of the newly introduced polynomial families, deriving the differential equations for which these polynomials serve as solutions, exploring the applications of the obtained identities in other fields of mathematics and physics, and examining the orthogonality properties of these new polynomials. Such studies would further broaden the theoretical and applied significance of the proposed framework.