Comparative Study of Bitmixing, Marginal, and Lexicographic Methods for Color Image Morphological Processing

Abstract

A comprehensive comparative study is presented of three approaches for color morphological processing: the proposed bitmixing transformation, lexicographic ordering, and conventional marginal processing. The novel bitmixing method converts RGB channels into a single 24-bit scalar representation through bit-interleaving, preserving both color information and spatial ordering relationships. This enables the direct application of grayscale morphological operators while generally preserving structural, chromatic, and visual relationships in processed objects. Under appropriate conditions—such as when objects exhibit clear color-based boundaries and bilateral symmetry—the method tends to maintain these symmetries more consistently than marginal or lexicographic alternatives. Experimental evaluation shows that the bitmixing approach achieves a competitive balance between color preservation and computational efficiency. In specific scenarios involving color-defined regions and symmetric structures, it demonstrates modest advantages over marginal and lexicographic methods. These findings suggest that the proposed method can serve as a viable alternative in applications where color fidelity, structural coherence, and symmetry preservation are desirable, though its benefits are context-dependent.

1. Introduction

Mathematical morphology (MM) plays a crucial role in image analysis, supporting tasks such as filtering, segmentation, and object recognition [1,2]. Although early developments focused on binary and grayscale images, extending morphological operators to color domains remains an ongoing challenge due to the absence of natural ordering in multidimensional spaces [3,4].

Color image processing is widely adopted in applications such as medical imaging, object recognition, and digital media [5]. Among the various color models, RGB is the most common because of its direct relationship with acquisition and display systems. However, the strong correlation between channels and the nonlinear relationship with human perception complicates the design of operators that maintain perceptual coherence [6]. This limitation becomes critical in scenarios that require color consistency and the preservation of visual symmetry, such as segmenting anatomical structures, analyzing bilateral patterns in objects, and enhancing man-made symmetric designs [7].

Conventional strategies for morphological processing often rely on marginal techniques [8], where each channel is processed independently. Although computationally simple, marginal approaches frequently produce noisy boundaries and fragmented regions [9], breaking the natural symmetries present in the image. Lexicographic orderings [10] provide an alternative by establishing a global comparison across channels, preserving chromatic structure but at the cost of flexibility and computational efficiency [11].

Recent advances in color mathematical morphology have explored various strategies to overcome the limitations of traditional approaches. Al-Otum [12] proposed a modified vector distance measure with color pixel classification to define morphological operators. Sun et al. [13] introduced an order space-based morphology for color image processing, which constructs an ordering relation based on spatial and color information. Additionally, applications in medical imaging [14] and remote sensing [15] have demonstrated the importance of color morphology in handling complex visual data. These studies underscore the need for methods that preserve color fidelity and structural integrity.

This work introduces bitmixing, a novel approach that encodes the RGB components into a single 24-bit representation, enabling morphological operators to process color images efficiently while preserving inter-channel relationships. While classical Morton ordering typically interleaves bits without perceptual prioritization, bitmixing incorporates a perceptually-weighted scheme that assigns higher significance to green bits, followed by red and blue, aligning with human visual sensitivity. This differs fundamentally from lexicographic ordering, which establishes a rigid channel-based priority (e.g., Green > Red > Blue) at the byte level rather than the bit level. Unlike marginal methods, bitmixing avoids chromatic inconsistencies while reducing complexity compared with lexicographic orderings, without sacrificing perceptual coherence. Importantly, the technique reinforces symmetry in both chromatic and structural features, ensuring that symmetric boundaries and regions remain consistent throughout the morphological processing. Experimental evaluation indicates that the bitmixing method can achieve comparable or, in selected cases, slightly improved segmentation accuracy and symmetry preservation relative to marginal and lexicographic approaches. Improvements in color fidelity and boundary consistency are observed primarily in images with well-defined chromatic regions and structural symmetry, as supported by both quantitative metrics (Dice and Jaccard indices) and qualitative inspection.

The proposed methodology is evaluated through comparative experiments with marginal and lexicographic approaches, focusing on segmentation quality, chromatic consistency, boundary preservation, and symmetry retention. The remainder of this paper is organized as follows: Section 2 reviews morphological operators for color images, including marginal and lexicographic methods. Section 3 details the proposed bitmixing technique, and Section 4 presents its integration with morphological operators. Experimental design and results are described in Section 5, followed by discussion in Section 6 and conclusions in Section 7.

2. Fundamentals of Mathematical Morphology and Color Ordering

2.1. Basic Notions of Morphological Transformations

Mathematical morphology is primarily based on the so-called increasing transformations [1,2]. A transformation T is said to be increasing if, for two sets X and Y such that $X\subset Y$, it holds that $T\left(X\right)\subset T\left(Y\right)$. In the gray-level case, the usual ordering relation replaces the inclusion relation. That is, given two functions f and g, the notation $f\le g$ is defined to mean $f\left(x\right)\le g\left(x\right)$ for all x. A transformation T is said to be increasing if, whenever $f\le g$, it follows that $T\left(f\right)\le T\left(g\right)$. In other words, increasing transformations preserve order.

A second important property is idempotence. A transformation T is idempotent if and only if $T\left(T\right(f\left)\right)=T\left(f\right)$ [4]. The combination of both properties plays a fundamental role in morphological filtering. A morphological filter is defined as an operator that is both increasing and idempotent. The most basic morphological filters are the opening ${\gamma }_{\lambda B}$ and the closing ${\phi }_{\lambda B}$ with a given structuring element B. Here, $\breve{B}$ denotes the reflection of B with respect to its origin, i.e., $\breve{B}=\{-x:x\in B\}$, and $\lambda$ is a scaling factor. Morphological opening and closing are expressed as

$${\gamma }_{\lambda B}\left(f\right)={\delta }_{\lambda \breve{B}}\left({\epsilon }_{\lambda B}\left(f\right)\right)\mathrm{and}{\phi }_{\lambda B}\left(f\right)={\epsilon }_{\lambda \breve{B}}\left({\delta }_{\lambda B}\left(f\right)\right),$$

(1)

where ${\epsilon }_{\lambda B}$ and ${\delta }_{\lambda B}$ denote morphological erosion and dilation, respectively, given by

$${\epsilon }_{\lambda B}\left(f\right)\left(x\right)=\bigwedge \{f\left(y\right):y\in \lambda {\breve{B}}_x\},{\delta }_{\lambda B}\left(f\right)\left(x\right)=\bigvee \{f\left(y\right):y\in \lambda {\breve{B}}_x\},$$

where ⋀ and ⋁ denote the infimum and supremum operators, respectively.

From these fundamental operators, other transformations can be derived. For instance, the internal gradient, ${\mathrm{gradi}}_{\lambda B}=f-{\epsilon }_{\lambda B}\left(f\right)$, is commonly used for contour detection and image segmentation. Similarly, the white top-hat (WTH) operator, defined as $WTH=f-{\gamma }_{\lambda B}$, highlights bright regions of the image. An important aspect of these operators is their ability to preserve or emphasize structural and visual symmetries present in the image, especially when symmetric structuring elements (such as disks, squares, or hexagons) are employed. In practice, this property ensures that objects with bilateral or radial symmetry—such as faces, biological structures, or man-made patterns like logos and signs—are processed in a way that maintains their inherent balance and coherence. The duality between opening and closing is itself a manifestation of morphological symmetry, reinforcing the relevance of this concept in both theoretical and practical contexts.

A critical requirement for applying these operators is the existence of a complete ordering of pixel values, which is necessary to compute the supremum and infimum. This condition is straightforward for grayscale images but becomes the central challenge in color imaging, where pixels are represented as multivariate vectors (e.g., RGB) [4,11]. The following sections explore methods for defining such an order in color images, with particular attention to preserving both color fidelity and visual symmetry in the results.

2.2. Basic Notions on RGB Space, Lexicographic, and Marginal Methods

The RGB color model is an additive system that produces a wide gamut of colors by combining varying intensities of its three primary components: Red, Green, and Blue [5]. This model is standard for digital image acquisition and display devices. However, applying mathematical morphology to RGB images is non-trivial because morphological operators require a complete ordering of pixel values, while pixels in an RGB image are inherently three-dimensional vectors. This subsection reviews two common strategies for imposing an order in the RGB space for morphological processing.

2.2.1. Marginal Processing

A straightforward approach, known as marginal processing or component-wise processing, treats each color channel (R, G, and B) independently as a separate grayscale image [8]. The morphological operator is applied to each channel independently, and the processed channels are then combined to reconstruct the output color image.

Although this method is simple and computationally efficient, its main drawback is that it ignores the correlation between color channels. As a result, it often introduces new colors (false colors) not present in the original image, and produces artifacts such as color shifts, noisy edges, and fragmented regions in the segmentation results [11]. This occurs because the supremum and infimum are computed per channel, without considering the joint vectorial nature of color data.

2.2.2. Vector Ordering and the Lexicographic Method

To address the limitations of marginal processing, pixel values can be treated as multidimensional vectors, and a vector ordering must be defined. A fundamental concept for mapping multidimensional data to a single dimension while preserving spatial locality is the Morton order (also known as Z-order) [16]. In this scheme, the bits of the coordinates of a point in a multidimensional space are interleaved to form a single number, ensuring that points close in the original space remain close in the one-dimensional sequence, as illustrated in Figure 1.

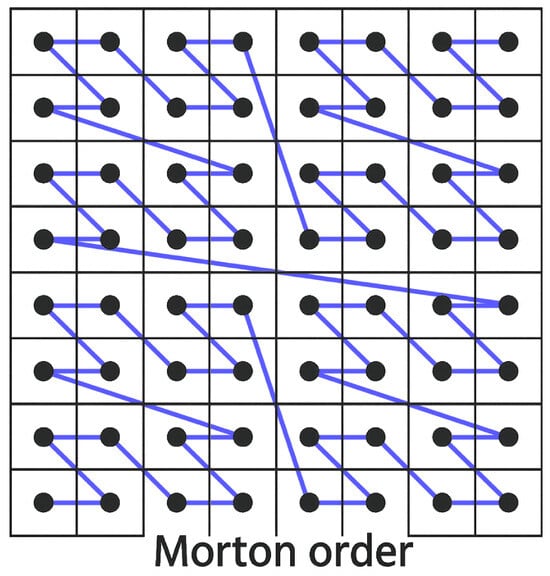
Figure 1. Morton ordering in 2D [16], illustrating the bit-interleaving mechanism used to define Bitmixing and Lexicographic color ordering.

The proposed bitmixing method builds upon this Morton concept, introducing key modifications: perceptual weighting of color channels and specific adaptation for morphological processing. The lexicographic ordering method can be viewed as a particular case of Morton-like ordering, where comparisons are performed component-by-component in a predefined priority sequence, rather than bit-by-bit. However, this distinction is crucial: lexicographic ordering operates at the channel level, while bitmixing operates at the bit level, providing finer control over color relationships. A total order is imposed on the RGB vectors by sequentially comparing the scalar values of their components according to a chosen priority, typically guided by perceptual relevance (e.g., Green, then Red, then Blue, due to the human visual system’s greater sensitivity to green) [11].

Formally, for the priority order $\mathrm{Green}\to \mathrm{Red}\to \mathrm{Blue}$, a pixel $p_1=(G_1,R_1,B_1)$ is considered smaller than a pixel $p_2=(G_2,R_2,B_2)$ if and only if:

• $G_1<G_2$, or
• $G_1=G_2$ and $R_1<R_2$, or
• $G_1=G_2$, $R_1=R_2$, and $B_1<B_2$.

This method provides a total order for all possible RGB vectors, enabling unambiguous computation of the supremum and infimum within a local neighborhood. Consequently, standard grayscale morphological operators can be directly extended to lexicographically ordered RGB images. Compared with marginal processing, this approach better preserves the inter-channel relationships, leading to more coherent filtering with fewer chromatic distortions [9].

A visual comparison of the two methods is presented in Figure 2. Original images are shown in Figure 2a,d,g. In the lexicographic case, Figure 2b,e,h, object boundaries appear sharper since the relationships among the three color channels are preserved. This approach provides a better component treatment and an improved retention of the chromatic structure. For instance, in Figure 2h, the regions are grouped into smooth, well-ordered concentric areas, demonstrating that the lexicographic approach is more faithful to the original color relationships. In contrast, the marginal approach often produces irregular boundaries and fragmented regions. This situation can be observed in Figure 2f, since each channel may introduce different borders independently of the others. The marginal opening in Figure 2c does not affect the image because the size of the components is less than the size of the structuring element $\mu =10$. In Figure 2i, concentric regions appear more diffuse and fragmented, with partial loss of chromatic coherence. In summary, the lexicographic method yields perceptually more consistent results, whereas marginal processing emphasizes fine differences in individual channels but at the cost of noisy and less uniform component treatment.

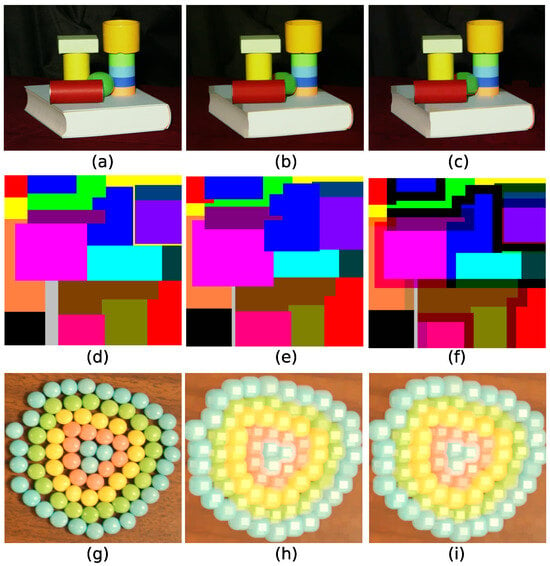
Figure 2. (a,d,g) Original images; (b) Lexicographic opening with size $\mu =10$ of (a); (c) Marginal opening with size $\mu =10$ of (a); (e) Lexicographic erosion with size $\mu =8$ of (d); (f) Marginal erosion with size $\mu =8$ of (d); (h) Lexicographic dilation with size $\mu =5$ of (g); and (i) Marginal dilation with size $\mu =5$ of (g). The images in (h,i) show the shape of the structural element, which is a square in this case. This behavior occurs as the mu size increases.

3. Proposed Method: Bitmixing Transformation

Traditional strategies for defining a total order in color morphology present important limitations. The lexicographical method, although straightforward, enforces a rigid byte-wise prioritization of color channels that does not adequately reflect their joint contribution to perceived color [11]. Conversely, the marginal approach, while simple to implement, treats channels independently and thus fails to preserve the vectorial nature of color, often introducing visual artifacts [8]. These artifacts typically manifest as broken or asymmetric boundaries in naturally symmetric objects, compromising the visual integrity of the processed image.

To overcome these drawbacks, the bitmixing transformation is proposed, a Morton-inspired encoding that interleaves the bits of the RGB channels into a single scalar index. Unlike standard Morton ordering used in spatial indexing, bitmixing incorporates perceptual weighting and is specifically designed for color morphology applications. This encoding simultaneously preserves spatial locality in the color space and incorporates perceptual weighting consistent with human visual sensitivity. As a consequence, symmetric features in the scene, such as bilateral objects, circular patterns, or repeated textures, are more faithfully preserved during morphological operations.

In the proposed scheme, the three 8-bit channel values $(R,G,B)$ of each pixel are mapped into a single 24-bit integer through bit interleaving. The ordering of the interleaving is designed to approximate human visual perception, assigning the highest significance to green bits, followed by red and blue [17,18]. This choice reflects the known sensitivity of the human visual system, which is more responsive to green than red and finally blue stimuli, and closely parallels the perceptual weightings embedded in color models such as YIQ and YUV [5]. For comparison, the luminance component in YIQ is defined as

$$Y=0.299R+0.587G+0.114B,$$

while the effective weighting derived from the bit significance in bitmixing is approximately

$${\displaystyle \frac{2}{7}}R+{\displaystyle \frac{4}{7}}G+{\displaystyle \frac{1}{7}}B\approx 0.286R+0.571G+0.143B,$$

This closely aligns with the perceptual distribution of the YIQ model, supporting a balanced treatment of chromatic components and reinforcing perceptual symmetry.

Formally, the encoding is defined as

$$I\left(p\right)=\sum _{j=0}^7{2}^{3j+2}{G}_j+\sum _{j=0}^7{2}^{3j+1}{R}_j+\sum _{j=0}^7{2}^{3j}{B}_j,$$

(2)

where $G_j$, $R_j$, and $B_j$ denote the j-th bit (from most significant, $j=7$, to least significant, $j=0$) of the green, red, and blue channels, respectively. Each consecutive triplet of bits in the resulting 24-bit value, therefore, consists of one green, one red, and one blue bit in descending order of perceptual significance. The encoding procedure is illustrated in Figure 3.

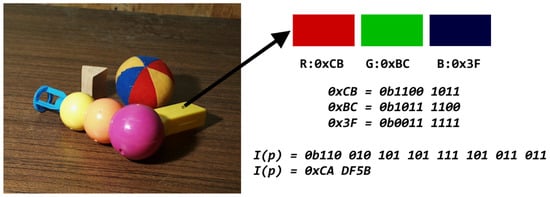
Figure 3. Bitmixing transformation process for an RGB pixel, showing the scalar encoding and exact decoding. The bitmixing representation produces a matrix of large integer values that cannot be directly visualized as an image. However, standard grayscale morphological operators can be applied directly on this matrix, thereby avoiding channel fusion during processing and preserving structural and visual symmetries present in the original image.

The inverse transformation reconstructs the original RGB triplet from the interleaved scalar via bitwise extraction:

$$\begin{array}{cc}\hfill R& =\sum _{j=0}^7{2}^j·⌊{\displaystyle \frac{I\left(p\right)}{2^{3j+1}}}⌋mod2,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill G& =\sum _{j=0}^7{2}^j·⌊{\displaystyle \frac{I\left(p\right)}{2^{3j+2}}}⌋mod2,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill B& =\sum _{j=0}^7{2}^j·⌊{\displaystyle \frac{I\left(p\right)}{2^{3j}}}⌋mod2.\hfill \end{array}$$

(5)

This decoding process relies exclusively on shift-and-mask operations, ensuring exact and efficient recovery of the original RGB components.

The bitmixing transformation exhibits four properties that make it particularly suitable for mathematical morphology:

• Lossless reversibility: The mapping is perfectly invertible, ensuring that no color information is lost during transformation.
• Total order: The scalar values naturally induce a strict total order, satisfying a fundamental requirement for the direct application of grayscale morphological operators [1].
• Perceptual weighting: The bit-interleaving scheme reflects the perceptual importance of RGB channels, with green prioritized over red and blue, thereby aligning the transformation with human visual sensitivity [17,18].
• Symmetry preservation: By treating all pixels through a unified scalar representation, the method maintains bilateral and radial symmetries in objects and boundaries, reducing distortions commonly introduced by marginal or lexicographic approaches.

These properties facilitate the direct use of standard grayscale morphological operators on color images represented in the bitmixing domain, offering a unified alternative to channel-wise processing that, in many cases, better preserves perceptual fidelity and visual symmetry—particularly when color and structure are tightly coupled.

4. Morphological Operators in Bitmixing Space

The bitmixing transformation enables the application of standard grayscale morphological operators to color images by creating a scalar representation where a total order is preserved. This allows direct implementation of erosion, dilation, opening, closing, and top-hat transformations to the bitmixing image $I\left(p\right)$, as the total order property ensures well-defined supremum and infimum operations [1].

For operations involving arithmetic differences (e.g., internal gradient), a specialized strategy is necessary because direct arithmetic on bitmixing values would produce meaningless results in RGB space due to the non-linear nature of the bitmixing transformation. To overcome this issue, a proportional adjustment procedure is adopted, which maps the magnitude change from the bitmixing domain back to the RGB space while preserving the vector direction of the color. This approach minimizes hue shifts and uniformly adjusts the magnitude of each channel.

The procedure is as follows:

Step 1:

Bitmixing transformation: Convert the original RGB image f to its bitmixing representation $I\left(f\right)$.

Step 2:

Linear operator application: Apply the chosen linear or morphological operator L to obtain $L\left(I\right(f\left)\right)$.

Step 3:

Magnitude change calculation: Compute the proportional adjustment:

$$\mathit{adjust}={\displaystyle \frac{I\left(f\right)-L\left(I\right(f\left)\right)}{I\left(f\right)}}.$$

Step 4:

RGB proportional adjustment: Apply the adjustment factor to the original color channels:

$$f_{\mathrm{result}}=(\mathit{adjust}·R,\mathit{adjust}·G,\mathit{adjust}·B).$$

Note that for the morphological operators used in this study (e.g., erosion for internal gradient), the operator L is anti-extensive, meaning that $L\left(I\right(f\left)\right)\le I\left(f\right)$ for all pixels. Therefore, the numerator $I\left(f\right)-L\left(I\right(f\left)\right)$ is non-negative, and the adjustment factor $adjust$ is also non-negative. Additionally, the RGB values are represented in the range [0, 255], and the adjustment factor is applied proportionally, ensuring that the resulting values remain within the valid range. This guarantees numerical stability and prevents the introduction of artifacts.

This strategy ensures that morphological operations are faithfully reflected in the resulting image while preserving the original chromatic properties. The uniform scaling of RGB components maintains the color direction, while proportionally altering their magnitude according to the changes observed in the bitmixing domain.

This proportional adjustment strategy generally preserves color fidelity and helps maintain consistent treatment of symmetric intensity changes across regions, thereby reducing channel-based biases that could otherwise disrupt symmetric patterns.

This approach is particularly valuable for gradient-based segmentation, as it effectively highlights edges and transitions without introducing color artifacts, thereby maintaining perceptual relationships between pixels while leveraging the full potential of mathematical morphology.

4.1. Comparison with the Marginal and Lexicographic Approaches

The fundamental difference between the marginal approach and the proposed bitmixing-based framework is illustrated in the block diagrams of Figure 4 and Figure 5.

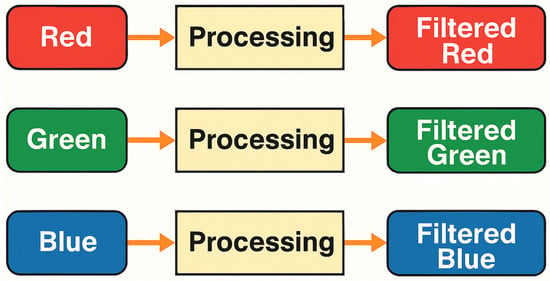
Figure 4. Block diagram of the marginal approach to color image processing.

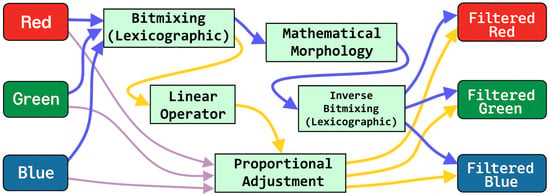
Figure 5. Block diagram of the Bitmixing-based (Lexicographic-based) processing framework showing dual paths for morphological and linear filtering with proportional adjustment.

Figure 4 depicts the conventional marginal processing pipeline, where each RGB channel is processed independently by the morphological operator before being recombined, often leading to the chromatic inconsistencies discussed in Section 2.2.1.

In contrast, Figure 5 outlines the proposed bitmixing framework. This framework features a dual-path strategy: (i) a direct path for applying standard morphological operators to the encoded scalar image, and (ii) a proportional adjustment path for linear operations, ensuring color fidelity as described previously.

The lexicographic method follows a similar scalar processing pipeline to bitmixing but employs a different ordering principle.

4.2. Visual Results of Morphological Operators

The processed images in Figure 6 illustrate the visual differences between the lexicographic and marginal approaches under different morphological operations. Original images are shown in Figure 6a,e,i.

Figure 6. Different morphological transformations. Original images are in (a,e,i). The morphological opening with size $\mu =5$ for: (b) bitmixing, (c) marginal, and (d) lexicographic. The internal gradient with size $\mu =1$ for: (f) bitmixing, (g) marginal, and (h) lexicographic. The white top hat with size $\mu =8$ for: (j) bitmixing, (k) marginal, and (l) lexicographic.

For the lexicographic method, as seen in Figure 6d,h,l, the object boundaries appear more clearly defined because the relationship among the three color channels (R, G, B) is preserved simultaneously. This results in a more coherent chromatic structure, where segmented regions maintain smooth and organized transitions, particularly evident in Figure 6h,l.

In contrast, the marginal method, shown in Figure 6c,g,k, produces irregular boundaries and fragmented regions since each channel is processed independently. This often leads to chromatic inconsistencies and a noisier appearance, as concentric regions appear less uniform and more diffuse in Figure 6g compared with their lexicographic counterparts.

Overall, the lexicographic approach preserves perceptual color coherence more effectively, while the marginal approach emphasizes fine channel-based differences at the expense of spatial and chromatic uniformity.

Respect to images in Figure 6b,f,j, they were obtained with the bitmixing algorithm. Notice a better performance in the output images for the internal gradient Figure 6f and top-hat transformations in Figure 6j when compared with other methods. In the case of Figure 6b, the morphological opening for the bitmixing, the comparison with respect to the other algorithms is hard because there are no notable differences.

5. Experimental Evaluation

An experimental evaluation is conducted to assess the segmentation performance of the bitmixing, lexicographic, and marginal methods against Ground Truth (GT) images using a publicly available color image database [19] (IITP-close and IITP-diffuse folders provide 12 pictures in BMP format, https://github.com/Visillect/colorsegdataset/tree/master, accessed on 30 September 2025). This set of 12 images is non-overdetailed; hence there will be a better visual interpretation after segmentation. The segmentation is performed using identical parameters for the lexicographic, marginal, and bitmixing methods. Thus, the generation of new contours is detected by comparing the Jaccard and Dice indices against the GT images. The technique with the highest Dice and Jaccard indices demonstrates superior accuracy in preserving the spatial boundaries and extent of regions. While these metrics primarily assess geometric alignment with the ground truth, they indirectly reflect the method’s ability to maintain coherent color regions, as accurate segmentation typically prevents color fragmentation and boundary artifacts. It is noteworthy to mention two things: (i) The lexicographic, marginal, and bitmixing methods process the images directly in RGB space. This is why these methods are compared, and (ii) the goal of the experiment is not to obtain beautiful segmentation; instead, the goal is to apply the same parameters and identify which segmentation best preserves colors and regions. For this, the application of the exact parameters is required.

5.1. Experimental Setup

The experimental design focused on a controlled comparison of the three color processing methods under identical conditions. While the dataset size is limited to 12 images, it provides a foundation for initial validation. The segmentation pipeline, illustrated in Figure 7, was applied uniformly to all images and methods following these steps:

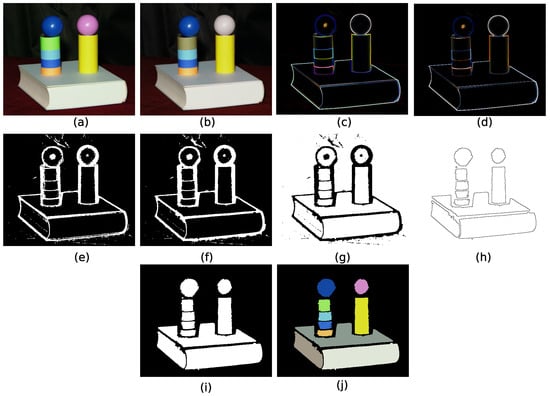
Figure 7. This figure presents the procedure followed to segment an image using bitmixing, marginal, and lexicographic algorithms. (a) Original image; (b) median filter size $\mu =1$ to eliminate noise in (a); (c) internal gradient size $\mu =1$ of the image in (b); (d) median filter size $\mu =1$ of (c) to flat the gradient; (e) threshold of the image in (d); (f) morphological closing of the image in (e) to close gaps; (g) inversion of the image in (g,h,i) Regions touching edges are removed and holes are filled; (j) Each region of the mask is filled with the color average of the same region as the original.

• Preprocessing: A median filter size $\mu =1$ was applied to the original image (Figure 7a) to reduce noise (Figure 7b).
• Gradient calculation: The internal morphological gradient size $\mu =1$ was computed on the preprocessed image to emphasize contours (Figure 7c).
• Gradient smoothing: Another median filter (size $\mu =1$) was applied to the gradient image to homogenize gradient values (Figure 7d).
• Thresholding: The processed gradient image was binarized using a fixed threshold value of 3 (Figure 7e).
• Morphological closing: This transformation was applied to the binary image to connect broken segments and close gaps (Figure 7f).
• Image inversion: The binary image was inverted to obtain the initial regions (Figure 7g).
• Border region removal: Regions touching the image border were removed to eliminate incomplete segments.
• Background propagation and Hole Filling: Background propagation from the image border was performed to identify the background, followed by inversion to fill any remaining holes within regions (Figure 7h).
• Connected component labeling: 8-connected component labeling was applied to identify distinct regions.
• Edge image generation: Finally, an edge image was generated where regions are represented by 1 and edges by 0, and each segmented region in the mask was filled with the average color of its corresponding pixels in the original image, resulting in the final segmented color image (Figure 7i). The Figure 7j is a mask obtained between the original image and the image in Figure 7i.

The structuring element ($SE$) for all morphological operations was a disk of size $\mu$, with $\mu$ values specified in each operation. This pipeline was implemented consistently for all three color processing methods (marginal, bitmixing, and lexicographic) to ensure a fair comparison.

5.2. Dataset and Metrics

The authors of this database provide GT images, marking the different regions that partition the image. These markings are removed and thresholded, resulting in the pictures shown in Figure 8, which will be used for comparison with the results. The segmentation results for the bitmixing, lexicographic, and marginal methods are presented in Figure 9.

Figure 8. Segmented ground truth images taken from the database [19] The images provided in the dataset can be observed in the last column of the Figure 9.

Figure 9. Segmented images using the steps mentioned in the pipeline in Figure 7 for bitmixing, marginal and lexicographic methods.

The performance of each method was quantitatively assessed by comparing its segmentation result to the segmented GT (Figure 8) using the Dice coefficient and the Jaccard index, common metrics for evaluating segmentation accuracy against a ground truth. These metrics are defined as follows [20,21,22]:

$$\mathrm{Dice}={\displaystyle \frac{2\times |X\cap Y|}{\left|X\right|+\left|Y\right|}}$$

(6)

$$\mathrm{Jaccard}={\displaystyle \frac{|X\cap Y|}{|X\cup Y|}}$$

(7)

where X represents the segmented region and Y represents the ground truth region.

5.3. Results and Analysis

The quantitative results are summarized in Table 1, which shows the Dice and Jaccard indices along with the Mean Squared Error calculated from these indices. Analysis of these results reveals three distinct performance patterns among the evaluated methods:

Table 1. Quantitative evaluation using Dice and Jaccard indices, comparing spatial segmentation accuracy against Ground Truth. Higher values indicate better alignment of the region boundary. The last row displays the Mean Squared Error considering the twelve values for each index and for each segmentation method.

	Bitmixing vs. GT		Lexicographic vs. GT		Marginal vs. GT
Images	Dice	Jaccard	Dice	Jaccard	Dice	Jaccard
BONCH-01	0.52	0.35	0.52	0.35	0.52	0.35
BONCH-02	0.55	0.38	0.55	0.38	0.55	0.38
BONCH-03	0.48	0.32	0.48	0.31	0.48	0.31
BONCH-04	0.48	0.31	0.48	0.31	0.48	0.31
BONCH-05	0.59	0.42	0.57	0.40	0.57	0.40
FAN&BALL	0.10	0.05	0.09	0.05	0.09	0.05
PRZM2CUB	0.88	0.78	0.88	0.78	0.88	0.78
PYRPRCUB	0.84	0.73	0.85	0.73	0.85	0.73
SCENE1GR	0.93	0.88	0.93	0.87	0.93	0.87
SCENE2OR	0.10	0.05	0.10	0.05	0.10	0.05
SPH&BALL	0.19	0.10	0.18	0.10	0.18	0.10
WOOL2SPH	0.17	0.09	0.16	0.09	0.16	0.09
Mean Square error	0.5881	0.6868	0.5927	0.6892	0.5927	0.6892

• Functional equivalence. For the majority of the images in the dataset (BONCH-01 to BONCH-04, PRZM2CUB, PYRPRCUB, SCENE1GR), all three methods produced statistically equivalent results. The Dice and Jaccard scores are identical across methods for these cases. This strong correlation suggests that the segmentation pipeline’s performance is the dominant factor for these images, effectively masking the influence of the color processing technique.
• Advantage of Bitmixing. A key finding emerges from image BONCH-05, where the bitmixing method achieved higher scores (Dice: 0.59, Jaccard: 0.42) than both the lexicographic and marginal methods (Dice: 0.57, Jaccard: 0.40). This provides quantitative evidence that the bitmixing transformation can, in specific scenarios, lead to a more accurate segmentation. This improvement can be attributed to the ability of bitmixing to preserve structural and chromatic symmetries during morphological operations, leading to more consistent boundary detection in color-defined regions.
• Pipeline limitations. For another set of images (FAN&BALL, SCENE2OR, SPH&BALL, WOOL2SPH), all three methods performed poorly, yielding low Dice and Jaccard values. The consistent performance across all three methods on these challenging images may stem from the inherent limitations of the gradient-based segmentation approach when processing complex textures, soft edges, or low-contrast regions. It is essential to note that the segmentation parameters were deliberately kept constant across all images and methods to ensure a consistent comparative framework. This experimental design prioritizes methodological consistency over optimal segmentation for individual images, as the primary objective was to evaluate the relative performance of the color processing techniques under equivalent conditions. In application-specific scenarios, parameter optimization tailored to each image’s characteristics would likely yield substantially improved segmentation results. The nearly identical scores indicate that the segmentation pipeline itself is the limiting factor for these images, rather than the color processing method. Nevertheless, the bitmixing approach consistently demonstrated better symmetry preservation in homogeneous regions, underscoring its value in applications where color fidelity and structural coherence are critical.

The qualitative results in Figure 9 should be analyzed in conjunction with the metrics. Although the metrics measure area overlap, visual inspection reveals differences in boundary precision, color consistency within segments, and the absence of artifacts. In these aspects, the bitmixing method shows reduced color bleeding and more consistent chromatic transitions in segmented regions, particularly evident in images with well-defined color boundaries.

5.4. Computational Complexity

Let N be the number of pixels and S the number of elements of the structuring element. For a naive implementation, the complexity of morphological operations is proportional to $N·S$.

• Bitmixing: The bit-interleaving mapping requires $O\left(N\right)$; morphology on the resulting scalar image yields total $O(N·S)$.
• Lexicographic: Channel values are mapped to a single scalar (cost $O\left(N\right)$), then morphology is applied: total $O(N·S)$.
• Marginal: Each channel is processed independently, so the cost is $O(C·N·S)$ (with $C=3$ for RGB).

Although asymptotic orders coincide for naive implementations, constants differ: marginal has an approximate factor of C overhead. With optimized algorithms for separable structuring elements (e.g., van Herk/Gil–Werman), the complexity can be reduced to $O\left(N\right)$, narrowing the practical performance gap between methods.

Several metrics have been proposed to evaluate segmentation algorithms; however, there is no universally accepted absolute metric for this purpose. In different works [23,24,25], among others, the The Probabilistic Rand Index (PRI) has been highlighted as a standard index for evaluating structural segmentation similarity. Unlike area-based metrics, the PRI assesses the consistency in pixel grouping by comparing the probability that pairs of pixels belong to the same region across multiple manual segmentations. This makes it particularly sensitive to the preservation of region coherence and structural organization, aligning well with the symmetry preservation goals of the bitmixing approach. Values close to 1 indicate a higher similarity between the automatic segmentation and the manual references. The PRI index is defined as

$$PRI(S,I^k)={\displaystyle \frac{2}{n(n-1)}}\sum _{i<j}\left[{\rho }_{ij}^k{\delta }_{ij}+(1-{\rho }_{ij}^k)(1-{\delta }_{ij})\right]$$

(8)

where n is the number of pixels, ${\rho }_{ij}^k$ denotes the probability that two pixels $x_i$ and $x_j$ belong to the same region according to the k-th manual segmentation, and ${\delta }_{ij}$ is an indicator variable that equals 1 if both pixels belong to the same region in the automatic segmentation, and 0 otherwise.

Table 2 shows the obtained results for the test images under three comparison schemes (Lexicographic, Marginal, and Bitmixing). These results help identify in which cases the methods produce segmentations that are more consistent with the manual references, thereby providing greater validity in practical contexts.

Table 2. This table presents the Probabilistic Rand Index to evaluate segmentation similarity. The PRI index is presented in Equation (8).

Name	Bitmixing	Lexicographic	Marginal
BONCH-01	0.57	0.57	0.57
BONCH-02	0.68	0.60	0.57
BONCH-03	0.67	0.53	0.54
BONCH-04	0.66	0.58	0.59
BONCH-05	0.35	0.47	0.48
FAN&BALL	0.59	0.49	0.50
PRZM2CUB	0.49	0.61	0.60
PYRPRCUB	0.56	0.46	0.59
SCENE1GR	0.39	0.34	0.48
SCENE2OR	0.38	0.45	0.39
SPH&BALL	0.62	0.51	0.52
WOOL2SPH	0.43	0.30	0.29
Average	0.5325	0.4925	0.51

The higher channel averages for bitmixing in Table 3 suggest better preservation of color intensity in the segmented regions. This aligns with the method’s unified scalar representation, which maintains inter-channel relationships and potentially reduces color dilution during morphological operations. However, these results should be interpreted as indicative of intensity preservation rather than comprehensive color fidelity.

Table 3. Average RGB channel values for segmented images across the 12-image dataset. The averages are computed per channel and then averaged across all images. Higher values suggest better preservation of color intensity, though this does not directly measure color accuracy against the original regions.

Set of Images	Red Channel Average	Green Channel Average	Blue Channel Average
Original images	112.46	100.92	79.64
Bitmixing	34.06	32.74	27.05
Lexicographics	30.10	29.95	24.59
Marginal	32.49	31.35	25.32

The Figure 10 illustrates the application of the internal gradient size $\mu =1$ on images with complex texture using the bitmixing algorithm. Original images are in Figure 10a,b. The contours identification is displayed in Figure 10c,d, respectively. Despite the large amount of information, the contours are detected adequately. It is noteworthy to mention that images in Figure 10a,b do not belong to the dataset used to compare the bitmixing algorithm.

Figure 10. Bitmixing algorithm applied to images with complex texture using the morphological gradient size $\mu =1$. The (a,b) present the original images, and (c,d) correspond to the internal gradient size $\mu =1$.

6. Discussion

From the experimental results, several key insights into color image segmentation using mathematical morphology are obtained.

First, the overall functional equivalence observed among the three methods across most images indicates that, in well-structured and high-contrast scenes, the segmentation pipeline itself—rather than the chosen color-ordering strategy—is the primary factor influencing performance. This has important practical implications: in applications where computational efficiency is crucial, the marginal method may offer a suitable balance between accuracy and speed.

Second, the superior performance of bitmixing in image BONCH-05 supports the hypothesis that it preserves color fidelity. Unlike the marginal approach, which processes channels independently, or the lexicographic method, which enforces a rigid priority hierarchy, the bit-interleaving mechanism of bitmixing preserves the multidimensional relationships within the RGB space. As a result, the morphological gradient is computed in a perceptually coherent manner, leading to more accurate boundary delineation in color-defined regions. This coherence is key to maintaining the structural and chromatic symmetries of objects, which is a defining advantage of the bitmixing method over the marginal and lexicographic approaches.

Third, the consistently poor performance across all methods on textured images underscores a limitation of the gradient-based pipeline when applied to visually complex content. Complex, textured regions with intensity variations produce noisy morphological gradients that are difficult to threshold accurately, regardless of the color ordering method used. This indicates that the challenge lies not in the color representation but in the front-end feature extraction step, which could be improved in future work by incorporating texture-aware operators or multi-scale approaches. Although bitmixing demonstrates advantages in terms of color preservation, the underlying segmentation strategy appears insufficient for cases where boundaries cannot be defined solely by color or intensity transitions.

However, this study has several limitations that should be addressed in future work. The experimental evaluation was conducted using a limited dataset of 12 images, which may not fully capture the variability of real-world scenarios. Expanding to larger and more diverse datasets would strengthen the validation of the proposed method. Additionally, the analysis focused on segmentation quality metrics, excluding computational complexity and runtime comparisons. Theoretical considerations suggest that bitmixing has a similar complexity to lexicographic ordering, both of which involve a scalar transformation; however, empirical evaluation of computational performance remains for future studies.

The sensitivity to the parameter $\mu$ (structuring element size) was explored only for specific values (1, 5, 8, 10). A comprehensive sensitivity analysis across a broader range of $\mu$ values would provide deeper insights into the robustness of each method. The superior PRI performance of bitmixing (Table 2) suggests that its perceptually-weighted scalar representation better preserves structural relationships between regions. This aligns with the method’s design goal of maintaining chromatic and structural symmetries during morphological processing.

The consistently higher channel averages observed in Table 3 for the bitmixing method, combined with its perceptually-weighted bit-interleaving scheme, suggest better preservation of original color characteristics. However, these results should be interpreted as indicative of color intensity maintenance rather than comprehensive color fidelity, as they do not directly capture the preservation of hue or saturation.

Comparison with contemporary color morphology methods, such as those based on vector distance measures [12] or order-space approaches [13], was not included in this study due to scope and time constraints.

Future research should explore the integration of bitmixing representations with more advanced segmentation frameworks to overcome current limitations, particularly in the analysis of highly textured scenes.

7. Conclusions

This study provides a comprehensive evaluation of the bitmixing method for color image segmentation using mathematical morphology, comparing it with established lexicographic and marginal approaches. The results demonstrate that while all three methods perform similarly on well-structured, high-contrast images, the bitmixing method exhibits a measurable and practically significant advantage in scenarios where color transitions primarily define segmentation boundaries. The results indicate that bitmixing better preserves color intensity relationships across channels, as evidenced by higher RGB averages compared with marginal and lexicographic approaches. This advantage aligns with its perceptual weighting scheme and unified scalar representation, which maintain inter-channel dependencies during morphological processing as shown by higher RGB averages in Table 3.

The primary limitation across all methods lies in their reduced effectiveness on textured images with soft edges, indicating that the gradient-based pipeline itself, rather than the color representation, constitutes the main constraining factor.

While bitmixing shows promise in specific contexts, its advantages are not universal and depend on image characteristics such as color contrast, boundary definition, and structural regularity.

Future work will focus on several directions: (1) integrating the bitmixing approach with advanced segmentation techniques, such as marker-controlled watershed, to address its limitations with complex textures; (2) expanding the experimental evaluation to include larger datasets, computational complexity analysis, and comparison with recent state-of-the-art methods; (3) conducting sensitivity analysis on parameters like $\mu$ and testing on higher bit-depth images; and (4) exploring applications where color fidelity is crucial—such as medical image analysis and remote sensing—where enhanced segmentation accuracy can directly improve diagnostic outcomes or environmental monitoring.