Basic Vaidya White Hole Evaporation Process

Abstract

We developed a self-consistent double-null description of an evaporating white-hole spacetime by embedding the outgoing Vaidya solution in a coordinate system that remains regular across the future horizon. Starting from the radiation-coordinate form, we specialize in retarded time so that a monotonically decreasing mass function $M\left(u\right)$ encodes outgoing positive-energy flux. Expressing the metric in null coordinates $(u,v)$, Einstein’s equations for a single-directional null-dust stress–energy tensor, $T_{uu}=\rho \left(u\right)$, then reduce to one first-order PDE for the areal radius: ${\mathsf{\partial }}_{v}r=B\left(u\right)\left(1-2M\left(u\right)/r\right)$. Its integral, $r+2M\left(u\right)ln|r-2M(u\left)\right|=v-C\left(u\right)$, defines an implicit foliation of outgoing null cones. The metric coefficient follows algebraically as $f(u,v)=1-2M\left(u\right)/r$. Residual gauge freedom in $B\left(u\right)$ and $C\left(u\right)$ is fixed so that u matches the Bondi retarded time at null infinity, while v remains analytic at the apparent horizon, generalizing the Kruskal prescription to dynamical mass loss. In the limit $M\left(u\right)\to M$, the construction reduces to the familiar Eddington–Finkelstein and Kruskal forms. Our solution, therefore, provides a compact analytic framework for studying white-hole evaporation, Hawking-like energy fluxes, and back-reaction in spherically symmetric settings without encountering coordinate singularities.

1. Introduction

Classical general relativity permits a time-reversed analog of the Schwarzschild black hole—the white hole—which, although it is believed to be unstable under realistic perturbations [1,2,3], remains a valuable theoretical laboratory. Its geometry exposes time-asymmetric aspects of horizon thermodynamics, clarifies the causal structure of a radiating spacetime, and offers a controlled setting for testing semiclassical back-reaction schemes. Quantitative studies of evaporating white holes, however, are scarce because most familiar gauges become singular precisely where one wishes to probe outgoing fluxes and dynamical horizons.

A natural template for spherical radiation is the Vaidya metric [4], whose standard single-null form $d{s}^2=-(1-2M\left(u\right)/R)d{u}^2-2dudR+R^{2}d{\mathrm{\Omega }}^2$ describes outgoing flux when the Bondi mass $M\left(u\right)$ decreases with retarded time u. Unfortunately, the coordinate pair $(u,R)$ fails at the apparent horizon $R=2M\left(u\right)$; curvature scalars remain finite, but the metric components diverge. For black holes, this weakness is cured by the Kruskal–Szekeres coordinates; an exact dynamical analog for the white-hole spacetime has not yet been fully exploited.

Here, we construct double-null coordinates $(u,v)$ that remain regular across the future horizon for arbitrary monotonic mass functions $M\left(u\right)$. Adopting the retarded-sign convention ensures that the null dust flows outward, modeling Hawking-like energy loss. Under spherical symmetry, the full Einstein system reduces to a single first-order PDE, ${\mathsf{\partial }}_{v}r=B\left(u\right)(1-2M\left(u\right)/r)$, for the areal radius $r(u,v)$. This equation is integrable in a closed implicit form, $r+2M\left(u\right)ln|r-2M(u\left)\right|=v-C\left(u\right)$. Two residual gauge functions, $B\left(u\right)$ and $C\left(u\right)$, encode the freedom to rescale and shift v. Choosing $B\left(u\right)=1$ and fixing $C\left(u\right)$ so that v is analytic at $r=2M\left(u\right)$ yields the metric $d{s}^2=-2(1-$$2M\left(u\right)/r)dudv + r^2(u,v)d{\mathrm{\Omega }}^2$, which reduces to the advanced Eddington–Finkelstein coordinates when $M^{\prime }\left(u\right)=0$ and generalizes the Kruskal prescription to dynamical horizons.

Then we present a thermodynamic and geometric account of an evaporating Vaidya–white hole within a spherically symmetric null-dust setting. Using the dynamical/isolated-horizon framework, we assign instantaneous horizon quantities on the future horizon, $r_H\left(u\right)=2M\left(u\right)$: the surface gravity $\kappa \left(u\right)=1/\left[4M\right(u\left)\right]$, the Hawking temperature $T_H\left(u\right)=\hslash /\left[8\pi k_{B}M\left(u\right)\right]$, and the Bekenstein–Hawking entropy $S_{BH}\left(u\right)=k_{B}A\left(u\right)/\left(4{\ell }_P^2\right)$, with $A\left(u\right)=16\pi M^2\left(u\right)$. In this quasi-stationary regime, the first-law balance, $dM=\kappa dA/\left(8\pi \right)$, is recovered consistently with the field equations and Bondi mass loss, and the generalized second law holds to leading order by comparing $d{S}_{BH}/du$ with the near-thermal entropy flux carried by Hawking quanta. To connect these analytic relations with causal geometry, we next provide a numerical illustration of the areal radius $r(u,v)$ obtained from the implicit double-null relation, solving uniquely for r on a $(u,v)$ grid. Three representative evaporation laws for $M\left(u\right)$—exponential, power-law, and linear—are examined to contrast asymptotic shrinkage with finite-time termination. We trace the horizon contraction $r_h\left(u\right)=2M\left(u\right)$, its changing causal character, and its far-field behavior, $r\simeq v$; thus, we obtain a smooth scheme for thermodynamics and horizon evolution during white-hole evaporation.

2. Vaidya Metric in White Hole

We first extend this idea by applying the Vaidya metric to white-hole evaporation. The basic white-hole algebra and notation are shown in Appendix A. We start with the Vaidya metric written in radiation coordinates, $(r,\theta ,\varphi ,\omega )$ [4]:

$$d{s}^2=2ϵdrd\omega -\left(1-{\displaystyle \frac{2M\left(\omega \right)}{r}}\right)d{\omega }^2+r^{2}d{\mathrm{\Omega }}^2$$

(1)

with $ϵ=1$ for advanced time and $ϵ=-1$ for retarded time.

We focus on the evaporation process with mass outflow, thus applying $ϵ=-1$. We assume that the mass function $M\left(\omega \right)$ is monotonically decreasing, $\dot{M}={\displaystyle \frac{dM\left(\omega \right)}{dt}}\le 0$ [5]. The evaporation is then constructed in the double-null coordinates as follows [6]:

$$d{s}^2=-2f(u,v)dudv+r^2(u,v)d{\mathrm{\Omega }}^2,$$

(2)

where $d{\mathrm{\Omega }}^2=d{\theta }^2+{sin}^2\theta d{\varphi }^2$ is the unit 2-sphere, $r(u,v)$ is the areal radius, and $f(u,v)$ is an undetermined metric function to be determined later. Given $f>0$, the metric signature remains $(-,+,+,+)$. The coordinates u and v are chosen to be null, so surfaces of constant u or v are null hypersurfaces. For an outgoing radiation field, we take $ϵ=-1$, which means that the null dust flows along the u-direction, and the mass decreases with increasing retarded time u. The stress–energy tensor corresponds to a single-directional null dust:

$$T_{ab}=\rho \left(u\right)k_a{k}_b,$$

(3)

with $k_a$ as a null vector field tangent to outgoing radial null geodesics, so that $k_a\propto {\nabla }_{a}u$. We then take $k_a={\nabla }_{a}u$ by setting the normalization $k_u=1$, with all other components $k_v,k_{\theta },k_{\varphi }=0$. Hence, $T_{uu}=\rho \left(u\right)$.

$T_{ab}$ only has a $uu$-component, consistent with purely outgoing radiation. Physically, $\rho \left(u\right)\ge 0$ is related to the mass-loss rate. In particular, we assume that the mass function $M\left(u\right)$ is monotonically decreasing in u. The standard Vaidya relation for mass loss is given by the following:

$${\displaystyle \frac{dM\left(u\right)}{du}}=-4\pi r^2{T}_{uu}<0,$$

(4)

so that $T_{uu}={\displaystyle \frac{-M^{\prime }\left(u\right)}{4\pi r^2}}$ (with $M^{\prime }=dM/du$) represents the energy density of the outgoing null flux [7]. All other $T_{ab}$ components vanish, and $M\left(u\right)$ corresponds to the Bondi mass as measured at null infinity. We present the Penrose diagram for the Vaidya-evaporating white hole in Figure 1. We set $\mathcal{K}$ to be a spacelike hypersurface before the event horizon (technically, the anti-event horizon—hereafter referred to simply as the horizon) is formed. ${\mathcal{K}}_A={\mathcal{K}}_w+{\mathcal{K}}_{in}$ denotes the hypersurface at the moment when the white hole evaporates completely; ${\mathcal{K}}_w$ represents the part of the hypersurface outside the horizon, and ${\mathcal{K}}_{in}$ corresponds to the inside part. ${\mathcal{K}}^{\prime }$ indicates the hypersurface after the evaporation [8].

In this work, we idealize the outgoing matter as a null dust without pressure, so that $T_{ab}$ only has a $uu$-component. This corresponds to radiation flowing outward without resistance or lateral pressure. Physically, any pressure associated with a null fluid would introduce additional stress components, such as radial pressure or tangential stresses. Such a case would require a generalized Vaidya solution [9]. Moreover, a pure null dust can be viewed as an extremely anisotropic fluid in which the effective radial pressure equals the energy density [10]. If one were to include a distinct null-fluid pressure term, the Einstein equations would no longer reduce to the single PDE used in this work, and an equation of state relating pressure and density would become essential. Thus, for tractability, we assume a pressureless outgoing flux, as is standard in the classical Vaidya model.

3. Einstein Field Equation

Given the above ansatz, we now write down the nontrivial Einstein field equations. Spherical symmetry and the null-dust form of $T_{ab}$ yield a system of equations for $f(u,v)$ and $r(u,v)$. In the vacuum situation, where $T_{uu}=0$, we have the following:

$$r_{uu}={\displaystyle \frac{f_u}{f}}{r}_u,$$

(5)

where we note that $r_u=\mathsf{\partial }r/\mathsf{\partial }u$ and $r_v=\mathsf{\partial }r/\mathsf{\partial }v$. The Einstein equations with outgoing null dust, $T_{ab}=\rho \left(u\right){\nabla }_{a}u{\nabla }_{b}u$, are given as follows:

$$G_{uu}=-{\displaystyle \frac{2}{f}}\left(r_{uu}-{\displaystyle \frac{f_u}{f}}{r}_u\right)=8\pi T_{uu}⟹r_{uu}-{\displaystyle \frac{f_u}{f}}{r}_u=-4\pi f{T}_{uu}\left(u\right),$$

(6)

$$G_{uv}=-{\displaystyle \frac{2\left(r_u{r}_v+r{r}_{uv}\right)}{fr}}+{\displaystyle \frac{f}{2}}=0⟹2{\displaystyle \frac{r_u{r}_v+r{r}_{uv}}{f}}=f{\displaystyle \frac{r}{2}}.$$

(7)

And we have the following:

$$2{\displaystyle \frac{r_u{r}_v}{f}}={\displaystyle \frac{2M(u,v)}{r}}-1,$$

(8)

where we define a local mass function $M(u,v)={\displaystyle \frac{r_u{r}_{v}r}{f}}+{\displaystyle \frac{r}{2}}$. In fact, the above can be recognized as the defining equation for the Misner–Sharp mass in spherical symmetry. Rearranging, one convenient definition is as follows [11]:

$$1-{\displaystyle \frac{2M(u,v)}{r}}\equiv -{\displaystyle \frac{2r_u{r}_v}{f}}.$$

(9)

Using this definition, one can see that $M(u,v)$ is constant along outgoing rays. In the outgoing Vaidya case, one of the Einstein equations implies ${\mathsf{\partial }}_{v}M=0$, so that the mass function depends only on u. We therefore set $M(u,v)=M\left(u\right)$ henceforth. The remaining field equation is the $uu$-component, which relates the change in $M\left(u\right)$ to the metric functions. Plugging $M=M\left(u\right)$ into the local mass definition and using Equation (5), one finds the radial equation of motion for outgoing geodesics. It can be written as a first-order PDE for $r(u,v)$:

$${\displaystyle \frac{\mathsf{\partial }r}{\mathsf{\partial }v}}=B\left(u\right)\left(1-{\displaystyle \frac{2M\left(u\right)}{r}}\right).$$

(10)

Equation (10) is separable and can be formally integrated for a general $M\left(u\right)$. Treating u as a parameter, we integrate the radial equation to obtain Equation (11):

$$\int {\displaystyle \frac{dr}{1-\frac{2M\left(u\right)}{r}}}=\int B\left(u\right)dv$$

(11)

Here, $B\left(u\right)$ is an arbitrary function of u arising from integration.

4. Analytical Solution

Equation (10) is precisely the single first-order nonlinear PDE to which the Einstein equations reduce for the Vaidya metric. It governs how the areal radius $r(u,v)$ evolves as one moves along increasing v for each fixed u. $B\left(u\right)$ can be chosen to be positive so that v increases toward the future for each fixed u. Performing the r-integral in Equation (11), one obtains the following:

$$r-2M\left(u\right)+2M\left(u\right)ln|r-2M(u\left)\right|=B\left(u\right)v+C\left(u\right),$$

(12)

Here, $C\left(u\right)$ is an arbitrary integration function of u, where the additive constant $-2M\left(u\right)$ may be absorbed into the arbitrary function $C\left(u\right)$. A suitable choice of $C\left(u\right)$ will be made to ensure the coordinates are regular across any horizon.

Now, with $r(u,v)$, we can construct the metric function $f(u,v)$. One convenient way to obtain f is to use the relation $g^{uv}=-1/f$ together with the definition of $M\left(u\right)$. Equivalently, we can differentiate the implicit solution above with respect to v. Differentiating yields back the radial PDE Equation (11), $r_v=B\left(u\right)\left(1-2M/r\right)$. Thus, solving for $f=-g_{uv}$:

$$f(u,v)={\displaystyle \frac{r_v}{B\left(u\right)}},$$

(13)

so that

$$f(u,v)=1-{\displaystyle \frac{2M\left(u\right)}{r(u,v)}}.$$

(14)

This is the desired metric coefficient in double-null coordinates, valid for an arbitrary mass function $M\left(u\right)$. The function $B\left(u\right)$ determines the normalization of v along each outgoing null cone with fixed u, while $C\left(u\right)$ sets the origin of v on each cone. Neither of them changes the scaling of the retarded coordinate u.

One may now exploit the coordinate freedom encoded in the functions $B\left(u\right)$ and $C\left(u\right)$. First, fix the overall scaling of the outgoing coordinate v by choosing $B\left(u\right)=1$. This choice makes the retarded coordinate u coincide with the usual Bondi retarded time at future null infinity. Second, use the additive freedom $v\to v+\sigma \left(u\right)$ to select $C\left(u\right)$ so that the metric remains analytic at the outgoing apparent (or event) horizon $r=2M\left(u\right)$; in the static Schwarzschild case, this yields the familiar Kruskal choice, $C\left(u\right)=-2M$.

With these choices, the implicit solution of the radial equation is as follows:

$$r+2M\left(u\right)ln|r-2M(u\left)\right|=v,$$

(15)

and the metric coefficients are as follows:

$$\begin{array}{cc}\hfill & d{s}^2=-2\left(1-{\displaystyle \frac{2M\left(u\right)}{r}}\right)dudv+r^{2}d{\mathrm{\Omega }}^2,\hfill \\ \hfill & f(u,v)=1-{\displaystyle \frac{2M\left(u\right)}{r(u,v)}}.\hfill \end{array}$$

(16)

In the static limit $M\left(u\right)=M$, these reduce to the advanced Eddington–Finkelstein form; with a different $C\left(u\right)$, one recovers the Kruskal–Szekeres extension. For a dynamical $M\left(u\right)$, a suitably chosen $C\left(u\right)$ likewise ensures a smooth extension across any future horizon that forms.

Together with the implicit relation for $r(u,v)$ in Equation (12), this describes a general radiating white-hole spacetime. The outgoing Vaidya–white-hole metric is often presented in retarded-null coordinates $(u,R)$. To recover that form, one can use the freedom in v to set $C\left(u\right)$ such that v coincides with the ingoing null coordinate at flat infinity. Then u is the retarded time, and $R=r$ is the areal radius. The metric then takes the form:

$$d{s}^2=-\left(1-{\displaystyle \frac{2M\left(u\right)}{R}}\right)d{u}^2-2dudR+R^{2}d{\mathrm{\Omega }}^2,$$

(17)

which indeed represents the standard outgoing Vaidya metric describing a radiating white hole or an evaporating black hole. In our double-null coordinates, the same physics is encoded, but the coordinates remain regular at the outgoing horizon by construction. The function $C\left(u\right)$ has been chosen so that $(u,v)$ extend across $r=2M\left(u\right)$, unlike the simpler $(u,R)$ coordinates, which break down at the horizon.

In summary, we started with Einstein’s equations for a null-dust stress–energy tensor and derived a single first-order PDE for $r(u,v)$. Its integration introduced an arbitrary function of u, denoted $C\left(u\right)$, which must be specified by a regularity condition. The general solution for an arbitrary $M\left(u\right)$ is given implicitly by the relations above. For the white-hole case, $M\left(u\right)$ decreases monotonically, and one chooses the integration constants to obtain an outgoing radiation solution that is regular on the outgoing horizon. Our construction generalizes the Schwarzschild–Kruskal coordinates to the dynamical case of a varying mass. The result is the double-null Vaidya metric [6].

5. Thermodynamics in Vaidya–White Hole

In this chapter, we continue by introducing a spherically symmetric null-dust configuration. The dynamical-horizon framework provides a first-law-type balance without charge and rotation, and we then introduce the thermodynamic description of the evaporating Vaidya–white hole.

5.1. The First Law

In the quasi-stationary regime of our outgoing Vaidya geometry, the white-hole future horizon at $r_H\left(u\right)=2M\left(u\right)$ has instantaneous surface gravity:

$$\kappa \left(u\right)={\left.{\displaystyle \frac{1}{2}}{\mathsf{\partial }}_r\left(1-{\displaystyle \frac{2M\left(u\right)}{r}}\right)\right|}_{r=2M\left(u\right)}={\displaystyle \frac{1}{4M\left(u\right)}},$$

(18)

and the Hawking temperature is as follows:

$$T_H\left(u\right)={\displaystyle \frac{\hslash \kappa \left(u\right)}{2\pi k_B}}={\displaystyle \frac{\hslash }{8\pi k_{B}M\left(u\right)}}.$$

(19)

We can also obtain the Bekenstein–Hawking entropy as follows:

$$S_{BH}\left(u\right)={\displaystyle \frac{k_{B}A\left(u\right)}{4{\ell }_P^2}}=4\pi k_B{\displaystyle \frac{M^2\left(u\right)}{m_P^2}},A\left(u\right)=4\pi r_H^2=16\pi M^2\left(u\right),$$

(20)

where ${\ell }_P=\sqrt{\hslash G/c^3}$ is the Planck length, $m_P=\sqrt{\hslash c/G}$ is the Planck mass, $k_B$ is Boltzmann’s constant, and A is the horizon area.

For spherically symmetric null dust, the dynamical/isolated-horizon framework gives a first-law-type balance:

$$dM={\displaystyle \frac{\kappa }{8\pi }}dA,$$

(21)

consistent with the field equations and the Bondi mass loss in Equation (4). This is the standard first law applied to slowly evolving trapping horizons and ensures the correct thermodynamic bookkeeping in our double-null chart [12,13,14,15].

5.2. General Second Law

Taking the outgoing luminosity $L\left(u\right)=-dM/du$ in geometrized units, the entropy flux carried by near-thermal Hawking quanta satisfies $d{S}_{\mathrm{rad}}/du\approx {\displaystyle \frac{4}{3}}L/T_H$. Using $S_{BH}=4\pi M^2$ gives $d{S}_{BH}/du=8\pi MdM/du$. Hence,

$${\displaystyle \frac{d}{du}}\left(S_{BH}+S_{\mathrm{rad}}\right)\approx -{\displaystyle \frac{8\pi M}{3}}dM/du>0$$

(22)

where $S_{BH}$ is the Bekenstein–Hawking entropy of the horizon, and $S_{\mathrm{rad}}$ is the entropy of the outgoing Hawking radiation. Because $dM/du<0$ for evaporation, the generalized second law holds to leading order in the quasi-static approximation [16,17].

5.3. White-Hole Heat Capacity

It is essential to discuss the heat capacity as part of the white-hole thermodynamic analysis. In general, the heat capacity is defined in the usual way for a white hole. We define the following:

$$C\equiv {\displaystyle \frac{\mathsf{\partial }E}{\mathsf{\partial }T}},$$

(23)

where $E=M{c}^2$ and T is the Hawking temperature associated with the event horizon. For the Schwarzschild case, $\left|T\right|={\displaystyle \frac{\hslash c^3}{8\pi GM{k}_B}}$. Differentiating gives

$$C_{\mathrm{WH}}={\displaystyle \frac{\mathsf{\partial }\left(M{c}^2\right)}{\mathsf{\partial }T}}=-{\displaystyle \frac{8\pi G{k}_B}{\hslash c}}{M}^2<0,$$

(24)

thus, under standard conditions, the white hole has the same negative heat capacity as a Schwarzschild black hole of the same mass [18,19]. Physically, this means that any loss of energy through radiation causes the horizon to heat up, which in turn increases the emission rate.

6. Numerical Illustration of Areal Radius and Horizon Evolution in Vaidya Evaporation

6.1. Mass Function Models

Consider three representative functional forms for the time-dependent mass $M\left(u\right)$ of an evaporating white hole. Each model captures a different evaporation law for $M\left(u\right)$.

The first corresponds to exponential decay:

$$M\left(u\right)=M_0{e}^{-\lambda u}.$$

(25)

This models an asymptotic decay in which the mass decreases continuously at a rate proportional to its current value. The mass approaches zero only as $u\to \infty$.

Then we consider the power-law decay:

$${\displaystyle M\left(u\right)=\frac{M_0}{{(1+\beta u)}^n}.}$$

(26)

Here, the mass loss slows down over time following a power law—for large u, $M\left(u\right)\sim u^{-n}$, again vanishing only asymptotically. The parameter n controls the steepness of the decay, with larger values of n corresponding to faster decay at late times.

Finally, the linear decay is given by the following:

$$M\left(u\right)=M_0-\mu u$$

(27)

This is an idealized model in which the mass decreases at a constant rate $\mu$. Unlike the other cases, the linear law can reach $M=0$ at a finite retarded time $u_{\mathrm{end}}=M_0/\mu$, representing complete evaporation in finite time. For $u>u_{\mathrm{end}}$, one would have $M\left(u\right)=0$.

We assume $M_0=1$ as the initial mass in all cases. The default parameters chosen are $\lambda =0.2$, $\beta =0.2$, $n=1$, and $\mu =0.1$.

6.2. Areal Radius

For the outgoing white-hole Vaidya solution in double-null coordinates ($u,v$), surfaces of constant u are outgoing null hypersurfaces, and v is an ingoing null coordinate. The areal radius $r(u,v)$ satisfies a first-order equation from Einstein’s equations which, with a horizon-regular gauge choice, integrates to the implicit relation Equation (15).

The apparent event horizon is $r_h\left(u\right)=2M\left(u\right)$. Because $dM/du<0$ during evaporation, $r_h\left(u\right)$ decreases with u, so the horizon contracts as the white hole loses mass. Unlike the stationary Schwarzschild horizon, this horizon moves inward (toward smaller r) with increasing u. If the mass vanishes at a finite time (in the linear model, e.g., $u=10$ with our parameters), then $r_h\to 0$, and the horizon terminates. Beyond that moment, spacetime becomes effectively Minkowski, with no trapped region. In contrast, for exponential and power-law decays, the mass approaches zero only as $u\to \infty$, so the horizon persists for all u, but its radius asymptotically tends to zero.

The causal character of the horizon can differ, depending on the evaporation rate. In the slowly varying, asymptotic decay regime, the horizon is nearly null or slightly timelike, analogous to that of an evaporating black hole. With rapid mass loss, the horizon retreats more steeply—that is, it becomes spacelike and receding. Thus, the linear model near its endpoint tends toward a more spacelike horizon, whereas the power-law model with $n=1$ remains closer to null.

6.3. Numerical Setup and Uniqueness

We solve the implicit equation for $r(u,v)$ on a grid with $u\in [0,10]$ and $v\in [0,20]$. For fixed u, the left-hand side is strictly increasing in r, from $-\infty$ as $r\to 2M{\left(u\right)}^{+}$ to $+\infty$ as $r\to \infty$, so the solution exists and is unique for each $(u,v)$. We obtain r by a standard root-finding method.

6.4. Areal Radius as a Function of $(u,v)$

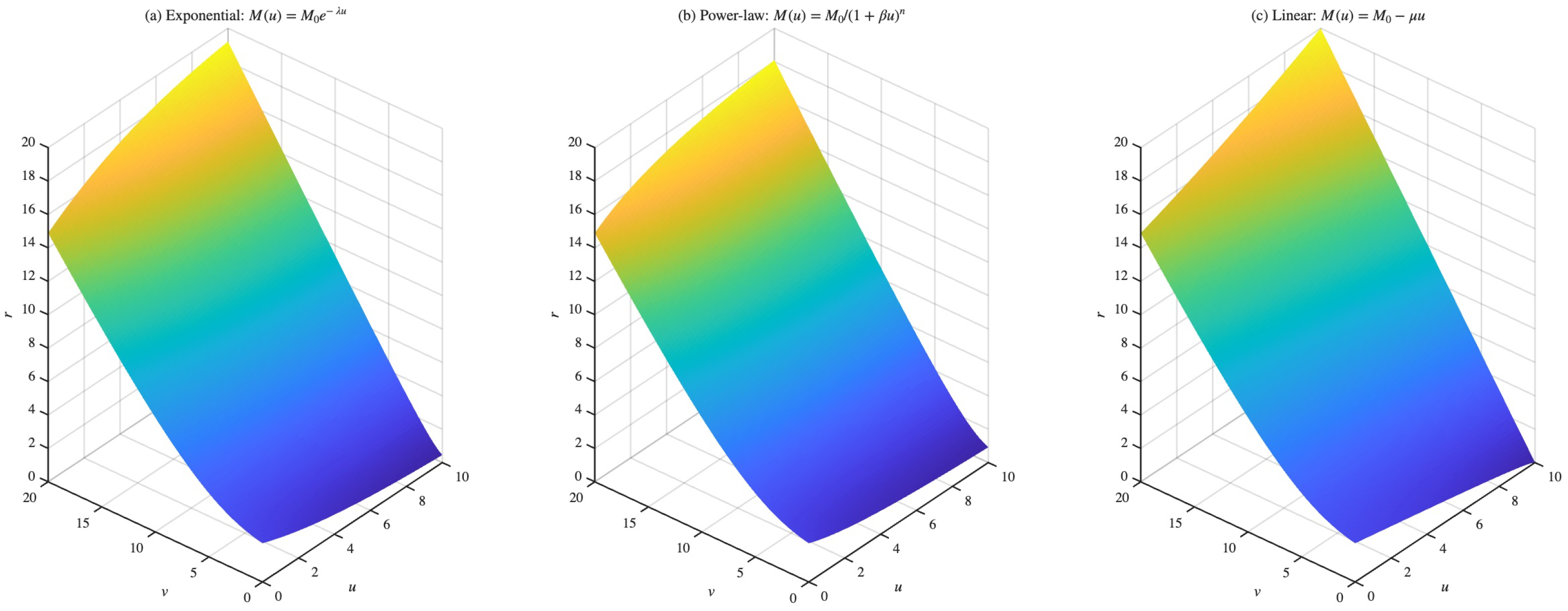
Figure 2 shows $r(u,v)$ for the three mass laws. Each panel depicts a 3D surface with u (horizontal) and v (depth). For any fixed u, r increases with v, since

$${\mathsf{\partial }}_{v}r=1-{\displaystyle \frac{2M\left(u\right)}{r}}>0(r>2M\left(u\right)).$$

(28)

At large v, all surfaces approach $r\approx v$. Far from the source, the spacetime is nearly flat, and outgoing null cones satisfy $r\simeq v$ up to a slow logarithmic correction. Near the horizon, where $r\approx 2M\left(u\right)$, the surfaces develop a steep gradient due to the logarithmic term in the coordinate relation, which causes v to vary rapidly with small changes in r.

For the exponential, the surface begins near $r=2M_0=2$ at $u=0$. The true horizon is reached only as $v\to -\infty$, so the plotted leading slice lies just above it. As u increases, $2M\left(u\right)$ shrinks exponentially, and the surface bends downward near the small-v edge.

Then, for the power-law model, the surface falls more slowly with u, reflecting the milder late-time mass loss; at a given u, it lies above the exponential case.

Last for the linear, the horizon radius shrinks linearly and reaches zero at $u=10$. At exactly $u=10, M=$ 0 and the implicit relation reduces to $r=v$; hence the end-slice lies on the plane $r=v$. For $u>10$, the spacetime is flat and there is no horizon.

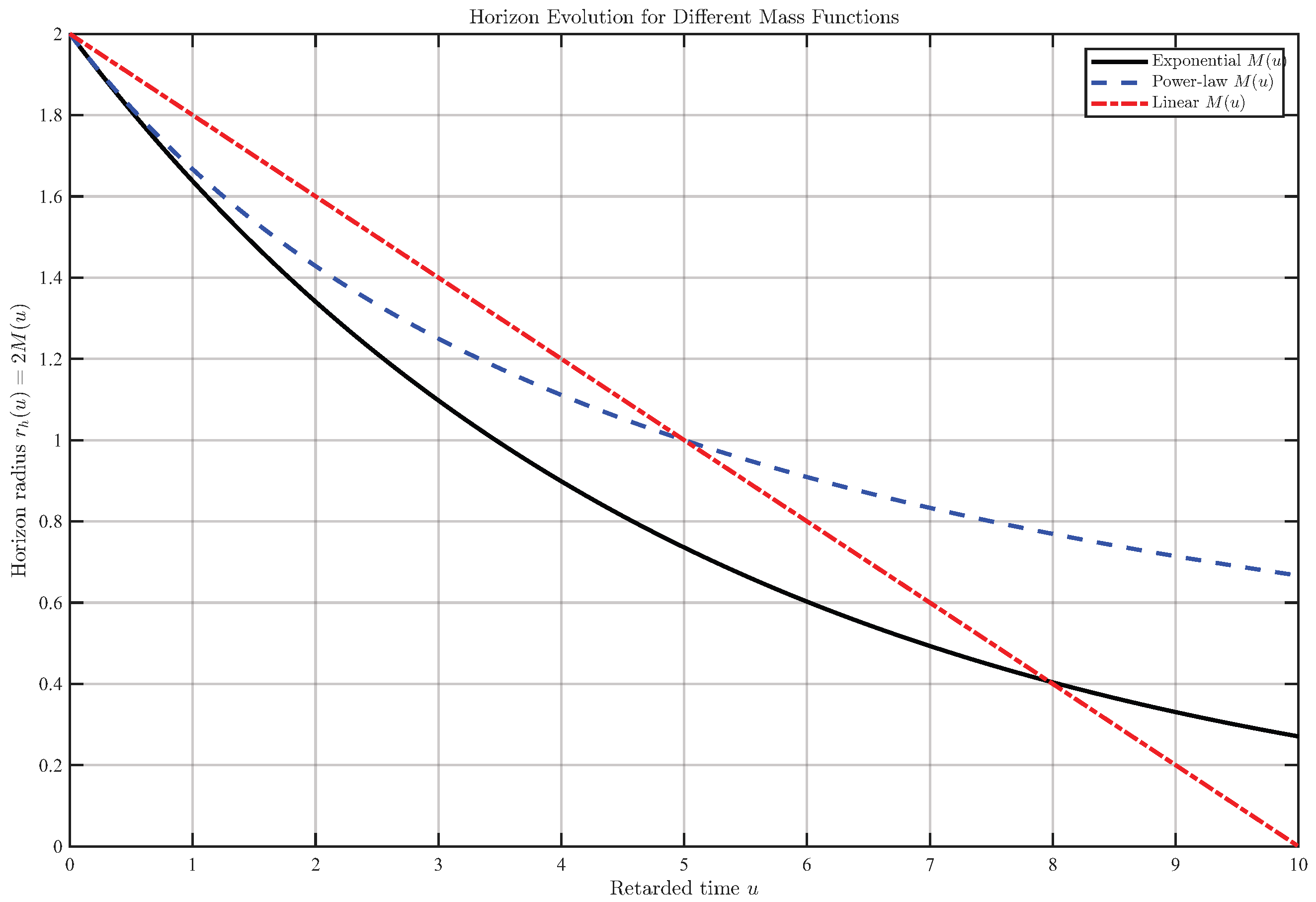
6.5. Horizon Shrinkage over Time

Figure 3 confirms the shrinkage of the horizon and the direct comparison of these decay laws. Initially, all three models have the same horizon radius $r_h\left(0\right)=2$. At early times $u\lesssim 2$, the exponential and power-law curves are nearly identical, as expected since the parameters were chosen so that their initial mass-loss rates are equal. The linear model’s horizon contracts more slowly at first, so the red dash-dot line lies above the others in the range $u\in (0,2)$. By $u\approx 5$, however, the exponential curve has fallen below the power-law curve, reflecting that exponential decay eventually outpaces the $1/(1+0.2u)$ law in reducing the mass. At $u=10$, the horizons have shrunk substantially: the power-law model retains the largest radius $r_h\approx 0.67$, the exponential model is smaller $r_h\approx 0.27$, and the linear model has vanished. Thus, by comparing these models, we could see how different evaporation rates affect the late-time size of the white-hole horizon. The qualitative trend of a shrinking horizon is the same in all cases, but complete evaporation in finite time drastically shortens the horizon’s lifespan, whereas asymptotic decay laws leave an ever-diminishing yet long-lived horizon.

6.6. Analytical Collapse Time

We let $u_c$ denote the retarded time at which the apparent horizon disappears; for instance, we define $u_c=inf\{u\ge 0:M\left(u\right)=0\}$ so that $r_H\left(u_c\right)=0$. For any monotone mass-loss law $dM/du=-\mathcal{L}\left(M\right)$, the collapse time is as follows:

$$u_c={\int }_0^{M_0}{\displaystyle \frac{dM}{\mathcal{L}\left(M\right)}},$$

(29)

which converges in a finite $u_c$ if and only if the integrand is integrable at $M\to 0$. Applying this to our three benchmark profiles yields the following:

$$u_c^{\mathrm{linear}}={\displaystyle \frac{M_0}{\mu }},u_c^{\exp }=+\infty ,u_c^{\mathrm{pwl}}=+\infty .$$

(30)

Thus, the linear model evaporates in a finite retarded time, as seen in Figure 3, whereas exponential and power-law profiles shrink asymptotically and never reach $r_H=0$ at finite u. For a practical comparison, we also give the time required to reach a small residual mass $\epsilon >0$:

$$u_{\epsilon }^{linear}=\left(M_0-\epsilon \right)/\mu ,u_{\epsilon }^{exp}=(1/\lambda )ln\left(M_0/\epsilon \right),u_{\epsilon }^{\mathrm{pwl}}={\beta }^{-1}[{\left(M_0/\epsilon \right)}^{1/n}-1].$$

(31)

Thus, we give an analytical collapse time for the horizon in these three situations.

6.7. Stability and Final Evaporation

Realistically, an evaporating white hole is an unstable configuration. Any perturbation by infalling matter or radiation tends to convert the white hole into a black hole [20]. Thus, our solution represents an idealized case with no ingoing flux. In a physical setting, a white hole would die long before completing its evaporation if surrounded by even trace amounts of matter. On the other hand, if a white hole could remain perfectly isolated, it would continue to radiate away its mass. Owing to its negative heat capacity, the luminosity increases as the mass decreases, potentially culminating in a final explosive burst of radiation when M becomes very small. This is actually a white hole exploding, which releases the remaining energy in a short pulse.

However, given the instability, a truly explosive emission would require an almost perfect vacuum environment and a relatively low initial mass, so that the evaporation time would not be astronomically long. Even then, as Ori & Poisson note in [21], observing a white-hole explosion in the current epoch would be difficult unless it occurred at high redshift in the early universe. We include this discussion to emphasize that, while mathematically allowed in our model, an evaporating white hole is likely a transient and unstable object in practice.

7. Conclusions

We have presented a self-contained double-null formulation of the outgoing Vaidya spacetime that remains manifestly regular across a dynamical white-hole horizon. By recasting Einstein’s equations with null dust into a single first-order PDE for the areal radius and solving it in a closed implicit form, we have shown that every physically admissible mass profile $M\left(u\right)$ admits a smooth extension analogous to the Kruskal chart for the Schwarzschild solution. This construction eliminates the coordinate pathologies that plague the traditional single-null gauge, offers an exact analytic framework for tracking Hawking-like energy flux and Bondi mass loss, and provides curvature-finite coordinates suitable for semiclassical or numerical back-reaction studies.

The double-null Vaidya scheme developed here furnishes both the mathematical clarity and the physical flexibility needed to probe the time-reversed frontier of black-hole physics, offering a precise platform on which the viability and implications of radiating white holes can be rigorously assessed.

The analysis afterward introduces the thermodynamic aspect of an evaporating Vaidya–white hole. The instantaneous horizon properties satisfy the first-law identity $dM=\kappa dA/\left(8\pi \right)$, while the generalized second law, $d\left(S_{BH}+S_{\mathrm{rad}}\right)/du>0$, follows at leading order from the near-thermal luminosity $L\left(u\right)=-dM/du$. Numerically, the areal radius solution $r(u,v)$ is unique and monotonic in v, approaching $r\simeq v$ far from the source and developing steep gradients near $r\approx 2M\left(u\right)$ due to the logarithmic structure of the coordinate relation. The horizon radius $r_h\left(u\right)=2M\left(u\right)$ decreases monotonically for all models, but its late-time behavior is controlled by the evaporation law. With the illustrative parameters, the exponential and power-law cases shrink asymptotically, whereas the linear model exhibits a finite-time disappearance at $u_{\mathrm{end}}=10$. Near its endpoint, the linear case drives a more spacelike, rapidly receding horizon, while slower mass loss leaves a larger anti-trapped region. These results provide a clear baseline within the double-null chart and quasi-stationary approximation for the future incorporation of charge and rotation, stronger back-reaction, or non-thermal corrections.

This basic framework opens several avenues for further investigation:

(i) Coupling the geometry to explicit quantum stress tensors to test the robustness of white-hole evaporation.

(ii) Exploring the global causal structure and potential instability channels through perturbative analyses.

(iii) Extending the method to incorporate charge, angular momentum, or modified-gravity corrections.

Although white holes have not yet been detected, our results may be relevant to several astrophysical scenarios. An evaporating white hole radiating away its mass would produce a transient high-energy signal, essentially a sudden release of all its confined energy. In this sense, complete evaporation mimics the final explosion of an evaporating black hole, which has been conjectured to yield a burst of gamma rays or other particles. Experimental searches for such bursts have so far found none, suggesting that, if white holes exist, they are exceedingly rare or very short-lived.

It should be mentioned that some quantum-gravity models propose that black holes might transition into white holes, leading to a sudden explosive event that could be observable [22]. Such ideas have been invoked to explain phenomena such as fast radio bursts or unexplained cosmic-ray showers. While speculative, these notions motivate further exploration of the basic physics of white-hole evaporation. Our study provides a groundwork for this effort—by describing the classical geometry and thermodynamics of an evaporating white hole, we offer a stepping stone toward more complete models. Moreover, the extreme instability of white holes implies that, if they did play a role in nature, it was likely during the early universe [2,21].

In summary, the obtained results deepen our theoretical insight into time-reversed black-hole behavior and could help guide future searches for exotic transient astrophysical events consistent with a white-hole origin.