An Iterative Design Method for CIHFS-DEMATEL Products Incorporating Symmetry Structures: Multi-Attribute Decision Optimization Based on Online Reviews and Credibility

Abstract

In the digital context, how to achieve symmetrical integration between subjective evaluation and structural stability becomes the key to improving the design effect of iterative product optimization. In this paper, we propose an iterative design method for CIHFS-DEMATEL products that incorporates structural symmetry analysis. The method is based on online review mining and constructs a credibility-based interval hesitant fuzzy set (CIHFS) to symmetrically express the ambiguity and credibility differences in the decision-maker’s subjective evaluation. In turn, a novel exact score function called credibility interval hesitant fuzzy score function (CHFSF), incorporating information symmetric weights, is proposed to realize the bidirectional symmetric mapping between subjective fuzzy inputs and objective exact outputs. Subsequently, the CIHFS-DEMATEL model is introduced to identify the causal paths and a symmetric interaction structure between potential users’ demands. Finally, the demand module mapping matrix is constructed to realize the symmetric decision-making closure loop from demand to solution. Taking the “Intelligent Classified Trash Can” as a case study, we verify the superiority of the method in terms of recognition accuracy, rationality of weight allocation, and structural stability. This study emphasizes the structural symmetry between “input–evaluation–output”, which provides a theoretical foundation and practical framework for the optimal design of products with complex multi-source information.

1. Introduction

In the booming digital economy, an increasing number of consumers tend to shop online and post product reviews on various platforms. It has been shown that online reviews have become an important source of information for users to make purchasing decisions [1]. These reviews not only reflect the user’s emotional inclination toward the product but also hide potential user needs (PUNs) that have not yet been fully explored by the business. In order to enhance the competitiveness of products, enterprises need to fully absorb user feedback in the product iteration process, so that the design is closer to the real demand [2]. Therefore, how to efficiently and accurately mine valuable information from users’ online reviews is becoming an important research direction for iterative product design.

However, online comments are usually expressed in natural language, the content is ambiguous and redundant, the number is huge, and the characteristics of the needs expressed by users are often unclear and ill-structured [3]. This makes enterprises face high cognitive costs and information-processing pressure when recognizing review information, extracting user requirements, and formulating design solutions. To address this problem, in recent years, latent Dirichlet allocation (LDA) topic modeling techniques have been widely used in text mining to extract keywords and potential topics in comments. For example, Tang et al. [4], Ying [5], and Dai et al. [6] applied the LDA model to the domains of new energy vehicle infrastructure, hotel experience, and healthcare services, respectively, and successfully realized the identification and extraction of user concerns from their online reviews. However, in the systematic application of product iteration design, traditional LDA methods can only perform keyword extraction. This method fails to establish structural symmetry between thematic frameworks and technical modules. It also fails to enable the reverse validation of keywords through actual iteration schemes. This often results in a disconnect between PUN and practical iteration solutions. Consequently, this paper constructs a complete, symmetrical closed-loop integration of “thematic analysis–technical mapping–decision optimization”. This effectively reduces information loss during the transmission of thematic keywords to iterative solutions, enhancing the structural symmetry and coherence of iterative design.

In addition to the text mining level, in the actual product iteration process, enterprises also need to build multi-attribute decision-making (MADM) models based on the correlation between user needs and product technology modules to determine the key optimization directions. However, in this process, the decision-makers’ assessment is generally characterized by incomplete information, subjectivity, and cognitive inconsistency, leading to significant hesitancy, ambiguity, and credibility differences in the judgment results [7]. An interval hesitant fuzzy set (IHFS) is widely used to express the uncertainty of subjective evaluation and has been preliminarily applied in multi-attribute decision-making problems. For example, Zeng [8], Zhan et al. [9], and Xie et al. [10] proposed assessment models based on this theory for construction noise evaluation, marine turbine fault diagnosis, and 3D-printing material selection, respectively. However, the traditional IHFS method generally ignores the key dimension of “credibility of the information source”, which makes it difficult to reflect the differences in the quality of decision-makers’ ratings and the credibility of the information.

To address this problem, Jin et al. [11] proposed the theory of basic uncertain information (BUI). By introducing the self-assessment credibility of decision-makers, this theory effectively enhances the scientific nature of information quality assessment. In subsequent studies, Yang et al. [12] and Liu et al. [13] also extended the theory to MADM scenarios such as evaluating the quality of electronic word-of-mouth (eWOM) data generated by consumers and assessing green recycling suppliers for shared electric bicycles. However, the current BUI methodology has not yet been integrated with fuzzy expressions to characterize both the “uncertainty” and the “credibility” of the information assessed by the decision-maker.

Therefore, this paper integrates IHFS with BUI to propose the concept of credibility-based interval hesitant fuzzy sets (CIHFSs). Structurally, CIHFSs symmetrically accommodate both the uncertainty and reliability of evaluative information: it employs fuzzy interval values to assess hesitancy while using credibility parameters to evaluate information quality. Both elements form part of CIHFSs’ symmetrical core structure, effectively resolving the one-dimensional representation limitations inherent in traditional IHFS and BUI. This provides a more scientifically grounded basis for subsequent symmetrical adjustments to decision-maker weights and interpretation of outcomes.

At the same time, how to transform this vaguely expressed information into definite values that can be used in calculations is also a key part of the MADM decision-making process. A hesitant fuzzy score function (HFSF) can effectively achieve this goal, and its role is to transform the hesitant fuzzy set into an exact value through a series of mathematical mapping rules, and, in this way, to compare and rank each hesitant fuzzy set [14]. Existing studies have made various improvements for HFSF, such as Farhadinia [15], proposing a novel ranking function, Liao et al. [16], introducing a mean-variance model, and Chen et al. [17], integrating the interval width with the degree of hesitation. However, none of these functions can effectively deal with CIHFS-type data containing credibility, nor can they unify the consideration of decision-maker weights and information quality. Therefore, this paper designs a credibility interval hesitant fuzzy score function (CHFSF) based on the principle of information fusion and expected utility theory. Compared with existing fuzzy scoring functions, the core innovation of CHFSFs lies in achieving symmetrically weighted fusion between subjective evaluators’ fuzzy assessments and the system’s objective default valuations. Dynamic adjustment of subjective evaluation weights and objective default valuations ensures subjective and objective contributions maintain a symmetrically balanced relationship, thereby avoiding unreasonable scenarios such as excessive subjective dominance or objective detachment from reality. Consequently, when mapping a CIHFS to a deterministic value with adjustable weights and controllable credibility, the CHFSF ensures dynamic adjustment and symmetrical equilibrium between credibility and the system’s objective default valuation. This approach enhances the interpretability of results while simultaneously improving the computational efficiency of fuzzy data operations.

In addition, there are often interactions and influences between PUNs, such as the coupling between hygiene, appearance, and ease of use. However, most of the traditional MADM methods assume that the attributes are independent of each other, which makes it difficult to reveal the impact of this complex correlation structure on the decision outcome. The decision-making trial and evaluation laboratory method (DEMATEL) is good at explaining causal paths between related attributes, and has been used in areas such as hospital management [18], logistics and transportation [19], and ecological product valuation [20]. However, in the actual scoring process, the DEMATEL also faces the problem of subjectivity in decision-maker scoring. For this reason, this paper constructs a DEMATEL method based on a credibility-based interval hesitant fuzzy set (CIHFS-DEMATEL) on the basis of CIHFS expression. CIHFS-DEMATEL primarily constructs the DEMATEL method upon the CIHFS framework, establishing substantive distinctions from existing DEMATEL approaches. In its expression form, this method employs a CIHFS—incorporating fuzzy interval values and credibility parameters—as data input in place of deterministic values, thereby simultaneously capturing decision-makers’ hesitancy during evaluation and the quality of information; subsequently, the CHFSF precise scoring function converts fuzzy information into precise causal strength values. Following this transformation, a DEMATEL causal relationship evaluation matrix is constructed to output the weight values for each attribute. Furthermore, CIHFS-DEMATEL incorporates a structurally symmetric design, forming a closed-loop system of “fuzzy input–confidence regulation–precise output”. This approach overcomes the limitations of traditional DEMATEL in three aspects: input format, information processing mechanisms, and result reliability, thereby ensuring the scientific validity and rationality of causal weightings.

Of particular note is the rigorous symmetrical mapping relationship between subjective evaluation expression and final weight output within the MADM process. At the micro level, weight fluctuations corresponding to evaluative value ambiguity among different decision-makers exhibit symmetrical correlation with weight adjustments corresponding to credibility. At the macro level, the causal influences between PUNs constitute a “bidirectionally reciprocal” symmetrical interaction network, thereby maintaining the structural stability requirements of the decision-making system. Therefore, when constructing the product iteration model, properly reflecting the “structural symmetry” between the information input, fuzzy transformation, and output structure not only enhances the stability of the model, but also has theoretical significance for the generalization of the method. Based on this, this paper explores how to incorporate the principle of “structural symmetry” into the CIHFS-DEMATEL framework to realize a balanced transformation from fuzzy information to structural weights.

In summary, this paper constructs an MADM method for iterative product design integrating data mining, fuzzy expression, and causal modeling on the basis of existing research. The main research objectives are as follows:

• Semantic clustering of online reviews using the LDA topic modeling approach to identify a product’s PUNs;
• Constructing a CIHFS-based weight adjustment method for decision-makers and introducing an information credibility control mechanism;
• Proposing a CHFSF that fuses decision-maker weights with information fusion to achieve a plausible transformation of fuzzy into real numbers;
• Constructing the CIHFS-DEMATEL method to analyze the causal relationship between user requirements and calculate the requirement weights;
• Establishing the mapping relationship between user requirements and technical modules and completing the importance ranking and design optimization of technical modules.

In order to verify the feasibility and validity of this method, this paper takes the “Intelligent Classified Trash Can” as an example to carry out the application research, combining the data-mining platform with the decision-maker evaluation system, and completing the complete closed-loop process from the mining of user comments to the iteration of product functions.

The rest of this paper is organized as follows: Section 2 and Section 3 provide an overview of the research methodology, mathematical algorithms, and application models; Section 4 provides case experiments and validation of the results; and finally, Section 5 presents the conclusions and future research directions.

2. Methods and Related Work

2.1. Online Review Mining with LDA Theme Analysis

With the rapid development of e-commerce platforms and social media, user-generated content (UGC) has increasingly become an important source for identifying potential user needs (PUNs) in iterative product design. Online reviews, serving as natural feedback from consumers after product use, form the basis for a symmetrical mapping between user subjective expression and PUNs. For instance, the distribution of high-frequency vocabulary within review texts exhibits structural symmetry with PUN priority. Consequently, user reviews—rich in explicit or implicit suggestions for improvement and insights into pain points—have progressively become a vital reference for product iteration design. However, in the face of massive unstructured review texts, how to efficiently extract structured demand topics is still a major challenge. For this reason, this paper introduces the latent Dirichlet allocation (LDA) topic analysis model as a core mining tool.

LDA, as an unsupervised topic modeling algorithm, is able to compress a large amount of text into a finite distribution of topics, which, in turn, identifies high-frequency keywords and hidden topics of user concern [21]. It has been shown that the LDA model performs stably in review mining tasks such as catering, tourism, and medical care [22,23,24], so this study applies it for the first time to the user demand extraction process at the early stage of product iteration, and the specific process is shown in Figure 1, which mainly consists of (1) obtaining product-targeted reviews and performing initial text cleaning; (2) segmenting the text into individual terms and removing stop words to output text information such as lexical properties and word frequencies; (3) constructing bag-of-words model and training the LDA model; and (4) extracting users’ potential concerns based on topic distribution.

2.2. Transformation of LDA Topics into Multi-Attribute Decision Attributes

The keywords and themes extracted by the LDA topic model essentially constitute semantic expression units of user focus and requirements. During product iteration design, these thematic terms can serve as foundational sources for evaluation attributes within MADM. However, as an unsupervised probabilistic model, LDA exhibits inherent limitations in review mining, particularly when its thematic outputs are directly employed as evaluation attributes: the method provides only lexical distributions and semantic clustering at the topic level, lacking any capacity to quantify the importance or priority of identified needs. It also fails to translate these semantic units into structured decision attributes. Concurrently, during a single product iteration cycle, design resources are often severely constrained. Decision-makers must effectively prioritize and filter numerous PUNs. Relying solely on LDA’s raw outputs in this context risks undermining subsequent prioritization decisions due to the absence of quantifiable evaluation dimensions. Consequently, it is necessary to transform the qualitative themes extracted by LDA into measurable, comparable decision attributes and construct a systematic attribute set.

In response to this issue, scholars have begun to explore integrating LDA topics with MADM methodologies in studies concerning tourist destination selection, electric vehicle acceptance, and mobile payment satisfaction [25,26,27], utilizing the extracted topics as multi-attribute evaluation factors. However, such research has predominantly focused on scenarios such as service design or consumer preference decision making, with its application in the field of product iteration design yet to be fully developed. Concurrently, existing research typically treats LDA-extracted thematic keywords as static inputs for evaluation attributes, failing to adequately consider the symmetrical matching relationship between product technical modules and users’ latent needs. Furthermore, traditional MADM methods such as TOPSIS and VIKOR struggle to accommodate the inherent fuzziness in decision-makers’ assessments during ranking processes. Therefore, this paper integrates LDA topics with MADM methods, further incorporating fuzzy expression techniques to enhance the subjective flexibility of requirement assessment. This approach bridges the gap between LDA topic extraction and fuzzy MADM evaluation, laying the groundwork for subsequent fuzzy decision modeling.

2.3. Interval-Valued Hesitant Fuzzy Set Fused with Basic Uncertain Information

During the evaluation phase of MADM, decision-makers or users are often required to assign subjective scores to the evaluation objects. Due to individual cognitive differences and incomplete information, the scoring data frequently contain ambiguity, hesitation, and uncertainty. To more accurately reflect the cognitive state during the decision-making process, interval hesitant fuzzy sets (IHFSs) are commonly employed in models expressing decision-makers’ evaluation preferences.

The core strength of IHFS lies in expressing fuzzy judgment results through one or more sets of interval numbers. Compared with traditional fuzzy sets, it better captures cognitive characteristics, such as decision-makers’ hesitation and ambiguity in complex decision-making scenarios. In recent years, many scholars have been attempting to extend its formal framework and explore its application in MADM [28,29,30] as well as practical domains such as corporate decision making [31,32]. However, the IHFS structurally expresses “evaluation hesitancy” from a single dimension only, lacking a symmetrical consideration of “information source credibility.” This inability to distinguish the quality of different evaluation information results in significant limitations when applying an IHFS within MADM, making it difficult to meet the demand for accurately capturing decision-makers’ evaluation quality during product iterations. Against this backdrop, scholars have developed various effective direct search methods for solving optimization problems in fuzzy systems. For instance, the inner–outer direct search (IODS) optimization technique proposed by Panigrahi, PK and Nayak, S [33,34] combines internal and external computations with an exploratory search to transform fuzzy nonlinear systems of equations into unconstrained optimization problems. The research’s refined approach to handling triangular fuzzy numbers (TFNs) provides a crucial reference for quantifying multi-attribute decision uncertainty in the present study.

In summary, to address the limitations of IHFSs, this paper introduces basic uncertain information (BUI) [11] into the IHFS framework. By assigning a “credibility” parameter to each set of interval value scores, it characterizes the decision-maker’s subjective level of confidence in their judgment results, thereby achieving a symmetrical structural optimization between subjective evaluation and information credibility. Based on this, this paper proposes a credibility-based IHFS model (credibility-based interval hesitant fuzzy set (CIHFS)). Structurally, the CIHFS symmetrically integrates the fuzziness and reliability of evaluation information: multiple interval sets characterize the decision-maker’s hesitation, while precise credibility parameters quantify information reliability. Mathematically, this symmetrical integration enables the CIHFS to retain the expressive power of hesitant fuzziness while enhancing information completeness and credibility through symmetrical integration. Compared with an IHFS, the CIHFS introduces a credibility dimension to construct a symmetrical structure capable of simultaneously evaluating fuzzy intervals and assessing information reliability. This provides a basis for subsequent weight adjustments and result verification, reducing the interference of subjective bias in decision making.

2.4. Credibility Interval Hesitant Fuzzy Score Function (CHFSF) Construction

Since the CIHFS expression is a collection of fuzzy intervals and exact real numbers, it cannot be directly applied to the MADM process, which requires exact numerical computation. Therefore, it needs to be converted to a single real number score with the help of a hesitant fuzzy score function (HFSF). However, existing HFSFs and their extended forms [35,36,37] predominantly target hesitant fuzzy sets or interval hesitant fuzzy sets. These approaches fail to incorporate the critical dimension of information credibility in computations, neglect the synergistic consideration of decision-maker weights and information quality, and lack mathematical compatibility with the CIHFS structure, which encompasses both fuzzy interval values and credibility parameters. Therefore, to enhance the conversion efficiency and information utilization of the CIHFS in MADM, it is necessary to construct a scoring function that can be directly applied to the CIHFS.

In the field of precise conversion of fuzzy information, the fuzzy inexact Levenberg–Marquardt optimization (FILMO) algorithm proposed by Panigrahi, PK and Nayak, S [38,39] employs an Armijo-type step size approach to provide effective convergence guarantees for fuzzy unconstrained optimization problems. This research’s approach to dynamically adjusting fuzzy parameters offers valuable insights for constructing the CHFSF in this paper, enabling rational control over the transition from fuzzy evaluation to precise conversion.

Based on this, this paper proposes the credibility interval hesitant fuzzy score function (CHFSF), which is grounded in the principles of information fusion and expected utility theory and can be directly applied to the CIHFS. Compared with other fuzzy scoring functions, the core innovation of the CHFSF lies in its construction of a symmetrically weighted fusion framework between fuzzy evaluation and the system’s objective default valuation. Through credibility parameters, it ensures that the contribution of both components in the final assessment value maintains a symmetrical balance and undergoes dynamic adjustment. This prevents excessive dominance by either side, guarantees the rationality of precise conversion of fuzzy values, and effectively overcomes the limitations of existing fuzzy scoring functions that rely solely on subjective ratings or disregard information quality.

In summary, the CHFSF not only maps CIHFS to a deterministic value with adjustable weights and controllable credibility while preserving the advantages of fuzzy processing, but also ensures seamless integration of the CIHFS into MADM methods.

2.5. PUN Causal Analysis with CIHFS-DEMATEL Modeling

In actual product design, there are often symmetric or asymmetric interactions between different PUNs, such as dependence, facilitation, or inhibition, and ranking based solely on decision-maker assessment scores may ignore these structural factors [40]. Decision-making trial and evaluation laboratory (DEMATEL) [41] specializes in the problem of causal influence between attributes in a system and is one of the mainstream approaches in MADM today [42,43,44,45].

However, existing DEMATEL methods typically require decision-makers to evaluate using deterministic values and rely excessively on subjective ratings. They lack quantitative constraints on information quality, resulting in evaluation outcomes that fail to accommodate the inherent ambiguity and hesitation in the assessment process. Moreover, these methods struggle to distinguish differences in the credibility of information evaluated by different decision-makers, allowing subjective cognitive biases to directly influence decision outcomes. To this end, this paper proposes the CIHFS-DEMATEL method. Compared with existing DEMATEL approaches, this method allows decision-makers to express the degree of influence between each PUN using CIHFS forms. This enables the evaluation process to integrate “fuzzy interval values” reflecting hesitancy with “confidence parameters” reflecting information reliability, thereby achieving a symmetrical unification of information fuzziness and reliability at the information structure level. Subsequently, the CHFSF scoring function converts CIHFS fuzzy information into precise numerical values, which are then input into the DEMATEL method to construct the causal weight matrix. This conversion process preserves the richness of decision-makers’ subjective evaluations while ensuring symmetry and consistency in causal relationship processing. Furthermore, by leveraging credibility parameters to quantitatively control information quality, it effectively depicts the symmetric influence network among PUNs. Therefore, compared with the logic in existing DEMATEL methods that relies on single deterministic inputs and lacks credibility constraints, the CIHFS-DEMATEL framework for evaluating structural symmetry better aligns with real-world decision-making scenarios. It achieves enhanced symmetry across three dimensions—information representation, quality control, and structural modeling—providing systematic theoretical support and methodological implementation for decision analysis. This significantly improves the scientific rigor and rationality of requirement prioritization and screening.

2.6. Convergent Product Iterative Design Process Construction

Based on the aforementioned technical approach, this paper ultimately proposes a product iteration design methodology that integrates LDA text mining, CIHFS fuzzy representation, and CIHFS-DEMATEL causal modeling. The overall workflow is shown in Figure 2.

The iterative design methodology for this product comprises four major steps: review collection and preprocessing, topic extraction and attribute construction, fuzzy evaluation and causal analysis, and design implementation. First, online reviews about the product are scraped from e-commerce platforms. Through preprocessing steps such as data cleansing and LDA topic analysis, information related to potential user demand keywords is extracted. Second, the design team identifies optimization points for technical modules based on product characteristics, establishing attribute points for subsequent evaluation while constructing potential user needs to complete topic extraction and attribute construction. Third, decision-makers use the CIHFS to assess the correlation between user needs and technical modules and employ CIHFS-DEMATEL to analyze causal relationships among PUNs, sequentially deriving the need–technical module relationship matrix and need weight vectors. Finally, the importance of each technical module is calculated based on the demand–technical module relationship matrix and the demand weight vector. This completes the mapping of technical modules to potential user demands, guiding subsequent iterative product design.

Compared with existing methods, this process achieves “multi-level symmetrical closed-loop integration” across text analysis, requirement extraction, fuzzy expression, and structural decision making. For instance, comment data structures align with requirement theme structures; requirement theme structures correspond with fuzzy evaluation structures; and fuzzy evaluation structures map to decision output structures. Each level maintains one-to-one correspondence in information dimensions, endowing the entire process with enhanced information adaptability, expressive flexibility, and structural insight capabilities. Subsequent sections will validate the effectiveness and generalizability of this method in complex requirement identification and technical decision making through an empirical case study involving intelligent waste-sorting equipment. Meanwhile, this paper will take intelligent waste classification equipment as an empirical case to verify the effectiveness and generalizability of the method in complex demand identification and technology decision making.

3. Methods Elaboration

In the field of MADM decision-making method innovation based on online reviews and fuzzy assessment methods, the group has previously conducted in-depth research and tested the effectiveness of the corresponding methods by applying them to examples such as personalized movie recommendations [46,47], vaccination willingness assessment [48,49], and product iterative design [50]. On this basis, in order to solve the key bottlenecks of traditional iterative product design such as the difficulty of user demand acquisition, weak fuzzy information processing, and simplified attribute relationship modeling, this paper proposes an iterative product design method that integrates the processes of online comment mining, interval hesitant fuzzy expression, decision-maker confidence quantification, and demand indicator correlation expression of CIHFS-DEMATEL product iterative design. The method takes user review data as the source and engineering attribute evaluation as the drop-off point, forming a closed-loop process of “semantic extraction–uncertainty modeling–causal weight calculation–scenario mapping”. Its innovations include the following: (1) extending the BUI to the IHFS environment and proposing a CIHFS model that can simultaneously measure the decision-maker’s fuzzy information and information credibility; (2) proposing the credibility-driven credibility interval hesitant fuzzy score function (CHFSF), which can be used to convert the exact value of CIHFS while taking into account the subjective preference and reliability of information; (3) improving the DEMATEL method by using the CIHFS as the main form, so as to adapt to the uncertainty of information transfer and dependency modeling; and (4) constructing the bidirectional mechanism of transforming the “user demand–technology module”, so as to form the full-process and quantifiable product iterative toolchain.

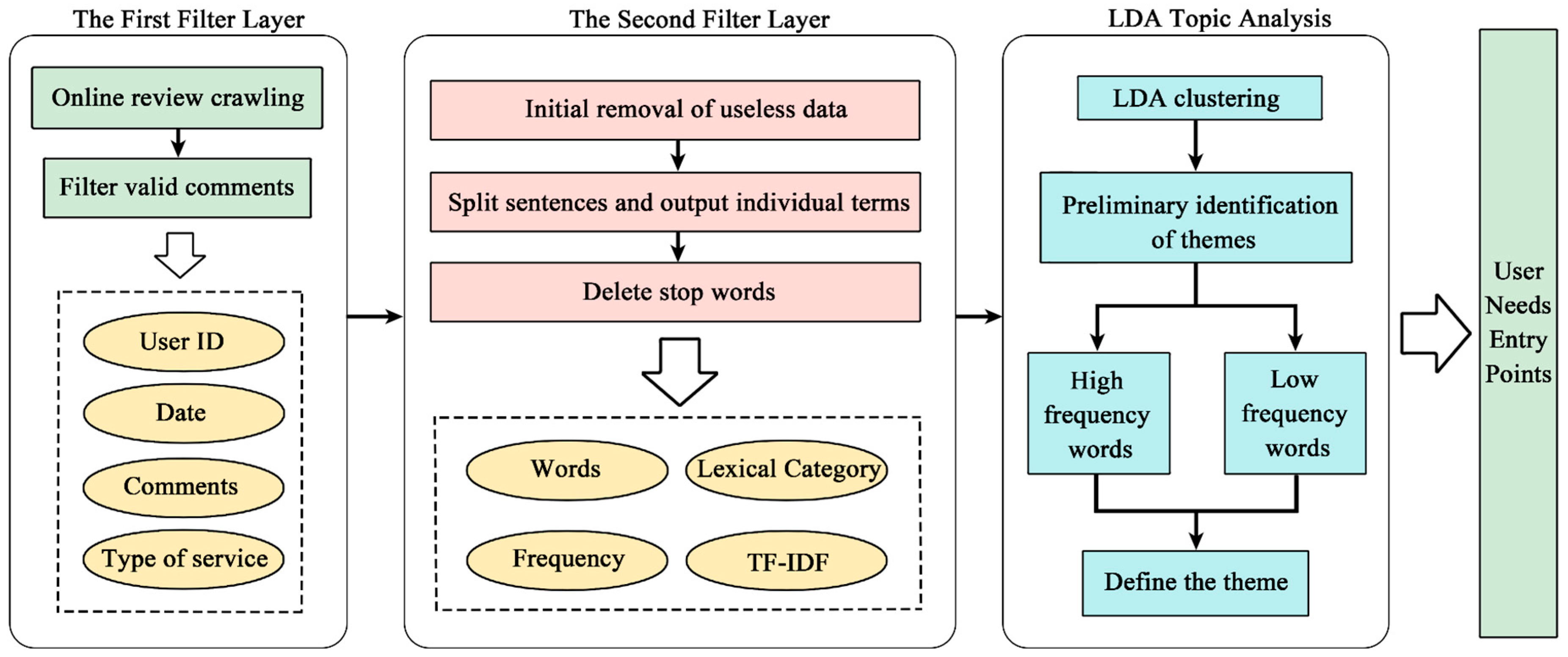
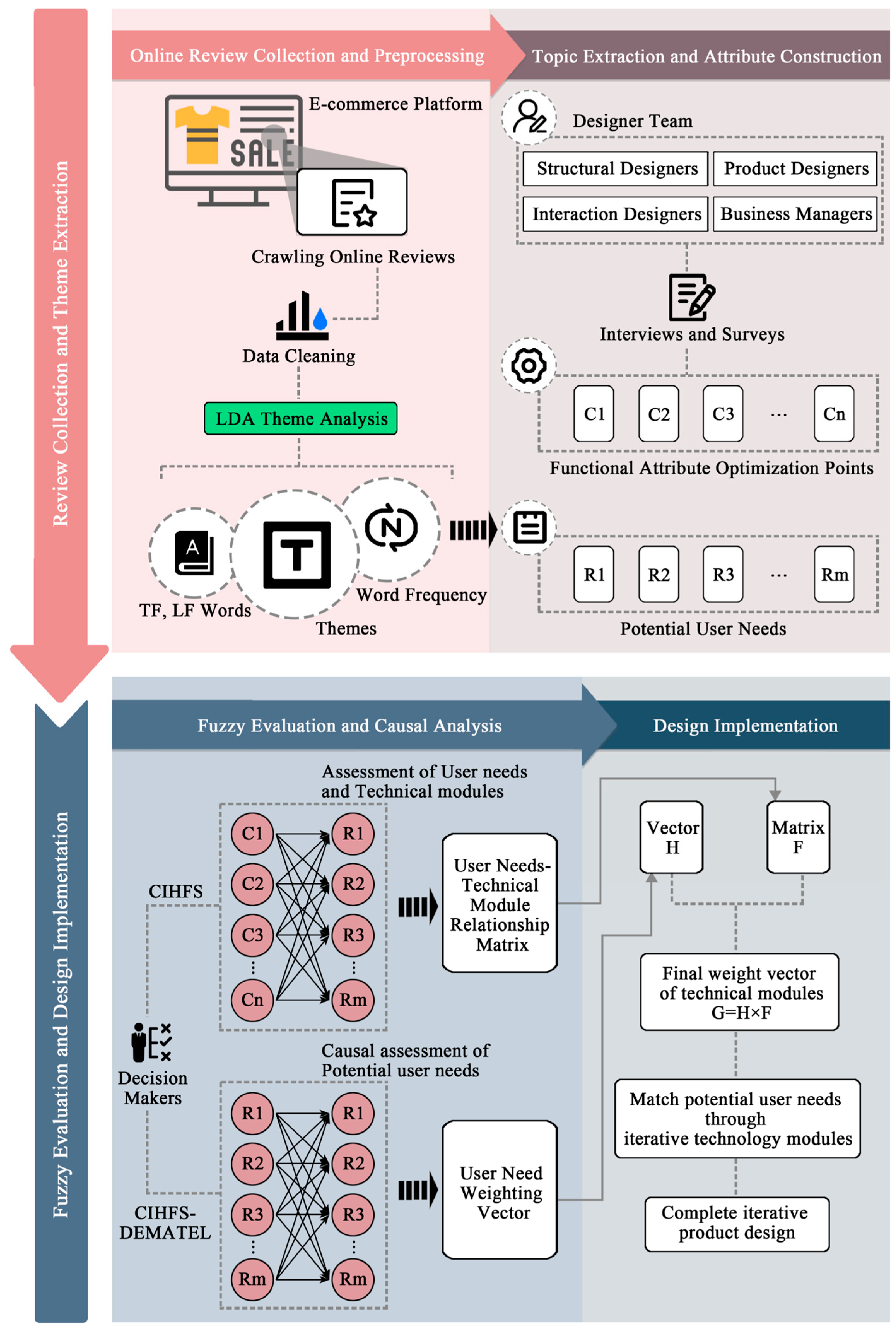
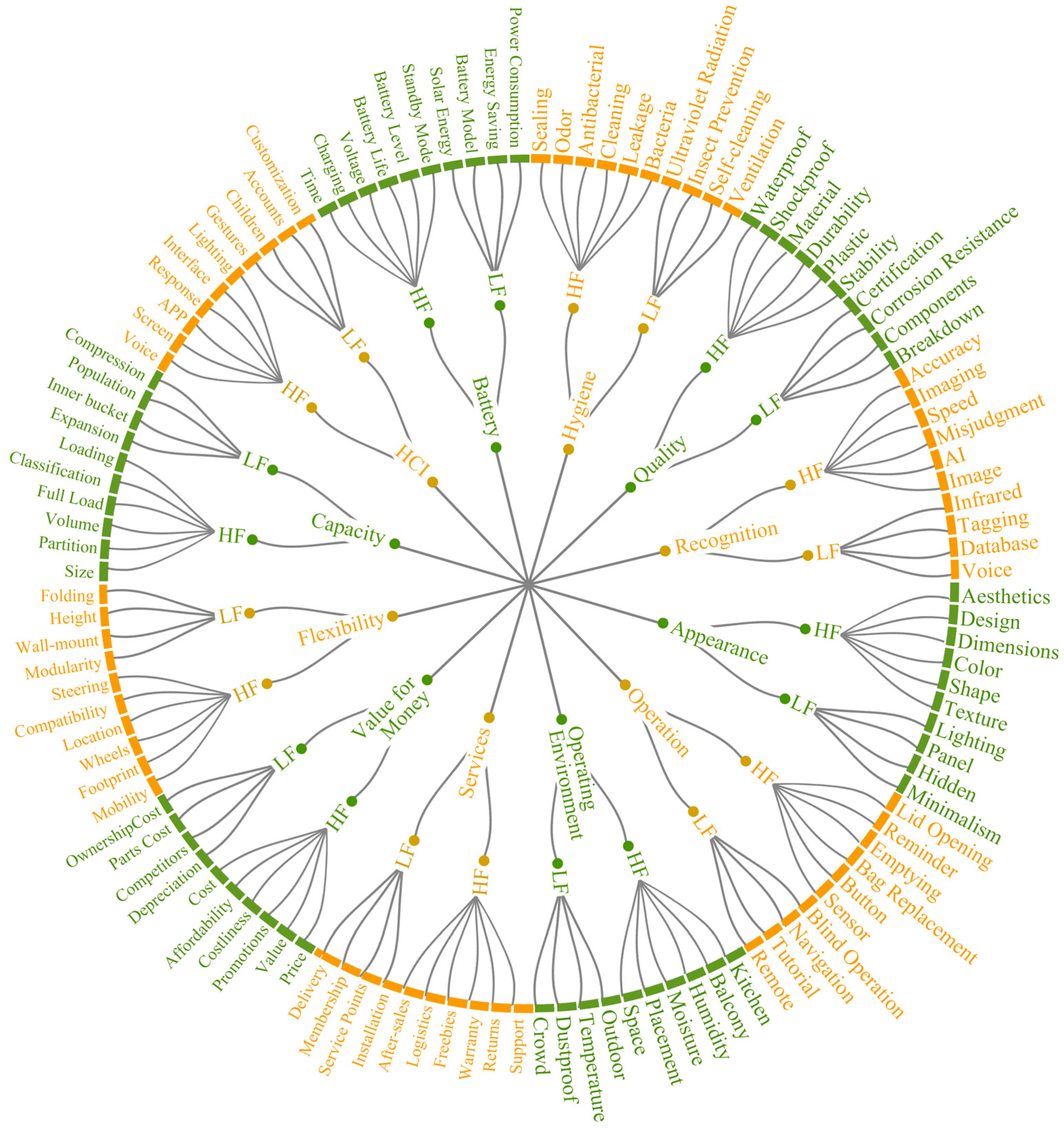
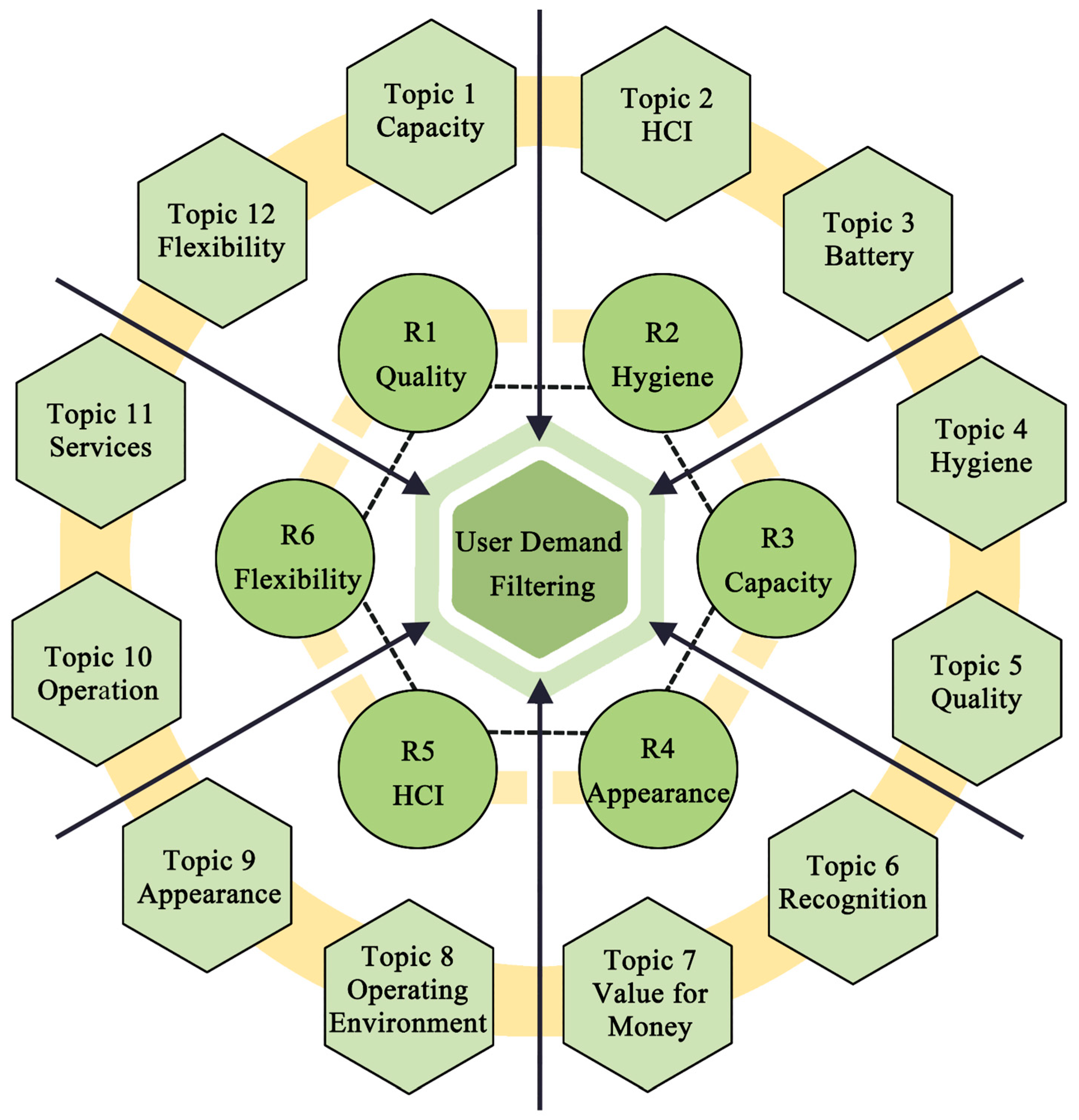
3.1. Weight Determination Model Based on CHFSF

Due to the increasing complexity of decision-making environments and the limitations of human thinking, decision-makers are bound to be hesitant and ambiguous in their evaluations, and the use of fuzzy numbers in decision making can better simulate human thinking than exact values. An interval-valued hesitant fuzzy set (IHFS), as one of the important extended forms of fuzzy numbers, is able to allow decision-makers to express their preferences through multiple intervals, and is considered to be a powerful tool for expressing uncertain information in the MADM process [51]. However, when scoring, people will inevitably have uncertainty about the scores given, but the existing interval hesitation fuzzy set does not fully consider this situation, but completely trusts the subjective judgments given by each decision-maker, which leads to a strong subjectivity in the decision-making results. Based on this, this paper combines basic uncertain information (BUI) with an interval-valued hesitant fuzzy set (IHFS), and proposes a credibility-based interval hesitant fuzzy set (CIHFS), which symmetrically integrates two key dimensions of the decision-maker’s subjective assessment: the uncertainty of the evaluation value and the level of confidence in the evaluation, as described below.

• Basic concepts

Suppose there are $m$ potential user needs (PUNs) to be evaluated $R=\left\{R_1,R_2,\dots ,R_m\right\}$, a product with $n$ technical modules $C=\left\{C_1,C_2,\dots ,C_n\right\}$, and $k$ product assessment decision-makers $d=\left\{d_1,d_2,\dots ,d_k\right\}$.

The weighting of PUNs is $h=\left\{h_l\left|l=1,2,\dots ,m\right.\right\}$, $h_l\in \left[0,1\right]$, ${\displaystyle \sum _{l=1}^m{h}_l}=1$.

The technical modules of the product are weighted $z=\left\{z_i\left|i=1,2,\dots ,n\right.\right\}$, $z_i\in \left[0,1\right]$, and ${\displaystyle \sum _{i=1}^n{z}_i}=1$.

The weights of the decision-makers are $w=\left\{w_j\left|j=1,2,\dots ,k\right.\right\}$, $w_j\in \left[0,1\right]$, and ${\displaystyle \sum _{j=1}^k{w}_j}=1$.

Assuming $b=〈\left\{\left[{\gamma }_1^L,{\gamma }_1^U\right],\left[{\gamma }_2^L,{\gamma }_2^U\right],\dots ,\left[{\gamma }_i^L,{\gamma }_i^U\right]\right\};c〉$ is a credibility-based interval hesitant fuzzy set (CIHFS), where $\left[{\gamma }_i^L,{\gamma }_i^U\right]$ represents the interval of evaluation values provided by the decision-maker and satisfies $0\le {\gamma }_i^L\le {\gamma }_i^U\le 1$, $i=1,2,\dots ,l_{\tilde{h}}$. $l_{\tilde{h}}$ denotes the number of elements; $c$ represents the degree of certainty, indicating the decision-maker’s subjective confidence in their own assessment results, and satisfies $c\in \left[0,1\right]$.

Example: A decision-maker assigns a score of $b=〈\left\{\left[0.3,0.4\right],\left[0.5,0.6\right];0.8\right\}〉$ to a certain indicator using the CIHFS. It can be interpreted that the decision-maker’s assessment of that indicator falls between values $\left[0.3,0.4\right]$ and $\left[0.5,0.6\right]$, with a confidence level of $c=0.8$ for the assigned value. The number of elements is $l_{\tilde{h}}=2$.

2.

Adjustment of the weight of information for decision-makers

In current product iteration design decision making, decision-maker weights are typically assigned subjectively to reflect the relative importance of the evaluation information they provide during the process. However, the knowledge backgrounds of participating evaluators often vary, and this subjective weighting approach may undermine the scientific rigor and objectivity of the final assessment results. Specifically, subjective weighting fails to distinguish variations in the credibility of information provided by different decision-makers. Consequently, information—regardless of its reliability—is assigned equal contribution weight in the final assessment. This approach clearly undermines the formation of reliable decision conclusions.

Therefore, this paper proposes a decision-maker weight allocation method whose core logic involves quantifying quality through information credibility and adjusting decision-maker weights based on this quality assessment. The method first assumes equal weights among decision-makers. It then determines each decision-maker’s trustworthiness based on their certainty regarding the product. Following this evaluation, it proposes a method for adjusting product decision-maker weights, ensuring dynamic weighting based on information credibility. The specific adjustment approach and mathematical logic are outlined below.

Assuming $b=〈\left\{\left[{\gamma }_1^L,{\gamma }_1^U\right],\left[{\gamma }_2^L,{\gamma }_2^U\right],\dots ,\left[{\gamma }_i^L,{\gamma }_i^U\right]\right\};c〉$ is a credibility-based interval hesitant fuzzy set (CIHFS), the decision-maker’s hesitancy [52,53] is defined as

$$\varphi \left(b\right)={\displaystyle \frac{1}{3}}\times \left(c\times s\left({\tilde{h}}_i\left(x\right)\right)+(1-{\displaystyle \frac{1}{l_{\tilde{h}}}})+(1-c)\right)$$

(1)

where $s\left({\tilde{h}}_i\left(x\right)\right)={\displaystyle \frac{1}{3l_{\tilde{h}}}}{\displaystyle \sum _{i=1}^{l_{\tilde{h}}}\left({\left({\gamma }_i^L\right)}^2+{\left({\gamma }_i^U\right)}^2+{\gamma }_i^L\times {\gamma }_i^U\right)-\frac{1}{4{l_{\tilde{h}}}^2}}{\left[{\displaystyle \sum _{i=1}^{l_{\tilde{h}}}({\gamma }_i^L+{\gamma }_i^U)}\right]}^2$ is the variance of the interval-valued hesitant fuzzy element, $c$ is the degree of certainty, and $l_{\tilde{h}}$ is the number of elements.

When the degree of hesitation under a certain index attribute is higher under the category to be evaluated, which proves that the product evaluation decision-maker is more hesitant to make an assessment under a certain attribute, the degree of certainty of the evaluation is lower. Based on the relationship between similarity and distance, the trustworthiness of the decision-maker’s evaluation is then defined as

$$R(b)=1-\varphi \left(b\right)$$

(2)

The decision-maker weights are adjusted according to the obtained trustworthiness to obtain more realistic decision-maker weights. The formula for adjusting the decision-maker’s weight is

$$w^{\prime }={\displaystyle \frac{w}{1+w-\frac{1}{mn}{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^{n}R\left(b_{ij}^k\right)}}}}$$

(3)

where $w\in \left[0,1\right]$ is the weight of the decision-maker before adjustment, $w^{\prime }\in \left[0,1\right]$ is the weight of the decision-maker after adjustment, and ${\displaystyle \frac{1}{mn}}{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^{n}R\left(b_{ij}^k\right)}}$ is the average certainty of the decision-maker.

Normalization of $w^{\prime }$ yields a weight $w^{″}$ for the final product decision-maker as

$$w^{″}={\displaystyle \frac{w^{\prime }}{{\displaystyle \sum _{j=1}^k{w}^{\prime }}}}$$

(4)

3.2. Credibility Interval Hesitant Fuzzy Score Function (CHFSF)

In practical product iteration design and multi-attribute decision-making (MADM) tasks, computational models typically require inputs as deterministic real numbers. However, the core constituent units of the CIHFS consist of one or more fuzzy interval values coupled with an exact confidence parameter, rendering them unsuitable for direct participation in subsequent operations. Therefore, it is necessary to develop a scoring function tailored for CIHFS that maps the fuzzy information and uncertainty evaluations expressed within CIHFS into computable deterministic values. This transformation is essential to meet the requirements for subsequent quantitative evaluation and priority ranking.

Based on this, this study integrates multi-source information fusion theory [54], expected utility theory [55], and the defuzzification concept in fuzzy decision-making to propose the credibility interval hesitant fuzzy score function (CHFSF). Structurally, the CHFSF embodies a weight symmetry mechanism between subjective information and objective references, enabling flexible control over the final precise value output through credibility parameters and decision-maker weight values.

From a mathematical logic perspective, the CHFSF first performs precision conversion on the fuzzy sets within it, then integrates various effective information, such as credibility parameters and decision-maker weights, to achieve quantitative analysis of the entire CIHFS unit. Overall, the core objective of the CHFSF is to map the fuzzy information and credibility features within the CIHFS into computable, deterministic values. This not only fulfills subsequent quantitative evaluation and priority ranking requirements but also enhances the conversion efficiency and utilization rate of fuzzy assessment information.

According to the multi-source information fusion (MSIF) theory, when the same evaluation indicator comes from more than one source, the fusion weights should be assigned according to the quality of information [56]. In this model, the fuzzy evaluation given by the decision-maker and the system default valuation $\eta$ constitute two types of basic information sources, while the credibility parameter $c\in \left[0,1\right]$ in the fuzzy evaluation reflects the trust level of the decision-maker’s evaluation. In order to maintain the balance of the input information, the score function designed in this paper is structured to give a symmetrical weighting relationship between the two: the fuzzy evaluation part of the decision-maker is weighted as $c_i^{*}$, and the default valuation part of the system is weighted as $1-c_i^{*}$, so as to make the subject–object information proportionally and equitably integrated in the confidence space.

In addition, expected utility theory (EUT) emphasizes that under uncertainty, rational decision making should be based on a weighted summation of multiple possible state utilities [57]. The CHFSF achieves precise conversion of evaluation information in CIHFS fuzzy environments by treating decision-makers’ subjective assessments and system default valuations $\eta$ as two core information sources, then performing expectation calculations based on their subjective credibility. Compared with existing fuzzy scoring functions that primarily focus on optimizing fuzzy processing while failing to establish a direct link between information quality and score calculation, and lacking a symmetric mapping mechanism between subjective and objective information, the CHFSF innovates by constructing a structured conversion framework from “fuzzy input–credibility regulation–precise output.” This framework not only maps CIHFS to quasi-exact numerical values, but more importantly, it preserves the structural flexibility and expressive adequacy of evaluation information through a credibility mechanism. This effectively reduces information entropy loss during mapping, thereby achieving symmetric logic from input to output in the information conversion process. It fills the theoretical gap in existing fuzzy scoring function methods regarding the correspondence between information types and numerical reliability.

At the operational level, this paper combines the “interval midpoint method [58]” and “credibility weighting [59]”, which are commonly used in hesitant fuzzy decision making, to design the following score function:

Assuming $b=〈\left\{\left[{\gamma }_1^L,{\gamma }_1^U\right],\left[{\gamma }_2^L,{\gamma }_2^U\right],\dots ,\left[{\gamma }_i^L,{\gamma }_i^U\right]\right\};c〉$ is a credibility-based interval hesitant fuzzy set (CIHFS), $0\le {\gamma }_i^L\le {\gamma }_i^U\le 1$, $i=1,2,\dots ,l_{\tilde{h}}$.

$${\mu }_i={\displaystyle \frac{{\displaystyle \sum _{i=1}^{l_{\tilde{h}}}({\gamma }_i^L+{\gamma }_i^U)}}{2\times l_{\tilde{h}}}}$$

(5)

$${x_i}^{\ast }=1-{\displaystyle \prod _{i=1}^n{(1-{\mu }_i)}^{w_i^{″}}}$$

(6)

$$c_i^{*}={\displaystyle \sum _{i=1}^n{w}_i^{″}{c}_i}$$

(7)

$${x^{\prime }}_i=c_i^{*}{x}_i^{*}+\eta \left(1-c_i^{*}\right)$$

(8)

where ${\mu }_i\in \left(0,1\right)$ is the mean value of the scoring interval, $l_{\tilde{h}}$ is the number of elements, ${x_i}^{\ast }$ is the scoring interval synthesis operator, $w_i^{″}$ is the adjusted decision-maker weight, $c_i^{*}$ is the certainty-weighted synthesis operator, $c_i$ is the original certainty, $x_i^{\prime }$ is the final certainty value, and $\eta$ is the default value under the lack of confidence condition, which is often taken to be 0.5, indicating a neutral reference.

The score function not only converts the uncertainty interval hesitant fuzzy expression into a unique real value but also maintains the structural flexibility and expressive adequacy in fuzzy evaluation. At the structural level, the function embodies the following mathematical and decision-making properties:

Property 1.  

Range boundedness: In the CIHFS, since all interval value sets satisfy $0\le {\gamma }_i^L\le {\gamma }_i^U\le 1$, the credibility parameters $c\in \left[0,1\right]$, $\eta \in \left[0,1\right]$, so $x_i^{\prime }\in \left[0,1\right]$

Property 2.  

Monotonicity: The final value $x_i^{\prime }$ monotonically converges toward the mean $c$ of the rating interval as the credibility coefficient ${\mu }_i$ increases. This indicates that higher trust levels result in a greater contribution of the decision-maker’s assessment value to the final value $x_i^{\prime }$, aligning with real-world logic.

Property 3.  

Boundary properties: If $c=1$, it indicates that the decision-maker’s assessment is fully credible.Then $x_i^{\prime }={\mu }_i$, the final value $x_i^{\prime }$ is entirely dependent on the decision-maker’s assessment. If $c=0$, it indicates that the decision-maker’s assessment is completely unreliable.Then, $x_i^{\prime }=\eta$, and the final value $x_i^{\prime }$ is entirely dependent on the neutral reference default value. The above assumptions all demonstrate the interpretability of the CHFSF under extreme scenarios.

Property 4.  

Continuity and derivability: The final value $x_i^{\prime }$ is a linear function of the certainty-weighted synthesis operator $c_i^{*}$. It is continuous and first-order derivable on $\left[0,1\right]$. This ensures that minor variations in the credibility within the CIHFS induce only smooth fluctuations in the final determination value $x_i^{\prime }$, thereby preventing abrupt changes in the final determination value $x_i^{\prime }$ results and enhancing the ranking stability of the CHFSF model.

Example: A decision-maker with a weight of $w_i^{″}=0.3856$ scoring an indicator as $b=〈\left\{\left[0.3,0.5\right],\left[0.6,0.8\right];0.8\right\}〉$ using the credibility interval hesitant fuzzy score function (CHFSF) is calculated as

$$\mu ={\displaystyle \frac{0.3+0.5+0.6+0.8}{2\times 2}}=0.55$$

$$x^{\ast }=1-{(1-0.55)}^{0.3856}=0.2650$$

$$c^{*}=0.3856\times 0.8=0.3085$$

$$x^{\prime }=0.3085\times 0.2650+0.5\times \left(1-0.3085\right)=0.4275$$

The finalized value $x^{\prime }=0.4275$ can serve as input for technical module scoring, size comparison, weight calculation, and priority ranking. This value retains information from all decision-makers while incorporating rational system evaluation, demonstrating strong representativeness and scalability.

Considering that the simplest application scenario in the MADM after converting fuzzy information into precise real numbers is to compare the magnitudes of two fuzzy pieces of information, this paper selects two methods for converting fuzzy information into precise real numbers proposed by Quirós, P et al. [60] and Liang et al. [61] for comparative research. This section first briefly describes the scoring functions proposed by Quirós, P et al. and Liang et al. [60,61].

First of all, a scoring function proposed by Quirós, P et al. for interval hesitant fuzzy sets is designed to compare the sizes of two distinct intervals. The scoring function proposed by Quirós, P et al. [60] is defined as follows:

For an interval-valued fuzzy set $\tilde{h}=\left\{\left[{\gamma }_1^L,{\gamma }_1^U\right],\left[{\gamma }_2^L,{\gamma }_2^U\right],\dots ,\left[{\gamma }_i^L,{\gamma }_i^U\right]\right\}$, satisfying $0\le {\gamma }_i^L\le {\gamma }_i^U\le 1$, $i=1,2,\dots ,l_{\tilde{h}}$, $l_{\tilde{h}}$ denotes the number of elements, and the score function $H\left(\tilde{h}\right)$ and the accuracy function $M\left(\tilde{h}\right)$ are as follows:

$$H\left(\tilde{h}\right)={\displaystyle \sum _{i=1}^{l_{\tilde{h}}}\left({\gamma }_i^U-{\gamma }_i^L\right)}$$

(9)

$$M\left(\tilde{h}\right)={\displaystyle \frac{1}{l_{\tilde{h}}}}{\displaystyle \sum _{i=1}^{l_{\tilde{h}}}\left(\frac{{\gamma }_i^L+{\gamma }_i^U}{2}\right)}$$

(10)

Assuming two interval-valued fuzzy sets are denoted as ${\tilde{h}}_1$ and ${\tilde{h}}_2$, and letting $l_{{\tilde{h}}_1}$ and $l_{{\tilde{h}}_2}$ be the number of elements in ${\tilde{h}}_1$ and ${\tilde{h}}_2$, respectively, then

• If $M\left(\widetilde{h_1}\right)<M\left(\widetilde{h_2}\right)$, then $\widetilde{h_1}\le \widetilde{h_2}$;
• If $M\left(\widetilde{h_1}\right)=M\left(\widetilde{h_2}\right)$, and $H\left(\widetilde{h_1}\right)<H\left(\widetilde{h_2}\right)$, then $\widetilde{h_1}\le \widetilde{h_2}$;
• If $M\left(\widetilde{h_1}\right)=M\left(\widetilde{h_2}\right)$, $H\left(\widetilde{h_1}\right)=H\left(\widetilde{h_2}\right)$, and $l_{{\tilde{h}}_1}<l_{{\tilde{h}}_2}$, then $\widetilde{h_1}\le \widetilde{h_2}$;
• If $M\left(\widetilde{h_1}\right)=M\left(\widetilde{h_2}\right)$, $H\left(\widetilde{h_1}\right)=H\left(\widetilde{h_2}\right)$, $l_{{\tilde{h}}_1}=l_{{\tilde{h}}_2}$, and ${\gamma }_1^U\left(\widetilde{h_1}\right)\le {\gamma }_1^U\left(\widetilde{h_2}\right)$, and ${\gamma }_1^L\left(\widetilde{h_1}\right)\le {\gamma }_1^L\left(\widetilde{h_2}\right)$, $i=1,2,\dots ,l_{\tilde{h}}$, then $\widetilde{h_1}\le \widetilde{h_2}$.

Liang et al. [61] define a group satisfaction function for the random MADM problem under interval-based hesitant fuzzy sets, aiming to map each complex set containing multiple interval values onto a single real number as the data input for subsequent MADM problems. The proposed scoring function is defined as follows:

For an interval-valued fuzzy set $\tilde{h}=\left\{\left[{\gamma }_1^L,{\gamma }_1^U\right],\left[{\gamma }_2^L,{\gamma }_2^U\right],\dots ,\left[{\gamma }_i^L,{\gamma }_i^U\right]\right\}$, satisfying $0\le {\gamma }_i^L\le {\gamma }_i^U\le 1$, $i=1,2,\dots ,l_{\tilde{h}}$, $l_{\tilde{h}}$ denotes the number of elements, and the steps for calculating the group satisfaction function are as follows:

$$s\left(\tilde{h}\right)={\displaystyle \frac{1}{2l_{\tilde{h}}}}{\displaystyle \sum _{i=1}^{l_{\tilde{h}}}\left({\gamma }_i^L+{\gamma }_i^U\right)}$$

(11)

$$v\left(\tilde{h}\right)={\displaystyle \frac{1}{3l_{\tilde{h}}}}{\displaystyle \sum _{i=1}^{l_{\tilde{h}}}\left[{\left({\gamma }_i^L\right)}^2+{\left({\gamma }_i^U\right)}^2+{\gamma }_i^L{\gamma }_i^U\right]}-{\displaystyle \frac{1}{4{l_{\tilde{h}}}^2}}{\left[{\displaystyle \sum _{i=1}^{l_{\tilde{h}}}\left({\gamma }_i^L+{\gamma }_i^U\right)}\right]}^2$$

(12)

$$\phi \left(\tilde{h}\right)={\displaystyle \frac{s\left(\tilde{h}\right)}{1+v\left(\tilde{h}\right)}}$$

(13)

where $l_{\tilde{h}}$ represents the number of elements; $s\left(\tilde{h}\right)$ indicates the overall level, with higher values signifying greater overall quality; $v\left(\tilde{h}\right)$ reflects internal dispersion and group divergence; and $\phi \left(\tilde{h}\right)$ denotes group satisfaction, with higher values indicating greater satisfaction with the rating.

Example: One decision-maker with weight $w_1^{″}=0.4$ assigns score $b_1=〈\left\{\left[0.2,0.4\right],\left[0.6,0.8\right];0.6\right\}〉$ to a certain indicator using an uncertain interval hesitant fuzzy set, while another decision-maker with weight $w_2^{″}=0.6$ assigns score $b_2=〈\left\{\left[0.15,0.45\right],\left[0.65,0.75\right];0.8\right\}〉$ to another indicator using the same uncertain interval hesitant fuzzy set.

Since the scoring function proposed by Quirós, P et al. and Liang et al. [60,61] only involves the calculation of interval numbers, subsequent comparative verification will disregard the effects of expert weighting and information credibility, setting $\widetilde{h_1}=\left\{\left[0.2,0.4\right],\left[0.6,0.8\right]\right\}$, and $\widetilde{h_2}=\left\{\left[0.15,0.45\right],\left[0.65,0.75\right]\right\}$.

According to Equations (9) and (10), it can be concluded that $M\left(\widetilde{h_1}\right)=0.5, M\left(\widetilde{h_2}\right)=0.5, H\left(\widetilde{h_1}\right)=0.4, H\left(\widetilde{h_2}\right)=0.4$. Therefore, based on this method, it is evident that the precise numerical values obtained cannot directly distinguish the relative magnitudes of ${\tilde{h}}_1$ and ${\tilde{h}}_2$.

According to Equations (11)–(13), it can be concluded that $s\left(\widetilde{h_1}\right)=0.5, s\left(\widetilde{h_2}\right)=0.5, v\left(\widetilde{h_1}\right)=0.043, v\left(\widetilde{h_2}\right)=0.044, \phi \left(\widetilde{h_1}\right)=0.479, \phi \left(\widetilde{h_2}\right)=0.479$. Therefore, based on this method, it is equally difficult to directly determine the relative magnitudes of ${\tilde{h}}_1$ and ${\tilde{h}}_2$.

According to Equations (5)–(8), it can be concluded that ${\mu }_1=0.5, {\mu }_2=0.5, {x_1}^{\ast }=0.242, {x_2}^{\ast }=0.340, c_1^{*}=0.24, c_2^{*}=0.48, x_1^{\prime }=0.438, x_2^{\prime }=0.493$. Therefore, based on the CHFSF method, we can directly determine that $b_1<b_2$.

As demonstrated by the above examples, under certain special circumstances, the scoring functions proposed by Quirós, P et al., and Liang et al. [60,61] for interval-hesitant fuzzy sets cannot achieve sufficiently scientific and precise conversion. Even when using CHFSF calculations, the average scores for both rating intervals remain equal at ${\mu }_i$. However, after incorporating indicators such as expert weight and credibility, the precise value results exhibit certain differences. This further demonstrates that relying solely on information within interval hesitant fuzzy sets for precision conversion cannot yield sufficiently objective and scientific precise values. More critically, the two methods proposed by Quirós, P et al. and Liang et al. [60,61] fail to account for expert weight contribution rates and subjective factors during scoring. Consequently, they not only fall short of meeting CIHFS’s precise value conversion requirements but also propagate the uncertainty inherent in expert assessments into subsequent MADM decision making, thereby compromising decision effectiveness.

In summary, precise conversion of fuzzy information requires not only consideration of interval values but also thorough assessment of the uncertainty attributes and reliability of expert evaluations. By symmetrically integrating these critical elements, CHFSF effectively addresses the shortcomings of traditional scoring function methods, thereby fully demonstrating its rationality and scientific validity.

3.3. CIHFS-DEMATEL Method

In iterative product design, the relationships among potential user needs need to be fully considered. Decision-making trial and evaluation laboratory (DEMATEL) is often used to analyze the correlations among metrics [41]. However, existing DEMATEL methods typically rely on decision-makers’ provided deterministic values when assessing causal relationships among indicators. This approach not only struggles to capture the hesitancy inherent in decision-making processes and variations in assessment credibility but also fails to distinguish the contribution levels of different-quality evaluation information to the final outcome. To address this, this paper integrates the CIHFS framework with the DEMATEL method, constructing a decision-making approach that simultaneously accounts for fuzzy causal relationships and ensures structural symmetry. First, the CIHFS serves as the carrier for expressing causal strength. By utilizing “interval value sets” and “credibility parameters,” it characterizes evaluation hesitation and reliability, respectively, overcoming the limitation of traditional DEMATEL methods that rely solely on deterministic values. Subsequently, the CHFSF facilitates the transformation from fuzzy inputs to deterministic causal strengths. This process not only preserves the structural symmetry of bidirectional relationships among requirements but also assigns higher weight contributions to high-credibility evaluation information, addressing the existing DEMATEL method’s indiscriminate treatment of information quality. Finally, the transformed precise values are input into DEMATEL to construct a comprehensive influence matrix, yielding the final weight values. The CIHFS-DEMATEL process fully integrates the multidimensional logic of “fuzziness–credibility–structurality.” While maintaining symmetrical conversion between input fuzziness and output structurality, it enhances the interpretability and scientific validity of evaluation results. This provides theoretical support and methodological assurance for introducing structural symmetry into decision-making models. Based on the above approach, the corresponding attribute weight determination model is constructed as follows:

• Constructing direct impact matrices between indicators

Each decision-maker scores each indicator in two-by-two comparisons using the uncertainty interval hesitant fuzzy meta form to quantify the causal influence relationship between functional elements, and each scoring value adopts a scale value of 0–1, where 0, 0.25, 0.5, 0.75, and 1.0 denote a very weak, weak, moderate, strong, and extremely strong influence, respectively, and since the DEMATEL method uses deterministic values for the calculation, the scoring of each decision-maker is completed using Formulas (5)–(8) for the scoring value of each decision-maker to do the refinement process.

After transforming the hesitant fuzzy elements of each uncertainty interval into the deterministic values used by DEMATEL, the initial direct impact matrix A is formed together.

$$A=\left[\begin{array}{cccc}0& x_{12}& \dots & x_{1n}\\ x_{21}& 0& \dots & x_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& \dots & 0\end{array}\right]$$

(14)

where $x_{ij}$ denotes the intensity of the direct effect of element $i$ on element $j$.

2.

Direct impact matrix data processing

The matrix A is normalized to yield the canonical matrix B.

$$B={\displaystyle \frac{x_{ij}}{\max \left({\displaystyle \sum _{j=1}^n{x}_{ij}}\right)}}$$

(15)

The integrated impact matrix T is calculated. The integrated system matrix T reflects the combined effect of the influences between the elements in the system, where I is the unit matrix.

$$T=B{\left(I-B\right)}^{-1}=\left(B+B^2+\dots B^k\right)={\displaystyle \sum _{K=1}^{\infty }{B}^k}$$

(16)

The center and cause degrees are calculated. The influence degree $D_i$ and the influenced degree $F_i$ of each element are calculated by Formulas (17) and (18), and the center degree $M_i$ and the cause degree $R_i$ of the system importance are further calculated by Formulas (19) and (20).

$$D_i={\displaystyle \sum _{j=1}^n{x}_{ij}},\left(i=1,2,\dots ,n\right)$$

(17)

$$F_i={\displaystyle \sum _{j=1}^n{x}_{ji},\left(i=1,2,\dots ,n\right)}$$

(18)

$$M_i=D_i+F_i$$

(19)

$$R_i=D_i-F_i$$

(20)

According to Formula (21), the center degree $M_i$ and cause degree $R_i$ of each indicator are combined to normalize them, the weight value of each indicator is calculated, and the weight value of each indicator is aggregated to obtain the potential user demand weight vector $H=\left(h_l\left|l=1,2,\dots ,m\right.\right)$

$$h_l={\displaystyle \frac{D_i+F_i}{{\displaystyle \sum _{k=1}^n\left(D_i+F_i\right)}}}$$

(21)

3.4. Adjustment of Indicator Importance Based on PUN and Engineering Considerations

The central challenge for companies in selecting and deciding on product iteration design points is how to strike a balance between potential user needs (PUNs) and engineering realizability. Although PUN information can map out the key points of product iterative design and manufacturing innovation, and then point out the direction for product development, it still needs to be manifested into technical module elements when it is realized. In the process of transformation, it is necessary to take into account the correlation between PUNs and the mapping relationship between PUNs and technology modules, both of which are indispensable. In terms of the user demand dimension, the potential demand weight and its interdependence will directly reflect the market demand priority. If this dimension is ignored, it will lead to difficulties in aligning research and development resources with the real user needs, thus reducing the competitiveness of the product in the market. From the engineering realization dimension, the correlation matrix between the technical modules and the PUN quantifies the ability of the modules to satisfy the needs. If this dimension is not taken into account, enterprises may ignore the strategic significance of high-value demands and over-invest in technical modules with weak demand correlation, resulting in a loss of research and development resources.

In summary, whether it is user demand or engineering realization, decision making that only considers a single dimension will lead to the risk of technology deviation from the market or resource mismatch. The only way to achieve a balance between the potential user demand and engineering realization is to combine the potential user demand weights with the correlation matrix and re-rank the importance of technology modules according to the correlation between the two. Based on this, this study combines the demand weight vector with the correlation matrix to generate the importance of the technology modules, which is handled as follows.

According to formula (22), combining the decision matrix $F={(f_{ij})}_{m\times n}$ of the relationship between the user’s potential needs and the technology module and the weight vector $H$ of the relationship between the indicators, they are summarized to obtain the importance vector of the technology module $G={(z_i)}_{1\times n}$.

$$G=H\times F$$

(22)

4. Case Studies

4.1. Product Iteration Object Selection

The product iteration design research object is selected as “Mayflower smart sorting bin WYH-GB1023”, as shown in Figure 3. The product has high brand awareness, good sales, and a moderate price. Online user reviews come from online e-commerce platforms such as Tmall and JD. There are more than 200,000 positive reviews, more than 2100 neutral reviews, and more than 1000 bad reviews for this product across the platform. In fact, the higher the number of online reviews of the product, the better it is received in the market and the more user demand information it has. Selecting this product as a product iteration design study has the advantage of rich information and sufficient optimization direction. Therefore, it is more convincing to validate it as the object of the product iterative method, which also better reflects the practical application value of this research and the method.

4.2. Arrangement of Research Tools

This study is based on the Windows 11 64-bit operating system, Octopus software V8.6.7., ROSTCM 5.8.0.603, and Python 3.6 software to build the experimental platform for designing the research and installing various types of third-party libraries, such as Jieba. Among them, the Octopus software is used for the data collection work; Python 3.6 and ROST CM6 are used for the work of comment segmentation, LDA clustering, and data visualization.

The data collection time was 5 July 2025, and a total of 10,311 original online review corpus data were obtained, and the actual review data crawled include user name, user location, purchase date, model number, and review text. Taking the review of “May Flower Intelligent Classified Trash Can” as an example, a total of 3149 pieces of original user review data from January 2023 to June 2025 were collected through the crawler. After crawling the comment data and removing the duplicates and blank comments, a total of 2817 valid comments were collected. Some of the comment data are shown in

Table 1. Crawled review information sheet.

User	Comment Content	Date	Region
j***3	The exterior design is quite good, and I am quite satisfied with it. The smart sorting trash can has a large capacity. It does not make much noise when running. Appearance: very good.	Feb. 2025	Jiangsu, China
W***0	This user has not entered any comments.	Apr. 2025	Wuhan, China
U***e	This trash can is really practical and convenient! [Emoji] Its simple and elegant appearance blends perfectly into the home environment when paired with a gray carpet. It has a large capacity and can hold a lot of trash, so you don’t have to worry about running out of space. The material is thick and of good quality, so you can use it with confidence and peace of mind. The lid design is especially effective at preventing odors, so you don’t have to worry about unpleasant smells anymore. Overall, it is very cost-effective and worth buying! [Emoji] [Emoji]	Jan. 2024	Henan, China
B***c	I have repurchased this product multiple times for my office. It has a simple design, no odor, is practical, durable, and easy to clean.	Dec. 2023	Guangdong, China

.

4.3. Preliminary Data Processing

First, we removed useless data from the comment data. Second, we used Jieba to segment Chinese sentences into individual terms and removed stop words that had no practical meaning. We then performed data mining on the results after segmentation and stop word removal. After processing, we obtained word frequency statistics, including words, part of speech, frequency, number of occurrences, and word frequency. The statistical results (partial) are shown in

Table 2. Partial results of word statistics.

Words	Part of Speech	Frequency	tf-idf	Words	Part of Speech	Frequency	tf-idf
Trash can	Noun	641	0.0066	Lid	Noun	81	0.0023
Sound	Noun	398	0.0059	Large	Adjective	80	0.0022
Appearance	Noun	379	0.0056	Clean	Adjective	79	0.0022
Capacity	Noun	376	0.0056	Quality	Noun	79	0.0022
Cost-effectiveness	Noun	96	0.0027	Exquisite	Adjective	67	0.0020

.

4.4. Potential User Needs and Technical Module Selection

First, LDA clustering was performed to identify the themes of the reviews, with the number of themes K set to 5 to enable a more in-depth exploration and analysis of the thematic structure within the review data. To reveal the intrinsic connections between keywords, this study employed logical naming conventions to label the clustering results of the online reviews for this smart waste sorting bin. Finally, based on word frequency, we selected six high-frequency (HF) words and four low-frequency (LF) words for each topic, as shown in Figure 4. After screening, the content of each topic mainly focused on aspects such as capacity, interaction, hygiene, battery life, and appearance, which are related to the product itself, its services, and user experience requirements.

The extracted user themes were categorized based on probability, and duplicate user requirement information was consolidated. The themes were divided into six categories from highest to lowest priority: Quality (R1), Hygiene (R2), Capacity (R3), Appearance (R4), Human–Computer Interaction (R5), and Flexibility (R6). These themes were considered as potential user needs (PUNs) in this study, as shown in Figure 5.

As is well known, a product consists of multiple technical modules designed under various engineering considerations. By analyzing the functional characteristics of this product and incorporating the recommendations of six experienced designers and faculty members from university industrial design programs, the optimization objectives for the design of this smart waste sorting bin were categorized into eight main areas: Appearance (C1), Automatic Recognition (C2), Human–Machine Interaction (C3), Automatic Packaging (C4), Partition Section (C5), Movable (C6), Autonomous Obstacle Avoidance (C7), and APP Control (C8). These eight optimization points will serve as key technical module keywords for further research.

4.5. Decision-Maker Decision Evaluation Based on CIHFS

The scoring for this study was conducted simultaneously by a decision-making group. The decision-making group consisted of four members, including two product designers, one user experience designer, and one university professor specializing in product design. Decision-makers were required to evaluate PUNs based on technical module optimization points. During the evaluation process, they were instructed to use credibility-based interval hesitant fuzzy elements to express their evaluations. Due to space constraints, only the specific evaluation values provided by one decision-maker $d_1$ are presented here, as shown in

Table 3. Decision matrix provided by Expert $d_1$.

	C1	C2	C3	C4	C5	C6	C7	C8
R1	<{[0.2,0.4], [0.4,0.5];0.5}>	<{[0.6,0.8], [0.8,0.9];0.7}>	<{[0.4,0.5], [0.5,0.6];0.6}>	<{[0.7,0.9];0.8}>	<{[0.5,0.6], [0.7,0.8];0.6}>	<{[0.3,0.5];0.5}>	<{[0.6,0.8];0.7}>	<{[0.3,0.5], [0.6,0.7];0.4}>
R2	<{[0.1,0.3];0.4}>	<{[0.7,0.9];0.8}>	<{[0.2,0.4], [0.6,0.7];0.5}>	<{[0.7,0.8];0.9}>	<{[0.7,0.8], [0.8,0.9];0.7}>	<{[0.2,0.4];0.4}>	<{[0.4,0.6], [0.7,0.8];0.6}>	<{[0.1,0.3], [0.4,0.6];0.3}>
R3	<{[0.2,0.3], [0.4,0.5];0.5}>	<{[0.2,0.5];0.6}>	<{[0.5,0.6], [0.6,0.8];0.7}>	<{[0.5,0.7], [0.7,0.8];0.7}>	<{[0.6,0.7];0.9}>	<{[0.7,0.8], [0.8,0.9];0.8}>	<{[0.3,0.5], [0.5,0.7];0.5}>	<{[0.1,0.3];0.4}>
R4	<{[0.8,0.9];0.9}>	<{[0.1,0.4];0.5}>	<{[0.6,0.8];0.8}>	<{[0.3,0.4], [0.4,0.5];0.6}>	<{[0.1,0.3], [0.4,0.5];0.4}>	<{[0.4,0.6], [0.7,0.8];0.7}>	<{[0.1,0.3], [0.4,0.5];0.3}>	<{[0.2,0.4], [0.4,0.6];0.5}>
R5	<{[0.5,0.7];0.7}>	<{[0.6,0.8];0.8}>	<{[0.7,0.8], [0.8,0.9];0.9}>	<{[0.6,0.9];0.8}>	<{[0.3,0.6];0.6}>	<{[0.5,0.6], [0.7,0.8];0.7}>	<{[0.4,0.7];0.7}>	<{[0.7,0.9];0.9}>
R6	<{[0.3,0.4], [0.5,0.6];0.6}>	<{[0.2,0.3], [0.4,0.5];0.5}>	<{[0.4,0.7];0.7}>	<{[0.4,0.6],[0.6,0.7];0.6}>	<{[0.5,0.6], [0.6,0.7];0.7}>	<{[0.8,0.9];0.9}>	<{[0.7,0.9];0.8}>	<{[0.6,0.8];0.8}>

. For detailed data provided by other decision-makers, please refer to

Table A1. Decision matrix provided by Expert $d_2$.

	C1	C2	C3	C4	C5	C6	C7	C8
R1	<{[0.3,0.5], [0.6,0.7];0.6}>	<{[0.7,0.9];0.8}>	<{[0.4,0.6], [0.7,0.8];0.7}>	<{[0.8,0.9];0.9}>	<{[0.6,0.8];0.7}>	<{[0.4,0.6], [0.7,0.8];0.5}>	<{[0.7,0.9];0.8}>	<{[0.3,0.5];0.4}>
R2	<{[0.2,0.4];0.5}>	<{[0.7,0.8];0.9}>	<{[0.3,0.5], [0.5,0.6];0.6}>	<{[0.5,0.6];0.9}>	<{[0.7,0.9];0.8}>	<{[0.3,0.5];0.4}>	<{[0.5,0.7], [0.8,0.9];0.6}>	<{[0.2,0.4], [0.4,0.5];0.3}>
R3	<{[0.1,0.3], [0.4,0.5];0.4}>	<{[0.2,0.4], [0.4,0.5];0.5}>	<{[0.3,0.5];0.6}>	<{[0.6,0.8], [0.8,0.9];0.7}>	<{[0.8,1.0];0.9}>	<{[0.7,0.9];0.8}>	<{[0.4,0.6];0.5}>	<{[0.1,0.3];0.3}>
R4	<{[0.7,0.9];0.8}>	<{[0.1,0.3], [0.4,0.5];0.4}>	<{[0.5,0.7];0.7}>	<{[0.3,0.5], [0.6,0.7];0.5}>	<{[0.2,0.4], [0.4,0.5];0.4}>	<{[0.4,0.6], [0.7,0.8];0.6}>	<{[0.1,0.3], [0.3,0.4];0.3}>	<{[0.2,0.4];0.4}>
R5	<{[0.4,0.6];0.7}>	<{[0.5,0.7], [0.7,0.8];0.7}>	<{[0.8,0.9];0.9}>	<{[0.7,0.9];0.8}>	<{[0.4,0.6];0.6}>	<{[0.6,0.8];0.7}>	<{[0.5,0.7];0.7}>	<{[0.7,0.9];0.8}>
R6	<{[0.2,0.5], [0.6,0.7];0.4}>	<{[0.1,0.4];0.3}>	<{[0.3,0.6], [0.7,0.8];0.5}>	<{[0.2,0.5];0.4}>	<{[0.5,0.7];0.6}>	<{[0.7,0.8];0.9}>	<{[0.7,0.9];0.8}>	<{[0.5,0.8];0.7}>

,

Table A2. Decision matrix provided by Expert $d_3$.

	C1	C2	C3	C4	C5	C6	C7	C8
R1	<{[0.2,0.4], [0.4,0.5];0.5}>	<{[0.6,0.8], [0.8,0.9];0.7}>	<{[0.3,0.5];0.6}>	<{[0.7,0.9], [0.9,1.0];0.8}>	<{[0.5,0.7];0.6}>	<{[0.3,0.4], [0.6,0.7];0.5}>	<{[0.6,0.9];0.7}>	<{[0.2,0.4];0.4}>
R2	<{[0.1,0.3];0.4}>	<{[0.8,0.9];1.0}>	<{[0.2,0.4], [0.5,0.6];0.5}>	<{[0.6,0.7];0.9}>	<{[0.7,0.9];0.8}>	<{[0.1,0.3], [0.4,0.5];0.3}>	<{[0.4,0.6], [0.5,0.6];0.6}>	<{[0.1,0.3], [0.4,0.5];0.3}>
R3	<{[0.1,0.2], [0.3,0.4];0.5}>	<{[0.3,0.5];0.6}>	<{[0.2,0.4], [0.4,0.5];0.5}>	<{[0.6,0.8];0.7}>	<{[0.8,0.9];0.9}>	<{[0.7,0.9];0.8}>	<{[0.3,0.5], [0.6,0.7];0.5}>	<{[0.1,0.3];0.4}>
R4	<{[0.6,0.8];0.7}>	<{[0.1,0.3], [0.3,0.5];0.4}>	<{[0.4,0.6];0.6}>	<{[0.2,0.4], [0.4,0.5];0.5}>	<{[0.1,0.3], [0.3,0.5];0.3}>	<{[0.3,0.5];0.5}>	<{[0.1,0.3];0.2}>	<{[0.2,0.3], [0.4,0.6];0.4}>
R5	<{[0.3,0.6];0.5}>	<{[0.5,0.7], [0.7,0.8];0.6}>	<{[0.7,0.9];0.8}>	<{[0.6,0.8];0.7}>	<{[0.3,0.5], [0.6,0.7];0.5}>	<{[0.5,0.6], [0.6,0.7];0.6}>	<{[0.4,0.6], [0.6,0.7];0.6}>	<{[0.6,0.8], [0.8,0.9];0.7}>
R6	<{[0.2,0.5];0.4}>	<{[0.1,0.4];0.3}>	<{[0.3,0.6], [0.6,0.7];0.5}>	<{[0.2,0.5];0.4}>	<{[0.5,0.7];0.6}>	<{[0.8,0.9];0.9}>	<{[0.7,0.9];0.8}>	<{[0.5,0.7];0.6}>

and

Table A3. Decision matrix provided by Expert $d_4$.

	C1	C2	C3	C4	C5	C6	C7	C8
R1	<{[0.2,0.4], [0.3,0.6];0.5}>	<{[0.7,0.9];0.8}>	<{[0.2,0.3], [0.4,0.5];0.4}>	<{[0.8,0.9];0.9}>	<{[0.6,0.8];0.7}>	<{[0.3,0.5];0.4}>	<{[0.4,0.7];0.6}>	<{[0.2,0.4], [0.5,0.6];0.4}>
R2	<{[0.1,0.3], [0.4,0.5];0.4}>	<{[0.2,0.3], [0.4,0.5];0.5}>	<{[0.3,0.5];0.6}>	<{[0.5,0.7], [0.8,0.9];0.7}>	<{[0.7,0.9];0.8}>	<{[0.4,0.5], [0.6,0.8];0.7}>	<{[0.3,0.6], [0.6,0.7];0.5}>	<{[0.1,0.3], [0.4,0.5];0.3}>
R3	<{[0.7,0.9];0.8}>	<{[0.1,0.3];0.4}>	<{[0.6,0.7], [0.8,0.9];0.8}>	<{[0.2,0.4];0.5}>	<{[0.1,0.3], [0.3,0.4];0.3}>	<{[0.4,0.6];0.6}>	<{[0.1,0.3], [0.3,0.4];0.2}>	<{[0.3,0.5];0.5}>
R4	<{[0.5,0.7];0.7}>	<{[0.6,0.8];0.8}>	<{[0.6,0.7];1.0}>	<{[0.7,0.9];0.8}>	<{[0.4,0.6], [0.7,0.8];0.6}>	<{[0.6,0.9];0.8}>	<{[0.5,0.8];0.7}>	<{[0.8,0.9];0.9}>
R5	<{[0.3,0.5], [0.5,0.6];0.5}>	<{[0.2,0.4], [0.5,0.6];0.4}>	<{[0.5,0.6], [0.7,0.9];0.7}>	<{[0.4,0.6], [0.7,0.8];0.5}>	<{[0.6,0.8];0.7}>	<{[0.7,0.8];0.9}>	<{[0.7,0.9];0.8}>	<{[0.7,0.9];0.8}>
R6	<{[0.2,0.4];0.5}>	<{[0.7,0.9];0.8}>	<{[0.3,0.5], [0.6,0.7];0.6}>	<{[0.6,0.7];0.9}>	<{[0.6,0.8];0.7}>	<{[0.3,0.5], [0.5,0.6];0.4}>	<{[0.4,0.6], [0.6,0.7];0.6}>	<{[0.2,0.3], [0.3,0.4];0.4}>

in the Appendix A. Additionally, prior to data calculation, the initial weights for the four decision-makers were temporarily set as $\left(w={({\displaystyle \frac{1}{4}},{\displaystyle \frac{1}{4}},{\displaystyle \frac{1}{4}},{\displaystyle \frac{1}{4}})}^T\right)$.

Step 1: Calculate the hesitation and trustworthiness of the four decision-makers regarding demand $R_m$ under technology module $C_n$ using Formulas (1) and (2). Then, adjust the decision-maker weights, as follows, via Formulas (3) and (4):

$${w_k}^{″}={\left(0.24752,0.25861,0.24286,0.25099\right)}^T$$

Step 2: The evaluation matrix for each decision-maker (as shown in Table 3) is calculated using Formulas (5) to (8). The CHFSF not only converts all fuzzy scores from decision-makers into precise numerical values but also integrates the scoring matrices of all decision-makers by incorporating indicators such as decision-maker weights and certainty-weighted composite operators. The decision matrix $F={(f_{ij})}_{m\times n}$ integrating the relationship between output requirements and engineering metrics is detailed in

Table 4. Decision matrix for the relationship between requirements and engineering metrics.

	C1	C2	C3	C4	C5	C6	C7	C8
R1	0.4568	0.7164	0.4895	0.7944	0.6079	0.4961	0.6499	0.4673
R2	0.3975	0.6873	0.4697	0.6500	0.7326	0.4602	0.5669	0.4533
R3	0.4969	0.4136	0.5436	0.5966	0.6893	0.6862	0.4821	0.4025
R4	0.6980	0.4631	0.5929	0.5402	0.4676	0.5783	0.4595	0.5301
R5	0.5059	0.5827	0.7396	0.6589	0.5332	0.6312	0.6043	0.7355
R6	0.4555	0.4907	0.5331	0.4995	0.5831	0.7057	0.6937	0.5537

.

Step 3: Invite the original decision-making group. Four decision-makers use the CIHFS format to comparatively score the interdependent relationships among six potential user needs. Scores are assigned on a 0–1 scale, where 0, 0.25, 0.5, 0.75, and 1 represent extremely weak, weak, moderate, strong, and extremely strong influence, respectively. Similarly, due to space limitations, only the scores for decision-maker $d_1$ are listed here, as shown in

Table 5. Evaluation matrix for relationships between user needs by Expert $d_1$.

	R1	R2	R3	R4	R5	R6
R1	<{[0,0];1.0}>	<{[0.25,0.5];0.6}>	<{[0.5,0.75];0.7}>	<{[0.25,0.5];0.5}>	<{[0.75,1];0.9}>	<{[0,0.25];0.4}>
R2	<{[0.5,0.75];0.7}>	<{[0,0];1.0}>	<{[0.75,1];0.9}>	<{[0,0.25];0.3}>	<{[0.5,0.75];0.8}>	<{[0.25,0.5];0.5}>
R3	<{[0,0.25];0.4}>	<{[0.5,1];0.8}>	<{[0,0];1.0}>	<{[0.25,0.5];0.6}>	<{[0,0.25];0.3}>	<{[0.75,1];0.9}>
R4	<{[0.75,1];0.9}>	<{[0.25,0.5];0.6}>	<{[0.5,0.75];0.7}>	<{[0,0];1.0}>	<{[0.5,0.75];0.7}>	<{[0.5,0.75];0.8}>
R5	<{[0.5,0.75];0.8}>	<{[0.75,1];0.9}>	<{[0.25,0.5];0.5}>	<{[0.75,1];0.9}>	<{[0,0];1.0}>	<{[0.5,0.75];0.6}>
R6	<{[0,0.5];0.5}>	<{[0.25,0.75];0.7}>	<{[0.5,1];0.8}>	<{[0.25,0.5];0.6}>	<{[0.75,1];0.9}>	<{[0,0];1.0}>

. For detailed data provided by other decision-makers, please refer to

Table A4. Evaluation matrix for relationships between user needs by Expert $d_2$.

	R1	R2	R3	R4	R5	R6
R1	<{[0,0];1.0}>	<{[0.5,1];0.6}>	<{[0.75,1];0.9}>	<{[0.25,0.75];0.7}>	<{[0.5,0.75];0.8}>	<{[0,0.5];0.5}>
R2	<{[0.5,0.75];0.8}>	<{[0,0];1.0}>	<{[0.75,1];0.8}>	<{[0,0.25];0.3}>	<{[0.75,1];0.9}>	<{[0.25,0.5];0.6}>
R3	<{[0.25,0.5];0.6}>	<{[0.75,1];0.9}>	<{[0,0];1.0}>	<{[0.5,1];0.8}>	<{[0,0.25];0.4}>	<{[0.75,1];0.9}>
R4	<{[0,0.5];0.5}>	<{[0.25,0.75];0.7}>	<{[0.25,0.75];0.7}>	<{[0,0];1.0}>	<{[0.75,1];0.9}>	<{[0,0.25];0.3}>
R5	<{[0.25,0.75];0.7}>	<{[0.5,1];0.8}>	<{[0,0.5];0.5}>	<{[0.5,0.75];0.8}>	<{[0,0];1.0}>	<{[0.5,1];0.4}>
R6	<{[0,0.25];0.3}>	<{[0,0.5];0.4}>	<{[0.25,1];0.7}>	<{[0,0.25];0.3}>	<{[0.75,1];0.9}>	<{[0,0];1.0}>

,

Table A5. Evaluation matrix for relationships between user needs by Expert $d_3$.

	R1	R2	R3	R4	R5	R6
R1	<{[0,0];1.0}>	<{[0.75,1];0.8}>	<{[0.5,0.75];0.7}>	<{[0,0.25];0.4}>	<{[0.25,0.75];0.7}>	<{[0.25,0.5];0.6}>
R2	<{[0.25,0.5];0.6}>	<{[0,0];1.0}>	<{[0.5,0.75];0.7}>	<{[0.25,0.75];0.7}>	<{[0,0.5];0.5}>	<{[0.5,1];0.8}>
R3	<{[0,0.25];0.3}>	<{[0.75,1];0.9}>	<{[0,0];1.0}>	<{[0.5,1];0.8}>	<{[0,0.25];0.4}>	<{[0.75,1];0.9}>
R4	<{[0.5,1];0.8}>	<{[0,0.25];0.3}>	<{[0.25,0.5];0.5}>	<{[0,0];1.0}>	<{[0.75,1];0.9}>	<{[0,0.5];0.5}>
R5	<{[0.25,0.75];0.7}>	<{[0.5,0.75];0.7}>	<{[0,0.25];0.4}>	<{[0.75,1];0.9}>	<{[0,0];1.0}>	<{[0.75,1];0.9}>
R6	<{[0,0.5];0.5}>	<{[0.25,1];0.7}>	<{[0.5,0.75];0.7}>	<{[0,0.25];0.3}>	<{[0.5,1];0.8}>	<{[0,0];1.0}>

and

Table A6. Evaluation matrix for relationships between user needs by Expert $d_4$.

	R1	R2	R3	R4	R5	R6
R1	<{[0,0];1.0}>	<{[0.25,0.75];0.7}>	<{[0,0.5];0.5}>	<{[0.5,1];0.8}>	<{[0.75,1];0.9}>	<{[0.25,0.5];0.6}>
R2	<{[0.5,1];0.8}>	<{[0,0];1.0}>	<{[0.75,1];0.9}>	<{[0,0.25];0.4}>	<{[0.25,0.75];0.7}>	<{[0.5,0.75];0.8}>
R3	<{[0,0.25];0.3}>	<{[0.5,0.75];0.7}>	<{[0,0];1.0}>	<{[0.25,0.5];0.6}>	<{[0,0.25];0.4}>	<{[0.75,1];0.7}>
R4	<{[0.75,1];0.9}>	<{[0.25,0.5];0.6}>	<{[0.5,1];0.8}>	<{[0,0];1.0}>	<{[0.5,1];0.4}>	<{[0.25,0.75];0.7}>
R5	<{[0.5,0.75];0.8}>	<{[0.75,1];0.9}>	<{[0,0.5];0.5}>	<{[0.75,1];0.9}>	<{[0,0];1.0}>	<{[0.25,0.75];0.3}>
R6	<{[0.25,0.75];0.7}>	<{[0,0.5];0.5}>	<{[0.75,1];0.9}>	<{[0.5,0.75];0.8}>	<{[0.75,1];0.9}>	<{[0,0];1.0}>

in the Appendix A.

Step 4: Similarly, using the CHFSF, the scores for each decision-maker are converted to precise values via Formulas (5)–(8), and a direct influence matrix in the form of Formula (14) is constructed, as shown in

Table 6. DEMATEL direct impact matrix.

	R1	R2	R3	R4	R5	R6
R1	0	0.6243	0.6151	0.4948	0.7208	0.3887
R2	0.5847	0	0.7780	0.3886	0.6026	0.5404
R3	0.3785	0.7512	0	0.5737	0.3593	0.8187
R4	0.7046	0.4225	0.5588	0	0.7209	0.4463
R5	0.5501	0.7516	0.3838	0.7919	0	0.6212
R6	0.3978	0.4581	0.6880	0.4246	0.8083	0

.

Step 5: According to Formulas (15)–(20), the center degree $M_i$ and cause degree $R_i$ of each functional element are calculated, and the specific results are shown in

Table 7. User requirement DEMATEL calculation results.

	${\mathit{D}}_{\mathit{i}}$	${\mathit{F}}_{\mathit{i}}$	${\mathit{M}}_{\mathit{i}}={\mathit{D}}_{\mathit{i}}+{\mathit{F}}_{\mathit{i}}$	${\mathit{R}}_{\mathit{i}}={\mathit{D}}_{\mathit{i}}-{\mathit{F}}_{\mathit{i}}$
R1	14.079	13.024	27.103	1.055
R2	14.242	14.808	29.050	−0.567
R3	14.110	14.723	28.832	−0.613
R4	14.104	13.393	27.497	0.712
R5	15.074	15.431	30.505	−0.357
R6	13.807	14.037	27.844	−0.230

.

Step 6: Based on the results of Table 7, the weight vector of each PUN $H$ is derived using Formula (21), and its weight relationship is shown in Figure 6.

$$H=\left(0.1587,0.1701,0.1688,0.1610,0.1786,0.1630\right)$$

Step 7: According to Formula (22), the technology module importance vector $G$ is derived, and its weight relationship is shown in Figure 7.

$$G=\left(0.5001,0.5590,0.5638,0.6234,0.6030,0.5937,0.5759,0.5262\right)$$

4.6. Program Effect Presentation

Based on the quantitative data, it can be concluded that the order of importance of the technology modules regarding this smart sorting garbage can (from highest to lowest) is $C_4$ (0.6234), $C_5$ (0.6030), $C_6$ (0.5937), $C_7$ (0.5759), $C_3$ (0.5638), $C_2$ (0.5590), $C_8$ (0.5262), and $C_1$ (0.5001). Therefore, the design team will take the four technical modules, Automatic Packaging ($C_4$), Partition Section ($C_5$), Movable ($C_6$), and Autonomous Obstacle Avoidance ($C_7$), as the priority considerations for the iterative design of this product. At the same time, due to the relatively small gap in importance of the technology modules, and considering factors such as alignment with user needs, product functionality completeness, and technical structure implementation, the design team will also take into account the remaining four technical modules: APP Control ($C_8$), Human–Machine Interaction ($C_3$), Automatic Recognition ($C_2$), and Appearance ($C_1$). The specific design solutions are presented in Figure 8, Figure 9 and Figure 10

4.7. Product Overview and Features

The design team analyzed the main technical modules of the smart household waste sorting bin in terms of appearance, structure, functionality, and other aspects to effectively meet the PUNs. After determining the relevant iterative components based on the module importance ranking data, iterative design was carried out. The degree of alignment between each technical module and the PUN is shown in Figure 11.

After iterative design, the smart household waste sorting bin mainly has the following functions:

• Waste sorting

The waste bin has four separate compartments for recyclable waste, dry waste, wet waste, and hazardous waste. Users simply place their waste in front of the camera, and the recognition system accurately detects the type of waste. Once detection is complete, the corresponding compartment door opens, and users can dispose of their waste, thus completing the entire waste-sorting process.

2.

Free movement

To adapt to the complex spatial environment of the home, the trash can is equipped with distance sensors and radar-scanning modules, greatly improving its obstacle avoidance capabilities. At the same time, it uses Mecanum wheels instead of traditional steering wheels to achieve flexible, all-around movement, meeting the needs of various usage scenarios in the home.

3.

Cleanliness and hygiene

This technology module is designed to improve hygiene and convenience during use. When the corresponding compartment is full, the automatic packaging structure tightens the garbage bag opening and seals it with plastic, completing the packaging process. After the user removes the garbage bag, the fan turns on to create negative pressure, causing the new garbage bag to automatically adhere to the inner wall of the bin, completing the automatic replacement of the garbage bag.

4.

Intelligent interaction

The trash can features a user-friendly interactive design with a touchless sensor button on the top to ensure hygiene and cleanliness during use. It also has voice recognition functionality, allowing users to call the robot at any time using voice commands, significantly reducing the distance required to dispose of trash and improving user convenience and satisfaction.

5.

Mobile app

The app design follows the principle of simplicity, with clean pages and convenient operations to enhance the user experience. Users can use the app to remotely control the product, view real-time capacity and power levels, customize driving routes, view waste disposal records, and view nearby waste collection sites, among other personalized functions. These features enhance the product’s intelligence, user satisfaction, and practical value.

4.8. Sensitivity Analysis

In the method proposed in this paper, the only adjustable parameter involved is the default value $\eta$ representing the lack of confidence in the CHFSF. To validate the robustness of the proposed method, this section compares the scores of demand interactions based on data from four decision-makers using the CIHFS format (Table 6 data; due to space limitations, only the scores for decision-maker $d_1$ are listed). By assigning different values to $\eta$ and applying Equations (5)–(8), and Equations (14)–(21) to compute the weight values for each potential user demand, thereby conducting a sensitivity analysis. The corresponding results are shown in Table 8.

As shown in

Table 8. Weight values and ranking of potential user needs (PUN) under different values of $\eta$.

Value	Weighting Values for Each PUN						Prioritization of PUN
	R1	R2	R3	R4	R5	R6
$\eta =0.3$	0.1568	0.1719	0.1685	0.1592	0.1819	0.1616	$R_5>R_2>R_3>R_6>R_4>R_1$
$\eta =0.4$	0.1578	0.1709	0.1687	0.1601	0.1801	0.1623
$\eta =0.5$	0.1587	0.1701	0.1688	0.1610	0.1786	0.1630
$\eta =0.6$	0.1594	0.1693	0.1688	0.1617	0.1772	0.1636
$\eta =0.7$	0.1601	0.1686	0.1689	0.1624	0.1759	0.1641	$R_5>R_3>R_2>R_6>R_4>R_1$
$\eta =0.8$	0.1607	0.1680	0.1689	0.1630	0.1747	0.1646

, with increasing values of $\eta$, the weight values of each PUN exhibit a gradual trend of change, with numerical fluctuations remaining minimal and far below the critical threshold affecting decision effectiveness. This demonstrates that moderate variations in the value of $\eta$ have little impact on the decision outcome, thereby proving that the CIHFS-DEMATEL method employed in this study possesses a certain degree of robustness.

Meanwhile, when $0.3\le \eta \le 0.6$, the ranking of potential user needs remains unchanged at $R_5>R_2>R_3>R_6>R_4>R_1$. However, when $0.7\le \eta \le 0.8$, the ranking shifts to $R_5>R_3>R_2>R_6>R_4>R_1$. This demonstrates that the CIHFS-DEMATEL method’s ranking results are sensitive to parameter values.

5. Conclusions and Outlook

Against the backdrop of increasingly shortened product lifecycles, accelerated evolution of user demands, and widespread adoption of digital platforms, traditional product iteration design methods still exhibit significant limitations in handling multi-source fuzzy information, identifying potential user needs (PUNs), and optimizing technical pathways. To address this, this paper proposes a CIHFS-DEMATEL product iteration design method that integrates online review mining with decision-maker credibility assessment and applies it to practical product iteration design scenarios.

This method is based on latent user needs embedded in online reviews. First, it extracts PUN themes using the LDA approach. Next, it constructs a credibility-based interval hesitant fuzzy set (CIHFS) to characterize the ambiguity and credibility differences in decision-makers’ ratings. Simultaneously, the CHFSF (credibility interval hesitant fuzzy score function), which integrates subjective credibility with system default valuations, is employed to convert fuzzy information into precise values. Subsequently, the CIHFS is integrated into the DEMATEL method to uncover causal relationships among demands while accounting for decision-makers’ subjective influences, thereby constructing an impact network of potential user demands. Finally, by combining the demand module mapping matrix with the demand weight vector, the importance ranking of technical modules is derived, enabling iterative optimization of product design. This paper demonstrates the framework’s significant advantages in demand identification accuracy, decision-making structure rationality, and optimization result stability through the case study of a smart sorting bin.

To further validate the applicability of the proposed methodology, the research team employed identical methods and processes to conduct iterative design analyses on products such as smart wristband wearables and consumer-grade drones. For the smart wristband wearable device, we extracted five potential user needs (PUNs) from online reviews: health-monitoring accuracy, battery life, wearing comfort, data privacy and security, and interaction convenience. These were categorized into five technical modules: heart rate sensor, low-power chip, flexible strap, data encryption, and touch interaction. Through CIHFS-DEMATEL method calculations, the resulting importance ranking of technical modules for smart wristband wearables (highest to lowest) was low-power chips, heart rate sensors, data encryption, flexible straps, and touch interaction. This framework guided subsequent iterative design optimizations to precisely address diverse user needs like extended battery life and accurate monitoring. For consumer-grade drones, analyzing user needs against technical modules revealed five key PUNs extracted from online reviews: aerial photography quality, endurance capability, obstacle avoidance reliability, low-altitude control stability, and portability/storage. These correspond to five technical modules: high-definition lenses, high-energy batteries, multi-sensor obstacle avoidance, flight control systems, and foldable body structures. Using the CIHFS-DEMATEL method, the technical module importance ranking for consumer drones (highest to lowest) was determined as: high-energy batteries, high-definition lenses, flight control systems, multi-sensor obstacle avoidance, and foldable body structures. This prioritizes addressing high-frequency user pain points like “short battery life, blurry aerial photos, and low-altitude control lag.”

The practical validation in other product domains demonstrates that this research methodology is not only applicable to the iterative design of smart trash cans but can also be extended to user requirement identification and iterative design scenarios across diverse products. This confirms the transferability, applicability, universal value, and broad application potential of the proposed approach in iterative product optimization design. The following sections summarize the research contributions, limitations, and future work directions.

The theoretical contributions of this study are primarily reflected in the following four aspects:

• Fuzzy modeling innovations

This paper proposes the CIHFS model, which integrates interval hesitant fuzzy expressions with credibility parameters. It symmetrically evaluates subjective psychological factors such as hesitation, fuzziness, and uncertainty when decision-makers provide assessment values, significantly enhancing the precision and explanatory power of fuzzy numbers in expressing subjective cognitive differences. Theoretically, the CIHFS framework introduces the concept of “two-dimensional symmetric integration” to hesitant fuzzy set theory. This innovation addresses the theoretical gap where traditional fuzzy sets could only express subjective cognition from a single dimension, thereby enriching the theoretical system of fuzzy decision making.

2.

Information fusion mechanism

This paper constructs the CHFSF scoring function based on expected utility theory and information fusion principles, establishing a numerical mapping structure between subjective ratings and system valuation. It addresses the common shortcomings of existing fuzzy scoring functions—namely, their failure to integrate information credibility and subjective-objective information fusion, as well as their inability to directly handle CIHFS-related issues—thereby ensuring the rationality and stability of the conversion process. Theoretically, the CHFSF overcomes the limitations of traditional scoring functions that prioritize numerical conversion while neglecting structural balance, introducing a new theoretical paradigm of “symmetrical weighting” for information fusion in MADM problems.

3.

Causal weight identification

This paper proposes the CIHFS-DEMATEL method, which addresses the issue of causal weights in traditional DEMATEL being susceptible to subjective bias during uncertain decision making by incorporating credibility constraints and multidimensional information fusion. This approach significantly enhances interpretability and reliability. Theoretically, CIHFS-DEMATEL refines the symmetric structure of causal modeling, bridging the gap in traditional DEMATEL’s inability to symmetrically characterize causal relationships under uncertainty and expanding the theoretical applicability of DEMATEL methods.

4.

Demand-program transformation mechanisms

A symmetric transformation mechanism based on mapping matrices was established between user requirements and technical modules, enabling bidirectional mapping and collaborative optimization between latent user needs and technical components. This provides structurally stable decision-making foundations for complex product iterations. In a theoretical contribution, this work provides a symmetrical structure for bidirectional mapping between “user requirements and technical modules,” overcoming limitations in traditional iterative design’s requirement alignment. It delivers a structurally symmetrical and stable theoretical tool for iterative decision-making in complex products.

From a methodological perspective, this paper exhibits clear structural symmetry characteristics in the decision-making modeling process and holds significant theoretical extension value: First, the symmetric mapping relationship established by the CHFSF function between subjective information and objective outputs ensures the consistency between the expression of hesitation information and the computational process, providing a new methodological perspective on structural balance for information transformation in MADM problems; second, the CIHFS-DEMATEL method emphasizes the symmetrical causal network structure of mutual influence and dependency among demand nodes. This symmetrical design of the “input–computation–output” tripartite structure not only enhances the model’s interpretability and universal adaptability but also refines the structural modeling theory for systemic decision making. It provides a reusable symmetrical methodological framework for decision modeling in comparable products or services, further elevating the universality and scalability of this study’s theoretical contributions.

Despite the positive outcomes of this study, certain limitations remain: First, the application of LDA topic modeling in review mining requires further optimization. For instance, the manual presetting of the number of topics K still relies on trial-and-error experimentation, lacking a data-driven adaptive determination method. Unsupervised clustering makes topic interpretation overly dependent on expert experience, fails to integrate non-textual information within reviews, and lacks the ability to capture demand evolution over time. These limitations can easily lead to demand granularity bias and ambiguous semantic clustering boundaries, compromising the objectivity of PUN extraction. Second, the credibility parameter assignment strategy in CIHFS remains dependent on decision-maker experience, lacking unified quantitative standards or data calibration mechanisms. Differences in decision-maker expertise may cause parameter assignment bias, thereby affecting the consistency of decision outcomes.

Therefore, future research will address these limitations through three key extensions:

(1)

To overcome the empirical dependency issue in LDA topic clustering, introduce advanced semantic clustering models such as BERTopic and multimodal LDA to achieve adaptive optimization of topic counts, thereby enhancing the precision and objectivity of PUN extraction.

(2)

Addressing the subjective bias in CIHFS credibility parameters by integrating historical evaluator assessments with feedback correction mechanisms. This establishes a credibility modeling approach featuring “empirical assignment–data calibration–dynamic updating” to enhance parameter adaptability and consistency across diverse decision-making scenarios. In subsequent research, we will draw upon existing fuzzy optimization methods such as IODS technology [33,34,38] and the data-driven approach from the FILMO algorithm [38] to further enhance the method’s adaptability in complex scenarios.

(3)

To address the limitations of the method’s application scenarios, the CIHFS-DEMATEL approach will be extended to iterative design tasks for complex products such as smart home appliances and new energy vehicles, as well as service systems like smart logistics and healthcare services. This expansion aims to validate the method’s framework boundaries and extension potential across multiple scenarios, thereby further refining the methodological system.

In summary, the CIHFS-DEMATEL product iteration design method proposed in this paper achieves a symmetric mapping from latent user needs to technical modules through steps including CIHFS fuzzy modeling, CHFSF precise value conversion, and CIHFS-DEMATEL causal analysis. Its theoretical contribution lies in refining the symmetric modeling logic for uncertain decision making, while its practical value enhances the adaptability of product iteration design to user needs. Simultaneously, it provides a systematic solution for product iteration centered on user needs while accommodating multi-source fuzzy information processing scenarios, demonstrating strong theoretical extension value and practical operability.