Abstract
Value-added services (VASs) are widely used to incentivize user adoption in the platform economy. While considering the symmetry of cross-network externalities of a platform, i.e., suppliers and manufacturers exert balanced and mutually reinforcing influences on each other’s participation, this study develops a stylized game model to investigate platforms’ optimal bilateral user pricing decisions and VAS provision strategies, such as outsourcing to a third-party service provider (Model OS) or in-house provision (Model PS). Then, the platform’s and the third-party service provider’s optimal pricing decisions are derived, and the equilibrium results are compared. The findings demonstrate that a platform should implement Model PS when the outsourced VAS cost coefficient is sufficiently high or the outsourced VAS quality and cost coefficient are low concurrently. Only when the outsourced VAS quality is relatively high and cost coefficient is in a low range should a platform choose Model OS. Additionally, to address the problem of declines in supply chain members’ profits caused by investment in low-quality outsourced VASs (VAS utility provided by a third party exceeds the specific value 1.38), this study also proposes a feasible VAS cost-sharing contract (Model CS) to incentivize the third-party provider to provide investment in high-quality VASs. The contract design can achieve a “win-win” outcome when the sharing ratio is at a moderate rate (especially a range from 0.291 to 0.5) and the outsourced VAS cost coefficient meets suitable thresholds.
1. Introduction
1.1. Background and Motivation
Digital information technology is accelerating the spread of two-sided manufacturing platforms, attracting significant attention. A report by Grand View Research projects that the global market of two-sided manufacturing platforms is expanding at an annual rate of 8.8% and is expected to reach USD 101.12 billion by 2028. For example, Alibaba.com and XoMetry.com connect manufacturers and customers who need customized parts and prototypes. These manufacturing platforms act as intermediaries by providing basic services to facilitate component trading between suppliers and manufacturers, charging both sides access fees for profitability [,].
Exemplifying a bilateral market structure that integrates suppliers and manufacturers, the two-sided manufacturing platform exhibits a distinct market characteristic, that is, the cross-network externality symmetry, which refers to the correlation and mutual influence of joining utility between suppliers and manufacturers [,]. This symmetry reflects an equilibrium where both sides of the market exert comparable and interdependent effects on each other’s participation incentives. Given the effects of the cross-network externality symmetry, two-sided platforms widely use pricing strategies such as subsidizing one side and charging the other side in practice [,,]. However, with rapid development of the platform and the intensification of competition among two-sided platform enterprises, the subsidization strategy considering the cross-network externality symmetry no longer remains effective as usual in expanding the market scale [,]. Instead, the level of value-added service (VAS) investment (hereafter referred to as VAS level), a highly profitable and rapidly growing business, has become a more effective operational strategy for two-sided platforms [,,]. Commonly used VAS for two-sided manufacturing platforms include functions such as priority ranking, effective matching, payment security, and logistics supervision, which aim to enhance participants’ engagement and expand the positive effect of the symmetry of cross-network externalities [,]. This symmetry reflects an equilibrium where both sides of the market exert comparable and interdependent effects on each other’s participation incentives.
Although VAS investment can stimulate participants to access more, it also increases the cost and affects the platforms’ pricing and VAS provision strategies. In practice, the costs associated with value-added services are often substantial, covering expenses such as servers, module management, specialized staff salaries, and other related expenses. Some platforms, like China texnet.com and the Shenyang Iron & Steel i5 platform, have faced issues of over-investment, resulting in reduced revenues and even website closures []. Moreover, outsourcing has become an effective strategy because it reduces heavy operating costs and allows platforms to focus on their core competencies [,]. For example, HOIZAL.com outsources its software service and financing services to third-party service providers (e.g., Delixi electric; KMES software company; and Haier financial services), and 1688.com outsources its logistics services to third-party service providers (e.g., S.f.Holding express and China cainiao express) []. However, platforms may suffer from a bad reputation and low access rates due to low-quality services provided by third parties. Consequently, these examples indicate that when VAS costs are high, platforms must optimize their service strategies and maintain quality to ensure sustainable competitiveness.
1.2. Research Questions and Innovations
Following established practices, we examined a two-sided platform with symmetric cross-network externalities to determine its optimal bilateral pricing and VAS provision strategy. In detail, we aimed to answer the following questions: (1) What are the optimal pricing decisions for bilateral participants that a platform should adopt, particularly under conditions of symmetric interdependence where suppliers and manufacturers exhibit balanced cross-network influences? Moreover, how do the relative strengths of these symmetry cross-network externalities—reflecting the degree of equilibrium in mutual participation effects—interact with the VAS level to shape the platform’s optimal pricing and service strategies? (2) Platforms have two VAS provision mode options, including providing VASs in-house or outsourcing VASs to a third party. Which strategy can enable the platform to achieve more profits? (3) What impact does a VAS cost-sharing contract have on supply chain members’ optimal operational decisions and profit distributions? Is there a mutually acceptable VAS cost-sharing arrangement between a platform and third party? And which conditions must be met for the platform and third party to accept this contract?
To answer the above questions, this study examines a two-sided manufacturing platform that facilitates component trading and operates as a monopoly. Utilizing a stylized game model and analyzing the utility of suppliers and manufacturers, this study derives the bilateral participants’ optimal pricing decisions and the profits of both parties (e.g., the platform and the third party) under two different VAS provision strategies. Then, we compare the proposed two VAS provision strategies to explore the service outsourcing choice of the platform under equilibrium. The results show that if the outsourced VAS cost coefficient is sufficiently high or the outsourced VAS quality and cost coefficient are relatively low concurrently, the platform should choose to provide VASs by itself. Only when the outsourced VAS quality is relatively high and cost coefficient is in a low range should the platform opt to outsource the VAS to the third party. Finally, we examine the role of VAS cost-sharing contracts in improving the performance of the platform and third parties. We find that a VAS cost-sharing contract is successful in improving the whole supply chain’s performance when the outsourced VAS cost coefficient is relatively high. Additionally, we give the optimal VAS cost-sharing ratio and clarify the conditions for achieving the VAS cost-sharing contract.
Within the contemporary landscape of Industry 4.0, while platform-mediated servitization is gaining attention [,], the strategic implications of symmetric cross-network externalities and the comparative analysis of different VAS provision models remain underexplored. This paper delivers three major contributions:
(1) Motivated by emerging VAS business practices, we examine how a VAS outsourcing strategy affects a two-sided platform’s optimal decisions, thereby supplementing the literature on two-sided market service outsourcing. By constructing two different VAS provision modes that account for balanced reciprocity between platform sides, our findings reveal how symmetrical interdependence shapes optimal strategies. These results offer practical guidance for pricing bilateral participants on platforms. They specifically address maintaining equilibrium under symmetric cross-network externalities, where equivalent utility flows between suppliers and manufacturers create mutually reinforcing effects.
(2) We discuss the optimal VAS provision choice for the platform when introducing the third-party service provider and offer a comparative analysis of three VAS provisioning models and the optimal decisions, revealing the non-obvious trade-offs in each, which is crucial for strategic decision-making in Industry 4.0.
(3) This study identifies a complete characterization of an optimal VAS cost-sharing ratio and clarifies the conditions for achieving a VAS cost-sharing contract. Additionally, we demonstrate that a VAS cost-sharing contract can improve the overall performance of a platform and third party as well as achieve a “win-win” outcome.
1.3. Paper Organization and Structure
The rest of this study is organized as follows. Section 2 briefly reviews the relevant literature. Section 3 describes the model. Section 4 compares the two proposed VAS provision strategies and identifies the optimal VAS provision strategy that maximizes both participant access rates and platform entrance fees. Section 5 investigates the role of a VAS cost-sharing contract. Section 6 extends the main model to a bilaterally differentiated VAS setting. Section 7 summarizes the main findings and summarizes and discusses their managerial implications. All proofs are included in the Appendix A.
2. Literature Review
There are two streams of literature that are closely related to this paper as they contribute to emerging research on two-sided platforms: (1) two-sided manufacturing platform operation and (2) service outsourcing strategy. We critically review the previous relevant literature and discuss the literature gaps that this study aims to fulfill.
2.1. Two-Sided Manufacturing Platform Operation
Two-sided manufacturing platforms can strengthen the integration of manufacturing resources and capabilities [,]. Previous studies primarily focus on the foundational architecture and early construction of two-sided manufacturing platforms [,,] and on operational aspects such as resource-sharing strategies [,,], machine scheduling [,], capacity matching and composition [,,], and task decomposition [,]. Recent research has demonstrated that two-sided platforms must strategically leverage symmetrical cross-network externalities—where balanced, reciprocal influences exist between user groups—when implementing pricing strategies. Specifically, platforms should account for this equilibrium in mutual network effects when determining optimal charge–subsidy allocations between sides. For example, Gao (2018) [] analyzed the pricing strategy of two-sided platforms where participants can engage on both sides, demonstrating that a platform should acquire higher profit margins from one side to offset the costs of subsidizing users who participate on both sides. Huang et al. (2022) [] revealed that both subsidization and first-party application strategies can benefit the platform owner and earn higher profits, but only subsidization could improve social welfare. Yuan et al. (2022) [] considered a two-sided software platform with asymmetric cross-network effects to analyze the platform’s optimal pricing strategy. They found that the platform should adopt a penetration pricing strategy when the user-to-developer network effect is strong and a skimming pricing strategy otherwise. Carroni et al. (2024) [] investigated the impact of superstar exclusive content provision on platform competition, taking into account the effects of indirect cross-network externalities in scenarios where service providers engage in multi-homing. The findings revealed that cross-network externalities are key in shaping market outcomes.
However, as competition among platform enterprises intensifies, subsidy-based pricing strategies that consider symmetric cross-network externalities are becoming less effective for expanding the base of users. Instead, platforms are increasingly adopting non-price controls to drive user adoption, sparking significant discussion among academics and practitioners. Li and Agarwal (2016) [] studied a platform’s choice to integrate its user base with a complementary platform, and they found that the platform’s integration allowed users to reap the benefits of the integration and increase their value. Dou and Wu (2021) [] investigated a new non-pricing strategy, monetization of exclusive access to external users (piggybacking). The study found the profitability of piggybacking depends on the piggybacking cost and the strengths of the cross-side network effects. Other non-pricing strategies include offering VAS levels to attract user adoption. Zhang et al. (2021) [] investigated bilateral VAS and pricing strategies in two-sided platforms, revealing that platform efficiency drives bilateral VAS differentiation and cross-network externalities substantially impact platforms’ optimal strategic choices. Sui et al. (2023) [] compared the VASs and pricing strategy of two competing platforms, finding that lower marginal costs in platform investments yield dual benefits of increased VASs and decreased user fees. An and Liu (2023) [] explored platforms’ investment strategies for two-sided beneficial value-added services and found that the value-added service levels and ad prices of the investment platforms remained constant and then decreased with marginal investment costs. This study contributes to the literature on two-sided manufacturing platforms by investigating a critical non-pricing strategy: the outsourcing of VASs. In practice, these platforms face a fundamental strategic dilemma: while offering VASs is essential for facilitating transactions and strengthening user engagement, the decision of whether to provide these services in-house or outsource them is complex. To address this gap, our research develops an analytical framework that incorporates the distinctive characteristic of symmetric cross-network externalities. Within this framework, we identify a platform’s optimal VAS provisioning strategy and derive the corresponding optimal pricing strategies for both sides of the market.
2.2. Service Outsourcing Strategy
Outsourcing service functions to third-party providers lowers the entry barriers to the high-potential service market and allows firms to concentrate on their core business by avoiding the substantial costs associated with establishing and operating service networks [,,]. A concise overview of existing scholarship on service outsourcing was presented by Choi et al. (2016) [] and Tsai et al. (2012) []. So far, a significant number of studies pay close attention to logistics service outsourcing. For example, Liu et al. (2018) [] investigated differential fairness considerations among logistics service providers within a competitive outsourcing framework, where a logistics integrator contracts with two rival functional providers. Zhang et al. (2019) [] examined retailers’ information-sharing strategies for logistics services undertaken by manufacturers or retailers. Lou et al. (2020) [] investigated logistics service outsourcing decisions in a retailer-led supply chain and found that, although offering logistics services by the retailer can alleviate the double marginalization effect, it is not always the optimal choice. Doratiotto et al. (2023) [] evaluated the factors that influence logistics outsourcing and the impact of logistics outsourcing on measurements of companies’ logistics performance. They found that the factors of collaboration and process characteristics are the most influential on the logistics performances of companies. Yang et al. (2024) [] explored manufacturers’ logistics outsourcing strategies with online freight platforms and traditional logistic service providers. They found that differences in transportation service levels and prices significantly affected the equilibrium of the manufacturer and traditional logistics service providers.
In addition, a larger number of studies focus on extended warranty service outsourcing. Zhang et al. (2020) [] explored outsourcing strategies for manufacturer warranty services in a dual-channel supply chain. They found that if the retailer is unable to provide the service for both channels, they may choose to give up control of services in the retail channel under certain conditions. Huang et al. (2021) [] studied two warranty service provision strategies for competing manufacturers, considering factors such as the competition intensity, service costs, and product reliability. They found that manufacturers are more likely to outsource warranty services when a service provider has a significant cost advantage or the competition is more intense. Cao et al. (2023) [] investigated the optimal maintenance service outsourcing strategy considering extended warranty services. They found that the optimal maintenance service outsourcing strategy depended on the cost coefficient of development maintenance services. Ullah et al. (2023) [] considered a situation in which manufacturers outsource warranty services to retailers. They found that outsourcing warranty services via blockchain always benefits both manufacturers and retailers, as it boosts consumer confidence in the warranty quality. Meng et al. (2024) [] studied the conditions under which the warranty service for remanufactured products is outsourced to retailers. They found that, when retailers have lower warranty costs, independent remanufacturers prefer to outsource the remanufactured product warranty to the retailer. While the existing literature provides a foundation, the specific interplay between service outsourcing strategies and pricing decisions for two-sided manufacturing platforms remains a significant, underexplored area. This study directly addresses this gap by presenting what is, to our knowledge, the first analytical model to compare the two primary VAS provisioning strategies—in-house provision versus outsourcing to third-party providers—within the context of platforms characterized by symmetric cross-network externalities. Furthermore, we extend the analysis by rigorously examining the impact of VAS cost-sharing contracts on the performance of all supply chain members, a critical yet thoroughly underexplored mechanism in this domain.
Table 1 summarizes the differences between this study and the related literature. While this study is grounded in the context of two-sided manufacturing platforms, the proposed model possesses broader applicability across various digital platform ecosystems. For instance, in logistics platforms (e.g., Freightos, Flexport, etc.), the model framework can be adapted to analyze how data sharing and algorithmic matching enhance supply chain visibility and operational efficiency. In financial technology platforms (e.g., Ant Group, PayPal, etc.), the model’s framework could elucidate the dynamics between user trust, network effects, and platform governance. Similarly, for software marketplaces (e.g., Apple’s App Store, Google Play, etc.), the model provides a lens to examine the interplay between developer innovation, user adoption, and platform curation policies. Future research could empirically validate and refine this model within these specific domains.

Table 1.
Comparison of this study with prior studies (√: covered; ×: not covered).
3. The Model
This study investigates the bilateral pricing problem and VAS provision strategy for two-sided platforms characterized by symmetric cross-network externalities—where suppliers and manufacturers exhibit balanced, reciprocal influences that create equilibrium in platform participation dynamics. We consider a two-sided manufacturing platform (e.g., XoMetry.com, DHGate.com, etc.) owner that facilitates the trade of components between suppliers (s) and manufacturers (m). The basic framework is illustrated in Figure 1. Due to the attractiveness of the VAS strategy [,], the platform needs to rethink the best strategy for providing VASs. To this end, we construct two theoretical models that are established to capture the platform’s divergent strategic pathways, namely, (1) self-operate VASs (Model PS) or (2) the platform outsources VASs to a third-party service provider (Model OS). Specifically, the former mode allows the platform to attract more bilateral participants through ensuring user-compatible service levels, but it weakens platform core business attention and bears additional operating costs. The latter mode allows the platform to offer VAS levels at a controllable investment cost but with an unstable quality of service.
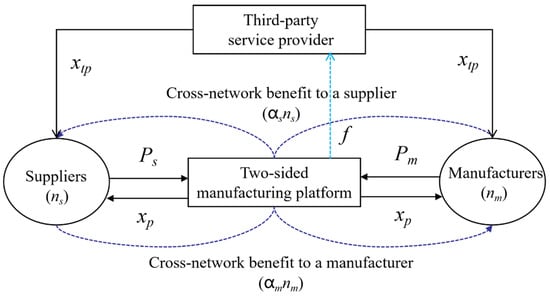
Figure 1.
Basic framework of a two-sided manufacturing platform.
In Model PS, the platform offers basic services, , namely, the intrinsic value of joining the platform (e.g., information browsing and searching), and charges the () side participants an access fee, . Consistent with prior studies, we assume the basic services follow uniform distributions, that is, . Moreover, suppliers and manufacturers make rational decisions based on the perceived value and network size. We use and to represent the positive cross-network externality symmetry between suppliers and manufacturers, that is, increased supplier participation enhances component matching probability for manufacturers, while greater manufacturer presence creates additional value for suppliers, where []. For analytical tractability and to maintain focus on platform VAS strategy, we explicitly exclude intra-side cross-network externalities from our model specification [,]. represents the VAS utility provided by platform. Hence, referring to previous research by Armstrong (2006) [], Zhang et al. (2021) [], and Sui et al. (2024) [], suppliers and manufacturers who use the platform for access find the following utility: ; .
The modeled platform firm’s revenue mainly stems from suppliers and manufacturers’ participation fees [,]. In addition to basic services, value-added services (e.g., priority ranking, payment security, and logistics supervision) are being introduced by many platforms to tap into the potential of users’ participation. Meanwhile, the platform needs to spend a certain amount on providing VASs, which will affect the platform’s VAS investment levels and pricing. Referring to Dou et al. (2016) [] and Dan et al. (2018) [], we suppose that the variable cost of unit VAS is , where represents the constant marginal cost. The variable costs of VASs such as installation, cleaning, and financial services have a linear relationship with the service level. In Section 6, we expand our base model to take into consideration a scenario in which the platform provides its bilateral players with differential VAS investment levels.
In Model OS, an independent third-party service provider is hired by the platform to provide a VAS for its bilateral participants. For example, HOIZAL.com outsources its software service and financing service to third-party service providers (e.g., Delixi electric; KMES software; and Haier financial services), and 1688.com outsources its logistics services to third-party service providers (e.g., S.f.Holding express and China cainiao express). In this context, the players follow the Stackelberg game. As a game leader, the third-party service provider first announces the price to the platform of providing the unit VAS . The platform, as the follower in the Stackelberg game, decides the bilateral participants’ prices . Meantime, the third-party service provider needs to spend a certain amount on providing unit VAS. Similarly, we adopt a variable cost function to describe the VAS investment cost, where is the VAS cost coefficient of the third-party service provider. The variable cost of the VAS increases with the service level . The main notations used in this study are summarized in Table 2.

Table 2.
Summary of main notations.
3.1. Self-Operate VAS (Model PS)
In Model PS, the platform conducts its own service system and offers the VAS by itself. In this case, the platform decides the participants’ price and offers the VAS for its bilateral participants. The superscript “PS” denotes Model PS. Based on the analysis above, we can obtain the profit function of the platform, which is given by
Recall the utility of a supplier and the utility of a manufacturer accessing the platform; the supplier and the manufacturer will access the platform only if its utility is non-negative (). Thus, bilateral participants’ access rate of the platform can be expressed as
Solving the system of Equations (2) and (3) simultaneously, we can obtain the access rates of bilateral participants as follows:
It is easy to know from Equations (4) and (5) that and are affected by two aspects, which are the negative impact of the platform’s access fees and positive impact of the VAS utility. Thus, the profit function of the platform can be further rewritten as
By computing the Hessian matrix of about , it is known that the Hessian matrix is positive definite. And our analysis is conducted under the following conditions: . The results characterize the equilibrium decisions of the platform under Model PS in Lemma 1. In addition, proofs of the positive definite condition and equilibrium results are given in Appendix A. Our analysis is conducted under the following conditions: .
Lemma 1.
Under Model PS, the optimal solutions of the platform are
, , , .
Based on Lemma 1, we can obtain the results below which describe how the key factors, including the cross-network externality symmetry degree and VAS level, affect the optimal decisions of the platform in Model PS.
Proposition 1.
When the platform undertakes a VAS, we have the following:
- (i)
- With the increase of , the optimal prices and optimal access rate increase;
- (ii)
- With the increase of , the optimal prices and optimal access rate increase, while decreases;
- (iii)
- With the increase of , the optimal prices and optimal access rate increase, while decreases.
Proposition 1(i) indicates that when the VAS level provided by the platform for its bilateral participants increases, bilateral participants have a higher willingness to access because they derive more service utility, thus promoting bilateral participants’ access rate too. Meanwhile, the platform will also increase the price for bilateral participants to make more profits and make up for the cost of improving the service level for bilateral participants. Propositions 1(ii) and (iii) reveal that when the manufacturers’ (suppliers) cross-network externality degree increases, the platform will increase the price for suppliers (manufacturers) but decrease the price for manufacturers (suppliers). This result is consistent with the findings of many other studies, such as Zheng et al. (2023) [] and Dou et al. (2024) [], that suggest platforms should charge a lower price to those who exhibit higher network externality and a high price to the other side which benefits from the increasing cross-network utility. The reason behind this outcome is that the platform is willing to attract more manufacturers (suppliers) when () increases, thus the platform will decrease the price for manufacturers to encourage them to access. Under symmetric equilibrium conditions, suppliers and manufacturers experience mutually balanced cross-network utility flows, where suppliers gain proportional benefits from manufacturer participation that improve their access rate, while simultaneously manufacturers receive equivalent utility gains from supplier participation that enhance their own access rate, maintaining perfect reciprocity in platform value exchange. Therefore, the platform will also increase the price for suppliers and make up for the loss of decreasing the price for manufacturers. Figure 2 presents some numerical examples to exhibit the impacts of the service level and cross-network externality symmetry on the platform’s optimal solutions .
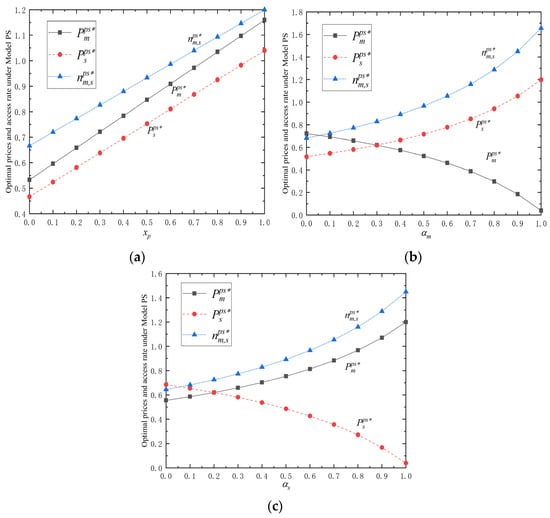
Figure 2.
Optimal prices and access rates under Model PS with the change in (a) service level (); (b) cross-network externality (); (c) cross-network externality ().
Corollary 1.
According to the optimal profit of the platform not providing the VAS (), which is shown in Zhang et al. [], the value of the platform providing the VAS by itself (Model PS), , is given by , where denotes the platform’s profit without providing the VAS.
Commonly used VASs for two-sided manufacturing platforms, including priority ranking, effective matching, payment security, and logistics supervision, are strategically designed to amplify the symmetrical nature of cross-network externalities. These services simultaneously enhance engagement for both suppliers and manufacturers in balanced proportions, thereby reinforcing the reciprocal value exchange and maintaining equilibrium in platform participation dynamics. According to Corollary 1, the platform should offer VASs and take into consideration the allure of the VAS approach. This finding further illustrates that investing in VASs as a highly profitable and rapidly growing business has become a more effective operational strategy for two-sided platforms [,,]. In addition, Zhang et al. (2021) [] also show that when bilateral participants have higher degrees of cross-network externality symmetry, a two-sided platform is better able to provide VASs. In the following, we concentrate more on a platform’s calculated decision to offer VAS provision.
3.2. VAS Is Outsourced to the Third Party (Model OS)
In Model OS, the platform hires an independent third party to provide a VAS. In this case, the third party provides the VAS for the platform’s bilateral participants and announces the price of each unit VAS. The platform decides the participants’ price . The decision sequence in Model OS is as follows: the third party announces the unit outsourcing price and provides the VAS first, then the platform decides the bilateral participants’ price. The superscript “OS” denotes Model OS. Based on the analysis above, we can obtain the profit function of the platform and the third party as follows.
The utility of a supplier under Model OS is equal to . And the utility of a manufacturer under Model OS is equal to . Both sides’ participants will access the platform only if its utility is non-negative (). Thus, we obtain
Following a similar solving approach as described in Section 3.1, we can calculate the access rates of bilateral participants as follows:
Then, the profit function of the platform and the third-party can be further rewritten. In this dynamic game, we solve for the subgame-perfect Nash equilibrium, such that is the best response when are given. Details of the calculation process can be found in the Appendix A. Then, we obtained the optimal decisions of the platform and the third party in Lemma 2. And our analysis was conducted under the following conditions: .
Lemma 2.
Under Model OS, platform’s optimal solutions are
, , , . The optimal solutions of the third-party are , .
Based on Lemma 2, we discuss how the outsourced VAS level affects the optimal decisions and profits of the platform and the third party, as Proposition 2 shows.
Proposition 2.
When the service is outsourced to the independent third party, we have the following:
- (i)
- With the increase of , the optimal access rate and profits increase when ; otherwise, decrease when ;
- (ii)
- With the increase of , the optimal prices increase.
Proposition 2(i) shows that when the VAS level provided by the third party increases, the platform will increase the price for bilateral participants and the price of unit VAS simultaneously. The platform increases the bilateral participants’ prices for two aspects, one is the higher service utility that bilateral participants obtained as stated in Proposition 1(i), and the other reason is the increased payment to the third party for improving the VAS level. To ground this finding in a tangible context, our simulation models a scenario akin to a logistics platform (e.g., similar to FedEx’s SenseAware service), introducing advanced, real-time tracking (VAS). This quantitatively validates the theoretical mechanism: the platform capitalizes on the enhanced utility for users (who can now track their shipments in near real-time) while also passing on part of the higher costs incurred for the third-party service provider to maintain this advanced infrastructure. In the low outsourced VAS cost scenario (e.g., a software marketplace where adding a new AI-powered code-review tool primarily involves marginal cloud computing costs), both platform participation and profits surge with VAS enhancement. The simulation outputs indicate a profit growth of over 30% for both parties when the VAS level is high under this cost structure. Conversely, in the high outsourced VAS cost scenario (e.g., a financial technology platform integrating a new, compliance-heavy fraud detection system that requires significant regulatory licensing and expert manpower), the picture changes dramatically. As shown in Figure 3, beyond a certain VAS threshold, profits begin to decline despite a modest increase in user access rate. The managerial insight is that third-party providers must conduct a rigorous cost–benefit analysis before committing to high-cost value-added feature development, ensuring that the anticipated demand expansion is sufficient to offset the substantial costs involved.
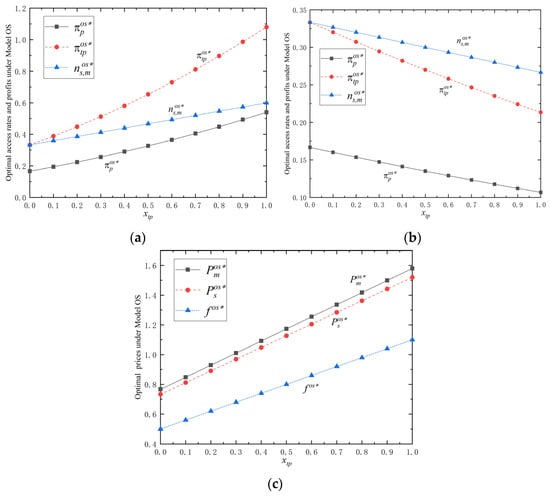
Figure 3.
Optimal solutions under Model OS with the change in outsourced service level : (a) (); (b) (); (c) ().
In conclusion, our model and simulations collectively paint a nuanced picture: strategically increasing a VAS is a powerful lever for growth, but its success is contingent on the economic reality of the service being offered. The key is not merely to add features, but to intelligently select and price those value-added services whose cost structures allow for a net positive return, thereby truly enhancing ecosystem value without falling into the trap of excessive, profit-eroding investment []. Figure 3 presents some numerical examples to better understand the findings of Proposition 2.
4. Comparative Analysis
Having analyzed both models independently, we now compare the equilibrium outcomes of Model PS and Model OS to guide platforms’ outsourcing decisions. In the following Proposition 3 and 4, we will analyze which VAS provision strategy choice can determine larger entry fees and access rates for its bilateral participants.
Proposition 3.
The following formulas are established by comparing the variables of the two modes:
- (i)
- The optimal suppliers’ price: (a) if , , (b) if , when ; otherwise, when .
- (ii)
- The optimal manufacturers’ price: (a) if , , (b) if , when ; otherwise, when , where , , , and .
Proposition 3 compares the optimal bilateral participants’ price of the two VAS provision modes. First, the platform charges a higher bilateral suppliers’ price under Model PS than under Model OS only when the VAS level provided by the third party is relatively low. That is to say, the platform has stronger pricing power to set a higher price for its suppliers when the platform offers a relatively high VAS level by itself. Conversely, when the VAS level provided by a third party is relatively high, the platform will set a lower price for suppliers to compensate for the lower service utility that suppliers obtain. Second, the platform charges a higher bilateral manufacturers’ price under Model PS than under Model OS only when the VAS level provided by the third party is relatively low. The fundamental reason for the optimal manufacturers’ price is similar to the supplier-side price.
Proposition 4.
The optimal bilateral participants’ access rate:
- (i)
- If , when ; otherwise, when .
- (ii)
- If , .
The threshold defines when outsourcing (the OS model) becomes optimal for the platform. Outsourcing is attractive when the VAS utility provided by the third-party service provider exceeds a critical level. This critical level decreases with the platform’s internal VAS costs c and the competitive VAS quality intensity , meaning the platform is more likely to outsource when its own operations are costly or the market is competitive. However, a strong third-party service provider’s VAS cost, k, raises the bar for outsourcing, as it makes in-house operation more valuable. Thus, Proposition 4 shows that the optimal bilateral participants’ access rate under Model OS is greater than that of Model PS only when the outsourced VAS cost is low and VAS level provided by the third party is in a high range. The rationale is straightforward: enhanced VAS provision (whether platform-supplied or third-party) boosts bilateral participants’ service utility, thereby directly increasing their access probability. In other cases, such as when the outsourced VAS cost is high or the VAS level provided by third party is relatively low, Model PS can determine a larger access rate for its bilateral participants. This is because the relatively low outsourced service quality may hurt bilateral participants’ enthusiasm to join the platform.
Proposition 5.
A platform’s optimal VAS provision strategy under symmetric cross-network effects—where balanced, reciprocal influences between participants create equilibrium conditions—is jointly determined by and
, presented as follows:
- (i)
- When and , the platform should implement Model PS; otherwise, the platform should implement Model OS when . The profit comparison of the platform and the third party under two models is shown in Figure 4.
- (ii)
- When , the platform should implement Model PS.
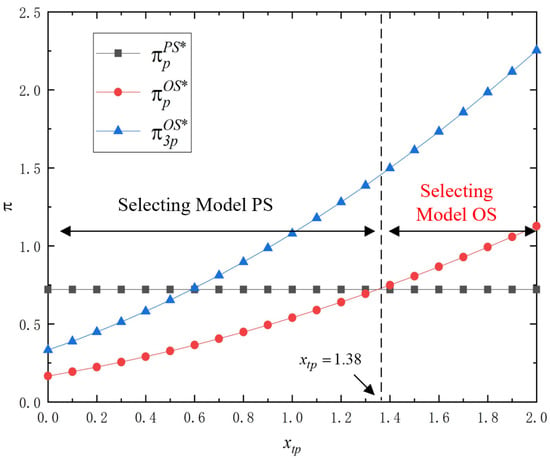
Figure 4.
Platform’s optimal VAS provision choice ().
Observe that the key factors for whether the platform should choose the option of outsourcing its VAS are the outsourced VAS’s quality and cost of the third party. To translate this finding into actionable strategy, we define “low cost and level” as scenarios where a third party offers a basic, cost-efficient service (e.g., a simple data analytics dashboard for an e-commerce platform). Counterintuitively, the model reveals that in these cases, the platform’s profit is maximized by bringing the service in-house (Model PS). The simulation shows that under these conditions, self-provisioning yields a 10–15% higher profit for the platform compared to outsourcing. The rationale is that the platform can leverage its existing infrastructure and brand trust to offer a marginally better version of this basic service, thereby capturing all the value and exercising greater pricing power over its users, without the burden of managing a third-party relationship for a non-differentiating service. However, Figure 3 also demonstrates that in the “low-cost, high-level” quadrant, outsourcing (Model OS) becomes unequivocally superior, boosting the bilateral participants’ access rate by over 20% and overall platform profit by a similar margin. Here, the value generated by the third party’s superior service in attracting and retaining users far outweighs the loss of direct control. This mirrors the real-world strategy of platforms like Shopify, which relies on an ecosystem of expert app developers to provide high-value services that Shopify itself does not build. Moreover, the platform should opt for self-provided VASs when encountering excessive outsourcing costs that undermine operational efficiency, as Proposition 5(ii) reveals. This quantifies the severe financial damage of a poor outsourcing decision and underscores the non-negotiable need for cost-effective partnerships. Next, we aim to incentivize the third party to provide high-quality VAS level in terms of the VAS cost-sharing contract design.
5. VAS Cost-Sharing Contract Design
In this section, we propose a VAS cost-sharing contract (Model CS) in which the platform shares a portion, μ, to the third party when the VAS is outsourced to the third party. Under the cost-sharing contract, the platform pays the service fee per participant to the third party and additionally shares a fraction, , of the third party’s service cost . We use a superscript, “CS”, which denotes Model CS. In Model CS, the utility functions of the bilateral participants are the same as those of Model OS, but the profit functions change. The profit functions are presented as follows:
With a similar calculating procedure as that employed in Model OS, we provide the optimal solution of the platform and the third party in Lemma 3.
Lemma 3.
Under Model CS, , , , and ; and .
Next, we look at how the platform and the third party’s best choices are impacted by the VAS cost-sharing agreement. Based on the optimal solutions characterized in Lemma 2 and 3, we derive the following key properties.
Proposition 6.
The VAS cost-sharing contract can decrease the outsourced price of unit VAS and increase the bilateral participants’ price while decreasing the access rate of the bilateral participants. Put mathematically, , , .
Proposition 6 shows that the platform may obtain favorable outsourced pricing of unit VAS with the use of a VAS cost-sharing contract. The third-party provider has clear economic incentives to reduce service prices when the platform shares a portion of VAS costs, as this cost-sharing arrangement effectively lowers the provider’s marginal costs. However, for the platform, the funds paid for the VAS cost primarily come from the platform increasing the bilateral participants’ price. Improving the price for its participants leads to a decrease in the access rate of the bilateral participants. Therefore, the bilateral participants’ price is high and bilateral participant access rates are systematically lower when operating under VAS cost-sharing contracts than in scenarios without such arrangements.
Proposition 7.
Given an active VAS cost-sharing agreement between the platform and third-party provider, there exists a Pareto zone, , , in which both the platform’s and the third party’s profits will improve, where .
Proposition 7 reveals the coordination conditions of the VAS cost-sharing contract. Intuitively, when the platform shares part of the cost, the third-party service provider can benefit from the VAS cost-sharing contract. However, Proposition 7(i) shows that” when the outsourced VAS cost coefficient is relatively low, there exists a “lose-lose” outcome, i.e., , . In this case, the third party is incentivized to deliver high-quality services to maximize compensation while simultaneously optimizing operational efficiency to minimize costs. Therefore, the VAS cost-sharing agreement will not be accepted by the third party. To accomplish the objective of raising the player’s overall performance and achieving a win-win situation, Proposition 7(ii) shows the VAS cost-sharing contract as a successful strategy when the outsourced VAS cost coefficient is relatively high. In Figure 5, we simulate the players’ profit with the change in the VAS cost-sharing ratio by setting . When the platform considers utilizing the VAS cost-sharing contract, the platform’s and the third party’s profits should satisfy the condition: , . We find that only when , , the conditions are satisfied concurrently. Through adopting the VAS cost-sharing contract, the platform should initially bear some part of a relatively high service cost to obtain a relatively low outsourced VAS price and attract the third party to accept the contract.
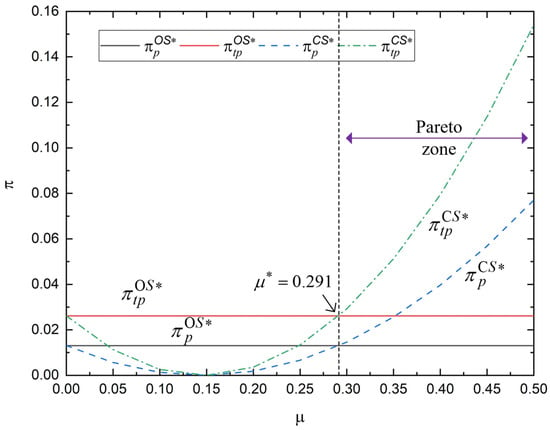
Figure 5.
Pareto zone with VAS cost-sharing contract.
6. Model Extensions
To assess the robustness of our core findings, in this section, our baseline model is extended to construct a platform that provides differentiated VASs to its bilateral participants. Specifically, (1) when the platform offers a VAS by itself, the utility of bilateral participants are and . We use a superscript, “P-BD”, to denote this scenario. (2) when the platform hires the independent third party to provide a VAS, the utility of bilateral participants is ; . We use a superscript, “O-BD”, to denote this scenario.
Based on Equation (1), the profit function of the platform under Model P-BD is
Based on Equations (7) and (8), the profit function of the platform and the third party under Model O-BD are
With a similar calculating procedure as those employed in Model PS and Model OS, we provide the optimal solution of the platform and the third party in Table 3. In addition, proofs of the equilibrium results are consistent with Model PS and Model OS. Thus, we omit them here.

Table 3.
The optimal solutions under Model P-BD and Model O-BD.
We discovered certain findings, which are summed up in Remark 1, by using numerical analysis, as illustrated in Figure 6.
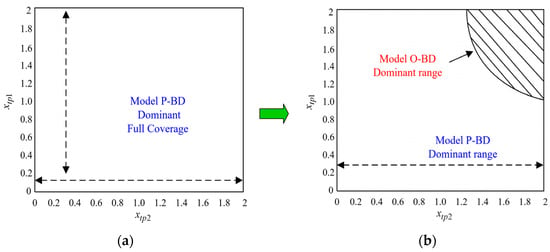
Figure 6.
Platform’s preferred VAS provision choice under bilaterally differentiated VAS. (a) ; (b) .
Remark 1.
When considering the bilateral differentiated VAS strategy, the main results of the platform’s VAS provision strategy choice in the basic model also hold. The platform should implement Model P-BD so long as the outsourced VAS cost coefficient is high. Otherwise, the platform should implement Model O-BD only when the outsourced VAS cost coefficient is low and the VAS level is a high range.
In Figure 6a, we simulate the profit of the platform under Model P-BD and Model O-BD with the change in the outsourced VAS level by setting . Under this scenario (), even if the outsourced VAS level is high, the platform is always prone to offering bilateral differentiated VAS to its participants by itself, which is in line with the findings of Proposition 5(ii). Similarly, in Figure 6b, we simulate the profit of the platform under Model P-BD and Model O-BD with the change in the outsourced VAS level by setting . Under this scenario (), there exists a Model O-BD dominant range in which the platform is inclined to hire the independent third party to provide bilateral differentiated VASs. Notably, the Model O-BD dominant range must satisfy the condition of the third-party service provider’s VAS cost coefficient being low and VAS level being high. This result is also consistent with the findings of Proposition 5(i). Therefore, we demonstrate that the results of the optimal platform’s VAS provision strategy choice continue to hold qualitatively both in identical and differentiated VASs.
7. Conclusions
The strategic value of two-sided platforms for manufacturer–supply chain collaboration has grown substantially, driven by concurrent developments in information technology and the intensification of economic globalization. Meanwhile, value-added services (VASs) provided by platforms have become a critical part of enhancing competitiveness, and platforms are facing the challenge of whether to outsource VAS investment. To address the challenge, we first developed a basic model for a two-sided platform in which the VAS level and cross-network externality symmetry strength affected the participating utility of suppliers and manufacturers through pricing decisions. On this basis, we constructed two theoretical models, which were Model PS and Model OS, to derive the optimal solutions for the platform and the third party and explore the platform’s optimal selection of VAS mode. Moreover, we considered VAS cost-sharing contracts to further explore platform cooperation strategies and tested the models’ robustness considering differentiated bilateral VASs.
7.1. Main Conclusions
This paper yields three main findings that complement the operating mechanism of two-sided manufacturing platforms. First, we obtained optimal bilateral participant pricing strategies and analyzed the impact of key parameters, such as the cross-network externality symmetry and the VAS level, on the platform’s and the third party’s optimal decisions. In addition, in comparison with not providing VAS, our analysis revealed that two-sided platforms derive greater strategic advantages from VAS provision when participants exhibit positive degrees of cross-network externality symmetry, where balanced, reciprocal utility flows between user groups create mutually reinforcing participation incentives. Second, a platform’s preferred VAS provision strategy is jointly determined by a third party’s outsourced VAS quality and cost coefficient. So long as the outsourced VAS cost coefficient is high, the platform should choose Model PS. When the outsourced VAS quality and cost coefficient are relatively low concurrently, the platform should also select Model PS. Only when the outsourced VAS quality is relatively high and cost coefficient is in a low range should the platform opt for Model OS. Additionally, this optimal VAS provision strategy also remains unchanged when considering platforms that provide differentiated VASs for its bilateral participants. Third, we gave the optimal VAS cost-sharing ratio and clarified the conditions for achieving a VAS cost-sharing contract. Introducing a VAS cost-sharing contract is helpful to improve the performance of the platform and the third party when the outsourced VAS cost coefficient is relatively high. Conversely, when the outsourced VAS cost coefficient is relatively low, VAS cost-sharing contracts should not be implemented.
7.2. Managerial Insights
Several significant managerial implications can be derived from our findings, offering actionable guidance for platform managers across different growth stages. (1) In the preliminary stage, it is crucial for a two-sided platform to ignite network effects by providing targeted VASs to both participant groups. By capitalizing on symmetry in cross-network effects, the platform can design VASs that create reciprocal value, simultaneously boosting attraction for both sides. For example, a nascent B2B industrial equipment platform might provide digital inventory management software for manufacturers and financing solutions for buyers. These VASs reduce friction and enhance participation value for both user groups, creating a virtuous cycle of growth. (2) During the development process, as platform scales and internal VAS costs rise significantly, a strategic transition toward third-party provisioning becomes essential to maintain innovation and cost-efficiency. The key is to curate a high-quality ecosystem of partners. For example, an expanding smart-home two-sided platform ecosystem (e.g., Samsung SmartThings) would shift from building all compatible devices itself to certifying thousands of third-party device manufacturers. This strategy rapidly expands variety for consumers while the platform focuses on core platform stability and standards. (3) In the latter stage of platform development, implementing VAS cost-sharing contracts with key third-party providers can deepen partnerships and create sustainable “win-win” outcomes. This involves sharing risks and incentives to align interests closely. For example, an established two-sided software platform (e.g., Salesforce) might partner with a consulting firm to develop a specialized industry module. The platform shares the development cost, incentivizing the partner to offer the solution at a preferential rate to the platform’s clients. This enhances the platform’s value proposition while giving the consulting firm access to a vast customer base.
7.3. Further Research
Further research can be conducted in the following aspects. First, although the management implications derived from this study are theoretically clear, a limitation lies in the fact that a comprehensive numerical sensitivity analysis of the model parameters has not yet been conducted. Future research can quantitatively test the robustness of the conclusions of this study by systematically perturbing key (small) parameters. Second, participants on one or both sides often lack information regarding the prices charged to participants on the other side. Therefore, considering how information availability influences price structures would be a challenging yet fascinating area for further study. Third, as platforms play a solely functional role as intermediaries, an increasing number of concerns have been raised about the insufficient corporate social responsibility of platforms []. Further research should consider how the factor of corporate social responsibility on platforms’ development goals shape the existing results.
Author Contributions
Conceptualization, H.Z., Y.Y. and S.W.; Methodology, H.Z. and J.L.; Software, H.Z. and Y.Y.; Validation, T.S., J.L. and S.W.; Formal analysis, Y.Y. and J.L.; Resources, J.L.; Writing—original draft, H.Z. and J.L.; Writing—review & editing, H.Z. and Y.Y.; Visualization, S.W.; Supervision, T.S. and S.W.; Project administration, T.S. and S.W.; Funding acquisition, T.S. and S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant No. 71771080.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Proof of Theorem 1.
According to Equation (6), we know that a platform’s profit under Model PS is . Hence we have the first derivative, , . Given , , we can know the Hessian matrix and . Therefore, there exist optimal prices to maximize the platform’s profit. Then, let and ; we can obtain the optimal decisions for the platform, as shown in Lemma 1. □
Proof of Proposition 1.
Based on the optimal solutions in Lemma 1 and , we have (i) , , , . (ii) , , , . (iii) , . , . Merging these results, we can summarize them as Proposition 1. □
Proof of Lemma 2.
Under Model OS, the third party is the leader of a Stackelberg game. Using backward induction, we first drive the platform’s first-order condition of with respect to : , . Then, solving the platform’s first-order condition and anticipating the subgame-perfect strategy, we obtain the first derivative of the third party that . Let ; we can obtain the optimal decisions of the third party as shown in Lemma 2. Substituting the optimal decisions of the third party into the expression of , , we can obtain the optimal decisions of the platform as shown in Lemma 2. The condition of the Hessian matrix is similar to that in Lemma 1, so we omit it. Then, we can obtain that to ensure the positive number of suppliers and manufacturers on the platform, that is, . □
Proof of Proposition 2.
Based on the optimal solutions in Lemma 2, we have (i) , , . (ii) . According to , we can obtain that when , ; otherwise, when . Then, , . We need to judge the value of under the condition of . By calculating, we can obtain that when , ; otherwise, when . □
Proof of Proposition 3.
Based on the optimal solutions in Lemma 1 and 2, we have . First, we need to judge the value of . By calculating, we can obtain that when , ; otherwise, when . Then, it is easy to know . Let be the sole root of the numerator of the function . By calculating, when , ; otherwise, when . Note that the expression of . The calculation process of is similar to the above analysis. Thus, we omit it to reduce complexity. □
Proof of Proposition 4.
Based on the optimal solutions in Lemma 1 and 2, we have . Let be the sole root of the numerator of the function . By calculating, we can obtain that , when ; otherwise, when . If , . Note that the expression of . The calculation process of is similar to the above analysis. Thus, we omit it to reduce complexity. □
Proof of Proposition 5.
Based on the optimal solutions in Lemma 1 and 2, we have . Then, we need to judge the value of . Let , be the root of the quadratic function. Note that the expression of and . By calculating, we can obtain that (i) if , will be the positive root of this function. In this case, when , ; otherwise, when . (2) If , will be the positive root of this function. In this case, when , ; otherwise, when . However, the condition of equal to cannot satisfy . Thus, only exists if . Merging these results, we can summarize them as Proposition 5. □
Proof of Lemma 3.
With the same reasoning as in Model OS, the proof of Lemma 3 is similar to that of Lemma 2. Therefore, we omit it here. □
Proof of Proposition 6.
Based on the optimal solutions in Lemma 2 and Lemma 3, we have ; ; ; and . □
Proof of Proposition 7.
Based on the optimal solutions in Lemma 2 and Lemma 3, we have (i) . Based on the molecular component of , we need to judge the value of . Let be the sole root of this function, .
We can obtain that when , , then . When , , then .
In such a case, we assume that the cost-sharing ratio does not exceed 50%. The same setting is also used in []. In addition, if , . Therefore, the outsourced VAS cost coefficient should satisfy . (ii) . Observe that the calculation process of is the same as . Finally, merging these results, we can summarize them as Proposition 7. □
References
- Chaudhuri, A.; Datta, P.P.; Fernandes, K.J.; Xiong, Y. Optimal pricing strategies for manufacturing-as-a service platforms to ensure business sustainability. Int. J. Prod. Econ. 2021, 234, 108065. [Google Scholar] [CrossRef]
- Cao, K.; Su, Y.; Han, G.; Wang, J. Optimal maintenance service outsourcing strategy considering extend warranty service. Manag. Dec. Econ. 2023, 44, 1344–1358. [Google Scholar] [CrossRef]
- Rochet, J.; Tirole, J. Platform competition in two-sided market. J. Eur. Econ. Assoc. 2003, 1, 990–1029. [Google Scholar] [CrossRef]
- Armstrong, M. Competition in two-sided markets. RAND J. Econ. 2006, 37, 668–681. [Google Scholar] [CrossRef]
- Zimmermann, S.; Angerer, P.; Provin, D.; Nault, B. Pricing in C2C sharing platforms. J. Asso. Infor. Sys. 2018, 19, 672–688. [Google Scholar] [CrossRef]
- Birge, J.; Candogan, O.; Chen, H. Optimal commissions and subscriptions in networked markets. Manu. Ser. Opera. Manag. 2021, 23, 569–588. [Google Scholar] [CrossRef]
- Huang, P.; Lyu, G.; Xu, Y. Quality Regulation on two-sided platforms: Exclusions, subsidization, and first-party applications. Manag. Sci. 2022, 68, 4415–4434. [Google Scholar] [CrossRef]
- Dou, Y.; Wu, D. Platform competition under network effects: Piggybacking and optimal subsidization. Infor. Sys. Res. 2021, 32, 820–835. [Google Scholar] [CrossRef]
- Sui, R.; Liu, M.; Liu, Y.; Zha, X. Two-sided dynamic pricing and value-added service investment strategies of competitive platforms considering indirect network effects. Int. J. Prod. Econ. 2024, 272, 109262. [Google Scholar] [CrossRef]
- Dou, G.; He, P.; Xu, X. One-side value-added service investment and pricing strategies for a two-sided platform. Int. J. Prod. Res. 2016, 54, 3808–3821. [Google Scholar] [CrossRef]
- Dan, B.; Zhang, S.; Zhou, M. Strategies for warranty service in a dual-channel supply chain with value-added service competition. Int. J. Prod. Res. 2018, 56, 5677–5699. [Google Scholar]
- Li, J.; Wang, Y.; Liu, Z.; Cai, X.; Xie, W. Joint optimal strategies on service investment and drug pricing for a two-sided online pharmaceutical platform. Int. J. Prod. Econ. 2022, 252, 108556. [Google Scholar] [CrossRef]
- Zhang, X.; Sui, R.; Dan, B.; Guan, Z. Bilateral value-added services and pricing strategies of the third-party platform considering the cross-network externality. Comp. Ind. Eng. 2021, 155, 107196. [Google Scholar] [CrossRef]
- Sui, R.; Zhang, X.; Dan, B.; Zhang, H.; Liu, Y. Bilateral value-added service investment in platform competition with cross-side network effect under multihoming. Euro. J. Oper. Res. 2023, 304, 952–963. [Google Scholar] [CrossRef]
- Lou, Y.; Feng, L.; He, S.; He, Z.; Zhao, X. Logistics service outsourcing choices in a retailer-led supply chain. Trans. Res. Part. E. 2020, 141, 101944. [Google Scholar] [CrossRef]
- Huang, H.; Liu, F.; Zhang, P. To outsource or not to outsource? Warranty service provision strategies considering competition, costs and reliability. Int. J. Prod. Econ. 2021, 242, 108298. [Google Scholar] [CrossRef]
- Leng, J.; Guo, J.; Xie, J.; Zhou, X.; Liu, A.; Gu, X.; Mourtzis, D.; Qi, Q.; Liu, Q.; Shen, W.; et al. Review of manufacturing system design in the interplay of Industry 4.0 and Industry 5.0 (Part II): Design processes and enables. J. Manu. Sys. 2025, 79, 528–562. [Google Scholar] [CrossRef]
- Bai, C.; Li, H.; Xiao, Y. Industry 4.0 technologies: Empirical impacts and decision framework. Prod. Oper. Manag. 2022. [Google Scholar] [CrossRef]
- Adamson, G.; Wang, L.; Holm, M.; Moore, P. Cloud manufacturing-a critical review of recent development and future trends. Int. J. Comp. Inte. Manu. 2017, 30, 347–380. [Google Scholar] [CrossRef]
- Anderson, E.G.; Lopez, J.; Parker, G.G. Leveraging value creation to drive the growth of B2B platforms. Prod. Oper. Manag. 2022, 31, 4501–4514. [Google Scholar] [CrossRef]
- Ren, L.; Zhang, L.; Tao, F.; Zhao, C.; Chai, X.; Zhao, X. Cloud manufacturing: From concept to practice. Ent. Info. Sys. 2015, 9, 186–209. [Google Scholar] [CrossRef]
- Moghaddam, M.; Cadaviad, M.; Kenley, R.; Deshmukh, A. Reference architectures for smart manufacturing: A critical review. J. Manu. Sys. 2018, 49, 215–225. [Google Scholar] [CrossRef]
- Rožman, N.; Diaci, J.; Corn, M. Scalable framework for blockchain-based shared manufacturing. Rob. Comp.-Int. Manu. 2021, 71, 102139. [Google Scholar] [CrossRef]
- Cao, X.; Bo, H.; Liu, Y.; Liu, X. Effects of different resource-sharing strategies in cloud manufacturing: A Stackelberg game-based approach. Int. J. Prod. Res. 2021, 61, 520–540. [Google Scholar] [CrossRef]
- Delaram, J.; Houshamand, M.; Ashtiani, F.; Valilai, O. A utility-based matching mechanism for stable and optimal resource allocation in cloud manufacturing platforms using deferred acceptance algorithm. J. Manu. Sys. 2021, 60, 569–584. [Google Scholar] [CrossRef]
- Hu, Y.; Pan, L.; Gu, D.; Wang, Z.; Liu, H.; Wang, Y. Matching of manufacturing resources in cloud manufacturing environment. Symmetry 2021, 13, 1970. [Google Scholar] [CrossRef]
- Wei, Q.; Wu, Y.; Cheng, T.; Sun, F.; Jiang, Y. Online hierarchical parallel machine scheduling in shared manufacturing to minimize the total completion time. J. Oper. Res. Soc. 2022, 74, 2432–2454. [Google Scholar] [CrossRef]
- Zheng, F.; Wang, Z.; Xu, Y.; Liu, M. Single machine scheduling with uncertain processing times and carbon emission constraint in the shared manufacturing environment. Ann. Oper. Res. 2023, 719. [Google Scholar] [CrossRef]
- Tong, H.; Zhu, J. A two-stage method for large-scale manufacturing service stable matching under uncertain environments in cloud manufacturing. Comp. Ind. Eng. 2022, 171, 108391. [Google Scholar] [CrossRef]
- Zhang, X.; Cao, D.; Dan, B.; Rui, J.; Zhang, S. The capacity matching problem of the third-party shared manufacturing platform with capacity time windows and order splitting. Int. J. Prod. Res. 2024, 62, 6167–6185. [Google Scholar] [CrossRef]
- Jin, H.; Jiang, C.; Lv, S. A hybrid whale optimization algorithm for quality of service-aware manufacturing cloud service composition. Symmetry 2024, 16, 46. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, Z.; Wang, J.; Wang, Z.; Liu, H. Task decomposition based on cloud manufacturing platform. Symmetry 2021, 13, 1311. [Google Scholar] [CrossRef]
- Duan, K.; Fong, S.; Siu, S.; Song, W.; Guan, S. Adaptive incremental genetic algorithm for task scheduling in cloud environments. Symmetry 2018, 10, 168. [Google Scholar] [CrossRef]
- Gao, M. Platform pricing in mixed two-sided markets. Int. Econ. Rev. 2018, 59, 1103–1129. [Google Scholar] [CrossRef]
- Yuan, N.; Feng, H.; Li, M.; Feng, N. Penetration or skimming? Pricing strategies for software platforms considering asymmetric cross-side network effects. J. Asso. Infor. Sys. 2022, 23, 966–998. [Google Scholar] [CrossRef]
- Carroni, E.; Madio, L.; Shekhar, S. Superstars exclusivity in two-sided markets. Manag. Sci. 2024, 70, 991–1011. [Google Scholar] [CrossRef]
- Li, Z.; Agarwal, A. Platform integration and demand spillovers in complementary markets: Evidence from Facebook’s integration of Instagram. Manag. Sci. 2016, 63, 3438–3458. [Google Scholar] [CrossRef]
- An, F.; Liu, G. Two-sided beneficial value-added service investment and pricing strategies in asymmetric/symmetric investment scenarios. Symmetry 2023, 15, 1246. [Google Scholar] [CrossRef]
- Kurvinen, M.; Toyryla, I.; Murthy, D.P. Warranty Fraud Management: Reducing Fraud and Other Excess Costs in Warranty and Service Operations; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Yoo, S.H.; Jung, D.; Park, K. Product design outsourcing in a supply chain: Impacts of the design and conformance quality trade-off. Oper. Res. 2021, 1, 4029–4055. [Google Scholar] [CrossRef]
- Harrington, J.E., Jr. The effect of outsourcing pricing algorithms on market competition. Manag. Sci. 2022, 68, 6889–6906. [Google Scholar] [CrossRef]
- Choi, T.; Wallace, S.; Wang, Y. Risk management and coordination in service supply chains: Information, logistic and outsourcing. J. Oper. Res. Soc. 2016, 67, 159–164. [Google Scholar] [CrossRef]
- Tsai, M.; Lai, K.; Lloyd, A.; Lin, H. The dark side of logistic outsourcing-unraveling the potential risks leading to failed relationships. Trans. Res. Part. E. 2012, 448, 178–189. [Google Scholar] [CrossRef]
- Liu, W.; Wang, D.; Shen, X.; Yan, X.; Wei, X. The impacts of distributional and peer-induced fairness concerns on the decision-making of order allocation in logistics service supply chain. Trans. Res. Part. E. 2018, 116, 102–122. [Google Scholar] [CrossRef]
- Zhang, S.; Dan, B.; Zhou, M. After-sale service deployment and information sharing in a supply chain under demand uncertainty. Euro. J. Oper. Res. 2019, 279, 351–363. [Google Scholar] [CrossRef]
- Doratiotto, K.; Vieira, J.; Silva, L.; Favero, L. Evaluating logistics outsourcing: A survey conducted with Brazilian industries. Benchmarking 2023, 30, 788–810. [Google Scholar] [CrossRef]
- Yang, C.; Bian, J.; Guo, X.; Jiang, W. Logistics outsourcing strategy with online freight platforms. Omega. 2024, 125, 103042. [Google Scholar] [CrossRef]
- Zhang, Y.; He, Z.; He, S.; Cai, K.; Wang, D. Manufacturer warranty service outsourcing strategies in a dual-channel supply chain. Int. Trans. Oper. Res. 2020, 27, 2899–2926. [Google Scholar] [CrossRef]
- Ullah, A.; Ayat, M.; He, Y.; Lev, B. An analysis of strategies for adopting blockchain technology in the after-sales service supply chain. Comp. Ind. Eng. 2023, 179, 109194. [Google Scholar] [CrossRef]
- Meng, L.; Xue, J.; Zhang, B.; Xia, H. Outsourcing or in-house: Remanufactured product warranty of independent remanufacture. Kybernetes 2024. [Google Scholar] [CrossRef]
- Hagiu, A.; Halaburda, H. Information and two-sided platform profits. Int. J. Ind. Org. 2014, 34, 25–35. [Google Scholar] [CrossRef]
- Zheng, R.; Shou, B.; Chen, Y. Differential pricing in social network with strategic consumers. Prod. Oper. Manag. 2023, 32, 2638–2655. [Google Scholar] [CrossRef]
- Dou, Y.; Zhang, X.; Wu, D. Intertemporal price competition in the two-sided market: Reexamining the seesaw principle for startup platforms. Prod. Oper. Manag. 2024, 10591478241245143. [Google Scholar] [CrossRef]
- Rebekka, K.; Birte, M.; Christian, H. A novel sustainable management tool for small and medium-sized food manufactures—Advantages and improvement opportunities. Man. Rev. 2024, 35, 35–65. [Google Scholar]
- Tang, Y.; Guo, P.; Tang, C.; Wang, Y. Gender-related operational issues arising from on-demand ride-hailing platforms: Safety concerns and system configuration. Prod. Oper. Manag. 2021, 30, 3481–3496. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).