GeoText: Geodesic-Based 3D Text Generation on Triangular Meshes

Abstract

Embedding text on 3D triangular meshes is essential for conveying semantic information and supporting reliable identification and authentication. However, existing methods often fail to incorporate the geometric properties of the underlying mesh, resulting in shape inconsistencies and visual artifacts, particularly in regions with high curvature. To overcome these limitations, we present GeoText, a framework for generating 3D text directly on triangular meshes while faithfully preserving local surface geometry. In our approach, the control points of TrueType Font outlines are mapped onto the mesh along a user-specified placement curve and reconstructed using geodesic Bézier curves. We introduce two mapping strategies—one based on a local tangent frame and another based on straightest geodesics—that ensure natural alignment of font control points. The reconstructed outlines enable the generation of embossed, engraved, or independent 3D text meshes. Unlike Boolean-based methods, which combine text meshes through union or difference and therefore fail to lie exactly on the surface—breaking the symmetry between embossing and engraving—our offset-based approach ensures a symmetric relation: positive offsets yield embossing, whereas negative offsets produce engraving. Furthermore, our method achieves robust text generation without self-intersections or inter-character collisions. These capabilities make GeoTextwell suited for applications such as 3D watermarking, visual authentication, and digital content creation.

1. Introduction

Visualization on 3D meshes plays a vital role in simulation and data analysis [1,2]. As the demand for 3D digital content increases, techniques such as embedding data into 3D models [3,4,5] and displaying information as text [6,7,8,9,10] have become essential in applications including augmented reality (AR) environments, digital watermarking, and model identification. A key challenge in these applications is embedding text while faithfully preserving the geometry of the underlying mesh.

A common approach projects a 2D binary font image (e.g., a bitmap) onto a locally flat region of the mesh [6,7]. This method is simple and direct but has notable drawbacks. First, the mesh must be locally subdivided to provide enough resolution to capture the font details. Second, it often causes distortion and visual artifacts on highly curved or complex surfaces. Third, because it depends on rasterized images, the resolution of the inserted text is scale-dependent, leading to aliasing or blurring.

To overcome these limitations, Dhiman et al. [8] and Li et al. [9] proposed generating 3D text meshes directly from vector-based font information. Specifically, Li et al. [9] employed TrueType Fonts (TTFs) [11], which define character outlines using Bézier curves. In their approach, points are sampled along the curves, and the front faces are constructed using Delaunay triangulation. The back faces are generated by duplicating the front faces with an offset along the z-axis, and the two regions are connected to form a closed 3D mesh. The resulting text mesh is then embedded into the target model through Boolean operations [12,13] such as union or difference. Although effective on smooth surfaces, Boolean embedding produces text that does not conform to the target surface geometry, resulting in flattened shapes on curved or intricate regions (Figure 1a).

Figure 1. Comparison of 3D text ‘B’ generation on the Bunny model using (a) Boolean operations and (b) our method.

In this paper, we propose a direct and geometry-aware method for generating 3D text on triangular meshes that overcomes these limitations. Our approach begins by projecting TrueType Font outlines onto the mesh along a user-defined geodesic curve [14], which naturally specifies the placement region. The outlines are then reconstructed on the mesh using geodesic Bézier curves [15] that conform to the underlying geometry. This process produces font outlines that adapt smoothly to complex and highly curved regions (Figure 1b). Moreover, our method is simpler and more efficient than Boolean-based workflows, which typically involve multiple complex stages such as intersection detection, mesh cutting, subshell identification, and subshell merging. These stages often introduce numerical instabilities and computational overhead, making Boolean-based approaches less efficient and error-prone compared to our method. As a result, computation time during embedding is significantly reduced. Finally, we introduce two mapping strategies—static and dynamic—that provide flexible text placement and support a wide range of applications, including embossing, engraving, and the generation of independent text meshes.

The main contributions of this paper are as follows:

• We propose a method that projects TrueType Font outlines onto triangular meshes using straightest geodesic vectors and reconstructs them with geodesic Bézier curves, enabling faithful text generation that conforms to the underlying geometry.
• We introduce two mapping strategies—static and dynamic. The static mapping considers only the mesh geometry, while the dynamic mapping incorporates the user-defined placement curve to allow flexible text placement and deformation.
• We present a simple and efficient framework that requires only three main steps—font outline extraction, outline mapping, and text generation—whereas Boolean-based approaches typically involve multiple complex operations.

This paper is organized as follows. Section 2 reviews prior work on text generation on meshes and geodesic-based techniques, with a focus on geodesic distance, straightest geodesics, and geodesic curves. Section 3 presents our method, which projects font outlines onto the mesh using two mapping strategies, reconstructs them with geodesic curves, and finally generates the 3D text. Section 4 addresses potential issues, including self-intersections within font outlines and collisions between neighboring characters. Section 5 presents our experimental results, a performance analysis, and examples of applications of the proposed method. Finally, Section 6 concludes the paper.

2. Related Work

The goal of our method is to generate 3D text directly on triangular meshes. To capture the geometric features of the surface, TrueType Font outlines are projected onto the mesh using straightest geodesics [16], and reconstructed with geodesic Bézier curves [15]. This section reviews prior studies related to our approach, with a focus on text generation on meshes and geodesic-based techniques such as geodesic distance, straightest geodesics, and geodesic curves on triangular meshes.

Cao et al. [6] projected locally flat regions of a mesh onto a 2D plane and mapped binary font images onto it. Similarly, Yan et al. [7] projected bitmap-based font images directly onto mesh surfaces. Both methods rely on 2D font data and are limited to flat regions, requiring local subdivision of the mesh to accommodate text details. Dhiman et al. [8] proposed generating 3D text meshes in real-time augmented reality (AR) environments by constructing text from contours derived from 2D curves. Li et al. [9] generated 3D text meshes by sampling TrueType Font (TTF) outlines and applying constrained Delaunay triangulation. The resulting meshes were embedded into target models using Boolean operations such as union and difference. However, Boolean-based methods are mostly restricted to planar surfaces and often fail on highly curved or complex regions. More recently, Singh et al. [10] proposed a learning-based approach for embedding text watermarks, where a trained network predicts embedding locations. Although effective on simple models, this method demands heavy computation and shows limited accuracy on complex models due to restricted training diversity.

Euclidean distance is defined as the length of a straight line between two points, whereas geodesic distance is the shortest path constrained to a mesh surface. Many algorithms have been proposed to improve its efficiency and accuracy. The MMP algorithm by Mitchell et al. [17] and the CH algorithm by Chen et al. [18] are classical methods, with time complexities of $O(n^{2}logn)$ and $O\left(n^2\right)$, respectively. Bommes et al. [19] introduced a window propagation approach that incrementally expands distances from a source point. Tang et al. [20] proposed an approximation that places virtual sources on a 2D plane for each triangle and propagates distances to the vertices. Trettner et al. [21] improved efficiency through virtual propagation with CPU and GPU parallelization while keeping memory costs low. Sharp et al. [22] developed an edge-flip algorithm for geodesic path computation, and Li et al. [23] proposed a distance function guaranteeing $C^2$ continuity. Among these options, we adopt an approximation algorithm [20,21] to support user interaction.

The concept of Bézier curves has been extended to mesh domains using geodesic distance. Park et al. [24] generalized Bézier curves to Riemannian manifolds, and Morera et al. [15] developed geodesic Bézier curves for triangular meshes by replacing Euclidean interpolation in the de Casteljau algorithm with geodesic interpolation. Ha et al. [14] further extended this idea to geodesic Hermite splines, enabling smooth and continuous curves with accurate interpolation of given points on meshes. Polthier et al. [16] introduced the concept of straightest geodesics, which differ from shortest-path geodesics. A straightest geodesic is defined by a starting point and a direction vector; it coincides with a standard geodesic along edges but minimizes curvature when passing through vertices. In our method, we adopt straightest geodesics to project font outlines onto the mesh and reconstruct them with geodesic Bézier curves, enabling effective 3D text generation that conforms to the underlying mesh geometry.

3. Three-Dimensional Text Generation on Triangular Meshes

The overall pipeline for generating 3D text on triangular meshes comprises three main steps: (i) extracting font outline information, (ii) mapping the outlines onto the mesh, and (iii) generating the final 3D text. Figure 2 illustrates this process.

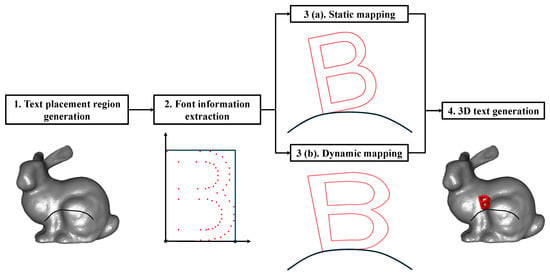
Figure 2. Pipeline of the proposed framework, consisting of three stages: font outline extraction, outline mapping, and 3D text generation.

3.1. Extraction of Font Outlines

TrueType Fonts (TTFs) [11] are a vector-based font format in which each character outline is represented by closed contours consisting of linear segments $L\left(t\right)$ and quadratic Bézier curves $C\left(t\right)$. They are defined as follows:

$$\begin{array}{cc}\hfill L\left(t\right)& =(1-t){\mathbf{p}}_0+t{\mathbf{p}}_1,\hfill \\ \hfill C\left(t\right)& ={(1-t)}^2{\mathbf{p}}_0+2t(1-t){\mathbf{p}}_1+t^2{\mathbf{p}}_2,\hfill \end{array}$$

(1)

where $t\in [0,1]$ and ${\mathbf{p}}_i\in {\mathbb{R}}^2$ are control points. We extract font outlines using the FreeType library [25], which provides the 2D control points for each linear and quadratic segment (Figure 3). Each segment is then uniformly sampled with respect to the parameter t, and connecting the sampled points sequentially forms a closed polyline that represents the original outline (Figure 3c). Since the raw coordinates obtained from FreeType are not normalized, each outline is uniformly scaled so that the horizontal length of its bounding box is set to one. After normalization, the x-coordinates of all control points lie within $[0,1]$ (Figure 3a), ensuring consistent sizing across different characters.

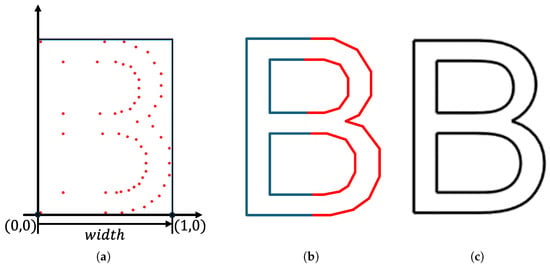
Figure 3. Example of font outline extraction from the FreeType library: (a) control points of linear and quadratic segments; (b) control polygons of $L\left(t\right)$ (in blue) and $C\left(t\right)$ (in red); (c) reconstructed font outline from (b).

3.2. Mapping Font Outlines onto Mesh

In our method, the text placement region on a mesh is defined by a user-specified geodesic curve $D\left(t\right)$ [14]. The curve is created interactively by selecting a sequence of points on the mesh surface. These points are connected by geodesic paths, and the resulting polyline is interpolated into a smooth geodesic curve. In practice, this enables users to sketch the desired trajectory of the text on the mesh by clicking a series of points. The control points ${\mathbf{p}}_i$ defining each character outline are then distributed along a parameter interval $[t_s,t_e]\subset [0,1]$ of the curve $D\left(t\right)$. A local coordinate frame is constructed along the curve to support text alignment and deformation, and each control point is subsequently mapped onto the mesh using one of two mapping strategies.

3.2.1. Local Tangent Frames

Given the mapping interval $[t_s,t_e]$, we first compute a local tangent frame $F\left(t_s\right)=\{\mathbf{T}\left(t_s\right),\mathbf{N}\left(t_s\right)\}$ at the point $D\left(t_s\right)$. This frame serves as the local coordinate system for text placement (Figure 4) and is defined as follows:

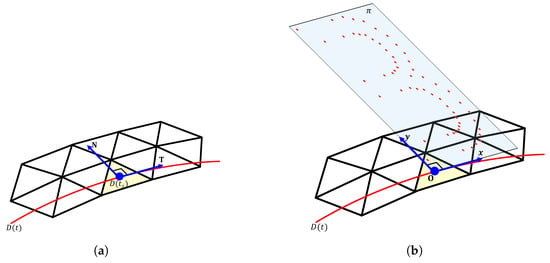
Figure 4. (a) Local tangent frame constructed at $D\left(t_s\right)$. (b) Control points represented in the local coordinate system, lying on plane $\pi$.

• $\mathbf{T}\left(t_s\right)$: the tangent vector at $D\left(t_s\right)$, used as the local x-axis.
• $\mathbf{N}\left(t_s\right)$: the normal vector obtained by rotating $\mathbf{T}\left(t_s\right)$ by ${90}^{\circ }$ around the triangle normal $\overrightarrow{n}$ at $D\left(t_s\right)$, used as the local y-axis.

Since $\mathbf{T}\left(t_s\right)$, $\mathbf{N}\left(t_s\right)$, and $D\left(t_s\right)$ lie on the same triangle of the mesh, all control points expressed in this local coordinate system lie on a plane $\pi$ (Figure 4b) given by

$$\pi :\overrightarrow{n}·(\mathbf{q}-D\left(t_s\right))=0,\mathbf{q}\in {\mathbb{R}}^3.$$

(2)

3.2.2. Mapping Strategies

We propose two mapping methods for projecting each control point ${\mathbf{p}}_i=(x_i,y_i)$ in Equation (1) onto the mesh surface. The first method, referred to as static mapping, maps each control point onto the mesh while preserving its relative position in the local tangent frame $F\left(t_s\right)$. Each control point ${\mathbf{p}}_i=(x_i,y_i)$ is scaled to ${\widehat{\mathbf{p}}}_i=(d_g{x}_i,d_g{y}_i)$ using a scaling factor $d_g$, the geodesic distance between $D\left(t_s\right)$ and $D\left(t_e\right)$, which controls the overall text size. The point ${\widehat{\mathbf{p}}}_i$ is then mapped onto the mesh by tracing a straightest geodesic vector ${\overrightarrow{v}}_i=(d_g{x}_i,d_g{y}_i)$ from $D\left(t_s\right)$, as described in [16] (see Figure 5).

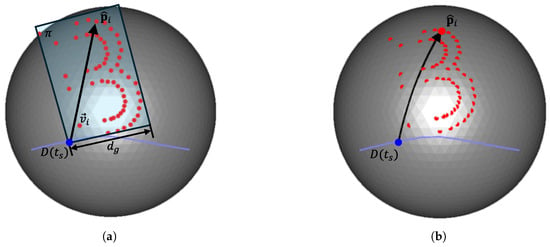
Figure 5. Example of static mapping: (a) vector ${\overrightarrow{v}}_i$ from $D\left(t_s\right)$ to ${\widehat{\mathbf{p}}}_i$ in plane $\pi$; (b) the corresponding straightest geodesic from $D\left(t_s\right)$ on the mesh surface.

The second method, referred to as dynamic mapping, incorporates both the target mesh and the placement curve $D\left(t\right)$. Since the x-coordinate $x_i$ of each control point ${\mathbf{p}}_i=(x_i,y_i)$ is normalized to the interval $[0,1]$, it can be directly used as a curve parameter $t_i$ over the mapping interval $[t_s,t_e]$ as follows:

$$t_i=(1-x_i)t_s+x_i{t}_e,x_i\in [0,1].$$

(3)

A local tangent frame $F\left(t_i\right)=\{\mathbf{T}\left(t_i\right),\mathbf{N}\left(t_i\right)\}$ is computed at the point $D\left(t_i\right)$, and the corresponding control point ${\mathbf{p}}_i=(x_i,y_i)$ is mapped to the point ${\widehat{\mathbf{p}}}_i=(0,y_{i}L)$ on $F\left(t_i\right)$ (see Figure 6). Here, L, defined by

$$L={\int }_{t_s}^{t_e}∥D^{\prime }\left(t\right)∥dt,$$

(4)

denotes the arc length of the curve $D\left(t\right)$ over the interval $[t_s,t_e]$ and controls the overall text size. Finally, similarly to the static mapping method, the point ${\widehat{\mathbf{p}}}_i$ is mapped onto the mesh by tracing the straightest geodesic vector ${\overrightarrow{v}}_i=(0,y_{i}L)$ starting from $D\left(t_i\right)$ (see Figure 6).

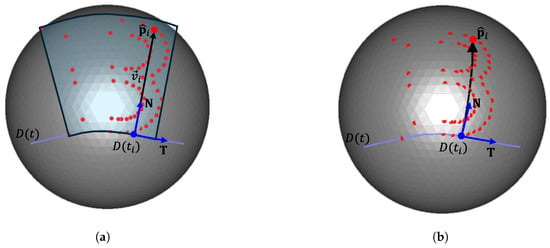
Figure 6. Example of dynamic mapping: (a) vector ${\overrightarrow{v}}_i$ from $D\left(t_i\right)$ to ${\widehat{\mathbf{p}}}_i$ in the local tangent frame; (b) the corresponding straightest geodesic from $D\left(t_i\right)$ on the mesh surface.

The dynamic mapping strategy enables more flexible deformation of character shapes by adapting to the placement curve $D\left(t\right)$. However, it may also introduce challenges such as self-intersections within the generated outlines, which are further discussed in Section 4.

3.3. Three-Dimensional Text Generation

As described in Section 3.1, font outlines are composed of multiple Bézier curves. To represent these outlines on the mesh, each curve is uniformly sampled to produce a closed polyline. Instead of linear interpolation in Euclidean space, we employ geodesic interpolation, which naturally embeds the outlines onto the mesh surface. Specifically, we adopt the geodesic de Casteljau algorithm [15], which recursively interpolates between control points along surface geodesics, as shown in Algorithm 1. This extends the classical de Casteljau algorithm from Euclidean space to triangular meshes, ensuring that the resulting curve lies on the underlying mesh and faithfully reflects its geometric features. The operator glerp(a,b,t) returns the point interpolated by the parameter t along the geodesic path between two points, $\mathbf{a}$ and $\mathbf{b}$, on the mesh. The resulting geodesic Bézier curves are then uniformly sampled to generate a closed polyline (Figure 7). The resulting polyline serves as the cutting boundary for mesh segmentation, following the triangle-cutting strategy [26] (Figure 8b). From this process, the following geometric elements are obtained (Figure 8c):

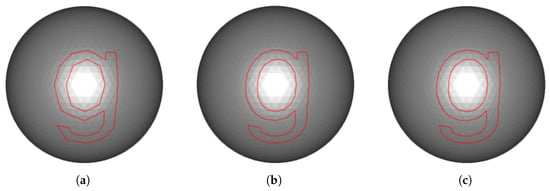
Figure 7. Comparison of the sampled curves of character ‘g’ on a sphere using (a) two, (b) three, and (c) four samples per curve.

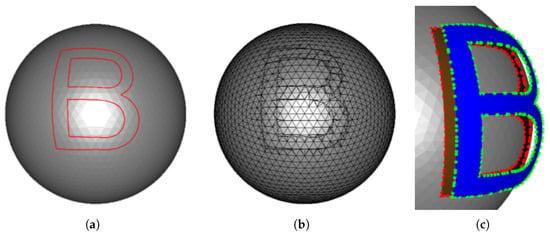
Figure 8. Outline-based mesh segmentation for the character ‘B’: (a) the outline generated by geodesic Bézier curves; (b) the mesh trimmed along the outline in (a); (c) the final result after trimming, where blue faces represent $T_F$ and red–green vertex pairs indicate $V_{pair}$.

• $T_F$: the set of triangles enclosed by the polyline,
• $V_{pair}$: the set of vertex pairs introduced along the cut boundary.

Algorithm 1 Geodesic de Casteljau [15]

Require:  Control points $\{{\mathbf{p}}_0^{\left(0\right)},{\mathbf{p}}_1^{\left(0\right)},\dots ,{\mathbf{p}}_n^{\left(0\right)}\}$ on the mesh surface, parameter $t\in [0,1]$ Ensure:  $C\left(t\right)$, the point on the geodesic Bézier curve at parameter t   1: for$i=1,\dots ,n$do   2:      for $j=0,\dots ,n-i$  do   3:         ${\mathbf{p}}_j^{\left(i\right)}\leftarrow \mathtt{glerp}\left({\mathbf{p}}_j^{(i-1)},{\mathbf{p}}_{j+1}^{(i-1)},t\right)$   4:      end for   5: end for   6: return$C\left(t\right)\leftarrow {\mathbf{p}}_0^{\left(n\right)}$

Depending on the desired output, the 3D text can be generated in one of two ways:

• Embedding onto the mesh surface: To generate embossed or engraved text, the triangles in $T_F$ are displaced along their average normal direction by a user-defined offset $d_{offset}$. Positive values $(+d_{offset})$ yield embossing, while negative values $(-d_{offset})$ yield engraving. The side surfaces are constructed by connecting the vertex pairs in $V_{pair}$, resulting in a closed 3D text region that conforms to the underlying mesh surface (Figure 9).
  

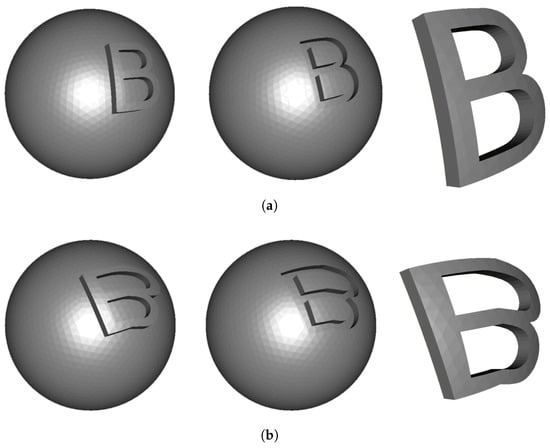  Figure 9. Examples of 3D text generation using (a) static mapping and (b) dynamic mapping, illustrating embossing, engraving, and independent text meshes.
• Generating an independent text mesh: To construct an isolated text mesh, the set $T_F$ is used as the front face. The back face is generated by duplicating and offsetting the front face by $d_{offset}$ along the average normal direction, with assigned reversed normals. Finally, boundary vertex pairs between the two faces are connected to form the side faces, producing a watertight 3D text mesh that reflects the geometric features of the surface (Figure 9).

4. Avoiding Self-Intersections and Inter-Character Collisions

In Section 3, we introduced two mapping strategies for embedding text on a mesh. Although these strategies effectively generate outlines that conform to the underlying surface geometry, the shape of the user-defined placement curve $D\left(t\right)$ can still induce intersection artifacts. We consider two cases: (i) self-intersections within a single character (glyph) outline (Figure 10); and (ii) inter-character collisions when adjacent characters are placed in close proximity along $D\left(t\right)$ (Figure 11). This section addresses these issues to ensure robust and visually consistent text insertion.

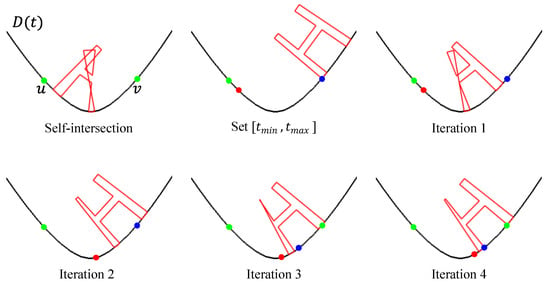
Figure 10. Self-intersection avoidance by interval refinement via binary search. Green points indicate the self-intersection interval $[u,v]$ where self-intersection occurs. Red and blue points denote the bracketing parameters $[t_{min},t_{max}]$. When self-intersection occurs at the midpoint, $t_{min}$ is updated; otherwise, $t_{max}$ is updated while conforming to the geometric features.

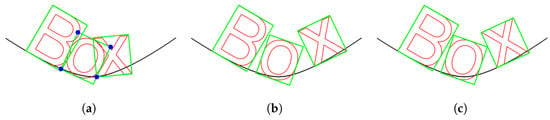
Figure 11. Detection and resolution of inter-character collisions using linear search. (a) Collision example: green boxes indicate oriented bounding boxes (OBBs), and blue points denote vertices with a winding number of one relative to another OBB. (b,c) Linear search results with different step sizes, $\Delta t=0.01$ and $\Delta t=0.005$, respectively. Smaller step sizes improve the accuracy of collision detection and resolution, ensuring that characters remain separated while conforming to the underlying surface.

4.1. Self-Intersections of Font Outlines

In the dynamic mapping strategy, each control point of a font outline is mapped onto the mesh using the corresponding normal vector $\mathbf{N}\left(t_i\right)$ of the placement curve at the point $D\left(t_i\right)$. However, when integral curves of the normal field $\left\{\mathbf{N}\left(t_i\right)\right\}$ intersect, the resulting outline may exhibit self-intersections, leading to undesirable shape distortions (Figure 10). This issue can be analyzed in terms of the offset curve $O\left(t\right)$, defined as the placement curve $D\left(t\right)$ shifted by a text height h along its unit normal direction:

$$O\left(t\right)=D\left(t\right)+h{\displaystyle \frac{\mathbf{N}\left(t\right)}{\parallel \mathbf{N}\left(t\right)\parallel }}.$$

(5)

A self-intersection of the offset curve $O\left(t\right)$ occurs when

$$h>{\displaystyle \frac{1}{\left|\kappa \right(t\left)\right|}},$$

(6)

where $\kappa \left(t\right)$ denotes the curvature of the curve $D\left(t\right)$. This condition highlights that on curves with high curvature, offset curves are prone to self-intersection. One possible strategy is to restrict the text height h, but this reduces flexibility in text design. In contrast, our algorithm automatically adjusts the mapping interval based on this condition, thereby avoiding self-intersections without imposing explicit constraints on h. More generally, a self-intersection interval $[u,v]$ can be identified by solving

$$D\left(u\right)+h·{\displaystyle \frac{\mathbf{N}\left(u\right)}{\parallel \mathbf{N}\left(u\right)\parallel }}=D\left(v\right)+h·{\displaystyle \frac{\mathbf{N}\left(v\right)}{\parallel \mathbf{N}\left(v\right)\parallel }},u\ne v.$$

(7)

If the mapping interval $[t_s,t_e]$ overlaps with a self-intersection interval $[u,v]$, i.e., $[t_s,t_e]\cap [u,v]\ne ⌀$, the projected control points may induce self-intersections in the font outlines. However, as illustrated in Figure 10, such overlap does not necessarily lead to intersections, since the outcome depends on both the font shape and the geometry of the curve.

To mitigate this problem, we determine an optimal mapping interval for the control points. Specifically, if self-intersection occurs in the initial interval $[t_s,t_e]$, the start parameter $t_s^{\ast }$ is refined via binary search within the range $[t_{min},t_{max}]=[t_s,v]$. Here, $t_{min}$ denotes the largest parameter value at which self-intersection still occurs, and $t_{max}$ denotes the smallest parameter value at which no intersection is observed. The binary search iteratively updates $[t_{min},t_{max}]$ until the following termination condition is satisfied:

$$|t_{max}-t_s^{\ast }|<\epsilon .$$

(8)

Finally, the corresponding end parameter $t_e^{\ast }$ is determined by preserving the curve length:

$$L(t_s,t_e)=L(t_s^{\ast },t_e^{\ast }).$$

(9)

4.2. Inter-Character Collisions

In addition to the self-intersection problem discussed in Section 4.1, collisions between adjacent character outlines may also occur when multiple characters are placed along the curve $D\left(t\right)$. Unlike self-intersections, such collisions can occur under both static and dynamic mapping strategies. To detect collisions, each outline is enclosed by an oriented bounding box (OBB) (Figure 11). Collision detection between two OBBs is performed by evaluating winding numbers [27]. The winding number $W(\gamma ,\mathbf{q})$ measures how many times a closed curve $\gamma$ winds around a point $\mathbf{q}$. For a bounding box B, it is defined as

$$W(B,\mathbf{q})=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathbf{q}\in \mathrm{interior}\left(B\right),\hfill \\ 0,\hfill & \mathrm{if}\mathbf{q}\in \mathrm{exterior}\left(B\right).\hfill \end{array}\right.$$

(10)

Given two bounding boxes, $B_i$ and $B_j$, with vertex sets $V\left(B_i\right)=\{{\mathbf{q}}_1^i,{\mathbf{q}}_2^i,{\mathbf{q}}_3^i,{\mathbf{q}}_4^i\}$ and $V\left(B_j\right)=\{{\mathbf{q}}_1^j,{\mathbf{q}}_2^j,{\mathbf{q}}_3^j,{\mathbf{q}}_4^j\}$, we evaluate $W(B_i,{\mathbf{q}}^j)$ for ${\mathbf{q}}^j\in V\left(B_j\right)$, and $W(B_j,{\mathbf{q}}^i)$ for ${\mathbf{q}}^i\in V\left(B_i\right)$. A collision is reported if at least one vertex satisfies $W(B,\mathbf{q})=1$, implying that the corresponding character outlines overlap.

When placing characters sequentially along $D\left(t\right)$, the OBB of each new character is checked against those of previously placed ones. If a collision is detected, the mapping interval of the new character is shifted forward. Specifically, for the k-th character with interval $[t_s^k,t_e^k]$, we update

$$t_s^k\leftarrow t_s^k+\Delta t,$$

(11)

until the non-overlapping condition

$$B_{k-1}\cap B_k=⌀,$$

(12)

is satisfied. In practice, the step size $\Delta t$ is initialized with a small value and adaptively increased when a collision is detected, or decreased when no collision occurs. This incremental adjustment ensures that each newly placed character is positioned further along the curve in the presence of collisions while allowing tighter placement otherwise, thereby preserving visual clarity in the generated text.

5. Experimental Results

The proposed method was implemented in C++17 on a desktop system with an Intel Core i9-14900K CPU, 64 GB of RAM, and an NVIDIA RTX 4060 Ti GPU running Windows 11. Outline information was extracted from TrueType Fonts using the FreeType library (version 2.14.1) [25]. The static and dynamic mapping methods described in Section 3 were parallelized on the CPU. Table 1 summarizes the properties of the target 3D meshes, and Table 2 lists the font properties of the test characters (Arial).

Table 1. Properties of the 3D models used in the experiments.

Model	Box	Bunny	Armadillo	Pumpkin
# of vertices	1538	8327	172,974	165,701
# of triangles	3026	16,650	345,955	331,398
Feature	Sharp features	Smooth surfaces	Noisy surface	High curvature with noise

Table 2. Properties of the character outlines extracted from the Arial font.

Character	B	L	O
# of control points	60	6	42
Outline type	Composite outline	Line segments only	Curves only
Control-point extraction time (ms)	0.764	0.342	0.498

5.1. Results of 3D Text Generation

Our method provides intuitive control over both the placement and the shape of 3D text through a user-specified placement curve. In the static mapping strategy, the placement curve is embedded directly on the mesh, and the resulting text conforms to local geometric features without noticeable distortion. In contrast, the dynamic mapping strategy adapts the character shapes to both the underlying mesh and the placement curve, enabling more flexible and expressive deformations.

Figure 12 illustrates the results obtained with static mapping, where text is generated robustly on smooth surfaces, sharp edges, and complex geometries such as regions with high curvature or noise. Figure 13 presents the results of dynamic mapping, where the character shapes smoothly adapt to the placement curve and exhibit diverse expressive deformations. As shown in Figure 14, long text strings can also be generated by sequentially arranging multiple characters along the curve, without causing intersection artifacts.

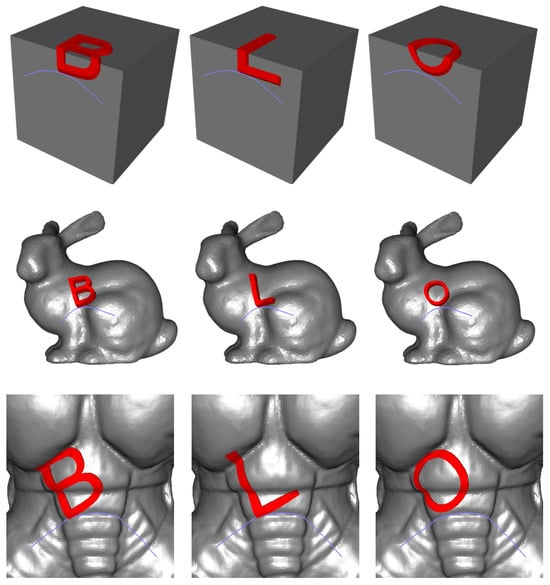
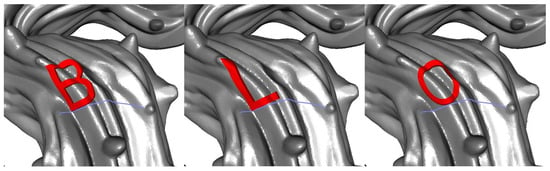
Figure 12. Examples of 3D text generation using the static mapping strategy on the Box, Bunny, Armadillo, and Pumpkin models.

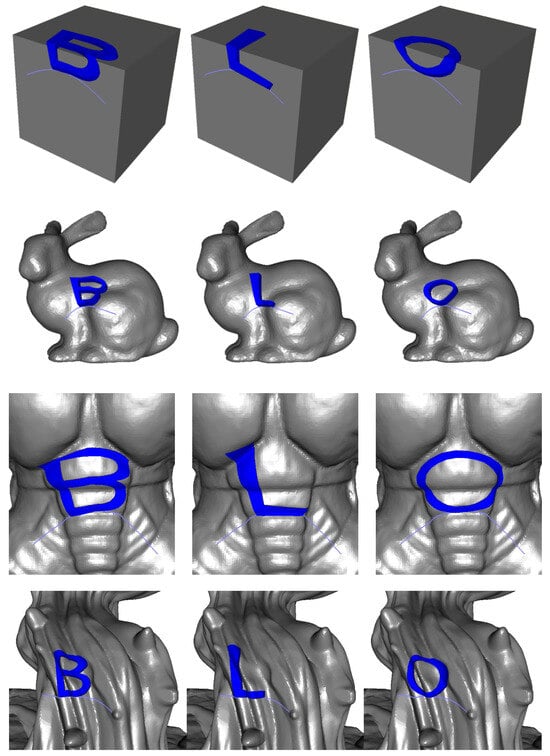
Figure 13. Examples of 3D text generation using the dynamic mapping strategy on the Box, Bunny, Armadillo, and Pumpkin models.

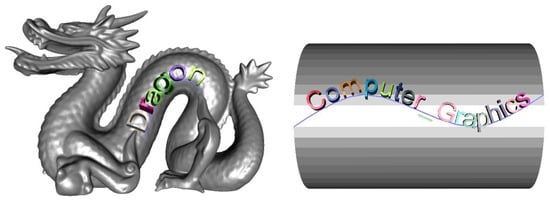
Figure 14. Generation of long text strings by sequentially arranging characters along a placement curve.

As shown in Figure 15, our method also supports a wide range of complex TrueType Fonts and robustly generates their contours. In general, TrueType Fonts define outer contours in a clockwise orientation and inner contours in a counter-clockwise orientation. However, certain fonts intentionally deviate from this convention for stylistic purposes, which may lead to unintended results. This limitation suggests the need for further investigation in future work.

Figure 15. Outlines of the character ‘B’ in various fonts (top row) and the corresponding 3D text mesh results (bottom row). Red lines indicate outer contours, while blue lines represent inner contours.

5.2. Performance Analysis

Table 3 reports the computation time required for each stage of 3D text generation on the Bunny model. The pipeline is divided into three stages: (i) outline mapping, (ii) geodesic curve generation, and (iii) 3D text generation. The total execution time is the sum of these stages. All experimental settings, including placement curves, text sizes, and positions, were kept consistent.

Table 3. Computation time (ms) for generating each character on the Bunny model.

Character	B		L		O
Mapping	Static	Dynamic	Static	Dynamic	Static	Dynamic
Outline mapping	3	6	3	4	2	4
Curve generation	2	3	1	1	1	2
Text generation	19	20	15	15	17	17
Total	24	29	19	20	20	23

For the same character, dynamic mapping consistently requires more time than static mapping. This additional cost primarily arises from computing local tangent frames for every control point, whereas static mapping computes it only once. By contrast, the times required for geodesic curve generation and 3D text creation show negligible differences between the two methods. Within the same mapping strategy, the outline mapping time generally decreases as the number of control points decreases. However, for characters with very few control points (e.g., ‘L’), the parallelization overhead becomes dominant, resulting in increased execution time. This issue could be alleviated by introducing adaptive scheduling strategies that selectively disable parallelization for simple cases.

Table 4 reports the elapsed times for generating character ‘B’ on the target meshes listed in Table 1. Across all mesh complexities, dynamic mapping requires more computation than static mapping. The difference is negligible for relatively simple models such as Box and Bunny, but becomes pronounced for more complex geometries such as the Armadillo and Pumpkin models.

Table 4. Computation time (ms) for generating the character ‘B’ on the models listed in Table 1.

Model	Box		Bunny		Armadillo		Pumpkin
Mapping	Static	Dynamic	Static	Dynamic	Static	Dynamic	Static	Dynamic
Outline mapping	2	3	5	9	90	160	84	150
Curve generation	2	2	3	3	71	70	75	76
Text generation	7	7	20	21	532	530	527	525
Total	11	12	28	33	693	760	686	751

Table 5 and Table 6 report the computation time for embedding the string “GeoText” into different models using static and dynamic mapping, respectively. In the static mapping case, the average time for resolving inter-character collisions (Avg. collision) is reported, while in the dynamic mapping case, the average time for handling character self-intersections (Avg. self-int.) is included. In both cases, the overall execution time increases with the number of vertices and faces in the target mesh, as the amount of geodesic distance computation grows accordingly. It is also observed that text generation dominates the total execution time for large and complex models (e.g., Armadillo and Pumpkin).

Table 5. Computation time (ms) for generating the string “GeoText” using static mapping on the models in Table 1.

Model	Box	Bunny	Armadillo	Pumpkin
Avg. collision	12	46	485	440
Outline mapping	9	24	280	219
Curve generation	8	10	335	333
Text generation	57	159	4950	4852
Total	86	239	6050	5844

Table 6. Elapsed time (ms) for generating the string “GeoText” using dynamic mapping on the models in Table 1.

Model	Box	Bunny	Armadillo	Pumpkin
Avg. self-int.	5	75	581	353
Avg. collision	15	40	832	758
Outline mapping	10	40	347	352
Curve generation	9	11	335	314
Text generation	66	162	5211	5174
Total	104	328	7306	6951

To quantitatively evaluate geometric accuracy, we conducted an experiment using a sphere of radius 5. As shown in Figure 16, the Gaussian curvature of the underlying sphere surface ($\kappa =1/25=0.04$, green line) was compared with that of the vertices of the embedded text region (red dots). Boundary vertices were excluded from the evaluation because their local neighborhoods degenerate into half-discs during curvature estimation, leading to inconsistent values. The results in Figure 16b demonstrate that the curvature in the embedded region closely matches the curvature of the underlying mesh, with only minor deviations due to numerical computation. This confirms that the proposed method effectively preserves the curvature of the underlying mesh when generating 3D text.

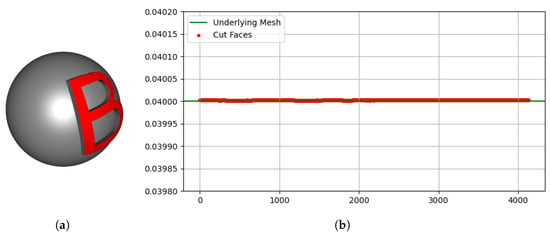
Figure 16. Comparison of Gaussian curvature between the underlying sphere and the embedded text region: (a) the sphere mesh with the embedded character ‘B’ in red; (b) a curvature comparison graph, where the x-axis represents the ordered vertex indices within the embedded region, and the y-axis indicates the corresponding Gaussian curvature values.

As shown in Figure 17, our method differs significantly from the Boolean-based approach [12,13] in terms of both performance and visual quality. The Boolean method requires constructing a text mesh and performing Boolean operations with the target mesh, which is computationally expensive. While the performance gap is small for short text strings, it increases rapidly as the number of characters grows.

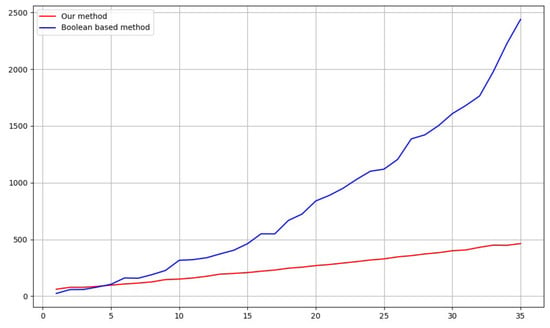
Figure 17. Comparison of computation time between the Boolean-based method and our method. The x-axis shows the number of characters, and the y-axis indicates the computation time (ms).

5.3. Applications

Our method has potential applications in digital security, copyright protection, and digital content creation. One notable application is 3D digital watermarking [4]. Text can be directly embedded on a 3D model as a visible annotation (Figure 18a), thereby explicitly conveying model ownership while also serving as a design element. In addition, by refining the mesh surface using geodesic Bézier curves that approximate the character outlines, invisible watermarks can be embedded without altering the apparent geometry (Figure 18b). This enables copyright protection while preserving the visual fidelity of the model.

Figure 18. Watermarking of the text “DGU” on the Buddha model: (a) visible surface watermarking; (b) invisible watermarking via mesh refinement (wireframe view).

In addition, the generated 3D text meshes can be used in human–bot authentication systems such as CAPTCHAs. Traditional CAPTCHAs rely on 2D text, whereas extending them to the 3D domain introduces additional complexity that remains intuitive for human users but challenging for automated recognition systems [28] (see Figure 19). In particular, rendering text on curved surfaces, adding surface noise, and introducing viewpoint variations pose additional challenges to AI-based recognition.

Figure 19. Examples of 3D CAPTCHAs: (a) CAPTCHA representing the string “A2fNee”; (b) CAPTCHA representing the string “5xEecD”.

Finally, our method is applicable to digital content creation, including product design, online advertising, real-time augmented reality (AR), and video games, where 3D models often require embedded text for branding, interaction, or aesthetic purposes. Current 3D modeling software such as Blender provides embedding through features like the shrinkwrap modifier [29]. However, as shown in Figure 20a, this approach can be unintuitive on complex models and may introduce noticeable distortions, degrading text readability and visual consistency. In contrast, our method allows users to intuitively define text insertion regions via a freeform curve on the model and ensures natural, undistorted text even on complex geometries (Figure 20b). This capability supports more accurate and expressive visual representations across diverse digital content applications.

Figure 20. Insertion of the text “Hand” on the hand of the Armadillo model: (a) using the shrinkwrap modifier in Blender; (b) using the proposed method.

6. Conclusions

This paper presents a framework for generating 3D text on triangular meshes. The method extracts control points from TrueType Font outlines and projects them onto the target mesh along a user-defined geodesic curve using two mapping strategies: static and dynamic. By employing geodesic Bézier interpolation instead of conventional linear interpolation, the generated text conforms more faithfully to the underlying surface features, enabling robust and visually coherent embeddings even on complex, high-curvature meshes. In addition, potential issues during text arrangement—such as self-intersections of font outlines and collisions between adjacent characters—were addressed through offset-curve analysis and winding-number-based collision detection on discrete surfaces. The framework supports both text embedding on meshes via engraving and embossing, as well as the generation of independent 3D text meshes.

Our experimental results show that, although dynamic mapping incurs higher computational cost than static mapping, it offers greater flexibility by adapting not only to the geometric features of the mesh but also to the shape of the placement curve. To verify that the generated 3D text reflects the geometric properties of the underlying mesh, we compared the Gaussian curvature of the embedded text with that of the mesh, confirming that the method faithfully preserves these features. Compared with Boolean-based methods, the proposed approach enables stable and efficient text generation without distortion. These capabilities make the method applicable to security-related tasks such as digital 3D watermarking and 3D CAPTCHA, as well as to digital content creation in domains including online advertising, augmented reality (AR), and video games.

In future work, we aim to further improve the robustness and efficiency of the framework. First, enhancing compatibility with diverse font specifications and handling irregular glyph topologies remain important directions. Second, we plan to explore more accurate and efficient computation techniques, including GPU acceleration, to enable real-time applications with an intuitive user interface (UI). For supplementary visual demonstrations, please refer to the accompanying video available at https://youtu.be/4-y2DitqcvY (accessed on 8 October 2025).