Performance Prediction of Air Source Heat Pumps Under Cold and Hot Ambient Temperatures Using ANFIS and ANN Models
Abstract
1. Introduction
2. Materials and Methods
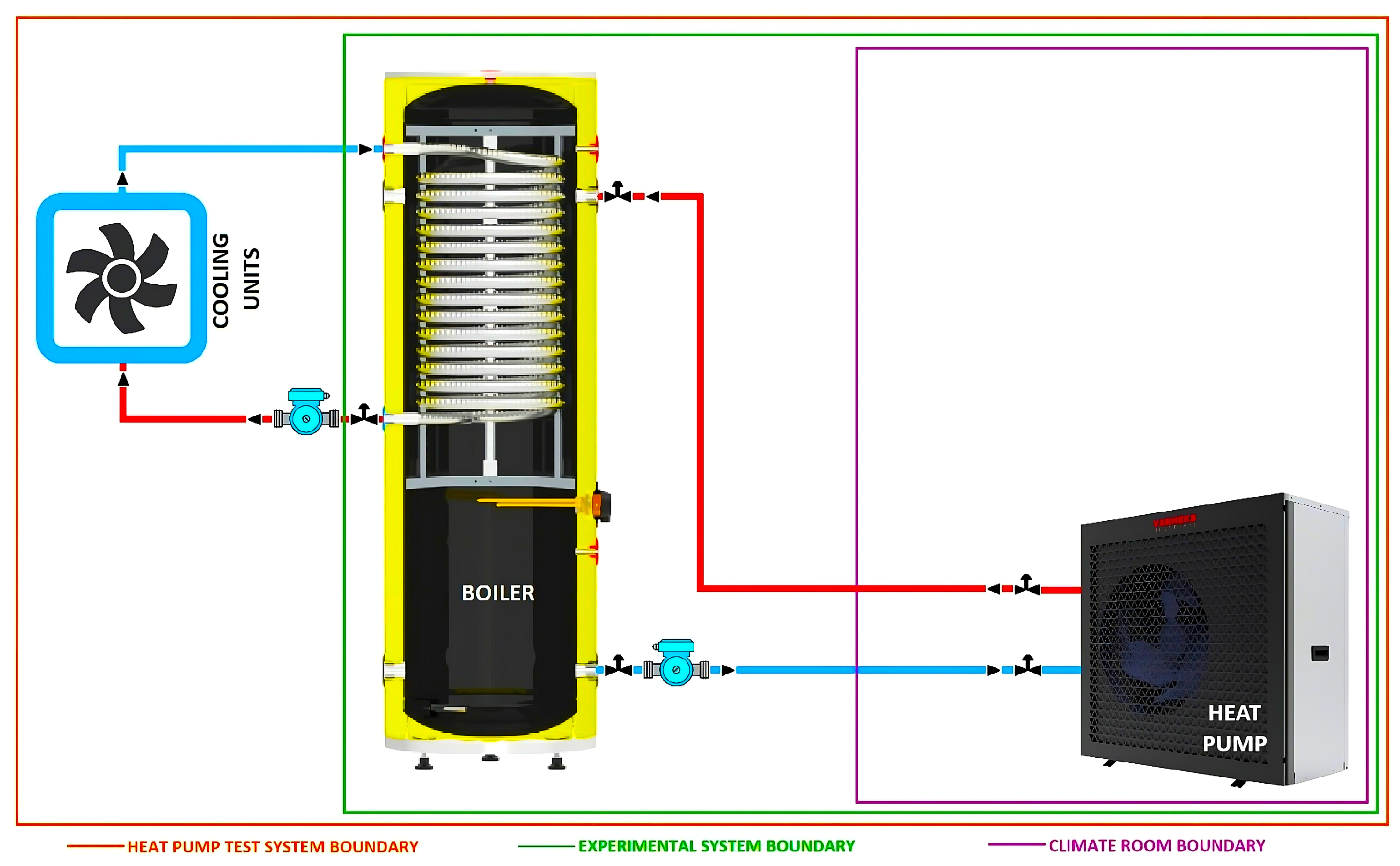
2.1. Experimental Setup and Campaigns
2.1.1. Experimental Setup
2.1.2. Experimental Campaigns
2.2. ANN and ANFIS Models
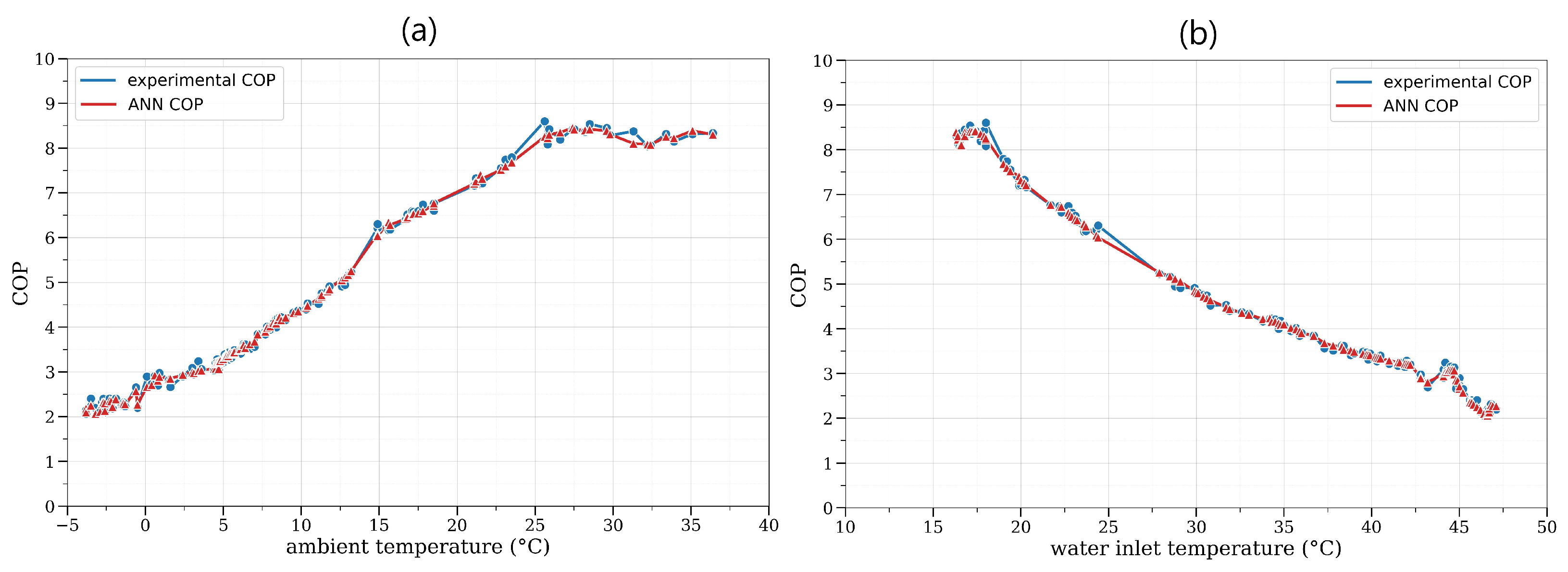
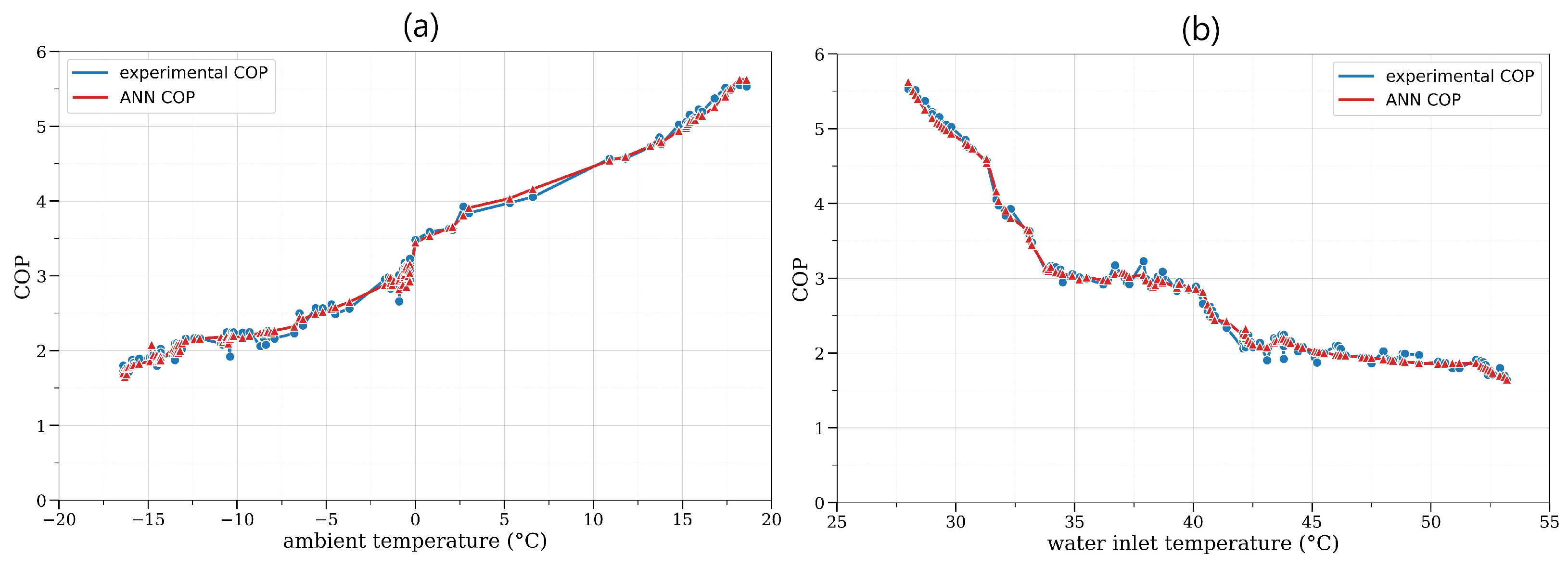
2.2.1. ANN Model
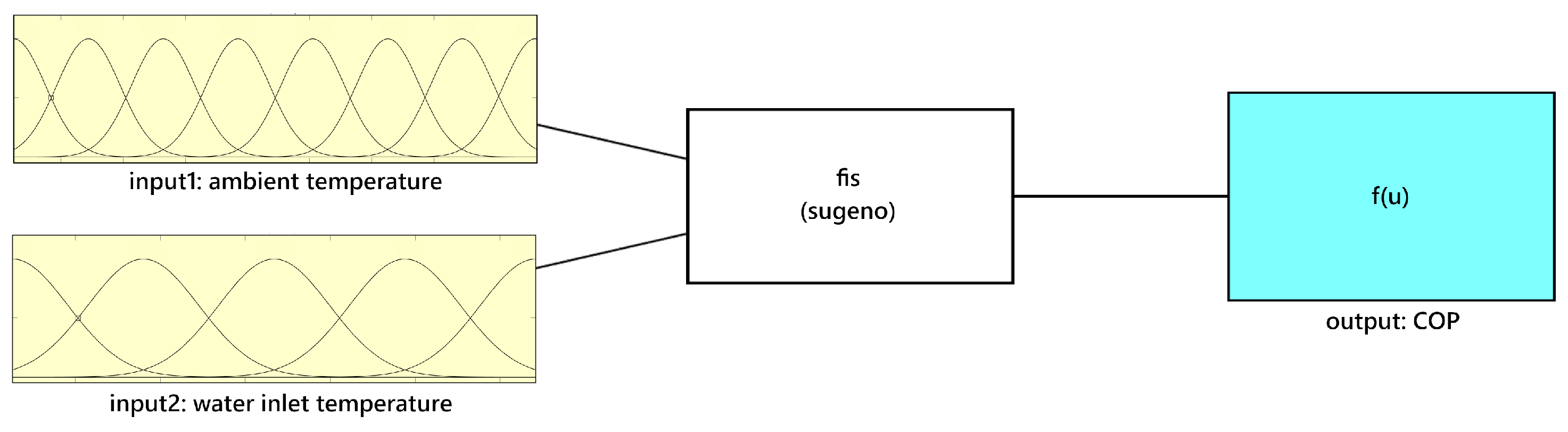
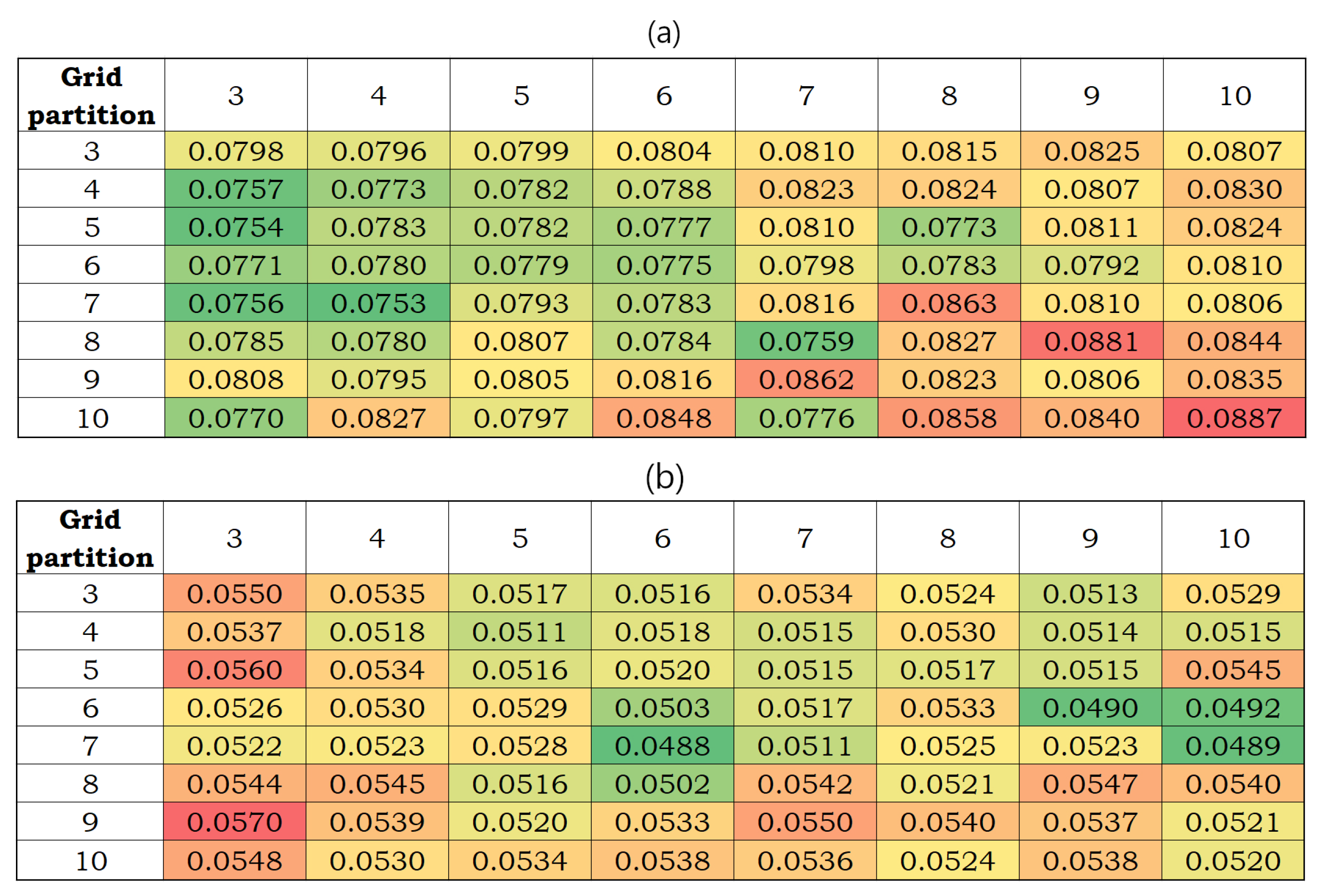
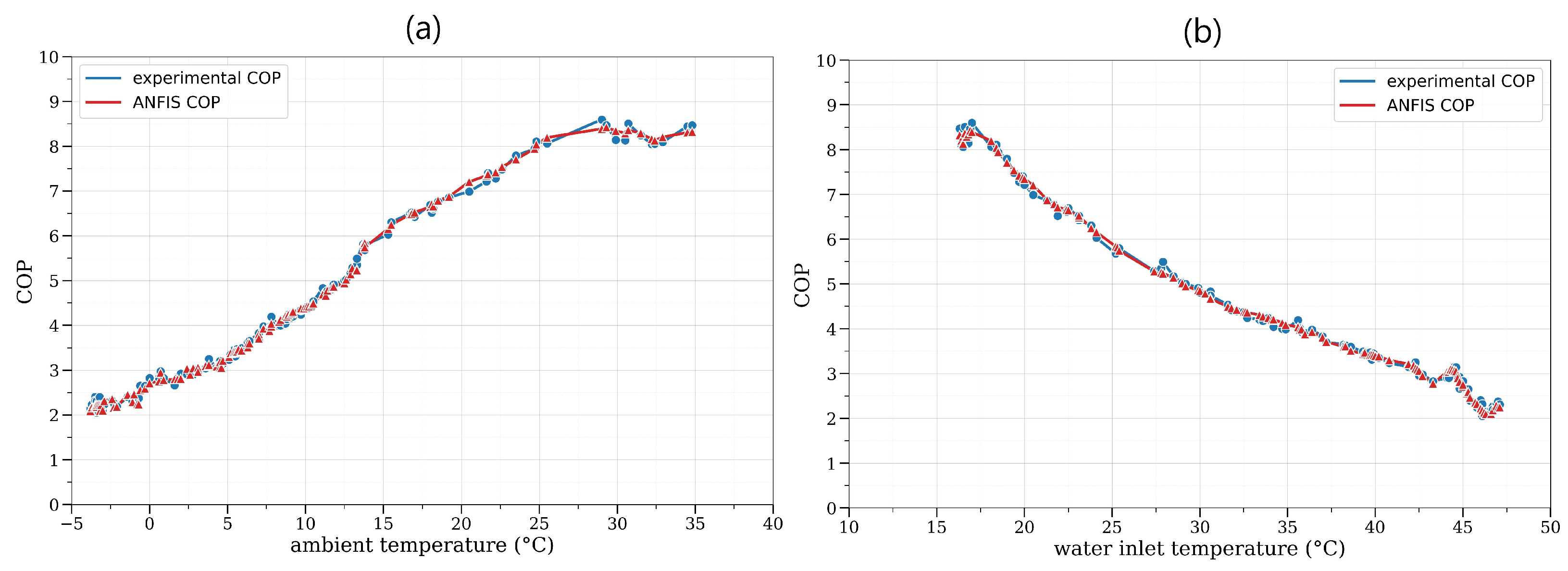
2.2.2. Adaptive Neuro-Fuzzy Inference System (ANFIS) Model
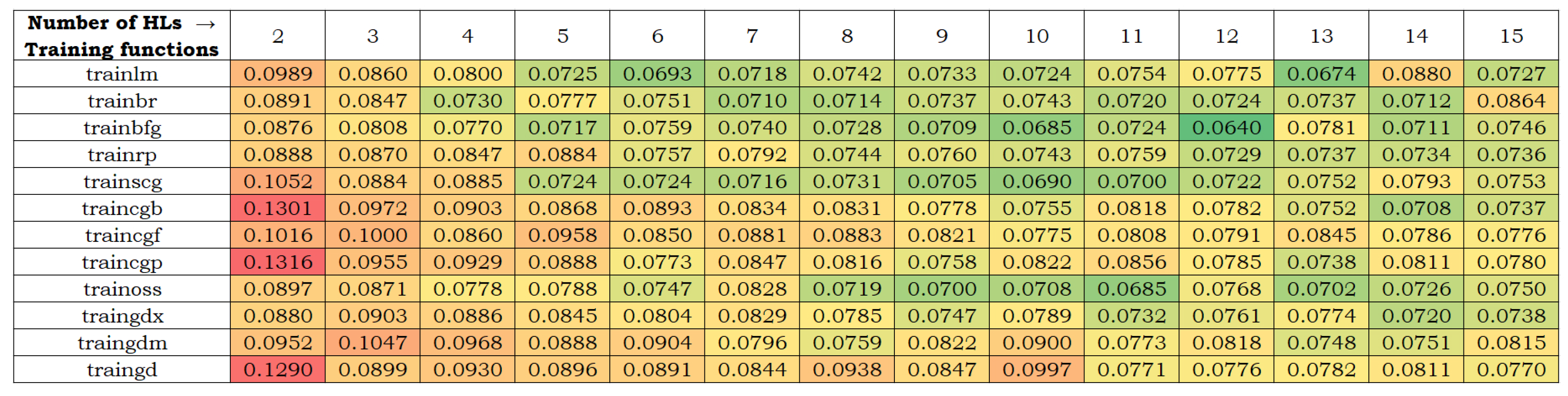
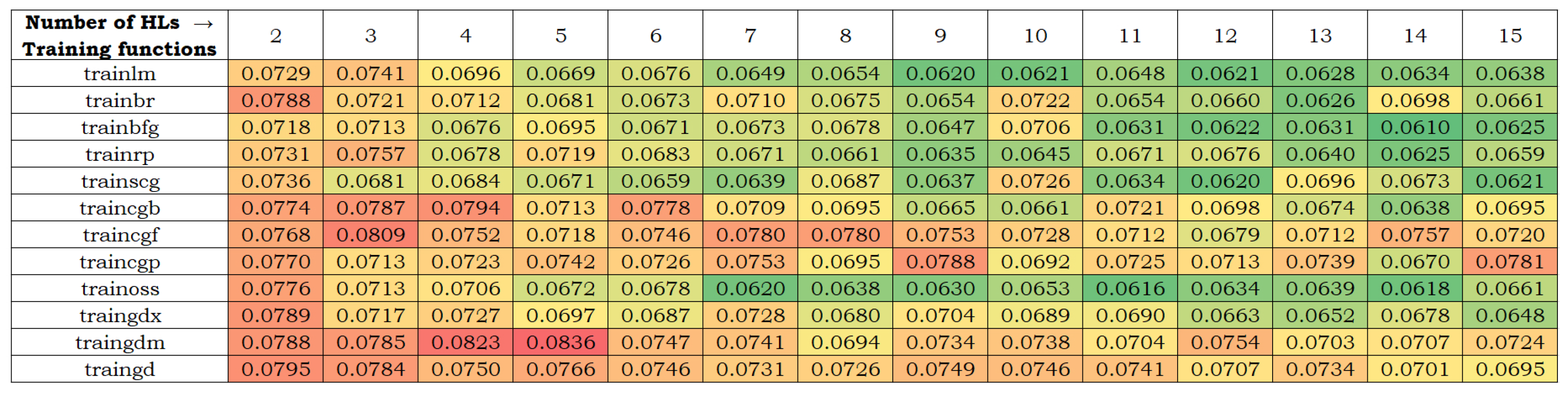
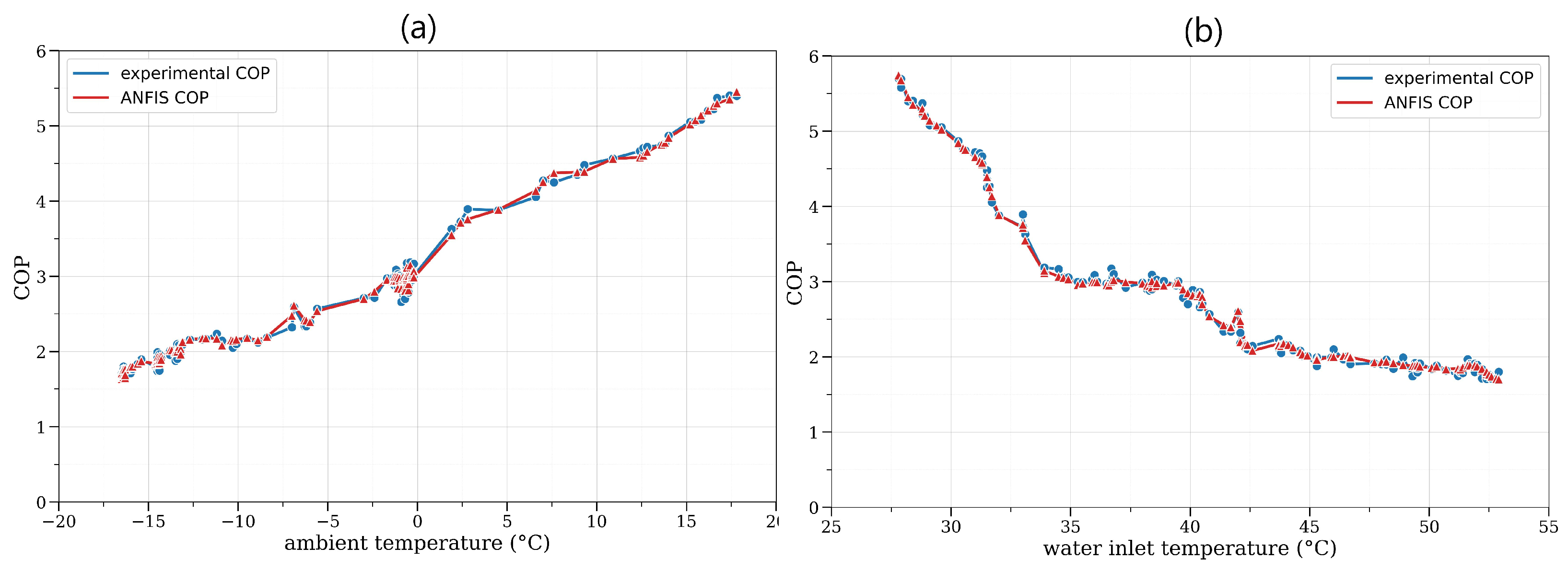
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, M.-Y.; Garud, K.S.; Jeon, H.-B.; Lee, H.-S. A Study on Performance Characteristics of a Heat Pump System with High-Pressure Side Chiller for Light-Duty Commercial Electric Vehicles. Symmetry 2020, 12, 1237. [Google Scholar] [CrossRef]
- de Melo Resende, S.I.; Diniz, H.A.G.; Machado, L.; de Faria, R.N.; de Oliveira, R.N. Dynamic modeling of an R290 direct-expansion solar-assisted heat pump: Performance analysis for efficient hot water production under different conditions. J. Build. Eng. 2025, 100, 111687. [Google Scholar] [CrossRef]
- Buyukzeren, R.; Kahraman, A. A comparative study on the application of solar thermal collector and photovoltaic combinations to assist an air source heat pump. J. Therm. Anal. Calorim. 2024, 149, 9413–9428. [Google Scholar] [CrossRef]
- Özden, E.; Kaya, M.N. Comprehensive analysis of key design parameters affecting the efficiency of flat plate solar thermal collectors. CaseStudies Therm. Eng. 2025, 73, 106458. [Google Scholar] [CrossRef]
- Seifi, A.; Riahi, H. Estimating daily reference evapotranspiration using hybrid gamma test-least square support vector machine, gamma test-ann, and gamma test-anfis models in an arid area of iran. J. Water Clim. Chang. 2020, 11, 217–240. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J. Prediction of long-term monthly air temperature using geographical inputs. Int. J. Climatol. 2014, 34, 179–186. [Google Scholar] [CrossRef]
- Esen, H.; Inalli, M.; Sengur, A.; Esen, M. Forecasting of a ground-coupled heat pump performance using neural networks with statistical data weighting pre-processing. Int. J. Therm. Sci. 2008, 47, 431–441. [Google Scholar] [CrossRef]
- Esen, H.; Inalli, M. Ann and anfis models for performance evaluation of a vertical ground source heat pump system. Expert Syst. Appl. 2010, 37, 8134–8147. [Google Scholar] [CrossRef]
- Zhuang, Z.; Ben, X.; Yan, R.; Pang, J.; Li, Y. Accurately predicting heat transfer performance of ground heat exchanger for ground-coupled heat pump systems using data mining methods. Neural Comput. Appl. 2017, 28, 3993–4010. [Google Scholar] [CrossRef]
- Sun, W.; Hu, P.; Lei, F.; Zhu, N.; Jiang, Z. Case study of performance evaluation of ground source heat pump system based on ann and anfis models. Appl. Therm. Eng. 2015, 87, 586–594. [Google Scholar] [CrossRef]
- Garud, K.S.; Seo, J.H.; Cho, C.P.; Lee, M.Y. Artificial neural network and adaptive neuro-fuzzy interface system modelling to predict thermal performances of thermoelectric generator for waste heat recovery. Symmetry 2020, 12, 259. [Google Scholar] [CrossRef]
- Naresh, C.; Bose, P.; Rao, C. Artificial neural networks and adaptive neuro-fuzzy models for predicting wedm machining responses of nitinol alloy: Comparative study. SN Appl. Sci. 2020, 2, 314. [Google Scholar] [CrossRef]
- Gupta, A.K.; Kumar, P.; Sahoo, R.K.; Sahu, A.K.; Sarangi, S.K. Performance measurement of plate fin heat exchanger by exploration: Ann, anfis, ga, and sa. J. Comput. Des. Eng. 2017, 4, 60–68. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Singh, V.P. Comparison of different heuristic and decomposition techniques for river stage modeling. Environ. Assess. 2018, 190, 392. [Google Scholar] [CrossRef]
- Khan, M.R.; Sadeed, A.; Kalam, S.; Abu-Khamsin, S.; Abdulraheem, A.; Khan, R.A.; Abbasi, A. Integration of formation and drilling parameters to generate a deterministic rop model. In Proceedings of the Offshore Technology Conference, OTC, Houston, TX, USA, 2–5 May 2022; p. D012S057R005. [Google Scholar]
- Moghaddas, F.; Kabiri-Samani, A.; Zekri, M.; Azamathulla, H.M. Combined apso-ann and apso-anfis models for prediction of pressure loss in air-water two-phase slug flow in a horizontal pipeline. J. Hydroinform. 2021, 23, 88–102. [Google Scholar] [CrossRef]
- Ye, K.; Demirezen, G.; Fung, A.; Janssen, E. The use of artificial neural networks (ann) in the prediction of energy consumption of air-source heat pump in retrofit residential housing. IOP Conf. Ser. Earth Environ. Sci. 2020, 463, 012165. [Google Scholar] [CrossRef]
- Guzel, M.H.; Unal, R.E.; Onder, A.; Sen, M.A.; Kose, F. The fuzzy logic-based modeling of a micro-scale sloped solar chimney power plant. J. Mech. Sci. Technol. 2021, 35, 1301–1308. [Google Scholar] [CrossRef]
- Ünler, T.; Seyfi, L. Experimental investigation of range measurement error for radar under different weather conditions. Proc. Bulg. Acad. Sci. 2022, 75, 1325–1333. [Google Scholar] [CrossRef]
- Dave, H.; Vakharia, V.; Panchal, H.; Siddiqui, M.I.H.; Dobrotă, D. Ann and multilayer-elm based prediction of combustion, performance and emission characteristics of a diesel engine fuelled with diesel-dtbp blends. Case Stud. Therm. Eng. 2025, 72, 106323. [Google Scholar] [CrossRef]
- Naphon, P.; Arisariyawong, T.; Wiriyasart, S.; Srichat, A. Anfis for analysis friction factor and nusselt number of pulsating nanofluids flow in the fluted tube under magnetic field. Case Stud. Therm. Eng. 2020, 18, 100605. [Google Scholar] [CrossRef]
- Ye, B.; Zhou, W. Efficiency increment of cfd modeling by using anfis artificial intelligence for thermal-based separation modeling. CaseStudies Therm. Eng. 2024, 60, 104820. [Google Scholar] [CrossRef]
- EN 14511-2; Air Conditioners, Liquid Chilling Packages and Heat Pumps for Space Heating and Cooling and Process Chillers, with Electrically Driven Compressors—Part 2: Test Conditions. European Committee for Standardization (CEN): Brussels, Belgium, 2018.
- Yang, X. Artificial Neural Networks. In Handbook of Research on Geoinformatics; Karimi, H.A., Ed.; IGI Global: Hershey, PA, USA, 2009; pp. 122–128. [Google Scholar]
- Abraham, A. Artificial neural networks. In Handbook of Measuring System Design; John Wiley & Sons: Chichester, UK, 2005. [Google Scholar]
- Wu, Y.C.; Feng, J.W. Development and application of artificial neural network. Wirel. Pers. Commun. 2018, 102, 1645–1656. [Google Scholar] [CrossRef]
- Yen, J. Fuzzy logic—a modern perspective. IEEE Trans. Knowl. Data Eng. 1999, 11, 153–165. [Google Scholar] [CrossRef]
- Mendel, J.M. Fuzzy logic systems for engineering: A tutorial. Proc. IEEE 1995, 83, 345–377. [Google Scholar] [CrossRef]
- Karaboga, D.; Kaya, E. Adaptive network based fuzzy inference system (ANFIS) training approaches: A comprehensive survey. Artif. Rev. 2019, 52, 2263–2293. [Google Scholar] [CrossRef]

| Climate Room Data | |
| Max. ambient temperature | 40 °C |
| Min. ambient temperature | −17 °C |
| Temperature adjustment | 0.1 °C |
| Humidity variation limit | 5 % |
| Data recording period | 15 s |
| Experimental Data | |
| Min. water inlet temperature | 15 °C |
| Max. water inlet temperature | 55 °C |
| Ambient humidity | 75–80% |
| Flow rate | 1.65 m3/h |
| COP | 1.5–8.5 |
| Range and standard accuracy of device/sensor | |
| Temperature sensor | −50 to 250 °C and 0.1% |
| Magnetic flowmeter | 0 to 6.36 m3/h and 0.5% |
| Humidity sensor | 5 to 100 % and 5% |
| Training Algorithm | Abbreviation |
|---|---|
| Levenberg–Marquardt | trainlm |
| Bayesian regularization | trainbr |
| BFGS Quasi–Newton | trainbfg |
| Resilient backpropagation | trainrp |
| Scaled conjugate gradient | trainscg |
| Conjugate gradient with Powell–Beale restarts | traincgb |
| Conjugate gradient with Fletcher–Reeves updates | traincgf |
| Conjugate gradient with Polak–Ribière updates | traincgp |
| One-step secant | trainoss |
| Gradient descent with adaptive learning | traingdx |
| Gradient descent with momentum | traingdm |
| Gradient descent | traingd |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaya, M.N.; Büyükzeren, R.; Pektaş, A. Performance Prediction of Air Source Heat Pumps Under Cold and Hot Ambient Temperatures Using ANFIS and ANN Models. Symmetry 2025, 17, 1728. https://doi.org/10.3390/sym17101728
Kaya MN, Büyükzeren R, Pektaş A. Performance Prediction of Air Source Heat Pumps Under Cold and Hot Ambient Temperatures Using ANFIS and ANN Models. Symmetry. 2025; 17(10):1728. https://doi.org/10.3390/sym17101728
Chicago/Turabian StyleKaya, Mehmet Numan, Rıza Büyükzeren, and Abdülkadir Pektaş. 2025. "Performance Prediction of Air Source Heat Pumps Under Cold and Hot Ambient Temperatures Using ANFIS and ANN Models" Symmetry 17, no. 10: 1728. https://doi.org/10.3390/sym17101728
APA StyleKaya, M. N., Büyükzeren, R., & Pektaş, A. (2025). Performance Prediction of Air Source Heat Pumps Under Cold and Hot Ambient Temperatures Using ANFIS and ANN Models. Symmetry, 17(10), 1728. https://doi.org/10.3390/sym17101728






