Fuzzy Graphic Binary Matroid Approach to Power Grid Communication Network Analysis

Abstract

Matroid is a mathematical structure that extends the concept of independence. The fuzzy graphic binary matroid serves as a generalization of linear dependence, and its properties are examined. Power grid networks, which manage the generation, transmission, and distribution of electrical energy from power plants to consumers, are inherently a complex system. A key objective in analyzing these networks is to ensure a reliable and uninterrupted supply of electricity. However, several critical issues must be addressed, including uncertainty in communication links, detection of redundant or sensitive circuits, evaluation of network resilience under partial failures, and optimization of reliability in interconnected network systems. To support this goal, the concept of a fuzzy graphic binary matroid is applied in the analysis of power grid communication network, offering a framework that not only incorporates fuzziness and binary conditions but also enables systematic identification of weak circuits, redundancy planning, and reliability enhancement. This approach provides a more realistic representation of operational conditions, ensuring better fault tolerance and improved efficiency of the grid.

1. Introduction

Graph theory provides a powerful framework for abstracting and solving complex problems through the analysis of connectivity and structure [1]. The field traces its origin to 1736, when Leonhard Euler resolved the renowned Konigsberg Bridge Problem, thereby establishing the foundation for modern network analysis [2]. The discipline’s first formal textbook was published by Denes Konig in 1936. A significant advancement occurred in 1965 when Zadeh introduced fuzzy set theory in his seminal paper [3], addressing critical limitations in modeling real-world ambiguity by a mathematical bridge between human reasoning and computational systems. Fuzzy graphs extend classical graph structures by incorporating fuzzy set principles, allowing vertices and edges to possess membership values instead of strict binary relationships.

A matroid is a mathematical structure that provides a framework for understanding linear independence, effectively bridging concepts from graph theory and linear algebra [4]. The theory of matroid was introduced by Hassler Whitney in 1935, who recognized that its axioms form a common abstraction of independence found in both graphs and matrices [5]. In 1936, Saunders Mac Lane explored connections between matroids and projective geometry. Van der Waerden explored analogies between algebraic dependence and linear dependence, contributing significantly to the algebraic foundation of the matroid theory in 1937. In 1940, Richard Rado expanded the scope of matroid theory by introducing independence systems, which generalized the idea of independent sets. The significant contributions from Tutte [6], who played a central role in expanding the field of matroid theory in 1950. Graphic matroids have practical applications in network reliability analysis and electrical grid design, where they are used to model and analyze the robustness and failure modes of networks [7]. Tutte was first to fully develop the theory of graphic matroids, defining a matroid in terms of the cycles of a graph and introducing the notion of dual matroids [8]. Pitsoulis [9] introduced two recognition algorithms for signed-graphic matroid, providing necessary and sufficient conditions for identifying a matroid in 2010.

The foundation of fuzzy graph [10] theory was first established by Kaufmann in 1973. Rosenfeld significantly advanced the field in 1975 by developing fuzzy graphs through the integration of fuzzy relations with fuzzy sets [11]. This innovative framework provided a more adaptable representation of relationships, overcoming the limitations of graph structures. Rosenfeld offered a significant advantages for modeling systems, including social networks, transportation networks, and biological network interactions.

Domination sets are vital in optimizing network design, particularly in ensuring that certain key nodes control or monitor the entire network [12]. The concept of domination sets, explored by Talebi and Rashmanlou in 2019 [12] presents opportunities for optimizing network design by ensuring that critical nodes efficiently control entire networks. Future developments in network analysis will likely focus on enhancing the handling of uncertainty and imprecision through advanced fuzzy and vague graph models [13,14]. Rashmanlou et al. (2018) introduced interval-valued fuzzy graphs, which offer potential for future exploration in uncertain environments [15]. Shoaib et al. (2020) contribute to this field with complex Pythagorean fuzzy graphs, offering a way to manage even more dimensions of uncertainty [16]. Future implications for energy management systems and sustainable infrastructure can be done by quantifying energy and network performance under various conditions [17].

Recent advancements in fuzzy graph theory and its applications to multi-attribute decision-making (MADM) problems highlight the growing relevance of uncertainty modeling in complex systems. The study by Rao et al. (2025) introduces a q-rung orthopair fuzzy Zagreb index, enhancing decision-making efficiency by incorporating flexible degrees of membership and non-membership, offering improved sensitivity in ranking alternatives under uncertainty [18]. Kosari et al. investigated topological indices in fuzzy graphs and their role in decision-making processes in 2024. Their analysis presents generalized measures that help quantify network attributes, thereby enabling better insight into system behavior and supporting optimal decision strategies in uncertain environments. This work builds a bridge between topological indices and fuzzy set theory for robust MADM frameworks [19].

Kosari et al. [20] examine vague fuzzy graphs to model the connectivity structure in university buildings, providing practical insight into infrastructure design and optimization in 2023. Expanding on the structural metrics of fuzzy graphs. He propose a novel formulation of perfectly regular fuzzy graphs and demonstrate their utility in psychological sciences, particularly in modeling cognitive stability and regular behavioral patterns [21]. This work emphasizes the capacity of fuzzy graphs to model imprecise human-centric data with high granularity. In 2024, Khan et al. explored interval-valued picture fuzzy hypergraphs, introducing a richer framework to represent complex, layered relationships in decision-making [22]. The integration of hypergraph structures with picture fuzzy sets allows for more expressive modeling of group preferences and interactions, accommodating multiple forms of indeterminacy. Shi et al. in 2024 utilize the connectivity index of cubic fuzzy graphs to identify potential tsunami danger zones [23].

In 1988, Goetschal and Voxman introduced the concept of fuzzy matroids, which integrate both graphical and algebraic structures through the use of membership degrees [24]. Building on this foundation, Sabana and Sameena [25] proposed a new class of matroid derived from fuzzy graphs in 2019. In 2021, Sabana and Sameena extended the theory by introducing the concept of representable fuzzy matroids, and developed a framework for constructing fuzzy matroid from fuzzy vector spaces [26]. Isomorphism and structural characteristics of fuzzy matroids was studied in [27], deepening the theoretical understanding of their properties. Binary and regular matroids were characterized by Anushka Murthy [28]. A matroid is termed binary if it admits a representation over the finite field [29], where the independent sets correspond to linearly independent subsets of matrix columns. A central structural property of binary matroids is the symmetric difference condition [30]. Rashmanlou et al. (2020) proposed a novel method for solving the shortest path problem using multi-valued logic and fuzzy set theory to account uncertainties in real-world networks [31].

1.1. Research Gap

Matroids provide a unifying framework for studying independence in various mathematical structures. Their fundamental properties have been studied since 1935, with several advancements explored in subsequent years. The concept of graphic matroids was introduced in 1965, and in 1988, the concept of fuzzy sets was integrated with matroids. In 2019, matroids were defined using fuzzy graphs. Building on these concepts, the fuzzy graphic matroid was introduced by incorporating the principles of fuzzy matroids and fuzzy graphs. Among the various extensions of fuzzy graphs, fuzzy graphic matroids have attracted significant research interest. This is primarily because they have been studied and applied in areas such as cryptography, network analysis, and optimization problems. However, there is limited research available on fuzzy graphic matroids in the existing literature. This motivates us to explore advanced aspects of fuzzy graphic matroids further.

1.2. Motivation

The communication network of the power grid is a critical component of modern electrical power systems, essential for enabling the secure and reliable exchange of information between various entities. As of today, societies become increasingly dependent on electricity, ensuring the continuous and efficient operation of these networks is important. Traditional methods often face challenges in modeling and optimizing the grid’s performance, especially in scenarios involving unreliable connections or components. Fuzzy graphic matroid theory, with its versatile applications across multiple fields, offers a powerful approach to address these challenges. By modeling the power grid communication network structure as a fuzzy graphic binary matroid, it becomes easier to analyze and optimize its components, identify critical links, and enhance overall reliability.

1.3. Novelty and Key Contributions

Power grid network analysis is vital for the stable and efficient functioning of modern electrical systems. This framework models a novel contribution to the study of power grid network analysis that helps to optimize the flow of electricity, minimize energy losses, and ensure that the grid operates efficiently. This analysis, using fuzzy graphic binary matroids, identifies weak links in the system and helps improve the overall resilience of the network.

(1)

The application of fuzzy graphic binary matroids to power grid networks provides the tools to identify critical links and ensures optimal network performance of the power grid communication network.

(2)

The fuzzy graphic binary matroid helps to simplify complex systems into a manageable model for better decision-making and computational efficiency.

1.4. Organization of the Paper

The paper is organized as follows: Section 2 provides the necessary background and foundational concepts required for the paper. The detailed conditions for the formation and application of fuzzy graphic binary matroids over the finite field ${\mathcal{F}}_2$ are presented and defined in Section 3. Section 4 explores the network structure represented as a fuzzy graphic binary matroid. The reliability and performance of the communication links within the grid are analyzed and the critical components. Section 5 presents the findings derived from the application of fuzzy graphic binary matroid theory to the power grid network. The paper is concluded in Section 6.

2. Preliminaries

Definition 1 

([32]). Let E be a ground set and I be the set of all independent sets. The pair $\mathcal{M}=(E,I)$ is called a matroid, with the following properties:

(i) 

$\varphi \in I$

(ii) 

If $T_1\in I,T_2\subset T_1$, then $T_2\in I$

(iii) 

If $T_1,T_2\in I; |T_2|\ge |T_1|$, then there exists an element $x\in T_2\setminus T_1$ such that $T_1\cup \left\{x\right\}\in I$.

Definition 2 

([33]). Let ${\sigma }^{*}:V⟶[0,1]$ is a fuzzy vertex set of G and ${\mu }^{*}:V\times V⟶[0,1]$ is a fuzzy edge set of G where the membership value of each edge $e_{ij}$ satisfies the condition ${\mu }^{*}\left(e_{ij}\right)\le min({\sigma }^{*}\left(e_i\right),{\sigma }^{*}\left(e_j\right))\mathrm{for}\mathrm{every}{e}_i,e_j\in V$. The pair $G=({\sigma }^{*},{\mu }^{*})$ is called a fuzzy graph.

Let $\mathbb{I}:X⟶[0,1]$ be a fuzzy subset on $\mathbb{E}$. If $M,N\in \mathfrak{F}\left(\mathbb{E}\right)$, then

(i)

$supp\left(M\right)=\{e_{ij}\in \mathbb{E}|M\left(e_{ij}\right)>0\}$, a crisp set

(ii)

$m\left(M\right)=min\left\{M\left(e_{ij}\right)\right|e_{ij}\in supp\left(M\right)\}$

(iii)

$M\cup N=max\{M\left(e_{ij}\right),N\left(e_{ij}\right)\},e_{ij}\in \mathbb{E}$

(iv)

$M\cap N=min\{M\left(e_{ij}\right),N\left(e_{ij}\right)\},e_{ij}\in \mathbb{E}$.

Note: For the sake of convenience, different notations are used here.

Definition 3 

([34]). Let $\mathbb{E}$ be a finite set and $\mathbb{I}\in \mathfrak{F}\left(\mathbb{E}\right)$ be the family of independent sets. The pair $FM=(\mathbb{E},\mathbb{I})$ is a fuzzy matroid if the following conditions are satisfied:

(i) 

$\varphi \in \mathbb{I}$

(ii) 

$M\subset N$ and $N\in M,\mathrm{where}M\subset N,M\left(e_{ij}\right)\le N\left(e_{ij}\right)\mathrm{forall}{e}_{ij}\in \mathbb{E}$

(iii) 

If $M,N\in \mathbb{I}$ with $\left|\mathrm{supp}\right(M\left)\right|\le \left|\mathrm{supp}\right(N\left)\right|$, there exists $P\in \mathbb{I}$ such that

(a) 

$M\subset P\subseteq M\cup N$

(b) 

$m\left(P\right)$ = $\min \left\{m\right(M),m(N\left)\right\}.$

Definition 4 

([35]). A fuzzy graph $G(\sigma ,\mu )$ that satisfies the independence property of a fuzzy matroid is defined to be a fuzzy graphic matroid. It is defined on the edge set of the fuzzy graph $G(\sigma ,\mu )$ and it is denoted by $\mathfrak{M}\left(G\right)$.

Definition 5 

([35]). The dual of a fuzzy graphic matroid on $\mathbb{E}$ is ${\mathfrak{M}}^{*}\left(G\right)$ whose bases are the complements of the bases $\mathfrak{M}\left(G\right)$.

Remark 1. 

If $\mathfrak{M}\left(G\right)$ is a fuzzy graphic matroid, then the sub-bases are the spanning sets and the hypobases are the hyperplanes.

Definition 6 

([35]). A minor of a fuzzy graphic matroid $\mathfrak{M}\left(G\right)$ is formed by two operations:

• An edge $e_{ij}$ is deleted from $\mathbb{E}$ without changing the independence or rank of $\mathfrak{M}\left(G\right)$.
• An edge $e_{ij}$ is contracted from $\mathbb{E}$ and the rank of every fuzzy set is decreased.

3. Fuzzy Graphic Binary Matroids

A $\mathfrak{M}\left(G\right)$ is said to be a fuzzy graphic binary matroid if it satisfies the following conditions:

(i)

Fuzzy Membership value: The membership function ${\mu }_{ij}:\mathbb{E}\to [0,1]$ that assigns a membership value to each edge $e_{ij}\in \mathbb{E}$ such that each edge is either included or excluded from circuits. There exists a threshold value $\alpha \in [0,1]$ such that

−

If $e_{ij}\ge \alpha$, then the edge is considerd as 1.

−

If $e_{ij}<\alpha$, then the edge is considerd as 0.

(ii)

Totally Unimodular Matrix: A matrix is called totally unimodular if every square submatrix has a determinant equal to either $0,1,or-1$.

(iii)

Symmetric Difference Property: For any two circuits ${\mathbb{C}}_1$ and ${\mathbb{C}}_2$ in $\mathfrak{M}\left(G\right)$, the symmetric difference ${\mathbb{C}}_1\Delta {\mathbb{C}}_2$ is a union of disjoint circuits. The edges in ${\mathbb{C}}_1\Delta {\mathbb{C}}_2$ form disjoint cycles or an empty set.

Example 1. 

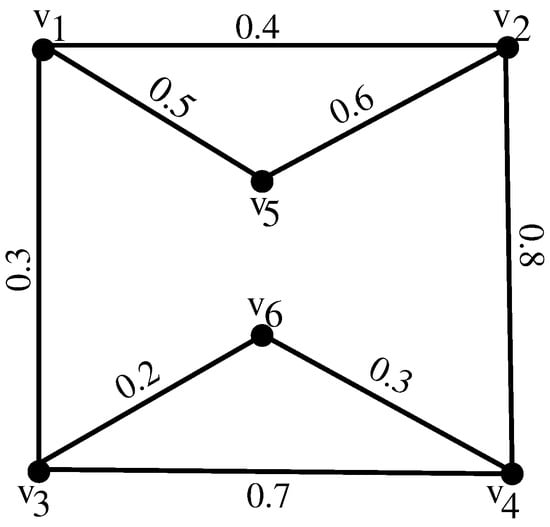
In Figure 1, $\mathbb{E}=\{e_{12}\left(0.4\right),e_{24}\left(0.8\right),e_{34})\left(0.7\right),e_{13}\left(0.3\right),e_{15}\left(0.5\right),e_{25}\left(0.6\right),e_{36}\left(0.2\right),e_{46}\left(0.3\right)$.

Figure 1. Fuzzy graph.

Let $\alpha =0.4$, the incidence matrix obtained after thresholding is

$$\begin{array}{ccccccc}& v_1& v_2& v_3& v_4& v_5& v_6\\ e_1& 1& 0& 0& 0& 1& 0\\ e_2& 0& 1& 0& 0& 1& 0\\ e_3& 1& 1& 0& 0& 0& 0\\ e_4& 0& 1& 0& 1& 0& 0\\ e_5& 0& 0& 0& 1& 0& 1\\ e_6& 0& 0& 1& 0& 0& 1\\ e_7& 0& 0& 1& 1& 0& 0\end{array}$$

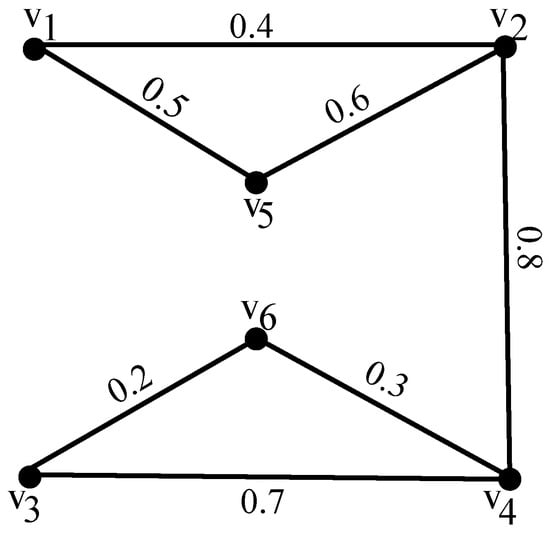
The fuzzy graph as shown in Figure 2 is obtained after applying the thershold value $\alpha =0.4$.

Figure 2. Fuzzy graph after thersholding.

The circuits ${\mathbb{C}}_1,{\mathbb{C}}_2\in \mathbb{E}$.

$${\mathbb{C}}_1\Delta {\mathbb{C}}_2=\{e_{12},e_{25},e_{15}\}\Delta \{e_{34},e_{36},e_{46}\}$$

(1)

Theorem 1. 

A fuzzy graphic matroid is binary if and only if its family of circuits is closed under symmetric difference.

Proof of Theorem 1. 

Let $\mathfrak{M}\left(G\right)$ be a fuzzy graphic matroid. If $\mathfrak{M}\left(G\right)$ is binary, then it is representable over a finite field ${\mathcal{F}}_2$.

Necessary Condition: If $\mathfrak{M}\left(G\right)$ is binary, then every circuit in $\mathfrak{M}\left(G\right)$ can be represented as a linear combination of other circuits over ${\mathcal{F}}_2$. Let ${\mathbb{C}}_1$ and ${\mathbb{C}}_2$ be circuits in $\mathfrak{M}\left(G\right)$. Since $\mathfrak{M}\left(G\right)$ is binary, the circuit difference ${\mathbb{C}}_1\setminus {\mathbb{C}}_2$ can be expressed as a linear combination of circuits in $\mathfrak{M}\left(G\right)$.

$${\mathbb{C}}_1\setminus {\mathbb{C}}_2=\sum _{i=1}^k{a}_i{C}_i$$

(2)

${\mathbb{C}}_i$ are the circuits in $\mathfrak{M}\left(G\right)$ and $a_i\in {\mathcal{F}}_2$. Hence, by the circuit difference property, the difference of any two circuits in $\mathfrak{M}\left(G\right)$ is expressible as a linear combination of other circuits. Therefore, $\mathfrak{M}\left(G\right)$ satisfies the circuit difference property.

Sufficient Condition: Suppose that $\mathfrak{M}\left(G\right)$ satisfies the condition of a fuzzy graphic binary matroid, which implies that any pair of circuits ${\mathbb{C}}_1$ and ${\mathbb{C}}_2$ in $\mathfrak{M}\left(G\right)$ can be expressed as linear combinations of other circuits in $\mathfrak{M}\left(G\right)$ over ${\mathcal{F}}_2$. The circuit difference property implies that every circuit can be expressed in terms of other circuits. The incidence matrix A of the fuzzy graph G encodes the relationship among the circuits. Since A is totally unimodular, the linear dependence among circuits is consistent with the constraints of total unimodularity. Therefore, $\mathfrak{M}\left(G\right)$ satisfies the circuit difference property. □

Theorem 2. 

If two circuits share exactly an edge, then the symmetric difference between the circuits contains at least one disjoint circuit.

Proof of Theorem 2. 

Let ${\mathbb{C}}_1$ and ${\mathbb{C}}_2$ be the circuits in $\mathfrak{M}\left(G\right)$. If ${\mathbb{C}}_1$ and ${\mathbb{C}}_2$ shares exactly one edge then the removal of the edge $e_{ij}$ from the symmetric difference leaving the set $({\mathbb{C}}_1\oplus {\mathbb{C}}_2)\setminus \left\{e_{ij}\right\}$. The symmetric difference of two circuits that share edges results in a new circuit or a union of disjoint circuits. If ${\mathbb{C}}_1$ and ${\mathbb{C}}_2$ share exactly one edge, then the remaining edges must form at least one disjoint circuit. The connected components of edges must be independent, and by the definition of a circuit, the set of remaining edges forms a minimal dependent set. Therefore, the symmetric difference of the circuits ${\mathbb{C}}_1$ and ${\mathbb{C}}_2$ contains at least one disjoint circuit in the fuzzy graphic matroid. □

Lemma 1. 

If a fuzzy graphic matroid is binary, then it can be represented by a matrix A over ${\mathcal{F}}_2$ such that any columns corresponding to a circuit in $\mathfrak{M}\left(G\right)$ are dependent over ${\mathcal{F}}_2$.

Proof of Lemma 1. 

If $\mathfrak{M}\left(G\right)$ is binary, then by the definition of a binary matroid there exists a matrix A over ${\mathcal{F}}_2$ representing the fuzzy graphic binary matroid such that the columns of $M\left(G\right)$ corresponds to a circuit of $\mathfrak{M}\left(G\right)$. Hence, the linear combination of columns in any circuit sums to zero in ${\mathcal{F}}_2$. □

Lemma 2. 

If a matrix $M\left(G\right)$ over ${\mathcal{F}}_2$ represent a fuzzy graphic binary matroid, then determinant $det\left(M^{\prime }\right)\left(G\right)$ for any square submatrix $M^{\prime }\left(G\right)$ in M is $0,1$, and $-1$.

Proof of Lemma 2. 

Let $\mathfrak{M}\left(G\right)$ be binary. The dependent sets holds over ${\mathcal{F}}_2$ and therefore, the determinant of any square submatrix $M^{\prime }\left(G\right)$ in A must be $0,1$, and $-1$ for a binary matrix over ${\mathcal{F}}_2$. □

Lemma 3. 

If a matrix $M\left(G\right)$ of a fuzzy graph G is totally unimodular, then the fuzzy graphic matroid is binary.

Proof of Lemma 3. 

Let A be an $m\times n$ totally unimodular matrix, then every square submatrix of A has a determinant $\{0,\pm 1\}$. A fuzzy graphic matroid on a ground set $\mathbb{E}$ is binary if there exists a representation matrix over ${\mathcal{F}}_2$ such that the circuits of $G(\sigma ,\mu ,\mathfrak{M})$ correspond to the columns of the incidence matrix A. Since A is unimodular, every entry of A must be an integer, and every square submatrix $A^{\prime }\left(G\right)$ is totally unimodular. □

Theorem 3. 

A fuzzy graphic matroid is binary if and only if the incidence matrix A of the fuzzy graph G is totally unimodular.

Proof of Theorem 3. 

A fuzzy graphic matroid is binary if it can be represented over a finite field. The circuits in the fuzzy graphic matroid can be expressed as a linear combination of other circuits over ${\mathcal{F}}_2$.

Necessary Condition: Assume that $\mathfrak{M}\left(G\right)$ is binary. Every circuit in $\mathfrak{M}\left(G\right)$ can be expressed as a sum of other circuits. The incidence matrix A defines the relationship between the vertices and edges of the fuzzy graph G. Since the circuits in the fuzzy graph G are represented as a sum of other circuits, the matrix formed by these circuits also behaves as a linear combination over ${\mathcal{F}}_2$. The incidence matrix satisfies certain properties that ensure it is totally unimodular. Any linear combination of the rows of A corresponding to the circuits results in a matrix where the submatrix has the determinant $\{0,\pm 1\}$. Therefore, $\mathfrak{M}\left(G\right)$ is binary.

Sufficient Condition: If the incidence matrix is totally unimodular, then every submatrix of the circuits $\mathfrak{M}\left(G\right)$ remains within the set of values $\{0,1\}$. All the circuits in $\mathfrak{M}\left(G\right)$ can be expressed as a sum of other circuits over ${\mathcal{F}}_2$. The total unimodularity of the incidence matrix implies that $\mathfrak{M}\left(G\right)$ can be represented over ${\mathcal{F}}_2$. □

Theorem 4. 

If a fuzzy graphic matroid is binary, then every minor of $\mathfrak{M}\left(G\right)$ is binary.

Proof of Theorem 4. 

Let G be a fuzzy graph and $\mathbb{E}$ be the ground set of a fuzzy graphic matroid. The fuzzy graphic matroid is represented by the incidence matrix $M\left(G\right)$. If $\mathfrak{M}\left(G\right)$ is binary, then the incidence matrix A is totally unimodular and it can be represented over ${\mathcal{F}}_2$. The fuzzy graphic matroid is binary, and every minor of $\mathfrak{M}\left(G\right)$ is binary. The minor of a fuzzy graphic matroid is obtained by a sequence of contraction and deletion of edges in the ground set of a fuzzy graph G. If $e_{ij}\in \mathbb{E}$ is an edge of G, then deletion of $e_{ij}$ results in a fuzzy graph $G^{\prime }$. The incidence matrix of $G^{\prime }$ is $A\left(G^{\prime }\right)$ obtained by removing the column corresponding to $e_{ij}$ from A. Since the deletion of a column does not affect the total unimodularity of a matrix, ${\mathfrak{M}}^{\prime }\left(G\right)$ is binary.

Similarly, the contraction of the edge $e_{ij}\in \mathbb{E}$ corresponds to the elementary row operation on A by removal of the row and column corresponding to the vertices and edges incident to the edge $e_{ij}$. The matrix formed after the removal of a row and column of an edge $e_{ij}$ is totally unimodular. Since the fuzzy graphic matroid formed by contraction of an edge $e_{ij}$ of a fuzzy graph G is binary. The deletion and contraction of an edge from a fuzzy graph G preserves the total unimodularity. Therefore, every minor of $\mathfrak{M}\left(G\right)$ obtained by contraction and deletion of an edge $e_{ij}$ has a totally unimodular incidence matrix. Consequently, every minor of $\mathfrak{M}\left(G\right)$ can be represented over ${\mathcal{F}}_2$. □

Theorem 5. 

$\mathfrak{M}\left(G\right)$ is represented over ${\mathcal{F}}_2$ if and only if its incidence matrix A can be transformed into a totally unimodular matrix.

Proof of Theorem 5. 

Let G be a fuzzy graph, and the fuzzy graphic binary matroid is defined on the edge set $\mathbb{E}$, and its incidence matrix represents the relationship between the vertices and edges. The fuzzy graphic matroid $\mathfrak{M}\left(G\right)$ is said to be representable over the finite field $\mathcal{F}$ if there exists a matrix representation of the fuzzy graphic binary matroid whose entries belong to $\mathcal{F}$. This condition holds if and only if the incidence matrix is totally unimodular.

Necessary condition: Let $\mathfrak{M}\left(G\right)$ be representable over ${\mathcal{F}}_2$. The incidence matrix can be transformed into a matrix with entries in ${\mathcal{F}}_2$ by elementary row operations. Since $\mathfrak{M}\left(G\right)$ is binary, the matrix must be totally unimodular, which ensures that the fuzzy graphic matroid is binary. Therefore, any set of dependent edges can be expressed as a linear combination over ${\mathcal{F}}_2$.

Sufficient condition: If the incidence matrix of a fuzzy graph G is totally unimodular. A totally unimodular matrix has the property that every square submatrix has a determinant $\{0,\pm 1\}$, which implies that the matrix can be transformed into a matrix with entries in ${\mathcal{F}}_2$. Consequently, $\mathfrak{M}\left(G\right)$ can be represented over ${\mathcal{F}}_2$ as its circuits can be expressed as linear combinations over the finite field. □

Lemma 4. 

The dual of a fuzzy graphic binary matroid is binary.

Proof of Lemma 4. 

Let $\mathfrak{M}\left(G\right)$ be a fuzzy graphic matroid represented by an incidence matrix A. If $\mathfrak{M}\left(G\right)$ is binary, then the incidence matrix $M\left(G\right)$ is totally unimodular. The dual of $\mathfrak{M}\left(G\right)$ is represented by the transpose of the incidence matrix $A{\left(G\right)}^T$. Since the transpose of a totally unimodular matrix is totally unimodular. Therefore, the dual of a $\mathfrak{M}\left(G\right)$ is binary and it can be represented over ${\mathcal{F}}_2$ by a totally unimodular matrix $A{\left(G\right)}^T$. □

Theorem 6. 

If $\mathfrak{M}\left(G\right)$ is a fuzzy graphic binary matroid, then adding an edge to the fuzzy graph G corresponding to a totally unimodular matrix is also binary.

Proof of Theorem 6. 

Let $\mathfrak{M}\left(G\right)$ be a fuzzy graphic binary matroid and $\mathbb{E}$ be the edge set of a fuzzy graph G. The incidence matrix of fuzzy graph G is totally unimodular. The binary property implies that every submatrix of A has determinant $\{0,\pm 1\}$ and $\mathfrak{M}\left(G\right)$ becomes representable over a finite field ${\mathcal{F}}_2$. Let $e_{ij}$ be an edge added to the fuzzy graph G and $e_{ij}\notin \mathbb{E}$, which results in a new fuzzy graph $G^{\prime }$. The incidence matrix $A\left(G^{\prime }\right)$ is obtained by appending the incidence vector of $e_{ij}$ to the matrix A. Since A is unimodular and $e_{ij}$ corresponds to a totally unimodular vector, the augmented matrix $A\left(G^{\prime }\right)$ remains totally unimodular. The preservation of total unimodularity implies that every square submatrix of $A\left(G^{\prime }\right)$ has a determinant $\{0,\pm 1\}$. Therefore, adding an edge $e_{ij}$ to a fuzzy graph G that corresponds to a totally unimodular matrix preserves the condition of the fuzzy graphic binary matroid, and $\mathfrak{M}\left(G\right)$ is representable over ${\mathcal{F}}_2$. □

Theorem 7. 

A fuzzy graphic matroid is binary if it can be decomposed into a direct sum of binary matroids corresponding to a totally unimodular submatrix of the incidence matrix of G.

Proof of Theorem 7. 

Let G be a fuzzy graph. The incidence matrix A of the fuzzy graph G encodes the relationships between the vertices and edges of a fuzzy graph G, where the independence corresponds to the acyclic subgraphs of G. If $\mathfrak{M}\left(G\right)$ can be decomposed into a direct sum of the fuzzy graphic matroid $\mathfrak{M}{\left(G\right)}_1,\mathfrak{M}{\left(G\right)}_2,\dots ,\mathfrak{M}{\left(G\right)}_k$ where each fuzzy graphic matroid $\mathfrak{M}{\left(G\right)}_k$ corresponds to a totally unimodular submatrix $A_i$ of A. Since $A_i$ is totally unimodular, the corresponding fuzzy graphic matroid is binary. If the incidence matrix of the direct sum of the diagonal and the diagonal matrices preserves total unimodularity, then the direct sum of binary fuzzy graphic matroids remains binary. Therefore, the fuzzy graphic matroid represented by the diagonal matrix formed by $\mathfrak{M}{\left(G\right)}_1,\mathfrak{M}{\left(G\right)}_2,\dots ,\mathfrak{M}{\left(G\right)}_k$ is binary.

Conversely, if $\mathfrak{M}\left(G\right)$ is binary, then its incidence matrix is totally unimodular, which implies that it can be decomposed into a direct sum of submatrices, each of which is totally unimodular. Therefore, $\mathfrak{M}\left(G\right)$ can be expressed as a direct sum of fuzzy graphic binary matroids. This completes the proof. □

Theorem 8. 

A fuzzy graphic matroid is binary if and only if every circuit in $\mathfrak{M}\left(G\right)$ can be represented as a linear combination over ${\mathcal{F}}_2$ of other circuits in $\mathfrak{M}\left(G\right)$ that do not share edges with a fuzzy graph G.

Proof of Theorem 8. 

Let $\mathfrak{M}\left(G\right)$ be a fuzzy graphic matroid and $\mathbb{E}$ be the ground set of $\mathfrak{M}\left(G\right)$ defined on the edge set of a fuzzy graph G. The circuits of the $\mathfrak{M}\left(G\right)$ correspond to the cycles of a fuzzy graph G.

Necessary Condition: Assume that $\mathfrak{M}\left(G\right)$ is binary. $\mathfrak{M}\left(G\right)$ can be represented as a linear combination over a finite field ${\mathcal{F}}_2$, and its incidence matrix A is totally unimodular. Consequently, any dependent edges between the cycles of a fuzzy graph G can be expressed as a linear combination over ${\mathcal{F}}_2$. Let $\mathbb{C}\subseteq \mathbb{E}$ be a circuit in $\mathfrak{M}\left(G\right)$. Since, $\mathfrak{M}\left(G\right)$ is binary, the circuits of $G(\sigma ,\mu ,\mathfrak{M})$ can be written as a linear combination over ${\mathcal{F}}_2$ of other circuits ${\mathbb{C}}_1,{\mathbb{C}}_2,\dots ,{\mathbb{C}}_n$ as follows:

$$\mathbb{C}={\mathbb{C}}_1\oplus {\mathbb{C}}_2\oplus \dots \oplus {\mathbb{C}}_n$$

(3)

The symmetric difference ensures that if an edge appears an even number of times in the linear combination, then it is removed from the circuit. The circuits ${\mathbb{C}}_1,{\mathbb{C}}_2,\dots ,{\mathbb{C}}_n$ must be disjoint sets in $\mathfrak{M}\left(G\right)$. Therefore, every circuit in $\mathfrak{M}\left(G\right)$ can be expressed as a linear combination of other circuits.

Sufficient Condition: Assume that every circuit in $\mathfrak{M}\left(G\right)$ can be expressed as a linear combination over ${\mathcal{F}}_2$ of other circuits in $\mathfrak{M}\left(G\right)$. For any circuit in $\mathfrak{M}\left(G\right)$, there exist ${\mathbb{C}}_1,{\mathbb{C}}_2,\dots ,{\mathbb{C}}_n$ such that the circuits that do not share common edges in the fuzzy graph G. This implies that all the circuits in $\mathfrak{M}\left(G\right)$ satisfy the symmetric difference property. This completes the proof. □

4. Fuzzy Graphic Binary Matroid in Power Grid Network

In this section, a fuzzy graphic binary matroid is applied to model a power grid communication network of a region through the proposed algorithm. The algorithm helps in identifying weak links before complete failure; therefore, the network can achieve better reliability and reduce the risk of communication failures. The analysis of a power grid network using fuzzy graphic binary matroid offers a rigorous mathematical framework to model, evaluate, and optimize the reliability and fault tolerance of communication structures within power systems.

The analysis using fuzzy graphic binary matroid aids in the following:

• Identifying redundant paths to ensure communication continuity during partial failures.
• Detecting vulnerable components where failure risks are concentrated.
• Suggesting optimization strategies, such as upgrading low-reliability links or reinforcing specific circuits.

4.1. Problem Formulation

Let ${\sigma }^{*}:V⟶[0,1]$ and ${\mu }^{*}:\mathbb{E}⟶[0,1]$ be the membership function of vertices and edges of a fuzzy graph G. The fuzzy graphic binary matroid is defined from the edge set of a fuzzy graph G with $\mathbb{E}$ be the ground set and $\mathbb{I}=2^n$ be the family of independent sets.

Defining the fuzzy graphic binary matroid over G using the set of dependent edges.

• Each independent fuzzy set corresponds to an acyclic subgraph.
• Circuits in the fuzzy graphic matroid correspond to fundamental cycles in the fuzzy graph.

Using the fuzzy graphic matroid circuit property:

• If $\mathbb{C}$ is a minimal dependent set in $\mathbb{E}$, the symmetric difference property ensures redundancy and fault tolerance.

Reliability Analysis: For each cycle C, the cycle reliability is

$$R=mi{n}_{e_{ij}\in \mathbb{C}}{\mu }^{*}\left(e_{ij}\right)$$

(4)

The network reliability is determined by the reliability of the fundamental cycles as follows:

$$R_N=mi{n}_{e_{ij}\in \mathbb{C}}\left(R_C\right)$$

(5)

This identifies the weakest critical circuits affecting the reliability of the network.

4.2. Algorithm Description

For a fuzzy graphic matroid $\mathfrak{M}\left(\mathtt{G}\right)=(\mathbb{E},\mathbb{I})$ having rank function $\mathbb{R}$, the ground set of a fuzzy graphic matroid $\mathbb{E}$ is the set of edges of a fuzzy graph G. The step-wise procedure to construct the power grid network is given below:

Step (i)

Construction of fuzzy graph: Let G be a fuzzy graph having n vertices and m edges. G is a pair of functions $\sigma :V⟶[0,1]$ and $\mu :V\times V⟶[0,1]$. Here, the vertices represents the power grid substations and the inter-connections between the substations are represented by edges with fuzzy weights ${\mu }_{ij}$.

Step (ii)

Defining the Fuzzy Graphic Matroid: Let $\mathbb{E}$ be the ground set of a fuzzy graphic matroid and $\mathbb{I}$ be the independent edges of a fuzzy graph G.

Step (iii)

Identifying the fundamental circuits: Cycles in the network indicate redundancy and alternative communication paths. Also, identifying the cycles assesses the network’s resilience.

Step (iv)

Checking binary condition for redundancy: The binary condition in a fuzzy graphic matroid requires that every cycle can be expressed as the symmetric difference of other cycles. This condition ensures that the network has sufficient redundancy, allowing alternative paths if certain links fail.

$$\mathrm{Minimum}\mathrm{reliability}=\min \left({\mu }_{ij}\right)$$

Step (v)

Analyzing network reliablity: The overall network reliability is evaluated by the reliability of each cycle. The cycle reliability is determined by the minimum fuzzy membership value among its edges. This reflects the weakest link in the cycle which indictates the overall reliability of that communication path.

Step (vi)

Optimizing the network design: Based on the reliability analysis, the weakest links can be identified and addressed to enhance the network’s overall reliability.

5. Implementation, Results, and Discussion

In this study, a fuzzy graphic binary matroid approach is used to model a power grid communication network, which is crucial for capturing the inherent uncertainties in the transmission of data in the network. In this approach, the power grid is represented as a fuzzy graph, where vertices correspond to substations and edges represent communication links, each associated with a membership value that quantifies its reliability. The fuzzy graphic binary matroid is constructed by treating the edge set as the ground set and defining independent sets as those that form acyclic subgraphs, capturing the network’s structural dependencies. Fundamental circuits in this matroid correspond to communication loops, which are essential for redundancy and fault tolerance. The binary nature of the matroid ensures that every cycle can be expressed as the symmetric difference of other cycles, supporting a resilient and reconfigurable network structure. The weakest link in each cycle determines its overall reliability and identifies critical failures and vulnerabilities in the network. The power grid comprises several substations and is interconnected through various communication links. The communication links between substations are categorized as follows based on their type, which influences their reliability:

• Fiber optic cables (Highly reliable, underground)
• Wireless links (Moderately reliable, susceptible to interference)
• Satellite links (Less reliable, affected by weather conditions)

The substations of the power grid network are considered as the vertices of the fuzzy graph G, and the communication link between the network is represented by the edges of a fuzzy graph G. The data considered in this study are not derived directly from real events.

In Table 1, the reliability of each edge connecting the zones of the city are given with membership value ${\mu }_{ij}$. Let $\mathbb{E}=\{e_{AB},e_{AC},e_{AM},e_{BD},e_{AB},e_{BC},e_{BE},e_{EC},e_{CD},e_{DM},e_{CM},e_{EF},e_{FG}{e}_{GH},e_{HM},e_{HI},e_{IM},e_{IJ},e_{JM},e_{DF},e_{CF},e_{GM},e_{EG},e_{JH},e_{CI},e_{BI}\}$ be the edges shown in the Figure 3 and $\mathbb{I}=2^n$ be the independent sets of a fuzzy graph G where n is number of edges.

Table 1. Zones of a city and their reliability values of the edges connecting the zones.

Edges	Substation	Substation	Type of link	Reliability $\left({\mathit{e}}_{\mathit{ij}}\right)$
$e_{AB}$	Zone A	Zone B	Fiber	0.7
$e_{AC}$	Zone A	Zone C	Fiber	0.8
$e_{AM}$	Zone A	Control Center	Fiber	0.6
$e_{BD}$	Zone B	Zone D	Fiber	0.7
$e_{AB}$	Zone A	Zone B	Fiber	0.7
$e_{BC}$	Zone B	Zone C	Wireless	0.6
$e_{BE}$	Zone B	Zone E	Fiber	0.7
$e_{EC}$	Zone E	Zone C	Fiber	0.8
$e_{CD}$	Zone C	Zone D	Wireless	0.8
$e_{DM}$	Zone D	Control Center	Satellite	0.7
$e_{CM}$	Zone C	Control Center	Satellite	0.8
$e_{EF}$	Zone E	Zone F	Fiber	0.8
$e_{FG}$	Zone F	Zone G	Fiber	0.7
$e_{GH}$	Zone G	Zone H	Fiber	0.9
$e_{HM}$	Zone H	Control Center	Fiber	0.9
$e_{HI}$	Zone H	Zone I	wireless	0.8
$e_{IM}$	Zone I	Control Center	Satellite	0.7
$e_{IJ}$	Zone I	Zone J	Fiber	0.9
$e_{JM}$	Zone J	Control Center	Fiber	0.8
$e_{DF}$	Zone D	Zone F	Wireless	0.8
$e_{CF}$	Zone C	Zone F	Fiber	0.8
$e_{GM}$	Zone G	Control Center	Wireless	0.8
$e_{EG}$	Zone E	Zone G	Wireless	0.8
$e_{JH}$	Zone J	Zone H	Wireless	0.8
$e_{CI}$	Zone C	Zone I	Fiber	0.8
$e_{BI}$	Zone B	Zone I	Fiber	0.8

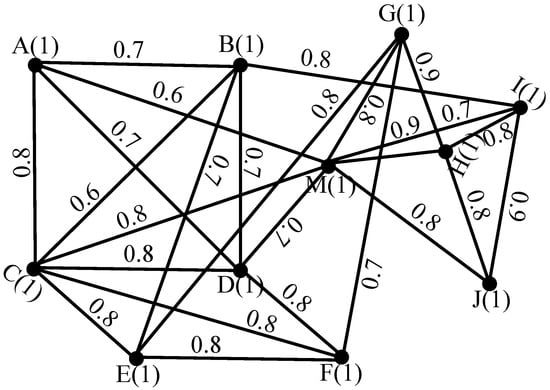
Figure 3. Fuzzy graph representation of a power grid network.

The incidence matrix for the $\mathfrak{M}\left(G\right)$ is given below:

$$A=\left|\begin{array}{ccccccccccccccc}0.9& 0.8& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0.8& 0.8& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0.7& 0\\ 0& 0& 0& 0.8& 0.8& 0& 0& 0& 0& 0& 0& 0.6& 0& 0& 0\\ 0& 0& 0& 0& 0.8& 0.8& 0.7& 0.9& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0.8& 0.8& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0.7& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0.8& 0& 0& 0& 0& 0.8& 0& 0& 0& 0\\ 0.9& 0& 0& 0& 0& 0& 0& 0.9& 0.8& 0& 0.8& 1& 0& 0& 0\\ 0& 0.8& 0.8& 0& 0& 0& 0& 0& 0& 0& 0& & 0& 0.8& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0.8& 0.7\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0.8& 0& 0.6& 0.7& 0& 0.7\end{array}\right|$$

Setting the threshold value as $\alpha =0.5$ ensures that only links with at least 50% reliability confidence contribute to the analysis, filtering out highly uncertain or poor-quality links without being overly restrictive.

$$A=\left|\begin{array}{ccccccccccccccc}1& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 1& 1& 0& 0& 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 1& 1& 1& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 1& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0& 1& 1& 0& 1& 1& 0& 0& 0\\ 0& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 0& 1& 1& 0& 1\end{array}\right|$$

The incidence matrix of the fuzzy graph is totally unimodular. Hence, it satisfies the condition of a fuzzy graphic binary matroid.

The cycles in the network indicate redundancy and alternative communication paths. The cycles covering different parts of the network highlighting redundancy and multiple communication paths are given below:

• Cycle 1:  $C_1=\{e_{AB},e_{BE},e_{EC},e_{AC}\}$
• Cycle 2:  $C_2=\{e_{BC},e_{CF},e_{EF},e_{BE}\}$
• Cycle 3:  $C_3=\{e_{CF},e_{FG},e_{GH},e_{HM},e_{CM}\}$
• Cycle 4:  $C_4=\{e_{GH},e_{EG},e_{BE},e_{BI},e_{HI}\}$
• Cycle 5:  $C_5=\{e_{IJ},e_{JM},e_{HM},e_{HI}\}$
• Cycle 6:  $C_6=\{e_{AM},e_{AC},e_{CM}\}$
• Cycle 7:  $C_7=\{e_{CM},e_{CF},e_{DF},e_{DM}\}$
• Cycle 8:  $C_8=\{e_{CR},e_{RM},e_{MT},e_{TC}\}$

The minimal dependent edges in these cycles forms a circuit in fuzzy graphic matroid $\mathfrak{M}\left(G\right)$.

The minimum reliability value of the circuit in $\mathfrak{M}\left(G\right)$ is given by

• Cycle 1:  $C_1=\{e_{AB}\left(0.7\right),e_{BE}\left(0.7\right),e_{EC}\left(0.8\right),e_{AC}\left(0.8\right)\}=0.7$
• Cycle 2:  $C_2=\{e_{BC}\left(0.6\right),e_{CF}\left(0.8\right),e_{EF}\left(0.8\right),e_{BE}\left(0.7\right)\}=0.6$
• Cycle 3:  $C_3=\{e_{CF}\left(0.8\right),e_{FG}\left(0.7\right),e_{GH}\left(0.9\right),e_{HM}\left(0.9\right),e_{CM}\left(0.8\right)\}=0.7$
• Cycle 4:  $C_4=\{e_{GH}\left(0.9\right),e_{EG}\left(0.8\right),e_{BE}\left(0.7\right),e_{BI}\left(0.8\right),e_{HI}\left(0.8\right)\}=0.7$
• Cycle 5:  $C_5=\{e_{IJ}\left(0.9\right),e_{JM}\left(0.8\right),e_{HM}\left(0.9\right),e_{HI}\left(0.8\right)\}=0.8$
• Cycle 6:  $C_6=\{e_{AM}\left(0.6\right),e_{AC}\left(0.8\right),e_{CM}\left(0.8\right)\}=0.6$
• Cycle 7:  $C_7=\{e_{CM}\left(0.6\right),e_{CF}\left(0.8\right),e_{DF}\left(0.8\right),e_{DM}\left(0.7\right)\}=0.6$
• Cycle 8:  $C_8=\{e_{CR}\left(0.9\right),e_{RM}\left(0.8\right),e_{MT}\left(0.9\right),e_{TC}\left(0.7\right)\}=0.7$

The overall network reliability is influenced by these cycle reliabilities. Cycles with lower reliability values indicate potential vulnerabilities where the network may fail if certain links within these cycles fail.

Overall Network Reliability Assessment:

• Highest Cycle Reliability: $C_5=0.8$
• Lowest Cycle Reliability: $C_2=0.6;C_6=0.6;C_7=0.6$

The weakest links to enhance the network’s overall reliability. Based on the reliability analysis, the minimum reliability value $\left(0.6\right)$ is addressed, and the cycles $C_2,C_6$, and $C_7$ are the weakest link among the overall network.

5.1. Comparision with the Coventional Methods

Graph-theoretic models encode interactions as crisp edges (i.e., either present or absent), failing to account for the varying degrees of interaction strength and reliability that exist in network systems. In contrast, fuzzy graph theory provides a more flexible model by representing interactions with membership values, typically in the range $[0,1]$, which reflect the degree of interaction or confidence in the interaction between the substations. Traditional models for power grid reliability, such as crisp graph theory and probabilistic methods, have notable limitations. Crisp graphs represent connections as either present or absent, thereby neglecting intermediate reliability states that often exist in real systems. Similarly, a probabilistic approach is effective for smaller systems that will become computationally intensive in large grids and lack a structured mechanism to systematically identify weak regions.

In contrast, the fuzzy graphic binary matroid framework integrates fuzziness with binary conditions, offering a structured approach to reliability assessment. It captures uncertainty through fuzzy weights, ensures binary compatibility via thresholding, and identifies minimal dependent sets where failure significantly reduces the rank. This enables operators to detect weak circuits and prioritize maintenance, thereby providing both structural and functional reliability insights.

5.2. Advantages of the Study

• The study aligns with modern smart grid requirements, where data transmission reliability is critical for automated control, fault detection, and load balancing.
• The algorithm helps in planning future expansions of the network while maintaining reliability through optimal cycle formation.
• The fuzzy graphic matroid captures independence and circuit properties that help identify minimal sets of communication links needed for connectivity.
• Identifying critical failure points through circuit analysis helps prioritize maintenance and recovery efforts.

5.3. Limitations of the Study

• Computing rank in large networks becomes computationally expensive since fuzzy independence must be checked for many subsets of edges.
• Selecting an optimal fuzzy basis becomes NP-hard, limiting practical applicability.
• This study typically captures a snapshot of the network without accounting for temporal variations in link reliability, which are critical for accurate fault prediction and recovery.
• The fuzzy graphic matroid framework focuses on connectivity and redundancy, but may not fully capture other interdependencies, such as communication protocol constraints and bandwidth limitations.
• The computational cost for identifying all circuits and fuzzy independent sets in very large power grid networks can be high.

5.4. Results and Discussion

The power grid network under analysis consists of 10 zones. Each zone is connected to a central control unit in a city, which is modeled using a fuzzy graphic binary matroid. The critical circuit of the network is found by addressing the minimum reliability value. Communication between these zones plays a vital role in the overall reliability of the power grid. The network is modeled using cycles, where each cycle represents a different path of communication between substations. The cycles $C_2,C_6$, and $C_7$ exhibits the lowest reliability value of $0.6$. The circuits with these cycles require significant maintenance and improvement. The satellite networks are more prone to weather-related disturbances and have lower bandwidth; their performance could degrade over time, leading to further issues. To enhance the network reliability, replacing satellite networks with fiber networks in these critical cycles is essential. Hence, the network could achieve better reliability and reduce the risk of communication failures.

6. Conclusions and Future Work

In this paper, the authors present the conditions for fuzzy graphic binary matroids and propose a systematic method for analyzing the reliability of the power grid network. The framework effectively identifies critical circuits that require greater attention for maintenance to enhance network performance and stability. By applying fuzzy graphic binary matroid principles, the study ensures both structural and functional reliability of the system. The identification of weak circuits allows operators to prioritize resources toward sensitive parts of the network. This contributes to improved decision-making in preventive and corrective maintenance. The findings demonstrate that matroid-based analysis offers a structured approach to network reliability assessment.

As future work, the determination of maintenance cost and optimal time allotment for addressing the identified critical circuits will be explored. This will enable prioritization of resources towards the sensitive sections of the network. Incorporating cost–time analysis will strengthen decision-making for preventive and corrective maintenance. This will provide a more practical and efficient framework for managing large-scale power grid networks.