The Geodetic Number for the Unit Graphs Associated with Rings of Order P and P²

Abstract

Let $G\left(R\right)$ be the unit graph associated with a ring R. Let p be a prime number and let R be a finite ring of order p or $p^2$ and be one of the rings ${\mathbb{Z}}_p,{\mathbb{Z}}_{p^2},GF\left(p^2\right),{\mathbb{Z}}_p(+){\mathbb{Z}}_p$ or ${\mathbb{Z}}_p\times {\mathbb{Z}}_p$. We determine the geodetic number $g\left(G\right(R\left)\right)$ associated with each such ring.

1. Introduction

The study of graphs associated with the algebraic structure of a ring R has received attention from many researchers. These graphs are used to represent the abstract substructure of a ring R. Many researchers have studied the relations between properties of graphs associated with a ring R and the algebraic structure of R. Beck [1] presented the zero-divisor graph; a graph defined by the set of elements of a ring R such that any different vertices u and v are adjacent if $uv=0.$ Anderson et al. [2] studied the zero-divisor graph $\Gamma \left(R\right)$ of a commutative ring. They investigated the interaction between the ring’s theoretical properties of R and the graph’s theoretical properties of $\Gamma \left(R\right).$ Anderson and Badawi [3] introduced the total graph; a simple graph that is defined by the set of elements of a ring R in which any distinct vertices x and y are adjacent if their sum is a zero-divisor in $R.$

The unit graph that is associated with a ring R is denoted by $G\left(R\right)$; it is a simple graph defined by a ring R in which two different vertices are adjacent if their sum is a unit in R. Grimaldi [4] studied the unit graph over ${\mathbb{Z}}_n,$ analyzing the graph $G\left({\mathbb{Z}}_n\right)$ in terms of the covering number, the chromatic polynomial of the graph $G\left({\mathbb{Z}}_n\right)$, the Hamilton cycles and independence number. Ashrafi et al. [5] investigated the unit graph $G\left(R\right)$ for an associative ring R, where different characterization results were obtained regarding the diameter, girth, connectedness and chromatic index of $G\left(R\right).$ Furthermore, unit graphs of rings of polynomials and power series have been discussed in [6]. Further, there are several publications that are devoted to this topic (see [2,7,8]).

Harary et al. [9] presented the definition of the geodetic number as a new graph theoretical parameter. Let $G=(V,E)$ be a connected graph. Let $H\subseteq V$, such that for every $v\in V,$ then two vertices x and y exist in H such that v lies on one of the geodesics $x-y.$ Then, H is called a geodetic set with cardinality greater than or equal to 2. Let $\mathcal{H}=\left\{\right|H|:H$ be geodetic$\}.$ The geodetic number for a connected graph G is denoted by $g\left(G\right),$ where $g\left(G\right)=min\mathcal{H}$.

Furthermore, Harary et al. [9] presented a formula expressing the geodetic number $g\left(G\right)$ as a function of the number of vertices for some specific graphs. The geodetic number was determined for the complete graphs $K_n,$ the complete bipartite graphs $K_{m,n}$ with $m,n\ge 2,$ the cycle graphs $C_n,$ the wheel graphs $W_{1,n}$ and the graph $P_r\times P_s$, where $P_r,P_s$ are path graphs. For a certain graph G, there are many applications of the geodetic number, including Location Theory and Convexity Theory, see [10].

The focus of our study is on calculating the geodetic number for the unit graph $G\left(R\right)$ for the rings R of order p and $p^2$. We hope this will open the way to further studies for more general rings. We note that for any connected graph G, the geodetic number $g\left(G\right)\ge 2$. In general, for any connected graph G, $2\le g\left(G\right)\le n.$ In this paper, for a disconnected graph G, we consider $g\left(G\right)$ to be $\infty .$ Furthermore, Chartrand et al. [11] showed that, for any connected graph G, $g\left(G\right)\le n-diam\left(G\right)+1$, where $dim\left(G\right)=max\left\{d\right(u,v):u,v\in V\}.$ Several researchers have studied this topic and presented some results [12,13,14,15,16,17,18].

2. Preliminaries

Suppose R is a finite ring of order $n.$ Let $n={\prod }_{i=1}^k{p}_i^{{\alpha }_i}$, where $p_i$ are distinct primes. Then, the additive Abelian group of R is a direct product of an additive cyclic group $C_{{}_m}=⟨a;ma=0⟩$, where $m=p_i^{e_j}$ such that ${\sum }_j{e}_j={\alpha }_i$ $\forall i,i=1,\cdots k.$ Hence, up to isomorphism, the number of rings of order n depends on the way that the exponents of ${\alpha }_i$ are represented. As usual, in a ring $R,$ an element a is said to be a unit if it has a multiplicative inverse b in which $ab=ba=1.$ The set $U\left(R\right)$ will denote the set of all units in R.

Consider ${\mathbb{Z}}_p,$ the ring of all integers modulo $p.$ The set ${\mathbb{Z}}_p^{\times }$ will denote ${\mathbb{Z}}_p\setminus \left\{0\right\}.$ The ring ${\mathbb{Z}}_p\times {\mathbb{Z}}_p$ is the set of ordered two-tuples from ${\mathbb{Z}}_p$ such that addition and multiplication are defined $(\mathrm{mod}$ $p)$ component wise. The ring ${\mathbb{Z}}_p(+){\mathbb{Z}}_p$ is defined to be the set of ordered two-tuples from ${\mathbb{Z}}_p$ with the operations:

$$\begin{array}{c}(a,b)+(c,d)=(a+c(\mathrm{mod}p),b+d(\mathrm{mod}p\left)\right)\\ (a,b)·(c,d)=\left(ac\right(\mathrm{mod}p),ad+bc(\mathrm{mod}p\left)\right).\end{array}$$

The ring ${\mathbb{Z}}_p(+){\mathbb{Z}}_p$ is called the idealization of ${\mathbb{Z}}_p$ as a ${\mathbb{Z}}_p-$module, see [19]. Note that the previous rings ${\mathbb{Z}}_p,{\mathbb{Z}}_p\times {\mathbb{Z}}_p$ and ${\mathbb{Z}}_p(+){\mathbb{Z}}_p$ are commutative rings with unities $1,(1,1)$ and $(1,0)$, respectively. Moreover, the set of units for $R={\mathbb{Z}}_p\times {\mathbb{Z}}_p$ is $U\left(R\right)=\{(x,y):x,y\in {\mathbb{Z}}_p^{\times }\}.$ If $R={\mathbb{Z}}_p(+){\mathbb{Z}}_p,$ then $U\left(R\right)=\left\{\right(x,y):$ $x\in {\mathbb{Z}}_p^{\times }\}$, where ${(x,y)}^{-1}=(x^{-1},-y{x}^{-2}).$ The ring $GF\left(p^n\right)$ will denote a finite field of order $p^n,$ a commutative ring with a unity in which all non-zero elements are a unit.

All graphs will be simple; they do not contain any loops or multiple edges. The null graph will be assumed to be a disconnected graph in which any two distinct vertices are non-adjacent. Let $G=(V,E)$ be a graph and let $u\in V.$ The set of neighbors of $u,$ denoted by $N_G\left(u\right),$ is defined to be the set of all vertices that are adjacent to $u.$ If u and v are distinct vertices, the geodesic between u and v, denoted by $u-v,$ is the shortest path that connects u and $v;$ its length is denoted by $d(u,v).$ We denote by $I[u,v]$ the set of all vertices in V that lies on some geodesic between u and v that includes u and $v.$ Consider H to be a subset of V. Let $I\left[H\right]={\bigcup }_{u,v\in H}I[u,v]$. Then, H will be called a geodetic set in G if $I\left[H\right]=V.$ The geodetic number for a connected graph G is denoted by $g\left(G\right);$ it is the minimum cardinality of geodetic sets in $G.$

3. The Unit Graph Associated with Rings of Order p

Suppose R is a finite ring of order $p.$ Then, its additive Abelian group is the cyclic group $C_p=⟨a:pa=0⟩$ for some $a\in R.$ Since the product of two elements $x,y\in R$ is equal to $nm{a}^2\in C_p,$ then $R=⟨a:a^2=0⟩$ or $R=⟨a:a^2=a⟩.$ Therefore, $R\simeq$ $C_p\left(0\right),$ the trivial ring in which the generator has a trivial square, or $R\simeq {\mathbb{Z}}_p$ under the operations modulo $p.$ If $R=$ $C_p\left(0\right),$ then $G\left(R\right)$ is a null graph of order $p,$ and hence $g\left(G\right(R\left)\right)=\infty .$ Assume $R={\mathbb{Z}}_p.$ If $x+y=0(\mathrm{mod}$ $p)$, then $d(x,y)=2$; otherwise, $d(x,y)=1$. Mainly, for every prime p, $x+y=0(\mathrm{mod}$ $p)$ if and only if $y=p-x\ne x$ except for $p=2.$ Hence, $G\left(R\right)$ is a connected simple graph with $1\le d(x,y)\le 2.$

The Geodetic Number for the Unit Graph $G\left({\mathbb{Z}}_p\right)$

In Theorem 1, we determine the geodetic number for the unit graph $G\left({\mathbb{Z}}_p\right)$.

Theorem 1.

The geodetic number for the unit graph $G\left({\mathbb{Z}}_p\right)$ is equal to 2.

Proof. 

Let V be the vertex set of the graph $G\left({\mathbb{Z}}_p\right)$ with order $p.$ If $p=2,$ then $\left|V\right|=2$ and hence $g\left(G\left({\mathbb{Z}}_p\right)\right)=2.$ Now, for $p>2,$ choose $a\in$ ${\mathbb{Z}}_p^{\times }.$ Let $H_a=\{a,p-a\}$, where $a\in$ ${\mathbb{Z}}_p^{\times }.$ Then, for every $x\in {\mathbb{Z}}_p\setminus H_a,$ we have $d(x,a)=d(x,p-a)=1.$ Hence, $I\left[H_a\right]=V$ and so $g\left(G\left({\mathbb{Z}}_p\right)\right)=2.$ □

For instance, consider the unit graph $G\left({\mathbb{Z}}_5\right).$ Let $u_i=i$ $\forall i\in {\mathbb{Z}}_5.$ Then, by Figure 1, the sets $H_1=\{u_1,u_4\}$ and $H_2=\{u_2,u_3\}$ are geodetic sets, where $I\left[H_j\right]=V$ for each $j=1,2.$ Thus, $g\left(G\left({\mathbb{Z}}_5\right)\right)=2.$

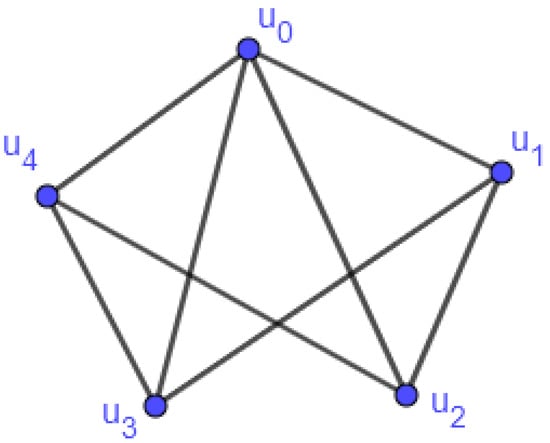
Figure 1. The unit graph $G\left({\mathbb{Z}}_5\right)$.

4. The Unit Graph Associated with Rings of Order p²

Suppose R is a finite ring of order $p^2.$ Hence, its additive Abelian group is the cyclic group $C_{p^2}=⟨x:p^{2}x=0⟩$ or $C_p\times C_p=⟨x,y:px=py=0⟩.$

In fact, Waterhouse in [20] classified the finite rings of order m with an additive cyclic group $C_m$ as described in Proposition 1.

Proposition 1.

(Waterhouse) If R is a finite ring with a cyclic additive group $C_m$ and $A=\{d:d$ divides $m\},$ then R is isomorphic to only one of the rings:

$$R_d=⟨a;ma=0,a^2=da⟩,$$

where a is an additive generator of $C_m$.

Remark 1.

Up to isomorphism, we have in total three rings with an additive Abelian group $C_{p^2}$; R $=R_1=⟨r;p^{2}r=0,r^2=r⟩$, $R=R_p=⟨r;p^{2}r=0,r^2=pr⟩$ or $R=R_{p^2}=⟨r;p^{2}r=0,r^2=0⟩.$

Now, assume R has an additive Abelian group $C_p\times C_p.$ Therefore, $R=⟨r,s:pr=ps=0⟩$ such that for every $x,y\in R,xy=a{r}^2+b{s}^2+crs+dsr$ for some $a,b,c$ and d in $R.$

Fine [21] has shown that, up to isomorphism, there are exactly eight rings with an additive Abelian group $C_p\times C_p.$ If the generators of R have a trivial square, i.e., $r^2=s^2=0,$ then in order to achieve the associative property, we have $rs=0$. Thus, the multiplication is trivial and so $R=(C_p\times C_p)\left(0\right)$. If $R=⟨r,s:pr=ps=0,r^2=0,s^2=s,rs=sr=0⟩,$ then R is isomorphic to the ring ${\mathbb{Z}}_p+C_p\left(0\right).$ If $R=⟨r,s:pr=ps=0,r^2=0,s^2=s,rs=sr=r⟩,$ then R is isomorphic to the ring ${\mathbb{Z}}_p(+){\mathbb{Z}}_p$, where $r=(0,1)$ and $s=(1,0).$ Otherwise, assume that $r^2\ne 0$ and $s^2\ne 0.$ Then, R can be isomorphic to one of the following rings: ${\mathbb{Z}}_p\times {\mathbb{Z}}_p,GF\left(p^2\right),$ or it is one of the following rings:

• $R=⟨a,b;pa=pb=0,a^2=a,b^2=b,ab=a,ba=b⟩.$
• $R=⟨a,b;pa=pb=0,a^2=a,b^2=b,ab=b,ba=a⟩.$
• $R=⟨a,b;pa=pb=0,a^2=b,ab=0⟩.$

The following remark draws from [21].

Remark 2.

If R is a ring of order $p^2$ and its additive Abelian group is $C_p\times C_p,$ then there are only eight rings up to isomorphism.

Obviously, for any ring R, the presence of a unity element is necessary for the connectedness of $G\left(R\right)$. Thus, it will inevitably affect the possibility of studying its geodetic number. This leads us to classify all the rings of order $p^2$ in terms of containing a unity element.

Remark 3.

Assume R is a finite ring of order $p^2.$ By Remarks 1 and 2, we have 11 types and so R is one of the following rings:

1. 

If R is any one of ${\mathbb{Z}}_{p{}^2},{\mathbb{Z}}_p\times {\mathbb{Z}}_p,{\mathbb{Z}}_p(+){\mathbb{Z}}_p$, then it has a unity of $1,(1,1)$ or $(1,0)$, respectively. Furthermore, since $GF\left(p^2\right)$ is a field, it has a unity of 1.

2. 

If $R=R_p=⟨a;p^{2}a=0,a^2=pa⟩$, then for each $x\in R,xa=\left(ka\right)a=kpa$ for some $k\in {\mathbb{Z}}_{p^2}$. So, if $xa=a$, then $pa=0$, which contradicts the assumption that R has an order $p^2$. Furthermore, if $R=R_{p^2}$, the multiplication is trivial. Hence, the rings $R_p$ and $R_{p^2}$ do not contain a unity element.

3. 

If $R={\mathbb{Z}}_p+C_p\left(0\right),$ then $\forall (a,b)\in R,(a,b)(0,1)=(0,0)\ne (0,1).$ Hence, there is no $1\in R.$ Similarly, if $R=C_p\times C_p\left(0\right)$, it is clear that it does not have a unity element.

4. 

If $R=⟨a,b;pa=pb=0,a^2=a,b^2=b,ab=a,ba=b⟩$, assume $x=na+mb\in R$, in which $xy=yx=y\forall y\in R$. Then, $a=xa=na+mb$ and $b=xb=na+mb$ and hence, $a=b$, a contradiction. Thus, R does not have a unity element in this case. Similarly, it can be shown that the ring $R=⟨a,b;pa=pb=0,a^2=a,b^2=b,ab=b,ba=a⟩$ does not have a unity element.

5. 

If $R=⟨a,b;pa=pb=0,a^2=b,ab=0⟩$, we have $ba=a^3=ab=0$ and $b^2=a^{2}b=0$. Thus, $xb=(na+mb)b=0\ne b$. Hence, there is no $1\in R.$

According to Remark 3, we only have to specify the geodetic number for the unit graphs associated with the rings $GF\left(p^2\right),{\mathbb{Z}}_{p^2},{\mathbb{Z}}_p(+){\mathbb{Z}}_p$ and ${\mathbb{Z}}_p\times {\mathbb{Z}}_p.$

4.1. The Geodetic Number for the Unit Graphs Associated with the Rings $GF\left(p^2\right)$ and ${\mathbb{Z}}_{p^2}$

In this section, we study the unit graphs for the rings $GF\left(p^2\right)$ and ${\mathbb{Z}}_{p^2}.$ We determine the minimal cardinality for the geodetic sets in these graphs based on the study of the set of neighbors for each vertex depending on the algebraic properties of each ring.

4.1.1. The Unit Graph over the Ring $GF\left(p^2\right)$

In the following theorem, we determine the geodetic number for the unit graph over the finite field $GF\left(p^2\right).$

Theorem 2.

The geodetic number for the unit graph $G\left(GF\left(p^2\right)\right)$ is equal to 2.

Proof. 

It is well known that for any p prime, the field $GF\left(p^2\right)$ is isomorphic to the ring ${}^{{\mathbb{Z}}_p\left[x\right]}{∕}_{⟨q\left(x\right)⟩}$, where $q\left(x\right)=a_0+a_{1}x+x^2$ is an irreducible monic polynomial over ${\mathbb{Z}}_p$. Let V be the vertex set of $G\left(GF\left(p^2\right)\right),$ then:

$$V=\{a+bX:a,b\in {\mathbb{Z}}_p,X=x+⟨q\left(x\right)⟩,x^2=-a_0-a_{1}x\}.$$

Therefore, for any two different vertices $u=a+bX$ and $v=c+dX,$ we have $u+v=0$ if and only if $c=p-a$ and $d=p-b.$ Let $u=a+bX$ be a non-zero vertex in $V,$ let $v=(p-a)+(p-b)X\in V$ and let $H=\{u,v\}.$ Then, H is geodetic set, where for every $w\notin H,$ we have $d(w,u)=d(w,v)=1.$ Therefore, $w\in I[u,v]=I\left[H\right]$ and so $g\left(G\right(R\left)\right)=2.$ □

As an example, consider the unit graph $GF\left(9\right).$ Since $GF\left(9\right)$ is isomorphic to the ring ${}^{{\mathbb{Z}}_3\left[x\right]}{∕}_{⟨x^2+1⟩}$, the vertex set is $V=\{0,1,2,X,2X,1+X,1+2X,2+X,2+2X\}.$

In Figure 2, assume $u_i=i$, where $i\in V$. We describe the unit graph $G\left(GF\right(9\left)\right)$ as an illustration of the geodetic sets for this graph with a minimal cardinality.

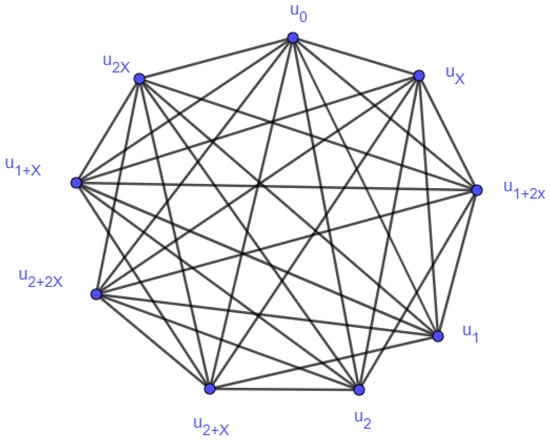
Figure 2. The unit graph $G\left(GF\right(9\left)\right)$.

4.1.2. The Unit Graph over the Ring $G\left({\mathbb{Z}}_{p^2}\right)$

We discuss the unit graph $G\left({\mathbb{Z}}_{p^2}\right)$and we determine the geodetic number $g\left(G\left({\mathbb{Z}}_{p^2}\right)\right)$ for each prime p.

Remark 4.

If $p=2,$ the subset $H=\{0,2\}$ is a geodetic set in $G\left({\mathbb{Z}}_{p^2}\right)$, where $I\left[H\right]=V\left(G\left({\mathbb{Z}}_4\right)\right)$. Hence, $g\left(G\left({\mathbb{Z}}_4\right)\right)=2.$

In Theorem 3, we show that for $p>2,$ $g\left(G\left({\mathbb{Z}}_{p^2}\right)\right)$ is equal to $4.$

Theorem 3.

The geodetic number for the unit graph $G\left({\mathbb{Z}}_{p^2}\right),$ for $p>2,$ is equal to $4.$

Proof. 

In ${\mathbb{Z}}_{p^2},$ each element has the form $i+jp,$ where $0\le i,j\le p-1.$ Hence, $U\left({\mathbb{Z}}_{p^2}\right)={\mathbb{Z}}_{p^2}\setminus \{jp:0\le j\le p-1\}$ with an order $p^2-p.$ Thus, $\forall i,j\in {\mathbb{Z}}_p,$ the set of neighbors $N_{G\left({\mathbb{Z}}_{p^2}\right)}(i+jp)={\mathbb{Z}}_{p^2}\setminus \{(p-i)+kp:0\le k\le p-1\}.$ The vertex set of $G\left({\mathbb{Z}}_{p^2}\right)$ can be decomposed as a union of the classes $A_i=\{i+jp:0\le j\le p-1\},0\le i\le p-1.$ Now, for any two distinct vertices u and v in $V\left(G\left({\mathbb{Z}}_{p^2}\right)\right)$, we have $d(u,v)=1$ if $v\in N_{G\left({\mathbb{Z}}_{p^2}\right)}\left(u\right).$ If $u=i_0+j_{0}p$ and $v=(p-i_0)+j_{0}p$ for some $i_0,j_0\in {\mathbb{Z}}_p,$ then $d(u,v)=2$, where $x=i_1+j_{0}p$ for some $i_1\in {\mathbb{Z}}_p\setminus \{i_0,p-i_0\}.$ Then, $u⟶x⟶v$ is a path of length 2. Hence, $G\left({\mathbb{Z}}_{p^2}\right)$ is a connected graph with $1\le d(u,v)\le 2.$

Now, let $H\subseteq V\left(G\left({\mathbb{Z}}_{p^2}\right)\right)$ be a geodetic set in $G\left({\mathbb{Z}}_{p^2}\right).$ Let $a,b\in H$, in which $d(a,b)>1.$ Then, $a,b\in A_0$ or $a\in A_i$ and $b\in A_{p-i}$ for some $i\in {\mathbb{Z}}_p$ and $i\ne 0.$ Assume that $a,b\in H\cap A_0.$ Then, $a=cp$ and $b=dp$ for some $c,d\in {\mathbb{Z}}_p$ and hence, for all $x\in V\setminus A_0$, $P(a,b):$ $a=cp\to x\to b=dp$ is a path of length 2 and exists in $G\left({\mathbb{Z}}_{p^2}\right).$ Hence, $\{a,b\}\cup \{A_1,A_2,\cdots ,A_{p-1}\}\subseteq I[a,b]$ but $A_0⊈I[a,b].$ Since H is geodetic, it must have another two elements $r\in A_i$ and $s\in A_{p-i}$ for some $i=1,\cdots ,p-1$ and therefore, its cardinality is greater than or equal to $4.$

Now, suppose that $a\in A_i\cap H,b\in A_{p-i}\cap H$ for some $i\ne 0.$ So, $a=i+kp$ and $b=(p-i)+tp$ for some $k,t\in {\mathbb{Z}}_p.$ Hence, for all $x\in {\bigcup }_{j\ne i,j\ne p-i}{A}_j$, we have:

$$P(a,b):a=i+kp\to x\to b=(p-i)+tp$$

as the shortest path from a to b including $x.$ Thus, for $j\ne i$ and $j\ne p-i,$ ${\bigcup }_j{A}_j\cup \{a,b\}\subseteq I[a,b]$ with $A_i\cup A_{p-i}I[a,b].$ Thus, since H is a geodetic set, H must contain two more elements r and s in which $r,s\in A_0$ or $r\in A_j$ and $s\in A_{p-j}$ for some $j\ne i.$ According to the discussion above, we conclude that H will be a geodetic set if and only if it has at least four elements.

On the other hand, consider $H_0=\{0,p,1,p-1\}.$ We can easily verify that $I\left[H_0\right]=V\left(G\left({\mathbb{Z}}_{p^2}\right)\right).$ Thus, $H_0$ is a geodetic set and therefore, $g\left(G\left({\mathbb{Z}}_{p^2}\right)\right)=4.$ □

4.2. The Geodetic Number for the Unit Graphs Associated with the Rings ${\mathbb{Z}}_p(+){\mathbb{Z}}_p$ and ${\mathbb{Z}}_p\times {\mathbb{Z}}_p$

Let $\widehat{G}$ be the unit graph associated with the ring ${\mathbb{Z}}_p(+){\mathbb{Z}}_p.$ Let $\widehat{U}$ be the unit graph associated with the ring ${\mathbb{Z}}_p\times {\mathbb{Z}}_p.$ We determine the geodetic numbers $g\left(\widehat{G}\right)$ and $g\left(\widehat{U}\right).$

4.2.1. The Geodetic Number for the Unit Graph $\widehat{G}$

We discuss the unit graph $\widehat{G}$. Note that any two distinct vertices $(a,b)$ and $(c,d)$ in $\widehat{G}$ are adjacent if $a+c$ is a unit in ${\mathbb{Z}}_p.$

Remark 5.

If $p=2,$ the set $H=\left\{\right(0,1),(0,0\left)\right\}$ is geodetic in $\widehat{G}$ and hence, $g\left(\widehat{G}\right)=2$ for $p=2.$

Next, in Theorem 4, we determine $g\left(\widehat{G}\right)$ for $p>2.$

Theorem 4.

For $p>2,$ the geodetic number for the unit graph $\widehat{G}$ is equal to $4.$

Proof. 

The vertex set of $\widehat{G}$ is $V\left(\widehat{G}\right)=\{(a,b):a,b\in {\mathbb{Z}}_p\}$, which has an order $p^2.$ Thus, for every $(a,b)\in V\left(\widehat{G}\right),$ the set of neighbors for $(a,b)$ is $N_{\widehat{G}}\left((a,b)\right)=\{(c,d):c\in {\mathbb{Z}}_p\setminus \{p-a\},d\in {\mathbb{Z}}_p\}.$ Suppose $u=(i,k)$ and $v=(j,l)$ are distinct vertices in $V\left(\widehat{G}\right).$ If $j\ne p-i,$ then $d(u,v)=1.$ Otherwise, assume that $i+j=0(\mathrm{mod}$ $p).$ Now, if $i,j$ are non-zeros, then $u=(i,k)⟶(0,k)⟶(j,l)=v$ is a path in $\widehat{G}$ and so $d(u,v)=2.$ If $i=j=0,$ since u and v are distinct in $V\left(\widehat{G}\right),$ say $k\ne 0.$ Thus, $u=(0,k)⟶(k,l)⟶(0,l)=v$ is a path in $\widehat{G}$ and so $d(u,v)=2.$ Thus, $\forall u,v\in V\left(\widehat{G}\right),$ we have $1\le d(u,v)\le 2$ and hence $\widehat{G}$ is connected.

Now, let $H\subseteq V\left(\widehat{G}\right)$ be a geodetic set. Consider the set $A_i\subseteq V\left(\widehat{G}\right)$ such that $A_i=\{(i,j):0\le j\le p-1\},0\le i\le p-1.$ Then, $V\left(\widehat{G}\right)$ is the disjoint union of $A_i$ with a cardinality p for each $i.$ Let $a=(i,k),b=(j,l)$ belong to H such that $d(a,b)>1.$ If $a,b\in H\cap A_0,$ then $d(a,b)=2$ and therefore, for all $x\in A_i,$ if $i\ne 0,$ a path $a⟶x⟶b$ exists in $\widehat{G}$. Thus, $\{A_i$: $i\ne 0\}\cup \{a,b\}\subseteq I[a,b]$ but $A_0⊈I[a,b]$. Note that for every $w\in$ $H\cap (A_0\cup A_j)\setminus \{a,b\}$ with $j\ne 0,$ then $A_0⊈I[w,a]\cup I[w,b]\cup I[a,b].$ Thus, H must have at least two other vertices in addition to a and b for H to be geodetic.

In the same manner, assume that $a,b\in H$ such that $a\in H\cap A_i$ and $b\in H\cap A_{p-i}$ for some $i\ne 0.$ Then, $A_i\cup A_{p-i}⊈I[a,b].$ Furthermore, for every $w\in (A_0\cup A_j)\setminus \{a,b\}$ and $j\ne 0,$ if w is added to $H,$ the situation will remain the same. Thus, H must contain at least two other vertices c and d from $A_j$ and $A_{p-j}$, respectively, for some $j\ne i$ and $j\ne 0.$ Therefore, the cardinality of H is greater than $4.$

Consider $H_0=\{a,b,c,d\}\subseteq V\left(\widehat{G}\right)$ such that $a\in A_i,b\in A_{p-i},c\in A_j,d\in A_{p-j}$ for some $i,j\in {\mathbb{Z}}_p$ and $i\ne j$. Then, $I\left[H_0\right]=V\left(\widehat{G}\right)$ and hence, $g\left(\widehat{G}\right)=4.$ □

4.2.2. The Geodetic Number for the Unit Graph $\widehat{U}$

Consider the unit graph $\widehat{U}$. Let $V\left(\widehat{U}\right)=\{(a,b):a,b\in {\mathbb{Z}}_p\}$ be the set of vertices of order $p^2$. Thus, for each $(a,b)\in V\left(\widehat{U}\right)$, the set of neighbors is defined by:

$$N_{\widehat{U}}\left((a,b)\right)=\{(c,d):c\in {\mathbb{Z}}_p\setminus \{p-a\},d\in {\mathbb{Z}}_p\setminus \{p-b\}\}.$$

In particular, if $p=2,$ the unit graph $\widehat{U}$ $=G({\mathbb{Z}}_2\times {\mathbb{Z}}_2)$ is disconnected. For instance, $d\left(\right(0,0),(1,0\left)\right)=\infty$ and hence, $g\left(\widehat{U}\right)=\infty .$

Lemma 1.

Consider $\widehat{U}$ provided that $p\ge 3.$ Then, $\widehat{U}$ is connected, and for each two distinct vertices u and v in $V\left(\widehat{U}\right),$ we have $1\le d(u,v)\le 2$.

Proof. 

Let u and v be distinct in $V\left(\widehat{U}\right)$, in which $d(u,v)\ne 1.$ Assume that $u=(x,y)$ and $v=(p-x,t)$ for some $x,y,t\in {\mathbb{Z}}_p.$ Hence, we have to show that a $(u-v)$ geodesic exists in $\widehat{U}$ with a length equal to 2.

Suppose $x=0.$ Since u and v are distinct, we have to consider y or t to be non-zero, say $y>0.$ Then, $P:(0,y)⟶(y,y)⟶(0,t)$ is a $u-v$ geodesic provided that $t\ne -y.$ Otherwise, if $t=-y,$ then $P:(0,y)⟶(-y,0)⟶(0,-y)$ is a $u-v$ geodesic. Furthermore, if $x=y=0,$ let $l\notin \{0,t\}.$ Then, $P:(0,0)⟶(l,t)⟶(0,t)$ is a $u-v$ geodesic.

Now, suppose that $x\ne 0.$ Then, according to t, we have the following cases:

• Suppose $t=p-y$. Then, $u=(x,y)$ and $v=(p-x,p-y).$ If $y\ne 0$, consider the $u-v$ geodesic $P:(x,y)\to (0,0)\to (p-x,p-y)$. If $y=0$, consider the $(u-v)$ geodesic $P:(x,0)\to (0,p-x)\to (p-x,0)$.
• Suppose $t\ne p-y$. If $t\ne 0$, consider the $u-v$ geodesic $P:(x,y)\to (0,t)\to (p-x,t)$. If $t=0$, then $u=(x,y)$ and $v=(p-x,0)$ and so $y\ne 0$. Thus, we consider $P:(x,y)\to (0,y)\to (p-x,0)$ as the $(u-v)$ geodesic.

□

Lemma 2.

The geodetic number for the unit graph $\widehat{U}$ is greater than $2.$

Proof. 

Assume H is a geodetic set in $V\left(\widehat{U}\right).$ Let $u,v\in H$ such that $d(u,v)\ne 1$. Thus, $u=(a,b)$ for some $a,b\in {\mathbb{Z}}_p$ and $v\in \{(p-a,j),(i,p-b):i,j\in {\mathbb{Z}}_p\}.$ Assume that $v=(p-a,j_0)$ for some $j_0\in {\mathbb{Z}}_p.$ Let $A\subseteq V\left(\widehat{U}\right)$ such that:

$$B=\{(a,k),(p-a,e),(t,p-b),(r,p-j_0):k\ne b,e\ne j_0\}.$$

Then, $B\ne ⌀$ and $B⊈I[u,v]$. For instance, if $u=(a,b)$ and $v=(p-a,j_0)$ with $a\ne 0$ and $j_0\ne b,$ then $(a,j_0)\in A$ but $(a,j_0)\notin I[u,v].$ If $a\ne 0$ and $j_0=b$, then $u=(a,b)$ and $v=(p-a,b)$ and hence, $(0,p-b)\in B$ but $(0,p-b)\notin I[u,v].$ If $a=0$, then $u=(0,b)$ and $v=(0,j_0)$ with $j_0\ne b.$ Hence, we may assume that $b\ne 0$ and so, $(b,p-b)\in B$ with $(b,p-b)\notin I[u,v].$

Similarly, if $u=(a,b)$ and $v=(i_0,p-b)$ for some $i_0\in {\mathbb{Z}}_p$, we have:

$$D=\{(p-a,e),(t,p-b),(p-i_0,k),(r,b):t\ne i_0,r\ne a\}$$

as a non-empty set with D$⊈I[u,v]$. Therefore, for any geodetic set in $\widehat{U}$, the cardinality must be greater than 2 and hence, $g\left(\widehat{U}\right)\ge 2$ as required. □

Remark 6.

If $p=3,$ it is immediately clear that $H=\left\{\right(0,1),(0,2),(0,3\left)\right\}$ is a geodetic set in $\widehat{U}$, where $I\left[H\right]=V\left(\widehat{U}\right)$. Therefore, for $\widehat{U}$ $=G({\mathbb{Z}}_3\times {\mathbb{Z}}_3),$ $g\left(\widehat{U}\right)=3$.

Next, we consider the unit graph $\widehat{U}$ for $p\ge 5.$

Lemma 3.

For $p\ge 5,$ the geodetic number for $\widehat{U}$ is greater than $3.$

Proof. 

Let H be a geodetic set in $V\left(\widehat{U}\right)$. In Lemma 2, we have proven that the cardinality of H is greater than $2.$ Now, let u and v be distinct vertices in H, in which $d(u,v)>1.$ Then, $u=(a,b)$ and $v\in \{(p-a,j),(i,p-b):i,j\in {\mathbb{Z}}_p\}$ for some $a,b\in {\mathbb{Z}}_p.$ Now, assume that $v=(p-a,j_0)$ for some $j_0\in {\mathbb{Z}}_p$. Furthermore, let $W=\{(a,k),(p-a,e),(t,p-b),(r,p-j_0)\}\subseteq$ $V\left(\widehat{U}\right)\setminus \{u,v\}.$ Then, $W⊈I[u,v].$ Since we have shown that $g\left(\widehat{U}\right)>2$ for $p\ge 5,$ it is sufficient to show that $\forall u,v,w$ is distinct in $V\left(\widehat{U}\right),$ and the set $\{u,v,w\}$ is not geodetic.

• Suppose that $w=(a,k_0)\in$ $H\cap A$, where $k_0\ne b.$ Thus, $u=(a,b),v=(p-a,j_0)$ and $w=(a,k_0)$ with $d(u,v)=d(w,v)=2$ and

  $$d(w,u)=\left\{\begin{array}{c}2,\mathrm{if}{k}_0=p-b\mathrm{or}a=0\hfill \\ \multicolumn{1}{c}{1,\mathrm{if}{k}_0\ne p-b\mathrm{and}a\ne 0}\end{array}\right..$$
  If $d(w,u)=1$ and $j_0=b,$ then $u=(a,b),v=(p-a,b)$ and $w=(a,k_0)$ and so, $(p-a,k_0)\notin I[u,v]\cup I[w,v]\cup I[u,w].$ If $j_0\ne b,$ then $(p-a,b)\notin I[u,v]\cup I[w,v]\cup I[u,w].$
  Now, assume that $d(w,u)=2.$ Then, we have the following cases:
  Case 1: If $a=0,$ then, $u=(0,b),v=(0,j_0)$ and $w=(0,k_0).$ Let $t_0\in {\mathbb{Z}}_p$, in which $t_0\notin \{b,j_0,k_0\}$. Then, $(0,t_0)\notin I[w,v]\cup I[u,v]\cup I[w,u].$
  Case 2: If $k_0=p-b$ and $a\ne 0,$ let $t_0\in {\mathbb{Z}}_p$ such that $t_0\ne j_0.$ Then, $u=(a,b),v=(p-a,j_0)$ and $w=(a,p-b)$ and therefore, $(p-a,t_0)\notin I[w,v]\cup I[u,v]\cup I[w,u].$
• Suppose that $w=(p-a,e_0)\in$ $H\cap A$ for some $e_0\ne j_0.$ Then, $u=(a,b),v=(p-a,j_0)$ and $w=(p-a,e_0)$ with $d(u,v)=d(u,w)=2$ and

  $$d(v,w)=\left\{\begin{array}{c}1,\mathrm{if}{e}_0\ne p-j_0\mathrm{and}a\ne 0\\ \multicolumn{1}{c}{2,\mathrm{if}{e}_0=p-j_0\mathrm{or}a=0}\end{array}\right..$$
  If $d(v,w)=1$ and $j_0=b,$ then $u=(a,b),v=(p-a,b)$ and $w=(p-a,e_0)$ with $a\ne 0$ and $e_0\ne j_0=b$ by assumption. Therefore,

  $$(a,e_0)\notin I[u,v]\cup I[u,w]\cup I[v,w],$$

  while, if $j_0\ne b,$ then $(a,j_0)\notin I[u,v]\cup I[u,w]\cup I[v,w].$
  Now, assume that $d(v,w)=2$ with $a=0.$ Then, $u=(0,b),v=(0,j_0)$ and $w=(0,e_0)$ and so, $(0,t_0)\notin I[w,v]\cup I[u,v]\cup I[w,u]$ for some $t_0\in {\mathbb{Z}}_p\setminus \{b,j_0,e_0\}$. Then, $(0,t_0)\notin I[w,v]\cup I[u,v]\cup I[w,u].$ If $d(v,w)=2$ with $e_0=p-j_0$ and $a\ne 0,$ let $t_0\in {\mathbb{Z}}_p$ $\setminus \{j_0,b\}.$ Then, $u=(a,b),v=(p-a,j_0)$ and $w=(p-a,p-j_0)$ and therefore, $(a,t_0)\notin I[w,v]\cup I[u,v]\cup I[w,u].$
• Suppose that $w=(t_0,p-b)\in$ $H\cap A$ for some $t_0\in {\mathbb{Z}}_p.$ Then, $u=(a,b),v=(p-a,j_0)$ and $w=(t_0,p-b)$ with $d(u,v)=d(u,w)=2$ and,

  $$d(w,v)=\left\{\begin{array}{c}1,\mathrm{if}{t}_0\ne a\mathrm{and}{j}_0\ne b\\ \multicolumn{1}{c}{2,\mathrm{if}{t}_0=a\mathrm{or}{j}_0=b}\end{array}\right..$$
  Assume that $d(w,v)=1$ with $a\ne 0.$ Since $t_0\ne a,$ then $(a,x)\notin I[u,v]\cup I[u,w]\cup I[v,w]$ $\forall x\in {\mathbb{Z}}_p\setminus \left\{b\right\}.$ If $a=0,$ then $u=(0,b),v=(0,j_0)$ and $w=(t_0,p-b)$ with $0\ne t_0\ne a$ and hence, $(p-t_0,p-j_0)\notin I[u,v]\cup I[u,w]\cup I[v,w]$.
  If $d(w,u)=2,$ assume that $u=(a,b),v=(p-a,j_0)$ and $w=(a,p-b).$ Then, $(a,t)\notin I[u,v]\cup I[u,w]\cup I[v,w]$ for all $t\in {\mathbb{Z}}_p\setminus \{b,j_0,p-b\}$. Otherwise, assume that $u=(a,b),v=(p-a,b)$ and $w=(t_0,p-b)$. In this case, we have $(a,t)\notin I[u,v]\cup I[u,w]\cup I[v,w]$ for some $t\notin \{b,p-b\}.$
• Suppose that $w=(r,p-j_0)\in$ $H\cap A$ for some $r\in {\mathbb{Z}}_p.$ Then, $u=(a,b),v=(p-a,j_0)$ and $w=(r,p-j_0)$ with $d(u,v)=d(w,v)=2$ and,

  $$d(w,u)=\left\{\begin{array}{c}1,\mathrm{if}r\ne p-a\mathrm{and}{j}_0\ne b\\ \multicolumn{1}{c}{2,\mathrm{if}r=p-a\mathrm{or}{j}_0=b}\end{array}\right..$$
  Assume that $d(w,u)=1.$ Then, $u=(a,b),v=(p-a,j_0)$ and $w=(r,p-j_0)$ with $r\ne p-a$ and $j_0\ne b.$ If $a\ne 0$ and $j_0>0,$ then $(p-a,p-j_0)\notin I[u,v]\cup I[u,w]\cup I[v,w].$ If $a=0,$ then $u=(0,b),v=(0,j_0)$ and $w=(r,p-j_0)$ and therefore, $(t,p-j_0)\notin I[u,v]\cup I[u,w]\cup I[v,w]$ for all $t\in {\mathbb{Z}}_p^{\times }\setminus \left\{r\right\}.$ If $j_0=0,$ then $u=(a,b),v=(p-a,0)$ and $w=(r,0)$ and therefore, $(a,t)\notin I[u,v]\cup I[u,w]\cup I[v,w]$ $\forall t$ $\in {\mathbb{Z}}_p^{\times }\setminus \left\{b\right\}.$
  If $d(w,u)=2,$ then $u=(a,b),v=(p-a,b)$ and $w=(p-a,p-b)$ or $w=(r_0,p-b)$ for some $r_0\in {\mathbb{Z}}_p$. Then, $a\ne 0$ and therefore, $(a,t)\notin I[u,v]\cup I[u,w]\cup I[v,w]$ for all $t\in {\mathbb{Z}}_p\setminus \left\{b\right\}.$

According to the cases above, the set $\{u,v,w\}$ is not geodetic for all $w\in A$. Hence, $g\left(\widehat{U}\right)>3$ as required. □

In the next theorem, we determine the geodetic number for the unit graph $\widehat{U}$ for every odd prime $p\ge 5.$

Theorem 5.

The geodetic number for the unit graph $\widehat{U}$ for a prime number $p,$ $p\ge 5,$ is equal to $4.$

Proof. 

Let $V\left(\widehat{U}\right)=\{(a,b):a,b\in {\mathbb{Z}}_p\}$ be the vertex set of the graph $\widehat{U}$. Let $a\in {\mathbb{Z}}_p\setminus \left\{0\right\}$ and let $u_1=$ $(a,a),u_2=(p-a,p-a),u_3=(a,p-a)$ and $u_4=(p-a,a)$ be distinct vertices in $V\left(\widehat{U}\right).$ We show that $H=\{u_1,u_2,u_3,u_4\}$ is a geodetic set in $V\left(\widehat{U}\right).$

For every $w\in V\left(\widehat{U}\right)\setminus H,$ if $w=(i,j)$ such that $\{i,j\}\cap \{a,p-a\}=⌀,$ then $d(w,u_r)=1$ for all $1\le r\le 4.$ Therefore, assume that $\{i,j\}\cap \{a,p-a\}\ne \varphi .$ This leads to one of the following cases:

• Assume that $w=(p-a,x)$ for some $x\in {\mathbb{Z}}_p$. Since $w\notin H,$ we have $x\notin \{a,p-a\}.$ Thus, $w\in I[u,v]$, where a path $P(u_2,u_4)$ exists in $\widehat{U}$ and is defined by

  $$P(u_2,u_4):u_2=(p-a,p-a)⟶w=(p-a,x)⟶u_4=(p-a,a).$$
• Assume that $w=(a,y)\in V\left(\widehat{U}\right)\setminus H$ for some $y\in {\mathbb{Z}}_p$. Then, $y\notin \{a,p-a\}$ and hence $w\in I[u,v]$, where there is a path $P(u_1,u_3)$ in $\widehat{U}$ defined by

  $$P(u_1,u_3):u_1=(a,a)⟶w=(a,y)⟶u_3=(a,p-a)$$
• Assume that $w=(t,p-a)\in V\left(\widehat{U}\right)\setminus H$ for some $t\in {\mathbb{Z}}_p$. Then, $t\notin \{a,p-a\}$ and hence $w\in I[u,v]$, where there is a path $P(u_2,u_3)$ in $\widehat{U}$:

  $$P(u_2,u_3):u_2=(p-a,p-a)⟶w=(t,p-a)⟶u_3=(a,p-a).$$
• Assume that $w=(l,a)\in V\left(\widehat{U}\right)\setminus H$ for some $l\in {\mathbb{Z}}_p$. Then, $l\notin \{a,p-a\}$ and hence $w\in I[u,v]$, where a path $P(u_1,u_4)$ in $\widehat{U}$ is defined by

  $$P(u_1,u_4):u_1=(a,a)⟶w=(l,a)⟶u_4=(p-a,a).$$

Thus, from the previous cases, we find that $I\left[H\right]=V\left(\widehat{U}\right)$ and so, H is geodetic. Thus, by Lemma 3, $g\left(\widehat{U}\right)=4.$ □

5. Conclusions

In this paper, we have focused on studying the geodetic number for the unit graphs $G\left(R\right)$ associated with rings of orders p and $p^2,$ where p is a prime number. It turned out that $G\left(R\right)$ only exists if such rings have unity and hence are commutative. It was found that the geodetic number $g\left(G\right(R\left)\right)$ is defined only if R is one of the following rings: ${\mathbb{Z}}_p,{\mathbb{Z}}_{p^2},GF\left(p^2\right),$ ${\mathbb{Z}}_p(+){\mathbb{Z}}_p$ or ${\mathbb{Z}}_p\times {\mathbb{Z}}_p.$ For the remaining cases of rings of order p and $p^2,$ the unit graphs do not exist, since such rings lack unity elements. Furthermore, we have determined the geodetic number for the unit graphs associated with such rings based on the algebraic structure of each ring. This resulted in several conclusions. It was found that the geodetic number for each of the unit graphs $G\left({\mathbb{Z}}_p\right)$ and $G\left(GF\left(p^2\right)\right)$ is 2. For the unit graph $G\left({\mathbb{Z}}_{p^2}\right),$ it was shown that the geodetic number is 4 for $p\ge 3$, while $g\left(G\left({\mathbb{Z}}_{p^2}\right)\right)=2$ for $p=2.$ The unit graphs $G\left({\mathbb{Z}}_p(+){\mathbb{Z}}_p\right)$ and $G({\mathbb{Z}}_p\times {\mathbb{Z}}_p)$ are denoted by $\widehat{G}$ and $\widehat{U}$, respectively. It was shown that the geodetic number $g\left(\widehat{G}\right)=2$ for $p=2$, while $g\left(\widehat{G}\right)=4$ for $p>2.$ For the graph $\widehat{U},$ it was found that $g\left(\widehat{U}\right)=\infty$ for $p=2$ and $g\left(\widehat{U}\right)=3$ for $p=3$, while $g\left(\widehat{U}\right)=4$ for $p\ge 5.$ We have not discussed the geodetic number of rings of order $p^3$ and higher. Commutativity is not guaranteed in such rings. This makes the research more involved in this case.