High-Field Nonresonant Response of Zundel Cations to Intense Terahertz Radiation

Abstract

The fundamental unit for comprehending the physicochemical properties of water, the Zundel cation configuration H₅O₂⁺, has yet to be exhaustively evaluated in terms of its interaction with terahertz (THz) electromagnetic waves, characterized by sub-picosecond oscillation periods or pulse widths. In this study, we embark on an investigation of the broad resonance and high-field nonresonant effects of intense THz radiation (ITR) on Zundel cations, utilizing a multifaceted methodological approach that includes density functional theory (DFT) calculations, finite difference time domain (FDTD) algorithm of the Schrödinger equation, and ab initio molecular dynamics (AIMD) simulations. Our analysis reveals that the proton potential energy surface (PES) varies in response to the external electric (E) field, suggesting that the interaction frequency of the central proton with the electromagnetic wave encompasses the THz band. This resonance effect is associated with proton behavior that may oscillate or demonstrate periodic tunneling. Moreover, our work uncovers the high-field nonresonant effects of ITR on Zundel cations, manifesting in proton transfer and vibrational excitation of the system. Our findings contribute to the understanding of the interaction between Zundel species and electromagnetic waves by presenting a microscopic view of proton transfer as informed by wavefunction evolution.

1. Introduction

Ever since G. Zundel introduced the double-minimum potential well model, the intriguing characteristics of Zundel cations have commanded attention in the context of water’s physical and chemical properties [1,2,3,4,5]. The ab initio calculation method has delivered accurate potential energy surface (PES) of Zundel cations [6], bolstering full-dimensional quantum dynamics simulations of the Zundel cluster [7], as well as quantum simulations of proton transfer [8]. Meanwhile, molecular dynamics (MD) methods permit simulations of the complex system of bulk water, comprising numerous water molecules. Ab initio molecular dynamics (AIMD) simulations, for example, Car-Parrinello MD, density-functional tight-binding (DFTB) MD [9], and divide-and-conquer DFTB (DC-DFTB) MD simulations [10], offer profound insights into the proton transfer process within bulk water. The resultant proton diffusion coefficients align with experimental findings. Furthermore, path integral molecular dynamics (PIMD) simulations have spotlighted nuclear quantum effects (NQEs), such as proton tunneling and zero-point energy in high-pressure ice hydrogen bonds [11], bulk water [12,13,14], and liquid water under an external E field [15]. The significance of quantum effects in proton transfer has been corroborated by potential-induced dioxygen reduction experiments at ambient temperature [16]. The NQEs of protons in hydrogen-bonded molecular chains have also been observed via scanning tunneling microscopy/atomic force microscopy (STM/AFM) measurements [17]. Both theoretical and experimental evidence substantiate the vital role the quantum effect of the nucleus plays within the hydrogen bond system.

Under the widely endorsed Grotthuss mechanism, the remarkable mobility of protons within liquid water owes to the proton “hopping” mechanism between neighboring water molecules within Zundel cations [2,3]. Recent experimental advances in this domain are equally exciting. Transient infrared (IR) pump–probe spectra have unveiled the pivotal role fluctuating E fields play in proton motion within the Zundel configuration [18]. Vibrational spectroscopy within clusters has further detailed proton transfer within ultracold clusters of isotope water molecules [19]. Notably, two-dimensional infrared (2D-IR) spectroscopy demonstrated that Zundel cations are copious in bulk water with an approximate 1-picosecond lifespan, underscoring their importance in aqueous proton transport [20].

The THz frequency range accommodates the frequencies associated with the formation and rupture of hydrogen bonds within water, and the low-frequency vibrational modes of the hydrogen bond network. The swift progression in THz science and technology now permits the generation of intense THz radiation (ITR) with sub-picosecond E field fluctuations, facilitating interactions with an array of substances [21,22]. The energy of THz photons is also comparable to hydrogen bond energy. THz spectroscopy has been employed to monitor the characteristic vibrational modes of hydrated ions [23]. Given the temporal and frequency selectivity, THz waves could conceivably interact with the Zundel configuration. However, comprehensive theoretical simulations or experimental investigations scrutinizing these molecular level interactions remain scant.

In the present study, we employ DFT calculations to ascertain the PES of Zundel species under the influence of an external E field. This provides an energy landscape that characterizes the resonant interaction of Zundel cations with THz electromagnetic waves. The evolution of the proton wavefunction, as dictated by the time-dependent (TD) Schrödinger equation, unveils details about the oscillation and transfer of protons under the nonresonant influence of the high-field of the ITR. Ultimately, we use AIMD simulations to simulate the potent nonresonant effect of ITR on the Zundel cation.

2. Methods

2.1. PES Scans of Zundel Cations

The Zundel cation (H₂O···H⁺···OH₂) structure as shown in Figure 1a was optimized using the B3LYP-D4 [24,25] functional and def2-QZVPP atomic basis sets with auxiliary basis [26,27,28], facilitated by the ORCA 5.0 software package [29,30]. To significantly accelerate the computational process while maintaining virtually no loss in precision, the ORCA software employs the resolution of the identity (RI) approximation method as its default approach for calculating Coulomb interactions [31,32]. Figure S1 illustrates the optimized equilibrium configuration of the Zundel cation, where the two oxygen atoms are spaced 2.40 Å apart.

After optimizing the structure to obtain the ground state equilibrium configuration, the next step is to perform PES scans under external E field variations. When there are substantial structural deviations from the equilibrium state in the course of the PES scans, relying solely on single point energy calculations at the B3LYP-D4/def2-QZVPP level may not ensure the precision of energy calculations. It is necessary to select a more accurate double-hybrid functional. The PES of the proton within the Zundel cation along the transfer coordinate Z was computed via DFT methodology using the ORCA 5.0 package. Considering both robustness and performance in calculating weak intermolecular interactions, the PWPB95-D4 [24,33] functional and def2-QZVPP basis set were employed in PES scans. The scanning ranges for the oxygen atomic spacing ranged from 2.1 Å to 3.2 Å and for the proton position Z scanning ranged from −1 Å to 1 Å, with a spatial step of 0.05 Å.

The PES data were computed for Z-direction E field intensities increasing from 0 to 8 V/nm, with a field strength scanning step size of 0.4 V/nm, yielding a total of 19,803 data points across the PES under varied external E field conditions. Due to computational resource limitations, we conducted a rigid scan rather than a relaxed one, as additional structural optimizations would result in an impractical computational time burden because structural optimization for each scanning point takes several tens of minutes in ORCA. So, in the PES scans, only Z, R_O-O, and E field intensity are varied, while the other geometric parameters remain at their ground state equilibrium values.

While more accurate global PESs are accessible for the Zundel configuration [6], our dynamic processes are conducted under the influence of a time-varying external E field. This necessitates the utilization of PESs that account for variations in external field dimensions. Due to limitations in computational resources, we conducted PES scans at a reduced level of atomic basis sets and functional calculations, while incorporating external E field dimensions.

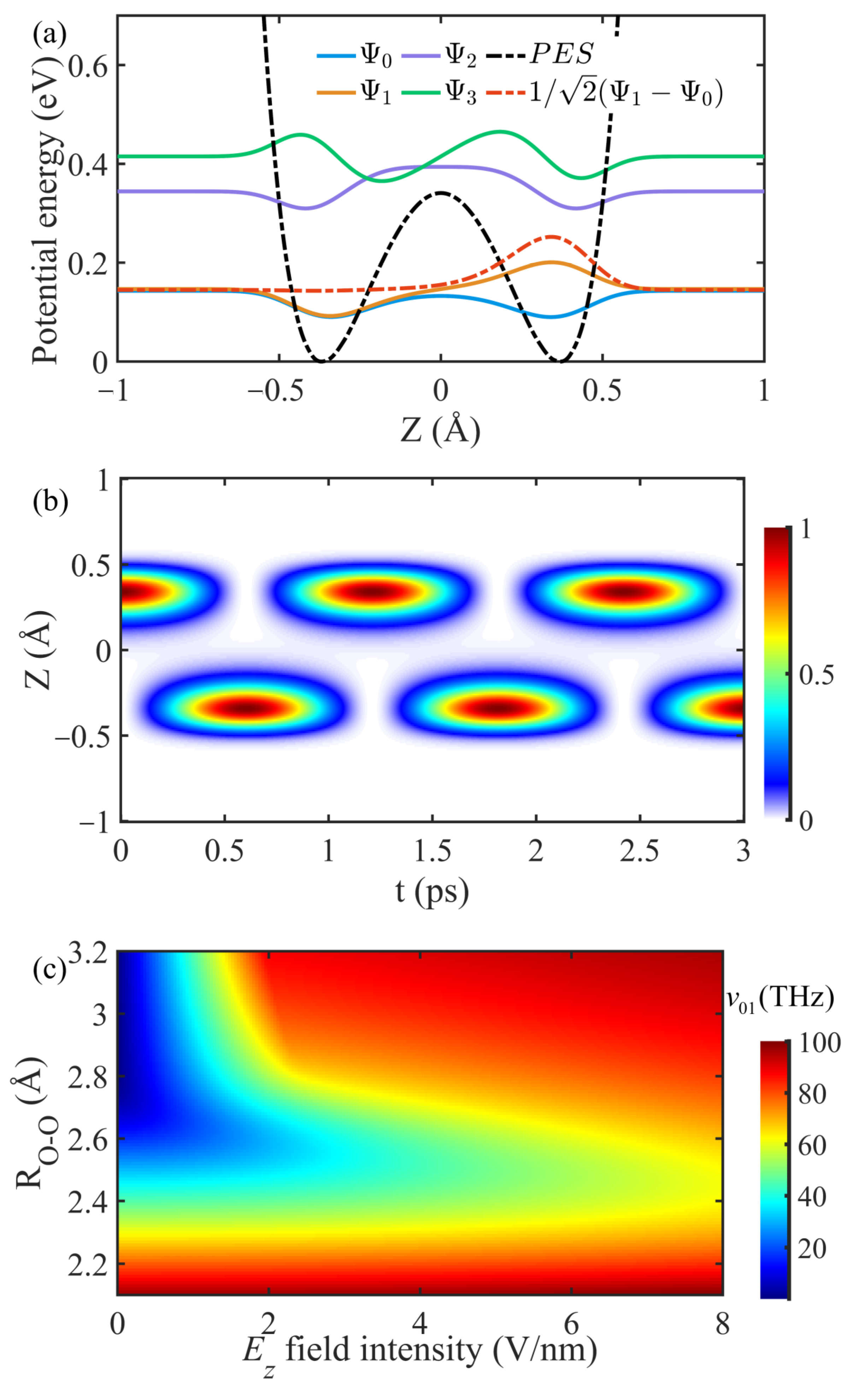
2.2. Solving the TD Schrödinger Equation via the FDTD Method

The one-dimensional TD Schrödinger equation is

$$i\hslash \frac{\partial }{\partial t}\Psi (z,t)=\left(-\frac{{\hslash }^2}{2\mathrm{m}}\frac{{\partial }^2}{\partial z^2}+U\left(\mathrm{t}\right)\right)\Psi (z,t).$$

(1)

Here, ħ represents the reduced Planck constant and U(t) denotes the TD potential function. The spatial scale of the molecule is on the order of nanometers, while the wave packet length of each ITR pulse is on the order of tens of micrometers. Consequently, the impact of ITR on molecular systems can be effectively modeled as a time-varying uniform E field acting on the entire molecular system. Thus, we can utilize the data obtained from PES scans to determine how the potential energy function varies with time. Initially, we need to specify the variation of the applied E field, denoted as E(t), and in conjunction with the discussions in Section 2.1 regarding the determination of PESs U(E) at different E field strengths, ultimately arrive at the TD potential function U(t). For convenience, we denote the first and second time derivatives of the wavefunction as v and a:

$$\begin{array}{l}v(t)=\frac{\partial }{\partial t}\Psi (z,t)\\ a(t)=\frac{{\partial }^2}{\partial t^2}\Psi (z,t)\end{array}.$$

(2)

The next step involves uniformly discretizing the TD Schrödinger equation in space and employing the velocity Verlet integration method for time integration [34,35]

$$\begin{array}{l}\Psi (z,t+\Delta t)=\Psi (z,t)+v(t)\Delta t+\frac{1}{2}a(t){(\Delta t)}^2\\ v(t+\Delta t)=v(t)+\frac{1}{2}\left[a(t)+a(t+\Delta t)\right]\end{array}.$$

(3)

By specifying the initial values of the wavefunction and iteratively solving, we can obtain the temporal evolution of the wavefunction. In this study, the spatial step is 0.01 Å and the integration time step is 1 attosecond, using a one-dimensional model Hamiltonian’s reduced mass equivalent to a proton’s mass.

2.3. AIMD and AI-PIMD Simulations of Zundel Cations

The ORCA 5.0 package’s AIMD module was utilized to simulate the influence of intense field THz waves on Zundel cations, with the B3LYP-D4 functional and the def2-SVP basis set. The system was initialized at 300K, with a simulation time step of 0.5 fs, recording the system’s dipole moment at each frame. The system was initially simulated for 25 picoseconds, with an ITR E field pulse applied over 2 ps, followed by a further 25 ps of simulation. The time domain waveform of the E field can be expressed as

$$E(t)=E_{\max }\exp \left[-2\log 2{\left(\frac{t-t_c}{\tau }\right)}^2\right]\sin (2\pi ft-\frac{\pi }{2}),$$

(4)

where E_max, t_c, τ, and f are the peak of the E field, the pulse center, the pulse width, and the frequency of the ITR, respectively. When t_c = 0.5 ps, τ = 0.2 ps, and f = 3 THz, the time-domain waveform and power spectrum of the ITR are shown in Figure S2a,b.

AI-PIMD simulations of ITR effects on Zundel cations were executed using the CP2K software [36], with an initial temperature of 300K, a time step of 1 fs, and 8 ring polymer beads allocated to each atom. The system dipole at each frame was calculated with respect to the system’s charge center, with a simulation time of 25 + 1 + 25 ps, where the central 1ps applies an ITR with a peak value of 10 V/nm.

2.4. Calculation of IR Spectrum

The IR absorption spectrums were derived via the Fourier transform of the autocorrelation function of the time derivative of the dipole moment [37]

$$A(\omega )\propto {{\displaystyle \int 〈\frac{d\mathit{\mu }(\tau )}{dt}\frac{d\mathit{\mu }(t+\tau )}{dt}〉}}_{\tau }{e}^{-i\omega t}dt,$$

(5)

where μ is the dipole moment of the system. During the MD simulation, the system’s dipole moment at each frame was computed to facilitate the calculation of the IR absorption spectrum. Transient IR absorption lines were obtained from dipole data within a 0.5 ps time window.

To establish a correlation between the infrared spectra obtained in MD simulations and molecular vibrational mode frequencies, structural optimization and vibrational analyses were conducted at the B3LYP-D4/def2-svp level [26,27], ensuring congruence with AIMD simulations.

3. Results and Discussion

3.1. Deformation of Proton PES under Elevated Static E Fields

The proton PES exhibits a pronounced dependence on the intermolecular water distance (R_O-O), with modulations in response to variations in the local E field. As demonstrated in Figure 1b, the PES of Zundel cations, obtained via Density Functional Theory (DFT) computations, reveals alterations under the influence of external E fields. As E field strength escalates from 0 to 8 V/nm, a progressive deformation of the PES is observed, exhibiting a strong tendency towards one side. Augmentation of the E field results in the loss of symmetry in the double potential well, leading to its eventual vanishing.

3.2. Resonant Interaction between THz Waves and Zundel Cations

Resonance interaction is a basic form of interaction between electromagnetic waves and matter. One of the basic conditions of resonance is that the energy level of matter matches the light quantum energy of electromagnetic waves. Therefore, it is necessary to examine the energy levels of molecules from the PES. Figure 2a shows the symmetric PES when R_O-O is 2.8 Å, depicted by the black dotted line. In the case of static potential wells, the proton wavefunction adheres to the stationary Schrödinger equation,

$$H{\Psi }_i=E_i{\Psi }_i,i=0,1,2,\cdots ,$$

(6)

where E_i denotes energy eigenvalues, with the Hamiltonian H determined by the PES. This equation facilitates the derivation of eigen wavefunctions for the proton in the Z-direction, alongside their corresponding energy eigenvalues. The four lowest energy wavefunctions are represented in Figure 2a.

The blue (even parity) and yellow lines (odd parity) represent wavefunctions corresponding to the ground eigenstate and the first excited eigenstate, respectively. The first two energy levels of the proton, when considering a specific energy barrier at the center of the double-minimum potential, demonstrate close energetic values with a mere energy gap of 3.4 meV. When we consider the initial proton state as a linear superposition of these two eigenstates (illustrated by the red dotted line in Figure 2a), it is evident that the proton’s most probable density is initially situated in the positive coordinate well (with negligible density in negative coordinates). Then, the time evolution of the proton wavefunction, according to the time-dependent Schrödinger equation, is

$$\Psi (z,t)=\frac{1}{\sqrt{2}}\left({\Psi }_1{e}^{-\frac{i}{\hslash }{E}_{1}t}-{\Psi }_0{e}^{-\frac{i}{\hslash }{E}_{0}t}\right),$$

(7)

which can be resolved by the Schrödinger equation via the FDTD algorithm. Figure 2b depicts the evolution of the proton probability density distribution. The proton oscillation between two wells in the one-dimensional model is seen to have a frequency of 0.83 THz, calculated from the oscillation period in Figure 2b, concordant with the theoretical value derived from the energy level difference

$${\nu }_{01}=(E_1-E_0)/h,$$

(8)

where h is the Planck constant. The proton’s maximum kinetic energy during this oscillation, 0.145 eV, is less than the central energy barrier of 0.34 eV, indicating the occurrence of quantum tunneling. Consequently, even two water molecules 2.8 Å apart can experience an exchange of extra protons within a picosecond timescale. However, this model, being static, fails to account for the impact of random polarization fields on the Zundel cation in liquid water, an effect which disrupts the potential well’s symmetry.

Broadening our discussion, Figure 2c reveals a wide frequency range for this periodic tunneling behavior, dependent on variations in R_O-O and Ez fields. An elongation of the distance between adjacent water molecules induces a decrease in the oscillation frequency of protons within the double-minimum well. Simultaneously, fluctuations of the E field in the Z-direction influence the tunneling frequency for a fixed R_O-O distance. The E field component in the Z-direction elevates the energy level difference between the ground state and the first excited state, correspondingly increasing the oscillation frequency. Generally, in bulk water, the distance between the two oxygen atoms in Zundel cations is typically between 2.2 and 2.8 Å [20]. This results in the photon energy corresponding to the energy level difference between the ground state and the first excited state being above 30 THz. When R_O-O falls below 2.5 Å, the double-minimum potential diminishes and yields a single-minimum well, indicating a shared proton between the two water molecules. Additionally, the lifetime of Zundel geometries, being limited to 1 ps, suggests that oscillation frequencies lower than 1 THz would contribute minimally to the proton transfer process. These limitations suggest the existence of a periodic “hopping” process, where protons tunnel across the energy barrier between adjacent water molecules at THz frequencies.

3.3. Proton Transfer during Collisional Events

The static symmetric double-well potential in liquid water is unsustainable amidst local polarized E field fluctuations and dynamic hydrogen-bonded networks. Proton transfer within the Zundel cation may accompany water molecule collisions and local E field fluctuations. Figure 3 elucidates the proton transfer process during the ‘collision’ of two water molecules within a Zundel cation, simulated based on the FDTD solution of the time-dependent Schrödinger equation. Initially, the proton resides in the potential well on the positive coordinate side with a kinetic energy of 0.12 eV. Proton transfer completion occurs at 0.5 ps, 1.0 ps, and 2.0 ps, as demonstrated in Figure 3a–c, correlating with the approach and separation of water molecules (3.0 Å→2.8 Å→3.0 Å). The lowest intermediate energy barrier height is 0.34 eV when R_O-O is 2.8 Å, roughly three times the kinetic energy of the proton. Hence, proton transfer occurs with a certain probability during collision events, with this probability increasing with longer collision times. This transfer process during collisions encompasses oscillation features typical of the static symmetric double-well potential, requiring two oxygen atoms to maintain close proximity over a sufficient period to facilitate proton transfer. This requisite duration is contingent on the oscillation period of the symmetric double-well illustrated in Figure 2c. In stark contrast, results based on classical Newtonian particle kinematics (Figure 3d–f) suggest that proton transfer is unattainable in these three collision scenarios. Given initial proton positions and kinetic energy (0.12 eV), identical to those in Figure 3a–c, the probability of proton transfer, due to the particle’s kinetic energy being less than the barrier height (0.34 eV), is effectively null. This limitation illustrates that classical MD simulations cannot account for such phenomena.

Given that the separation between two oxygen atoms typically falls below 2.8 Å, the phenomenon of proton transfer within Zundel cations is predominantly devoid of reliance on quantum tunneling effects. Consequently, encounters involving distances of 2.8 Å between the oxygen atoms in Zundel cations occur exceedingly infrequently. Nevertheless, the discourse within this segment remains capable of shedding light on the quantum tunneling mechanism intrinsic to extended proton transfer processes akin to hydrogen bonds. Such phenomena are prevalent across a multitude of biochemical processes, prominently including enzyme catalysis.

3.4. Proton Transfer Induced by High-Field Nonresonant Interaction

E field oscillations can impact the structure or proton transition dynamics of the Zundel cationic system. Hydrogen bond oscillations and transformations within bulk water, which transpire on a picosecond timescale, introduce local E field fluctuations in the THz band. Utilizing the simplified one-dimensional model and time-dependent (TD) Schrödinger equation, Figure 4 delineates the influence of sinusoidal and THz E fields on the proton transition process. The variability in the E field induces oscillation and proton translocation within Zundel cations, as demonstrated in Figure 4c,f. As the E field induces a deformation in the potential PES of the proton, a PES inversion facilitates proton movement along the evolving valley floor of the PES, thus effectuating proton transfer. Simultaneously, E field fluctuations reduce the intermediate barrier height and transiently create a near-symmetrical double barrier. Such alterations enable proton transference via periodic tunneling, a process that does not necessitate the proton’s kinetic energy to exceed the intermediate barrier height within the Zundel configuration.

The oscillatory collision of water molecules within bulk water, grounded in the hydrogen-bonded network and slow E field changes, underpins the alteration in Zundel configuration. Present advancements in THz science and technology facilitate the production of sub-picosecond electromagnetic pulses with a spectral distribution in the THz range, which matches the rapid dynamic process of water. Figure 4d–f highlight the impact of intense terahertz radiation (ITR) on Zundel configuration protons, as resolved by the TD Schrödinger equation. A directionally polarized ITR, through the high-field nonresonant effect, induces proton oscillation and excites the proton from the ground state to a superposition state, incorporating higher eigenstates. In this context, the ITR’s directionally high field applies work to the protons, instigating proton oscillations, despite the ITR’s power spectrum range failing to match the proton transition frequency.

3.5. Vibrational Excitation Instigated by ITR’s Nonresonant Interaction

Given that both the hydrogen-bonded network vibrations and local E field fluctuations of water molecules within bulk water occur in the THz band, examining the effect of THz waves on Zundel cations is of paramount importance. The previously mentioned one-dimensional approach possesses limitations in studying cation responses to THz waves, which underscores the need for further exploration via AIMD simulations. The system’s equilibrium time is 5 ps and the average kinetic energy of the Zundel cation for the following 20 ps registers at 0.104 eV. As Figure S2a illustrates, post 20 ps, an ITR with a peak E field of 10 V/nm is applied. The pulse center is positioned at 21 ps, with power concentrated around 3 THz, as depicted in Figure S2b.

Figure 5a and Figure S3 elucidate the shift in the system’s infrared (IR) absorption spectrum before and after ITR pumping of varying intensities. It can be observed that both pre- and post-pumping of terahertz waves, and the spectral absorption peaks in the vicinity of 30 THz, 52 THz, and 113 THz align precisely with the outcomes derived from comprehensive quantum simulations [38]. The most notable change is the appearance of a low-frequency absorption peak at around 10 THz due to the ITR increasing the system’s average kinetic energy to 0.638 eV. This newly conferred energy accentuates the weak low-frequency vibration of Zundel cations, thus emerging as an IR absorption near 10 THz. An examination of Figure S3a,b reveals a significantly greater impact on the IR spectrum at a peak intensity of 1.0 V/nm compared to 0.1 V/nm, although neither notably shifts the absorption peaks’ position and height. The system’s dipole variation along the E field polarization axis during ITR, as exhibited in Figure 5b, demonstrates a significantly greater impact from an ITR peak of 10 V/nm on the system dipole, echoing the E field time domain waveform in Figure S2a.

Adopting a similar approach, ITR’s effect on Zundel cations was simulated via ab initio path integral molecular dynamics (AI-PIMD). Figure 5c presents the dipole moment changes of the system during ITR’s action, mirroring the E field waveform of ITR. An inspection of Figure S4a–c reveals minor changes in the infrared spectrum’s band intensity after the ITR action, likely due to the random orientation introduced by the Zundel cation’s rotation during the interaction. However, Figure S4a indicates an enhancement in absorption near 3 THz following the ITR action, aligning with the central frequency of the applied ITR shown in Figure S2b.

The system’s transient vibrational modes are analyzed, as displayed in Figure 6, which illustrates Zundel cations’ four IR-active vibrational modes within the low (0–20 THz), medium (30–60 THz), and high (>100 THz) frequency ranges. The vibrational mode constantly fluctuates with time and the vibration energy is exchanged between different modes, underscoring the coupling between the vibrations. The peak intensity variation of the transient IR spectrum over time vividly captures these ultrafast transient processes, inclusive of, but not restricted to, the 32.1 THz vibration mode corresponding to proton transfer. Examination of Figure 6b,c reveals that ITR with peak intensities of 1.0 V/nm or lower induces limited changes in the vibrational modes and IR spectra of the Zundel cations. Lower intensity THz waves are more prone to resonant interactions than high-field nonresonant interactions.

A recent study based on stochastic theory and trajectory decomposition techniques has made contributions towards understanding proton transfer processes and spectral signatures [39,40]. Proton translocation between two water molecules involves significant separations and a free-energy barrier, deviating from normal mode behavior and characterized by two nonvibrational time scales: a dispersed 200–300 fs waiting period leading to a subtle shoulder near 3 THz in the absorption spectrum and a well-defined spectral contribution around 36  THz with a mean transfer event duration of approximately 14 fs [40]. Notably, Figure 6 exhibits a sustained absorption peak in the vicinity of 32 to 40 THz, a range corresponding to the spectral characteristics attributed to proton translocation events. Furthermore, the faint absorption features observed below 10 THz are explicable by the intervals between successive translocation events.

4. Conclusions

In conclusion, we have employed first-principle calculations to conduct a theoretical investigation of both resonant and nonresonant modulation of Zundel cations by THz waves. The PES image of protons discloses the quantum mechanical underpinnings of the resonant interaction with THz waves, potentially leading to proton transfer and oscillation. Additionally, the extraordinarily high E field inherent to the ITR may incite oscillations or transfers of shared protons through nonresonant interactions. On a broader scale, our AIMD simulations and transient IR spectroscopy reveal the vibrational relaxation process resulting from the nonresonant interaction between ITR and Zundel cations. ITR has the capacity to induce or amplify the 10 THz low-frequency vibrational modes of the Zundel configuration through high-field nonresonant effects, a phenomenon we anticipate can be identified using THz spectroscopy. These theoretical findings elucidate the microscopic molecular mechanism of THz wave action, particularly high-field THz waves, on Zundel cations, thereby enhancing our understanding of the fundamental physics underlying the interaction between water and THz waves.