Analysis of Results of Digital Electroencephalography and Digital Vectors of Coronavirus Images upon Applying the Theory of Covariance Functions

Abstract

This paper analyses the structures of covariance functions of digital electroencephalography measurement vectors and digital vectors of two coronavirus images. For this research, we used the measurement results of 30-channel electroencephalography (E1–E30) and digital vectors of images of two SARS-CoV-2 variants (cor2 and cor4), where the magnitudes of intensity of the electroencephalography parameters and the parameters of the digital images of coronaviruses were encoded. The estimators of cross-covariance functions of the digital electroencephalography measurements’ vectors and the digital vectors of the coronavirus images and the estimators of auto-covariance functions of separate vectors were derived by applying random functions constructed according to the vectors’ parameter measurement data files. The estimators of covariance functions were derived by changing the values of the quantised interval k on the time and image pixel scales. The symmetric matrices of correlation coefficients were calculated to estimate the level of dependencies between the electroencephalography measurement results’ vectors and the digital vectors of the coronavirus images. The graphical images of the normalised cross-covariance functions for the electroencephalography measurement results’ vectors and the digital vectors of the coronavirus images within the period of all measurements are asymmetric. For all calculations, a computer program was developed by applying a package of Matlab procedures. A probabilistic interdependence between the results of the electroencephalography measurements and the parameters of the coronavirus vectors, as well as their variation on the time and image pixel scales, was established.

1. Introduction

The COVID-19 pandemic which has constrained the world forces us to review virus populations and the technologies of their observation [1,2,3], as well as to pay particular attention to analyses of viruses of zoo-genetic origin [4,5,6,7,8] and mathematical modelling of COVID-19-related phenomena [9,10,11,12,13]. In this paper, the authors would like to draw attention to the application of covariance functions for an analysis of the parameters of digital images of coronaviruses and present some results based on electroencephalography measurements.

For an analysis of vectors of electroencephalography measurement results and vectors of coronavirus images, the mathematics of covariance functions was introduced. Upon the application of the proposed theory, the strength of probabilistic interdependence between all the vectors was established. The variation in the structure of covariance functions of the vectors on the quantisation scale was established depending on the variations in time (t) and pixels (p). The data on the results of the electroencephalography measurements were fixed in the time interval of one second, and the resolution of the coronavirus images was one pixel. The electroencephalography measurement results (A00062408 raw data) were taken from [14] and the coronavirus images were obtained from [4]. The symmetric matrices of correlation coefficients were calculated to estimate the level of dependencies between the electroencephalography measurement results’ vectors and the digital vectors of the coronavirus images.

The disposition of the electroencephalography measurement electrodes and the scheme of their nomenclature, as well as the images of the coronavirus variants cor2 and cor4, are provided in Figure 1, Figure 2 and Figure 3 below.

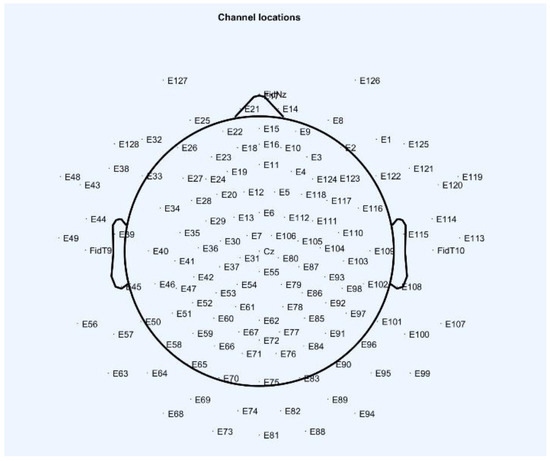
Figure 1. The disposition of the electroencephalography measurement electrodes and the scheme of their nomenclature (EEGLAB software; [15]).

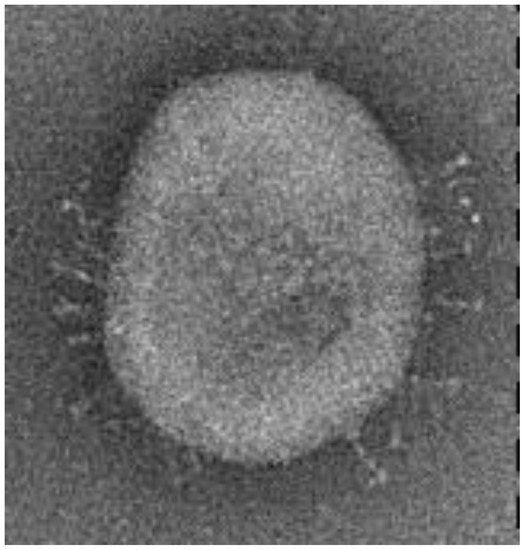
Figure 2. The microscopic view of coronavirus variant cor2 [4].

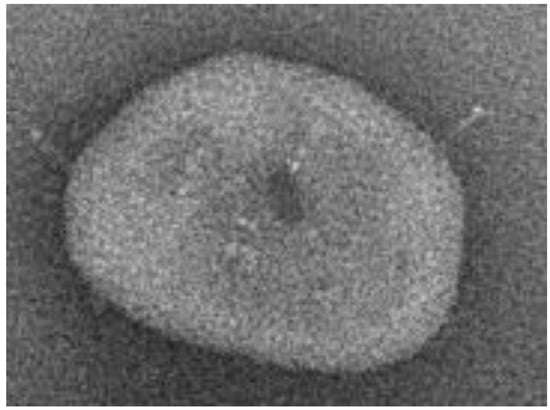
Figure 3. The microscopic view of coronavirus variant cor4 [4].

The measurement data from 30 electroencephalographic electrodes (out of 128) were analysed. In Figure 4 below, the data time series (10,000 s) of the normalised digital vectors for three electrodes (t1-no1, t2-no2, and t3-no3) and the coronavirus images (t4-cov2 and t5-cov4) are presented.

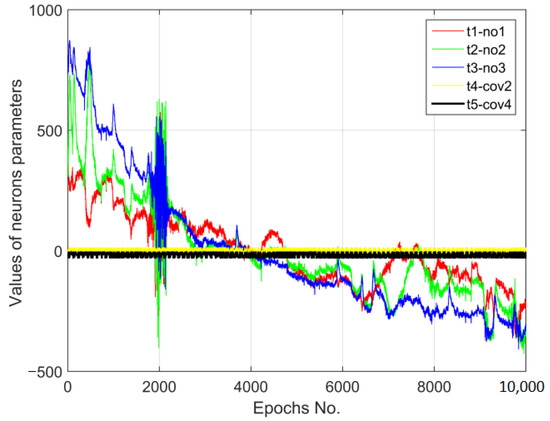
Figure 4. The data time series of the normalised digital vectors for electroencephalography measurement results and the images of coronavirus variants cor2 and cor4.

An analysis of variation in the normalised cross-covariance and auto-covariance functions for the electroencephalography measurement vectors and vectors $\phi$ of the coronavirus images was performed upon applying quantised intervals. The magnitudes of the normalised cross-correlation functions show the magnitudes of the cross-correlation coefficients of single vectors in the relevant quantised intervals (all the couples of the vectors are used). In Figure 5, Figure 6, Figure 7 and Figure 8, the quantised interval is shown along the abscissa axis and the magnitudes of the normalised covariance functions (the magnitudes of the correlation coefficients) are shown along the ordinate axis.

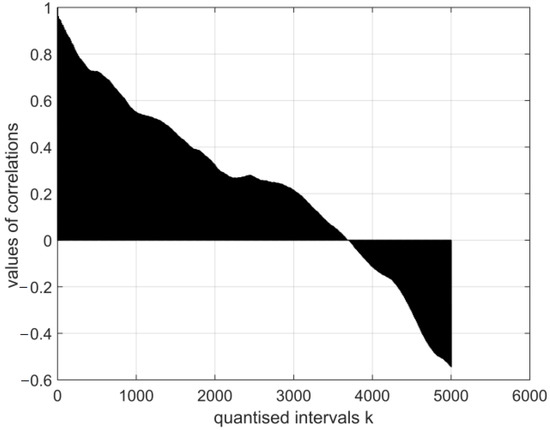
Figure 5. The normalised auto-covariance function for a digital vector of the encephalogram E1. The range of variation in the values of the function: $r\to \left(1.0:-0.5\right)$.

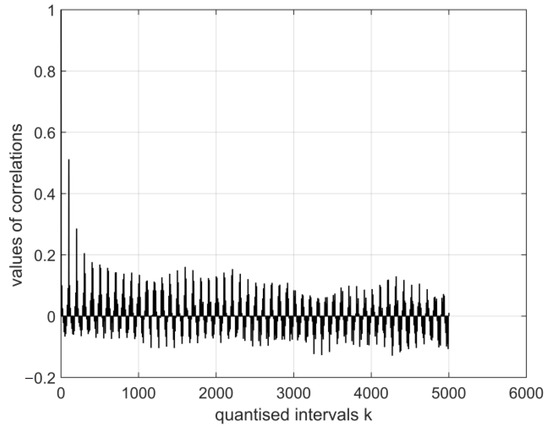
Figure 6. The normalised auto-covariance function for a digital vector of the coronavirus cor2 image. The range of variation in the values of the function: $r\to \left(1.0:0.1\right)$ (E1:E12).

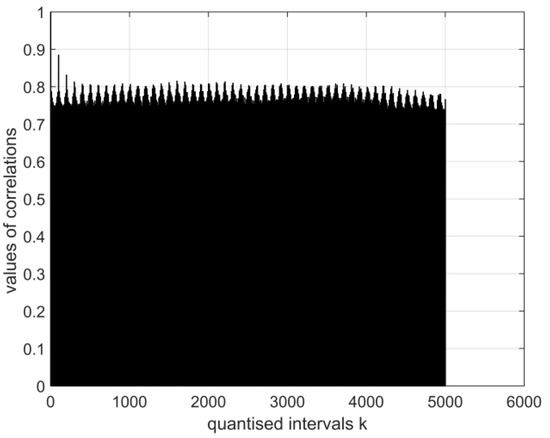
Figure 7. The normalised auto-covariance function for a digital vector of the image of coronavirus variant cor4. The range of variation in the values of the function: $r\to \left(1.0:0.8\right)$ (E1:E12).

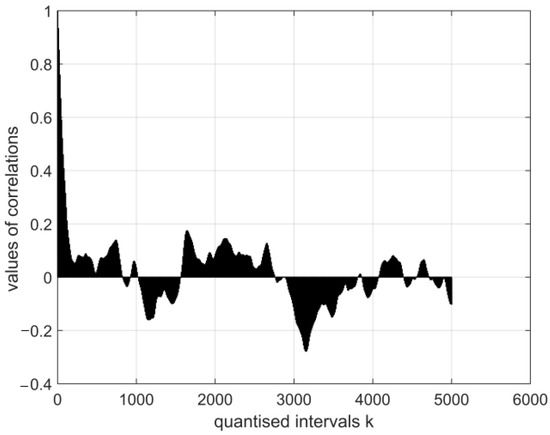
Figure 8. The normalised auto-covariance function for the electroencephalography measurement vector E7. The range of variation in the values of the function: $r\to \left(1.0:-0.3\right)$.

The calculated magnitudes of the correlation coefficients of relevant parameters show the level of their probabilistic interdependence.

2. The Theoretical Model

The foundation of the theoretical model is the idea of a stationary random function, which main features show that the measurement errors $\mathsf{\Delta }$ are absolutely random and possibly slightly systematic, i.e., the mathematical expectancy gradually approaches zero ($M\mathsf{\Delta }=\mathrm{const}\to 0$), their dispersion $D\mathsf{\Delta }=const$, and the magnitudes of the covariance functions of the measured digital signals pertain to the differences in the parameter $\tau$ only, which means, on the quantised interval k, the differences on the moments in time and on the image pixel scales.

The estimators of covariance functions of pair relevant digital vectors or the auto-covariance functions of single separate vectors are derived using the expressions of data arrays in the shape of random functions. For the processing of digital signals, a discrete transformation is applied [16,17].

In each digital data vector $\phi$, a trend of measurement data is eliminated. It is defined that the random functions constructed according to the data of the vectors φ are stationary (in a wide sense), i.e., the mean value of such a function $M\left\{\varphi \left(t\right)\right\}\to const,$ and the covariance function $K_{\varphi }\left(\tau \right)$ depends on the differences of the parameter $\tau$ only. The auto-covariance function of a random, single separate vector or the cross-covariance function of pair of random different vectors $K_{\varphi }\left(\tau \right)$ is written as follows [17,18,19]:

$$K_{\phi }\left(\tau \right)=M\left\{\delta {\overline{\phi }}_1\left(u\right)·\delta {\overline{\phi }}_2\left(u+\tau \right)\right\}$$

(1)

or

$$K_{\varphi }\left(\tau \right)=\frac{1}{T-\tau }\underset{0}{\overset{T-\tau }{{\displaystyle \int }}}\delta {\varphi }_1\left(u\right)\delta {\varphi }_2\left(u+\tau \right)du,$$

(2)

Here, $\mathsf{\delta }{\phi }_1={\phi }_1-{\overline{\phi }}_1$ and $\mathsf{\delta }{\phi }_2={\phi }_2-{\overline{\phi }}_2$ for the centered vectors $\phi$ when the trend is eliminated; $u$ is the parameter of the vectors; $\tau =k·\rho$ is the quantised interval; $k$ is the amount of measurements; $\rho$ is the meaning of the standard of measurement; $T$ is the moment in time; and $M$ is the symbol of the average value.

The estimator ${K^{\prime }}_{\varphi }\left(\tau \right)$ of the covariance function according to the given measurement data on the relevant parameters could be derived according to the following formula:

$${K^{\prime }}_{\varphi }\left(\tau \right)={K^{\prime }}_{\varphi }\left(k\right)=\frac{1}{n-k}{\sum }_{i=1}^{n-k}\delta {\varphi }_1\left(u_i\right)\delta {\varphi }_2\left(u_{i+k}\right),$$

(3)

where $n$ is the total number of discrete ranges.

Formula (3) was applied both as the auto-covariance function and as the cross-covariance function. In the case of auto-covariance function, the vectors ${\varphi }_1\left(u\right)$ and ${\varphi }_2\left(u+\tau \right)$ are the values of separate vectors. In the case of cross-covariance function, they are the values of pair discrepant vectors.

The estimator of a normalized covariance function is expressed using the following formula:

$${R^{\prime }}_{\varphi }\left(k\right)=\frac{{K^{\prime }}_{\varphi }\left(k\right)}{{K^{\prime }}_{\varphi }\left(0\right)}=\frac{{K^{\prime }}_{\varphi }\left(k\right)}{{{\sigma }^{\prime }}_{\varphi }^2},$$

(4)

Here, ${{\sigma }^{\prime }}_{\varphi }$ is the estimator of the standard deviation of a random function.

After applying the following difference, the trend is eliminated from any vector of the measurement data:

$$\delta \phi =\phi -\overline{\phi },$$

(5)

Here, $\delta \phi$ is the data vector from which the trend is eliminated, and $\overline{\phi }$ is the vector’s trend (the average value).

An estimator of a covariance matrix of the i-th vector is expressed based on the following formula:

$$K^{\prime }\left(\delta {\varphi }_i\right)=\frac{1}{n-1}\delta {\varphi }_i^T\delta {\varphi }_i$$

(6)

An estimator of a cross-covariance matrix of the parameters of two vectors ${\phi }_i$ and ${\phi }_j$ is written as follows:

$$K^{\prime }\left(\delta {\varphi }_i,\delta {\varphi }_j\right)=\frac{1}{n-1}\delta {\varphi }_i^T\delta {\varphi }_j,$$

(7)

Here, the sizes of the vectors $\delta {\varphi }_i \mathrm{and} \delta {\varphi }_j$ should be equal.

The estimators $K^{\prime }\left(\delta {\varphi }_i\right)$ and $K^{\prime }\left(\delta {\varphi }_i,\delta {\varphi }_j\right)$ of covariance matrices are transformed into the estimators of correlation coefficient matrices $R^{\prime }\left(\delta {\varphi }_i\right)$ and $R^{\prime }\left(\delta {\varphi }_i,\delta {\varphi }_j\right)$:

$$R^{\prime }\left(\delta {\varphi }_i\right)=D_i^{-1/2}{K}^{\prime }\left(\delta {\varphi }_i\right)D_i^{-1/2},$$

(8)

$$R^{\prime }\left(\delta {\varphi }_i,\delta {\varphi }_j\right)=D_{ij}^{-1/2}{K}^{\prime }\left(\delta {\varphi }_i,\delta {\varphi }_j\right)D_{ij}^{-1/2},$$

(9)

Here, $D_i \mathrm{and} D_{ij}$ are the diagonal matrices formed from the principal diagonal members of the estimators $K^{\prime }\left(\delta {\varphi }_i\right)$ and $K^{\prime }\left(\delta {\varphi }_i,\delta {\varphi }_j\right)$ of the corresponding covariance matrices.

The precision of the derived correlation coefficient r is expressed using the standard deviation ${\sigma }_r,$ the magnitude of which could be estimated as follows:

$${\sigma }_r^{\prime }=\frac{1}{\sqrt{k}}\left(1-r^2\right)$$

(10)

Here, k is the value of the quantised interval, and r is the magnitude of the correlation coefficient. The maximum value of estimator of the standard deviation is derived in the case when r is near zero and k = 5000, so we have ${\sigma }_r^{\prime }=0.01.$ For example, when $r\approx 0.5,$ ${\sigma }_r^{\prime }=0.005$.

3. The Results of the Analysis

The number of electroencephalography measurement vectors is 30: ne = 30 (it is marked as E1–E30). Each vector includes n = 10,000 digital parameters. The number of coronaviruses nc = 2, and each image of them has n = 10,000 pixels. In the vectors of both types, the number n of the parameters is the same.

The magnitudes of the quantised interval of the normalised covariance functions chang in the range between 1 and n/2; here, n = 10,000—the number of values of each vector. For ne and nc of every vector, the estimate $K{\prime }_{\phi }\left(\tau \right)$ of the normalised auto-covariance function $K_{\phi }\left(\tau \right)$ was derived, and 32 graphical images of the normalised auto-covariance functions were received. In addition, the estimates $K{\prime }_{\phi }\left(\tau \right)$ of the normalised auto-covariance functions were calculated for all 32 vectors, and 496 graphical expressions of them were obtained. In the calculations, their most distinctive images were provided.

The graphical images of the normalised auto-covariance functions for the electroencephalography measurement vectors differ. This can be seen in Figure 5, Figure 6, Figure 7 and Figure 8 below.

All normalised auto-covariance functions show the maximum magnitude of the correlation coefficient $r\to 1.0$ (the normalised standard deviation) in the quantised interval $k\to 0\left({\tau }_k\to 0 \mathrm{s}\right)$ and then fall to r$\to 0$ in the interval $k\to 1000: 3500 \left({\tau }_k\to 1000: 3500 \mathrm{s}\right)$. The graphical images of the normalised auto-covariance functions of the coronavirus images differ (Figure 6 and Figure 7 above). The magnitudes of the normalised auto-covariance functions of cor2 parameters differ in the interval $r_c\to$ (1.0: 0.1). The magnitudes of the normalised auto-covariance functions of cor4 parameters vary in the range $r_c$ $\to$ (1.0: −0.8). These results show that the two coronaviruses are of different kinds and structures.

The standard deviations of the parameters describe the accuracy of measuring the parameters of the vectors. The values of the standard deviations of the parameters for the electroencephalography measurement results for vectors E vary in the range ${\sigma }_e\to \left({\sigma }_7-{\sigma }_9\right)\to ($98$-565)$ s. The values of the standard deviations of the parameters for the digital vectors of the coronavirus images vary in the range ${\sigma }_c\to \left(9.4-10.3\right)$ of pixels. Thus, the data on the electroencephalography measurement results’ vectors do not have high accuracy.

The values of the normalised cross-covariance functions for the digital electroencephalography measurement results’ vectors within the period of all measurements vary in different ranges: r$\to \left(0.9:-0.5\right), r\to \left(0.6:-0.7\right), \mathrm{and} r\to \left(0.4:-0.1\right)$. The graphical images of the changes in the dependences differ. This can be seen in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 below.

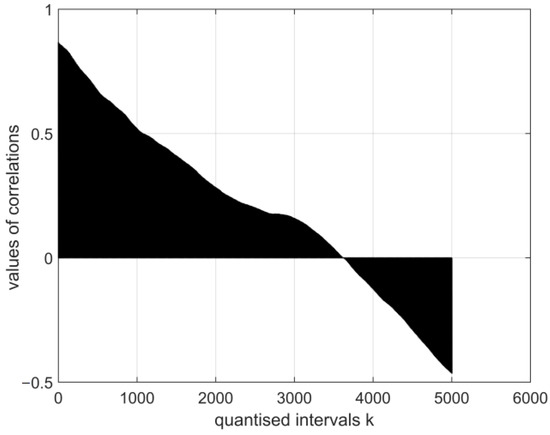
Figure 9. The normalised cross-covariance function for the digital electroencephalography measurement vector E1. The range of variation in the values of the function: $r\to \left(0.8:-0.6\right)$.

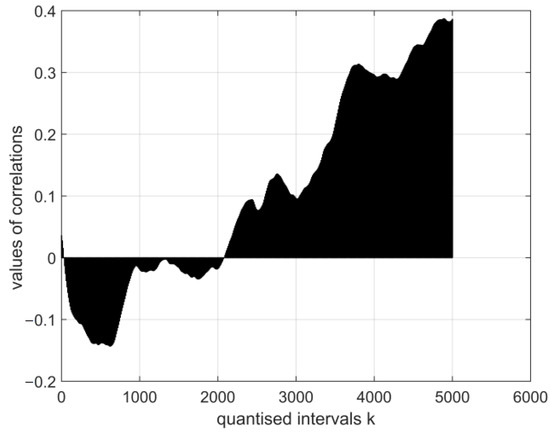
Figure 10. The normalised cross-covariance function for the digital electroencephalography measurement vector E27. The range of variation in the values of the function: $r\to \left(-0.15:0.4\right)$.

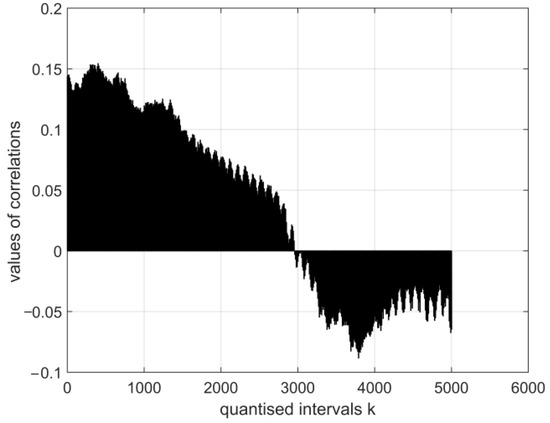
Figure 11. The normalised cross-covariance function for the digital electroencephalography measurement vector E1 and a digital vector of the image of coronavirus variant cor2. The range of variation in the values of the function: $r\to \left(0.15:-0.1\right)$.

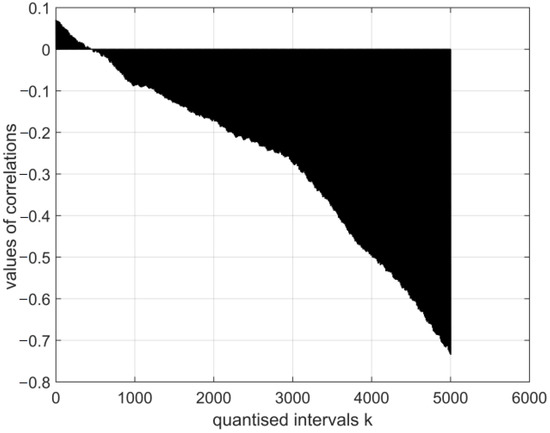
Figure 12. The normalised cross-covariance function for the electroencephalography measurement vector and a digital vector of the image of coronavirus variant cor4. The range of variation in the values of the function: $r\to \left(0.1:-0.75\right)$.

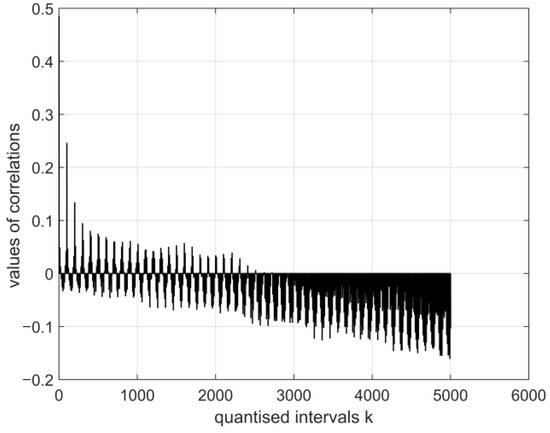
Figure 13. The normalised cross-covariance function for the digital vectors of the images of coronavirus variants cor2 and cor4. The range of variation in the values of the function: $r\to \left(0.05: 0.14\right)$, $\left(\mathrm{E}1: \mathrm{E}12\right)$.

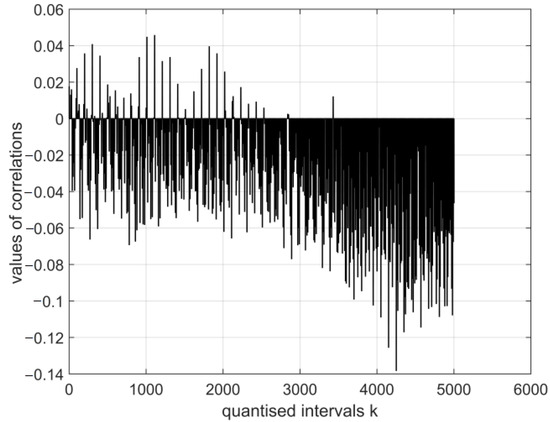
Figure 14. The normalised cross-covariance function for the digital vectors of the image of coronavirus variants cor2 and cor4s. The range of variation in the values of the function: $r\to \left(0.05:-0.14\right),$ $\left(\mathrm{E}13:\mathrm{E}30\right)$.

The magnitudes of the normalised cross-covariance functions for the digital electroencephalography measurement results’ vectors and the vectors of the coronavirus images within the period of all measurements also differ in different ranges: r$\to \left(0.15:-0.1\right), r\to \left(0.1:-0.7\right), r\to \left(0:-0.3\right), \mathrm{and} r\to \left(0:-0.4\right).$ The graphical images of the changes in the dependences differ as well. The magnitudes of the normalised cross-covariance functions for the electroencephalography measurement results’ vectors and the digital vectors of the coronavirus images within the period of all measurements are negative.

The magnitudes of the normalised cross-covariance functions for the digital vectors of the images of coronavirus variants cor2 and cor4 differ in the range $r\to \left(0.5:-0.15\right)$ based on the calculation in the system with vectors (E1–E12). The values of the digital vectors of the images of cor2 and cor4 differ in the range r$\to$(0.04: −0.14) based on the calculation in the system with vectors (E13–E30).

The graphical images of the normalised cross-covariance functions for the electroencephalography measurement results’ vectors and the digital vectors of the coronavirus images within the period of all measurements are asymmetric.

4. Conclusions

• The magnitudes of the normalised auto-covariance functions for the electroencephalography measurement results’ vectors in all quantised intervals vary in the range $r_e\to$ (1: −0.6). Their graphical expressions are asymmetric and similar. The values of the functions show the probabilistic interdependence of parameters of the relevant vectors.
• The magnitudes of the normalised auto-covariance functions for the digital vectors of the coronavirus cor2 image parameters differ in the range $r_c\to$ (1.0: 0.1). The magnitudes of the normalised auto-covariance functions for the digital vectors of coronavirus cor4 image parameters vary in the range $r_c\to$(1.0: −0.8). Thus, the structures of both viruses differ. In a considerable part of quantised intervals, the vector of the coronavirus cor2 image has negative values of normalised auto-covariance functions when $r_c$ = −0.8.
• The magnitudes of the normalised cross-covariance functions for the digital electroencephalography measurement results’ vectors E in all quantised intervals vary in the range $r_e\to$ (0.9: −0.6). The graphical expressions of the functions are asymmetric and similar.
• The magnitudes of the normalised cross-covariance functions for the electroencephalography measurement results’ vectors E and the vectors of the images of cor2 and cor4 vary in different ranges when $r\to$ (0.15: −0.7). The magnitudes of the normalised cross-covariance functions for the electroencephalography measurement results’ vectors E and the digital vectors of the coronavirus images within the period of all measurements are negative. Consequently, their probabilistic interdependence is negative as well.
• The magnitudes of the normalised cross-covariance functions for the digital vectors of the images of cor2 and cor4 differ in the interval r $\to$ (0.5: −0.15) based on the calculation in the system with vectors (E1–E12). The magnitudes of the normalised cross-covariance functions for the digital vectors of the images of cor2 and cor4 vary in the interval r $\to$(0.04: −0.14) based on the calculation in the system with vectors (E13–E30). Thus, in this case, their values are very low, and this shows an absence of interdependence between cor2 and cor4.