Abstract
Recently, in light of the significant attention devoted to pseudohalide CN− and cyano radical CN physico-chemical property studies and superhalide behavior exploration in CN−-ligated metal compounds, the photoelectron angular distribution nature of pseudohalide CN− has been directly demonstrated via the photoelectron velocity map imaging technique to be comparable to Cl−. For the halide Cl−, photoelectrons were observed at 266 nm (4.66 eV) to peak, perpendicular to the laser polarization associated with the detachment of p-orbital symmetry. For the analogous pseudohalide CN−, photoelectrons were present at a peak in laser polarization at 266 nm, which can be explained as detachment from mainly atomic s-like orbital symmetry. Although both are often regarded as having the same high electron affinity and similarly strong chemical bonding capabilities to stabilize complexes, their photoelectron angular distributions are distinctly different, which indicates their intrinsically different electronic–structure symmetry (HOMO nature). The approach based on symmetry consideration in this work could be utilized to explain the photoelectron angular distributions of pseudohalide and classic halide ligands via the advanced photoelectron velocity map imaging tool.
1. Introduction
Photoelectron spectroscopy (PES) is based on the photoelectric effect principle and provides an excellent connection to photoelectric experiments in modern quantum theory when discussing transitions in atoms and molecules [1]. This versatile and useful technique engages undergraduate students or novice researchers of physics and chemistry in modern quantum mechanics to accurately elucidate spectroscopic data and extract internal structural information of atoms and molecules. Notably, it provides straightforward evidence for the quantized shell model [2].
Photoelectron velocity map imaging (PE-VIM) is a variant of photoelectron spectroscopy, and serves as a powerful probe of atomic and molecular electronic structure, chemical bonding, and interactions due to its high energy resolution, photoelectron angular distribution (PAD) availability, and high efficiency [3]. PAD often reveals the symmetry nature of parent initial electronic states and final neutral electronic states. With the aid of PAD analyses as complementary information, photoelectron imaging has been developed as a sensitive probe for the symmetry properties of the corresponding parent MO and the dynamics of the detachment process, from which electrons are emitted [4,5,6,7,8,9,10,11].
CN− is the simplest pseudohalide, as it is a closed-shell species, and has an electron binding energy of 3.82 eV, comparable with that of Cl−, which has the highest electron affinity (3.6 eV) of all elements in the periodic table [1]. In classic halide-ligated clusters, superhalogen properties have been extensively explored in recent decades due to their exotically higher electron affinities (as high as 14 eV) [12,13]. CN−-ligated compounds have also been extensively explored recently due to their special stability and chemistry resembling that of true halides [14,15,16,17,18,19]. However, CN−-ligated compounds also exhibit distinctly geometric, electronic, and spectral properties compared to other halides. For example, the cyanide anion, CN− is a good hydrogen-bonding acceptor for both the C terminus and N terminus, in which the N terminus of cyanide is a slightly better hydrogen bond acceptor than the C terminus. Interestingly, negative-ion hydrogen-bonded complexes with one H2O as proton donors and pseudohalide CN− and halide Cl− as proton acceptors were compared in theoretical study and an IR vibrational spectra experiment. Both complexes have stable geometries, with the hydrogen-bonded proton being non symmetrically bound [20]. Nevertheless, in contrast to only one stable Cl−···H2O isomer being observed in vibrational spectroscopy experiments [21,22], two stable, singly hydrogen-bonded isomers, NC–···H2O and CN–···H2O, have been confirmed via cryogenic ion vibrational spectroscopy, in which the CN–···H2O isomer was slightly more stable than the NC–···H2O isomer [23]. Close investigations of OH stretching oscillations in previously reported results indicate that the magnitude of frequency redshifts (with respect to free OH stretch, ~3700 cm−1) correlated with the hydrogen bond strength for a singly hydrogen-bonded complex. The OH stretching frequency of Cl−···H2O has been measured as 3285 cm−1 [21], and the OH stretching frequency of CN–···H2O isomer and NC–···H2O isomer have been determined as 3034 cm−1 and 2896 cm−1, respectively [23]. The slightly less red-shifted hydrogen-bonded O-H stretching frequency indicates that halide Cl− is a slightly poorer hydrogen bond acceptor than pseudohalide CN−, in which the C terminus of CN− displays the strongest hydrogen bond strength. This situation is ascribed to the different electronic structure features of CN− in comparison to halide Cl−.
In addition, CN− and its neutral radical have also been reported in many groups [24,25,26]. Their spectra and reaction properties have also been investigated [27,28,29,30]. Especially, during near-threshold photodetachment in CN−, detachment reaches a more isotropic distribution (β ≈ 1.7 to β ≈ 0), with photon energies ranging from 4.40 to 3.87 eV (eKE: 0.01~0.53 eV) [31]. It has been unraveled that long-range interaction (electron−molecular dipole) plays an important role in the anion photodetachment process. The photodetachment cross-section measurements of CN− near the threshold also suggest the dependence of the long-range interaction between the permanent dipole moment of CN and the outgoing electron, although this process was investigated as s-wave detachment [32].
Despite their importance in many aspects, the PAD properties of ligands of CN− and halide Cl− have not yet been directly compared. This short article demonstrates how pseudohalide CN− and halide Cl− can be unambiguously identified by directly measuring their PADs, and in terms of the measured PADs, elucidates that the HOMO symmetry natures of the two species are substantially different. Additionally, using a photon energy of 4.66 eV, the asymmetry parameter β of CN− photodetachment reached the +2 limit in the asymptotic limit (a purely parallel transition or pure s-like orbital symmetry detachment). This situation is an important extension of the threshold photodetachment experiment of CN−. Additionally, this work presents a good case suitable for undergraduate students and novice researchers to deeply understand the intrinsic electronic–structure symmetry and chemical bonding natures between pseudohalides and halides via a PAD approach.
2. Materials and Methods
The negative ion photoelectron velocity-map imaging system has been discussed in detail elsewhere and is only briefly introduced here [33]. CN and Cl anions were generated via laser ablation of a rotating metal target (99.9%) in the presence of a supersonic beam of helium (99.999%) carrier gas with trace CH3CN or chlorides, and steered to a McLaren Wiley time-of-flight, mass selected, and crossed with a laser beam (Nd:YAG laser) in the PE-VMI chamber. Negligible background electron signals enabled the 266 nm photodetachment spectra to be recorded without background subtraction. The detached photoelectrons were extracted using a PE-VIM spectrometer, and recorded using a charge-coupled device camera. Each image was accumulated using 104–105 laser shots at a 10 Hz repetition rate. The final raw image stood for the projection of the photoelectron density in the 3D laboratory frame onto the 2D imaging detector. The original 3D distribution was reconstructed using the Basis Set Expansion (BASEX) inverse Abel transform method, and the photoelectron spectrum was acquired [34]. The new photoelectron spectra were calibrated using known atomic anion spectra. When the electron kinetic energy (eKE) was 1 eV, the energy resolution was typically ~30 meV. The Gaussian 09 suite of programs was used for theoretical calculations [35]. The CN and Cl anions were calculated at the level of Becke-3-parameter-Lee-Yang-Parr (B3LYP) theory [36], and the augmented correlation-consistent polarized valence triple-ζ basis set aug-cc-pVTZ was utilized for carbon, nitrogen, and chlorine atoms [37].
3. Results and Discussion
Anion PE-VMI spectra of CN− and Cl− are displayed in Figure 1; it is apparent that double peaks of Cl− ascribed to the transitions of 1S0 → 2P3/2 and 1S0 → 2P1/2 [1]. The first peak of 3.61 ± 0.01 eV was defined as the electron affinity of the Cl atom. For CN−, only a single peak located at 3.86 ± 0.01 eV was visible, at a detachment wavelength of 266 nm, corresponding to the transition of X 1Σ+ → X′ 2Σ+ [38]. This indicated no geometric change between the anion ground state and the neutral ground state of CN. Further visual inspection of PADs in Figure 1 shows that the two images exhibit apparently different PAD characteristics. For Cl−, the electrons detached from the 1S0 state to the spin–orbit states of 2P3/2 and 2P1/2 appeared to possess a strong anisotropy distribution perpendicular to the laser polarization (double arrow in Figure 1). On the contrary, for CN−, the electrons detached from the X 1Σ+ state to the X′ 2Σ+ state were preferentially distributed along the laser polarization.
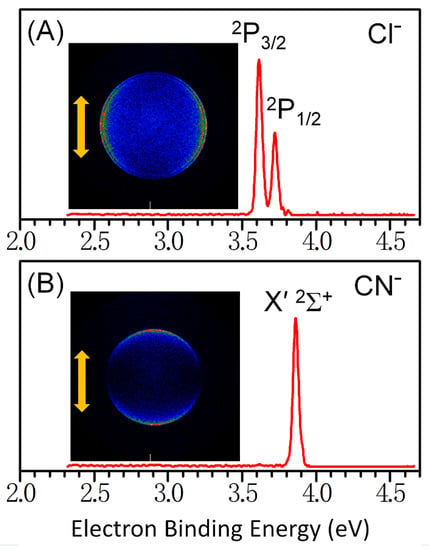
Figure 1.
Photoelectron velocity-map imaging of (A) Cl− and (B) CN−; experimental spectra used a 4.661 eV (266 nm) photon energy.
Basically, in anion PE-VMI experiments, the polarization of the detaching laser (linear polarization) is parallel to the surface of the imaging detector. The resulting PAD possesses cylindrical symmetry. The angular distribution of ejected photoelectrons for a single photon process is fitted to a formula [39]:
where θ is the angle between the laser polarization axis and the direction of the ejected electron, σ is the photodetachment cross section, and β is an asymmetry parameter ranging from −1 (aligned perpendicular to the laser polarization axis) to 2 (aligned parallel to the laser polarization axis). Additionally, β = 0 represents a perfectly isotropic s-wave of outgoing electrons [40].
Figure 2A,B depict the PADs of Cl– by integrating radial intensity (across peaks) versus angle in each spin–orbit state after inverse Abel transformation of the photoelectron images, normalized to 1 as the maximum intensity. The PAD plots are also essentially numerical representations of the anisotropies revealed by the images shown in Figure 1; due to symmetry, only half of the ring, from 0° to 180° (defined to be along the laser polarization direction), is plotted in each case. Both plots indicate a perpendicular transition, with maximum intensity at θ = 90°. The asymmetry parameters, β, from the fitting analysis were determined to be −0.8 ± 0.1 for both cases, which is very close to the −1 limit of a purely perpendicular transition associated with typical p orbital electron emission as O− [39]. On the contrary, for the PAD of CN–, the maxima along the laser polarization at θ = 0° and 180° and the minimum perpendicular to the laser polarization at θ = 90° are clearly shown. Additionally, the final asymmetry parameters, β, and uncertainties were calculated as 2.0 ± 0.1, exhibiting a purely parallel transition as H− [40].
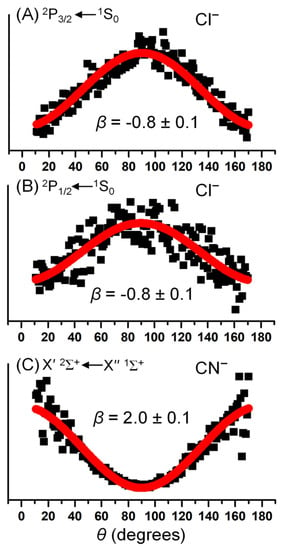
Figure 2.
Representative photoelectron angular distribution analysis for the (A) 2P3/2 state of Cl, (B) 2P1/2 state of Cl, and (C) X′2Σ+ state of CN at 266 nm. The solid squares represent experimental angular intensities, I(θ), and the solid red lines represent the best fit to data using the model function described in the text. The asymmetry parameters, β, from the fitting analysis are listed in each figure.
Although CN− has been termed a pseudohalide (due to its many similar properties to halides) why does its asymmetry parameter of the photoelectron distribution yield this distinct difference from that of atomic Cl−? Electronic–structure symmetry should be essential for determining the details of the PADs. To understand how electronic–structure symmetry influences the PADs, we calculated the valence orbitals for Cl− and CN− at the level of B3LYP/aug-cc-pVTZ in Gaussian 09. Figure 3 displays the calculated HOMOs for electrons detached from Cl− and CN−; it is apparent that for Cl−, HOMO is a typical p atomic orbital symmetry, whereas, for CN−, calculations show that HOMO is a σ bond, which consists of 43% s orbital, 33% p orbital of C atom, and 23% p orbital of N atom. Additionally, the HOMO of CN− can be nominally described as a superposition of an sp hybrid orbital centered on the carbon atom and a p orbital centered on the nitrogen atom, which in fact enables its whole shape to resemble an s-like atomic orbital symmetry.
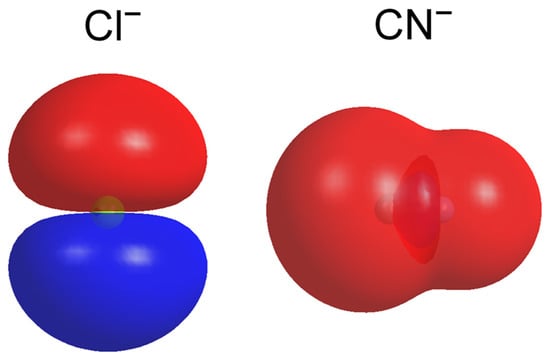
Figure 3.
The contour plots of the HOMOs of the ground states of CN− and Cl− calculated at the level of B3LYP (the basis set of aug-cc-pVTZ for C, N, and Cl) (isovalue = 0.01 a.u.).
In one-photon, electric-dipole allows atomic transition, angular momentum conservation must be conformed, and the photodetachment selection rule is Δl = ±1 as the absorbed photon carries one quantum of angular momentum. During photodetachment, the absorbed photon is transferred to the electron. As illustrated in Scheme 1, generally speaking, photodetachment from an orbital with typical s symmetry character (l = 0) leads to a free-electron wave characterized by a single l = 1, corresponding to a p wave symmetry. Under the electric-dipole approximation, a photodetachment is accessed as long as the transition dipole moment . Here, μ = −er is the dipole operator, while φi and φf represent the initial and final states of the electron upon photodetachment, respectively. As laser light is z-polarized, only Mz is addressed:
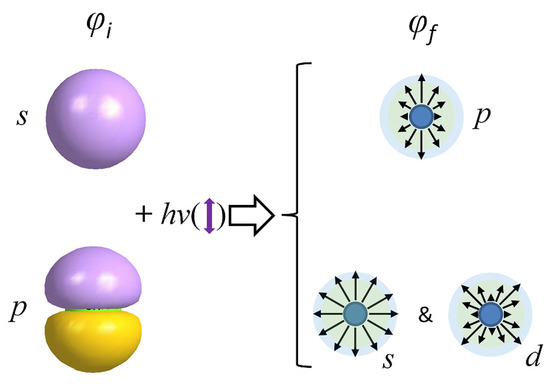
Scheme 1.
Pictorial representation of photodetached electron angular distribution for detachment from the s and p initial orbitals. The purple double arrow indicates the directions of the laser polarization.
As the normalized angular component of φi (s symmetry orbital) can be expressed as Y0,0(θ, ϕ) = (1/4π)1/2, the normalized angular component of φf is Y1,m(θ, ϕ) (l = 1), so that the possible values of m are 0 and ±1. To satisfy , we must restrict the photoelectrons to l = 1 and m = 0, i.e., the pz wave (Scheme 1), while x and y polarized p waves are forbidden, because . In fact, the experimentally observed PADs were essentially the same as those corresponding to a pz wave. The normalized angular dependence of the pz wave is described by Y1,0(θ, ϕ) = (3/4π)1/2cosθ, which yields a cos2θ probability distribution and corresponds to Equation (1) with the asymmetry parameter β = 2 [41]. In this sense, for the CN− photoelectron image, the highly positive β = 2.0 (pz-character of PAD) was consistent with its HOMO nature with s-like atomic orbital symmetry. In general, PADs for photodetachment from s-symmetry orbitals are independent of the photoelectron kinetic energy.
For cases of photodetachment from a non-s symmetry orbital, both the l = li + 1 and l = li − 1 waves contribute to the photoelectron wave function. Thus, photodetachment from an orbital with p symmetry character (li = 1) yields interference between s (l = 0) and d (l = 2) partial waves based on angular momentum conservation (Scheme 1). In terms of the selection rules Δl = ± 1 and Δm = 0, we may model the photoelectron as a linear combination of outgoing s and d0,±1 waves. The resulting photoelectron intensity is described by the angular and radial parts of the corresponding waves [41]:
Here, the cross term (Y0,0*Y2,0) in Equation (3) represents interference of the s and d free-electron waves. Its sign (positive or negative) depends on the condition of R2 = R0 or R2 = −R0, respectively. In fact, the radial components of the l = 0 and l = 2 partial waves have opposite signs, R2 = −R0 [41]. The p symmetry orbital photodetachment may yield negative β parameters due to the only negative interference term (−2Y0,0*Y2,0). β parameter may not be intuitively acquired over the entire range, as d±1 partial-waves (Y2, ±1) have zero intensity at θ = 0° and 90°; the parallel (θ = 0°) and perpendicular (θ = 90°) photoelectron wave functions can be written as:
and
respectively, where η = η2 − η0 denotes a relative phase shift due to interaction with the remaining neutral. The photoelectron intensities are succinctly deduced as:
and
Next, we define β parameter as
yielding
Here, Rl is the radial dipole integral for a partial-wave of l. According to the Wigner threshold laws, for detachment near threshold [42], where ε is the electron kinetic energy and σl is the cross-section of the l-type partial wave, which is dependent on Rl: ; the radial terms in Equation (9) could be replaced with kinetic energy terms: , where A is a proportionality constant that represents the ratio of radial matrix elements. Equation (9) can then be rearranged into a form that reveals the energy dependence of β from a p-orbital:
where with l = 1. Equation (10) indicates that as ε → 0, β → 0. Obviously, photodetachment from a p-symmetry orbital yields isotropic distributions near zero photoelectron kinetic energy. However, as photoelectron kinetic energy continues to increase, the asymmetry parameters of β become negative, typically decreasing to a minimum (near −1) below ~2 eV. As the ε increases further, the asymmetry parameters of β increase, becoming positive before ultimately leveling off near β = 1 [43]. Hence, based on the consideration of PAD results for Cl−, a significantly negative parameter, with β = −0.8 at photoelectron kinetic energy of ~1 eV, is typical of detachment from a p-symmetry orbital.
Thus, PAD is demonstrated as a sensitive tool for investigating the electronic–structure symmetry of atoms and molecules. This experimental demonstration of PAD for CN− distinctly differed from that of Cl−, although we usually refer to CN− as a pseudohalide. Computations of the HOMOs for both allowed the PADs to be predicted and compared using experimental results. It is interesting to note that the p-symmetry component plays a negligible role in PAD beyond the threshold photodetachment of CN−, although some p orbital symmetry should be considered due to the cylindrical symmetry along the bond axis. According to the Wigner threshold law, emitted s-wave electrons dominate and result in isotropic distribution at the threshold photo-detachment [43]. However, in this regard, the β = 2.0 at eKE ~ 0.8 eV beyond the threshold photo-detachment indicates that the pure s-symmetry parent orbital dominated and the p-symmetry component’s influence was negligible. Even in the near-threshold photodetachment measurements, only the s-symmetry detachment was evidenced in the prior experiment. Experimental PADs at low photoelectron energies had pronounced deviation from free-electron model predictions, which is ascribed to the long-range interaction (electron−molecular dipole) for a polar molecule.
4. Conclusions
This work incorporated the advanced photoelectron velocity map imaging technique into electronic–structure detection to better understand the essential difference in orbital symmetry between pseudohalides and halide anions (CN− vs. Cl−, respectively, in this work). For the halide Cl−, photoelectrons were observed to peak at 266 nm (4.66 eV), perpendicular to laser polarization due to electron emission from the typically parent p orbital symmetry. For the analogous pseudohalide CN−, photoelectrons presented peaks along the laser polarization entirely at 266 nm, which were attributed to s-like atomic orbital photodetachment. Although both are often considered to have the same high electron affinity and extremely strong chemical bonding capability to stabilize complexes, their photoelectron angular distributions are quite different, which indicates their different symmetry nature of HOMO. Thus, this study may be useful to undergraduate students and researchers interested in deeply understanding the different molecular orbital symmetries and chemical bonding natures of pseudohalides and classic halides when using the advanced photoelectron velocity map imaging tool.
Funding
This research was funded by the National Science Foundation of China (No. 21873003). This work was also funded by the Hefei Comprehensive National Science Center (No. GXXT-2020-004), the University Annual Scientific Research Plan of Anhui Province (No. 2022AH010013), and the Open Foundation of Key Laboratory of High Power Laser and Physics, Chinese Academy of Sciences (SGKF202106).
Data Availability Statement
All data are fully available.
Acknowledgments
The author acknowledges additional computational support from the Super Computation Center of Shenzhen.
Conflicts of Interest
The author declares no conflict of interest.
References
- Rienstra-Kiracofe, J.C.; Tschumper, G.S.; Schaefer, H.F.; Nandi, S.; Ellison, G.B. Atomic and Molecular Electron Affinities: Photoelectron Experiments and Theoretical Computations. Chem. Rev. 2002, 102, 231–282. [Google Scholar] [CrossRef]
- Benigna, J. Photoelectron Spectroscopy in Advanced Placement Chemistry. J. Chem. Educ. 2014, 91, 1299–1305. [Google Scholar] [CrossRef]
- Neumark, D.M. Slow Electron Velocity-Map Imaging of Negative Ions: Applications to Spectroscopy and Dynamics. J. Phys. Chem. A 2008, 112, 13287–13301. [Google Scholar] [CrossRef] [PubMed]
- Otto, R.; Ma, J.; Ray, A.W.; Daluz, J.S.; Li, J.; Guo, H.; Continetti, R.E. Imaging Dynamics on the F + H2O → HF + OH Potential Energy Surfaces from Wells to Barriers. Science 2014, 343, 396–399. [Google Scholar] [CrossRef]
- Kim, J.B.; Weichman, M.L.; Sjolander, T.F.; Neumark, D.M.; Klos, J.; Alexander, M.H.; Manolopoulos, D.E. Spectroscopic observation of resonances in the F + H2 reaction. Science 2015, 349, 510–513. [Google Scholar] [CrossRef]
- Continetti, R.E.; Guo, H. Dynamics of transient species via anion photodetachment. Chem. Soc. Rev. 2017, 46, 7650–7667. [Google Scholar] [CrossRef]
- DeVine, J.A.; Weichman, M.L.; Laws, B.; Chang, J.; Babin, M.C.; Balerdi, G.; Xie, C.; Malbon, C.L.; Lineberger, W.C.; Yarkony, D.R.; et al. Encoding of vinylidene isomerization in its anion photoelectron spectrum. Science 2017, 358, 336–339. [Google Scholar] [CrossRef] [PubMed]
- Weichman, M.L.; DeVine, J.A.; Babin, M.C.; Li, J.; Guo, L.; Ma, J.; Guo, H.; Neumark, D.M. Feshbach resonances in the exit channel of the F + CH3OH → HF + CH3O reaction observed using transition-state spectroscopy. Nat. Chem. 2017, 9, 950–955. [Google Scholar] [CrossRef]
- Wang, T.; Yang, T.; Xiao, C.; Sun, Z.; Zhang, D.; Yang, X.; Weichman, M.L.; Neumark, D.M. Dynamical resonances in chemical reactions. Chem. Soc. Rev. 2018, 47, 6744–6763. [Google Scholar] [CrossRef] [PubMed]
- Bellm, S.M.; Reid, K.L. Reevaluation of the use of photoelectron angular distributions as a probe of dynamical processes: Strong dependence of such distributions from S1 paradifluorobenzene on photoelectron kinetic energy. Phys. Rev. Lett. 2003, 91, 263002. [Google Scholar] [CrossRef]
- Xing, X.-P.; Wang, X.-B.; Wang, L.-S. Imaging Intramolecular Coulomb Repulsions in Multiply Charged Anions. Phys. Rev. Lett. 2008, 101, 083003. [Google Scholar] [CrossRef]
- Yawei, L.I.; Wang, Q. Progress in superhalogen research: Structures, properties and potential applications. Sci. Sin. 2013, 43, 142–162. [Google Scholar]
- Freza, S.; Skurski, P. Enormously large (approaching 14 eV) electron binding energies of [HnFn+1]− (n = 1–5, 7, 9, 12) anions. Chem. Phys. Lett. 2010, 487, 19–23. [Google Scholar] [CrossRef]
- Okabayashi, T.; Okabayashi, E.Y.; Koto, F.; Lshida, T.; Tanimoto, M. Detection of Free Monomeric Silver(I) and Gold(I) Cyanides, AgCN and AuCN: Microwave Spectra and Molecular Structure. J. Am. Chem. Soc. 2009, 131, 11712. [Google Scholar] [CrossRef] [PubMed]
- Xue-Bin, W.; Yi-Lei, W.; Jie, Y.; Xiao-Peng, X.; Jun, L.; Lai-Sheng, W. Evidence of significant covalent bonding in Au(CN)2−. J. Am. Chem. Soc. 2009, 131, 16368–16370. [Google Scholar]
- Wu, X.; Qin, Z.; Xie, H.; Cong, R.; Wu, X.; Tang, Z.; Fan, H. Photoelectron Imaging and Theoretical Studies of Group 11 Cyanides MCN (M = Cu, Ag, Au). J. Phys. Chem. A 2010, 114, 12839–12844. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.-T.; Xiong, X.-G.; Dau, P.D.; Wang, Y.-L.; Li, J.; Wang, L.-S. The mixed cyanide halide Au(I) complexes, [XAuCN]− (X = F, Cl, Br, and I): Evolution from ionic to covalent bonding. Chem. Sci. 2011, 2, 2101. [Google Scholar] [CrossRef]
- Samanta, D.; Wu, M.M.; Jena, P. Unique Spectroscopic Signature of Nearly Degenerate Isomers of Au(CN)3 Anion. J. Phys. Chem. Lett. 2011, 2, 3027–3031. [Google Scholar] [CrossRef]
- Samanta, D.; Wu, M.M.; Jena, P. Au(CN)n Complexes: Superhalogens with Pseudohalogen as Building Blocks. Inorg. Chem. 2011, 50, 8918–8925. [Google Scholar] [CrossRef]
- Del Bene, J.E. An ab initio study of the structures and enthalpies of the hydrogen-bonded complexes of the acids H2O, H2S, HCN, and HCl with the anions OH−, SH−, CN−, and Cl−. Struct. Chem. 1990, 1, 19–27. [Google Scholar] [CrossRef]
- Choi, J.-H.; Kuwata, K.T.; Cao, Y.-B.; Okumura, M. Vibrational Spectroscopy of the Cl−(H2O)n Anionic Clusters, n = 1−5. J. Phys. Chem. A 1998, 102, 503–507. [Google Scholar] [CrossRef]
- Horvath, S.; McCoy, A.B.; Elliott, B.M.; Weddle, G.H.; Roscioli, J.R.; Johnson, M.A. Anharmonicities and Isotopic Effects in the Vibrational Spectra of X−·H2O, ·HDO, and ·D2O [X = Cl, Br, and I] Binary Complexes. J. Phys. Chem. A 2010, 114, 1556–1568. [Google Scholar] [CrossRef] [PubMed]
- Kelly, J.T.; Knorke, H.; Asmis, K.R. Isolating the Isomeric Hydrogen Bonding Signatures of the Cyanide–Water Complex by Cryogenic Ion Trap Vibrational Spectroscopy. J. Phys. Chem. Lett. 2017, 8, 5349–5354. [Google Scholar] [CrossRef] [PubMed]
- Shi, D.-H.; Li, W.-T.; Sun, J.-F.; Zhu, Z.-L. MRCI study on spectroscopic and molecular properties of several low-lying electronic states of the CN radical. J. Quant. Spectrosc. Radiat. Transfer 2011, 112, 2335–2346. [Google Scholar] [CrossRef]
- Kumar, S.S.; Hauser, D.; Jindra, R.; Best, T.; Roučka, Š.; Geppert, W.D.; Millar, T.J.; Wester, R. Photodetachment as destruction mechanism for CN− and C3N− anions in circumstellar envelopes. Astrophys. J. 2013, 776, 25. [Google Scholar] [CrossRef]
- Khamesian, M.; Douguet, N.; Dos Santos, S.F.; Dulieu, O.; Raoult, M.; Brigg, W.J.; Kokoouline, V. Formation of CN− C3N−, and C5N− Molecules by Radiative Electron Attachment and their Destruction by Photodetachment. Phys. Rev. Lett. 2016, 117, 123001.1–123001.5. [Google Scholar] [CrossRef]
- Estillore, A.D.; Visger, L.M.; Kaiser, R.I.; Suits, A.G. Crossed-Beam Imaging of the H Abstraction Channel in the Reaction of CN with 1-Pentene. J. Phys. Chem. Lett. 2010, 1, 2417–2421. [Google Scholar] [CrossRef]
- Abeysekera, C.; Joalland, B.; Ariyasingha, N.; Zack, L.N.; Sims, I.R.; Field, R.W.; Suits, A.G. Product Branching in the Low Temperature Reaction of CN with Propyne by Chirped-Pulse Microwave Spectroscopy in a Uniform Supersonic Flow. J. Phys. Chem. Lett. 2015, 6, 1599–1604. [Google Scholar] [CrossRef]
- Joalland, B.; Jamal-Eddine, N.; Kłos, J.; Lique, F.; Trolez, Y.; Guillemin, J.-C.; Carles, S.; Biennier, L. Low-Temperature Reactivity of C2n+1N– Anions with Polar Molecules. J. Phys. Chem. Lett. 2016, 7, 2957–2961. [Google Scholar] [CrossRef]
- Gans, B.; Boyé-Péronne, S.; Garcia, G.A.; Röder, A.; Schleier, D.; Halvick, P.; Loison, J.-C. Unveiling the Ionization Energy of the CN Radical. J. Phys. Chem. Lett. 2017, 8, 4038–4042. [Google Scholar] [CrossRef]
- Hart, C.A.; Lyle, J.; Spellberg, J.; Krylov, A.I.; Mabbs, R. Role of the Electron–Dipole Interaction in Photodetachment Angular Distributions. J. Phys. Chem. Lett. 2021, 12, 10086–10092. [Google Scholar] [CrossRef] [PubMed]
- Simpson, M.; Notzold, M.; Schmidt-May, A.; Michaelsen, T.; Bastian, B.; Meyer, J.; Wild, R.; Gianturco, F.A.; Milovanovic, M.; Kokoouline, V.; et al. Threshold photodetachment spectroscopy of the astrochemical anion CN−. J. Chem. Phys. 2020, 153, 184309. [Google Scholar] [CrossRef]
- Qin, Z.; Wu, X.; Tang, Z. Note: A novel dual-channel time-of-flight mass spectrometer for photoelectron imaging spectroscopy. Rev. Sci. Instrum. 2013, 84, 066108. [Google Scholar] [CrossRef]
- Dribinski, V.; Ossadtchi, A.; Mandelshtam, V.A.; Reisler, H. Reconstruction of Abel-transformable images: The Gaussian basis-set expansion Abel transform method. Rev. Sci. Instrum. 2002, 73, 2634–2642. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Bradforth, S.E.; Kim, E.H.; Arnold, D.W.; Neumark, D.M. Photoelectron spectroscopy of CN−, NCO−, and NCS−. J. Chem. Phys. 1993, 98, 800–810. [Google Scholar] [CrossRef]
- Cooper, J.; Zare, R.N. Angular Distributions in Atomic Anion Photodetachment. J. Chem. Phys. 1968, 48, 942–943, Erratum in J. Chem. Phys. 1968, 49, 4252. [Google Scholar] [CrossRef]
- Grumbling, E.R.; Pichugin, K.; Mabbs, R.; Sanov, A. Photoelectron Imaging as a Quantum Chemistry Visualization Tool. J. Chem. Educ. 2011, 88, 1515–1520. [Google Scholar] [CrossRef]
- Mabbs, R.; Grumbling, E.R.; Pichugin, K.; Sanov, A. Photoelectron imaging: An experimental window into electronic structure. Chem. Soc. Rev. 2009, 38, 2169–2177. [Google Scholar] [CrossRef]
- Wigner, E.P. On the Behavior of Cross Sections Near Thresholds. Phys. Rev. A 1948, 73, 1002–1009. [Google Scholar] [CrossRef]
- Sanov, A. Laboratory-Frame Photoelectron Angular Distributions in Anion Photodetachment: Insight into Electronic Structure and Intermolecular Interactions. Annu. Rev. Phys. Chem. 2014, 65, 341–363. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).