Differential Evolution Using Enhanced Mutation Strategy Based on Random Neighbor Selection

Abstract

Symmetry in a differential evolution (DE) transforms a solution without impacting the family of solutions. For symmetrical problems in differential equations, DE is a strong evolutionary algorithm that provides a powerful solution to resolve global optimization problems. DE/best/1 and DE/rand/1 are the two most commonly used mutation strategies in DE. The former provides better exploitation while the latter ensures better exploration. DE/Neighbor/1 is an improved form of DE/rand/1 to maintain a balance between exploration and exploitation which was used with a random neighbor-based differential evolution (RNDE) algorithm. However, this mutation strategy slows down convergence. It should achieve a global minimum by using 1000 × D, where D is the dimension, but due to exploration and exploitation balancing trade-offs, it can not achieve a global minimum within the range of 1000 × D in some of the objective functions. To overcome this issue, a new and enhanced mutation strategy and algorithm have been introduced in this paper, called DE/Neighbor/2, as well as an improved random neighbor-based differential evolution algorithm. The new DE/Neighbor/2 mutation strategy also uses neighbor information such as DE/Neighbor/1; however, in addition, we add weighted differences after various tests. The DE/Neighbor/2 and IRNDE algorithm has also been tested on the same 27 commonly used benchmark functions on which the DE/Neighbor/1 mutation strategy and RNDE were tested. Experimental results demonstrate that the DE/Neighbor/2 mutation strategy and IRNDE algorithm show overall better and faster convergence than the DE/Neighbor/1 mutation strategy and RNDE algorithm. The parametric significance test shows that there is a significance difference in the performance of RNDE and IRNDE algorithms at the 0.05 level of significance.

1. Introduction

Today, the modern world has entered a post peta scale era; the requirements are growing exponentially for computation and data processing, and the need for high-performance computation is increasing day by day; thus, the trend has changed from serial execution to high-performance computation. For achieving high-performance computation, several hurdles need to be tackled. Examples are those problems where the solution is very hard to find, or the solution merely exists or is very hard to achieve, e.g., NP-complete problems. To achieve the solution to those problems, we have very well-known heuristic techniques which provide the solution to these types of problems, but those solutions are not completely optimized. However, using optimization algorithms, such as the differential evolution (DE) and particle swarm optimization (PSO), optimized solutions to such problems can still be found.

Moreover, we will observe and discuss its variants, as it is already known that the original DE was first proposed by Storn and Price [1] in 1995; this drew the attention of many researchers as it was the simplest algorithm that provided the optimized solutions to many real-world problems. Thus, based on the original DE algorithm, different variants were introduced later. Some of the well-known approaches were the hybridization with other techniques, modification of mutation strategies, adaptation of mutation strategy and parameter settings, and use of neighbor information.

1.1. Problem Statement

The local optima issue is a challenging issue if the population loses its diversity in the differential evolution algorithm. The selection of parents is important to incorporate diversity in mutation and crossover operations’ DE algorithm. The perturbation of a vector that evolves the population around the neighborhood will be stuck in local optima because of the imbalance between the exploration and exploitation capability of the algorithm. The RNDE algorithm utilizes only one difference vector and a neighbor best vector from a set of N neighbors, where N is taken from the interval of $N_{LL}$ and $N_{UL}$. Less diversity and slow convergence degrade the convergence speed of the RNDE Algorithm 1 [2].

Algorithm 1: Improved Random Neighbor-Based Differential Evolution

1: Randomly initialize population 2: Evaluate the objective function 3: FEs = NP 4: while  $FEs<Max\left(FEs\right)$  do 5:  Calculate the number of neighbor’s Ni for each individual  $N_i=N_{lb}+(N_{ub}-N_{lb}).\frac{f\left(X_i\right)-f_{min}+\psi }{{\sum }_{j=1}^{NP}(f(X_j-f_{min})+\psi }$ 6:   for  $i=1:NP$  do 7:   Randomly choose Ni neighbors for ith individual and the best one Xnbest 8:   Generate IRNDE mutant vector      $V_i$ according to $V_i=X_{nbest}+F(X_{r1}-X_{r2})+F(X_{r3}-X_{r4})$ 9:   Execute the crossover operation to generate a trial vector $U_i$ 10:   Evaluate the trial vector $U_i$ 11:   FEs = FEs + 1 12:    if  $Xi>f\left(U_i\right)$  then 13:     $X_i>U_i$ 14:   else 15:    Update CR by using adaptive shift 16:    if  $f\left(U_i\right)>f\left(X_i\right)$  then 17:     Flag = − Flag 18:    end if 19:    if Flag==1  then 20:      $CR={CR}_{\mathit{large}}+0.1\ast \mathit{randn}$ 21:    else 22:      $CR={CR}_{\mathit{small}}+0.1\ast \mathit{randn}$ 23:    end if 24:   end if 25:  end for 26: end while

1.2. Research Significance

The selection of the number of parents used in the perturbation of any individual is considered important in the evolution of the DE algorithm. The RNDE algorithm utilizes a difference vector that reduces the diversity in the population and, as a result, the algorithm converges slowly. The perturbation of one neighborhood’s best vector results in more exploitation than exploration and ultimately results in being stuck in local optima that can be fixed by increasing the exploration capability of the DE algorithm.

1.3. Research Contributions

• This paper presents a novel mutation strategy in the RNDE algorithm to maintain the balance between the exploration and exploitation of the DE algorithm. The proposed IRNDE is helpful in increasing the convergence speed and average fitness solution quality of results.
• Experimental results show that the performance of the improved RNDE algorithm is superior, as compared to the RNDE algorithm for the standard test suit of benchmark functions.
• Convergence graphs confirm the quick convergence of the proposed IRNDE algorithm and statistical results show the significance of the IRNDE algorithm.

1.4. Research Question and Hypothesis

• Ways to increase population diversity and incorporate a balance between exploration and exploration during the evolution process of the RNDE algorithm.
• Finding significance in the performance of the RNDE algorithm and proposed algorithm.

In the rest of the paper, Section 2 shows how the DE algorithm works; a brief literature review is presented in Section 3; material and methods are given in Section 4; results and discussion are presented in Section 5; statistical analysis is given in Section 5.4; conclusion and future are given in the last section.

2. Principle of the Classical Differential Evolution Algorithm

As mentioned earlier, the purpose of the DE algorithm is to provide optimized solutions [3]. The algorithm keeps searching for the best individual among the given population [4]. It is also considered that DE can solve the problem for immediate goals using a given population and a set of parameters [5]. It is a population-based algorithm, such as genetic algorithms, and uses crossover and mutation as operators; the last step is the selection step. Moreover, it is self-adaptive, where all solutions have the same chance of being selected, no matter what their fitness values are [6]. It follows the greedy approach, especially in the selection phase. DE uses NP (number of population) D-dimensional parameter vectors, and it is a parallel direct search method. Once we obtain the result or new offspring from the DE algorithm, we compare the new offspring/generation with their parents and we evaluate both the parents and the new generation based on their fitness value. We obtain a new individual by applying mutation, crossover, and selection operators. Those who are better at fitness are kept, no matter whether it is a new generation or their parents. In the selection operation, the greedy selection is applied to select the individual among the target vector and trial vector [7]. DE uses NP, a Population Size, and D-dimensional parameter vectors, and it is a parallel direct search method. The individual is represented by $X_{i,j},i=1,2,\dots ,NP,j=1,2,\dots ,D$ and the population size for the population of each generation G. The classical DE works in three phases: mutation, crossover, and selection.

2.1. Mutation Phase

The mutation phase is used to generate a mutant vector or donor vector that is then used in a crossover operation. To calculate each target vector $X_{i,j},i=1,2,$…$,NP$, the donor or the mutant vector is generated according to

$$V_{i,G+1}=X_{r1,G}+F.\left(X_{r2,G}-X_{r3,G}\right)$$

(1)

This equation during the $G^{th}$ generation generates a donor vector, $V_{i,G+1}$. $r_1$, $r_2$, $r_3$$ϵ$$1,2,\dots ,NP$, with a mutually different integer and $F>0$. The random integers $r1$, $r2$, and $r3$ are taken from the running index i; thus, the NP should be greater or equal to four to meet the condition. F is the real time constant factor, in which $ϵ$$[0,2]$, and is responsible for amplification of differential variations of $(X{r}_2,G-X{r}_3,G)$. It shows the two-dimensional illustration which is responsible for the generation of $V_{i,G+1}$.

2.2. Crossover Phase

The crossover is introduced to increase the diversity of the disconcerted parameter vectors [8]. The trial vector is

$$V_i{,}_{G+1}=X_{r1,G}+F.\left(X_{r2,G}-X_{r3,G}\right)$$

(2)

$$U_{i,G+1}=\left(u_{1i,G+1},{\mathrm{u}}_{2i,G+1},{...,u}_{Di,G+1}\right)$$

(3)

where $j=1,2,\dots ,D$.

In the crossover phase, $randb\left(j\right)$ is the $jth$ calculation of an unvarying random number generator with outcome $ϵ$$[0,1]$. CR is the crossover constant $ϵ$$[0,1]$, and this is set by the user. The $rnbr\left(i\right)$ is the randomly chosen index $ϵ$$1,2,\dots ,D$ which should make sure that $u_{i,G+1}$ always obtains at least one parameter from $v_{i,G+1}$.

2.3. Selection Phase

The selection phase is responsible for deciding whether an individual should become a member of G + 1 or not. Hence, trial vector $u_{i,G+1}$ is always compared with target vector $v_{i,G+1}$ by using the greedy approach and if $u_{i,G+1}$ to achieve minimum fitness value $x_{i,G}$, then $x_{i,G+1}$ is set to $u_{i,G+1}$; otherwise, the old value $x_{i,G}$ is taken [1].

2.4. Commonly Used Mutation Strategies

As the focus of the current study is DE neighbor information, for classical DE and in other variants of DE, the most commonly used group of mutation strategies [9] are given below

$$V_i=X_{r1}+F.\left(X_{r2}-X_{r3}\right)$$

(4)

$$V_i=X_{\mathrm{best}}+F.\left(X_{r1}-X_{r2}\right)$$

(5)

$$V_i=X_i+F.{(X}_{\mathrm{best}}-X_i)+F.\left(X_{r1}-X_{r2}\right)$$

(6)

$$V_i=X_{r1}+F.\left(X_{r2}-X_{r3}\right)+F.\left(X_{r4}-X_{r5}\right)$$

(7)

$$V_i=X_{\mathrm{best}}+F.\left(X_{r1}-X_{r2}\right)+F.\left(X_{r3}-X_{r4}\right)$$

(8)

The above-mentioned mutation strategies are used, not only in neighbor information types of DE algorithms, but also by different researchers of different variants of DE. Moreover, these strategies are also used in the classical version of DE.

2.5. Major Contributions of Study

A number of studies by various researchers are available in the literature to handle the local optima issue, balance between exploration and exploitation, improve the convergence speed and improve the solution quality of the DE algorithm. A few of the variants introduced by researchers include tournament selection-based DE [10], rank-based DE [11], fuzzy-based DE [12], self-adaptive DE [13], adaptive DE [14], and Pool-based DE [15] to maintain the balance between exploration and exploitation as well as to improve the convergence performance of the DE algorithm in their research work.

There are two commonly used mutation strategies for DE. The first is DE/best/1, which provides better exploitation, as it obtains the best population but results in poor exploration. On the other hand, in the second strategy of DE/rand/1, in which exploration is better as it obtains the base vector randomly, exploitation is not good, as there is no balance between exploration and exploitation. So far, to overcome this issue, the DE/Neighbor/1 mutation strategy and random neighbor-based differential evolution (RNDE) algorithm were introduced in [2] and tested on 27 extensively used benchmark functions a few years earlier. The authors stated that the DE/Neighbor/1 and RNDE algorithm is successful in maintaining the balance between exploration and exploitation. It is built to use the lower and upper bound limits to control the balance between exploration and exploitation. However, this mutation strategy shows a slow convergence. It should achieve a global minimum as the function falls within 1000 × D, but due to exploration and exploitation balancing trade-offs, it is unable to obtain a global minimum within the range of 1000 × D in some of the objective functions.

This study introduces a new approach, based on the RNDE variant, namely, the improved random neighbor-based differential evolution (IRNDE). The proposed algorithm uses neighbor information similar to RNDE; however, in addition, we added a new concept: weighted differences after various tests. The proposed IRNDE is tested on the same 27 commonly used benchmark functions on which RNDE was tested. Experiments are performed to compare its performance with RNDE. Results demonstrate faster convergence of IRNDE and its superior performance compared to RNDE.

The rest of this article is organized as follows. The related work is given in Section 3, which is followed by a description of the proposed IRNDE algorithm in Section 4. Section 5 presents the results, while the conclusion is given in Section 6.

3. Related Work

Many researchers proposed models/techniques to improve the DE algorithm to provide better and more optimized results [16,17]. Few researchers provided techniques or other algorithms that work with the DE algorithm to provide hybrid techniques obtaining more optimized and satisfactory results. DE algorithm has attracted many scholars around the globe; according to their work, the DE algorithm can be categorized in the following sections.

3.1. Hybridization with Other Techniques

The study [18] proposed a hybrid algorithm CADE which combines a customized canonical version of CA and DE. The canonical CA uses the ’Accept()’ function which selects the best individual from the population; then, it is updated in the belief space knowledge source by using the ’Update()’ function. The ’Influence()’ function selects the knowledge source that affects the evolution of the next generation of the population. The authors state that in CA, the major source of exploration is topographic knowledge, which is the knowledge about the functional landscape. Moreover, DE can also provide a complementary source of exploration knowledge hence it makes the perfect complement of CA. Both algorithms share the same population space and hence follow high-level teamwork. The study [19] proposed a mechanism, called ADE-ALC, which is abbreviated to the adaptive DE algorithm with an aging leader and challenges, which is helpful to solve optimization problems. It is introduced in the framework of DE, which helps in maintaining the diversity of the population. Moreover, in the DE algorithm, it is critical to retain the diversity of the evolutionary population in solving multimodal optimization problems. ADE-ALC achieves the optimal solution with fast-converging speed. In the ADE-ADC approach, the key parameters are updated that depend on the given probability distribution that could learn from their successful experience in the next generation. In the end, the effectiveness of the ADE-ALC algorithm is checked by numerical results of twenty-five benchmark test functions, where they found that ADE-ALC shows better or at least competitive optimization performance in terms of statistical performance. The authors proposed a hybrid technique in [20] to provide a statistically better performance in the optimization problems. The authors used a combination of the DE algorithm and the stochastic fractal search algorithm. As the hybrid approach is used, the combination of both algorithms has the strength of both competent algorithms and produces better results than the single algorithm. Moreover, to test the performance of the hybrid approach, they used the IEEE 30 benchmark suite, IEEE CEC2014. The results show a better performance of the hybrid approach compared to a single algorithm, and results show the statistical superiority of the hybrid approach.

3.2. Modification of Mutation Strategies

The study [21] proposed an approach to improve the search efficiency of the DE algorithm. The performance of DE is badly affected by parameter settings and evolutionary operators, e.g., the mutation, crossover, and selection process. To overcome this issue, the authors proposed a new technique, called a combined mutation strategy. A guiding individual-based parameter setting method and a diversity-based selection strategy are used. The proposed algorithm uses the concept of sub-population and divides the population into two subcategories, superior and inferior. Experiments are performed using CEC 2005 and CEC 2014 benchmarks. Moreover, their algorithm is different from greedy selection strategies; hence, they proved their algorithm produced more efficient results than previous proposed techniques. The study [22] points out that DE uses only the best solution to deal with global optimization problems. Similarly, mutation strategies in the existing literature utilize only one best solution. The authors challenged this concept and introduced the concept of m best candidates. The authors proposed that m best candidates should be selected to obtain the better gain or better achievement. A technique called the collective information-powered DE (CIPDE) algorithm is proposed to obtain the m best candidates and enhance the power of DE. The CEC2013 benchmark functions are used for experiments that prove that the CIPDE technique is much better than existing mutation strategies. The study [23] proposed a new technique in which they improved the structure of the DE algorithm. The authors argue that the performance of DE is based on control parameters and the mutation strategy; if we enhance both the selection of proper mutation strategy and control parameter, we can obtain better results. An automated system is proposed to produce an evolution matrix that later takes the place of the control parameter crossover rate, Cr. Furthermore, parameter F is renewed in the evolution process. The mutation strategy along with the time stamp system is also progressive in this study. The experiment results showed that the proposed technique is very competitive with the existing strategies.

3.3. Adaptation of Mutation Strategy and Parameter Settings

The study [24] proposed a new algorithm that can investigate problem landscape information and the performance histories of operators for dynamically selecting the most suitable DE operator during the evolution process. The need for this mutation strategy is justified by the fact that predominantly existing works use a single mutation strategy. The authors present the concept of using multiple mutation strategies. Multiple mutation strategy-based algorithms are reported to provide far better results than single mutation-based algorithms. In such algorithms, the emphasis is to obtain the better performing evolutionary operator, which will be totally based on performance history for creating new offspring. This procedure is carried out dynamically; it selects the most suitable evolutionary operator. Experimental results using 45 optimization problems show the efficacy of the proposed algorithm. The study [21] proposed a new and improved version of the DE algorithm. Firstly, the search strategy of the previous DE is improved by using the information of individuals to set the parameter of DE and update the population, and the combined mutation strategy is produced by combining two single mutation strategies. Secondly, the fitness value of the original and guiding individual is used. Finally, a diversity-based selection strategy is developed by applying a greedy selection strategy. The performance is evaluated using CEC 2005 and CEC 2014 benchmarks, and better results are reported. The study [25] investigates the high-level ensemble in the mutation strategies of DE algorithms. For this purpose, a multi-population-based framework (MFT) was introduced. An ensemble of differential evolution variants (EDEV) based on three high, popular, and efficient DE versions is utilized. JADE-adaptive DE with optional external archive, CoDE DE with composite trial vector generation strategies and control parameters, and EPSDE DE algorithm with an ensemble of parameters and mutation strategies are joined. Furthermore, the whole population of EDEV is divided into four subcategories. In the end, the EDEV-based test is run on the CEC 2005 and CEC 2014, which shows better performance of EDEV.

3.4. Use of Neighbor Information

The study [26] proposed an adaptive social learning (ASL) strategy for the DE algorithm so that neighborhood relationship information of individuals in the current population can be extracted; this is called the social learning of DE (SL-DE). In the classical DE algorithm, parents in mutation are randomly selected from the population. However, in the ASL strategy, the selection of parents is intelligently guided. In ASL, every individual can only interact with their neighbor and parents. To check the efficacy of SL-DE, it is applied to the advanced DE algorithm. Results demonstrate that SL-DE can achieve a better performance than most of the existing variants of DE. The study [27] proposed the technique in which the authors applied the global numerical optimization and the index-based neighborhood on DE. In this technique, the authors used information and population to enhance the performance of DE. In the existing literature, neighborhood information of the current population has not been systematically exploited in DE design. The authors proposed neighborhood-adaptive DE (NaDE). The NaDE technique is based on the pool of index-based neighborhood topologies. Firstly, several neighborhood interactions for every discrete individual are recorded and later used adaptively for specific function selection. Secondly, the authors introduced a neighborhood-directional mutation operator in NaDE to obtain the new resolution in the designated neighborhood topology. Finally, NaDE is easy to operate and implement and can be matched with earlier DE versions on different kinds of optimization problems. The authors proposed a new approach called enhancing De with a random neighbors-based strategy in [2]. Traditionally, DE/rand/1 and DE/best/1 mutation strategies are used with DE. In DE/rand/1, the base vector is chosen from the population randomly for better exploration. On the other hand, the DE/best/1 strategy has better exploitation and poor exploration. To overcome this issue, the authors proposed DE/Neighbor/1. In the proposed technique, for each individual population at every generation, the neighbors are chosen from the population in a random manner and the base factor of the DE/Neighbor/1 mutation strategy should be the best one among neighbors. Xiong et al. [28] introduced a speciation-based DE algorithm in their research work. The presented algorithm utilizes the mechanism of the adaptive neighborhood by considering multimodal benchmark functions. They used the concept of achievement to store inferior individuals in each iteration and remove similar-performing individuals using the mechanism of crowding relief. In their presented approach, the use can fine-tune the parameters adaptively. Liao et al. [29] considered the system of non-linear equations using the DE algorithm in their research work. They utilized neighborhood-based information to increase the exploitation capability of the DE algorithm. The size of the neighborhood is dynamically selected with the adjustment of parameter adaption in the state of evolution. The search efficiency of the DE algorithm was enhanced by achieving significant results. The research work [30] presented binary differential evolution based on a self-adaptive neighborhood method for change detection in super-pixels. The change detection process is carried out by using a binary DE mutation strategy to reduce the dimension of super-pixels. Lio et al. [31] introduced a variable neighborhood-based DE algorithm by utilizing a history archive in their research work. During the evolution process, the neighborhood size is dynamically controlled in their presented approach. The information exchange process is performed between the current population and the population stored in the achieved research. The information exchange is helpful to escape from local optima during the evolutionary process. Liu et al. [32] considered the economic dispatch problem by incorporating a direction-inducted strategy in neighborhood-based DE algorithm in their research work. They have used a new mutation strategy named a neighborhood-based non-elite direction strategy that enhances the exploitation capability of the presented algorithm. Sheng el al. [33] introduced the concept of an adaptive neighborhood-based mutation in the DE algorithm. The presented technique is helpful to focus on an intensive search followed by an initial search by the DE algorithm. They also used a Gaussian local search to evolve promising individuals during the search process. Wang et al. [34] introduced an adaptive memetic-based neighborhood crossover strategy in their research work. They used the concept of a multi-nitching sampling for the evolution of the sub-population to ensure intensive search. They also presented the design of adaptive elimination-based local search in their research work. Their neighborhood crossover strategy focuses on an exploitation capability in the DE algorithm to encourage a good quality solution. Cai et al. [35] presented a self-organizing DE algorithm in their research work that is helpful in guiding the search process by utilizing neighborhood information. The adaptive adjustment of various individuals in the explored works use a cosine similarity in the self-organizing map. Segredo et al. [36] proposed a neighborhood based on proximity in the DE algorithm that is helpful to balance between exploration and exploitation during the evolution process. They used Euclidean-based distance to measure the similarity between neighbors of individuals and termed it a similarity-based neighborhood search. Baioletti et al. [37] presented algebraic differential evolution based on a variable neighborhood concept in their research work. Their presented algorithm utilizes the information of three neighborhoods for shifting and swapping purposes to form permutations. Tian and Gao [38] introduced the adaptive evolution method by using the neighborhood mechanism in the DE algorithm. They used a selection probability based on the selection of individuals, as well as two mutation operators based on the neighborhood to improve the evolution process. They also used a simple reduction method to adjust the population size to incorporate diversity in the DE algorithm. Tarkhaneh and Moser [39] performed a cluster analysis by incorporating a neighborhood search and Archimedean spiral in the DE algorithm in their research work. Mantegna Levy’s flight mechanism was used in the Archimedean spiral by generating robust solutions to balance between exploration and exploitation during the searching process. In this section, we analyzed the DE variants in terms of mutation strategies, use of neighbor information, hybridization of the DE algorithm, etc. Experimental results and performance reports from these works indicate that the performance of DE can be enhanced in several ways. Some of the studies used hybrid approaches to achieve the enhancement while others used a combination of something likr test functions, etc. We can say that, to some extent, researchers were able to obtain a better performance from enhanced versions rather than from the simple version of the DE algorithm. However, to achieve a better performance of DE, they had to make a trade-off. We realize that there are many research challenges for DE to further improve its performance. This research aims to enhance the concept of random neighbors; the focus is to obtain a faster convergence compared to the existing random neighbors approach.

4. Materials and Methods

4.1. DE with Random Neighbor-Based Mutation Strategy

For this research, we selected the random neighbor-based differential evolution (RNDE) approach by [2]. It was proposed to achieve a balance between a better exploration and exploitation, which cannot be achieved using traditional DE/rand/1 and DE/best/1 mutation strategies. The mutation phase is RNDE, given as

$$V_i=X_{\mathrm{nbest}}+F.\left(X_{r1}-X_{r2}\right)$$

(9)

The number of neighbors N plays a critical role in leading the balance between exploration and exploitation by using the upper and lower bound limits. A small value of N makes the mutation strategy similar to the DE/rand/1 strategy, which results in better exploration and poor exploitation. Contrarily, the large value of N (near to NP) makes the mutation strategy similar to DE/best/1, which provides a better exploitation. The large value of N is not a wise choice because it can make the algorithm become stuck in the local optimum. The authors also proposed a self-adaptive strategy that dynamically updates N and the number of neighbors for each individual $X_i$, as follows

$$N_i=N_{lb}+(N_{ub}-N_{lb}).\frac{f\left(X_i\right)-f_{min}+\psi }{{\sum }_{j=1}^{NP}\left(f\left(X_j\right)-f_{min}\right)+\psi }$$

(10)

where $N_{lb}$ and $N_{ub}$ show lower bounds and upper bounds, respectively, $f_{min}$ is the smallest best value of the objective function in the population in the current generation and $\psi$ is used as the smallest constant to avoid a zero division-error.

The RNDE is successful in maintaining the balance between exploration and exploitation, as it was built to use the lower and upper bound limits to control the balance between exploration and exploitation. However, as the whole focus of the RNDE algorithm is to maintain the balance between exploration and exploitation, this mutation strategy makes convergence very slow, thus requiring a larger number of iterations in achieving the global optimum.

4.2. Proposed Approach

To overcome the slower convergence problem of RNDE, this study proposes an improved random neighbor-based mutation strategy for DE (IRNDE). The flow chart of the proposed IRNDE is given in Figure 1. IRNDE also uses neighbor information, such as the RNDE algorithm and DE/Neighbor/1 mutation strategy; however, in addition, we added another term of weighted differences in the DE/neighbor/2 mutation strategy after various tests. As we added an extra-weighted vector in the mutation phase, the upper and lower bound limits of N, which is denoted by neighbors, are also increased. The proposed IRNDE mutation equation is given as

$$V_i=X_{\mathrm{nbest}}+F.\left(X_{r1}-X_{r2}\right)+F.\left(X_{r3}-X_{r4}\right)$$

(11)

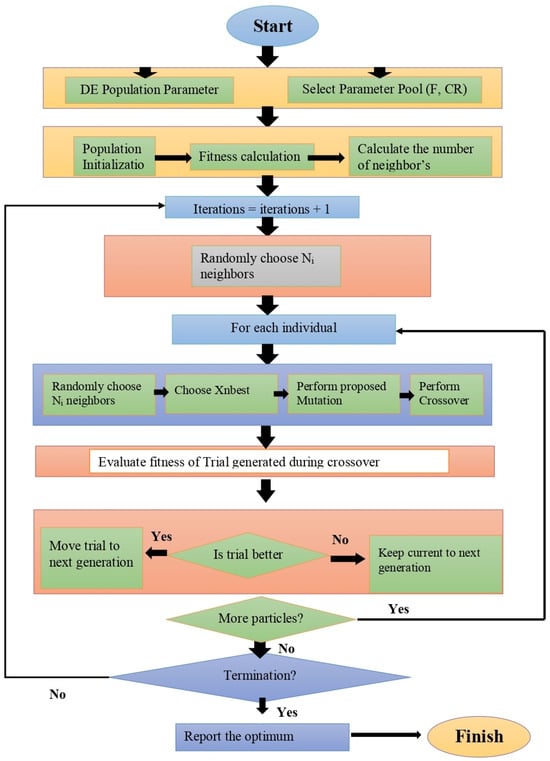
Figure 1. Flowchart of proposed IRNDE algorithms.

The original/base RNDE algorithm and DE/Neighbor/1 mutation strategy have one weighted difference vector

$$V_i=X_{\mathrm{nbest}}+F\left(X_{r1}-X_{r2}\right)$$

(12)

On the contrary, the proposed IRNDE algorithm and DE/neighbor/2 mutation strategy have two weighted difference vectors

$$V_i=X_{\mathrm{nbest}}+F\left(X_{r1}-X_{r2}\right)+F\left(X_{r3}-X_{r4}\right)$$

(13)

In addition, the upper and lower neighbor bounds limits are also adjusted accordingly. In the base algorithm RNDE, the mutation strategy DE/Neighbor/1 lower bound $N_{lb}$ was set to 3, and the $N_{ub}$ upper bound was set to 10 after experimentation. For the proposed IRNDE, using the DE/neighbor/2 mutation strategy, we updated upper and lower bound limits accordingly, and set $N_{lb}$ to 5 and $N_{ub}$ to 12.

We used lower bound 5 because minimum vectors are 5 in our mutation equation. Moreover, the range of implication factor F in the base algorithm RNDE and the proposed algorithm IRNDE is between 0 to 2 and was varied according to the nature of the objective functions. The value of F is kept differently for each function until the best result is achieved. However, we have faced many difficulties during the implementation of IRNDE. In the RNDE algorithm, N denotes the neighbors and is very important in maintaining the balance between exploration and exploitation. If the individual from the population learns the best information from their neighbors, the efficiency of the overall algorithm will be enhanced and more fit offspring can be obtained.

Another major change from the original DE, which is used both by RNDE and the proposed IRNDE, is the dynamic updation of CR, if the trial vector is worse than the target/current vector. The idea behind the dynamic update of CR is that if the trial vector is worse than the target/current vector, i.e., $f\left(Ui\right)\ge f\left(Xi\right)$, it means current CR cannot provide the best solution; it needs to be updated. Conversely, if a small value of CR is not suitable, then this method can shift the value to the larger one. This strategy, called the adaptive shift strategy, is based on $C{R}_l$ and $C{R}_s$ and uses a standard deviation of 0.1 and the random number denoted by $randn$, which is a real number between 0 and 1. To fulfill this, RNDE uses two terms $C{R}_l$ and $C{R}_s$, where $C{R}_l$ means large and $C{R}_s$ means the smaller value of CR. The value of $C{R}_l$ is set to 0.85 and the value of $C{R}_s$ is set to 0.1 after conducting many experiments. If the fitness of the trial vector is worse than the target vector, then CR is updated using the negation from $C{R}_l$ to $C{R}_s$ or $C{R}_s$ to $C{R}_l$ using the following equations

$$CR=C{R}_l+0.1\times randn$$

(14)

$$CR=C{R}_u+0.1\times randn$$

(15)

In IRNDE, the crossover phase is given as

$$U_{ij}=\left\{\begin{array}{cc}{V}_{ij},\hfill & \mathrm{if}ran{d}_j(0,1)\le CR\mathrm{or}j=j_{rand}\hfill \\ X_{ij}\hfill & otherwise\hfill \end{array}\right.$$

(16)

Equation (16) is responsible for performing the crossover operation, as it is used in the same classical DE crossover phase studies. Moreover, where $G=1,2,\dots ,D$, and $i=1,2,\dots ,NP$$j_{rand}$ randomly choose an integer from $1,2,\dots ,D$, $ran{d}_j$ is a random value consistently distributed in [0, 1], $j=1,2,\dots ,D$, and, normally, CR should be in between [0, 1], as it is a crossover probability.

However, in RNDE and IRNDE, CR is dynamically updated, because if the value of CR is large, then the CR-made trial vector learns more from the mutant vector and less from the target vector; this causes an increase in the population diversity and is contrary to a small value of CR, making the trial vector learn more from the target vector and less from the mutant vector. IRNDE selection phase is denoted as

$$U_{ij}=\left\{\begin{array}{cc}{V}_{ij},\hfill & \mathrm{if}ran{d}_j(0,1)\le CR\mathrm{or}j=j_{rand}\hfill \\ X_{ij}\hfill & otherwise\hfill \end{array}\right.$$

(17)

Equation (17) shows the selection phase of IRNDE, which is different from the classical DE. As in classical DE, greedy choice is used between the $U_i$ trial vector and $X_i$ target vector, and if $U_i$ is better, then $X_i$ is replaced with $U_i$. Hence, it survives in the next generation; however, in RNDE and IRNDE, if the $U_i$ trial vector is not better than the $X_i$ target vector, then $X_i$ will be replaced with $X_i$ and will dynamically update the CR. This is where $NP$ shows the number of individuals in the population, $FEs$ is the number of function evaluations, $Max\left(FEs\right)$ is the maximum number of functions evaluated, $V_i$ is the mutant vector around the individual $X_i$ (or called a target vector),$U_i$ is the trial vector, $f_{min}$ is the minimum (best) value of the objective function in the population at the current generation, and $xi$ is the smallest constant in the computer to avoid a zero-division-error. $Flag$ is used to inverse the value of $CR$ and is initialized with 0, $CR$ is the crossover probability, $C{R}_{large}$ is the large mean value which is generated by Gaussian distribution, $C{R}_{small}$ is a small mean value that is generated by the Gaussian distribution, and 0.1 is the standard deviation. After some experimentation and surveys, $C{R}_{large}$ is set to 0.85 and $C{R}_{small}$ is set to 0.1.

5. Results and Discussions

To evaluate the effectiveness of the proposed algorithm IRNDE and the new enhanced mutation strategy, namely DE/Neighbor/2, we utilized 27 commonly used benchmark functions in which the previous RNDE algorithm and DE/Neighbor/1 mutation strategy were tested. For fair testing with the base algorithm, we implement both RNDE and the proposed IRNDE using the DE/Neighbor/1 mutation strategy and DE/Neighbor/2 mutation strategy, respectively, on the same parameter settings.

5.1. Parameter Settings

As mentioned earlier, the original/base RNDE algorithm and DE/Neighbor/1 mutation strategy have one amplified difference vector, however, the proposed IRNDE algorithm and DE/neighbor/2 mutation strategy have two amplified difference vectors used to generate the mutant vector or donor vector. In addition, upper and lower bounds limits for the calculation of neighbors are also adjusted accordingly. In the base algorithm, the RNDE mutation strategy DE/Neighbor/1 lower bound $N_{lb}$ was set to 3, and the $N_{ub}$ upper bound was set to 10 after some research and experimentation. We have improved the mutation equation in our algorithm and added an extra weighted difference vector in the proposed IRNDE mutation strategy DE/neighbor/2. We have updated the upper and lower bound limits as well and set $N_{lb}=$ 5 and $N_{ub}=$ 12.

The lower bound is set to 5 because minimum vectors are 5 in our mutation equation. Moreover, the range of implication factor F in the base algorithm RNDE and the proposed algorithm IRNDE was between 0 and 2 and has been varied according to the nature of the objective functions. The value of F is kept different for each function until the best result is achieved. Finally, the selection phase is the same as used in the original DE algorithm except for the updating process of CR, which is already explained.

5.2. Benchmark Functions

For experimental evaluation, we have used a test suite with 27 benchmark functions, which are also used by the RNDE algorithm. The details of the test suit are provided in Table 1.

Table 1. Test suite with 27 benchmark functions.

Function	Name	Search Range	Global Optimum
Unimodal Functions
f1	Sphere	[−100, 100]	0
f2	Schwefel2.22	[−10, 10]	0
f3	Schwefel1.2	[−100, 100]	0
f4	Schwefel2.21	[−100, 100]	0
f5	Rosenbrock’s	[−30, 30]	0
f6	Step	[−1.28, 1.28]	0
f7	Quartic with Noise	[−100, 100]	0
Multimodal Functions
f8	Schwefel2.26	[−500, 500]	−418.98
f9	Rastrigin’s	[−5.12, 5.12]	0
f10	Ackley	[−32, 32]	0
f11	Griewank’s	[−600, 600]	0
f12	Penalized1	[−50, 50]	0
f13	Penalized2	[−50, 50]	0
Shifted Unimodal Functions
f14	Shifted Sphere Function	[−100, 100]	−450
f15	Shifted Schwefel’s Problem 1.2	[−100, 100]	−450
f16	Shifted Rotated High Conditioned Elliptic Function	[−100, 100]	−450
f17	Shifted Schwefel’s Problem 1.2 with Noise in Fitness	[−100, 100]	−450
f18	Schwefel’s Problem 2.6 with Global Optimum on Bounds	[−100, 100]	−310
Shifted Multimodal Functions
f19	Shifted Rosenbrock’s Function	[−100, 100]	390
f20	Shifted Rotated Griewank’s Function without Bounds	[0, 600]	−180
f21	Shifted Rotated Ackley’s Function with Global Optimum on Bounds	[−32, 32]	−140
f22	Shifted Rastrigin’s Function	[−5, 5]	−330
f23	Shifted Rotated Rastrigin’s Function	[−5, 5]	−330
f24	Shifted Rotated Weierstrass Function	[−0.5, 0.5]	90
f25	Schwefel’s Problem 2.13	[$-\pi$, $\pi$]	−460
f26	Shifted Expanded Griewank’s plus Rosenbrock’s Function (F8F2)	[−3, 1]	−130
f27	Shifted Rotated Expanded Scaffer’s F6 Function	[−100, 100]	−300

5.3. Results

The list given in Table 1 is the list of benchmark functions, their ranges, and their global minimum. These are the functions that we used to check the performance of both algorithms, RNDE and IRNDE. For experiments, 5000 iterations are used to evaluate the performance of both algorithms. Convergence graphs are shown only for f1 to f6; however, tabular data are presented for f1 to f15.

Figure 2 shows the graphical representation of the fitness results of f1 to f6, where iterations are 5000, population NP = 150, and dimension D = 50. Moreover, the overall enhancement of the proposed algorithm IRNDE can be clearly observed.

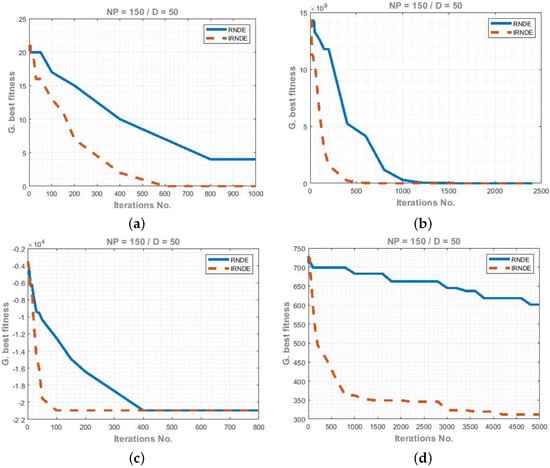
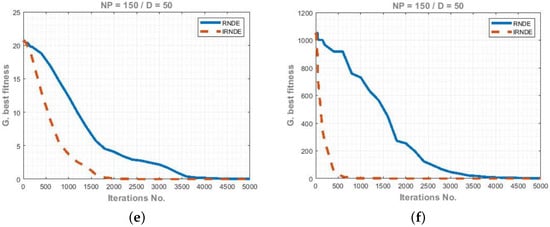
Figure 2. Convergence graphs of f1 to f6 for RNDE and IRNDE. (a) Function f1 convergence graph of RNDE and IRNDE for NP = 150, D = 30, Iterations = 5000, (b) Function f2 convergence graph of RNDE and IRNDE for NP = 150, D = 30, Iterations = 5000, (c) Function f3 convergence graph of RNDE and IRNDE for NP = 150, D = 30, Iterations = 5000, (d) Function f4 convergence graph of RNDE and IRNDE for NP = 150, D = 30, Iterations = 5000, (e) Function f5 convergence graph of RNDE and IRNDE for NP = 150, D = 30, Iterations = 5000, and (f) Function f6 convergence graph of RNDE and IRNDE for NP = 150, D = 30, Iterations = 5000.

The performance of both algorithms, RNDE and IRNDE, is analyzed with respect to variations in the number of populations (NP) and dimensions that are denoted by D. Results of fitness values are reported in Table 2 for population size NP = 150, dimension size D = 50, and iterations = 5000. The results are divided into the pair of five benchmark functions: f1 to f5, f6 to f10, and f11 to f15. It can be clearly observed that the proposed algorithm IRNDE has performed far better than the base algorithm RNDE. There is a visible difference, as the proposed algorithm IRNDE is reducing more quickly than the base algorithm RNDE.

Table 2. Fitness values of function f1 to f5 for NP = 150, D = 50, and iterations = 5000.

Iterations	f1		f2		f3		f4		f5
	RNDE	IRNDE	RNDE	IRNDE	RNDE	IRNDE	RNDE	IRNDE	RNDE	IRNDE
1	107,166	107,166	197,013	197,013	91.4529	91.4529	2.19833e+71	2.19833e+71	4.31944e+08	4.31944e+08
5	107,166	107,166	197,013	197,013	91.4529	91.4529	1.56318e+71	1.25631e+69	4.31944e+08	4.31944e+08
10	106,763	98,577.1	197,013	197,013	91.4529	91.4529	1.56318e+71	9.13478e+68	4.31944e+08	4.31944e+08
15	106,763	98577.1	197,013	197,013	91.4529	91.4529	1.36815e+71	6.45164e+68	4.31944e+08	4.31944e+08
20	106,763	98577.1	196,295	168,441	91.4529	91.4529	6.09134e+69	5.62354e+67	4.31944e+08	4.31944e+08
30	102,924	93,241.7	196,295	168,441	91.4529	91.4529	1.10354e+69	3.20042e+67	4.31944e+08	4.31944e+08
40	93,490.6	93,241.7	196,295	168,441	91.4529	91.4529	8.49963e+68	1.1789e+65	4.31944e+08	4.31944e+08
50	93,490.6	91,660.3	196,295	168,441	91.4529	91.4529	3.2853e+67	6.41441e+63	4.31944e+08	4.31944e+08
100	86,431.9	56,403.3	196,295	168,441	91.4065	89.2837	1.27491e+63	3.44804e+55	4.04911e+08	2.99116e+08
150	69,868.9	40,416.5	171,358	143,138	90.3058	89.2837	1.15333e+62	5.90041e+53	4.04911e+08	2.77088e+08
200	64,281	34,341.9	171,358	143,138	90.3058	89.0754	4.09299e+60	2.93405e+51	3.90937e+08	1.99466e+08
400	31,954.4	6800.34	164,102	113,800	89.5071	85.3248	8.52268e+57	6.13965e+47	2.92851e+08	1.51033e+07
600	17,025.5	1761.99	153,406	96,057.6	89.5071	74.6393	5.21376e+49	9.92589e+44	2.45835e+08	1.92694e+06
800	7159.23	271.509	153,406	96,057.6	88.0884	67.8502	1.49244e+47	4.0476e+43	1.54781e+08	350747
1000	2954.65	85.033	113,349	78,643.5	85.2505	56.0395	2.36147e+46	3.02577e+42	5.83435e+07	57207.6
1200	1411.61	12.6946	113,349	78571.1	81.3025	51.9173	4.34581e+45	7.79156e+40	1.66845e+07	23060.8
1400	705.528	3.36049	113,349	78,508.4	64.4952	43.103	3.27444e+42	1.04872e+38	1.06145e+07	6365.95
1600	330.4	0.705804	103,116	77,692	64.4952	38.9589	2.92916e+37	9.65888e+34	3.61785e+06	3784.11
1800	143.321	0.148906	103,116	76,766.7	58.7125	27.6752	2.68602e+33	1.27846e+34	1.06625e+06	1897.68
2000	72.6645	0.027825	102008	70697.2	49.5419	24.4122	2.62547e+33	1.74314e+32	861487	1077.72
2200	28.5524	0.00816997	100,863	61497.6	48.856	21.7797	2.3213e+31	2.27938e+30	263,768	916.068
2400	15.1582	0.00170155	97,335.3	51,589.8	43.1867	18.7337	2.27744e+30	1.26613e+27	195775	700.118
2600	5.75624	0.000385194	94,308.2	51,589.8	39.6438	14.7789	2.27744e+30	2.4849e+26	112,458	642.347
2800	2.84793	8.46806e-05	94308.2	46713.4	36.3745	12.6463	1.06585e+30	1.44058e+26	108,988	578.795
3000	1.30338	1.73096e-05	89,843.4	45,302.9	32.3394	9.99071	3.97908e+28	2.10136e+24	80144.5	515.251
3200	0.591442	4.38451e-06	89,843.4	38085.9	27.8329	8.72914	3.97908e+28	9.46517e+23	49,036	462.433
3400	0.243082	1.02105e-06	85,722.3	38,085.9	25.2841	6.37169	3.97908e+28	2.44522e+22	38,846.7	347.158
3600	0.112868	2.96409e-07	58,333.6	37,141.8	25.2841	0.4367	3.97908e+28	3.53667e+20	30,109.7	347.158
3800	0.0454132	4.85207e-08	58,087.2	33,533.5	22.1458	4.33106	3.97908e+28	3.23352e+19	21,079.1	301.099
4000	0.0233552	1.12556e-08	58,087.2	32429.3	20.2136	3.77252	1.09389e+28	1.09388e+18	19,657.9	248.39
4200	0.0104778	2.35218e-09	50,409.5	28,602.2	19.4409	3.06997	2.02774e+26	5.27283e+16	13542.1	188.169
4400	0.00507579	3.57897e-10	48,908.5	24,143	16.6239	2.6146	1.14581e+21	2.90392e+16	7989.71	129.291
4600	0.00191955	5.69887e-11	48,908.5	21,842.5	14.7613	2.18745	1.14581e+21	4.48367e+12	5393.15	75.9085
4800	0.000790519	1.34205e-11	48,908.5	19,772.3	14.4084	1.63888	1.14581e+21	1.43737e+11	4743.71	56.1816
5000	0.000285069	2.70302e-12	48,861.7	19,772.3	12.7042	1.38764	1.14581e+21	1.43737e+11	4269.41	49.7603

Results given in Table 3 are generated using population size NP = 150, dimension size D = 50, and iterations = 5000 for f6 to f10. It can be observed that the proposed algorithm IRNDE shows better performance compared to the base algorithm RNDE.

Table 3. Fitness values of function f6 to f10 for NP = 150, D = 50, and iterations = 5000.

Iterations	f6		f7		f8		f9		f10
	RNDE	IRNDE	RNDE	IRNDE	RNDE	IRNDE	RNDE	IRNDE	RNDE	IRNDE
1	21	21	1.42628e+10	1.42628e+10	−3516.54	−3516.54	728.486	728.486	20.7073	20.7073
5	20	21	1.42628e+10	1.42628e+10	−4303.27	−4484.28	710.839	728.486	20.7073	20.7073
10	20	19	1.42628e+10	1.42628e+10	−6262.3	−6764.29	710.839	728.486	20.6636	20.6009
15	20	19	1.42628e+10	1.42628e+10	−6282.13	−6935.1	710.839	724.258	20.6636	20.6009
20	20	19	1.42628e+10	1.12205e+10	−7428.17	−10,057	710.839	724.258	20.6636	20.5467
30	20	16	1.42628e+10	1.12205e+10	−9398.02	−14,537.2	710.839	724.258	20.6381	20.5467
40	20	16	1.42628e+10	1.05978e+10	−9534.25	−16,106.3	710.839	682.222	20.5408	20.5467
50	20	16	1.32638e+10	1.05978e+10	−10322.7	−19,528.8	710.839	679.314	20.4485	20.4571
100	17	13	1.26344e+10	6.24556e+09	−12489.3	−20,949	698.499	594.514	20.3311	19.7722
150	16	11	1.17699e+10	3.04017e+09	−14,918.2	−20,949	698.499	533.429	19.8555	19.2148
200	15	7	1.17699e+10	1.56747e+09	−16,420	−20,949	698.499	494.476	19.7466	17.9631
400	10	2	5.23897e+09	2.18584e+08	−20,949	−20,949	698.499	455.163	18.7771	13.0003
600	7	0	4.14472e+09	1.98573e+07	−20,949	−20,949	698.499	404.723	16.8826	8.77267
800	4	0	1.17689e+09	2.39732e+06	−20,949	−20,949	698.499	362.02	14.5523	5.26086
1000	4	0	2.94735e+08	229054	−20,949	−20,949	682.614	362.02	12.3433	3.72313
1200	3	0	5.57891e+07	34096.6	−20,949	−20,949	682.614	352.496	9.90552	2.51792
1400	2	0	1.79379e+07	2328.99	−20,949	−20,949	682.614	349.761	7.68546	1.84401
1600	2	0	4.92482e+06	268.371	−20,949	−20,949	682.614	349.212	5.72134	0.697559
1800	1	0	1.60315e+06	22.3301	−20,949	−20,949	661.983	349.212	4.52571	0.242736
2000	1	0	291,084	1.7914	−20,949	−20,949	661.983	349.212	4.08072	0.0935032
2200	1	0	149,086	0	−20,949	−20,949	661.983	346.007	3.42992	0.0420455
2400	1	0	64,393.3	0	−20,949	−20,949	661.983	346.007	2.92868	0.01849
2600	0	0	22,563.6	0	−20,949	−20,949	661.983	346.007	2.76194	0.00828884
2800	0	0	6538.42	0	−20,949	−20,949	661.983	346.007	2.45848	0.00367194
3000	0	0	1510.69	0	−20,949	−20,949	645.042	323.189	2.18228	0.00170531
3200	0	0	434.261	0	−20,949	−20,949	645.042	323.189	1.65711	0.00071923
3400	0	0	96.3754	0	−20,949	−20,949	637.334	323.189	0.958296	0.000306232
3600	0	0	29.8399	0	−20,949	−20,949	637.334	319.548	0.389258	0.000158771
3800	0	0	6.60063	0	−20,949	−20,949	618.245	319.548	0.233483	6.64578e-05
4000	0	0	3.47587	0	−20,949	−20,949	618.245	319.548	0.176824	3.53399e-05
4200	0	0	0	0	−20,949	−20,949	618.245	311.84	0.113753	1.68176e-05
4400	0	0	0	0	−20,949	−20,949	618.245	311.84	0.0665963	6.99799e-06
4600	0	0	0	0	−20,949	−20,949	618.245	311.84	0.041563	3.74626e-06
4800	0	0	0	0	−20,949	−20,949	601.333	311.84	0.0263947	1.71841e-06
5000	0	0	0	0	−20,949	−20,949	601.333	311.84	0.0188713	8.13691e-07

The results for f11 to f15 are given in Table 4, which is indicative of the superior performance of the proposed IRNDE for f11 to f15. Results demonstrate that the proposed IRNDE algorithm can obtain a global optimum with less numbers of iterations than the RNDE algorithm.

Table 4. Fitness values of function f11 to f15 for NP = 150, D = 50, and iterations = 5000, * indicates global optimum could not reach.

Iterations	f11		f12		f13		f14		f15
	RNDE	IRNDE	RNDE	IRNDE	RNDE	IRNDE	RNDE	IRNDE	RNDE	IRNDE
1	1055.15	1055.15	1.08539e+09	1.08539e+09	2.00701e+09	2.00701e+09	168,301	168,301	398,585	398,585
5	1055.15	1055.15	1.0548e+09	1.08539e+09	2.00701e+09	2.00701e+09	159,042	166,735	355,510	334,098
10	1055.15	1039.8	1.05323e+09	1.08539e+09	2.00701e+09	2.00701e+09	125,808	163,621	355,510	283,650
15	1055.15	1039.8	1.05323e+09	1.08539e+09	2.00701e+09	2.00701e+09	125,808	162,531	335,683	250,962
20	1052.27	937.941	1.05323e+09	1.08539e+09	2.00701e+09	2.00701e+09	120,207	131,129	335,683	250,962
30	1052.27	937.941	1.05323e+09	1.08539e+09	2.00701e+09	2.00701e+09	120,207	118,288	335,683	250,962
40	1052.27	894.572	1.05323e+09	1.08539e+09	2.00701e+09	2.00701e+09	106,490	114,755	335,683	250,962
50	1002.21	710.905	1.05323e+09	1.08539e+09	2.00701e+09	2.00701e+09	106,490	109,345	263,847	228,577
100	1002.21	542.417	1.05323e+09	1.01396e+09	1.88035e+09	1.94988e+09	85847.8	64180.9	224,621	185,333
150	1002.21	347.765	1.05323e+09	5.11633e+08	1.88035e+09	1.11306e+09	81634.2	55196.3	224,621	155,871
200	966.712	270.401	9.49775e+08	4.21792e+08	1.84609e+09	8.48217e+08	69772.1	34856.8	224,452	155,871
400	917.708	52.6602	5.81916e+08	3.97822e+07	1.3873e+09	7.41636e+07	24635.1	5930.8	209,400	152,495
600	917.708	13.7598	5.63661e+08	953763	1.26871e+09	3.5074e+06	12060.9	1400.9	177,338	144,816
800	759.071	3.21318	4.32972e+08	1005.07	1.2686e+09	43217.1	5247.32	−48.6701	170,882	125,566
1000	729.991	1.60481	2.97419e+08	22.796	7.18698e+08	767.809	2420.72	−370.845	154,607	97,994.6
1200	632.36	1.10341	4.74073e+07	9.4321	4.88062e+08	38.0572	838.294	−432.312	154,607	97,768.6
1400	564.399	1.01736	1.54405e+07	4.53885	1.71841e+08	16.5448	114.425	−446.984	153,222	94,129.1
1600	450.362	0.658333	3.30737e+06	4.25549	4.75411e+07	3.86112	−167.851	−449.317	153,222	79,506.3
1800	272.759	0.22698	310,283	2.83376	1.47191e+07	1.10332	-296.65	−449.78	141,583	77,475.6
2000	254.433	0.0445405	75,962.6	2.3151	3.43088e+06	0.308245	−398.253	−449.961	135,500	74,589.6
2200	198.676	0.00737067	126.916	2.12297	1.16831e+06	0.0776809	−424.14	−449.993	135,500	69,304.9
2400	124.491	0.00171678	31.6576	1.76203	258,691	0.0147251	−437.264	−449.998	127,620	62,349.5
2600	96.0986	0.000409527	19.7927	1.47519	19,247.4	0.00279349	−444.947	−450	127,620	56,522
2800	66.9394	9.89848e-05	12.1895	0.995179	296.106	0.000594427	−446.741	−450	123,796	55,272.9
3000	46.4022	2.55152e-05	11.0036	0.913088	62.8248	0.000129401	−449.27	−450	121,615	51,567.8
3200	34.6919	5.18012e-06	7.55257	0.536102	52.5342	2.94385e-05	−449.568	−450	112,014	47,125.5
3400	21.599	6.62209e-07	6.5113	0.282837	33.2308	7.30486e-06	−449.82	−450	97,448.5	45,670.9
3600	17.9387	1.96707e-07	6.23303	0.0455196	14.0115	1.12448e-06	−449.929	−450	97,356.9	44,078.9
3800	10.8625	4.72381e-08	5.51551	0.00797489	6.56287	2.64319e-07	−449.976	−450 *	95,037.9	43,505.3
4000	7.99392	9.67328e-09	3.45958	0.00158262	3.8305	5.15215e-08	−449.988	−450	95,037.9	30,530.6
4200	5.55138	1.67994e-09	3.33907	0.000302378	1.87559	6.99077e-09	−449.994	−450	79,005.2	28,242.5
4400	4.71148	4.01571e-10	3.33907	6.66714e-05	0.657885	1.60463e-09	−449.997	−450	79,005.2	27,167.2
4600	3.69465	6.71285e-11	3.27146	1.49248e-05	0.458076	2.50137e-10	−449.999	−450	79,005.2	27,167.2
4800	2.52784	1.32597e-11	3.27146	3.3658e-06	0.255931	5.15735e-11	−450	−450	76,609.3	18,035
5000	2.1493	2.38842e-12	3.27146	6.39102e-07	0.107353	9.56412e-12	−450*	−450	69,629.2	17,402.5

In Table 5, results are given for both RNDE and IRNDE regarding the best, mean, and worst values with standard deviation and number of iterations needed to reach the global optimum. Results are generated using the population size NP = 150, dimension size D = 10, and iterations = 5000. It can be observed that f14 RNDE at the 5000th iteration still could not reach the global optimum, as −450 is the rounded value and the original value is (−449.99983911013300), whereas IRNDE reached the global optimum in 3976 iterations. While observing the number of iterations for f1 to f27, it can be observed that IRNDE can achieve a global optimum with much less numbers of iterations compared to RNDE, which shows the superiority of the proposed IRNDE algorithm.

Table 5. Number of function evaluations for functions f1 to f15 for NP = 150, D = 10, and iterations = 1000 × D.

		10 Runs Fitness Evaluations for NP = 150/D = 10
		Best	Median	Worst	Mean ± Std. Dev.	Success Rate	RNDE vs. IRNDE (# of Iterations)
f1	RNDE	504	518	526	5.157e+2 ± 8.68012e+0	100%	516
	IRNDE	340	345	357	3.468e+2 ± 5.05085e+0	100%	348
f2	RNDE	1457	1480	1528	1.4885e+3 ± 2.25549e+1	100%	1549
	IRNDE	784	819	875	8.26e+2 ± 3.32031e+1	100%	802
f3	RNDE	820	846	874	8.456e+2 ± 1.42533e+1	100%	477
	IRNDE	590	625	647	6.207e+2 ± 1.82638e+1	100%	336
f4	RNDE	808	823	847	8.251e+2 ± 1.19856e+1	100%	832
	IRNDE	342	349	359	3.495e+2 ± 5.01664e+0	100%	618
f5	RNDE	1652	1715	1757	1.7163e+3 ± 3.54622e+1	100%	1737
	IRNDE	1034	1072	1132	1.0773e+3 ± 3.23661e+1	100%	1087
f6	RNDE	1	15	27	1.45e+1 ± 7.15309e+0	100%	13
	IRNDE	7	13	22	1.34e+1 ± 4.29987e+0	100%	12
f7	RNDE	187	192	204	1.955e+2 ± 6.62067e+0	100%	205
	IRNDE	122	132	139	1.316e+2 ± 5.05964e+0	100%	138
f8	RNDE	18	27	31	2.66e+1 ± 3.62706e+0	100%	30
	IRNDE	9	11	17	1.22e+1 ± 2.65832e+0	100%	11
f9	RNDE	830	871	908	8.742e+2 ± 2.23696e+1	100%	915
	IRNDE	906	1126	1265	1.1178e+3 ± 1.04919e+2	100%	1227
f10	RNDE	797	817	839	8.198e+2 ± 1.18771e+1	100%	815
	IRNDE	552	565	574	5.653e+2 ± 7.33409e+0	100%	569
f11	RNDE	1729	2065	2328	2.037e+3 ± 2.02333e+2	100%	2621
	IRNDE	1996	2586	3700	2.7613e+3 ± 5.16669e+2	100%	3453
f12	RNDE	446	468	493	4.671e+2 ± 1.26179e+1	100%	484
	IRNDE	321	331	344	3.327e+2 ± 7.39444e+0	100%	328
f13	RNDE	472	488	506	4.879e+2 ± 1.13671e+1	100%	476
	IRNDE	332	338	346	3.393e+2 ± 4.49815e+0	100%	327
f14	RNDE	503	511	524	5.112e+2 ± 6.47731e+0	100%	503
	IRNDE	337	353	359	3.512e+2 ± 7.56894e+0	100%	353
f15	RNDE	1440	1484	1558	1.4951e+3 ± 3.86018e+1	100%	1539
	IRNDE	810	824	887	8.363e+2 ± 2.70803e+1	100%	858
f16	RNDE	496	522	542	5.204e+2 ± 1.26947e+1	100%	499
	IRNDE	343	350	359	3.519e+2 ± 5.95259e+0	100%	345
f17	RNDE	1471	1532	1603	1.5474e+3 ± 4.45676e+1	100%	1496
	IRNDE	844	858	907	8.693e+2 ± 2.34902e+1	100%	832
f18	RNDE	616	643	679	6.494e+2 ± 1.96932e+1	100%	652
	IRNDE	513	535	558	5.346e+2 ± 1.12862e+1	100%	518
f19	RNDE	265	274	295	2.777e+2 ± 9.84378e+0	100%	265
	IRNDE	220	227	238	2.292e+2 ± 5.82714e+0	100%	233
f20	RNDE	400	431	484	4.396e+2 ± 2.63236e+1	100%	518
	IRNDE	228	261	308	2.683e+2 ± 2.55345e+1	100%	352
f21	RNDE	343	355	369	3.562e+2 ± 8.25698e+0	100%	365
	IRNDE	297	304	320	3.063e+2 ± 8.28721e+0	100%	310
f22	RNDE	388	396	411	3.991e+2 ± 7.37036e+0	100%	393
	IRNDE	257	268	274	2.681e+2 ± 5.21643e+0	100%	267
f23	RNDE	286	308	316	3.066e+2 ± 1.01784e+1	100%	306
	IRNDE	195	206	213	2.059e+2 ± 5.46606e+0	100%	196
f24	RNDE	761	803	831	8.008e+2 ± 1.98203e+1	100%	773
	IRNDE	616	634	649	6.343e+2 ± 1.09143e+1	100%	612
f25	RNDE	3620	5080	9495	5.83986e+3 ± 2.00043e+3	70%	3217
	IRNDE	286	423	1088	4.74111e+2 ± 2.39794e+2	90%	1608
f26	RNDE	179	182	216	1.918e+2 ± 1.31976e+1	100%	172
	IRNDE	108	117	123	1.164e+2 ± 4.16867e+0	100%	127
f27	RNDE	214	223	229	2.234e+2 ± 4.74224e+0	100%	228
	IRNDE	162	169	171	1.683e+2 ± 2.71006e+0	100%	169

Results given in Table 5, Table 6 and Table 7 report the performance of both RNDE and IRNDE for dimensions D of 10, 30, and 50. The performance is analyzed with respect to the number of fitness evaluations (NFE). This test is based on 10 runs of fitness evaluation and will keep running until the terminating condition is satisfied, where the termination condition is set as 10,000 × D. The size of D varies from 10, and 30 to 50. For example, if the number of dimensions is D = 30 then the algorithm has to run for 10,000 × 30 = 300,000 iterations to achieve the global minimum. Moreover, if the algorithm reaches the global minimum in 300,000 iterations, then we record in how many iterations the global minimum is achieved; if the algorithm is not able to achieve the global minimum in 300,000 iterations, it will consider and mark that the global minimum is not achieved so the output will be the error, as shown for f9 and f25 in Table 6 and Table 7, where both RNDE and IRNDE are unable to obtain the global minimum. Similarly from the above-mentioned discussion, it is concluded that if there is a change in dimensions, then the iterations must change as there is a direct relation between dimensions and iterations.

Table 6. Number of function evaluations for functions f1 to f15 for NP = 150, D = 30, and iterations = 1000 × D.

		10 Runs Fitness Evaluations for NP = 150/D = 30
		Best	Median	Worst	Mean ± Std. Dev.	Success Rate	RNDE vs. IRNDE (# of Iterations)
f1	RNDE	2555	2627	2745	2.6491e+3 ± 6.40424e+1	100%	2675
	IRNDE	1736	1753	1792	1.7634e+3 ± 2.09401e+1	100%	1802
f2	RNDE	57,202	59,993	66,380	6.05669e+4 ± 2.46933e+3	100%	57,718
	IRNDE	23,162	23,828	24,961	2.39414e+4 ± 5.28169e+2	100%	24,016
f3	RNDE	8581	8825	9258	8.9154e+3 ± 2.28402e+2	100%	9119
	IRNDE	5464	5532	5841	5.6021e+3 ± 1.32403e+2	100%	5546
f4	RNDE	4294	4340	4476	4.356e+3 ± 6.34333e+1	100%	4480
	IRNDE	3086	3169	3395	3.1891e+3 ± 8.24155e+1	100%	3303
f5	RNDE	12504	12915	13721	1.30622e+4 ± 4.15667e+2	100%	13,426
	IRNDE	7377	7580	7803	7.5919e+3 ± 1.51639e+2	100%	7659
f6	RNDE	179	225	272	2.27e+2 ± 3.39706e+1	100%	227
	IRNDE	118	143	168	1.437e+2 ± 1.75439e+1	100%	142
f7	RNDE	1150	1224	1289	1.2318e+3 ± 4.22816e+1	100%	1239
	IRNDE	811	840	902	8.455e+2 ± 2.53213e+1	100%	886
f8	RNDE	70	108	137	1.017e+2 ± 2.17718e+1	100%	102
	IRNDE	25	35	58	3.68e+1 ± 8.9666e+0	100%	52
f9	RNDE	39881	43,293	48,764	4.37697e+4 ± 2.6549e+3	100%	41,835
	IRNDE	-	-	-	-	0%	6.58946e+1
f10	RNDE	3998	4089	4208	4.0932e+3 ± 7.4265e+1	100%	4147
	IRNDE	2700	2730	2770	2.7372e+3 ± 2.18469e+1	100%	2718
f11	RNDE	4072	4147	4297	4.1676e+3 ± 8.43567e+1	100%	4146
	IRNDE	1827	2017	2161	2.0213e+3 ± 1.14815e+2	100%	2092
f12	RNDE	2569	2701	2840	2.6904e+3 ± 7.63081e+1	100%	2782
	IRNDE	1719	1739	1823	1.7558e+3 ± 3.35354e+1	100%	1752
f13	RNDE	2586	2616	2719	2.6462e+3 ± 5.21575e+1	100%	2661
	IRNDE	1738	1769	1838	1.7794e+3 ± 3.34139e+1	100%	1809
f14	RNDE	2646	2667	2742	2.6824e+3 ± 3.43615e+1	100%	2630
	IRNDE	1746	1780	1833	1.7887e+3 ± 3.41989e+1	100%	1867
f15	RNDE	58341	60,131	62,726	6.07395e+4 ± 1.69443e+3	100%	59,989
	IRNDE	23,938	24,436	24,956	2.44474e+4 ± 3.02649e+2	100%	23,667
f16	RNDE	2574	2642	2752	2.651e+3 ± 5.04094e+1	100%	2674
	IRNDE	1770	1803	1842	1.8056e+3 ± 2.39499e+1	100%	1780
f17	RNDE	61,575	61,985	65,619	6.29908e+4 ± 1.38551e+3	100%	62,862
	IRNDE	25,129	26,032	27,197	2.62584e+4 ± 7.24199e+2	100%	27,668
f18	RNDE	4695	4781	4878	4.7949e+3 ± 6.23154e+1	100%	4890
	IRNDE	3486	3638	3821	3.6549e+3 ± 8.90661e+1	100%	3741
f19	RNDE	1018	1039	1088	1.0458e+3 ± 1.88255e+1	100%	1023
	IRNDE	805	823	844	8.251e+2 ± 1.46246e+1	100%	803
f20	RNDE	4386	4728	5203	4.7566e+3 ± 2.72762e+2	100%	4829
	IRNDE	2633	2936	3887	3.0857e+3 ± 3.68177e+2	100%	3050
f21	RNDE	1257	1279	1311	1.2815e+3 ± 1.75768e+1	100%	1307
	IRNDE	1029	1050	1056	1.0457e+3 ± 1.02746e+1	100%	1082
f22	RNDE	2078	2151	2228	2.1589e+3 ± 4.80681e+1	100%	2653
	IRNDE	1399	1424	1507	1.4387e+3 ± 3.33801e+1	100%	1532
f23	RNDE	1629	1685	1734	1.6867e+3 ± 3.29209e+1	100%	1699
	IRNDE	1084	1121	1181	1.1264e+3 ± 2.89988e+1	100%	1111
f24	RNDE	6375	6465	6618	6.4829e+3 ± 8.03388e+1	100%	6556
	IRNDE	4785	4939	5162	4.946e+3 ± 1.2686e+2	100%	4926
f25	RNDE	50,303	-	-	-	10%	2549.54
	IRNDE	-	-	-	-	0%	966.653
f26	RNDE	1988	2448	3554	2.5159e+3 ± 4.72809e+2	100%	1570
	IRNDE	985	1202	1350	1.1722e+3 ± 1.12576e+2	100%	937
f27	RNDE	1069	1104	1148	1.1106e+3 ± 2.85081e+1	100%	1088
	IRNDE	765	788	806	7.859e+2 ± 1.30933e+1	100%	778

Table 7. Number of function evaluations for functions f1 to f15 for NP = 150, D = 50, and iterations = 1000 × D.

		10 Runs Fitness Evaluations for NP = 150/D = 50
		Best	Median	Worst	Mean ± Std. Dev.	Success Rate	RNDE vs. IRNDE (# of iterations)
f1	RNDE	7214	7445	7721	7.4651e+3 ± 1.41869e+2	100%	7391
	IRNDE	3869	3921	4028	3.9451e+3 ± 5.64298e+1	100%	3888
f2	RNDE	109,913	113,260	120,046	1.14284e+5 ± 2.98052e+3	100%	109,893
	IRNDE	67,118	69,546	70,788	6.91903e+4 ± 1.32311e+3	100%	74,815
f3	RNDE	38,400	39,679	41,609	4.01089e+4 ± 9.56063e+2	100%	37,964
	IRNDE	22,579	23,704	24,492	2.35874e+4 ± 6.57373e+2	100%	24,331
f4	RNDE	19,633	21,491	22,899	2.14575e+4 ± 8.63521e+2	100%	20,941
	IRNDE	12,048	14,038	15,583	1.4151e+4 ± 1.31694e+3	100%	11,980
f5	RNDE	53,747	56,423	65,062	5.67883e+4 ± 3.33907e+3	100%	57,945
	IRNDE	21,985	22,926	23,565	2.29314e+4 ± 5.33276e+2	100%	23,786
f6	RNDE	2093	2695	3858	2.7862e+3 ± 4.73772e+2	100%	2801
	IRNDE	390	558	644	5.562e+2 ± 7.65721e+1	100%	464
f7	RNDE	4389	4620	4960	4.6433e+3 ± 1.99158e+2	100%	4743
	IRNDE	2012	2074	2110	2.0685e+3 ± 3.06132e+1	100%	2166
f8	RNDE	174	220	378	2.451e+2 ± 6.85492e+1	100%	472
	IRNDE	40	60	77	6.e+1 ± 1.09341e+1	100%	64
f9	RNDE	363687	-	-	-	10%	2.69166e+1
	IRNDE	-	-	-	-	0% 2.17122e+2
f10	RNDE	11,610	11,833	12,182	1.19068e+4 ± 1.86668e+2	100%	12,179
	IRNDE	5818	5979	6111	5.9913e+3 ± 9.06116e+1	100%	6069
f11	RNDE	20,074	21,698	23,867	2.19229e+4 ± 1.05793e+3	100%	22,594
	IRNDE	3846	4025	4310	4.0539e+3 ± 1.37402e+2	100%	4014
f12	RNDE	16,969	18,456	24,620	1.90873e+4 ± 2.41333e+3	100%	21,185
	IRNDE	5077	5680	6303	5.7656e+3 ± 4.00958e+2	100%	5537
f13	RNDE	8787	9155	10266	9.484e+3 ± 5.46782e+2	100%	9104
	IRNDE	3997	4158	4232	4.154e+3 ± 6.94358e+1	100%	4149
f14	RNDE	7136	7254	7679	7.3257e+3 ± 1.76951e+2	100%	7320
	IRNDE	3905	3945	4055	3.9735e+3 ± 5.40684e+1	100%	3999
f15	RNDE	111,558	113,908	123,780	1.15099e+5 ± 3.86545e+3	100%	115,568
	IRNDE	64,774	68,523	71,652	6.89078e+4 ± 1.95258e+3	100%	68,125
f16	RNDE	7278	7311	7637	7.3623e+3 ± 1.05346e+2	100%	7636
	IRNDE	3836	3996	4063	3.9862e+3 ± 7.47274e+1	100%	4004
f17	RNDE	117,296	124,557	128,845	1.24642e+5 ± 3.76015e+3	100%	125,185
	IRNDE	74,880	78,511	82,122	7.8798e+4 ± 2.27369e+3	100%	80,990
f18	RNDE	15,527	16,158	17,455	1.64022e+4 ± 6.10143e+2	100%	17,064
	IRNDE	12,863	13,177	13,876	1.32738e+4 ± 3.59021e+2	100%	12,389
f19	RNDE	1896	1937	2031	1.9478e+3 ± 4.20972e+1	100%	1949
	IRNDE	1519	1530	1580	1.5368e+3 ± 1.88078e+1	100%	1531
f20	RNDE	14,092	16,088	20,233	1.67794e+4 ± 2.10221e+3	100%	21,606
	IRNDE	13,981	18,900	34,239	2.20096e+4 ± 5.75139e+3	100%	25,853
f21	RNDE	2333	2433	2483	2.4255e+3 ± 4.67529e+1	100%	2434
	IRNDE	1873	1933	2044	1.9509e+3 ± 5.22865e+1	100%	1949
f22	RNDE	5807	6420	7360	6.4919e+3 ± 4.23616e+2	100%	6823
	IRNDE	3137	3243	3660	3.3141e+3 ± 1.69914e+2	100%	3916
f23	RNDE	4805	5018	5360	5.0267e+3 ± 1.55067e+2	100%	5029
	IRNDE	2509	2575	2685	2.5812e+3 ± 5.33621e+1	100%	2592
f24	RNDE	15,928	16,317	16,709	1.63417e+4 ± 2.60714e+2	100%	15,566
	IRNDE	12,581	13,007	13,582	1.31475e+4 ± 3.50596e+2	100%	12,686
f25	RNDE	401842	-	-	-	10%	3.44991e+3
	IRNDE	-	-	-	-	0%	7.49417e+5
f26	RNDE	5996	7521	8927	7.407e+3 ± 9.59153e+2	100%	6808
	IRNDE	3368	4557	6620	4.7084e+3 ± 1.10688e+3	100%	4394
f27	RNDE	2314	2404	2460	2.4018e+3 ± 5.12636e+1	100%	2415
	IRNDE	1644	1686	1750	1.6957e+3 ± 3.59755e+1	100%	1710

Moreover, we performed the abovementioned tests on the same well-known 27 benchmark functions that were used by the RNDE algorithm for its evaluation. In addition, we also discussed the different scenarios, such as how many iterations are required for both algorithms to achieve the global minimum if the algorithms obtain the worst, median, or best population data and what the success rate of both algorithms is in achieving the global minimum during the calculation of NFE. Finally, Figure 3 and Figure 4 show a bar graph of the median values of both algorithms and demonstrate the performance of both algorithms. It is noteworthy to point out that the proposed IRNDE outperforms the RNDE algorithm.

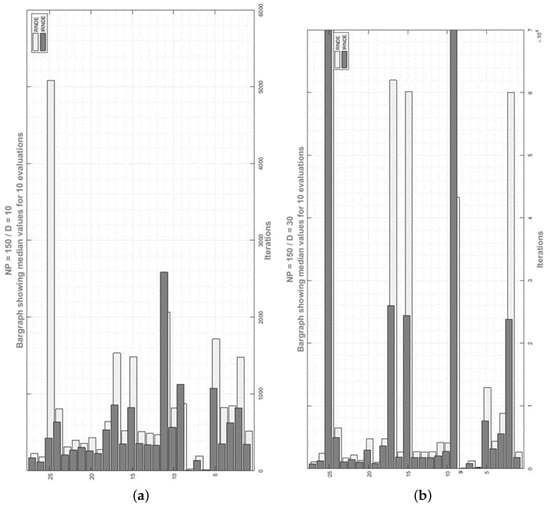
Figure 3. Number of fitness evaluations for RNDE and IRNDE. (a) NFE comparison of RNDE and IRNDE when NP = 150 and D = 10; (b) NFE comparison of RNDE and IRNDE when NP = 150 and D = 30.

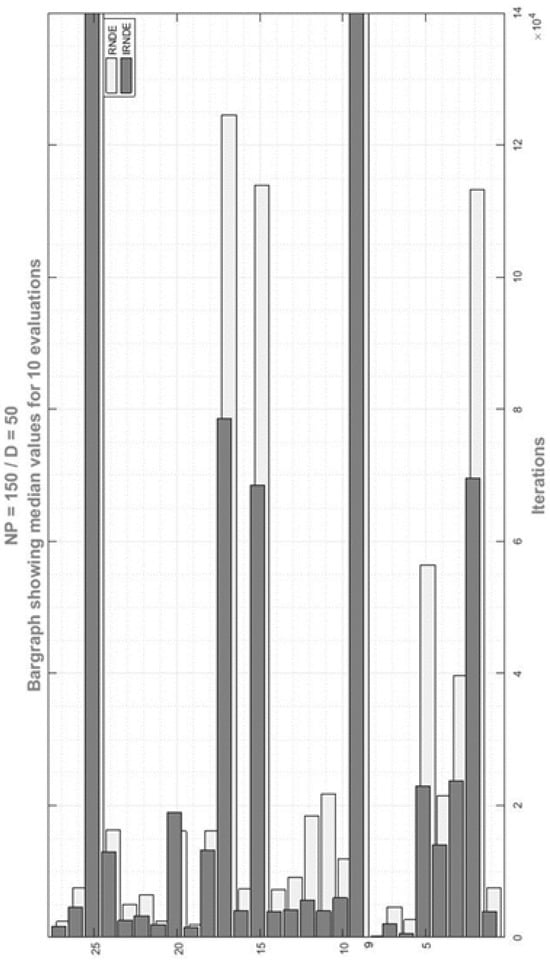
Figure 4. NFE comparison of RNDE and IRNDE when NP = 150 and D = 50.

5.4. Statistical Significance

The statistical significance performance of average fitness values of two algorithms are analyzed using the two-sampled pair t-test significant test. The null hypothesis states that there is no significance difference between the average fitness performance of the RNDE algorithm (${\mathsf{\mu }}_1$) and IRNDE algorithm (${\mathsf{\mu }}_2$). The s.t $\mathsf{\mu }1-\mathsf{\mu }2=0$ and alternate hypothesis state that there is a significance difference between the average fitness performance of the RNDE algorithm and IRNDE algorithm(${\mathsf{\mu }}_2$) s.t $\mathsf{\mu }1\ne \mathsf{\mu }2$. We used a 0.05 level of significance test to generate significant t-Test results, which are reported in Table 8 of this paper. The degree of freedom used in the research was 34 for 35 observations used to generate test statistics, the sample mean, variance, Pearson correlation, and p values for two-tailed critical t-test values. We generated significant values for fifteen functions; the results of the rest of the functions were similar. It can be observed from the table that all p-values except $f_4$ and $f_{14}$ are less than the level of significance (0.05). It can be summarized that overall there is a significant difference in the performance of the RNDE algorithm and IRNDE algorithm.

Table 8. Statistically paired two-sample significance t-test for means of RNDE vs. IRNDE.

Function	Algorithm	Mean	Variance	Pearson Correlation	t-Stat	p-Value
f1	RNDE	3.16e+04	2.00e+09	-	-	-
	IRNDE	2.65e+04	1.75e+09	9.79e-01	3.23e+00	2.77e-03
f2	RNDE	1.23e+05	3.08e+09	-	-	-
	IRNDE	9.24e+04	3.78e+09	9.72e-01	1.21e+01	7.92E-14
f3	RNDE	5.92e+01	9.70e+02	-	-	-
	IRNDE	4.53e+01	1.42e+03	9.69e-01	7.66e+00	6.71e-09
f4	RNDE	1.94e+70	3.02e+141	-	-	-
	IRNDE	6.36e+69	1.38e+141	6.40e-01	1.82e+00	7.82e-02
f5	RNDE	1.55e+08	3.83e+16	-	-	-
	IRNDE	1.21e+08	3.48e+16	9.25e-01	2.71e+00	1.04e-02
f6	RNDE	7.00e+00	7.35e+01	-	-	-
	IRNDE	5.14e+00	6.32e+01	9.59e-01	4.50e+00	7.47e-05
f7	RNDE	4.58e+09	3.97e+19	-	-	-
	IRNDE	3.19e+09	2.89e+19	9.10e-01	3.10e+00	3.86e-03
f8	RNDE	-1.72e+04	3.59e+07	-	-	-
	IRNDE	-1.85e+04	2.79e+07	8.99e-01	2.82e+00	7.95e-03
f9	RNDE	6.70e+02	1.39e+03	-	-	-
	IRNDE	4.44e+02	2.64e+04	7.98e-01	9.92e+00	1.43E-11
f10	RNDE	9.63e+00	7.74e+01	-	-	-
	IRNDE	7.37e+00	8.45e+01	9.51e-01	4.69e+00	4.35e-05
f11	RNDE	5.00e+02	2.03e+05	-	-	-
	IRNDE	2.54e+02	1.67e+05	7.69e-01	4.93e+00	2.14e-05
f12	RNDE	3.85e+08	2.30e+17	-	-	-
	IRNDE	3.05e+08	2.25e+17	9.19e-01	2.46e+00	1.92e-02
f13	RNDE	7.72e+08	8.16e+17	-	-	-
	IRNDE	5.73e+08	7.80e+17	8.91e-01	2.83e+00	7.72e-03
f14	RNDE	3.74e+04	3.17e+09	-	-	-
	IRNDE	3.68e+04	3.73e+09	9.78e-01	2.63e-01	7.94e-01
f15	RNDE	1.82e+05	9.61e+09	-	-	-
	IRNDE	1.23e+05	1.01e+10	9.84e-01	1.93e+01	6.53E-20

6. Conclusions

Differential evolution is a strong evolutionary algorithm that provides a powerful solution to resolve global optimization problems. However, the existing mutation strategies, DE/best/1 and De/rand/1, do not provide a balance between better exploitation and exploration. So far, to overcome this issue, the DE/Neighbor/1 mutation strategy and RNDE algorithm have been introduced. The DE/Neighbor/1 mutation strategy maintains a balance between exploration and exploitation, as it was built to use the lower and upper bound limits. However, this mutation strategy makes the whole procedure or convergence very slow, and requires a higher number of iterations for convergence. This study overcomes this limitation by introducing IRNDE with a DE/neighbor/2 mutation strategy. Contrary to the DE/Neighbor/1 mutation strategy in the RNDE algorithm, the proposed IRNDE adds weighted differences after various tests. The proposed IRNDE algorithm and DE/neighbor/2 mutation strategy are tested on the same 27 commonly used benchmark functions, on which the DE/Neighbor/1 mutation strategy and RNDE algorithm were tested. Experimental results demonstrate that the new mutation strategy DE/neighbor/2 and IRNDE algorithm is better and faster overall in convergence. Moreover, while performing successful tests on both state-of-the-art algorithms, we have gone through different situations during the implementation of benchmark functions concerning minimum, mean, and worst values. Although it has been proven that the proposed algorithm IRNDE is better and more successful overall, not only in maintaining the balance between exploration and exploitation but also in converging more quickly than the base RNDE algorithm, it may not provide optimal results in some scenarios. For results using 27 benchmark functions’ test suites, the proposed algorithm IRNDE performs better than the base algorithm RNDE except for the f9 Rastrigin function and f25 Schwefels Problem. The experimental results of the average fitness ensures the significant difference between the performance of RNDE and IRNDE algorithms using a two-tailed paired t-test at a 0.05 level of significance. The limitation of this study is that it is applied to constrained problems. Applying this study to unconstrained problems could be a good idea in future work. Finally, we intend to apply the proposed algorithm to complex, real-world problems, such as steganography, which remains an attractive topic. Another future work of this study could be the usage of memory to store the convergence track of parameters associated with the proposed algorithm based on user-defined time periods.