Abstract
Recent measurements in the top quark sector at the CERN Large Hadron Collider are discussed. This review discusses the most recent measurements of inclusive and differential top quark cross-sections in strong and electroweak production of top quarks and related measurements, such as top quark properties, as well as searches, including EFT approaches.
1. Introduction
The top quark, t, is the heaviest known elementary particle and was discovered at the Tevatron collider in 1995 by the CDF and DØ collaborations [1,2] with a mass around . It was re-discovered at the Large Hadron Collider (LHC) at all center-of-mass energies the LHC operated at during Run 1 and Run 2: 7 [3,4], 8 [5,6], and 13 [7,8] TeV and even in proton-Pb collisions [9]. Most recently, the LHC has re-started operations at the highest energies of 13.6 TeV, which marks the official start of the Run 3 collider operations. The top quark plays a special role in the standard model (SM) and also in many extensions. Measurements of the top quark mass together with measurements of the W boson mass and the mass of the Higgs boson discovered in 2012 [10,11] provide now a strong self-consistency test of the SM [12,13,14,15,16]. The top quark has an extremely short lifetime of s, which prevents the formation of top quark hadrons in general, while a small fraction might form short-lived bound top quark states, aka “toponium” [17]. The time-scale of depolarization of the top quarks is beyond , allowing us to uniquely observe bare quark properties by measuring the properties of the top quarks. One example is the access to the spin of top quarks, the extent of their correlation, and the top quarks’ polarization itself. Reconstructing the quantum spin state of top quarks allows accessing an elusive behavior of quantum mechanical particles: entanglement, where the wave functions of two originally entangled particles possess an inseparable component of the wave functions even when they are moving apart. Measurements in this area open up an exciting new probe into the inner workings of quantum mechanics at the fundamental level with far-reaching implications and related research prospects in quantum information science at colliders [18,19]. Additionally, its large Yukawa coupling gives the top quark a special role in the interplay with the Higgs boson and the Higgs field, which affects extensions of the SM and also the evolution of the SM to high scales, where e.g., the stability of the electroweak vacuum is critically affected by the interplay of the top quark mass and the Higgs boson mass [20,21,22,23].
At any of the LHC energies, the top quark is produced so copiously that the LHC is referred to as a “top quark factory”. Top quarks are produced either as top quark-antiquark pairs () via the strong interaction (/), providing a direct test of quantum chromodynamics (QCD), or as single top quarks via electroweak processes, testing the electroweak theory and providing a direct probe of the CKM matrix element . Three different channels contribute to the production of single top quarks: the t-channel , the associated -channel , and the s-channel . Owing to the proton–proton initial state, the latter has a very small production cross-section at the LHC with a low signal-to-background fraction, making any observation extremely challenging. Any and all production modes are employed for measurements of top quark properties, searches, and, more recently, constraints on (SM) effective field theory (EFT) operators [24,25,26,27].
In the SM, the branching fraction for top quarks decaying into Wb is essentially 100%, where the subsequent decay of the W into or ’ is utilized to denote the decay channel. Namely, either the dileptonic () final state, where ℓ can be an electron or a muon (including those that stem from decays), the lepton+jets ( jets) final state, or the all-hadronic final state into all-jets. Jets originating from a b quark are usually identified by means of multivariate discriminant techniques (“b-tagging”) built using the combination of variables describing the properties of secondary vertices and of tracks with large impact parameters relative to the primary vertex. Depending on the number of top quarks in the final state, there can be a single lepton or more, one or more jets, some of them b-tagged, and mixtures of leptons and jets. For example, in top quark pair production in the jets final state, one of the two W bosons (stemming from the decay of the top quarks) decays leptonically, and the other W boson decays hadronically.
In this review, we selected a sample of measurements that highlight the current status of experimental top quark physics. The review begins with summarizing the evolution of analysis techniques over the past two decades in Section 2, before discussing measurements on inclusive and differential top quark and top-quark pair production cross-sections in Section 3. Measurements of top quark properties are summarized in Section 4, including measurements of angular correlations related to asymmetries in the production of top quarks, as well as measurements of the correlation of the spin of the top quark, all covered in Section 4.1. Section 4.2 outlines the current status of precision measurements of the mass of the top quark. Where available, combinations of ATLAS and CMS results are presented as well. This review focuses on measurements. Searches for beyond-the-SM physics contributions (BSM) are only briefly captured in Section 5, and otherwise discussed in more detail elsewhere in this special issue [28,29,30]. However, we include Section 5.1 to briefly discuss results involving EFT approaches, which are derived from cross-section measurements discussed in earlier Sections. Lastly, we conclude our review in Section 6. Any review is always a compromise on the level of measurement details provided and cannot do justice to the complexity of measurements in the top quark sector, and much more complete information can be found online on the publication lists of each experiment.
2. Techniques & Methods
Top quark physics has evolved from the first discovery back in 1995 to the precision frontier, translating to sub-percent level uncertainties based on millions of top quarks. This transition required a dramatic shift also in analysis techniques and methods. Back then, the analysis of statistically limited data sets at the Tevatron relied on parametric fits, ideogram, and likelihood techniques, all exploited for the discovery of the top quark [1,2,31,32,33]. Later on, the matrix element method [34] allowed for unprecedented precision of the early top quark mass measurements by means of squeezing out all statistical information available in the data on an event-by-event basis.
Once the LHC turned on and Run 1 data started to be analyzed using both ATLAS and CMS, results were less affected by statistics, while the systematic uncertainties were not yet significant nor a dominant fraction of total uncertainties. Clearly, this was the golden age allowing for a much larger set of measurements in all areas of top quark physics relying on more straightforward “brute force” applications of the Tevatron analysis strategies, such as simple cut-and-count methods. Hence, the incentive to develop a coherent larger long-term strategy on understanding systematic uncertainties was not yet strong but clearly growing. Some of the more sophisticated methods were being ported from the Tevatron environment to the LHC Run 1 analysis, e.g., various ideogram methods for measuring the mass [35]. The latter showed a large impact of modeling uncertainties, calling for the first dedicated measurements of those, such as the gap fraction measurements and the first efforts for tuning Monte Carlo (MC) inputs [36,37,38]. With the full LHC Run 1 data set and even more so in the transition to Run 2, systematic uncertainties became dominant for most measurements of cross-sections, mass, and other properties of the top quark. To cope with this changing situation the first full multi-dimensional likelihood fits with nuisance parameters were employed [39], which allowed to reduce of systematic uncertainties by a factor of two. The large sample of top quark data also allowed for increasing the depth and wealth of information provided. In addition, to the detector level and fully unfolded parton level, now also intermediate “particle level” results became available in a variety of phase spaces [36,40].
Finally, Run 2 provides such a vast sample of top quarks in basically all decay channels and even some of the associated production modes that many measurements became exposed to the higher-order statistic effects. Meaning the sample size of systematic variations is affecting the templates employed to extract the parameters of interest, e.g., Ref. [41], which is still causing concerns going into the future. Given the abundance of top quarks, profile-likelihood fits are essentially the gold standard for any measurement of single-valued and inclusive quantities [42,43,44,45], soon followed by full multi-dimensional inputs for likelihood unfolding of differential distributions [46,47], which again resulted in a factor two reduction of systematic uncertainties. To further progress in understanding model uncertainties, dedicated ancillary measurements become more important and urgently needed, e.g., Ref. [44]. The application of sophisticated statistical methods harvesting the wealth and power of the top quark data yields a larger power to constrain systematic uncertainties, but on the other hand, the results are increasingly more complex. Especially, correlations of modeling/theory uncertainties across the measured phase space are important and can not be neglected anymore for a consistent interpretation of the results. Here, interpretation means the comparison of results to theoretical predictions by a statistical quantifier and searches for contributions beyond the SM, either directly or indirectly, by means of effective field theory methods.
3. Inclusive and Differential Cross-Sections
Measurements of inclusive and differential cross-sections deepen our understanding of the theory of modeling the production of top quarks. In particular, measurements of pair production test perturbative QCD (pQCD) and provide important information that can improve the simulation of QCD processes. As noted earlier, single top quark production provides tests of the electroweak theory, and since new physics can change individual production channels, all production modes of single and pair top quark production are needed to check for possible contributions of new physics. Furthermore, many of what are herein called top quark properties are, in fact, differential top quark cross-sections of a particular kinematic quantity, for example, the top quark polarization and the charge asymmetry at the LHC (or forward-backward asymmetry at the Tevatron). To challenge the SM pQCD predictions and to identify evidence of new physics in their modeling, the distributions of these observables need to be tested as accurately as possible and improved where needed.
Theoretical predictions of the and single top production processes exist at various orders of perturbation in SM theory. The most recent prediction for production is a fully re-summed next-to-next-to-leading log (NNLL) at next-to-next-to-leading order (NNLO) pQCD calculation and includes electroweak (EW) correction up to next-to-leading order (NLO) as well; single top quark production cross-sections typically have NLO accuracy with the resummation of higher-order logarithms [48,49,50,51,52,53,54,55,56,57,58,59,60]. The total uncertainty from factorization and renormalization scale variations and uncertainties of the parton density distribution function (PDF) is approximately 4–5% for the LHC and evaluated by taking the envelope of the scale uncertainties added in quadrature to the envelope of the total uncertainty of the MSTW2008NNLO, CT10NNLO, and NNPDF2.3NNLO PDF sets [61,62,63,64,65] here. Table 1 summarizes the predictions for and single top quark production at the LHC (using GeV) and the Tevatron (using GeV, and the MSTW2008NNLO, only).

Table 1.
Theoretical predictions for total top quark production cross-sections and their uncertainties for various center-of-mass energies at the LHC [49,53,60,66,67,68,69].
3.1. Precision Frontier
3.1.1. Measurements of Single Top Quark Production Cross-Sections
As introduced in Section 1, there are two dominant channels for producing single top quarks at the LHC: the t-channel and the associated -channel . The s-channel cross-section is only four times larger at the LHC compared to the Tevatron (see Table 1), which makes s-channel measurements at the Tevatron competitive. At the LHC, the predicted single top quark cross-sections in the t- and -channel are not much smaller compared to the pair production cross-section, hence allowing for similarly precise and detailed studies of the top quark in events containing only one top quark. Given the large available data sets already towards the end of Run 1 and even more so for Run 2, simple counting measurements are not competitive anymore in terms of total uncertainties. Instead, more sophisticated algorithms are widely used to further optimize individual analyses; for example, multivariate analysis techniques (MVA) or deep learning approaches [70,71,72] are utilized.
Highlights of results in the single top quark sector are precision measurements of production cross-sections, elements of the Cabbibo–Kobajashi–Maskawa (CKM) matrix related to the top quark, the polarization of single top quarks, as well as exploitation of single top quark events to constrain the proton structure with respect to the ratio of up and down quark content. The latter is possible with measurements of the ratio of t versus quarks.
Historically, the single top quark production was first observed at the Tevatron in 2009 in the t-channel production mode [73,74] and the program culminated in a simultaneous measurement of the s- and t-channel electroweak single top-quark production cross-sections using three multivariate analyses to separate the signal from the background. At D0, these three methods were combined in order to measure the s-, t- and -channel cross-sections in one analysis [75], which was later combined with CDF to form the legacy single top quark cross-section measurements at the Tevatron [76]. This includes the s-channel single top quark production, which has been observed in the combination of earlier results by CDF and D0 [76]. With the start of the operations of the LHC, it was certain that the LHC is not just a top quark factory based on pair production alone, but that it is also producing an abundance of events containing single top quark events. The larger production cross-section allowed for, at first, more straightforward techniques [77,78], with a selection mostly relying on two leptons, one from top-W boson decay, one from “direct” W boson decay, while lately, the application of MVA techniques in LHC measurements allows for one of the W bosons to decay hadronically, e.g., for a “single lepton” tW channel with decent signal-to-background fraction. The most up-to-date measurements at the LHC are by CMS in the t-channel using 13 TeV data and by ATLAS also in the t-channel but using 8 TeV data [45,79]. Figure 1 shows the current situation of measurements of the inclusive single top quark production cross-sections at the LHC [80,81,82,83,84] for all production channels, including combinations of ATLAS and CMS data. Most recently, ATLAS has seen evidence for the production of single top quarks in the s-channel [84]. However, as mentioned earlier the s-channel is challenging at the LHC and hence, is the least well-measured process in -collisions.
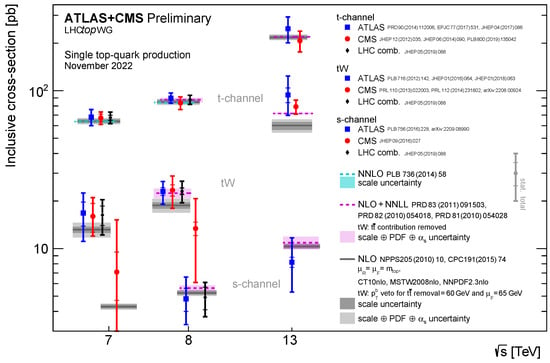
Figure 1.
Summary of predicted and measured single top quark production cross-sections at the LHC [85].
3.1.2. Measurements of Production Cross-Sections
The production of pairs is mediated via the QCD interaction of strongly interacting colored gluons and quarks. State-of-the-art theoretical predictions are currently at NNLO, including NNLL corrections, including electroweak corrections at NLO. Typical uncertainties of predictions are at the level of a relative 3.5% and include uncertainties due to renormalization and factorization scales, choice of PDF, and the value of the strong coupling constant (). Measurements are competitive, and the most precise ones are at the level of around 3% relative total uncertainty. With the growing top quark sample collected over the various LHC operations, the analysis started to focus on the dilepton decay channel since it provides a more background-free sample, limiting uncertainties from the modeling of those background contributions. Since then, the most precise cross-section measurements utilize the dilepton decay channel, which has proven to be experimentally well understood, as demonstrated by Figure 2. Precise inclusive cross-section measurements are sensitive to the top quark mass, , and in particular also the high Björken x gluon contribution to the proton structure. Given the precision with which cross-sections are measured, results are also sensitive to contributions beyond the SM (BSM), which can potentially enhance the total cross-section. An example is supersymmetric (SUSY) extensions of the SM, where compressed and degenerate SUSY parameter choices lead to low mass splittings of top squarks and the lightest SUSY particle (LSP) that can escape more direct detection. An example of the prospects of a search for a top squark exploiting a top quark property via a measurement of differential cross-sections is discussed in Section 4.
Starting from the measurements of LHC Run 1, cut-and-count was replaced by techniques that exploit the expected event topology of decays, in particular the expected number of jets identified to originate from b quarks (“b-jets”) in the final state. The ATLAS Run 1 measurement uses the expected number of b jets to constrain the total b-jet identification and selection efficiency and thereby reduces the uncertainty significantly [6]. CMS went another way in using the same parametrization, expanding the visible phase space to zero b jets and performing a likelihood fit with nuisance parameters instead [39], leading to about a factor two improvement with reference to the more simple cut-and-count method utilized earlier. With the onset of Run 2 measurements at a center-of-mass energy of 13 TeV, both collaborations rely on applications of similar techniques to yield comparable precision in the dilepton decay channel [8,41]. Profile likelihood techniques are widely exploited to squeeze down uncertainties even further, e.g., in the jets channel with ATLAS [86]. A summary of recent measurements of the inclusive production cross-section measurements covering all center-of-mass energies at the LHC is given in Figure 2. In particular, measurements of cross-sections using the heavy ion operation of the LHC are getting into the precision level, e.g., by CMS using 5 TeV data with less than 8% uncertainty [87,88].
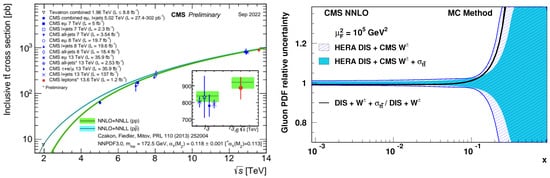
Figure 2.
Left: Measured cross-sections at different centers of mass energies compared to the predicted dependence [85], including a result at 13.6 TeV [89]. Right: Improved constraints on the high gluon PDF by including the cross-section measured at 5 TeV.
Different center-of-mass energies provide access to complementary physics reach, or even in collisions of nuclei where evidence for top quark production was reported by CMS [90]. Another example is the aforementioned inclusive cross-section measurement at 5 TeV [91]. The lower center-of-mass energy provides larger sensitivity to high x gluon PDFs through more centrally produced top quarks compared to higher center-of-mass energies. Figure 2 shows resulting constraints on the high x gluon contribution to the proton structure via the xFitter framework [92].
The first measurement of the production cross-section in proton–proton collisions at 13.6 TeV [89] was presented at the TOP22 conference by CMS employing a total integrated luminosity of fb. This early measurement goes back to the concepts in the early days of top quark physics at the Tevatron, namely to constrain detector and object reconstruction efficiencies with data. A maximum likelihood fit is performed to event categories defined by the number and flavors of the leptons and the number of jets and b-jets. Ultimately, an inclusive production cross-section of (stat+syst) (lumi) pb is measured, which is in agreement with the standard model prediction of pb (see Table 1).
3.2. Differential Cross-Section Measurements in t, , and Production
Single and multi-differential cross-section measurements are the most powerful tool to challenge the SM and the intricacies of top quark modeling. In most general terms, a differential cross-section, , as a function of the variable X can be calculated by extracting the number of observed signal events in bin i, , which needs to be corrected for effects of limited acceptance and efficiency of the detector, branching fraction, integrated luminosity, and finally the bin width of the particular variable X. Any measurement of a cross-section relies on MC samples to correct the data for the detector efficiency and also in order to extrapolate, if desired, from the fiducial phase space to the total phase space via acceptance corrections. For this purpose, all cross-section measurements rely on MC samples at leading-order or next-to-leading order pQCD. The process of correcting the data for detector effects is commonly called unfolding; various approaches to this stage of the analysis exist. They differ in complexity and range from un-regularized and regularized matrix unfolding [93] to likelihood techniques, as well as Bayesian full nuisance fit methods [94].
By now, a multitude of highly precise differential cross-section measurements is at our disposal to further challenge and test the SM and the modeling of the production and decay of events. Results by both ATLAS and CMS provide accurate measurements and stringent constraints on the top quark mass, PDFs, as well as . For example, Ref. [95] represents one of the first results exploiting top quark data to constrain all three quantities simultaneously. Figure 2(right) and Figure 3 show the outcome of these simultaneous fits to the early data at the LHC.
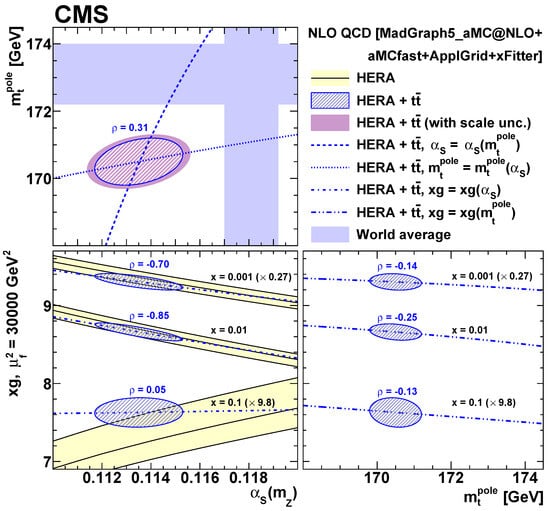
Figure 3.
Constraints on the strong coupling, the top quark pole mass at NLO, and the gluon PDF from a double multi-differential cross-section measurement [95].
These techniques have been pioneered at the Tevatron but, owing to the limited amount of statistics, in a one-dimensional approach as a top quark pole mass extractions only, using NNLO+NNLL pQCD calculations [96]. Nowadays, double- and even triple-differential cross-section measurements at the LHC [95] in the dilepton and jets decay channels (see Figure 4) provide excellent statistical power and (multi)differential information to constrain SM parameters and PDFs when compared to state-of-the-art predictions up to NNLO+NNLL [66,97]. In the context of the “TOP 2022 conference,” CMS has presented the first measurement of the production cross-section at 13.6 TeV [89].
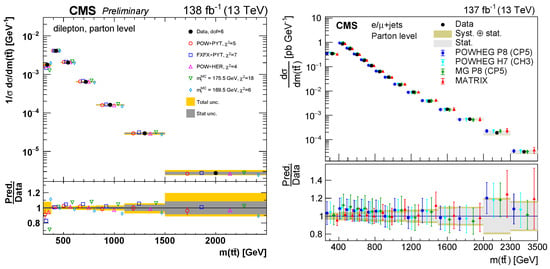
Figure 4.
Differential cross-section as a function of the mass of the pair in the dilepton (left) and jets channel (right) [98,99].
In the future, the constraints on the high-x gluon content of the proton will become crucial for the physics program at the high-luminosity phase of the LHC (HL-LHC). In particular, to understand tails of gluon–gluon fusion-induced processes such as high transverse momentum Higgs boson production, which “lives” at the high-x domain of the proton content. Hence, the gluon-dominated production, in particular in the high rapidity regime, will provide valuable constraints on the high-x gluon content of the proton for global PDF fits [100].
With the size of the available top quark sample at the LHC, there is a plethora of applications for parameter extractions. For example, the differential cross-section, in particular as a function of can be used to extract the Yukawa coupling, , of the top quark by investigating modifications of the cross-section at the production threshold. It is especially that region where virtual Higgs boson loop effects provide sensitivity to . Results of this alternative approach to access are shown in Figure 5 for the jets channel. While the method provides good constraints on , it suffers from large systematic uncertainties and a precise understanding of the threshold regime, e.g., coming from possible bound-state effects.
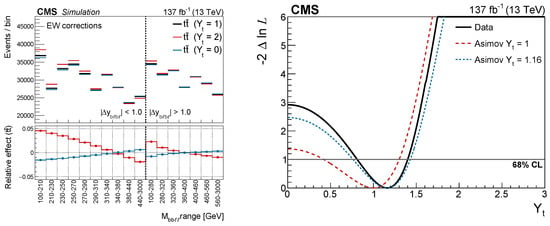
Figure 5.
Fitted distribution and its dependence on the Yukawa coupling (left) and likelihood result (right) [43].
3.3. Rare Cross-Section Frontier: Boosted Phase Space, Associated Productions, 4 Top Quark
Measurements of production in the boosted regime give access to high-scale contributions, possibly affected more strongly by BSM processes through virtual or loop contributions. In addition, the boosted phase space can also give alternative access to SM quantities by comparing measurements with predictions and explicitly exploiting one of the features of boosted top quarks, with a lower contribution from threshold effects. Experimentally, boosted top quarks are challenging and require dedicated “top quark taggers” to retain reconstruction efficiency because these highly boosted top quarks result in collimated decay products that are either partially or fully merged. For example, boosted top quark events where the lepton (muon or electron) appears as non-isolated due to its proximity to the b-jet. Dedicated algorithms for jet and lepton cleaning at the trigger and analysis level allows reconstructing the decay products of events in the jets channel even without requiring isolation for the leptons. The other top quark in those events decays hadronically, and the decay products have angular distances that are smaller than the jet clustering distance parameter. Hence, all those decay products are reconstructed into a single jet, or “boosted” topology. However, when the pair is produced near the production threshold, every decay product ends up in a single jet or “semi-resolved” topology, and with a rising boost, the hadronic W boson decay products get merged first, which represents the “semi-resolved” topology. The first step in extending measurements into the highly boosted phase space is dedicated measurements in the boosted phase space to establish reconstruction methods [101] (Figure 6).
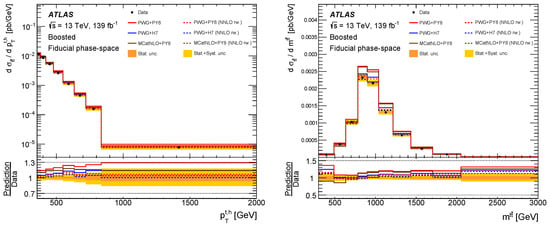
Figure 6.
Measured differential cross-section as a function of the hadronic top quark (left) and (right) [101].
Any differential cross-section can be exploited to search for BSM contributions via EFT approaches, but the boosted phase space is, of course, especially interesting since it is a “high scales” region of interest. ATLAS exploits, for example, the transverse momentum distribution of the top quark, , in all-hadronic decays to search for contributions from and via EFT approaches [101], which alter the couplings between gluons and quarks producing top quarks (see Section 5.1).
A recent measurement by the CMS collaboration, interpolating between the resolved and boosted regime, gives consistent access to full-spectrum differential cross-sections [99] in the resolved, semi-resolved, and boosted regime. This CMS analysis employs unfolding with nuisance parameters to combine the individual data-taking periods at GeV. Figure 7 shows the cross-section distribution starting at the production threshold and reaching all the way up to 3000 GeV—the highly boosted regime. The boosted regime is also accessible up to similar scales via the reaching as high as 1500 GeV, also reached with ATLAS measurements.
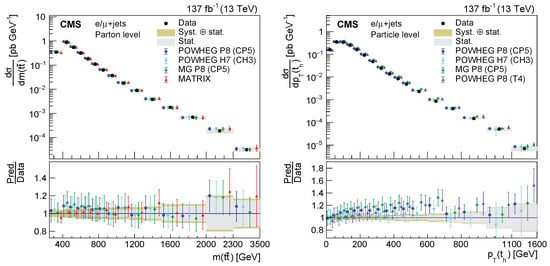
Figure 7.
Differential production cross-section as a function of the invariant mass (left) and the hadronically decaying top quark (right). The measurement covers the resolved and boosted regime simultaneously [99].
Precise measurements of the inclusive cross-sections of inclusive associated production of vector bosons with pairs have been carried out early on in Run 2. These processes are of particular interest because they can receive sizable contributions from BSM phenomena. Associated production of vector bosons allows accessing enhanced charge asymmetry in top production via production of + W, the coupling of the Z boson to pairs via + Z [102], and, of course, also the coupling to the photon which allows accessing the top quark electric charge. Any of the processes are, at times, also an important background to several searches for BSM phenomena, which is especially true for the associated production of additional pairs, e.g., pairs. The latter is a highly relevant process producing background contributions to the measurement of pairs in association with the Higgs boson.
More rare associated production channels are the production of single top quarks with a vector boson, such as producing a top quark, a Z boson, and a quark (jet): tZq events. This process has been observed using ATLAS [103] and is now also measured differentially by CMS [104]. The latter also allows to access the spin asymmetry, which is sensitive to the polarization of the top quark. Figure 8 shows summaries of the tZq and other associated vector boson production results. The ratio of the Zq to Z rates gives access to the polarization of the top quark.
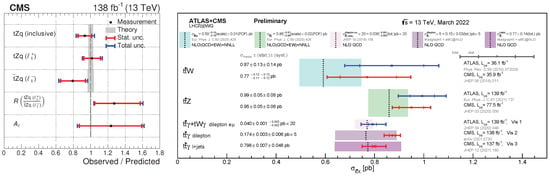
Figure 8.
Left: Measured cross-sections of top quark production in association with a Z boson compared to the SM predictions [104]. Right: Summary of associated production of vector bosons at the LHC [85].
Searches for four-top production [105,106,107] are one of the most, if not the most exciting, processes yet to be measured at the LHC. The current limits are shown in Figure 9a with tantalizing hints for a cross-section enhancement when compared to the SM cross-section prediction of fb [108]. The production of four top quarks provides also constraints on the top quark Yukawa coupling as shown in Figure 9. While the constraints are slightly weaker than from the direct measurement [43], these will gain in power with statistics and more precise calculations for four top productions, while the measurement from the production threshold, discussed earlier, is already limited by systematic uncertainties.
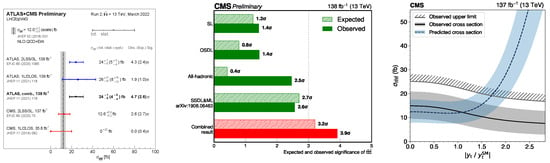
Figure 9.
Left: Measurements at ATLAS and CMS production cross-section compared to the SM prediction. Middle: Latest results on production cross-section by CMS. Right: constraints on the top quark Yukawa coupling from the measured cross-section [105,106,107].
3.4. Implications
Ever more precise differential cross-section distributions of production offer unique ways to challenge the SM and call for further developments and a deeper understanding of the SM theory. Especially, the extremes of the production phase space of offer a unique window into the inner workings of production, such as highly boosted pairs. Any and all of these are currently limited by systematic uncertainties, i.e., normalized differential distributions offer the lowest uncertainties of around 5–6%,k limited by a variety of uncertainties. Any progress towards smaller uncertainties requires the concerted effort of the entire community, and progress on experimental and theoretical topics is happening via the LHC Top working group (LHCtopWG [85]). The next Section 4 provides an example for a top squark search which will exploit future measurements of differential distributions in production at the HL-LHC; typical systematic uncertainties are assumed to be lower by about a factor of two. Such improvements demonstrate the unprecedented power of the HL-LHC, which will produce around one billion top quark events. Even now, the LHC is a top quark factory, which also means that the associated production of bosons enters the precision realm and offers entirely new tests of the SM, not just in differential precision tests of the SM but also in terms of the coupling of to these bosons. Overall, we conclude with a strong statement that differential measurements in , associated production of bosons and pairs of semi-heavy pairs, and even the production of + pairs all provide ample ways of constraining models and sources of new physics.
4. Top Quark Properties
Measurements of top quark properties have been a highly sensitive probe as to whether the top quark is indeed the SM top quark. It all started at the Tevatron with measurements of the top quark mass, moving on to the charge of the top quark, spin correlations, and more.
4.1. Measurements of Angular Correlations
Angular correlations are sensitive probes to test the validity of the SM predictions, given the level of detail that needs to be modeled accurately in order to achieve a decent description of the data. A variety of measurements of angular correlations has been done over the years, such as charge or forward–backward asymmetries, as well as measurements of top quark spin correlations and polarization. The different initial state makes measurements of angular correlations in events, for example, forward–backward asymmetries, at the Tevatron complementary to those at the LHC. In general, the size of the asymmetries at the Tevatron or at the LHC is related to the relative weight of the quark anti-quark annihilation channel in pair production since events arising from initial states are forward–backward symmetric. Consistently, this results in angular correlations being different quantities at the various center-of-mass energies of the LHC operation. The charge asymmetry at the LHC arises from the fact that quarks have, on average, a larger longitudinal momentum than anti-quarks, which in the case of a collider leads to a wider rapidity distribution in the case of t production compared to the . At the Tevatron, the t and rapidity distributions are shifted with respect to each other, allowing accessing by a measurement of the difference in rapidity. The CDF and D0 combined experimental results [109], show indications for deviations from the SM predictions by about one to two standard deviations (s.d.), whereas the results from the LHC are not yet sensitive to the predicted level of the charge asymmetry in the SM. A variety of results at both ATLAS and CMS exist [47,110], including an ATLAS+CMS combination [111], and we only mention two results here briefly. ATLAS has evidence for the charge asymmetry being different from zero but not yet for the predicted SM value of [47], while CMS recently put out a measurement of in the highly boosted phase space of GeV [110]. The latter measurement benefits from a binned maximum likelihood fit, which yields a reduced impact of systematic uncertainties on the result. In either case of these ATLAS and CMS results, the measured top quark charge asymmetry is in good agreement with the standard model prediction at NNLO in pQCD with electroweak corrections at NLO. Future prospects include measurements of the charge asymmetry in the associated production of W bosons and via different variables that are more sensitive to the charge asymmetry.
Angular distributions of leptons stemming from the decay of the top quark can be measured precisely and utilized to probe variables sensitive to the spin correlations and polarization of top quarks. Measurements at all center-of-mass energies of the LHC [112,113,114,115,116] and prior to that at the Tevatron [117], have established that the spins of top quarks are correlated as predicted by the SM.
The latest measurements at ATLAS [116] and CMS [118] show good agreement with each other; see Figure 10. When comparing ATLAS and CMS data to the SM predictions a mild tension is observed that is reduced with higher order corrections at next-to-next-to-leading order (NNLO) [119], and through techniques that reduce the effect of theoretical uncertainties on the acceptance corrections [120].
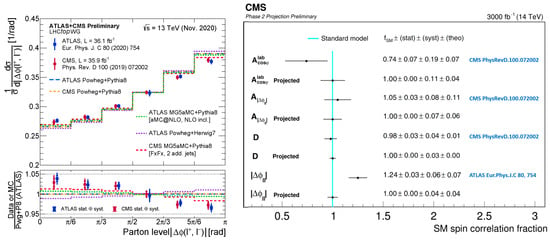
Figure 10.
Left: Independent measurements of the opening angle between the decay leptons of the pair are compared to SM predictions [116,118]. Right: A projection of the expected precision of the spin correlation and polarization of top quarks at the HL-LHC [121].
Current and future efforts at the LHC are focused on accessing the spin correlation and polarization information to an ever greater differential depth using full Run 2 data and beyond, hence, allowing us to understand better the clearly visible mis-modeling of the distribution of the opening angle of the decay leptons, , of the top quarks shown earlier. Recently, CMS has done a projection of how precise this and other angular distributions can be measured with the data collected during the HL-LHC [121]. An integrated luminosity of 3000 at TeV provides a vast top quark data sample, which is unlimited in terms of statistical power. A generic future CMS detector simulation is employed via delphes to provide a first study of the performance of the expected precision of measurement of the strength of expected SM spin correlations. Unprecedented precision in measuring spin correlation variables is expected, with D the most accurate variable with a 3% total uncertainty. Figure 10 (right) shows the result of this study in comparison to existing measurements by ATLAS and CMS using partial Run 2 data. The metric for that comparison is by means of the strength of the top quark spin correlation relative to the SM prediction.
Second, as an application of utilizing these measured angular distributions and to study a specific model that predicts zero spin correlation, prospects for a search for supersymmetric partners of the top quark in the compressed SUSY model are studied as well. The reconstruction of the system allows for 19 spin correlation variables to be computed. These are used to form a discriminant between the background SM and the (hypothesized) signal SUSY processes through a Deep Neural Network (DNN), used in a binned likelihood fit. Prospects using 3000 of data at TeV indicate that the top squark-LSP mass corridor up to the 1 TeV range should easily be able to discover a non-SM signal. In the absence of a discovery, this analysis can exclude top squarks up to masses of 600 GeV (see Figure 11) and push down existing limits, especially below top squark masses of 300 GeV, by about one order of magnitude [121].
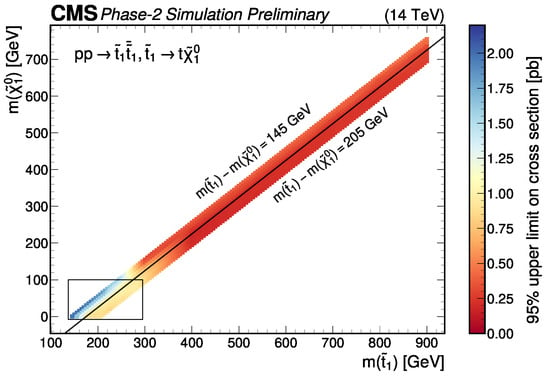
Figure 11.
A projection of the expected sensitivity for the discovery of top squarks all the way up to 800 GeV [121].
4.2. Top Quark Mass
A large number of measurements of the top quark mass have been carried out at the LHC, and it is not possible to summarize all the details adequately in this review. Instead, we focus only on those demonstrating the latest status and that are most relevant to the current discussion in the top quark mass sector. Figure 12a shows the summary (March 2022) of top quark mass measurements accessing the mass via kinematic or “direct” methods. The typical uncertainties of the ATLAS [122] and CMS [123] combined top quark mass values are less than 0.5 GeV in absolute units or below 0.3% in relative uncertainty. Both experiments have measured the top quark mass in the dilepton, jets, and all-hadronic decay channels and are preceded by a multitude of measurements at the Tevatron culminating in the latest Tevatron combination [124] and even a world-first combination documented in Ref. [125]. Individual Tevatron results have been combined with LHC results published up to 2014, and the world average is indicated in Figure 12a with the vertical grey band, providing a typical relative uncertainty of 0.5%. The degradation of precision stems from the lack of up-to-date LHC results in the world combination [125]. Most of these combinations have been performed using the BLUE method [126,127,128], but recent measurements using profile likelihood techniques have also triggered further developments of—in that case—a more accurate approximate likelihood method [129] that is now becoming standard for LHC top quark combinations.
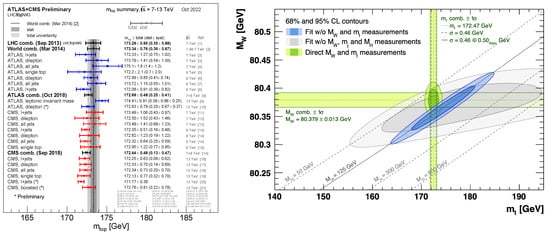
Figure 12.
Left: Summary of measurements of the top quark mass relying on direct techniques [85]. Right: The versus plane showing the GFitter global fit result relying top quark mass results as determined by the direct technique [16].
The latest measurements of the top quark mass at the LHC Run 2 showcase the potential of the top quark factory for precise determination of the top quark mass. An example is a CMS measurement employing profile likelihood methods with five observables [130]. Similar to previous measurements, the main estimator for the top quark mass is given by the invariant mass of the three jets originating from the same top quark: one b jet and two light jets from the W boson. For that purpose, the full system is reconstructed by minimizing a , taking into account the expected resolutions on the objects and the combinatorics. In addition, observables are considered that provide the best constraint on the top quark mass and at the same time help to understand the dominant systematic uncertainties. Namely, those observables that are sensitive to the jet energy scale but can constrain it by e.g., leveraging the known W boson mass, and observables that give access to the difference in detector response between light and b-quark jets, as well as observables that help further constrain the top quark mass for events where the kinematic fit did not provide a high purity result. Figure 13 (left) shows how adding these observables, and with them, their constraining power, successively to the analysis improves the total precision of the extracted top quark mass. Additional observables, Figure 13 (right), are the input to the ML fit and their post-fit probability density functions. The green and yellow bands represent the 1 s.d. and 2 s.d. uncertainty bands. Another noteworthy detail of this analysis is that it includes a consistent treatment with respect to the effect of statistical fluctuations that affect the modeling of the systematic uncertainties directly in the likelihood. This is an issue that will become increasingly important with more data and when more subtle uncertainties need to be accounted for.
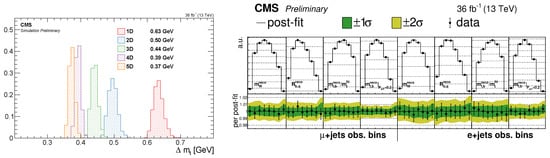
Figure 13.
Left: Adding additional observables improves the constraining power of the ML fit employed to extract the top quark mass [130]. Right: Additional observables that are the input to the ML fit and their post-fit probability density functions [130].
Figure 12 (right) shows the versus plane, where is obtained by the GFitter collaboration [16] via a combination of the individual combined results of ATLAS and CMS using direct methods—an updated result including latest measurements can be found at Ref. [131]. That combined and its uncertainty gets an additional theoretical uncertainty of 500 MeV assigned to account for a potential difference between the measured “MC mass” and the pole mass of the top quark. Historically, and surely since the early measurements at the Tevatron got reasonably precise, this MC-versus-pole-mass controversy has received lots of attention from the experimental and theoretical communities. Given the increasing precision of the LHC measurements beyond 0.3%, the topic receives renewed attention, asking for an accurate assessment of the differences and uncertainties related to this conversion, a recent overview article is provided in Ref. [132]. The value of is the world average of available measurements at the time of this fit. A recent update on the W boson mass measurement by CDF [133] is further away from the world average, and the result and its impact are currently being discussed in the community [131]. Together with the measurement of the mass of the Higgs boson [10,11] this is a strong self-consistency test of the SM with implications on the stability of the SM vacuum [20]. The current measurements and the theoretical extrapolation at NNLO of the SM seem to indicate that the vacuum is meta-stable or, maybe even more peculiar, sitting right at the boundary of stability and meta-stability.
In addition to the presented direct measurements, alternative measurements of the top quark mass have also been performed with the aim to either increase the precision by constructing the measurement such that the systematic uncertainties are complementary to direct measurements or with the aim to improve the understanding of the measured quantity in terms of well-defined renormalization schemes. The most common alternative top quark mass measurement technique is the extraction from the production cross-section. At the Tevatron, these techniques were limited by the available statistics to focus on the top quark mass only, while the larger statistics available at the LHC allow not only the use of inclusive but also more and more differential techniques. This wealth of information and data now permits simultaneous fits of the strong coupling constant and the top quark mass, even measurements of in the boosted phase space by a “Jet mass” proxy [134] reach uncertainties of below 0.9 GeV.
Even more orthogonal measurements using alternative approaches to measuring the top quark mass employ, for example, the invariant mass of the muon from the leptonic decay of the W boson together with a soft muon in the b jet as a top-mass sensitive observable [135]. Given the dependency on muons, this measurement approach is less sensitive to uncertainties and effects that arise from jet energy scale and top quark production modeling. However, since the soft muon comes from the decay of B hadrons, the uncertainty on is dominated by the knowledge of the B fragmentation and the B decay branching fractions. Figure 14 shows, as an example, the post-fit distribution selecting same-sign muon pairs to construct the top mass sensitive observable.
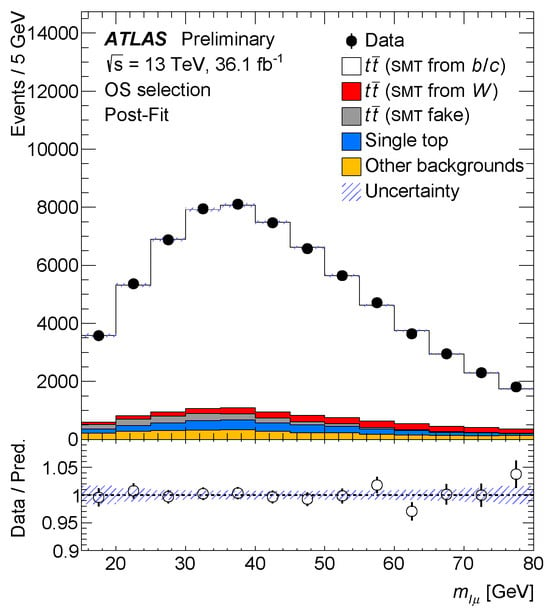
Figure 14.
Post-fit distribution using the same-sign opposite-sign selection.
Once corrections beyond leading order enter calculations in pQCD, the couplings exhibit a scale dependence well known from e.g., the strong coupling. In the no-mass limit, this running described by renormalization group equations (RGE) even governs the dependence of observables on the physical scales. In certain renormalization schemes, the masses are also subject to this fundamental effect of QCD. Beyond proving this fundamental effect, measurements of the “running” of the top quark mass are sensitive to new physics affecting the RGEs. While these would also be reflected on final state distributions, a change in the RGEs from BSM contributions is often easier to access.
The first study of the scale dependence of the top quark mass was performed with the CMS collaboration [46] at NLO, finding good agreement with the SM RGEs when using the top-quark pair invariant mass as a proxy for the scale, as also shown in Figure 15. The sensitivity of the measurement to this subtle effect relies heavily on high dimensional likelihood unfolding with nuisance parameters discussed in Section 2, and on mitigating the dependence of the measurement on the MC mass-related acceptance corrections [136]. Recently, also an extension to state-of-the-art NNLO calculations has been presented, showing similarly good agreement with the SM while improving the accuracy of the results [137].
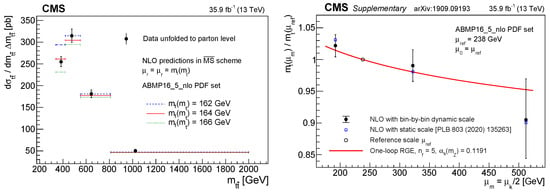
Figure 15.
Running of the top quark mass. Left: Differential production cross-section measured as a function of compared to different choices for the top quark mass. Right: Extracted top quark mass running as a function of the process scale compared to one-loop SM RGE [46].
4.3. Top Quark Width
The top quark width can be calculated precisely in the SM [138,139], and deviations could hint at new physics. However, indirect measurements of the width assume SM couplings and are therefore not very suited for a more model-independent measurement. Direct top quark width measurements circumvent this problem and are solely based on width-sensitive final state distributions. These direct measurements have been pioneered at the Tevatron by the CDF and D0 experiments [140,141], and further improved at LHC with the Run I data set [142]. One of the latest examples of such a direct measurement is performed by the ATLAS collaboration [42]. It uses the invariant mass of the lepton and b-tagged jet, , to harvest the power of differential distributions; see Figure 16. The result also exploits the invariant mass of the pair, , for constraining uncertainties arising from the jet energy scale. The measured width of the top quark is GeV, in agreement with the Standard Model prediction.
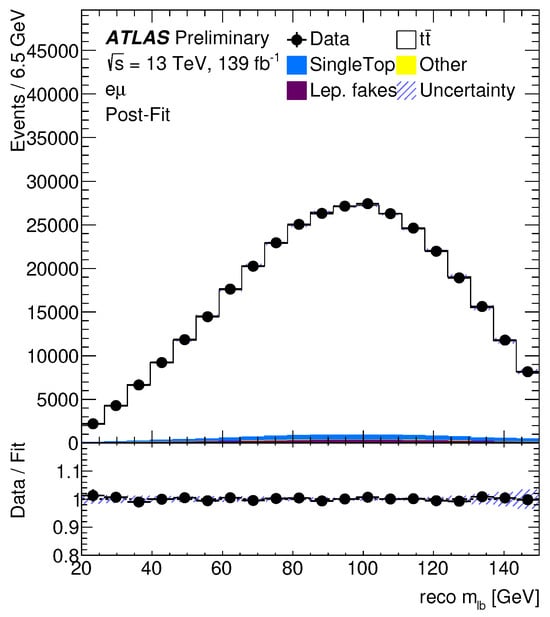
Figure 16.
Observables used in the fit of the top quark width. The post-fit uncertainties are calculated using the correlation matrix obtained from the fit [42].
5. Searches in the Top Quark Sector: FCNC, SUSY, and EFT
There is a rich landscape of searches carried out in the top quark sector, but despite this section, we are not discussing those searches in more detail here since there is a separate review on, e.g., vector-like top quarks. Instead, we only mention the ones most specific to top quarks, namely a hypothetical flavor-changing neutral current (FCNC). Recent searches for the existence of such an FCNC in top quark production or decay [143,144] is evident in the transition of an up or charm quark to a top quark, latest results are shown in Figure 17.
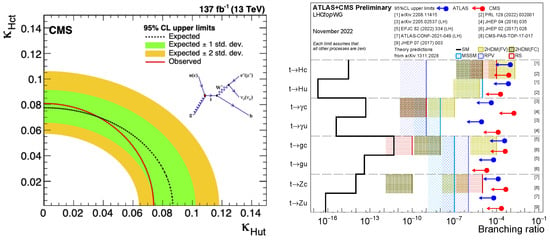
Figure 17.
Left: Search for the existence of FCNC currents using CMS data [144]. Right: Overview of a variety of 95% confidence level observed limits on FCNC currents by ATLAS and CMS [85]. Each limit assumes that all other FCNC processes vanish.
A summary of the best limits at the 95% confidence level observed limits on the branching ratios of the top quark decays via FCNC is shown in Figure 17 (right). Results using ATLAS and CMS include top quark decays to a quark (u or c) and a neutral boson ( or H) and are compared to several new physics models.
5.1. EFT Methods
In the absence of direct experimental observation of contributions beyond the SM and new particles, direct searches aimed at single BSM models are more and more turned into global searches—an approach that is surely discussed in more detail in the separate review on searches for new physics. Instead, we focus on the more general and model-independent EFT approach highlighting three examples of how EFT techniques are leveraged in top quark physics to reveal new physics, namely by deriving EFT constraints by means of multi-process, property-based, or differential fully correlated measurements. The first example shows its strength in a regime where multiple processes cannot be disentangled easily; one can harvest the power of the data using multi-process analyses, i.e., for more global EFT constraints [145] on processes enhancing final states with multiple leptons. Figure 18 shows a recent result by CMS aimed at constraining BSM contributions that manifest themselves in multi-lepton final states. These multi-lepton stem from the decay of top quarks produced in association with gauge bosons: H, Z, W, tZq, and tHq. Such a combined fit of EFT parameters properly accounts for correlations between the different channels in terms of systematic uncertainties.
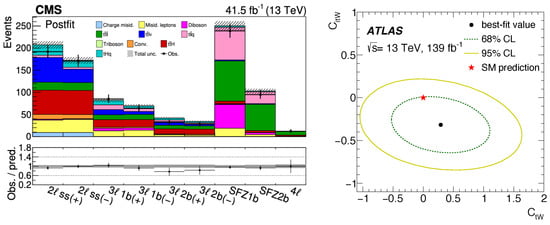
Figure 18.
Left: Example of a multi-process EFT analysis focused on multi-lepton final states with a variety of signal processes [145]. Right: The angular differential distributions used to access the polarization information of the top quark in single top production are used to derive limits on the Wilson coefficients [146].
Even expanding on this multi-process EFT analysis is possible and allows gaining additional sensitivity to dimension-6 operators by exploiting machine learning and apply on control and signal regions to maximize the statistical power of the LHC data. An example at the LHC is published by CMS [147] and implements novel machine learning techniques to boost sensitivity to new physics.
In addition to new physics enhancing rare processes in a variety of final states, one can rely on the power of the LHC being a top quark factory. A second example of a typical EFT analysis is the one presented with ATLAS on utilizing a measurement of a top quark property, i.e., its polarization, to extract EFT constraints [146]. The SM predicts top quarks to be not polarized if produced in pair production. However, the production of single top quarks is mediated by the electroweak force and hence, produces highly polarized top quarks. ATLAS measured the polarization of top quarks and anti-top quarks from the distributions of the direction cosines of the charged-lepton momentum in the top-quark rest frame. The normalized differential cross-sections are corrected to a fiducial region at the stable-particle level and are utilized to search for new physics appearing in the complex Wilson coefficients, results shown in Figure 18 (right).
Any extraction of bounds on new physics in an EFT framework utilizing one or multiple differential cross-section distributions in n dimensions “suffers” from not properly accounting for correlations between bins of all the variables in terms of (a) statistical uncertainties and (b) any and all systematic uncertainties. Earlier in this review, we discussed a CMS result on the measurement of the full spin density production and polarization information in dilepton events [118]; see Section 4.1. This measurement is utilized in a subsequent analysis to constrain the phase space of new physics contributions via an EFT approach utilizing a total of 22 variables sensitive to spin correlations and polarization of the top quark. However, the measured distribution of a variable is obviously correlated to all others, and in addition, also systematic uncertainties are correlated between the bins of these variables. A powerful tool to determine correlations is commonly referred to as the “bootstrap method” [148], which, in essence, treats every single data event as a Poisson counting experiment with expectation value 1 and draws toys, e.g., 10,000 times and each time repeat the unfolding. This approach allows us to statistically correlate all measured single differential cross-section distributions in terms of their statistical uncertainties. Now, if this approach is expanded to also utilize MC samples implementing parameter variations (systematic uncertainties) one can finally obtain correlations of total systematic uncertainty. Figure 19 shows the correlations of systematic uncertainties in the CMS spin density analysis. Hence, the bootstrap method allows a simultaneous model-to-data fit properly, accounting for correlations of statistical and systematical uncertainty between variables. This method is, of course, also highly applicable when challenging the SM, an example using ATLAS can be found in Ref. [149]. In the case of CMS, the statistical and systematic covariance matrices consisting of 132 × 132 bins are provided for the set of all measured bins and are used in simultaneous fits to constrain the contributions from dimension-six effective EFT operators and, at the time, providing a significantly improved limit compared to other existing measurements.
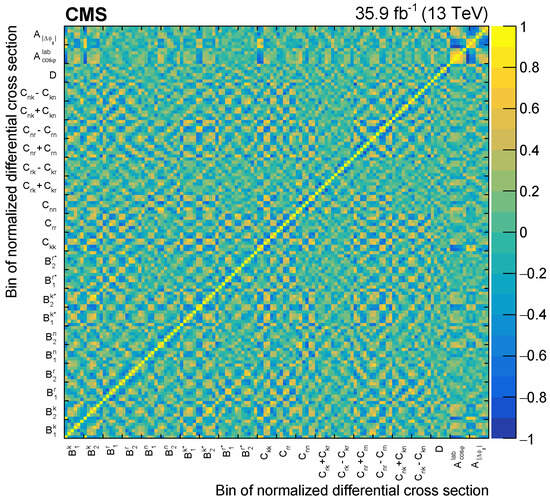
Figure 19.
Matrix showing full correlations of systematic uncertainties between the six bins of, and between, variables (a total of 22 as labeled on the axis), as measured and determined by the CMS spin density analysis [118].
To conclude this very short overview of results using EFT techniques we provide the summary overview as obtained using the ATLAS and CMS Collaborations [85]. Figure 20 shows the 95% confidence level observed limits on the effective field theory Wilson coefficients of the dimension-6 operators related to top quark interactions with vector bosons. The results are reported as individual constraints assuming new physics contributions from one specific operator at a time.
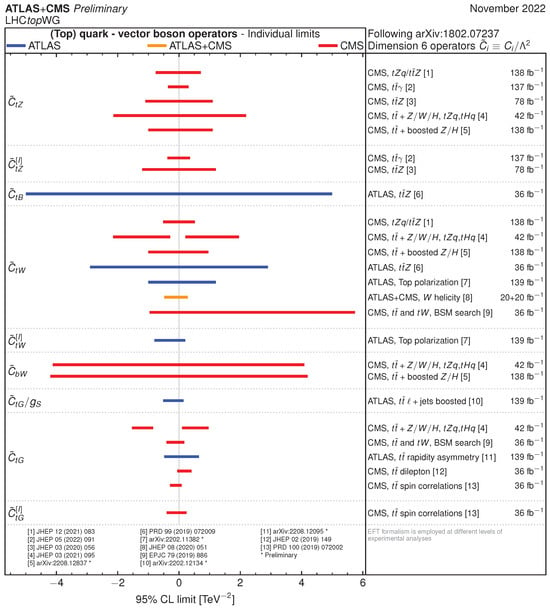
Figure 20.
Summary of the 95% confidence level observed limits on the effective field theory Wilson coefficients of the dimension-6 operators [85].
6. Conclusions
The LHC experiments have provided a plethora of top quark results in the past decade that have superseded or complemented previous measurements at the Tevatron. Just recently, exciting new results were presented by the LHC collaborations, including a first measurement of the production cross-section using LHC Run 3 data at 13.6 TeV [89], cementing the role of top quark pair production as a standard-candle process. In consequence, precise studies of single- and multi-differential cross-sections for production, also in association with additional bosons and quark anti-quark pairs, can be performed. These offer unique ways to test the SM and call for further developments and a deeper understanding of the SM theory. Measurements of top quark properties at the LHC are challenging the currently best available theoretical predictions, e.g., the latest measurements of top quark spin correlations at ATLAS and CMS show good agreement with each other but reveal a mild tension to the SM that is reduced when higher order corrections (NNLO) are taken into consideration. Measurements of angular correlations, i.e., charge asymmetries, are not yet sensitive to the SM expectation, but ATLAS has shown evidence of the charge asymmetry being different from zero. The wealth of top quark mass measurements is now dominated by individual measurements with a smaller uncertainty than combinations of LHC or even world averages of existing top quark mass data.
The HL-LHC phase is on the horizon, and the available sample will exceed one billion top quarks at the end of the HL-LHC. Harvesting the potential of this data set requires a dedicated effort by the top quark community to improve and align the precision of experimental results and the predictions they are confronted with, i.e., by investigating novel variables that have a particularly precise predicted value or profiting from uncertainties canceling. The most dominant experimental systematic uncertainties currently arise from signal modeling, with efforts in the LHCtopWG [85] along the way to unify the treatment and provide a solid basis for comparison studies. Equally important is to aim the analysis strategies at regimes that are robust against these uncertainties, on the one hand, but on the other hand, also to perform ancillary studies that can improve our understanding of these effects. Finally, more multi-process analyses become possible and can be carried out to constrain and limit the impact of systematic uncertainties while resulting in a more global picture of the involved processes and their interplay. This will be in particular important for EFT interpretations but will need the effort to understand how such analyses can be optimized in a rigorous way, also considering the application of ML in EFT. Already the complexity and timeline of current LHC analyses pose a dire need for joined and more centralized technical development of tools and reconstruction setups so that there are fewer technical obstacles and maintenance (person power) costs for analyses in the future.
We conclude with excellent prospects for top quark physics challenging the SM at an unprecedented level, even opening an exciting new probe to study quantum information aspects and maximizing the discovery potential for new physics.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abe, F.; Akimoto, H.; Akopian, A.; Albrow, M.G.; Amendolia, S.R.; Amidei, D.; Antos, J.; Anway-Wiese, C.; Aota, S.; Apollinari, G.; et al. Observation of Top Quark Production in Collisions with the Collider Detector at Fermilab. Phys. Rev. Lett. 1995, 74, 2626–2631. [Google Scholar] [CrossRef] [PubMed]
- Abachi, S.; Abbott, B.; Abolins, M.; Adam, I.; Adams, D.L.; Adams, M.; Ahn, S.; Aihara, H.; Alitti, J.; Alvarez, G.; et al. Observation of the Top Quark. Phys. Rev. Lett. 1995, 74, 2632–2637. [Google Scholar] [CrossRef] [PubMed]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Fabjan, C.; Friedl, M.; Ghete, V.M.; Hammer, J.; et al. First Measurement of the Cross Section for Top-Quark Pair Production in Proton-Proton Collisions at = 7 TeV. Phys. Lett. B 2011, 695, 424–443. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abdallah, J.; Abdelalim, A.A.; Abdesselam, A.; Abdinov, O.; Abi, B.; Abolins, M.; Abramowicz, H.; Abreu, H.; et al. Measurement of the top quark-pair production cross section with ATLAS in pp collisions at = 7 TeV. Eur. Phys. J. C 2011, 71, 1577. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Fabjan, C.; Friedl, M.; Ghete, V.M.; et al. Measurement of the production cross section in the dilepton channel in pp collisions at = 8 TeV. J. High Energy Phys. 2014, 2, 24. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; AbouZeid, O.S.; Abramowicz, H.; et al. Measurement of the production cross-section using eμ events with b-tagged jets in pp collisions at = 7 and 8 TeV with the ATLAS detector. Eur. Phys. J. C 2014, 74, 3109, Addendum in Eur. Phys. J. C 2016, 76, 642. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Flechl, M.; Friedl, M.; et al. Measurement of the top quark pair production cross section in proton-proton collisions at = 13 TeV. Phys. Rev. Lett. 2016, 116, 052002. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; Abdallah, J.; Abeloos, B.; Aben, R.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; Abreu, H.; et al. Measurement of the production cross-section using eμ events with b-tagged jets in pp collisions at = 13 TeV with the ATLAS detector. Phys. Lett. B 2016, 761, 136–157, Erratum in Phys. Lett. B 2017, 772, 879–879. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Ahuja, S.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; et al. Observation of top quark production in proton-nucleus collisions. Phys. Rev. Lett. 2017, 119, 242001. [Google Scholar] [CrossRef]
- Aad, G.; Abajyan, T.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Bansil, H.S.; Abdinov, O.; Aben, R.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Damiao, D.D.J.; Bergauer, T.; Dragicevic, M.; Friedl, M.; et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 2012, 716, 30–61. [Google Scholar] [CrossRef]
- de Blas, J.; Pierini, M.; Reina, L.; Silvestrini, L. Impact of the recent measurements of the top-quark and W-boson masses on electroweak precision fits. arXiv 2022, arXiv:2204.04204. [Google Scholar] [CrossRef] [PubMed]
- de Blas, J.; Ciuchini, M.; Franco, E.; Goncalves, A.; Mishima, S.; Pierini, M.; Reina, L.; Silvestrini, L. Global analysis of electroweak data in the Standard Model. Phys. Rev. D 2022, 106, 033003. [Google Scholar] [CrossRef]
- de Blas, J.; Chowdhury, D.; Ciuchini, M.; Coutinho, A.M.; Eberhardt, O.; Fedele, M.; Franco, E.; di Cortona, G.G.; Miralles, V.; Mishima, S.; et al. HEPfit: A code for the combination of indirect and direct constraints on high energy physics models. Eur. Phys. J. C 2020, 80, 456. [Google Scholar] [CrossRef]
- Flächer, H.; Goebel, M.; Haller, J.; Hoecker, A.; Mönig, K.; Stelzer, J. Revisiting the global electroweak fit of the Standard Model and beyond with Gfitter. Eur. Phys. J. C 2009, 60, 543–583. [Google Scholar] [CrossRef]
- Haller, J.; Hoecker, A.; Kogler, R.; Mönig, K.; Peiffer, T.; Stelzer, J. Update of the global electroweak fit and constraints on two-Higgs-doublet models. Eur. Phys. J. C 2018, 78, 675. [Google Scholar] [CrossRef]
- Fuks, B.; Hagiwara, K.; Ma, K.; Zheng, Y.J. Signatures of toponium formation in LHC run 2 data. Phys. Rev. D 2021, 104, 034023. [Google Scholar] [CrossRef]
- Afik, Y.; de Nova, J.R.M.n. Entanglement and quantum tomography with top quarks at the LHC. Eur. Phys. J. Plus 2021, 136, 907. [Google Scholar] [CrossRef]
- STAR Collaboration. Tomography of ultrarelativistic nuclei with polarized photon-gluon collisions. Sci. Adv. 2023, 9, eabq3903. [Google Scholar] [CrossRef]
- Alekhin, S.; Djouadi, A.; Moch, S. The top quark and Higgs boson masses and the stability of the electroweak vacuum. Phys. Lett. B 2012, 716, 214–219. [Google Scholar] [CrossRef]
- Holthausen, M.; Lim, K.S.; Lindner, M. Planck scale boundary conditions and the Higgs mass. J. High Energy Phys. 2012, 2012, 37. [Google Scholar] [CrossRef]
- Elias-Miró, J.; Espinosa, J.R.; Giudice, G.F.; Isidori, G.; Riotto, A.; Strumia, A. Higgs mass implications on the stability of the electroweak vacuum. Phys. Lett. B 2012, 709, 222–228. [Google Scholar] [CrossRef]
- Xing, Z.; Zhang, H.; Zhou, S. Impacts of the Higgs mass on vacuum stability, running fermion masses, and two-body Higgs decays. Phys. Rev. D 2012, 86, 013013. [Google Scholar] [CrossRef]
- Grzadkowski, B.; Iskrzyński, M.; Misiak, M.; Rosiek, J. Dimension-six terms in the Standard Model Lagrangian. J. High Energy Phys. 2010, 2010, 85. [Google Scholar] [CrossRef]
- Buchmüller, W.; Wyler, D. Effective lagrangian analysis of new interactions and flavour conservation. Nucl. Phys. B 1986, 268, 621–653. [Google Scholar] [CrossRef]
- Falkowski, A.; Rattazzi, R. Which EFT. J. High Energy Phys. 2019, 10, 255. [Google Scholar] [CrossRef]
- Degrande, C.; Greiner, N.; Kilian, W.; Mattelaer, O.; Mebane, H.; Stelzer, T.; Willenbrock, S.; Zhang, C. Effective field theory: A modern approach to anomalous couplings. Ann. Phys. 2013, 335, 21–32. [Google Scholar] [CrossRef]
- Veatch, J. Searches for Resonant Scalar Boson Pair Production Using Run 2 LHC Proton-Proton Collision Data. Symmetry 2022, 14, 260. [Google Scholar] [CrossRef]
- de la Torre, H.; Farooque, T. Looking beyond the Standard Model with Third Generation Quarks at the LHC. Symmetry 2022, 14, 444. [Google Scholar] [CrossRef]
- Schramm, S. Searching for New Physics in Hadronic Final States with Run 2 Proton-Proton Collision Data at the LHC. Symmetry 2022, 14, 1173. [Google Scholar] [CrossRef]
- Abdallah, J.; Abreu, P.; Adam, W.; Adzic, P.; Albrecht, T.; Alemany-Fernandez, R.; Kersevan, B.P.; Allmendinger, T.; Allport, P.P.; Amaldi, U.; et al. Measurement of the mass and width of the W boson in e+e- collisions at = 161–209 GeV. Eur. Phys. J. C 2008, 55, 1–38. [Google Scholar] [CrossRef]
- Aaltonen, T.; Abulencia, A.; Adelman, J.; Affolder, T.; Akimoto, T.; Albrow, M.G.; Eusebi, R.; Amerio, S.; Amidei, D.; Anastassov, A.; et al. Measurement of the top-quark mass in all-hadronic decays in p anti-p collisions at CDF II. Phys. Rev. Lett. 2007, 98, 142001. [Google Scholar] [CrossRef] [PubMed]
- Abazov, V.M.; Abbott, B.; Abolins, M.; Acharya, B.S.; Adams, M.; Adams, T.; Dyshkant, A.; Ahn, S.H.; Ahsan, M.; Alexeev, G.D.; et al. Measurement of the top quark mass in the lepton+jets channel using the ideogram method. Phys. Rev. D 2007, 75, 092001. [Google Scholar] [CrossRef]
- Abbott, B.; Abolins, M.; Abramov, V.; Acharya, B.S.; Adam, I.; Adams, D.L.; Hedin, D.; Anderson, S.; Andeen, T.; Anastasoaie, M.; et al. Measurement of the top quark mass in the dilepton channel. Phys. Rev. D 1999, 60, 052001. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Fabjan, C. Measurement of the top-quark mass in events with lepton+jets final states in pp collisions at = 7 TeV. J. High Energy Phys. 2012, 2012, 105. [Google Scholar] [CrossRef]
- Hollar, J.; Nayak, A.; Calpas, B.; Bargassa, P.; Beirao Da Cruz E Silva, C.; Faccioli, P.; Dragicevic, M.; Fabjan, C.; Friedl, M.; et al.; CMS Collaboration Measurement of jet multiplicity distributions in production in pp collisions at = 7TeV. Eur. Phys. J. C 2015, 74, 3014, Erratum in Eur. Phys. J. C 2015, 75, 216. [Google Scholar] [CrossRef]
- The ATLAS Collaboration; Aad, G.; Alconada Verzini, M.J.; Alonso, F.; Anduaga, X.S.; Dova, M.T.; Monticelli, F.G.; Wahlberg, H.P.; Abbott, B.; Abdallah, J.; et al. Measurement of the production cross-section as a function of jet multiplicity and jet transverse momentum in 7 TeV proton-proton collisions with the ATLAS detector. J. High Energy Phys. 2015, 1, 20. [Google Scholar] [CrossRef]
- The ATLAS Collaboration; Aad, G.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdelalim, A.A.; Abdesselam, A.; Abdinov, O.; Abi, B.; Abolins, M.; et al. Measurement of production with a veto on additional central jet activity in pp collisions at sqrt(s) = 7 TeV using the ATLAS detector. Eur. Phys. J. C 2012, 72, 2043. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Flechl, M.; et al. Measurement of the t-tbar production cross section in the e-mu channel in proton-proton collisions at sqrt(s) = 7 and 8 TeV. J. High Energy Phys. 2016, 8, 29. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; AbouZeid, O.S.; Abramowicz, H.; et al. Differential top-antitop cross-section measurements as a function of observables constructed from final-state particles using pp collisions at = 7 TeV in the ATLAS detector. J. High Energy Phys. 2015, 6, 100. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Dragicevic, M.; Flechl, M.; Ghete, V.M.; et al. Measurement of the production cross section, the top quark mass, and the strong coupling constant using dilepton events in pp collisions at = 13 TeV. Eur. Phys. J. C 2019, 79, 368. [Google Scholar] [CrossRef] [PubMed]
- Measurement of the Top-Quark Decay Width in Top-Quark Pair Events in the Dilepton Channel at s=13 TeV with the ATLAS Detector; Technical Report; CERN: Geneva, Switzerland, 2019; All Figures including auxiliary Figures are available at ATLAS-CONF-2019-038; Available online: https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/CONFNOTES/ATLAS-CONF-2019-038 (accessed on 10 April 2023).
- The CMS Collaboration. Measurement of the top quark Yukawa coupling from kinematic distributions in the dilepton final state in proton-proton collisions at = 13 TeV. Phys. Rev. D 2020, 102, 092013. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Measurements of jet observables sensitive to b-quark fragmentation in events at the LHC with the ATLAS detector. arXiv 2022, arXiv:hep-ex/2202.13901. [Google Scholar]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Bergauer, T.; Dragicevic, M.; Escalante Del Valle, A.; Flechl, M.; Jeitler, M.; Krammer, N.; et al. Measurement of CKM matrix elements in single top quark t-channel production in proton-proton collisions at = 13 TeV. Phys. Lett. B 2020, 808, 135609. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Bergauer, T.; Brandstetter, J.; Dragicevic, M.; Escalante Del Valle, A.; Flechl, M.; Jeitler, M.; et al. Running of the top quark mass from proton-proton collisions at = 13TeV. Phys. Lett. B 2020, 803, 135263. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Inclusive and Differential Measurement of the Charge Asymmetry in Events at 13 TeV with the ATLAS Detector. 2019. Available online: https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/CONFNOTES/ATLAS-CONF-2019-026/ (accessed on 10 April 2023).
- Beneke, M.; Falgari, P.; Klein, S.; Schwinn, C. Hadronic top-quark pair production with NNLL threshold resummation. Nucl. Phys. B 2012, 855, 695–741. [Google Scholar] [CrossRef]
- Bärnreuther, P.; Czakon, M.; Mitov, A. Percent Level Precision Physics at the Tevatron: First Genuine NNLO QCD Corrections to →+X. Phys. Rev. Lett. 2012, 109, 132001. [Google Scholar] [CrossRef]
- Czakon, M.; Mitov, A. NNLO corrections to top-pair production at hadron colliders: The all-fermionic scattering channels. J. High Energy Phys. 2012, 12, 054. [Google Scholar] [CrossRef]
- Czakon, M.; Mitov, A. NNLO corrections to top pair production at hadron colliders: The quark-gluon reaction. J. High Energy Phys. 2013, 1, 80. [Google Scholar] [CrossRef]
- Czakon, M.; Fiedler, P.; Mitov, A. Total Top-Quark Pair-Production Cross Section at Hadron Colliders Through (). Phys. Rev. Lett. 2013, 110, 252004. [Google Scholar] [CrossRef]
- Czakon, M.; Mitov, A. Top++: A Program for the Calculation of the Top-Pair Cross-Section at Hadron Colliders. Comput. Phys. Commun. 2014, 185, 2930. [Google Scholar] [CrossRef]
- Aliev, M.; Lacker, H.; Langenfeld, U.; Moch, S.; Uwer, P.; Wiedermann, M. HATHOR: HAdronic Top and Heavy quarks crOss section calculatoR. Comput. Phys. Commun. 2011, 182, 1034–1046. [Google Scholar] [CrossRef]
- Kant, P.; Kind, O.M.; Kintscher, T.; Lohse, T.; Martini, T.; Mölbitz, S.; Rieck, P.; Uwer, P. HatHor for single top-quark production: Updated predictions and uncertainty estimates for single top-quark production in hadronic collisions. Comput. Phys. Commun. 2015, 191, 74–89. [Google Scholar] [CrossRef]
- Kidonakis, N. Two-loop soft anomalous dimensions for single top quark associated production with a W− or H−. Phys. Rev. D 2010, 82, 054018. [Google Scholar] [CrossRef]
- Kidonakis, N. Top Quark Production. In Proceedings of the Helmholtz International Summer School on Physics of Heavy Quarks and Hadrons, Dubna, Russia, 15–28 July 2013; pp. 139–168. [Google Scholar] [CrossRef]
- Kidonakis, N. Next-to-next-to-leading logarithm resummation for s-channel single top quark production. Phys. Rev. D 2010, 81, 054028. [Google Scholar] [CrossRef]
- Kidonakis, N. Next-to-next-to-leading-order collinear and soft gluon corrections for t-channel single top quark production. Phys. Rev. D 2011, 83, 091503. [Google Scholar] [CrossRef]
- Kidonakis, N. Single top quark production at the Fermilab Tevatron: Threshold resummation and finite-order soft gluon corrections. Phys. Rev. D 2006, 74, 114012. [Google Scholar] [CrossRef]
- Martin, A.D.; Stirling, W.J.; Thorne, R.S.; Watt, G. Parton distributions for the LHC. Eur. Phys. J. C 2009, 63, 189–285. [Google Scholar] [CrossRef]
- Martin, A.D.; Stirling, W.J.; Thorne, R.S.; Watt, G. Uncertainties on alpha(S) in global PDF analyses and implications for predicted hadronic cross sections. Eur. Phys. J. C 2009, 64, 653–680. [Google Scholar] [CrossRef]
- Lai, H.L.; Guzzi, M.; Huston, J.; Li, Z.; Nadolsky, P.M.; Pumplin, J.; Yuan, C.P. New parton distributions for collider physics. Phys. Rev. D 2010, 82, 074024. [Google Scholar] [CrossRef]
- Gao, J.; Guzzi, M.; Huston, J.; Lai, H.L.; Li, Z.; Nadolsky, P.; Pumplin, J.; Stump, D.; Yuan, C.P. CT10 next-to-next-to-leading order global analysis of QCD. Phys. Rev. D 2014, 89, 033009. [Google Scholar] [CrossRef]
- Ball, R.D.; Bertone, V.; Carrazza, S.; Deans, C.S.; Del Debbio, L.; Forte, S.; Guffanti, A.; Hartland, P.H.; Latorre, J.I.; Rojo, J.; et al. Parton distributions with LHC data. Nucl. Phys. B 2013, 867, 244–289. [Google Scholar] [CrossRef]
- Czakon, M.; Heymes, D.; Mitov, A. High-precision differential predictions for top-quark pairs at the LHC. Phys. Rev. Lett. 2016, 116, 082003. [Google Scholar] [CrossRef] [PubMed]
- Ball, R.D.; Butterworth, J.; Cooper-Sarkar, A.M.; Courtoy, A.; Cridge, T.; Roeck, A.D.; Feltesse, J.; Forte, S.; Giuli, F.; Gwenlan, C.; et al. The PDF4LHC21 combination of global PDF fits for the LHC Run III. J. Phys. G 2022, 49, 080501. [Google Scholar] [CrossRef]
- Campbell, J.; Neumann, T.; Sullivan, Z. Single-top-quark production in the t-channel at NNLO. J. High Energy Phys. 2021, 2, 40. [Google Scholar] [CrossRef]
- Kidonakis, N.; Yamanaka, N. Higher-order corrections for tW production at high-energy hadron colliders. J. High Energy Phys. 2021, 5, 278. [Google Scholar] [CrossRef]
- Hoecker, A.; Speckmayer, P.; Stelzer, J.; Therhaag, J.; von Toerne, E.; Voss, H.; Backes, M.; Carli, T.; Cohen, O.; Christov, A.; et al. TMVA—Toolkit for Multivariate Data Analysis. arXiv 2007, arXiv:physics/0703039. [Google Scholar]
- Guest, D.; Cranmer, K.; Whiteson, D. Deep Learning and Its Application to LHC Physics. Annu. Rev. Nucl. Part. Sci. 2018, 68, 161–181. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Aaltonen, T.; Adelman, J.; Akimoto, T.; Amerio, S.; Amidei, D.; Anastassov, A.; Annovi, A.; Antos, J.; Apollinari, G.; Apresyan, A.; et al. First Observation of Electroweak Single Top Quark Production. Phys. Rev. Lett. 2009, 103, 092002. [Google Scholar] [CrossRef]
- Abazov, V.M.; Abbott, B.; Abolins, M.; Acharya, B.S.; Adams, M.; Adams, T.; Aguilo, E.; Ahsan, M.; Alexeev, G.D.; Alkhazov, G.; et al. Observation of Single Top Quark Production. Phys. Rev. Lett. 2009, 103, 092001. [Google Scholar] [CrossRef] [PubMed]
- Abazov, V.M.; Abbott, B.; Acharya, B.S.; Adams, M.; Adams, T.; Agnew, J.P.; Alexeev, G.D.; Alkhazov, G.; Alton, A.; Askew, A.; et al. Evidence for S-Channel Single Top Quark Production in Collisions at = 1.96 TeV. Phys. Lett. B 2013, 726, 656–664. [Google Scholar] [CrossRef]
- Aaltonen, T.; Abazov, V.M.; Abbott, B.; Acharya, B.S.; Adams, M.; Adams, T.; Agnew, J.P.; Alexeev, G.D.; Alkhazov, G.; Alton, A.; et al. Observation of s-Channel Production of Single Top Quarks at the Tevatron. Phys. Rev. Lett. 2014, 112, 231803. [Google Scholar] [CrossRef] [PubMed]
- Aad, G.; Abbott, B.; Abdallah, J.; Abdinov, O.; Aben, R.; Abolins, M.; AbouZeid, O.S.; Abramowicz, H.; Abreu, H.; Abreu, H.; et al. Evidence for single top-quark production in the s-channel in proton-proton collisions at = 8 TeV with the ATLAS detector using the Matrix Element Method. Phys. Lett. B 2016, 756, 228–246. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Flechl, M.; et al. Search for s channel single top quark production in pp collisions at = 7 and 8 TeV. J. High Energy Phys. 2016, 9, 27. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; Abdallah, J.; Abdinov, O.; Abeloos, B.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; Abreu, H.; et al. Probing the W tb vertex structure in t-channel single-top-quark production and decay in pp collisions at = 8 TeV with the ATLAS detector. J. High Energy Phys. 2017, 4, 124. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; Abbott, D.C.; Abdinov, O.; Abed Abud, A.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, O.S.; et al. Combinations of single-top-quark production cross-section measurements and |fLVVtb| determinations at = 7 and 8 TeV with the ATLAS and CMS experiments. J. High Energy Phys. 2019, 5, 88. [Google Scholar] [CrossRef]
- Tumasyan, A.; Adam, W.; Andrejkovic, J.W.; Bergauer, T.; Chatterjee, S.; Dragicevic, M.; Escalante Del Valle, A.; Jeitler, M.; Krammer, M.; Lechner, L.; et al. Observation of tW production in the single-lepton channel in pp collisions at = 13 TeV. J. High Energy Phys. 2021, 11, 111. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abbott, D.C.; Abed Abud, A.; Abeling, K.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; et al. Measurement of single top-quark production in association with a W boson in the single-lepton channel at = 8TeV with the ATLAS detector. Eur. Phys. J. C 2021, 81, 720. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Escalante Del Valle, A.; et al. Measurement of the production cross section for single top quarks in association with W bosons in proton-proton collisions at = 13 TeV. J. High Energy Phys. 2018, 10, 117. [Google Scholar] [CrossRef]
- Measurement of single top-quark production in the s-channel in proton–proton collisions at = 13 TeV with the ATLAS detector. arXiv 2022, arXiv:hep-ex/2209.08990.
- LHCtopWG Joined Experimental and Theory LHC Working Group. Available online: https://twiki.cern.ch/twiki/bin/view/LHCPhysics/LHCTopWG (accessed on 23 February 2023).
- Aad, G.; Abbott, B.; Abbott, D.C.; Abed Abud, A.; Abeling, K.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; et al. Measurement of the production cross-section in the lepton+jets channel at = 13 TeV with the ATLAS experiment. Phys. Lett. B 2020, 810, 135797. [Google Scholar] [CrossRef]
- Search for new physics using effective field theory in 13 TeV pp collision events that contain a top quark pair and a boosted Z or Higgs boson. arXiv 2022, arXiv:hep-ex/2208.12837.
- Tumasyan, A.; Adam, W.; Andrejkovic, J.W.; Bergauer, T.; Chatterjee, S.; Dragicevic, M.; Escalante Del Valle, A.; Jeitler, M.; Krammer, N.; Lechner, L.; et al. Measurement of the inclusive production cross section in proton-proton collisions at = 5.02 TeV. J. High Energy Phys. 2022, 4, 144. [Google Scholar] [CrossRef]
- First Measurement of the Top Quark Pair Production cross Section in Proton-Proton Collisions at s = 13.6 TeV; CERN: Geneva, Switzerland, 2022. [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Bergauer, T.; Dragicevic, M.; Erö, J.; Escalante Del Valle, A.; Frühwirth, R.; Jeitler, M.; et al. Evidence for Top Quark Production in Nucleus-Nucleus Collisions. Phys. Rev. Lett. 2020, 125, 222001. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Flechl, M.; et al. Measurement of the inclusive cross section in pp collisions at = 5.02 TeV using final states with at least one charged lepton. J. High Energy Phys. 2018, 3, 115. [Google Scholar] [CrossRef]
- Abdolmaleki, H.; Amoroso, S.; Bertone, V.; Botje, M.; Britzger, D.; Camarda, S.; Cooper-Sarkar, A.; Fiaschi, J.; Giuli, F.; Glazov, A.; et al. xFitter: An Open Source QCD Analysis Framework. A resource and reference document for the Snowmass study. arXiv 2022, arXiv:hep-ph/2206.12465. [Google Scholar]
- Schmitt, S. TUnfold: An algorithm for correcting migration effects in high energy physics. J. Instrum. 2012, 7, T10003. [Google Scholar] [CrossRef]
- D’Agostini, G. Improved iterative Bayesian unfolding. arXiv 2010, arXiv:1010.0632. [Google Scholar]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Bergauer, T.; Brandstetter, J.; Dragicevic, M.; Escalante Del Valle, A.; Flechl, M.; Fruehwirth, R.; et al. Measurement of normalised multi-differential cross sections in pp collisions at = 13 TeV, and simultaneous determination of the strong coupling strength, top quark pole mass, and parton distribution functions. Eur. Phys. J. C 2020, 80, 658. [Google Scholar] [CrossRef]
- Abazov, V.M.; Abbott, B.; Acharya, B.S.; Adams, M.; Adams, T.; Agnew, J.P.; Alexeev, G.D.; Alkhazov, G.; Alton, A.; Askew, A.; et al. Measurement of the inclusive production cross section in collisions at = 1.96 TeV and determination of the top quark pole mass. Phys. Rev. D 2016, 94, 092004. [Google Scholar] [CrossRef]
- Grazzini, M.; Kallweit, S.; Wiesemann, M. Fully differential NNLO computations with MATRIX. Eur. Phys. J. C 2018, 78, 537. [Google Scholar] [CrossRef]
- Measurement of Differential cross Sections for the Production of Top Quark Pairs and of Additional Jets in pp Collisions at = 13.6 TeV; Technical Report; CERN: Geneva, Switzerland, 2022.
- Tumasyan, A.; Adam, W.; Andrejkovic, J.W.; Bergauer, T.; Chatterjee, S.; Dragicevic, M.; Escalante Del Valle, A.; Jeitler, M.; Krammer, N.; Lechner, L.; et al. Measurement of differential production cross sections in the full kinematic range using lepton+jets events from proton-proton collisions at = 13 TeV. Phys. Rev. D 2021, 104, 092013. [Google Scholar] [CrossRef]
- Projection of Measurements of Differential Ttbar Production cross Sections in the e/u+jets Channels in pp Collisions at the HL-LHC; CERN: Geneva, Switzerland, 2018; Available online: http://cds.cern.ch/record/2803771?ln=en (accessed on 10 April 2023).
- ATLAS Collaboration. Measurements of differential cross-sections in top-quark pair events with a high transverse momentum top quark and limits on beyond the Standard Model contributions to top-quark pair production with the ATLAS detector at = 13 TeV. arXiv 2022, arXiv:hep-ex/2202.12134. [Google Scholar]
- Aad, G.; Abbott, B.; Abbott, D.C.; Abed Abud, A.; Abeling, K.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; et al. Measurements of the inclusive and differential production cross sections of a top-quark–antiquark pair in association with a Z boson at = 13 TeV with the ATLAS detector. Eur. Phys. J. C 2021, 81, 737. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abbott, D.C.; Abed Abud, A.; Abeling, K.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; et al. Observation of the associated production of a top quark and a Z boson in pp collisions at = 13 TeV with the ATLAS detector. J. High Energy Phys. 2020, 7, 124. [Google Scholar] [CrossRef]
- Tumasyan, A.; Adam, W.; Andrejkovic, J.W.; Bergauer, T.; Chatterjee, S.; Damanakis, K.; Dragicevic, M.; Escalante Del Valle, A.; Jeitler, M.; Krammer, N.; et al. Inclusive and differential cross section measurements of single top quark production in association with a Z boson in proton-proton collisions at = 13 TeV. J. High Energy Phys. 2022, 2, 107. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abbott, D.C.; Abed Abud, A.; Abeling, K.; Abhayasinghe, D.K.; Abidi, S.H.; Abramowicz, H.; Abreu, H.; Abulaiti, Y.; et al. Measurement of the production cross section in pp collisions at = 13 TeV with the ATLAS detector. J. High Energy Phys. 2021, 11, 118. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Abreu, A.; Adam, W.; Ambrogi, F.; Bergauer, T.; Brandstetter, J.; Dragicevic, M.; Escalante Del Valle, A.; Flechl, M.; Fruehwirth, R.; et al. Search for production of four top quarks in final states with same-sign or multiple leptons in proton-proton collisions at = 13 TeV. Eur. Phys. J. C 2020, 80, 75. [Google Scholar] [CrossRef]
- Evidence for the Simultaneous Production of Four Top Quarks in Proton-Proton Collisions at = 13 TeV; Technical Report; CERN: Geneva, Switzerland, 2022; All Figures including auxiliary Figures are available at CMS-PAS-TOP-21-005; Available online: https://cds.cern.ch/record/2827591 (accessed on 10 April 2023).
- Frederix, R.; Pagani, D.; Zaro, M. Large NLO corrections in W± and hadroproduction from supposedly subleading EW contributions. J. High Energy Phys. 2018, 2, 31. [Google Scholar] [CrossRef]
- Aaltonen, T.; Abazov, V.M.; Abbott, B.; Acharya, B.S.; Adams, M.; Adams, T.; Agnew, J.P.; Alexeev, G.D.; Alkhazov, G.; Alton, A.; et al. Combined Forward-Backward Asymmetry Measurements in Top-Antitop Quark Production at the Tevatron. Phys. Rev. Lett. 2018, 120, 042001. [Google Scholar] [CrossRef] [PubMed]
- ATLAS Collaboration. Measurement of the charge asymmetry in events with highly Lorentz-boosted top quarks in pp collisions at = 13 TeV. arXiv 2022, arXiv:hep-ex/2208.02751. [Google Scholar]
- Aaboud, M.; Aad, G.; Abbott, B.; Abdinov, O.; Abeloos, B.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; Abreu, H.; et al. Combination of inclusive and differential charge asymmetry measurements using ATLAS and CMS data at = 7 and 8 TeV. J. High Energy Phys. 2018, 4, 33. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Fabjan, C.; Friedl, M.; Ghete, V.M.; et al. Measurements of Spin Correlations and Top-Quark Polarization Using Dilepton Final States in pp Collisions at = 7 TeV. Phys. Rev. Lett. 2014, 112, 182001. [Google Scholar] [CrossRef] [PubMed]
- Aad, G.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; AbouZeid, O.S.; Abramowicz, H.; et al. Measurements of spin correlation in top-antitop quark events from proton-proton collisions at = 7TeV using the ATLAS detector. Phys. Rev. D 2014, 90, 112016. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Flechl, M.; et al. Measurements of t t-bar spin correlations and top quark polarization using dilepton final states in pp collisions at sqrt(s) = 8 TeV. Phys. Rev. D 2016, 93, 052007. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; Abdallah, J.; Abdinov, O.; Abeloos, B.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; Abreu, H.; et al. Measurements of top quark spin observables in events using dilepton final states in = 8 TeV pp collisions with the ATLAS detector. J. High Energy Phys. 2017, 3, 113. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; Abbott, D.C.; Abdinov, O.; Abed Abud, A.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; et al. Measurements of top-quark pair spin correlations in the eμ channel at = 13 TeV using pp collisions in the ATLAS detector. Eur. Phys. J. C 2020, 80, 754. [Google Scholar] [CrossRef]
- Abazov, V.; Abbott, B.; Acharya, B.; Adams, M.; Adams, T.; Agnew, J.; Alexeev, G.; Alkhazov, G.; Alton, A.; Askew, A.; et al. Measurement of spin correlation between top and antitop quarks produced in collisions at s=1.96 TeV. Phys. Lett. B 2016, 757, 199–206. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Dragicevic, M.; Escalante Del Valle, A.; Flechl, M.; et al. Measurement of the top quark polarization and spin correlations using dilepton final states in proton-proton collisions at = 13 TeV. Phys. Rev. D 2019, 100, 072002. [Google Scholar] [CrossRef]
- Behring, A.; Czakon, M.; Mitov, A.; Papanastasiou, A.S.; Poncelet, R. Higher order corrections to spin correlations in top quark pair production at the LHC. Phys. Rev. Lett. 2019, 123, 082001. [Google Scholar] [CrossRef] [PubMed]
- Aad, G.; Abbott, B.; Abbott, D.C.; Abud, A.A.; Abeling, K.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; et al. Measurement of the production cross-section and lepton differential distributions in eμ dilepton events from pp collisions at = 13TeV with the ATLAS detector. Eur. Phys. J. C 2020, 80, 528. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Projection of the Top Quark Spin Correlation Measurement and Search for Top Squark Pair Production at the HL-LHC. 2022. All Figures Including Auxiliary Figures Are Available at CMS-PAS-FTR-18-034. Available online: https://inspirehep.net/literature/2110182 (accessed on 10 April 2023).
- Aaboud, M.; Aad, G.; Abbott, B.; Abdinov, O.; Abeloos, B.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; et al. Measurement of the top quark mass in the ➝ lepton+jets channel from = 8 TeV ATLAS data and combination with previous results. Eur. Phys. J. C 2019, 79, 290. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Flechl, M.; et al. Measurement of the top quark mass using proton-proton data at = 7 and 8 TeV. Phys. Rev. D 2016, 93, 072004. [Google Scholar] [CrossRef]
- CDF and D0 Collaborations. Combination of CDF and D0 Results on the Mass of the Top Quark using up to 9.7 fb−1 at the Tevatron. arXiv 2014, arXiv:hep-ex/1407.2682. [Google Scholar]
- ATLAS, CDF, CMS Collaborations, DO. First combination of Tevatron and LHC measurements of the top-quark mass. arXiv 2014, arXiv:1403.4427. [Google Scholar]
- Lyons, L.; Gibaut, D.; Clifford, P. How to combine correlated estimates of a single physical quantity. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1988, 270, 110–117. [Google Scholar] [CrossRef]
- Nisius, R. BLUE: A Software Package to Combine Correlated Estimates of Physics Observables within ROOT Using the Best Linear Unbiased Estimate Method—Program Manual, Version 2.1.0. 2016. Available online: http://blue.hepforge.org (accessed on 10 April 2023).
- Nisius, R. On the combination of correlated estimates of a physics observable. Eur. Phys. J. C 2014, 74. [Google Scholar] [CrossRef]
- Kieseler, J. A method and tool for combining differential or inclusive measurements obtained with simultaneously constrained uncertainties. Eur. Phys. J. C 2017, 77, 792. [Google Scholar] [CrossRef]
- A Profile Likelihood Approach to Measure the Top Quark Mass in the Lepton+Jets Channel at s = 13 TeV; Technical Report; CERN: Geneva, Switzerland, 2022; All Figures including auxiliary Figures are available at CMS-PAS-TOP-20-008; Available online: https://cds.cern.ch/record/2806509 (accessed on 10 April 2023).
- Haller, J.; Hoecker, A.; Kogler, R.; Mönig, K.; Stelzer, J. Status of the global electroweak fit with Gfitter in the light of new precision measurements. arXiv 2022, arXiv:2211.07665. [Google Scholar]
- Hoang, A.H. What Is the Top Quark Mass? Annu. Rev. Nucl. Part. Sci. 2020, 70, 225–255. [Google Scholar] [CrossRef]
- Hays, C. High precision measurement of the W-boson mass with the CDF II detector. PoS 2022, ICHEP2022, 898. [Google Scholar] [CrossRef]
- Measurement of the jet mass distribution and top quark mass in hadronic decays of boosted top quarks in proton-proton collisions at = 13 TeV. arXiv 2022, arXiv:hep-ex/2211.01456.
- Measurement of the Top Quark Mass Using a Leptonic Invariant Mass in pp Collisions at sqrts = 13 TeV with the ATLAS Detector; Technical Report; CERN: Geneva, Switzerland, 2019; All Figures including auxiliary Figures are available at ATLAS-CONF-2019-046; Available online: https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/CONFNOTES/ATLAS-CONF-2019-046 (accessed on 10 April 2023).
- Kieseler, J.; Lipka, K.; Moch, S.O. Calibration of the Top-Quark Monte Carlo Mass. Phys. Rev. Lett. 2016, 116, 162001. [Google Scholar] [CrossRef] [PubMed]
- Defranchis, M.M.; Kieseler, J.; Lipka, K.; Mazzitelli, J. Running of the top quark mass at NNLO in QCD. arXiv 2022, arXiv:2208.11399. [Google Scholar]
- Jezabek, M.; Kuhn, J.H. QCD Corrections to Semileptonic Decays of Heavy Quarks. Nucl. Phys. B 1989, 314, 1–6. [Google Scholar] [CrossRef]
- Gao, J.; Li, C.S.; Zhu, H.X. Top-Quark Decay at Next-to-Next-to-Leading Order in QCD. Phys. Rev. Lett. 2013, 110, 042001. [Google Scholar] [CrossRef]
- Aaltonen, T.A.; Amerio, S.; Amidei, D.; Anastassov, A.; Annovi, A.; Antos, J.; Apollinari, G.; Appel, J.A.; Arisawa, T.; Artikov, A.; et al. Direct Measurement of the Total Decay Width of the Top Quark. Phys. Rev. Lett. 2013, 111, 202001. [Google Scholar] [CrossRef]
- Abazov, V.M.; Abbott, B.; Acharya, B.S.; Adams, M.; Adams, T.; Alexeev, G.D.; Alkhazov, G.; Alton, A.; Alverson, G.; Aoki, M.; et al. An Improved determination of the width of the top quark. Phys. Rev. D 2012, 85, 091104. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; Abdinov, O.; Abeloos, B.; Abidi, S.H.; AbouZeid, O.S.; Abraham, M.L.; Abramowicz, H.; Abreu, H.; et al. Direct top-quark decay width measurement in the lepton+jets channel at = 8 TeV with the ATLAS experiment. Eur. Phys. J. C 2018, 78, 129. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abbott, D.C.; Abed Abud, A.; Abeling, K.; Abhayasinghe, D.K.; Abidi, S.H.; Aboulhorma, A.; Abramowicz, H.; Abreu, H.; et al. Search for flavour-changing neutral-current interactions of a top quark and a gluon in pp collisions at = 13 TeV with the ATLAS detector. Eur. Phys. J. C 2022, 82, 334. [Google Scholar] [CrossRef]
- Tumasyan, A.; Adam, W.; Andrejkovic, J.W.; Bergauer, T.; Chatterjee, S.; Damanakis, K.; Dragicevic, M.; Escalante Del Valle, A.; Jeitler, M.; Krammer, N.; et al. Search for flavor-changing neutral current interactions of the top quark and the Higgs boson decaying to a bottom quark-antiquark pair at = 13 TeV. J. High Energy Phys. 2022, 2, 169. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Escalante Del Valle, A.; Jeitler, M.; Krammer, N.; Lechner, L.; Liko, D.; et al. Search for new physics in top quark production with additional leptons in proton-proton collisions at = 13 TeV using effective field theory. J. High Energy Phys. 2021, 3, 095. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Measurement of the polarisation of single top quarks and antiquarks produced in the t-channel at = 13 TeV and bounds on the tWb dipole operator from the ATLAS experiment. arXiv 2022, arXiv:hep-ex/2202.11382. [Google Scholar]
- Tonon, N.; Aarup Petersen, H.; Aldaya Martin, M.; Asmuss, P.; Baxter, S.; Bayatmakou, M.; Behnke, O.; Bermúdez Martínez, A.; Bhattacharya, S.; Bin Anuar, A.A.; et al. Probing effective field theory operators in the associated production of top quarks with a Z boson in multilepton final states at = 13 TeV. J. High Energy Phys. 2021, 2021, 83. [Google Scholar] [CrossRef]
- Bohm, G.; Zech, G. Introduction to Statistics and Data Analysis for Physicists, 3rd ed.; Verlag Deutsches Elektronen-Synchrotron: Hamburg, Germany, 2017; p. 488. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abbott, D.C.; Abud, A.A.; Abeling, K.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; et al. Measurements of top-quark pair differential and double-differential cross-sections in the ℓ+jets channel with pp collisions at = 13 TeV using the ATLAS detector. Eur. Phys. J. C 2019, 79, 1028. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).