New Lifetime Distribution with Applications to Single Acceptance Sampling Plan and Scenarios of Increasing Hazard Rates

Abstract

This article is an extension of the Chris-Jerry distribution (C-JD) in that a two-parameter Chris-Jerry distribution (TPCJD) is suggested and its characteristics are studied. Based on the determined domain of attraction and other major statistical properties, the proposed TPCJD seems to fit into the Gumbel domain. Additionally, it has been confirmed that the stress strength is reliable. The tail study suggests that the TPCJD’s substantial tail makes it suited for a range of applications. The study took into account the single acceptance sampling approach using both simulation and real-life situations. The parameters of the TPCJD were estimated by some classical and Bayesian approaches. The mean squared errors (MSE), linear-exponential, and generalized entropy loss functions were deployed to obtain the Bayesian estimators aided by the Markov chain Monte Carlo (MCMC) simulation. An analysis of lifetime data on two events justified the use of the proposed distribution after comparing the results with some standard lifetime models.

1. Introduction

In the field of distribution theory, significant effort has gone toward creating novel flexible distributions that might be used for lifetime data sets. The methods used in statistical analysis are significantly influenced by the presumed probability distributions, and a wide range of methodologies have been developed and employed by numerous authors. The majority of the extensions of well-known distributions provide a better fit for various life events. For more information on the goodness of fit criterion, see [1,2,3]. Even though they perform better in some data sets, using innovative distributions produced by enlarging and changing the classical distributions has a cost. The Chris-Jerry distribution was shown to be more applicable and to perform better than some well-known Lindley class of distributions—see [2,4,5,6,7,8,9,10,11,12,13,14,15,16] for details.

Due to the complexity involved in estimating additional parameters introduced via extending existing distributions, parsimony in parameters becomes key in the choices of distributions.

Therefore, the study’s motivation stems from the requirement to improve the one-parameter C-JD so that:

• A new distribution is created by adding a shape parameter to the C-JD with one parameter.
• Despite additional parameters, the suggested distribution’s parameters are tractable using both conventional and Bayesian estimates.
• Enhanced flexibility and characteristics of the current distributions.
• The Weibull, Gamma, Lomax, Burr III, Exponentiated Inverse Exponential, and Generalised Inverse Exponential distributions all provide better fits than the one-parameter C-JD.

The organization of the rest of the sections of this article is as follows: Section 2, where we derive the new distribution, Section 3, where we derive some useful characteristics, such as the classical estimation method, Section 4, where we apply the single acceptance sampling plan to the proposed TPCJD, and Section 5, where we apply the Bayesian technique for the estimation of the parameters of the suggested distribution and two-lifetime data.

2. The Two Parameter Chris-Jerry (TPCJD)

The C-JD, due to Onyekwere and Obulezi [2], has p.d.f and c.d.f, respectively, as

$$f(x;\theta )=\frac{{\theta }^2}{\theta +2}(1+\theta x^2){\mathrm{e}}^{-\theta x};x>0,$$

(1)

and

$$F_{CJ}(x,\theta )=1-\left[1+\frac{\theta x\left(\theta x+2\right)}{\theta +2}\right]{\mathrm{e}}^{-\theta x},x>0,\theta >0.$$

(2)

The TPCJD is obtained similarly to that of the C-JD, with the mixing proportion $p=\frac{\lambda \theta }{\lambda \theta +2}$. Thus, the TPCJD’s p.d.f and c.d.f are, respectively

$${\displaystyle g(x;\lambda ,\theta )=\frac{{\theta }^2}{\lambda \theta +2}(\lambda +\theta x^2){\mathrm{e}}^{-\theta x};x>0,\theta >0,\lambda >0,}$$

(3)

and

$$G(x;\lambda ,\theta )=1-\frac{1}{\theta \lambda +2}({\theta }^2{x}^2+2\theta x+\theta \lambda +2){\mathrm{e}}^{-\theta x},$$

(4)

$\ni ,\lambda$, and $\theta$ are the shape and scale parameters, respectively. The PDF and CDF plots are shown in Figure 1.

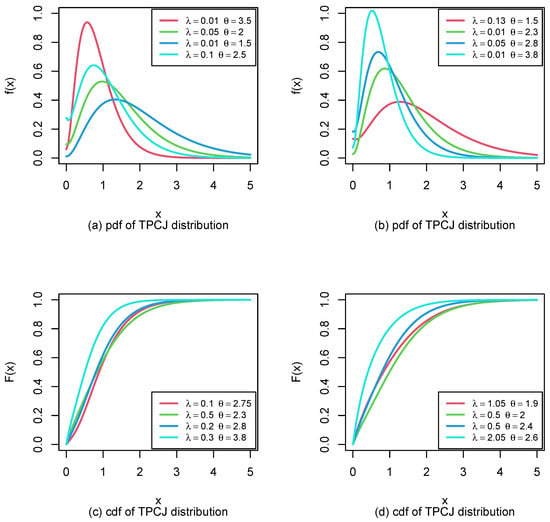
Figure 1. TPCJD’s pdf and the cdf plots.

The Reliability function of the TPCJD is

$$S(x;\lambda ,\theta )=\frac{1}{\theta \lambda +2}({\theta }^2{x}^2+2\theta x+\theta \lambda +2){\mathrm{e}}^{-\theta x}.$$

(5)

The Reliability function of the TPCJD is such that $S_x\left(0\right)=1$ and $S_x(\infty )=0$. The hazard rate function of the TPCJD is

$$h(x;\lambda ,\theta )=\frac{{\theta }^2(\lambda +\theta x^2)}{{\theta }^2{x}^2+2\theta x+\theta \lambda +2}.$$

(6)

From the hazard rate function, it is easy to see that

i.

$h\left(0\right)=\frac{\lambda {\theta }^2}{\theta \lambda +2}$.

ii.

$h(\infty )=\theta$.

3. The Characteristics of the TPCJD

3.1. Complete Moment

The rth crude moment of the TPCJD in the complete sense is given as

$${\mu }_r^{{}^{\prime }}=E\left(X^r\right)=\frac{\Gamma (r+1)}{{\theta }^r(\theta \lambda +2)}(\lambda \theta +r^2+3r+2).$$

(7)

The first four non-central moments are obtained by replacing r in (7) by $1,2,3,4$ respectively.

$$\mu ={\mu }_1^{{}^{\prime }}=\frac{(\lambda \theta +6)}{\theta (\theta \lambda +2)};{\mu }_2^{{}^{\prime }}=\frac{2(\lambda \theta +12)}{{\theta }^2(\theta \lambda +2)};{\mu }_3^{{}^{\prime }}=\frac{6(\lambda \theta +20)}{{\theta }^3(\theta \lambda +2)};{\mu }_4^{{}^{\prime }}=\frac{24(\lambda \theta +30)}{{\theta }^4(\theta \lambda +2)}.$$

(8)

3.2. Variance of the TPCJD

In this subsection, the variance of the TPCJD is given by

$${\displaystyle {\sigma }^2={\mu }_2^{{}^{\prime }}-{\left({\mu }_1^{{}^{\prime }}\right)}^2=\frac{{\lambda }^2{\theta }^2+16\theta \lambda +12}{{\theta }^2{\left(\theta \lambda +2\right)}^2}.}$$

(9)

The third and fourth central moments are respectively

$$\begin{array}{cc}\hfill {\mu }_3& {\displaystyle =\mu {{}_3}^{{}^{\prime }}-3\mu {{}_2}^{{}^{\prime }}\mu {{}_1}^{{}^{\prime }}+2\mu {{}_1}^{{}^{\prime }}{}^3=\frac{2{\lambda }^3\theta {}^3+60{\lambda }^2\theta {}^2+72\lambda \theta +48}{\theta {}^3\left(\theta \lambda +2\right){}^3},}\hfill \\ \hfill {\mu }_4& =\mu {{}_4}^{{}^{\prime }}-4\mu {{}_3}^{{}^{\prime }}\mu +6\mu {{}_2}^{{}^{\prime }}{\mu }^2-3{\mu }^4=\frac{9\lambda {}^4\theta {}^4+384\lambda {}^3\theta {}^3+1224\lambda {}^2\theta {}^2-1728\lambda \theta +720}{\theta {}^4\left(\theta \lambda +2\right){}^4}\hfill \end{array}$$

(10)

The survival and hazard functions plots are shown in Figure 2.

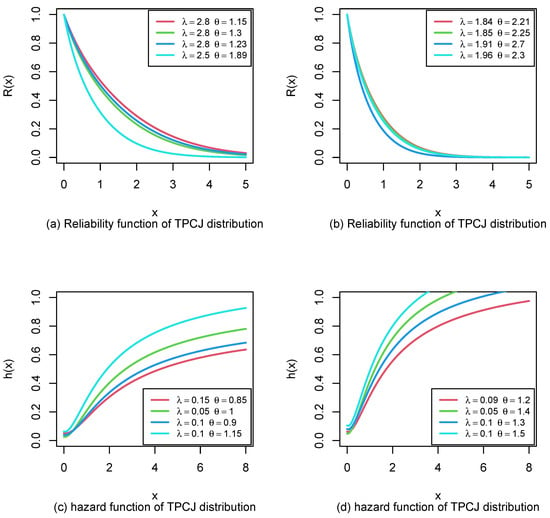
Figure 2. Reliability rate and hazard rate functions of the TPCJD.

Figure 2 provides useful insight into the behaviour of the TPCJD, having an increasing shape. Therefore, from Figure 2, it is possible to model data sets with increasing failure rates with the TPCJD.

3.3. Skewness, Kurtosis, Coefficient of Variation, and Index of Dispersion

The moment coefficient of skewness, coefficient of kurtosis, coefficient of variation, and index of dispersion of the TPCJ distributed random variable X are respectively given as

$$\gamma =\frac{{\mu }_3^{{}^{\prime }}-3\mu {\mu }_2^{{}^{\prime }}+2{\left(\mu \right)}^3}{{\sigma }^{2\frac{3}{2}}}=\frac{2{\lambda }^3{\theta }^3+60{\lambda }^2{\theta }^2+72\lambda \theta +48}{{\left({\lambda }^2{\theta }^2+16\theta \lambda +12\right)}^{\frac{3}{2}}},$$

(11)

$$\begin{array}{ccc}\hfill \beta & =& \frac{{\mu }_4^{{}^{\prime }}-4\mu {\mu }_3^{{}^{\prime }}+6{\left(\mu \right)}^2{\mu }_2^{{}^{\prime }}-3{\left(\mu \right)}^4}{{\sigma }^4}\hfill \\ \hfill & =& \frac{9^4}{\lambda }{\theta }^4+384{\lambda }^3{\theta }^3+1224{\lambda }^2{\theta }^2-1728\lambda \theta +720{\left({\lambda }^2{\theta }^2+16\theta \lambda +12\right)}^2,\hfill \end{array}$$

$$\zeta =\frac{\sigma }{\mu }\times \frac{100}{1}=\frac{\sqrt{{\lambda }^2{\theta }^2+16\theta \lambda +12}}{\lambda \theta +6}\times 100\%,$$

(12)

and

$$\eta =\frac{{\sigma }^2}{\mu }=\frac{{\lambda }^2{\theta }^2+16\theta \lambda +12}{{\theta }^3{\lambda }^2+8\lambda {\theta }^2+12\theta }.$$

(13)

3.4. Moment-Generating Function of TPCJD

The moment-generating function of a X ∼ TPCJ($\lambda ,\theta$) is given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_X\left(t\right)& =\mathit{E}\left({\mathrm{e}}^{tx}\right)={\int }_0^{\infty }{\mathrm{e}}^{tx}f\left(x\right)dx\hfill \\ \hfill & =\frac{{\theta }^2}{\lambda \theta +2}{\int }_0^{\infty }{\mathrm{e}}^{tx}(\lambda +\theta x^2){\mathrm{e}}^{-\theta x}dx\hfill \\ \hfill & =\frac{{\theta }^2}{\lambda \theta +2}\left[\lambda {\int }_0^{\infty }{\mathrm{e}}^{-(\theta -t)x}dx+\theta {\int }_0^{\infty }{x}^2{\mathrm{e}}^{-(\theta -t)x}\right]\hfill \\ \hfill & =\frac{{\theta }^2}{\lambda \theta +2}\left[\frac{\lambda \Gamma \left(1\right)}{(\theta -t)}+\frac{\theta \Gamma \left(3\right)}{{(\theta -t)}^3}\right]\hfill \\ \hfill & =\frac{{\theta }^2\left[\lambda {(\theta -t)}^{-1}+2\theta {(\theta -t)}^{-3}\right]}{\lambda \theta +2}.\hfill \end{array}\end{array}$$

(14)

The moment-generating function of the proposed TPCJD is defined only when $t<\theta$.

3.5. Characteristic Function of TPCJD

The characteristic function of a X ∼ TPCJ($\theta$) is given by

$${\varphi }_X\left(it\right)=\frac{{\theta }^2\left[\lambda {(\theta -it)}^{-1}+2\theta {(\theta -it)}^{-3}\right]}{\lambda \theta +2}.$$

(15)

3.6. The Order Statistics

The order statistics of the TPCJD are given by

$$f_{r:n}(x;\lambda ,\theta )=\frac{n!}{(r-1)!(n-r)!}{f}_{TPCJD}(x;\lambda ,\theta ){\left[F_{TPCJD}(x;\theta )\right]}^{r-1}{\left[1-F_{TPCJD}(x;\lambda ,\theta )\right]}^{n-r},$$

(16)

$\ni ,f_{TPCJD}(x;\lambda ,\theta )$ and $F_{TPCJD}(x;\lambda ,\theta )$ are defined in Equations (3) and (4), respectively. Hence, we have

$$\begin{array}{cc}\hfill f_{r:n}(x;\lambda ,\theta )=& \frac{n!}{(r-1)!(n-r)!}\frac{{\theta }^2}{\lambda \theta +2}\left(\lambda +\theta x^2\right){\mathrm{e}}^{-\theta x}{\left\{1-\frac{1}{\theta \lambda +2}({\theta }^2{x}^2+2\theta x+\theta \lambda +2){\mathrm{e}}^{-\theta x}\right\}}^{r-1}\hfill \\ & {\left\{\frac{1}{\theta \lambda +2}({\theta }^2{x}^2+2\theta x+\theta \lambda +2){\mathrm{e}}^{-\theta x}\right\}}^{n-r}.\hfill \end{array}$$

(17)

We obtain the PDF of the largest order statistics by substituting $r=n$ in Equation (17)

$$f_{n:n}(x;\lambda ,\theta )=\frac{n{\theta }^2}{\lambda \theta +2}\left(\lambda +\theta x^2\right){\mathrm{e}}^{-\theta x}{\left\{1-\frac{1}{\theta \lambda +2}({\theta }^2{x}^2+2\theta x+\theta \lambda +2){\mathrm{e}}^{-\theta x}\right\}}^{n-1}.$$

(18)

We obtain the PDF of the smallest order statistics by substituting $r=1$ in Equation (17)

$$f_{1:n}(x;\lambda ,\theta )=\frac{n{\theta }^2}{\lambda \theta +2}\left(\lambda +\theta x^2\right){\left\{\frac{1}{\theta \lambda +2}({\theta }^2{x}^2+2\theta x+\theta \lambda +2)\right\}}^{n-1}{\mathrm{e}}^{-\theta nx}.$$

(19)

3.7. Information Measure and the Behavior of TPCJD

Entropy is a measure of disorder in a system for a non-negative integer—say $\omega \ne 1$. For $X\sim$ TPCJD, the Rény entropy is obtained as:

$$R_{\omega }\left(x\right)=\underset{n\to \infty }{lim}\left({\mathit{I}}_{\omega }\left(f_n\right)-logn\right)=\frac{1}{1-\omega }log{\int }_0^{\infty }{f}^{\infty }\left(x\right)dx.$$

(20)

For $\omega \to 1$, we have the special case of Shannon Entropy $R_s\left(x\right)$

$$\begin{array}{cc}\hfill R_{\omega }\left(x\right)& =\frac{1}{1-\omega }log\left\{{\int }_0^{\infty }{\left\{\frac{{\theta }^2}{\lambda \theta +2}\left(\lambda +\theta x^2\right){\mathrm{e}}^{-\theta x}\right\}}^{\omega }dx\right\}\hfill \\ \hfill & =\frac{1}{(1-\omega )}log\left\{\frac{{\theta }^{2\omega }}{{(\theta +2)}^{\omega }}{\int }_0^{\infty }{\left((\lambda +\theta x^2){\mathrm{e}}^{-\theta x}\right)}^{\omega }dx\right\}\hfill \\ \hfill \mathrm{From} \mathrm{binomial} \mathrm{theorem},{(a+b)}^n& =\sum _{x=0}^n\left(\genfrac{}{}{0pt}{}{n}{x}\right)a^{n-x}{b}^x.\hfill \\ \hfill \mathrm{Therefore},& ={(\lambda +\theta x^2)}^{\omega }=\sum _{j=0}^{\omega }\left(\genfrac{}{}{0pt}{}{\omega }{j}\right){\lambda }^{\omega -j}{\left(\theta x^2\right)}^j\hfill \\ \hfill & =\frac{1}{(1-\omega )}log\left\{\frac{{\theta }^{2\omega }}{{(\theta +2)}^{\omega }}{\int }_0^{\infty }\sum _{j=0}^{\omega }\left(\genfrac{}{}{0pt}{}{\omega }{j}\right){\lambda }^{\omega -j}{\left(\theta x^2\right)}^j{\mathrm{e}}^{-\theta x\omega }dx\right\}\hfill \\ \hfill & =\frac{1}{(1-\omega )}log\left\{\frac{{\theta }^{2\omega }}{{(\theta +2)}^{\omega }}\sum _{j=0}^{\omega }\left(\genfrac{}{}{0pt}{}{\omega }{j}\right){\lambda }^{\omega -j}{\theta }^j{\int }_0^{\infty }{x}^{2j}{\mathrm{e}}^{-\theta x\omega }dx\right\}\hfill \\ \hfill & =\frac{1}{1-\omega }log\left\{{\theta }^{2\omega }{\left(\frac{\theta +\lambda }{\lambda \theta +2}\right)}^{\omega }\frac{\Gamma (2j+1)}{{\left(\theta \omega \right)}^{2j+1}}\right\}.\hfill \end{array}$$

(21)

The asymptotic behavior of the TPCJ distributed random variable is obtained by taking the limit of the PDF as $x\to 0$ and as $x\to \infty$.

$$\begin{array}{c}\hfill \underset{x\to 0}{lim}\frac{{\theta }^2}{\lambda \theta +2}\left(\lambda +\theta x^2\right){\mathrm{e}}^{-\theta x}=\frac{\lambda {\theta }^2}{\lambda \theta +2},\end{array}$$

(22)

and

$$\underset{x\to \infty }{lim}\frac{{\theta }^2}{\lambda \theta +2}\left(\lambda +\theta x^2\right){\mathrm{e}}^{-\theta x}=0.$$

(23)

3.8. The Odds Function

The Odds function is a reliability tool for modelling a data set that shows a non-monotone hazard rate. It is defined to be the ratio of the CDF to the survival function

$$O(x;\lambda ,\theta )=\frac{F_{TPCJ}(x;\lambda ,\theta )}{S_{TPCJD}(x;\lambda ,\theta )}$$

(24)

$$O_{TPCJ}(x;\lambda ,\theta )=\frac{1-\frac{1}{\theta \lambda +2}({\theta }^2{x}^2+2\theta x+\theta \lambda +2){\mathrm{e}}^{-\theta x}}{\left\{\frac{1}{\theta \lambda +2}({\theta }^2{x}^2+2\theta x+\theta \lambda +2){\mathrm{e}}^{-\theta x}\right\}}=\left(\theta \lambda +2\right){\left({\theta }^2{x}^2+2\theta x+\theta \lambda +2\right)}^{-1}{e}^{\theta x}-1.$$

(25)

3.9. The Stress–Strength Reliability Analysis

The reliability of a system is a function of its strength. Therefore, when a higher stress exacts on the system, the system collapses and hence is not reliable. Suppose $Y\sim$ TPCJD $({\theta }_1,{\lambda }_1)$ and $X\sim$ TPCJD $({\theta }_2,{\lambda }_2)$ are two independent continuous random variables representing the strength and stress of a system, respectively. Following that, the stress–strength reliability can be expressed as

$$\begin{array}{c}\hfill R=P(X<Y)=\underset{0}{\overset{\infty }{\int }}\underset{0}{\overset{x}{\int }}f(y,x)dydx,\end{array}$$

where $f(y,x)$ is the joint probability density function of Y and X. $f(y,x)=f\left(y\right)f\left(x\right)$ from basic knowledge of independence of two random variables

$$f\left(y\right)=\frac{{\theta }_1^2}{{\lambda }_1{\theta }_1+2}({\lambda }_1+{\theta }_1{y}^2){\mathrm{e}}^{-{\theta }_{1}y};\mathrm{and}f\left(x\right)=\frac{{\theta }_2^2}{{\lambda }_2{\theta }_2+2}({\lambda }_2+{\theta }_2{x}^2){\mathrm{e}}^{-{\theta }_{2}x}.$$

(26)

Therefore

$$\begin{array}{cc}\hfill R& =\frac{{\theta }_1{\theta }_2}{({\lambda }_1{\theta }_1+2)({\lambda }_2{\theta }_2+2)}\left\{\underset{0}{\overset{x}{\int }}({\lambda }_2+{\theta }_2{x}^2)e^{-{\theta }_{2}x}\underset{0}{\overset{\infty }{\int }}({\lambda }_1+{\theta }_1{y}^2)e^{-{\theta }_{1}y}dy\right\}dx\hfill \\ \hfill & =\frac{{\theta }_2}{{\theta }_1({\lambda }_2{\theta }_2+2)}\underset{0}{\overset{x}{\int }}({\lambda }_2+{\theta }_2{x}^2)e^{-{\theta }_{2}x}dx=\frac{{\lambda }_2{\theta }_2(e^{-{\theta }_{2}x}-1)+\gamma \left(3,{\theta }_{2}x\right)}{{\theta }_1{\theta }_2({\lambda }_2{\theta }_2+2)}.\hfill \end{array}$$

(27)

Figure 3 discusses stress–strength reliability plots with different parameters by using Equation (28).

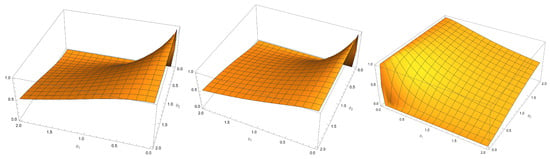
Figure 3. Stress–strength reliability plots with different parameters.

3.10. Maximum Likelihood Estimation of the TPCJD

Let $\left(x_1,x_2,\dots ,x_n\right)$ be n random samples drawn from TPCJD, then the likelihood function is given as

$$\begin{array}{cc}\hfill \ell \left(f_{TPCJ}(x;\lambda ,\theta )\right)& =\prod _{i=1}^n\frac{{\theta }^2}{\lambda \theta +2}(\lambda +\theta x_i^2){\mathrm{e}}^{-\theta x_i}\hfill \\ \hfill & =\frac{{\theta }^{2n}}{{(\lambda \theta +2)}^n}{\mathrm{e}}^{-\theta \sum x_i}\prod _{i=1}^n(\lambda +\theta x_i^2).\hfill \end{array}$$

(28)

Next, take the logarithm of ℓ and differentiate partially with respect to $\lambda$ and $\theta$ to obtain the following non-linear equations

$$\begin{array}{c}\hfill \psi =\ell (x;\theta )=2nln\theta -nln(\lambda \theta +2)-\theta \sum _{i=1}^n{x}_i+\sum _{i=1}^{n}ln(\lambda +\theta x_i^2),\end{array}$$

(29)

$$\begin{array}{c}\hfill \frac{\partial \psi }{\partial \widehat{\theta }}=\frac{2n}{\widehat{\theta }}-\frac{\lambda n}{\lambda \widehat{\theta }+2}-\sum x_i+\sum _{i=1}^n\left(\frac{x_i^2}{\lambda +\widehat{\theta }{x}_i^2}\right),\end{array}$$

(30)

$$\begin{array}{c}\hfill \frac{\partial \psi }{\partial \widehat{\lambda }}=-\frac{n\theta }{\widehat{\lambda \theta }+2}+\sum _{i=1}^n\left(\frac{1}{\widehat{\lambda }+\widehat{\theta }{x}_i^2}\right).\end{array}$$

(31)

Set $\frac{\partial \psi }{\partial \widehat{\theta }}=0$, which yields the following quadratic result

$$\frac{2n}{\widehat{\theta }}-\frac{n}{\widehat{\theta }+2}-\sum x_i+\sum _{i=1}^n\left(\frac{x_i^2}{1+\widehat{\theta }{x}_i^2}\right)=0.$$

(32)

Set $\frac{\partial \psi }{\partial \widehat{\lambda }}=0$, which yields the following quadratic result

$$\begin{array}{c}\hfill -\frac{n\theta }{\widehat{\lambda \theta }+2}+\sum _{i=1}^n\left(\frac{1}{\widehat{\lambda }+\widehat{\theta }{x}_i^2}\right)=0.\end{array}$$

(33)

Approximate Confidence Interval (ACI) of the MLEs

The approximate confidence intervals of the parameters are based on the asymptotic distribution of the maximum likelihood estimates of the u parameters $\Phi =(\theta ,\lambda )$. The asymptotic variances and covariances of $\theta$ and $\lambda$ are the elements of the inverse of the Fisher information matrix. Hence,

$$I_{ij}^{-1}(\theta ,\lambda )={\left[\begin{array}{cc}\left[2\right]\psi \theta & \psi \theta \lambda \\ \psi \lambda \theta & \left[2\right]\psi \lambda \end{array}\right]}^{-1}=\left[\begin{array}{cc}var\left(\widehat{\theta }\right)& cov(\widehat{\theta },\widehat{\lambda })\\ cov(\widehat{\lambda },\widehat{\theta })& var\left(\widehat{\lambda }\right),\end{array}\right]$$

(34)

where

$$\begin{array}{c}\hfill [2]\psi \theta =-\frac{2n}{{\theta }^2}-\frac{2\lambda }{{\left(\lambda \theta +2\right)}^2}-\sum _{i=1}^n{\left(\frac{x^2}{\lambda +\theta x^2}\right)}^2,\\ \hfill [2]\psi \lambda =\frac{n{\theta }^2}{{\left(\lambda \theta +2\right)}^2}-\sum _{i=1}^n\frac{1}{{\left(\lambda +\theta x^2\right)}^2},\\ \hfill \psi \theta \lambda =-\frac{2n}{{\left(\lambda \theta +2\right)}^2}-\sum _{i=1}^n{\left(\frac{x}{\lambda +\theta x^2}\right)}^2,\\ \hfill \psi \lambda \theta =-\frac{2\theta }{{\left(\lambda \theta +2\right)}^2}-\sum _{i=1}^n{\left(\frac{x}{\lambda +\theta x^2}\right)}^2.\end{array}$$

(35)

Therefore, a $100(1-\gamma )\%$ approximate confidence intervals for $\theta$ and $\lambda$ are, respectively,

$$\begin{array}{c}\hfill \widehat{\theta }\pm Z_{\frac{\gamma }{2}}\sqrt{var\left(\widehat{\theta }\right)};\widehat{\lambda }\pm Z_{\frac{\gamma }{2}}\sqrt{var\left(\widehat{\lambda }\right)},\end{array}$$

(36)

$\ni ,Z_{\frac{\gamma }{2}}$ follows the percentile standard normal distribution with right-tailed probability.

3.11. The Least Squares Estimation (LSE)

From Swain et al. [17], we can derive the LSEs of the parameters $\lambda$ and $\theta$ as follows:

$$E\left[F\left(x_{i:n}\right|\lambda ,\theta )\right]=\frac{i}{n+1}.$$

$$V\left[F\left(x_{i:n}\right|\lambda ,\theta )\right]=\frac{i(n-i+1)}{{(n+1)}^2(n+2)}.$$

Minimize the function $L(\lambda ,\theta )$ to obtain the estimates ${\widehat{\lambda }}_{LSE}$ and ${\widehat{\theta }}_{LSE}$ of the parameters $\lambda$ and $\theta$ as follows

$$L(\lambda ,\theta )=\underset{(\theta ,\lambda )}{argmin}\sum _{i=1}^n{\left[F\left(x_{i:n}\right|\lambda ,\theta )-\frac{i}{n+1}\right]}^2.$$

(37)

Resolving the following non-linear systems of equations produces the estimates

$$\begin{array}{cc}\hfill \sum _{i=1}^n{\left[F\left(x_{i:n}\right|\lambda ,\theta )-\frac{i}{n+1}\right]}^2{\Delta }_1\left(x_{i:n}\right|\lambda ,\theta )& =0.\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill \sum _{i=1}^n{\left[F\left(x_{i:n}\right|\lambda ,\theta )-\frac{i}{n+1}\right]}^2{\Delta }_2\left(x_{i:n}\right|\lambda ,\theta )& =0.\hfill \end{array}$$

(39)

where

$$\begin{array}{cc}\hfill {\Delta }_1\left(x_{i:n}\right|\lambda ,\theta )& =\left(\frac{-\theta \lambda -1}{\theta \lambda +2}\right)\left({\theta }^2{x}^2+2\theta x+\theta \lambda +2\right){\mathrm{e}}^{-\theta x}.\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill {\Delta }_2\left(x_{i:n}\right|\lambda ,\theta )& =\left(-2\theta x^2-2x-\theta \right)\left({\theta }^2{x}^2+2\theta x+\theta \lambda +2\right){\mathrm{e}}^{-\theta x}.\hfill \end{array}$$

(41)

More papers discussed these methods as [18,19].

3.12. The Weighted Least Squares Estimation (WLSE)

Minimize the function $W(\lambda ,\theta )$ to obtain the estimates ${\widehat{\lambda }}_{WLSE}$ and ${\widehat{\theta }}_{WLSE}$ of the proposed TPCJD parameters $\lambda$ and $\theta$ as follows

$$W(\lambda ,\theta )=\underset{(\lambda ,\theta )}{argmin}\sum _{i=1}^n\frac{{(n+1)}^2(n+2)}{i(n-i+1)}{\left[F\left(x_{i:n}\right|\lambda ,\theta )-\frac{i}{n+1}\right]}^2.$$

(42)

Resolving the following non-linear systems of equations produces the estimates

$$\begin{array}{cc}\hfill \sum _{i=1}^n\frac{{(n+1)}^2(n+2)}{i(n-i+1)}\left[F\left(x_{i:n}\right|\lambda ,\theta )-\frac{i}{n+1}\right]{\Delta }_1\left(x_{i:n}\right|\lambda ,\theta )& =0.\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill \sum _{i=1}^n\frac{{(n+1)}^2(n+2)}{i(n-i+1)}\left[F\left(x_{i:n}\right|\lambda ,\theta )-\frac{i}{n+1}\right]{\Delta }_2\left(x_{i:n}\right|\lambda ,\theta )& =0,\hfill \end{array}$$

(44)

${\Delta }_1(x.|\lambda ,\theta )$ and ${\Delta }_2(x.|\lambda ,\theta )$ are respectively defined in (40) and (41).

3.13. The Maximum Product Spacing Estimators (MPSE)

The Kullback–Leibler measure is approximated by the maximum product spacing method and, of course, it is a good alternative method to the maximum likelihood. Considering increasing ordered data, the maximum product spacing for the TPCJD can be derived as follows

$$Gs(\lambda ,\theta |data)={\left(\prod _{i=1}^{n+1}{D}_l(x_i,\lambda ,\theta )\right)}^{\frac{1}{n+1}},$$

(45)

where $D_l(x_i,\lambda ,\theta )=F(x_i;\lambda ,\theta )-F(x_{i-1};\lambda ,\theta )$, $i=1,2,3,\dots ,n$.

An alternative function to maximize in order to obtain the estimates is

$$H(\lambda ,\theta )=\frac{1}{n+1}\sum _{i=1}^{n+1}ln{D}_i(\lambda ,\theta ).$$

(46)

For the first derivative, we solved the function $H\left(\vartheta \right)$ and the associated nonlinear equations with respect to $\lambda$ and $\theta$. That is, $\frac{\partial H\left(\varphi \right)}{\partial \lambda }$ = 0 and $\frac{\partial H\left(\varphi \right)}{\partial \theta }$ = 0, where $\varphi =(\lambda ,\theta )$, the estimates of the parameters are derived.

3.14. Cramér-Von-Mises Estimation (CVME)

We minimized the function $C(\lambda ,\theta )$ to obtain the estimates ${\widehat{\lambda }}_{CVME}$, and ${\widehat{\theta }}_{CVME}$ of the TPCJD parameters $\lambda$, and $\theta$ as follows

$$C(\lambda ,\theta )=\underset{(\lambda ,\theta )}{argmin}\left\{\frac{1}{12n}+\sum _{i=1}^n{\left[F\left(x_{i:n}\right|\lambda ,\theta )-\frac{2i-1}{2n}\right]}^2\right\}.$$

(47)

Resolving the following non-linear systems of equations produces the estimates

$$\begin{array}{cc}\hfill \sum _{i=1}^n\left(F\left(x_{i:n}\right|\lambda ,\theta )-\frac{2i-1}{2n}\right){\Delta }_1\left(x_{i:n}\right|\lambda ,\theta )& =0\hfill \\ \hfill \sum _{i=1}^n\left(F\left(x_{i:n}\right|\lambda ,\theta )-\frac{2i-1}{2n}\right){\Delta }_2\left(x_{i:n}\right|\lambda ,\theta )& =0,\hfill \end{array}$$

(48)

${\Delta }_1(x.|\lambda ,\theta )$ and ${\Delta }_2(x.|\lambda ,\theta )$ are, respectively, defined in (40) and (41).

3.15. The Anderson–Darling Estimation (ADE)

We minimized the function $A(\lambda ,\theta )$ to obtain the estimates ${\widehat{\lambda }}_{ADE}$, and ${\widehat{\theta }}_{ADE}$ of the TPCJD parameters $\lambda$ and $\theta$ as follows

$$A(\lambda ,k,\theta )=\underset{(\lambda ,\theta )}{argmin}\sum _{i=1}^n(2i-1)\left\{lnF\left(x_{i:n}\right|\lambda ,\theta )+ln\left[1-F\left(x_{n+1-i:n}\right|\lambda ,\theta )\right]\right\}.$$

(49)

Resolving the following non-linear systems of equations produces the estimates

$$\begin{array}{cc}\hfill \sum _{i=1}^n(2i-1)\left[\frac{{\Delta }_1\left(x_{i:n}\right|\lambda ,\theta )}{F\left(x_{i:n}\right|\lambda ,\theta )}-\frac{{\Delta }_1\left(x_{n+1-i:n}\right|\lambda ,\theta )}{1-F\left(x_{n+1-i:n}\right|\lambda ,\theta )}\right]& =0,\hfill \\ \hfill \sum _{i=1}^n(2i-1)\left[\frac{{\Delta }_2\left(x_{i:n}\right|\lambda ,\theta )}{F\left(x_{i:n}\right|\lambda ,\theta )}-\frac{{\Delta }_2\left(x_{n+1-i:n}\right|\lambda ,\theta )}{1-F\left(x_{n+1-i:n}\right|\lambda ,\theta )}\right]& =0,\hfill \end{array}$$

(50)

where ${\Delta }_1(x.|\lambda ,\theta )$ and ${\Delta }_2(x.|\lambda ,\theta )$ are as defined in (40) and (41), respectively.

3.16. The Right-Tailed Anderson–Darling Estimation (RTADE)

We minimized the function $R(\lambda ,\theta )$ to obtain the estimates ${\widehat{\lambda }}_{RTADE}$ and ${\widehat{\theta }}_{RTADE}$ of the TPCJD parameters $\lambda$ and $\theta$ as follows

$$R(\lambda ,\theta )=\underset{(\lambda ,\theta )}{argmin}\left\{\frac{n}{2}-2\sum _{i=1}^{n}F\left(x_{i:n}\right|\lambda ,\theta )-\frac{1}{n}\sum _{i=1}^n(2i-1)ln\left[1-F\left(x_{n+1-i:n}\right|\lambda ,\theta )\right]\right\}.$$

(51)

Resolving the following non-linear systems of equations produces the estimates

$$\begin{array}{cc}\hfill -2\sum _{i=1}^n\frac{{\Delta }_1\left(x_{i:n}\right|\lambda ,\theta )}{F\left(x_{i:n}\right|\lambda ,\theta )}+\frac{1}{n}\sum _{i=1}^n(2i-1)\left[\frac{{\Delta }_1\left(x_{n+1-i:n}\right|\lambda ,\theta )}{1-F\left(x_{n+1-i:n}\right|\lambda ,\theta )}\right]& =0,\hfill \\ \hfill -2\sum _{i=1}^n\frac{{\Delta }_2\left(x_{i:n}\right|\lambda ,\theta )}{F\left(x_{i:n}\right|\lambda ,\theta )}+\frac{1}{n}\sum _{i=1}^n(2i-1)\left[\frac{{\Delta }_2\left(x_{n+1-i:n}\right|\lambda ,\theta )}{1-F\left(x_{n+1-i:n}\right|\lambda ,\theta )}\right]& =0,\hfill \end{array}$$

(52)

${\Delta }_1(x.|\lambda ,\theta )$ and ${\Delta }_2(x.|\lambda ,\theta )$ are respectively defined in (40) and (41). We obtained the estimates in (32), (33), (43), (44), (46), (48), (50), and (52) by iterative algorithm in R.

3.17. The Tail Analysis of TPCJD

In this subsection, we zoomed into the tails of the TPCJD to investigate characteristics. Firstly, the ratio of the TPCJD’s survival function to that of the exponential survival function was investigated to ascertain the tail weight. This will give an idea of the speed of decay of the TPCJD’s survival function.

Secondly, the mean residual life function (or the mean excess loss function) was derived. This will provide the expected loss over a specified threshold, conditioned on the event that the threshold has already been exceeded.

Thirdly, we determined the maximum domain of attraction of TPCJD. Given that the extreme value theorem provides three extreme types (Gumbel, Frechet, and Weibull), the goal here is to ascertain which of the types the TPCJD tail falls into.

3.17.1. Comparing Tail Weights

The comparing tail weights are given by

$$\begin{array}{cc}\hfill \frac{TPCJ{D}_{survival}}{Exponentia{l}_{survival}}& =\frac{\frac{1}{\theta \lambda +2}\left({\theta }^2{x}^2+2\theta x+\lambda \theta +2\right){\mathrm{e}}^{-\theta x}}{{\mathrm{e}}^{-\theta x}}\hfill \\ \hfill & =\frac{{\theta }^2{x}^2+2\theta x+\lambda \theta +2}{\theta \lambda +2}.\hfill \end{array}$$

(53)

Dividing through by $x^2$ and taking limit as $x\to \infty$

$$\frac{{\theta }^2{x}^2+2\theta x+\lambda \theta +2}{\theta \lambda +2}\to \infty asx\to \infty .$$

(54)

The distribution of the TPCJD has a heavier tail than that of the exponential distribution.

3.17.2. The Mean Residual Life Function

The mean residual life function $m\left(x\right)$ is obtained as follows

$$m\left(x\right)=\frac{1}{1-F\left(x\right)}{\int }_x^{\infty }[1-F\left(t\right)]dt.$$

(55)

Substituting into the formula, we obtain

$$\begin{array}{cc}\hfill m\left(x\right)& =\frac{1}{1-\left\{1-\frac{({\theta }^2{x}^2+2\theta x+\theta \lambda +2){\mathrm{e}}^{-\theta x}}{\lambda \theta +2}\right\}}{\int }_x^{\infty }1-\left\{1-\frac{({\theta }^2{t}^2+2\theta t+\theta \lambda +2){\mathrm{e}}^{-\theta t}}{\lambda \theta +2}\right\}dt\hfill \\ \hfill & =\frac{\lambda \theta +2}{({\theta }^2{x}^2+2\theta x+\theta \lambda +2){\mathrm{e}}^{-\theta x}}{\int }_x^{\infty }\frac{({\theta }^2{t}^2+2\theta t+\theta \lambda +2){\mathrm{e}}^{-\theta t}}{\theta \lambda +2}dt\hfill \\ \hfill & =\frac{1}{({\theta }^2{x}^2+2\theta x+\theta \lambda +2){\mathrm{e}}^{-\theta x}}\left[{\int }_x^{\infty }{\theta }^2{t}^2{\mathrm{e}}^{-\theta t}dt+{\int }_x^{\infty }2\theta t{\mathrm{e}}^{-\theta t}dt+{\int }_x^{\infty }\theta \lambda {\mathrm{e}}^{-\theta t}dt+2{\int }_x^{\infty }{\mathrm{e}}^{-\theta t}dt\right]\hfill \\ \hfill & m\left(x\right)=\frac{{\mathrm{e}}^{-\theta x}[\theta t^2-2x-\frac{2}{\theta }]+2{\mathrm{e}}^{-\theta x}[x+\frac{1}{\theta }]+\lambda {\mathrm{e}}^{-\theta x}+\frac{2}{\theta }{\mathrm{e}}^{-\theta x}}{[{\theta }^2{x}^2+2\theta x+\theta x+2]{\mathrm{e}}^{-\theta x}}=\frac{\theta t^2+\lambda +\frac{2}{\theta }}{{\theta }^2{x}^2+2\theta x+\theta \lambda +2}.\hfill \end{array}$$

(56)

3.17.3. The Domain of Attraction

For each of the Gumbel, Frechet, and Weibull distributions, known as the extreme value distributions, we briefly list the necessary and sufficient requirements that must be met for a distribution function $F(.)$ to be a member of the maximum domain of attraction $\left(D\right)$.

Theorem 1.

Let the right extremity of F be given by $w\left(F\right)$

(1)

$F\in D\left(Gumbel\right).\iff k\left(t\right)>0\ni {lim}_{t\to w\left(F\right)}\frac{1-F(t+K(t)x}{1-F\left(t\right)}=exp(-x),x\ge 0,w\left(F\right)\le \infty .$

(2)

$F\in D\left(Frechet\right).\iff w\left(F\right)=\infty$ and ${lim}_{t\to \infty }\frac{1-F\left(tx\right)}{1-F\left(t\right)}=x^{-\alpha },x\ge 0.$

(3)

$F\in D\left(Weibull\right).\iff w\left(F\right)<\infty$ and ${lim}_{t\to 0}\frac{1-F\left(w\right(F)-tx}{1-F\left(w\right(F)-t)}=x^{\alpha },x\ge 0.$

By using the probability density function and distribution function in Equations (3) and (4), we call $\lambda$ the shape parameter and $\theta$ the shape parameter of the TPCJD, respectively, and we can determine the domain of attraction for the TPCJD.

Making use of the necessary and sufficient conditions for Gumbel $F\in D\left(Gumbel\right).\iff k\left(t\right)>0\ni {lim}_{t\to w\left(F\right)}\frac{1-F(t+K(t)x}{1-F\left(t\right)}=exp(-x),x\ge 0,w\left(F\right)\le \infty$

Therefore, setting $k=\frac{1}{\theta }$ and $w\left(F\right)=\infty$

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim}\frac{1-F(t+\frac{x}{\theta }}{1-F\left(t\right)}& =\underset{t\to w\left(F\right)}{lim}\frac{1-\left(1-\frac{\left({\theta }^2{(t+\frac{x}{\theta })}^2+2\theta (t+\frac{x}{\theta })+\theta \lambda +2\right){\mathrm{e}}^{-\theta (\theta +\frac{x}{\theta })}}{\theta \lambda +2}\right)}{1-\left(1-\frac{\left({\theta }^2{t}^2+2\theta t+\theta \lambda +2\right){\mathrm{e}}^{-\theta t}}{\theta \lambda +2}\right)}\hfill \\ \hfill & \underset{t\to \infty }{lim}\frac{\left({\theta }^2{t}^2+2\theta tx+2x^2+2\theta t+2x+\theta \lambda +2\right){\mathrm{e}}^{-\theta (t+\frac{x}{\theta })}}{\left[{\theta }^2{t}^2+2\theta t+\theta \lambda +2\right]{\mathrm{e}}^{-\theta t}}.\hfill \end{array}$$

(57)

Dividing through by $t^2$ and taking limit as $t\to \infty$

$$\frac{{\theta }^2{\mathrm{e}}^{-\theta (t+\frac{x}{\theta })}}{{\theta }^2{\mathrm{e}}^{-\theta t}}={\mathrm{e}}^{-x}.$$

(58)

As a result, the TPCJD falls under the Gumbel domain of attraction. The Gumbel domain of attraction is characterized by distributions with a significant range of tail heaviness and either infinite or finite upper endpoints.

4. Single Acceptance Sampling Plan (SASP) for TPCJD

Assume that the lifetime of a good is determined by the TPCJD, whose parameters are $(\lambda ,\theta )$, as stated in Equation (3), and that the producer’s declared industry standard for the lifespan of units is symbolized by $M_0$. The primary objective is to decide whether or not to accept the proposed lot given that the actual median life cycle of the units, m, is longer than the suggested lifetime, $M_0$. The test must be completed by the time provided by $T_0$ in order to count the number of failures, which is typical practice in life testing.

Given the evidence that $M\ge M_0$, given a probability of at least ${\alpha }^{*}$ (consumer’s risk), utilizing a single acceptance sampling plan, Singh and Tripathi [20] gave us some recommendations on how to accept the suggested lot. Additionally, Maya et al. [21] developed a lifetime acceptance sampling plan and provided the HEB distribution. The experiment is conducted during a time period of $T_0=a{M}_0$, which is longer than the claimed median lifetime with any positive constant a. Steps:

• Select a random sample of n units from the proposed lot.
• Run the following evaluation for $T_0$ time units:
  If c or fewer units (the acceptance number) fail over the course of the experiment, accept the entire lot; if not, reject the entire lot.

We note that the suggested sampling strategy is provided by and that the likelihood of accepting a lot takes into account suitable large lots to aid in the application of the binomial distribution.

$$L\left(p\right)=\sum _{i=0}^c\left(\begin{array}{c}n\hfill \\ i\hfill \end{array}\right)p^i{(1-p)}^{n-i},i=1,2,\dots ,n,$$

(59)

According to Equaiton (4), $\ni ,p$ is defined as $p=F_{TPCJ}\left(T_0;\lambda ,\theta \right)$. The function $L\left(p\right)$ is used to represent the operational characteristic function of the sampling plan as well as the acceptance probability of the lot as a function of the failure probability. Using $T_0=a{M}_0$, $p_0$ can also be represented as follows:

$$p_0=F_{TPCJ}(T_0=a{M}_0;\lambda ,\theta )=1-\frac{1}{\theta \lambda +2}({\theta }^2{T}_0^2+2\theta T_0+\theta \lambda +2){\mathrm{e}}^{-\theta T_0}.$$

(60)

Now, the problem is to determine for given values of ${\alpha }^{*}\left(0<{\alpha }^{*}<1\right),M_0$ and c, the smallest positive integer n such that

$$L\left(p_0\right)=\sum _{i=0}^c\left(\begin{array}{c}n\hfill \\ i,\hfill \end{array}\right)p_0^i{\left(1-p_0\right)}^{n-i}\le 1-{\alpha }^{*},$$

(61)

where $p_0$ is given by Equation (60).

We make the following assumptions for the operating characteristic probability and the minimal values of n, which satisfies the inequality in Equation (61) as contained in Table 1, Table 2, Table 3 and Table 4:

Table 1. The SASP for the TPCJD with parameter: $\theta =0.20$ for different values of $\lambda$.

$\mathit{\alpha }$*	c	$\mathit{a}=0.1$		$\mathit{a}=0.2$		$\mathit{a}=0.4$		$\mathit{a}=0.8$		$\mathit{a}=1$
		$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$
$\lambda =0.15$
0.25	0	49	0.75124	13	0.76046	3	0.81034	1	1	1	1
	2	291	0.75137	77	0.75423	18	0.76268	5	0.86067	4	0.87500
	4	568	0.75034	150	0.75264	35	0.75164	10	0.80543	8	0.77344
	8	1152	0.75035	304	0.75190	70	0.75151	20	0.77993	15	0.78802
	10	1452	0.75037	383	0.75194	88	0.75095	25	0.77799	19	0.75966
0.75	0	233	0.25096	61	0.25431	14	0.25488	4	0.25836	2	0.50000
	2	659	0.25082	173	0.25280	39	0.25487	10	0.30751	7	0.34375
	4	1055	0.25069	277	0.25268	62	0.25914	17	0.25304	12	0.27441
	8	1817	0.25046	478	0.25084	107	0.25796	29	0.26007	21	0.25172
	10	2190	0.25046	576	0.25109	129	0.25821	35	0.25863	25	0.27063
0.95	0	503	0.05022	132	0.05032	29	0.05264	7	0.06675	5	0.06250
	2	1058	0.05012	277	0.05075	61	0.05352	16	0.05028	11	0.05469
	4	1539	0.05002	404	0.05009	90	0.05026	23	0.05612	16	0.05923
	8	2427	0.05005	637	0.05032	142	0.05089	37	0.05293	26	0.05388
	10	2852	0.05007	749	0.05017	167	0.05096	43	0.06059	30	0.06802
$\lambda =0.20$
0.25	0	41	0.75452	12	0.76285	3	0.80668	1	1	1	1
	2	247	0.75056	72	0.75130	18	0.75314	5	0.85996	4	0.87500
	4	481	0.75050	139	0.75409	34	0.75812	10	0.80417	8	0.77344
	8	976	0.75002	282	0.75275	68	0.76011	20	0.77799	15	0.78802
	10	1230	0.75009	356	0.75085	86	0.75429	25	0.77582	19	0.75966
0.75	0	197	0.25153	57	0.25207	13	0.27555	4	0.25751	2	0.50000
	2	558	0.25080	161	0.25119	38	0.25856	10	0.30596	7	0.34375
	4	894	0.25004	257	0.25295	61	0.25591	17	0.25118	12	0.27441
	8	1539	0.25005	443	0.25230	105	0.25646	29	0.25759	21	0.25172
	10	1854	0.25056	535	0.25021	127	0.25272	35	0.25591	25	0.27063
0.95	0	426	0.05015	122	0.05092	28	0.05501	7	0.06631	5	0.06250
	2	896	0.05002	257	0.05077	60	0.05252	15	0.06899	11	0.05469
	4	1302	0.05020	374	0.05075	88	0.05083	23	0.05537	16	0.05923
	8	2054	0.05016	591	0.05037	139	0.05121	37	0.05201	26	0.05388
	10	2414	0.05014	695	0.05018	163	0.05254	43	0.05949	30	0.06802

Table 2. The SASP for the TPCJD with parameters: $\theta =0.30$ for different values of $\lambda$.

$\mathit{\alpha }$*	c		$\mathit{a}=0.1$		$\mathit{a}=0.2$		$\mathit{a}=0.4$		$\mathit{a}=0.8$		$\mathit{a}=1$
			$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$
$\lambda =0.15$
0.25	0		27	0.75694	10	0.75867	3	0.79430	1	1	1	1
	2		163	0.75079	58	0.75240	17	0.75099	5	0.85753	4	0.87500
	4		317	0.75104	112	0.75444	32	0.75653	10	0.79982	8	0.77344
	8		643	0.75059	227	0.75326	64	0.75693	20	0.77131	15	0.78802
	10		810	0.75100	286	0.75316	80	0.76251	25	0.76829	19	0.75966
0.75	0		130	0.25117	46	0.25134	13	0.25113	4	0.25461	3	0.25000
	2		368	0.25007	129	0.25356	36	0.25115	10	0.30069	7	0.34375
	4		588	0.25110	207	0.25176	57	0.25747	16	0.30450	12	0.27441
	8		1013	0.25062	357	0.25009	98	0.25968	28	0.29459	21	0.25172
	10		1221	0.25058	430	0.25075	119	0.25157	34	0.28766	25	0.27063
0.95	0		280	0.05038	98	0.05096	27	0.05009	7	0.06483	5	0.06250
	2		589	0.05033	207	0.05018	56	0.05299	15	0.06663	11	0.05469
	4		857	0.05022	301	0.05027	82	0.05190	23	0.05289	16	0.05923
	8		1352	0.05020	475	0.05030	130	0.05123	36	0.06152	26	0.05388
	10		1589	0.05019	558	0.05054	153	0.05105	43	0.05585	30	0.06802
$\lambda =0.20$
0.25	0		24	0.75487	9	0.76668	3	0.78919	1	1	1	1
	2		143	0.75091	54	0.75018	16	0.76950	5	0.85651	4	0.87500
	4		278	0.75119	104	0.75274	31	0.76114	10	0.79798	8	0.77344
	8		564	0.75041	210	0.75386	62	0.76283	20	0.76848	15	0.78802
	10		711	0.75004	265	0.75218	78	0.76237	25	0.76510	19	0.75966
0.75	0		114	0.25118	42	0.25624	12	0.27195	4	0.25341	3	0.25000
	2		322	0.25122	120	0.25027	35	0.25250	10	0.29850	7	0.34375
	4		516	0.25029	191	0.25382	56	0.25062	16	0.30167	12	0.27441
	8		888	0.25062	330	0.25092	96	0.25369	28	0.29087	21	0.25172
	10		1070	0.25093	398	0.25018	116	0.25081	34	0.28361	25	0.27063
0.95	0		246	0.05001	91	0.05034	26	0.05185	7	0.06422	5	0.06250
	2		516	0.05042	191	0.05071	55	0.05088	15	0.06566	11	0.05469
	4		751	0.05026	278	0.05065	80	0.05133	23	0.05188	16	0.05923
	8		1185	0.05019	439	0.05056	127	0.05002	36	0.06007	26	0.05388
	10		1393	0.05010	516	0.05060	149	0.05105	43	0.05438	30	0.06802

Table 3. The SASP for the TPCJD with parameters: $\theta =0.40$ for different values of $\lambda$.

$\mathit{\alpha }$*	c		$\mathit{a}=0.1$		$\mathit{a}=0.2$		$\mathit{a}=0.4$		$\mathit{a}=0.8$		$\mathit{a}=1$
			$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$
$\lambda =0.15$
0.25	0		32	0.75278	11	0.75491	3	0.79952	1	1	1	1
	2		190	0.75135	63	0.75330	17	0.76393	5	0.85857	4	0.87500
	4		370	0.75123	122	0.75427	33	0.75338	10	0.80167	8	0.77344
	8		751	0.75048	248	0.75078	66	0.75303	20	0.77416	15	0.78802
	10		946	0.75099	312	0.75193	83	0.75206	25	0.77150	19	0.75966
0.75	0		152	0.25076	50	0.25216	13	0.26121	4	0.25584	2	0.50000
	2		429	0.25134	141	0.25190	37	0.25108	10	0.30292	7	0.34375
	4		687	0.25104	226	0.25059	59	0.25168	16	0.30737	12	0.27441
	8		1184	0.25019	389	0.25060	101	0.25670	29	0.25274	21	0.25172
	10		1427	0.25020	469	0.25022	122	0.25454	35	0.25059	25	0.27063
0.95	0		328	0.05001	107	0.05078	27	0.05455	7	0.06546	5	0.06250
	2		689	0.05009	225	0.05096	58	0.05121	15	0.06762	11	0.05469
	4		1002	0.05006	328	0.05050	84	0.05304	23	0.05393	16	0.05923
	8		1580	0.05016	518	0.05029	134	0.05026	37	0.05025	26	0.05388
	10		1857	0.05013	609	0.05021	157	0.05187	43	0.05738	30	0.06802
$\lambda =0.20$
0.25	0		26	0.75542	10	0.75291	3	0.79258	1	1	1	1
	2		155	0.75286	56	0.75655	16	0.77731	5	0.85719	4	0.87500
	4		303	0.75053	109	0.75487	32	0.75077	10	0.79920	8	0.77344
	8		614	0.75066	221	0.75343	63	0.76353	20	0.77036	15	0.78802
	10		774	0.75040	279	0.75135	80	0.75362	25	0.76722	19	0.75966
0.75	0		124	0.25159	44	0.25770	12	0.27844	4	0.25421	2	0.50000
	2		351	0.25075	126	0.25158	35	0.26356	10	0.29995	7	0.34375
	4		562	0.25035	201	0.25379	57	0.25029	16	0.30355	12	0.27441
	8		967	0.25090	347	0.25173	98	0.25016	28	0.29334	21	0.25172
	10		1166	0.25046	418	0.25243	118	0.25108	34	0.28630	25	0.27063
0.95	0		268	0.05001	95	0.05160	26	0.05471	7	0.06462	5	0.06250
	2		563	0.05007	201	0.05076	56	0.05078	15	0.06630	11	0.05469
	4		818	0.05031	293	0.05028	81	0.05290	23	0.05255	16	0.05923
	8		1291	0.05017	462	0.05061	129	0.05075	36	0.06103	26	0.05388
	10		1517	0.05023	543	0.05068	152	0.05005	43	0.05536	30	0.06802

Table 4. The SASP for the TPCJD with parameters: $\theta =0.50$ for different values of $\lambda$.

$\mathit{\alpha }$*	c		$\mathit{a}=0.1$		$\mathit{a}=0.2$		$\mathit{a}=0.4$		$\mathit{a}=0.8$		$\mathit{a}=1$
			$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{p}}_{\mathbf{0}}\mathbf{\right)}$
$\lambda =0.15$
0.25	0		19	0.75465	8	0.76158	3	0.77770	1	1	1	1
	2		112	0.75189	46	0.75416	15	0.77568	5	0.85416	4	0.87500
	4		218	0.75118	89	0.75426	29	0.76969	10	0.79377	8	0.77344
	8		442	0.75048	180	0.75378	59	0.75791	20	0.76198	15	0.78803
	10		557	0.75036	227	0.75252	74	0.75981	25	0.75775	19	0.75966
0.75	0		89	0.25254	36	0.25619	12	0.25089	4	0.25068	3	0.25000
	2		252	0.25165	102	0.25457	33	0.25402	10	0.29354	7	0.34375
	4		404	0.25042	164	0.25129	52	0.26493	16	0.29529	12	0.27441
	8		695	0.25112	282	0.25240	91	0.25018	28	0.28251	21	0.25172
	10		838	0.25073	340	0.25216	109	0.25731	34	0.27449	25	0.27063
0.95	0		192	0.05044	77	0.05197	24	0.05551	7	0.06284	5	0.06250
	2		404	0.05033	163	0.05117	52	0.05047	15	0.06350	11	0.05469
	4		588	0.05015	238	0.05032	75	0.05342	22	0.06585	16	0.05923
	8		928	0.05001	376	0.05001	119	0.05292	36	0.05688	26	0.05388
	10		1090	0.05024	441	0.05089	141	0.05008	43	0.05115	30	0.06802
$\lambda =0.20$
0.25	0		17	0.75009	7	0.77341	3	0.76986	1	1	1	1
	2		98	0.75054	42	0.75393	15	0.75847	5	0.85252	4	0.87500
	4		190	0.75146	81	0.75538	28	0.76963	10	0.79081	8	0.77344
	8		385	0.75107	164	0.75382	57	0.75652	20	0.75741	15	0.78803
	10		485	0.75128	207	0.75158	72	0.75066	25	0.75259	19	0.75966
0.75	0		78	0.25061	33	0.25401	11	0.27043	3	0.39557	3	0.25000
	2		220	0.25038	93	0.25364	32	0.25001	10	0.29012	7	0.34375
	4		352	0.25027	149	0.25278	51	0.25035	16	0.29090	12	0.27441
	8		606	0.25012	257	0.25112	87	0.25853	28	0.27678	21	0.25172
	10		730	0.25068	310	0.25022	105	0.25750	34	0.26826	25	0.27063
0.95	0		167	0.05062	70	0.05209	23	0.05630	7	0.06190	5	0.06250
	2		352	0.05020	149	0.05003	50	0.05077	15	0.06203	11	0.05469
	4		512	0.05018	216	0.05102	73	0.05013	22	0.06399	16	0.05923
	8		808	0.05008	342	0.05010	115	0.05151	36	0.05475	26	0.05388
	10		949	0.05034	402	0.05012	135	0.05250	42	0.06077	30	0.06802

For the operational characteristic probability and the minimal values of n that satisfy the inequality in Equation (61), as shown in Table 1, Table 2, Table 3 and Table 4: we make the following assumptions:

• The risk ${\alpha }^{*}$ for the consumer was set at $0.30,0.60$, and $0.95$.
• The acceptance number c assumes the following values $0,2,4,8,$ and 10.
• The constant a takes the following values $0.10,0.25,0.50,$ and $0.75$. If $a=1$, thus $T_0$ is the median life time $M_0=0.5\forall (\lambda ,\theta$).
• After trial and error, the following values are suitable for the parameters $(\lambda ,\theta )$ of the TPCJD:

  $$\lambda =(0.15,0.25,0.30,0.50)\mathrm{and}\theta =(0.20,0.30,0.40,0.50).$$

From Table 1, Table 2, Table 3 and Table 4, we make the following inference:

• As ${\alpha }^{*}$, c, and the required sample size n increase, the $L\left(p_0\right)$ decreases.
• The needed sample size n reduces as a rises, whereas $L\left(p_0\right)$ rises.
• The needed sample size n increases and $L\left(p_0\right)$ is lowers as $\lambda$ increases and $\theta$ remains constant.
• The needed sample size n grows and $L\left(p_0\right)$ shrinks as $\theta$ increases and fixed $\lambda$ remains constant.

Finally, for all scenarios, we verified that $L\left(p_0\right)\le 1-{\alpha }^{*}$. Also, for $a=1,p_0=0.5$ as $T_0=M_0$, hence in all results $\left(n,L\left(p_0\right)\right)$, for any values of the parameters $(\lambda ,\theta )$ considered are the same.

5. The Bayesian Estimation of the TPCJD Parameters

The parameters of the TPCJD’s Bayesian Estimates (BE) are derived in this section. There are three types of loss functions used: squared error, LINEX, and generalized entropy loss functions. The following independent gamma priors are utilized for $\lambda$ and $\theta$:

$$\begin{array}{c}\hfill \begin{array}{cc}{\pi }_1\left(\lambda \right)\propto {\lambda }^{s_1-1}{\mathrm{e}}^{-q_1\lambda }\hfill & \lambda >0, s_1>0, q_1>0,\hfill \\ {\pi }_2\left(\theta \right)\propto {\theta }^{s_2-1}{\mathrm{e}}^{-q_2\theta }\hfill & \theta >0, s_2>0, q_2>0.\hfill \end{array}\end{array}$$

(62)

To represent the previous knowledge about the unknown parameters, the hyper-parameters $s_j,q_j,j=1,2$ were used. The following is how we arrived at the joint prior for the parameter $\varphi =(\lambda ,\theta )$.

$$\begin{array}{cc}\hfill & \pi \left(\varphi \right)={\pi }_1\left(\lambda \right){\pi }_2\left(\theta \right),\hfill \\ \hfill & \pi \left(\varphi \right)\propto {\lambda }^{s_1-1}{\theta }^{s_2-1}{\mathrm{e}}^{\left\{-q_1\lambda -q_2\theta \right\}}.\hfill \end{array}$$

(63)

The associated posterior density for the observed data $\mathbf{x}=\left(x_1,x_2,\dots ,x_n\right)$ is given by:

$$\pi (\varphi \mid \mathbf{x})=\frac{\pi \left(\varphi \right)\ell \left(\varphi \right)}{{\int }_{\varphi }\pi \left(\varphi \right)\ell \left(\varphi \right)d\varphi },$$

Which implies that the posterior density function is:

$$\begin{array}{ccc}\hfill \pi (\varphi \mid \mathbf{x})& \propto & \frac{{\theta }^{2n+s_2-1}{\lambda }^{s_1-1}}{{(\lambda \theta +2)}^n}{\mathrm{e}}^{-\theta {\sum }_{i=1}^n{x}_i-q_1\lambda -q_2\theta }\prod _{i=1}^n(\lambda +\theta x^2).\hfill \end{array}$$

(64)

The setting, the nature of the issue, and the decision-maker’s preferences on errors all affect the choice of loss function in Bayesian inference. While generalized entropy and linear-exponential losses offer more flexibility to address cases where different types of errors have variable effects, squared error loss is a popular and simple option. The relative costs or preferences associated with various outcomes are frequently taken into account while selecting a loss function that is compatible with real-world applications such as regression, risk assessment, and quality control for the squared error loss (SEL) function, medical diagnosis and finance for Linear-exponential loss (LINEX), economics and finance, environmental decision-making, and machine learning for the generalized entropy loss function. Given any function, such as $l\left(\varphi \right)$, under the squared error loss (SEL) function, the Bayes estimator is given by

$${\widehat{\varphi }}_{B{E}_{SEL}}=E\left[l\left(\varphi \right)|\mathbf{x}\right]={\int }_{\varphi }l\left(\varphi \right)\pi \left(\varphi \right|x)d\varphi .$$

(65)

In some cases, a proposed LINEX loss can be made instead of the SEL provided by

$$\left(l\left(\varphi \right),\widehat{l}\left(\varphi \right)\right)={\mathrm{e}}^{\left\{\widehat{l}\left(\varphi \right)-l\left(\varphi \right)\right\}}-v\left(\widehat{l}\left(\varphi \right)-l\left(\varphi \right)\right)-1.$$

$\ni ,v\ne 0$ is a shape parameter. $v>1$ indicates that an underestimation is milder than an overestimation and the reverse is the case for $v<0$. Moreover, when $v\to 0$, the SE loss function replicates itself. A detailed study is found in Varian [22] and Doostparast et al. [23]. The Bayes estimates of $l\left(\varphi \right)$ under LINEX loss function are obtained as:

$${\widehat{\varphi }}_{B{E}_{LINEX}}=E\left[{\mathrm{e}}^{\left\{-vl\left(\varphi \right)\right\}}|\mathbf{x}\right]=-\frac{1}{v}log\left[{\int }_{\varphi }{\mathrm{e}}^{\left\{-vl\left(\varphi \right)\right\}}\pi \left(\varphi \right|x)d\varphi \right].$$

(66)

The third loss function is the general entropy loss (GEL) function proposed by Calabria and Pulcini [24], and is given as follows.

$$\left(l\left(\varphi \right),\widehat{l}\left(\varphi \right)\right)={\left(\frac{\widehat{l}\left(\varphi \right)}{l\left(\varphi \right)}\right)}^{\tau }-\tau log\left(\frac{\widehat{l}\left(\varphi \right)}{l\left(\varphi \right)}\right)-1,$$

where a break from symmetry is indicated by the shape parameter $\tau \ne 0$. for $\tau >0$, it considers overestimation to be more significant than underestimation, and the opposite is true for $\tau <0$. The Bayes estimator for the GE loss function is provided.

$${\widehat{\varphi }}_{B{E}_{GEL}}={\left[E\left({\left(l\left(\varphi \right)\right)}^{-\tau }|\mathbf{x}\right)\right]}^{-1/\tau }={\left[{\int }_{\varphi }{\left(l\left(\varphi \right)\right)}^{-\tau }\pi \left(\varphi \right|x)d\varphi \right]}^{-1/\tau }.$$

(67)

It is clear that the estimations generated by (65), (66), and (66) cannot be converted into closed-form expressions. Following that, in order to create posterior samples and produce appropriate Bayes estimates, we employed the Markov chain Monte Carlo (MCMC) method. In MCMC, a portion of the initial samples from the random samples of size M derived from the posterior density can be discarded (burned in), and the remaining samples are then utilized to compute Bayes estimates. The BEs of ${\varphi }^{\left(i\right)}=\left({\lambda }^{\left(i\right)},{\theta }^{\left(i\right)}\right)$ can be determined using MCMC under the SEL, LINEX, and GEL functions as follows:

$${\widehat{\varphi }}_{B{E}_{SEL}}=\frac{1}{M-l_B}\sum _{i=l_B}^M{\varphi }^{\left(i\right)},$$

(68)

$${\widehat{\varphi }}_{B{E}_{LINEX}}=-\frac{1}{v}log\left[\frac{1}{M-l_B}\sum _{i=l_B}^M{\mathrm{e}}^{\left\{-v{\varphi }^{\left(i\right)}\right\}}\right],$$

(69)

$${\widehat{\varphi }}_{B{E}_{GEL}}={\left[\frac{1}{M-l_B}\sum _{i=l_B}^M{\left({\varphi }^{\left(i\right)}\right)}^{-\tau }\right]}^{-1/\tau },$$

(70)

$\ni ,l_B$ is the number of burn-in samples. Read Ravenzwaaij et al. [25] for further details on MCMC.

Credible Intervals for Bayes Estimates

A $100(1-\gamma )\%$ credible intervals for the parameters $\varphi =(\theta ,\lambda )$ under the loss functions discussed are

$$\begin{array}{c}\hfill {\widehat{\varphi }}_{B{E}_{SEL}}\pm Z_{\frac{\gamma }{2}}\sqrt{var\left({\widehat{\varphi }}_{B{E}_{SEL}}\right)};{\widehat{\varphi }}_{B{E}_{LINEX}}\pm Z_{\frac{\gamma }{2}}\sqrt{var\left({\widehat{\varphi }}_{B{E}_{LINEX}}\right)};{\widehat{\varphi }}_{B{E}_{GEL}}\pm Z_{\frac{\gamma }{2}}\sqrt{var\left({\widehat{\varphi }}_{B{E}_{GEL}}\right)}.\end{array}$$

(71)

$\ni ,Z_{\frac{\gamma }{2}}$ is distributed according to percentile standard normal with right-tailed probability.

6. Simulation Study

In this section, we simulated data for the TPCJD to show how each of the non-Bayesian estimation methods performed. First, 1000 data points were generated from the TPCJD by considering the initial parameter values as

• $\lambda =0.50$ and $\theta =0.15,$
• $\lambda =0.05$ and $\theta =0.50,$
• $\lambda =0.50$ and $\theta =0.20,$
• $\lambda =0.15$ and $\theta =0.75,$

and sample sizes $n=50,100,150,200$. For each estimate $\widehat{\varphi }=(\widehat{\lambda },\widehat{\theta })$, the Bias and Root Mean Squared Error (RMSE) were calculated, respectively, as

$$Bias\left(\widehat{\varphi }\right)=\frac{1}{B}\sum _{i=1}^B({\widehat{\varphi }}_i-\varphi ),$$

and

$$RMSE\left(\widehat{\varphi }\right)=\sqrt{\frac{1}{B}\sum _{i=1}^B{({\widehat{\varphi }}_i-\varphi )}^2}.$$

To locate the desired estimates for the non-Bayesian process, we employed the Newton–Raphson algorithm. With the Bayesian approach, BEs are generated while accounting for prior knowledge using MCMC and the MH algorithm. We made the gamma distribution hyper-parameters for the prior data equal to double the parameter values. These values were filled in to provide the estimates we were looking for. The maximum likelihood estimates take initial guess values into consideration by using the MH method. In order to acquire the Bayes estimates under SEL, LINEX at $v=-1.5,1.5$, and the GEL at $\tau =-0.5,0.5$, we finally eliminate 2000 burn-in samples from the overall 10,000 samples produced from the posterior density. We calculate the bias and RMSE for each strategy. For the MCMC method, there are two types of graphs: marginal posterior and cumulative sum plots for lambda and theta. It is evident that the MCMC is a reliable method that, after a 5000 burn-in from a 10,000 sample draw, meets stability and convergences.

The simulation study’s Table 5, Table 6, Table 7, Table 8 and Table 9 allow for the following deductions.

Table 5. Average estimated Biases and RMSEs of various estimation techniques for the TPCJD for various sample sizes n and various parameter values $(\lambda =0.50,\theta =0.15)$.

Method			$\mathit{n}=50$			$\mathit{n}=100$			$\mathit{n}=150$			$\mathit{n}=200$
			Bias	RMSE		Bias	RMSE		Bias	RMSE		Bias	RMSE
MLE	$\lambda$		0.98406	8.24020		0.19537	1.34138		0.06881	0.52422		0.04189	0.31270
	$\theta$		0.02085	0.00299		0.00374	0.00049		0.00123	0.00009		0.00087	0.00008
MPSE	$\lambda$		0.63460	2.02765		0.35268	0.64016		0.24657	0.35237		0.17910	0.22907
	$\theta$		0.00441	0.00020		0.00313	0.00010		0.00217	0.00006		0.00160	0.00005
LSE	$\lambda$		0.49729	3.02560		0.23794	1.22444		0.13727	0.72793		0.12295	0.53421
	$\theta$		0.00148	0.00026		0.00114	0.00013		0.00058	0.00008		0.00056	0.00006
WLSE	$\lambda$		0.34174	1.83810		0.15752	0.70367		0.08703	0.42488		0.07030	0.30327
	$\theta$		0.00082	0.00022		0.00081	0.00011		0.00029	0.00006		0.00025	0.00005
CVME	$\lambda$		0.11572	2.33623		0.05629	1.07863		0.01883	0.67246		0.03427	0.49971
	$\theta$		0.00134	0.00027		0.00026	0.00013		0.00034	0.00008		0.00013	0.00006
ADE	$\lambda$		0.32773	1.57408		0.19434	0.63942		0.12533	0.37176		0.09907	0.27071
	$\theta$		0.00097	0.00020		0.00118	0.00010		0.00068	0.00006		0.00053	0.00005
RTADE	$\lambda$		0.29957	3.76597		0.14387	1.63933		0.05603	1.01888		0.05591	0.72909
	$\theta$		0.00023	0.00026		0.00028	0.00013		0.00019	0.00008		0.00005	0.00006
$B{E}_{SEL}$	$\lambda$		0.24209	0.13264		0.35021	0.14873		0.39953	0.17615		0.41281	0.17923
	$\theta$		0.55642	0.73418		0.45306	0.54725		0.32550	0.35261		0.29166	0.28644
$B{E}_{Linex1}$	$\lambda$		0.24011	0.13361		0.34921	0.14905		0.39898	0.17618		0.41246	0.17911
	$\theta$		0.57528	0.79468		0.46892	0.59307		0.33923	0.39141		0.30322	0.31117
$B{E}_{Linex2}$	$\lambda$		0.24403	0.13174		0.35115	0.14851		0.40006	0.17614		0.41316	0.17934
	$\theta$		0.53866	0.68188		0.43788	0.50656		0.31224	0.31923		0.28071	0.26553
$B{E}_{GEL1}$	$\lambda$		0.24598	0.13266		0.35287	0.14953		0.40118	0.17678		0.41424	0.18000
	$\theta$		0.54641	0.71282		0.44371	0.53012		0.31673	0.33832		0.28348	0.27645
$B{E}_{GEL2}$	$\lambda$		0.25365	0.13294		0.35810	0.15131		0.40437	0.17809		0.41699	0.18156
	$\theta$		0.52667	0.67225		0.42524	0.49767		0.29924	0.31103		0.26739	0.25782

Table 6. Average estimated Biases and RMSEs of various estimation methods for TPCJD at various sample sizes n and various values of the parameters $(\lambda =0.05,\theta =0.50)$.

Method			$\mathit{n}=50$			$\mathit{n}=100$			$\mathit{n}=150$			$\mathit{n}=200$
			Bias	RMSE		Bias	RMSE		Bias	RMSE		Bias	RMSE
MLE	$\lambda$		0.50123	0.96599		0.19988	0.24559		0.09586	0.08121		0.05498	0.03925
	$\theta$		0.10776	0.05159		0.03817	0.01385		0.01622	0.00490		0.00771	0.00146
MPSE	$\lambda$		0.14049	0.11223		0.06825	0.02984		0.05649	0.01694		0.04808	0.01212
	$\theta$		0.01374	0.00227		0.00577	0.00096		0.00526	0.00071		0.00498	0.00052
LSE	$\lambda$		0.10334	0.21173		0.04434	0.07900		0.04482	0.05154		0.02781	0.04006
	$\theta$		0.00499	0.00279		0.00062	0.00126		0.00134	0.00090		0.00066	0.00070
WLSE	$\lambda$		0.06572	0.10608		0.02266	0.03920		0.02496	0.02449		0.01530	0.01881
	$\theta$		0.00318	0.00231		0.00181	0.00106		0.00004	0.00075		0.00005	0.00056
CVME	$\lambda$		0.00093	0.16906		0.00548	0.07141		0.01141	0.04717		0.00301	0.03781
	$\theta$		0.00395	0.00282		0.00513	0.00130		0.00166	0.00090		0.00158	0.00071
ADE	$\lambda$		0.07279	0.09505		0.03851	0.03323		0.04173	0.02196		0.03338	0.01561
	$\theta$		0.00434	0.00223		0.00003	0.00100		0.00180	0.00073		0.00185	0.00054
RTADE	$\lambda$		0.03324	0.27959		0.02056	0.11357		0.02752	0.07766		0.01586	0.05842
	$\theta$		0.00249	0.00295		0.00316	0.00129		0.00061	0.00094		0.00068	0.00073
$B{E}_{SEL}$	$\lambda$		0.50971	0.50529		0.70084	0.59258		0.78370	0.66320		0.80666	0.68840
	$\theta$		0.29012	0.23360		0.20209	0.12317		0.16064	0.08764		0.14730	0.06507
$B{E}_{Linex1}$	$\lambda$		0.50288	0.51091		0.69789	0.59266		0.78226	0.66238		0.80561	0.68764
	$\theta$		0.29652	0.24615		0.20585	0.12837		0.16439	0.09334		0.15035	0.06836
$B{E}_{Linex2}$	$\lambda$		0.51626	0.50062		0.70367	0.59284		0.78509	0.66408		0.80768	0.68919
	$\theta$		0.28399	0.22235		0.19842	0.11831		0.15697	0.08241		0.14434	0.06209
$B{E}_{GEL1}$	$\lambda$		0.51672	0.50602		0.70540	0.59600		0.78683	0.66670		0.80935	0.69175
	$\theta$		0.28467	0.22668		0.19820	0.11969		0.15681	0.08400		0.14382	0.06264
$B{E}_{GEL2}$	$\lambda$		0.53066	0.50820		0.71443	0.60308		0.79296	0.67375		0.81463	0.69844
	$\theta$		0.27389	0.21350		0.19050	0.11306		0.14916	0.07706		0.13695	0.05812

Table 7. Average estimated Biases and RMSEs of various estimation methods for TPCJD at various sample sizes n and various values of the parameters $(\lambda =0.50,\theta =0.20)$.

Method			$\mathit{n}=50$			$\mathit{n}=100$			$\mathit{n}=150$			$\mathit{n}=200$
			Bias	RMSE		Bias	RMSE		Bias	RMSE		Bias	RMSE
MLE	$\lambda$		0.66151	4.71880		0.12123	0.80191		0.04520	0.26611		0.02131	0.18882
	$\theta$		0.02668	0.00526		0.00483	0.00075		0.00158	0.00015		0.00114	0.00016
MPSE	$\lambda$		0.52018	1.58390		0.27107	0.42405		0.16567	0.22040		0.13202	0.15708
	$\theta$		0.00564	0.00039		0.00379	0.00019		0.00239	0.00012		0.00198	0.00008
LSE	$\lambda$		0.46137	2.20969		0.18661	0.69514		0.10609	0.44090		0.09411	0.33995
	$\theta$		0.00240	0.00051		0.00100	0.00023		0.00061	0.00016		0.00032	0.00011
WLSE	$\lambda$		0.29156	1.30326		0.11733	0.43186		0.05161	0.25953		0.04786	0.20116
	$\theta$		0.00102	0.00042		0.00036	0.00019		0.00003	0.00013		0.00007	0.00009
CVME	$\lambda$		0.15891	1.68837		0.04634	0.60816		0.01445	0.40653		0.02571	0.31813
	$\theta$		0.00144	0.00051		0.00089	0.00023		0.00064	0.00016		0.00062	0.00011
ADE	$\lambda$		0.27784	1.15771		0.13737	0.38788		0.06992	0.24571		0.06791	0.18624
	$\theta$		0.00117	0.00039		0.00083	0.00018		0.00037	0.00013		0.00026	0.00009
RTADE	$\lambda$		0.28326	2.46754		0.13614	0.98523		0.04857	0.62202		0.07720	0.47625
	$\theta$		0.00008	0.00048		0.00012	0.00023		0.00033	0.00016		0.00000	0.00011
$B{E}_{SEL}$	$\lambda$		0.77372	1.23023		0.85554	0.99477		0.88717	0.94550		0.89972	0.92600
	$\theta$		0.38651	0.39608		0.33187	0.15161		0.32719	0.13314		0.32485	0.12363
$B{E}_{Linex1}$	$\lambda$		0.74852	1.51980		0.84729	0.99479		0.88095	0.94120		0.89437	0.92083
	$\theta$		0.39892	0.42990		0.33707	0.15656		0.33057	0.13559		0.32748	0.12543
$B{E}_{Linex2}$	$\lambda$		0.79079	1.15575		0.86346	0.99565		0.89318	0.95006		0.90488	0.93129
	$\theta$		0.37428	0.36472		0.32670	0.14681		0.32382	0.13073		0.32223	0.12187
$B{E}_{GEL1}$	$\lambda$		0.78409	1.22066		0.86352	1.00270		0.89436	0.95503		0.90643	0.93585
	$\theta$		0.38008	0.38662		0.32862	0.14903		0.32499	0.13167		0.32313	0.12251
$B{E}_{GEL2}$	$\lambda$		0.80442	1.20739		0.87929	1.01905		0.90853	0.97426		0.91963	0.95561
	$\theta$		0.36723	0.36809		0.32211	0.14391		0.32061	0.12875		0.31969	0.12029

Table 8. Average estimated Biases and RMSEs of various estimation methods for TPCJD at various sample sizes n and various values of the parameters $(\lambda =0.15,\theta =0.75)$.

Method			$\mathit{n}=50$			$\mathit{n}=100$			$\mathit{n}=150$			$\mathit{n}=200$
			Bias	RMSE		Bias	RMSE		Bias	RMSE		Bias	RMSE
MLE	$\lambda$		0.12535	0.25423		0.01855	0.04527		0.00328	0.01898		0.00349	0.01275
	$\theta$		0.07082	0.04897		0.01159	0.00737		0.00441	0.00247		0.00290	0.00137
MPSE	$\lambda$		0.14510	0.12222		0.07512	0.03064		0.05704	0.01836		0.04184	0.01322
	$\theta$		0.02341	0.00504		0.01535	0.00248		0.01011	0.00152		0.00734	0.00129
LSE	$\lambda$		0.09402	0.12030		0.04946	0.04895		0.04183	0.03595		0.02712	0.02310
	$\theta$		0.00854	0.00574		0.00639	0.00305		0.00278	0.00203		0.00205	0.00154
WLSE	$\lambda$		0.06632	0.07752		0.03226	0.03082		0.02748	0.02157		0.01770	0.01473
	$\theta$		0.00509	0.00488		0.00377	0.00260		0.00088	0.00164		0.00046	0.00133
CVME	$\lambda$		0.01467	0.09316		0.01141	0.04282		0.01661	0.03262		0.00851	0.02152
	$\theta$		0.00582	0.00578		0.00073	0.00305		0.00200	0.00204		0.00152	0.00155
ADE	$\lambda$		0.06254	0.06998		0.03625	0.02852		0.03229	0.02028		0.02074	0.01383
	$\theta$		0.00542	0.00463		0.00512	0.00248		0.00225	0.00157		0.00137	0.00128
RTADE	$\lambda$		0.05197	0.17665		0.02533	0.07156		0.03033	0.05023		0.01513	0.03353
	$\theta$		0.00198	0.00626		0.00076	0.00314		0.00005	0.00207		0.00080	0.00161
$B{E}_{SEL}$	$\lambda$		0.10377	0.03811		0.16702	0.03708		0.19165	0.04070		0.19857	0.04228
	$\theta$		1.11092	3.63592		0.78462	1.94456		0.62770	1.39507		0.57794	1.03423
$B{E}_{Linex1}$	$\lambda$		0.10297	0.03850		0.16672	0.03714		0.19152	0.04070		0.19849	0.04227
	$\theta$		1.21169	4.44912		0.84478	2.28887		0.68613	1.76432		0.62722	1.26033
$B{E}_{Linex2}$	$\lambda$		0.10455	0.03773		0.16731	0.03702		0.19177	0.04071		0.19866	0.04229
	$\theta$		1.02281	3.05876		0.73002	1.67776		0.57330	1.11956		0.53373	0.87114
$B{E}_{GEL1}$	$\lambda$		0.10610	0.03771		0.16840	0.03720		0.19255	0.04091		0.19933	0.04249
	$\theta$		1.08934	3.52907		0.76919	1.88976		0.61237	1.33692		0.56401	0.99529
$B{E}_{GEL2}$	$\lambda$		0.11075	0.03703		0.17113	0.03747		0.19431	0.04134		0.20082	0.04292
	$\theta$		1.04666	3.32551		0.73864	1.78528		0.58179	1.22588		0.53653	0.92296

Table 9. Confidence Intervals for MLEs and Credible Intervals for the Bayesian Estimates using $B{E}_{SEL}$, $B{E}_{Linex1}$, $B{E}_{Linex2}$, $B{E}_{GEL1}$, and $B{E}_{GEL2}$.

Initial Values	Lower MLE	Upper MLE	Lower ${\mathit{BE}}_{\mathit{SEL}}$	Upper ${\mathit{BE}}_{\mathit{SEL}}$	Lower ${\mathit{BE}}_{\mathit{Linex}1}$	Upper ${\mathit{BE}}_{\mathit{Linex}1}$	Lower ${\mathit{BE}}_{\mathit{Linex}2}$	Upper ${\mathit{BE}}_{\mathit{Linex}2}$	Lower ${\mathit{BE}}_{\mathit{GEL}1}$	Upper ${\mathit{BE}}_{\mathit{GEL}1}$	Lower ${\mathit{BE}}_{\mathit{GEL}2}$	Upper ${\mathit{BE}}_{\mathit{GEL}2}$
$\lambda =0.50$	0.00190	0.77385	0.77196	0.00051	0.38456	0.38405	0.00085	0.44259	0.44174	0.00008	0.31780	0.31772
$\theta =0.75$	0.41433	2.58905	2.17472	0.37938	2.42793	2.04855	0.42279	2.05945	1.63666	0.40221	1.87099	1.46878
$\lambda =1.0$	0.00005	1.55607	1.55602	0.00110	0.96420	0.96310	0.00014	0.63588	0.63574	0.00016	0.55624	0.55607
$\theta =0.50$	0.30178	1.58474	1.28295	0.33896	1.34911	1.01016	0.29789	1.15208	0.85420	0.31009	1.06971	0.75961
$\lambda =1.50$	0.00276	2.17717	2.17442	0.00796	1.71010	1.70214	0.07217	1.39138	1.31921	0.10819	1.24181	1.13362
$\theta =1.20$	0.97274	2.30087	1.32814	1.15623	1.86206	0.70583	1.21857	1.80650	0.58793	1.28516	1.79025	0.50509
$\lambda =0.25$	0.00001	0.49411	0.49410	0.00000	0.27732	0.27731	0.00003	0.17555	0.17552	0.00004	0.14845	0.14842
$\theta =2.0$	1.33200	6.46250	5.13050	1.32533	5.34055	4.01522	1.18540	4.60782	3.42242	1.24040	4.27824	3.03784

• The results of Table 5, Table 6, Table 7, Table 8 and Table 9 show the stability of the TPCJD because the Bias and RMSE for the parameters of the TPCJD are relatively small.
• As the sample size increases, we occasionally observe a decrease in the Bias and RMSE for all estimations.
• This indicates that using a variety of estimation techniques yields reliable Bias and RMSE results for big sample sizes.
• The MPSE estimate method offers better metrics than the LSE, WLSE, CVME, ADE, and RTADE approaches.
• All estimators’ Bias and RMSE values decrease as sample size rises, indicating improved model parameter estimation accuracy.
• LSE, WLSE, CVME, ADE, and RTADE are the parameters that are least biased when compared to all other parameters and different sample sizes.
• All sample sizes have a positive estimators’ bias.
• From Table 5, Table 6, Table 7, Table 8 and Table 9, we noted that the WLSE, LSE, CVME, ADE, RTADE, MLE, and Bayesian methods, respectively, give smaller values for accurate Bias and RMSE findings for large sample sizes.

7. Applications

In this section, the performance of the TPCJD is illustrated using two life data sets.

7.1. Application to Infant Mortality Rate Data

The first set of information is a description of the infant mortality rate per 1000 live births for a few chosen nations in 2021, as reported by a https://data.worldbank.org/indicator/SP.DYN.IMRT.IN (accessed on 2021). This real data set is presented as

56	10	22	3	69	6	7	11	4	4	19	13	7	27	12	3	4	11
84	27	25	6	35	14	11	12	6

Here, we compare the goodness of fit of the TPCJD with the Burr III distribution by Papadopoulos [26], Exponentiated Inverse Exponential (EIE) by [27], Weibull distribution, Gamma distribution, Lomax distribution, and the parent distribution called C-JD by Onyekwere and Obulezi [2], as shown in Table 10. The fitness metrics considered are the Negative log-likelihood (NLL), the Akaike information criterion (AIC), the corrected AIC (CAIC), the Bayesian information criterion (BIC), the Hannan–Quinn information criterion (HQIC), Anderson Darling (AD), and Cramér-von-Mises (CVM) statistics. The model with the lowest values of these metrics is chosen as the best performer.

Table 10. The fitness metrics and performance statistics for the models using the world infant mortality rate per 1000 live birth data.

Dist	NLL	AIC	CAIC	BIC	HQIC	${\mathit{W}}^{*}$	${\mathit{A}}^{*}$	K-S	p-Value	Scale	Shape
TPCJ	106.16	216.31	216.81	218.90	217.08	0.11	0.75	0.16	0.5345	399.51	0.06
Burr III	119.08	242.16	242.66	244.75	242.93	0.04	0.26	0.36	0.0021	9.50	0.04
EIE	103.88	211.76	212.26	214.36	212.54	0.08	0.50	0.17	0.4187	0.42	6.66
Weibull	106.11	231.36	231.86	233.95	232.13	0.13	0.82	0.32	0.0084	0.90	8.90
Gamma	105.76	217.90	218.40	220.49	218.67	0.13	0.82	0.18	0.3436	1.80	9.74
LOMAX	106.17	216.33	216.83	218.92	217.10	0.11	0.71	0.16	0.5158	232.81	13.37
C-J	112.39	226.77	226.93	228.07	227.16	0.17	1.10	0.28	0.0260	0.15	-

The fitness criterion states that the distribution that fits the data the best and has a p-value larger than $\alpha =0.05$ meets the requirement for fitness. The infant mortality rate is best suited by the proposed TPCJD, according to the findings in Table 10.

The TPCJD has the smallest values of the Negative Log-Likelihood (NLL), Akaike information criterion (AIC), Corrected AIC (CAIC), Bayesian information criterion (BIC), Hannan–Quinn information criterion (HQIC), Anderson–Darling and Cramer Van Miss, and Kolmogorov–Smirnov (K–S) statistics, and hence performs better with the infant mortality rate data compared to TPOD, OGE, Burr, GIE, EIE, and C-J, as shown in Table 10. The MLEs of the parameters of the fitted distributions are determined in Table 11. The standard error (Std. Error) and classical and Bayesian estimates for the TPCJD’s parameters are also provided in Table 11. Figure 4 shows the fitted density, CDF, and empirical Survival function for the underlying TPCJD. In contrast, Figure 5 is the PP plot of the fitted distributions using the infant mortality rate data. For the operational characteristic probability and the minimal values of n for data on infant mortality rates, we use the following assumptions; for more information, see Table 12.

Table 11. Using data on infant mortality rates, Bayesian and Non-Bayesian estimates of the TPCJD’s parameters.

Method		$\mathit{\lambda }$	$\mathit{\theta }$
MLE	Estimated value	399.51	0.06118
	Standard Error	1189.3266	0.02192
MPS	Estimated value	359.6895	0.05795
	Standard Error	726.20844	0.01689
LSE	Estimated value	12.00955	0.13564
	Standard Error	85.748090	0.26537
WLSE	Estimated value	4.09348	0.16306
	Standard Error	1.77336	0.01467
CVM	Estimated value	7.03324	0.15549
	Standard Error	38.82560	0.21236
ADE	Estimated value	1227.73996	0.05692
	Standard Error	20249.38073	0.03999
RTADE	Estimated value	354.44999	0.06383
	Standard Error	2351.7580	0.04899
BE	Estimated value	528.93682	0.06067
	Standard Error	62.37168	0.00146

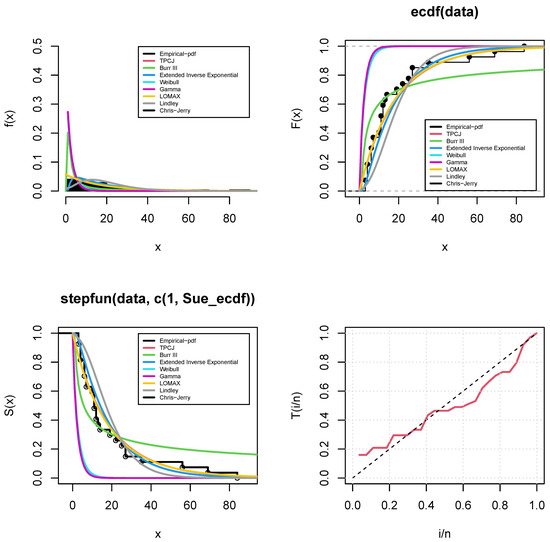
Figure 4. Statistical fitting of distributions to the world infant mortality rate per 1000 live birth data using empirical PDF, CDF, and survival plots.

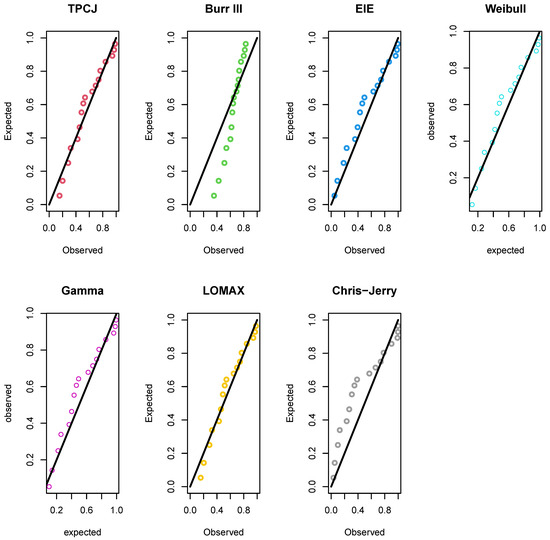
Figure 5. The PP plots of the distributions fitted to the world infant mortality rate per 1000 live birth data.

Table 12. The SASP for the TPCJD with parameters where $\lambda =399.51$ and $\theta =0.06118$.

P	c	n	$\mathit{a}=0.1$	n	$\mathit{a}=0.2$	n	$\mathit{a}=0.4$	n	$\mathit{a}=0.8$	n	$\mathit{a}=1$
0.25	0	5	0.752629	3	0.753243	2	0.754448	1	1	1	1
	2	26	0.756249	14	0.758651	8	0.765589	5	0.787914	4	0.875
	4	50	0.755859	26	0.771797	15	0.754474	9	0.781198	8	0.773437
	8	101	0.752716	53	0.756754	29	0.767708	17	0.800299	15	0.788025
	10	127	0.753183	66	0.765475	36	0.777253	22	0.751028	19	0.759659
0.75	0	20	0.259274	10	0.279388	5	0.323979	3	0.327964	2	0.5
	2	57	0.252101	29	0.265356	15	0.294139	9	0.260991	7	0.34375
	4	91	0.25294	47	0.255756	25	0.262584	14	0.281203	12	0.274414
	8	157	0.250631	81	0.254463	43	0.263966	24	0.290777	21	0.251722
	10	189	0.251913	98	0.250069	52	0.260579	29	0.290522	25	0.270628
0.95	0	43	0.050594	22	0.051029	11	0.059744	6	0.061598	5	0.0625
	2	90	0.05165	46	0.052408	24	0.054086	13	0.058115	11	0.054687
	4	131	0.051924	67	0.052901	35	0.055147	19	0.060895	16	0.059235
	8	208	0.050384	106	0.053527	56	0.052819	31	0.053015	26	0.053876
	10	244	0.051346	125	0.05278	66	0.052693	36	0.06187	30	0.068023

Given that the model is the best match among competing distributions, the model performance measurements for the TPCJD in Table 10 raise several questions. Other techniques were employed to estimate the parameters in order to assess the MLE method’s appropriateness. The Weighted Least Squares Estimates (WLSE) approach is the most effective, as shown in Table 11. This is a result of these estimates’ minimum standard errors. In addition to the fact that the proposed TPCJD fits the infant mortality rate data better than the traditional Weibull, Gamma, Lomax, Exponentiated Inverse Exponential, Burr III, and the C-JD, maximum likelihood estimation is not a good estimation procedure for estimating the parameters of the TPCJD.

7.2. Application to Data on Life of Fatigue Fracture of Kevlar 373/epoxy

The application is on the life of fatigue fracture of Kevlar 373/epoxy subjected to constant pressure at $90\%$ stress level until all had failed, as shown in Table 13 (see Andrews and Herzberg [28]).

Table 13. Kevlar 373/epoxy was subjected to a continuous $90\%$ stress level until all fatigue fractures failed.

0.0251	0.0886	0.0891	0.2501	0.3113	0.3451	0.4763	0.5650	0.5671	0.6566	0.6748
0.6751	0.6753	0.7696	0.8375	0.8391	0.8425	0.8645	0.8851	0.9113	0.9120	0.9836
1.0483	1.0596	1.0773	1.1733	1.2570	1.2766	1.2985	1.3211	1.3503	1.3551	1.4595
1.4880	1.5728	1.5733	1.7083	1.7263	1.7460	1.7630	1.7746	1.8475	1.8375	1.8503
1.8808	1.8878	1.8881	1.9316	1.9558	2.0048	2.0408	2.0903	2.1093	2.1330	2.2100
2.2460	2.2878	2.3203	2.3470	2.3513	2.4951	2.5260	2.9911	3.0256	3.2678	3.4045
3.4846	3.7433	3.7455	3.9143	4.8073	5.4005	5.4435	5.5295	6.5541	9.0960

In Table 14, by comparing the proposed TPCJD’s goodness of fit to that of the Burr, EIE, Weibull, GIE, Lomax, and C-J distributions at the instance of the time to the breakdown of an insulating fluid between electrodes at a voltage of 34 k.v. (minutes) data, we are able to demonstrate the suggested TPCJ distribution’s use. The measurements of fitness include Kolmogorov–Smirnov (K–S) statistics, Akaike information criterion (AIC), Corrected AIC (CAIC), Bayesian information criterion (BIC), Anderson–Darling (AD), Cramer von Mises (CVM), and Negative Log-Likelihood (NLL). The model with the fewest indices meets the performance criterion.

Table 14. Using data from the time it takes an insulating fluid between electrodes to break down at 34 k.v. (minutes), the metrics of fitness and performance indices for the models are shown.

Dist	NLL	AIC	CAIC	BIC	HQIC	W*	A*	K-S	p-Value	par[1]	par[2]
TPCJ	122.48	248.970	249.134	253.631	250.833	0.128	0.767	0.114	0.261	0.310	1.354
Burr III	128.57	261.144	261.309	265.806	263.007	0.273	1.643	0.148	0.066	0.666	2.231
EIE	126.52	257.047	257.211	261.708	258.910	0.149	0.891	0.158	0.039	0.034	0.065
Weibull	122.53	249.171	249.336	253.833	251.034	0.129	0.759	0.119	0.213	1.304	2.171
GIE	161.99	327.972	328.136	332.633	260.112	1.238	7.015	0.271	0.000	0.523	0.790
Lomax	127.12	258.249	258.414	262.911	329.835	0.119	0.708	0.166	0.026	1.042	5.319
C-J	124.21	250.414	250.469	252.745	251.346	0.166	0.973	0.115	0.244	-	1.172

The fitness criterion states that the distribution that fits the data the best and has a p-value larger than $\alpha =0.05$ meets the requirement for fitness. According to the results in Table 14, the proposed TPCJD fits the data for the most optimal time taken for an insulating fluid between electrodes to break down at a voltage of 34 k.v.

The Bayes Estimates (BE) and Weighted Least Squares Estimates (WLSE) outperformed the others, as shown in Table 15. This is a result of these estimates’ minimum standard errors. The standard error (Std. ErrorS) and classical and Bayesian estimates for the TPCJD’s parameters are provided in Table 15. The density, CDF, empirical reliability, and PP plots of the fitted distributions of the time to break down an insulating fluid between electrodes at 34 k.v. (minutes) data are presented in Figure 6 and Figure 7, respectively, for the underlying TPCJD. For the operating characteristic probability and the minimal values of n for fluid between electrodes at a voltage of 34 k.v. (minutes) data, see Table 16, we adopt the following assumptions.

Table 15. Using data from the time it takes for an insulating fluid between electrodes to break down at 34 k.v. (minutes), Bayesian and non-Bayesian estimates of the TPCJD’s parameters were concluded.

Methods		Parameters
		$\mathbf{\lambda }$	$\mathbf{\theta }$
MLE	Estimated value	0.30976	1.35394
	Standard Error	0.19859	0.12069
MPS	Estimated value	0.40753	1.29379
	Standard Error	0.25563	0.12376
LSE	Estimated value	0.21377	1.49792
	Standard Error	0.77708	0.56511
WLSE	Estimate value	0.23910	1.47511
	Standard Error	0.03402	0.02554
CVM	Estimated value	0.18468	1.51836
	Standard Error	0.72632	0.55747
ADE	Estimated value	0.27569	1.43510
	Standard Error	0.32428	0.21346
RTADE	Estimated value	0.47229	1.34924
	Standard Error	0.84916	0.33271
BE	Estimated value	0.37424	1.27970
	Standard Error	0.03354	0.04525

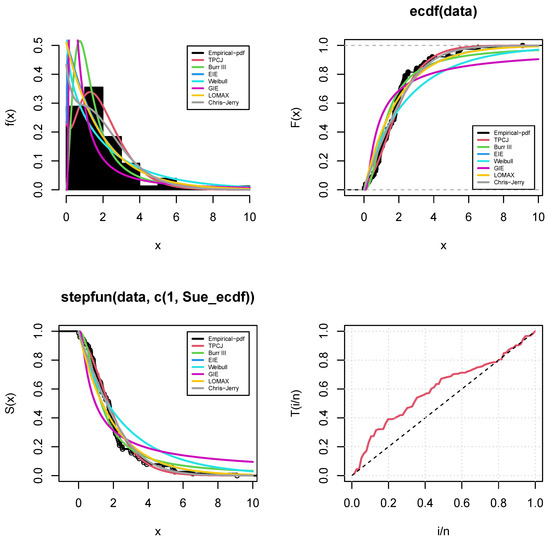
Figure 6. Using data on the amount of time needed for an insulating fluid between electrodes to break down at a voltage of 34 k.v., empirical PDF, CDF, and survival plots of fitted distribution were plotted.

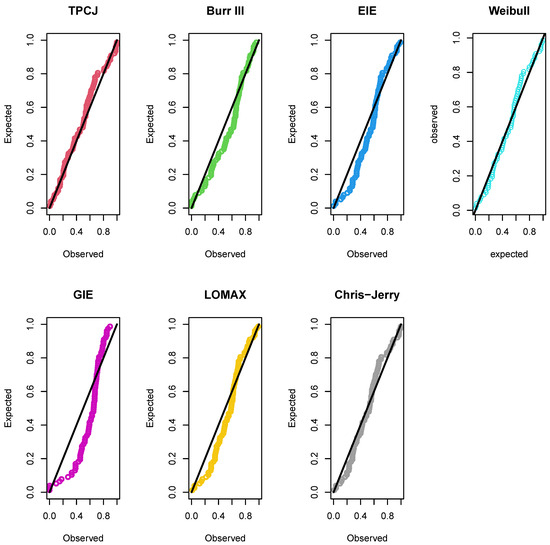
Figure 7. The fitted distributions’ PP graphs using the measured data for the number of minutes it takes for an insulating fluid between electrodes to break down at a voltage of 34 k.v.

Table 16. The SASP for the TPCJD with parameters where $\lambda =0.30976$ and $\theta =1.35394$.

P	c	n	A = 0.1	n	A = 0.2	n	A = 0.4	n	A = 0.8	n	A = 1
0.25	0	8	0.764176	4	0.791797	2	0.837431	1	1	1	1
	2	46	0.759814	24	0.754506	11	0.786577	5	0.836628	4	0.875002
	4	90	0.754889	46	0.754664	22	0.752272	10	0.762131	8	0.773442
	8	182	0.754824	92	0.759169	43	0.765333	19	0.776015	15	0.78803
	10	230	0.751647	116	0.757398	54	0.76509	24	0.758895	19	0.759665
0.75	0	37	0.250772	18	0.266366	8	0.288831	3	0.377084	3	0.250002
	2	104	0.250237	52	0.254697	24	0.253458	10	0.259185	7	0.343755
	4	166	0.251468	83	0.256271	38	0.259272	16	0.251505	12	0.27442
	8	286	0.250624	143	0.256385	66	0.250024	27	0.271959	21	0.251729
	10	344	0.252918	173	0.252495	79	0.258083	33	0.253714	25	0.270636
0.95	0	78	0.051895	39	0.051973	17	0.058504	7	0.053618	5	0.062501
	2	165	0.051224	82	0.052669	37	0.053413	14	0.070579	11	0.054689
	4	241	0.050291	120	0.05159	54	0.053646	21	0.065537	16	0.059237
	8	380	0.050684	190	0.051066	86	0.052095	34	0.061865	26	0.053879
	10	447	0.050444	224	0.050058	101	0.053123	41	0.051504	30	0.068026

8. Conclusions

A new life distribution, named the two-parameter Chris-Jerry distribution (TPCJD), has been proposed and studied here. The characteristics of the proposed distribution, moments, moment-generating function, and order statistics are derived. The MLEs, LSEs, WLSEs, CVMEs, ADEs, and RTADEs were derived and implemented. Bayesian inference with squared error loss, linear exponential loss, and generalized entropy loss functions were also studied, and the simulation of parameters based on the classical and Bayesian methods was carried out. Also, the asymptotic confidence intervals and credible intervals for the maximum likelihood estimates and Bayesian estimates were obtained. Applications to lifetime data using the infant mortality rate per 1000 live births for some selected countries in the year 2021 and the time to break down an insulating fluid between electrodes at 34 k.v. (minutes) data were also illustrated. From the metrics of fitness (K-S and p-value) and performance indices (LL, AD, CVM, AIC, CAIC, BIC, HQIC), the proposed TPCJD is better than the following fitted distributions: Burr distribution, Generalized Inverse Exponential (GIE) distribution, Exponentiated Inverse Exponential (EIE), Weibull, Gamma, Lomax, and Chris-Jerry distribution (C-JD).

9. Future Work

Further study on the proposed distribution can explore more characterizations, namely the normalized incomplete moment, conditional value at risk, buffered probability of exceedance, and Pietra and Gini indices for measuring income and population inequalities.