Characterizations of Γ Rings in Terms of Rough Fuzzy Ideals

Abstract

Fuzzy sets are a major simplification and wing of classical sets. The extended concept of set theory is rough set (RS) theory. It is a formalistic theory based upon a foundational study of the logical features of the fundamental system. The RS theory provides a new mathematical method for insufficient understanding. It enables the creation of sets of verdict rules from data in a presentable manner. An RS boundary area can be created using the algebraic operators union and intersection, which is known as an approximation. In terms of data uncertainty, fuzzy set theory and RS theory are both applicable. In general, as a uniting theme that unites diverse areas of modern arithmetic, symmetry is immensely important and helpful. The goal of this article is to present the notion of rough fuzzy ideals (RFI) in the gamma ring structure. We introduce the basic concept of RFI, and the theorems are proven for their characteristic function. After that, we explain the operations on RFI, and related theorems are given. Additionally, we prove some theorems on rough fuzzy prime ideals. Furthermore, using the concept of rough gamma endomorphism, we propose some theorems on the morphism properties of RFI in the gamma ring.

1. Introduction

L.A.Zadeh introduced the fuzzy set concept [1]. Fuzzy set theory is a method of investigation that can be used to solve problems involving ambiguous, subjective, and inaccurate senses or judgments. Fuzzy set theory is a valuable tool for describing the data. Many researchers have discussed fuzzy versions of various algebraic structures. One of the algebraic structures is the gamma ring. Almost all the axioms of the ring and gamma ring are the same. In 1964, the concept of the gamma ring was introduced by N.Nobusawa [2]. Nobusawa’s definition of the gamma rings was slightly weakened by W.E.Barnes [3]. These two papers were widely read by mathematicians after being published and had interesting results on gamma rings. Y.B.Jun et al. used the idea of the fuzzy set in the theory of gamma rings [4,5]. Gamma rings have been used to extend several fundamental ring theory conclusions. The number of generalizations that are identical to the corresponding parts of S.Kyuno’s ring theory was investigated using the gamma ring structure [6]. Many researchers developed theorems and examples of fuzzy sets on algebraic structures [7,8]. Pure mathematics uses algebraic structures to learn the symmetry of geometrical objects. The most important functions in ring theory are those that preserve ring operation, often called homomorphisms.

The extension of a fuzzy set is an intuitionistic fuzzy set (IFS). The IFS was introduced by Atanssov to tackle the problem of non-determinacy caused by a single membership function in the fuzzy set. The IFS is very useful in providing a flexible model to elaborate on the uncertainty and vagueness involved in decision making. Palaniappan et.al. developed and proved certain results on intuitionistic fuzzy ideals in both gamma near rings and the gamma ring structure [9,10,11]. In 2011, the structures of Artinian and Noetherian nearrings were examined by Ezhilmaran and Palaniappan [12]. Wen presented findings on the IF overlap function [13]. Alolaiyan et.al. and Altassan stated their findings on fuzzy isomorphisms of fuzzy subrings [14,15]. In 2013, Uddin proved gamma endomorphism’s function [16]. Pawlak proposed RS theory, a novel mathematical way of dealing with inexact and imprecise knowledge [17]. RS is a new branch of uncertainty mathematics intimately related to fuzzy set theory. RS theory is intended to handle uncertainty in addition to fuzzy set theory, which uses concepts such as approximation, dependence, and reduction of attributes. Almost all the applications of a RSs and fuzzy sets are similar. However, fuzzy sets and RSs have distinctive characteristics which make RSs better than fuzzy sets. In fuzzy sets, a membership function is determined a priori, and data are fitted to the theory, but an RS does not need any assumptions about the membership function. According to an RS, each subset of a universe is made up of two subsets called the lower and upper approximations. An RS identifies partial or total reliance, purges superfluous data, and supplies an approach to null values, missing data, dynamic data, and others. The various structures of algebra are explained in terms of an RS by Biswas and Nandha [18] and Z. Bonikowaski [19]. Ali examined some properties of generalized RSs as well as some properties of generalized upper and lower approximations [20]. B.Davvaz studied the new rough algebraic structural results [21,22,23,24,25]. The following are some rough algebraic structures described by mathematicians. V.S.Subha et al. Stated the fuzzy rough prime and semi-prime ideals in semigroups and discussed their properties. Bagirmaz described the rough image and inverse image of the prime ideals [26,27,28]. Zhan and Marynirmala proposed RFI and hearings [29]. Bo et.al. investigated three kinds of neutrosophic rough sets and multigranulation neutrosophic rough sets [30]. The concepts of rough sets have been extended to the fuzzy environment, in which the results are called the Rough Fuzzy Set (RFS) and fuzzy rough set. A pair of fuzzy sets called “RFS” is produced when a fuzzy set is approximated in a crisp approximation space. A RFS can be useful with improbability in classification, especially vagueness. Dubois and Prade showed the difference between an RFS and a fuzzy rough set [31]. Wang et al. and Zhan primarily focused on rough fuzzy subsemigroups and rough fuzzy prime ideals [32,33]. The objective of the current work is to provide the RFI in the gamma ring structure. In this article, some basic concepts are given in Section 2 and Section 3 contain the definition of RFI with examples and some properties of RFI. Section 4 and Section 5 explain the characteristic functions of RFI in gamma rings and some operations on RFI in gamma rings. Then, Section 6 deals with prime ideals in RFI. The two additional theorems of rough gamma endomorphism are demonstrated in Section 7. Section 8 concludes with a succinct summary.

2. Prerequisites

The required definitions are incorporated in this section.

Definition 1 ([3]). 

Consider $\left(N,\Gamma \right)$ an abelian group where $N=\left\{p,q,r\right\}$and $\Gamma =\left\{\alpha ,\beta ,\gamma \dots \right\}$, and for all$p,q,r ϵ N$and $\alpha ,\beta ϵ\Gamma$, the following conditions are satisfied:

(1) 

$p\alpha q ϵ N$;

(2) 

$\left(p+q\right)\alpha r=p\alpha r+q\alpha r, p\left(\alpha +\beta \right)q=p\alpha q+p\beta q, p\alpha \left(q+r\right)=p\alpha q+p\alpha r$;

(3) 

If $\left(p\alpha q\right)\beta r=p\alpha \left(q\beta r\right)$, then N is called a Γ Ring;

This was later the improved by W.E.Barnes [3]:

(1’) 

$p\alpha qϵN\alpha p\beta ϵ\mathsf{\Gamma }$;

(2’) 

$\left(p+q\right)\alpha r=p\alpha r+q\alpha r,p\left(\alpha +\beta \right)q=p\alpha q+p\beta q,p\alpha \left(q+r\right)=p\alpha q+p\alpha r$;

(3’) 

$\left(p\alpha q\right)\beta r=p\left(\alpha q\beta \right)\mathrm{r}=p\alpha \left(q\beta r\right)$;

(4’) 

$p\alpha q=0for all p,qϵN, which implies \alpha =0$.

Definition 2 ([17]). 

Suppose K = (U,R), in each subset $P\subseteq U, and an equivalence relation$ R$ϵIND\left(K\right)$. We associated two subsets $\underset{¯}{apr}\left(P\right)=\cup \{p_i\in U/R | \left[p_i\right]\subseteq P\}$ and $\overline{ apr}\left(P\right)=\cup \{p_i\in U/R | \left[p_i\right]\cap P \ne \varphi$}, called the apr-lower and apr-upper approximations of P, respectively. A set of pairs $\left(\overline{apr},\underset{¯}{apr}\right)$is called the RS in K and symbolized by $P=\left(\overline{apr},\underset{¯}{apr}\right)$.

Definition 3 ([31]). 

Let X be a set, R be an equivalence relation on X and $\eta$ be a fuzzy subset of N. Then upper and lower approximation of $\overline{apr}\left(p\right)$ and $\underset{¯}{apr}\left(p\right)$ of a fuzzy subsets $\eta$ by R are the fuzzy set $U$/R with membership funcution defined by

${\mu }_{\overline{apr}\left(\eta \right)}\left(X_i\right)=$ $sup\left\{{\mu }_{\eta }\left(x\right)/\omega \left(X_i\right)={\left[x\right]}_R\right\}$

${\mu }_{\underset{¯}{apr}\left(\eta \right)}\left(X_i\right)=$ $inf\left\{{\mu }_{\eta }\left(x\right)/\omega \left(X_i\right)={\left[x\right]}_R\right\}$where ${\mu }_{\overline{apr}\left(\eta \right)}\left(X_i\right)$(resp.${\mu }_{\underset{¯}{apr}\left(\eta \right)}\left(X_i\right))$

is the degree of membership of $X_{i }$in $\overline{apr}\left(\eta \right)$ (resp.$\underset{¯}{apr}\left(\eta \right)) . \left(\overline{apr}\left(\eta \right) , \underset{¯}{apr}\left(\eta \right) \right)$ is called an RFS.

Definition 4. 

A function $\theta :g_1\to g_2$ where $g_1$ and $g_2$ are $\Gamma$ Rings is said to be a $\Gamma$-homomorphism if

(1) 

$\theta \left(p+q\right)=\theta \left(p\right)+\theta \left(q\right)$;

(2) 

$\theta \left(p\alpha q\right)=\theta \left(p\right)\alpha \theta \left(q\right)$for all$p,q,ϵ N$,$\alpha ϵ\mathsf{\Gamma }.$

Definition 5. 

A function $\theta :g_1\to g_2$, where $\theta$ is a $\Gamma$-homomorphism and $g_1$ and $g_2$ are $\Gamma$ Rings, is called a $\Gamma$-endomorphism if$g_2\subseteq g_1.$

3. Main Contribution

A definition of RFI and an example are given in this section, and we then discuss the basic concepts of RFI.

Definition 6. 

An RFS in N is called a rough fuzzy upper ideal (resp. rough fuzzy lower ideal) (RFUI (resp. RFLI)) of a$\Gamma$Ring N for all$p,q ϵ N$and $\alpha ϵ \Gamma$ given the following:

(1) 

${\overline{apr}}_{\eta }\left(p-q\right)\ge \left\{{\overline{apr}}_{\eta }\left(p\right)\wedge {\overline{apr}}_{\eta }\left(q\right)\right\},{\overline{apr}}_{\eta }\left(p\alpha q\right)\ge {\overline{apr}}_{\eta }\left(q\right)\left[resp.{\overline{apr}}_{\eta }\left(p\alpha q\right)\ge {\overline{apr}}_{\eta }\left(p\right)\right]$;

(2) 

${\underset{¯}{apr}}_{\eta }\left(p-q\right)\le \left\{{\underset{¯}{apr}}_{\eta }\left(p\right)\vee {\underset{¯}{apr}}_{\eta }\left(q\right)\right\},{\underset{¯}{apr}}_{\eta }\left(p\alpha q\right)\le {\underset{¯}{apr}}_{\eta }\left(q\right)[resp.{\underset{¯}{apr}}_{\eta }\left(p\alpha q\right)\le {\underset{¯}{apr}}_{\eta }\left(p\right)$].

Example 1.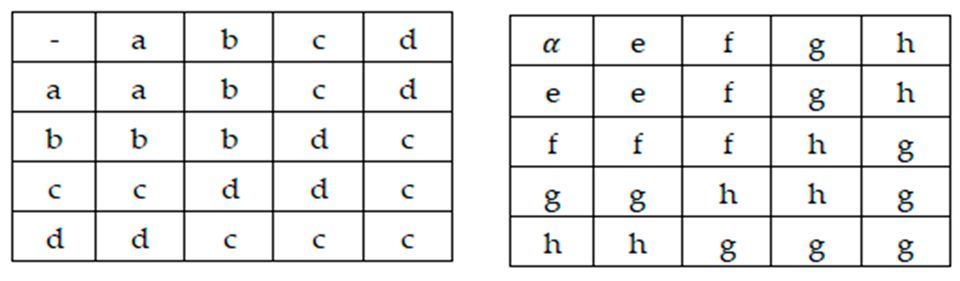 

Let N = {a, b, c, d} and $\alpha =$ {e, f, g, h} define N and $\alpha$ as follows:

${\overline{apr}}_{\eta }\left(p\right)=\left\{\begin{array}{c}0.5 ifx=a,e\\ 0.6 ifx=b,f\\ 0.6 ifx=c,d,g,h\end{array}\right.$, ${\underset{¯}{apr}}_{\eta }\left(p\right)$=$\left\{\begin{array}{c}0.7 ifx=a,e\\ 0.5 ifx=b,f\\ 0.4 ifx=c,d,g,h\end{array}\right.$

By routine calculation, clearly, N is an RF ideal of N.

Theorem 1. 

Consider $\chi$ an ideal of a Γ Ring. Then, the RFS in N is a RFI of N.

Proof. 

Let $p,q ϵ N$. If the elements $p,q$ are in the ideal $\chi$ and $\alpha ϵ \mathsf{\Gamma }$, then $p-q ϵ\chi$and $p\alpha q ϵ\chi$, since $\chi$is an ideal of N. Hence, ${\overline{apr}}_{\chi }\left(p-q\right)=1\ge \left\{{\overline{apr}}_{\chi }\left(p\right)\wedge {\overline{apr}}_{\chi }\left(q\right)\right\}$ and ${\overline{apr}}_{\chi }\left(p\alpha q\right)=1\ge {\overline{apr}}_{\eta }\left(q\right)$. Additionally, 0 = 1 − ${\overline{apr}}_{\chi }\left(p-q\right)={\overline{apr}}_{\overline{\chi }}\left(p-q\right)\le \left\{{\overline{apr}}_{\overline{\chi }}\left(p\right)\vee {\overline{apr}}_{\overline{\chi }}\left(q\right)\right\}$ and 0 = 1 − ${\overline{apr}}_{\chi }\left(p\alpha q\right)$ = ${\overline{apr}}_{\overline{\chi }}\left(p\alpha q\right)\le {\overline{apr}}_{\overline{\chi }}\left(q\right).$ If $p\mathrm{and}q$ are not in the ideal $\chi$, $\mathrm{then}{\overline{apr}}_{\chi }\left(p\right)=0$ or ${\overline{apr}}_{\chi }\left(q\right)=0$, and we find ${\overline{apr}}_{\chi }\left(p-q\right)\ge \left\{{\overline{apr}}_{\chi }\left(p\right)\wedge {\overline{apr}}_{\chi }\left(q\right)\right\}$ and ${\overline{apr}}_{\chi }\left(p\alpha q\right)\ge {\overline{apr}}_{\chi }\left(q\right).$ In addition, ${\overline{\mathrm{apr}}}_{\mathsf{\chi } \text{¯}}\left(\mathrm{p}-\mathrm{q}\right)\le \left\{{\overline{apr}}_{\overline{\chi }}\left(p\right)\vee {\overline{apr}}_{\overline{\chi }}\left(q\right)\right\}$ = {1 − ${\overline{apr}}_{\chi }\left(p\right)\}\vee \left\{1-{\overline{apr}}_{\chi }\left(q\right)\right\}$ = 1 and ${\overline{ apr}}_{\overline{\chi }}\left(p\alpha q\right)=1-{\overline{apr}}_{\chi }\left(p\alpha q\right)\le 1-{\overline{apr}}_{\chi }\left(q\right)={\underset{¯}{apr}}_{\overline{\chi }}\left(q\right)$. Therefore, is a RFI of N. Similiarly, is also a RFI of N. □

Definition 7. 

A RFUI (resp. RFLI) of a Γ Ring N is normal if${\overline{apr}}_{\eta }\left(0\right)=1 and {\underset{¯}{apr}}_{\eta }\left(0\right)=0$.

Example 2. 

Let R be the set of all integers. Then, R is a ring. Take N =$\Gamma$= R, and let a,b$ϵ N$,$\alpha ϵ \Gamma$. Suppose $a\alpha bϵ N$ is the product of a, $\alpha$, and b. Then, N is a $\Gamma$ Ring. Define the RFS in N as follows:

${\overline{apr}}_{\eta }\left(\mathrm{p}\right)=\left\{\begin{array}{c}1 if p=0 \\ t if p=\pm 1,\pm 2\dots , \end{array}\right.{\underset{¯}{apr}}_{\eta }\left(p\right)=\left\{\begin{array}{c}0 if p=0 \\ s if p=\pm 1,\pm 2\dots \end{array}\right.$

where t$ϵ \left[0,1\right)$, s$ϵ \left(0,1\right]$and t + s $\le 1$. By routine calculation, clearly $\eta$ is a RFI. Here, ${\overline{apr}}_{\eta }\left(0\right)=1 and {\underset{¯}{apr}}_{\eta }\left(0\right)=0$. Therefore, $\eta$ is normal.

Theorem 2. 

Assume that $\eta$ is a RFUI (resp. RFLI) of a Γ Ring N, and let${\overline{apr}}_{\eta }{}^{+}\left(p\right)={\overline{apr}}_{\eta }\left(p\right)+1-{\overline{apr}}_{\eta }\left(0\right),{\underset{¯}{ apr}}_{\eta }{}^{+}\left(p\right)={\underset{¯}{apr}}_{\eta }\left(p\right)-{\underset{¯}{apr}}_{\eta }\left(0\right). If {\overline{apr}}_{\eta }{}^{+}\left(p\right)+{\underset{¯}{apr}}_{\eta }{}^{+}\left(p\right)\le 1 for all pϵN$. Then is a normal RFUI (resp. RFLI) of N.

Proof. 

We observe that ${\overline{apr}}_{\eta }{}^{+}\left(0\right)=1,{\underset{¯}{apr}}_{\eta }{}^{+}\left(0\right)=0and {\overline{apr}}_{\eta }{}^{+}\left(p\right),{\underset{¯}{apr}}_{\eta }{}^{+}\left(p\right)ϵ\left[0,1\right] for every pϵN.$ Therefore, is a normal RFS. To prove it is a RFUI (resp. RFLI), let $p,q ϵ N$ and $\alpha ϵ \mathsf{\Gamma }$. Then, ${\overline{apr}}_{\eta }{}^{+}\left(p-q\right)$, and by our condition, we find ${\overline{ apr}}_{\eta }\left(p-q\right)+1-{\overline{ apr}}_{\eta }\left(0\right)\ge \left\{{\overline{apr}}_{\eta }\left(p\right)\wedge {\overline{apr}}_{\eta }\left(q\right)\right\}+1-{\overline{ apr}}_{\eta }\left(0\right)$=$\{{\overline{apr}}_{\eta }\left(p\right)+1-{\overline{apr}}_{\eta }\left(0\right)$}$\wedge \{{\overline{apr}}_{\eta }\left(q\right)+1-{\overline{apr}}_{\eta }\left(0\right)$} = ${\overline{ apr}}_{\eta }{}^{+}\left(p\right)\wedge {\overline{ apr}}_{\eta }{}^{+}\left(q\right) and {\overline{ apr}}_{\eta }{}^{+}\left(p\alpha q\right)={\overline{apr}}_{\eta }\left(p\alpha q\right)+1-{\overline{ apr}}_{\eta }\left(0\right)\ge {\overline{apr}}_{\eta }\left(q\right)+1-{\overline{apr}}_{\eta }\left(0\right)={\overline{ apr}}_{\eta }{}^{+}\left(q\right)$. A similar condition also holds for lower ideals. This shows that is a RFUI (resp. RFLI) of N. □

4. Characteristic Function on RFI in Γ Rings

The following section includes the characteristics of RFI and discusses some related theorems.

Theorem 3. 

$\eta$is an ideal of a Γ Ring N if and only if , where

${\overline{apr}}_{\tilde{\eta }}$(p) =$\left\{\begin{array}{l}1 p\in \eta \\ 0 otherwise\end{array}\right.$ and ${\underset{¯}{apr}}_{\tilde{\eta }}$ (p) =$\left\{\begin{array}{l}1 p\in \eta \\ 0 otherwise\end{array}\right.$

Then,$\tilde{\eta }$is a RFUI (resp. RFLI) of N.

Proof. 

Assume that $\eta$ is an ideal of N, and let $p,q\in N\mathrm{and}\alpha ϵ\mathsf{\Gamma }.\mathrm{If} p,q\in \eta ,$ and $p\alpha q\in \eta .$ Therefore, ${\overline{apr}}_{\tilde{\eta }}$($p-q$) = 1.

Apply the condition of the RFI and ${\overline{apr}}_{\tilde{\eta }}$($p\alpha q$) = 1$\ge {\overline{apr}}_{\tilde{\eta }}$($q)$ (as well as a similar p). Supposing the elements are not ideal, then we have ${\overline{apr}}_{\tilde{\eta }}$($p)=0$ and ${\underset{¯}{apr}}_{\tilde{\eta }}$ (p) = 0, and we find ${\overline{apr}}_{\eta }\left(p-q\right)\ge \left\{{\overline{apr}}_{\eta }\left(p\right)\wedge {\overline{apr}}_{\eta }\left(q\right)\right\},{\overline{apr}}_{\eta }\left(p\alpha q\right)\ge {\overline{apr}}_{\eta }\left(q\right) \left(\mathrm{also}\mathrm{resp}.p\right).$

In the same manner, lower ideals are also implemented. Hence, $\widetilde{ \eta }$ is a RFUI (resp. RFLI) of N. Conversely, let us assume that $\tilde{\eta }$ is a RFUI (resp. RFLI) of N. Let $p,q\in N\mathrm{and}\alpha ϵ \mathsf{\Gamma }.$ If $p,q\in \eta ,{\overline{apr}}_{\tilde{\eta }}$($p-q$)$\ge \left\{{\overline{apr}}_{\tilde{\eta }}\left(p\right)\wedge {\overline{apr}}_{\tilde{\eta }}\left(q\right)\right\}$ = 1, then ${\underset{¯}{apr}}_{\tilde{\eta }}(p-q$)$\le \left\{{\overline{apr}}_{\tilde{\eta }}\left(p\right)\vee {\overline{apr}}_{\tilde{\eta }}\left(q\right)\right\}$ = 0, and therfore $p-q\in \eta .{\overline{apr}}_{\tilde{\eta }}\left(p\alpha q\right)\ge {\overline{apr}}_{\tilde{\eta }}\left(q\right)=1$, (which is also similiar for the element p). ${\underset{¯}{apr}}_{\tilde{\eta }}(p\alpha q$)$\le {\underset{¯}{apr}}_{\tilde{\eta }}\left(q\right)=0$ such that $p\alpha q\in \eta$.

Therefore $\eta$ is a RFUI (resp. RFLI) of N. □

Theorem 4. 

Let I be the ideal of N. If the RFS in N is defined by

${\overline{apr}}_{\eta }$(p) = $\left\{\begin{array}{l}a if p\in I\\ b otherwise\end{array}\right.$and${\underset{¯}{apr}}_{\eta }$ (p) = $\left\{\begin{array}{l}c if p\in I\\ d otherwise\end{array}\right.$

then for all p$\in N and \alpha ϵ \Gamma$, where 0$\le b<a ,$0$\le d<c$, a + c$\le 1$, and b + d$\le 1,$then$\eta$is a RFUI (resp. RFLI) of N and U(${\overline{apr}}_{\eta };a)$= I = L(${\underset{¯}{apr}}_{\eta }$;c).

Proof. 

If $p,q\in \eta \mathrm{and}\alpha ϵ \mathsf{\Gamma }$, suppose atleast one of the p and q does not fit in I. Then, ${\overline{apr}}_{\eta }\left(p-q\right)\ge b$ = {${\overline{apr}}_{\eta }$(p)$\wedge {\overline{apr}}_{\eta }$(q)},${\underset{¯}{apr}}_{\eta }\left(p-q\right)\le d$. If $p,q\in I$, then $p-q\in I$, and so${\overline{apr}}_{\eta }\left(p-q\right)$ = a = {${\overline{apr}}_{\eta }$(p)$\wedge {\overline{apr}}_{\eta }\left(\mathrm{q}\right)$}. Suppose that $q\in I,p\in N$, and $\alpha ϵ\mathsf{\Gamma }.\mathrm{Then},\mathrm{p}\alpha q\in I\mathrm{and}{\overline{apr}}_{\eta }\left(p\alpha q\right)=a={\overline{apr}}_{\eta }\left(q\right)$ (also resp. the element p). In the case where $q\notin I,$ then ${\overline{apr}}_{\eta }$($p\alpha q)=b={\overline{apr}}_{\eta }$($q)$ (also resp. the element p). In addition to the same steps, we also used a lower approximation, resulting in$p,q\in \mathrm{I}, \mathrm{then} {\underset{¯}{apr}}_{\eta }\left(p-q\right)=d$. If $q\in I,$ then ${\underset{¯}{apr}}_{\eta }\left(p\alpha q\right)=c$, and if $q\notin I,\mathrm{then}{\underset{¯}{apr}}_{\eta }$ ($p\alpha q)=d.$ We can conclude that $\eta$ is a RFUI (resp. RFLI) of N. □

Theorem 5. 

An RFS $\eta =⟨{\overline{apr}}_{\eta },{\underset{¯}{apr}}_{\eta }⟩$ in a $\Gamma Ring N is an$RFUI (resp. RFLI) if andonly if${\eta }_{⟨t,s⟩}$ = {p$\in N|{\overline{apr}}_{\eta }\left(p\right) \ge t,{\underset{¯}{apr}}_{\eta }$ ($p)\le s\}$ is an upper (resp. lower) ideal of N for ${\overline{apr}}_{\eta }\left(0\right) \ge t$,${\underset{¯}{apr}}_{\eta }$ ($0)\le s.$

Proof. 

Let $\eta$ be a RFUI (resp. RFLI) of N, and let ${\overline{apr}}_{\eta }\left(0\right) \ge t$ and${\underset{¯}{ apr}}_{\eta }$ ($0)\le s$. If we take two elements p,q and $\alpha ϵ \mathsf{\Gamma },\mathrm{then}{\overline{apr}}_{\eta }\left(p\right) \ge t$,${\overline{apr}}_{\eta }\left(q\right) \ge t, and {\underset{¯}{apr}}_{\eta }$(p)$,{\underset{¯}{apr}}_{\eta }$(q)$\le s.$ We know the RFI conditions ${\overline{apr}}_{\eta }\left(p-q\right)$ = {${\overline{apr}}_{\eta }$(p)$\wedge {\overline{apr}}_{\eta }$(q)}$\ge t$ and ${\overline{apr}}_{\eta }\left(p\alpha q\right)\ge {\overline{apr}}_{\eta }\left(q\right)\ge$t (also resp. p).

Similarly, the same steps are also followed by lower ideals, and finally we have ${\underset{¯}{apr}}_{\eta }\left(p-q\right)\le s and {\underset{¯}{apr}}_{\eta }\left(p\alpha q\right)\le s$.

Therefore, is a RFUI (resp. RFLI) of N.

Conversely, assume that ${\eta }_{⟨t,s⟩}$ is a RFUI (resp. RFLI) of N. Then, ${\overline{apr}}_{\eta }\left(0\right)\ge t$ and ${\underset{¯}{apr}}_{\eta }$ ($0)\le s.$ Let $p,q\in N$ be such that ${\overline{apr}}_{\eta }\left(p\right)=t_1$, ${\overline{apr}}_{\eta }\left(q\right)=t_2$, and ${\underset{¯}{apr}}_{\eta }\left(p\right)=s_1$,${\underset{¯}{apr}}_{\eta }\left(q\right)=s_2$. Then, p and q such that $t_2\le t_1$ and $s_2\ge s_1$.

Without loss of generality, we may assume that it follows that such that $p,q\in {\eta }_{⟨t_1,s_1⟩}$. Since ${\eta }_{⟨t_1,s_1⟩}$ is an ideal of N, we have $p-q\in {\eta }_{⟨t_1,s_1⟩}$ and $p\alpha q\in {\eta }_{⟨t_1,s_1⟩}$ for all $\alpha ϵ\mathsf{\Gamma }$, where ${\overline{apr}}_{\eta }\left(p-q\right)\ge t_1\ge t_2$ = {${\overline{apr}}_{\eta }$(p)$\wedge {\overline{apr}}_{\eta }$(q)},${\overline{apr}}_{\eta }\left(p\alpha q\right))\ge t_1\ge t_2={\overline{apr}}_{\eta }\left(q\right)$ and ${\underset{¯}{apr}}_{\eta }\left(p-q\right)\le s_1\le s_2$ = {${\underset{¯}{apr}}_{\eta }$(p)$\wedge {\underset{¯}{apr}}_{\eta }$(q)},${\underset{¯}{apr}}_{\eta }\left(p\alpha q\right)))\le s_1\le s_2={\underset{¯}{apr}}_{\eta }\left(q\right)$.

We conclude that $\eta \mathrm{is}\mathrm{a}\mathrm{RFUI}$ (resp. RFLI) of N. □

Theorem 6. 

If the RFS RFUI (resp. RFLI) of a $\Gamma Ring,$ then the sets N${\overline{apr}}_{\eta }$ = {p$\in N$/${\overline{apr}}_{\eta }\left(p\right)={\overline{apr}}_{\eta }\left(0\right)\}$ and N${\underset{¯}{apr}}_{\eta }$ (P) = {p$\in N$/${\underset{¯}{apr}}_{\eta }\left(p\right)={\underset{¯}{apr}}_{\eta }\left(0\right)\}$ are upper (resp.lower) ideals.

Proof. 

Consider $p,q\in$ N ${\overline{apr}}_{\eta } and \alpha ϵ\mathsf{\Gamma }.$ Then, ${\overline{apr}}_{\eta }$($p$) = ${\overline{apr}}_{\eta }$(0) and ${\overline{apr}}_{\eta }$($q$) = ${\overline{apr}}_{\eta }$(0), since $\eta$ is a RFUI (resp. RFLI). ${\overline{apr}}_{\eta }$($p-q)\ge$ {${\overline{apr}}_{\eta }$($p$)$\wedge {\overline{apr}}_{\eta }$($q$)}=${\overline{apr}}_{\eta }$(0), but ${\overline{apr}}_{\eta }$(0)$\ge {\overline{apr}}_{\eta }$($p-q)$. Therefore, $p-q\in$ $N {\overline{apr}}_{\eta }$ and ${\overline{apr}}_{\eta }$($p\alpha q)\ge {\overline{apr}}_{\eta }$(q) = ${\overline{apr}}_{\eta }$(0) (also resp. the element $p$). Hence, $p\alpha q\in$ N${\overline{ apr}}_{\eta }$, and therefore $N{\overline{apr}}_{\eta }$ is the upper (resp. lower) ideal of M. We followed the same steps followed by the lower ideals and finally arrived at$p-q\in$ N${\underset{¯}{apr}}_{\eta } and p\alpha q\in$ N${\underset{¯}{apr}}_{\eta }$. Therefore, $N{\underset{¯}{apr}}_{\eta }$ is the upper (resp. lower) ideal of N. □

5. Operations on RFI in $\Gamma$ Rings

A few operators of RFI and their related theorems are presented in this section.

Definition 8. 

Let and be two rough fuzzy subsets of a Γ Ring N. Then, the rough sum of X and Y is defined to be the rough fuzzy setin N given by

${\overline{apr}}_{X\oplus Y}\left(P\right)=\left\{\begin{array}{c}{\displaystyle \underset{p=q+r}{\bigvee }}\left\{{\overline{apr}}_X\left(q\right)\wedge {\overline{apr}}_Y\left(r\right)\right\}ifp=q+r\\ 0 otherwise\end{array}\right.$

${\underset{¯}{apr}}_{X\oplus Y}\left(P\right)=\left\{\begin{array}{c}{\displaystyle \underset{p=q+r}{\bigwedge }}\left\{{\underset{¯}{apr}}_X\left(q\right)\vee {\underset{¯}{apr}}_Y\left(r\right)\right\}ifp=q+r\\ 1 otherwise\end{array}\right.$

Theorem 7. 

If and are two RFUI (resp. RFLI) ideals of N, then the rough sum is a RFUI (resp. RFLI) of N.

Proof. 

For any $p,q\in N$, we have ${\overline{apr}}_{X\oplus Y}\left(p\right)\wedge {\overline{apr}}_{X\oplus Y}\left(q\right)$, and by the definition of $A\oplus B$, we find

$=\vee \left\{{\overline{apr}}_X\left(x\right)\wedge {\overline{apr}}_Y\left(y\right):p=x+y\right\}\wedge \vee \left\{{\overline{apr}}_X\left(c\right)\wedge {\overline{apr}}_Y\left(d\right):q=c+d\right\}=\vee \{({\overline{apr}}_X\left(x\right)\wedge {\overline{apr}}_Y\left(y)\right)\wedge ({\overline{apr}}_X\left(c\right)\wedge {\overline{apr}}_Y\left(d\right)):p=x+y$,$q=c+d$}

By substituting $-q=-c-d$ into the above equation, we obtain

= $\vee \{({\overline{apr}}_X\left(x\right)\wedge {\overline{apr}}_Y\left(y)\right)\wedge ({\overline{apr}}_X\left(-c\right)\wedge {\overline{apr}}_Y\left(-d\right)):p=x+y,-q=-c-d\}$

$=\vee \left\{\left({\overline{apr}}_X\left(x\right)\wedge {\overline{apr}}_X\left(-c\right)\right)\wedge \left({\overline{apr}}_Y\left(y\right)\wedge {\overline{apr}}_Y\left(-d\right)\right)\right\}:p=x+y,-q=-c-d\}$

$\le \vee \left\{{\overline{apr}}_X\left(x-c\right)\wedge {\overline{apr}}_X\left(y-d\right):p-q=\left(x-c\right)+\left(y-d\right)\right\}$ = ${\overline{apr}}_{X\oplus Y}\left(p-q\right),$

We also we ${\overline{apr}}_{X\oplus Y}\left(p\right)=\vee \left\{({\overline{apr}}_X\left(x\right)\wedge {\overline{apr}}_Y\left(y\right):p=x+y\right\}\le \vee \left\{{\overline{apr}}_X\left(x\alpha q\right)\wedge {\overline{apr}}_X\left(y\alpha q\right)):p\alpha q=x\alpha q+y\alpha q\right\}$ = $\vee \left\{({\overline{apr}}_X\left(u\right)\wedge {\overline{apr}}_Y\left(v\right):p\alpha q=u+v\right\}$ = ${\overline{apr}}_{X\oplus Y}\left(p\alpha q\right)$. Similar conditions also hold for the lower ideals. Therefore, we conclude that $X\oplus Y$ is a RFUI (resp. RFLI) of N. □

Definition 9. 

Let be two rough fuzzy subsets of a Γ Ring N. Then, the composition of X and Y is in N, given by

${\overline{apr}}_{X\circ Y}=\left(p\right)=\bigvee \left\{\begin{array}{c}{\displaystyle \underset{1\le i\le k}{\bigwedge }}\left\{{\overline{apr}}_X\left(x_i\right)\wedge {\overline{apr}}_Y\left(y_i\right)\right\}:p={\displaystyle \sum _1^k}{x}_i\alpha y_i,x_i{y}_iϵN,\alpha ϵ\Gamma ,kϵZ^{+},\\ 0 otherwise\end{array}\right.$

${\underset{¯}{apr}}_{X\circ Y}\left(p\right)=\bigwedge \left\{\begin{array}{c}{\displaystyle \underset{1\le i\le k}{\bigvee }}\left\{{\underset{¯}{apr}}_A\left(x_i\right)\vee {\underset{¯}{apr}}_B\left(y_i\right)\right\}:p={\displaystyle \sum _1^k}{x}_i\alpha y_i,x_i{y}_iϵN,\alpha ϵ\Gamma ,kϵZ^{+},\\ 1 otherwise\end{array}\right.$

Theorem 8. 

Let be two RFI in a Ring N. Then, $X\circ Y$is a RFUI (resp. RFLI) in N.

Proof. 

For any $p,q\in N$, we have ${\overline{apr}}_{AX\circ Y}\left(p-q\right)$, and by the definition of$X\circ Y$, we have

${\overline{apr}}_{X\circ Y}\left(p-q\right)=\bigwedge \left\{{\displaystyle \underset{1\le i\le k}{\bigwedge }}{\overline{apr}}_X\left(u_i\right)\wedge {\overline{apr}}_Y\left(v_i\right):p-q={\displaystyle \sum _1^k}{u}_i\alpha v_i,u_i,v_iϵN,\alpha ϵ\mathsf{\Gamma },kϵZ^{+}\right\}$

$\ge \vee \{\left({\displaystyle \underset{1\le i\le m}{\bigwedge }}{\overline{apr}}_X\left(x_i\right)\wedge {\overline{apr}}_Y\left(y_i\right)\right)\wedge \left({\displaystyle \underset{1\le i\le k}{\bigwedge }}{\overline{apr}}_X\left(-c_i\right)\wedge {\overline{apr}}_Y\left(d_i\right)\right)$

$:p={\displaystyle \sum _1^m}{x}_i\alpha y_i,-q={\displaystyle \sum _1^n}-c_i\alpha d_i,x_i,y,-c_i,d_iϵM,\alpha ϵ\mathsf{\Gamma } and m.nϵZ^{+}\}$

$=\vee \{\left({\displaystyle \underset{1\le i\le m}{\bigwedge }}{\overline{apr}}_X\left(x_i\right)\wedge {\overline{apr}}_Y\left(y_i\right)\right)\wedge \left({\displaystyle \underset{1\le i\le k}{\bigwedge }}{\overline{apr}}_X\left(-c_i\right)\wedge {\overline{apr}}_Y\left(d_i\right)\right)$

$:p={\displaystyle \sum _1^m}{x}_i\alpha y_i,q={\displaystyle \sum _1^n}{c}_i\alpha d_i,x_i,y,-c_i,d_iϵM,\alpha ϵ\mathsf{\Gamma } and m.nϵZ^{+}\}$

$=\vee \left\{\left({\displaystyle \underset{1\le i\le m}{\bigwedge }}{\overline{apr}}_X\left(x_i\right)\wedge {\overline{apr}}_Y\left(y_i\right)\right):p={\displaystyle \sum _1^m}{x}_i\alpha y_i,x_i,y_iϵN,\alpha ϵ\mathsf{\Gamma }andmϵZ^{+}\right\}\wedge$

$\vee \left\{\left({\displaystyle \underset{1\le i\le k}{\bigwedge }}{\overline{apr}}_X\left(-c_i\right)\wedge {\overline{apr}}_Y\left(d_i\right)\right),q={\displaystyle \sum _1^n}{c}_i\alpha d_i,x_i,y_i,c_i,d_iϵN,\alpha ϵ\mathsf{\Gamma } and nϵZ^{+}\right\}$

${\overline{apr}}_{X\circ Y}\left(p-q\right)={\overline{apr}}_{X\circ Y}\left(p\right)\wedge {\overline{apr}}_{X\circ Y}\left(q\right)$

and ${\overline{apr}}_{X\circ Y}\left(p\right)=\vee \left\{\left({\displaystyle \underset{1\le i\le m}{\bigwedge }}{\overline{apr}}_X\left(x_i\right)\wedge {\overline{apr}}_Y\left(y_i\right)\right):p={\displaystyle \sum _1^m}{x}_i\alpha y_i{x}_i,y_iϵN,\alpha ϵ\mathsf{\Gamma }andmϵZ^{+}\right\}$

$\le \vee \left\{\left({\displaystyle \underset{1\le i\le m}{\bigwedge }}{\overline{apr}}_X\left(x_i\right)\wedge {\overline{apr}}_Y\left(y_i\right)\right):p\alpha q={\displaystyle \sum _1^m}{x}_i\alpha (y_i\alpha q)x_i,y_i\alpha qϵM,\alpha ϵ\mathsf{\Gamma }andmϵZ^{+}\right\}$

$=\vee \left\{\left({\displaystyle \underset{1\le i\le m}{\bigwedge }}{\overline{apr}}_X\left(u_i\right)\wedge {\overline{apr}}_Y\left(v_i\right)\right):p\alpha q={\displaystyle \sum _1^m}{u}_i\alpha v_i,u_i,v_iϵM,\alpha ϵ\mathsf{\Gamma }andmϵZ^{+}\right\}={\overline{apr}}_{X\circ Y}\left(p\alpha q\right)$.

The same steps are also followed by lower ideals, and finally we obtain ${\underset{¯}{apr}}_{X\circ Y}\left(p-q\right)={\underset{¯}{apr}}_{X\circ Y}\left(p\right)\wedge {\underset{¯}{apr}}_{X\circ Y}\left(q\right)$ and ${\underset{¯}{apr}}_{X\circ Y}\left(p\alpha q\right)\le {\underset{¯}{apr}}_{X\circ Y}\left(p\right)$. Therefore, $X\circ Y$is a RFUI (resp. RFLI) of N. □

Definition 10. 

Let be two RF subsets in a Ring N. Then, the product of A and B, constructed as A$\Gamma B,$is

${\overline{apr}}_{X\mathsf{\Gamma }Y}\left(P\right)=\left\{\begin{array}{c}{\displaystyle \underset{p=q\alpha r}{\bigvee }}\left\{{\overline{apr}}_X\left(q\right)\wedge {\overline{apr}}_Y\left(r\right)\right\}ifp=q\alpha r\\ 0 otherwise\end{array}\right.$

${\underset{¯}{apr}}_{X\mathsf{\Gamma }Y}\left(P\right)=\left\{\begin{array}{c}{\displaystyle \underset{p=q\alpha r}{\bigwedge }}\left\{{\underset{¯}{apr}}_X\left(q\right)\vee {\underset{¯}{apr}}_Y\left(r\right)\right\}ifp=q\alpha r\\ 1 otherwise\end{array}\right.$

Theorem 9. 

Let be two RFUIs (resp. RFLIs) of N. Then, A$\cap B$ is a RFUI (resp. RFLI) of N. If X is a rough fuzzy right ideal, and Y is a rough fuzzy left ideal, then$X\Gamma Y\subseteq X\cap Y.$

Proof. 

Consider X and Y to be RFUIs (resp. RFLIs) of N, and let p, q$ϵN.$ Then,${\overline{apr}}_{\mathrm{X}\cap Y}\left(p-q\right)={\overline{apr}}_{\mathrm{X}\cap Y}\left(p-q\right)\wedge {\overline{apr}}_{\mathrm{X}\cap Y}\left(p-q\right)$. By applying the condition of RFI and combining the terms p and q, we finally obtain {${\overline{apr}}_{\mathrm{X}\cap Y}\left(p\right)\wedge {\overline{apr}}_{\mathrm{X}\cap Y}\left(q\right)\}.$

Additionally, ${\overline{apr}}_{\mathrm{X}}\left(p\alpha q\right)\ge {\overline{apr}}_{\mathrm{X}}\left(q\right)\left[resp.{\overline{apr}}_{\mathrm{X}}\left(p\alpha q\right)\ge {\overline{apr}}_{\mathrm{X}}\left(p\right)\right]$ and ${\overline{apr}}_{\mathrm{Y}}\left(p\alpha q\right)\ge {\overline{apr}}_{\mathrm{Y}}\left(q\right)\left[resp.{\overline{apr}}_{\mathrm{Y}}\left(p\alpha q\right)\ge {\overline{apr}}_{\mathrm{Y}}\left(p\right)\right].$Now, ${\overline{apr}}_{\mathrm{X}\cap Y}\left(p\alpha q\right)={\overline{apr}}_{\mathrm{X}}\left(p\alpha q\right)\wedge {\overline{apr}}_Y\left(p\alpha q\right)\ge {\overline{apr}}_{\mathrm{X}}\left(q\right)\wedge {\overline{apr}}_{\mathrm{X}}\left(q\right)={\overline{apr}}_{\mathrm{X}\cap Y}\left(q\right) \left(also resp. p\right).$

The same steps are also followed by the lower ideals. Therefore, $X\cap Y$ is an RFUI (resp. RFLI) of N. To prove the second part if ${\overline{apr}}_{X\mathsf{\Gamma }Y}\left(p\right)=0 and {\underset{¯}{apr}}_{X\mathsf{\Gamma }Y}\left(p\right)=1,$there is nothing to show. By the definition of $X\mathsf{\Gamma }Y$, ${\overline{apr}}_X\left(p\right)$=${\overline{apr}}_X\left(q\alpha r\right)\ge {\overline{apr}}_X\left(q\right)$,${\underset{¯}{apr}}_X\left(p\right)$ = ${\underset{¯}{apr}}_X\left(q\alpha r\right)\le {\underset{¯}{apr}}_X\left(q\right)$, since X is a rough fuzzy right ideal, and Y is a rough fuzzy left ideal, we have ${\overline{apr}}_{\mathrm{X}}\left(p\right)={\overline{apr}}_{\mathrm{X}}\left(q\alpha r\right)\ge {\overline{apr}}_{\mathrm{X}}\left(q\right) and {\overline{apr}}_{\mathrm{Y}}\left(p\right)={\overline{apr}}_{\mathrm{Y}}\left(q\alpha r\right)\ge {\overline{apr}}_{\mathrm{Y}}\left(r\right)$ and ${\underset{¯}{apr}}_{\mathrm{X}}\left(p\right)={\underset{¯}{apr}}_{\mathrm{X}}\left(q\alpha r\right)\le {\underset{¯}{apr}}_{\mathrm{X}}\left(q\right) and {\underset{¯}{apr}}_{\mathrm{Y}}\left(p\right)={\underset{¯}{apr}}_{\mathrm{Y}}\left(q\alpha r\right)\le {\underset{¯}{apr}}_{\mathrm{Y}}\left(r\right).$

By definition we have

${\overline{apr}}_{X\Gamma Y}\left(P\right)={\displaystyle \underset{p=q\alpha r}{\bigvee }}\left\{{\overline{apr}}_X\left(q\right)\wedge {\overline{apr}}_Y\left(r\right)\right\}\le {\overline{apr}}_X\left(q\right)\wedge {\overline{apr}}_Y\left(r\right)={\overline{apr}}_{X\cap Y}\left(p\right),$

${\underset{¯}{apr}}_{X\mathsf{\Gamma }Y}\left(P\right)={\displaystyle \underset{p=q\alpha r}{\bigwedge }}\left\{{\underset{¯}{apr}}_X\left(q\right)\vee {\underset{¯}{apr}}_Y\left(r\right)\right\}\ge \left\{{\underset{¯}{apr}}_X\left(q\right)\vee {\underset{¯}{apr}}_Y\left(r\right)\right\}={\underset{¯}{apr}}_{X\cap Y}\left(p\right)$

Hence, $X\Gamma Y\subseteq X\cap Y.$ □

Corollary 1. 

If are two RFUIs (resp. RFLI) of N, then$X\cup Y$ is a RFUI (resp. RFLI) of N.

Definition 11. 

A $\Gamma$ Ring N is regular if there exists $p\in N,\forall x\in N$ and $\alpha ,\beta \in \Gamma$, and then x = x$\alpha p\beta x$.

Result 1. 

A $\Gamma$ Ring N is said to be regular$\iff if I\Gamma J=I\cap J$ for each right ideal I and for each left ideal J of N.

Theorem 10. 

A $\Gamma$ Ring N is regular if for each rough fuzzy right ideal X and for each rough fuzzy left ideal Y of N,$X\Gamma Y=X\cap Y.$

Proof. 

Suppose N is regular by Theorem 9, where $X\mathsf{\Gamma }Y\subseteq \mathrm{X}\cap Y.$ To prove $\mathrm{X}\cap Y\subseteq X\mathsf{\Gamma }Y$, let $x\in N$ and $\alpha ,\beta \in \Gamma .$ Then, by definition,$\exists p\in N$ such that x = x$\alpha p\beta x$. Thus ${\overline{apr}}_X\left(x\right)={\overline{apr}}_X\left(\mathrm{x}\alpha p\beta x\right)\ge {\overline{apr}}_X\left(\mathrm{x}\alpha p\right)\ge {\overline{apr}}_X\left(x\right)\mathrm{and}$, ${\underset{¯}{apr}}_X\left(x\right)={\underset{¯}{apr}}_X\left(\mathrm{x}\alpha p\beta x\right)\le {\underset{¯}{apr}}_X\left(\mathrm{x}\alpha p\right)\le {\underset{¯}{apr}}_X\left(x\right).{\overline{apr}}_X\left(\mathrm{x}\alpha a\right)\ge {\overline{apr}}_X\left(\mathrm{x}\right)\mathrm{and}{\underset{¯}{ apr}}_X\left(\mathrm{x}\alpha a\right)\le {\underset{¯}{apr}}_X\left(\mathrm{x}\right)$. On the other hand, ${\overline{apr}}_{X\mathsf{\Gamma }Y}\left(x\right)={\vee }_{\mathrm{x}=\mathrm{x}\alpha p\beta x}\left\{{\overline{apr}}_X\left(\mathrm{x}\alpha p\right)\wedge {\overline{apr}}_Y\left(x\right)\right\}\ge {\overline{apr}}_{\mathrm{X}}\left(x\right)\wedge {\overline{apr}}_{\mathrm{Y}}\left(x\right)={\overline{apr}}_{\mathrm{X}\cap Y}\left(x\right)$ and ${\underset{¯}{apr}}_{X\mathsf{\Gamma }Y}\left(P\right)={\vee }_{\mathrm{x}=\mathrm{x}\alpha p\beta x}\left\{{\underset{¯}{apr}}_X\left(\mathrm{x}\alpha p\right)\vee {\underset{¯}{apr}}_Y\left(x\right)\right\}\le \left\{{\underset{¯}{apr}}_X\left(x\right)\vee {\underset{¯}{apr}}_Y\left(x\right)\right\}={\underset{¯}{apr}}_{\mathrm{X}\cap Y}\left(x\right).$ Thus, $X\cap Y\subseteq X\Gamma Y$, and hence $X\Gamma Y=\mathrm{X}\cap Y.$ □

Definition 12. 

If$\left\{{\eta }_i\right\}{ }_{iϵj }$ is an arbitrary family of RFS in X, where${\eta }_i=⟨\wedge {\overline{apr}}_{{\eta }_i},\vee {\underset{¯}{apr}}_{{\eta }_i}⟩$for each $i\in J$, then$\left(i\right)\cap {\eta }_i=⟨\wedge {\overline{apr}}_{{\eta }_i},\vee {\underset{¯}{apr}}_{{\eta }_i}⟩\left(ii\right)\cup {\eta }_i=⟨\vee ,{\overline{apr}}_{{\eta }_i},,,\wedge ,{\underset{¯}{apr}}_{{\eta }_i}⟩$.

Theorem 11. 

If $\left\{{\eta }_i\right\}{ }_{iϵj}$ is a family of RFUI (resp. RELI) of N, then $\cup {\eta }_i=⟨\vee {\overline{apr}}_{{\eta }_i},\wedge {\underset{¯}{apr}}_{{\eta }_i}⟩;$ is a RFUI (resp. RFLI) of N.

Proof. 

Let $p,q\in N$ and $\alpha ϵ\mathsf{\Gamma }$. Then, $\left({{\displaystyle \cup }}_{i\in J}{\overline{apr}}_{{\eta }_i}\right)\left(p-q\right)$. By definition, we have $\left({\vee }_{i\in J}{\overline{apr}}_{{\eta }_i}\left(p-q\right)\right)\ge {\vee }_{i\in J}\left({\overline{apr}}_{{\eta }_i}\left(p\right)\wedge {\overline{apr}}_{{\eta }_i}\left(q\right)\right)=\left({\vee }_{i\in J}{\overline{apr}}_{{\eta }_i}\left(p\right)\right)\wedge \left({\vee }_{i\in J}{\overline{apr}}_{{\eta }_i}\left(q\right)\right)$=$\left({{\displaystyle \cup }}_{i\in J}{\overline{apr}}_{{\eta }_i}\right)\left(p\right)\wedge \left({{\displaystyle \cup }}_{i\in J}{\overline{apr}}_{{\eta }_i}\right)\left(q\right)$.

In addition, $\left({{\displaystyle \cup }}_{i\in J}{\overline{apr}}_{{\eta }_i}\right)\left(p\alpha q\right)={\vee }_{i\in J}{\overline{apr}}_{{\eta }_i}\left(p\alpha q\right)\ge {\vee }_{i\in J}{\overline{apr}}_{{\eta }_i}\left(q\right)=\left({{\displaystyle \cup }}_{i\in J}{\overline{apr}}_{{\eta }_i}\right)\left(q\right)$ and $\left({{\displaystyle \cup }}_{i\in J}{\overline{apr}}_{{\eta }_i}\right)\left(p\alpha q\right)\ge \left({{\displaystyle \cup }}_{i\in J}{\overline{apr}}_{{\eta }_i}\right)\left(p\right).$ The same is also true for lower ideals. Finally, we obtain $\left({{\displaystyle \cup }}_{i\in J}{\underset{¯}{apr}}_{{\eta }_i}\right)\left(p-q\right)=\left({{\displaystyle \cup }}_{i\in J}{\underset{¯}{apr}}_{{\eta }_i}\right)\left(p\right)\vee \left({{\displaystyle \cup }}_{i\in J}{\underset{¯}{apr}}_{{\eta }_i}\right)\left(q\right)$ and $\left({{\displaystyle \cup }}_{i\in J}{\underset{¯}{apr}}_{{\eta }_i}\right)\left(p\alpha q\right)\le \left({{\displaystyle \cup }}_{i\in J}{\underset{¯}{apr}}_{{\eta }_i}\right)\left(q\right).\left(\mathrm{resp}.\left({{\displaystyle \cup }}_{i\in J}{\underset{¯}{apr}}_{{\eta }_i}\right)\left(p\alpha q\right)\le \left({{\displaystyle \cup }}_{i\in J}{\underset{¯}{apr}}_{{\eta }_i}\right)\left(p\right)\right).$

Consequently, ${{\displaystyle \cup }}_{i\in J}{\eta }_i$ is a RFUI (resp. RFLI) of N. □

6. Rough Fuzzy Prime Ideals (RFPIs) in $\Gamma$ Rings

A few theorems are proven regarding the rough fuzzy prime ideals discussed in this section.

Definition 13. 

An ideal $\mathcal{P}$of the $\Gamma$ Ring N is said to be prime if, for any ideals X and Y of N,$X\Gamma Y\subseteq \mathcal{P}\Rightarrow X\subseteq \mathcal{P}$ or $Y\subseteq \mathcal{P}.$

Definition 14. 

Let $\mathcal{P}$ be a rough fuzzy ideal (RFI) of a $\Gamma$ Ring N. Then, $\mathcal{P}$ is said to be prime if $\mathcal{P}$ is not a constant mapping and, for any RFI X, Y of a $\Gamma$ Ring N, $X\Gamma Y\subseteq \mathcal{P}$ implies $X\subseteq \mathcal{P}$ or$Y\subseteq \mathcal{P} .$

Theorem 12. 

Let $\mathcal{U}$ be an ideal of a $\Gamma$ Ring N $\ni \mathcal{U}\ne N$ Then, $\mathcal{U}$ is a prime ideal of N if $\left({\overline{apr}}_{{\chi }_{\mathcal{U}}},{{\underset{¯}{apr}}_{\overline{\chi }}}_{\mathcal{U}}\right)$ is a RFPI of N.

Proof. 

Suppose that $\mathcal{U}$ is a prime ideal of N, and let $\mathcal{U}=\left({\overline{apr}}_{{\chi }_{\mathcal{U}}},{{\underset{¯}{apr}}_{\overline{\chi }}}_{\mathcal{U}}\right).$ Since$\mathcal{U}\ne N$,$\mathcal{P}$ is not a constant mapping on N. Let X and Y be two RFI of N such that $X\Gamma Y\subseteq \mathcal{P}$ and$X\not\subset \mathcal{P}$ or $Y\not\subset \mathcal{P}$. Then, $\exists p,q\in N$ such that${\overline{apr}}_X\left(p\right)>{\overline{apr}}_{\mathcal{P}}\left(p\right)={{\underset{¯}{apr}}_{\overline{\chi }}}_{\mathcal{U}}\left(p\right),{\underset{¯}{apr}}_X\left(p\right)<{\underset{¯}{apr}}_{\mathcal{P}}\left(p\right)={{\underset{¯}{apr}}_{\overline{\chi }}}_{\mathcal{U}}\left(p\right)$ and ${\overline{apr}}_Y\left(p\right)>{\overline{apr}}_{\mathcal{P}}\left(p\right)={{\underset{¯}{apr}}_{\overline{\chi }}}_{\mathcal{U}}\left(p\right),{\underset{¯}{apr}}_Y\left(p\right)>{\underset{¯}{apr}}_{\mathcal{P}}\left(p\right)<{{\underset{¯}{apr}}_{\overline{\chi }}}_{\mathcal{U}}\left(p\right)$. Thus, ${\overline{apr}}_X\left(p\right)\ne 0,{\underset{¯}{apr}}_X\left(p\right)\ne 1and{\overline{apr}}_Y\left(q\right)\ne 0,{\underset{¯}{apr}}_Y\left(q\right)\ne 1,$ but ${{\underset{¯}{apr}}_{\overline{\chi }}}_{\mathcal{U}}\left(p\right)=0$ and ${\underset{¯}{apr}}_{\chi }{}_{\mathcal{U}}\left(p\right)=0\mathrm{and}{\underset{¯}{apr}}_{\chi }{}_{\mathcal{U}}\left(q\right)=0$ such that $p\ne \mathcal{U}, q\ne \mathcal{U}. Since \mathcal{U}$ is a prime ideal of N, it follows from Theorem 5 [3] that there exists r$\in N$ and $\alpha ,\beta \in \Gamma$ such that $p\alpha r\beta q\notin \mathcal{U}$. Let c = $p\alpha r\beta q$. Then, ${{\underset{¯}{apr}}_{\overline{\chi }}}_{\mathcal{U}}\left(c\right)=0and {{\underset{¯}{apr}}_{\overline{\chi }}}_{\mathcal{U}}\left(c\right)$ = 1. Thus, $X\mathsf{\Gamma }Y\left(c\right)=\left(0,1\right)$, but ${\overline{apr}}_{X\mathsf{\Gamma }Y}\left(c\right)={\vee }_{c=m\gamma n}[{\overline{apr}}_X\left(m\right)\wedge {\overline{apr}}_Y\left(n\right)]\ge {\overline{apr}}_X\left(p\alpha r\right)\wedge {\overline{apr}}_Y\left(q\right)$ (by the definition of c)$\ge {\overline{apr}}_X\left(p\right)\wedge {\overline{apr}}_Y\left(q\right)>0 (since it is\ne 0$), and by following the same steps for the lower ideals, we find ${\underset{¯}{apr}}_X\left(p\right) \vee {\underset{¯}{apr}}_Y\left(q\right)<1$.

Then, $X\mathsf{\Gamma }Y\left(a\right)\ne \left(0,1\right)$. This contradicts the result. Hence, for any two RFI X and Y, $X\mathsf{\Gamma }Y\subseteq \mathcal{P}$, which implies $X\subseteq \mathcal{P}$or $Y\subseteq \mathcal{P}$. Hence, $\mathcal{P}$ is a RFPI of N. $(\Leftarrow )$Suppose that $\mathcal{P}$ is not a constant mapping on N, where $\mathcal{U}\ne N.$Let X and Y be two ideals of N such that $X\mathsf{\Gamma }Y\subseteq \mathcal{U}$, and let $\overline{X}=\left({\overline{apr}}_{{\chi }_X},{{\underset{¯}{apr}}_{\overline{\chi }}}_X\right)$ and $\overline{Y}=\left({\overline{apr}}_{{\chi }_Y},{{\underset{¯}{apr}}_{\overline{\chi }}}_Y\right)$ be two fuzzy ideals of N. Consider $\overline{X}\Gamma \overline{Y}\subseteq \mathcal{U}.$ Let $p\in N$ if $\overline{X}\Gamma \overline{Y}\left(x\right)=\left(0,1\right)$. Then, clearly $\overline{X}\Gamma \overline{Y}\subseteq \mathcal{U}$.

Suppose $\overline{X}\Gamma \overline{Y}\ne \left(0,1\right)$. Then, ${\overline{apr}}_{\overline{X}\mathsf{\Gamma }\overline{Y}}\left(p\right)={\vee }_{p=q\gamma r}[{\overline{apr}}_{{\chi }_X}\left(q\right)\wedge {\overline{apr}}_{{\chi }_Y}\left(r\right)]\ne 0$ and ${\underset{¯}{apr}}_{\overline{X}\mathsf{\Gamma }\overline{Y}}\left(p\right)={\wedge }_{p=q\gamma r}\left[{{\underset{¯}{apr}}_{\overline{\chi }}}_X\left(q\right)\vee {{\underset{¯}{apr}}_{\overline{\chi }}}_Y\left(r\right)\right]\ne 1$. There exists $q,r\in N$ with p = q$\alpha r$ such that ${\overline{apr}}_{{\chi }_X}\left(q\right)\ne 0$,${{\underset{¯}{apr}}_{\overline{\chi }}}_X\left(q\right)\ne 1$, and ${{\underset{¯}{apr}}_{\overline{\chi }}}_Y\left(r\right)\ne 0,{{\underset{¯}{apr}}_{\overline{\chi }}}_Y\left(r\right)\ne 1$. Therefore, ${{\overline{apr}}_{\chi }}_Y\left(q\right)=1,{{\underset{¯}{apr}}_{\overline{\chi }}}_Y\left(q\right)=0$ and ${{\overline{apr}}_{\chi }}_Y\left(r\right)=1,{{\underset{¯}{apr}}_{\overline{\chi }}}_Y\left(r\right)=0$.

This implies $q\in X and r\in Y.$Thus, p = q$\alpha r\in X\Gamma Y\subseteq \mathcal{U}$. Therefore, ${{\overline{apr}}_{\overline{\chi }}}_{\mathcal{U}}\left(p\right)=1, {{\underset{¯}{apr}}_{\overline{\chi }}}_{\mathcal{U}}\left(q\right)$ = 1. It follows that $X\Gamma Y\left(p\right)\subseteq \mathcal{U}$. Since $\mathcal{U}$ is a RFPI of N, either $\overline{X}\subseteq \mathcal{P}$ or $\overline{Y}\subseteq \mathcal{P}.$ Thus, either $\mathrm{X}\subseteq \mathcal{U}$ or Y $\subseteq \mathcal{U}.$ Hence, $\mathcal{U}$ is a prime ideal of N. □

7. Properties of Rough $\Gamma$-Endomorphism of $\Gamma$ Rings

In this section, we propose some theorems about the morphism properties of RFI in the gamma ring based on rough gamma endomorphism.

Definition 15. 

Mapping $\theta :N\to N$ of the Γ Ring N into itself is called a rough Γ-endomorphism of N. If for$p,q\in N, \alpha ϵ \Gamma$,then

$$\left(i\right)\overline{apr}\left(p+q\right)\theta =\overline{apr}\left(p\theta \right)+\overline{apr}\left(q\theta \right),\underset{¯}{apr}\left(p+q\right)\theta =\underset{¯}{apr}\left(p\theta \right)+\underset{¯}{apr}\left(q\theta \right)$$

(1)

$$\left(ii\right)\overline{apr}\left(p\alpha q\right)\theta =\overline{apr}\left(p\theta \alpha q\theta \right),\underset{¯}{apr}\left(p\alpha q\right)\theta =\underset{¯}{apr}\left(p\theta \alpha q\theta \right)$$

(2)

Let $\Delta$denote the set of all rough $\Gamma$-endomorphisms of the $\Gamma$ Ring N.The multiplication and addition on the set are as $\Delta$ follows. If $x,y\in \Delta$, then

$$\begin{array}{c}\overline{apr}\left(p\left(x\alpha y\right)\right)=\overline{apr}\left(\left(px\right)\alpha y)\right)p\in N, \alpha ϵ\mathsf{\Gamma },\underset{¯}{apr}\left(p\left(x\alpha y\right)\right)=\underset{¯}{apr}\left(\left(px\right)\alpha y\right)\\ p\in N, \alpha ϵ \mathsf{\Gamma }\end{array}$$

(3)

$$\begin{array}{c}\overline{apr}\left(p\left(x+y\right)\right)=\overline{apr}\left(px)+\overline{apr}\left(py\right)\right)p\in N,\underset{¯}{apr}\left(p\left(x+y\right)\right)=\underset{¯}{apr}\left(px\right)+\underset{¯}{apr}\left(py\right)\\ p\in N,\alpha ϵ \mathsf{\Gamma }\end{array}$$

(4)

Theorem 13. 

If $\Delta$is the set of all rough $\Gamma$-endomorphisms of a $\Gamma$ Ring N, then$\Delta$ is a $\Gamma$-endomorphism of a $\Gamma$ Ring with unity with respect to the usual operations.

Proof: 

Given that $\Delta$ is the set of all rough $\mathsf{\Gamma }$-endomorphisms of a $\mathsf{\Gamma }$-ring M, toprove $\Delta$ is a $\mathsf{\Gamma }$ Ring with unity, welet$x,y,z\in \Delta ,\alpha ϵ \mathsf{\Gamma },\mathrm{p}ϵ N$. Then, the condition of the $\mathsf{\Gamma }$ Ring is $\overline{apr}(p\left(x+y\right)\alpha c$ = $\overline{apr}\left(p\left(x+y\right)\right)\alpha z)$.

By applying the distributive law and the condition of rough gamma endomorphism, we finally get $\overline{apr} p\left(x\alpha z\right)+\overline{apr }p\left(y\alpha z\right)$ = $\overline{apr}\left(p\left(x\alpha z+y\alpha z\right)\right)$ $\mathrm{and}\overline{apr}\left(p\left(x\left(\alpha +\beta \right)z\right)\right)=\overline{apr}\left(\left(px\right)\alpha z\right)+\overline{apr}\left(\left(px\right)\beta z\right)=\overline{apr}\left(p\left(x\alpha z+x\beta z\right)\right)$, $x,z\in \Delta ,\alpha ,\beta ϵ\mathsf{\Gamma },\mathrm{p}ϵN.$

Similiarly, $\overline{apr}\left(p\left(x\alpha y\right)\beta z\right)=\overline{apr}\left(\left(\left(px\right)\alpha y\right)\beta z\right)=\overline{apr}\left(p\left(x\alpha (y\beta z\right)\right))\forall x,y,z\in \Delta ,\alpha ,\beta ϵ\mathsf{\Gamma }.$ Likewise, the three conditionsalso satisfythe lower case.

For all $x\in \Delta ,$ there exists a unity element $1\in \Delta$ such that $\overline{apr}\left(p\left(1\alpha x\right)\right)=\overline{apr}\left(\left(\left(p1\right)\alpha \right)x\right)=\overline{apr}\left(px\right),\alpha ϵ\mathsf{\Gamma },pϵN$, and hence $\overline{apr}\left(p\left(1\alpha x\right)\right)=\overline{apr}\left(p\left(x\alpha 1\right)\right)=px and\underset{¯}{apr}\left(p\left(1\alpha x\right)\right)=\underset{¯}{apr}\left(p\left(x\alpha 1\right)\right)=px.$ Thus $\Delta$ satisfies all the conditions of the $\Gamma$ Ring, andhence $\Delta$ is a $\Gamma$ Ring with unity. □

Theorem 14. 

Let $\Delta$ be the set of all rough endomorphisms of the $\Gamma$ Ring N. If $xϵ\Delta$, then a has a multiplicative inverse in $\Delta$ if and only if x is a one-to-one function.

Proof. 

Assume $\Delta$ to be the set of all rough $\Gamma$-endomorphisms of a $\Gamma$ Ring M. If $xϵ\Delta$, then x has an inverse in $\Delta .$ To prove x is a one-to-one function, let x have an inverse y in $\Delta .x\alpha y=y\alpha x=1, \alpha ϵ\Gamma .\mathrm{Then}, \mathrm{for}\mathrm{each}pϵN,$we get $\overline{apr}\left(\left(py\right)\alpha x\right)=\overline{apr}\left(p\left(y\alpha x\right)\right)=\overline{apr}\left(p\right).$ A similar condition holds for the lower approximation, which x is clearly on. Furthermore, $p_1,p_2ϵN$ such that $\overline{apr}\left(p_{1}x\right)=\overline{apr}\left(p_{2}x\right) and \overline{ apr}\left(p_1\right)=\overline{apr}\left(p_1.1\right)=\overline{apr}\left(p_1\left(x\alpha y\right)\right)=\overline{apr}\left(\left(p_1.1\right)\alpha y\right)=\overline{apr}\left(\left(p_2.1\right)\alpha y\right)=\overline{apr}\left(p_2\right).$ Therefore, x is a one-to-one mapping. Conversely, let us assume that the $\Gamma$-endomorphism x is a one-to-one mapping of N onto N so that each element of N is of the form $px,pϵN.$ We define a mapping d of N into N as follows: $\overline{apr}\left(\left(\left(px\right)\alpha \right)y\right)=\overline{apr}\left(p\right),pϵN,\alpha ϵ\mathsf{\Gamma }.$ If $p,qϵN$, then $\overline{apr}\left(\left(\left(px+qx\right)\alpha \right)y\right)$, and by this assumption, we get $\overline{apr}\left(p+q\right)$. Through asimple calculation, we finally get $\overline{apr}\left(\left(\left(px)\alpha )y)+\overline{apr}(((qx\right)\alpha \right)y\right)$ and $\overline{apr}\left(\left(px\alpha qx)\alpha )y)=\overline{apr}(((p\alpha q\right)x\alpha \right)y=\overline{apr}\left(p\alpha q\right)=\overline{apr}\left(\left(\left(px\right)\alpha \right)y\right)\alpha \overline{apr}\left(\left(\left(qx\right)\alpha \right)y\right)$.

A similar condition holds for the lower approximation. We see that b is a rough $\Gamma$-endomorphism of M. Furthermore, $\overline{apr}\left(\left(px\right)\alpha y\right)=\overline{apr}(p\left(x\alpha y\right)=\overline{apr}\left(p\right)$ for every p in N, and hence $x\alpha y=1$. Finally, $pϵN, \mathrm{where} \overline{apr}(\left(\left(px\right)\alpha \left(y\alpha x\right)\right)=\overline{apr}\left(\left(p\left(x\alpha y\right)\right)\alpha x\right)=\overline{apr}\left(\left(p\left(1\right)\right)\alpha x\right)=\overline{apr}\left(p\left(1\alpha x\right)\right)=\overline{apr}\left(px\right).$ Similiarly, $\underset{¯}{apr}(\left(\left(px\right)\alpha \left(y\alpha x\right)\right)=\underset{¯}{apr}\left(px\right)$. That is equivalent to the statement that $\overline{apr}\left(q\left(y\alpha x\right)\right)=\overline{apr}\left(q\right)$ and $\underset{¯}{apr}\left(q\left(y\alpha x\right)\right)=\underset{¯}{apr}\left(q\right)$ for every $q ϵN.$ Hence, $y\alpha x=1$, and y is the inverse of x in$\Delta$. □

8. Conclusions

Recently, many algebraic structures have been viewed in terms of rough structures. The chief purpose of RS analysis is the induction of approximation. The topical extension of RS theory has developed a new method for the decay of large datasets. In this paper, some new rough operations were discovered. Furthermore, we hashed out characterizations of rough fuzzy ideals and discussed some morphism properties. Finally, we introduced the rough gamma endomorphism and discussed the set of all rough Γ-endomorphisms of the Γ Ring as a gamma ring with unity. Error tolerance is a major limitation of the classical rough sets. In future work, the rough fuzzy concept may be applied in other algebraic structures such as Γ fields, Γ modules, Γ near rings, and Γ near fields. In addition, various algebraic structures and their properties may be investigated through rough soft sets. Researchers are finding a new way to visualize the various structures.