Abstract
We summarize recent results regarding single and double soft theorems of two different particles named dilatons, the Nambu-Goldstone boson of the spontaneously broken conformal field theories and the massless scalar particle of the closed string theories. Similarities and differences between the soft theorems of these two particles are discussed as well as their connections with the symmetries of the theories.
1. Introduction
Symmetries are one of the most powerful guiding principle for constructing consistent mathematical frameworks necessary to describe quantitatively the fundamental laws of nature. All the theories of the known interactions are based on such a principle and it turns out to be of great interest to understand how the symmetries, eventually hidden, are manifest in the behaviour of the physical observables. It is well known, for example, from the pioneering works by Low [1,2,3,4] for gauge theories and Weinberg [5,6,7] in gravity that gauge symmetries determine the behaviour of the S-matrix in the infrared region where gauge-bosons or gravitons carry low or soft momentum [8,9,10]. In this soft-regime, scattering amplitudes with a soft graviton or gauge boson factorize in the product of amplitudes with only hard or finite energy particles and a soft contribution. This behaviour is universal at leading order in the low momentum expansion and for tree level amplitudes extends to subleading order for amplitudes with soft gravitons [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. Loop amplitudes in four space-time dimensions, instead, are usually ill-defined because of the presence of infrared divergences. These divergences make even the leading soft factor not universal for Yang-Mills amplitudes [31] while for gravity and abelian theories their effect consists in adding logarithmic corrections to the subleading soft factors [32,33,34,35]. The soft regime of amplitudes with gravitons also provides predictions on the gyromagnetic factors of specific massive higher spin states emerging in Kaluza-Klein theories [36] that they have been confirmed by explicit amplitude calculations [37].
The deep relation between symmetries and IR-behaviour of the S-matrix, have been recently extended to the asymptotic symmetries of flat space-times introduced by Bondy, Metzner, van de Burg and Sachs to study the gravitational radiation at null infinity (BMS-group) [38,39]. The Ward-identities associated with the supertranslation generators of the BMS group give the leading soft behaviour of amplitudes with external gravitons while the subleading contribution originates from the super-rotation charges [40].
Symmetries determine also the IR behaviour of scattering processes with massless scalar states [41,42,43,44,45,46,47,48] although, recently, an alternative geometric proof of such theorems for scalar particles has been proposed in Ref. [49]. It is well known, for example, that when an internal symmetry is spontaneously broken, as in the non-linear -models (NLSM), the conservation law of the broken current requires the vanishing of amplitudes with emission at zero momentum of a Goldstone boson (Adler’s zero) [50,51,52,53].
The situation is different when a space-time symmetry is spontaneously broken as in the case of the breaking of the conformal group to the Poincaré symmetry. In this breaking only one Nambu-Goldstone boson, in the following named CFT-dilaton, appears in the spectrum of the theory [54]. Amplitudes with a CFT-dilaton and an arbitrary number of massless states are vanishing to leading order in the soft expansion of the dilaton momentum, but for massive hard states, differently from the Adler-zero case, these are divergent at zero dilaton momentum in full analogy with emission of soft-gauge bosons [44]. To the subleading order instead, amplitudes with one soft dilaton are determined by the conformal Ward-identity of broken scale invariance [55,56,57] while only recently it has been shown that the subsubleading behaviour of soft dilaton amplitudes is completely fixed from the Ward-identity associated with the breaking of the special conformal generators [44,58]. These relations hold for any non-anomalous conformal field theory and they have been tested in super-Yang Mills perturbatively up to one-loop and non-perturbatively in the contest of gravity/dual on the Coulomb branch and by considering instanton effective actions [58,59].
Symmetries are also manifest in the double soft behaviour of amplitudes computed in NLSM-models [52,60,61,62,63,64]. Amplitudes with two soft Nambu-Goldstone bosons factorize in amplitudes without the soft particles and a contribution that capture the algebra of the broken generators. For the dilaton, the double soft behaviour follows from the Ward-identities associated with the breaking of the dilatation and special conformal transformation generators. Furthermore, it turns out to be equal to two consecutive single soft expansions [58].
There is another particle named dilaton, it is the massless scalar of the gravitational multiplet of the closed string theories. Amplitudes with this dilaton, referred to in these notes as gravity dilaton, satisfy single and double soft-theorems, as well. These have been determined by computing amplitudes in bosonic, heterotic and superstring theories and expanding them in the relevant infrared region [10,41,43,45,47,48].
The same behaviour has also been derived with a different approach based on the property of the string theory to provide a unified expression for amplitudes with external gravitons, dilaton and Kalb-Ramonds states. The request of gauge invariance fixes, up to subsubleading order in soft expansion, the soft behaviour of the whole amplitude including the dilaton contribution [10,65]. This contribution in the case of a single soft gravity dilaton is conjectured to be universal being the same in all the cases studied and shares many features with those of the CFT-dilatons. This similarity has also led to argue the presence of hidden tree-level conformal symmetry in ordinary Einstein gravity [66]. However, the resemblance of the two theorems is less evident in the case of two soft dilatons because for the gravity dilaton, differently from the CFT-dilaton, the double soft behaviour cannot be obtained from two consecutive single soft expansions due to the presence of four-point interactions [67].
The aim of this article, based on the results obtained in the papers of Refs. [10,43,44,45,58,65,67] is to review the state of art of the single and double soft-theorems satisfied by dilaton amplitudes. It will be given the main results achieved in the literature providing few details on their derivations but highlighting similarities and differences between the IR-behaviour of the amplitudes with the two dilatons.
The paper is organized as follows. In the prelude of Section 1, are summarized the main features of conformal field theories necessary to introduce the results considered in the article. In its subsection are discussed the Ward-identities of the conformal field theory spontaneously broken and their connections with the infrared properties of amplitudes with CFT-dilatons. In Section 3 are introduced the main properties of the string amplitudes used in the subsection to discuss the soft theorems for the gravity-dilatons. In the discussion section are commented the achieved results.
2. CFT-Prelude
A conformal transformation is an invertible map that leave the metric invariant up to a scale factor (More details on conformal field theories and their breaking can be found in Refs. [54,68,69].). The conformal group is locally isomorphic to with d the space time dimensions and it can be seen as an extension with dilatations and special conformal transformations of the Poincarè group. The generators are:
with and the generators of the translations and Lorentz transformations respectively and the spin angular momentum operator. denotes the scaling dimension of the fields involved in the transformation. The action of the dilation and special transformation on a scalar field with conformal dimension is:
The Nöther currents associated to the scale and special conformal transformations
are conserved if the improved energy momentum tensor is conserved and traceless.
The conformal symmetry is spontaneosly broken when a scalar field acquires a non zero vacuum expectation value (vev).
The vacuum remains invariant under the Poncaré group but as consequence of the Goldstone’s theorem, one massless boson, the CFT-dilaton , appears in the spectrum parametrizing the oscillations around the nonconformal vacuum. The dilaton couples linearly to the energy momentum tensor of the broken theory and through the equations of motion contributes to its trace:
where v is a dimensionful constant related to the vev of the scalar field. As a consequence, the currents of the broken generators are not conserved being their divergences related to the trace of the energy momentum tensor through the identies:
In the spontaneously broken phase, the theory is not any more conformal but the memory of the original symmetry is conserved in the infrared behaviour of the S-matrix through the so called soft-theorems. These follow from the Ward-identities associated to the broken generators and assert that amplitudes with one or more soft-dilatons are obtained acting with suitable operators related to the broken generators on amplitudes without the soft particles.
Soft Theorems from Ward-Identities
We consider a conformal invariant field theory whose conformal symmetry is spontaneously broken by the vev acquired by some scalar field. In a such theory we analyse the matrix element among the divergences of set of broken currents and a string of scalar fields
denotes the usual Time-ordered product with all the derivative placed outside the time ordering [70]. The derivatives of these matrix elements with respect the current coordinates determine the Ward-identities of the spontaneously broken conformal field theory.
In the case of a single current, in momentum space, one gets:
The matrix element is evaluated up to the order in the momentum expansion q of the current. The first term on left side of this equation is neglected after an integration by part under the assumption of absence of poles at . For the broken dilation and special conformal transformation, Equation (7) through the divergences of the currents given in Equation (5) relates the correlation functions with the insertion of a dilaton field with low momentum to those without the dilaton but depending on the variations of the fields under the considered transformations. This identity contains soft-theorems at a very preliminary stage and the LSZ-reduction translates them in a relation between amplitudes. The LSZ-operator
is applied on both sides of Equation (7) with the on-shell limit performed only to the end of the calculation. The current whose divergence gives the amplitude with the insertion of the dilaton, is not truncated by the LZS-reduction formula. The presence in the divergence of the current of the operator amputates the dilaton propagator determining a relation between two truncated amplitudes. This in the case of the dilatation current, up to the order in the soft-expansion, gives:
with . Equation (9) the amplitude with the insertion of a soft dilaton is obtained acting with the generator of the dilatation, written in the momentum space, , on the amplitude without the dilaton. In the case of hard or finite energies massless field, the leading divergent contribution is vanishing. For massive hard particles, instead, the presence of the pole in q makes the leading soft-theorem of the dilaton very similar to that satisfied by the gauge bosons of the fundamental interactions. More details on such derivation are given in Refs. [44,58], here it is worthwhile to comment that in Equation (9) we have commuted the generator of the translations with the delta-function over the momenta and in the leading divergent term we have used the prescription to perform the on-shell limit before the soft one.
The same analysis is now performed for broken current generating the special conformal transformations. The calculation is very similar to the previous one with the only difference that the operator of the special conformal transformations commutes with the delta over the momenta and no extra factors, as the space-time dimension d as in Equation (9), is introduced. The resulting Ward-identity is:
The of the amplitude with one dilaton and n-hard states is obtained by decomposition the amplitudes as the sum of the leading, subleading and subsubleading soft terms:
where the and are operators dependent only on the momenta , while may depend on q as well and replacing such expression in Equation (10). The leading term cancels on both sides leading to an identity which determines:
The Ward-identities of the scale and special conformal transformation determine through the subsubleading order the amplidude with one soft-dilaton in terms of the amplitude without the ditaton through the relation:
The terms proportional to the mass of the external states show a pole in the momentum of the soft particle, in perfect analogy with the the Low and Weinberg soft behaviours, and are determined by the cubic couplings between a dilaton and two massive states. It may also be though as a q-expansion of the -points amplitude. The regular terms are not vanishing to the and are fixed by action of broken generators, dilatation and special conformal transformations , on the amplitude without the emission at zero momentum of the dilaton.
The double soft behaviour of the amplitude with the emission of two dilatons at zero momenta is determined starting from the matrix elements with the insertion of two broken currents and n-finite energy states. The two currents can be either of the same nature, dilatation or special conformal transformation, or of different kind. Three sets of double-soft Ward-identities may in principle be computed and they are related, through LZS-reduction, to the terms in the soft expansion of the amplitudes with the emission of two dilatons at zero momenta. This calculation has only been performed for external hard massless states and it is similar but more involved of the single soft identities. The leading term of the amplitude is obtained from the Ward-identities with two dilatation currents while the subleading behaviour is obtained from those with mixed broken generators. The subsubleading contribution of the amplitude would be determined by the Ward-identities with two special conformal transformation currents. These have not been possible to determine because as discussed in Ref. [58], they would require a formulation of the single soft-theorem to which is still missing. The universal behaviour of an amplitude with two dilatons at zero momenta is given in terms of the amplitude without the soft particles by the expression:
It is straightforward to verify that the double soft behaviour coincides with the one obtained by considering two consecutive single soft expansions. This observation has led to conjecture that the behaviour of amplitudes with multiple emission of soft dilatons is universal and it is fixed by the consecutive soft limits of amplitudes with dilatons at zero momentum emitted one after the other.
3. String Amplitudes
In string theories, amplitudes are very compact expressions given by complex integrals of correlation functions of vertex operators evaluated on Riemann surfaces of a given genus that represent the world-sheet of strings propagating in the space-time. At genus zero, the sphere is the relevant tree-level closed string world-sheet and the superstring vertex operators associated with the massless states in the and super-ghost pictures take the form (An introduction to superstring amplitudes can be found in the textbooks of Refs. [71,72].):
with the gravitational coupling constant and z the complex coordinate parametrizing the insertion on the world-sheet of the vertex operators
Here, and are Grassmannian variables, is the polarization of the massless state, k in the momentum of the external state, and the superfield notation is given by
This vertex describes collectively all massless states, these are the graviton , the antisymmetric two form and the scalar field (gravity dilaton) of the massless gravitational string multiplet. These fields are identified with the symmetric, anti-symmetric and trace of the external polarization, through the relation:
where
such that , and , while is an unphysical reference momentum. The relevant expectation values for the world-sheet fields are:
The superstring amplitude with massless external states is:
Here, is the volume of the Möbius group, the states with the indices 1 and 2 are in the picture, while the others are in the picture and the factor comes from the correlator of the superghosts.
Equation (23) is the starting point for computing amplitudes with external massless states. In such an expression, one vertex operator depending on the complex super-coordinate and momentum q is kept separated from all the other external legs. It will be considered the vertex of the soft particle whose momentum will be expanded up to order . Soft theorems will be obtained by integrating over the super-coordinate Z and expressing the result of the integration by an operator acting on the amplitude without the soft-leg. This operator, in general, contains string corrections, being the Regge slope. The leading order in gives the correct field theory result. Furthermore, Equation (23) provides in a unique expression the amplitudes for the graviton, the Kalb-Ramond and the gravity dilaton. The analyses of the IR properties of these amplitudes give, in a single expression, the soft theorems of these three different particles. In the next section, we will review those of the gravitational dilaton highlighting the similarities and differences with those of the conformal dilaton.
Soft-Dilaton Behaviour
The analyses of the infrared properties of amplitudes with Gravitational dilatons have a long history. They were already studied in the old dual models in connection with the renormalization of the Regge slope [41] and in the framework of closed string field theories [73]. In this section we review the recent extension of these old results by studying the soft properties of amplitudes with scalar particles. The starting point of this analysis is Equation (23) supplemented by the observation that the amplitude after having integrated over the Grassmann variables associated to the soft vertex reduces to an expression that is factorized at integrand level:
where the ⋆ denotes a convolution integral between the n-point amplitude and the integral S which collects all the dependence from the soft-leg. This quantity is the sum of three terms where receives contributions form the purely bosonic degrees of freedom and it is equal to the similar expression computed in bosonic string theory while and its complex conjugate receive contribution from the supersymmetric partners of the bosonic degrees of freedom. This decomposition turns out to be very useful because from one can deduce the soft function in bosonic string. These have been computed in Ref. [10], here we only cite their expressions. The bosonic contribution turns out to be:
The contribution dues to the superpartner degrees of freedom is:
The superkinetic quantities introduced in these expressions are given by:
with Grassmannian variables introduced to exponentiate the vertex operators. All the integrals in and have been computed in Refs. [10,43,45] up the in the expansion of the momentum of the graviton chosen to be the soft external leg. The result of the integrations, when the soft leg is projected on the external symmetric and traceless polarization, reproduces, according to Equation (19), the known soft theorems for gravitons. The projection on the dilaton state, instead, is written as the sum of two operators acting on the amplitude depending only on hard momenta:
where
with the spin-operator. Remarkably these operators are the generators of the dilatations and special conformal transformations acting in the momentum space. This result has also been confirmed by decomposing the -amplitude in a double copy three-point vertex, with a soft leg describing collectively a graviton, a dilaton and a Kalb-Ramond, factorized from an n-point amplitude [65]. The expansion of this amplitude in the soft momentum and the request of the gauge invariance imposed order by order in soft expansion, reproduces the dilaton infrared behaviour obtained by the explicit calculation of superstring amplitudes. The same calculation has also been performed in heterotic and bosonic string theories for massless and massive external state. Differently from the soft graviton behaviour which is universal up to subleading order, the tree-level soft behaviour of the dilaton is universal through the in all string theories. It doesn’t contain any string correction and therefore is a result that can also be obtained from amplitudes computed in the framework of the low energy effective string theories. This result has been extended at h-order in the loop expansion by computing in bosonic string theory amplitudes with one massless state in interaction with n-tachyon states treated as massive particles with mass . The calculation has been performed in space-time dimensions bigger than four to avoid infrared logarithmic divergences, the resulting soft-expansion reads:
Remarkably, the multiloop soft expansion is again free by string corrections to any order in the loop expansion. Instead, since the multiloop infrared behaviour has been obtained only in the bosonic string, it is not clear if universality holds to any loop.
In analogy with the dilaton of the broken conformal field theories, also the gravitational dilaton obeys a double soft factorization property. This has been determined by computing in bosonic string theory tree level amplidudes with n-tachyons and two massless states carrying low momenta. The simultaneos zero momentum limit is performed by rescaling, by a small parameter , the momenta of two massless states and expanding the amplitude in . The projection on the dilatons, up to the subleading order, gives:
This result is independent of the string slope and it has also been obtained by starting from Feynman diagrams computed in the low energy effective string theory. Two classes of exchange Feynman diagrams contribute to the infrared behaviour of the amplitudes (see Figure 1). The first class of diagrams involve only three-point vertices with two tachyons and one dilaton emitted from two different external lines. In the second class of diagrams, three and four-point vertices are emitted from a single external line. These are the vertices with two tachyons and one massless state, three massless states and a four point-vertex with two tachyons and two massless states. The contribution due to the four-point interaction is collected by the single pole term in second line in Equation (31). Gauge invariance is obtained by requiring the emission of the massless states from internal lines. The same expression is also obtained by joining a four-point amplitude, with two tachyons and two dilatons, to a n-point tachyon amplitude. It is straightforward to see that Equation (31) differs from the expression obtained by considering two consecutive single soft expansions in the term generated by the four-point interaction.
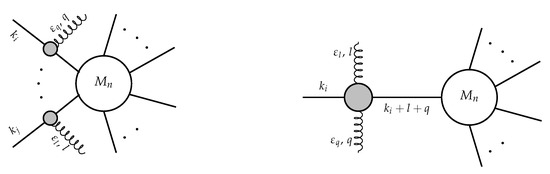
Figure 1.
Diagrams of two massless closed string states with polarization and momenta respectively and . External tachyon lines have momenta , with .
4. Discussion
In this paper, we have summarized the state of the art of the soft-theorems of two different particles named dilaton, the Nambu-Goldstone boson of the spontaneously broken conformal theories and the scalar of the massless gravitational multiplet of the string theories. Symmetries of the theory determine the single and double soft behaviour for both particles. Ward-identities associated with the scale and special conformal transformation control the soft-behaviour of amplitudes with conformal dilatons. Gauge-invariance of string (or string effective theory) amplitudes fixes the infrared behaviour of all the massless closed string multiplet. The single soft theorems for both particles are almost similar. They contain at subleading order the generators of the scale transformations and kinematically invariant factors related to the mass and scale dimensions of the amplitudes. The subsubleading order in both cases is fixed by the generators of the special conformal transformations. These analogies are less evident in the double soft behaviour of the two dilatons. Both contain the generators of the dilations, but for external massless finite energy particles, the amplitudes with conformal soft dilatons are finite at zero momentum while diverging for the gravity dilaton. Furthermore, the simultaneously low momentum limit for the conformal dilatons coincides with the consecutive one. That is not true in the case of the gravity dilaton for the presence of quartic interaction among two massive and two dilaton particles. Differences appear also at higher order in the perturbative expansion. In string theory, the dilaton remains massless to all loops and satisfies factorization properties similar to the tree-level one. In conformal theories, the dilaton, in general, become massive at one-loop because of the breaking of conformal invariance in quantum theories. We emphasize that it is still missing a symmetry principle that explains the infrared properties of the gravitational dilaton. These are inferred by direct amplitude calculations or by the request of gauge invariance of string amplitudes that describe in a unified expression scattering of gravitons, Kald-Ramonds and dilatons. Similarities between the soft theorems of the two dilatons suggest that also the IR properties of the gravity-dilaton might be determined by the breaking of some “hidden” symmetry of the theory.
Universality of the loop soft theorem for the gravity-dilaton is still an open issue. The loop factorization properties for this kind of particle have been derived only in bosonic string theory and for external tachyons treated as massive scalar fields [74]. They hold also in field theory because the soft operators are independent on the string slope but a their extension to other string models and for other kinds of hard states is still lacking.
We conclude these notes by observing that the gravity dilaton is a massless scalar that appears in all superstring theories and can play an important role in the so-called string cosmology. They have been proposed, for example, cosmological models where the primordial evolution of the background is driven by this massless scalar. On the other side, there are extensions of the Standard Model and gravity based on scale invariance which could solve the hierarchy problem. In all these cosmological contests it would be interesting to explore the role played by soft theorems in establishing relations among cosmological correlators.
Funding
This research received no external funding.
Acknowledgments
I would like to thank Paolo Di Vecchia, Matin Mojaza, Josh Nole and Mritunjay Verma for having accompanied me on this journey into the formulation of soft theorems for dilatons. I thank P. Di Vecchia for his helpful comments on the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
References
- Low, F.E. Scattering of light of very low frequency by systems of spin 1/2. Phys. Rev. 1954, 96, 1428. [Google Scholar] [CrossRef]
- Low, F.E. Bremsstrahlung of very low-energy quanta in elementary particle collisions. Phys. Rev. 1958, 110, 974. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Goldberger, M.L. Scattering of low-energy photons by particles of spin 1/2. Phys. Rev. 1954, 96, 1433. [Google Scholar] [CrossRef]
- Saito, S. Low-energy theorem for Compton scattering. Phys. Rev. 1969, 184, 1894. [Google Scholar] [CrossRef]
- Weinberg, S. Photons and Gravitons in s Matrix Theory: Derivation of Charge Conservation and Equality of Gravitational and Inertial Mass. Phys. Rev. 1964, 135, B1049. [Google Scholar] [CrossRef]
- Gross, D.J.; Jackiw, R. Low-Energy Theorem for Graviton Scattering. Phys. Rev. 1968, 166, 1287. [Google Scholar] [CrossRef]
- Jackiw, R. Low-Energy Theorems for Massless Bosons: Photons and Gravitons. Phys. Rev. 1968, 168, 1623. [Google Scholar] [CrossRef]
- Broedel, J.; de Leeuw, M.; Plefka, J.; Rosso, M. Constraining subleading soft gluon and graviton theorems. Phys. Rev. 2014, D90, 065024. [Google Scholar] [CrossRef]
- Bern, Z.; Davies, S.; Vecchia, P.D.; Nohle, J. Low-Energy Behavior of Gluons and Gravitons from Gauge Invariance. Phys. Rev. 2014, D90, 084035. [Google Scholar] [CrossRef]
- Vecchia, P.D.; Marotta, R.; Mojaza, M. Soft behavior of a closed massless state in superstring and universality in the soft behavior of the dilaton. J. High Energy Phys. 2016, 12, 20. [Google Scholar] [CrossRef]
- Elvang, H.; Jones, C.R.T.; Naculich, S.G. Soft Photon and Graviton Theorems in Effective Field Theory. Phys. Rev. Lett. 2017, 118, 231601. [Google Scholar] [CrossRef]
- Cachazo, F.; Strominger, A. Evidence for a New Soft Graviton Theorem. arXiv 2014, arXiv:1404.4091. [Google Scholar]
- Schwab, B.U.W.; Volovich, A. Subleading Soft Theorem in Arbitrary Dimensions from Scattering Equations. Phys. Rev. Lett. 2014, 113, 101601. [Google Scholar] [CrossRef]
- He, S.; Huang, Y.T.; Wen, C. Loop Corrections to Soft Theorems in Gauge Theories and Gravity. J. High Energy Phys. 2014, 1412, 115. [Google Scholar] [CrossRef]
- Larkoski, A.J. Conformal Invariance of the Subleading Soft Theorem in Gauge Theory. Phys. Rev. D 2014, 90, 087701. [Google Scholar] [CrossRef]
- Bianchi, M.; He, S.; Huang, Y.T.; Wen, C. More on Soft Theorems: Trees, Loops and Strings. Phys. Rev. D 2015, 92, 065022. [Google Scholar] [CrossRef]
- White, C.D. Diagrammatic insights into next-to-soft corrections. Phys. Lett. B 2014, 737, 216–222. [Google Scholar] [CrossRef][Green Version]
- Zlotnikov, M. Sub-sub-leading soft-graviton theorem in arbitrary dimension. J. High Energy Phys. 2014, 1410, 148. [Google Scholar] [CrossRef][Green Version]
- Kalousios, C.; Rojas, F. Next to subleading soft-graviton theorem in arbitrary dimensions. J. High Energy Phys. 2015, 1501, 107. [Google Scholar] [CrossRef]
- Du, Y.J.; Feng, B.; Fu, C.H.; Wang, Y. Note on Soft Graviton theorem by KLT Relation. J. High Energy Phys. 2014, 1411, 90. [Google Scholar] [CrossRef]
- Schwab, B.U.W. A Note on Soft Factors for Closed String Scattering. J. High Energy Phys. 2015, 1503, 140. [Google Scholar] [CrossRef]
- Vera, A.S.; Vazquez-Mozo, M.A. The Double Copy Structure of Soft Gravitons. J. High Energy Phys. 2015, 1503, 70. [Google Scholar] [CrossRef]
- Guerrieri, A.L. Soft behavior of string amplitudes with external massive states. Nuovo Cim. C 2016, 39, 221. [Google Scholar]
- Vecchia, P.D.; Marotta, R.; Mojaza, M. Soft Theorems from String Theory. Fortschr. Phys. 2016, 64, 389. [Google Scholar] [CrossRef]
- Bianchi, M.; Guerrieri, A.L. On the soft limit of closed string amplitudes with massive states. Nucl. Phys. B 2016, 905, 188. [Google Scholar] [CrossRef]
- Sen, A. Soft Theorems in Superstring Theory. J. High Energy Phys. 2015, 1706, 113. [Google Scholar] [CrossRef]
- Sen, A. Subleading Soft Graviton Theorem for Loop Amplitudes. J. High Energy Phys. 2017, 11, 123. [Google Scholar] [CrossRef]
- Laddha, A.; Sen, A. Sub-subleading soft graviton theorem in generic theories of quantum gravity. J. High Energy Phys. 2017, 11, 65. [Google Scholar] [CrossRef]
- Higuchi, S.; Kawai, H. Universality of soft theorem from locality of soft vertex operators. Nucl. Phys. B 2018, 936, 400–447. [Google Scholar] [CrossRef]
- Bhatkar, S.A.; Sahoo, B. Subleading Soft Theorem for arbitrary number of external soft photons and gravitons. J. High Energy Phys. 2019, 1, 153. [Google Scholar] [CrossRef]
- Bern, Z.; Davies, S.; Nohle, J. One Loop Corrections to Subleading Soft Behaviour of Gluons nd Gravitons. Phys. Rev. D 2014, 90, 085015. [Google Scholar] [CrossRef]
- Weinberg, S. Infrared Photons and Gravitons. Phys. Rew. 1965, 140, B516. [Google Scholar] [CrossRef]
- Laddha, A.; Sen, A. Logarithmic Terms in the Soft Expansion in Four Dimensions. J. High Energy Phys. 2018, 1810, 56. [Google Scholar] [CrossRef]
- Laddha, A.; Sen, A. Observational Signature of the Logarithmic Terms in the Soft Graviton Theorem. Phys. Rev. D 2019, 100, 024009. [Google Scholar] [CrossRef]
- Sahoo, B.; Sen, A. Classical and Quantum Results on Logarithmic Terms in the Soft Theorem in Four Dimensions. J. High Energy Phys. 2019, 1902, 86. [Google Scholar] [CrossRef]
- Marotta, R.; Verma, M. Soft Theorems from Compactification. J. High Energy Phys. 2020, 2, 8. [Google Scholar] [CrossRef]
- Marotta, R.; Taronna, M.; Verma, M. Revisiting higher-spin gyromagnetic couplings. J. High Energy Phys. 2021, 6, 168. [Google Scholar] [CrossRef]
- Bondi, H.; van Burg, M.G.J.; Metzner, A.W.K. Gravitational waves in general relativity. 7. Waves from axisymmetric isolated systems. Proc. R. Soc. Lond. A 1962, 269, 21–52. [Google Scholar]
- Sachs, R.K. Gravitational waves in general relativity. 8. Waves in asymptotically flat space-times. Proc. R. Soc. Lond. A 1962, 270, 103–126. [Google Scholar]
- Strominger, A. Lectures on the Infrared Structure of Gravity and Gauge Theory. arXiv 2017, arXiv:1703.05448. [Google Scholar]
- Ademollo, M.; D’Adda, A.; D’Auria, R.; Gliozzi, F.; Napolitano, E.; Sciuto, S.; Vecchia, P.D. Soft Dilatons and Scale Renormalization in Dual Theories. Nucl. Phys. 1975, B94, 221–259. [Google Scholar] [CrossRef]
- Shapiro, J. On the renormalization of Dual Models. Phys. Rev. 1975, D11, 2937. [Google Scholar] [CrossRef]
- Vecchia, P.D.; Marotta, R.; Mojaza, M. Soft theorem for the graviton, dilaton and the Kalb-Ramond field in the bosonic string. J. High Energy Phys. 2015, 1505, 137. [Google Scholar] [CrossRef]
- Vecchia, P.D.; Marotta, R.; Mojaza, M.; Nohle, J. New soft theorems for the gravity dilaton and the Nambu-Goldstone dilaton at subsubleading order. Phys. Rev. D 2016, 93, 085015. [Google Scholar] [CrossRef]
- Vecchia, P.D.; Marotta, R.; Mojaza, M. Subsubleading soft theorems of gravitons and dilatons in the bosonic string. J. High Energy Phys. 2016, 1606, 54. [Google Scholar] [CrossRef]
- Campiglia, M.; Coito, L.; Mizera, S. Can scalars have asymptotic symmetries? Phys. Rev. D 2018, 97, 46002. [Google Scholar] [CrossRef]
- Vecchia, P.D.; Marotta, R.; Mojaza, M. Multiloop Soft Theorem for Gravitons and Dilatons in the Bosonic String. J. High Energy Phys. 2019, 1, 38. [Google Scholar] [CrossRef]
- Vecchia, P.D.; Marotta, R.; Mojaza, M. Multiloop soft theorem of the dilaton in the bosonic string. Phys. Rev. D 2019, 100, 041902. [Google Scholar] [CrossRef]
- Cheung, C.; Helset, A.; Parra-Martinez, J. Geometric Soft Theorems. arXiv 2021, arXiv:2111.03045. [Google Scholar]
- Adler, S.L. Consistency conditions on the strong interactions implied by a partially conserved axial vector current. Phys. Rev. 1965, 137, B1022. [Google Scholar] [CrossRef]
- Adler, S.L. Consistency conditions on the strong interactions implied by a partially conserved axial-vector current. II. Phys. Rev. 1965, 139, B1638. [Google Scholar] [CrossRef]
- Weinberg, S. Current-Commutator Theory of Multiple Pion Production. Phys. Rev. Lett. 1966, 16, 879. [Google Scholar] [CrossRef]
- Blas, D.; Camalich, J.M.; Oller, J.A. Scalar resonance in graviton-graviton scattering at high-energies: The graviball. Phys. Lett. B 2022, 827, 136991. [Google Scholar] [CrossRef]
- Low, I.; Manohar, A.V. Spontaneously Broken Spacetime Symmetries and Goldstone’s Theorem. Phys. Rev. Lett. 2002, 88, 101602. [Google Scholar] [CrossRef]
- Callan, C.G., Jr. Broken scale invariance in scalar field theory. Phys. Rev. D 1970, 2, 1541. [Google Scholar] [CrossRef]
- Coleman, S.R.; Jackiw, R. Why dilatation generators do not generate dilatations? Ann. Phys. 1971, 67, 552–598. [Google Scholar] [CrossRef]
- Boels, R.H.; Wormsbecher, W. Spontaneously broken conformal invariance in observables. arXiv 2015, arXiv:1507.08162. [Google Scholar]
- Vecchia, P.D.; Marotta, R.; Mojaza, M. Double-soft behavior of the dilaton of spontaneously broken conformal invariance. J. High Energ. Phys. 2017, 2017, 1–43. [Google Scholar] [CrossRef]
- Bianchi, M.; Guerrieri, A.L.; Huang, Y.T.; Lee, C.J.; Wen, C. Exploring soft constraints on effective actions. J. High Energy Phys. 2016, 1610, 36. [Google Scholar] [CrossRef]
- Dashen, R.F.; Weinstein, M. Soft pions, chiral symmetry, and phenomenological lagrangians. Phys. Rev. 1969, 183, 1261. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Cachazo, F.; Kaplan, J. What is the Simplest Quantum Field Theory? J. High Energy Phys. 2010, 1009, 16. [Google Scholar] [CrossRef]
- Kampf, K.; Novotny, J.; Trnka, J. Tree-level Amplitudes in the Nonlinear Sigma Model. J. High Energy Phys. 2013, 1305, 32. [Google Scholar] [CrossRef]
- Low, I. Double Soft Theorems and Shift Symmetry in Nonlinear Sigma Models. Phys. Rev. D 2016, 93, 045032. [Google Scholar] [CrossRef]
- Du, Y.J.; Luo, H. On single and double soft behaviors in NLSM. J. High Energy Phys. 2015, 1508, 58. [Google Scholar] [CrossRef]
- Vecchia, P.D.; Marotta, R.; Mojaza, M. The B-field soft theorem and its unification with the graviton and dilaton. J. High Energy Phys. 2017, 1710, 17. [Google Scholar] [CrossRef][Green Version]
- Loebbert, F.; Mojaza, M.; Plefka, J. Hidden Conformal Symmetry in Tree-Level Graviton Scattering. J. High Energy Phys. 2018, 1805, 208. [Google Scholar] [CrossRef]
- Marotta, R.; Mojaza, M. Double-soft behavior of massless closed strings interacting with any number of closed string tachyons. J. High Energy Phys. 2020, 8, 83. [Google Scholar] [CrossRef]
- Francesco, P.D.; Mathieu, P.; Senechal, D. Conformal Field Theory; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar] [CrossRef]
- Higashijima, K. Nambu-Goldstone theorem for conformal symmetry. In Proceedings of the XX International Colloquium on Group Theoretical Methods in Physics (GROUP 20), Toyonaka, Japan, 4–9 July 1994; pp. 223–228. [Google Scholar]
- Coleman, S. Aspects of Symmetry: Selected Erice Lectures; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Polchinski, J. String Theory. An Introduction to the Bosonic String; Cambridge University Press: Cambridge, UK, 1998; Volume 1. [Google Scholar]
- Polchinski, J. String Theory. Superstring Theory and Beyond; Cambridge University Press: Cambridge, UK, 1998; Volume 2. [Google Scholar]
- Hata, H. Softh Dilaton Theorem in String Field Theory. Prog. Theor. Phys. 1992, 88, 1197. [Google Scholar] [CrossRef]
- Scherk, J. Zero slope limit of the dual resonance model. Nucl. Phys. 1971, B31, 222. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).